Прогиб от сосредоточенной нагрузки – Расчетные схемы для балок

Содержание

Влияние высоты балки на прогиб

Влияние поперечных сил на прогиб балки. Общие положения

Поперечные силы, действующие в том или ином поперечном сечении балки, определяются по соответствующей эпюре «Q». Отношение поперечных сил Q_x к площади поперечного сечения F_x рассматривается как касательные напряжения, действующие в данном сечении, хотя тут нет линейной зависимости. Максимальные касательные напряжения как правило действуют ближе к середине высоты балки.

Площадь поперечного сечения балки может быть не постоянной величиной, поэтому площадь рассматриваемого сечения обозначена как F_x, тем не менее дальше мы будем рассматривать только один частный случай, а именно балки с постоянными параметрами сечения по всей длине, в частности с площадью F.

Как правило при соотношении длины балки к высоте l/h > 10 (где h — высота, l — длина балки) влияние касательных напряжений в поперечных сечениях балки на прогиб относительно мало и не превышает 0.8%. А для балок с соотношением

l/h > 20 — и вовсе 0.2%. В таких случаях можно пользоваться упрощенными уравнениями метода начальных параметров, в частности:

∫dx∫M_xdx/EI = f_x (537.5)

Эта формула в частности означает, что в данном случае при определении прогиба интегрированием уравнения моментов учитываются только нормальные напряжения, действующие в поперечных сечениях балки. Как мы знаем, нормальные напряжения приводят к линейным деформациям, а величина линейной деформации зависит от значения момента инерции I и значения модуля упругости материала Е.

Если соотношение длины балки к высоте l/h < 10, то влияние поперечных сил на значение прогиба желательно учитывать. И чем меньше соотношение длины к высоте, тем больше будет влияние поперечных сил.

На первый взгляд это кажется странным. Ведь чем больше высота балки, тем больше будет жесткость балки. И тут даже не линейная зависимость, потому как например момент инерции поперечного прямоугольного сечения I = bh³/12.

Однако ничего странного тут нет, действительно, чем больше высота балки, тем больше в итоге жесткость балки и тем меньше прогиб балки. Но при этом необходимо учитывать возрастающее влияние касательных напряжений на это относительно небольшое значение прогиба.

То есть, чем больше высота балки по отношению к длине, тем сильнее балка, с точки зрения строительной механики рассматриваемая как стержень, приближается к пластине.

Как мы знаем, особенность касательных напряжений в том, что они в отличие от нормальных напряжений, приводящих к линейным деформациям, зависящим от модуля упругости материала балки Е, вызывают деформацию сдвига. Соответственно величина деформации сдвига зависит от значения модуля сдвига

G и при более точных расчетах это нужно учитывать.

Для этого может использоваться следующее уравнение, учитывающее действие касательных напряжений:

∫dx∫M_xdx/EI + k∫(Q_x/GF)dx = f_x (536.1)

где k — безразмерный коэффициент, зависящий от геометрической формы поперечного сечения.

— Для балок прямоугольного сечения k = 6/5

— Для балок сплошного круглого сечения k = 10/9,

— Для тонкостенных труб — k = 2.

Примечание: Нормальные напряжения, действующие вдоль оси х, и вызывающие линейные деформации вдоль оси х, сами по себе вроде бы не приводят к прогибу — вертикальному смещению нейтральной оси балки вдоль оси у. Однако в результате линейных деформаций, различных по высоте балки, изменяется угол наклона поперечного сечения, в результате прогиб зависит от угла наклона поперечного сечения. Поэтому для определения прогиба уравнение момента интегрируется дважды. В свою очередь касательные напряжения действуют вдоль оси

у и деформация сдвига происходит сразу вдоль оси у, поэтому для учета влияния касательных напряжений уравнение поперечных сил интегрируется один раз.

Возможно это и не самое правильное объяснение природы действия касательных напряжений, но зато достаточно наглядное. Другие возможные объяснения, в частности рассматривающие плоское напряженное состояние в различных точках балки, я здесь не привожу.

Определение прогиба балки с учетом поперечных сил

Рассмотрим влияние поперечных сил на значение прогиба на следующем достаточно простом примере.

Имеется консольная балка, на конце балки приложена сосредоточенная нагрузка, проще говоря, сила Q. Уравнения моментов и поперечных сил, действующих в поперечных сечениях такой балки, давно известны и очень просты:

М_х = Q(x — l) (536.2)

Q_x = Q (536.3)

Кроме того, нам известны начальные параметры для такой балки:

М₀ = Ql (536.4.1)

Q₀ = Q (536.4.2)

θ₀ = 0 (536.4.3)

f₀ = 0 (536.4.4)

Проинтегрировав уравнения момента и поперечных сил с учетом значений начальных параметров, получим:

f_x = Q(x³/6 — lx²/2)/EI — kQx/GF (536.5)

В данном случае отрицательный знак перед вторым членом уравнения в правой части учитывает отрицательное направление прогиба. Впрочем как и интегрируемое уравнение момента.

Максимальный прогиб балки будет в конце — в точке приложения сосредоточенной силы (

х = l), тогда:

— f_l = Ql³/3EI + kQl/GF (536.6)

В принципе все необходимые данные для определения прогиба уже есть, тем не менее попробуем привести правую часть уравнения к общему знаменателю, чтобы оценить влияние прогиба от поперечных сил на общее значение прогиба.

Модуль сдвига и модуль упругости материала связаны между собой следующей зависимостью:

Е = 2(1 + μ)G (318.3.9)

из этого следует, что

G = E/2(1 + μ) (536.7)

где μ — это коэффициент Пуассона.

А чтобы получить момент инерции сечения I, нужно площадь сечения F = bh умножить на h² и разделить на 12:

Fh²/12 = I (536.8.1)

из этого следует, что

F = 12I/h²

(536.8.2)

Тогда,

GF = 6EI/((1 + μ)h²) (536.9)

Подставим полученные значения в уравнение (536.6):

— f_l = Ql³/3EI + 2kQlh²(1 + µ)/12EI = (Ql³ + kQlh²(1 + μ)/2)/3EI (536.10)

А чтобы вынести в правой части уравнения (536.6) выражение Ql³ за скобки, умножим и разделим член уравнения (536.10) на l²:

— f_l = (Ql³(1 + kh²(1 + μ)/2l²)/3EI (536.11)

Если мы заменим достаточно длинное выражение kh²(1 + μ)2l² неким коэффициентом λ:

λ = k(1 + μ)h²/2l² (536.12)

То форма записи уравнения (536.11) значительно сократится:

— f_l = Ql³(1 + λ)/3EI (536.13)

При этом коэффициент λ как раз и будет показывать приращение прогиба, зависящее от высоты балки. То есть для того, чтобы оценить влияние на прогиб высоты балки при соответствующей длине, достаточно определить значение коэффициента λ. И даже абсолютные значения высоты и длины балки при этом не нужны, достаточно знать отношение длины к высоте.

Например для балки прямоугольного сечения, материал которой имеет коэффициент Пуассона μ = 0.3 и соотношение l/h = 10, т.е. h/l = 0.1, значение λ составит:

λ = 6(1 + 0.3)0.1²/2·5 = 0.0078

или 0.78% от прогиба, происходящего в результате действия нормальных напряжений.

При соотношении h/l = 0.2 влияние поперечных сил для такой балки оценивается в 3.1%, а при соотношении h/l = 0.5 — в 19.5%. При h/l = 1 в 78%.

И так далее.

doctorlom.com

Приведение сосредоточенной нагрузки к эквивалентной равномерно распределенной

1 вариант

Расстояние между сосредоточенными нагрузками одинаковое, при этом расстояние от начала пролета до первой сосредоточенной нагрузки равно расстоянию между сосредоточенными нагрузками. В этом случае сосредоточенные нагрузки также попадают на начало и на конец пролета, но при этом вызывают только увеличение опорной реакции, на значение изгибающих моментов и на прогиб крайние сосредоточенные нагрузки никак не влияют, а потому при расчетах несущей способности конструкции не учитываются. Рассмотрим это на примере балок перекрытия опирающихся на перемычку. Кирпичная кладка, которая может быть между перемычкой и балками перекрытия, и создавать при этом равномерно распределенную нагрузку, для простоты восприятия не показана.

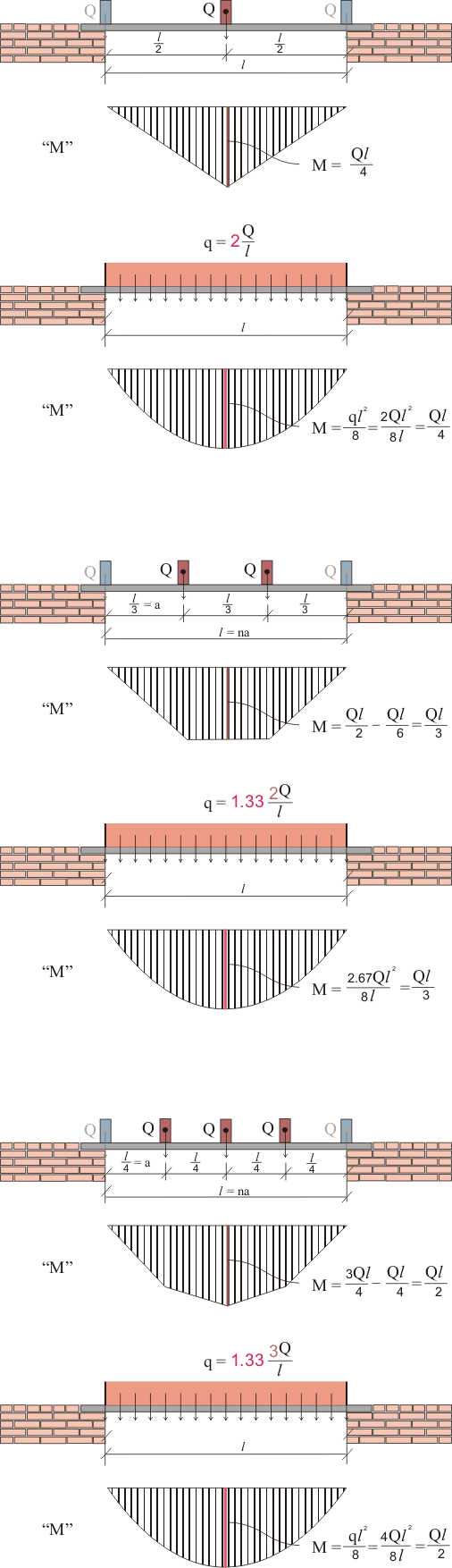
Рисунок 1. Приведение сосредоточенных нагрузок к эквивалентной равномерно распределенной нагрузке.

Как видно из рисунка 1, определяющим является изгибающий момент, который используется при расчетах конструкций на прочность. Таким образом, чтобы равномерно распределенная нагрузка создавала такой же изгибающий момент, как и сосредоточенная нагрузка, ее нужно умножить на соответствующий коэффициент перехода (коэффициент эквивалентности). А определяется этот коэффициент из условий равенства моментов. Думаю, рисунок 1 это очень хорошо иллюстрирует. А еще, анализируя полученные зависимости, можно вывести общую формулу для определения коэффициента перехода. Так, если количество приложенных сосредоточенных нагрузок является нечетным, т.е. одна из сосредоточенных нагрузок обязательно попадает на середину пролета, то для определения коэффициента эквивалентности можно использовать формулу:

γ = n/(n — 1) (305.1.1)

где n — количество пролетов между сосредоточенными нагрузками.

При этом эквивалентная равномерно распределенная нагрузка будет равна:

q_экв = γ(n-1)Q/l (305.1.2)

где (n-1) — количество сосредоточенных нагрузок.

Впрочем, иногда удобнее производить расчеты, исходя из количества сосредоточенных нагрузок. Если это количество выразить переменной m, то тогда

γ = (m +1)/m (305.1.3)

где m — количество сосредоточенных нагрузок.

При этом эквивалентная равномерно распределенная нагрузка будет равна:

q_экв = γmQ/l (305.1.4)

Когда количество сосредоточенных нагрузок является четным, т.е. ни одна из сосредоточенных нагрузок не попадает на середину пролета, то значение коэффициента можно принимать, как для следующего нечетного значения количества сосредоточенных нагрузок. В целом при соблюдении указанных условий загружения можно принимать следующие коэффициенты перехода:

γ = 2 — если на рассматриваемую конструкцию, например, балку попадает только одна сосредоточенная нагрузка посредине перемычки.

γ = 1.33 — для балки, на которую действуют 2 или 3 сосредоточенные нагрузки;

γ = 1.2 — для балки, на которую действуют 4 или 5 сосредоточенных нагрузок;

γ = 1.142 — для балки, на которую действуют 6 или 7 сосредоточенных нагрузок;

γ = 1.11 — для балки, на которую действуют 8 или 9 сосредоточенных нагрузок.

2 вариант

Расстояние между сосредоточенными нагрузками одинаковое, при этом расстояние от начала пролета до первой сосредоточенной нагрузки равно половине расстояния между сосредоточенными нагрузками. В этом случае сосредоточенные нагрузки не попадают на начало и на конец пролета.

Рисунок 2. Значения коэффициентов перехода при 2 варианте приложения сосредоточенных нагрузок.

Как видно из рисунка 2, при таком варианте загружения значение коэффициента перехода будет значительно меньше. Так, например, при четном количестве сосредоточенных нагрузок, коэффициент перехода вообще можно принимать равным единице. При нечетном количестве сосредоточенных нагрузок для определения коэффициента эквивалентности можно использовать формулу:

γ = (m +7)/(m +6) (305.2.1)

где m — количество сосредоточенных нагрузок.

При этом эквивалентная равномерно распределенная нагрузка все также будет равна:

q_экв = γmQ/l (305.1.4)

В целом при соблюдении указанных условий загружения можно принимать следующие коэффициенты перехода:

γ = 2 — если на рассматриваемую конструкцию, например, балку попадает только одна сосредоточенная нагрузка посредине перемычки, а попадают ли балки перекрытия на начало или конец пролета или расположены сколь угодно далеко от начала и конца пролета, в данном случае значения не имеет. А значение это имеет при определении сосредоточенной нагрузки.

γ = 1 — если на рассматриваемую конструкцию, действует четное количество нагрузок.

γ = 1.11 — для балки, на которую действуют 3 сосредоточенные нагрузки;

γ = 1.091 — для балки, на которую действуют 5 сосредоточенных нагрузок;

γ = 1.076 — для балки, на которую действуют 7 сосредоточенных нагрузок;

γ = 1.067 — для балки, на которую действуют 9 сосредоточенных нагрузок.

Не смотря на некоторую заковыристость определения, коэффициенты эквивалентности очень просты и удобны. Так как при расчетах очень часто известна распределенная нагрузка, действующая на квадратный или погонный метр, то чтобы не переводить распределенную нагрузку сначала в сосредоточенную, а потом снова в эквивалентную распределенную, достаточно просто умножить значение распределенной нагрузки на соответствующий коэффициент. Например, на перекрытие будет действовать нормативная распределенная нагрузка 400 кг/м², при этом собственный вес перекрытия составит еще 300 кг/м². Тогда при длине балок перекрытия 6 м на перемычку могла бы действовать равномерно распределенная нагрузка q = 6(400 + 300)/2 = 2100 кг/м. А дальше, если будет только одна балка перекрытия посредине пролета, то γ = 2, а

q_экв = γq = 2q (305.2.2)

И все.

Если ни одно из двух вышеприведенных условий не соблюдается, то использовать коэффициенты перехода в чистом виде нельзя, нужно добавить еще пару дополнительных коэффициентов, учитывающих расстояние до балок, не попадающих на начало и конец пролета перемычки, а также возможную несимметричность приложения сосредоточенных нагрузок. Вывести такие коэффициенты в принципе можно, однако в любом случае они будут понижающими во всех случаях, если рассматривать 1 вариант загружения и в 50% случаев, если рассматривать 2 вариант загружения, т.е. значения таких коэффициентов будут < 1. А потому для упрощения расчетов, а заодно и для большего запаса по прочности рассчитываемой конструкции вполне хватит коэффициентов, приведенных при первых двух вариантах загружения.

doctorlom.com

видео-инструкция по монтажу своими руками, как усилить перекрытия, расчет, фото и цена

Все фото из статьи

Деревянные балки широко применяются в частном строительстве — их используют при обустройстве полов и даже деревянных межэтажных перекрытий. Однако, для получения с их помощью прочных конструкций необходимо предварительно выполнить некоторые расчеты. В данной статье мы подробно рассмотрим как рассчитать самостоятельно балки на прогиб, который является крайне важным значением.

На фото — деревянные балки перекрытия

Общие сведения

Балка является конструкционным элементом, представляющим собой стержень, на который девствуют силы в направлении перпендикулярно его оси. Под воздействием этих сил любые балки, в том числе и деревянные,деформируются.

Незначительный прогиб является вполне допустимым явлением. К примеру, при ходьбе по деревянному полу мы зачастую ощущаем как он незначительно пружинит. Но если прогиб превышает допустимые значения, то это может привести к поломке детали.

Допустимой считается деформация, которая соответствует следующим требованиям:

Не превышает расчетные значения.
Не мешает комфортной эксплуатации дома.

Чтобы узнать насколько будет деформироваться деталь в том или ином случае, необходимо выполнить некоторые расчеты на жесткость и прочность.Следует отметить, что подобными работами обычно занимаются инженеры-строители. Однако в частном строительстве, ознакомившись с некоторыми формулами, их можно выполнить самостоятельно.

Незначительный прогиб перекрытий допускается

Надо сказать, что расчет прогиба деревянной балки является очень ответственной работой, ведь любая постройка должна соответствовать определенным требованиям прочности. Поэтому балки должны обладать определенной устойчивостью и жесткостью, чтобы конструкция с определенным запасом по прочности выдерживала запланированные нагрузки.

Расчет

Такие параметры, как прочность и жесткость связаны между собой. Поэтому вначале определяют жесткость детали, после чего, на основе полученных данных вычисляют деформацию.

Для этого совсем необязательно углубляться в сложные инженерные расчеты, для получения точных значений. Чтобы не ошибиться, лучше воспользоваться упрощенной схемой, которой вполне достаточно для частного строительства.

Состоит такой способ расчета из нескольких этапов:

Составление расчетной схемы и определение геометрических параметров балки.
Определение максимальной нагрузки, которая будет оказываться на деталь, в том числе от перегородок, установленных сверху конструкций и пр.
Вычисление максимального прогиба.

Ниже подробней рассмотрим все эти этапы.

Схема влияния расстояния между опорами на деформацию

Расчетная схема

Выполнить своими руками расчетную схему не сложно. Для этого нужно лишь знать форму поперечного сечения и размеры детали.

Кроме того, следует учитывать такие моменты, как:

Способ опирания детали.
Длина пролета, т.е. расстояние между опорами. К примеру, если выполняется перекрытие и расстояние между стенами составляет 4 м, то пролет «l» будет равняться 4м.

Если речь идет о перекрытиях, то принимается схема расчета, согласно которой нагрузка распределяется на деталь равномерно. В случаях, когда необходимо вычислить деформацию от сконцентрированного воздействия, к примеру, от установленной печи на перекрытие, используется схема с учетом сосредоточенной и направленной нагрузки F, которая равняется весу конструкции.

Размеры прямоугольной балки

Для определения прогиба «f» необходимо узнать такую геометрическую характеристику, как момент инерции сечения, которая обозначается буквой «j». Момент инерции рассчитывается по такой формуле:

J=bхh^3/12, где:

Буквенное обозначение	Значение
h	Высота сечения бруса
b	Ширина сечения

Обратите внимание! Момент инерции прямоугольного бруса зависит от того, как он расположен в пространстве. Если деталь будет уложена широкой стороной на стены, то момент инерции будет меньше, в то время как деформация больше. Примером тому является доска, которая уложенная на ребро прогибается значительно меньше, чем уложенная плашмя.

Определение максимальной нагрузки

Чтобы определить максимальную нагрузку нужно сложить все параметры бруса, такие как:

Его вес;
Вес квадратного метра перекрытия;
Воздействие от перегородок на перекрытия, также измеряется в килограммах на метр квадратный.

Помимо этого необходимо учитывать коэффициент, обозначающийся буквой«k», который равняется расстоянию между балками (измеряется в метрах). К примеру, если расстояние между ними составляет 700 мм, то значение коэффициента будет равняться 0,7.

Печи или другие конструкции создают дополнительную нагрузку на перекрытие

Совет! За помощью в расчетах при составлении проекта дома можно обратиться к специалистам. Однако,цена на их услуги бывает довольно высокой. Поэтому в большинстве случаев с поставленной задачей можно справиться самостоятельно.

Чтобы упростить расчеты, можно принять следующие усредненные параметры:

Вес перекрытия составляет 60 кг.
Нормативная временная нагрузка на перекрытие – 250 кг.
Нормативная нагрузка от перегородок – 75 кг.

Что касается веса деревянной детали, то его можно посчитать, зная плотность и объем древесины. К примеру, наиболее распространенный брус, который используют для перекрытий,имеет сечение 0,15х0,2м и весит в среднем 18 кг на погонный метр.

Теперь, зная все параметры можно вычислить максимальную нагрузку по такой формуле –q=(60+250+75)х0,6+18=249 кг/м.

Вычисление максимального прогиба

Следующим шагом является расчет деревянной балки на прогиб. Если нагрузка будет распределяться равномерно,то нужно воспользоваться следующей формулой — f=-5хqхl^4/384хEхJ.

Величина Е в данной формуле означает модуль упругости. Для древесины это значение составляет Е=100000 кгс/м². Если подставить полученные ранее величины, полученные при расчете бруса сечением 0,15х0,2м и длиной равной 4м, то максимальный прогиб будет равняться 0,83 см.

Деформация при сосредоточенной нагрузке F

Для вычисления деформации детали, на которую будет оказываться сосредоточенная нагрузка, следует воспользоваться такой формулой — f=-Fхl^3/48хEхJ, где F обозначает давление на брус, к примеру, вес печи, установленной на перекрытии.

Надо сказать, что модуль «E» у разных пород древесины может быть разным. Кроме того, этот показатель зависит от типа детали. К примеру, сплошной брус и оцилиндрованное бревно обладают разным модулем упругости.

Совет! Зачастую домашние мастера интересуются — как усилить деревянные балки перекрытия от прогиба? Для этих целей можно воспользоваться досками толщиной не менее 50 мм, которые крепятся к брусу.

Вот, собственно, и вся инструкция по расчету балок на прогиб.

Вывод

Самостоятельно вычислить прогиб балки из дерева, как мы выяснили, несложно. Для этого следует воспользоваться несколькими приведенными выше формулами и некоторыми средними нормативными значениями. При этом главное, как и в любых других расчетах, выполнять работу внимательно, чтобы не допустить ошибку.

Из видео в этой статье можно ознакомиться как сделать чердачное перекрытие по деревянным балкам своими руками.

rubankom.com

Вопросы по прогибу деревянных конструкций

21-01-2013: Доктор Лом

1. Такой прогиб является допустимым согласно общепринятых строительных норм и правил и, так сказать, для общего случая. При превышении допустимого прогиба балка не треснет, если она была предварительно рассчитана на прочность, но такой прогиб может мешать нормальной эксплуатации или эстетическому виду конструкции. Но случаи бывают разные, например, для оштукатуриваемых деревянных конструкций прогиб не должен превышать 1/350 пролета. Вы можете использовать для расчетов это значение.

2. Максимальный прогиб балки будет только при максимальной нагрузке, которая складывается из постоянной и временной (длительной и кратковременной). И прогиб балки также складывается из постоянного и временного. Чем больше доля кратковременной нагрузки (для конструкций по деревянному перекрытию эта доля может составлять более 60%, а для железобетонных плит до 30%, тем больше доля временного прогиба и тем больше вероятность, что напольная керамическая плитка будет отслаиваться или трескаться, или появятся трещины на стыках гипсокартона. Однако не забывайте, что это все равно составит не более 1 см на 4 метра (от кратковременной нагрузки), а это, смею Вас уверить, очень небольшой прогиб (в хрущевках железобетонные плиты размером на комнату иногда имеют прогиб до 10 см на 3 метра и никого это сильно не беспокоит и установке раздвижных дверей не мешает, в частности потому, что доля кратковременного прогиба в таких случаях составляет 10-15%). Указанное Вами ограничение по прогибу 5 мм нужно использовать для расчетов на прогиб только от временной нагрузки, какая она у Вас, я даже приблизительно не представляю.

3. Если Вы собираетесь укладывать на пол по деревянным балкам керамическую плитку, то конечно же Вам потребуются балки, обеспечивающие минимально возможный прогиб, т.е. сечение балки нужно подбирать не по прочности, а по прогибу. И кроме того, черновой пол, который скорее всего будет из досок, также должен минимально прогибаться при действии кратковременной нагрузки. И отслаиваться или трескаться керамическая плитка будет скорее от прогиба чернового пола, чем от прогиба балок.

4. Чтобы уменьшить прогиб балки можно уменьшить расстояние между балками (заодно это уменьшит и прогиб чернового пола), использовать металлические или железобетонные балки (а вообще почитайте статью про укладку плитки на пол).

В статье все вышесказанное заключалось в предложении: «подобрать такое сечение балки, прогиб которой устраивает или Вас или СНиП»

28-05-2013: Игорь

Добрый день Доктор Лом,

У меня вопрос по балкам перекрытия первого этажа.

Есть помещение 6м х 3.8м. Балки размером 3,8м х 0.05м х 0,15м. С шагом 0.55 м. Хочу нагрузить такие перекрытия двумя листами ЦСП вперехлест 12мм и 16мм, и на них положить плитку. Выдержал ли такие перекрытия керамический пол и мебель (кухня). Буду благодарен за ответы.

28-05-2013: Доктор Лом

В вашем случае определяющим будет расчет на прогиб, так как плитка очень не любит деформаций перекрытия и может при этом отслаиваться или трескаться. Достаточно подробно эта тема обсуждалась на форуме (ссылка на форум на главной странице сайта). Однако и по несущей способности нужен брус сечением как минимум 10х15 см, но если балки-лаги будут опираться на столбики, то это совсем другой расчет и многое будет зависеть от расстояния между столбиками.

10-09-2013: Артем

Подскажите пожалуйста. Вопрос по полу в срубе. Планирую лаги 200*100, шаг 60 см положить на цоколь. Пролет в комнате 4,7 м.(комната 4,7*8.3). Возможно ли положить лаги без опорных столбов? По таблице расчета получается прогиб 16 мм и запас по прогибу 1,19 раза. Будет ли пружинить или провисать пол? И еще буду делать в цоколе отверстия под лаги (на цоколь не могу ставить потому что рубщики вырезали окна слишком низко). На сколько их нужно углублять. Ну и вообще правильно ли я делаю?

10-09-2013: Доктор Лом

Да, можно положить лаги и без опорных столбов, вот только завести их при готовом срубе будет не просто. Как минимум с одной стороны придется делать сквозное отверстие.

По поводу заглубления со второй стороны отвечу так, чем длиннее будет опорная площадка, тем меньше будет деформация цокольного бруса под лагами. Подробности в статьях «Расчет опорной площадки стены на смятие» и «Расчет опорной площадки балки на смятие»

Определенный вами прогиб 1.6 см посредине лаги — это и есть, условно говоря, провисание пола при максимальной действующей нагрузке. Соответственно при минимальной нагрузке прогиба почти не будет. При ходьбе человека весом в 100 кг по середине комнаты прогиб (то, что вы обозначили как пружинные свойства) будет составлять до 2-3 мм. А если прыгать по полу, то и прогиб будет значительно больше. Устраивает вас такой пружинный прогиб или нет — решайте сами.

10-09-2013: Артем

Спасибо большое за развернутый ответ. А то писал на другом крупном форуме- ответили со второго раза, и то неправильно.

24-12-2013: алексей

Будьте так любезны, какой будет прогиб пола для помещения 3,5 м х 4. Предполагаемый сэндвич — балки 100х100х3900 с шагом 500 мм, с штроблением в стены по 200 мм, поперек доска сороковка, сверху плита фанера, на нее ламинат на ширину 2 метра, оставшиеся 1,5 метра плитка.

25-12-2013: Доктор Лом

Указанный вами сэндвич приведет к частичному перераспределению сосредоточенных нагрузок. При равномерно распределенной нагрузке состав сэндвича на несущую способность и на прогиб балок почти не влияет. Прогиб вы относительно легко можете определить по формуле, приведенной в статье, так как ваши балки будут шарнирно опертыми.

05-06-2014: владимир

подскажите пожалуйста как осознать нагрузку 400 кг/м я хочу построить мансарду над гаражом увеличить рабочее пространство .Деревянные балки показывают большой прогиб 7см 3см а если 4,6/250=1,84 см подшивать буду доской чем грозит увеличение прогиба и как узнать более точную нагрузку от моей мастерской

05-06-2014: Доктор Лом

400 кг/м² — это некая условная равномерно распределенная нагрузка, принимаемая для упрощения расчетов. Если в вашей мастерской стеллажи и всякое оборудование будут расположены возле стен, а посредине мастерской ничего громоздкого не будет, то нагрузка на перекрытие может быть меньше. Чтобы определить, насколько меньше, нужно составить с десяток расчетных схем, учитывающих виды нагрузок и время их приложения.

Если потолок будет подшит доской, то большой прогиб не будет иметь решающего значения, главное, чтобы прочности балок хватало.

04-06-2015: Василий

Добрый вечер, Доктор Лом. Деревянная балка перекрытия сарая сечением 10*10 см работает при проете 2м. По расчетам при увеличении пролета до 3 м сечение балки должно быть 13*13 см. Хочу усилить балку 10*10 двумя стальными уголками, прикрепленными по боковым стенкам балки. Какой номер уголка должен быть, чтобы комбинированная балка была эквивалентна балке 13*13 по прогибу?

04-06-2015: Доктор Лом

Вопрос не обычный, поэтому отвечу с цифрами для большей наглядности и таким образом произведу большую часть расчета.

1. Сначала вам следует определить разницу моментов сопротивления для балок сечением 10х10 и 13х13 см. Эта разница покажет, сколько не хватает до требуемого момента сопротивления деревянной балки. (13³ — 10³)/6 = 199.5 см³)

2. Определяете соотношение расчетных сопротивлений металла и древесины (например 2000/130 = 15)

3. Затем делите разницу на соотношение расчетных сопротивлений металла и древесины, т.е. переводите эту разницу в эквивалентную для металлической балки. ( 199.5/15 = 13.3 см³)

4. По сортаменту подбираете требуемое сечение (например можно использовать 2 равнополочных уголка сечением 75х5, суммарный момент сопротивления таких уголков составит 7.21х2 = 14.42 см³)

doctorlom.com

Прогиб металлической балки предел нормы. Вопросы по прогибу деревянных конструкций

21-01-2013: Доктор Лом

28-05-2013: Игорь

Добрый день Доктор Лом,

У меня вопрос по балкам перекрытия первого этажа.

28-05-2013: Доктор Лом

10-09-2013: Артем

10-09-2013: Доктор Лом

10-09-2013: Артем

24-12-2013: алексей

25-12-2013: Доктор Лом

05-06-2014: владимир

подскажите пожалуйста как осознать нагрузку 400 кг/м я хочу построить мансарду над гаражом увеличить рабочее пространство.Деревянные балки показывают большой прогиб 7см 3см а если 4,6/250=1,84 см подшивать буду доской чем грозит увеличение прогиба и как узнать более точную нагрузку от моей мастерской

05-06-2014: Доктор Лом

400 кг/м 2 — это некая условная равномерно распределенная нагрузка, принимаемая для упрощения расчетов. Если в вашей мастерской стеллажи и всякое оборудование будут расположены возле стен, а посредине мастерской ничего громоздкого не будет, то нагрузка на перекрытие может быть меньше. Чтобы определить, насколько меньше, нужно составить с десяток расчетных схем, учитывающих виды нагрузок и время их приложения.

04-06-2015: Василий

04-06-2015: Доктор Лом

2. Определяете соотношение расчетных сопротивлений металла и древесины (например 2000/130 = 15)

3. Затем делите разницу на соотношение расчетных сопротивлений металла и древесины, т.е. переводите эту разницу в эквивалентную для металлической балки. (199.5/15 = 13.3 см 3)

Определение прогиба производится только на действие постоянных и длительных нагрузок при коэффициенте надежности по нагрузке >по формуле на стр. 142 :

, где

для свободно опертой балки коэффициент равен:

При равномерно распределенной нагрузке;

При двух равных моментах по концам балки от силы обжатия.

Полная кривизна плиты на участках без трещин в растянутой зоне определяется по формулам (155 … 159) п.4.24.

Кривизна от постоянной и длительной нагрузки:

Момент от соответствующей внешней нагрузки относительно оси, нормальной к плоскости действия изгибающего момента и проходящей через центр тяжести приведенного сечения;

Коэффициент, учитывающий влияние длительной ползучести тяжелого бетона при влажности более 40%;

Коэффициент, учи

starer.ru

Расчет на ударную нагрузку с учетом массы конструкции

Иногда этот запас может быть слишком большим и потому не совсем оправданным, так как приведет к перерасходу материалов, т.е. необоснованному завышению стоимости конструкции. Потому, если есть уверенность в своих силах и знаниях, то иногда имеет смысл пересчитать значение динамического коэффициента с учетом массы деформирующейся конструкции.

Как уже говорилось, удар — это достаточно сложное физическое явление, в результате которого происходит много различных процессов, в частности падающее тело в момент падения имеет импульс

p = mV (288.1)

где v — уже рассматривавшаяся нами скорость тела в момент касания с рассматриваемой конструкцией. При этом и упавший груз и рассматриваемая конструкция имеют некоторую массу. Из закона сохранения энергии и вытекающего из него закона сохранения импульсов вытекает следующее уравнение:

m₁v₁ + m₂v₂ = m₁v’₁ + m₂v’₂ (296.1.1)

где m₁ — масса груза, m₂ — масса рассматриваемой конструкции, v₁ — скорость груза перед ударом, v’₁ — скорость груза после удара, соответственно v₂ — скорость рассматриваемой конструкции перед ударом, v’₂— скорость рассматриваемой конструкции после удара.

Если скорость рассматриваемой конструкции до начала удара принять v₂ = 0, то формула (288.11.2) преобразуется в

m₁v₁ = m₁v’₁ + m₂v’₂ (296.1.2)

Далее рассмотрим несколько граничных условий и промежуточных вариантов, характерных для столкновения тел:

1. Если масса рассматриваемой конструкции значительно меньше массы груза и для упрощения расчетов массой конструкции пренебречь, то

m₁v₁= m₁v’₁ (296.1.3)

Суть этой формулы в том, что при столкновении относительно тяжелого тела с относительно легким телом скорость движения тяжелого тела в момент столкновения практически не изменяется, что можно видеть и даже проверить самому, прыгая на батуте. Именно это допущение мы и использовали при расчете деформаций и динамических коэффициентов без учета массы деформирующегося тела.

2. Если масса падающего груза значительно меньше массы рассматриваемой конструкции, то формула (296.1.1) примет вид

m₁v₁ = — m₁v’₁ или v₁ = — v’₂ (296.1.4)

Суть этой формулы в том, что при столкновении очень легкого тела с очень тяжелым телом скорость движения тяжелого тела после столкновения практически не изменится, а вот легкое тело после столкновения начнет двигаться в противоположном направлении, проще говоря, отскочит от рассматриваемой конструкции, но в силу неизменного действия силы тяжести через некоторое время опять упадет на рассматриваемую конструкцию, снова отскочит и так будет продолжаться до тех пор, пока вся энергия не перейдет в указанные нами выше виды и легкое тело не упокоится с миром на поверхности тяжелого тела. Это можно наблюдать, роняя на пол теннисный или любой другой мяч.Тем не менее то, что легкое тело отскакивает от тяжелого почти с такой же скоростью (во всяком случае теоретически), означает, что на тяжелое тело действует такая же ударная сила, а значит деформируемую конструкцию все равно следует рассчитывать на действие ударной нагрузки и потому формула (288.5.3), позволяющая определить максимальную деформацию в зависимости от линейной скорости и частоты колебаний, остается в силе.

Если деформирующееся тело после столкновения движется по прямолинейной траектории (совершает поступательное движение) или по криволинейной траектории с радиусом, значительно превышающим размеры тела, то такое движение можно рассматривать как движение материальной точки, совпадающей с центром тяжести тела. Кроме того, чем больше радиус траектории, тем ближе криволинейное движение к прямолинейному по своим параметрам и вообще прямолинейное движение — это частный случай движения по криволинейной траектории с бесконечным радиусом.

Но если в качестве рассматриваемой конструкции выступает балка или плита, которая в результате удара прогибается, то такое движение никак нельзя назвать прямолинейным или вращательным относительно оси, расположенной на очень большом расстоянии, а потому масса не может рассматриваться, как одна из характеристик такого движения. Не является такое движение и вращательным относительно центра тяжести сечения. И потому момент инерции для описания такого движения также не подходит. А используется для корректного описания такого движения коэффициент жесткости с, учитывающий сложные и запутанные взаимоотношения между массой деформирующейся конструкции, длиной, моментом инерции поперечного сечения, и модулем упругости материала рассматриваемой конструкции.

Не смотря на столь припудренное определение коэффициента жесткости формула, позволяющая определить циклическую частоту, выглядит даже проще, чем при поступательном движении:

ω² = с/m (296.2.1)

А при угловых колебаниях (вращении относительно центра тяжести):

ω² = c/I (296.2.2)

Универсальность формулы (296.2.1) в том, что если колебания балки вызываются сосредоточенной нагрузкой, приложенной посредине пролета, при этом масса балки пренебрежимо мала по сравнению с массой груза, вызывающей деформацию, то исходя из формулы (288.10.1) следует, что если

ω² = Q/mf_ст (288.10.1)

то

с_Q = Q/f_ст = 48EI/l³ (296.3.1)

и в итоге мы получаем ту же формулу (288.11.3) для определения динамического коэффициента.

А вот когда нужно определить коэффициент жесткости для балки, колеблющейся под действием нагрузки от собственного веса, то ситуация усложняется. Во-первых следует учитывать, что балка может иметь не постоянное по длине сечение и даже не постоянный модуль упругости. Но даже если сечение, определяющее значения момента инерции, и модуль упругости постоянны по длине, то все равно отсутствует сосредоточенная сила, которая может рассматриваться как ударная нагрузка, а есть только распределенная по длине балки масса. В таких случаях используется понятие приведенной массы.

Существует несколько методов учета этой приведенной массы: метод Рэлея, формула Граммеля, формула Донкерли, метод Ритца, метод Бубнова-Галеркина. Эти методы используют разные подходы и разные физические модели процессов, происходящих в процессе ударной деформации, а потому и результаты при использовании различных методов разные, впрочем разница не столь уж и существенна. Единственное, что все эти методы объединяет — это насыщенность дифференциальными уравнениями и интегралами, которые представляют определенный интерес для любителей высшей математики. Здесь же, оставаясь в формате справочника, отмечу лишь основную проблему, которая возникает, при переходе от распределенной массы к условно сосредоточенной.

Когда мы рассматривали возможные соотношения между сосредоточенной и равномерно распределенной нагрузкой, то выяснили, что момент от равномерно распределенной нагрузки, умноженной на длину балки (что и дает нам значение условно приведенной нагрузки), будет в два раза меньше, чем от сосредоточенной нагрузки, равной по значению условно приведенной нагрузке и приложенной посредине пролета. Таким образом мы определили коэффициент перехода γ_п = 2. Соответственно приведенный коэффициент при переходе от равномерно распределенной нагрузки к сосредоточенной будет равен:

k_пр = 1/γ = 1/2 = 0.5 (296.4.1)

Однако прогиб от приведенной нагрузки будет не в 2, а приблизительно в 1.5 раза меньше, чем при сосредоточенной нагрузке (см. расчетные схемы для балок). Таким образом в этой ситуации некорректно применять один и тот же динамический коэффициент при определении прогиба, угла поворота поперечного сечения, нормальных и касательных напряжений. Между тем определяющими при расчете на ударные нагрузки являются нормальные напряжения, возникающие в поперечных сечениях под действием изгибающего момента, но расчет при этом производится в зависимости от значения прогиба. Чтобы с честью выйти из этой ситуации используют понятие приведенного прогиба, который имеет большее значение, чем прогиб при воздействии статической равномерно распределенной нагрузки и тогда:

f_пр = f_стk_пр = Q_прl³/48EI = qlk_прl³/48EI = ql⁴/96EI (296.5.1)

где Q_пр = ql = γFl — значение приведенной сосредоточенной силы, γ — плотность материала балки, F — площадь поперечного сечения.

Тогда условное значение коэффициента жесткости, необходимое для определения частоты колебаний, составит:

с_q = ql/f_пр = 96EI/l³ (296.3.2)

При таком подходе мы получаем максимально возможное значение приведенного прогиба по сравнению с вышеперечисленными методами, однако парадокс ситуации в том, что чем меньше статический прогиб, тем больше в итоге значение динамического коэффициента, а значит и меньше запас по прочности. Например, метод Рэлея приводит к следующему значению переходного коэффициента:

k^Р_пр = β = 17/35 = 0.4857 (296.4.2)

и тогда

f^Р_пр = 0.4857ql⁴/48EI = ql⁴/98.82EI (296.5.2)

соответственно

с^Р_q = 98.82EI/l³(296.3.3)

Если рассматривать приведенный прогиб как сумму прогиба от равномерно распределенной нагрузки и производной этого прогиба (а производная от прогиба — это угол поворота), то:

с_пр =ql/f_ст + q/f’_ст = 384EI/5l³ + 24EI/l³ = 100.8EI/l³ (296.3.4)

Как видим значения приведенных прогибов, полученные при разных способах определения, отличаются незначительно, максимальное расхождение составляет менее 5%. И не совсем понятно, зачем придумывать столько разных способов, чтобы вычислить максимальное значение приведенного прогиба, но напомню, что значение приведенного прогиба влияет на значение частоты колебаний, а когда частота свободных колебаний — колебаний груза, совпадает с частотой вынужденных колебаний — деформаций балки, то возникает резонанс, значительно увеличивающий амплитуду колебаний, что в итоге может привести к разрушению конструкции. На уроках физики изучение явления резонанса предваряется следующей байкой:

Когда-то давным-давно рота солдат бодрым строевым шагом вступала в побежденный город по широкому и прочному мосту. Однако частота собственных (вынужденных) колебаний пролета моста совпала с частотой четко отбиваемого строевого шага (частотой свободных колебаний), возникло явление резонанса, пролет обвалился и рота победителей погибла под обломками моста, так и не успев собрать трофеи, точнее трофеи в том смысле, в каком это понятие использовали древние греки, буквально засыпали солдат. С тех солдатам строго настрого запрещено проходить строевым шагом по мостам, акведукам и прочим инженерным сооружениям, включая плиты перекрытия, в которых могут возникнуть вынужденные колебания. Тем не менее свои выводы из этой истории сделали и строители и потому при расчете конструкций на различные виды нагрузок учитывается как минимально возможное так и максимально возможное значение частоты колебаний.

При расчете на ударные нагрузки конструкций жилых помещений явление резонанса как правило не учитывается, потому что по большому счету максимальный прогиб от действия ударной силы — это и есть проявление резонанса. А так как в результате достаточно быстрого перераспределения энергии удара, колебания такой системы при любом соотношении масс являются быстро затухающими, то возникновение ударной силы, большей чем при первом столкновении, в моменты последующих возможных столкновений практически не возможно. Тем не менее ударные нагрузки, прикладываемые к конструкции с более-менее постоянной частотой мы можем наблюдать в обычной квартире при работе стиральной машины, работающей в режиме отжима. Самый простой способ максимально уменьшить ударные нагрузки от прыгающей по помещению стиральной машинки — это изменить количество оборотов при отжиме и у хороших стиральных машин-автоматов для этого есть специальный регулятор. Если же переключателя скоростей нет, то можно рассчитать перекрытие на дополнительную ударную нагрузку возникающую от прыгающей стиральной машины, руководствуясь приведенным выше принципом.

В обще случае определить значение коэффициента жесткости (когда это возможно), частоту и период колебаний можно по следующей таблице:

Таблица 1: Основные параметры упругих систем с одной степенью свободы

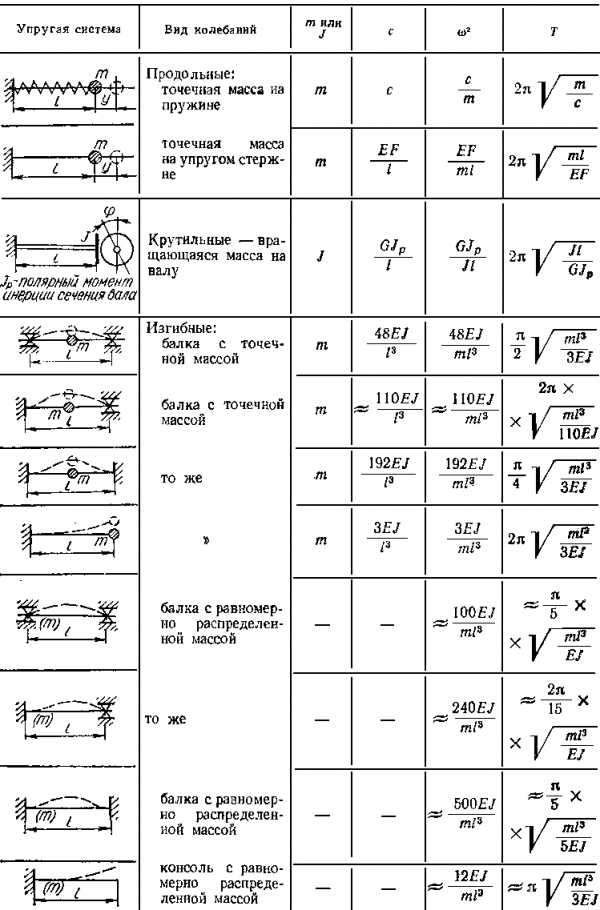
Если рассматривается случай приложения ударной нагрузки к изгибаемой конструкции, отличный от приведенных в таблице, то определить приближенное значение коэффициента жесткости можно по расчетным схемам для простых и статически не определимых балок. Приближенное потому, что при приложении сосредоточенной нагрузки не посредине пролета или при приложении не равномерно распределенной нагрузки колебания вряд ли будут гармоническими.

Таким образом формула для определения динамического коэффициента ударной нагрузки (288.11.3) при учете только массы деформирующейся конструкции примет вид

k_д = 1 + √1 + 2h/f_пр = 1 + √1 + 2h/(f_стk_пр) (296.7.1)

3. Если груз после падения продолжает движение вместе с рассматриваемой конструкцией, то формула (296.1.2) остается в силе

Это означает, что для определения максимального прогиба следует учитывать как массу падающего груза, так и параметры деформирующейся конструкции. Прогиб от действия сосредоточенной нагрузки, приложенной посредине балки, составляет f_ст = Ql³/48EI, прогиб от действия приведенной сосредоточенной нагрузки составляет f_пр = k_прf_ст, таким образом суммарный прогиб составляет:

f_сум = f_ст + f_пр = (Q + qlk_пр)l³/48EI = (1+ qlk_пр/Q)Ql³/48EI = f_ст(1 + k_пр(ql/Q) (296.8.1)

тогда значение динамического коэффициента ударной нагрузки с учетом масс обеих тел составит:

k_д = 1 + √1 + 2h/f_сум = 1 + √1 + 2h/(f_ст(1 +k_пр(ql/Q)) (296.7.2)

Не смотря на кажущуюся сложность, все приведенные выше формулы определения динамического коэффициента максимально просты, так как основаны на простейшей физической модели процессов, происходящих при ударе. Между тем, как уже говорилось, процессы, происходящие в соударяемых телах, достаточно сложные. Да и падать на перекрытие могут не только твердые тела, но и жидкости в различной упаковке, сыпучие материалы (песок, цемент и различные сухие строительные смеси), ну и тем более человек. Особенность таких падений в том, что перечисленные вещества, а тем более человек, падая на поверхность, даже очень жесткую, очень редко от нее отскакивают. Происходит это потому, что у жидкостей, а тем более сыпучих материалов отсутствуют жесткие внутренние связи, характерные для твердых тел, а человек, приземляясь после прыжка, старается присесть и таким образом искусственно продлить время контакта, а значит и максимально уменьшить ударную силу. Это означает, что ударная сила в таких случаях будет меньше и в зависимости от множества различных факторов (включая ловкость, если речь идет о человеке), которые требуют отдельного учета, расчетное снижение скорости, может снижаться от 1.1. до нескольких десятков раз. В связи с этим из соображений упрощения расчетов и обеспечения дополнительной прочности такие тонкости поведения жидких сыпучих и человеческих тел можно не учитывать. Но опять же, если есть уверенность в понимании происходящих процессов и в своих силах, то

Для сыпучих материалов в зависимости от размера фракций и плотности упаковки можно применять понижающий коэффициент k_п = 0.5-0.2 тогда формула (296.7.2) примет вид:

k_д = 1 + √1 + 2hk_п/f_сум = 1 + √1 + 2h/(f_ст(1 +k_пр(ql/Q)) (296.7.2)

Для человека упавшего головой на балку, тоже можно вычислить понижающий коэффициент в зависимости от наличия головного убора, пышности волос, толщины кожного и мышечного слоя, геометрии, жесткости и прочности черепа, но мой вам совет, не падайте головой на перекрытие, потому что в этом случае спасать придется уже не конструкцию перекрытия, а вас.

Пример расчета балки на ударную нагрузку с учетом масс балки и груза

А теперь посмотрим как изменится значение динамического коэффициента с учетом массы балки, на ранее рассматривавшемся примере. Напомню, рассматривается шарнирно закрепленная деревянная балка перекрытия длиной 4 м из древесины сечением 20х10 см. На средину балки с высоты 50 см падает гиря весом в 32 кг. Требуется определить прочность балки при ударной нагрузке с учетом массы балки.

1. При таком сечении и плотности древесины γ = 500 кг/м³ приведенная масса балки составит

ql = 500х0.2х0.1х4 = 40 кг

2. Прогиб балки при воздействии статической нагрузки от гравитационной массы гири мы уже определяли

f_cт = Ql³/48EI = 32х400³/(48х100000х6666.667) = 0.064 см

где Е = 10⁵ кгс/см² — модуль упругости древесины, I = bh³/12 = 6666.667 см⁴ — момент инерции поперечного сечения.

3. Тогда значение динамического коэффициента составит

k_д = 1 + √(1 + 2х50/0.064(1 + 0.5(40/32) = 32.02 (при использовании приведенного коэффициента 0.4875 значение динамического коэффициента составит 32.17)

напомню, значение динамического коэффициента без учета массы балки составляло 40.53, таким образом учет массы балки позволил уменьшить расчетное значение динамического коэффициента почти на треть.

4. Значение максимального изгибающего момента при таком динамическом коэффициенте составит

М_д = Qlk_д/4 = 32х400х31.02/4 = 102464 кг·см

5. Тогда при расчетном сопротивлении R = 140 кг/см² требуемый момент сопротивления составит

W_тр = М/R = 99279/140 = 731.9 см³

6. Момент сопротивления для балки сечением 20х10 см составит W = 2I/h = 6666.667/10 = 666.67см³ < W_тр = 731.9 см³.

Напомню, без учета массы балки требуемый момент сопротивления составлял 926.4 см³.

Вывод: Не смотря на все наши старания балка под действием такой ударной нагрузки может разрушиться. Однако в данном случае мы совершенно не учитывали упругие свойства гири, полагая ее совершенно жесткой, а также то, что на балке перекрытия будут уложены как минимум доски пола (без досок балки перекрытия как-то теряют изначальный смысл). А это означает, что расчетную массу балки следует еще увеличить, а если еще учесть упругие свойства как гири, так и древесины, и вполне вероятное развитие местных неупругих деформаций, то у рассматриваемой балки большие шансы на выживание.

doctorlom.com

Пример решения задачИ с сосредоточенными нагрузками — МегаЛекции

Методические указания

к расчетно-графической работе

“Изгиб прямоугольной плиты”

Казань

УДК 539.3

ББК 22.251

Методические указания к расчетно-графической работе “Изгиб прямоугольной плиты” / Составители: Каюмов Р.А., Зиннуров Р.А., Шакирзянов Ф.Р. – Казань: КГАСУ, 2013. – 12 с.

Печатается по решению редакционно-издательского совета Казанского государственного архитектурно-строительного университета.

Приводятся постановка задачи и формулы для вычисления внутренних силовых факторов и напряжений для шарнирно-опертой по контуру прямоугольной плиты на упругом основании под действием двух сосредоточенных нагрузок.

Определяются общая схема и последовательность выполнения расчетно-графической работы, даются рекомендации для ее самостоятельного выполнения и примеры решения задач.

Ил. 6; табл. 1

Рецензент: к.ф.-м.н., профессор, заведующий кафедрой «Теоретическая механика» КГАСУ Шигабутдинов Ф.Г.

УДК 539.3

ББК 22.251

Ó Казанский государственный архитектурно-строительный университет, 2013.

Ó Каюмов Р.А., Зиннуров Р.А., Шакирзянов Ф.Р, 2013

Рассматривается задача об изгибе шарнирно опертой по контуру прямоугольной фундаментной бетонной плиты толщины h, лежащей на грунте с коэффициентом постели k. Воздействие на плиту (рис.1) представляется в виде сосредоточенных сил P₁, P₂ (например, воздействие от колонн) и постоянной распределенной нагрузки q (например, вес плиты).

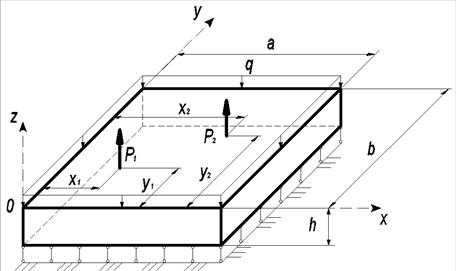
Рис. 1.

Геометрические (a, b, h, x₁, x₂, y₁, y₂), механические (модуль упругости Е=240 т/см² и коэффициент Пуассона =0.2) и силовые параметры ( ) выбираются по индивидуальному шифру из таблицы 1.

Таблица 1

А	Б	В	Г	А	Б	В	Г	А	Б	В
а(м)	b(м)	h(м)	x₁(м)	y₁(м)	x₂(м)	y₂(м)	P₁(т)	P₂(т)	q(т/м²)	k(т/см³)
2,2	5,0	0,1	0,5	0,2	2,0	1,8			0.5	0.001
2,4	4,8	0,15	0,6	0,4	1,8	1,6			1.0	0.003
2,6	4,6	0,2	0,7	0,5	1,6	1,4			1.5	0.005
2,8	4,2	0,3	0,8	0,6	1,4	1,2			2.0	0.007
3,0	3,9	0,4	1,0	0,8	1,2	1,0			2.5	0.01
3,2	3,5	0,45	1,2	1,0	1,0	0,8			3.0	0.012
3,4	3,1	0,5	1,4	1,2	0,8	0,6			3.5	0.015
3,6	2,7	0,55	1,6	1,4	0,6	0,5			4.0	0.017
3,8	2,3	0,6	1,8	1,6	0,4	0,4			4.5	0.018
4,0	2,0	0,65	2,0	1,8	0,2	0,2			5.0	0.02

Требуется найти выражение для прогиба плиты W(x,y), выражения для нормальных s_x, s_y и касательных напряжений t_xy и построить их эпюры. При заданных значениях проверить прочность плиты по критерию Г.А. Гениева (класс бетона B15, для которого ).
Толщину плиты принять равной h=a/40, сечение бетонных свай — А_св=100см² , высоту свай l=15 м, координаты первой бетонной сваи принять равными x₁, y₁ , остальные три расположить симметрично,
Решение задачи методом Бубнова-Галеркина
Дифференциальное уравнение изгиба плиты на упругом основании записывается в виде
(1)
где – цилиндрическая жесткость плиты, – координаты сосредоточенной нагрузки, – описательная функция (дельта-функция Дирака, аналогичная функциям типа модуль), согласно которой сила везде равно нулю кроме точки .
Для решения задачи изгиба плиты используем метод Бубнова-Галеркина. В этой задаче прогибы , ищем в виде двойного ряда:
(2)
Легко проверить, что такой вид решения обеспечивает выполнение условия шарнирного закрепления.
Значения для A_mn получаются следующим образом. Подставим соотношения (2) в уравнение (1) и умножим это уравнение на . Интегрирование по области, которую занимает пластина (т.е. в интервале ), приводит к результату:
(3)
Выражения для нормальных и касательных напряжений определяются из следующих соотношений:
, (4)
, (5)
. (6)

Расчет на прочность
Согласно критерию Г.А. Гениева, прочность бетона будет обеспечена если:
. (7)
Здесь – расчетные значения сопротивлению бетона сжатию и растяжению, – главные напряжения.
Главные напряжения , определяются по формулам:
. (8)
Максимальные сжимающие напряжения в плите возникают, согласно (4)-(6), при z=h/2, т.е. на ее верхней поверхности, а максимальные растягивающие напряжения возникают, согласно (4)-(6), при z = — h/2, т.е. на ее нижней поверхности. Подставляя (2) в (4)-(6) при z=h/2 строят эпюры напряжений в разных сечениях плиты. Это позволяет определить опасные точки и провести ее проверку прочности.

Пример решения задачИ с сосредоточенными нагрузками
Исходные данные:
Требуется найти выражение для прогиба плиты W(x,y), выражения для нормальных s_x, s_y и касательных напряжений t_xy и построить их эпюры. При заданных значениях проверить прочность плиты по критерию Г.А. Гениева.
Решение:
1. Определение прогибов
Дифференциальное уравнение изгиба плиты записывается в виде:
(9)
В соответствии с выше изложенным, прогибы ищем в виде следующего ряда:
(10)
где
Цилиндрическая жесткость плиты равна
Для упрощения расчетов учтем только несколько членов ряда ( ). Предварительно вычислим коэффициенты :
, ,
,
,
,
,
,
,
.
Тогда из соотношения (10) получим перемещение в виде:
(11)
Определим прогибы в точках. Например, в точке прогиб равен , а в середине плиты : см. Аналогично можно найти прогибы в промежуточных точках и построить эпюру прогибов (рис. 2).
Рис. 2. Эпюры прогибов
2. Определение напряжений
Из (4)-(6) предварительно найдем производные от функции прогибов для вычисления напряжений:
(12)
Тогда напряжения на верхней поверхности плиты (при z=h/2) вычисляются из следующих соотношений:
,
, (13)
.
Из (12) и (13) видно, для ряда (10) выполняются условия равенства нулю нормальных напряжений на контуре пластины.
Как и в случае с перемещениями, определим напряжения в узлах сетки: в углу плиты при напряжения равны: , , т/см² = 0.86 МПа. В середине плиты ( ) напряжения равны т/см² = 1.6 МПа, т/см² = -1.1 МПа, т/см² = 0.03 МПа. Аналогично можно найти напряжения во всех узлах и построить эпюры напряжений (рис. 4-6).
Рис. 4. Эпюра

Рис. 5. Эпюра

Рис.6. Эпюра
3. Расчет на прочность
Проверим прочность бетонной плиты по критерию Гениева. Примем в расчетах класс бетона B15, для которого .
Для того, чтобы плита была прочной, функция (7), определяющая уровень напряженности малого элемента плиты, должна быть меньше единицы во всех точках. Построим эпюру функции f и найдем его наибольшее значение (рис. 7).

Рис. 7. Функция, определяющая уровень напряженности плиты
Наибольшее значение функции напряженности по критерию Гениева равно:

Таким образом, можно сделать вывод, что условие прочности выполняется.
Литература
1. Александров А.В., Потапов В.Д. Основы теории упругости и пластичности. – М: Высшая школа, 1990. – С. 146-174.
2. Гениев Г.А., Киссюк В.Н., Тюпин Г.А. Теория пластичности бетона и железобетона. – М: Стройиздат, 1974. – 316 с.
3. Доннел Л.Г. Балки, пластины и оболочки. – М: Наука, 1982. – 567 с.
4. Самуль В.И. Основы теории упругости и пластичности. – М: Высшая школа, 1982. – С. 116-134.
5. Терегулов И.Г. Сопротивление материалов и основы теории упругости и пластичности. – М: Высшая школа, 1984. – 472 с.
6. Тимошенко С.П. Курс теории упругости. − Киев: Наукова думка, 1972. – 507 с.
7. Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки. − М: Наука, 1966. – 636 с.

Методические указания
к расчетно-графической работе
“Изгиб прямоугольной плиты”

Составители: д.ф.-м.н., профессор Каюмов Р.А.,
к.т.н., старший преподаватель Зиннуров Р.А.,
к.ф.-м.н., ассистент Шакирзянов Ф.Р.

Редактор

Редакционно-издательский отдел
Казанского государственного архитектурно-строительного университета

Подписано в печать Формат 60х84/16,
Заказ Печать ризографическая Усл.-печ. л. 1,0
Тираж 100 экз. Бумага офсетная № 1 Уч.-изд. л. 1,0
Печатно-множительный отдел КГАСУ
420043, Казань, Зеленая, 1

Рекомендуемые страницы:

Воспользуйтесь поиском по сайту:
megalektsii.ru