Построение эпюр для чайников – Эпюра поперечных сил

Содержание

Эпюра поперечных сил — как построить?

Привет! Сегодня будем учиться строить эпюры поперечных сил. В этой статье я расскажу, что такое поперечная сила, чем интересна и полезна при проведении расчетов на прочность и жесткость. По уже сложившейся традиции, как и с другими эпюрами, будем рассматривать три способа построения эпюры поперечных сил: подробный, упрощенный и быстрый. Для того чтобы рассчитать поперечную силу в сечении нужно уметь пользоваться уравнениями равновесия конструкции. Поэтому перед изучением данной статьи, если вы не знаете этого материала, рекомендую изучить его, перейдя по указанной ссылке выше. Ну что же перейдем непосредственно к обучению!

Эпюра поперечных сил — это график показывающий распределение поперечных сил в сечениях, загруженного элемента, работающего на поперечный изгиб.

Подробный способ построения эпюры поперечных сил

В качестве примера, возьмем балку, частично загрузим ее распределенной нагрузкой q, а часть оставим без нагрузки, чтобы рассмотреть всевозможные случаи:

Первым делом нужно определить все внешние силы, действующие на конструкцию, то есть помимо распределенной нагрузки на балку будет действовать реакции, возникающие в опорах. Если вы до сих пор не умеете их определять, то обязательно изучите этот материал. В этой статье, я подробно на этом останавливаться не буду. Вот какие значения реакций получаться для рассматриваемого примера:

Разбиваем балку на участки

После подготовительного этапа можно приступать к расчету поперечных сил. На отдельных участках балки поперечная сила будет меняться по определенному закону. Как раз, наша задача научиться определять эти законы. Зная закон изменения поперечной силы на участке, можно определить ее значения в любом сечении в пределах этого участка. Так как, поперечная сила меняется по линейному закону, для построения эпюры достаточно определить ординаты на границах участков. Границами участков служат места приложения сосредоточенных сил, а также начало и конец распределенной нагрузки, то есть для нашего случая нужно рассмотреть два участка.

Важно! Для эпюры изгибающих моментов, границей участков также служит место приложения сосредоточенного момента. На эпюру же поперечных сил моменты не оказывают никакого влияния. Однако, так как эпюры поперечных сил и изгибающих моментов строятся, обычно, вместе, то эту границу так же нужно намечать.

Метод сечений

Приступим непосредственно к расчету. Для установления закона изменения поперечной силы, будем использовать метод сечений. Мысленно рассекаем балку на две части, в пределах 1-го участка, на расстоянии x₁от правого торца балки.

Каждую часть балки уравновешиваем путем приложения сосредоточенной силы Q_y₁и момента M_x₁. Эти силовые факторы, заменяют действие частей балки друг на друга. Для определения этих величин, достаточно рассмотреть равновесие одной из рассеченных частей.

Правила знаков для поперечной силы

Очень важно на данном этапе выбрать правильное направление поперечной силы. Она должна иметь такое направление, при котором часть балки, при неподвижном (закрепленном) противоположном от рассечения месте, стремилась повернутся ПО часовой стрелке.

Также многие авторы рекомендуют просто запомнить такое правило:

Для правой отсеченной части, направлять поперечную силу вверх;
Для левой отсеченной части, направлять поперечную силу вниз.

Вводим систему координат для первого участка

Для удобства выберем правую часть, так как здесь меньше нагрузки, которую нужно учитывать в расчете. Также, мы можем не учитывать момент M_x1, так как в этом уроке, нас интересует только поперечная сила. В рассматриваемом сечении вводим локальную систему координат:

Ось z будет иметь горизонтальное направление;
Ось y будет направленна вертикально;
Ось x будет направленна перпендикулярно плоскости чертежа (на нас).

Записываем уравнение равновесия для первого участка и строим эпюру

Для нахождения поперечной силы на первом участке достаточно записать одно уравнение равновесия – сумму проекций все сил на вертикальную ось y. Эта сумма должна быть равна нулю:

Из полученного уравнения, следует:

Таким образом, поперечная сила в пределах первого участка равна 1 кН. Откладываем это значение на графике:

Положительное значение поперечной силы откладывается выше нулевой линии, отрицательное ниже (как в нашем случае). Эпюры штрихуются перпендикулярно нулевой линии, на каждом участке проставляются знаки, на границах участков указываются численные значения.

Расчет второго участка

Проделываем те же действия, что выполняли для первого участка. Рассекаем балку в пределах рассматриваемого участка на расстоянии z₂от левого торца балки:

Зарисовываем отдельно расчетный элемент, отбросив правую часть и заменив ее действие Q_y2и M_x2. Вводим локальную систему координат:

Для того чтобы рассчитать такой участок, с распределенной нагрузкой, воспользуемся хитростью, которой часто пользуются при решении задач по теоретической механике. Свернем эту нагрузку до сосредоточенной силы. Для этого умножим интенсивность q на длину действия нагрузки – z

Записываем уравнение равновесия для второго участка:

Выражаем поперечную силу:

Это закон, по которому меняется поперечная сила на втором участке. Чтобы получить значения для построения эпюры, нужно в это уравнение вместо z₂подставить координаты характерных сечений. Как и говорилось ранее, поперечная сила меняется по линейному закону (исключениями могут быть только схемы с трапециевидной нагрузкой), поэтому для построения эпюры достаточно вычислить значения на границах участка. В сечении A (при z₂=0) поперечная сила будет равна:

В середине пролета, при z₂=2м получим:

По полученным значениям, строим эпюру поперечных сил на втором участке:

Вот собственно и все! Эпюра поперечных сил построена. Согласитесь, длинное руководство получилось?! Так вот, далее я расскажу, как построить эту эпюру намного быстрее, а в конце покажу как это делается за несколько секунд.Сделайте небольшой перерыв на чай, и возвращайтесь к чтению!

Упрощенный способ построения эпюры

Итак, продолжим изучать технологии построения эпюры поперечных сил. В этом методе будем учится рассчитывать эту эпюру без вынесения отдельных участков балки и без записи уравнений равновесия. Будем выводить сразу следствия из этих уравнений. Также как, в первом случае, балку нужно разбить на 2 участка.

Первый участок

Запишем закон изменения поперечной силы на первом участке. Для этого отметим сечение С, отстающее от правого торца балки на величину z₁. Поперечная сила в этом сечении будет равна сумме проекций всех сил на вертикальную ось, находящихся справа (или слева) от сечения. Мы ведем расчет этого участка справа-налево, так как в данном случае справа нагрузки меньше.

Для того чтобы правильно записать уравнение поперечных сил для любого участка, нужно придерживаться следующих правил:

Если нагрузка относительно рассматриваемого сечения стремится повернуть ПО часовой стрелки, то в уравнении она учитывается со знаком «+»;
Если нагрузка относительно рассматриваемого сечения стремится повернуть ПРОТИВ часовой стрелки, то в уравнении она учитывается со знаком «-».

Продемонстрирую вышеописанные правила на нашем примере. Относительно сечения С, сила R_B, находящаяся справа от сечения, стремится повернуть против часовой стрелки, поэтому в уравнение она пойдет со знаком «-»:

Как видно из уравнения, поперечная сила, на первом участке, не зависет от координаты z₁, поэтому во всех сечениях она одинаковая.

Кстати, помните я писал, что нагрузку можно учитывать, как справа, так и слева? Так вот, давайте запишем уравнение, просуммировав нагрузку, находящуюся слева от сечения С и посмотрим результат.

Реакция R_A, относительно сечения С, стремится повернуть ПО часовой стрелке, в уравнение пойдет с плюсом:

Нагрузку q, сворачиваем до сосредоточенной силы, как в подробном способе. Она стремится повернутся ПРОТИВ часовой стрелке, в уравнение пойдет со знаком «минус»:

Подставляя численные значения нагрузки, получим следующий результат:

Теперь перейдем ко второму участку.

Второй участок

Здесь ситуация похожая, подробно комментировать уже не буду, приведу схему и расчет:

По выполненным расчетам двух участков, можно построить уже знакомую эпюру:

Как видите, эпюра поперечных рассчитывается достаточно просто. В последнем разделе я расскажу, как можно построить ее и вовсе устно.

Быстрый способ построения эпюры

Как вы уже, наверное, заметили, эпюра поперечных сил имеет скачки в тех местах, где прикладываются сосредоточенные усилия, а в местах где приложена распределенная нагрузка, эпюра постоянно меняется по линейному закону. Эти свойства эпюры можно использовать при построении. Давайте рассмотрим такую балку:

Определим для нее опорные реакции:

Расчет быстрым способом рекомендую производить слева-направо. В этом случае для скачков эпюры будут следующие правила знаков:

Если приложенная сила направленна вверх, то и скачек на эпюре будет вверх, на величину силы;
Если приложенная сила направленна вниз, то и скачек на эпюре будет вниз, на величину силы.

С учетом данных правил, получим вот такую эпюру поперечных сил:

Прокомментирую: в точке А, сила направленна вверх, эпюра поднимается на 4 кН, в точке С, опускается до нуля, т.к. приложенная сила направленна вниз и так далее. С сосредоточенным усилиями думаю все просто и понятно.

Там, где есть, распределенная нагрузка, эпюра меняется не скачкообразно, а постепенно. И чтобы узнать на сколько эпюра измениться от действия распределенной нагрузки от ее начала и до конца, нужно умножить интенсивность q на длину ее действия:

Вот собственно и все, что хотелось рассказать об эпюрах поперечных сил! Вы можете задавать любые вопросы по материалам статьи в комментариях ниже. Также рекомендую подписаться на наши соц. сети, чтобы не пропустить новые и интересные материалы.

После освоения данного урока, можете смело приступать к изучению техник построения эпюр изгибающих моментов. Данная статья является продолжением серии статей о том, как строятся эпюры для балок, работающих на поперечный изгиб.

Спасибо за внимание!)

sopromats.ru

Правила построения эпюр (сопромат)

Озвучим правила построения эпюр, вытекающие из метода сечений, и являющиеся следствием дифференциальных и интегральных зависимостей, некоторые из которых справедливы при обходе эпюр и слева направо. Зная правила построения эпюр, можно быстро найти грубую ошибку только по внешнему виду эпюр.

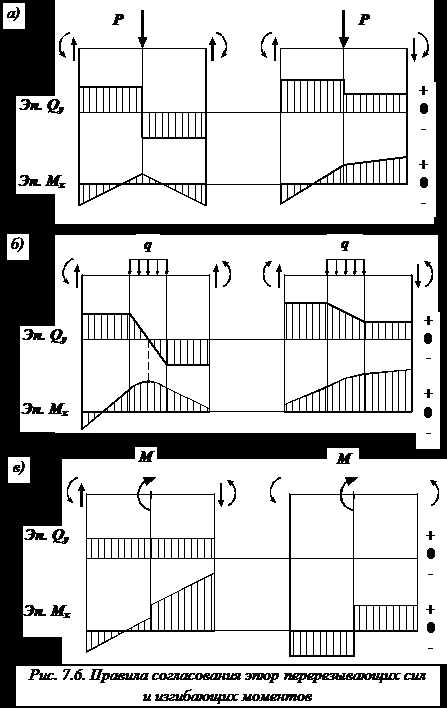
Правило построения эпюр – отсутствующая распределенная нагрузка

Если на участке балки отсутствует распределенная нагрузка (), то эпюра поперечных сил на этом участке представляет собой прямую, параллельную оси балки (рис. 7.6). По дифференциальной зависимости распределенной нагрузки и поперечной силы: поскольку , то и . Следовательно, .

Эпюра изгибающих моментов на участке, где , – прямая линия. Причем, если , то прямая идет вверх, а если , прямая идет вниз. Если , то изгибающий момент постоянен, поскольку .

Правило построение эпюр – скачки и изломы

Под сосредоточенной силой (P) на эпюре поперечных сил (рис. 7.6, а) имеется скачок на величину этой силы и по ее направлению, а на эпюре изгибающих моментов – излом, угол которого направлен навстречу нагрузке.

Правило построение эпюр – присутствует распределенная нагрузка

Если на участке балки имеется равномерно распределенная нагрузка: эпюра поперечных сил представляет собой наклонную прямую (рис. 7.6, б), идущую вниз, если нагрузка направлена вниз (и наоборот). Эпюра на этом участке, согласно третьей формуле дифференциальных зависимостей, изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке.

Правило построение эпюр – экстремум

Если эпюра поперечной силы проходит через нулевое значение, то в этом сечении балки на эпюре изгибающих моментов имеется экстремум (последнее вытекает из дифференциальной зависимости ). В точках, соответствующих началу и концу участка, в пределах которого действует распределенная нагрузка, параболическая и прямолинейная части эпюры переходят одна в другую плавно (без излома).

Правило построение эпюр – внешний момент

Сосредоточенный внешний момент M (рис. 7.6, в) никак не отражается на эпюре . На эпюре в месте приложения этого момента имеется скачок на его величину.

Заметим, что построение эпюр поперечных сил и изгибающих моментов ввел в практику расчета балок на изгиб французский ученый Жан Антуан Шарль Бресс (1822 – 1883 гг.) в 1859 г.

sopromato.ru

Как быстро построить эпюру моментов ?

В одном из уроков я писал про то как построить эпюру моментов используя метод сечений. Теперь предлагаю построить те же самые эпюры изгибающих моментов только быстрее. С помощью этого способа можно проверить себя, иногда сэкономить время на решении задач по сопромату. При построении эпюр воспользуемся принципом независимости действия сил.

Хитрости быстрого построения эпюры изгибающих моментов

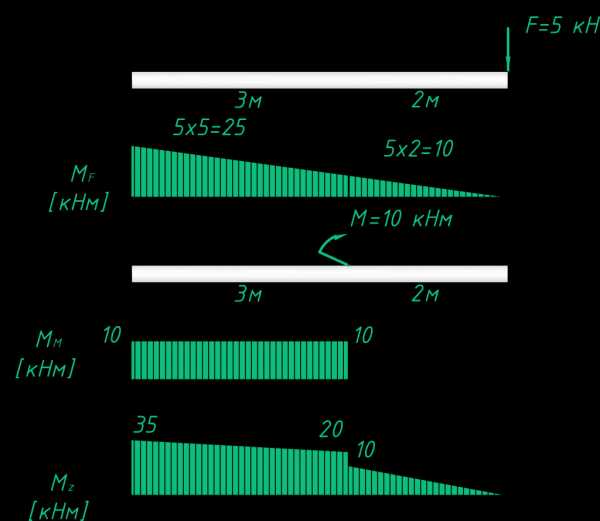
Наверно, внимательные читатели заметили, что эпюрой изгибающих моментов от сосредоточенной силы является прямоугольный треугольник. В точке приложения сосредоточенной силы момент будет равен нулю, так как плечо равно нулю. В наиболее удаленной точке от силы момент находим умножив силу на плечо.

Эпюра от единственного момента прямоугольная, ординаты эпюры равны этому моменту и постоянны по всей длине.

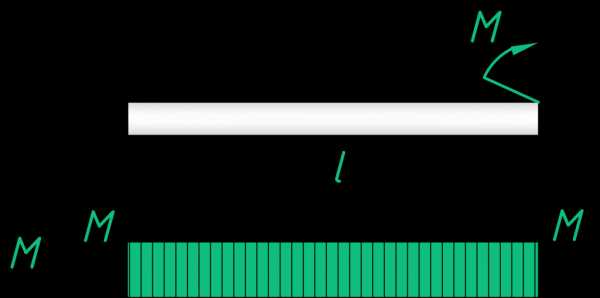
Теперь построим быстрым способом эпюру сначала от сосредоточенной силы, а затем от момента. Далее сложим ординаты двух полученных эпюр.

Умножая силу на плечо, для характерных точек, получаем первую эпюру от сосредоточенной силы. Сила растягивает верхние волокна, эпюру откладываем сверху.

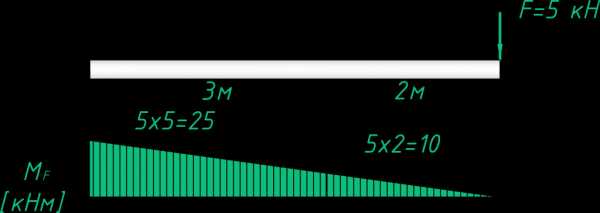
Строим эпюру от момента, внешний момент также растягивает верхние волокна:

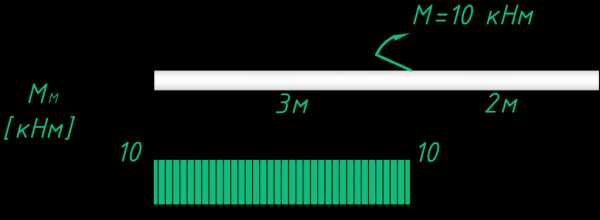
Теперь складываем ординаты двух эпюр в характерных точках. Получили эпюру один в один как при первом способе построения.

ssopromat.ru

Построение эпюр консольной балки | buildingbook.ru

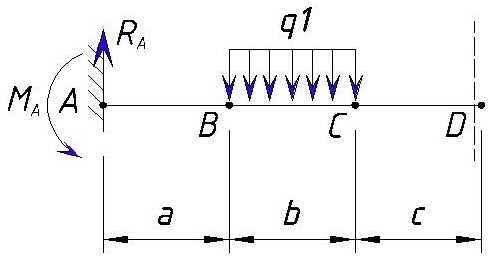
Мы уже рассматривали типовые эпюры консольной балки, теперь расскажем про построение эпюры консольной балки если на нее воздействуют сразу несколько нагрузок.

Чтобы легче было понять материал разберемся на примере:

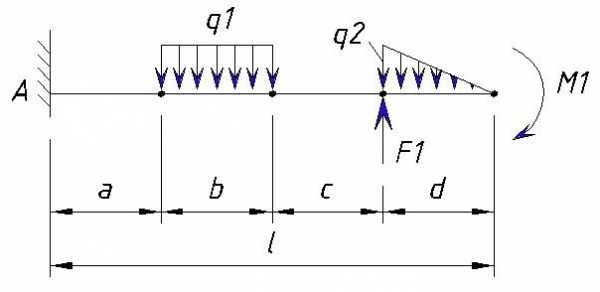
Значения нагрузок:

q1=10 кН/м

q2=60 кН/м

F1=10 кН

M1=20 кН·м

Расстояния между точками равны т,е. a=b=c=d=1м

Опорные реакции

Построение эпюр, как правило, начинают с определения опорных реакций.

Определяем поперечную силу и изгибающий момент в точке А.

Для начала зададим направление опорных реакций

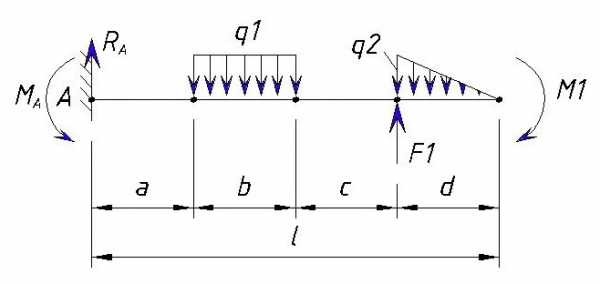
Т.к. система не подвижна, то сумма сил должна равняться нулю.

Нагрузки, направленные вверх, принимаются со знаком плюс.

Нагрузки, направленные вниз, принимаем со знаком минус.

Направление Ra мы приняли вверх. Если в процессе решения уравнение значение Ra будет отрицательным, значит она направлена в другую сторону.

В уравнении уравновешивающих сил вдоль оси Y изгибающий момент M1 не присутствует. Да и в консольной балке момент, приложенный на любом участке балки, не влияет на поперечные силы. Только если будет как минимум еще одна опора момент повлияет на опорную реакцию и, соответственно, на поперечные силы, но в данном уравнении его все равно не будет.

Из этого уравнения вычисляем значение опорной реакции Ra:

Подставляем значения нагрузок и вычисляем значение опорной реакции Ra:

Мы вычислили значение опорной реакции Ra. Значение положительное, значит направление нагрузки мы назначили правильно.

Далее составляем уравнение равновесия изгибающих моментов вокруг точки A. Если система неподвижна, сумма моментов вокруг любой точки равна нулю.

Уравнение равновесия моментов вокруг точки A для нашего примера будет выглядеть следующим образом:

Значение момента от действия силы вокруг определенной точки равно произведению этой силы на расстояние от заданной точки до центра приложения нагрузки. Чтобы было понятно какой изгибающий момент создает каждый вид нагрузки, давайте рассмотрим их по отдельности.

Изгибающий момент M1 влияет на опорный момент вне зависимости от того где он приложен, т.е. не важно приложен он в середине балки или на конце на опорный момент он будет влиять одинаково.

Сосредоточенная сила F1 создает изгибающий момент равный произведению его значения на плечо (расстояние от рассматриваемой точки до точки приложения силы). Т.е. чем больше плечо, тем больший изгибающий момент создает сила F1.

Равномерно-распределенная сила q1 создает момент, равный произведению этой нагрузки на длину приложения этой нагрузки и на плечо (расстояние от рассматриваемой точки до центра равномерно-распределенной нагрузки). Т.е. мы можем представить распределенную нагрузку как сосредоточенную в центре этой нагрузки и умножить это значение на плечо.

Переменная нагрузка сила q2 создает момент, равный произведению половины произведения этой нагрузки на длину приложения и на плечо (расстояние от рассматриваемой точки, до центра приложения нагрузки, который расположен на расстоянии 1/3 от общей длины приложения этой нагрузки, ближе к максимальному значению). В данном примере это выглядит так:

Из этого уравнения мы можем вычислить значение опорного момента Ma:

Подставляем значения и вычисляем значение опорного момента в точке A:

Мы вычислили значение опорного момента Ma. Значение опорного момента Ma положительное, поэтому направление действия момента задано правильно.

Назначение контрольных точек

Для начала определяем контрольные точки на балке. 2-е точки естественно будут начало и конец балки, а промежуточные точки будут места приложения нагрузок (в случае равномерно-распределенной или переменной нагрузки точками будут начало и коней приложения нагрузки). Рассмотрим на примере разделение консольной балки на участки:

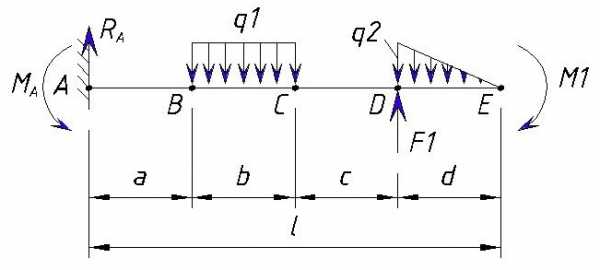
Точку заделки мы обозначили буквой «А».

Далее ближайшая точка «В» — это место приложения начала равномерно-распределенной нагрузки q1. Расстояние между точкой «А» и «B» равно a.

Далее следующая точка «С» — это конец приложения равномерно-распределенной нагрузки q1. Расстояние между точкой «B» и «C» равно b.

Следующая точка «D» — это начало приложения переменной нагрузки q1 и точка приложения силы F1. Расстояние между точкой «C» и «D» равно c.

Следующая точка «E» — это конец приложения переменной нагрузки q1, точка приложения изгибающего момента M1 и конец балки. Расстояние между точкой «D» и «E» равно d.

Построение эпюры Q (поперечной силы)

Разбиваем балку на участки между контрольными точками, т.е. участок AB (между точками A и B), участок BC (между участками B и C) и т.д.

В нашем примере у нас есть 4 участка: AB, BC, CD,DE.

Эпюру поперечных сил Q мы можем строить перемещаясь от точки А до точки E, рассчитывая значения в каждой точке, либо наоборот от точки E до точки A. В данном примере мы будем следовать от точки A, до точки E.

На каждом участке мы определяем значения и строим эпюру. По горизонтальной оси будут откладываться координаты, по вертикали откладываются значения (вверх от консольной балки откладываются положительные значения, вниз откладываются отрицательные значения).

Далее необходимо соединить эти точки линиями. Все точки, кроме точек между началом и концом переменной нагрузки, соединяются по прямой линии. Переменная нагрузка от начала, до конца соединяется изогнутой линией, напоминающей гиперболу, изогнутой вниз если нагрузка возрастает к месту заделки (если заделка слева) и изогнутой вверх если нагрузка к месту заделки спадает.

Правило знаков для построения эпюры Q

Если внешняя нагрузка, приложенная к рассматриваемой части, стремится повернуть сечение на заданном участке по часовой стрелке, то значение будет положительным и откладывается вверх.

Если внешняя нагрузка стремится повернуть сечение на заданном участке против часовой стрелки, то значение будет отрицательным и откладывается вниз.

Точка, вокруг которой поворачивают заданный участок не обязательно точка закрепления. Это точка, которую мы задаем на заданном участке в направлении к которой мы строим эпюру: если мы строим эпюру слева направо (как в данном примере), то это самая правая точка на заданном участке, если строим эпюру справа налево, то это самая левая точка на заданном участке.

Определяем напряжения Q на участке AB.

Рассмотрим участок AB. При рассмотрении участка AB мы как бы отбрасываем все остальные участки и не учитываем их на данном этапе. Кроме этого вначале мы не учитываем силы, приложенные в точке B.

Значение поперечной силы в точке А равно значению опорной реакции Ra, которое мы вычислили ранее. Не забываем про правило знаков — если сила стремится повернуть рассматриваемый участок по часовой стрелке, то значение принимается со знаком плюс, если против часовой, то со знаком минус. Мы как-бы откидываем закрепление балки в точке А, заменив ее силой Ra, и закрепляем в точке B. Сила Ra стремится повернуть участок вокруг точки B по часовой стрелке, поэтому Ra принимается со знаком плюс.

С правилом знаков поначалу возникают некоторые проблемы. Точка, вокруг которой мы мысленно вращаем данный участок, это не точка закрепления балки, а точка на участке, который мы в данный момент рассматриваем. Если мы строим эпюру слева направо (как в данной примере), это это будет самая правая точка, на рассматриваемом участке. Если строим эпюру справа налево, то это будет самая левая точка, на рассматриваемом участке.

Далее мы рассматриваем участок от точки А, до точки B, но при этом не учитываем нагрузки, которые приложены в самой точке B.

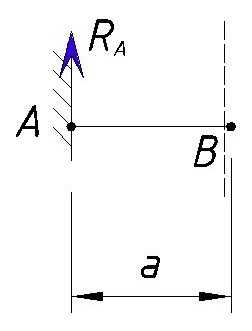
Пунктирной линией на рисунке обозначен участок, который мы рассматриваем.

На данном участке нет поперечных сил, кроме Ra, поэтому

Т.е. мы пока не учитываем силы, которые справа от этой точки и сила которая приложена именно в этой точке. Естественно силы, приложенные правее правее точки B влияют на значение поперечных сил на данном участке и они сейчас выражены в опорной реакции Ra. Как уже ранее выяснили сила Ra стремится повернуть сечение по часовой стрелке, поэтому Ra принимается со знаком «плюс» и откладывается вверх от оси.

Т.к. значение поперечной силы не изменилось, то эпюра Q на данном участке будет выглядеть как прямоугольник:

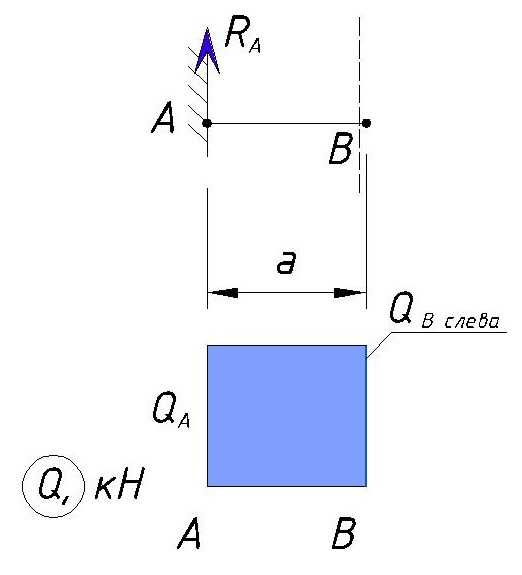
По вертикали мы откладываем значение поперечной силы, по горизонтали координаты балки.

Далее мы рассматриваем участок AB с учетом точки B, но принимаем участок не много правее точки B (на рисунке участок отсечен пунктирной линией)

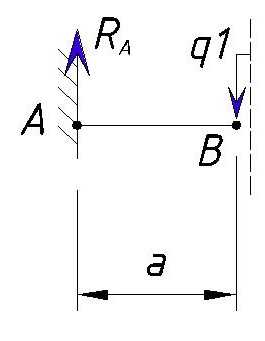
В точке B начинается равномерно-распределенная нагрузка q1, но мы рассматриваем участок правее точки как бы равный нулю, т.е. нагрузка q1 приложена в точке B, но еще имеет нулевую длину приложения нагрузки, поэтому она не изменяет значение поперечной силы в точке B.

Тут мы опять действуем согласно правилу знаков: точка, вокруг которой мы вращаем участок, находится не много правее точки B. Сила Ra стремится повернуть данный участок по часовой стрелке, поэтому она принимается со знаком «плюс». Чтобы было проще при построении эпюры слева направо сила, направленная вверх всегда будет со знаком «плюс», а сила направленная вниз будет со знаком «минус».

Эпюра Q на данном участке получается следующая:

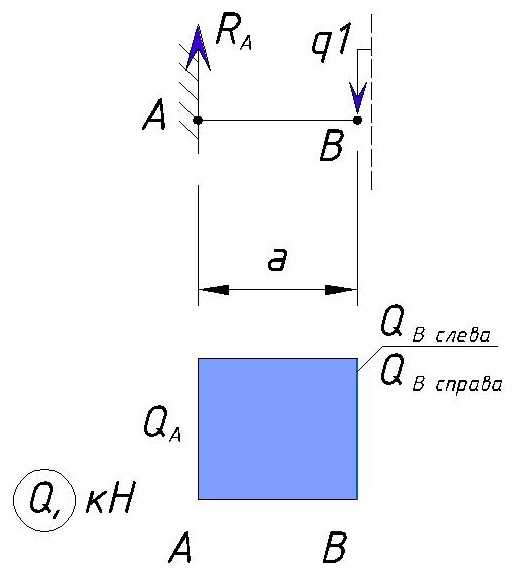
Определяем напряжения Q на участке BС.

Далее мы рассматриваем участок от точки B до точки C.

Пунктирными линиями я указал рассматриваемый участок.

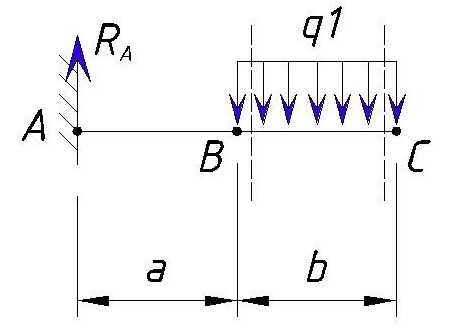
Значение поперечной силы в точке B справа мы уже вычислили ранее — это Q(B справа)=Ra=30 кН (именно значение, что справа).

На участке от точки B до точки C действует сила q1. По правилу знаков данная нагрузка стремится повернуть участок BC вокруг точки C против часовой стрелки, поэтому оно учитывается со знаком минус. Значение Q слева от точки C равно:

Строим эпюру поперечных сил на данном участке

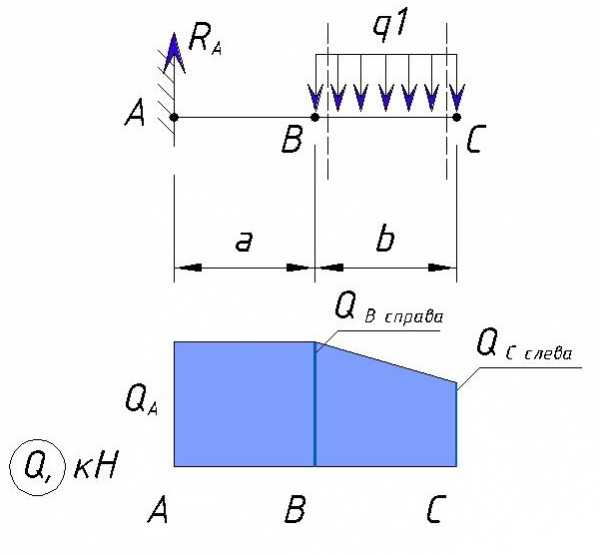
Далее рассматриваем участок BC, с точкой несколько правее точки C

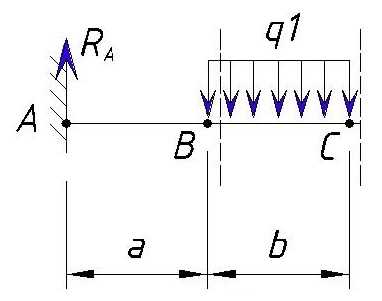
В точке C справа ничего не изменилось, поэтому

Эпюра Q на участке от A до C будет выглядеть следующим образом:

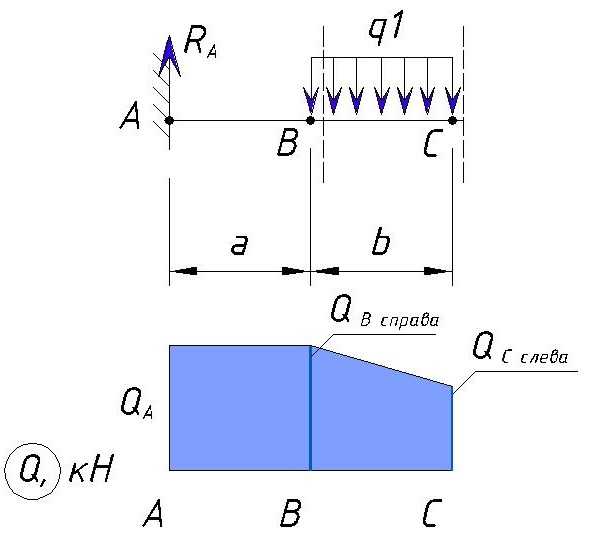
Определяем напряжения Q на участке СD.

Рассмотрим участок от точки C до точки D. Вначале рассматриваем участок левее точки D.

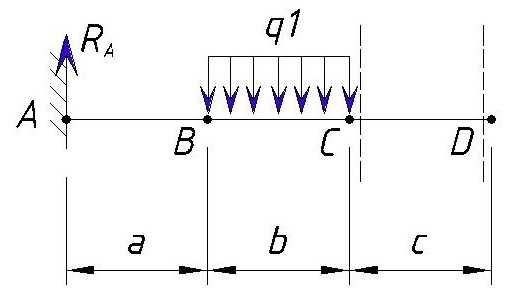
На данном участке нет поперечных сил, поэтому поперечная сила Q на данном участке не изменяется:

Эпюра на данном участке выглядит следующим образом:

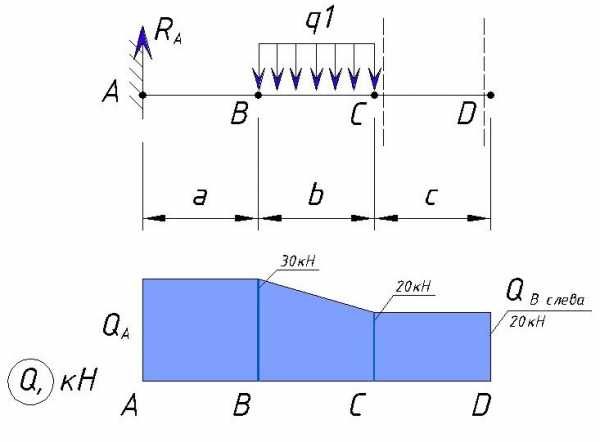
Далее рассмотрим участок с учетом сил, действующих в точке D

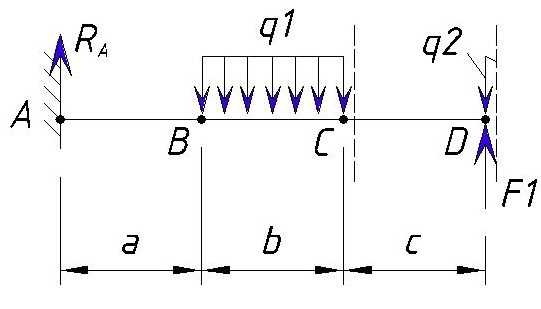
В точке D действует сосредоточенная сила F1 и начинает действовать переменная сила q2. Переменная сила q2 не влияет на поперечную силу в точке D т.к. она еще имеет нулевую длину приложения (правее этой точки она будет влиять, но это будет рассмотрено на участке DE). А сила F1 создает скачок поперечной нагрузки. Т.к. сила F1 стремится повернуть участок CD вокруг точки D по часовой стрелке сила F1 учитывается со знаком плюс (сила F1 вообще не может повернуть сечение вокруг точки D т.к. она приложена именно к этой точке, но тут точку вращения мы принимаем не много правее точки D т.к. это значение будет правее точки D).

Строим эпюру Q с учетом силы F1

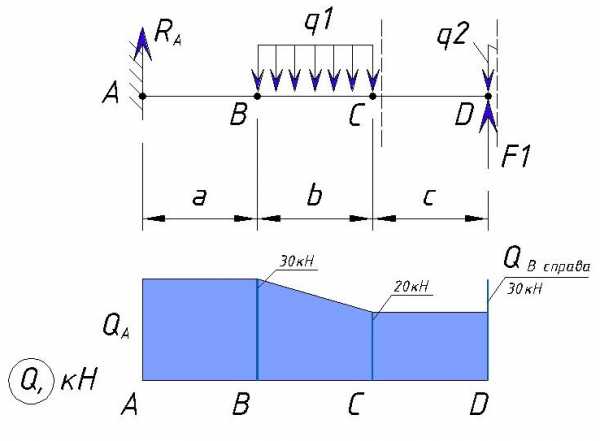
На эпюре мы видим скачок поперечной силы.

Определяем напряжения Q на участке DE.

Рассмотрим участок от точки D до точки E (слева)

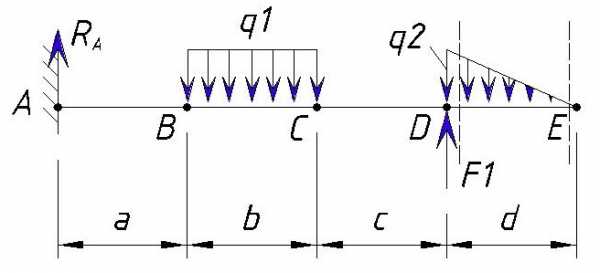
На участке от точки D до точки E приложена переменная нагрузка q2.

Определим значение Q в левее точки E. Сила q2 стремится повернуть сечение DE вокруг точки E против часовой стрелки, поэтому принимается со знаком минус. Значение поперечной силы в точке E слева равно:

Эпюра на этом участке будет выглядеть как изогнутая линия т.к. переменная нагрузка с увеличением длины уменьшает свое влияние на поперечную силу и сводится к нулю в конце участка

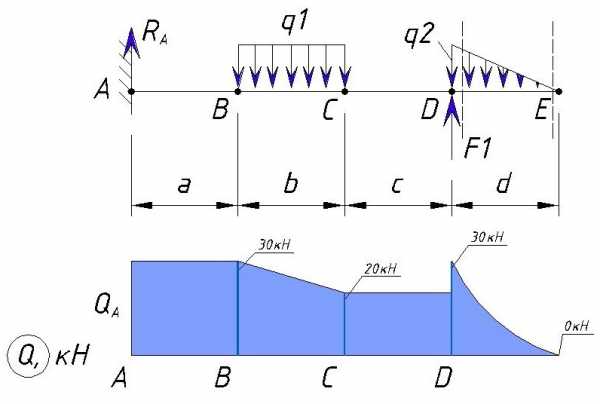
Далее рассматриваем участок DE с участком правее точки E

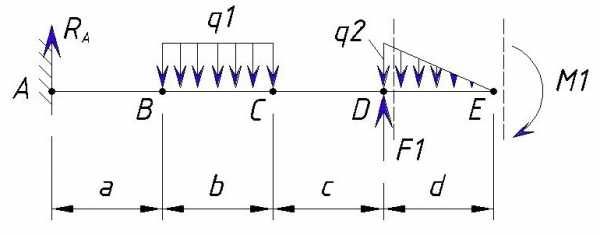
В точке E действует изгибающий момент M1, но он не влияет на поперечную силу, поэтому

Эпюра Q

В итоге эпюра поперечной силы Q для данного примера выглядит следующим образом:

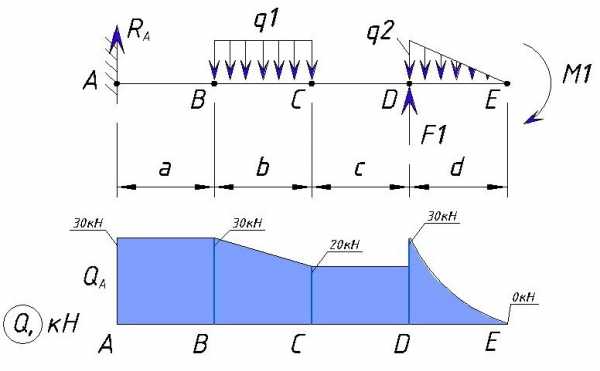
Как видим максимальная поперечная нагрузка, в данном примере, находится на участке от точки А до точки В, а также в точке D и равна Ra=30кН.

Вообще не во всех случаях обязательно рассматривать участок левее и правее заданной точки — только если в точке приложена сосредоточенная сила F эпюра Q осуществляет скачок, во всех остальных случаях Q(слева)=Q(справа). Я просто показал принцип построения эпюры.

В консольной балке напряжения Q в конце балки должны быть равны нулю. Конечно если на конце приложена сила F будет скачок напряжения, но Q(справа) будет равна нулю.

Построение эпюры M (изгибающий момент)

Для построения эпюры М мы используем те же контрольные точки и те же участки, что мы использовали при построении эпюры Q.

Последовательно передвигаясь от точки А к концу балки мы вычисляем значения моментов в контрольных точках и соединяем их в график который и будет указывать изгибающий момент в любой точке балки.

Изгибающий момент вычисляется произведением силы или центра приложения силы на плечо.

Для сосредоточенной силы мы умножаем значение нагрузки на расстояние до рассматриваемой точки. На графике эпюра M от действия сосредоточенной силы имеет прямую линию.

Чтобы определить изгибающий момент от действия равномерно-распределенной нагрузки определяем расстояние до середины рассматриваемого участка равномерно-распределенной нагрузки, умножаем на длину рассматриваемого участка и на величину нагрузки. На графике эпюра М от действия равномерно-распределенной нагрузки напоминает изогнутую линию, гиперболу.

Для переменной нагрузки изгибающий момент определяем следующим образом: определяется центр приложения нагрузки (длина приложения нагрузки делится в соотношении 1/3-2/3, центр приложения нагрузки находится ближе к максимальной нагрузке), определяем длину от этой точки до рассматриваемой, умножаем на длину приложения нагрузки, и умножаем на половину от приложенной нагрузки (q).На графике эпюра М от действия переменной нагрузки также как и для равномерно-распределенной напоминает изогнутую линию, но с большим изгибом.

Приложенный момент в точке просто суммируется с вычисляемым изгибающим моментом от других нагрузок. В точке где приложен момент эпюра совершает скачок. Значение момента не умножается на расстояние, а остается неизменным по всей длине.

Правило знаков для построения эпюры M

Тут есть 2-а метода: метод которым пользуются строители и метод, которым пользуются машиностроители.

У строителей изгибающий момент считается положительным, если внешняя нагрузка приводит к растяжению верхних волокон и график откладываем вверх. Если внешняя нагрузка приводит к растяжению нижних волокон, то изгибающий момент считается отрицательным и график откладывается вверх. Т.е. график всегда откладывается в сторону растянутых волокон.

У машиностроителей все наоборот — положительное значение откладывается в сторону сжатых волокон.

Ни в том, ни в другом случае ошибки нет, просто разные методы и итоговые значения будут одинаковыми, только знаки противоположными.

Не могу с уверенностью сказать почему у строителей изгибающий момент направлен в сторону растянутых волокон. Возможно из-за того, что при данном рассмотрении эпюра моментов во многих случаях повторяет изгиб балки.

Мы будем рассматривать метод, которым пользуются строители.

Определяем напряжение M на участке AB

Также как и при определении эпюры Q, эпюру М также строим по тем же участкам.

Значение изгибающего момента в точке равно значению опорного момента Ma, который мы вычислили ранее.

Также как и при построении эпюры Q мы рассматриваем участок с точкой левее точки B и правее этой точки, но если при построении эпюры Q мы не учитывали изгибающие моменты, то при построении эпюры изгибающих моментов мы должны учитывать и изгибающие моменты, и поперечные силы.

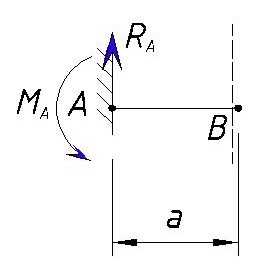
Изгибающий момент Ma стремится повернуть сечение вокруг точки B против часовой стрелки, а опорная реакция Ra по часовой стрелке. Теперь обратимся к правилу знаков. Изгибающий момент Ma стремится растянуть верхние волокна и сжать нижние, поэтому мы его учитываем со знаком плюс (читаем правило знаков для эпюры M). Опорная реакция Ra напротив стремится сжать верхние волокна и растянуть нижние, поэтому принимается со знаком минус. Напоминаю, что мы вращаем участок вокруг точки B, заделка в точке A заменена опорными реакциями Ra и Ma, т.е. если мы вместо заделки приложим эти силы, то система будет неподвижна.

Изгибающий момент в точке B слева будет равен:

На участке между точками A и B изгибающий момент изменяется прямолинейно т.к. на этом участке только реакция Ra изменяет значение, поэтому эпюра M на данном участке будет выглядеть так:

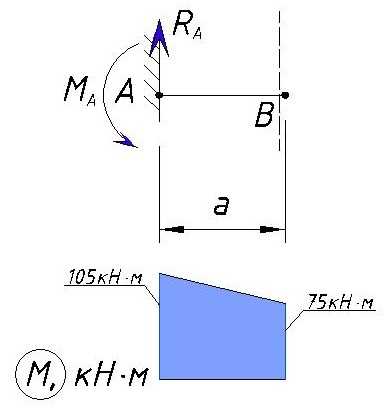
Теперь рассмотрим участок до точки B справа

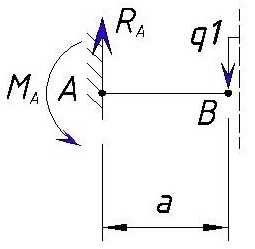
Тут добавляется равномерно распределенная нагрузка q1, но длина ее приложения еще равна нулю, поэтому она не влияет на изгибающий момент в точке B справа. Изгибающий момент справа от точки B буден равен значению слева от точки B.

Эпюра M выглядит следующим образом:

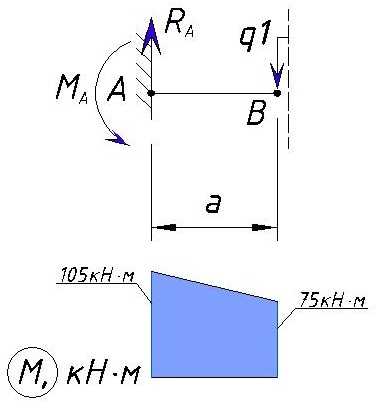
Определяем напряжение M на участке BС

Рассмотрим участок BC взяв участок без учета нагрузок в точке C (ну или как мы приняли левее точки C).

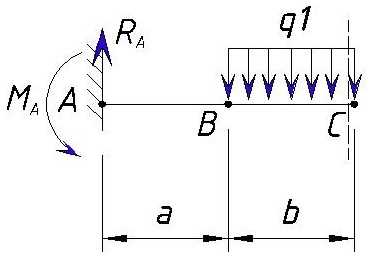
При вычислении изгибающего момента в точке C мы рассматриваем участок от точки A до С. Изгибающий момент в точке B вычисленный ранее является только значением в точке B и на точку C уже не влияет т.к. значение изгибающего момента изменяется в зависимости от плеча (расстояние от точки приложения нагрузки до рассматриваемой точки).

Изгибающий момент в точке С формируется из следующих составных:

1) Изгибающий момент Ma — опорная реакция в точке A. Значение изгибающего момента на изменяется от расстояния. Также как и для точки B значение изгибающего момента принимаем со знаком плюс т.к. он растягивает верхние волокна в точке C.

2) Опорная реакция Ra. Значение изгибающего момента в точке C напрямую зависит от плеча приложения нагрузки, поэтому в точке C опорная реакция Ra создает изгибающий момент в 2-а раза больше чем в точке B. Опорная реакция также сжимает верхние волокна, поэтому принимается со знаком минус.

3) Равномерно-распределенная нагрузка q1 создает изгибающий момент в точке C равный произведению этой нагрузки на длину ее приложения и на расстояние до центра ее приложения. По правилу знаков нагрузка q1 растягивает верхние волокна и принимается со знаком плюс.

Значение изгибающего момента в точки С слева равно:

На участке действия равномерно-распределенной нагрузки эпюра M имеет изогнутую форму. Изгиб направлен в сторону действия нагрузки. Эпюра на участке от A до C имеет следующий вид:

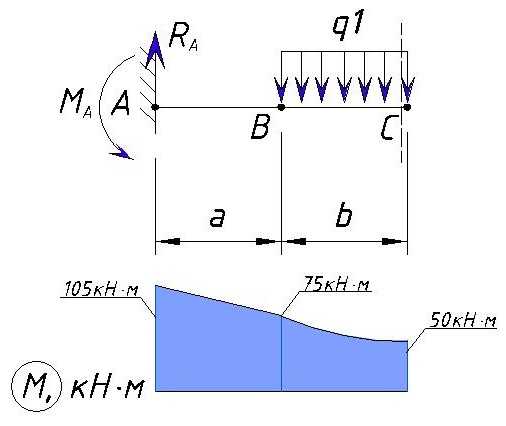
Теперь рассмотрим участок правее точки C

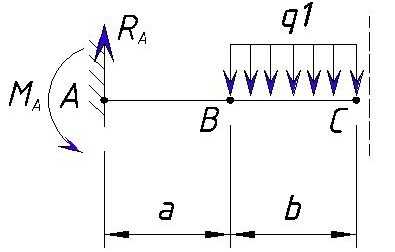
В принципе тут ничего не изменяется, новых нагрузок не появляется, расстояние (плечо) тоже остается тоже, поэтому эпюра с учетом этого участка выглядит также

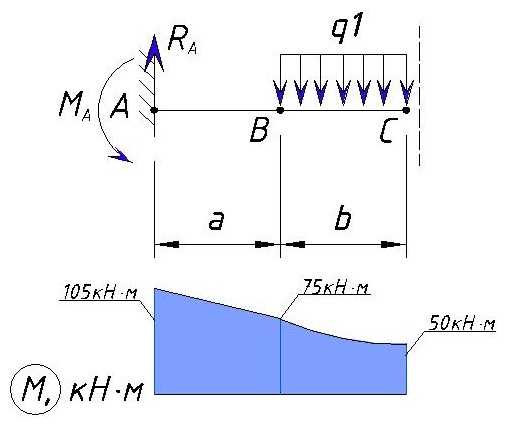
Определяем напряжение M на участке СD

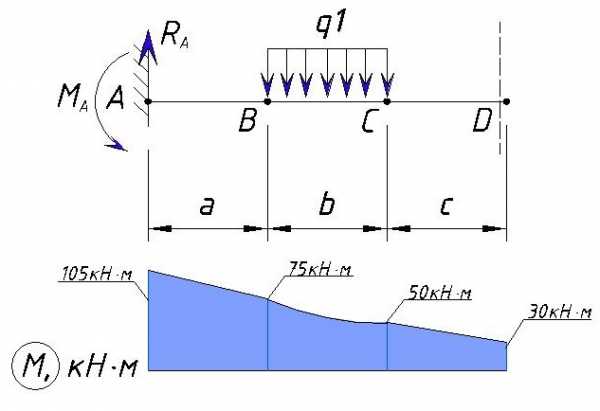
Также рассматриваем участок слева от точки D

Изгибающий момент в точке D формируется из следующих составных:

2) Опорная реакция Ra. Значение изгибающего момента в точке Dнапрямую зависит от плеча приложения нагрузки, поэтому в точке D опорная реакция Ra создает изгибающий момент в 3-и раза больше чем в точке B. Опорная реакция также сжимает верхние волокна, поэтому принимается со знаком минус.

3) Равномерно-распределенная нагрузка q1 создает изгибающий момент в точке D равный произведению этой нагрузки на длину ее приложения и на расстояние до центра ее приложения. По правилу знаков нагрузка q1 растягивает верхние волокна и принимается со знаком плюс.

Значение изгибающего момента в точки D слева равно:

На участке CD нет никаких нагрузок, поэтому изменение напряжения M прямолинейно

Рассмотрим точку D справа

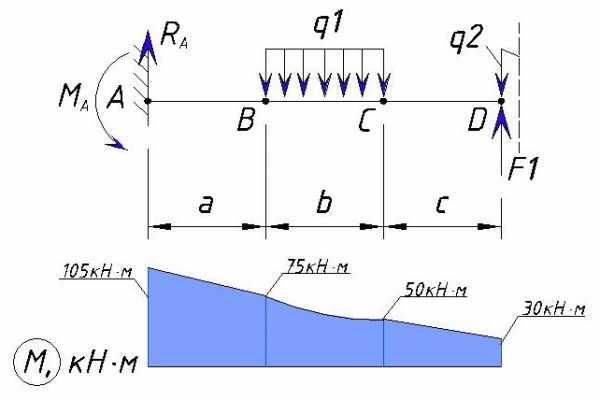
В точке D начинается приложение переменной нагрузки q2 и приложена сосредоточенная сила F1, но плечо приложения нагрузки еще равно нулю, поэтому значение изгибающего момента M в точке D справа не изменяется и равно значению слева от точки D.

Определяем напряжение M на участке DE

Рассматриваем участок слева от точки E

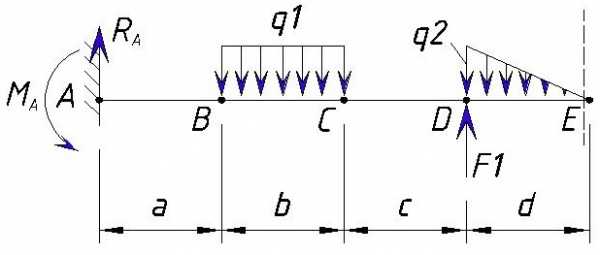
Изгибающий момент в точке E слева формируется из следующих составных:

2) Опорная реакция Ra. Значение изгибающего момента в точке E напрямую зависит от плеча приложения нагрузки, поэтому в точке E опорная реакция Ra создает изгибающий момент в 4-ре раза больше чем в точке B. Опорная реакция также сжимает верхние волокна, поэтому принимается со знаком минус.

3) Равномерно-распределенная нагрузка q1 создает изгибающий момент в точке E равный произведению этой нагрузки на длину ее приложения и на расстояние до центра ее приложения. По правилу знаков нагрузка q1 растягивает верхние волокна и принимается со знаком плюс.

4) Сосредоточенная сила F1 создает изгибающий момент, равный произведению силы на плечо. Т.к. действие силы стремится сжать верхние волокна (напоминаю мы рассматриваем действие силы вокруг точки E), то изгибающий момент принимаем со знаком минус.

5) Переменная нагрузка q2 создает изгибающий момент, равный произведению половины от максимальной силы, на длину приложения и на расстояние от центра сил (точка находится примерно 1/3 участка приложения сил ближе к максимальной нагрузке) до рассматриваемой точки

Значение изгибающего момента в точки E слева равно:

На участке DE изменение изгибающего момента не равномерно т.к. на этом участке имеется переменная нагрузка, эпюра имеет изогнутый вид

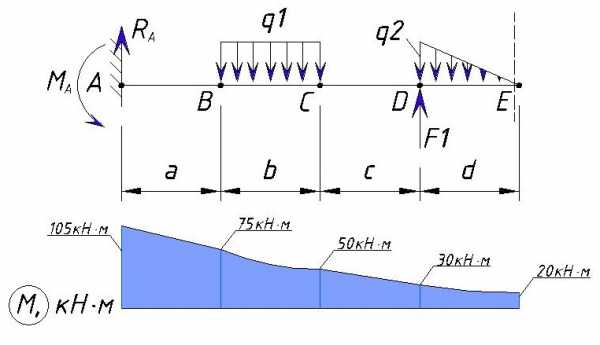
Теперь рассмотрим точку E с учетом приложенной к нему нагрузок (точка E справа)

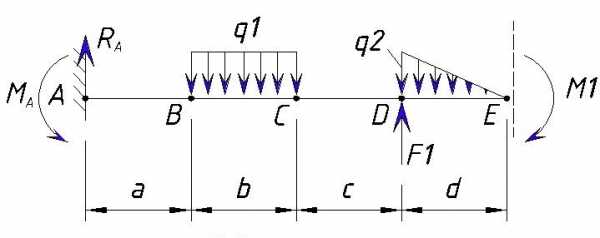
Тут добавляется момент M1. Действие изгибающего момента M1 стремится сжать верхние волокна поэтому мы принимаем его со знаком минус.

Значение изгибающего момента справа от точки E равно:

Действие изгибающего момента создает скачок в точке E. В итоге мы получаем такую эпюру изгибающих моментов для данного примера:

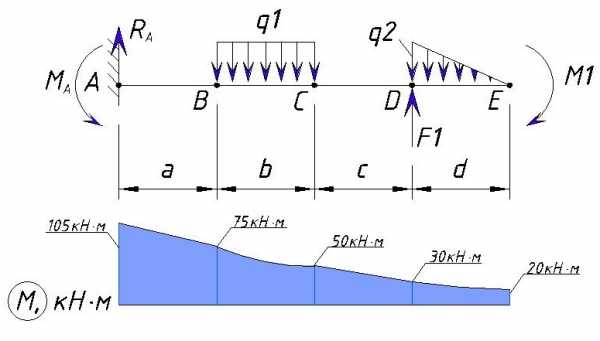
Значение изгибающего момента для консольной балки всегда равно нулю на свободном конце. Только если в конце балки приложен момент он будет отличатся на графике и будет равен значению этого момента, но изгибающий момент для E справа все равно будет равен нулю.

Также как и для эпюры Q не всегда обязательно рассматривать значения справа и слева от рассматриваемой точки. Только для точки в которой приложен изгибающий момент нужно рассматривать отдельно с учетом этого момента и без т.к. изгибающий момент создает скачок на эпюре моментов.

Эпюра Q и M

Покажем эпюры Q и M вместе чтобы увидеть где будут максимальные нагрузки

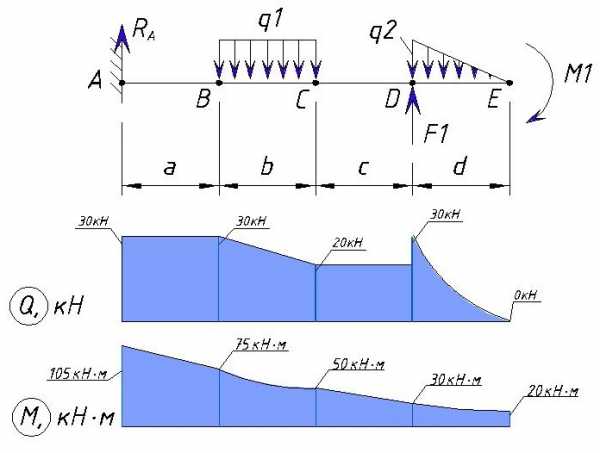
Надеюсь моя статья поможет в освоении азов сопротивления материалов.

Также ознакомитесь со статьей «Типовые эпюры консольной балки»

buildingbook.ru

Определение крутящих моментов и построение эпюры

Кручение стержня вызывается парами сил (сосредоточенными или распределенными), плоскость действия которых перпендикулярна продольной оси стержня. При кручении в поперечном сечении стержня возникает лишь один силовой фактор – крутящий момент M_к.

Согласно методу сечений величина и направление крутящего может быть найдены из уравнения равновесия моментов относительно оси стержня, составленного для оставленной части. То есть, крутящий момент в сечении численно равен алгебраической сумме моментов пар сил, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси стержня.

Правило знаков для крутящих моментов.

Крутящий момент считается положительным, если при взгляде на сечение со стороны внешней нормали он поворачивает сечение по ходу часовой стрелки и отрицательным — в противном случае.
При построение эпюры крутящих моментов положительные значения откладываются вверх от горизонтальной базовой линии, а отрицательные – вниз.

Это правило знаков условное и не совпадает с принятыми правилами знаков моментов, углов поворота в теоретической механике и математике, поскольку связано не с системой координат, а с видом деформации оставленной части.

Крутящий момент для сечения можно выразить так: $$M _к(x) = \sum M _{кi} + \sum \int m _i(x)\cdot dx$$

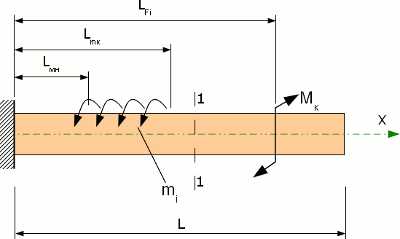
Распределенный крутящий момент m может быть постоянной или переменной интенсивности. Для постоянного распределенного момента m это выражение примет вид: $$M _к(x) = \sum M _{кi} + \sum m _i(x)\cdot (x- L_{mн}) — \sum m _i(x)\cdot (x- L_{mк})$$

где L_mн и L_mк – расстояние от начала координат до начала и до конца распределенного момента соответственно.

Дифференциальная зависимость внутренних усилий от распределенной нагрузки m:

dM_к = m·dx

Общий порядок расчета и построения эпюры.

Намечаем характерные сечения стержня.
Определяем крутящий момент в каждом характерном сечении.
По найденным значениям моментов строим эпюру.

Построение эпюр крутящих моментов (пример)

Построить эпюру крутящих моментов для жестко защемленного стержня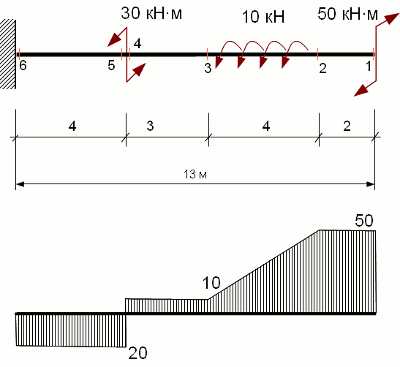

Пусть прямолинейный стержень нагружен внешними сосредоточенными крутящими моментами M_кв1=-30кН·м, M_кв2=50 кН·м, и распределенным моментом m₁=10кН. Реакции левой опоры можно не определять, т.к. в этом примере можно ограничиться рассмотрением лишь сил, приложенных к правым оставленным частям (справа от сечений).

1. Число характерных сечений — 6
Для заданного консольного стержня вычисления удобно вести, идя справа налево, начав их с 1–го сечения.

2. Проведем сечение 1. Определим крутящий момент в текущем сечении:

M_к1= M_кв2= 50 кНм

3. Проведем сечение 2. Отбросим левую часть, заменим ее действие крутящим моментом M_к2 и составим уравнение равновесия в моментах относительно оси бруса. Из уравнения равновесия получаем выражение для крутящего момента в сечении 2:

M_к2 = M_к1 = M_кв2 = 50 кНм

3. Проведем сечение 3, отбрасываем левую часть, составляем уравнение равновесия и получаем:

M_к3 = M_кв2 – m₁*4 = 50 – 10*4 = 10 кНм

4. Аналогично для сечения 4:

M_к4 = M_к3 = 10 кНм

5. Также для сечения 5:

M_к5= M_к4-M_кв1= 10 – 30 = -20 кНм

6. Для сечения 6:

M_к6= M_к5 =-20 кНм

7. По полученным значения строим эпюру крутящих моментов (см. рис.).

Скачок на левом конце эпюры дает величину опорного момента (реактивного момента в заделке) M_к6, так как реактивный момент – это внутреннее усилие, действующее в поперечном сечении, где соединены торец стержня и заделка.

Правила контроля правильности эпюр крутящих моментов

Для эпюр крутящих моментов характерны некоторые закономерности, знание которых позволяет оценить правильность построений.

Эпюры крутящих моментов всегда прямолинейные.
На участке, где нет распределенных моментов, эпюра M_к – прямая, параллельная оси; а на участке с распределенными моментами – наклонная прямая.
Под точкой приложения сосредоточенного момента на эпюре M_к будет скачок на величину этого момента.

Дополнительно

Еще один вариант построения эпюры крутящих моментов с использованием компьютера найдете на этой странице.

Пример из пособия МИИТ Построение эпюры крутящих моментов (формат pdf).

метки: внутренние усилия, кручение

sopromat.in.ua

Построение эпюры внутренних поперечных сил

Построим эпюру внутренних поперечных сил Q для консольной балки с заданной системой изгибающих нагрузок.

Покажем опорные реакции, которые были рассчитаны ранее и установим систему координат y-z так, чтобы ось z совпадала с продольной осью балки.

Для построения эпюр внутренних поперечных сил Q_y рассчитаем их значения на границах силовых участков.

Балка имеет 2 силовых участка (с.у.) — AB и BC.
Обозначим их на расчетной схеме римскими цифрами I и II соответственно.

Для расчета значений поперечных сил на каждом участке используем метод сечений.

Начнем с первого силового участка.
Проведем сечение в произвольном месте участка между точками A и B.
Это сечение условно делит балку на две части: левую и правую.
Можно рассмотреть любую из них, но лучше выбрать ту часть, к которой приложено меньше нагрузок.

Очевидно, это будет левая часть балки.

Расстояние от левой границы участка до сечения обозначим переменной z₁.
Возможные значения переменной z₁ находятся в пределах от 0 до 0,5м,
z₁=0 — если сечение переместить в точку A
z₁=0,5м — в точке B.

Отбросим на время правую часть балки.

Запишем имеющиеся данные:

I с.у. (AB) 0≤z₁≤0,5м

Поперечная сила в указанном сечении равна сумме всех вертикальных внешних сил, приложенных к рассматриваемой части балки.

К рассматриваемой левой части балки приложена только одна сила — опорная реакция R.

Поэтому сумма сил для первого участка будет состоять только из одного слагаемого R.

По правилу знаков, если сила стремится повернуть рассматриваемую часть балки относительно сечения по ходу часовой стрелки, она записывается положительной.

Q_yI=ΣF_i=R=60кН

В выражении отсутствует переменная z₁. Это указывает на то, что поперечная сила Q_yI одинакова для всех сечений I силового участка.

Переходим на второй силовой участок.

Так же начинаем с того, что проводим сечение в любом месте между точками B и C.
Здесь для рассмотрения лучше выбрать правую часть балки.

Обозначим переменной z₂ положение сечения относительно правой границы участка и мысленно отбросим левую часть балки.

II с.у. (BC) 0≤z₂≤1м

Q_yII=ΣF_i=q∙z₂-F=100z₂-40

Получено выражение, где имеется переменная Z₂.
Переменная имеет первую степень, поэтому ее графиком будет прямая.
Для её построения достаточно двух точек.

Этими точками будут значения Q_y на границах II силового участка, то есть при z₂=0 и при z₂=1м.

Рассчитаем их:

Q_yII(z₂=0)=100∙0-40=-40кН

Q_yII(z₂=1м)=100∙1-40=60кН

Теперь у нас есть все данные для построения эпюры Q_y.

Удлиним линии границ силовых участков, начертим базовую линию и укажем обозначение и размерность эпюры.
Обозначим полученные значения соответствующими точками на эпюре и соединим их.

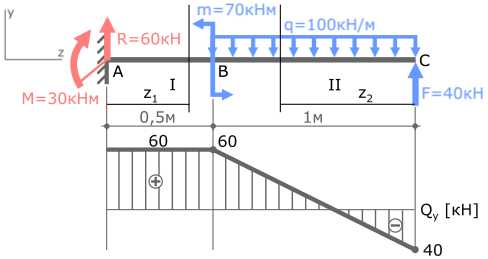
Эпюра Q_y для консольной балки построена. Ее желательно проверить.

Построение эпюры изгибающих моментов >
Другие примеры решения задач >

isopromat.ru

решение задач. Лекции. Изгиб. Определение напряжений. Построение эпюр изгибающих моментов и поперечных сил.

Меню сайта

Расчет геометрических характеристик сечений он-лайн ^NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.

Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн.
+ Полное расписанное решение!
Теперь и для статически неопределимых балок!

Расчет рам, ферм балок он-лайн ^NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы.

Лекции — теория, практика, задачи…

Примеры решения задач

Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое.

Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое).

Форум сопромата и механики

Книги — разная литература по теме.

Заказать задачу

Друзья сайта (ссылки)

WIKI^betta

Разработчикам (сотрудничество)

Веб-мастерам (партнёрка)

О проекте, контакты

Подпроекты

Базовый курс лекций по сопромату, теория, практика, задачи.

::Оглавление::

3. Изгиб. Определение напряжений.

3.5. Построение эпюр изгибающих моментов и поперечных сил.

Рассмотрим пример построения эпюр поперечных сил Q и изгибающих моментов M_x.

1. Изображаем расчетную схему (рис. 3.9, а).

2. Определяем реакции опор. Первоначально выбираем произвольное направление реакций (рис. 3.9, а)

Так как реакция R_B с минусом, изменяем выбранное направление на противоположное (рис. 3.9, б), а про минус забываем.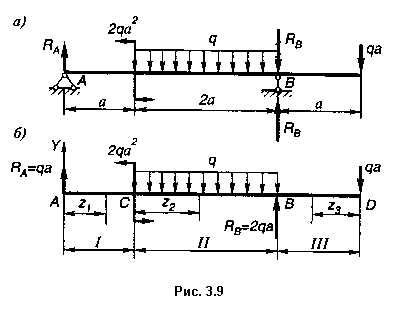

Проверка:

Y = 0,
R_A — 2qa + R_B — qa = qa — 2qa + 2qa — qa = 0.

3. Расчетная схема имеет три силовых участка.

I участок АС: 0 1 В сечении возникают внутренние усилия:

поперечная сила

Q = qa = const

и изгибающий момент

M_x = qa * z₁
при z₁ = 0 M_x = 0; при z₁ = a M_x = qa².

II участок CB: 0 2 На этом участке

при z₂ = 0 Q = qa, M_x = -qa²;

при z₂ = 2 Q = -qa, M_x = qa².

На 2-м участке в уравнении моментов аргумент z₂ имеет 2-ю степень, значит эпюра будет кривой второго порядка, т.е. параболой. На этом участке поперечная сила меняет знак (в начале участка +qa, а в конце -qa), значет на эпюре M_x будет экстремум в точке, Q = 0. Определяем координату сечения, в котором экстремальное значение M_x, приравнивая нулю выражение поперечной силы на этом участке.

Определяем величину экстремального момента (с учетом знака):

III учаток BD: 0 3

Здесь Q = qa = const; M_x = -qa*z₃; при z₃ = 0 M_x = 0; при z₃ = a M_x = -qa².

4. Строим эпюры Q и M_x (рис. 3.13, б и в).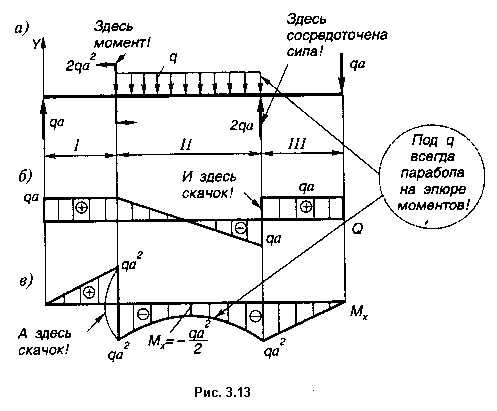

5. Проверка построения.

::Оглавление::

Примеры

Пример 1. Расчет статически определимой балки, подбор сечения.

Полезные ресурсы по теме «Изгиб»

1. Он-лайн программа (версия 2004 года), которая выдаст расписанное решение любой балки. Пример результата.
Кроме построения эпюр эта программа так же подбирает профиль сечения по условию прочности на изгиб, считает прогибы и углы поворота в балке.

2. Он-лайн программа (версия 2008 года), которая строит 4 вида эпюр и рассчитывает реакции для любых балок (даже для статически неопределимых).

Сообщество

Вход

Решение задач

Расчет редукторов

Для Android (рекомендую)

NEW Mobile Beam 2.0
Программа для расчета балок на прочность на Вашем Android устройстве…