1. 6 Понятие о деформациях и перемещения

Растяжение или сжатием стержня вызывается силами, действующими,

вдоль его оси. В этом случае в поперечных сечениях из шести внутренних си-

ловых факторов возникает только один — продольная сила N.

Рассмотрим случай осевого (центрального) растяжения или сжатия, когда внешние силы действуют по оси стержня(рисунок 2.1). Для определения внут-

ренних усилий (продольных сил) применим метод сечений. Проведем какое-

нибудь сечение, например а—а, и рассмотрим равновесие нижней отсеченной части. Воздействие верхней отброшенной части на нижнюю заменим продоль-

ной силой и предварительно направим ее от сечения, т. е. предположим, что си-

ла является растягивающей. Составим уравнение равновесия. Проецируя все силы, действующие на нижнюю часть, на направление параллельное оси стержня, и приравнивая сумму проекций нулю, получаем

N1+8F-5F=0,откуда N1 = — 3F.

Знак минус показывает, что направление силы N1 следует изменить на об-

ратное, т. е. продольная сила будет в данном случае не растягивающей, как мы предположили, а сжимающей. Аналогично найдем продольную силу в сечении b—b:N2=5P (растяжение). Условимся продольную силу, соответствующую рас-

тяжению считать положительной. Наглядное представление о законе изменения продольных сил по длине стержня дает график(эпюра продольных сил), ось абсцисс которого проводится параллельно оси стержня, а ось ординат ей пер-

пендикулярна. По оси ординат в выбранном масштабе откладывают значения продольных сил (с учетом знаков) в поперечных сечениях стержня(рисунок

2.1).

Если на поверхность призматического стержня нанести сетку линий, па-

раллельных и перпендикулярных оси стержня(рисунок 2.2, а), и приложить к нему растягивающую силу, то можно убедиться в том, что линии сетки и после деформации останутся взаимно перпендикулярными, за исключением неболь-

шого участка стержня вблизи точки приложения силы, который из рассмотре-

ния пока исключаем, но расстояния между ними изменятся (рисунок 2.2, б). Все горизонтальные линии, напримерcd, переместятся вниз, оставаясь горизон-

studfiles.net

Сопромат.in.ua: Деформация

Перемещение — изменение положения точки тела в пространстве вследствие изменения его формы и размеров под действием нагрузки. Полное перемещение точки в пространстве раскладывается на компоненты u, v и w, параллельные осям x, y и z, соответственно.

Деформация — изменение формы и размеров тела.

Перемещения рассматриваемой точки зависит от деформации всех нагруженных областей тела и включают также в себя перемещения как жесткого целого ненагруженных областей. Поэтому перемещения не могут характеризовать степень деформирования в окрестности рассматриваемой точки. Для этого используют понятие деформации. В отдельных случаях их величины могут совпадать (растяжение стержня), но в общем случае — это разные вещи.

Остановимся еще на одном важном моменте. Очень часто путают два понятия — «деформация» и «перемещение» — хотя ясно, что они не адекватны. Например, представим себе канат, прикрепленный к потолку. По канату на некоторую высоту поднялся человек. Очевидно, что под действием веса человека (пренебрегая весом каната) деформируется (растягивается) только верхняя часть каната, заключенная между потолком и местом, где находится человек. Нижняя часть каната не деформируется, а перемещается как твердое тело. Следовательно, не всегда перемещения сечений какого-то участка стержня непосредственно связаны с его деформацией.

Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. 3-е изд. — М.: Высшая школа, 2003.

Деформации могут быть угловые и линейные.

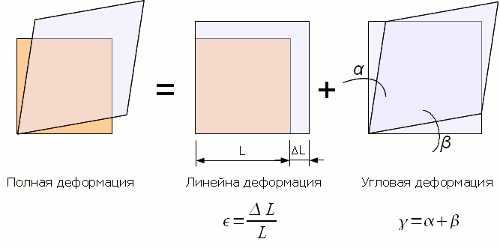
Линейная деформация характеризует изменение размеров тела. Различают

абсолютную деформацию ΔL и относительную деформацию ε = ΔL/L.

Угловая деформация характеризует изменение формы тела и чаще всего называется углом сдвига.

Угол сдвига — это изменение первоначально прямого угла. γ = α + β .

Полная деформация — это сумма линейной и угловой деформации.

Если взять малый элемент тела параллелепипед, ориентированный по осям x, y, z, то соответственно возникает три линейных деформации (вдоль осей x, y, z ) ε_x,ε_y, ε_z
$$\epsilon _x = {Δdx\over dx}, \quad \epsilon _y = {Δdy\over dy},\quad \epsilon _z = {Δdz\over dz} $$
и три угловые деформации [math]\gamma _{xy}, \gamma _{yz}, \gamma _{zx}[/math] в трех взаимно-перпендикулярных плоскостях.

Относительные линейные и угловые деформации – величины безразмерные.

Деформации упругие и пластические

Деформации делятся на упругие и пластические (остаточные).

• Упругими деформациями называются деформации, исчезающие после снятия вызвавших их сил.
• Пластичными деформациями называются деформации, не исчезающие после снятия вызвавших их сил.

Типы деформаций

В зависимости от приложенных к телу нагрузок различают несколько видов деформации, отличающиеся законом распределения напряжений по сечению тела.

Растяжение-сжатие

в поперечном сечении действует только одно внутреннее усилие, не равное нулю — продольное усилие. Конструкция В этом случае говорят о линейной деформации конструкции (характеризуется абсолютным и относительным удлинением, остальными деформациями пренебрегают).

Чистый сдвиг

в поперечном сечении действует только поперечная сила. В этом случае линейные относительные деформации равны нулю, углы сдвига не равны нулю (характеризуется изменением формы)

Кручение

в поперечном сечении действует только крутящий момент. Линейные относительные деформации равны нулю, углы сдвига не равны нулю.

Изгиб

в поперечном сечении действуют изгибающий момент и поперечная сила.

Сложное сопротивление

одновременное действие нескольких типов простых деформаций — растяжения-сжатия, кручения, изгиба.

Для каждого из указанных видов деформации существуют свои формулы для расчета на прочность.

Ссылки по теме

---

метки: деформация

sopromat.in.ua

3.1. Деформации, перемещения

Деформацией тела называется изменение его формы или разме­ров, или того и другого одновременно, без изменения мас­сы тела.

Деформация тела обычно связана с изменением взаимного по­ло­­же­ния отдельных его точек (рис. 3.1). При этом линия, соединяю­щая две точ­ки тела, называется линейным элементом данного нап­ра­в­­ления (ab— в нап­равлении осиоxиac— в направлении осиоy, рис. 3.1).

Изменение длины линейного элемента называется абсолютной ли­­­нейной деформацией или абсолютным удлинением по данному на­п­­рав­лению.

Отношение изменения длины бесконечно малого линейного эле­мен­та к первоначальной его длиненазывается относитель­ной линей­ной деформацией в точке по данному направлению.­

Рис. 3.1

Изменение прямого угла между двумя бесконечно малыми ли­ней­ными элементами, выходящими из одной точки, называется уг­лом сдвига в этой точке в плоскости линейных элементов.

Линейные и угловые деформации — величины безразмерные.

Изменение положения точки тела (изменение ее координат) в ре­зу­ль­та­те действия внешних сил называется линейным перемещением.

Вектор, проведенный из начального положения точки до дефор­ма­ции тела в конечное ее положение после деформации, называется пол­ным ли­ней­­ным перемещением этой точки. Проекция полного линейного пе­­ре­мещения точки на какое-либо направление называется ли­ней­ным перемещением точки по данному направлению.

Угол, составленный направ­ле­ни­­ем линейного элемента тела после деформации с его первоначальным направлением, на­зы­ва­ется угловым перемещением.

Приняты следующие обозначения для линейных и угловых де­фор­ма­ций:

— относительные линейные деформации по оси x-, по осиy — , по осиz-;

— угловые деформации (сдвиги) в плоскости xoy-, в плос­ко­с­тиyoz-, в плоскостиzox-.

Совокупность линейных деформаций по различным направ­ле­ни­ям и угловых деформацийпо различным плоскостям, прохо­дя­щим че­рез рассматриваемую точку, представляет собой деформи­ро­­ванное сос­­то­я­ние в точке.

Компоненты перемещений некоторой точки а, имею­щей до де­фор­­­ма­ции координатыx,y,z, обозначим черезu — по осиx, v — по осиy, w — по осиz. Эти компоненты линейного переме­ще­ния точки яв­ля­ются функ­ция­ми координат точкиа.

Перемещение соседней точки b, координаты которой отличают­ся от координат точкиaприращениямиdx,dy,dz, получим, разложив пе­ре­ме­ще­­­­ния в ряд Тейлора и ограничившись бесконечно малыми пер­во­го по­ря­д­­­ка:

,

,

.

3.2. Зависимости между деформациями и перемещениями. Формулы Коши

Бесконечно малый параллелепипед dxdydz, вырезанный из уп­ру­­гого тела около произвольной точки

а, вследствие различия пе­ре­ме­щений его то­чек деформируется, т. е. изменяется длина его ребер и ис­кажаются пер­во­­начально прямые углы между гранями (рис. 3.2).

Рис. 3.2

Длина ребра abравнаdx, ребраac — dy. После де­фор­ми­ро­ва­ния точ­киa, bиc займут новые положения -и. При этом точкаапо­лу­чит пе­­ремещение, составляющие которого в плоскости чертежаuиv. Точкаb, отстоящая от точкиана бесконечно малом расстоянииdx, по­лу­чит пе­ре­ме­щение, составляющие которого будут отличаться от сос­­тав­ля­ю­щих пе­ре­мещения точкиaна бесконечно ма­лую величину за счет измене­ния ко­ор­динатыx:

.

Составляющие перемещения точки с будут отличаться от сос­та­в­­­ля­ю­щих перемещения точки a на бесконечно малую величину за счет из­мене­ния координаты

y:

.

Проекция абсолютного удлинения ребра abна осьxпосле де­фор­ма­ции равна:

.

Относительное удлинение вдоль оси x, или, по другому, линей­ную де­формацию по направлению осиxзапишем как

.

Аналогично получим линейные деформации по направлениям ко­­ор­динатных осей yиz:

,.

Итак, линейная деформация по любому направлению равна ча­с­т­­­­ной производной составляющей перемещения в этом направ­ле­нии по пере­мен­­­ной в том же направлении.

Рассмотрим теперь изменения углов между ребрами парал­ле­ле­пи­пе­да:

.

Пренебрегая линейной деформацией по сравнению с едини­цей, по­­­­лучими, по аналогии,.

Ограничиваясь рассмотрением только малых деформаций, мож­но по­­лагать , тогда,.

Угол сдвига в плоскости xoy, т. е. искажение прямого углаbac, на­зы­вается угловой деформацией и определяется как сумма углов по­во­рота ре-

бер abиac:.

Аналогично найдем угловые деформации в двух других коорди­нат­ных плоскостях:

,.

Итак, угловая деформация в любой плоскости равна сумме ча­ст­­­ных производных составляющих перемещения в этой плоскости по пе­ре­мен­ным в перпендикулярных направлениях.

Суммируя все вышеизложенное, можно записать шесть основ­ных за­ви­си­мостей составляющих линейных и угловых деформаций от состав­ля­ющих перемещения:

,

(3.1)

,

.

Эти уравнения были получены О. Коши (1823 г.) и носят его имя.

В пределе, когда длина ребер параллелепипеда стремится к нулю, фор­­­му­лы (3.1) определяют линейные и угловые деформации в точке a.

Правило знаков для составляющих деформации:

1. Положительным линейным деформациям отвечают удлине­ния по соответствующим направлениям, а отрицательным — укороче­ния.

2. Положительным угловым деформациям соответствует умень­ше­­ние углов между положительными направлениями координатных осей, а от­ри­цательным — увеличение тех же углов.

studfiles.net

Деформации в сопромате

Реальные тела могут деформироваться, т. е. изменять свою форму и размеры. Деформации тел происходят вследствие нагружения их внешними силами или изменения температуры. При деформации тела его точки, а также мысленно проведенные линии или сечения перемещаются в плоскости или в пространстве относительно своего исходного положения.

При нагружении твердого тела в нем возникают внутренние силы взаимодействия частиц, оказывающие противодействие внешним силам и стремящиеся вернуть частицы тела в положение, которое они занимали до деформации.

 

При решении задач сопромата различают упругие деформации, исчезающие после прекращения действия вызвавших их сил, и пластические, или остаточные, деформации, не исчезающие после снятия нагрузок. В большинстве случаев для величин деформаций элементов конструкций устанавливают определенные ограничения.

 

 

В сопротивлении материалов изучаются следующие основные виды деформирования стержней или виды их деформаций: растяжение и сжатие, сдвиг (или срез), кручение, изгиб. Рассматриваются также более сложные деформации, получающиеся в результате сочетания нескольких основных видов деформаций.

 

Растяжение или сжатие возникает, например, в случае, когда к стержню вдоль его оси приложены противоположно направленные силы (рис. 3). При этом происходит поступательное перемещение сечений вдоль оси стержня, который при растяжении удлиняется, а при сжатии укорачивается. Изменение первоначальной длины стержня L называется абсолютным удлинением (при растяжении) или абсолютным укорочением (при сжатии).

 Отношение абсолютного удлинения (укорочения) к первоначальной длине L стержня или его участка называется средним относительным удлинением (укорочением) на длине L или средней линейной относительной деформацией стержня или его участка:

Истинное линейное относительное удлинение, или относительная линейная деформация в точке, определяется как относительная деформация участка при L→0:

На растяжение или сжатие работают многие элементы конструкций: стержни ферм, колонны, штоки поршневых машин, стяжные болты и др.

Сдвиг, или срез, возникает, когда внешние силы смешают два параллельных плоских сечения стержня одно относительно другого при неизменном расстоянии между ними (рис. 4). Величина смещения dS называется абсолютным сдвигом. Отношение абсолютного сдвига к расстоянию между смещающимися плоскостями (тангенс угла у) называется относительным сдвигом. Вследствие малости угла у можно принять

Относительный сдвиг является угловой деформацией, характеризующей перекос элемента.

На сдвиг, или срез, работают, например, заклепки и болты, скрепляющие элементы, которые внешние силы стремятся сдвинуть друг относительно друга.

 

Кручение возникает при действии на стержень внешних сил, образующих момент относительно его оси (рис. 5). Деформация кручения сопровождается поворотом поперечных сечений стержня друг относительно друга вокруг его оси. Угол поворота одного сечения стержня относительно другого, находящегося на расстоянии L, называется углом закручивания на длине L. Отношение угла закручивания ф к длине L называется относительным углом закручивания.

На кручение работают валы, шпиндели токарных и сверлильных станков и другие детали.

 

Изгиб (рис. 6) заключается в искривлении оси прямого стержня или в изменении кривизны кривого стержня. Происходящее при изгибе перемещение какой-либо точки оси стержня выражается вектором, начало которого совмещено с первоначальным положением точки, а конец — с положением той же точки в деформированном стержне, В прямых стержнях перемещения точек, направленные перпендикулярно к начальному положению оси, называются прогибами. Обозначим прогибы буквой w, а наибольший из них — буквой f. При изгибе также происходит поворот сечений стержня вокруг осей, лежащих в плоскостях сечений. Углы поворота сечений относительно своих начальных положений обозначим буквой ф.

 На изгиб работают балки междуэтажных перекрытий, мостов, оси железнодорожных вагонов, листовые рессоры, валы, зубья шестерен, спицы колес, рычаги и многие другие детали.

 

Описанные выше простейшие деформации стержня дают представление об изменении его формы и размеров в целом, но ничего не говорят о степени и характере деформированного состояния материала. Исследования показывают, что деформированное состояние тела является неравномерным и изменяется от точки к точке. При этом деформированное состояние в точке тела полностью определяется шестью компонентами деформации: тремя относительными линейными деформациями и тремя относительными угловыми деформациями.

funnystudy.ru

Напряжения. Перемещения и деформации.

   Как отмечалось выше, внутренние силы, действующие в некотором сечении со стороны отброшенной части тела, можно привести к главному вектору и главному моменту. Зафиксируем точку М в рассматриваемом сечении с единичным вектором нормали n. В окрестности этой точки выделим малую площадку F. Главный вектор внутренних сил, действующих на этой площадке, обозначим через P (рис. 1 а). При уменьшении размеров площадки соответственно

Рис.1. Композиция вектора напряжения. а) вектор полного напряжения б) вектор нормального и касательного напряжений

 

уменьшаются главный вектор и главный момент внутренних сил, причем главный момент уменьшается в большей степени. В пределе при получим

   Аналогичный предел для главного момента равен нулю. Введенный таким образом вектор р_n называется вектором напряжений в точке. Этот вектор зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки F, характеризуемой вектором п. Совокупность всех векторов напряжений в точке М для всевозможных направлений вектора п определяет напряженное состояние в этой точке.

   В общем случае направление вектора напряжений р_n не совпадает с направлением вектора нормали п. Проекция вектора р_n на направление вектора п называется нормальным напряжением , а проекция на плоскость, проходящую через точку М и ортогональную вектору n, — касательным напряжением (рис. 1 б).

Размерность напряжений равна отношению размерности силы к размерности площади. В международной системе единиц СИ напряжения измеряются в паскалях: 1 Па=1 Н/м².

   При действии внешних сил наряду с возникновением напряжений происходит изменение объема тела и его формы, т. е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела.

   Отнесем недеформированное тело к декартовой системекоординат Oxyz (рис. 2). Положение некоторой точки М в этой системе координат определяется радиус-вектором r(х, у, z). В деформированном состоянии точка М займет новое положение М^/ , характеризуемое радиус-вектором r‘ (х, у, z). Вектор u=r’—r называется вектором, перемещений точки М. Проекции вектора u на координатные оси определяют компоненты вектора перемещений и(х, у, z), v(х, у, z), w(х, у, z), равные разности декартовых координат точки тела после и до деформации.

   Перемещение, при котором взаимное расположение точек тела не меняется, не сопровождается деформациями. В этом случае говорят, что тело перемещается как жесткое целое (линейное перемещение в пространстве или поворот относительно некоторой точки). С другой стороны, деформация, связанная с изменением формы тела и его объема, невозможна без перемещения его точек.

Рис.2. Композиция вектора перемещения

 

   Деформации тела характеризуются изменением взаимного расположения точек тела до и после деформации. Рассмотрим, например, точку М и близкую к ней точку N, расстояние между которыми в недеформированном состоянии вдоль направления вектора s обозначим через (рис. 2). В деформированном состоянии точкиМ и N переместятся в новое положение (точки М’ и N’), расстояние между которыми обозначим через s’. Предел отношения

называется относительной линейной деформацией в точке М в направлении вектора s, рис.3. Рассматривая три взаимно перпендикулярных направления, например, вдоль координатных осей Ох, Оу и Oz, получим три компоненты относительных линейных деформаций характеризующих изменение объема тела в процессе деформации.

Для описания деформаций, связанных с изменением формы тела, рассмотрим точку М и две близкие к ней точки N и Р, расположенные в недеформированном состоянии в направлении двух взаимно ортогональных векторов s₁ и s₂. Расстояния между точками обозначим через и(рис. 4). В деформированном состоянии положение точек обозначим черезМ’, N’ и Р’. Угол между отрезками M’N’ и М’Р’ в общем случае будет отличным от прямого. При , изменение угламежду двумя ортогональными до деформации направлениями называетсяугловой деформацией. Как видно из рис. 4, угловая деформация складывается из двух углов и, связанных с поворотами отрезковM’N’ и М’Р’ ‘в.плоскости, образованной векторами s₁ и s₂, относительно этих векторов. Если заданы три взаимно ортогональных вектора, направленных вдоль координатных осей, то имеются три угловые деформации ,и, которые вместе с тремя линейными деформациями ,иполностью определяют деформированное состояние в точке.

Рис.3. Композиция линейной деформации

 

Рис. 4. Композиция угловой деформации

Определим упругие деформации стержня предполагая, что изменение его длины при растяжении , называемоеабсолютной продольной деформацией или удлинением, мало по сравнению с его первоначальной длиной . Тогда относительная продольная деформация будет равна

   Учитывая, что согласно закону Гука для одноосного растяжения (сжатия)

,

где Е—;модуль продольной упругости материала стержня, а нормальные напряжения определяются по формуле — (в нашем случае N_z=P), для абсолютной деформации получаем

(2)

   Произведение EF принято называть жесткостью поперечного сечения стержня при растяжении (сжатии), так как удлинение обратно пропорционально EF.

Рис.6. Модели продольной и поперечной деформаций

 

   Как показывают эксперименты, при растяжении стержня размеры его поперечного сечения уменьшаются (рис. 6), а при сжатии — увеличиваются. Это явление получило название эффекта Пуассона.

   По аналогии с продольной деформацией изменение размеров поперечного сечения (на рис. 6) будем называтьабсолютной поперечной деформацией, а — относительной поперечной деформацией. Относительные продольная и поперечная деформации, имеющие противоположные знаки, связаны между собой коэффициентом , являющимся константой материала и называемым коэффициентом поперечной деформации иликоэффициентом Пуассона:

Как известно, для изотропного материала .

   Формула (2) для удлинения стержня применима только в случае, когда по длине стержня ни жесткость поперечного сечения, ни продольная сила не изменяются (EF=const, N_z =const). Удлинение стержня со ступенчатым изменением EF и N_z (рис. 7) может быть определено как сумма удлинений ступеней, у которых EF и N_z постоянны:

(индекс k у модуля продольной упругости означает, что участки стержня могут быть изготовлены из различных материалов). В случае, когда N_z и EF меняются по длине стержня l непрерывно и их можно считать постоянными лишь в пределах ступеней длиной dz, обобщая формулу эту, получаем

   В качестве тестов для практики расчетов определенных интегралов рекомендую воспользоваться системой входных тестов Т-5, указанных в ПРИЛОЖЕНИИ.

Рис.7. Ступенчатый брус

 

   С упругими продольными деформациями стержня при растяжении (сжатии) связаны продольные перемещения его сечений. На рис. 8 приведены три случая определения таких перемещений, откуда видно, что перемещения поперечных сечений численно равны удлинениям заштрихованных частей стержня:

• перемещение свободного торцевого сечения 1—1 при неподвижном другом торцевом сечении (рис. 8, а) численно равно удлинению стержня;

• перемещение промежуточного сечения 2—2 (рис. 8, б) численно равно удлинению части стержня, заключенной между данным сечением и сечением неподвижным;

• взаимное перемещение сечений 3—3 и 4—4 (рис, 8, в) численно равно удлинению части стержня, заключенной между этими сечениями.

Рис.8. Модели перемещений

studfiles.net

Напряжение.

Мерой внутренних сил, величиной характеризующей интенсивность их распределения является напряжение.

Рассмотрим тело, находящееся под действием системы уравновешенных сил.

Будем исследовать внутренние силы в малой области, окружающей точку А. Проведем через данную точку сечение некоторой поверхностью. Внешняя нормаль этой поверхности в точке А — Отбросим часть, лежащую по правую сторону от сечения и заменим ее действие на оставшуюся часть внутренними силами. Выделим в окрестности точки А площадку. Результирующая внутренних сил, действующих на площадкепусть равняется.

Делим результирующую силу на, получаем величину среднего напряжения по площадке. Величиназависит от размеров площадки, перейдем к пределу, стягивая площадку к точке

Величина — называется вектором полного напряжения в данной точке по площадке с внешней нормалью.

Очевидно, что, выбирая другим образом ориентированную площадку, проходящую через данную точку, мы получаем другое значение вектора напряжения.

Совокупность всех векторов полного напряжения по площадкам, проходящим через данную точку, составляет напряженное состояние в данной точке.

Величину обычно раскладывают на две составляющие: нормальное напряжение, направленное по внешней нормали к площадке и касательное напряжение, лежащее в плоскости площадки.

Перемещения и деформации.

Рассмотрим тело, имеющее такое количество связей, что движение его как жесткого тела исключено. Перемещения точек тела обусловлены деформативностью материала.

Пусть под действием сил тело деформировалось, и точка перешла в новое положение. Тогда векторназывается вектором перемещения, а его проекции на координатные оси обозначены соответственно

Зададим в точке некоторое направлениеи пусть длина отрезкаВ деформированном состоянии длина отрезка изменилась и стала равнойТогда величину

называют линейной деформацией в данной точке по направлению АВ. Пусть угол между отрезками ЕС и ЕD – прямой.

После деформации тела величина угла изменится.

Величина называется угловой деформацией или углом сдвига.

Уже сейчас отметим, что между напряжениями и деформациями существует связь, и эта связь принципиально может быть установлена только экспериментальным путем.

Принципы сопротивления материалов.

Таких принципов (основных правил) три.

1. Принцип неизменности начальных размеров.

Будем считать, что перемещения, возникающие в системах, малы по сравнению с их размерами.

Так, например, определяя изгибающий момент в балке, мы не учитываем того обстоятельства, что в результате изгиба балки плечо у силы изменится.

2. Принцип независимости действия сил.

Если на систему действуют несколько сил, то напряжения (перемещения, деформации, внутренние силовые факторы), возникающие от совместного действия этих сил, можно определить следующим образом: определить от действия каждой из сил порознь и результаты сложить.

Справедливость этого принципа вытекает из принятия изложенного выше принципа неизменности начальных размеров и допущения, что между напряжениями и деформациями существует связь, определяемая простейшим законом – законом линейной упругости (закон Гука). В этом случае поведение наших конструкций будет описываться математически линейными системами, с этой точки зрения принцип независимости действия сил есть не что иное, как хорошо знакомый принцип суперпозиции.

3. Принцип Сен-Венана.

Способ приложения нагрузки не сказывается в точках, достаточно удаленных от места приложения нагрузки. Например, две совершенно одинаковых консольных балки нагружены одной и той же по величине силой , но в первом случае эта сила есть давление опирающейся на данную балку другой балки, а во втором случае к балке через проушину подвешен груз. Ясно, что характер распределения напряжений в месте нагружения здесь будет совершенно различным, но в сечениях достаточно удаленных от места приложения, нагрузки индивидуальные особенности передачи нагрузки сказываться не будут.

Принцип Сен-Венана дает возможность заменять действующие силы системами статически эквивалентными. Это позволяет схематизировать силы, действующие на конструкцию.

В частности, системы статически эквивалентные нулю вызывают напряжения лишь в локальной области. Например, полоса сжата клещами. В этом случае возникают только местные напряжения.

Принцип Сен-Венана имеет ограниченное применение для тонкостенных стержней.

studfiles.net

ПОНЯТИЕ О НАПРЯЖЕНИЯХ, ДЕФОРМАЦИЯХ И ПЕРЕМЕЩЕНИЯХ.

Рабочие гипотезы СОПРОМАТА

ОТВЕТ: В отличие от термеха, базирующегося на модели абс. твердого тела, в сопромате принята своя расчетная модель-модель идеализированного деформируемого тела. А для упрощения расчетов принимаются следующие допущения или гипотезы: 1) Материал тела имеет сплошное строение. 2) материал однороден, т.е. во всех точках свойства одинаковы. 3) материал изотропен, т.е. по всем направлениям свойства одинаковы. 4) до приложения внешних сил начальные напряжения в материале отсутствуют. 5) при решении реальных задач целесообразно использовать принцип суперпозиции, или принцип независимости действия сил, т.е. воздействие на конструкцию группы сил равно сумме воздействий от каждой силы в отдельности и не зависит от последовательности приложения этих сил.

ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ И МЕТОД ИХ ОПРЕДЕЛЕНИЯ.

ОТВЕТ: Под действием внешних сил на брус возникают внутренние силы или внутренние силовые факторы, для определения которых в сопромате принят единый расчетный метод – метод сечений. 1) разрезаем мысленно брус в исследуемом сечении на 2 части I и II. 2) Отбрасываем одну из частей. 3) Заменяем действие отбрасываемой части II на часть I внутренними силовыми факторами(в общем случае их 6). Q_x Q_y – поперечные силы, N_z – продольная сила, M_x M_y – изгибающие моменты, M_z – крутящий момент. 4) Уравновешиваем оставшуюся часть бруса и с помощью уравнений равновесия термеха находим искомые силовые факторы.

 

ПОНЯТИЕ О НАПРЯЖЕНИЯХ, ДЕФОРМАЦИЯХ И ПЕРЕМЕЩЕНИЯХ.

ОТВЕТ: Мерой интенсивности действия внутренних сил в окрестности точки рассматриваемого поперечного сечения являются напряжения, определяемые отношением силы к единице площади [Па]. Если в поп. сечении выделить элемент DА, к которому будет приложена сила DР, то DР/DА=р_m – среднее полное напряжение в рассматриваемой точке поперечного сечения. — полное истинное напряжение. Вектор раскладывают на и . — нормальное напряжение – вызывает разрушения путем отрыва. — касательное напряжение – вызывает разрушение путем сдвига. Перемещения и деформации – понятия, характеризующие изменение размеров и формы исследуемого тела. При этом перемещения являются следствием деформации.

ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТУПЕНЧАТЫХ БРУСЬЯХ С НЕСКОЛЬКИМИ СИЛОВЫМИ УЧАСТКАМИ.

ОТВЕТ: Растяжением или сжатием бруса называют такой его вид деформации, при котором все внешние силы направлены по продольной оси, а в поперечных сечениях возникает единственный внутренний силовой фактор – продольная сила N. Ее величину определяют, используя метод сечений: , т.е. продольная сила в рассматриваемом сечении бруса численно равна алгебраической сумме всех внешних сил, расположенных по одну сторону от сечения. Условились считать N>0, если она направлена в сторону от сечения, т.е. растягивает и N<0, если сжимает. Для полного суждения о прочности бруса необходимо построить график изменения продольной силы по длине бруса – эпюру продольной силы (Эп.N).

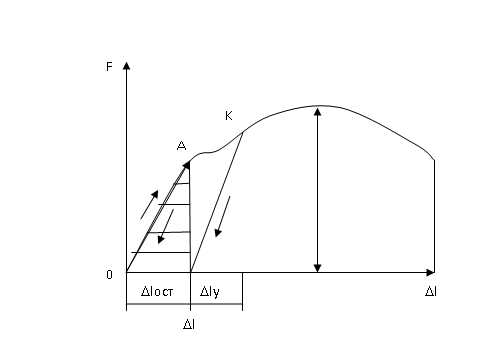
Напряжения и деформации при осевом растяжении-сжатии

В процессе деформирования в поперечных сечениях бруса при осевом растяжении-сжатии возникают только нормальные напряжения σ, причем они распределяются равномерно по поперечному сечению.

При растяжении-сжатии брус испытывает только линейные деформации.

– абсолютная продольная деформация груза (удлинение)

— относительная продольная деформация

— абсолютная поперечная деформация (сужение)

— относительная поперечная деформация

Связь между и : — коэффициент Пуассона.

Линейная закономерность, связывающая напряжения и деформации – закон Гука при осевом растяжении-сжатии.

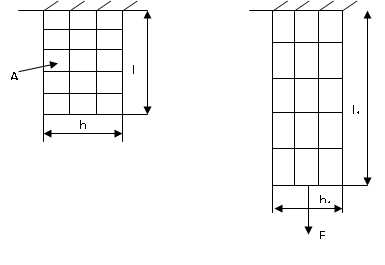
Определение геом. характеристик.

Рассмотрим определение геом. характеристик , для наиболее часто встречаемых поперечных сечений валов.

1.Сплошной вал

 

2.Полый вал

 

 

3.Тонкостенное трубчатое сечение

 

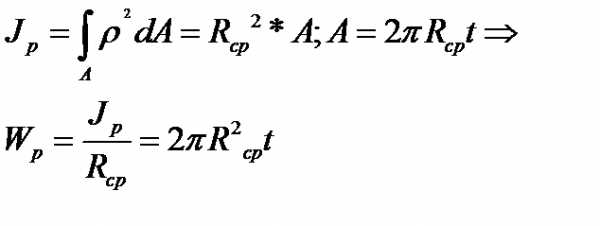
К тонкостенным отн-ся трубу с соотношением

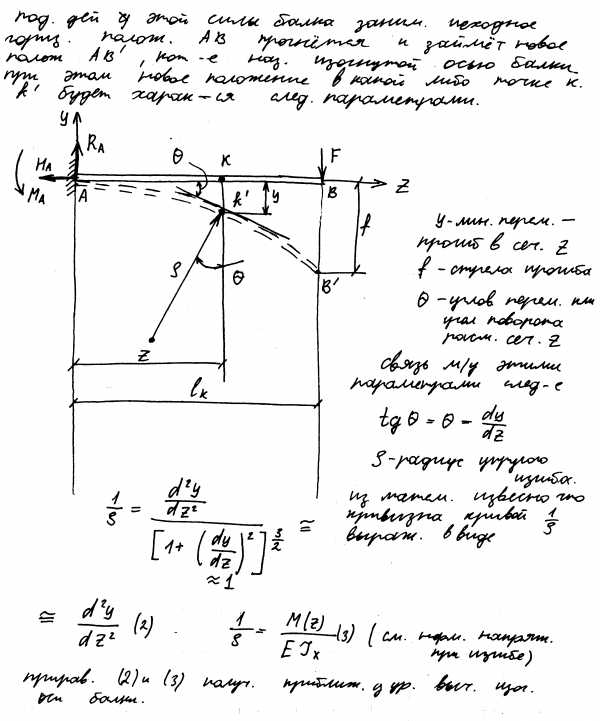
Определение перемещений при изгибе. Условие жесткости. Дифференциальное уравнение изогнутой оси балки.

 

 

 

 

 

 

 

 

Варианты расчета простых статически неопределимых балок

Существует несколько способов расчета простых балок:

1.Сравнение линейных перемещений.

ΔВ=ΔВq+ΔBRB=0(1) доп. уравнение деформаций

 

Слагаемые в(1) могут быть найдены исп-я готовые таблицы или универсальные уравнения. Применительно к рас-му предмету:

ΔBq=-qe⁴/8EIx; ΔBRB=RBe³ /3EIx;

 

ΔB=-qe⁴/8EIx +RBe³/3EIx =0 =>RB=3qe/8

 

2. Сравнение угловых перемещений.

Можно отбросить связь, препятствующая повороту опорного сечения А и записать

 

ΔA=ΔAq+ΔAMA=0(2)

Также ур-е деформации слагаемое означает углы поворота.

 

3.Составление замкнутой системы ур-я.

3 ур-я статики+ унивес. ур-е

yB=0.

43. Метод сил для расчета сложных СНС.

Метод при котором за неизвестное принимаются сосредоточенные моменты наз-ся методом сил. Он явл-ся наиболее распространенным и ис-ся для любых упругих систем (балки, рамы,эстакады итд.).

Например:

К трем ур-ям статики для решения данной СНС добавится 3 уравнения, выражающие рав-во 0 перемещений по направлениям всех отброшенных связей т.е. опорное сечение и не перемещаются им в горизонтальном или в вертикальном перемещениях и не переворачиваются.

X1 Δ1=0

X2 Δ2=0 (1)

X3 Δ3=0

Каждое уравнение системы(1) можно записать в развернутом виде:

Δ1=Δ11+Δ12+Δ13+Δ1f=0 (2)

Первый символ указывает направление; 2-й воз-е.

Δ1f-перемещение опорного сечения А в направлении действия X, вызванное внешней нагрузкой

(2) можно выразить через единичные перемещения и искомое неизвестное (это первые три слагаемых)

Δ11=δ11-x1 и тогда система примет закончен. вид.

δ11 x1+ δ12 x2+ δ13 x3+ Δ1f=0

δ21 x1+ δ22 x2+ δ23 x3+ Δ2f=0 (3)-система кумс.

δ31 x1+ δ32 x2+ δ33 x3+ Δ3f=0

Канонические ур-я метода сил-КУМС.

Число ур-й равно степени статической неопределимости.

 

Рабочие гипотезы СОПРОМАТА

ОТВЕТ: В отличие от термеха, базирующегося на модели абс. твердого тела, в сопромате принята своя расчетная модель-модель идеализированного деформируемого тела. А для упрощения расчетов принимаются следующие допущения или гипотезы: 1) Материал тела имеет сплошное строение. 2) материал однороден, т.е. во всех точках свойства одинаковы. 3) материал изотропен, т.е. по всем направлениям свойства одинаковы. 4) до приложения внешних сил начальные напряжения в материале отсутствуют. 5) при решении реальных задач целесообразно использовать принцип суперпозиции, или принцип независимости действия сил, т.е. воздействие на конструкцию группы сил равно сумме воздействий от каждой силы в отдельности и не зависит от последовательности приложения этих сил.

ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ И МЕТОД ИХ ОПРЕДЕЛЕНИЯ.

ОТВЕТ: Под действием внешних сил на брус возникают внутренние силы или внутренние силовые факторы, для определения которых в сопромате принят единый расчетный метод – метод сечений. 1) разрезаем мысленно брус в исследуемом сечении на 2 части I и II. 2) Отбрасываем одну из частей. 3) Заменяем действие отбрасываемой части II на часть I внутренними силовыми факторами(в общем случае их 6). Q_x Q_y – поперечные силы, N_z – продольная сила, M_x M_y – изгибающие моменты, M_z – крутящий момент. 4) Уравновешиваем оставшуюся часть бруса и с помощью уравнений равновесия термеха находим искомые силовые факторы.

 

ПОНЯТИЕ О НАПРЯЖЕНИЯХ, ДЕФОРМАЦИЯХ И ПЕРЕМЕЩЕНИЯХ.

ОТВЕТ: Мерой интенсивности действия внутренних сил в окрестности точки рассматриваемого поперечного сечения являются напряжения, определяемые отношением силы к единице площади [Па]. Если в поп. сечении выделить элемент DА, к которому будет приложена сила DР, то DР/DА=р_m – среднее полное напряжение в рассматриваемой точке поперечного сечения. — полное истинное напряжение. Вектор раскладывают на и . — нормальное напряжение – вызывает разрушения путем отрыва. — касательное напряжение – вызывает разрушение путем сдвига. Перемещения и деформации – понятия, характеризующие изменение размеров и формы исследуемого тела. При этом перемещения являются следствием деформации.



infopedia.su