Основные формулы. Динамика | FizPortal
Динамика.Динамика рассматривает силы в качестве причины движения тел. При этом следует различать:
- Динамику поступательного движения, или динамику материальной точки, и
- Динамику вращательного движения, или динамику твердого тела.
Второй закон Ньютона
m − масса тела, F1 + F2 + F3 + … = F − сумма всех сил, действующих на материальную точку.
Теорема о движении центра масс
Мсистaц.м. = F1вн + F2вн + …,
где Мсист − масса системы материальных точек (масса тела или системы тел), aц.м. − ускорение центра масс этой системы, F1вн + F2вн + … − сумма внешних сил, действующих на эту систему.
Третий закон Ньютона
Сила всемирного тяготения (гравитационная сила)
G = 6,67 × 10−11 H•м2/кг2 − гравитационная постоянная, m1 и m2 − массы материальных точек, r − расстояние между точками.
Сила тяжести
go = GM/R2,
g = GM/(R + h)2 = go/(1 + h/R)2,
где go − ускорение свободного падения вблизи поверхности планеты, g − ускорение свободного падения на высоте h от поверхности, R − радиус планеты, M − масса планеты. Для планеты Земля R = RЗ.
Первая космическая скорость
Вторая космическая скорость
RЗ − радиус Земли.
3-й Закон Кеплера
где T1 и T2 − периоды обращения двух планет вокруг Солнца, а a1 и a2 − длины больших полуосей их орбит.
Вес тела − сила, с которой тело действует на горизонтальную опору или растягивает подвес, находясь в поле тяготения Земли.
Вес тела в покое или движущегося по вертикали равномерно и прямолинейно
Вес тела, опускающегося с ускорением или поднимающегося с замедлением
Вес тела, поднимающегося с ускорением или опускающегося с замедлением
Перегрузки при подъеме с ускорением или спуске с замедлением
Сила упругости пружины
Сила упругости стержня, закрепленного на одном конце и свободного на другом
E − модуль упругости материала стержня (Юнга), σ − механическое напряжение, ε = |Δl|/lo − относительное удлинение стержня.
Сила трения.
Движущееся тело теряет свою энергию, не только преодолевая сопротивление окружающей среды, на из-за наличия трения. Сила трения действует на поверхности соприкосновения тел и затрудняет их перемещение относительно друг друга.
Сила трения скольжения
μ − коэффициент трения между телом и поверхностью, зависит от материала поверхностей, шероховатости тела и поверхности, от скорости тела относительно поверхности, N − сила нормального давления, которая прижимает тело к опоре.
Трение покоя проявляется в том случае, когда тело, находившееся в состоянии покоя, приводится в движение. При отсутствии скольжения, сила трения покоя равна силе, вызывающей движение тела.
fizportal.ru
Основы динамики
34. Динамика — это раздел механики, в котором изучаются связи между различными видами движений и причинами их вызывающими.
35. Первый закон Ньютона: существуют такие системы отсчёта, относительно которых тела движутся равномерно и прямолинейно, если на них не действуют другие тела или действие этих тел скомпенсировано.
36. Инерция — это свойство тела сохранять скорость своего движения неизменной по величине и направлению.
37. Инерциальная система отсчета — система отсчета, относительно которой свободная материальная точка, не подверженная воздействию других тел, движется равномерно и прямолинейно (по инерции).
38. Масса — это физическая величина, характеризующая инерционные и гравитационные свойства тел. Масса численно равна отношению ускорения a0 эталона массы m0=1 кг к ускорению a тела при их взаимодействии.
39. Плотность тела — это физическая величина, равная отношению массы тела к его объёму.
Измеряется в кг/м3.
40. Сила — это физическая величина, характеризующая действие на тело других тел или полей, в результате которого тело изменяет скорость своего движения или подвергается деформации. Сила измеряется в ньютонах. 1 Н= кг.м/с2. Сила — величина векторная. Она характеризуется числовым значением, направлением в пространстве и точкой приложения.
41. Второй закон Ньютона: ускорение, с которым движется тело, прямо пропорционально силе, приложенной к телу, и обратно пропорционально массе тела.
42. 1 ньютон — это сила, под действием которой тело массой 1 кг движется с ускорением 1 м/с2.
43. Третий закон Ньютона: Тела действуют друг на друга с силами равными по модулю, противоположными по направлению и одинаковыми по природе.
44. Закон всемирного тяготения: тела притягиваются друг к другу с силой прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
где G — гравитационная постоянная.
45. Гравитационная постоянная G численно равна силе, с которой притягиваются тела массами по 1 кг на расстоянии 1 м друг от друга.
46. Сила тяжести — это сила, с которой тело притягивается Землёй.
47. Вес тела — это сила, с которой тело давит на опору или растягивает подвес.
48. Силы трения — это силы, препятствующие перемещению одного тела по поверхности другого. Они возникают в результате зацепления друг за друга мелких выступов, находящихся на поверхностях тел. При шлифовке выступы и впадины уменьшаются, что приводит к уменьшению сил трения. Но, если поверхности отшлифовать очень хорошо, силы трения вновь начинают увеличиваться из-за действия межмолекулярных сил трущихся поверхностей. Для уменьшения сил трения кроме шлифовки применяют смазку и замену трения скольжения трением качения, которое обычно на порядок меньше сил трения скольжения.
49. Сила трения покоя — это сила, возникающая на границе соприкосновения тел при отсутствии относительного движения тел. Она численно равна силе, приложенной к телу, и может изменяться от нуля до максимального значения внешней силы, при котором тело начинает перемещаться. Сила трения покоя в некоторых случаях может быть больше силы трения скольжения.
50. Коэффициент трения — это число, показывающее долю силы трения от силы, прижимающей поверхности друг к другу.
Коэффициент трения зависит от рода трущихся поверхностей и от чистоты обработки поверхностей.
studfiles.net
7.2. Основные понятия, законы и формулы динамики
В динамике изучают законы движения тел с учетом причин, вызывающих это движение. Различают динамику материальной точки и динамику твердого тела.
Механическое движение тел изменяется в процессе их взаимодействия друг с другом.
Меру взаимодействия тел, в результате которого тела деформируются или приобретают ускорение, называют силой. Сила – величина векторная, она характеризуется числовым значением, направлением действия и точкой приложения к телу.
Если к материальной точке приложено
несколько сил
,
их действие можно заменить действием
одной силы
,
которая называетсяравнодействующей данных сил:
. | (7) |
Если реально действующие силы заменены равнодействующей, то в дальнейшем нужно считать, что к частице приложено не несколько сил, а только одна – равнодействующая.
Основой динамики и всей классической механики служат три закона Ньютона, сформулированные для материальной точки и тел, движущихся поступательно в инерциальных системах отсчета.
I)Первый закон Ньютона. Если равнодействующая всех сил, приложенных к МТ, равна нулю, то точка находится в состоянии покоя или равномерного прямолинейного движения: при.
Это свойство, присущее всем телам, называют инерцией, а тела, им обладающие, – инертными. Мерой инертности тел являетсямасса.
Из первого закона динамики следует, что свободное движение частиц с постоянной скоростью – движение по инерции – есть такое же естественное состояние частиц, как и покой. Каждая частица может двигаться с какой угодно постоянной скоростью без каких бы то ни было внешних воздействий со стороны, но изменить свое движение – сообщить себе ускорение – не может. Состояния покоя и равномерного прямолинейного движения с точки зрения динамики неразличимы.
II)Второй закон Ньютона. Скорость изменения импульса частицы равна силе, приложенной к частице, и происходит по направлению прямой, вдоль которой действует эта сила:
| (8) |
, где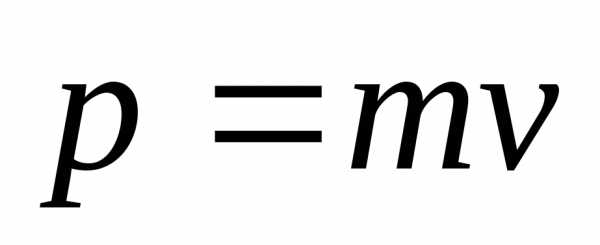 
– импульс (количество движения) частицы,
– сила, действующая на частицу.
В нерелятивистской механике масса не зависит от скорости (m=const). Тогда формула (8) эквивалентна формуле:
| (9) |
.Это уравнение является основным уравнением динамикиматериальной точки. При его использовании нужно иметь в виду следующее. Действие сил на материальную точку не зависит друг от друга. Каждая из сил, приложенных к частице, сообщает ей такое ускорение, как если бы других сил не было (принцип независимости действия сил). Результирующее ускорение частицы, находящейся под действием нескольких сил, равно геометрической сумме ускорений, сообщаемых каждой силой в отдельности. Модуль и направление ускорения таковы, как если бы на частицу действовала одна сила, равная векторной сумме приложенных сил, т. е. основное уравнение динамики точки справедливо как для отдельных сил, так и для их равнодействующей.
В тех случаях, когда на МТ действуют силы, равнодействующая которых с течением времени не меняется, движение точки будет равноускоренным.
При изучении криволинейного движения, и в частности движения по окружности, все силы, действующие на частицу в рассматриваемой точке, удобно разложить по направлениям касательному и нормальному к траектории движения. Компоненту силы вдоль касательной называют тангенциальнойсилой. Эта сила сообщает частице тангенциальное ускорение, и по второму закону Ньютона:
| (10) |
.Компоненту силы вдоль нормали называютнормальнойсилой. Эта сила сообщает частице нормальное ускорение:
, | (11) |
где R– радиус кривизны
траектории частицы в данной точке
пространства, при круговом движенииR– радиус описываемой окружности,v– модуль вектора скорости,ω– угловая скорость,
– базисный вектор (орт) в направлении
центра кривизны.
III)Третий закон Ньютона.Два тела действуют друг на друга с силами, равными по модулю и противоположными по направлению; приложены эти силы к разным телам.
Равенство модулей сил при взаимодействии имеет место всегда, независимо от того, находятся ли взаимодействующие тела в относительном покое или они движутся.
Наиболее распространенный случай взаимодействия тел – это взаимодействие материальной точки с поверхностью. Силы, действующие со стороны груза на опору и со стороны опоры на груз, называют соответственно силой давленияисилой реакции опоры.
Силы, которые противодействуют движению при касании тел, называются силами трения. Они направлены по касательной линии в месте контакта. Различают три вида сухого трения:трениепокоя, скольжения и качения. Модуль максимальной силы трения покоя определяют из соотношения:
? | (12) |
где μ– постоянный для данной пары соприкасающихся поверхностей коэффициент, называемыйкоэффициентом трения покоя,N– сила реакции опоры. При малых скоростях скольжения по этой же формуле рассчитывается и сила трения скольжения, т. к. в этом случае коэффициент трения скольжения мало отличается от коэффициента трения покоя.
Законы Ньютона сформулированы для инерциальных систем отсчета– систем, связанных с телами, на которые не действуют внешние силы. В системах движущихся ускоренно эти законы не выполняются.
studfiles.net
Формулы по кинематике, динамике, законам сохранения, молекулярной физике, электричеству, магнетизму, оптике. Тест
Формулы по кинематике, динамике, законам сохранения, молекулярной физике, электричеству, магнетизму, оптике. Тест — курсы по физике Skip navigation- Элементы математики
- действия с векторами
- выражение неизвестной
- Физические величины
- Единицы измерения
- внесистемные единицы
- Постоянные величины в физике
- плотность вещества
- предел прочности, модуль Юнга
- скорость звука
- удельная теплота
- диэлектрическая проницаемость
- удельное сопротивление
- электрохимический эквивалент
- Формулы
- I. Механика
- Кинематика
- равномерное движение
- относительность движения
- неравномерное движение
- равноускоренное движение
- ускорение свободного падения
- графики движения
- движение по окружности
- параболическое движение
- Динамика
- закон тяготения
- законы Ньютона
- силы в природе
- равнодействующая сила
- Законы сохранения
- импульс тела, импульс силы
- закон сохранения импульса
- работа и мощность
- кинетическая и потенциальная энергии
- закон сохранения энергии
- Статика
- плечо и момент силы
- условия равновесия
- центр тяжести, центр масс
- Колебания и волны
- колебательное движение
- гармонические колебания
- маятники
- превращение энергии при колебаниях
- упругие волны
- звуковые волны
- II. Молекулярная физика
- Молекулярная физика
- основные положения мкт
- давление
- основное уравнение мкт, температура
- уравнение идеального газа
- изопроцессы
- свойства жидкостей*
- свойства твердых тел
- Термодинамика
- количество теплоты
- работа, внутренняя энергия
- первый закон термодинамики
- второй закон термодинамики
- тепловые двигатели
- III. Основы электродинамики
- Электричество
- электрический заряд
- закон Кулона
- напряженность поля
- потенциал и работа поля
- диэлектрики, проводники
- электроемкость, конденсаторы
- энергия конденсатора
- Электрический ток
- электрический ток, сила и плотность
- закон Ома для участка цепи
- работа и мощность тока
- закон Ома для замкнутой цепи
- электрический ток в различных средах
- электрические явления
- Магнетизм
- магнитное поле
- сила Ампера
- сила Лоренца
- Электромагнетизм
- магнитный поток
- закон электромагнитной индукции
- самоиндукция, энергия поля
- электромагнитные колебания
- электромагнитные волны
- переменный ток
- трансформатор*
- IV. Оптика
- Волновая оптика
- свет как электромагнитные волны
- интерференция
- дифракция
- Геометрическая оптика
- законы распространения света
- линзы, оптические приборы
- V. Теория относительности
- Теория относительности
- постулаты теории относительности
- VI. Квантовая физика
- Световые кванты
- фотон
- фотоэффект
- квантовые постулаты Бора
- излучение и поглощение света
- Атомное ядро
- энергия связи ядра
- ядерные реакции
- закон радиоактивного распада
- элементарные частицы и их свойства
- Современная физика*
- физика элементарных частиц
- мир внутри атомного ядра
- время расщепляем на мгновения
- нанотехнологии и нанофизика
- вещество в экстремальных состояниях
fizmat.by
Физика. Основы динамики (формулы) — Сдать физику на 5
Второй закон Ньютона:
Второй закон Ньютона формулируется следующим образом:
Ускорение тела прямо пропорционально равнодействующей всех сил, приложенных к телу, и обратно пропорционально его массе.
Третий закон Ньютона:
Третий закон Ньютона гласит:
Взаимодействия двух тел друг на друга равны между собой и направлены в противоположные стороны.
Из этого закона следует, что если на какое-то тело действует сила, то обязательно существует другое тело, на которое первое действует с такой же по абсолютному значению силой, но направленной в противоположную сторону, т. е. силы взаимодействия двух тел всегда равны друг другу.
Сила тяжести:
Силой тяжести называют силу, с которой Земля притягивает к себе тело, находящееся вблизи ее поверхности. Сила тяжести всегда направлена вертикально вниз, к центру Земли. Она обозначается латинской буквой Fт (т — тяжесть). Сила тяжести приложена к центру тяжести тела.
Для находящегося вблизи поверхности Земли тела сила тяжести равна:
Сравнение масс тел:
Закон всемирного тяготения:
Закон всемирного тяготения был открыт великим английским ученым Исааком Ньютоном и гласит: сила, с которой две материальные точки с массами m1 и m2 притягивают друг друга, пропорциональна массам этих точек и обратно пропорциональна квадрату расстояния r2 между ними.
G – гравитационная постоянная.
Вес тела в ускоренно движущемся лифте:
Закон Гука:
Закон Гука является основным законом теории упругости, который гласит: сила упругости, возникающая при упругой деформации тела (растяжении или сжатии пружины) пропорциональна удлинению тела (пружины) и направлена в сторону, противоположную направлению перемещений частиц тела при деформации.
Если обозначить удлинение тела через x, а силу упругости через Fупр, то закон Гука можно представить в виде формулы:
E – модуль Юнга.
Сила трения скольжения:
Трение скольжения. приложим к телу силу, превышающую максимальную силу трения покоя – тело сдвинется с места и начнет двигаться. Трение покоя сменится трением скольжения.
Сила трения скольжения также пропорциональна силе нормального давления и силе реакции опоры:
Fтр = μN.
fizikuna5.ru
Динамика — раздел теоретической механики.
Динамика
Основные понятия и аксиомы динамики
Динамика есть часть теоретической механики, изучающая механическое движение тел в зависимости от сил, влияющих на это движение.
Основы динамики заложил итальянский ученый Галилео Галилей (1564-1642), который опроверг существовавшее в науке со времен Аристотеля (IV в. до н.э.) заблуждение о том, что из двух тел, падающих на Землю, более тяжелое движется быстрее. Галилей установил, что причиной изменения скорости тела является сила, т. е. любое ускорение или замедление вызывается силовым воздействием.
На основе выводов Г. Галилея англичанин И. Ньютон сформулировал основные аксиомы (законы) движения, ставшие фундаментом, на который сотни лет опирается классическая физика, в том числе и современная.
Динамика основывается на ряде положений, которые являются аксиомами и называются законами динамики.
Прежде чем перейти к рассмотрению этих законов, необходимо раскрыть сущность понятий материальной точки и изолированной материальной точки.
Под материальной точкой подразумевают некое тело, имеющее определенную массу (т. е. содержащее некоторое количество материи), но не имеющее линейных размеров (бесконечно малый объем пространства).
Изолированной считается материальная точка, на которую не оказывают действие другие материальные точки.
В реальном мире изолированных материальных точек, как и изолированных тел, не существует, это понятие является условным.
***
Первый закон Ньютона (первый закон динамики)
Первый закон динамики, называемый аксиомой инерции, формулируется в применении к материальной точке так: изолированная материальная точка либо находится в покое, либо движется прямолинейно и равномерно.
В кинематике было установлено, что прямолинейное равномерное движение является единственным видом движения, при котором ускорение равно нулю, поэтому аксиому инерции можно сформулировать следующим образом: ускорение изолированной материальной точки равно нулю.
Итак, изолированная от влияния окружающих тел материальная точка не может сама себе сообщить ускорение. Это свойство тел называют инерцией или инертностью, т. е. инертность (инерция) – свойство тел сохранять скорость по модулю и направлению (в т. ч. и покой – состояние, при котором скорость равна нулю). Изменить скорость, т. е. сообщить материальной точке ускорение способна только приложенная к ней сила.
***
Второй закон Ньютона (второй закон динамики)
Зависимость между силой и сообщаемым ею ускорением устанавливает второй закон Ньютона, который гласит, что ускорение, сообщаемое материальной точке силой, имеет направление силы и пропорционально ее модулю.
Если сила F1 сообщает материальной точке ускорение a1, а сила F2 сообщает этой же точке ускорение a2, то на основании второго закона Ньютона можно записать:
F1/F2 = a1/a2 или F1/a1 = F2/a2.
Следовательно, для данной материальной точки отношение любой силы к вызываемому ею ускорению есть величина постоянная. Эту величину (отношение силы к ускорению) называют массой материальной точки, и обозначают ее m:
F/a = m = const.
На основании этого равенства можно сделать выводы:
— две материальные точки, имеющие одинаковые массы, получат от одной и той же силы одинаковые ускорения;
— чем больше масса точки, тем большую силу необходимо приложить, чтобы придать данной точке требуемое ускорение.
***
Что такое масса тела
Масса – одна из основных характеристик любого материального объекта, определяющая его инертные и гравитационные свойства. Ньютон называл массой количество материи, заключенной в теле, считая массу каждого тела величиной постоянной.
Современное представление о мире, после открытий, совершенных А. Эйнштейном, опровергает этот вывод И. Ньютона – масса не является постоянной величиной для тела, она зависит от скорости, с которой это тело движется. Так, например, наблюдения за движением заряженных частиц в ускорителях показали, что инертность частицы (т. е. способность сохранять свою скорость) возрастает с увеличением ее скорости.
Теория относительности устанавливает следующую зависимость между массой тела, находящегося в покое, и массой движущегося тела:
m = m0/√(1 – v2/c2),
где m – масса движущегося тела, m0 – масса покоящегося тела (масса покоя), v = скорость движения тела, c – скорость света.
Из этой формулы видно, что чем больше скорость движения тела, тем больше его масса и, следовательно, тем труднее сообщить ему дальнейшее ускорение. При скоростях близких к скорости света масса тела стремится к бесконечности, и для дальнейшего ускорения такого тела требуется сила бесконечной величины.
Очевидно, что материальное тело не может двигаться со скоростью света, поскольку не существует реальная сила, способная ускорить его до такого состояния.
На основании теории относительности современная наука дает массе такое определение: масса есть мера инертности тела.
Однако заметное изменение массы (инертности) тела наблюдается лишь при очень больших скоростях, близких к скорости света, поэтому в классической физике массу принимают величиной постоянной, при этом погрешности, возникающие в расчетах, являются ничтожно малыми.
Второй закон Ньютона выражается равенством:
F = ma,
которое называется основным уравнением динамики и читается так: сила есть вектор, равный произведению массы точки на ее ускорение.
Основное уравнение динамики является уравнением движения материальной точки в векторной форме.
Ускорение свободного падения
Опытным путем установлено, что под действием притяжения Земли в вакууме тела падают с одинаковым ускорением, которое называется ускорением свободного падения.
Следует отметить, что это явление будет верным для конкретного географического места на поверхности планеты или над ее поверхностью – ускорение свободного падения не является постоянной величиной и зависит, в частности, от расстояния между центром тяжести тела и центром тяжести нашей планеты, а также от существования центробежной силы инерции, вызываемой вращением Земли.
Так, на полюсах ускорение свободного падения g ≈ 9,83 м/с2, а на экваторе g ≈ 9,78 м/с2. Но в приближенных расчетах принимают среднее значение, равное примерно g ≈ 9,81 м/с2, при этом погрешности результатов незначительны.
Итак, сила тяжести тела равна его массе, умноженной на ускорение свободного падения. Если сила тяжести одного тела G1 = m1/g, а второго тела – G2 = m2/g, то
G1/G2 = (m1g)/(m2g) = m1/m2,
т. е. силы тяжести тел пропорциональны их массам, что позволяет сравнивать массы различных тел путем взвешивания (сравнивания их сил тяжести при помощи весов).
Из второго закона Ньютона следует, что под действием постоянной силы находившаяся в покое свободная материальная точка движется прямолинейно равнопеременно (с постоянным ускорением).
Движение под действием постоянной силы может быть и прямолинейным и криволинейным (в последнем случае материальная точка имеет начальную скорость, вектор которой не совпадает с вектором силы). Пример движения под действием постоянной силы – свободное падение тел.
***
Третий закон Ньютона
К основным законам динамики относится и рассмотренная в Статике аксиома взаимодействия, или третий закон Ньютона.
Применительно к материальной точке закон формулируется так: силы взаимодействия двух материальных точек по модулю равны между собой и направлены в противоположные стороны (действие равно противодействию).
На основании этого закона можно сделать вывод, что сила, как мера взаимодействия между телами, не может проявляться без пары, т. е. если возникает какое-либо силовое воздействие, то существует и «двойник» этого силового воздействия, равный по модулю и противоположный по вектору.
***
Дифференциальные уравнения движения материальной точки
Правильные ответы на тестовые вопросы по разделу «Динамика»:
Тест №1 2-3-2-1-1
Тест №2 4-2-4-3-1
Тест №3 3-1-1-2-4
Тест №4 4-2-1-2-3
Тест №5 1-1-4-3-2
Тест №6 1-3-3-2-4
Тест №7 2-2-4-1-3
k-a-t.ru
Статика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Основы статики
К оглавлению…
Статикой называется раздел механики, изучающий условия равновесия тел. Равновесием называют такое состояние тела или системы тел, в котором оно не движется в данной системе отсчета. Различают три вида равновесия:
- Устойчивое равновесие. Если систему вывести из состояния устойчивого равновесия, то она самопроизвольно в него вернется, то есть при выведении из положения равновесия возникает сила, возвращающая систему к равновесию. Для этого необходимо, чтобы потенциальная энергия системы в состоянии устойчивого равновесия имела минимальное значение. Любая физическая система стремится к состоянию устойчивого равновесия. Это значит, что любой самопроизвольный процесс всегда проходит с уменьшением потенциальной энергии.
- Неустойчивое равновесие. В данном случае при выведении из состояния равновесия возникают силы, уводящие систему от равновесия, и система самопроизвольно не может в него вернуться. В состоянии неустойчивого равновесия потенциальная энергия системы имеет максимальное значение.
- Безразличное равновесие. При выведении из состояния равновесия в системе не возникает ни возвращающих, ни уводящих в сторону сил.
Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к невращающемуся телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение (действительно, ведь ускорение тела при этом равно нулю). В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей силы все силы, действующие на тело, можно прикладывать к центру масс. Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело.
Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю. Иными словами, векторная сумма всех сил, приложенных к телу должна быть равна нолю:
Момент силы. Правило моментов
К оглавлению…
Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил. Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения. Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.
Для описания причин вызывающих вращения и условия равновесия тела в статике вводится новое понятие — момент силы. Произведение модуля силы F на плечо d и называется моментом силы M. Таким образом момент силы в статике вычисляется по формуле:
Обычно в физике используется следующее правило знаков: если сила поворачивает тело по часовой стрелке, то ее момент считается положительным, а если против – то отрицательным. Момент силы может и равняться нулю, если сила проходит (сама или продолжением) через ось. Обратите внимание: если Вы перепутаете, и возьмете знаки моментов наоборот (по часовой стрелке со знаком минус, а против часовой со знаком плюс), то ничего страшного не произойдет. Поэтому, важно запомнить, что моменты сил, вращающих тело в различных направлениях относительно часовой стрелки, берутся с различными знаками.
Обратите внимание, что момент силы зависит не только от величины силы, но и от ее плеча. Следовательно, одно и то же значение момента можно получить двумя способами: взять большую силу и малое плечо или взять малую силу и большое плечо. Вывод: чем больше плечо, тем меньшую силу необходимо прилагать для получения одного и того же результата.
Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
При записи этого условия в ходе решения конкретной задачи по статике моменты сил необходимо записывать с учётом их знаков. В Международной системе единиц (СИ) моменты сил измеряются в ньютоно-метрах (Н∙м).
Обратите внимание: в общем случае, когда тело может двигаться поступательно и вращаться, для равновесия необходимо выполнение обоих условий: равенство нулю равнодействующей силы и равенство нулю суммы всех моментов.
Алгоритм решения задач на правило моментов (задач по статике):
- Нарисовать рисунок. Следует помнить, что сила тяжести, действующая на тело изображается один раз. Если же в задаче идет речь об изломанной палочке, то удобнее рисовать отдельно силы тяжести, действующие на каждую часть палочки, считая массы частей пропорциональными их длинам. В отличие от динамики, где силы изображаются из одной точки, в статике важно точно указать точку приложения силы.
- Выбрать ось вращения в точке приложения самой ненужной в задаче силы или сил (той силы, которую определять не надо и не хочется из-за природного чувства лени). При этом плечо (и, следовательно, момент) этой силы обратится в нуль независимо от ее величины, и в дальнейших вычислениях эту силу можно не учитывать совсем.
- Записать правило моментов относительно данной оси, на забывая про правило знаков.
- При необходимости записать также условие согласно которому равнодействующая сила равна нолю.
- Выразить искомую силу.
Рычаги и блоки
К оглавлению…
Как вы знаете из практики, иногда необходимо изменить направление силы, увеличить или уменьшить ее величину. Этой цели служат простые механизмы: устройства, преобразующие величину или направление силы с помощью механических явлений. Для всех простых механизмов справедливо золотое правило механики: выиграл в силе – проиграл в перемещении (или наоборот). Это значит, что при увеличении силы за счет некоторого механизма неизбежно будет уменьшено и перемещение. Рассмотрим основные типы простых механизмов изучаемых в школьной физике:
- Равноплечий рычаг (весы). Рычаг, ось вращения которого проходит через его геометрический центр.
- Неравноплечий рычаг. Рычаг ось вращения которого проходит через произвольную точку.
- Неподвижный блок. Это диск с закрепленной осью, через который переброшена нить. Неподвижный блок используется для изменения направления приложения силы. Если трение в блоке отсутствует, нить невесома, то сила ее натяжения до и после блока не изменяется. Таким образом, неподвижный блок не дает ни выигрыша в силе, ни проигрыша в перемещении.
- Подвижный блок. Это диск, ось которого может двигаться поступательно. Подвижный блок позволяет уменьшить силу в два раза, одновременно с этим вдвое увеличивая перемещение.
- Наклонная плоскость. Это устройство применяется для поднятия тяжестей. При достаточно малых значениях угла наклона и небольшом коэффициенте трения сила, которую необходимо приложить чтобы поднимать некоторое тело вдоль наклонной плоскости может быть значительно меньше веса тела. Таким образом, подъем становится легче. Естественно, при этом в полном соответствии с «золотым правилом» увеличивается перемещение тела.
Центр тяжести тела
К оглавлению…
Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело. В общем случае центр тяжести может и не лежать внутри тела, а выходить за его пределы (например, различные изогнутые длинные предметы, кольца, полукольца и так далее).
Рассмотрим основные методы определения положения центра масс тел для некоторых конкретных случаев, возникающих при решении задач по статике:
1. У однородных тел правильной формы (шары, прямоугольники, стержни) центр тяжести совпадает с геометрическим центром. Следует запомнить, что центр тяжести однородной треугольной пластины лежит в точке пересечения ее медиан. Для однородных симметричных тел центр тяжести всегда расположен на оси симметрии.
2. Определение положения центра тяжести системы из двух тел с известными центрами тяжести. Здесь можно использовать замечательное свойство центра тяжести. Подперев центр тяжести, мы обеспечим равновесие тела. Таким образом, центр тяжести системы из двух тел лежит на отрезке, соединяющем их центры тяжести, и делит его в отношении, обратном отношению масс тел:
где: l1 – расстояние от центра масс до тела с массой m1, а l2 – до тела с массой m2.
3. Определение положения центра тяжести любой системы тел с известными положениями центров тяжести. Необходимо ввести систему координат (естественно, начало координат выбрать в точке, относительно которой необходимо рассчитать положение центра тяжести), определить в ней координаты центров тяжести всех тел и найти координаты центра тяжести системы по формуле:
Аналогичные уравнения получаются для остальных координатных осей, если таковые необходимо рассматривать в задаче (просто переменная x меняется на y или z соответственно).
4. Однородное тело правильной формы с вырезом правильной формы. Проще всего свести задачу к обратной: мысленно вставить вырез обратно и получить тело правильной формы с известным положением центра тяжести. Далее представить его в виде двух тел: страшного с вырезом и самого выреза. А теперь все просто. У одного из тел (выреза) мы знаем положения центра тяжести. У другого – нет. Зато знаем положение центра тяжести системы двух тел. Составив уравнение для определения общего центра тяжести получим выражение с одной неизвестной – центром тяжести тела с вырезом. Решив уравнение получим искомый ответ.
5. Теорема Паппа. Применяется для определения положения центра тяжести плоской пластины, которая при вращении вокруг некоторой оси образует тело с легко вычисляемым объемом. Необходимо мысленно повернуть пластину на один оборот, нарисовать рисунок и применить теорему:
Формулировка теоремы: объем тела, полученного при вращении пластины, равен произведению ее площади на путь, пройденный центром тяжести при вращении:
educon.by
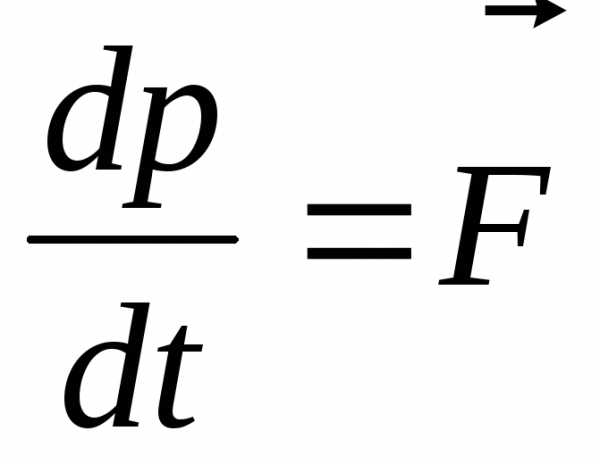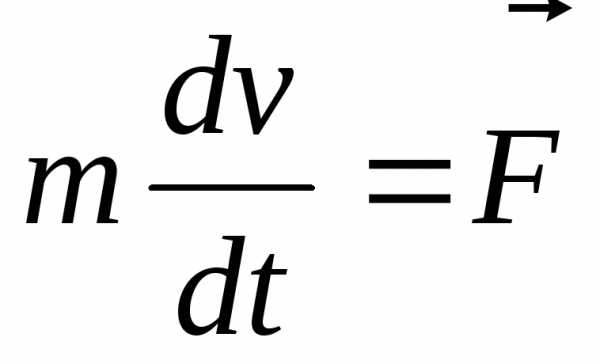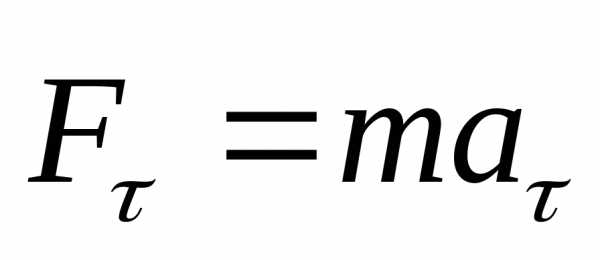