Сила реакции опоры: определение и формула
Статика — один из разделов современной физики, который изучает условия нахождения тел и систем в механическом равновесии. Для решения задач на равновесие важно знать, что такое сила реакции опоры. Данная статья посвящена подробному рассмотрению этого вопроса.
Второй и третий законы Ньютона
Прежде чем рассматривать определение силы реакции опоры, следует вспомнить о том, что вызывает движение тел.
Причиной нарушения механического равновесия является действие на тела внешних или внутренних сил. В результате этого действия тело приобретает определенное ускорение, которое вычисляется с помощью следующего равенства:
F = m*a
Эта запись известна как второй закон Ньютона. Здесь сила F является результирующей всех действующих на тело сил.
Если одно тело воздействует с некоторой силой F1¯ на второе тело, то второе оказывает действие на первое с точно такой же по абсолютной величине силой F2¯, но она направлена в противоположном направлении, чем F1¯. То есть справедливо равенство:
F1¯ = -F2¯
Эта запись является математическим выражением для третьего ньютоновского закона.
При решении задач с использованием этого закона школьники часто допускают ошибку, сравнивая эти силы. Например, лошадь везет телегу, при этом лошадь на телегу и телега на лошадь оказывают одинаковые по модулю силы. Почему же тогда вся система движется? Ответ на этот вопрос можно правильно дать, если вспомнить, что обе названные силы приложены к разным телам, поэтому они друг друга не уравновешивают.
Сила реакции опоры
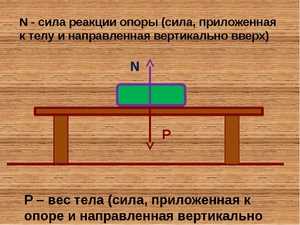
Сначала дадим физическое определение этой силы, а затем поясним на примере, как она действует. Итак, силой нормальной реакции опоры называется сила, которая действует на тело со стороны поверхности. Например, мы поставили стакан с водой на стол. Чтобы стакан не двигался с ускорением свободного падения вниз, стол воздействует на него с силой, которая уравновешивает силу тяжести. Это и есть реакция опоры. Ее обычно обозначают буквой N.
Сила N — это контактная величина. Если имеется контакт между телами, то она появляется всегда. В примере выше значение величины N равно по модулю весу тела. Тем не менее это равенство является лишь частным случаем. Реакция опоры и вес тела — это совершенно разные силы, имеющие различную природу. Равенство между ними нарушается всегда, когда изменяется угол наклона плоскости, появляются дополнительные действующие силы, или когда система движется ускоренно.
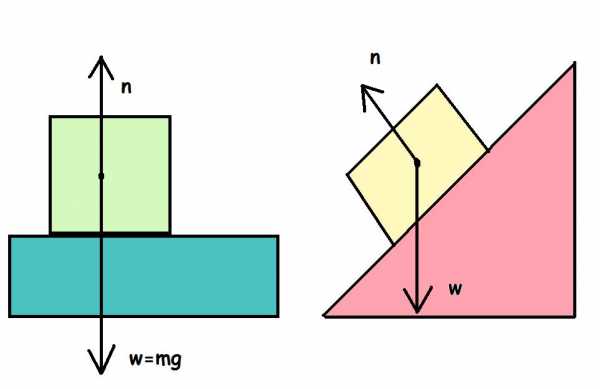
Сила N называется нормальной потому, что она всегда направлена перпендикулярно плоскости поверхности.
Если говорить о третьем законе Ньютона, то в примере выше со стаканом воды на столе вес тела и нормальная сила N не являются действием и противодействием, поскольку обе они приложены к одному телу (стакану с водой).
Физическая причина появления силы N
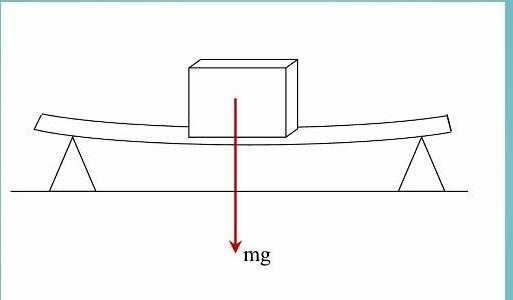
Как было выяснено выше, сила реакции опоры препятствует проникновению одних твердых тел в другие. Почему появляется эта сила? Причина заключается в деформации. Любые твердые тела под воздействием нагрузки деформируются сначала упруго. Сила упругости стремится восстановить прежнюю форму тела, поэтому она оказывает выталкивающее воздействие, что проявляется в виде реакции опоры.
Если рассматривать вопрос на атомном уровне, то появление величины N — это результат действия принципа Паули. При небольшом сближении атомов их электронные оболочки начинают перекрываться, что приводит к появлению силы отталкивания.
Многим может показаться странным, что стакан с водой способен деформировать стол, но это так. Деформация настолько мала, что невооруженным глазом ее невозможно наблюдать.
Как вычислять силу N?
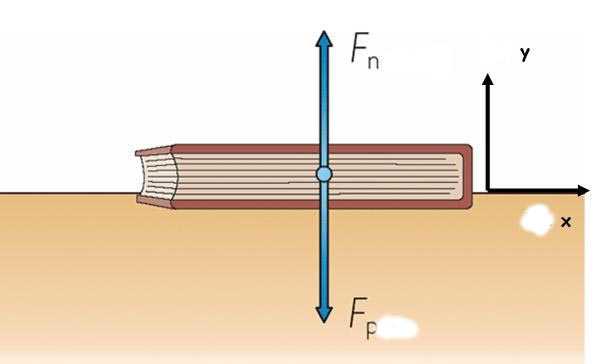
Сразу следует сказать, что какой-то определенной формулы силы реакции опоры не существует. Тем не менее имеется методика, применяя которую, можно определить N для совершенно любой системы взаимодействующих тел.
Методика определения величины N заключается в следующем:
- сначала записывают второй закон Ньютона для данной системы, учитывая все действующие в ней силы;
- находят результирующую проекцию всех сил на направление действия реакции опоры;
- решение полученного уравнения Ньютона на отмеченное направление приведет к искомому значению N.
При составлении динамического уравнения следует внимательно и правильно расставлять знаки действующих сил.
Найти реакцию опоры можно также, если пользоваться не понятием сил, а понятием их моментов. Привлечение моментов сил справедливо и является удобным для систем, которые имеют точки или оси вращения.
Далее приведем два примера решения задач, в которых покажем, как пользоваться вторым ньютоновским законом и понятием момента силы для нахождения величины N.
Задача со стаканом на столе
Выше уже был приведен этот пример. Предположим, что пластиковый стакан объемом 250 мл наполнен водой. Его поставили на стол, а сверху на стакан положили книгу массой 300 грамм. Чему равна сила реакции опоры стола?
Запишем динамическое уравнение. Имеем:
m*a = P1 + P2 — N
Здесь P1 и P2 — вес стакана с водой и книги соответственно. Поскольку система находится в равновесии, то a=0. Учитывая, что вес тела равен силе тяжести, а также пренебрегая массой пластикового стакана, получаем:
m1*g + m2*g — N = 0 =>
N = (m1 + m2)*g
Учитывая, что плотность воды равна 1 г/см3, и 1 мл равен 1 см3, получаем согласно выведенной формуле, что сила N равна 5,4 ньютона.
Задача с доской, двумя опорами и грузом

Доска, массой которой можно пренебречь, лежит на двух твердых опорах. Длина доски равна 2 метра. Чему будет равна сила реакции каждой опоры, если на эту доску посередине положить груз массой 3 кг?
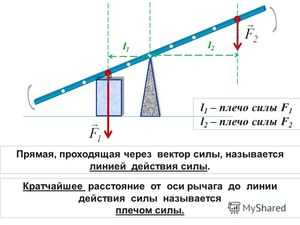
Прежде чем переходить к решению задачи, следует ввести понятие момента силы. В физике этой величине соответствует произведение силы на длину рычага (расстояние от точки приложения силы до оси вращения). Система, имеющая ось вращения, будет находиться в равновесии, если суммарный момент сил равен нулю.
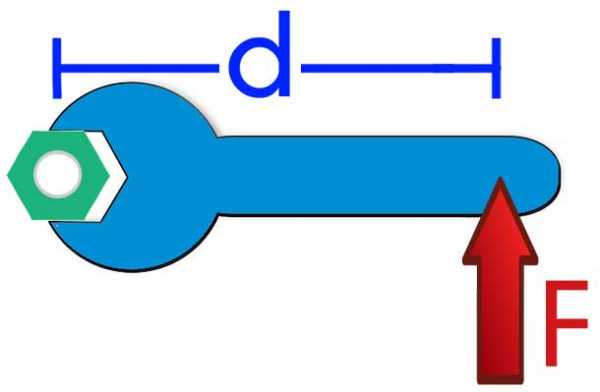
Возвращаясь к нашей задаче, вычислим суммарный момент сил относительно одной из опор (правой). Обозначим длину доски буквой L. Тогда момент силы тяжести груза будет равен:
M1 = -m*g*L/2
Здесь L/2 — рычаг действия силы тяжести. Знак минус появился потому, что момент M1 осуществляет вращение против часовой стрелки.
Момент силы реакции опоры будет равен:
M2 = N*L
Поскольку система находится в равновесии, то сумма моментов должна быть равной нулю. Получаем:
M1 + M2 = 0 =>
N*L + (-m*g*L/2) = 0 =>
N = m*g/2 = 3*9,81/2 = 14,7 Н
Заметим, что от длины доски сила N не зависит.
Учитывая симметричность расположения груза на доске относительно опор, сила реакции левой опоры также будет равна 14,7 Н.
fb.ru
симметричная задача на примере балки с двумя опорами
Расчет реакций относится к разделу физики с названием «Статика», которая рассматривает структуру и системы, находящиеся в покое.
Силой реакции опоры называется усилие противодействия опоры действующему на нее объекту, при этом она равна по модулю и противоположна по направлению усилию, с которым объект действует на опору, согласно третьему закону Ньютона.

Система между некоторой структурой и опорой, которая препятствует линейному или угловому перемещению этой структуры, называется системой опоры. Существует несколько типов опор:
- Шарнир (валик) — опора первого порядка, ограничивающая смещение в пространстве в одном измерении и обладающее реакцией опоры перпендикулярной основанию.
- Плоская опора — опора второго порядка, которая ограничивает перемещение в пространстве в двух измерениях (горизонтальном и вертикальном) и разрешает только движение вращения структуры.
Расчет равновесных систем связан с вычислением результирующего динамического момента. В ньютоновской (классической) механике момент силы определяется как векторное произведение усилия, действующего на опору, на вектор, образованный между точкой опоры и точкой приложения этого усилия. Момент силы также называют динамическим моментом или просто моментом.
Далее в статье приводится пример расчета реакции для наиболее распространенной задачи: балки с двумя опорами.
Решение задачи о реакции опоры балки
Как было сказано выше, балка с двумя опорами является типичной и наиболее простой задачей статики. Задача состоит в расчете реакций в точках А и В ввиду действующих на балку усилий.
Знание этих величин необходимо для правильного понимания диаграмм моментов и диаграмм сил данной системы, и является важной частью статики в школьных и университетских курсах. Существует компьютерная программа SkyCiv, которая предоставляет мощный инструмент по расчету таких реакций для различных равновесных систем.
Возвращаясь к поставленной выше задаче, напомним, что основным ее условием является статическое состояние, то есть отсутствие каких-либо линейных перемещений и вращений объектов. В простой физике последний факт означает, что сумма векторов всех усилий равна нулю (то есть сумма усилий, направленных вверх, равна таковым, направленным вниз). Вторым условием равновесия системы является равенство нулю динамических моментов, приложенных относительно определенной точки опоры.
Чтобы определить реакции подпорок балки, следуйте нижеизложенным двум способам решения задачи:
- используя равенство нулю суммы динамических моментов;
- используя равенство нулю суммы действующих усилий.

Первый способ: через моменты
Для начала нужно положить, что сумма всех моментов относительно точки реакции равна нулю, то есть ΣMi = 0, где Мi — момент усилия. Расчет таких моментов для нашей задачи очень прост, и состоит в перемножении действующих усилий на расстояния от точки их приложения до точки реакции.
Будем считать, что наша балка имеет длину 4 метра и расположена на двух подпорках А и В. Посредине балки вертикально вниз действует усилие в 20 кН, и нужно рассчитать реакции каждой подпорки, то есть Ay и By . Описанная задача представлена на рисунке.
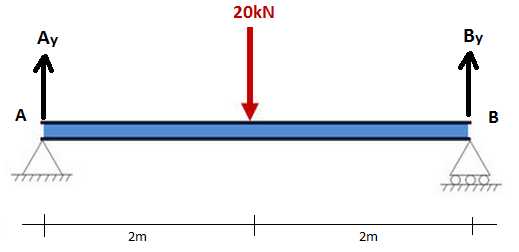
Например, рассчитаем сумму всех динамических моментов относительно точки реакции В, учитывая ее равенство нулю в равновесии. Выбор точки В, относительно которой будет проводиться расчет, является произвольным, точно так же можно выбрать точку А. Таким образом, просуммируем все динамические моменты относительно точки В, полагая эту сумму равной нулю:
ΣMв = 0 = 20*2 — A y * 4 ==> A y = 10 кН.
Отметим, что в формуле выше мы выбрали положительное направление для моментов, действующих против часовой стрелки, и отрицательное направление для моментов, действующих по часовой стрелке. Такой выбор знаков моментом является наиболее общим, однако, вы можете выбрать и наоборот. Необходимо помнить, что всегда нужно использовать одно и то же соглашение на знак моментов, начиная сначала и следуя ему на протяжении всего решения конкретной задачи.
Таким образом, мы получили нашу первую формулу, из которой определили силу реакции опоры в точке А. Аналогичная формула запишется для определения реакции в точке В. В нашем случае, ввиду симметричности действующего вертикально вниз усилия в 20 кН относительно точек подпорок, реакция в точке В будет равна таковой в точке А, то есть 10 кН.
Второй способ: через силы
Для существования равновесия сумма всех вертикальных сил должна быть равна нулю, то есть ΣF y = 0, где индекс Y определяет конкретную вертикальную силу в системе. Помните, что в данном случае мы должны включать в расчет все действующие в системе силы. Принимая во внимание последний факт, проводим суммирование всех вертикальных сил, в итоге получаем следующую формулу:
ΣF y = 0 = A y + В y — 20 кН, откуда 0 = 10 кН + В y — 20 кН, и В y = 10 кН.
Так же, как и в случае моментов сил, силы являются векторными величинами и имеют знак, здесь мы приняли за положительные силы те, которые действуют вверх, и за отрицательные те, которые действуют вниз. Выбор знака остается за вами, однако, напоминаем, что этот выбор не должен изменяться в процессе решения задачи. Отметим, что в формуле выше мы использовали результат, полученный в предыдущем пункте, когда вычислили силу реакции Ay.
Таким образом, мы решили, поставленную в начале этого параграфа задачу о расчете сил реакций опоры балки, используя при этом две системы уравнений, уравнения момента силы и уравнения силы, и получили ответы: силы реакции в точках А и В равны между собой и составляют 10 кН. Напоминаем, что физический смысл полученного равенства заключается в том, что действующая на балку внешняя сила приложена точно посередине балки. В случае ее приложения в другой точке, приведенные формулы также будут действительны и процесс расчета остается тем же самым.
Видео
Эта видеоподборка поможет вам лучше разобраться в теме и закрепить полученные знания.
liveposts.ru
Сила нормальной реакции — WiKi
Си́ла норма́льной реа́кции (иногда нормальная реакция опоры) — сила, действующая на тело со стороны опоры и направленная перпендикулярно («по нормали», «нормально») к поверхности соприкосновения. Распределена по площади зоны соприкосновения. Подлежит учёту при анализе динамики движения тела. Фигурирует в законе Амонтона — Кулона.
Одним из часто обсуждаемых примеров для иллюстрации силы нормальной реакции является случай нахождения небольшого тела на наклонной плоскости. При этом для простоты считается, что сила реакции приложена в одной точке соприкосновения.
Для расчёта в этом случае используется формула
N — сила нормальной реакции, f — сила трения покоя- |N→|=mgcosθ{\displaystyle |{\vec {N}}|=mg\cos \theta },
где |N→|{\displaystyle |{\vec {N}}|} — модуль вектора силы нормальной реакции, m{\displaystyle m} — масса тела, g{\displaystyle g} — ускорение свободного падения, θ{\displaystyle \theta } — угол между плоскостью опоры и горизонтальной плоскостью.
Выписанной формулой отражается тот факт, что вдоль направления, перпендикулярного наклонной плоскости, движения нет. Это значит, что величина силы нормальной реакции равна проекции силы тяжести mg{\displaystyle mg} на указанное направление.
Из закона Амонтона — Кулона следует, что для модуля вектора силы нормальной реакции справедливо соотношение:
- |N→|=|F→|μ,{\displaystyle |{\vec {N}}|={\frac {|{\vec {F}}|}{\mu }},}
где F→{\displaystyle {\vec {F}}} — сила трения скольжения, а μ{\displaystyle \mu } — коэффициент трения.
Поскольку сила трения покоя вычисляется по формуле
- |f→|=mgsinθ,{\displaystyle |{\vec {f}}|=mg\sin \theta ,}
можно экспериментальным путём найти такое значение угла θ{\displaystyle \theta }, при котором сила трения покоя будет равна силе трения скольжения:
- mgsinθ=μmgcosθ.{\displaystyle mg\sin \theta =\mu mg\cos \theta .}
Отсюда выражается коэффициент трения:
- μ=tg θ.{\displaystyle \mu =\mathrm {tg} \ \theta .}
ru-wiki.org
Сила тяжести, трения, реакции опоры, упругости, Архимеда, сопротивления, вес. Направление, точка приложения, природа возникновения
Тестирование онлайн
Что надо знать о силе
Сила — векторная величина. Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом
Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!
Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
Сила тяжести
На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле
Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.
Сила трения
Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:
Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила реакции опоры
Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».
Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.
Специальной формулы для нахождения этой силы нет. Обозначают ее буквой , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как
Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила упругости
Закон Гука
Сила упругости направлена противоположно деформации.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
При последовательном соединении, например, пружин жесткость рассчитывается по формуле
При параллельном соединении жесткость
Жесткость образца. Модуль Юнга.
Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.
Подробнее о свойствах твердых тел здесь.
Вес тела
Вес тела — это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору (не на предмет)!
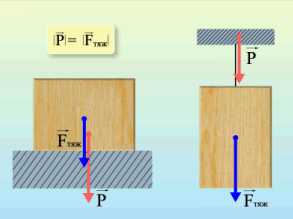
Формулы определения веса нет. Обозначается эта силы буквой .
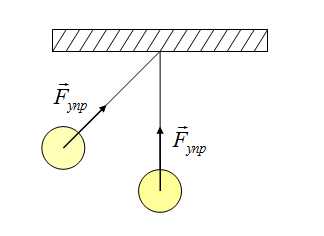
Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.
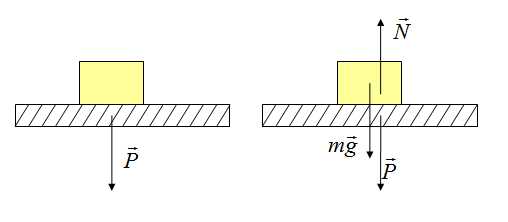
Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью. Невесомость — состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!

Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила
Обратите внимание, вес — сила, измеряется в Ньютонах. Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!
Перегрузка — отношение веса к силе тяжести
Сила Архимеда
Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:В воздухе силой Архимеда пренебрегаем.
Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше — тонет.

Электрические силы
Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона, сила Ампера, сила Лоренца, подробно рассмотрены в разделе Электричество.
Схематичное обозначение действующих на тело сил
Часто тело моделируют материальной точкой. Поэтому на схемах различные точки приложения переносят в одну точку — в центр, а тело изображают схематично кругом или прямоугольником.
Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.
Главное запомнить
1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы
Рассмотрим взаимное притяжение предмета и Земли. Между ними, согласно закону гравитации возникает сила
А сейчас сравним закон гравитации и силу тяжести
Величина ускорения свободного падения зависит от массы Земли и ее радиуса! Таким образом, можно высчитать, с каким ускорением будут падать предметы на Луне или на любой другой планете, используя массу и радиус той планеты.
Расстояние от центра Земли до полюсов меньше, чем до экватора. Поэтому и ускорение свободного падения на экваторе немного меньше, чем на полюсах. Вместе с тем, следует отметить, что основной причиной зависимости ускорения свободного падения от широты местности, является факт вращения Земли вокруг своей оси.
При удалении от поверхности Земли сила земного тяготения и ускорения свободного падения изменяются обратно пропорционально квадрату расстояния до центра Земли.
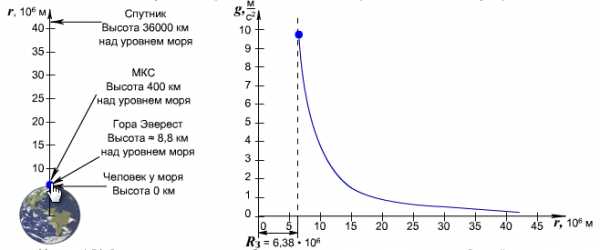
fizmat.by
Сила нормальной реакции — Википедия. Что такое Сила нормальной реакции
Материал из Википедии — свободной энциклопедии
Си́ла норма́льной реа́кции (иногда нормальная реакция опоры) — сила, действующая на тело со стороны опоры и направленная перпендикулярно («по нормали», «нормально») к поверхности соприкосновения. Распределена по площади зоны соприкосновения. Подлежит учёту при анализе динамики движения тела. Фигурирует в законе Амонтона — Кулона.
Одним из часто обсуждаемых примеров для иллюстрации силы нормальной реакции является случай нахождения небольшого тела на наклонной плоскости. При этом для простоты считается, что сила реакции приложена в одной точке соприкосновения.
Для расчёта в этом случае используется формула
N — сила нормальной реакции, f — сила трения покоя- |N→|=mgcosθ{\displaystyle |{\vec {N}}|=mg\cos \theta },
где |N→|{\displaystyle |{\vec {N}}|} — модуль вектора силы нормальной реакции, m{\displaystyle m} — масса тела, g{\displaystyle g} — ускорение свободного падения, θ{\displaystyle \theta } — угол между плоскостью опоры и горизонтальной плоскостью.
Выписанной формулой отражается тот факт, что вдоль направления, перпендикулярного наклонной плоскости, движения нет. Это значит, что величина силы нормальной реакции равна проекции силы тяжести mg{\displaystyle mg} на указанное направление.
Из закона Амонтона — Кулона следует, что для модуля вектора силы нормальной реакции справедливо соотношение:
- |N→|=|F→|μ,{\displaystyle |{\vec {N}}|={\frac {|{\vec {F}}|}{\mu }},}
где F→{\displaystyle {\vec {F}}} — сила трения скольжения, а μ{\displaystyle \mu } — коэффициент трения.
Поскольку сила трения покоя вычисляется по формуле
- |f→|=mgsinθ,{\displaystyle |{\vec {f}}|=mg\sin \theta ,}
можно экспериментальным путём найти такое значение угла θ{\displaystyle \theta }, при котором сила трения покоя будет равна силе трения скольжения:
- mgsinθ=μmgcosθ.{\displaystyle mg\sin \theta =\mu mg\cos \theta .}
Отсюда выражается коэффициент трения:
- μ=tg θ.{\displaystyle \mu =\mathrm {tg} \ \theta .}
wiki.sc
Сила нормальной реакции Википедия
Си́ла норма́льной реа́кции (иногда нормальная реакция опоры) — сила, действующая на тело со стороны опоры и направленная перпендикулярно («по нормали», «нормально») к поверхности соприкосновения. Распределена по площади зоны соприкосновения. Подлежит учёту при анализе динамики движения тела. Фигурирует в законе Амонтона — Кулона.
Одним из часто обсуждаемых примеров для иллюстрации силы нормальной реакции является случай нахождения небольшого тела на наклонной плоскости. При этом для простоты считается, что сила реакции приложена в одной точке соприкосновения.
Для расчёта в этом случае используется формула
N — сила нормальной реакции, f — сила трения покоя- |N→|=mgcosθ{\displaystyle |{\vec {N}}|=mg\cos \theta },
где |N→|{\displaystyle |{\vec {N}}|} — модуль вектора силы нормальной реакции, m{\displaystyle m} — масса тела, g{\displaystyle g} — ускорение свободного падения, θ{\displaystyle \theta } — угол между плоскостью опоры и горизонтальной плоскостью.
Выписанной формулой отражается тот факт, что вдоль направления, перпендикулярного наклонной плоскости, движения нет. Это значит, что величина силы нормальной реакции равна проекции силы тяжести mg{\displaystyle mg} на указанное направление.
Из закона Амонтона — Кулона следует, что для модуля вектора силы нормальной реакции справедливо соотношение:
- |N→|=|F→|μ,{\displaystyle |{\vec {N}}|={\frac {|{\vec {F}}|}{\mu }},}
где F→{\displaystyle {\vec {F}}} — сила трения скольжения, а μ{\displaystyle \mu } — коэффициент трения.
Поскольку сила трения покоя вычисляется по формуле
- |f→|=mgsinθ,{\displaystyle |{\vec {f}}|=mg\sin \theta ,}
можно экспериментальным путём найти такое значение угла θ{\displaystyle \theta }, при котором сила трения покоя будет равна силе трения скольжения:
ru-wiki.ru
Определение и физическая причина возникновения силы реакции опоры. Примеры решения задач
Задачи на равновесие в физике рассматриваются в разделе статики. Одной из важных сил, которая присутствует в любой механической системе, находящейся в равновесии, является сила реакции опоры. Что она собой представляет и как ее можно вычислить? Эти вопросы подробно раскрываются в статье.

Каждый из нас ежедневно ходит по поверхности земли или по полу, открывает дверь, сидит на стуле, облокотившись на стол, поднимается по лестничной площадке. Во всех этих случаях существует сила реакции опоры, которая обеспечивает возможность осуществления перечисленных действий. Эту силу в физике обозначают буквой N и называют нормальной.
В соответствии с определением, нормальная сила N — это сила, с которой опора действует на тело, находящееся с ней в физическом контакте. Нормальной ее называют потому, что она направлена вдоль нормали (перпендикуляра) к поверхности.
Нормальная реакция опоры всегда возникает, как ответное действие внешней силы на ту или иную поверхность. Чтобы это понять, следует вспомнить третий закон Ньютона, который гласит, что любому действию существует противодействие. Когда тело давит на опору, опора оказывает воздействие на тело с такой же по модулю силой, что и тело на нее.
Причина появления нормальной силы N
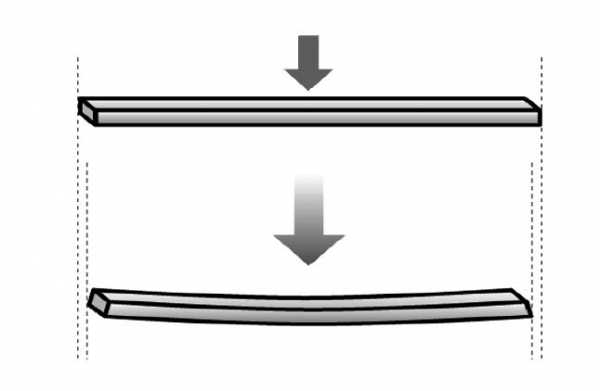
Эта причина кроется в силе упругости. Если два твердых тела, независимо от материалов, из которых они сделаны, привести в соприкосновение и слегка прижать друг к другу, то каждое из них начинает деформироваться. В зависимости от величины воздействующих сил деформация изменяется. Например, если на тонкую доску, находящуюся на двух опорах, поставить груз массой 1 кг, то она слегка прогнется. Если же этот груз увеличить до 10 кг, величина деформации возрастет.
Появившаяся деформация стремится восстановить исходную форму тела, создавая при этом некоторую упругую силу. Последняя оказывает воздействие на тело и называется реакцией опоры.
Если посмотреть на более глубокий, масштабный уровень, то можно увидеть, что сила упругости появляется в результате сближения атомных оболочек и последующего их отталкивания из-за действия принципа Паули.
Как рассчитывать нормальную силу?
Выше уже было сказано, что ее величина по модулю равна результирующей силе, направленной перпендикулярно к рассматриваемой поверхности. Это означает, что для определения реакции опоры необходимо сначала составить уравнение движения, пользуясь вторым законом Ньютона, вдоль прямой, которая перпендикулярна поверхности. Из этого уравнения можно найти величину N.
Другой способ определения силы N заключается в привлечении физического условия равновесия моментов сил. Этот способ удобно использовать, если в системе имеются оси вращения.
Моментом силы называют величину, которая равна произведению действующей силы на длину рычага относительно оси вращения. В системе, находящейся в равновесии, сумма моментов сил всегда равна нулю. Последнее условие используется для нахождения неизвестной величины N.

Отметим, что при наличии одной опоры в системе (одной оси вращения), нормальная сила всегда будет создавать нулевой момент. Поэтому для таких задач следует применять описанную выше методику с использованием ньютоновского закона для определения реакции опоры.
Конкретной формулы для расчета силы N не существует. Она определяется в результате решения соответствующих уравнений движения или равновесия для рассматриваемой системы тел.
Ниже приведем примеры решения задач, где покажем, как вычислять нормальную реакцию опоры.
Задача с наклонной плоскостью

Брус находится в покое на наклонной плоскости. Масса бруса равна 2 кг. Плоскость к горизонту наклонена под углом 30o. Чему равна нормальная сила N?
Данная задача является не сложной. Чтобы получить ответ на нее, достаточно рассмотреть все силы, которые действуют вдоль перпендикулярной к плоскости линии. Таких сил всего две: N и проекция силы тяжести Fgy. Поскольку они действуют в разных направлениях, то уравнение Ньютона для системы примет вид:
m*a = N — Fgy
Так как брус находится в покое, то ускорение равно нулю, поэтому уравнение преобразуется в следующий вид:
N = Fgy
Проекцию силы тяжести на нормаль к плоскости найти не сложно. Из геометрических соображений находим:
N = Fgy = m*g*cos(α)
Подставляя данные из условия, получаем: N = 17 Н.
Задача с двумя опорами
На две опоры положена тонкая доска, масса которой является незначительной. На 1/3 от левой опоры на доску положили груз массой 10 кг. Необходимо определить реакции опор.
Поскольку в задаче имеются две опоры, то для ее решения можно воспользоваться условием равновесия через моменты сил. Для этого положим сначала, что одна из опор является осью вращения. Например, правая. В этом случае условие равновесия моментов примет вид:
N1*L — m*g*2/3*L = 0
Здесь L — расстояние между опорами. Из этого равенства следует, что реакция N1 левой опоры равна:
N1 = 2/3*m*g = 2/3*10*9,81 = 65,4 Н.
Аналогичным образом находим реакцию правой опоры. Уравнение моментов для этого случая имеет вид:
m*g*1/3*L — N2*L = 0.
Откуда получаем:
N2 = 1/3*m*g = 1/3*10*9,81 = 32,7 Н.
Отметим, что сумма найденных реакций опор равна силе тяжести груза.
fb.ru