Правило Верещагина»Метод Верещагина»Способ Верещагина

 

 

Заказать решение           Способ оплаты

 

 Недостатком метода Мора является необходимость получать значения внутренних силовых факторов, входящих в подинтегральные выражения формул (2.18) и (2.19), в общем виде, как функций от z, что становится достаточно трудоемким уже при двух – трех участках разбиения в балках и особенно – в рамах.

Оказывается, что от этого недостатка можно уйти, если непосредственное интегрирование в формулах Мора заменить так называемым перемножением эпюр. Такая замена возможна в тех случаях, когда хотя бы одна из перемножаемых эпюр является прямолинейной. Этому условию соответствуют все системы, состоящие из прямолинейных стержней. Действительно, в таких системах эпюра, построенная от обобщенной единичной силы, всегда будет прямолинейной.

Способ вычисления интеграла Мора путем замены непосредственного интегрирования перемножением соответствующих эпюр называется способом (или правилом) Верещагина

и заключается в следующем: чтобы перемножить две эпюры, из которых хотя бы одна является прямолинейной, нужно площадь одной эпюры (если есть криволинейная эпюра, то обязательно ее площадь) умножить на ординату другой эпюры, расположенную под центром тяжести первой.

Докажем справедливость этого правила. Рассмотрим две эпюры (рис.28). Пусть одна из них (Mn) является грузовой и имеет криволинейное очертание, а вторая  соответствует единичной нагрузке и является линейной.

Из рис.28 следует, что  Подставим значения  в выражение

где — дифференциал площади  эпюры  Mn.

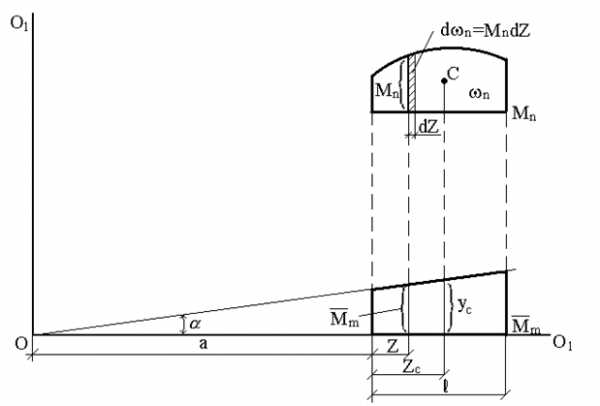Рис. 28

Интеграл представляет собой статический момент площади относительно оси О – О1, при этом:

где zc – абсцисса центра тяжести площади , тогда:

Учитывая, что  получим:
                                           (2.20)
 Выражение (2.20) определяет результат перемножения двух эпюр, а не перемещения. Чтобы получить перемещение, этот результат нужно разделить на жесткость, соответствующую внутренним силовым факторам, стоящим под знаком интеграла.

 

Основные варианты перемножения эпюр

 

Очевидно, что разнообразие приложенных нагрузок и геометрических схем конструкций приводит к различным, с точки зрения геометрии, перемножаемым эпюрам. Для реализации правила Верещагина нужно знать площади геометрических фигур и координаты их центров тяжести. На рис.29 представлены некоторые основные варианты, возникающие в практических расчетах.

Для перемножения эпюр сложной формы их необходимо разбивать на простейшие. Например, для перемножения двух эпюр, имеющих вид трапеции, нужно одну из них разбить на треугольник и прямоугольник, умножить площадь каждого из них на ординату второй эпюры, расположенную под соответствующим центром тяжести, и результаты сложить. Аналогично поступают и для умножения криволинейной трапеции на любую линейную эпюру.

Если указанные выше действия проделать в общем виде, то получим для таких сложных случаев формулы, удобные для использования в практических расчетах (рис.30). Так, результат перемножения двух трапеций (рис.30,а):

                               (2.21)

 

Рис. 29

По формуле (2.21) можно перемножить и эпюры, имеющих вид «перекрученных» трапеций (рис.30,б), но при этом произведение ординат, расположенных по разные стороны от осей эпюр, учитывается со знаком минус.

Если одна из перемножаемых эпюр очерчена по квадратной параболе (что соответствует нагружению равномерно распределенной нагрузкой), то для перемножения со второй (обязательно линейной) эпюрой ее рассматривают как сумму (рис.30,в) или разность (рис.30,г) трапециидальной и параболической эпюр. Результат перемножения в обоих случаях определяется формулой:

                                   (2.22)

но значение  f при этом определяется по-разному (рис. 30, в, г).

Рис. 30

Возможны случаи, когда ни одна из перемножаемых эпюр не является прямолинейной, но хотя бы одна из них ограничена ломаными прямыми линиями. Для перемножения таких эпюр их предварительно разбивают на участки, в пределах каждого из которых по крайней мере одна эпюра являетя прямолинейной.
Рассмотрим использование правила Верещагина на конкретных примерах.

 

Пример 15. Определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис.31,а), способом Верещагина.

Последовательность расчета способом Верещагина – такая же, как и в методе Мора, поэтому рассмотрим три состояния балки: грузовое – при действии распределенной нагрузки q; ему соответствует эпюра Mq (рис.31,б), и два единичных состояния  — при действии силы  приложенной в точке С (эпюра , рис.31,в), и момента , приложенного в точке В (эпюра , рис.31,г).

Прогиб балки в середине пролета:

.

Аналогичный результат был получен ранее методом Мора (см. пример 13). Следует обратить внимание на тот факт, что перемножение эпюр выполнялось для половины балки, а затем, в силу симметрии, результат удваивался. Если же площадь всей эпюры Mq умножить на расположенную под ее центром тяжести ординату эпюры (на рис.31,в), то величина перемещения будет совершенно иной и неправильной так как эпюра  ограничена ломаной линией. На недопустимость такого подхода уже указывалось выше.

А при вычислении угла поворота сечения в точке В можно площадь эпюры Mq умножить на расположенную под ее центром тяжести ординату эпюры (, рис.31,г), так как эпюра  ограничена прямой линией:

Этот результат также совпадает с результатом, полученным ранее методом Мора (см. пример 13).

 

Рис. 31

 

Пример 16. Определить горизонтальное и вертикальное перемещения точки А в раме (рис.32,а).

Как и в предыдущем примере, для решения задачи необходимо рассмотреть три состояния рамы: грузовое и два единичных. Эпюра моментов MF, соответствующая первому состоянию, представлена на рис.32,б. Для вычисления горизонтального перемещения прикладываем в точке А по направлению искомого перемещения (т.е. горизонтально) силу , а для вычисления вертикального перемещения силу  прикладываем вертикально (рис.32,в,д). Соответствующие эпюры  и  показаны на рис.32,г,е.

Горизонтальное перемещение точки А:

При вычислении  на участке АВ трапеция (эпюра  MF) разбита на треугольник и прямоугольник, после чего треугольник с эпюры «умножен» на каждую из этих фигур. На участке ВС криволинейная трапеция разделена на криволинейный треугольник и прямоугольник, а для перемножения эпюр на участке СД использована формула (2.21).

Знак » — «, полученный при вычислении , означает, что точка А перемещается по горизонтали не влево (в этом направлении приложена сила ), а вправо.
Вертикальное перемещение точки А:

Здесь знак » — » означает, что точка А перемещается вниз, а не вверх.

Отметим, что единичные эпюры моментов, построенные от силы , имеют размерность длины, а единичные эпюры моментов построенные от момента , являются безразмерными.

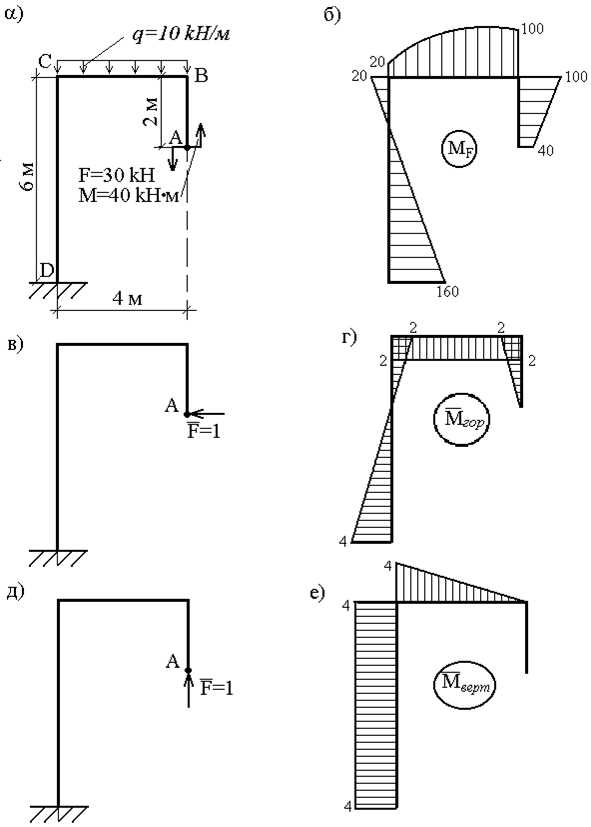
Рис.32

Пример 17. Определить вертикальное перемещение точки А плоско-пространственной системы (рис.33,а).

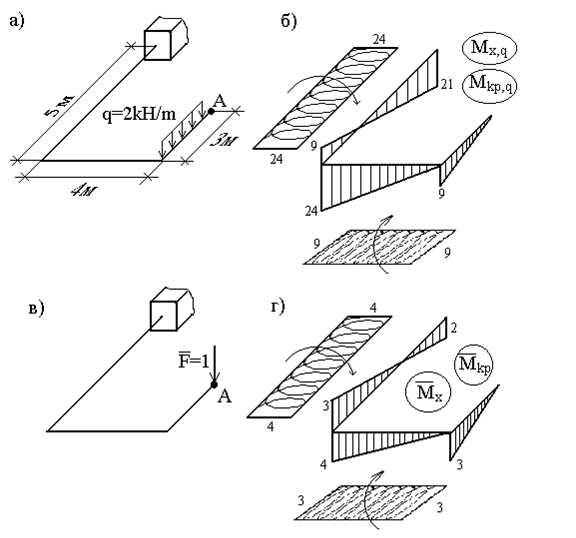
Рис.23

 Как известно (см. гл.1), в поперечных сечениях стержней плоско-пространственной системы возникают три внутренних силовых фактора: поперечная сила Qy, изгибающий момент Mx и крутящий момент Mкр. Так как влияние поперечной силы на величину перемещения незначительно (см. пример 14, рис.27), то при вычислении перемещения методом Мора и Верещагина из шести слагаемых остаются только два.

Для решения задачи построим эпюры изгибающих моментов Mx,q и крутящих моментов Мкр,q от внешней нагрузки (рис.33,б), а затем в точке А приложим силу  по направлению искомого перемещения, т.е. вертикального (рис.33,в), и построим единичные эпюры изгибающих моментов  и крутящих моментов (рис.33,г). Стрелками на эпюрах крутящих моментов показаны направления закручивания соответствующих участков плоско-пространственной системы.

Вертикальное перемещение точки А:

При перемножении эпюр крутящих моментов произведение берется со знаком «+», если стрелки, указывающие направление кручения, сонаправленны, и со знаком » — » – в противном случае.

 

Заказать решение

funnystudy.ru

Правило Верещагина (способ перемножения эпюр)

Во многих случаях интегрирования по Мору можно избежать и применить способ«перемножения» эпюр. Одним из таких способов является способ Симпсона, но также можно определить перемещения по способу (правилу) Верещагина. Этот способ А.К. Верещагин предложил в 1924 году, будучи студентом.

Рассмотрим последовательность действий по правилу Верещагина. Начальный этап такой же, как по формуле Мора и способу Симпсона, т.е. вначале строится грузовая эпюра от действующих нагрузок (действительное состояние), затем рассматриваем балку во вспомогательном состоянии. Вспомогательное состояние получается следующим образом: сначала всю заданную нагрузку нужно удалить, затем

приложить «единичный силовой фактор» в том месте, где требуется определить перемещение, и по направлению этого искомого перемещения. Причем, когда определяем линейное перемещение (прогиб балки), то в качестве «единичного силового фактора» принимается сосредоточенная сила, равная единице , а если требуется найти угол поворота, то приложить следует сосредоточенную пару сил, момент, равный единице. Строится эпюра единичных моментов или эпюра от единичной нагрузки. Далее перемещение вычисляется по формуле:

, где в числителе — произведение площади грузовой эпюры на ординату  единичной (обязательно прямолинейной), взятой под центром тяжести грузовой эпюры, а в знаменателе — жесткость сечения.

Этот способ становится понятным,если доказать, что результат перемножения двух эпюр ,одна и которых произвольна ,а другая линейна, равен

 произведению площади грузовой эпюры на ординату  единичной,  взятой под центром тяжести грузовой эпюры.

Следует иметь в виду, что способы «перемножения» эпюр  применимы только при наличии двух условий:

1. Изгибная жесткость балки на рассматриваемом участке должна быть постоянной(EI=Const),
2. Одна из двух эпюр моментов на этом участке (грузовая или единичная)   должна быть обязательно линейной. При этом обе эпюры не должны в пределах данного участка иметь перелома. 

Пусть грузовая эпюра произвольна, а единичная линейна (так как единичной нагрузкой бывает обычно либо сосредоточенная сила, либо пара сил, то единичная эпюра М⁰  оказывается ограниченной прямыми линиями). Пусть грузовая эпюра М(z) имеет криволинейное очертание, а эпюра М⁰ – прямолинейное (см. рисунок). Произведение   можно рассматривать как элемент  площади эпюры М, заштрихованной на рисунке.

Так как ордината М⁰ равна то произведение  , а весь интеграл , где

 — статический момент площади эпюры М(z) относительно оси ординат

Но! Статический момент площади ,как известно, это произведение самой площади на координату центра тяжести. Тогда

, где  — это

ордината в единичной эпюре, расположенной под центром тяжести грузовой эпюры. Окончательно, перемещение равно:

Таким образом, результат перемножения двух эпюр равен произведению площади грузовой эпюры на ординату другой (обязательно прямолинейной), взятой под центром тяжести грузовой эпюры.

Правило знаков: если обе «перемножаемые» ординаты в двух эпюрах расположены по одну сторону от оси эпюры (то есть они одного знака), то перед их произведением мы должны поставить знак «плюс», а если они по разные стороны от оси эпюры, то перед произведением ставим знак «минус».

prosopromat.ru

метод Верещагина

Лекция 13 (продолжение). Примеры решения на вычисление перемещений методом Мора-Верещагина и задачи для самостоятельного решения

 

Определение перемещений в балках

Пример 1.

Определить перемещение точки К балки (см. рис.) при помощи интеграла Мора.

Решение.

1) Составляем уравнение изгибающего момента от внешней силы M_F.

2) Прикладываем в точке К единичную силу F = 1.

3) Записываем уравнение изгибающего момента от единичной силы .

4) Определяем перемещения

 

Пример 2.

Определить перемещение точки К балки по способу Верещагина.

Решение.

1) Строим грузовую эпюру.

2) Прикладываем в точке К единичную силу.

3) Строим единичную эпюру.

4) Определяем прогиб

;     ;

 

Пример 3.

Определить углы поворота на опорах А и В для заданной балки (см. рис.).

Решение.

Строим эпюры от заданной нагрузки и от единичных моментов, приложенных в сечениях А и В (см. рис.). Искомые перемещения определяем с помощью интегралов Мора

,

, которые вычисляем по правилу Верещагина.

Находим параметры эпюр

    C₁ = 2/3,     C₂ = 1/3,

а  затем  и  углы  поворота  на опорах А и В  

 

Пример 4.

Определить угол поворота сечения  С для заданной балки (см. рис.).

Решение.

Определяем опорные реакции R_A=R_B,

,     ,R_A = R_B = qa.

Строим эпюры изгибающего момента от заданной нагрузки и от единичного момента, приложенного в сечении С, где ищется угол поворота. Интеграл Мора вычисляем по правилу Верещагина.  Находим  параметры  эпюр      

        C₂ = —C₁ = -1/4,

а по ним и искомое перемещение

.

 

Пример 5.

Определить  прогиб  в  сечении С для заданной балки (см. рис.).

Решение.

1. Построение эпюр изгибающих моментов.

Эпюра M_F  (рис. б)

Опорные реакции:

ВЕ:   ,,

,   R_B + R_E = F,   R_E = 0;

АВ:  ,R_А = R_В = F;        ,.

Вычисляем моменты в характерных точках  ,M_B = 0,   M_C = Fa   и   строим   эпюру  изгибающего момента от заданной нагрузки.

Эпюра (рис. в).

В сечении С, где ищется прогиб, прикладываем единичную силу и строим от нее эпюру изгибающего момента, вычисляя сначала опорные реакцииВЕ — ,,= 2/3;,,= 1/3,   а затем моменты в характерных точках,,.

2. Определение искомого прогиба. Воспользуемся правилом Верещагина и вычислим предварительно параметры эпюр и:

  ,    

    

Прогиб сечения С

.

 

Пример 6.

Определить   прогиб   в   сечении С для заданной балки (см. рис.).

Решение.

Строим эпюры изгибающих моментов от заданной нагрузки и от единичной силы, приложенной в точке С. Пользуясь правилом Верещагина, вычисляем параметры эпюр ,

     

и находим искомый прогиб

.

 

Пример 7.

Определить прогиб в сечении С для заданной балки (см. рис.).

Решение.

1. Построение эпюр изгибающих моментов.

Опорные реакции:

,   ,     R_A = 2qa,

,  R_A + R_D = 3qa,     R_D = qa.   

Строим эпюры изгибающих моментов от заданной нагрузки и от единичной силы, приложенной в точке С. 

2. Определение перемещений. Для вычисления интеграла Мора воспользуемся формулой Симпсона, последовательно применяя ее к каждому из трех участков, на которые разбивается балка.

Участок АВ:   

Участок ВС:   

Участок СD:   

Искомое перемещение

.

 

Пример 8.

Определить прогиб сечения А и угол поворота сечения Е для заданной балки (рис. а).

Решение.

1. Построение эпюр изгибающих моментов.

Эпюра М_F (рис. в). Определив опорные реакции

,   ,R_B = 19qa/8,    

,     R_D = 13qa/8, строим эпюры поперечной силы Q и изгибающего момента   М_F  от заданной нагрузки.

Эпюра  (рис. д). В сеченииА, где ищется прогиб, прикладываем единичную силу и строим от нее эпюру изгибающего момента.

Эпюра (рис. е). Эта эпюра строится от единичного момента, приложенного в сеченииЕ, где ищется угол поворота.

2. Определение перемещений. Прогиб сечения А находим, пользуясь правилом Верещагина. Эпюру М_F на участках ВС и CD разбиваем на простые части (рис. г). Необходимые вычисления представляем в виде таблицы.

 

Номер части	1	2	3	4	5	6	7
	—qa3/6	2qa3/3	—qa3/2	qa3/4	qa3/4	—qa3	—qa3/2
Ci	-3a/4	-3a/4	-5a/6	-2a/3	—a/3	—a/6	0
	qa4/8	—qa4/2	5qa4/12	—qa4/6	—qa4/12	qa4/6	0	—qa4/24

 

Получаем     .

Знак “минус” в результате означает, что точка А перемещается не вниз, как была направлена единичная сила, а вверх.

Угол поворота сечения Е находим двумя способами: по правилу Верещагина и по формуле Симпсона.

По правилу Верещагина, перемножая эпюры M_F и , по аналогии с предыдущим получим

,

.

Для нахождения угла поворота по формуле Симпсона вычислим предварительно изгибающие моменты посредине участков:

Искомое перемещение, увеличенное в EI_x раз,

.

 

Пример 9.

Определить, при каком значении коэффициента k прогиб сечения С будет равен нулю. При найденном значении k построить эпюру изгибающего момента и изобразить примерный вид упругой линии балки (см. рис.).

 

Решение.

Строим   эпюры  изгибающих моментов   от   заданной    нагрузки и от единичной силы, приложенной в сечении С, где ищется прогиб.

По условию задачи V_C = 0. С другой стороны, . Интеграл на участкеАВ вычисляем по формуле Симпсона, а на участке ВС – по правилу Верещагина.

Находим предварительно

Перемещение сечения С      ,

 

Отсюда     ,.

При найденном значении k определяем значение опорной реакции в точке А:   ,,, исходя из которого находим положение точки экстремума на эпюреМ согласно условию   .

По значениям момента в характерных точках

,       ,

строим эпюру изгибающего момента (рис. г).

 

Пример 10.

Определить вертикальное перемещение точки В консольной балки, изображенной на рисунке.

Решение.

Строим эпюру изгибающих моментов М от действия внешней сосредоточенной силы F:   М_В = 0, М_А = –F2l (эпюра линейная).

По условию задачи требуется определить вертикальное перемещение у_В точки В консольной балки, поэтому строим единичную эпюру от действия вертикальной единичной силыF_i  = 1, приложенной в точке В.

Учитывая, что консольная балка состоит из двух участков с разной жесткостью на изгиб, эпюры иМ перемножаем с помощью правила Верещагина по участкам отдельно. Эпюры М ипервого участка перемножаем по формуле, а эпюры второго участка – как площадь эпюрыМ второго участка Fl²/2 на ординату 2l/3 эпюры второго участка под центром тяжести треугольной эпюрыМ этого же участка.

В этом случае формула дает:

 

Пример 11.

Определить вертикальное перемещение точки В однопролетной балки, изображенной на рисунке. Балка имеет постоянную по всей длине жесткость на изгиб EI.

Решение.

Строим эпюру изгибающих моментов М от действия внешней распределенной нагрузки: М_А  = 0; M_D  = 0;

.

Прикладываем в точке В единичную вертикальную силу F_i = 1 и строим эпюру (см. рис.):

откуда R_a = 2/3;

 откуда R_d = 1/3, поэтому M_a = 0; M_d  = 0; .

Разделим рассматриваемую балку на 3 участка. Перемножение эпюр 1-го и 3-го участков не вызывает трудностей, так как перемножаем треугольные эпюры. Для того чтобы применить правило Верещагина ко 2-му участку, разобьем эпюру М 2-го участка на две составляющие эпюры: прямоугольную и параболическую с площадью (см. таблицу).

Центр тяжести параболической части эпюры М лежит посередине 2-го участка.

Таким образом, формула при использовании правила Верещагина дает:

 

Пример 12.

Определить максимальный прогиб в двухопорной балке, нагруженной равномерно распределенной нагрузкой интенсивности q (см. рис.).

Решение.

Находим изгибающие моменты:

— от заданной нагрузки

— от единичной силы, приложенной в точке С, где ищется прогиб .

Вычисляем искомый наибольший прогиб, который возникает в среднем сечении балки

 

Пример 13.

Определить прогиб в точке В балки, показанной на рисунке.

Решение.

Строим эпюры изгибающих моментов от заданной нагрузки и единичной силы, приложенной в точке В. Чтобы перемножить эти эпюры, надо балку разбить на три участка, так как единичная эпюра ограничена тремя различными прямыми.

Операция перемножения эпюр на втором и третьем участках осуществляется просто. Затруднения возникают при вычислении площади и координат центра тяжести основной эпюры на первом участке. В таких случаях намного упрощает решение задачи построение расслоенных эпюр. При этом удобно одно из сечений принять условно за неподвижное и строить эпюры от каждой из нагрузок, приближаясь справа и слева к этому сечению. Целесообразно за неподвижное принимать сечение в месте перелома на эпюре единичных нагрузок.

Расслоенная эпюра, в которой за неподвижное принято сечение В, представлена на рисунке. Вычислив площади составных частей расслоенной эпюры и соответствующие им ординаты единичной эпюры, получаем

.

 

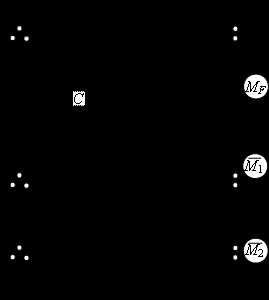
Пример 14.

Определить перемещения в точках 1 и 2 балки (рис. а).

 

Решение.

Приведем эпюры М и Q для балки при а=2 м; q=10 кН/м; С=1,5а; М=0,5qa²; Р=0,8qa; М₀=М; =200 МПа (рис.б и в).

Далее определяем перемещения в точках 1 и 2 балки (рис. а). Состояние балки под действием заданной нагрузки обозначим q.

Определим вертикальное перемещение центра сечения, где приложен сосредоточенный момент. Для  этого рассмотрим балку в состояниипод действием только сосредоточенной силыприложенной в точке 1 перпендикулярно оси балки (по направлению искомого перемещения) (рис. г).

Вычислим опорные реакции, составив три уравнения равновесия

Проверка 

Реакции найдены верно.

Для построения эпюры рассмотрим три участка (рис. г).

1 участок

2 участок

3 участок

По этим данным строим эпюру (рис. д) со стороны растянутых волокон.

Определим по формуле Мора с помощью правила Верещагина. При этом криволинейную эпюру, на участке между опорами, можно представить в виде сложения трех эпюр. Стрелка

Знак «минус» означает, что точка 1 перемещается вверх (в направлении противоположном ).

Определим вертикальное перемещение точки 2, где приложена сосредоточенная сила. Для этого рассмотрим балку в состояниипод действием только сосредоточенной силыприложенной в точке 2 перпендикулярно оси балки (по направлению искомого перемещения) (рис. е).

Эпюра строится аналогично предыдущей.

Далее по формуле Мора

Точка 2 перемещается вверх.

Определим угол поворота сечения, где приложен сосредоточенный момент.

Для этого рассмотрим балку в состоянии под действием только сосредоточенного момента, приложенного в сечении 1 против часовой стрелки (рис. ж).

studfiles.net

АНДРЕЙ КОНСТАНТИНОВИЧ ВЕРЕЩАГИН | ПроСопромат.ру

Андрей Константинович Верещагин (1896  -1959) — талантливый советский ученый и изобретатель — родился  в г. Козлове Тамбовской области. В 30-х годах двадцатого века город Козлов был переименован в Мичуринск в честь учёного-селекционера И.В. Мичурина.   Отец Верещагина был прекрасным врачом, о котором до сих пор хранят память в городе, мать также из семьи врача, однако Андрей Константинович по каким-то причинам не захотел продолжать профессию и в 1921 г. поступил в Московский институт инженеров транспорта.

В 1924 г., будучи студентом, А.К. Верещагин предложил наглядный способ вычисления интеграла Мора, а именно правило для вычисления интеграла Максвелла — Мора для частного случая прямого стержня постоянного поперечного сечения —  «Каждое из слагаемых, входящих в интеграл Мора, равно произведению площади нелинейной эпюры изгибающих моментов на ординату линейной эпюры ,соответствующую центру тяжести нелинейной, деленному на жесткость сечения данного участка балки». Главным образом, в сопромате имя Верещагина связывают с этим способом.

После окончания теоретического курса Андрей Константинович оставил институт и поступил на физико-математический факультет Московского университета, который окончил в 1930 г. Затем он работал в различных научно-исследовательских институтах и стал крупным специалистом в области минной электротехники.  А.К. Верещагин считается основоположником отечественной школы минной электротехники. В 1937 — 1938 гг. преподавал в Военно-морской академии, а в 1947 — 1948 гг. — во Всесоюзном заочном энергетическом институте.

Во время Великой Отечественной войны Верещагин принимал активное участие в обороне Одессы и Севастополя.

В 1956 г.  А.К. Верещагин вышел в отставку по состоянию здоровья в звании инженера-полковника. А.К. Верещагин внес большой вклад в развитие военной техники.

Запись опубликована 01.10.2014 автором admin в рубрике Великие учёные.

prosopromat.ru

Определение перемещений способом Верещагина — Строительная механика

 

Способ Верещагина: : интеграл перемножения двух функций, ограничивающих эпюры, причем одна из которых представляет собой прямую линию, а другая является криволинейной, равен произведению площади фигуры криволинейной эпюры, на ординату из эпюры, ограниченной прямой линией, которую берут под центром тяжести площади эпюры, ограниченной произвольной линией.

 

Способ Верещагина

 

 

 

Соответственно, перемещение:

 

 

Ордината y_c должна быть взята из эпюры, ограниченной прямой линией.

 

 

Способ Верещагина

 

Примеры перемножения эпюр, представляющих различные фигуры:

 

Рисунок 1. Перемножение различных фигур способом Верещагина

 

— перемножение треугольников (рис. 1, а и б):

 

 

— перемножение трапеций (рис. 1, б и в):

 

 

 

Перемножение различных фигур

 

— перемножение для выпуклой криволинейной фигуры:

 

 

— перемножение для вогнутой криволинейной фигуры:

 

 

Произведение ординат эпюр, расположенных по одну сторону от нулевой линии, берется со знаком «+», по разные стороны – со знаком «–». Формула для трапеций применима и когда эпюры в виде треугольников – в этих случаях треугольник рассматривается как трапеция с нулевой стороной.

Когда ни одна из эпюр не ограничена одной прямой линией, но одна из них или ограничена несколькими прямыми линиями, как на рисунке ниже, то в этом случае эти эпюры разбивают на отдельные участки, так, что на каждом из них эпюры ограничены одной прямой линией:

Пример задачи с решением.

 

 

Перемножение эпюр

 

 

 

5stroymeh.ru

Определение перемещения методом Мора. Правило Верещагина

УО «БГУИР»

кафедра инженерной графики

РЕФЕРАТ

на тему:

«ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ МЕТОДОМ МОРА. ПРАВИЛО ВЕРЕЩАГИНА»

МИНСК, 2008

Рассмотрим теперь общий метод определения перемещений, пригодный для любой, линейно деформируемой системы при любой нагрузке. Этот метод предложен выдающимся немецким ученым О. Мором.

Пусть, например, требуется определить вертикальное перемещение точки А балки, представленной на рис. 7.13, а. Заданное (грузовое) состояние обозначим буквой к. Выберем вспомогательное состояние той же балки с единичной

силой, действующей в точке A и в направлении искомого перемещения. Вспомогательное состояние обозначим буквой i(рис. 7.13,6).

Вычислим работу внешних и внутренних сил вспомогательного состояния на перемещениях, вызванных действием сил грузового состояния.

Работа внешних сил будет равна произведению единичной силы на искомое перемещение ya

а работа внутренних сил по абсолютной величине равна интегралу

Имеем

или

(1)

Формула (7.33) и есть формула Мора (интеграл Мора), которая дает возможность определить перемещение в любой точке линейно-деформируемой системы.

В этой формуле подынтегральное произведение MiMkположительно, если оба изгибающих момента имеют одинаковый знак, и отрицательно, если Miи Мк имеют разные знаки.

Если бы мы определяли угловое перемещение в точке А, то в состоянии iследовало бы приложить в точке А момент, равный единице (без размерности).

Обозначая буквой Δ любое перемещение (линейное или угловое), формулу (интеграл) Мора напишем в виде

(2)

В общем случае аналитическое выражение Miи Мк может быть различным на разных участках балки или вообще упругой системы. Поэтому вместо формулы (2) следует пользоваться более общей формулой

(3)

Если стержни системы работают не на изгиб, а на растяжение (сжатие), как, например, в фермах, то формула Мора имеет вид

(4)

В этой формуле произведение NiNKположительно, если оба усилия растягивающие или оба сжимающие. Если стержни одновременно работают и на изгиб и на растяжение (сжатие), то в обычных случаях, как показывают сравнительные расчеты, перемещения можно определять, учитывая лишь изгибающие моменты, так как влияние продольных сил весьма мало.

По тем же соображениям, как отмечалось ранее, в обычных случаях можно не учитывать влияния поперечных сил.

Вместо непосредственного вычисления интеграла Мора можно пользоваться графо-аналитическим приемом «способом перемножения эпюр», или правилом Верещагина.

Рассмотрим две эпюры изгибающих моментов, из которых одна Мк имеет произвольное очертание, а другая Мi прямолинейна (Рис 7.14, а и б).

Сечение стержня на участке AВ будем считать постоянным. В этом случае

(5)

Величина MKdzпредставляет собой элементарную площадь dωk эпюры Мк (заштрихована на рисунке). Таким образом,

(6)

Но

(7)

следовательно,

(8)

Но

представляет собой статический момент площади эпюры Мк относительно некоторой оси у, проходящей через точку О, равный ωkzc, где ωk — площадь эпюры моментов; zс — расстояние от оси у до центра тяжести эпюры Мк. Из чертежа видно, что (9)

где Мсi — ордината эпюры Mi, расположенная под центром тяжести эпюры Мк (под точкой С). Следовательно,

(10)

т. е. искомый интеграл равен произведению площади эпюры Мк (любой по очертанию) на расположенную под ее центром тяжести ординату прямолинейной эпюры Мсi. Значение величины ωкМсi считается положительным, если обе эпюры располагаются по одну сторону стержня, и отрицательным, если они располагаются по разные стороны. Положительный результат перемножения эпюр означает, что направление перемещения совпадает с направлением единичной силы (или момента).

Необходимо помнить, что ордината Мсiберется обязательно в прямолинейной эпюре. В том частном случае, когда обе эпюры прямолинейные, можно умножить площадь любой из них на соответствующую ординату другой.

Для стержней переменного сечения правило Верещагина перемножения эпюр неприменимо, так как в этом случае уже нельзя выносить величину EJиз-под знака интеграла. В этом случае следует выразить EJкак функцию абсциссы сечения и затем уже вычислять интеграл Мора (1).

При ступенчатом изменении жесткости стержня интегрирование (или перемножение эпюр) производят для каждого участка отдельно (со своим значением EJ) и затем суммируют результаты.

В табл. 1 приведены значения площадей некоторых простейших эпюр и координат их центра тяжести.

Таблица 1

Для ускорения вычислений можно использовать готовые таблицы перемножения эпюр (табл.2).

В этой таблице, в клетках на пересечении соответствующих элементарных эпюр, приведены результаты перемножения этих эпюр.

При разбивке сложной эпюры на элементарные, представленные в табл. 1 и 7.2, следует иметь в виду, что параболические эпюры получены от действия только одной распределенной нагрузки.

В тех случаях, когда в сложной эпюре криволинейные участки получаются от одновременного действия сосредоточенных моментов, сил и равномерно распределенной нагрузки, во избежание ошибки следует сложную эпюру предварительно «расслоить», т. е. разбить ее на ряд самостоятельных эпюр: от действия сосредоточенных моментов, сил и от действия равномерно распределенной нагрузки.

Можно также применить другой прием, не требующий расслоения эпюр, а требующий лишь выделения криволинейной части эпюры по хорде, соединяющей крайние ее точки.

Покажем оба способа на конкретном примере.

Пусть, например, требуется определить вертикальное перемещение левого конца балки (рис. 7.15).

Суммарная эпюра от нагрузки представлена на рис. 7.15, а.

Таблица 7.2

Эпюра от действия единичной силы в точке А представлена на рис. 7.15, г.

mirznanii.com

Определение прогиба балки в середине пролета

Для двухопорной двутавровой балки (двутавр №12 по ГОСТ ГОСТ 8239-89) необходимо определить прогиб в середине пролета (сечение C), используя метод Мора — Верещагина. Данные для расчета указаны на схеме.

Ход выполнения расчета

Сначала строим эпюру изгибающих моментов, для рассчитываемой балки:

Расслаиваем эпюру на простейшие фигуры:

Построение единичной эпюры

Прикладываем единичное усилие по направлению искомого перемещения (в точке С) и строим от этой силы эпюры моментов:

Вычисление прогиба

Вычисляем прогиб сечения C по методу Мора — Верещагина (слева направо):

\[ { V }_{ C }=\frac { 1 }{ E{ I }_{ x } } (\frac { q{ \cdot 2 }^{ 3 } }{ 12 } \cdot \frac { 1 }{ 2 } \cdot 1+\frac { 1 }{ 2 } \cdot 2\cdot 2\cdot \frac { 2 }{ 3 } \cdot 1+\frac { 1 }{ 2 } \cdot 2\cdot 2\cdot \frac { 2 }{ 3 } \cdot 1)=\frac { 10кН{ м }^{ 3 } }{ 3E{ I }_{ x } } \]

По сортаменту двутавров выписываем значение момента инерции балки и вычисляем численное значение прогиба:

\[ { I }_{ x }=350{ см }^{ 4 } \]

\[ { V }_{ C }=\frac { 10кН{ м }^{ 3 } }{ 3E{ I }_{ x } } =\frac { 10\cdot { 10 }^{ 9 }Н\cdot { см }^{ 3 } }{ 3\cdot 2\cdot { 10 }^{ 7 }\frac { Н }{ { см }^{ 2 } } \cdot 350{ см }^{ 4 } } =0.476см \]

sopromats.ru