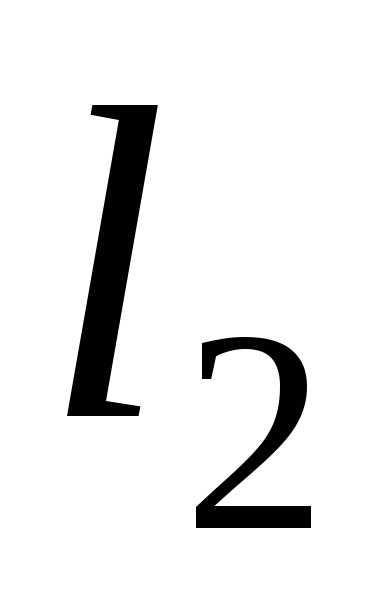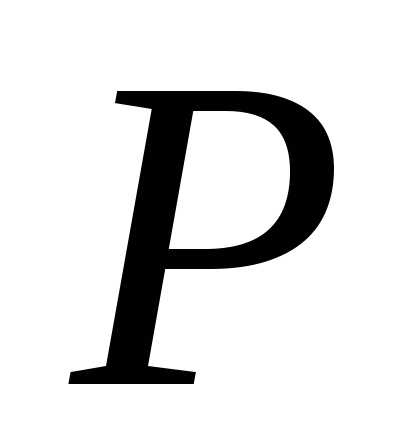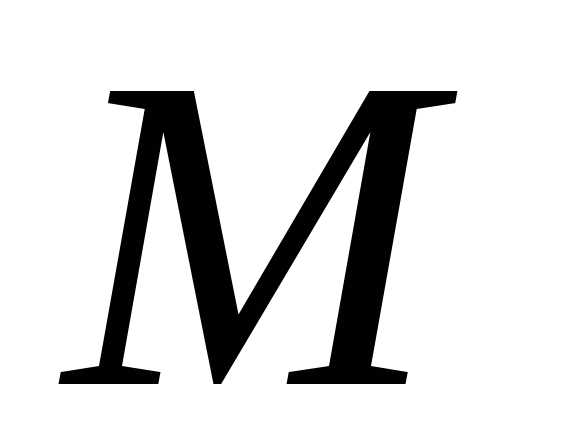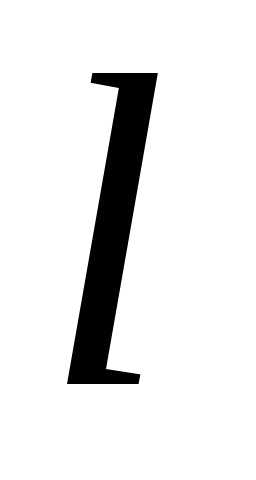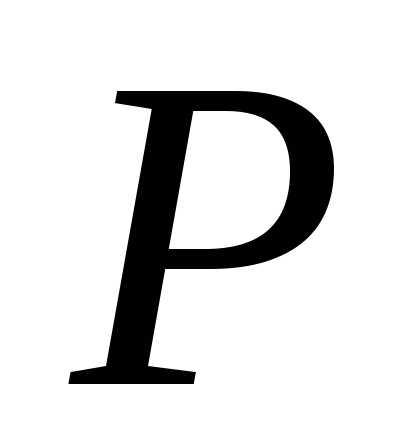ЗАДАЧА № 7. ПОСТРОЕНИЕ ЭПЮР ДЛЯ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ РАМ
36
Ближайшее из сортамента значение момента сопротивления составляет 289 см3, оно соответствует двутавру № 24, этот двутавр и следует использовать для балки.
В балке на двух опорах Мmax = 22 кН м,Qmax = 22 кН.
Требуемый момент сопротивления из условия прочности по нормальным
напряжениям |
| Wx≥ | M max | = | 22 103 | =1,83 10−3 | м3. | Момент | сопротивления | ||||||||||||||||
| [σ] | 12 106 | |||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
прямоугольного сечения Wx | = | b h3 | , т. к. | b = | 2 | h , то | Wx= | 2h4 | . Требуемая высота | ||||||||||||||||
6 | 3 | 18 | |||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
балки составит: | h = 3 18Wx |
| =0,254 м. Округляем до четного числа и получаемh | ||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
|
|
|
| ||
= 0,26 м. Ширина балки составит b = 0,18 м. |
|
|
|
|
|
| |||||||||||||||||||
| Проверим балку с выбранными размерами поперечного сечения по | ||||||||||||||||||||||||
условию |
| Qmax |
|
|
| прочности |
|
|
| по |
| касательным |
| напряжениям: | |||||||||||
τmax= | 3 |
|
|
|
| = | 3 |
| 22 103 |
| ≈ 0,71МПа, | что меньше допустимых напряжений | |||||||||||||
|
|
| |||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
| ||||||||||||||||
2 |
| b h | 2 | 0,26 0,18 | |||||||||||||||||||||
[τ]= 1,5 МПа.
В том случае, если условие прочности по касательным напряжениям не выполняется, то размеры поперечного сечения следует увеличить.
Требуется: для заданной схемы статически определимой рамы построить эпюры внутренних силовых факторов (Nz,Qу,Mх).
Условия задания:
Рама загружена силами (Р1 иР2), моментом (М) и равномерно распределенной нагрузкой (q). Расчетные схемы представлены на рис. 24, числовые данные в табл. 7.
Последовательность выполнения задания:
1.Вычертить расчетную схему рамы с заданными нагрузками. Проставить числовые значения размеров и нагрузок. Изобразить реакции и вычислить их величину.
2.Построить эпюры Nz,Qу,Mх на каждом участке. Эпюры строят на контуре рамы. Контур рамы для построения каждой эпюры следует чертить заново в том же масштабе, что и расчетную схему. Контур рамы выделяют утолщенной линией. На всех эпюрах проставить числовые значенияNz,Qу,Mх с указанием размерности.
|
| P1 | q |
|
|
| |
| a | a | c |
q | 2b |
|
|
|
| M | P2 |
|
|
| |
|
| Схема 1 |
|
q
2a
b
P1
P2 2a/3
b
M
Схема 3
q
b
P2
q
M
Схема 5
37
P1 |
| c |
a | a | P2 |
q | q |
|
b |
|
|
| b |
|
M |
|
|
Схема 2 |
| |
M | q | P2 |
|
| |
a | a | c |
b |
|
|
|
| P1 |
q |
| b |
b |
| |
Схема 4 |
| |
P1 | M |
|
|
| |
c |
|
|
| 2b | q |
|
| |
| 2a |
|
P2 |
|
|
| Схема 6 |
|
Рис. 24. Расчетные схемы к задаче № 7
| P2 |
|
a |
| a |
b |
|
|
P1 |
| M |
q |
|
|
b | b | q |
|
| |
|
| c |
Схема 7 |
| |
| q | P2 |
b | P1 |
|
|
| |
| a |
|
b | 2a |
|
|
| P2 |
| Схема 9 |
|
| a | P2 |
|
| |
q |
| a |
b b | ||
|
| P1 |
|
| q |
| b |
|
| M |
|
|
| Схема 8 |
q
| 2a | P2 |
| b | q |
q |
| |
|
| |
|
| M |
b | b | c |
Схема 0
Рис. 24. Расчетные схемы к задаче № 7 (окончание)
Таблица 7
Числовые данные к задаче № 7
№ | № | Р1, кН | Р2, кН | М, | q, | № | а, м | b, м | с, м |
схемы | кН м | кН/м | |||||||
0 | 00 | 26 | 34 | 24 | 12 | 000 | 3,0 | 4,0 | 1,0 |
1 | 10 | 28 | 32 | 26 | 14 | 100 | 3,2 | 3,8 | 1,0 |
2 | 20 | 30 | 30 | 28 | 16 | 200 | 3,4 | 3,6 | 1,0 |
3 | 30 | 32 | 28 | 30 | 18 | 300 | 2,4 | 3,4 | 2,0 |
4 | 40 | 34 | 26 | 32 | 20 | 400 | 2,6 | 4,2 | 1,6 |
5 | 50 | 36 | 24 | 34 | 22 | 500 | 2,8 | 4,4 | 1,4 |
6 | 60 | 38 | 32 | 36 | 24 | 600 | 3,0 | 4,6 | 1,3 |
7 | 70 | 40 | 30 | 38 | 16 | 700 | 3,2 | 4,8 | 1,2 |
8 | 80 | 38 | 28 | 40 | 18 | 800 | 3,4 | 5,0 | 1,1 |
9 | 90 | 36 | 26 | 40 | 10 | 900 | 3,6 | 4,5 | 1,0 |
39
Пример решения задачи № 7
Для продольных сил (Nz) и поперечных сил (Qу) сохраняют принятые ранее правила знаков. Ординаты эпюрNz иQу откладывают перпендикулярно к оси элементов рамы в произвольную сторону, но обязательно указывается знак.
Для изгибающих моментов специального правила знаков нет, а при вычислении момента в любом сечении знак принимается произвольно. Но результат вычислений всегда откладывается со стороны сжатого волокна элемента рамы.
Рассмотрим жестко защемленную плоскую раму (рис. 25, а). В жесткой заделке возникают три реакции, но строить эпюры внутренних силовых факторов для такого типа рамы можно без вычисления реакций в заделке.
Рама имеет 4 участка. Построение эпюры Nz.
Первый участок 0 ≤ z1 ≤ 3 м.
N1 = 0.
Второй участок 0 ≤ z2 ≤ 3 м.
N2 = 0.
Третий участок 0 ≤ z3 ≤ 4 м.
N3 =− Р =− 20 кН (сжатие «−»).
Четвертый участок 0 ≤ z4 ≤ 6 м.
N4 =− q 4 =− 40 кН (сжатие «−»).
Эпюра продольных сил показана на рис. 25, б. Из эпюры видно, что вертикальная реакция в защемлении RА = 40 кН и направлена вверх, вызывая сжатие в стойке рамы.
Построение эпюры Qу.
Первый участок 0 ≤ z1 ≤ 3 м.
Q1 = 0.
Второй участок 0 ≤ z2 ≤ 3 м.
Q2 =Р = 20 кН (знак «+», т. к. силаР стремится повернуть сечение по ходу часовой стрелки).
Третий участок 0 ≤ z3 ≤ 4 м.
Q3 =q z3. При z3 = 0,Q3 = 0, z3 = 4 м,Q3 = 40 кН.
Четвертый участок 0 ≤ z4 ≤ 6 м.
Q4 =− Р =− 20 кН.
Эпюра поперечных сил показана на рис. 25, в. Из эпюры видно, что горизонтальная реакция защемления НА = 20 кН и направлена вправо.
Построение эпюры Мх.
Первый участок 0 ≤ z1 ≤ 3 м.
М1 =М = 40 кН м (сжатым является правое волокно в сечении, поэтому ордината отложена вправо от оси стойки).
Второй участок 0 ≤ z2 ≤ 3 м.
М2 =М − Р z2. Приz2 = 3 мМ2 =− 20 кН м.
Третий участок 0 ≤ z3 ≤ 4 м.
40
М3 =М –Р 3− q z3 z3/2. Приz3 = 0,М3 =− 20 кН м,z3 = 4 м,
М3 =− 100 кН м (сжаты нижние волокна). Эпюра изгибающих моментов имеет вид квадратичной параболы.
Четвертый участок 0 ≤ z4 ≤ 6 м.
Вверхнем левом углу стойки М4 =М − Р 3− q 4 2 =− 100 кН м.
Вопоре А М4 =М +Р 3− q 4 2 = 20 кН м.
Эпюра изгибающих моментов представлена на рис. 25, г. Реактивный момент в защемлении МА = 20 кН м.
Проверка правильности определения реакций из уравнений статики.
∑X = 0,H A − P = 20−20= 0;
∑Y = 0,RA −q 4= 40−10 4= 0;
∑M = 0,M A + q 4 2− P 3− M = 20+10 4 2−20 3−40= 0.
q=10 êÍ/ì
|
| 40 | 20 |
4 | z3 |
| |
z |
| ||
| 2 | P=20 êÍ |
|
6 ì | z | б) | Nz |
| 4 ì | ì | |
|
| ||
| 3 |
| |
|
|
| |
H | 1 |
|
|
A | z | Ì=40 êÍ ì |
|
MARA |
|
| |
|
|
| |
| 100 | 20 |
г) | 100 | 40 |
| ||
| Mx |
|
| 20 | 40 |
Рис. 25. Пример построения эпюр внутренних силовых факторов в жестко защемленной раме
Рассмотрим раму на двух шарнирных опорах (рис. 26, а). Определим реакции в опорах рамы из уравнений статики
∑X= 0, HA − P= 0 HA = 20 кН;
41
∑M A = 0,q 4 2− P 3− M − RB 4= 0 |
| RB = −5 кН; |
∑M B = 0,RA 4−q 4 2− P 3− M = 0 |
| RA = 45кН. |
Построение эпюры Nz. Первый участок 0≤ z1 ≤ 6 м.N1 =− RВ =− 45 кН (сжатие). Второй участок 0≤ z2 ≤ 4 м.N2 =− НА =− 20 кН (сжатие). Третий участок 0≤ z3 ≤ 3 м.N3 =RВ = 5 кН (растяжение). Четвертый участок 0≤ z4 ≤ 3 м.
N4 =RВ = 5 кН.
Эпюра продольных сил представлена на рис. 26, б. Построение эпюры Qу.
Первый участок 0 ≤ z1 ≤ 6 м.
Q1 =− НА =− 20 кН.
Второй участок 0 ≤ z2 ≤ 4 м.
Q2 =RА − q z2. Приz2 = 0Q2 = 45 кН, приz2 = 4 мQ2 = 5 кН.
Третий участок 0 ≤ z3 ≤ 3 м.
Q3 = 0.
Четвертый участок 0 ≤ z4 ≤ 3 м.
Q4 =Р = 20 кН.
Эпюра поперечных сил показана на рис. 26, в. Построение эпюры Мх.
Первый участок 0 ≤ z1 ≤ 6 м.
М1 =НА z1 (сжаты правые волокна стойки). Приz1 = 6 мМ1 = 120 кН м.
Второй участок 0 ≤ z2 ≤ 4 м.
М2 =НА 6− q z2 z2/2. Приz2 = 4 мМ2 =− 20 кН м.
Третий участок 0 ≤ z3 ≤ 3 м.
М3 =М = 40 кН м (сжаты правые волокна стойки). Четвертый участок 0≤ z4 ≤ 3 м.
М4 =М − Р z4. Приz4 = 3 мМ4 =− 20 кН м.
Эпюра изгибающих моментов показана на рис. 26, г.
z2 | q=10 êÍ/ì | |
| ||
| 4 ì |
|
ó | õ | 3 ì |
| 4 | |
|
| z |
|
| 3 ì |
1 |
| 3 |
z |
| z |
A
RA
| 20 |
|
Ð=20 êÍ | б) | Nz |
|
| |
M=40 êÍ ì |
|
|
B | 4540 | 5 |
RB | 20 | |
|
|
45 | 5 |
|
| 120 | 20 |
|
|
|
|
| 20 |
в) | Qy | г) | 120 | Mx |
|
| 20 |
|
|
| |
| 20 |
|
|
| 40 |
|
|
|
|
|
Рис. 26. Пример построения эпюр внутренних силовых факторов в раме на двух шарнирных опорах
ЗАДАЧА № 8. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛКАХ
Требуется: для заданной схемы статически определимой балки определить вертикальное перемещение указанного сечения (уД илиуЕ) и угол поворота сечения в одной из опор балки (θА илиθВ), используя графоаналитический метод.
Условия задания:
Балка загружена силой Р и моментомМ. Расчетные схемы представлены на рис. 27, числовые данные в табл. 8.
Последовательность выполнения задания:
1.Начертить расчетную схему балки с размерами и значениями внешних нагрузок.
2.Начертить грузовую эпюру Мр − эпюру изгибающих моментов от заданных внешних сил.
3.Составить единичное состояние. Начертить единичную эпюру
Mi изгибающих моментов.
43
4. Перемещения в балке определить методом перемножения эпюр. Выражения для площадей эпюр и положения центров тяжести приведены в табл. 9. Выражения интеграла Мора для различных сочетаний единичных и грузовых эпюр приведены в табл. 9 а.
| M | P | B |
| P |
|
| M |
A | D | E |
| A | E |
| B | |
|
|
| D |
|
| |||
a | b | c |
|
| a | b |
| c |
| Схемы 1, 0 |
|
| Схемы 2, 7, 9 |
| |||
M | D | E | B |
| D | M | E | B |
A | A |
| ||||||
| P |
| P |
| ||||
a | b |
|
| a |
| c | ||
c |
|
| b |
| ||||
| Схемы 3, 6, 8 |
|
| Схемы 4, 5 |
|
| ||
|
| Рис. 27. Расчетные схемы к задаче № 8 |
|
|
| |||
Таблица 8
Числовые данные к задаче № 8
№ | № | Р, кН | М, | Угол | № | а, м | b, м | с, м | Сечение |
схемы |
|
| кН м |
|
|
|
|
|
|
1 | 10 | 6,0 | 4,0 | θА | 100 | 1,2 | 1,4 | 1,4 | Е |
2 | 20 | 8,0 | 6,0 | θВ | 200 | 1,4 | 1,6 | 1,2 | D |
3 | 30 | 4,0 | 8,0 | θА | 300 | 1,6 | 1,2 | 1,8 | Е |
4 | 40 | 10,0 | 4,0 | θВ | 400 | 1,0 | 1,8 | 1,2 | D |
5 | 50 | 6,0 | 10,0 | θА | 500 | 1,2 | 1,4 | 1,6 | Е |
6 | 60 | 8,0 | 6,0 | θВ | 600 | 1,8 | 1,6 | 1,2 | D |
7 | 70 | 4,0 | 8,0 | θА | 700 | 1,4 | 1,0 | 1,6 | Е |
8 | 80 | 10, | 4,0 | θВ | 800 | 1,6 | 1,4 | 1,2 | D |
9 | 90 | 6,0 | 8,0 | θА | 900 | 1,8 | 1,2 | 1,0 | Е |
0 | 00 | 8,0 | 6,0 | θВ | 000 | 1,0 | 1,6 | 1,4 | D |
studfiles.net
Построение эпюр в составных рамах [wiki.eduVdom.com]
Эпюры внутренних усилий в составных рамах можно построить так же, как и в простых, однако часто эту процедуру
удается упростить, если:
1) предварительно найти реакции в соединительных шарнирах;
2) учесть, что при переходе через соединительный шарнир характер эпюр не меняется, если при этом не меняется
характер нагрузки.
Решим задачу определения эпюр внутренних усилий в составной раме:
Делим раму на участки . Для построения эпюр достаточно знать только одну опорную реакцию – Rв,
которую можно найти из условий равновесия части BC:
Rв = q/2.
Находим реакции в соединительном шарнире:
Xс = q Yс = ql.
Теперь построение эпюр на участке 3-2 заданной рамы можно свести к построению эпюр в консоли,
защемленной на правом конце – в точке 2 и загруженной распределенной нагрузкой и найденными реакциями Xс, Yс
Переходя к рассмотрению левой части рамы – AC,
можно отбросить правую часть – BC,
заменив ее действие найденными реакциями отброшенной части: Xс ; Yс .
Отметим, что при переходе через соединительный шарнир C
от участка 2-3 к участку 3-4 меняется характер нагрузки q
а вместе с ней и характер эпюр M и Q ,
но не меняется нагрузка qx, поэтому на всем ригеле N = const.
Правильность построения эпюр (рис. в-д) можно проверить, рассматривая равновесие рамы в целом или ее ригеля.
Нетрудно догадаться, что для рамы, состоящей из двух дисков, рассмотренная выше схема решения будет целесообразной,
если один из дисков присоединен к земле только одной связью.
В тех же случаях, когда диски имеют по две опорные связи, часто удается построить эпюры без определения реакций в
соединительном шарнире.
Построение эпюр внутренних усилий в трех шарнирной раме
Построить эпюры внутренних усилий в трех шарнирной раме .
Решение:
Делим раму на участки и определяем опорные реакции(рис б): $$ \sum M_{B}=0; Y_{A}=ql/4 $$ $$ \sum M_{C}^{\left ( AC \right )}=0;X_{A}=ql/4; $$ $$ \sum X=0; X_{B} =3ql/4; $$$$ \sum X=0; X_{B} =3ql/4; $$ $$ \sum Y=0; Y_{B} =3ql/4; $$ Проверка: $$ \sum M_{C}^{\left ( BC \right )}=X_{B}\cdot l-Y_{B}\cdot l-ql\cdot l/2=3ql^{2}/4-ql^{2}/4-ql^{2/2} =0 $$
Эпюры на участке 1-2 строим как в консоли соответствующей длины, закрепленной в точке 2.
Момент на левом конце ригеля находим из условий равновесия второго узла.
Поскольку ригель не загружен и эпюра M здесь должна быть линейной,
проводим прямую через найденную ординату эпюры M = (q/4)l*2 и шарнир C,
а затем продолжаем ее до 4 узла.
На правой стойке эпюру M можно построить как в консоли,
закреплен-ной в 4 узле и загруженной распределенной нагрузкой и найденными реакциями Xв, Yв.
Однако проще рассмотреть этот участок как простую двух опорную балку,
загруженную концевым моментом в 4 узле (соответствующая эпюра показана пунктиром – рис. в) и распределенной
нагрузкой.
Эпюры Q и N в этом примере нетрудно построить в соответствии с определением (рис. г, д).
Для контроля правильности построения эпюр можно рассмотреть равновесие ригеля (рис. д).
Рекомендуем
subjects/stroymeh/эпюры_в_составных_рамах.txt · Последние изменения: 2013/10/04 01:03 — ¶
wiki.eduvdom.com
2.2.3. Построение эпюр в составных рамах
Эпюры внутренних усилий в составных рамах можно построить так же, как и в простых, однако часто эту процедуру удается упростить, если:
– предварительно найти реакции в соединительных шарнирах;
– учесть, что при переходе через соединительный шарнир характер эпюр не меняется, если при этом не меняется характер нагрузки.
Пример 2.4. Построить эпюры M, Q, N (рис. 2.5, а).
Решение. Делим раму на участки (рис. 2.5, а). Для построения эпюр достаточно знать только одну опорную реакцию – RB, которую можно найти из условий равновесия части BC:
MC(BC) = 0; RB = ql/2.
Находим реакции в соединительном шарнире:
SX (BC) = 0; XC = ql/2.
SY (BC)= 0; YC = ql.
Теперь построение эпюр на участке 3-2 заданной рамы можно свести к построению эпюр в консоли, защемленной на правом конце – в точке 2 и загруженной распределенной нагрузкой и найденными реакциями XC, YC (аналогично участку 5-3 в примере 2.3 на рис. 2.4, в).
Переходя к рассмотрению левой части рамы – AC можно отбросить правую часть – BC, заменив ее действие найденными реакциями отброшенной части: XC = XC ; YC = YC. При этом эпюры на участках 3-4 и 4-5 заданной рамы строятся так же, как на участках 1-2 и 2-3 в примере 2.3 (рис. 2.4, в).
Отметим, что при переходе через соединительный шарнир C от участка 2-3 к участку 3-4 меняется характер нагрузки qy, а вместе с ней и характер эпюр M и Q , но не меняется нагрузка qx, поэтому на всем ригеле N = const.

Рис.2.5
Правильность построения эпюр (рис. 2.5, в-д) можно проверить, рассматривая равновесие рамы в целом или ее ригеля (рис. 2.5, е).
Нетрудно догадаться, что для рамы, состоящей из двух дисков, рассмотренная выше схема решения будет целесообразной, если один из дисков присоединен к земле только одной связью – как в примере 2.4. В тех же случаях, когда диски имеют по две опорные связи, часто удается построить эпюры без определения реакций в соединительном шарнире.
Пример 2.5. Построить эпюры внутренних усилий в трехшарнирной раме (рис. 2.6, а).
Решение. Делим раму на участки и определяем опорные реакции (рис. 2.6, б):
MB = 0; YA = ql/4;
MC(AС) = 0; XA = ql/4;
X = 0; XB = 3ql/4;
Y = 0; YB = ql/4.
Проверка:
MC(ВС) = XBl – YBl – qll/2 = 3ql2/4 – ql2/4 – ql2/2 = 0.
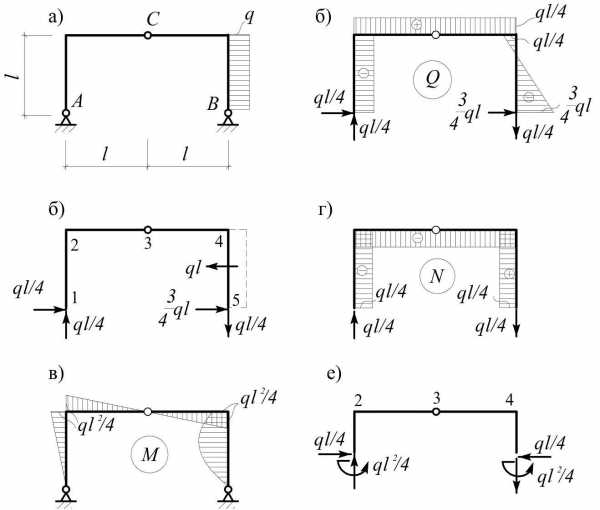
Рис.2.6
Эпюры на участке 1-2 строим как в консоли соответствующей длины, закрепленной в точке 2. Момент на левом конце ригеля находим из условий равновесия второго узла. Поскольку ригель незагружен и эпюра M здесь должна быть линейной, проводим прямую через найденную ординату эпюры M = ql2/4 и шарнир C, а затем продолжаем ее до 4 узла.
На правой стойке эпюру M можно построить как в консоли, закрепленной в 4 узле и загруженной распределенной нагрузкой и найденными реакциями XB, YB. Однако проще рассмотреть этот участок как простую двухопорную балку, загруженную концевым моментом в 4 узле (соответствующая эпюра показана пунктиром – рис. 2.6, в) и распределенной нагрузкой.
Эпюры Q и N в этом примере нетрудно построить в соответствии с определением (рис. 2.6, г, д).
Для контроля правильности построения эпюр можно рассмотреть равновесие ригеля (рис. 2.6, д).
studfiles.net
4. Особенности построения эпюр внутренних усилий в рамах
Рама – это стержневая система, состоящая из двух и более стержней, лежащих в одной плоскости и жестко соединенных в местах стыков.
Порядок построения эпюр внутренних усилий (эпюра Q, эпюраМ) аналогичен тому, как это делается для балок с несколькими участками и прямолинейной осью (см. РГР №4), с той лишь разницей, что оси отдельных участков стержней на раме не лежат на одной линии. В этой связи правило знаков дляQиM, принятое при построении эпюр в балках, неудобно. Для удобства построения эпюр внутренних усилий в рамах принимаем правило построения эпюр внутренних усилий на сжатом волокне стержней, составляющих раму.
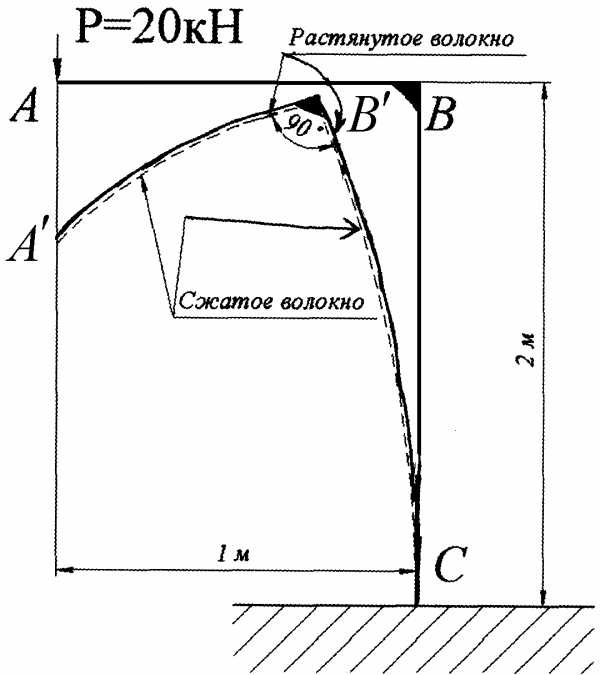
Рассмотрим раму, состоящую из двух стержней ABиBCс опорой в точкеC в виде жесткой заделки (рис. 1.7).СтержниABиBC жестко соединены в точкеB (в процессе деформации под действием внешней нагрузки). Построим эпюру внутренних изгибающих моментов для такой стержневой системы.
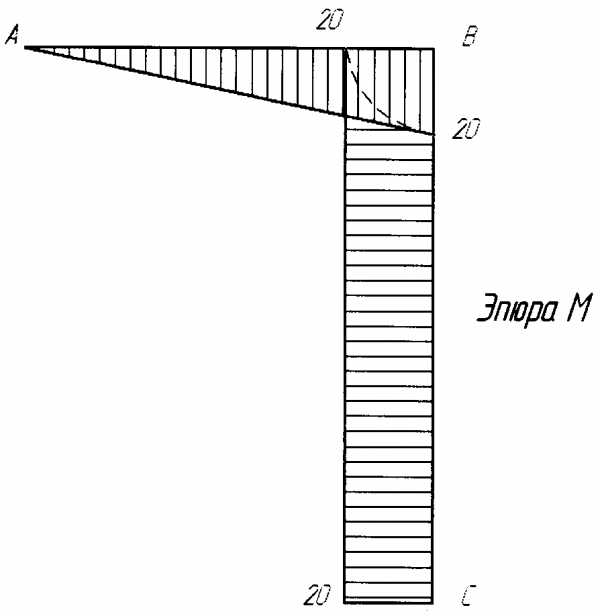
Для построения эпюры M (рис. 1.8) необходимо вычислить значения внутренних изгибающих моментов на левой и правой границах каждого из стержней, составляющих раму. Это можно сделать путем составления уравнения внутренних изгибающих моментов для участков рамы, с последующей подстановкой в них координат точек, где вычисляется внутреннее усилие, или путем непосредственного определения значений внутренних усилий в заданных точках. Двигаясь со свободного края рамы (стержня AB) вычислим моменты в точках A и B. Соответственно МА = 0, МВ = 20 кНм. В стержне AB при действии силы P будут сжаты нижние волокна, поэтому значения моментов откладываем вниз от оси стержня AB. Завершаем построение эпюры M на стержне AB, соединив точки и прямой линией. Далее рассматриваем стержень BC. Все нагрузки, приложенные к стержню AB, приводим к точке B. Анализ напряженного состояния стержня BC показывает, что он нагружен сжимающей силой и изгибающим моментом .
| |
Рис. 1.7. | Рис. 1.8. |
Таким образом, на стыке стержней АВ и BC внутренний изгибающий момент будет равен 20 кНм. Так как никаких других изгибающих нагрузок на стержень ВС не действует, внутренний изгибающий момент будет постоянным на участке ВС. Откладываем значение 20 кНм слева от оси стержня BC в точки B и C и соединяем эти точки прямой линией; слева – потому что волокна слева от оси стержня будут сжаты. Так как сжимающая нагрузка Р, приложенная к стержню ВС, не является определяющей, то на этапе расчета на изгиб рамы ею пренебрегаем. Она будет учтена при проверочном расчете, который выходит за рамки задания.
Примеры расчета
Часть I. Расчет на прочность статически неопределимой балки
Задание
Для балки, выбранной на рис. 1.9, выполнить следующие расчеты:
Раскрыть статическую неопределимость, используя метод сил;
Построить эпюры поперечных сил Q. и изгибающих моментов М;
Из условия прочности по нормальным напряжениям при изгибе подобрать сечение двутаврового профиля по допускаемым напряжениям . Линейные размеры и величины нагрузок взять в табл. 1.2.
Исходные данные
Расчетная схема балки приведена на рис. 1.10,а.
Решение
1. Определение степени статической неопределимости балки.
Как известно, плоская статически определимая система содержит три связи. При этом защемление дает три связи, шарнирнонеподвижная опора –две связи, а шарнирно подвижная –одну связь. Поэтому степень статической неопределимости плоской стержневой системы N определяется по формуле
N= С – 3, (1.10)
где С – общее число связей;N – степень статической неопределимости системы.
Таблица 1.2
№ стро-ки | № схемы | Балка | № схемы | Рама | ||||||||||
| | | | | | | | | | | | |||
м | кН | кН/м | кНм | м | кН | кН/м | кНм | |||||||
1 | 1 | 1,0 | 1,5 | 0,5 | 10 | 10 | 10 | 1 | 1,0 | 2,0 | 0,4 | 50 | — | — |
2 | 2 | 1,5 | 2,0 | 1,0 | 20 | 10 | 15 | 2 | 1,2 | 2,2 | 0,5 | — | 20 | — |
3 | 3 | 2,0 | 2,5 | 1,5 | 30 | 15 | 20 | 3 | 1,4 | 2,4 | 0,6 | — | — | 100 |
4 | 4 | 2,5 | 3,0 | 2,0 | 40 | 15 | 20 | 4 | 1,6 | 2,6 | 0,7 | 60 | — | — |
5 | 5 | 3,0 | 2,5 | 2,5 | 50 | 20 | 30 | 5 | 1,8 | 2,8 | 0,8 | — | 30 | — |
6 | 6 | 2,5 | 2,0 | 3,0 | 60 | 20 | 35 | 6 | 2,0 | 3,0 | 0,9 | — | — | 120 |
7 | 7 | 2,0 | 1,5 | 2,5 | 70 | 25 | 40 | 7 | 2,2 | 3,2 | 0,8 | 70 | — | — |
8 | 8 | 1,5 | 1,0 | 2,0 | 80 | 25 | 45 | 8 | 2,4 | 3,4 | 0,7 | — | 10 | — |
9 | 9 | 1,0 | 0,5 | 1,5 | 90 | 30 | 50 | 9 | 2,6 | 3,6 | 0,6 | — | — | 150 |
0 | 0 | 0,5 | 1,0 | 1,0 | 100 | 30 | 55 | 0 | 2,8 | 3,8 | 0,5 | 80 | — | — |
е | г | д | в | д | е | а | е | а | б | г | е | е | е | |

Рис. 1.9.
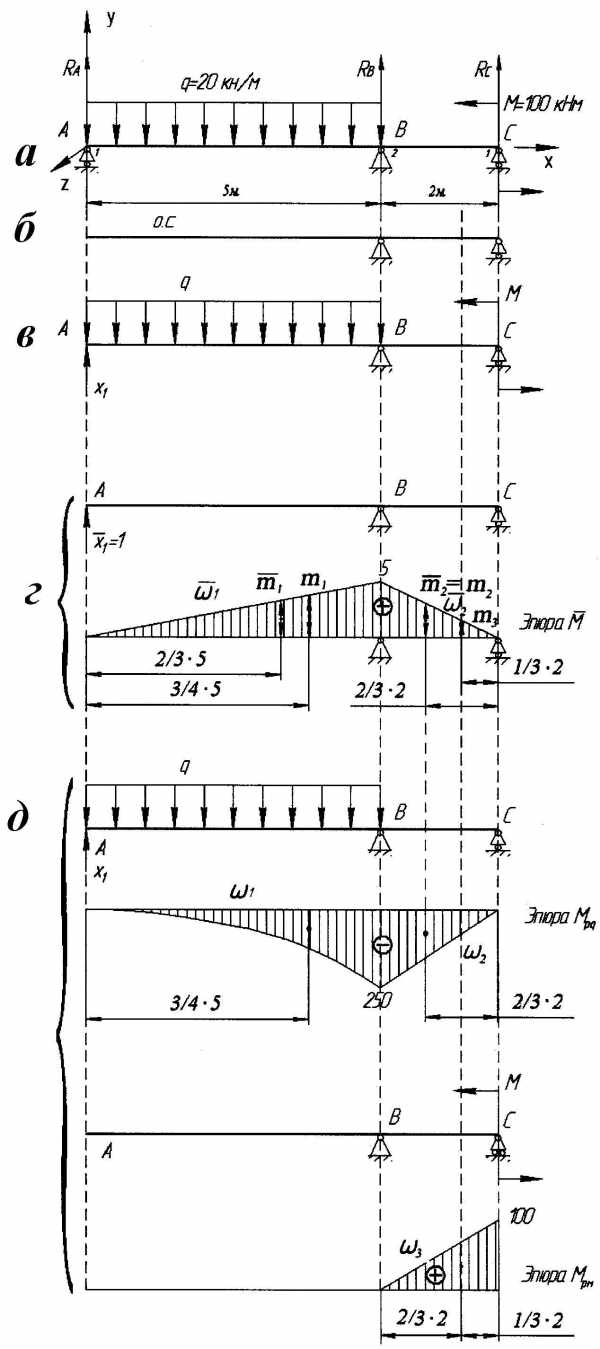
Рис. 1.10.
В нашем случае С = 2+1+1, так как имеем две шарнирно подвижных и одну шарнирно неподвижную опору. На схеме (рис. 1.10,а) для каждой опоры проставлено количество связей. Поэтому, используя формулу (1.10), получимN = 4 — 3 =1. Следовательно, в нашем случае балка один раз статически неопределима.
2. Выбираем основную
систему (о.с), т.е. статически определимую,
геометрически неизменяемую систему,
которая получается из исходной статически
неопределимой путем отбрасывания
«лишних» связей. В нашем случае отбрасываем
опоруА и полученная о.с. показана
на схеме (рис. 1.10,б). Такая схема удобна
тем, что в процессе построения эпюр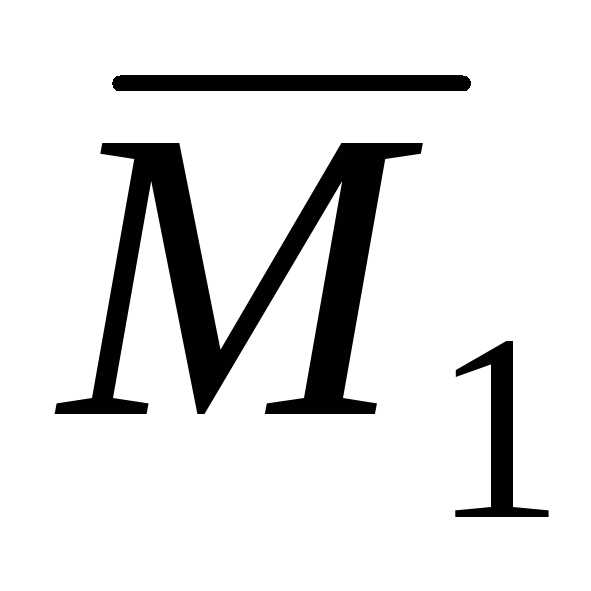 и
и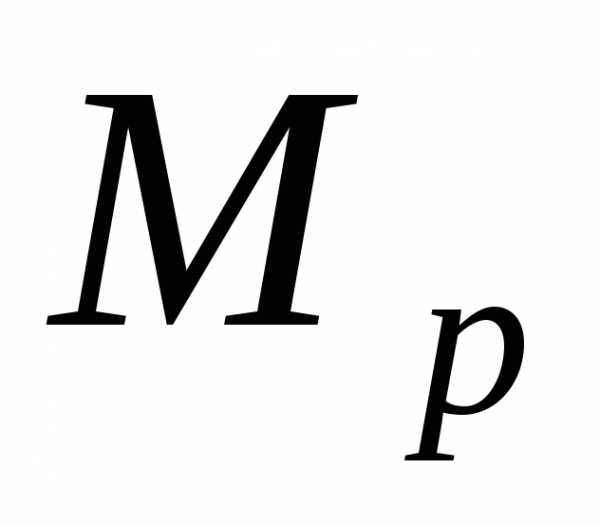 не нужно определять
реакции опор, так как эпюры могут быть
построены и без определения реакций
опор. В некоторых случаях такой подход
крешению задачи
невозможен и при построении эпюр
не нужно определять
реакции опор, так как эпюры могут быть
построены и без определения реакций
опор. В некоторых случаях такой подход
крешению задачи
невозможен и при построении эпюр 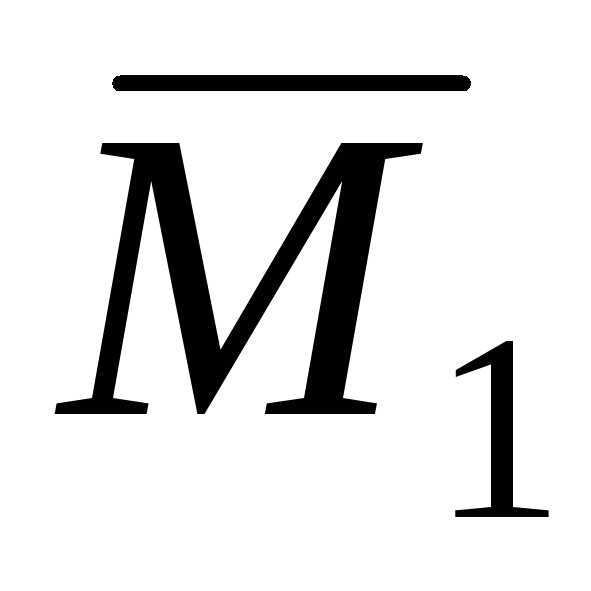 и
и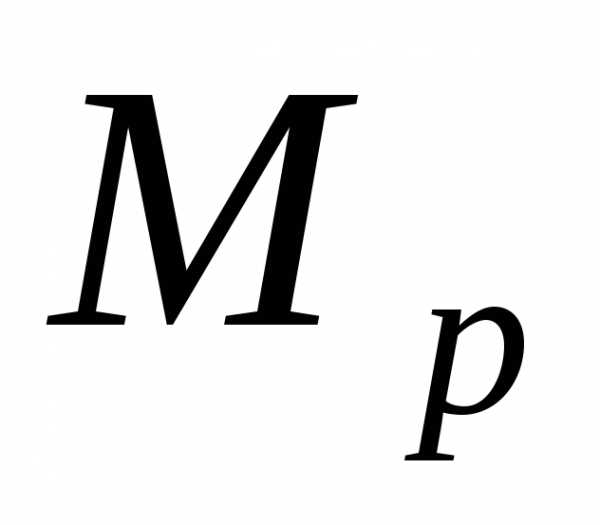 ,
предварительно необходимо определять
реакции опор.
,
предварительно необходимо определять
реакции опор.
3. Загружаем о.с. внешней нагрузкой и
«лишней» неизвестной  (рис. 1.10,в).
(рис. 1.10,в).
4. Составляем систему канонических уравнений метода сил.
Так как рассматриваемая балка один раз статически неопределима, то для нее записывается одно уравнение (1.7):
,
откуда
 ,
(1.11)
,
(1.11)
где  – перемещение
по линии действия силы Х1 от
этой силы, равной
единице;
– перемещение
по линии действия силы Х1 от
этой силы, равной
единице; 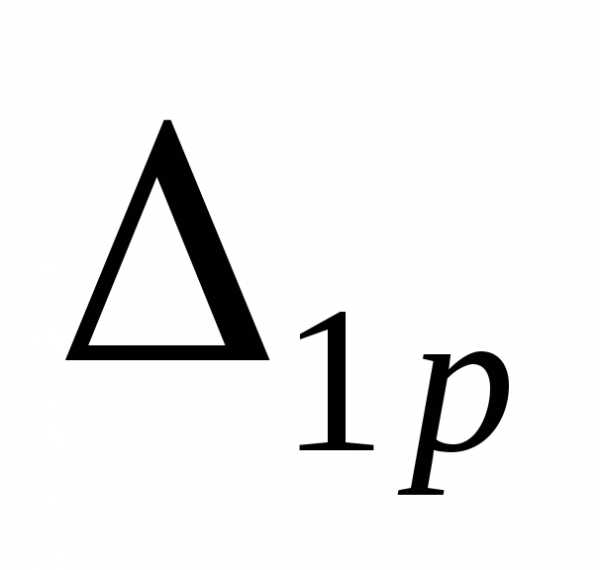 –перемещение
по линии
действия силы Х1 от
внешней нагрузки.
–перемещение
по линии
действия силы Х1 от
внешней нагрузки.
Для определения коэффициентов 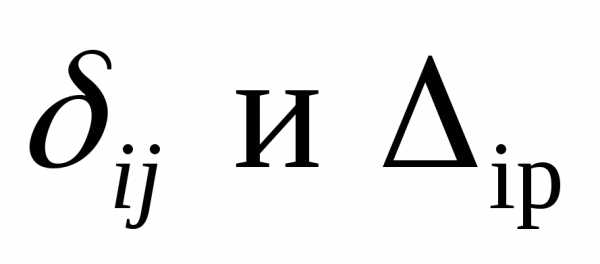 используем правило
Верещагина. Если
эпюры изгибающих моментов Мр или
используем правило
Верещагина. Если
эпюры изгибающих моментов Мр или 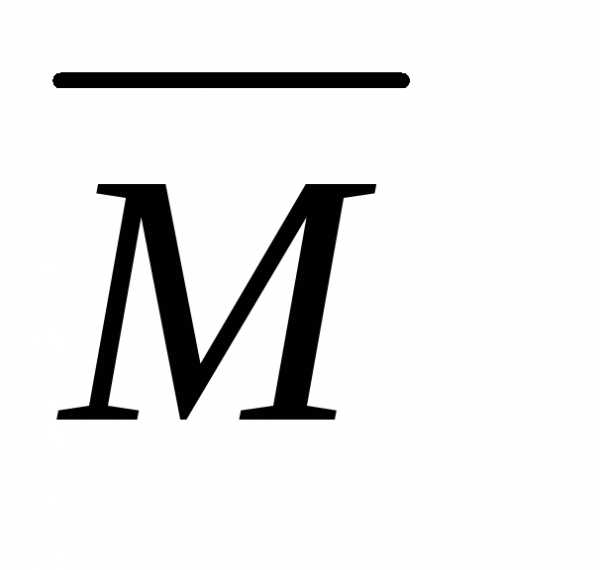 содержат
несколько участков,
то правило Верещагина должно быть
использовано для каждого из участков
по отдельности.
содержат
несколько участков,
то правило Верещагина должно быть
использовано для каждого из участков
по отдельности.
Поэтому
в общем случае искомое
перемещение, например 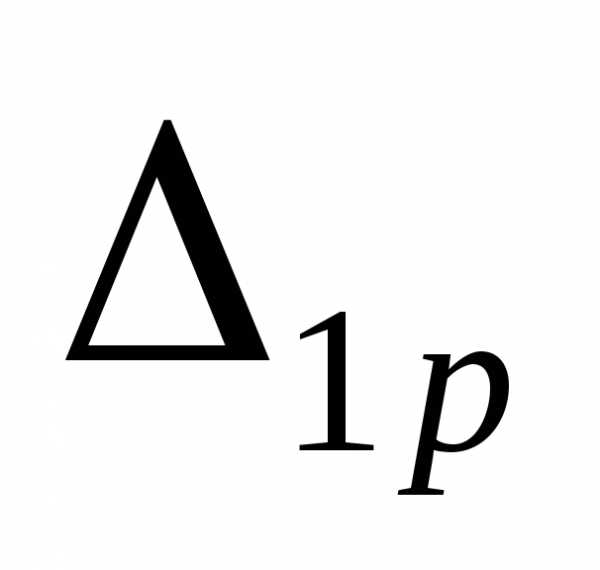 , определяется
по формуле
, определяется
по формуле
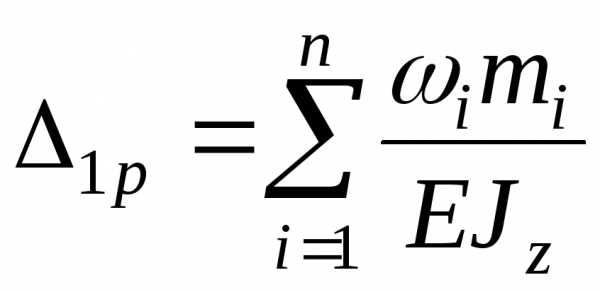 ,
(1.12),
,
(1.12),
где n – количество
участков, на которые разбиваются
эпюры изгибающих моментов  ;
; i– площадь
грузовой эпюры,
т.е. эпюры Мр на i-м участке;
i– площадь
грузовой эпюры,
т.е. эпюры Мр на i-м участке; 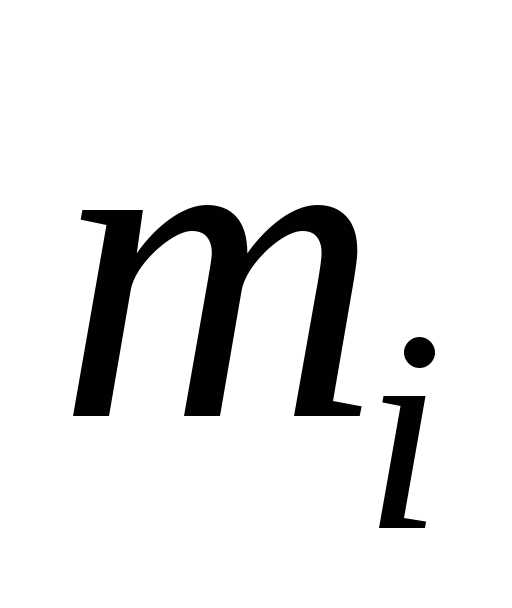 –
ордината эпюры
–
ордината эпюры 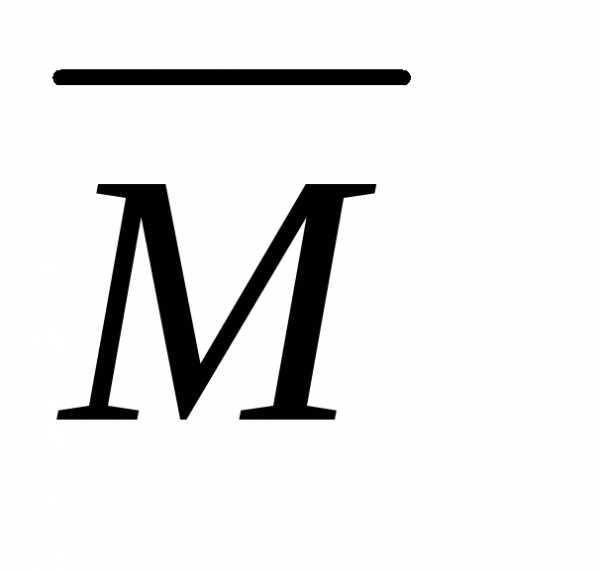 на i—м участке,
расположенная под
центром тяжести эпюры Mpi ; EJ – жесткость
стержня.
на i—м участке,
расположенная под
центром тяжести эпюры Mpi ; EJ – жесткость
стержня.
5. Определяем коэффициент  .
.
Для этого предварительно строим в о.с.
эпюру изгибающего момента  от действия силы
от действия силы  (рис. 1.10,г.). Далее, используя формулу
(1.8), «умножаем»
эпюру
(рис. 1.10,г.). Далее, используя формулу
(1.8), «умножаем»
эпюру 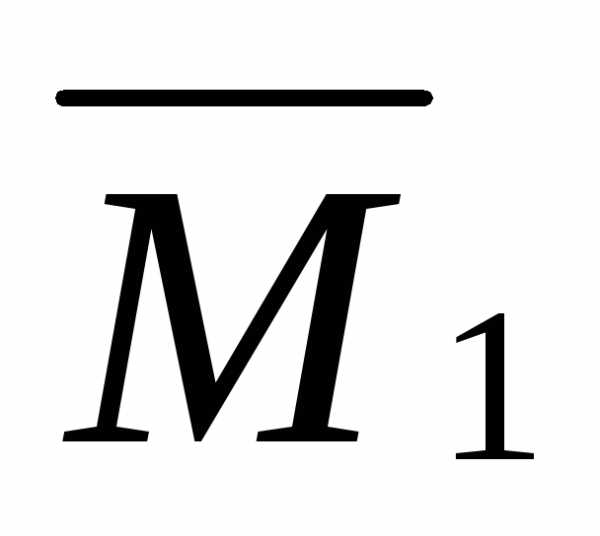 саму на себя.
Получим
саму на себя.
Получим
где 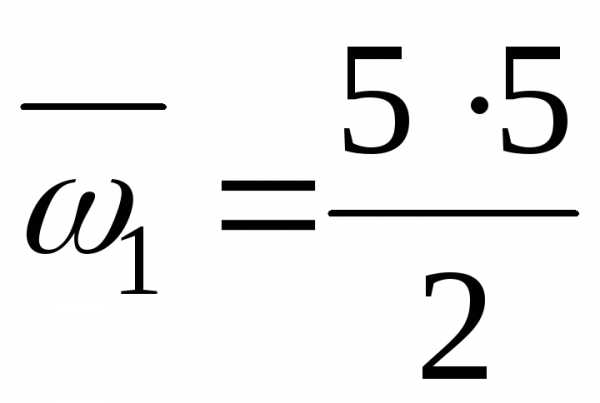 – площадь первого участка эпюры
– площадь первого участка эпюры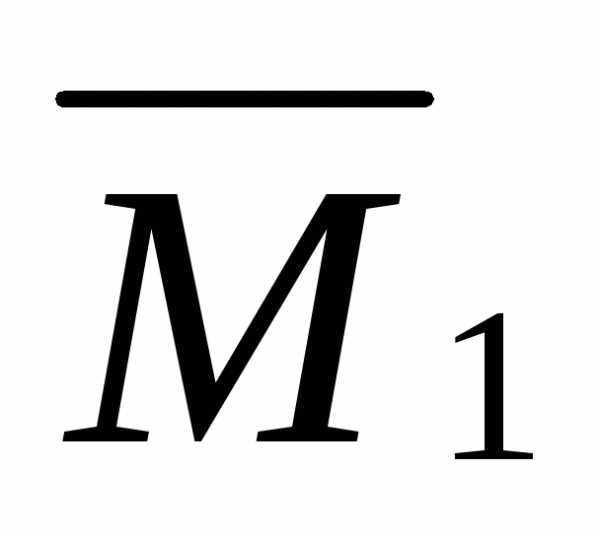 ;
;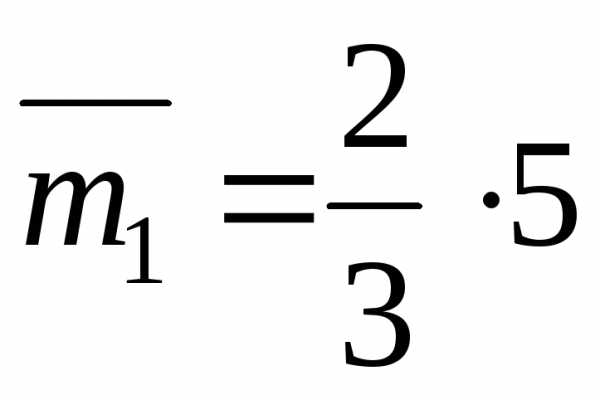 – ордината
центра тяжести площади
первого участка эпюры
– ордината
центра тяжести площади
первого участка эпюры 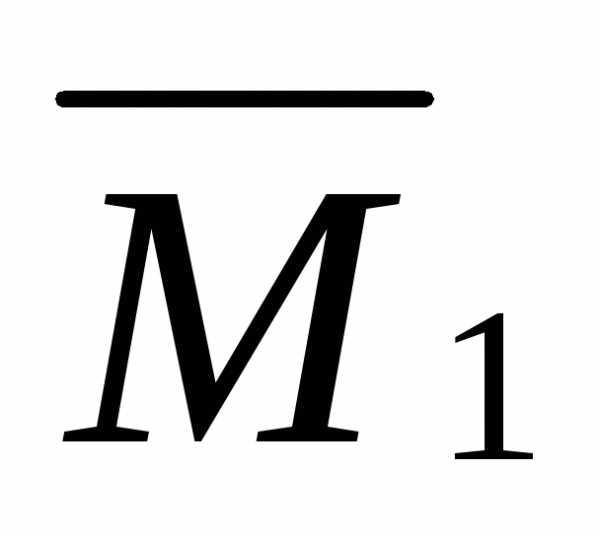 ;
; – площадь
второго участка эпюры
– площадь
второго участка эпюры 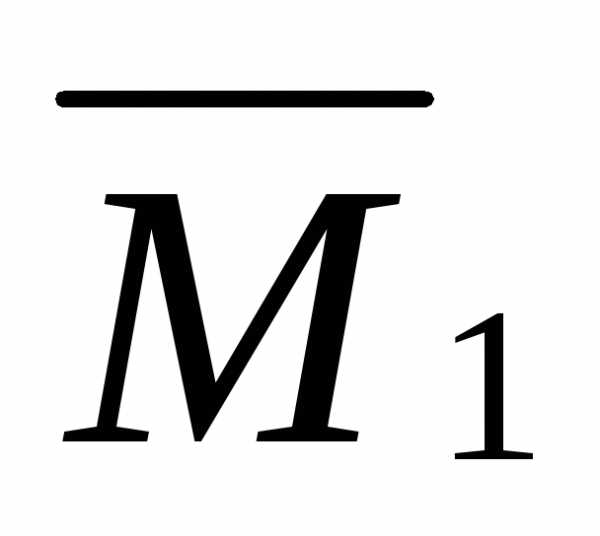 ;
; 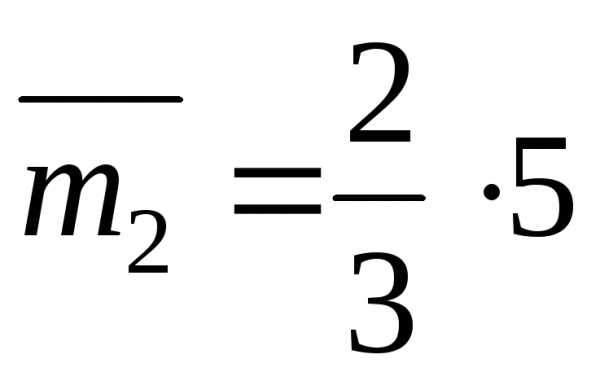 – ордината
центра тяжести площади
второго участка эпюры
– ордината
центра тяжести площади
второго участка эпюры 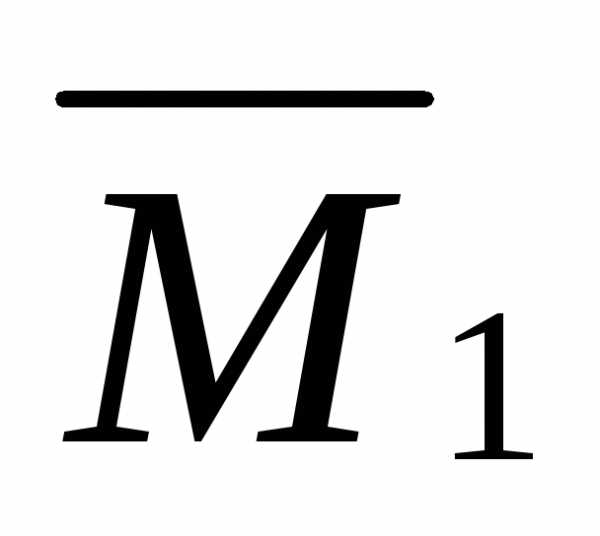 .
.
6. Определяем коэффициент  .
.
Для
определения коэффициента 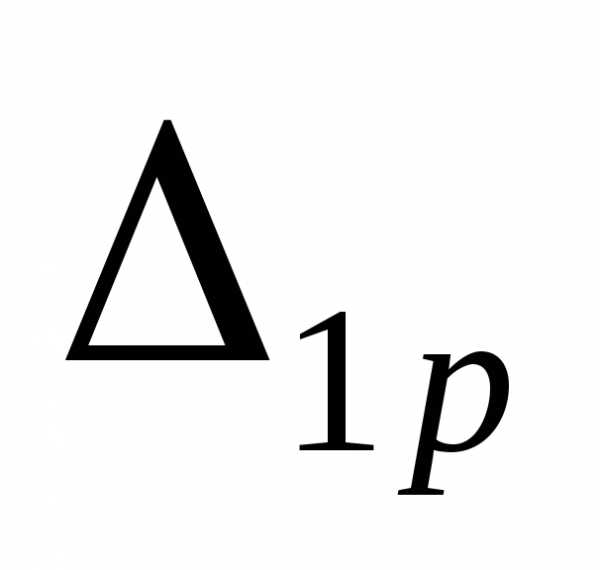 необходимо
построить эпюру изгибающего
момента Мр от действия
внешней
нагрузки, приведенной на рис.
1.10,в. Для
упрощения процесса перемножения эпюр
будем строить эпюры внутренних изгибающих
моментов от каждой внешней нагрузки
отдельно, используя принцип независимости
действия сил (принцип суперпозиции).
Результат построения показан на рис.
1.10,д. При этом нет необходимости
предварительно определять реакции
опор. Достаточно на консоли АВ построить
эпюру изгибающего момента от распределенной
нагрузки q (Mpq)
(это вогнутая парабола с высотой 250 кНм)
и соединить ординату эпюры Mpq на опоре В с ординатой эпюры Mpq на опоре С,
равной 0. Аналогично определив ординаты
эпюры MpМ на опоре В и на опоре С,
соединяем их прямой линией. Очевидно,
что.
При этом также очевидно, что для получения
результата необходимо перемножить
эпюруMpq с эпюрой
необходимо
построить эпюру изгибающего
момента Мр от действия
внешней
нагрузки, приведенной на рис.
1.10,в. Для
упрощения процесса перемножения эпюр
будем строить эпюры внутренних изгибающих
моментов от каждой внешней нагрузки
отдельно, используя принцип независимости
действия сил (принцип суперпозиции).
Результат построения показан на рис.
1.10,д. При этом нет необходимости
предварительно определять реакции
опор. Достаточно на консоли АВ построить
эпюру изгибающего момента от распределенной
нагрузки q (Mpq)
(это вогнутая парабола с высотой 250 кНм)
и соединить ординату эпюры Mpq на опоре В с ординатой эпюры Mpq на опоре С,
равной 0. Аналогично определив ординаты
эпюры MpМ на опоре В и на опоре С,
соединяем их прямой линией. Очевидно,
что.
При этом также очевидно, что для получения
результата необходимо перемножить
эпюруMpq с эпюрой 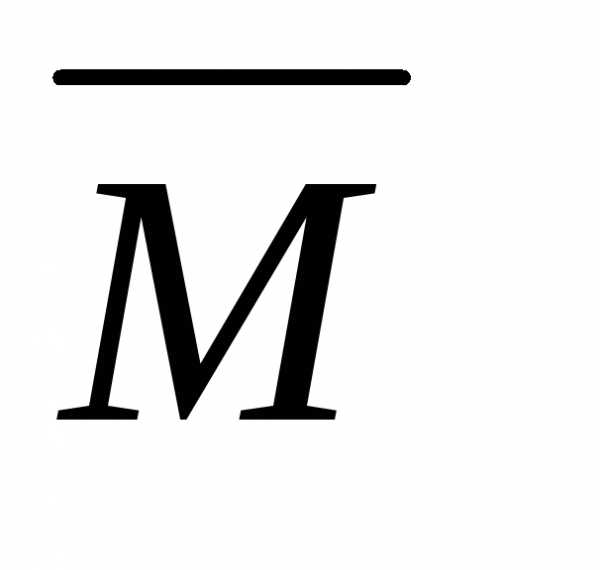 на
двух участках, а эпюруMpМ с эпюрой M – на одном.
на
двух участках, а эпюруMpМ с эпюрой M – на одном.
Далее, используя формулу (1.12),
«перемножаем» эпюры Мр и 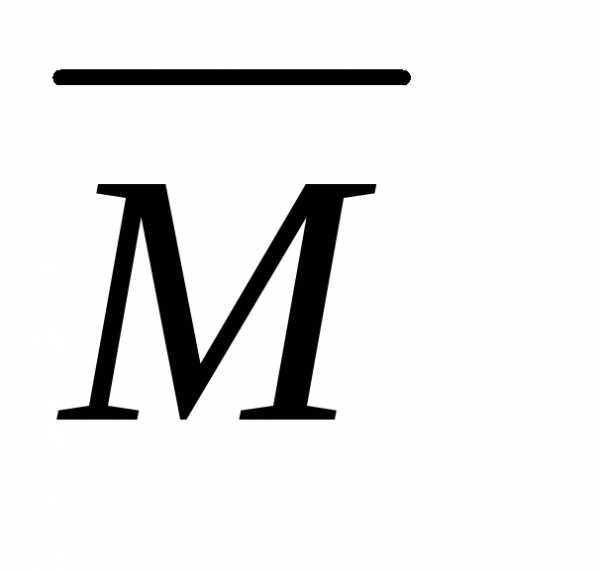 . При этом на первом участке нужно
«умножить» вогнутую параболу натреугольник, на
втором – эпюру, состоящую из треугольника
– на треугольник, а на третьем – эпюру,
состоящую из треугольника – также на
треугольник, но с вершинами, не лежащими
на одной вертикали.
. При этом на первом участке нужно
«умножить» вогнутую параболу натреугольник, на
втором – эпюру, состоящую из треугольника
– на треугольник, а на третьем – эпюру,
состоящую из треугольника – также на
треугольник, но с вершинами, не лежащими
на одной вертикали.
7. Вычисляем значение лишней неизвестной
.
Так как , статическая неопределимость балки раскрыта. Далее решение строится обычным образом для расчета балки на изгиб.
8. Загружаем о.с. внешней нагрузкой и силойХ1(рис. 1.11,а).
9. Строим эпюру внутренней поперечной силы Qуи внутреннего изгибающего момента Мz.(рис. 1.11,б и рис. 1.11,в).Предварительно необходимо определить реакции опор B и С.
.
.
Знак минус означает, что реакция RCнаправлена в сторону, противоположную предварительно выбранной и направленной вверх. ЗачеркиваемRCи показываем истинное направление реакции опоры.
Проверка:
; .
На балке два участка. Составляем уравнения для QиМ на участках:
Участок I:
На участке особенная точка  Определяем ее координаты и находим
максимальный момент на участкеI.
Определяем ее координаты и находим
максимальный момент на участкеI.
Из анализа эпюры Mz следует, что максимальный по модулю изгибающий момент действует в сечении по опореС:.
10. Подбираем поперечное сечение балки в виде двутавра из условия прочности по нормальным напряжениям
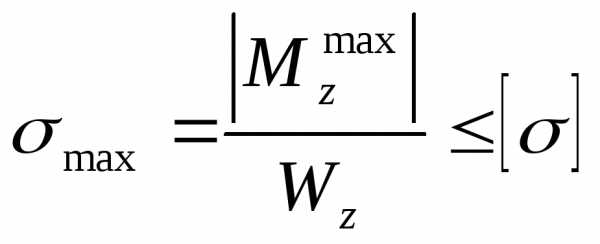 ,
.
,
.

Рис. 1.11.
Из сортамента (Прил. 2) выбираем двутавр I№33, у которого момент сопротивления. Действующие максимальные напряжения:
.
Максимальные действующие напряжения меньше допускаемых. Прочность обеспечена.
Примечание: стандартом допускается превышение максимальных действующих напряжений над допускаемыми, но не более чем на 5%.
studfiles.net
Особенности построения эпюр внутренних усилий в рамах — МегаЛекции
Рама – это стержневая система, состоящая из двух и более стержней, лежащих в одной плоскости и жестко соединенных в местах стыков.
Порядок построения эпюр внутренних усилий (эпюра Q, эпюра М) аналогичен тому, как это делается для балок с несколькими участками и прямолинейной осью (см. РГР №4), с той лишь разницей, что оси отдельных участков стержней на раме не лежат на одной линии. В этой связи правило знаков для Q и M, принятое при построении эпюр в балках, неудобно. Для удобства построения эпюр внутренних усилий в рамах принимаем правило построения эпюр внутренних усилий на сжатом волокне стержней, составляющих раму.
Рассмотрим раму, состоящую из двух стержней AB и BC с опорой в точке C в виде жесткой заделки (рис. 1.7). Стержни AB и BC жестко соединены в точке B (в процессе деформации под действием внешней нагрузки ). Построим эпюру внутренних изгибающих моментов для такой стержневой системы.
Для построения эпюры M (рис. 1.8) необходимо вычислить значения внутренних изгибающих моментов на левой и правой границах каждого из стержней, составляющих раму. Это можно сделать путем составления уравнения внутренних изгибающих моментов для участков рамы, с последующей подстановкой в них координат точек, где вычисляется внутреннее усилие, или путем непосредственного определения значений внутренних усилий в заданных точках. Двигаясь со свободного края рамы (стержня AB) вычислим моменты в точках A и B. Соответственно МА = 0, МВ= 20 кНм. В стержне AB при действии силы P будут сжаты нижние волокна, поэтому значения моментов откладываем вниз от оси стержня AB. Завершаем построение эпюры M на стержне AB, соединив точки и прямой линией. Далее рассматриваем стержень BC. Все нагрузки, приложенные к стержню AB, приводим к точке B. Анализ напряженного состояния стержня BC показывает, что он нагружен сжимающей силой и изгибающим моментом .
| Рис. 1.7. | Рис. 1.8. |
Таким образом, на стыке стержней АВ и BC внутренний изгибающий момент будет равен 20 кНм. Так как никаких других изгибающих нагрузок на стержень ВС не действует, внутренний изгибающий момент будет постоянным на участке ВС. Откладываем значение 20 кНм слева от оси стержня BC в точки B и C и соединяем эти точки прямой линией; слева – потому что волокна слева от оси стержня будут сжаты. Так как сжимающая нагрузка Р, приложенная к стержню ВС, не является определяющей, то на этапе расчета на изгиб рамы ею пренебрегаем. Она будет учтена при проверочном расчете, который выходит за рамки задания.
ПРИМЕРЫ РАСЧЕТА
Часть I. расчет на прочность статически
Неопределимой балки
Задание
Для балки, выбранной на рис. 1.9, выполнить следующие расчеты:
1. Раскрыть статическую неопределимость, используя метод сил;
2. Построить эпюры поперечных сил Q. и изгибающих моментов М;
3. Из условия прочности по нормальным напряжениям при изгибе подобрать сечение двутаврового профиля по допускаемым напряжениям . Линейные размеры и величины нагрузок взять в табл. 1.2.
Исходные данные
Расчетная схема балки приведена на рис. 1.10,а.
Решение
1. Определение степени статической неопределимости балки.
Как известно, плоская статически определимая система содержит три связи. При этом защемление дает три связи, шарнирно неподвижная опора – две связи, а шарнирно подвижная – одну связь. Поэтому степень статической неопределимости плоской стержневой системы N определяется по формуле
N= С – 3, (1.10)
где С – общее число связей; N – степень статической неопределимости системы.
Таблица 1.2
| № стро-ки | № схемы | Балка | № схемы | Рама | ||||||||||
| м | кН | кН/м | кНм | м | кН | кН/м | кНм | |||||||
| 1,0 | 1,5 | 0,5 | 1,0 | 2,0 | 0,4 | - | - | |||||||
| 1,5 | 2,0 | 1,0 | 1,2 | 2,2 | 0,5 | - | - | |||||||
| 2,0 | 2,5 | 1,5 | 1,4 | 2,4 | 0,6 | - | - | |||||||
| 2,5 | 3,0 | 2,0 | 1,6 | 2,6 | 0,7 | - | - | |||||||
| 3,0 | 2,5 | 2,5 | 1,8 | 2,8 | 0,8 | - | - | |||||||
| 2,5 | 2,0 | 3,0 | 2,0 | 3,0 | 0,9 | - | - | |||||||
| 2,0 | 1,5 | 2,5 | 2,2 | 3,2 | 0,8 | - | - | |||||||
| 1,5 | 1,0 | 2,0 | 2,4 | 3,4 | 0,7 | - | - | |||||||
| 1,0 | 0,5 | 1,5 | 2,6 | 3,6 | 0,6 | - | - | |||||||
| 0,5 | 1,0 | 1,0 | 2,8 | 3,8 | 0,5 | - | - | |||||||
| е | г | д | в | д | е | а | е | а | б | г | е | е | е |
Рис. 1.9.
Рис. 1.10.
В нашем случае С = 2+1+1, так как имеем две шарнирно подвижных и одну шарнирно неподвижную опору. На схеме (рис. 1.10,а) для каждой опоры проставлено количество связей. Поэтому, используя формулу (1.10), получим N = 4 — 3 =1. Следовательно, в нашем случае балка один раз статически неопределима.
2. Выбираем основную систему (о.с), т.е. статически определимую, геометрически неизменяемую систему, которая получается из исходной статически неопределимой путем отбрасывания «лишних» связей. В нашем случае отбрасываем опору А и полученная о.с. показана на схеме (рис. 1.10,б). Такая схема удобна тем, что в процессе построения эпюр и не нужно определять реакции опор, так как эпюры могут быть построены и без определения реакций опор. В некоторых случаях такой подход к решению задачи невозможен и при построении эпюр и , предварительно необходимо определять реакции опор.
3. Загружаем о.с. внешней нагрузкой и «лишней» неизвестной (рис. 1.10,в).
4. Составляем систему канонических уравнений метода сил.
Так как рассматриваемая балка один раз статически неопределима, то для нее записывается одно уравнение (1.7):
,
откуда
, (1.11)
где –перемещение по линии действия силы Х1 от этой силы, равной единице; – перемещение по линии действия силы Х1 от внешней нагрузки.
Для определения коэффициентов используем правило Верещагина. Если эпюры изгибающих моментов Мрили содержат несколько участков, то правило Верещагина должно быть использовано для каждого из участков по отдельности.
Поэтому в общем случае искомое перемещение, например , определяется по формуле
, (1.12),
где n – количество участков, на которые разбиваются эпюры изгибающих моментов ; i– площадь грузовой эпюры, т.е. эпюры Мрна i-мучастке; – ордината эпюры на i-мучастке, расположенная под центром тяжести эпюры Mpi; EJ –жесткость стержня.
5. Определяем коэффициент .
Для этого предварительно строим в о.с. эпюру изгибающего момента от действия силы (рис. 1.10,г.). Далее, используя формулу (1.8), «умножаем» эпюру саму на себя. Получим
где – площадь первого участка эпюры ; – ордината центра тяжести площади первого участка эпюры ; – площадь второго участка эпюры ; – ордината центра тяжести площади второго участка эпюры .
6. Определяем коэффициент .
Для определения коэффициента необходимо построить эпюру изгибающего момента Мрот действия внешней нагрузки, приведенной на рис. 1.10,в. Для упрощения процесса перемножения эпюр будем строить эпюры внутренних изгибающих моментов от каждой внешней нагрузки отдельно, используя принцип независимости действия сил (принцип суперпозиции). Результат построения показан на рис. 1.10,д. При этом нет необходимости предварительно определять реакции опор. Достаточно на консоли АВ построить эпюру изгибающего момента от распределенной нагрузки q (Mpq) (это вогнутая парабола с высотой 250 кНм) и соединить ординату эпюры Mpq на опоре В с ординатой эпюры Mpqна опоре С, равной 0. Аналогично определив ординаты эпюры MpМ на опоре В и на опоре С, соединяем их прямой линией. Очевидно, что . При этом также очевидно, что для получения результата необходимо перемножить эпюру Mpqс эпюрой на двух участках, а эпюру MpМ с эпюрой M – на одном.
Далее, используя формулу (1.12), «перемножаем» эпюры Мри . При этом на первом участке нужно «умножить» вогнутую параболу на треугольник, на втором – эпюру, состоящую из треугольника – на треугольник, а на третьем – эпюру, состоящую из треугольника – также на треугольник, но с вершинами, не лежащими на одной вертикали.
7. Вычисляем значение лишней неизвестной
.
Так как , статическая неопределимость балки раскрыта. Далее решение строится обычным образом для расчета балки на изгиб.
8. Загружаем о.с. внешней нагрузкой и силой Х1 (рис. 1.11,а).
9. Строим эпюру внутренней поперечной силы Qу и внутреннего изгибающего момента Мz. (рис. 1.11,б и рис. 1.11,в). Предварительно необходимо определить реакции опор B и С.
.
.
Знак минус означает, что реакция RC направлена в сторону, противоположную предварительно выбранной и направленной вверх. Зачеркиваем RC и показываем истинное направление реакции опоры.
Проверка:
; .
На балке два участка. Составляем уравнения для Q и М на участках:
Участок I:
На участке особенная точка Определяем ее координаты и находим максимальный момент на участке I.
Из анализа эпюры Mzследует, что максимальный по модулю изгибающий момент действует в сечении по опоре С: .
10. Подбираем поперечное сечение балки в виде двутавра из условия прочности по нормальным напряжениям
, .
Рис. 1.11.
Из сортамента (Прил. 2) выбираем двутавр I №33, у которого момент сопротивления . Действующие максимальные напряжения:
.
Максимальные действующие напряжения меньше допускаемых. Прочность обеспечена.
Примечание: стандартом допускается превышение максимальных действующих напряжений над допускаемыми, но не более чем на 5%.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Методические указания по дисциплине «Сопротивление материалов», страница 6
Эпюра М ограничена квадратичной параболой с выпуклостью вниз. Экстремального значения изгибающего момента не надо определять т.к. эпюра Q ось не пересекает.
Определим продольную силу N. (рис. 2.11).
2.10 Построение эпюр для пространственной рамы способом сложения действия сил.
В пространственных конструкциях при определении внутренних силовых факторов действует следующее правило знаков.
33
Продольные силы N растягивающие считаются положительными
(N>0), а сжимающие – отрицательными (N<0).
Поперечные силы и имеют знаки, совпадающие со знаками проекций этих сил на главные центральные оси инерции в сечении (оси x и y).
Изгибающие моменты и будут положительными, если, изгибая стержень, они растягивают материал в первой четверти поперечного сечения (M>0). Если материал в первой четверти сжат, действующий изгибающий момент будет отрицательным (M<0).
Эпюры изгибающих моментов строятся по-прежнему со стороны растянутого волокна.
Крутящий момент будет положительным (>0), если поворачивает сечение по часовой стрелке, и отрицательным (<0), если поворот происходит против часовой стрелки. Эпюра штрихуется спиралью, чтобы можно было отличить её от эпюр изгибающих моментов.
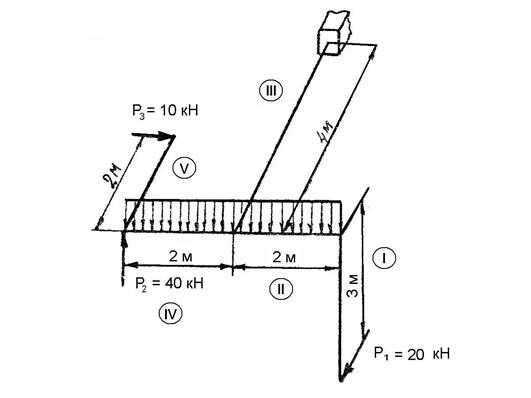
Рис. 2.12.
34
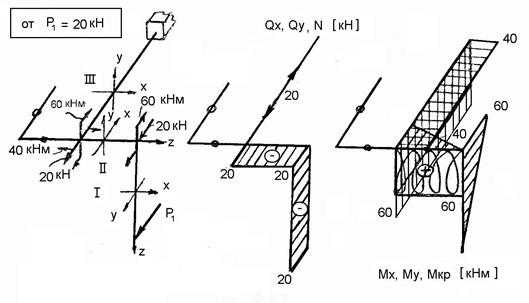
Рис. 2.13.
Сразу ″зануляем″ нерабочие участки рамы (рис. 2.13.) По раме идем от свободного конца к заделке: 1-2-3 участки, перенося силу из узла в узел.
Условное обозначение продольных сил на эпюрах приведены на рис. 2.14.
Рис. 2.14.
кН- const;
; ; ;
Растянуто заднее волокно.
35
;
кН – const;
; ; ;
Растянуто заднее волокно.
– const;
; кН– const;
– const;
Растянуто нижнее волокно.
— const;
Растянуто правое волокно.
.
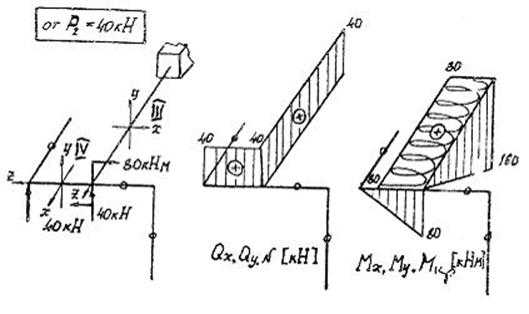
Рис. 2.15.
Сразу ″зануляем″ нерабочие участки рамы идем от свободного конца к заделке: 4-3 участки (рис 2.15)
36
кН – const;
; ; ;
Растянуто нижнее волокно.
кН — const;
; ; ;
Растянуто нижнее волокно.
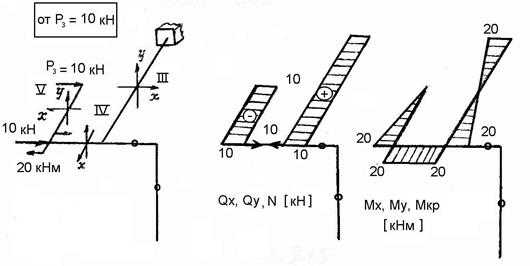 — const.
— const.
Рис. 2.16.
Сразу ″зануляем″ нерабочие участки рамы идем от свободного конца к заделке: 5→4→3 участки (рис 2.16)
кН – const;
; ; .
Растянуто левое волокно.
кН – const;
37
– const.
Растянуто нижнее волокно.
кН– const;
;
; .
В начале участка растянуто правое волокно, в конце – левое.
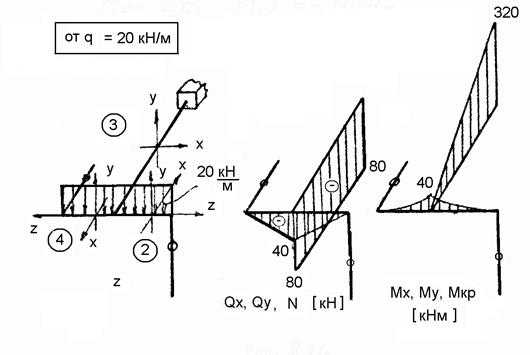
Рис. 2.17.
″Зануляем″ нерабочие участки рамы. Идем от свободных концов к заделке (рис 2.17).
;
; кН;
; ; кНм.
Растянуто верхнее волокно.
38
; ; кН;
;
; кНм.
Растянуто верхнее волокно.
кН – const;
; ; кНм.
Растянуто верхнее волокно.
Суммируем эпюры от всех нагрузок
(рис. 2.18)
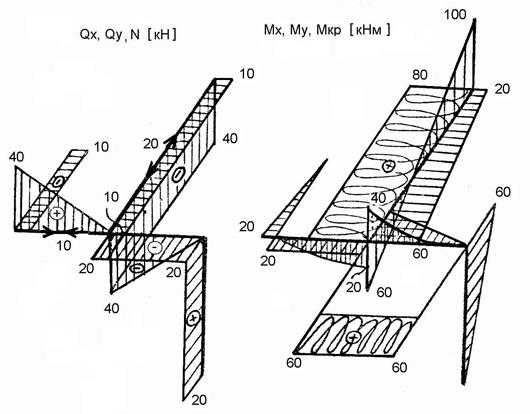
Рис. 2.18.
39
Опасное сечение в заделке, где одновременно действуют:
кН; кН; кН;
; кНм; кНм.
40
Расчетно-графическое задание.
Построить эпюры всех действующих сил. Данные взять из таблицы 1.
Строка | a | ||||||
1 | 40 | 100 | 60 | 100 | 150 | 50 | 1 |
2 | 150 | 60 | 30 | 120 | 60 | 20 | 2 |
3 | 20 | 100 | 50 | 40 | 140 | 60 | 3 |
4 | 40 | 120 | 60 | 80 | 150 | 20 | 2 |
5 | 80 | 40 | 20 | 130 | 50 | 40 | 3 |
41
Вставить варианты
1-50
51-100
42
Библиографический список
Основной
1. Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов. М., Высшая школа, 1995 г.
2. Сопротивление материалов. Под ред. Костенко С.А., М., Высшая школа, 2000 г.
3. Ицкович Г.Н. Сопротивление материалов. М., Высшая школа, 1998 г.
Дополнительный
4. Смирнов А.Ф. и др. Сопротивление материалов. Высшая школа, М., 1975, 480 с., с ил.
5. Беляев Н.М. Сопротивление материалов. – М., 1976 (и все другие издания).
6. Феодосьев В.И. Сопротивление материалов. – Наука, 1974 (и все другие издания).
7. Дарков А.В., Шпиро Г.С. Сопротивление материалов. – Высшая школа, 1980 (и все другие издания).
8. Писаренко Г. С. и др. Сопротивление материалов. Киев, 1986
43
Составитель В.Н. Яременко
Методические указания для студентов всех специальностей.
Издательский центр МГТУ им.Г.И.Носова
455000, Магнитогорск, пр.Ленина, 38
Полиграфический участок МГТУ
vunivere.ru
Особенности построения эпюр внутренних усилий в рамах
Дом Особенности построения эпюр внутренних усилий в рамахпросмотров — 554
Рама — ϶ᴛᴏ стержневая система, состоящая из двух и более стержней, лежащих в одной плоскости и жестко соединенных в местах стыков.
Порядок построения эпюр внутренних усилий (эпюра Q, эпюра М) аналогичен тому, как это делается для балок с несколькими участками и прямолинейной осью (см. РГР №4), с той лишь разницей, что оси отдельных участков стержней на раме не лежат на одной линии. В этой связи правило знаков для Q и M, принятое при построении эпюр в балках, неудобно. Для удобства построения эпюр внутренних усилий в рамах принимаем правило построения эпюр внутренних усилий на сжатом волокне стержней, составляющих раму.
Рассмотрим раму, состоящую из двух стержней AB и BC с опорой в точке C в виде жесткой заделки (рис. 1.7). Стержни AB и BC жестко соединены в точке B (в процессе деформации под действием внешней нагрузки ). Построим эпюру внутренних изгибающих моментов для такой стержневой системы.
Для построения эпюры M (рис. 1.8) крайне важно вычислить значения внутренних изгибающих моментов на левой и правой границах каждого из стержней, составляющих раму. Это можно сделать путем составления уравнения внутренних изгибающих моментов для участков рамы, с последующей подстановкой в них координат точек, где вычисляется внутреннее усилие, или путем непосредственного определения значений внутренних усилий в заданных точках. Двигаясь со свободного края рамы (стержня AB) вычислим моменты в точках A и B. Соответственно МА = 0, МВ= 20 кНм. В стержне AB при действии силы P будут сжаты нижние волокна, в связи с этим значения моментов откладываем вниз от оси стержня AB. Завершаем построение эпюры M на стержне AB, соединив точки и прямой линией. Далее рассматриваем стержень BC. Все нагрузки, приложенные к стержню AB, приводим к точке B. Анализ напряженного состояния стержня BC показывает, что он нагружен сжимающей силой и изгибающим моментом .
| Рис. 1.7. | Рис. 1.8. |
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, на стыке стержней АВ и BC внутренний изгибающий момент будет равен 20 кНм. Так как никаких других изгибающих нагрузок на стержень ВС не действует, внутренний изгибающий момент будет постоянным на участке ВС. Откладываем значение 20 кНм слева от оси стержня BC в точки B и C и соединяем эти точки прямой линией; слева – потому что волокна слева от оси стержня будут сжаты. Так как сжимающая нагрузка Р, приложенная к стержню ВС, не является определяющей, то на этапе расчета на изгиб рамы ею пренебрегаем. Она будет учтена при проверочном расчете, который выходит за рамки задания.
Читайте также
Рама – это стержневая система, состоящая из двух и более стержней, лежащих в одной плоскости и жестко соединенных в местах стыков. Порядок построения эпюр внутренних усилий (эпюра Q, эпюра М) аналогичен тому, как это делается для балок с несколькими участками и… [читать подробенее]
oplib.ru