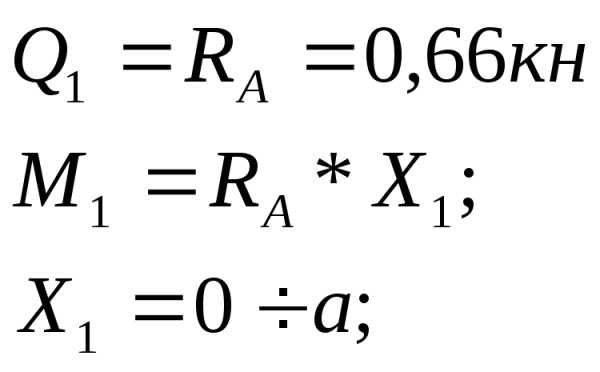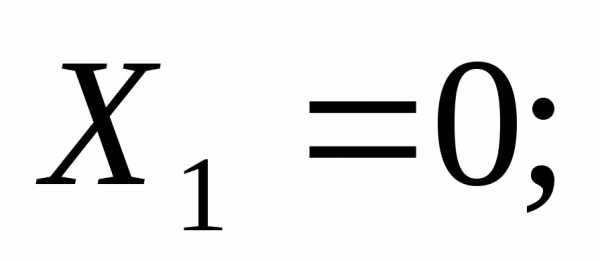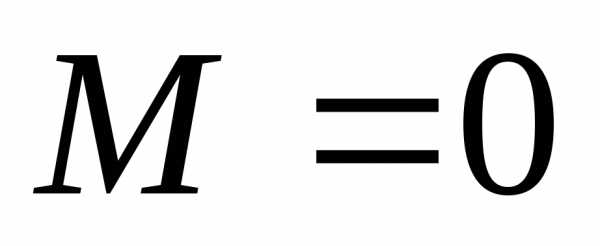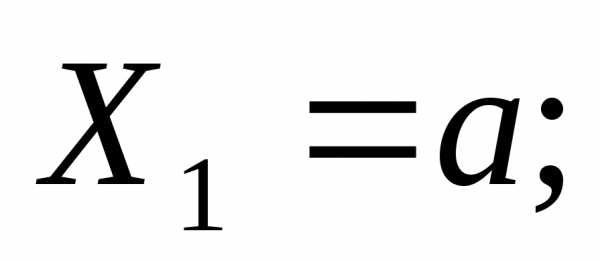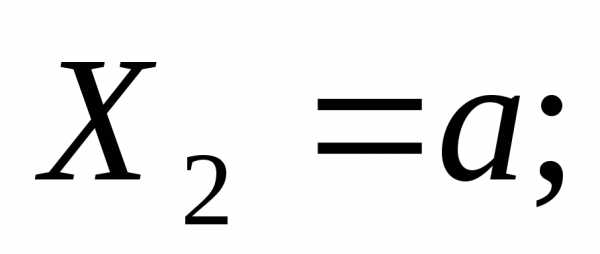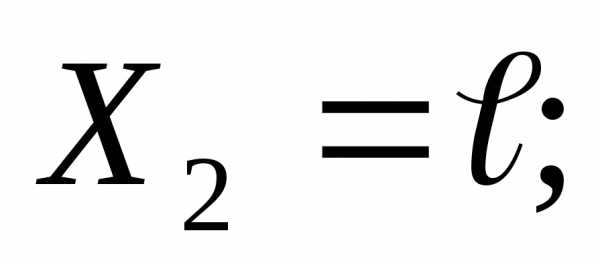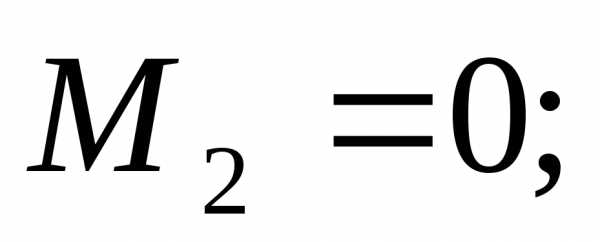Поперечная сила и изгибающий момент.
В поперечных сечениях балки возникает поперечная сила Q и изгибающий моментM.
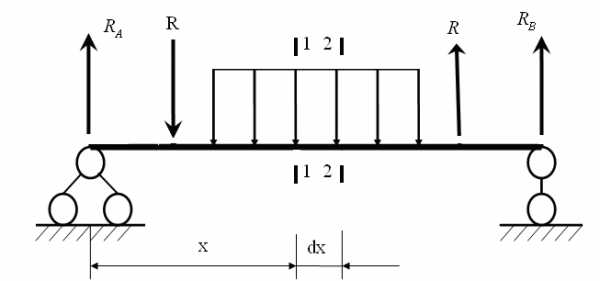
| Разрежем балку на расстоянии Х. Заменим действие отброшенной части (правой) внутренними усилиями Q и M; рассмотрим левую часть балки. Q – поперечная сила — результирующая всех внутренних усилий алгебраически равна сумме всех сил, расположенных левее сечения. M – изгибающий момент результирующий момент всех внешних сил, численно равен алгебраической сумме моментов всех усилий, расположенных левее сечения. Составим уравнения равновесия для левой части: |
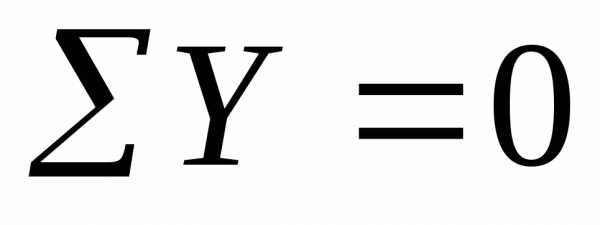 →→
→→
∑МсечХ=0; →→;
Можно вместо левой части рассмотреть правую часть. Результат будет тот же, но с обратным знаком.
В связи с этим для того, чтобы в одном и том же сечении Q и M имели одинаковые знаки независимо от того какая часть рассматривается, примем следующее
ПРАВИЛО ЗНАКОВ (см. рисунок):
Поперечную силу будем считать положительной, если равнодействующая сила левее сечения направлена вверх, а правее сечения направлена вниз.
Изгибающий момент будет считаться положительным, если равнодействующий момент левых сил направлен по ходу часовой стрелки, а правых – против часовой стрелки.
Зависимость между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки.
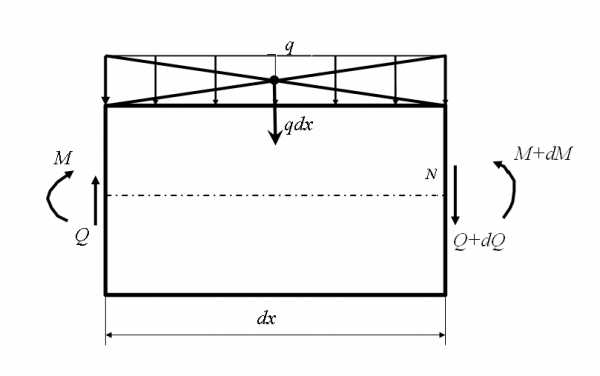
| Выделим из балки участок бесконечно малой длины так чтобы по границам этого участка и по самом участке сосредоточенные силы отсутствовали. Ввиду малости участка распределенную
нагрузку Составим уравнения равновесия: или
|
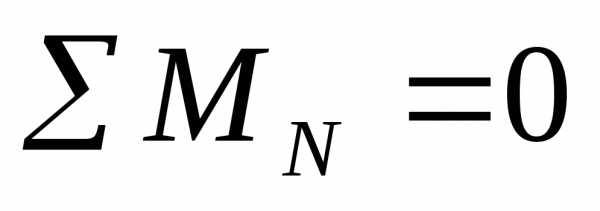 ;;
;;
Пренебрегая бесконечно малыми величинами второго порядка, получаем:или
Продифференцировав последнее
выражение по Х, получаем: 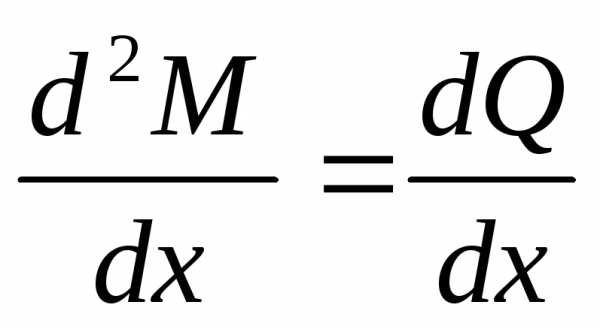 ;или
;или
Построение эпюр изгибающих моментов и поперечных сил.
Внутренние усилия Q и M зависят от координатыХ,поэтому удобно иметь графики зависимостиQ и M от расстоянияХ,эти графики называютсяэпюрамипоперечных сил и изгибающих моментов. Построение эпюрQ и M рассмотрим на частных примерах.
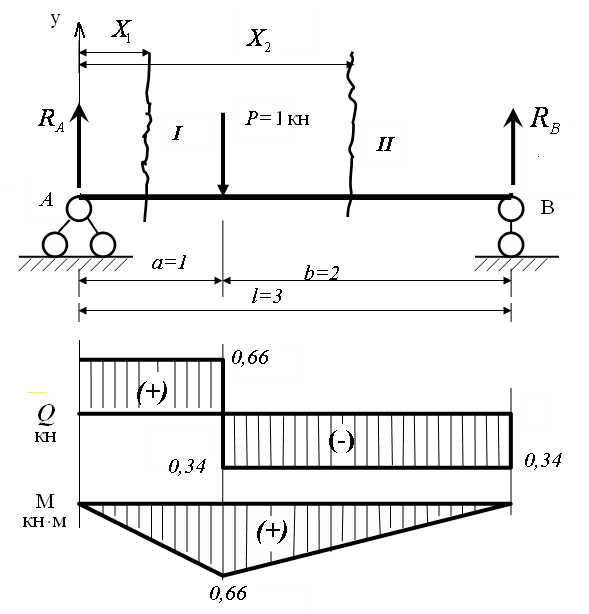
Положительные изгибающие моментыбудем откладывать в сторону растянутых волокон. | Пример 1. Построить эпюры Q иM. 1) Определяем опорные реакции: 2) Разбиваем балку на участки. 3) Участок 1: (рассекаем на расстоянии Х1) Участок 2: (рассекаем на расстоянии Х2) при при . |
Пример 2. Построить эпюры Q иM.
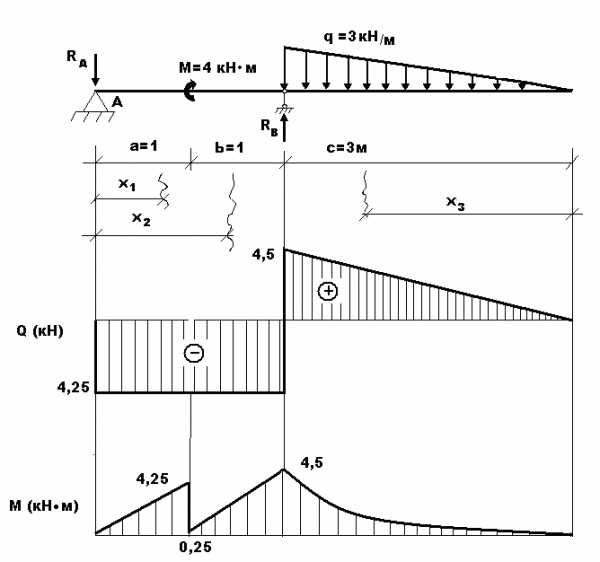
Определим опорные реакции:
Проверка
,
Следовательно, опорные реакции определены верно.
2) Построим эпюры QиM:
Участок I:
Участок II:
Участок III:
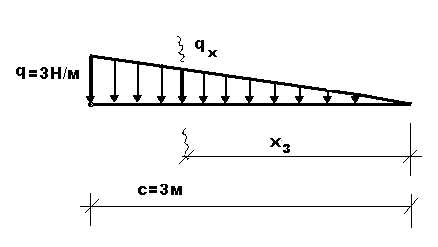
| Идем справа налево Из подобия треугольников . находим: |
studfiles.net
Изгибающий момент и поперечная сила
Основные понятия об изгибе. Чистый и поперечный изгиб балки
Чистым изгибом называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только изгибающий момент.
Деформация чистого изгиба будет, например, иметь место, если к прямому брусу в плоскости, проходящей через ось, приложить две равные по величине и противоположные по знаку пары сил.
На изгиб работают балки, оси, валы и другие детали конструкций. Если брус имеет хоть одну ось симметрии, и плоскость действия нагрузок совпадает с ней, то имеет место прямой изгиб, если же это условие не выполняется, то имеет место косой изгиб.
При изучении деформации изгиба будем мысленно представлять себе, что балка (брус) состоит из бесчисленного количества продольных, параллельных оси волокон.
Чтобы наглядно представить деформацию прямого изгиба, проведем опыт с резиновым брусом, на котором нанесена сетка продольных и поперечных линий.
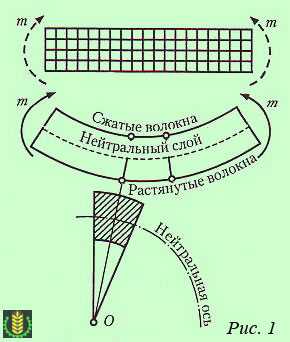
Подвергнув такой брус прямому изгибу, можно заметить, что (рис. 1):
— поперечные линии останутся при деформации прямыми, но повернутся под углом друг другу;
— сечения бруса расширятся в поперечном направлении на вогнутой стороне и сузятся на выпуклой стороне;
— продольные прямые линии искривятся.
Из этого опыта можно сделать вывод, что:
— при чистом изгибе справедлива гипотеза плоских сечений;
— волокна, лежащие на выпуклой стороне растягиваются, на вогнутой стороне – сжимаются, а на границе между ними лежит нейтральный слой волокон, которые только искривляются, не изменяя своей длины.
Полагая справедливой гипотезу о не надавливании волокон, можно утверждать, что при чистом изгибе в поперечном сечении бруса возникают только нормальные напряжения растяжения и сжатия, неравномерно распределенные по сечению.
Линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной осью. Очевидно, что на нейтральной оси нормальные напряжения равны нулю.
Изгибающий момент и поперечная сила
Как известно из теоретической механики, опорные реакции балок определяют, составляя и решая уравнения равновесия статики для всей балки. При решении задач сопротивления материалов, и определении внутренних силовых факторов в брусьях, мы учитывали реакции связей наравне с внешними нагрузками, действующими на брусья.
Для определения внутренних силовых факторов применим метод сечений, причем изображать балку будем только одной линией – осью, к которой приложены активные и реактивные силы (нагрузки и реакции связей).
Рассмотрим два случая:
1.К балке приложены две равные и противоположные по знаку пары сил.
Рассматривая равновесие части балки, расположенной слева или справа от сечения 1-1 (рис. 2), видим, что во всех поперечных сечениях возникает только изгибающий момент Ми, равный внешнему моменту. Таким образом, это случай чистого изгиба.
Изгибающий момент есть результирующий момент относительно нейтральной оси внутренних нормальных сил, действующих в поперечном сечении балки.
Обратим внимание на то, что изгибающий момент имеет разное направление для левой и правой частей балки. Это говорит о непригодности правила знаков статики при определении знака изгибающего момента.
2. К балке приложены активные и реактивные силы (нагрузки и реакции связей), перпендикулярные оси (рис 3). Рассматривая равновесие частей балки, расположенных слева и справа, видим, что в поперечных сечениях должны действовать изгибающий моментМи и поперечная сила Q.
Из этого следует, что в рассматриваемом случае в точках поперечных сечений действуют не только нормальные напряжения, соответствующие изгибающему моменту, но и касательные, соответствующие поперечной силе.
Поперечная сила есть равнодействующая внутренних касательных сил в поперечном сечении балки.
Обратим внимание на то, что поперечная сила имеет противоположное направление для левой и правой частей балки, что говорит о непригодности правила знаков статики при определении знака поперечной силы.
Изгиб, при котором в поперечном сечении балки действуют изгибающий момент и поперечная сила, называется поперечным.
У балки, находящейся в равновесии вод действием плоской системы сил, алгебраическая сумма моментов всех активных и реактивных сил относительно любой точки равна нулю; следовательно, сумма моментов внешних сил, действующих на балку левее сечения, численно равна сумме моментов всех внешних сил, действующих на балку правее сечения.
Таким образом, изгибающий момент в сечении балки численно равен алгебраической сумме моментов относительно центра тяжести сечения всех внешних сил, действующих на балку справа или слева от сечения.
У балки, находящейся в равновесии под действием плоской системы сил, перпендикулярных оси (т. е. системы параллельных сил), алгебраическая сумма всех внешних сил равна нулю; следовательно сумма внешних сил, действующих на балку левее сечения, численно равна алгебраической сумме сил, действующих на балку правее сечения.
Таким образом, поперечная сила в сечении балки численно равна алгебраической сумме всех внешних сил, действующих справа или слева от сечения.
Так как правила знаков статики неприемлемы для установления знаков изгибающего момента и поперечной силы, установим для них другие правила знаков, а именно: Если внешняя нагрузка стремится изогнуть балку выпуклостью вниз, то изгибающий момент в сечении считается положительным, и наоборот, если внешняя нагрузка стремится изогнуть балку выпуклостью вверх, то изгибающий момент в сечении считается отрицательным (рис 4a).
Если сумма внешних сил, лежащих по левую сторону от сечения, дает равнодействующую, направленную вверх, то поперечная сила в сечении считается положительной, если равнодействующая направлена вниз, то поперечная сила в сечении считается отрицательной; для части балки, расположенной справа от сечения, знаки поперечной силы будут противоположными (рис. 4b). Пользуясь этими правилами, следует мысленно представлять себе сечение балки жестко защемлённым, а связи отброшенными и замененными реакциями.
Еще раз отметим, что для определения реакций связей пользуются правилами знаков статики, а для определения знаков изгибающего момента и поперечной силы – правилами знаков сопротивления материалов.
Правило знаков для изгибающих моментов иногда называют «правилом дождя», имея в виду, что в случае выпуклости вниз образуется воронка, в которой задерживается дождевая вода (знак положительный), и наоборот – если под действием нагрузок балка выгибается дугой вверх, вода на ней не задерживается (знак изгибающих моментов отрицательный).
Эпюры внутренних усилий при прямом изгибе.
Прямым изгибом называется такой вид простого сопротивления, когда внешние силы приложены перпендикулярно продольной оси бруса (балки) и расположены в одной из главных плоскостей в соответствие с конфигурацией поперечного сечения балки.
Как известно, при прямом изгибе в поперечном сечении возникают два вида внутренних усилий: поперечная сила и внутренний изгибающий момент.
Рассмотрим пример расчетной схемы консольной балки с сосредоточенной силой Р, рис. 1 а., …

а) расчетная схема, б) левая часть, в) правая часть, г) эпюра поперечных сил, д) эпюра изгибающих моментов
Рис.1. Построение эпюр поперечных сил и внутренних изгибающих моментов при прямом изгибе:
Наиболее рациональным следует признать сечение, обладающее минимальной площадью при заданной нагрузке (изгибающем моменте) на балку. В этом случае расход материала на изготовление балки, будет минимальным. Для получения балки минимальной материалоемкости нужно стремиться к тому, чтобы по возможности наибольший объем материала работал при напряжениях, равных допускаемым или близким к ним. Прежде всего рациональное сечение балки при изгибе должно удовлетворять условию равнопрочности растянутой и сжатой зон балки.Иными словами необходимо, чтобы наибольшие напряжения растяжения (max ) н наибольшие напряжения сжатия (max ) одновременно достигали допускаемых напряжений и .
Поэтому для балки из пластичного материала (одинаково работающего на растяжение и сжатие: ), условие равнопрочности выполняется для сечений, симметричных относительно нейтральной оси. К таким сечениям относится, например, прямоугольное сечение (рис. 6, а), при котором обеспечено условие равенства . Однако в этом случае материал, равномерно распределенный по высоте сечения, плохо используется в зоне нейтральной оси. Чтобы получить более рациональное сечение, необходимо возможно большую часть материала переместить в зоны, максимально удаленные от нейтральной оси. Таким образом, приходим к рациональному для пластичного материала сечению в форме симметричного двутавра (рис. 6): 2 горизонтальных массивных листа, соединенные стенкой (вертикальным листом), толщина которой назначается из условий прочности стенки по касательным напряжениям, а также из соображений ее устойчивости. К двутаврому сечению близко по критерию рациональности так называемое коробчатое сечение (рис. 6, в).
Рис.6. Распределение нормальных напряжений в симметричных сечениях
Рассуждая аналогично, приходим к выводу, что для балок из хрупкого материала наиболее рациональным будет сечение в форме несимметричного двутавра, удовлетворяющего условию равнопрочности на растяжение и сжатие (рис. 27):
которое вытекает из требования
Рис.7. Распределение напряжений несимметричного профиля сечения балки.
Идея рациональности поперечного сечения стержней при изгибе реализована в стандартных тонкостенных профилях, получаемых методами горячего прессования или прокатки из рядовых и легированных конструкционных высококачественных сталей, а также алюминия и алюминиевых сплавов, получивших широкое распространение в строительстве, машиностроении, авиационном машиностроении. Широко распространены показанные на рис. 7: а—двутавр, б— швеллер, в — неравнобокий уголок, г—равнобокий уголок. Реже встречаются тавр, таврошвеллер, зетовый профиль и др.
Рис.8. Используемые профили сечений: а) двутавр, б ) швеллер, в) неравнобокий уголок, г) равнобокий уголок
Формула осевого момента сопротивления при изгибе выводится просто. Когда поперечное сечение балки симметрично относительно нейтральной оси, нормальные напряжения в наиболее удаленных точках (при ) определяются по формуле:
Геометрическую характеристику поперечного сечения балки, равную называют осевым моментом сопротивления при изгибе. Осевой момент сопротивления при изгибе измеряется в единицах длины в кубе (как правило, в см3). Тогда .
формула осевого момент сопротивления при изгибе для прямоугольного поперечного сечения: ;
формула осевого момент сопротивления при изгибе для круглого поперечного сечения: .
Похожие статьи:
poznayka.org
Как определить поперечную силу и изгибающий момент ?
В этой статье будем говорить как определяется поперечная сила и изгибающий момент. Оба эти внутренних силовых фактора появляются при поперечном изгибе. При чистом изгибе, когда на конструкцию действует только моменты, в поперечных сечениях появляются только изгибающие моменты.
Изгибающий момент действует в плоскости перпендикулярной к поперечному сечению и совпадает с одной из главных центральных осей.
Поперечная сила действует в плоскости поперечного сечения.
Пример определения поперечной силы и изгибающего момента
Давайте посмотрим, так сказать, воочию на эти внутренние силовые факторы. Рассмотрим балку, закрепленную с левого торца жесткой связью и нагруженной с другого торца силой P.
Воспользуемся любимым методом сечений. Рассечем балку в произвольном сечении на расстоянии x1 от свободного торца балки.
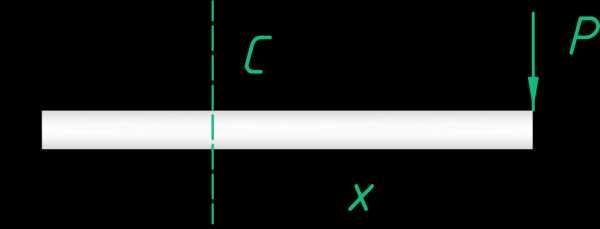
Заменим действие одной части балки на другую внутренними силовыми факторами, так сказать уравновесим обе части балки.
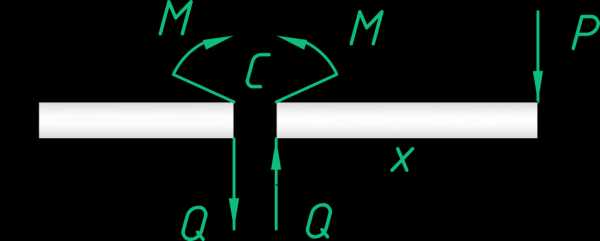
Если записать уравнения статики для одной из частей, например, для правой части балки, то получим:
∑Fkx= -P+Q=0. Тогда Q=P, то есть поперечная сила будет равна внешней силе.
∑Mc= P·x1-M=0. Тогда M= P·x1, то есть изгибающий момент в исследуемом сечении будет равен произведению внешней силы на расстояние от свободного торца до сечения.
Теперь рассмотрим балку подверженную только чистому изгибу. На свободном торце балки приложим только момент силы.

В поперечных сечениях, как говорилось выше, будут возникать только изгибающие моменты и только одной величины. Не трудно догадаться, что внутренний изгибающий момент будет равен внешнему моменту.
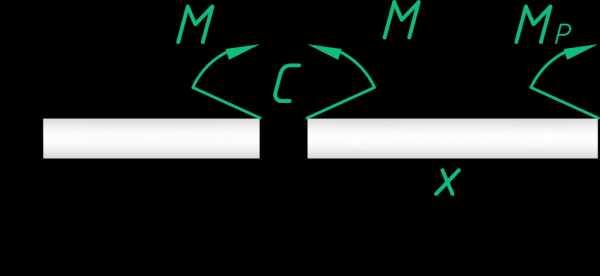
Важно научиться строить правильно эпюры изгибающих моментов и поперечных сил. Перед тем как читать статью про построение эпюр, рекомендую сначала ознакомиться с правилом знаков.
ssopromat.ru
Опорные реакции, максимальный изгибающий момент и прогиб балки — Расчет строительства
Admin Расчет строительства| Схема балки и нагрузки | Опорная реакция | Максимальный изгибающий момент | Стрела прогиба | Расстояние места максимального изгибающею момента от опоры А |
 Формула — Опорные реакции, максимальный изгибающий момент и прогиб балки
Формула — Опорные реакции, максимальный изгибающий момент и прогиб балки Формула — Опорные реакции, максимальный изгибающий момент и прогиб балки
Формула — Опорные реакции, максимальный изгибающий момент и прогиб балки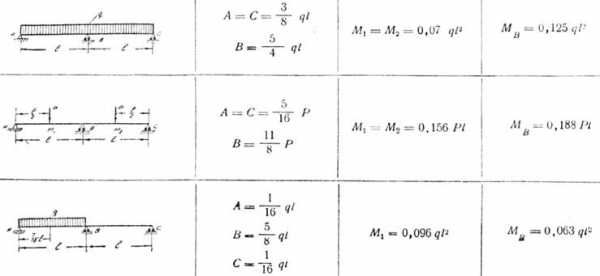 Формула — Опорные реакции, максимальный изгибающий момент и прогиб балки
Формула — Опорные реакции, максимальный изгибающий момент и прогиб балки Формула — Опорные реакции, максимальный изгибающий момент и прогиб балки
Формула — Опорные реакции, максимальный изгибающий момент и прогиб балки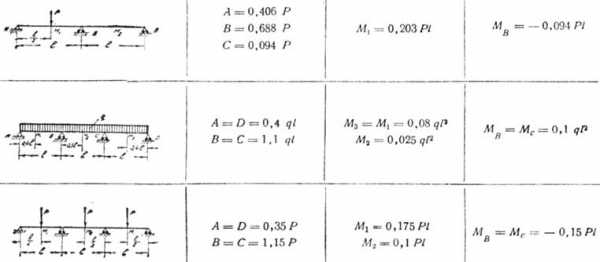 Формула — Опорные реакции, максимальный изгибающий момент и прогиб балки
Формула — Опорные реакции, максимальный изгибающий момент и прогиб балкиAbout Author
admin
arxipedia.ru
Изгибающий момент – внутренний силовой фактор
Здравствуйте. Здорово, что Вы проявляете интерес к нашему проекту SoproMats, спасибо! Эта статья будет посвящена внутреннему силовому фактору – изгибающему моменту. Фактору, который возникает в поперечных сечениях балок, работающих на изгиб. Здесь поделимся информацией как он обозначается, измеряется, определяется и т.д. В общем все, что нужно знать об изгибающем моменте. Также в конце статьи поделимся ссылочками, на важные материалы про изгибающий момент.
Что такое изгибающий момент?
Изгибающий момент – это внутренний силовой фактор, возникающий в элементах конструкций, деталях, работающих на изгиб: такие конструктивные элементы как балка, рама, плита и т.д.
Зачем нужен?
Зная изгибающий момент в сечении, а также геометрические размеры этого сечения, можно определить нормальное напряжение в его конкретной точке и исследовать ее напряженно-деформированное состояние. Определение изгибающих моментов является неотъемлемой частью любого прочностного расчета деталей, работающих на изгиб. Для наглядной визуализации распределения изгибающих моментов строят эпюры, которые позволяют выявить наиболее подверженные к разрушению места балки. Как правило, то сечение, в котором изгибающий момент имеет максимальное значение, является самым опасным у балки. За редкими исключениями. Поэтому так важно уметь определять эту величину.
Как обозначается?
Изгибающий момент обозначается буквой M с индексом, который указывает на название оси, относительного которой происходит изгиб. Обычно это ось x, поэтому в этой статье будем использовать такое обозначение — Mx.
Как определяется?
Для определения этой величины используется метод сечений. По которому считается, что если балка находится в равновесии, то и отдельные части балки также будут находится в равновесии, если действие каждой части друг на друга, заменить равными силовыми факторами. Используя этот метод в совокупности с уравнениями равновесия статики, можно определить изгибающий момент в любом сечении, более подробно посмотрим этот процесс на примере ниже.
В чем измеряется?
Данная величина измеряется в Н·м. В расчетах, в основном, используется размерность — кН·м, и этот вариант будем использовать в этой статье. Иногда считают в кгс·м и т·м.
Статьи про изгибающие моменты:
Как построить эпюру изгибающего момента? В материале этой статьи написано, как можно построить эпюру различными методами.
sopromats.ru
Поперечная сила и изгибающий момент
Поперечным изгибом называется такой вид деформирования бруса, при котором внешние нагрузки действуют перпендикулярно к его продольной оси. Деформация изгиба заключается в искривлении оси бруса.
Брус с прямой осью, работающий на изгиб, называется балкой. Если плоскость действия внешних нагрузок проходит через ось балки и одну из главных центральных осей поперечного сечения, изгиб называется прямым. В этом случае ось балки искривляется в плоскости действия нагрузок и является плоской кривой.
В сечениях балки возникают два внутренних силовых фактора: изгибающий момент Мх и поперечная сила Qy
Правила контроля построения эпюр Q и М при изгибе (рис. 6.1).
Дифференциальные зависимости между q, Qy и Мх имеют вид:
- В сечении, где приложена сосредоточенная сила, — на эпюре Qy скачок по модулю равный этой силе, на эпюре Мх – излом навстречу силе.
- В сечении, где приложена сосредоточенная пара сил m — на эпюре Мх скачок по модулю равный этой паре сил. На эпюре Qy это не сказывается.
- Если на участке имеется равномерно распределенная нагрузка q, то Qy изменяется по линейному закону, Мх – по параболе, выпуклостью навстречу нагрузке q (Мх = Мэкстр – в сечении, где Qy меняет свой знак).
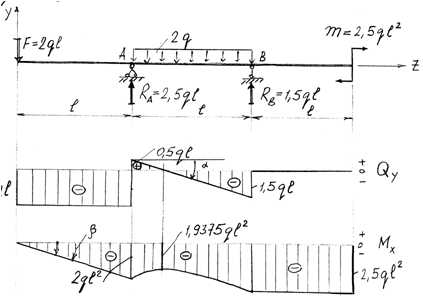
Рис. 6.1
Изгиб называется чистым, если в сечении балки возникает только изгибающий момент Мх.
Примеры решения задач >
Прочность и напряжения при изгибе >
isopromat.ru
Изгибающий момент — балка — Большая Энциклопедия Нефти и Газа, статья, страница 1
Изгибающий момент — балка
Cтраница 1
Изгибающий момент балки определяется, считая ее свободно опертой по краям. [2]
Изгибающий момент балки в сечении х равен сумме моментов сил Л и Р относительно центра тяжести названного сечения. [3]
Максимальный изгибающий момент балки, свободно опертой на двух опорах и нагруженной силой Р посредине, равен Мх. [4]
Отдельные линии осциллограммы обозначают: / — изгибающий момент балки моста в горизонтальной плоскости Ми г; 2 — то же в вертикальной плоскости Ми. [6]
Приведенные материалы показывают, что, взяв изгибающие моменты балки постоянного сечения за координатные функции и проведя ортогонализацию, мы получаем распределение изгибающих моментов очень близким к фактическому. Естественно, что и прогибы, определенные по этим изгибающим моментам, также должны быть близки к их точным значениям; поэтому, вычислив кинетическую и потенциальную энергию для выбранных — таким образом прогибов и изгибающих моментов, мы должны получить очень близкие к истинным значения частот колебаний. [7]
Тем же построением легко решается задача об изгибающем моменте балки для любого ее сечения. Изгибающим моментом балка или односторонним моментом для какого-нибудь сечения назы — вается общий момент относительно эгпаго сечения сил, расположенных по одну сторону от этого сечения. Так как балка находится в равновесии, то общий момент всех действующих на нее сил относительно любого сечения равен нулю; поэтому общий момент сил, расположенных по одну сторону сечения, равен по величине и противоположен по знаку общему моменту сил, расположенных по другую сторону сечения. Определим момент сил, расположенных, например, слева от сечения А ( черт. [8]
В предельном равновесии — непосредственно перед разрушением — изгибающие моменты балки находят статическим или кинематическим способом. [9]
Следует отметить, что при точном расчете всей рамы изгибающий момент балки 6 будет SAfe5735 кГ — м, что опять указывает на хорошее совпадение обоих методов. [10]
Все поперечные сечения ниже сечения IV — IV работают только на изгиб. Эпюра изгибающих моментов балки приведена на фиг. [11]
Каждая сила, действующая на балку ( например, нагрузка балки, регкция опор), имеет момент относительно какого-нибудь поперечного сечения балки, равный произведению силы на расстояние точки приложения силы от данного сечения. Сумма М ( х) моментов всех сил, приложенных к части балки, расположенной по одну сторону от данного сечения, с абсциссой А, называется изгибающим моментом балки относительно данного сечения. [12]
Каждая сила, действующая на балку ( например, нагрузка балки, реакция опор), имеет момент относительно какого-нибудь поперечного сечения балки, равный произведению силы на расстояние точки приложения силы от данного сечения. Сумма М ( х) моментов всех сил, приложенных к части балки, расположенной по одну сторону от данного сечения, с абсциссой х, называется изгибающим моментом балки относительно данного сечения. В курсе сопротивления материалов доказывается, что изгибающий момент балки равен EJ / R, где Е — так называемый модуль упругости, зависящий от материала балки: J — момент инерции площади поперечного сечения балки относительно горизонтальной линии, проходящей через центр тяжести площади поперечного сечения; R — радиус кривизны оси изогнутой балки, который выражается формулой ( § 6, гл. [14]
Каждая сила, действующая на балку ( например, нагрузка балки, реакция опор), имеет момент относительно какого-нибудь поперечного сечения балки, равный произведению силы на расстояние точки приложения силы от данного сечения. Сумма М ( х) моментов всех сил, приложенных к части балки, расположенной по одну сторону от данного сечения, с абсциссой х, называется изгибающим моментом балки относительно данного сечения. [15]
Страницы: 1 2
www.ngpedia.ru
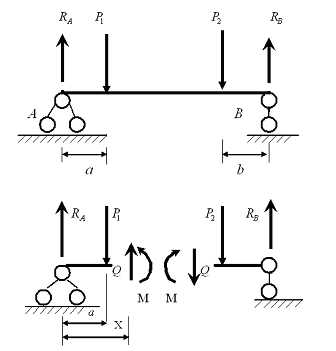
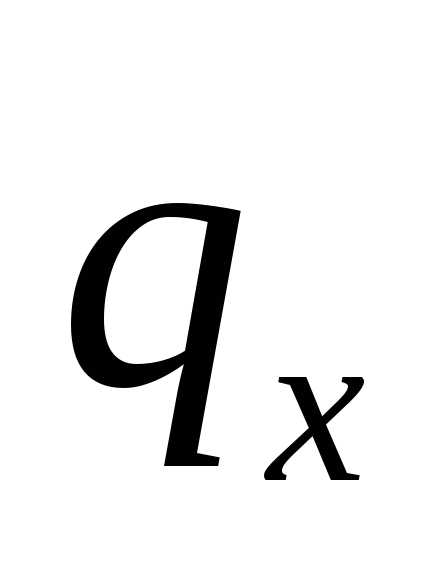 примем равномерно распределенной
примем равномерно распределенной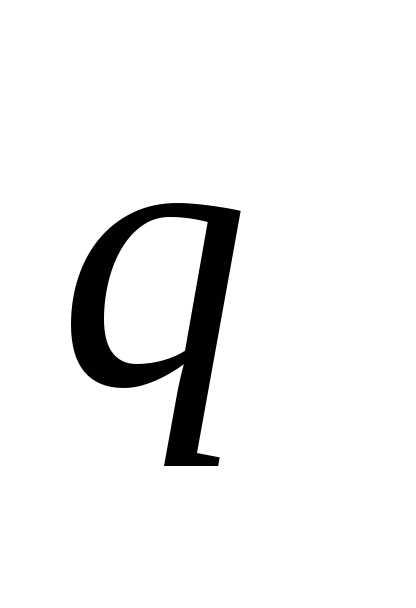 .
.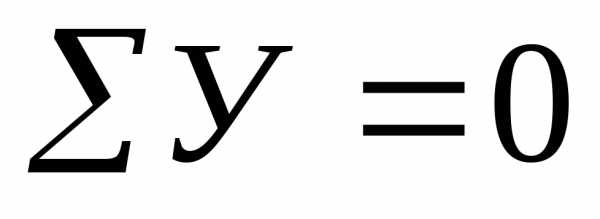 ;
;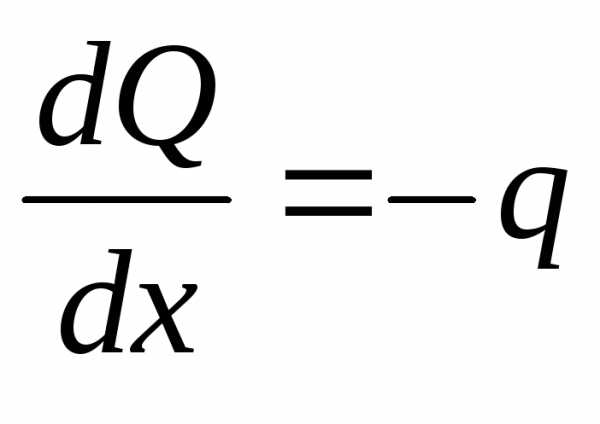
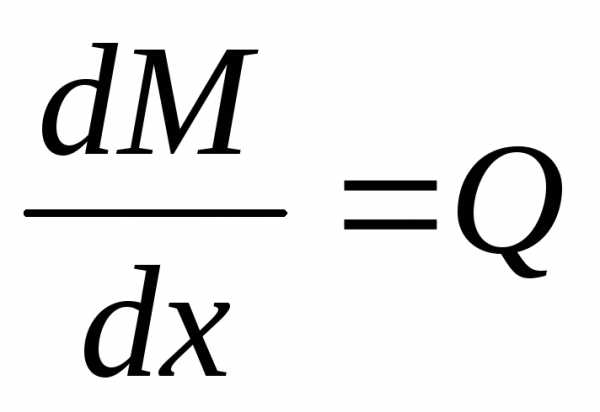
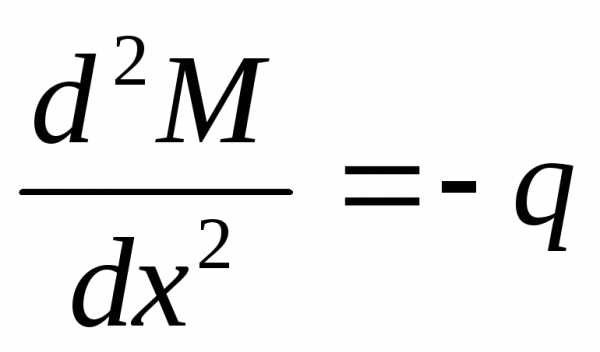
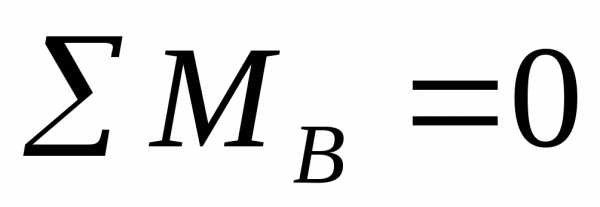 ;
;