Основные формулы для расчета прогиба балки

 

Балка является основным элементом несущей конструкции сооружения. При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.

Балки в доме

При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах. Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно. Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.

Виды балок

Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению. Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.

Деревянные

Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.

Деревянные перекрытия

Для расчета максимального прогиба следует учитывать:

1. Материал. Различные породы дерева обладают разным показателем прочности, твердости и гибкости.
2. Форма поперечного сечения и другие геометрические характеристики.
3. Различные виды нагрузки на материал.

Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.

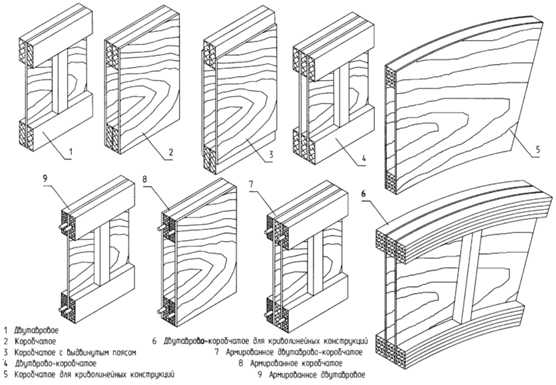
Конструкции из древесины хвойных пород

Стальные

Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.

Стальные перекрытия

Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:

• электросварка;
• заклепки;
• болты, винты и другие виды резьбовых соединений.

Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.

Для проведения расчета балки на прогиб может помочь видео: 

Прочность и жесткость балки

Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.

Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали. Расчет конструкции по опытным формулам не всегда эффективен. Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности. Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.

Существует два основных метода расчета прочности и жесткости:

1. Простой. При использовании данного метода применяется увеличительный коэффициент.
2. Точный. Данный метод включает в себя использование не только коэффициентов для запаса прочности, но и дополнительные вычисления пограничного состояния.

Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.

Расчет балок на прогиб

Расчет на жесткость

Для расчета прочности балки на изгиб применяется формула:

Где:

M – максимальный момент, который возникает в балке;

W_n,min – момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.

R_y является расчетным сопротивлением стали при изгибе. Зависит от вида стали.

γ_c представляет собой коэффициент условий работы, который является табличной величиной.

Расчет жесткости или величины прогиба балки является достаточно простым, поэтому расчеты может выполнить даже неопытный строитель. Однако для точного определения максимального прогиба необходимо выполнить следующие действия:

1. Составление расчетной схемы объекта.
2. Расчет размеров балки и ее сечения.
3. Вычисление максимальной нагрузки, которая воздействует на балку.
4. Определение точки приложения максимальной нагрузки.
5. Дополнительно балка может быть проверена на прочность по максимальному изгибающему моменту.
6. Вычисление значения жесткости или максимально прогиба балки.

Чтобы составить расчетную схему, потребуются такие данные:

• размеры балки, длину консолей и пролет между ними;
• размер и форму поперечного сечения;
• особенности нагрузки на конструкцию и точно ее приложения;
• материал и его свойства.

Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.

Расчет моментов инерции и сопротивления сечения

Для выполнения расчетов жесткости потребуется значение момент инерции сечения (J) и момента сопротивления (W). Для расчета момента сопротивления сечения лучше всего воспользоваться формулой:

Важной характеристикой при определении момента инерции и сопротивления сечения является ориентация сечения в плоскости разреза. При увеличении момента инерции увеличивается и показатель жесткости.

Определение максимальной нагрузки и прогиба

Для точного определения прогиба балки, лучше всего применять данную формулу:

Где:

q является равномерно-распределенной нагрузкой;

E – модуль упругости, который является табличной величиной;

l – длина;

I – момент инерции сечения.

Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.

Особенности расчета на прогиб

Расчет на прогиб проводится обязательно для любых перекрытий. Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:

1. Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.
2. Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.
3. Варианты нагружения консольного стержня, который закреплен жестко.
4. Действие на конструкцию сложной нагрузки.

Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.

Пример подсчета прогиба

Чтобы понять процесс расчета жесткости балки и ее максимального прогиба, можно использовать простой пример проведения расчетов. Данный расчет проводится для балки с такими характеристиками:

• материал изготовления – древесина;
• плотность составляет 600 кг/м3;
• длина составляет 4 м;
• сечение материала составляет 150*200 мм;
• масса перекрывающих элементов составляет 60 кг/м²;
• максимальная нагрузка конструкции составляет 249 кг/м;
• упругость материала составляет 100 000 кгс/ м²;
• J равно 10 кг*м².

Для вычисления максимальной допустимой нагрузки учитывается вес балки, перекрытий и опор. Рекомендуется также учесть вес мебели, приборов, отделки, людей и других тяжелых вещей, который также будут оказывать воздействие на конструкцию. Для расчета потребуются такие данные:

• вес одного метра балки;
• вес м2 перекрытия;
• расстояние, которое оставляется между балками;
• временная нагрузка;
• нагрузка от перегородок на перекрытие.

Чтобы упросить расчет данного примера, можно принять массу перекрытия за 60 кг/м², нагрузку на каждое перекрытие за 250 кг/м², нагрузки на перегородки 75 кг/м², а вес метра балки равным 18 кг. При расстоянии между балками в 60 см, коэффициент k будет равен 0,6.

Если подставить все эти значения в формулу, то получится:

q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

Для расчета изгибающего момента следует воспользоваться формулой f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦].

Подставив в нее данные, получается f = (5 / 384) * [(qn * L4) / (E * J)] = (5 / 384) * [(249 * 44) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

Именно это и является показателем прогиба при воздействии на балку максимальной нагрузки. Данные расчеты показывают, что при действии на нее максимальной нагрузки, она прогнется на 0,83 см. Если данный показатель меньше 1, то ее использование при указанных нагрузках допускается.

Использование таких вычислений является универсальным способом вычисления жесткости конструкции и величины их прогибания. Самостоятельно вычислить данные величины достаточно легко. Достаточно знать необходимые формулы, а также высчитать величины. Некоторые данные необходимо взять в таблице. При проведении вычислений крайне важно уделять внимание единицам измерения. Если в формуле величина стоит в метрах, то ее нужно перевести в такой вид. Такие простые ошибки могут сделать расчеты бесполезными. Для вычисления жесткости и максимального прогиба балки достаточно знать основные характеристики и размеры материала. Эти данные следует подставить в несколько простых формул.

 

 

viascio.ru

Расчет металлической балки на прогиб: учимся составлять формулы

Приветствую тебя, читатель экспресс-курса — «сопромат для чайников» на сайте – SoproMats.ru. Меня зовут Константин Вавилов, я являюсь автором статей по сопромату и других материалов данного ресурса. В этой статье, будем рассматривать универсальную методику расчета прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.

В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.

Что такое прогиб балки?

Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).

Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.

ν-прогиб сечения C; θ-угол поворота сечения C.

Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.

Метод начальных параметров

Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)

Под начальными параметрами понимаются уже известные перемещения:

• в опорах прогибы равны нулю;
• в жесткой заделке прогиб и угол поворота сечения равен нулю.

Учитывая эти хитрости, их называют еще граничными условиями, определяются перемещения в других частях балки.

Расчет прогибов балки

Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:

Реакции опор

Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.

Если ты не знаешь, как определять реакции, то рекомендую изучить данный материал, где я как раз рассказываю, как они определяются на примере этой балки:

Система координат

Далее вводим систему координат, с началом в левой части балки (точка А):

Распределенная нагрузка

Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.

Если бы нагрузка была приложена вот таким способом:

То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:

Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.

Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:

Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:

\[ { V }_{ A }=0\quad при\quad x=0 \]

\[ { V }_{ B }=0\quad при\quad x=8м \]

Записываем уравнение метода начальных параметров для сечения C:

\[ E{ I }_{ z }{ V }_{ C }=… \]

Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:

\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]

Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:

\[ E{ I }_{ z }{ V }_{C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 4+… \]

Учет внешней нагрузки

И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. Здесь есть несколько особенностей:

• Сосредоточенные силы и распределенные нагрузки, которые направленны вверх, то есть совпадают с направлением оси y, в уравнении записываются со знаком «плюс». Если они направленны наоборот, соответственно, со знаком «минус»:

• Моменты, направленные по часовой стрелке – положительные, против часовой стрелки – отрицательные:

• Все сосредоточенные моменты нужно умножать дробь:

\[ M\cdot \frac { { x }^{ 2 } }{ 2 } \]

• Все сосредоточенные силы нужно умножать дробь:

\[ F\cdot \frac { { x }^{ 3 } }{ 6 } \]

• Начало и конец распределенных нагрузок нужно умножать на дробь:

\[ q\cdot \frac { { x }^{ 4 } }{ 24 } \]

Откуда такие цифры и степени взялись? Все эти вещи вытекают при интегрировании дифференциального уравнения упругой линии балки, в методе начальных параметров все эти выводы опускаются, то есть он является как бы упрощенным и универсальным методом.

Формулы прогибов

С учетом всех вышеописанных правил запишем окончательное уравнение для сечения C:

\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 4+\frac { { R }_{ A }\cdot { 4 }^{ 3 } }{ 6 } -\frac { F\cdot { 4 }^{ 3 } }{ 6 } -\frac { q\cdot { 2 }^{ 4 } }{ 24 } \]

В этом уравнении содержится 2 неизвестные величины – искомый прогиб сечения C и угол поворота сечения A.

Поэтому, чтобы найти прогиб, составим второе уравнение для сечения B, из которого можно определить угол поворота сечения A. Заодно закрепим пройденный материал:

\[ E{ I }_{ z }{ V }_{ B }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 8+\frac { { R }_{ A }\cdot { 8 }^{ 3 } }{ 6 } -\frac { F\cdot { 8 }^{ 3 } }{ 6 } -\frac { q\cdot 6^{ 4 } }{ 24 } +\frac { q\cdot 2^{ 4 } }{ 24 } =0 \]

Упрощаем уравнение:

\[ E{ I }_{ z }{ \theta }_{ A }\cdot 8+874.67=0 \]

Выражаем угол поворота:

\[ { \theta }_{ A }=-\frac { 874.67 }{ 8E{ I }_{ z } } =-\frac { 109.33кН{ м }^{ 2 } }{ E{ I }_{ z } } \]

Подставляем это значение в наше первое уравнение и находим искомое перемещение:

\[ E{ I }_{ z }{ V }_{ C }=\frac { -109.33\cdot 4E{ I }_{ z } }{ E{ I }_{ z } } +\frac { { R }_{ A }\cdot { 4 }^{ 3 } }{ 6 } -\frac { F\cdot { 4 }^{ 3 } }{ 6 } -\frac { q\cdot { 2 }^{ 4 } }{ 24 } =-\frac { 280кН{ м }^{ 3 } }{ E{ I }_{ z } } \]

Вычисление прогиба

Значение получили в общем виде, так как изначально не задавались тем, какое поперечное сечение имеет рассчитываемая балка. Представим, что металлическая балка имеет двутавровое поперечное сечение №30. Тогда:

\[ { V }_{ C }=-\frac { 280кН{ м }^{ 3 } }{ E{ I }_{ z } } =-\frac { 280\cdot { 10 }^{ 9 }Н\cdot { см }^{ 3 } }{ 2\cdot { 10 }^{ 7 }\frac { Н }{ { см }^{ 2 } } \cdot 7080{ см }^{ 4 } } =-2см \]

Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.

На этом, пожалуй, закончу данный урок. Если у вас возникли какие-либо вопросы по представленным материалам, задавайте вопросы в комментариях к этой статье. А также рекомендую вам посмотреть другие примеры определение прогибов этим методом. Там вы найдете более сложные задачи, определение углов поворотов, примеры расчета консольных балок (с жесткой заделкой).

sopromats.ru

формула, механизм и примеры вычисления прогиба по стандартам

Для строительства прочного, надежного и долговечного здания, нужно знать такой показатель, как прогиб балки (формула), то есть величину жесткости.

Данное направление изучается в таких науках (дисциплинах), как “Сопротивление материалов”, “Теория прочности”, “Механика строительная” и прочее.

Прочность и жесткость балки

Балки в доме

Современные строительные технологии, применяемые для просчета стройконструкций, называемых также стержневыми, по качествам прочности и жесткости дают уникальную возможность на первом же этапе проектировки вычислить величину прогиба.

Кроме этого, можно, опираясь на рассчитанные данные, составить заключение о вероятности использования строительной конструкции.

Какой вопрос позволяет решать указанная далее формула для расчета жесткости? Данные, полученные таким путем, говорят о самых больших изменениях в геометрии детали, что могут возникнуть в строительной конструкции.

Несмотря на некоторую бюрократизацию методик для вычисления прогиба, используются опытные формулы, а если воздействие реальных нагрузок отличается от идеальных или усредненных, вопрос решается введением дополнительных коэффициентов для запаса прочности. Понятия «жесткость» и «прочность» связаны и абсолютно неразделимы.

Хотя некоторые различия все-таки есть. Но только в том случае, если рассматривать данные показатели в автомашинах. В стройконструкциях главное нарушение конструкции объектов случается потому, что снижаются или нивелируются полностью вопросы, связанные с запасом прочности, вследствие чего здания нельзя эксплуатировать.

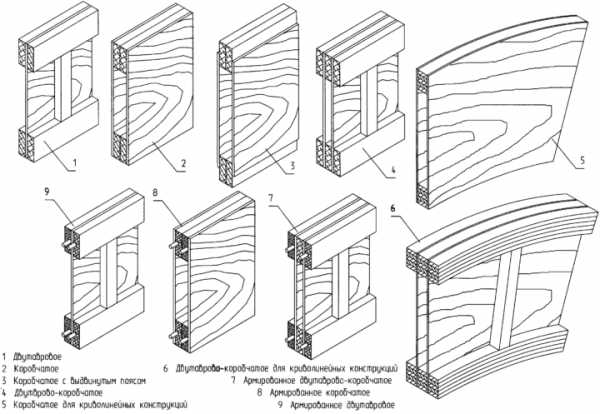
Деревянные балки из древесины хвойных пород

На сегодня в таких предметах изучения, как «Сопромат» и другие, приняты 2 метода для расчета прочности и жесткости:

• Простой. При просчитывании показателей на основе этого метода используют увеличенный коэффициент.
• Точный. Тут используются не только коэффициенты, показывающие запас прочности, но также осуществляется вычисление пограничного состояния (какую нагрузку может выдержать балка).

Как рассчитывать прогиб для балки дома

Чтобы просчитать, подходит ли конкретная балка для строительства дома, нужно знать такие показатели:

• M – это тот максимальный момент, который возникает в балке, находящийся по эпюру моментов. Эпюр – это специальный чертеж с изображением пространственная фигура изображается на плоскости.
• W _{n, mіn} – момент сопротивления сечения (его значение находят по таблице).
• R_y – сопротивление, что оказывает материал, из которого изготовлен элемент конструкции дома, изгибаясь от нагрузки.
• У_c – дополнительный показатель (его можно найти в одной из многочисленных таблиц строительных нормативов).

Формула для расчета прогиба представляет из себя неравенство следующего вида (формула № 1):

М / (W _{n, min}* R_y * У_c) ≤1

Чтобы правильно применить формулу, нужно действовать так:

• Нарисовать схематично балку и ее будущее расположение под крышей дома. Чтобы верно изобразить на чертеже все части исследуемого объекта, нужно знать форму и линейные размеры балки, поперечного сечения, характер будущих нагрузок, материал, из которого балка изготовлена.
• Записать ее точные размеры.
• Рассчитать по указанной формуле, чему равно частное максимального момента балки к произведению остальных трех величин.
• Сравнить полученный результат с единицей: если он меньше или равен 1, то вычисления дают положительный ответ.

Зная значение параметров рассматриваемой балки и сил, действующих на нее, сделав нехитрые вычисления, можно быстро справится с задачей вычисления допустимого прогиба балки дома.

Как вычислить вспомогательные величины

Для получения полной информации о значениях, необходимых для достижения конечной цели вычислений, нужно узнать, каков момент сопротивление сечения (формула № 2):

W_{n(требуемое)} = М _мах / (R_y * У_c)

Необходимо обязательно уитывать ориентирование рассматриваемого балочного сечения, так как с уменьшением моментов инерций жесткость балок снижается, чего допускать нельзя. Для выяснения максимального значения нагрузки f, которое может выдержать балка, надо вычислить его по такой формуле № 3:

f = (5 / 384) * [(q_n * L⁴) / (E * J)] £ [¦], где

• L – продольный размер, в метрах
• E – коэффициент, показывающий упругость (для каждого материала или сплава он будет разным)
• J – момент инерции по сечению
• q_n – это нагрузка, равномерно-распространенная, выражается в кг/м или в Н/м

Показатель J рассчитывается так:

J = b * h³ / 12

Обозначения:

• b – диаметр сечений
• h – вертикальный размер сечения

Примером для сечений, величиной 15 на 20 сантиметров:

J = 0,15 * (0,2)³ / 12 = 10 000 см⁴ или 0,0001 м⁴

Кроме указанных расчетных или табличных величин, среди важных факторов, которые нужно учитывать при определении максимальных нагрузок, выделяют такие: статические (которые действуют постоянно, независимо от переменных внешних факторов), периодические (действие ветра, вибрации, ударов).

Пример подсчета прогиба

Прогиб балки (формула, пример расчета) вычисляется так. Допустим, есть балка, для которой нужно рассчитать прогиб, с такими параметрами:

• Материал изготовления – дерево.
• Плотность 600 кг/м³.
• Длина балки L – 4 м, остальные размеры: 15 см х 20 см.
• Масса перекрывающих элементов – 60 кг/м².
• Максимальная нагрузка q равна 249 кг/м.
• E (насколько упруго дерево) – 100 000 кгс/ м².
• J балок – 10 кг*м².

Максимально допустимая нагрузка вычисляется с учетом веса не только балочной конструкции, но и перекрытия, а также опор.

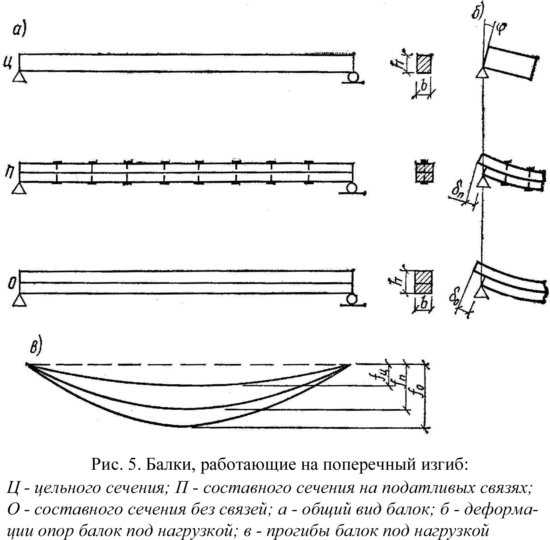
Расчет на поперечный прогиб

Не лишним будет учесть тяжесть, которую будут оказывать люди или приборы, механизмы и другие тяжелые вещи, если вычисляется прогиб балок этажа дома. Нужны такие данные, как:

• Сколько весит один пог. метр рассматриваемой балки.
• Сколько весит каждый м² перекрытия.
• Какова временная нагрузка на перекрытие.
• Сколько составляет нагрузка от перегородок на 1 м² перекрытия.
• Каков коэфф. k (это промежуток, оставляемый между балками).

Чтобы упростить пример расчетов, принимают масс перекрытия за 60 кг/м², нормальную непостоянную нагрузку на каждое перекрытие – 250 кг/м², нагрузки от перегородок равными 75 кг/м², тяжесть части деревянных балок – 18 кг/погонный метр. Когда расстояние между перекрытиями равно составляет 600 мм, тогда коэффициент k равен 0,6. Подставляем в формулу все эти значения:

q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

Изгибающий момент нужно вычислить по формуле №3, учитывая все указанные выше данные. Получается:

 f = (5 / 384) * [(q_n * L⁴) / (E * J)] = (5 / 384) * [(249 * 4⁴) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

Это – показатель уровня прогиба во время воздействия максимальной нагрузки. Что именно он обозначает? Получается, что менее, чем на один сантиметр прогнется балка при указанной максимальной нагрузке. После этого нужно сравнить полученный результат с единицей: 0,83 меньше 1.

При расчетах деформации важных строящегося здания используют указанные выше простые формулы. Прогиб балки по формуле СНиП является универсальным способом вычисления жесткости балок и величины их прогибания.

Как посчитать балку на изгиб – на видео:

Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.

foxremont.com

Расчет прогиба балки на двух опорах

Процесс проектирования современных строений и построек регулируется огромным количеством различных строительных норм и правил. В большинстве случаев нормы требуют обеспечения определенных характеристик, например, деформации или прогиба балок плит перекрытия под статической или динамической нагрузкой. Например, СНиП № 2.09.03-85 определяет для опор и эстакад прогиб балки не более чем в 1/150 длины пролета. Для чердачных перекрытий этот показатель составляет уже 1/200, а для межэтажных балок и того меньше – 1/250. Поэтому одним из обязательных этапов проектирования является выполнение расчета балки на прогиб.

Способы выполнить расчет и проверку на прогиб

Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.

Просчитать прогиб конструкции можно несколькими способами:

• Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
• Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
• Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.

Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.

Методика выполнения расчета на прогиб

Прежде чем приступать к расчету, нужно будет вспомнить некоторые зависимости из теории сопротивления материалов и составить расчетную схему. В зависимости от того, насколько правильно выполнена схема и учтены условия нагружения, будет зависеть точность и правильность расчета.

Используем простейшую модель нагруженной балки, изображенной на схеме. Простейшей аналогией балки может быть деревянная линейка, фото.

В нашем случае балка:

1. Имеет прямоугольное сечение S=b*h, длина опирающейся части составляет L;
2. Линейка нагружена силой Q, проходящей через центр тяжести изгибаемой плоскости, в результате чего концы поворачиваются на небольшой угол θ, с прогибом относительно начального горизонтального положения, равным f;
3. Концы балки опираются шарнирно и свободно на неподвижных опорах, соответственно, не возникает горизонтальной составляющей реакции, и концы линейки могут перемещаться в произвольном направлении.

Для определения деформации тела под нагрузкой используют формулу модуля упругости, который определяется по соотношению Е=R/Δ, где Е – справочная величина, R— усилие, Δ— величина деформации тела.

Вычисляем моменты инерции и сил

Для нашего случая зависимость будет выглядеть так: Δ = Q/(S·Е). Для распределенной вдоль балки нагрузки q формула будет выглядеть так: Δ = q·h/(S·Е).

Далее следует наиболее принципиальный момент. Приведенная схема Юнга показывает прогиб балки или деформацию линейки так, если бы ее раздавливали под мощным прессом. В нашем случае балку изгибают, а значит, на концах линейки, относительно центра тяжести, приложены два изгибающих момента с разным знаком. Эпюра нагружения такой балки приведена ниже.

Чтобы преобразовать зависимость Юнга для изгибающего момента, необходимо обе части равенства умножить на плечо L. Получаем Δ*L = Q·L/(b·h·Е).

Если представить, что одна из опор жестко закреплена, а на второй будет приложен эквивалентный уравновешивающий момент сил M_max = q*L*2/8, соответственно, величина деформации балки будет выражаться зависимостью Δх = M·х/((h/3)·b·(h/2)·Е). Величину b·h²/6 называют моментом инерции и обозначают W. В итоге получается Δх = M·х/(W·Е) основополагающая формула расчета балки на изгиб W=M/E через момент инерции и изгибающий момент.

Чтобы точно выполнить расчет прогиба, потребуется знать изгибающий момент и момент инерции. Величину первого можно посчитать, но конкретная формула для расчета балки на прогиб будет зависеть от условий контакта с опорами, на которых находится балка, и способа нагружения, соответственно для распределенной или концентрированной нагрузки. Изгибающий момент от распределенной нагрузки считается по формуле Mmax = q*L²/8. Приведенные формулы справедливы только для распределенной нагрузки. Для случая, когда давление на балку сконцентрировано в определенной точке и зачастую не совпадает с осью симметрии, формулу для расчета прогиба приходится выводить с помощью интегрального исчисления.

Момент инерции можно представить, как эквивалент сопротивления балки изгибающей нагрузке. Величину момента инерции для простой прямоугольной балки можно посчитать по несложной формуле W=b*h³/12, где b и h – размеры сечения балки.

Из формулы видно, что одна и та же линейка или доска прямоугольного сечения может иметь совершенно разный момент инерции и величину прогиба, если положить ее на опоры традиционным способом или поставить на ребро. Недаром практически все элементы стропильной системы крыши изготавливаются не из бруса 100х150, а из доски 50х150.

Реальные сечения строительных конструкций могут иметь самые разные профили, от квадрата, круга до сложных двутавровых или швеллерных форм. При этом определение момента инерции и величины прогиба вручную, «на бумажке», для таких случаев становится нетривиальной задачей для непрофессионального строителя.

Формулы для практического использования

На практике чаще всего стоит обратная задача – определить запас прочности перекрытий или стен для конкретного случая по известной величине прогиба. В строительном деле очень сложно дать оценку запасу прочности иными, неразрушающими методами. Нередко по величине прогиба требуется выполнить расчет, оценить запас прочности здания и общее состояние несущих конструкций. Мало того, по выполненным измерениям определяют, является деформация допустимой, согласно расчету, или здание находится в аварийном состоянии.

Совет! В вопросе расчета предельного состояния балки по величине прогиба неоценимую услугу оказывают требования СНиПа. Устанавливая предел прогиба в относительной величине, например, 1/250, строительные нормы существенно облегчают определение аварийного состояния балки или плиты.

Например, если вы намерены покупать готовое здание, простоявшее достаточно долго на проблемном грунте, нелишним будет проверить состояние перекрытия по имеющемуся прогибу. Зная предельно допустимую норму прогиба и длину балки, можно безо всякого расчета оценить, насколько критическим является состояние строения.

Строительная инспекция при оценке прогиба и оценке несущей способности перекрытия идет более сложным путем:

• Первоначально измеряется геометрия плиты или балки, фиксируется величина прогиба;
• По измеренным параметрам определяется сортамент балки, далее по справочнику выбирается формула момента инерции;
• По прогибу и моменту инерции определяют момент силы, после чего, зная материал, можно выполнить расчет реальных напряжений в металлической, бетонной или деревянной балке.

Вопрос – почему так сложно, если прогиб можно получить, используя для расчета формулу для простой балки на шарнирных опорах f=5/24*R*L²/(E*h) под распределенным усилием. Достаточно знать длину пролета L, высоту профиля, расчетное сопротивление R и модуль упругости Е для конкретного материала перекрытия.

Ответ  прост — необходимо непросто рассчитать, но и сохранить на бумаге ход выполнения проверочного расчета, чтобы сделанные выводы о состоянии перекрытия можно было проверить и перепроверить по всем этапам проверки.

Совет! Используйте в своих расчетах существующие ведомственные сборники различных проектных организаций, в которых в сжатом виде сведены все необходимые формулы для определения и расчета предельного нагруженного состояния.

Заключение

Аналогичным образом поступает большинство разработчиков и проектантов серьезных построек. Программа – это хорошо, она помогает очень быстро выполнить расчет прогиба и основных параметров нагружения перекрытия, но важно также предоставить заказчику документальное подтверждение полученных результатов в виде конкретных последовательных расчетов на бумаге.

Что еще почитать по теме?

Автор статьи:

Сергей Новожилов — эксперт по кровельным материалам с 9-летним опытом практической работы в области инженерных решений в строительстве.

Понравилась статья? Поделись с друзьями в социальных сетях:

Facebook

Twitter

Вконтакте

Одноклассники

Google+

proroofer.ru

Расчет балок на прогиб. Максимальный прогиб балки: формула

Балка – элемент в инженерии, представляющий собой стержень, который нагружают силы, действующие в направлении, перпендикулярном стержню. Деятельность инженеров зачастую включает в себя необходимость расчета прогиба балки под нагрузкой. Этой действие выполняется для того, чтобы ограничить максимальный прогиб балки.

Типы

На сегодняшний день в строительстве могут использоваться балки, изготовленные из разных материалов. Это может быть металл или дерево. Каждый конкретный случай подразумевает под собой разные балки. При этом расчет балок на прогиб может иметь некоторые отличия, которые возникают по принципу разницы в строении и используемых материалов.

Деревянные балки

Сегодняшнее индивидуальное строительство подразумевает под собой широкое применение балок, изготовленных из дерева. Практически каждое строение содержит в себе деревянные перекрытия. Балки из дерева могут использоваться как несущие элементы, их применяют при изготовлении полов, а также в качестве опор для перекрытий между этажами.

Ни для кого не секрет, что деревянная, так же как и стальная балка, имеет свойство прогибаться под воздействием нагрузочных сил. Стрелка прогиба зависит от того, какой материал используется, геометрических характеристик конструкции, в которой используется балка, и характера нагрузок.

Допустимый прогиб балки формируется из двух факторов:

• Соответствие прогиба и допустимых значений.
• Возможность эксплуатации здания с учетом прогиба.

Проводимые при строительстве расчеты на прочность и жесткость позволяют максимально эффективно оценить то, какие нагрузки сможет выдерживать здание в ходе эксплуатации. Также эти расчеты позволяют узнать, какой именно будет деформация элементов конструкции в каждом конкретном случае. Пожалуй, никто не будет спорить с тем, что подробные и максимально точные расчеты – это часть обязанностей инженеров-строителей, однако с использованием нескольких формул и навыка математических вычислений можно рассчитать все необходимые величины самостоятельно.

Для того чтобы произвести правильный расчет прогиба балки, нужно также брать во внимание тот факт, что в строительстве понятия жесткости и прочности являются неразрывными. Опираясь на данные расчета прочности, можно приступать к дальнейшим расчетам относительно жесткости. Стоит отметить, что расчет прогиба балки – один из незаменимых элементов расчета жесткости.

Обратите ваше внимание на то, что для проведения таких вычислений самостоятельно лучше всего использовать укрупненные расчеты, прибегая при этом к достаточно простым схемам. При этом также рекомендуется делать небольшой запас в большую сторону. Особенно если расчет касается несущих элементов.

Расчет балок на прогиб. Алгоритм работы

На самом деле алгоритм, по которому делается подобный расчет, достаточно прост. В качестве примера рассмотрим несколько упрощенную схему проведения расчета, при этом опустив некоторые специфические термины и формулы. Для того чтобы произвести расчет балок на прогиб, необходимо выполнить ряд действий в определенном порядке. Алгоритм проведения расчетов следующий:

• Составляется расчетная схема.
• Определяются геометрические характеристики балки.
• Вычисляется максимальную нагрузку на данный элемент.
• В случае возникновения необходимости проверяется прочность бруса по изгибающему моменту.
• Производится вычисление максимального прогиба.

Как видите, все действия достаточно просты и вполне выполнимы.

Составление расчетной схемы балки

Для того чтобы составить расчетную схему, не требуется больших знаний. Для этого достаточно знать размер и форму поперечного сечения элемента, пролет между опорами и способ опирания. Пролетом является расстояние между двумя опорами. К примеру, вы используете балки как опорные брусья перекрытия для несущих стен дома, между которыми 4 м, то величина пролета будет равна 4 м.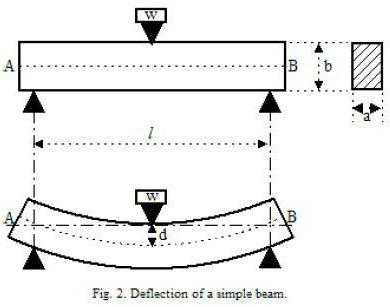

Вычисляя прогиб деревянной балки, их считают свободно опертыми элементами конструкции. В случае балки перекрытия для расчета принимается схема с нагрузкой, которая распределена равномерно. Обозначается она символом q. Если же нагрузка несет сосредоточенный характер, то берется схема с сосредоточенной нагрузкой, обозначаемой F. Величина этой нагрузки равна весу, который будет оказывать давление на конструкцию.

Момент инерции

Геометрическая характеристика, которая получила название момент инерции, важна при проведении расчетов на прогиб балки. Формула позволяет вычислить эту величину, мы приведем ее немного ниже.

При вычислении момента инерции нужно обращать внимание на то, что размер этой характеристики зависит от того, какова ориентация элемента в пространстве. При этом наблюдается обратно пропорциональная зависимость между моментом инерции и величиной прогиба. Чем меньше значение момента инерции, тем больше будет значение прогиба и наоборот. Эту зависимость достаточно легко отследить на практике. Каждый человек знает, что доска, положенная на ребро, прогибается гораздо меньше, чем аналогичная доска, находящаяся в нормальном положении.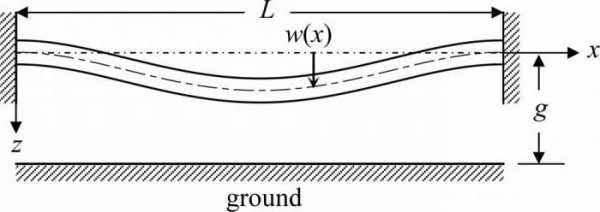

Подсчет момента инерции для балки с прямоугольным сечением производится по формуле:

J=b*h^3/12, где:

b – ширина сечения;

h – высота сечения балки.

Вычисления максимального уровня нагрузки

Определение максимальной нагрузки на элемент конструкции производится с учетом целого ряда факторов и показателей. Обычно при вычислении уровня нагрузки берут во внимание вес 1 погонного метра балки, вес 1 квадратного метра перекрытия, нагрузку на перекрытие временного характера и нагрузку от перегородок на 1 квадратный метр перекрытия. Также учитывается расстояние между балками, измеренное в метрах. Для примера вычисления максимальной нагрузки на деревянную балку примем усредненные значения, согласно которым вес перекрытия составляет 60 кг/м², временная нагрузка на перекрытие равна 250 кг/м², перегородки будут весить 75 кг/м². Вес самой балки очень просто вычислить, зная ее объем и плотность. Предположим, что используется деревянная балка сечением 0,15х0,2 м. В этом случае ее вес будет составлять 18 кг/пог.м. Также для примера примем расстояние между брусьями перекрытия равным 600 мм. В этом случае нужный нам коэффициент составит 0,6.

В результате вычисления максимальной нагрузки получаем следующий результат: q=(60+250+75)*0,6+18=249 кг/м.

Когда значение получено, можно переходить к расчету максимального прогиба.

Вычисление значения максимального прогиба

Когда проводится расчет балки, формула отображает в себе все необходимые элементы. При этом стоит учитывать, что формула, используемая для расчетов, может иметь несколько иной вид, если расчет проводится для разных типов нагрузок, которые будут оказывать влияние на балку.

Сначала приведем вашему вниманию формулу, используемую для расчета максимального прогиба деревянной балки с распределенной нагрузкой.

f=-5*q*l^4/384*E*J.

Обратите внимание, что в данной формуле Е – это постоянная величина, которая получила название модуль упругости материала. Для древесины эта величина равна 100 000 кгс/ м².

Продолжив вычисления с нашими данными, использованными для примера, получим то, что для балки из древесины, сечение которой составляет 0,15х0,2 м, а длина равна 4 м, величина максимального прогиба при воздействии распределенной нагрузки равна 0,83 см.

Обращаем внимание, что когда производится расчет прогиба с учетом схемы с сосредоточенной нагрузкой, формула приобретает следующий вид:

f=-F*l^3/48*E*J, где:

F – сила давления на брус.

Также обращаем внимание на то, что значение модуля упругости, используемое в расчетах, может различаться для разных видов древесины. Влияние оказывают не только порода дерева, но и вид бруса. Поэтому цельная балка из дерева, клееный брус или оцилиндрованное бревно будут иметь разные модули упругости, а значит, и разные значения максимального прогиба.

Вы можете преследовать разные цели, совершая расчет балок на прогиб. Если вы хотите узнать пределы деформации элементов конструкции, то по завершении расчета стрелки прогиба вы можете остановиться. Если же ваша цель – установить уровень соответствия найденных показателей строительным нормам, то их нужно сравнить с данными, которые размещены в специальных документах нормативного характера.

Двутавровая балка

Обратите внимание на то, что балки из двутавра применяются несколько реже в силу их формы. Однако также не стоит забывать, что такой элемент конструкции выдерживает гораздо большие нагрузки, чем уголок или швеллер, альтернативой которых может стать двутавровая балка.

Расчет прогиба двутавровой балки стоит производить в том случае, если вы собираетесь использовать ее в качестве мощного элемента конструкции.

Также обращаем ваше внимание на то, что не для всех типов балок из двутавра можно производить расчет прогиба. В каких же случаях разрешено рассчитать прогиб двутавровой балки? Всего таких случаев 6, которые соответствуют шести типам двутавровых балок. Эти типы следующие:

• Балка однопролетного типа с равномерно распределенной нагрузкой.
• Консоль с жесткой заделкой на одном конце и равномерно распределенной нагрузкой.
• Балка из одного пролета с консолью с одной стороны, к которой прикладывается равномерно распределенная нагрузка.
• Однопролетная балка с шарнирным типом опирания с сосредоточенной силой.
• Однопролетная шарнирно опертая балка с двумя сосредоточенными силами.
• Консоль с жесткой заделкой и сосредоточенной силой.

Металлические балки

Расчет максимального прогиба одинаковый, будь это стальная балка или же элемент из другого материала. Главное — помнить о тех величинах, которые специфические и постоянные, как к примеру модуль упругости материала. При работе с металлическими балками, важно помнить, что они могут быть изготовлены из стали или же из двутавра. Прогиб металлической балки, изготовленной из стали, вычисляется с учетом, что константа Е в данном случае составляет 2·105Мпа. Все остальные элементы, вроде момента инерции, вычисляются по алгоритмам, описанным выше.

Расчет максимального прогиба для балки с двумя опорами

В качестве примера рассмотрим схему, в которой балка находится на двух опорах, а к ней прикладывается сосредоточенная сила в произвольной точке. До момента прикладывания силы балка представляла собой прямую линию, однако под воздействием силы изменила свой вид и вследствие деформации стала кривой.

Предположим, что плоскость ХУ является плоскостью симметрии балки на двух опорах. Все нагрузки действуют на балку в этой плоскости. В этом случае фактом будет то, что кривая, полученная в результате действия силы, также будет находиться в этой плоскости. Данная кривая получила название упругой линии балки или же линии прогибов балки. Алгебраически решить упругую линию балки и рассчитать прогиб балки, формула которого будет постоянной для балок с двумя опорами, можно следующим образом.

Прогиб на расстоянии z от левой опоры балки при 0 ≤ z ≤ a

F(z)=(P*a²*b²)/(6E*J*l)*(2*z/a+z/b-z³/a²*b)

Прогиб балки на двух опорах на расстоянии z от левой опоры при а ≤ z ≤l

f(z)=(-P*a²*b²)/(6E*J*l)*(2*(l-z)/b+(l-z)/a-(l-z)³/a+b²), где Р – прикладываемая сила, Е – модуль упругости материала, J – осевой момент инерции.

В случае балки с двумя опорами момент инерции вычисляется следующим образом:

J=b₁h₁³/12, где b₁ и h₁ – значения ширины и высоты сечения используемой балки соответственно.

Заключение

В заключение можно сделать вывод о том, что самстоятельно вычислить величину максимального прогиба балки разных типов достаточно просто. Как было показано в этой статье, главное — знать некоторые характеристики, которые зависят от материала и его геометрических характеристик, а также провести вычисления по нескольким формулам, в которых каждый параметр имеет свое объяснение и не берется из ниоткуда.

fb.ru

Формулы для расчетов на изгиб

σ — нормальные напряжения,
τ — касательные напряжения,
Q_y – внутренняя поперечная сила,
M_x – внутренний изгибающий момент,
I_x – осевой момент инерции сечения балки,
W_x – осевой момент сопротивления сечения,
[σ], [τ] – соответствующие допустимые напряжения,
E – модуль упругости I рода (модуль Юнга),
y — расстояние от оси x до рассматриваемой точки сечения балки.

Расчет внутренних поперечных сил и изгибающих моментов

Формула кривизны балки в заданном сечении

Расчет нормальных напряжений в произвольной точке сечения балки

Условие прочности по нормальным напряжениям при изгибе (проверочный расчет)

Осевые моменты инерции I и сопротивления W

• прямоугольного сечения
  
  h – высота сечения,
  b – ширина сечения балки.
• круглого сечения балки
  
  D — диаметр сечения

Касательные напряжения в произвольной точке сечения определяются по формуле Журавского:

Здесь:

S_x^* — статический момент относительно оси x отсеченной части сечения

b — ширина сечения на уровне рассматриваемой точки

Условие прочности балки по касательным напряжениям

Дифференциальное уравнение линии изогнутой оси балки

Уравнения метода начальных параметров (МНП)

θ_z, y_z — соответственно угол наклона и прогиб сечения балки на расстоянии z от начала координат,
θ₀, y₀ — соответственно угол наклона и прогиб сечения балки в начале координат,
m, F, q — соответственно все изгибающие моменты, сосредоточенные силы и распределенные нагрузки приложенные к балке,
a, b — расстояние от начала координат до сечений где приложены моменты и силы соответственно,
c — расстояние от начала координат до начала распределенной нагрузки q.

Другие формулы >
Примеры решения задач >
Краткая теория >

isopromat.ru

Основы сопромата, расчет прогиба балки

Cодержание:

Основы сопромата кратко.

1. Виды опор.

1.1. Шарнирные опоры.

Расчетная длина (пролет) балки.

1.2. Опорные связи шарнирно закрепленной балки.

1.3 Жесткое защемление на опорах.

1.4. Скользящие заделки.

2. Нагрузки (внешние силы).

3. Напряжения (внутренние силы).

4. Реакции опор.

5. Уравнения статического равновесия.

4.1. Определение опорных реакций.

6. Уравнения изгибающего момента.

7. Балка на двух шарнирных опорах.

8. Консольная балка.

9. Метод сечений.

10. Определение момента сопротивления.

11. Определение угла поворота.

12. Определение прогиба.

13. Определение угла поворота через прогиб.

14. Список использованной литературы.

Расчет прогиба балки не то, чтобы такой уж сложный, но для того, чтобы каждый раз не повторять одни и те же операции при расчете и этим максимально сократить время расчета, специалисты по сопромату уже давно вывели формулы для наиболее вероятных вариантов опор балок и нагрузок, действующих на балки. Достаточно только определиться с расчетной моделью балки и формула для расчета прогиба к Вашим услугам. Но аксиомы: «если хочешь, чтобы работа была сделана хорошо, сделай это сам» пока никто не отменял. Дело в том, что в разного рода справочниках и пособиях иногда бывают опечатки или ошибки, поэтому использовать готовые формулы не всегда есть хорошо.

11. Определение угла поворота.

(вернуться к основному содержанию)

Прогиб строительной конструкции, а в нашем случае балки — единственная величина, которую проще всего определить опытным путем и сложнее всего теоретическим. Когда мы прикладывали к линейке нагрузку (давили на нее пальцем или мощью своего интеллекта), то невооруженным глазом видели, что линейка прогибалась:

Рисунок 11.1. Перемещение центра тяжести поперечного сечения балки в центре балки и угол поворота продольной оси, проходящей через центр тяжести поперечного сечения, на одной из опор.

Если бы мы хотели определить величину прогиба опытным путем, то достаточно было бы измерить расстояние от стола, на котором лежат книги (на рисунке не показан) до верха или низа линейки, затем приложить нагрузку и измерить расстояние от стола до верха или низа линейки. Разница в расстояниях — это и есть искомый прогиб (на фотографии величина прогиба обозначена оранжевой линией):

Фотография 1.

Но попробуем прийти к тому же результату, следуя по тернистому пути теории сопромата.

Так как балка прогнулась (в хорошем значении этого слова), получается, что и продольная ось, проходящая через центры тяжести поперечных сечений всех точек балки, и до приложения нагрузки совпадавшая с осью х, сместилась. Это смещение центра тяжести поперечного сечения по оси у называется прогибом балки f. Кроме того, очевидно, что на опоре эта самая продольная ось теперь находится под некоторым углом θ к оси х, а в точке действия сосредоточенной нагрузки угол поворота = 0, так как нагрузка у нас приложена посредине и балка прогнулась симметрично. Угол поворота принято обозначать «θ«, а прогиб «f» (во многих справочниках по сопромату прогиб обозначается как «ν«, «w» или любыми другими литерами, но нам, как практикам, удобнее использовать обозначение «f«, принятое в СНиПах).

Как определить этот самый прогиб мы пока не знаем, но зато мы знаем, что нагрузка, действуя на балку, создает изгибающий момент. А изгибающий момент создает внутренние нормальные сжимающие и растягивающие напряжения в поперечных сечениях балки. Эти самые внутренние напряжения приводят к тому, что в верхней части балка сжимается, а в нижней растягивается, при этом длина балки по оси, проходящей через центры тяжести поперечных сечений остается такой же, в верхней части длина балки уменьшается, а в нижней части увеличивается, причем чем дальше расположены точки поперечных сечений от продольной оси, тем больше будет деформация. Определить эту самую деформацию мы можем используя еще одну характеристику материала — модуль упругости.

Если мы возьмем кусок бинтовой резины и попробуем его растянуть, то обнаружим, что резина растягивается очень легко, а выражаясь по научному деформируется на значительную величину при воздействии даже небольшой нагрузки. Если мы попробуем проделать то же самое с нашей линейкой, то растянуть ее даже на десятые доли миллиметра руками вряд ли получится, даже если прилагать к линейке нагрузку в десятки раз большую, чем к бинтовой резине. Это свойство любого материала описывается модулем Юнга, который часто называется просто модулем упругости. Физический смысл модуля Юнга при максимально допустимом загружении рассчитываемой конструкции примерно следующий: модуль Юнга показывает отношение нормальных напряжений, (которые при максимально допустимом загружении равны расчетному сопротивлению материала к относительной деформации при таком загружении:

E = R/Δ (11.1.1)

а это значит, что для работы материала в области упругих деформаций значение внутренних нормальных напряжений, действующих не абстрактно, а на вполне определенную площадь сечения, с учетом относительной деформации не должно превышать значения модуля упругости:

E ≥ N/ΔS (11.1.2)

в нашем случае балка имеет прямоугольное сечение, поэтому S = b·h, где b — ширина балки, h — высота балки.

Измеряется модуль Юнга в Паскалях или кгс/м². Для абсолютного большинства строительных материалов модули упругости определены эмпирическим путем, узнать значение модуля для того или иного материала можно по справочнику или сводной таблице.

Определить величину деформации для поперечного сечения, к которому приложена равномерно распределенная нагрузка или сосредоточенная сила в центре тяжести поперечного сечения, очень просто. В таком сечении возникают нормальные сжимающие или растягивающие напряжения, равные по значению действующей силе, направленные противоположно и постоянные по всей высоте балки (согласно одной из аксиом теоретической механики):

Рисунок 507.10.1

и тогда определить относительную деформацию, если известны геометрические параметры балки (длина, ширина и высота) несложно, простейшие математические преобразования формулы (11.1.2) дают следующий результат:

Δ = Q/(S·Е) (11.2.1) или Δ = q·h/(S·Е) (11.2.2)

Так как расчетное сопротивление показывает какую максимальную нагрузку можно приложить к определенной площади, то в данном случае мы можем рассматривать действие сосредоточенной нагрузки на всю площадь сечения нашей конструкции. В некоторых случаях важно определить деформации именно в точке приложения сосредоточенной нагрузки, но сейчас мы эти случаи не рассматриваем. Чтобы определить суммарную деформацию, нужно обе части уравнения умножить на длину балки:

Δl = Q·l/(b·h·Е) (11.2.3) или Δl = q·h·l/(b·h·Е) (11.2.4)

Но в рассматриваемом нами случае на поперечные сечения балки действует не сосредоточенная сила, приложенная к центру тяжести поперечного сечения, а изгибающий момент, который можно представить в виде следующей нагрузки:

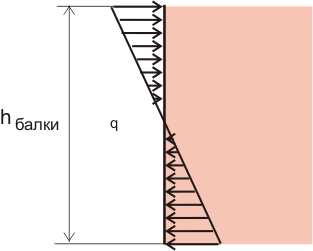
Рисунок 149.8.3 

При такой нагрузке максимальные внутренние напряжения и соответственно максимальные деформации будут происходить в самой верхней и в самой нижней части балки, а посредине никаких деформаций не будет. Равнодействующую для такой распределенной нагрузки и плечо действия сосредоточенной силы мы находили в предыдущей части (2), когда определяли момент сопротивления балки. Поэтому теперь без особого труда можем определить суммарную деформацию в самой верхней и в самой нижней части балки:

Δх = M·х/((h/3)·b·(h/2)·Е) (11.3.1)

или

Δх = M·х/(W·Е) (11.3.2)

так как W = b·h²/6 (10.6)

Эту же формулу мы можем получить и другим способом. Как мы знаем, момент сопротивления поперечного сечения балки должен удовлетворять следующему условию:

W ≥ М / R (10.3)

Если мы будем рассматривать эту зависимость как уравнение и заменим в этом уравнении значение R на ΔЕ, получим следующее уравнение:

W = М / ΔЕ (11.4.1)

И тогда:

М = WΔЕ (11.4.2) a Δ = M/(W·Е) (11.4.5) и соответственно Δх = M·х/(W·Е) (11.3.2)

В результате деформации, которую мы только что определили, наша балка могла была бы выглядеть так:

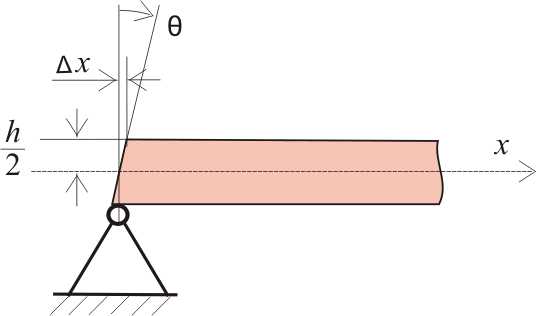
Рисунок 11.2. Предполагаемая (для наглядности) деформация балки

то есть в результате деформаций самая верхняя и самая нижняя точки поперечного сечения сместятся на величину Δх. А это значит, что зная величину деформации и высоту балки, мы можем определить угол поворота θ поперечного сечения на опоре балки. Из школьного курса геометрии мы знаем, что отношение катетов прямоугольного треугольника (в нашем случае катеты Δх и h/2) равно тангенсу угла θ:

tgφ = Δх/(h/2) (11.5.1)

и тогда

tgφ = 2 M·х/(h·W·Е) (11.5.3)

Если вспомнить, что момент инерции — это момент сопротивления поперечного сечения, умноженный на расстояние от центра тяжести до крайней точки сечения или наоборот, момент сопротивления — это момент инерции, разделенный на расстояние от центра тяжести до крайней точки сечения:

W = I/(h/2) (10.7) или I = W·h/2 (10.7.2)

то мы можем заменить момент сопротивления на момент инерции:

tgφ = M·х/(I·Е) (11.5.4)

хотя делать это было не обязательно, но таким образом мы получили формулу угла поворота почти такой, как она дается во всех учебниках и справочниках по сопромату. Главное отличие в том, что обычно речь идет о угле поворота, а не о тангенсе угла. И хотя при малых деформациях значения тангенса угла и угол сопоставимы, но тем не менее угол и тангенс угла — это разные вещи (впрочем в некоторых справочниках, например: Фесик С.П. «Справочник по сопротивлению материалов» Киев: Будiвельник. — 1982 переход от тангенса к углу упоминается, хотя и без достаточных на мой взгляд объяснений). Более того, если быть совсем уж точным, то таким способом мы определяем отношение продольной деформации к высоте балки

Рассчитываемые элементы далеко не всегда имеют прямоугольное сечение, как наша рассматриваемая линейка. В качестве балок и перемычек могут использоваться различные горячекатаные профили, тесанные и не тесанные бревна и вообще все, что угодно. Тем не менее понимание принципов расчета момента инерции позволяет определить момент инерции для поперечного сечения любой, даже очень сложной геометрической формы. В абсолютном большинстве случаев вычислять самому момент инерции нет необходимости, для металлических профилей сложного сечения (уголки, швеллера, двутавры и др.) момент инерции, как впрочем и момент сопротивления определяется по сортаменту. Для элементов круглого овального, треугольного сечения и некоторых других видов сечения определить момент инерции можно по соответствующей таблице.

Если рассматривать суммарную деформацию всей балки, т.е. по всей длине l, то очевидно, что суммарная деформация при наших нагрузках не может быть только с одной стороны балки, как показано на рисунке 11.3.а:

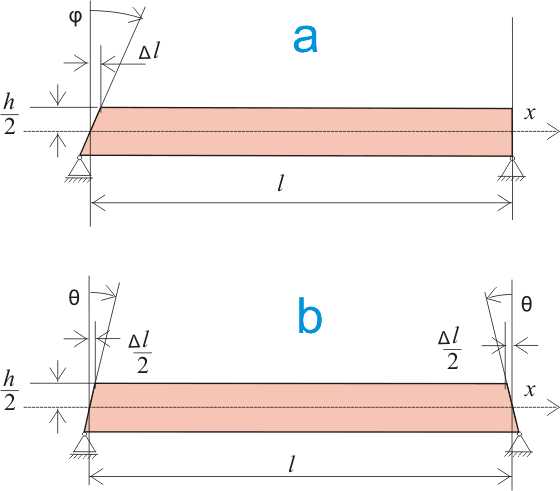
Рисунок 11.3.

Так как к нашей балке нагрузка приложена посредине, в результате чего реакции на опорах, возникающие в результате действия нагрузки равны между собой и каждая равна половине приложенной нагрузки, то скорее при этих условиях суммарная деформация будет выглядеть так, как показано на рисунке 11.3.b и тогда в нашем конкретном случае угол наклона поперечного сечения на каждой из опор будет:

tgθ = M·х/(2IЕ) (11.5.5)

Пока мы определяли тангенс угла поворота простым графоаналитическим методом и в случае, когда нагрузка к балке приложена посредине, это у нас неплохо получилось. Но варианты приложения нагрузок к балке бывают всякие и хотя суммарная деформация всегда будет равна Δl, но угол наклона поперечных сечений на опорах может быть разным. Если мы присмотримся к формулам (11.5.4) и (11.5.5) повнимательнее, то увидим, что мы умножаем значение момента в некоторой точке на величину х, которая с точки зрения теоретической механики ни чем не отличается от понятия — «плечо действия силы». Получается, что для определения тангенса угла поворота мы должны умножить значение момента на плечо действия момента, и значит, понятие «плечо» можно применить не только к силе, но и к моменту. Когда мы использовали понятие плеча действия силы, открытое еще Архимедом, то мы и предполагали как далеко это может нас завести. Метод, показанный на рисунке 5.3, дал нам значение плеча момента = х/2. Теперь попробуем определить плечо момента другим способом (графоаналитический метод). Тут нам пригодятся эпюры, построенные для балки на шарнирных опорах:

               

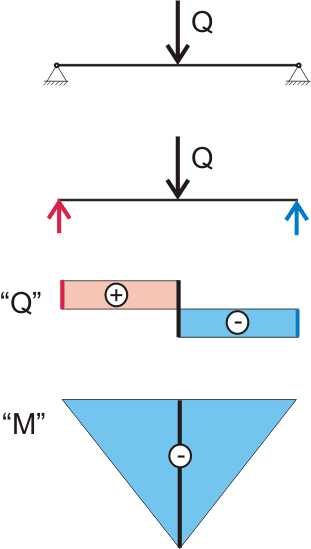
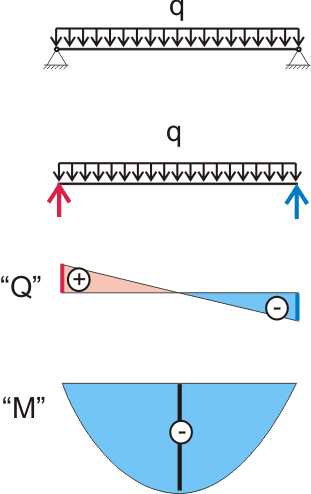
          Рисунок 149.7.1                                                             Рисунок 149.7.2

Теория сопротивления материалов позволяет рассматривать внутренние нормальные напряжения, характеризуемые эпюрой «М» рисунка 149.7.1 для балки с постоянной жесткостью, как некую внешнюю фиктивную нагрузку. Тогда площадь эпюры «М» от начала балки до середины пролета — это фиктивная опорная реакция материала балки на равномерно изменяющуюся нагрузку. А фиктивный изгибающий момент — это площадь эпюры «М», умноженная на расстояние от центра тяжести эпюры «М» до рассматриваемой точки. Так как значение изгибающего момента посредине пролета составляет Ql/4, то площадь такой фигуры составит Ql/4(l/2)(1/2) = Ql²/16. А если это значение разделить на жесткость ЕI, то мы получим значение тангенса угла поворота.

Забегая наперед, определим значение прогиба. Расстояние от центра тяжести треугольной эпюры «М» до середины пролета равно l/6, тогда фиктивный изгибающий момент составит (Ql²/16)l/2 — (Ql²/16)l/6 = Ql³/48. Тогда прогиб f = Ql³/48EI. А так как эпюра моментов у нас расположена снизу балки, то такая фиктивная нагрузка будет в итоге давать отрицательное значение угла поворота и прогиба, что в общем-то логично, так как при таком действии нагрузки прогиб — смещение центра тяжести поперечного сечения будет происходить вниз по оси у.

Характерная особенность графоаналитического метода состоит в том, что количество вычислений можно еще сократить. Для этого нужно умножить площадь эпюры фиктивной нагрузки на расстояние от центра тяжести эпюры до начала координат, а не до рассматриваемой точки на оси. Например, для вышеприведенного случая (Ql²/16)l/3 = Ql³/48

При равномерно распределенной нагрузке эпюра моментов описывается квадратичной параболой, определить площадь такой фигуры и расстояние до центра тяжести сложнее, но для того нам и нужны знания по геометрии, чтобы можно было определить площадь любой фигуры и положение центра тяжести такой фигуры.

Таким образом получается, что для балки, на которую действует сосредоточенная нагрузка в середине балки при х=l/2:

tgθ = М·(x/2)/(ЕI) = ((Ql/4)·(l/4))/(ЕI) = Ql²/(16EI) (11.6.1)

То, что мы только что делали называется интегрированием, ведь если умножить значение значение эпюры «Q» (рисунок 149.7.1) на длину действия нагрузки, мы тем самым определим площадь прямоугольника со сторонами «Q» и х, при этом площадь данного прямоугольника равняется значению эпюры «М» в точке х.

Теоретически получается, что мы можем определить значение тангенса угла поворота, интегрируя одно из уравнений моментов, составленных для нашей балки. Максимальное значение тангенса угла поворота для балки на двух шарнирных опорах, на которую действует сосредоточенная нагрузка посредине (рисунок 149.7.1), будет при х=l/2

tgθ = ∫Mdx/(EI) = ∫Axdx/(EI)= Ax²/(2EI) = (Q/2)·(l/2)²/(2ЕI) = Ql²/(16EI) (11.6.2)

где А — это реакция опоры = Q/2

При распределенной нагрузке интегрирование уравнения моментов: q(l/2)·x — qx²/2 для левой части балки дает следующий результат:

tgθ = ∫Mdx/(EI) = q·(l/2)·(l/2)²/(2ЕI) -q·(l/2)³/(6ЕI) = ql³/(24EI) (11.6.3)

Тот же результат мы получим и при использовании графо-аналитического метода.

Когда мы определяли угол поворота, то для наглядности предположили, что балка деформировалась так, как показано на рисунке 5.2, потом так, как показано на рисунке 11.3.b, потом мы выяснили, что если бы второй опоры не было, то балка повернулась вокруг первой опоры, но в действительности вторая опора есть и потому так балка деформироваться (при нашей нагрузке на балку) не может. Так как на опоре нет никакого вращающего момента и соответственно никаких внутренних напряжений, способных изменить геометрическую форму балки, то геометрическая форма балки на опоре остается неизменной, а внутренние напряжения, увеличивающиеся по ходу балки, деформируют балку все сильнее и это приводит к тому, что балка поворачивается вокруг шарнирных опор и этот угол поворота равен углу наклона поперечного сечения θ (так как мы рассматриваем балку-параллелепипед):

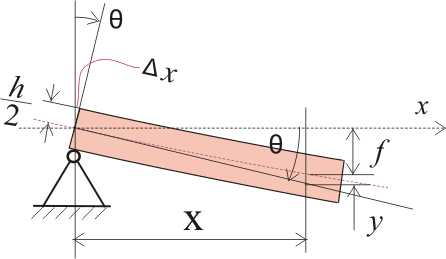
Рисунок 11.4. Реальная деформация балки.

 

Если мы просто постоим эпюру углов поворота для балки со сосредоточенной нагрузкой посредине по уравнениям для левой и для правой части балки, то эпюра будет выглядеть так:

Рисунок 11.5.

Данная эпюра была бы правильной только для балки, изображенной на рисунке 5.3.а. Очевидно, что в нашем случае эпюра так выглядеть не может и для построения правильной эпюры нужно учесть, что поперечные сечения балки имеют наклон на обоих опорах, причем наклон этот одинаковый по значению, но разный по направлению а наклон поперечного сечения балки посредине =0. Если мы опустим эпюру на Ql²/16EI, которое мы получаем при интегрировании уравнения моментов для левой части балки и которое показывает угол наклона поперечного сечения именно на опоре, то получим эпюру следующего вида:

Рисунок 11.6.

Данная эпюра абсолютно точно показывает, изменение угла поворота поперечных сечений, вдоль всей балки, а значение тангенса угла поворота на левой опоре балки не что иное, как некая постоянная С₁, которую мы получаем, если интегрирование выполнять корректно. И тогда уравнение угла поворота для балки при данной нагрузке на участке 0<x<0.5l будет выглядеть так:

tgθ_х = — tgθ_A + Ax²/(2EI) (11.6.5)

Эпюра углов поворота для балки с распределенной нагрузкой визуально ни чем не отличается от эпюры углов поворота для балки со сосредоточенной нагрузкой, разница только в том, что эпюра углов поворота для балки с распределенной нагрузкой — это кубическая парабола. Уравнение угла поворота для балки с равномерно распределенной нагрузкой будет выглядеть так:

tgθ_х = — tgθ_A + Ax²/(2EI) — qx³/(6ЕI) (11.6.6)

По поводу знаков в данном уравнении. «-» означает, что рассматриваемый член уравнения как бы пытается повернуть балку против часовой стрелки относительно рассматриваемого поперечного сечения, а «+» — по часовой стрелке. Впрочем и по эпюре углов поворота видно, что значение tgθ_А должно быть отрицательным. Таким образом, если сечение имеет наклон по часовой стрелке относительно оси х, то оно будет отрицательным, а если против часовой стрелки — то положительным.

 

Ну и теперь самое главное, все эти разборки с углом поворота поперечного сечения нужны нам были для того, чтобы определить прогиб балки.

12. Определение прогиба.

(вернуться к основному содержанию)

Как мы видим из рисунка 11.4, треугольник с катетами h/2 и Δх является подобным треугольнику с катетом Х и вторым катетом, равным f+у, а это значит, что теперь мы можем определить значение прогиба:

tgθ = (f + y)/Х (12.1)

тогда

f + y = tgθ·X (12.2.1) или f + y = М·x·Х/(2ЕI) (12.2)

при малых значениях х значение у близко к 0, но в более дальних точках сечения значение у увеличивается. Значение у — это и есть влияние на величину прогиба наличия второй опоры. Отметим, что это значение у показывает разницу между реальным наклоном продольной оси балки и наклоном продольной оси балки, если бы балка просто поворачивалась вокруг опоры, и получается, что значение у зависит от изменения угла поворота. Кроме того, мы опять получили уравнение, в котором значение прогиба в некоторой точке зависит от тангенса угла поворота (12.2.1) и таким образом получается, что у угла поворота тоже есть «плечо действия». Например при у=f/2 (если присмотреться к левой части фотографии 1, то посредине балки это где-то так и будет) мы бы получили следующую формулу для определения прогиба:

f = М·x²/(3ЕI) (12.3.1)

Но мы не будем ничего предполагать, а воспользуемся интегрированием. Если мы проинтегрируем уравнение моментов для левой части балки, то получим значение у (эпюра для у показана бирюзовым цветом на фотографии 1):

у =∫∫∫(Q/2)dх =2 (Q/2)·(l/2)³/6EI = Ql³/(96EI) (12.3.2)

или площадь фиолетовой эпюры для левой части балки(рисунок 5.5), но нам нужна площадь голубой эпюры на левом участке балки (рисунок 5.6), которая в 2 раза больше площади фиолетовой эпюры. Таким образом:

f =2∫∫∫(Q/2)dх =2 (Q/2)·(l/2)³/6EI = Ql³/(48EI) (12.3.3)

Почему площадь голубой эпюры в 2 раза больше площади фиолетовой эпюры, объяснить очень легко. Площадь треугольника равна 1/2 от площади прямоугольника с теми же сторонами, площадь фигуры, описанной квадратной параболой, составляет 1/3 от площади прямоугольника с теми же сторонами. Если бы мы развернули фиолетовую эпюру, то получили бы прямоугольник, образованный голубой и фиолетовой эпюрами. Соответственно, если из площади прямоугольника вычесть 1/3, то мы получим 2/3. У этого логического ряда есть продолжение — площадь фигуры, описанной кубической параболой, составляет 1/4 от площади прямоугольника с теми же сторонами и так далее.

Мы можем найти значение прогиба и другим способом. Из рисунка 11.4 и формул (12.2) следует, что:

f_х = — tgθx + ∫tgθdx (12.3.4)

f_l/2 = — (Ql²/16EI) l/2 + (Ql³/96EI) = -(Ql³/48EI) (12.3.5)

В данном случае знак «-» показывает, что центр поперечного сечения балки переместится вниз по оси у относительно оси х. А теперь вернемся к фотографии 1. Под продольной осью балки изображена эпюра у, именно это значение в точке l/2 мы и вычли, решая уравнение (12.3.3).  Кроме того получается, что соотношение между f и у зависит от коэффициента предыдущего интегрирования, т.е. у = kf или f = y/k. Когда мы интегрировали уравнение сил, то получили коэффициент 1/2. Впрочем, такое же значение мы получили и тогда, когда определяли плечо действия момента. Если продолжить этот логический ряд, то получается, что при определении прогиба от распределенной нагрузки мы должны использовать коэффициент 1/3, то есть прогиб в середине балки мы можем вычислить по следующей формуле:

f= 2∫∫∫(ql/2)dx — 3∫∫∫∫qdх = (2(qlx³/6) — 3(qx⁴/24))/EI = 5ql⁴/(384EI) (12.4.4)

или

f_х= — ∫tgθdx + ∫∫∫(ql/2)dx -∫∫∫∫qdх (12.4.5)

f_l/2 = (- ql³x/24 + (qlx³/6) — (qx⁴/24))/EI = — 5ql⁴/(384EI) (12.4.6)

В данном случае знак «-» означает, что центр тяжести поперечного сечения перемещается вниз по оси у.

Примечание: Предложенный метод определения прогиба несколько отличается от общепринятых, так как я старался сделать основной упор на наглядность.

Если определять прогиб графоаналитическим методом, то площадь фиктивной нагрузки — эпюры моментов, описываемой квадратной параболой, будет составлять (согласно таблице 378.1) (2ql²/(8·3))l/2 = ql³/24. А расстояние от центра тяжести эпюры до начала координат составляет 5/8, Тогда фиктивный момент равен (ql3/24)(5l/(8·2)) = 5ql⁴/384.

Конечно же, сосредоточенная нагрузка к балке может быть приложена и не посредине, распределенная нагрузка может быть не только равномерно распределенной и действовать не по всей длине балки, да и варианты крепления балки на опорах бывают разные. Но для того и существуют готовые формулы, чтобы ими пользоваться.

-Позвольте! — Скажете вы, — Все это хорошо, но как быть с касательными напряжениями? Ведь они действуют вдоль оси у и потому должны как-то влиять на прогиб!

Все верно. Касательные напряжения действительно влияют на прогиб, однако для балок с соотношением l/h > 10 это влияние очень незначительно и потому допустимо для определения прогиба пользоваться изложенным в данной статье методом.

Но это еще не все, как мы уже говорили, определить значение прогиба опытным путем достаточно просто по методу, описанному в самом начале статьи. Так так ничего лучшего под рукой не было, то я взял деревянную линейку, прообраз которой я так долго описывал (см. фотографию 1). Деревянная линейка имела размеры около 91.5 см, ширину b=4.96 см и высоту h=0.32 cм (высоту и ширину определял штангенциркулем). Затем я положил линейку на опоры, при этом расстояние между опорами составило около 90 см и таким образом получил балку с пролетом l=90 см. Под воздействием собственного веса линейка конечно же немного прогнулась, но столь малый прогиб меня не интересовал. Я измерил рулеткой (точность до 1 мм) расстояние от пола до низа линейки (77.65 см), затем приложил посредине условно сосредоточенную нагрузку (поместил посредине мерный стакан весом около 52 грамм с 250 граммами воды) и измерил расстояние от пола до низа линейки при нагрузке (75.5 см). Разница этих двух измерений и составила искомый прогиб. Таким образом величина прогиба определенного опытным путем составила 77.65 — 75.5 = 2.15 см. Осталось только найти модуль упругости для древесины, определить момент инерции для данного сечения и точно посчитать нагрузку. Модуль упругости Е для древесины = 10⁵ кгс/см², момент инерции прямоугольного сечения I_z = bh³/12 = 4.98·0.32³/12 = 0.01359872 см⁴, полная нагрузка — 0.302 кг.

Расчет прогиба по формуле дал: f = Ql³/(48EI) = 0.302·90³/(48·10⁵·0.0136) = 3.37 см. Напомню, что прогиб, определенный опытным путем, составил: f = 2.15 см. Возможно следовало учесть влияние на прогиб первой производной функции — тангенса угла поворота? Ведь угол наклона, судя по фотографии, достаточно большой.

Проверяем: tgθ = Ql²/(16EI) = 0.302·90²/(16·10⁵·0.0136) = 0.11233. Тогда согласно формулы (542.12) f = 3.37/((1 + 0.112²)^3/2) = 3.307 см. Т.е. влияние конечно есть, но оно не превышает 2% или 0.63 мм. 

Результат меня сначала удивил, но потом объяснений для такого расхождения нашлось несколько, в частности в середине поперечное сечение линейки было не прямоугольным, так как линейка была деформирована от времени и воздействия воды, соответственно момент инерции для такого сечения больше чем, для прямоугольного, кроме того, линейка изготовлена не из сосны, а из более твердой породы древесины, для которой и модуль упругости следует принимать больше. Да и с научной точки зрения одного результата совершенно недостаточно, чтобы говорить о каких-либо закономерностях. После этого я проверил величину прогиба для деревянного бруска с моментом инерции I=2.02 см⁴, длиной более 2 м при пролете 2 м под нагрузкой 2 кг, приложенной посредине бруска и тогда значение прогиба, определенного теоретическим путем и опытным путем, совпало до десятых долей миллиметра. Конечно, можно было бы и дальше продолжать эксперименты, но так уж получилось, что до меня это уже сделали сотни других людей и получили на практике результаты, очень близкие к теоретическим. А если еще учесть, что идеально изотропные материалы бывают только в теории, то это очень хорошие результаты.

13. Определение угла поворота через прогиб.

(вернуться к основному содержанию)

Определить значение угла поворота для шарнирно опертой балки, на которую действует только изгибающий момент M на одной из опор, например на опоре А, казалось бы, проще простого:

tgθ_х = — tgθ_A + Мx/(EI) — Аx²/(2ЕI) (13.1.1)

где А = М/l, (B = — M/l), но для этого нужно знать угол поворота на опоре А, а мы его не знаем, однако вычислить его помогает понимание того, что прогиб на опорах будет равен нулю и тогда:

f_A = tgθ_Bl — Bl³/(6EI) = 0; tgθ_B = — Ml³/(6l²EI) = — Ml/(6EI) (13.1.2)

f_B = tgθ_Al + Ml²/(2EI)- Al³/(6EI) = 0; tgθ_A = — Ml/(3EI) (13.1.3)

Как видим, угол поворота на опоре к которой приложен изгибающий момент, в два раза больше угла поворота на противоположной опоре, это очень важная закономерность, которая в дальнейшем нам очень пригодится.

Когда сосредоточенная нагрузка к балке приложена не по центру тяжести или распределенная нагрузка является неравномерной, то углы поворота на опорах определяются через прогиб, как в вышеприведенном примере. Другими словами — значения начальных параметров определяются в ходе решения дифференциальных уравнений.

doctorlom.com