Задачи на определение перемещений | ПроСопромат.ру

Для определения любого перемещения (линейного или углового) в методе Мора балка рассматривается в двух состояниях: действительном и вспомогательном. Вспомогательное состояние получается следующим образом: сначала всю заданную нагрузку нужно удалить, затем приложить «единичный силовой фактор» в том месте, где требуется определить перемещение, и по направлению этого искомого перемещения. Причем, когда определяем линейное перемещение (прогиб балки), то в качестве «единичного силового фактора» принимается сосредоточенная сила  , а если требуется найти угол поворота, то приложить следует сосредоточенную пару  .

Далее в одном и том же произвольном сечении обоих состояний (то есть и действительного, и вспомогательного) составляются аналитические выражения изгибающего момента, которые подставляются в формулу, называемую «интегралом Мора»:

где: знак Σ распространяется на все участки балки,

а EI – изгибная жесткость на участке.

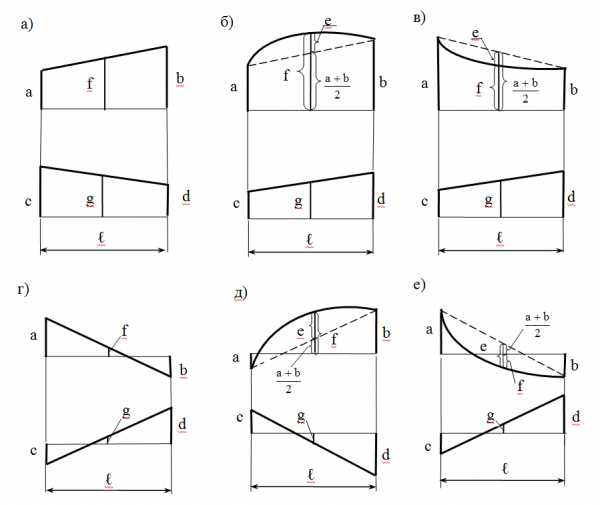
Во многих случаях интегрирования по Мору можно избежать и применить способ «перемножения» эпюр. Одним из таких способов является способ Симпсона, по которому значение интеграла Мора на участке длиной ℓ вычисляется по следующей формуле:

Здесь обозначено: a, b и с – соответственно крайние и средняя ординаты эпюры изгибающих моментов действительного состояния М,

 — крайние и средняя ординаты эпюры изгибающих моментов, но только вспомогательного состояния .

Правило знаков: если обе «перемножаемые» ординаты в двух эпюрах расположены

по одну сторону от оси эпюры (то есть они одного знака), то перед их произведением мы должны поставить знак «плюс: а если они по разные стороны от оси эпюры, то перед произведением ставим знак «минус».

Следует иметь в виду, что способы «перемножения» эпюр (кроме способа Симпсона известен еще способ Верещагина) применимы только при наличии двух условий:

1. Изгибная жесткость балки на рассматриваемом участке должна быть постоянной (EI=Const),
2. Одна из двух эпюр моментов на этом участке    должна быть обязательно линейной. При этом обе эпюры не должны в пределах данного участка иметь перелома.

При наличии нескольких участков на балке, удовлетворяющих указанным двум условиям, формула для определения перемещений принимает вид:

Если результат вычисления получается положительным, то, следовательно, направление искомого перемещения совпадает с направлением «единичного силового фактора» (  ), а если результат отрицательный, значит искомое перемещение происходит в направлении, противоположном этому фактору.

Формула Симпсона, записанная через моменты, выглядит следующим образом: перемещения (прогиб или угол поворота) равны

где  li – длина участка;

      EIi – жесткость балки на участке;

 M_F – значения изгибающих моментов с грузовой эпюры,  соответственно   в начале, в середине и в конце участка;

 –  значения изгибающих моментов с единичной эпюры, соответственно  в начале, в середине и в конце

 участка.

При перемножении эпюр будет полезным для определения ординат эпюр изгибающих моментов:

, где

Задача 

Определить угол поворота сечения на левой опоре φ_А 

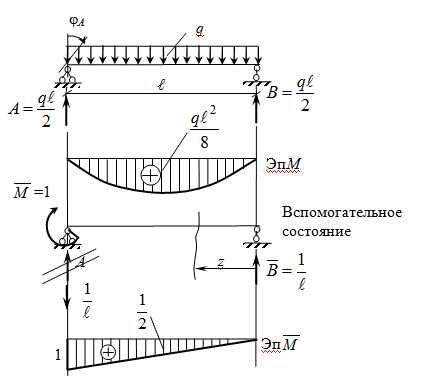
1)                 Находим опорные реакции действительного состояния  .

2)                 Строим эпюру моментов действительного состояния М.

3)                 Выбираем вспомогательное состояние для определения угла поворота φ_А.

4)                 Находим опорные реакции вспомогательного состояния

«Реагируем» на знак «минус».

5)            

Строим эпюру моментов вспомогательного состояния:

6)                «Перемножаем» эпюры 

Поскольку одна из них (а именно   ) линейна на всем пролете и не имеет перелома, а эпюра М тоже без перелома, то в формуле Симпсона будет всего один участок, и тогда

Знак «плюс» говорит о том, что сечение А поворачивается в сторону «единичного момента» 

prosopromat.ru

Прогиб консоли — Энциклопедия по машиностроению XXL

Когда компоненты напряжений найдены, перемещения и, v и W можно определить тем же путем, как это делалось в случае чистого изгиба (см. стр. 294). Рассмотрим кривую прогибов консоли. Кривизны этой линии в плоскостях хг и уг с достаточной степенью точности определяются значениями производных д и/дг и d v/dz при л = у = 0. Эти величины можно найти из уравнений  

[c.380]

Прогиб консоли. Взяв в качестве вспомогательного состояния решение задачи Сен-Венана об изгибе консоли из 120 и заменяя Р на Р», имеем  [c.465]

Пример 5.2. Определить прогиб консоли (рис. 5.10), нагруженной на конце силой Р.  [c.234]

Показать, что консоль равного сопротивления при изгибе при равномерной нагрузке и постоянной ширине имеет форму клина. Найти наибольший прогиб консоли и сравнить с прогибом консоли постоянного сечения.  [c.134]

Вычисляя, получаем, что прогиб консоли максимален при t = Т, причем функция у (Г, ж) равняется  [c.201]

Отсюда следует, что прогиб консоли максимален в точке х = I для нагрузки д (х) = 8 х — I). Следовательно, значение Ш (8) функционала (4.4) имеет вид  [c.202]

Теперь приложим груз Р в центре изгиба D, найденном теоретически отсчеты по индикаторам окажутся приблизительно равными. При этом перемещения всех точек сечения одинаковы и равны теоретическому прогибу консоли под действием сосредоточенной силы на конце, т. е. v = Pl /3EJ. Таким образом, сила Р, приложенная в центре изгиба, только изгибает брус, не вызывая его закручивания.  

[c.91]

Общность или не общность, о которой здесь идет речь, характеризуется возможностью или невозможностью проводить решение вне предположения о числовых характеристиках рассматриваемой конструкции. Так, если определяется прогиб консоли (рис. 103) под действием  [c.153]

Тормозной рычаг представляет собой балку, нагруженную на консоли силой пружины и опертую в средней части на ось колодки. Прогиб консоли определяется по формуле  [c.98]

Рассмотрим две следующие системы горизонтальное перемещение П-образной рамы (рис. 3-11) и прогиб консоли силой, приложенной на конце консоли. Консольный брус состоит из двух балок, раздвинутых на расстояние I и связанных между собой бесконечно жесткой в своей плоскости стенкой толщиной 6 = 0. Эта система аналогична брусу, показанному на рис. 3-10,6. Стойки рамы и балки консоли раздвинуты на одинаковое расстояние / они имеют равные высоты и площади поперечных сечений.  

[c.106]

Подставив в формулу (3-14) значение k и выполнив элементарные преобразования, покажем, что смещение П-образной рамы превышает прогиб консоли, т. е. что предложенная нами схема жестче ранее принятой. Именно  [c.107]

Если стержень имеет консоль, то. при первой форме колебаний ординаты прогибов консоли будут противоположного знака с ординатами прогибов стержня между опорами, и на этом участке направление сил следует- принять противоположным направлению сил между опорами. Определение прогибов может быть проведено графическим или графоаналитическим методом.  [c.401]

Рассмотреть изгиб консоли прямоугольного поперечного сечения силой, приложенной на конце. Найти области пластической деформации, предельное значение силы, прогибы консоли в упруго-пластическом состоянии.  

[c.118]

Формулы для прогибов консоли, нагруженной равномерно распределенной нагрузкой приведем без вывода.  [c.130]

Пример. Определить прогибы консоли постоянного сечения под действием сосредоточенной силы Р (рис. 18).  [c.408]

В 523 мы получили приближенна (51), взяв для форму кривой статического прогиба консоли постоянного поперечного сечения под равномерно распределенной нагрузкой. Мы также можем использовать кривую статического прогиба для сосредоточенной силы, приложенной на расстоянии а от заделанного конца. Тогда, так как любая полученная таким образом оценка будет обязательно превышать истинную величину, мы можем выбрать а так, чтобы получающееся при этом выражение для имело минимальное значение.  [c.641]

Кривая прогиба консоли постоянного поперечного сечения длины а, заделанной на одном конце и нагруженной сосредоточенной силой на другом, определяется уравнением )  

[c.641]

Со времени Эйлера этим уравнением пользовались для вычисления прогибов консолей и симметрично нагруженных свободно опертых балок. Навье применяет его для любого вообще случая поперечного загружения простой балки, причем кривая прогибов описывается у него в отдельных участках пролета балки  [c.94]

Сен-Венан показывает ), что прогиб консоли может быть вычислен элементарным путем, без интегрирования соответству-  [c.166]

Л. Эйлер приходит к следующему выводу среди всех кривых одной и той же лины, которые не только проходят через точки А и В, но также касаются заданных прямых линий, проведенных через (ти точки, следует определить ту кривую, которая делает выражение эЬ) минимальным. При помощи такого подхода Л. Эйлер приходит к уравнению (а) и использует его для различных частных случаев. Два простых случая становятся особенно важными для дальнейшего развития сопротивления материалов. Рассматривая малые прогибы консоли длиной L, вызванные силой Р, приложенной на ее конце Эйлер находит следующую зависимость  

[c.653]

И рекомендует эту формулу для вычисления изгибной жесткости К в том случае, если прогиб / найден экспериментально. Если в числителе этой формулы пренебречь / по сравнению с L, то получим обычную формулу для определения прогиба консоли при действии силы Р. Во втором случае Л. Эйлер рассматривает стержень, сжатый силой Р, и находит, что она начинает выпучиваться вбок, когда  [c.653]

Тогда прогиб консоли S = дИ/дР = -Р1 /EJz- Подсчитав этот  [c.285]

Стрелки /б прогиба главных балок и /к прогиба консолей при пролете балок Ig и вылете консоли Lk  [c.541]

Чтобы прогиб консоли не изменился при переходе к другому диаметру, в формуле  [c.66]

Прогибы консоли оказываются равными  [c.335]

Упругий прогиб консоли груза при этом консоль груза принимают условно за балку с заделкой и перемещение конца консоли определяют как  [c.154]

Сен-Венан нашел способ определения положения нейтральной оси сечения при косом изгибе решил задачу определения больших прогибов консоли (в случае неприменимости приближенного дифференциального уравнения изогнутой оси) решил задачу изгиба балки, материал которой не следует закону Гука исследовал изгиб кривых стержней плоских и двоякой кривизны вывел формулу для определения продольной деформации винтовых пружин провел дальнейшую разработку теории кручения призматических стержней развил вторую теорию прочности дал расчетную формулу для валов, работающих в условиях совместного действия кручения и изгиба показал, что в частном случае плоского напряженного состояния при аг = —вызывается чистый  [c.562]

Задача 118. Найти наибольший прогиб консоли АВ (фиг. 218), если J = 245 см,  [c.215]

Задача 246. На конце консоли АВ (фиг. 470) находится электродвигатель общим весом С, вращающийся с числом п оборотов в минуту. Маховик, вес которого равен О, насажен на вал электродвигателя с эксцентрицитетом е. Найти наибольший динамический прогиб консоли без учета свободных колебаний системы. Собственным весом консоли пренебречь.  [c.482]

Амплитуда вынужденных колебаний, т. е. искомый наибольший динамический прогиб консоли,  [c.482]

Обозначая через /д, = — к и = прогибы консоли от действия веса маховика О и веса электродвигателя с маховиком Q, окончательно будем иметь  [c.483]

L = 150 мм упругое перемещение от податливости конического соединения равно прогибу консольной части оправки при L [c.177]

Прогиб консоли от веса груза, электрической тали и собственного веса (рис. 189)  [c.352]

Общий вид машины представлен на рис. 150. Станина машины состоит из кор,нуса 1, верхней консоли 2 и нижней консоли 3. Основными элементами сварного корпуса являются четыре вертикальные колонки-трубы, передняя толстостенная плита, горизонтальные угольники, нижняя плита с ребрами, верхняя плита и две боковые двери. Колонки-трубы корпуса, соединенные между собой трубками, образуют ресивер сжатого воздуха, которым питается пневматический цилиндр привода сжатия электродов. На верхней консоли смонтированы верхняя контактная часть 4, ползун 5, пневматический цилиндр 6 привода сжатия электродов, верхний электрододержатель с электродом и гибкие соединения 7. На верхней консоли установлен электропневматический клапан 8, воздушный редуктор с манометром и дроссели. Нижняя консоль 3 прикрепляется к корпусу 1 двумя направляющими планка ми 9. В ней смонтированы нижний хобот с электрододержателем и контактная шина. Нижняя консоль с помощью винтового устройства 0 может перемешаться перемещение осуществляется после освобождения направляющих планок, которые после установки на требуемой высоте нижней консоли снова затягиваются. Для избежания прогиба консоли предусмотрено подпорное устройство 11.  [c.255]

Консоли. Консоли обычно имеют круглое сечение они изготовляются из меди или медных сплавов. На рис. 80. а показаны типовые консоли точечных машин с различными способами крепления электрододержателей с отъемной колодкой и без нее. Консоли точечных машин воспринимают большие усилия привода сжатия электродов прогиб консолей ведет к смещению электродов. Этот прогиб ограничивается ГОСТом 1,2 мм для консолей длиной до 500 мм, 1,6 мм — до 1200 мм и 2,5 мм — более 1200 мм. Поэтому в машинах средней и большой мощности предусмотрено усиление консолей чугунными или стальными кронштейнами (рис.  [c.85]

Рассмотрим прямоугольную пластинку системы пленка-подложка (толщина пленки гг, толщина подложки Н, длина /). Образец жестко закреплен с одного края в виде консоли. При выводе pa чeтfloй формулы предполагается, что остаточные напряжения п, одинаковы во всех точках покрытия. Удаление покрытия приводит к деформации образца под действием изгибающего момента М=ЕН / ( 2R), где Е — модуль упругости материала подложки, К — радиус кривизны пластины до изгиба. Измерив максимальный прогиб консоли / можно вычислить радиус кривизны / = ( /2/. С другой стороны изгибающий момент М связан с остаточными напряжениями формулой М = 1/2 о, — кИ. Приравнивая М к М как эквивалентные нагрузки получим выражение для расчета остаточных напряжений  [c.115]

Используя метод 51, найти кривую прогиба консоли постоянного сеченил, нагруженной так, как показано на рис. 17 А. На этом  [c.68]

Сен-Венан исследует также большие прогибы консоли, при которых кривизна 1/р не может быть заменена приближенным значением d yldx . Он дает решение в виде ряда, суммирование которого позволяет вычислить прогиб о с любой желаемой точностью ).  [c.167]

По-видимому, это утверждение Максвелла пе совсем правильно. Как отметил С. А. Бернштейн в статье Забытые страницы из истории русской строительной механики (Труды по истории техники АН СССР, вып. VII, М., 1954, стр. 35), в вышедшей в 1855 г. в Петербурге небольшой книге Беспалова Элементарный способ решения вопросов относительно сопротивления материалов и устойчивости сооружений метод Клапейрона приравнивания работ внешних и внутренних сил был применен к вычислению прогиба консоли под сосредоточенным грузом. При вычислении работы внутренних сил Беспалов пользуется перемножением эпюр напряжений и удлинений в произвольном волокне по длине балки и приходит к правильному значению прогиба. Этот прием на 30 лет опередил прием вычисления интегралов Мора, указанный Мюллер—Бреслау. (Прим. ред.)  [c.248]

Онределить угол поворота и прогиб консоли из двутавра № 22 в сечении, расположенном посредине длины (см. рис. 282), если Р=2,5 Г,  [c.131]

Для увеличения жесткости станка при тяжелых условиях работы применяют поддержки (ножницы), скрепляющие при помощи болтов хобот и консоль станка. Применение поддержек уменьшает прогиб консоли и хобота при работе. Винт для затяжки обеспечивает плотный контакт конического хвостовика оправки с поверхностью внутреннего конуса шпинделя, а торцовые шпонки — непроворачиваемость оправки относительно шпинделя.  [c.38]

---

mash-xxl.info

Расчет на прочность и прогиб балки при ударе в Excel

Опубликовано 12 Янв 2014
Рубрика: Механика | 3 комментария

Расчет на прочность при ударе в обычной работе инженера-конструктора встречается не очень часто. Поэтому возникновение такой задачи может поставить в тупик своей неожиданностью. Расчеты при ударных, то есть динамических нагрузках очень сложны и часто производятся…

…по эмпирическим – полученным из практических опытов — методикам и формулам. В этой статье мы рассмотрим расчет по приближенной теоретической формуле, которая, однако, позволяет быстро, просто, понятно и с достаточной для многих случаев жизни точностью учесть динамическую составляющую нагрузки!

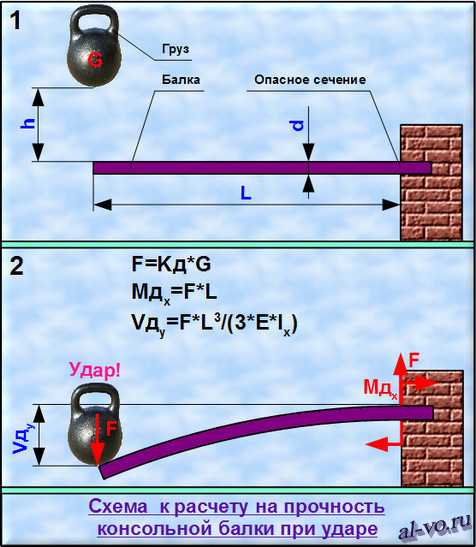
Выполним расчет на прочность и определим прогиб балки при воздействии ударной нагрузки на примере консоли.

Общий подход к статическим расчетам на прочность при изгибе подробно изложен в статье «Расчет балки на изгиб – «вручную»!», где приведены уравнения общего вида, позволяющие произвести расчет на прочность балки с любыми опорами и при любых нагрузках.

Расчеты выполним в программе MS Excel. Вместо MS Excel можно воспользоваться программой OOo Calc из свободно распространяемого пакета Open Office.

С правилами форматирования ячеек листа Excel, которые применены в статьях этого блога, можно ознакомиться на странице «О блоге».

Расчет консольной балки при ударе.

Расчет на прочность, который мы будем выполнять, является приблизительным.

Во-первых, предполагаем, что вся потенциальная энергия груза, падающего с некоторой высоты, переходит в кинетическую энергию, которая при соприкосновении груза с балкой полностью переходит в потенциальную энергию деформации. В реальности часть энергии превращается в тепло.

Во-вторых, мы не будем учитывать в расчете массу балки. То есть прогиб балки под действием собственного веса примем равным нулю! (Чем меньше вес балки относительно веса груза, тем точнее результаты, полученные по рассматриваемой методике расчета!)

В-третьих, прогиб балки при ударе будем определять как прогиб от статического воздействия груза с весом больше реального веса груза на величину, определяемую коэффициентом динамичности. То есть силу при ударе найдем как сумму веса и силы инерции груза при торможении.

В-четвертых, считаем, что груз не отскакивает при ударе, а перемещается на величину динамического прогиба вместе с балкой. То есть удар абсолютно неупругий!

В-пятых, учтем ограничение, что ошибка расчета не превысит 8…12% только в случае, если рассчитанный коэффициент динамичности будет не более 12!

На рисунке, расположенном ниже, изображена  расчетная схема.

Составим в Excel программу и в качестве примера выполним расчет на прочность и определим прогиб балки круглого сечения.

Исходные данные:

1. Вес груза G в Н записываем

в ячейку D3: 50

2. Высоту падения груза h в мм заносим

в ячейку D4: 400

3. Длину консольной балки L в мм вписываем

в ячейку D5: 2500

4. Осевой момент инерции поперечного сечения балки I_x в мм⁴ вычисляем для диаметра d=36 мм

в ячейке D6: =ПИ()*36^4/64 =82448

I_x=π*d⁴/64

5. Осевой момент сопротивления поперечного сечения балки W_x в мм³ вычисляем для диаметра d=36 мм

в ячейке D7: =ПИ()*36^3/32 =4580

W_x=π*d³/32

6. Допустимые напряжения материала балки (Ст3 сп5) при изгибе [σ_и] в Н/мм² записываем

в ячейку D8: 235

7. Модуль упругости материала балки E в Н/мм² вписываем

в ячейку D9: 215000

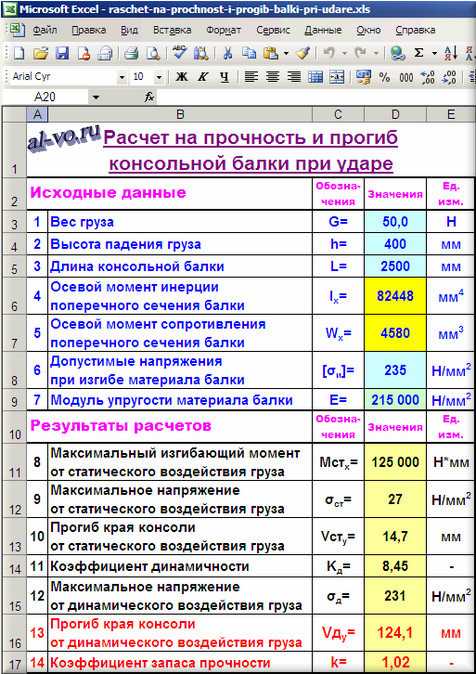
Результаты расчетов:

8. Максимальный изгибающий момент при статическом воздействии груза Mст_x в Н*мм определяем

в ячейке D11: =D3*D5 =125000

Mст_x=G*L

9. Максимальное напряжение при статическом воздействии груза σ_ст в Н/мм² вычисляем

в ячейке D12: =D11/D7 =27

σ_ст=Mст_x /W_x

10. Прогиб края консоли от статического воздействия груза Vст_y в Н/мм² рассчитываем

в ячейке D13: =D3*D5^3/3/D9/D6 =14,7

Vст_y=G*L³/(3*E*I_x)

11. Коэффициент динамичности K_д вычисляем

в ячейке D14: =1+(1+2*D4/D13)^0,5 =8,45

K_д=1+(1+2*h/Vст_y)^0,5

12. Максимальное напряжение при динамическом воздействии груза σ_д в Н/мм² вычисляем

в ячейке D15: =D12*D14 =231

σ_д=σ_ст*K_д

13. Прогиб балки в точке удара при динамическом воздействии груза Vд_y в мм определяем

в ячейке D16: =D13*D14 =124,1

Vд_y=Vст_y*K_д

14. Коэффициент запаса прочности k вычисляем

в ячейке D17: =D8/D15 =1,02

k=[σ_и]/σ_д

Заключение.

Созданный расчет в Excel можно использовать для расчета на прочность при ударе консольных балок любого сечения. Для этого в исходных данных необходимо предварительно рассчитать  осевые моменты инерции и сопротивления соответствующего сечения.

Для балок с другими вариантами опор следует найти прогиб и напряжение от статического воздействия груза по соответствующим схеме опор формулам, затем по приведенной в п.11 формуле рассчитать коэффициент динамичности и определить прогиб балки в точке удара и максимальное напряжение в опасном сечении при ударе.

Опасное сечение – это сечение, в котором напряжение максимально и, соответственно, в котором начнется изгиб при достижении напряжением предельного значения. Определяется это сечение индивидуально для конкретных схем из эпюр и расчетов.

Коэффициент динамичности зависит – как следует из формулы – от высоты падения груза и величины прогиба при статическом приложении нагрузки. Чем больше высота падения, тем больше коэффициент динамичности. Это понятно, но почему этот коэффициент возрастает при уменьшении статического прогиба? Дело в том, что, чем меньше статический прогиб, тем жестче балка и тем быстрее остановится падающий груз после касания. Чем меньше время и путь торможения груза, тем больше ускорение (точнее торможение – ускорение с отрицательным знаком), а значит больше и сила инерции, которая по второму закону Ньютона, как известно, равна произведению массы тела на ускорение! Спрыгнуть на батут с высоты четырех метров можно легко, а вот на бетонный пол – чревато последствиями…

Подписывайтесь на анонсы статей в окне, расположенном в конце каждой статьи или в окне вверху страницы.

Не забывайте подтверждать подписку кликом по ссылке в письме, которое тут же придет к вам на указанную почту (может прийти в папку «Спам»)!!!

Оставляйте ваши комментарии, уважаемые читатели! Ваш опыт и мнение будут интересны и полезны коллегам!!!

Прошу уважающих труд автора  скачивать файл после подписки на анонсы статей!

Ссылка на скачивание файла: raschet-na-prochnost-i-progib-balki-pri-udare (xls 20,0KB).

Другие статьи автора блога

На главную

Статьи с близкой тематикой

Отзывы

al-vo.ru

Плоский изгиб (консольная балка) — Студопедия.Нет

Для балки, изображенной на рисунке 22, данные к эадаче  приведены в таблице 7, необходимо:

 1. Определить опорные реакции.

      2. Написать выражения изгибающего момента М и поперечной   

            си­лы для Q каждого участка в общем виде.

      3. Построить эпюры М и Q.

      4. Подобрать балку круглого сечения из стали 20.

                                                                         Таблица 7

 Данные к задаче 4

 

Номер	Схема	l	а1/ а	М	F	q
строки	По рис.5	М		кНм	кН	кН/м
1	1	1,1	1	10	10	1
2	2	1,2	2	20	20	2
3	3	1,3	3	3	3	3
4	4	1,4	4	4	4	4
5	5	1,5	5	5	5	5
6	6	1,6	6	6	6	6
7	7	1,7	7	7	7	7
8	8	1,8	8	8	8	8
9	9	1,9	9	9	9	9
0	10	2	10	15	15	10
	Е	Д	Б	Г	В	Е

Задача 5

              Плоский изгиб (консольная балка). Определение перемещений

    Используя результаты, полученные в задаче 6, для балки, изображен­ной на

рисунке 22, необходимо построить эпюру прогибов.

 

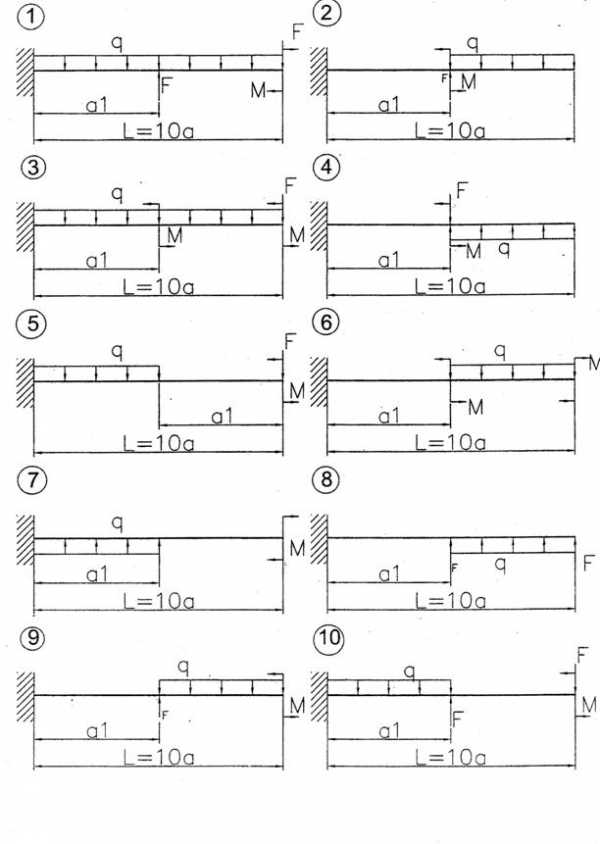
Рисунок 22 − Схемы балок к задаче 4

 

Задача 6

Плоский изгиб (двухопорная балка)

       Для балки, изображенной на рисунке 23, необходимо:

  1. Определить опорные реакции.

 2. Написать выражения изгибающего момента М и поперечной си­лы Q для  каждого участка в общем виде.

 3. Построить эпюры М и Q.

4. Подобрать балку двутаврового поперечного сечения при [σ]=160 МПа.                

 Если по данным задачи опоры оказываются в одной точке, следует вместо                

a₁  взять 0,5 a₁.   

                                                                                                               Таблица 8

Данные к задаче 8

Номер	Схема	l	a1 /а	a2 /а	M	F	q
строки	по рис. 6	м			кНм	кН	кН/м
1	1	6	1	9	10	10	1
2	2	7	2	8	20	20	2
3	3	3	3	7	3	3	3
4	4	4	4	6	4	4	4
5	5	5	5	5	5	5	5
6	6	6	6	6	6	6	6
7	7	7	7	7	7	7	7
8	8	8	8	8	8	8	8
9	9	9	9	9	9	9	9
0	10	10	10	10	15	15	10
	Е	Д	Б	В	Г	Д	Е

 

 

Задача 7

               Плоский изгиб (двухопорная балка). Определение перемещений

  Используя результаты, полученные  в задаче 8, для  балки,

изображенной на рисунке 23, необходимо построить эпюру про­гибов.

 

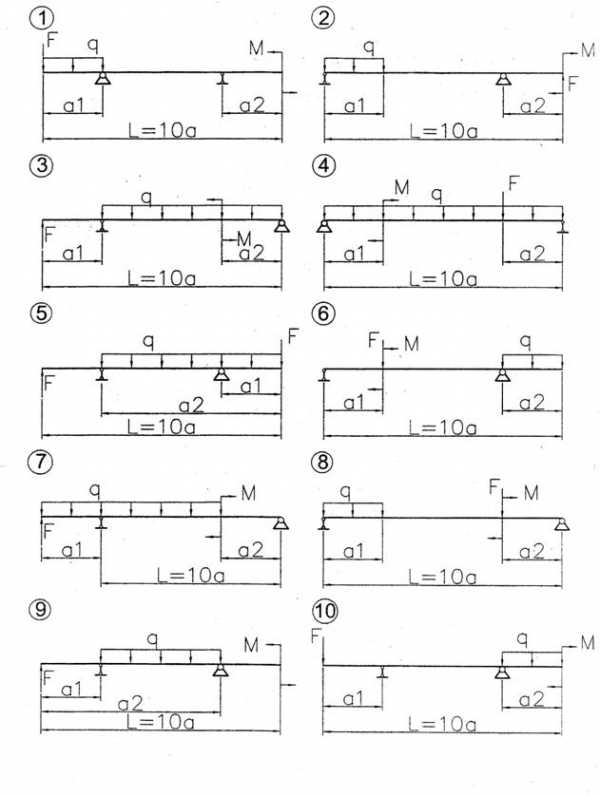
Рисунок 23 − Схемы балок к задаче 6

 

РАСЧЕТ НА ПРОЧНОСТЬ СТАТИЧЕСКИ

НЕОПРЕДЕЛИМОЙ БАЛКИ

 

Понятие о статически неопределимой системе

 

            Статически неопределимой называется система, в которой реакции и внутренние усилия не могут быть найдены только из уравнений равновесия и опреде­ляются из дополнительных уравнений, вытекающих из деформированного состояния системы. Статически неопределимые системы имеют так называемые «лишние» связи: внешние (опорные) или внутренние. Будем рассматривать только внешние статически неопределимые системы. Степень статической не­определимости определяется разностью между числом неизвестных реак­ций и числом независимых уравнений статики. Будем рассматривать геометрически неизменяемые балки, не содержащие шарниров.

   Обозначим:

  n — степень статической неопределимости,

  s — число опорных связей.

  Для неподвижного закрепления плоеной геометрически неизменяе­мой системы требуется три определенным образом расположенные опорные связи. Число независимых уравнений статики для плоской системы равно трём. Следовательно, степень статической неопреде­лимости такой системы может быть определена по формуле

                                               n = s – 3                                       

   Например, для балки, изображённой на рисунке 24, а, число опорных cвязей s = 4 и, следовательно, степень статической неопределимости n= 4 — 3 = 1; для балок, изображенных на рисунке 24, 6 и на рисунке 24, в, степени статической неопределимости равны n= 2 и n= 4 соответственно.

 

 

 

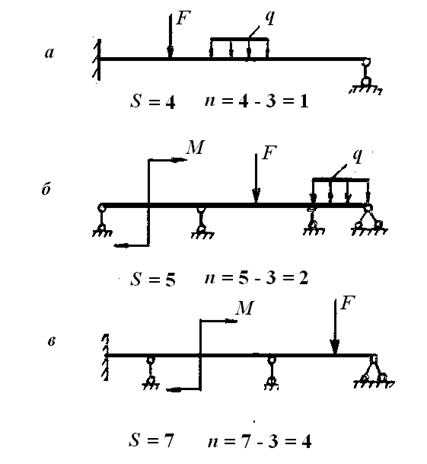
  Рисунок 24 − Определение степени статической неопределимости n

 

Для раскрытия статической неопределимости к уравнениям статики нужно составить столько дополнительных уравнений, сколько раз статически неопределима система. Эти дополнительные уравнения составляются из условий совместности деформаций.

   Расчет статически неопределимой системы сводится к определению неизвестных реакций и построению эпюр внутренних усилий (изгибающих моментов М и попеpeчных сил Q, на основании которых подбираются размеры попеpeчных сечений или про­веряются напряжения в опасных сечениях.

    Существуют различные методы раскрытия статической неопределимости: метод сравнения перемещений, метод сил, метод перемещений. Рассмотрим метод сравнения перемещений.

 

Метод сравнения перемещений

            Метод сравнения перемещений (деформаций) наиболее простой. Суть этого метода заключается в том, что дополнительные уравнения составляются из условий равенства нулю прогибов на опорах балки.         Рассмотрим этот метод на примере.

Пример 6

 

            Для балки, изображённой на рисунке 25, требуется определить                опорные реакции и построить эпюры поперечных сил Q_y и изгибающих моментов М_Z

   

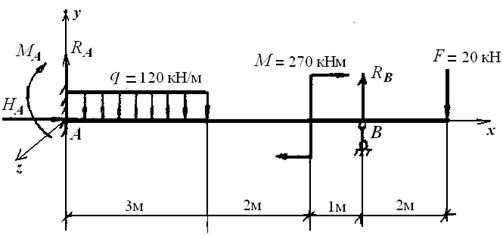
            Рисунок 25 − Расчетная схема статически неопределимой балки

 

   Балка имеет 4 опорные связи и является один раз статически неопределимой. Для определения неизвестных реакций М_А, R_А, H_Аи R_B  имеем только три уравнения равновесия статики:

                1. ∑Х = 0;                                                                 (11)

                      откуда следует, что H_А = 0.

                  2. ∑Y = 0;                                                                  (12)

                     R_А  − q∙3+ R_B− F = 0;  

                     R_А+ R_B= 380.

                 3. ∑ М_B    = 0;                                                             (13)

                    М_А + 6∙ R_А  − q∙3∙4,5 + M  + F∙2 = 0;

                      М_А + 6∙ R_А  = 1310.                          

           Дополнительное четвертое уравнение составим, исходя из условия, что на опоре В прогиб y_B равен нулю. Прогиб в опоре определим, используя универсальное уравнение упругой линии (ме­тод начальных параметров), которое применительно к данной задаче имеет вид:

                   4. EI y_B  = 0;                                                                     (14) 

EI y_B = EI y₀ + EIφ₀ ∙x + М_А ∙6² /2 + R_А ∙6³ /6 − q∙6⁴ /24 + q∙3⁴ /24 + М ∙1² /2 = 0.

                  Так как качало координат помещено в защемлении, начальные параметры  y₀ = 0 и φ₀ = 0, где y₀ − прогиб балки при х = 0, φ₀ − угол поворота сечения балки при х = 0.       

                    С учетом этого уравнение (14) имеет вид

                                                           М_А + 2∙ R_А = 330.

                               Решая совместно уравнения (3) и (4), получим:

                                 ,

—                                откуда R_А = 245 кН, М_А = − 160 кHм.

   Затем, подставив в уравнение (12) найденное значение реакции R_А, определим реакцию R_B = 380 – 245 = 135 кН.

    Для проверки правильности вычисленных реакций составим уравнение

моментов всех сил относительно опоры А:

                    ∑ m_А   = −120∙3∙1,5 + 270 −135∙6 + 20∙8 = 0

    Равенство нулю суммы моментов означает, что реакции определены

правильно. Определив значения реакций М_А, R_А, и R_B, можно приступить к

построению эпюр внутренних усилий.

    На рисунке 26 приведены: схема балки, эпюры поперечных сил       

Q_y, кН и изгибающих моментов М_Z, кНм.

 

      Рисунок 26 − Расчет статически неопределимой балки.

                  Эпюры поперечных сил Q_y и изгибающих моментов М_Z

  Рассмотрим ещё один пример расчета статически неопределимой балки.

Пример 7

    Определить размеры h, b прямоугольного поперечного сечения стальной балки (рисунок 27), если [σи] = 160 МПа, E = 2·105 МПа и h/b = 2. Определить прогибы посредине пролета балки и на конце консоли. Число неизвестных реакций 4, уравнений статики 3: балка один раз статически неопределима. Целесообразные уравнения статики:

                          ;

       .                    (15)

      Рисунок 27 − Расчетная схема статически неопределимой балки

   Число неизвестных реакций 4, уравнений статики 3: балка один раз статически неопределима. Целесообразные уравнения статики:

                              ;

       .                    (15)  

Дополнительное уравнение составим, исходя из условия, что на опоре Bпрогиб равен нулю:

.    Так как начало координат помещено в защемлении, начальные параметры y₀ = 0 и φ₀ = 0. Тогда из уравнения прогибов получим:

                                                                                      (16)

Из уравнений (15) и (16) следует: С_у= 7,75 кН, m_c = 7 кН∙м.

Определим опорную реакцию B:

,

откуда В  = 4,25 кН.

       

                

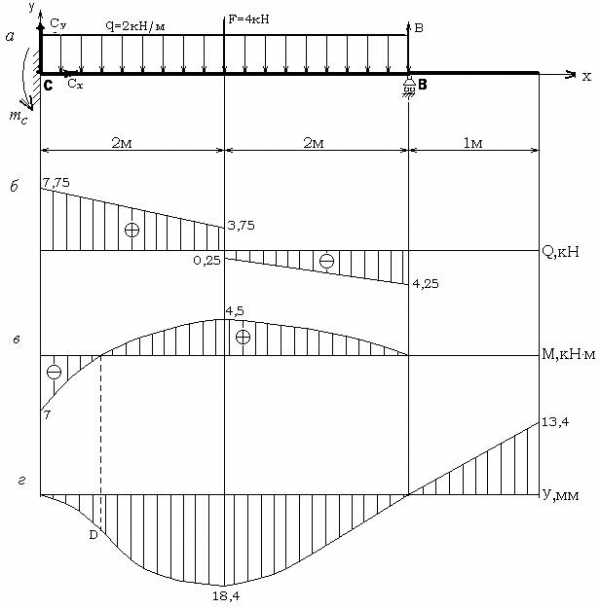
                           Рисунок 28 − Пример 9. Эпюры поперечных сил Q,

                                изгибающих  моментов M и прогибов y

 

 Проверка вычислений реакций:

.

Эпюры  и   показаны на рисунке 51, б, в.

Размеры сечения балки определим из условия прочности по нормальным напряжениям:

; ;

 

Момент инерции сечения

Жесткость сечения

Прогиб посередине пролета балки  

                        ;

.

 

Прогиб на конце консоли  (х = 5 м):

 

откуда  

Изогнутая   ось балки   показана   на  рисунке 51, г. Необходимо отметить,

что консольная часть балки не деформируется , но перемещается за счет деформации пролетной части. Точка D – точка перегиба упругой линии.

 

 

Задача 8

studopedia.net

Определение перемещений | ПроСопромат.ру

Виды перемещений. Дифференциальное уравнение упругой линии балки

При плоском изгибе балки её упругая линия, лежащая в плоскости действия внешних сил, искривляется, точки этой линии получают некоторые перемещения.

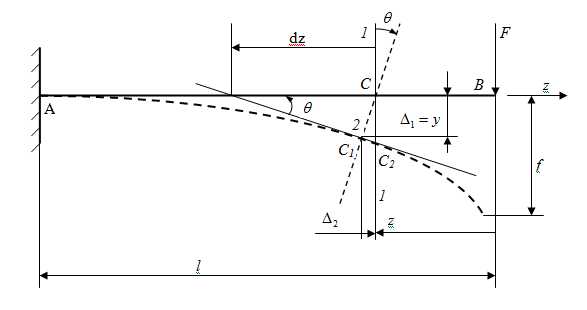
Произвольно выбранная точка С перемещается как в направлении, перпендикулярном АВ, так и вдоль этой линии на величину . Наибольший практический интерес представляет перемещение , которое называется прогибом балки. Угол между направлениями 1-1 и 2-2 называется углом поворота сечения балки. Таким образом , перемещения бывают линейные и угловые.

Наряду с расчётом балки на прочность необходимо производить и расчёт на жёсткость, то есть определять прогибы и углы поворота балки. Существует несколько способов решения задачи о деформациях балок.  Рассмотрим аналитический способ. Установим зависимость координаты   – уравнение упругой линии.

Из рисунка видно ,что Но! В упругой стадии работы материала углы поворота настолько малы ,что можно считать угол равным его тангенсу. Вспомнив геометрический смысл производной, можно принять угол поворота равным  первой производной прогиба по абсциссе сечения.

Правила знаков для перемещений, знаки перемещений

Угол считается положительным, если сечение поворачивается против хода часовой стрелки и наоборот. Прогиб считают положительным согласно принятому направлению осей координат. Если ось координат направлена вверх, то положительным будет прогиб вверх, а отрицательным —  вниз.

Для нахождения зависимости y=f(z) используем известное соотношение  между кривизной оси с изгибающим моментом и жесткостью сечения балки          

При постоянных моменте, кривизне и жесткости  балка изгибается по окружности.

Из математики известно, что кривизна кривой может быть выражена так:

Пренебрегая   получим приближённое дифференциальное уравнение изогнутой оси балки:                     

Или 

При приближённом дифференциальном уравнении изогнутой оси балки пользуются принципом малости перемещений, а если перемещения очень большие, то используют точное дифференциальное уравнение. В технике допускаемая величина прогиба , где   — длина пролёта балки. Уравнение    представляет собой линейное дифференциальное уравнение второго порядка с разделяющимися переменными и может быть проинтегрировано в общем виде:

где v- линейное перемещение (прогиб), θ – угловое перемещение, С₁ и С₂ – постоянные интегрирования.

С₁– угол поворота в начале координат, умноженной на величину ЕI;

С₂  – прогиб балки в начале координат, умноженный на EI.

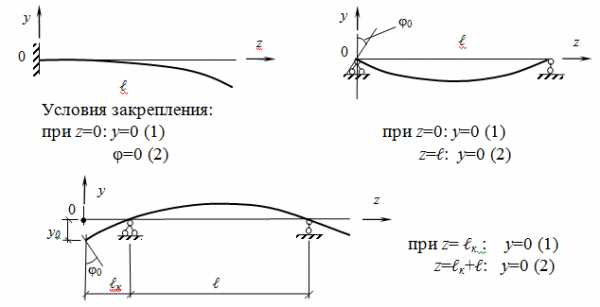
Значения этих постоянных определяют из граничных условий ,т.е. условий опирания балки и условий на границах смежных участков.  Вот эти условия:

— у свободно лежащей балки прогибы на обеих опорах равны нулю. При симметричном нагружении у такой балки угол поворота в середине пролета также равен нулю;

— у консольной балки в заделке и прогиб и угол поворота равны нулю;

— на границе смежных участков балки прогиб и угол поворота одинаковы как для левого, так и для правого участка.

Определение перемещений по методу начальных параметров (или по универсальным формулам прогибов и углов поворота сечений)

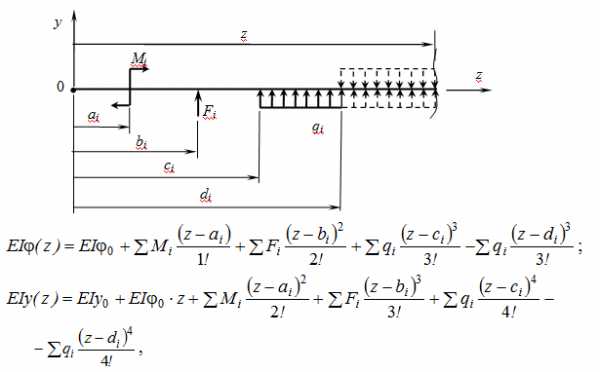
где у₀ и φ₀ – начальные параметры, то есть прогиб и угол поворота в начале координат, которые определяются из условий закрепления балки:

Порядок определения перемещений по универсальным формулам:

1. Определить все опорные реакции.
2. Поместить начало координат обязательно в крайнее сечение балки (левое или правое).
3. Ось у направить вверх, ось z — вдоль балки.
4. Найти начальные параметры из условий закрепления балки (возможные случаи показаны выше).
5. Зная начальные параметры у₀ и φ₀, по универсальным формулам определить интересующие нас перемещения.

При использовании универсальных формул необходимо выполнять следующие требования:

а) В универсальные формулы включать только те внешние силы, которые действуют между началом координат (т.0) и сечением, в котором определяются перемещения. Следует помнить, что опорные реакции – тоже внешние силы.

б) Каждая внешняя сила (Мi, Fi, qi) вводится со знаком изгибающего момента, который эта сила вызывает в сечении, где определяется перемещение.

prosopromat.ru

2QM.ru: Расчет балок на прогиб. Максимальный прогиб балки: формула

Балка – элемент в инженерии, представляющий собой стержень, который нагружают силы, действующие в направлении, перпендикулярном стержню. Деятельность инженеров зачастую включает в себя необходимость расчета прогиба балки под нагрузкой. Этой действие выполняется для того, чтобы ограничить максимальный прогиб балки.

Содержание статьи

Типы

На сегодняшний день в строительстве могут использоваться балки, изготовленные из разных материалов. Это может быть металл или дерево. Каждый конкретный случай подразумевает под собой разные балки. При этом расчет балок на прогиб может иметь некоторые отличия, которые возникают по принципу разницы в строении и используемых материалов.

Деревянные балки

Сегодняшнее индивидуальное строительство подразумевает под собой широкое применение балок, изготовленных из дерева. Практически каждое строение содержит в себе деревянные перекрытия. Балки из дерева могут использоваться как несущие элементы, их применяют при изготовлении полов, а также в качестве опор для перекрытий между этажами.

Ни для кого не секрет, что деревянная, так же как и стальная балка, имеет свойство прогибаться под воздействием нагрузочных сил. Стрелка прогиба зависит от того, какой материал используется, геометрических характеристик конструкции, в которой используется балка, и характера нагрузок.

Допустимый прогиб балки формируется из двух факторов:

• Соответствие прогиба и допустимых значений.
• Возможность эксплуатации здания с учетом прогиба.

Проводимые при строительстве расчеты на прочность и жесткость позволяют максимально эффективно оценить то, какие нагрузки сможет выдерживать здание в ходе эксплуатации. Также эти расчеты позволяют узнать, какой именно будет деформация элементов конструкции в каждом конкретном случае. Пожалуй, никто не будет спорить с тем, что подробные и максимально точные расчеты – это часть обязанностей инженеров-строителей, однако с использованием нескольких формул и навыка математических вычислений можно рассчитать все необходимые величины самостоятельно.

Для того чтобы произвести правильный расчет прогиба балки, нужно также брать во внимание тот факт, что в строительстве понятия жесткости и прочности являются неразрывными. Опираясь на данные расчета прочности, можно приступать к дальнейшим расчетам относительно жесткости. Стоит отметить, что расчет прогиба балки – один из незаменимых элементов расчета жесткости.

Обратите ваше внимание на то, что для проведения таких вычислений самостоятельно лучше всего использовать укрупненные расчеты, прибегая при этом к достаточно простым схемам. При этом также рекомендуется делать небольшой запас в большую сторону. Особенно если расчет касается несущих элементов.

Расчет балок на прогиб. Алгоритм работы

На самом деле алгоритм, по которому делается подобный расчет, достаточно прост. В качестве примера рассмотрим несколько упрощенную схему проведения расчета, при этом опустив некоторые специфические термины и формулы. Для того чтобы произвести расчет балок на прогиб, необходимо выполнить ряд действий в определенном порядке. Алгоритм проведения расчетов следующий:

• Составляется расчетная схема.
• Определяются геометрические характеристики балки.
• Вычисляется максимальную нагрузку на данный элемент.
• В случае возникновения необходимости проверяется прочность бруса по изгибающему моменту.
• Производится вычисление максимального прогиба.

Как видите, все действия достаточно просты и вполне выполнимы.

Составление расчетной схемы балки

Для того чтобы составить расчетную схему, не требуется больших знаний. Для этого достаточно знать размер и форму поперечного сечения элемента, пролет между опорами и способ опирания. Пролетом является расстояние между двумя опорами. К примеру, вы используете балки как опорные брусья перекрытия для несущих стен дома, между которыми 4 м, то величина пролета будет равна 4 м.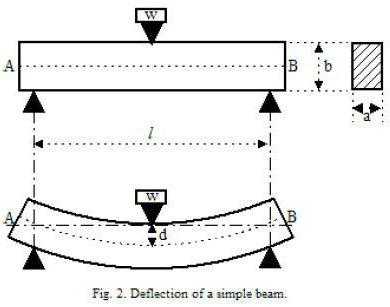

Вычисляя прогиб деревянной балки, их считают свободно опертыми элементами конструкции. В случае балки перекрытия для расчета принимается схема с нагрузкой, которая распределена равномерно. Обозначается она символом q. Если же нагрузка несет сосредоточенный характер, то берется схема с сосредоточенной нагрузкой, обозначаемой F. Величина этой нагрузки равна весу, который будет оказывать давление на конструкцию.

Момент инерции

Геометрическая характеристика, которая получила название момент инерции, важна при проведении расчетов на прогиб балки. Формула позволяет вычислить эту величину, мы приведем ее немного ниже.

При вычислении момента инерции нужно обращать внимание на то, что размер этой характеристики зависит от того, какова ориентация элемента в пространстве. При этом наблюдается обратно пропорциональная зависимость между моментом инерции и величиной прогиба. Чем меньше значение момента инерции, тем больше будет значение прогиба и наоборот. Эту зависимость достаточно легко отследить на практике. Каждый человек знает, что доска, положенная на ребро, прогибается гораздо меньше, чем аналогичная доска, находящаяся в нормальном положении.

Подсчет момента инерции для балки с прямоугольным сечением производится по формуле:

J=b*h^3/12, где:

b – ширина сечения;

h – высота сечения балки.

Вычисления максимального уровня нагрузки

Определение максимальной нагрузки на элемент конструкции производится с учетом целого ряда факторов и показателей. Обычно при вычислении уровня нагрузки берут во внимание вес 1 погонного метра балки, вес 1 квадратного метра перекрытия, нагрузку на перекрытие временного характера и нагрузку от перегородок на 1 квадратный метр перекрытия. Также учитывается расстояние между балками, измеренное в метрах. Для примера вычисления максимальной нагрузки на деревянную балку примем усредненные значения, согласно которым вес перекрытия составляет 60 кг/м², временная нагрузка на перекрытие равна 250 кг/м², перегородки будут весить 75 кг/м². Вес самой балки очень просто вычислить, зная ее объем и плотность. Предположим, что используется деревянная балка сечением 0,15х0,2 м. В этом случае ее вес будет составлять 18 кг/пог.м. Также для примера примем расстояние между брусьями перекрытия равным 600 мм. В этом случае нужный нам коэффициент составит 0,6.

В результате вычисления максимальной нагрузки получаем следующий результат: q=(60+250+75)*0,6+18=249 кг/м.

Когда значение получено, можно переходить к расчету максимального прогиба.

Вычисление значения максимального прогиба

Когда проводится расчет балки, формула отображает в себе все необходимые элементы. При этом стоит учитывать, что формула, используемая для расчетов, может иметь несколько иной вид, если расчет проводится для разных типов нагрузок, которые будут оказывать влияние на балку.

Сначала приведем вашему вниманию формулу, используемую для расчета максимального прогиба деревянной балки с распределенной нагрузкой.

f=-5*q*l^4/384*E*J.

Обратите внимание, что в данной формуле Е – это постоянная величина, которая получила название модуль упругости материала. Для древесины эта величина равна 100 000 кгс/ м².

Продолжив вычисления с нашими данными, использованными для примера, получим то, что для балки из древесины, сечение которой составляет 0,15х0,2 м, а длина равна 4 м, величина максимального прогиба при воздействии распределенной нагрузки равна 0,83 см.

Обращаем внимание, что когда производится расчет прогиба с учетом схемы с сосредоточенной нагрузкой, формула приобретает следующий вид:

f=-F*l^3/48*E*J, где:

F – сила давления на брус.

Также обращаем внимание на то, что значение модуля упругости, используемое в расчетах, может различаться для разных видов древесины. Влияние оказывают не только порода дерева, но и вид бруса. Поэтому цельная балка из дерева, клееный брус или оцилиндрованное бревно будут иметь разные модули упругости, а значит, и разные значения максимального прогиба.

Вы можете преследовать разные цели, совершая расчет балок на прогиб. Если вы хотите узнать пределы деформации элементов конструкции, то по завершении расчета стрелки прогиба вы можете остановиться. Если же ваша цель – установить уровень соответствия найденных показателей строительным нормам, то их нужно сравнить с данными, которые размещены в специальных документах нормативного характера.

Двутавровая балка

Обратите внимание на то, что балки из двутавра применяются несколько реже в силу их формы. Однако также не стоит забывать, что такой элемент конструкции выдерживает гораздо большие нагрузки, чем уголок или швеллер, альтернативой которых может стать двутавровая балка.

Расчет прогиба двутавровой балки стоит производить в том случае, если вы собираетесь использовать ее в качестве мощного элемента конструкции.

Также обращаем ваше внимание на то, что не для всех типов балок из двутавра можно производить расчет прогиба. В каких же случаях разрешено рассчитать прогиб двутавровой балки? Всего таких случаев 6, которые соответствуют шести типам двутавровых балок. Эти типы следующие:

• Балка однопролетного типа с равномерно распределенной нагрузкой.
• Консоль с жесткой заделкой на одном конце и равномерно распределенной нагрузкой.
• Балка из одного пролета с консолью с одной стороны, к которой прикладывается равномерно распределенная нагрузка.
• Однопролетная балка с шарнирным типом опирания с сосредоточенной силой.
• Однопролетная шарнирно опертая балка с двумя сосредоточенными силами.
• Консоль с жесткой заделкой и сосредоточенной силой.

Металлические балки

Расчет максимального прогиба одинаковый, будь это стальная балка или же элемент из другого материала. Главное — помнить о тех величинах, которые специфические и постоянные, как к примеру модуль упругости материала. При работе с металлическими балками, важно помнить, что они могут быть изготовлены из стали или же из двутавра. Прогиб металлической балки, изготовленной из стали, вычисляется с учетом, что константа Е в данном случае составляет 2·105Мпа. Все остальные элементы, вроде момента инерции, вычисляются по алгоритмам, описанным выше.

Расчет максимального прогиба для балки с двумя опорами

В качестве примера рассмотрим схему, в которой балка находится на двух опорах, а к ней прикладывается сосредоточенная сила в произвольной точке. До момента прикладывания силы балка представляла собой прямую линию, однако под воздействием силы изменила свой вид и вследствие деформации стала кривой.

Предположим, что плоскость ХУ является плоскостью симметрии балки на двух опорах. Все нагрузки действуют на балку в этой плоскости. В этом случае фактом будет то, что кривая, полученная в результате действия силы, также будет находиться в этой плоскости. Данная кривая получила название упругой линии балки или же линии прогибов балки. Алгебраически решить упругую линию балки и рассчитать прогиб балки, формула которого будет постоянной для балок с двумя опорами, можно следующим образом.

Прогиб на расстоянии z от левой опоры балки при 0 ≤ z ≤ a

F(z)=(P*a2*b2)/(6E*J*l)*(2*z/a+z/b-z3/a2*b)

Прогиб балки на двух опорах на расстоянии z от левой опоры при а ≤ z ≤l

f(z)=(-P*a2*b2)/(6E*J*l)*(2*(l-z)/b+(l-z)/a-(l-z)3/a+b2), где Р – прикладываемая сила, Е – модуль упругости материала, J – осевой момент инерции.

В случае балки с двумя опорами момент инерции вычисляется следующим образом:

J=b1h23/12, где b1 и h2 – значения ширины и высоты сечения используемой балки соответственно.

Заключение

В заключение можно сделать вывод о том, что самстоятельно вычислить величину максимального прогиба балки разных типов достаточно просто. Как было показано в этой статье, главное — знать некоторые характеристики, которые зависят от материала и его геометрических характеристик, а также провести вычисления по нескольким формулам, в которых каждый параметр имеет свое объяснение и не берется из ниоткуда.

2qm.ru