3)Эпюры продольных сил, поперечных сил, изгибающих моментов, крутящих моментов
Эпю́ра (фр. epure — чертёж) — особый вид графика, показывающий распределение величины нагрузки на объект. Например, для стержня продольнаяось симметрииберётся заобласть определения,и составляются эпюры для сил, напряжений и разных деформаций в зависимости отабсциссы.
Расчёт эпюр напряжения является базовой задачей такой дисциплины, как сопротивление материалов. В частности, только при помощи эпюры возможно определить максимально допустимую нагрузку на материал.
Построение эпюр продольных сил Nz
Продольная сила в сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня.
Правило знаков для Nz: условимся считать продольную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части стержня, вызывает растяжение и отрицательной — в противном случае.
Построение эпюр крутящих моментов Мкр.
Крутящий момент в сечении численно равен алгебраической сумме внешних моментов, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси Z.
Правило знаков для Мкр: условимся считать крутящий момент в сечении положительным, если при взгляде на сечение со стороны рассматриваемой отсеченной части внешний момент виден направленным против движения часовой стрелки и отрицательным — в противном случае.
Определение поперечных сил и изгибающих моментов — сечение 1
Отбросим правую часть балки и заменим ее действие на левую часть поперечной силой и изгибающим моментом . Для удобства вычисления закроем отбрасываемую правую часть балки листком бумаги, совмещая левый край листка с рассматриваемым сечением 1.
Поперечная сила в сечении 1 балки равна алгебраической сумме всех внешних сил, которые видим после закрытия
Видим только реакцию опоры, направленную вниз. Таким образом, поперечная сила равна:
кН.
Знак «минус» нами взят потому, что сила вращает видимую нами часть балки относительно первого сечения против хода часовой стрелки (или потому, что одинаково направлена с направлением поперечной силы по правилу знаков)
Изгибающий момент в сечении 1 балки, равен алгебраической сумме моментов всех усилий, которые мы видим после закрытия отброшенной части балки, относительно рассматриваемого сечения 1.
Видим
два усилия: реакцию опоры и
момент M. Однако у силы плечо
практически равно нулю. Поэтому изгибающий
момент равен: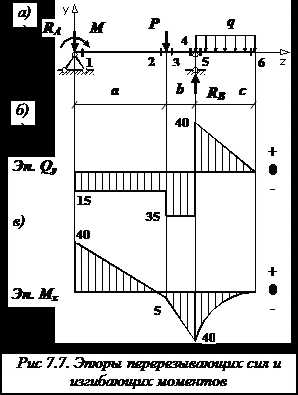
кН·м.
Здесь знак «плюс» нами взят потому, что внешний момент M изгибает видимую нами часть балки выпуклостью вниз. (или потому, что противоположно направлен направлению изгибающего момента по правилу знаков)
Определение поперечных сил и изгибающих моментов — сечение 2
В отличие от первого сечения, у силы реакциипоявилось плечо, равное а.
поперечная сила:
кН;
изгибающий момент:
кН·м.
Определение поперечных сил и изгибающих моментов — сечение 3
поперечная сила:
кН;
изгибающий момент:
кН ·м.
Определение поперечных сил и изгибающих моментов — сечение 4
Теперь удобнее закрывать листком левую часть балки.
поперечная сила:
кН;
изгибающий момент:
кН ·м.
Определение поперечных сил и изгибающих моментов — сечение 5
поперечная сила:
кН;
изгибающий момент:
кН ·м.
Определение поперечных сил и изгибающих моментов — сечение 1
поперечная сила и изгибающий момент:
.
По найденным значениям производим построение эпюры поперечных сил (рис. 7.7, б) и изгибающих моментов (рис. 7.7, в).
КОНТРОЛЬ ПРАВИЛЬНОСТИ ПОСТРОЕНИЯ ЭПЮР
Убедимся в правильности построения эпюр по внешним признакам, пользуясьправилами построения эпюр.
Проверка эпюры поперечных сил
Убеждаемся: под незагруженными участками эпюра поперечных сил идет параллельно оси балки, а под распределенной нагрузкой q – по наклоненной вниз прямой. На эпюре продольной силы три скачка: под реакцией – вниз на 15 кН, под силой P – вниз на 20 кН и под реакцией – вверх на 75 кН.
Проверка эпюры изгибающих моментов
На эпюре изгибающих моментов видим изломы под сосредоточенной силой P и под опорными реакциями. Углы изломов направлены навстречу этим силам. Под распределенной нагрузкой q эпюра изгибающих моментов изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. В сечении 6 на эпюре изгибающего момента – экстремум, поскольку эпюра поперечной силы в этом месте проходит через нулевое значение.
4) Стержень, балка, вал, брус, пластина, плита, оболочка
Основными расчетными типовыми элементами на которые делится целая конструкция, являются стержень, брус, оболочка, пластина, массивное тело, балка, ферма.
Стержень — тело, длина которого существенно превышает характерные размеры поперечного сечения.
Брус — это тот же стержень.
Балка — стержень или брус, работающий на изгиб.
Пластина — тело, у которого толщина существенно меньше двух других размеров.
Оболочка — тело, ограниченное криволинейными поверхностями (искривленная пластина).
Массивное тело — элемент конструкции с размерами одного и того же порядка.
Ферма — стержневая конструкция, работающая только на растяжение или сжатие.
Остальное см.конспект.
studfiles.net
2.1. Эпюры сил и моментов. Правила, применяемые при построении эпюр
Кисляков Н.И.Прикладная механика Л.3-4. 1101.03.17Лекция 3-4
Тема.2 Расчеты механизмов на прочность и жесткость
2.1. Эпюры сил и моментов. Правила, применяемые при построении эпюр
2.2. Продольные силы. Эпюры продольных сил
2.3. Крутящие моменты. Эпюры крутящих моментов
2.4. Балки и опоры. Реакции и их вычисление
2.5. Изгиб. Поперечные силы и моменты в сечениях при изгибе
2.6. Построение эпюр Q и M для балок
2.7. Дифференциальные зависимости при изгибе
Тема.2 Расчеты механизмов на прочность и жесткость
Усилия и моменты в разных сечениях одного и того же стержня различны.
Графики (диаграммы), показывающие, как изменяются внутренние усилия при переходе от сечения к сечению, называют эпюрами.
Правила, применяемые при построении эпюр:
1. Ось (базу), на которой строится эпюра, всегда выбирают так, чтобы она была параллельна или просто совпадала с осью стержня.
2. Ординаты эпюры откладывают от оси эпюры по перпендикуляру.
3. Штриховать эпюры принято линиями, перпендикулярными к базе.
4. Для усилий и моментов выбирают некоторый масштаб. Ординаты откладывают строго в масштабе. Кроме того, на эпюрах проставляют числа, показывающие величины характерных ординат, а в поле эпюры в кружочке ставят знак усилия.
2.2. Продольные силы. Эпюры продольных сил
Продольная (осевая) сила считается положительной, если она вызывает растяжение, и отрицательной, если вызывает сжатие. Внешние силы сами по себе ни положительны, ни отрицательны, но каждая дает в выражении для N слагаемое определенного знака.
В качестве примера построения эпюр осевых сил рассмотрим стержень (рис. 1), нагруженный в точках А, В и С сосредоточенными силами Р1 Р2, Р3, направленными вдоль оси.
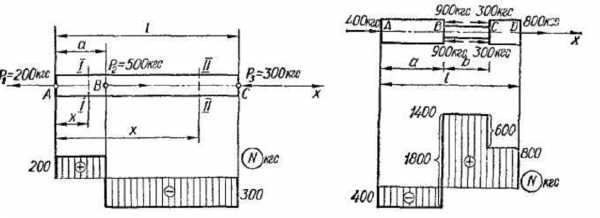
Рис 1 рис 2
Приступая к построению эпюры, стержень разбивают на участки.
Участком называют часть стержня между точками приложения сосредоточенных сил. Если на стержень действует распределенная нагрузка, участком называют часть стержня, в пределах которого распределенная нагрузка изменяется по одному закону. В рассматриваемом примере два участка — 1(АВ) и 2 (ВС).
Чтобы построить эпюры, нужно составить выражения для осевых сил в произвольном сечении каждого участка.
Продольная сила в сечении равна алгебраической сумме проекций на ось бруса сил, взятых по одну сторону от сечения!
Выберем начало координат в крайней левой точке стержня; ось х направим вдоль его оси. В произвольном сечении любого участка на расстоянии х от начала координат находим осевую силу как сумму проекций всех внешних сил, расположенных слева или справа от рассматриваемого сечения:
1
участок
(0  х < а) слева: N
(х)=
х < а) слева: N
(х)=  = 2000н; справа: N (х)=
= 2000н; справа: N (х)=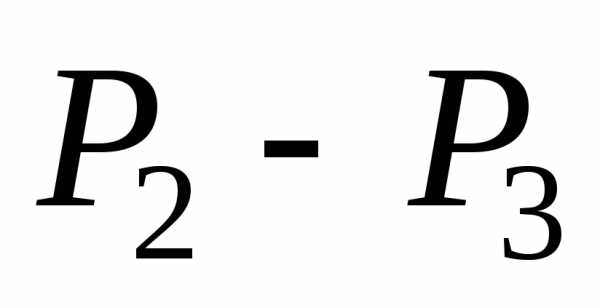 = (5000
— 3000) н = 2000 н.
= (5000
— 3000) н = 2000 н.
2
участок (а < х  l)
слева: N(х) =
l)
слева: N(х) =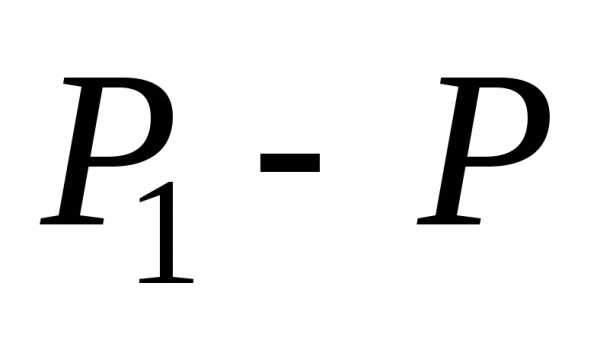 = (2000
— 5000) н = -3000н; справа: N
(х) = —P3 = -3000н.
= (2000
— 5000) н = -3000н; справа: N
(х) = —P3 = -3000н.
Поскольку эти величины не зависят от абсцисс сечения, то во всех сечениях первого участка продольная сила N — 2000 н, а для любого сечения второго участка она равна — 3000 н. Откладывая полученные ординаты от оси эпюры, строим эпюру N. Заметим, что штриховка эпюры показывает откладываемые ординаты. В сечениях А, В и С на эпюре получились скачки, равные соответственно 2000, 5000 и 3000 н, т. е. как раз тем силам, которые приложены к стержню в этих сечениях.
Если на стержень действуют только сосредоточенные силы, то линии эпюры параллельны ее оси (эпюра N состоит из прямоугольников и имеет скачки в тех сечениях, где приложены внешние силы). Так, нетрудно убедиться, что для стержня, изображенного на рис. 2, эпюра будет иметь такой вид, как показано на рисунке.
Если стержень расположен вертикально и учитывается его собственный вес, то линия эпюры наклонена к оси (для цилиндрического стержня) или криволинейна (для стержня с непрерывно меняющимися размерами сечения).
studfiles.net
Построение эпюр продольных сил — МегаЛекции
Рассмотрим порядок построения эпюр продольных сил в стержне, работающем на растяжение – сжатие (рис. 3.14).
1. В соответствии с общим алгоритмом построения эпюр прежде всего определяем все внешние силовые факторы, действующие на рассматриваемый стержень (рис. 3.14а). Активные силы заданы. Определим реакции связей. В рассматриваемом примере связью является заделка. В заделке при плоской системе сил в общем случае возникают три реакции – две силы и момент. Однако в данном примере активные силы приложены на оси стержня и действуют вдоль оси, представляющей прямую линию. Равнодействующая активных сил направлена вдоль этой прямой и может быть уравновешена силой, действующей также вдоль этой прямой. Таким образом, возникает только одна реакция, направленная вдоль оси стержня. Выбираем систему координат YOZ, изображаем реакцию связи , и так как направление ее неизвестно, предварительно направляем ее слева направо. Величину и истинное направление реакции определяем из уравнения статики (рис. 3.14а):
ΣFZ = 0; – P3 – P2 + P1 = – 7 – 3 + 5 = 0; = 5 кН.
Если при решении уравнения результат получают со знаком «минус», то направление реакции изменяют на обратное (влево от т. А).
2. Так как в рассматриваемом примере все силы приложены на оси и действуют вдоль нее, то уточнять расчетную схему не следует.
3. Разбиваем стержни на участки, проводя вертикальные линии через точки приложения сосредоточенных сил. Получаем три участка АВ, ВС и СD.
4. На каждом участке методом сечений определяем внутренние силовые факторы.
Рассмотрим участок АВ. Рассечем стержень на две части поперечным сечением на расстоянии z от начала координат (от т. А) и правую часть отбросим (рис. 3.14б). Абсцисса z в пределах участка АВ изменяется от 0 до 1 м, т.е. 0 ≤ z ≤ 1. На рассматриваемую часть стержня действует только внешняя сила , направленная вдоль оси стержня. Эта сила может быть уравновешена силой, также действующей вдоль оси стержня, т.е. продольной силой N. Прикладываем в рассматриваемом сечении продольную силу N. Так как направление силы N неизвестно (от сечения или на сечение), то направляем ее вдоль оси произвольно, например, от сечения. Записываем уравнение статики (составляем условие равновесия) для рассматриваемой части стержня:
ΣFZ = 0; + N = 5 + N = 0; N = — 5 кН.
Знак «минус» означает, что сила N должна действовать на сечение. Так как сила N не зависит от абсциссы z, то продольная сила по длине участка АВ не изменяется.
5. Выбираем ось отсчета в виде линии, параллельной оси стержня. При построении эпюры продольных сил принимают следующее правило знаков:
Продольную силу N считают положительной, если имеет место растяжение (N направлена от сечения) и отрицательной, если сжатие (N направлена на сечение).
При горизонтальном расположении оси отсчета положительные значения продольной силы откладывают вверх, отрицательные – вниз. Так как на участке АВ сила N действует на сечение, т.е. имеет место сжатие, то график изменения N на участке АВ представляет собой прямую, параллельную оси отсчета в отрицательной области значений (рис. 1д).
Рассмотрим участок ВС (рис. 3.14в, сеч. II-II). Абсцисса z при начале координат в т. А будет изменяться от 1 м до 1,5 м. Рассуждая так же, как и в предыдущем случае, убеждаемся, что в сечении II-II действует только продольная сила N. Записываем уравнение статики для рассматриваемой части стержня:
ΣFZ = 0; – P3 + N = 5 – 7 + N = 0; N = 7 – 5 = 2 кН.
Эпюра продольной силы на участке ВС представляет собой прямую, параллельную оси отсчета в положительной области значений (рис. 3.14д).
Аналогично можно найти продольную силу и на участке СD.
| =5 кН |
| =5 кН |
| =5 кН |
Рис. 3.14. Построение эпюр нормальных сил
Из эпюры продольных сил следует (рис. 3.14д), что в точках А, В, С и D значения продольной силы изменились скачком на величину сосредоточенных сил в этих точках. Эта закономерность справедлива при действии любой сосредоточенной силы и значительно облегчает построение эпюр продольных сил для стержней, нагруженных сосредоточенными силами.
Так, для рассмотренного примера можно было бы поступить следующим образом.
Рассмотрим стержень, начиная с т. А (слева направо). В т. А в соответствии с отмеченной закономерностью должен быть скачок на величину . Сила в сечении I-I (рис. 3.14а) может быть уравновешена внутренней силой N, равной по модулю и направленной на сечение, т.е. имеет место сжатие и ординату откладываем вниз от оси отсчета (скачок направлен вниз). Если выбрать другое сечение в пределах участка АВ, то результат не изменится. Таким образом, на участке АВ имеем:
NАВ = — = — 5 кН.
График представляет собой прямую, параллельную оси отсчета.
В т. В должен быть скачок на величину силы P3. Так как сила P3 направлена в сторону, противоположную силе , то скачок направлен вверх и продольная сила на участке ВС равна:
NВС = NАВ + 7 = -5 + 7 = 2 кН.
Учитывая скачок в т. С, для участка CD получаем:
NCD = NВС + 3 = 2 + 3 = 5 кН.
Если учесть скачок в точке D от силы P1, то находим:
NCD — P1 = 5 – 5 = 0,
что и должно быть, т.к. ΣFZ = 0.
В заключении отметим основные закономерности:
1. В поперечных сечениях прямого стержня, нагруженного силами, приложенными на оси стержня и направленными вдоль оси, возникает только один внутренний силовой фактор – продольная сила N, т.е. имеет место растяжение или сжатие.
2. В сечениях, где приложены сосредоточенные силы, действующие вдоль оси стержня, на эпюре продольных сил имеет место скачок на величину этих сил.
3. Форма и размеры поперечных сечений не влияют на величину продольных сил.
4. Продольная сила в рассматриваемом сечении равна алгебраической сумме проекций на продольную ось всех сил, действующих на рассматриваемую часть стержня. Проекцию любой силы берут со знаком «плюс», если соответствующая ей внутренняя продольная сила направлена от сечения, и «минус» — если на сечение.
Замечание: Это правило справедливо для любой системы внешних сил. В случае криволинейных стержней силы проектируют на ось, перпендикулярную рассматриваемому сечению.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Построение эпюры внутренних сил для стержня с продольно распределенной нагрузкой
Задача
Рассчитать значения внутренних продольных сил N и построить их эпюру для стержня к которому приложены сосредоточенная сила и продольная равномерно распределенная нагрузка
для дальнейшего расчета на прочность.
Пример решения
Предыдущий пункт решения задачи:
Рассматриваемый стержень имеет два силовых участка, обозначим их цифрами I и II.
Для расчета внутренних сил на них воспользуемся методом сечений.
Начнем с первого силового участка BC.
Мысленно рассекаем участок в произвольном месте между сечениями B и C.
Выбираем для рассмотрения левую часть стержня, так как к ней приложено меньшее количество нагрузок.
Внутренняя сила на I силовом участке равна сумме внешних сил (с учетом правила знаков при растяжении-сжатии) приложенных к рассматриваемой отсеченной части стержня:
Так как на данном участке нет распределенной нагрузки, полученное значение NI будет одинаковым для всех сечений первого участка.
Переходим на второй силовой участок CD.
Проведя сечение,
рассматриваем правую часть стержня.
На данном участке есть распределенная нагрузка поэтому необходимо показать расстояние от границы участка до рассматриваемого сечения обозначив его переменной z2.
Интервал возможных значений переменной z2 лежит в пределах от 0 до 50см, т.е. 0 ≤ z2 ≤ 0,5м.
Выражение для расчета NII
В полученном выражении переменная z2 в первой степени, следовательно, зависимость линейная.
Рассчитаем значения внутренней силы NII на границах участка при z2=0 и z2=0,5м.
По полученным данным строим эпюру N.
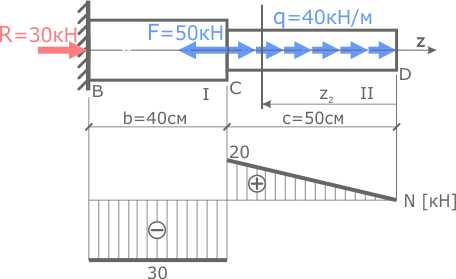
На I участке в соответствии с выбранным масштабом откладываем вниз от базовой линии значение 30 кН и проводим горизонтальную линию в пределах участка.
На II участке было получено 2 значения. Переменная z2 откладывалась от правой границы участка (сечения D) поэтому под сечением D где z2=0 ставим точку на базовой линии.
Под сечением C где z2=0,5м откладываем значение 20кН.
Полученные точки соединяем прямой линией, проставляем знаки, заштриховываем и проверяем построенную эпюру.
Другие примеры решения задач >
isopromat.ru
Построение эпюр продольных сил — Мегаобучалка
Рассмотрим порядок построения эпюр продольных сил в стержне, работающем на растяжение – сжатие (рис. 3.14).
1. В соответствии с общим алгоритмом построения эпюр прежде всего определяем все внешние силовые факторы, действующие на рассматриваемый стержень (рис. 3.14а). Активные силы заданы. Определим реакции связей. В рассматриваемом примере связью является заделка. В заделке при плоской системе сил в общем случае возникают три реакции – две силы и момент. Однако в данном примере активные силы приложены на оси стержня и действуют вдоль оси, представляющей прямую линию. Равнодействующая активных сил направлена вдоль этой прямой и может быть уравновешена силой, действующей также вдоль этой прямой. Таким образом, возникает только одна реакция, направленная вдоль оси стержня. Выбираем систему координат YOZ, изображаем реакцию связи , и так как направление ее неизвестно, предварительно направляем ее слева направо. Величину и истинное направление реакции определяем из уравнения статики (рис. 3.14а):
ΣFZ = 0; – P3 – P2 + P1 = – 7 – 3 + 5 = 0; = 5 кН.
Если при решении уравнения результат получают со знаком «минус», то направление реакции изменяют на обратное (влево от т. А).
2. Так как в рассматриваемом примере все силы приложены на оси и действуют вдоль нее, то уточнять расчетную схему не следует.
3. Разбиваем стержни на участки, проводя вертикальные линии через точки приложения сосредоточенных сил. Получаем три участка АВ, ВС и СD.
4. На каждом участке методом сечений определяем внутренние силовые факторы.
Рассмотрим участок АВ. Рассечем стержень на две части поперечным сечением на расстоянии z от начала координат (от т. А) и правую часть отбросим (рис. 3.14б). Абсцисса z в пределах участка АВ изменяется от 0 до 1 м, т.е. 0 ≤ z ≤ 1. На рассматриваемую часть стержня действует только внешняя сила , направленная вдоль оси стержня. Эта сила может быть уравновешена силой, также действующей вдоль оси стержня, т.е. продольной силой N. Прикладываем в рассматриваемом сечении продольную силу N. Так как направление силы N неизвестно (от сечения или на сечение), то направляем ее вдоль оси произвольно, например, от сечения. Записываем уравнение статики (составляем условие равновесия) для рассматриваемой части стержня:
ΣFZ = 0; + N = 5 + N = 0; N = — 5 кН.
Знак «минус» означает, что сила N должна действовать на сечение. Так как сила N не зависит от абсциссы z, то продольная сила по длине участка АВ не изменяется.
5. Выбираем ось отсчета в виде линии, параллельной оси стержня. При построении эпюры продольных сил принимают следующее правило знаков:
Продольную силу N считают положительной, если имеет место растяжение (N направлена от сечения) и отрицательной, если сжатие (N направлена на сечение).
При горизонтальном расположении оси отсчета положительные значения продольной силы откладывают вверх, отрицательные – вниз. Так как на участке АВ сила N действует на сечение, т.е. имеет место сжатие, то график изменения N на участке АВ представляет собой прямую, параллельную оси отсчета в отрицательной области значений (рис. 1д).
Рассмотрим участок ВС (рис. 3.14в, сеч. II-II). Абсцисса z при начале координат в т. А будет изменяться от 1 м до 1,5 м. Рассуждая так же, как и в предыдущем случае, убеждаемся, что в сечении II-II действует только продольная сила N. Записываем уравнение статики для рассматриваемой части стержня:
ΣFZ = 0; – P3 + N = 5 – 7 + N = 0; N = 7 – 5 = 2 кН.
Эпюра продольной силы на участке ВС представляет собой прямую, параллельную оси отсчета в положительной области значений (рис. 3.14д).
Аналогично можно найти продольную силу и на участке СD.
| =5 кН |
| =5 кН |
| =5 кН |
Рис. 3.14. Построение эпюр нормальных сил
Из эпюры продольных сил следует (рис. 3.14д), что в точках А, В, С и D значения продольной силы изменились скачком на величину сосредоточенных сил в этих точках. Эта закономерность справедлива при действии любой сосредоточенной силы и значительно облегчает построение эпюр продольных сил для стержней, нагруженных сосредоточенными силами.
Так, для рассмотренного примера можно было бы поступить следующим образом.
Рассмотрим стержень, начиная с т. А (слева направо). В т. А в соответствии с отмеченной закономерностью должен быть скачок на величину . Сила в сечении I-I (рис. 3.14а) может быть уравновешена внутренней силой N, равной по модулю и направленной на сечение, т.е. имеет место сжатие и ординату откладываем вниз от оси отсчета (скачок направлен вниз). Если выбрать другое сечение в пределах участка АВ, то результат не изменится. Таким образом, на участке АВ имеем:
NАВ = — = — 5 кН.
График представляет собой прямую, параллельную оси отсчета.
В т. В должен быть скачок на величину силы P3. Так как сила P3 направлена в сторону, противоположную силе , то скачок направлен вверх и продольная сила на участке ВС равна:
NВС = NАВ + 7 = -5 + 7 = 2 кН.
Учитывая скачок в т. С, для участка CD получаем:
NCD = NВС + 3 = 2 + 3 = 5 кН.
Если учесть скачок в точке D от силы P1, то находим:
NCD — P1 = 5 – 5 = 0,
что и должно быть, т.к. ΣFZ = 0.
В заключении отметим основные закономерности:
1. В поперечных сечениях прямого стержня, нагруженного силами, приложенными на оси стержня и направленными вдоль оси, возникает только один внутренний силовой фактор – продольная сила N, т.е. имеет место растяжение или сжатие.
2. В сечениях, где приложены сосредоточенные силы, действующие вдоль оси стержня, на эпюре продольных сил имеет место скачок на величину этих сил.
3. Форма и размеры поперечных сечений не влияют на величину продольных сил.
4. Продольная сила в рассматриваемом сечении равна алгебраической сумме проекций на продольную ось всех сил, действующих на рассматриваемую часть стержня. Проекцию любой силы берут со знаком «плюс», если соответствующая ей внутренняя продольная сила направлена от сечения, и «минус» — если на сечение.
Замечание: Это правило справедливо для любой системы внешних сил. В случае криволинейных стержней силы проектируют на ось, перпендикулярную рассматриваемому сечению.
megaobuchalka.ru
Тема 9. Растяжение и сжатие. Продольные силы и их эпюры. Закон Гука — Мегаобучалка
Растяжением или сжатием называется такой вид деформаций, при котором в любом поперечном сечений бруса возникают только продольная сила . Брусья с примолинейной осью называют стержнями (рис.1).
Рис. 35.
Примой брус постоянного поперечного сечения , длиной , жестко защемленный одним концом и нагруженный на другом конце растягивающей силой F (рис.35). Под действием этой силы, брус удлинится на некоторою величину которую назовем абсолютным удлинением. Отношение абсолютного удлинения к первоначальной длине назовем относительным удлинением и обозначим .
При расчете, мы будем считать, что растяжение и сжатие бруса связано только с приложенными внешними силами, то есть учитываем только напряжения, действующие на стержень, температуру и время действий сил не будем учитывать.
При растяжении и сжатии продольные силы определяется методом сечении. Правило знаков будем определять следующим образом: растягивающие, то есть, направленные от сечения, продольные силы будем считать положительными, сжимающие, то есть направленные к сечению, будем считать отрицательными.
Для наглядного изображения распределения вдоль оси бруса продольных сил и нормальных напряжений строят графики, называемые эпюрами, причем для нормальных напряжений применяется то же правило знаков, что и для продольных сил.
При растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению и вычисляемые по формуле:
площать поперечного сечения бруса,
Очевидно, что при растяжении и сжатии форма сечения на напряжения не влияет.
Условие прочности бруса при растяжении и сжатии определяется следующим образом:
Здесь называют допускаемым напряжением, максимальная продольная сила.
Напряжения и деформаций при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука, по имени установившего этот закон английского физика Гоберта Гука. Закон Гука при растяжении и сжатии справедлив лишь в определенных пределах нагружения и формируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению бруса.
Математически закон Гука можно вписать в виде равенства:
Коэффициент пропорциональности Е характеризует жесткость материала и называется модулем продольной упругости. Модуль упругости и напряжения выражаются в одинаковых единицах.
Если в формулу закона Гука поставим выражения и то получим:
Контрольные вопросы
1. Что такое растяжение-сжатие?
____
2. По какому методу определяется нормальные силы?
__
3. По какой формуле определяется относительное удлинение или укорочение?
____
4. Какое напряжение появляется при растяжении-сжатии, и по какой формуле определяется?
____
5. Как пишется условие прочности при растяжении-сжатии?
____
6. Что такое модуль упругости, и в чем измеряется?
____
7. От чего зависит модуль упругости?
__
8. По какой формуле определяется абсолютное удлинение или укорочение бруса при растяжении-сжатии?
____
Пример 4.1.
Для данного ступенчатого бруса (рис.36.) построить эпюру продольных сил, эпюру нормальных напряжений и определить перемещение свободного конца, если .
Рис.36.
1. Разбиваем брус на участки как показоно на рис. 37а.
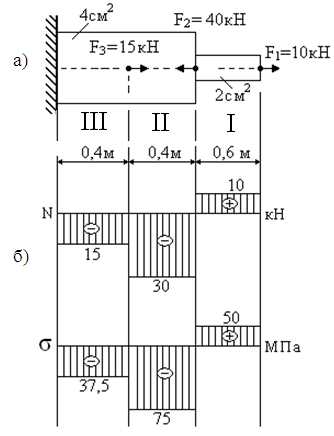
Рис.37.
2. По методу сечения определяем ординаты эпюр и каждого сечения.
4. Строим эпюру (рис. 37б.)
5. Определяем перемещение свободного конца бруса.
Пример 4.2.
Для данного ступенчатого бруса (рис.38.) построить эпюру продольных сил, эпюру нормальных напряжений и определить перемещение свободного конца, если .
Рис. 38.
1. Разбиваем брус на участки как показоно на рис. 39а.
2. По методу сечения определяем ординаты эпюр и каждого сечения.
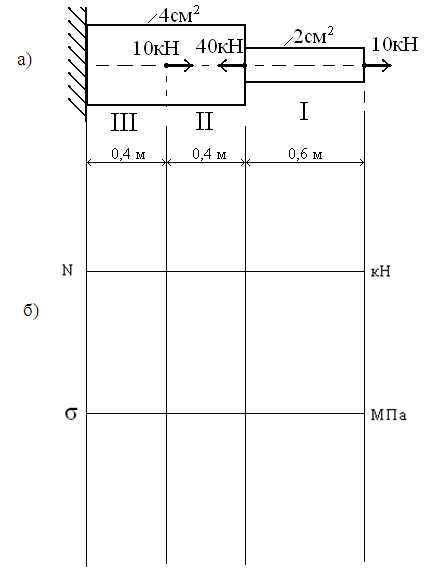
Рис. 39.
3. Строим эпюру (рис. 37б.)
4. Определяем перемещение свободного конца бруса.
Для решения первой задачи контрольной работы 2 следует выполнить следующие действия:
1) Изучить темы 7,8,9.
2) Ответить на контрольные вопросы по темам 7,8,9.
2) Выполнить самостоятельно пример 2.2.
Данные для своего варианта первой задачи контрольной работы 2 посмотрите в таблице 4. Расчетную схему надо посмотреть в рис.40.
Таблица 4 (для первой задачи контрольной работы 2)
| Номер варианта | Номер схемы на рис. 40. | |||||
| кН | ||||||
| I | 3,6 | 1,4 | ||||
| II | 2,4 | 1,1 | ||||
| III | 3,5 | 2,5 | ||||
| IV | 2,9 | 1,4 | ||||
| V | 1,9 | 1,1 | ||||
| VI | 3,7 | 2,3 | ||||
| VII | 4,4 | 2,6 | ||||
| VIII | 4,6 | 3,1 | ||||
| IX | 4,2 | 3,2 | ||||
| X | 3,1 | 1,5 | ||||
| I | 3,6 | 2,4 | ||||
| III | 3,5 | 2,5 | ||||
| V | 2,8 | 1,2 | ||||
| VII | 3,0 | 2,2 | ||||
| II | 2,8 | 1,4 | ||||
| IV | 2,4 | 1,2 | ||||
| VI | 3,6 | 2,6 | ||||
| IX | 2,1 | 1,0 | ||||
| VIII | 2,6 | 1,3 | ||||
| X | 3,8 | 1,6 | ||||
| V | 1,4 | 3,2 | 1,8 | |||
| III | 3,4 | 1,5 | ||||
| VII | 2,3 | 2,9 | 1,9 | |||
| VIII | 3,6 | 1,7 | ||||
| II | 2,9 | 1,6 | ||||
| I | 3,4 | 2,1 | ||||
| III | 3,5 | 2,4 | ||||
| V | 3,6 | 2,3 | ||||
| VII | 3,2 | 2,2 | ||||
| II | 3,6 | 2,6 |
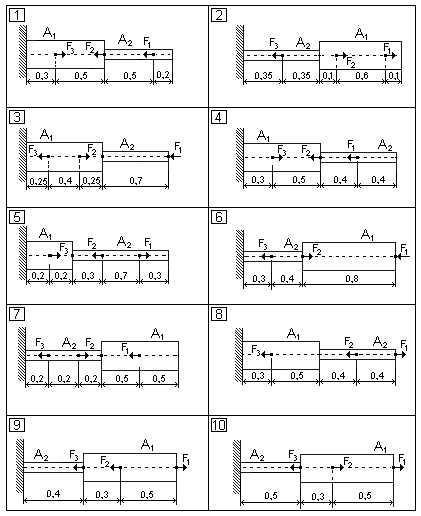
Рис. 40.
megaobuchalka.ru
Растяжением – сжатием называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила N. Прямые брусья, работающие на растяжение – сжатие, называются стержнями. Продольной силой называется равнодействующая всех внутренних нормальных сил, возникающих в этом сечении. Продольная сила в любом напряженном сечении бруса определяется методом сечений: она равна алгебраической сумме проекций всех внешних сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось. Если продольная сила по всей длине бруса не постоянна, то строят эпюру «N». Эпюра – это график изменения внутреннего силового фактора по длине бруса.
Правила построения эпюр нормальных напряжений:
N А
При растяжении длина детали увеличивается, а сечение уменьшается; при сжатии – наоборот. ∆l = l – l0 — абсолютное удлинение. относительное удлинение или продольная деформация. l0 Е – модуль упругости первого рода, характеризует жесткость материала. Nl ∆l = ——- EA Алгоритм решения задач на построение эпюр продольных сил и нормальных напряжений, расчет абсолютного удлинения стержня
N = —— A
Анализ наиболее часто встречающихся ошибок. Методические рекомендации по их устранению |
topuch.ru