продольных сил, нормальных напряжений и перемещений для ступенчатого стержня (бруса)
Приветствую, друзья! Сегодня дебютирует наш курс – «сопромат для чайников», Вы находитесь на сайте проекта SoproMats, который связан с сопроматом и не только. На этой страничке будет выложен первый урок из заявленного экспресс курса, который связан с таким простейшим видом деформации как растяжение (сжатие). В частности, будем учиться строить эпюры для бруса (стержня), который загружен растягивающей и сжимающей силой. Как правило, такое домашнее задание, одним из первых, дают всем студентам, которые начинают знакомиться с сопроматом. После изучения материалов данного урока вы научитесь строить следующие эпюры: продольных сил, нормальных напряжений, относительных деформаций и осевых перемещений поперечных сечений. Не пугайтесь мудреных названий, на самом деле все эти эпюры строятся очень просто. Что же давайте приступим к изучению!
Построение эпюры продольных сил
Так как это курс для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику. Если вы хотите более детально изучить рассматриваемые здесь вопросы, то могу предложить Вам другие материалы нашего сайта. Например, что касается данного блока статьи, то у нас есть материалы про продольную силу, где представлено полное досье на данный внутренний силовой фактор: что эта за сила, зачем нужна и т.д. Также есть отдельная статья по построению этой эпюры продольных сил, где я более подробно рассказываю о методике ее расчета и построения, а если точнее, то там рассмотрено целых 3 инструкции. Но если Вам некогда залазить в эти дебри, и хотите по-быстрому освоить продольную силу, то оставайтесь здесь, сейчас покажу как строится первая эпюра!
Кстати, вот объект нашего сегодняшнего исследования:
Чтобы построить эпюру продольных сил, нужно разбить наш брус на несколько участков, на которых эта эпюра будет иметь постоянное значение. Конкретно, для продольной эпюры, границами участков служат те точки, где прикладываются силы. То бишь, для нашего примера, нужно рассмотреть всего 2 участка:
Важно! На эпюру продольных сил, никак не влияет форма бруса, в отличие от других эпюр, которые будем дальше рассчитывать и строить.
На первом участке сила F1растягивает брус на величину 5кН, поэтому на этом участке, продольная сила будет положительной и равной:
Откладываем это значение на графике. Эпюры в сопромате, принято штриховать перпендикулярно нулевой линии, а также для продольных сил, на эпюрах проставляются знаки:
На втором же участке, сила F2 сжимает брус, тем самым в уравнение продольных сил, она пойдет с минусом:
Откладываем полученное значение на эпюре:
Вот так, достаточно просто, строится эта эпюра!
Построение эпюры нормальных напряжений
Переходим к эпюре нормальных напряжений. В отличие от продольных сил, нормальные напряжения зависят от формы бурса, а если точнее, то от площади его поперечных сечений и вычисляются они, по следующей формуле:
То бишь, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на его площадь.
Для того, чтобы построить эпюру нормальных напряжений, нужно рассчитать ее для любого сечения, каждого участка. В отличие, от продольной силы, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашего подопытного бруса, нужно наметить три участка и вычислить напряжение, соответственно, 3 раза:
Зададим брусу на первом участке (I) площадь поперечного сечения A1=2 см2, а вторая ступень бруса, допустим, будет иметь площадь A2=4 см2 (II, III участки). В вашей домашней задаче, эти величины будут даны по условию. Также в задачах, часто, просят определить эти площади из условия прочности, с учетом допустимого напряжения, обязательно сделаю статью про это.
Вычисляем напряжения на каждом участке:
По полученным значениям строим эпюру нормальных напряжений:
Построение эпюры перемещений
Самое время перейти к последней эпюре, которая называется эпюрой осевых перемещений поперечных сечений. Для краткости, ее еще называют просто эпюрой перемещений. Для расчета данного графика, пользуются следующей формулой:
Эта формула, является следствием закона Гука. Также ее можно записать как:
Сейчас покажу как ею пользоваться. Все характерные сечения бруса назовем буквами английского алфавита, чтобы потом в решении, было удобно ссылаться на них:
Традиционно расчет перемещений начинают с жестко защемленного торца. Так как сечение в заделке, не имеет возможности перемещаться, то и в решение записываем, что перемещение этого сечения равно нулю:
Далее, для построения эпюры нужно вычислить перемещения в характерных сечениях, которые находятся на границах участков (B, C и D). Этого будет достаточно, так как в пределах участков, эпюра будет меняться по линейному закону. Исключениями могут быть участки, на которых действует распределенная нагрузка, но это тема отдельной статьи.
Приступаем к расчету перемещения сечения B. По формуле, оно будет равно площади эпюры σ, на третьем участке, деленной на модуль упругости — E. При этом, обязательно, учитываем знак эпюры:
Для других сечений, перемещения будут вычисляться аналогичным образом:
ВАЖНО! Вы, наверное, заметили, что для каждого последующего сечения, в расчетах учитывается перемещение предыдущего. Это обязательно необходимо делать.
По полученным значениям, откладываем эпюру перемещений:
Вот так, достаточно просто можно построить эпюры для бруса, работающего на растяжение (сжатие). В рамках статьи, была рассмотрена достаточно простая расчетная схема, если Вы хотите развить свои навыки по построению эпюр, то приглашаю Вас на страничку про различные эпюры, где можно найти примеры расчета более сложных брусьев с распределенными нагрузками, где о каждой эпюре подготовлена отдельная статья.
Если Вам понравилась статья, расскажите о ней своим друзьям, подписывайтесь на наши социальные сети, где публикуется информация о новых статьях проекта. Также, там можно задать любой интересующий Вас вопрос о сопромате и не только.
sopromats.ru
Как строить эпюры
Растяжением – сжатием называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила N.
Прямые брусья, работающие на растяжение – сжатие, называются
Продольной силой называется равнодействующая всех внутренних нормальных сил, возникающих в этом сечении.
Продольная сила в любом напряженном сечении бруса определяется методом сечений: она равна алгебраической сумме проекций всех внешних сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось.
Если продольная сила по всей длине бруса не постоянна, то строят эпюру «N». Эпюра – это график изменения внутреннего силового фактора по длине бруса.
Правила построения эпюр продольных сил:
Разбиваем брус на участки, границами которых являются сечения, где приложены внешние силы.
В пределах каждого участка применяют метод сечений и определяют продольную силу. При этом если внешняя сила растягивает оставленную часть стержня, т.е. направлена от сечения — продольная сила положительна; если внешняя сила сжимает оставленную часть стержня, т.е. направлена к сечению – продольная сила отрицательна.
Откладываем полученные значения и строим эпюру продольных сил. Если на участке не действует равномерно распределенная нагрузка, то эпюра ограничена прямой, параллельной нулевой линии.
Правильность построения эпюр продольных сил определяется следующим образом: в сечениях, где приложена внешняя сила, на эпюре есть «скачки», равные по величине приложенной силе.
Правила построения эпюр нормальных напряжений:
Разбиваем брус на участки, границами которых являются точки приложения внешних сил и сечения, где меняется площадь.
На каждом участке вычисляем нормальные напряжения по формуле
N
А
Строим эпюру нормальных напряжений, по которой определяем опасное сечение. При растяжении – сжатии опасным является сечение, в котором величина нормальных напряжений наибольшая.
При растяжении длина детали увеличивается, а сечение уменьшается; при сжатии – наоборот.
∆l = l – l0 — абсолютное удлинение.
∆l
относительное удлинение или продольная деформация.
l0
Закон Гука при растяжении – сжатии:
Е – модуль упругости первого рода, характеризует жесткость материала.
Величина абсолютного удлинения вычисляется по формуле Гука:
Nl
∆l = ——-
EA
Алгоритм решения задач на построение эпюр продольных сил и
нормальных напряжений, расчет абсолютного удлинения стержня
Разбить нулевую линию на участки для построения эпюры продольных сил. Границы участков провести в сечениях, где приложены внешние силы.
- На каждом участке вычислить продольную силу методом сечений.
Отложить полученные значения и построить эпюру продольных сил. Правильность контролируется так: в сечениях, где к стержню приложены внешние силы, на эпюре продольных сил есть «скачки», численно равные этим силам.
Разбить нулевую линию на участки для построения эпюры нормальных напряжений. Границами участков являются сечения, в которых меняется площадь и приложены внешние силы.
На каждом участке вычислить нормальное напряжение по формуле
N
= ——
A
Отложить полученные значения и построить эпюру нормальных напряжений. По эпюре определить опасное сечение детали. Опасными являются сечения участка, на котором нормальные напряжения наибольшие.
Для каждого участка на эпюре нормальных напряжений рассчитать абсолютное удлинение по формуле Гука.
Определить суммарную величину абсолютного удлинения для всей детали в целом: найти алгебраическую сумму абсолютных удлинений всех участков. При этом если суммарная величина положительна – стержень удлинился, если отрицательна – стержень укоротился.
Анализ наиболее часто встречающихся ошибок.
Методические рекомендации по их устранению
Следует помнить, что на эпюре продольных сил границы участков проходят в точках приложения внешних сил, а на эпюре нормальных напряжений – в точках приложения внешних сил и в сечениях, где меняется площадь стержня.
Чтобы правильно подставить значения в формулу нормальных напряжений, нужно с участка эпюры напряжений, для которого ведется расчет, подняться на эпюру нормальных сил и посмотреть, каково значение продольной силы именно на этом участке. Затем подняться на чертеж детали и посмотреть, какова площадь сечения стержня именно на этом участке.
При расчете абсолютного удлинения в формулу Гука продольную силу следует подставлять с эпюры продольных сил, а величину площади сечения и длины данного участка – с чертежа детали.
В формулу нормальных напряжений и в формулу Гука следует подставлять значение продольной силы для данного участка.
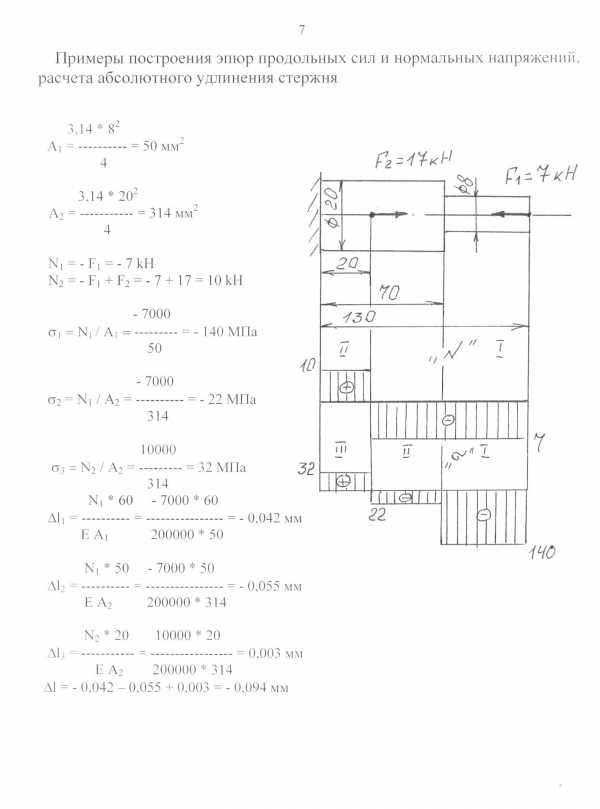

studfiles.net
Эпюра продольных сил — как построить?
В этой статье пойдет речь о том, как строятся эпюры продольных сил, какой метод используется при вычислении продольных сил. Также в статье будут разобраны примеры построения эпюр при различных видах нагрузок.
Пример построения эпюры продольных сил
Рассмотрим двухступенчатый брус нагруженный силами F1=5 кН, F2=3 кН, F3=6 кН
Решается подобная задача методом сечений. Для определения внутренних усилий по всей длине бруса нужно рассмотреть три участка.
Границами участков являются точки приложения внешних сил и места изменения геометрии бруса.
В жесткой заделке возникает сила реакции опоры, чтобы ее не определять, поступим по-хитрому, будем рассматривать участки поочередно, начиная от свободного торца тела.
Итак, 1-ый участок. Сечение сделаем на расстоянии x1 от 0 до l1 (0≤ x1≤ l1). Сила N1 будет равна: N1=-F1=-5 кН (знак «-» т.к. сила сжимающая).
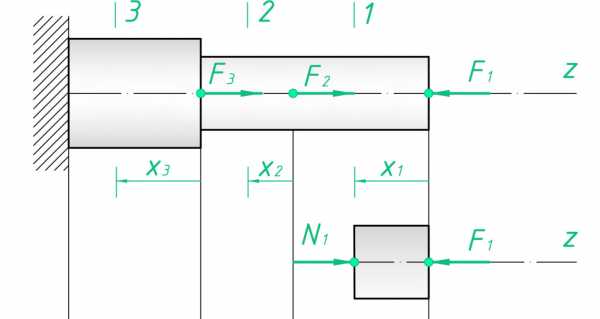
На втором участке (0≤ x2≤ l2) будет действовать уже 2 внешние силы, сила N2 будет равна сумме: N2=- F1+ F2=-2 кН.
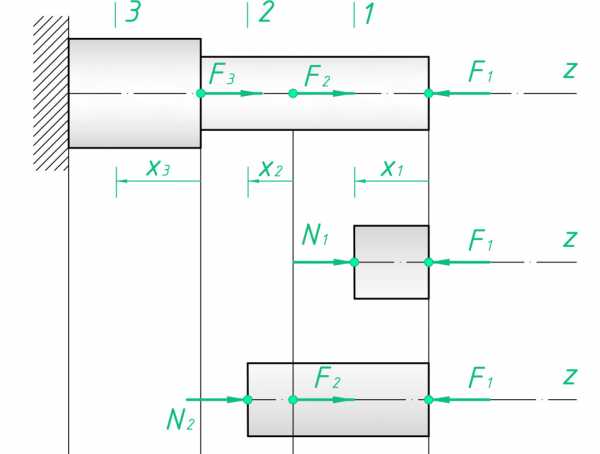
На третьем участке (0≤ x3≤ l3) N3=- F1+ F2+ F3=4 кН.
После нахождения внутренних усилий строим эпюру продольных сил N.
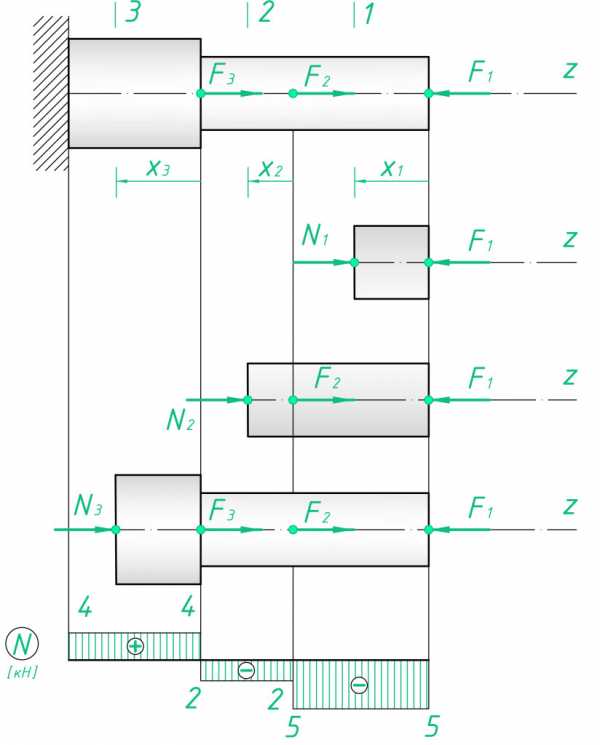
Рассмотрим брус немного другой конфигурации. Дано: F1=5 кН, F2=7 кН, q=2 кН/м, l3=2 м
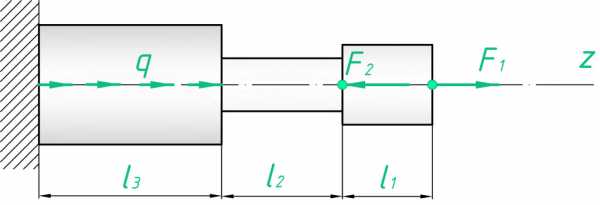
Также как и в предыдущей задаче будем рассматривать 3 участка. Для 1-го и 2-го участка внутренние силы будут равны:
Участок 1 (0≤ x1≤ l1) N1=F1=5 кН
Участок 2 (0≤ x2≤ l2) N2=F1-F2=-2 кН
Третий участок будет поинтересней. Здесь у нас действует распределенная нагрузка.
Если сосредоточенные силы действуют одинаково по всей длине бруса (эпюры прямоугольные), то распределенная нагрузка не так постоянна. Она усиливает свое влияние по мере увеличения расстояния, на котором она действует (эпюра треугольная).
То есть для нашей задачи на 3-ем участке (0≤ x3≤ l3) N3=F1— F2+q· x3
При x3=0 => N3=-2 кН
При x3=2 => N3=2 кН
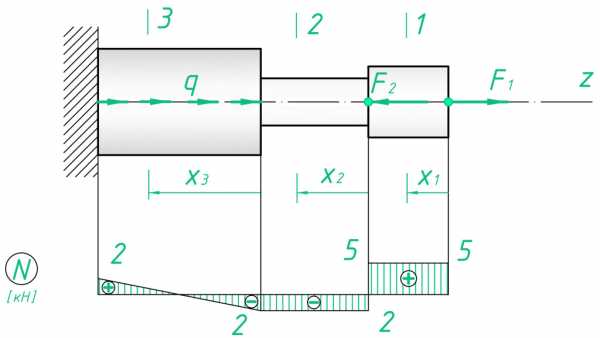
ssopromat.ru
Простейшие случаи сопротивления
Вид напряженного состояния | Nz | Qx | Qy | Mz | Mx | My |
Растяжение/сжатие | + | 0 | 0 | 0 | 0 | 0 |
Кручение | 0 | 0 | 0 | + | 0 | 0 |
Чистый изгиб относительно оси х | 0 | 0 | 0 | 0 | + | 0 |
Чистый изгиб относительно оси у | 0 | 0 | 0 | 0 | 0 | + |
Поперечный изгиб относительно оси х | 0 | 0 | + | 0 | + | 0 |
Поперечный изгиб относительно оси у | 0 | + | 0 | 0 | 0 | + |
Примечание: + означает наличие усилия, 0 его отсутствие
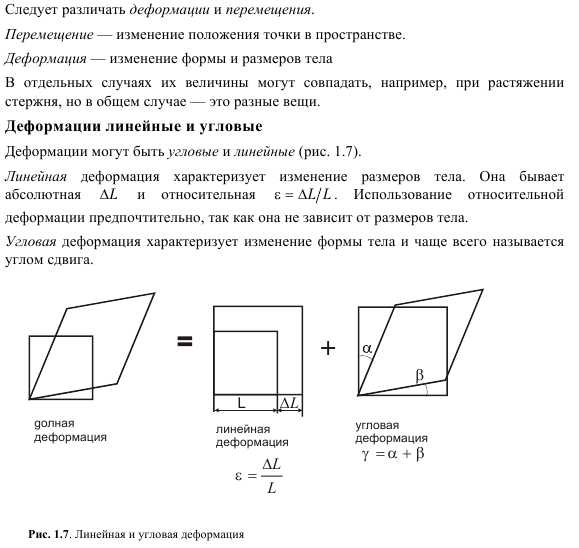
6.Деформация и перемещения.

7.Расчетная схема.

8.Продольная сила и её определение. Построение эпюры продольной силы.
Под растяжением или сжатием понимается такой вид нагружения, при котором в поперечных сечениях бруса возникают только нормальные силы (N), а все прочие внутренние силовые факторы равны нулю. Растягивающие нормальные силы (т.е. силы, направленные от поперечного сечения рис. 7.а) принято считать положительными, а сжимающие силы (т.е. силы направленные к поперечному сечению рис.7,б) – отрицательными. Этим правилом пользуемся при построении эпюр продольных сил.
Рис.7
Пример 1. Для бруса, находящегося в равновесии и нагруженного так, как показано на рис.8 а построить эпюру нормальных сил N. Разбиваем брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы.
I участок – СД, II участок – ВС, III участок – ВА.
Применяя метод сечений, оставляем правую и отбрасываем левую часть бруса: это позволяет не определять опорной реакции. Проводя произвольное сечение I-I на участке I и составляя для части бруса (рис. 8,б) уравнение равновесия Z=0, получим F-N=0, N=F
Очевидно, что все сечения на участке I равноценны. Таким образом, на участке I брус растянут силой F. Построим эпюру нормальных сил (рис.8,д). От нулевой линии, параллельной оси бруса, отложим вверх в масштабе на участке I ординаты, равные F и эпюру пометим знаком (+).
Проделаем подобные операции для участка II. Рассечём брус сечением 2-2 и рассмотрим правую отсечённую часть (рис.8,в)
Z=0 F+2F-N2=0 N2=3F
На эпюре нормальных сил на участке II отложим ординаты, равные 3F в том же масштабе, что и на участке I. Аналогично определяем нормальную силу на участке III. Проводим сечение 3-3 (рис. 8,в) и пишем уравнение равновесия Z=0
F+2F-4F+N3=0 N3=F
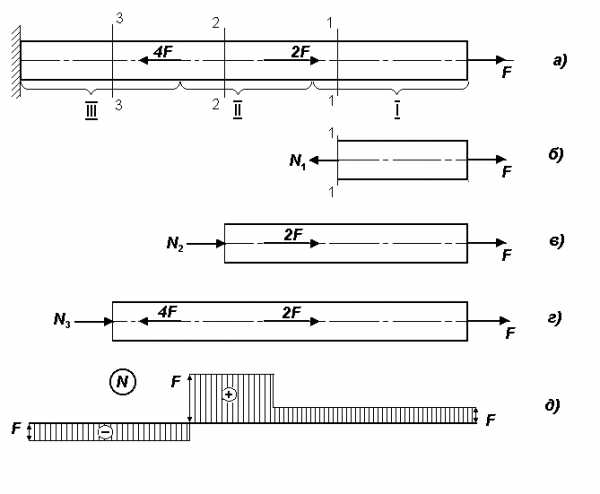
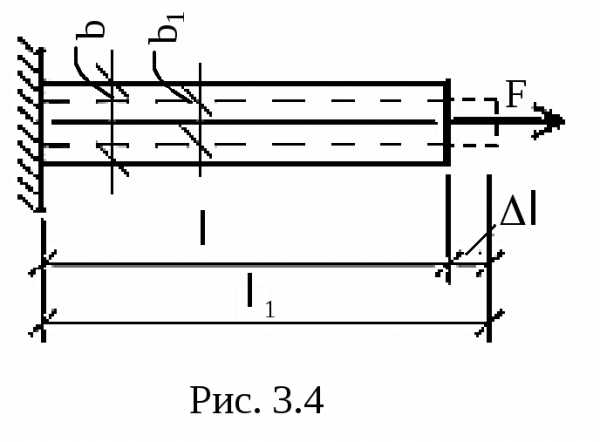
Усилие N3 направлено к сечению, т.е. сжимает участок III. Откладываем вниз от нулевой линии ординаты, равные F и ставим знак (-) на эпюре N (рис.8,д)
Таким образом, на рис.8,д построена эпюра нормальных сил для заданного бруса; Эпюры силовых факторов штрихуются линиями, перпендикулярными оси, т.к. они являются графиками, построенными в масштабе, т.е. каждая штриховая линия представляет собой продольную силу возникающую в соответствующем поперечном сечении.
9.Напряжения при растяжении-сжатии (нормально напряжение). Построение эпюры нормальных напряжений.
При растяжении (сжатии) бруса в его поперечных сечениях возникают только нормальные напряжения.
Гипотеза плоских сечений Я. Бернулли: сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к оси и при деформации.
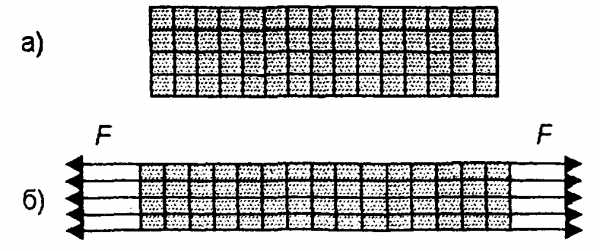
При растяжении (сжатии) бруса нормальные напряжения распределены по его поперечному сечению равномерно.
— нормальное напряжение, возникающее в материале при растяжении (сжатии), А — площадь поперечного сечения, N — сила вызывающая деформацию.
Для нормальных напряжений принимают то же правило знаков, что и для продольных сил, т.е. при растяжении считают напряжения положительными.
ПРИМЕР РЕШЕНИЯ ЗАДАЧ
Для
бруса со ступенчато-переменным поперечным
сечением построить эпюру нормальных
напряжений: Решение:
Решение:
Разбиваем брус на участки, начиная от свободного конца. Границами участков являются места приложения внешних сил и изменения размеров поперечного сечения, т.е. брус имеет пять участков.
При построении эпюры N достаточно было разбить брус только на три участка в местах приложения сил.
Нормальные напряжения вычисляем по формуле: σ = N/А
Аналогично:
В пределах каждого из участков напряжения постоянны, т.е. эпюра на данном участке — прямая, параллельная оси Х. Для расчётов на прочность интерес представляют в первую очередь те сечения, в которых возникают наибольшие напряжения. Интересно также отметить, что максимальные напряжения, возникающие в исследуемом образце, не всегда совпадают с максимальными продольными силами.
studfiles.net
Расчетно-графическая работа №5 «Построение эпюр продольных сил и нормальных напряжений при растяжении и сжатии»
Задание. Построить эпюры продольных сил и нормальных напряжений по длине бруса; определить удлинение (укорочение) бруса. Двухступенчатый стальной брус нагружен силами , и . Площади поперечных сеченийи. Принять. Данные для своего варианта приведены в таблице.
Таблица
параметры | Вариант | |||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
схема | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 |
20 | 26 | 20 | 17 | 16 | 10 | 26 | 40 | 14 | 28 | |
10 | 20 | 8 | 13 | 25 | 12 | 9 | 55 | 16 | 14 | |
5 | 10 | 4 | 8 | 28 | 13 | 3 | 24 | 10 | 5 | |
1,8 | 1,6 | 1,0 | 2,0 | 1,2 | 0,9 | 1,9 | 2,8 | 2,1 | 1,9 | |
3,2 | 2,4 | 1,5 | 2,5 | 2,8 | 1,7 | 2,6 | 3,4 | 2,9 | 2,4 | |
0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,4 | 0,3 | 0,2 | 0,5 | 0,6 | |
Вариант | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
схема | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 |
20 | 26 | 20 | 17 | 16 | 10 | 26 | 40 | 14 | 28 | |
10 | 20 | 8 | 13 | 25 | 12 | 9 | 55 | 16 | 14 | |
5 | 10 | 4 | 8 | 28 | 13 | 3 | 24 | 10 | 5 | |
1,8 | 1,6 | 1,0 | 2,0 | 1,2 | 0,9 | 1,9 | 2,8 | 2,1 | 1,9 | |
3,2 | 2,4 | 1,5 | 2,5 | 2,8 | 1,7 | 2,6 | 3,4 | 2,9 | 2,4 | |
0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,4 | 0,3 | 0,2 | 0,5 | 0,6 | |
Вариант | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
схема | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 |
20 | 26 | 20 | 17 | 16 | 10 | 26 | 40 | 14 | 28 | |
10 | 20 | 8 | 13 | 25 | 12 | 9 | 55 | 16 | 14 | |
5 | 10 | 4 | 8 | 28 | 13 | 3 | 24 | 10 | 5 | |
1,8 | 1,6 | 1,0 | 2,0 | 1,2 | 0,9 | 1,9 | 2,8 | 2,1 | 1,9 | |
3,2 | 2,4 | 1,5 | 2,5 | 2,8 | 1,7 | 2,6 | 3,4 | 2,9 | 2,4 | |
0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,4 | 0,3 | 0,2 | 0,5 | 0,6 | |
Расчетно-графическая работа №6 «Определение коэффициента запаса прочности при растяжении и сжатии».
Задание: Для заданного стального бруса (сталь Ст.3) с построить эпюры продольных сил и нормальных напряжений по длине бруса; определить удлинение (укорочение) бруса; определить коэффициент запаса. Данные для своего варианта даны в таблице .
Таблица.
Вариант | Схема | a | b | c | |||||||
кН | м | ||||||||||
1 | 1 | 12 | 6 | 12 | 120 | 260 | 0,2 | 0,4 | 0,6 | ||
2 | 2 | 15 | 7 | 30 | 100 | 320 | 0,15 | 0,4 | 0,55 | ||
3 | 3 | 18 | 22 | 9 | 160 | 360 | 0,2 | 0,5 | 0,55 | ||
4 | 4 | 18 | 52 | 5 | 120 | 310 | 0,1 | 0,25 | 0,5 | ||
5 | 5 | 20 | 80 | 42 | 140 | 350 | 0,65 | 0,75 | 0,5 | ||
6 | 6 | 20 | 13 | 53 | 130 | 410 | 0,1 | 0,3 | 0,6 | ||
7 | 7 | 20 | 62 | 23 | 150 | 420 | 0,4 | 0,5 | 0,3 | ||
8 | 8 | 30 | 41 | 8 | 190 | 610 | 0,4 | 0,4 | 0,8 | ||
9 | 1 | 13 | 5 | 12 | 110 | 270 | 0,25 | 0,45 | 0,6 | ||
10 | 2 | 14,5 | 8,5 | 27 | 125 | 310 | 0,18 | 0,25 | 0,65 | ||
11 | 3 | 17,5 | 23 | 8 | 150 | 350 | 0.22 | 0,48 | 0,7 | ||
12 | 4 | 17 | 51 | 6 | 125 | 320 | 0.2 | 0,35 | 0,8 | ||
13 | 5 | 21 | 79 | 40 | 150 | 330 | 0,55 | 0,75 | 0,5 | ||
14 | 6 | 21 | 12 | 50 | 125 | 400 | 0,25 | 0,4 | 0,5 | ||
15 | 7 | 21 | 64 | 22 | 140 | 440 | 0,65 | 0,55 | 0,3 | ||
16 | 8 | 31 | 39 | 9 | 185 | 620 | 0.3 | 0,4 | 0,7 | ||
17 | 1 | 11 | 8 | 13 | 130 | 280 | 0,45 | 0,45 | 0,4 | ||
18 | 2 | 11 | 8 | 13 | 130 | 280 | 0,35 | 0,35 | 0,4 | ||
19 | 3 | 16,5 | 24 | 7,5 | 155 | 370 | 0,25 | 0,62 | 0,75 | ||
20 | 4 | 16 | 49 | 6 | 130 | 300 | 0,55 | 0,55 | 0,9 | ||
21 | 5 | 21 | 79 | 40 | 150 | 330 | 0,55 | 0,75 | 0,4 | ||
22 | 6 | 22 | 14 | 54 | 130 | 420 | 0,35 | 0,5 | 0,4 | ||
23 | 7 | 22 | 65 | 22 | 145 | 450 | 0,75 | 0,6 | 0,35 | ||
24 | 8 | 29 | 38 | 11 | 200 | 620 | 0,4 | 0,5 | 0,6 | ||
25 | 1 | 10 | 9 | 14 | 125 | 250 | 0,4 | 0,25 | 0,5 | ||
26 | 2 | 15,5 | 7,5 | 28,5 | 140 | 350 | 0,25 | 0,45 | 0,75 | ||
27 | 3 | 13,5 | 23 | 10 | 167 | 380 | 0,3 | 0,75 | 0,8 | ||
28 | 4 | 15 | 50 | 7 | 120 | 290 | 0,25 | 0,45 | 0,8 | ||
29 | 5 | 18 | 78 | 41 | 160 | 360 | 0,45 | 0,8 | 0,6 | ||
30 | 6 | 20 | 13 | 53 | 130 | 410 | 0,1 | 0,3 | 0,6 | ||
studfiles.net
Последовательность выполнения расчета на прочность при растяжении или сжатии.
Разбить брус на участки. Границы участков проходят там, где приложены внешние силы и там, где изменяются размеры поперечного сечения.
Определить значение продольной силы на каждом участке.
Строим эпюру N.
Определяем значение нормальных напряжений в поперечных сечениях каждого участка и строим эпюру σ.
Определяем удлинение (укорочение) бруса.
Выполняем проверочный расчет на прочность по опасному сечению, , если брус не догружен на15 % и перегружен на 5 %, то условие прочности выполняется.
Примеры решения задач
Пример 1. На стальной ступенчатый брус (Е=2·МПа) действуют силы=20 кН иПлощади поперечных сечений равны800 мм2. Длины участков указаны, на рисунке : а= 0,2 м. Построить эпюры продольных сил и определить удлинение бруса.
Решение:
Разобьем брус на участки ( три участка) и, применяя метод сечений, определим значения продольных сил ,, на каждом из них:(сжатие),(растяжение).
Строим эпюру продольных сил.
Определяем нормальные напряжения на каждом участке: .
Тогда ;
Строим эпюру нормальных напряжений.
Используя формулу для вычисления изменения длины бруса, состоящего из нескольких участков, получим, где, по формуле Гука, удлинение бруса на первом участке, аналогично,,, удлинение бруса на втором и третьем участках.
Следовательно,
Следовательно, брус укоротился на 0,015 мм.
Пример
2. Для
заданного ступенчатого бруса,
изготовленного из стали марки Ст3
построить эпюры продольных сил и
нормальных напряжений и выполнить
проверочный расчет на прочность.
Допускаемое напряжение принять 
Решение
Разбиваем брус на участки (пять участков) и, применяя метод сечений, определим значения продольных сил ,,,на каждом из них.(растяжение),(растяжение),(сжатие),(сжатие),(растяжение).
Строим эпюру продольных сил.
Определяем нормальные напряжения на каждом участке: .
Тогда ;
Строим эпюру нормальных напряжений.
Используя формулу для вычисления изменения длины бруса, состоящего из нескольких участков, получим, где, по формуле Гука, удлинение бруса на первом участке, аналогично,,,удлинение бруса на втором, третьем, четвертом и пятом участках.
Следовательно,
Выполняем проверочный расчет на прочность по опасному сечению (участок 2). . Условие прочности выполняется.
Практическая работа № 6 «Построение эпюр продольных сил и нормальных напряжений при растяжении и сжатии»
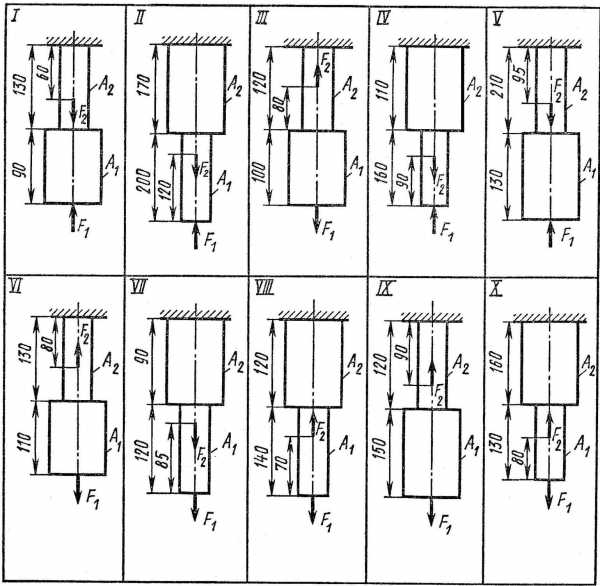
Цель: Двухступенчатый стальной брус, длина ступеней которого указана на схеме, нагружены силами F1 и F2. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить удлинение (укорочение) бруса, приняв МПа.
Задача: Числовые значения сил F1 и F2, а так же площадей поперечных сечений ступеней А1 и А2 взятьиз таблицы.
Вариант | № схемы | F1, кН | F2, кН | А1, см2 | А2, см2 | Вариант | № схемы | F1, кН | F2, кН | А1, см2 | А2, см2 |
1 | IX | 22,0 | 30,6 | 2,7 | 2,1 | 18 | VI | 3,0 | 6,0 | 0,5 | 0,9 |
2 | VII | 16,0 | 8,0 | 1,4 | 0,4 | 19 | IV | 8,0 | 18,0 | 2,0 | 3,0 |
3 | V | 3,5 | 12,0 | 2,5 | 1,8 | 20 | II | 4,0 | 9,2 | 0,5 | 0,6 |
4 | III | 15,0 | 30,0 | 2,1 | 1,6 | 21 | IX | 12,0 | 34,0 | 2,2 | 1,8 |
5 | I | 10,0 | 20,0 | 1,2 | 0,8 | 22 | VII | 19,0 | 9,8 | 0,9 | 0,6 |
6 | X | 12,0 | 30,0 | 2,1 | 2,5 | 23 | V | 18,0 | 38,0 | 3,0 | 1,8 |
7 | VIII | 14,0 | 16,0 | 2,4 | 2,8 | 24 | III | 20,0 | 32,0 | 2,5 | 2,2 |
8 | VI | 6,0 | 3,0 | 0,4 | 0,8 | 25 | I | 12,0 | 20,0 | 0,7 | 0,9 |
9 | IV | 10,8 | 29,0 | 1,8 | 2,0 | 26 | X | 14,2 | 30,0 | 1,5 | 2,4 |
10 | II | 3,3 | 8,0 | 0,4 | 0,5 | 27 | VIII | 10,0 | 16,0 | 2,2 | 3,0 |
11 | IX | 10,8 | 30,0 | 2,8 | 2,4 | 28 | VI | 6,0 | 3,0 | 0,4 | 0,8 |
12 | VII | 8,3 | 30,5 | 1,5 | 0,8 | 29 | IV | 7,6 | 20,5 | 2,8 | 3,2 |
13 | V | 27,0 | 27,0 | 2,8 | 2,0 | 30 | II | 4,8 | 10,0 | 0,4 | 0,8 |
14 | III | 14,0 | 18,0 | 2,3 | 2,1 | 31 | IX | 11,0 | 24,0 | 2,0 | 1,6 |
15 | I | 12,0 | 10,0 | 1,2 | 0,8 | 32 | VII | 8,0 | 8,4 | 2,0 | 1,4 |
16 | X | 14,0 | 40,0 | 2,0 | 2,0 | 33 | V | 1,4 | 20,0 | 2,6 | 1,5 |
17 | VIII | 16,0 | 12,0 | 1,1 | 3,0 | 34 | III | 30,0 | 36,0 | 2,4 | 1,6 |
studfiles.net
Построение эпюры нормальных напряжений при растяжении-сжатии
Задача
Построить эпюру нормальных напряжений для стержня постоянного сечения, нагруженного продольными силами.
Поперечное сечение стержня — квадрат со сторонами a=22мм. Допустимые напряжения [σ]=160МПа
Решение
Предыдущие пункты решения задачи:
Расчет нормальных напряжений при растяжении-сжатии производится по формуле:
т.е. напряжения в рассматриваемом сечении определяются отношением соответствующей величины внутренней силы к площади поперечного сечения стержня.
Площадь поперечного сечения стержня постоянна по всей его длине, и составляет
Очевидно, что в пределах участка стержня, на котором внутренняя сила и площадь постоянны, напряжения так же будут иметь одинаковую величину.
Здесь, при одинаковой площади, внутренние силы различаются на трех силовых участках. Соответственно на этих участках нормальные напряжения тоже будут отличаться.
Знак напряжений зависит от знака соответствующей внутренней продольной силы.
Значения внутренних сил принимаются с построенной ранее эпюры N.

Расчет напряжений
Нормальные напряжения на I силовом участке (KM)
На II участке (CK)
На III участке (BC)
По этим данным строим эпюру нормальных напряжений.
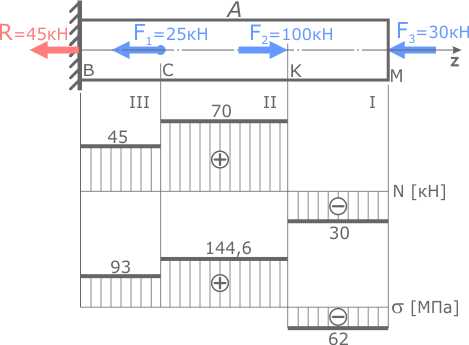
По построенной эпюре видно, что напряжения не превышают заданных допустимых значений, следовательно, рассчитанные размеры стержня обеспечивают его прочность.
Расчет деформации стержня >
Другие примеры решения задач >
isopromat.ru