2.4. Построение эпюр поперечных сил и изгибающих моментов по “характерным”сечениям

Дифференциальные зависимости между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом и изложенные выше следствия из этих зависимостей позволяют не только контролировать правильность построения эпюр внутренних силовых факторов при изгибе, но и строить эпюры поперечных сил и изгибающих моментов по “характерным” сечениям. Этот метод существенно отличается от аналитического метода, так как в результате его применения нельзя получить уравнения распределения внутренних силовых факторов в пределах рассматриваемого участка изгибаемого элемента конструкции. С помощью этого метода можно получить лишь численные значения поперечной силы и изгибающего момента в том или ином сечении. Однако такой подход в сочетании с использованием следствий из дифференциальных зависимостей между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом позволяет быстро и качественно строить эпюры различной сложности. “Характерными” будем называть поперечные сечения, расположенные бесконечно близко к границам участка изгибаемого элемента конструкции.

Рассмотрим применения этого метода на примере.

Пример 2.8. Построить эпюры поперечных сил и изгибающих моментовдля изображенной на рис.2.16,а балки по методу“характерных” сечений.

Рис.2.16

Решение:

1. Определяем опорные реакции. Для этого составим два уравнения равновесия:

; (а)

. (б)

Из уравнения (а) находим величину реакции :

кН.

Из уравнения (б) находим величину реакции :

кН.

Выполняем проверку. Для этого составим уравнение проекций всех сил, действующих на балку, на вертикальную ось :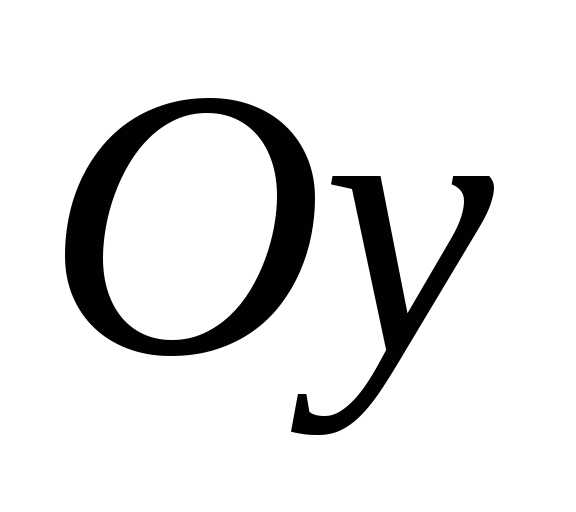

.

2. Разбиваем балку на участки и проставляем “характерные” сечения 1 6 на границах участков.

3. Определяем величины для поперечной силы в каждом из “характерных” сечений:

кН; кН;кН;

кН; кН;кН.

Откладываем от базисной линии найденные значения для поперечной силы в каждом из “характерных” сечений и соединяем полученные точки, руководствуясь следствиями из дифференциальных зависимостей между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом.

На участке №1 распределенная нагрузка отсутствует. Следовательно, на основании первого следствия из дифференциальных зависимостей поперечная сила будет постоянной. Соединяем точки, соответствующие значениям поперечной силы, найденным в сечениях №1 и №2, горизонтальной прямой. На втором участке действует распределенная нагрузка постоянной интенсивности. Следовательно, на основании следствия №2 из дифференциальных зависимостей поперечная сила должна меняться по линейному закону. Поэтому соединяем точки соответствующие значениям поперечной силы, найденным в сечениях №3 и №4 наклонной прямой. На участке №3 распределенная нагрузка так же, как и на участке №1, отсутствует. Следовательно, на основании первого следствия из дифференциальных зависимостей поперечная сила будет постоянной. Соединяем точки, соответствующие значениям поперечной силы, найденным в сечениях №5 и №6 горизонтальной прямой.

При построении эпюры поперечных сил следует обращать внимание на возможные скачки в тех сечениях, в которых приложены сосредоточенные силы. Так, в сечениях №2 и №3 значения для поперечной силы отличаются на величину силы . В сечениях №4 и №5 значения для поперечной силы отличаются на величину реакции. В сечении №6 также наблюдается скачок на величину силыв направлении ее действия при построении эпюры слева направо.

4. Находим значения для изгибающих моментов в “характерных” сечениях:

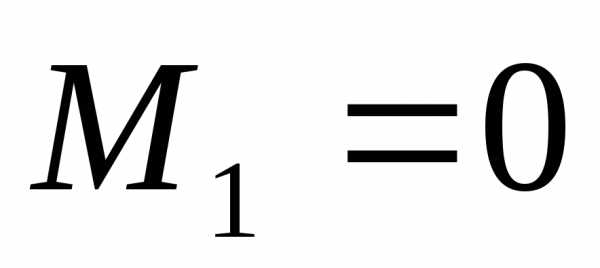; кНм;кНм;

кНм; кНм;.

Откладываем от базисной линии найденные значения для изгибающих моментов в “характерных” сечениях и соединяем полученные точки, руководствуясь следствиями из дифференциальных зависимостей между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом.

На участке №1 распределенная нагрузка отсутствует. Следовательно, на основании первого следствия из дифференциальных зависимостей изгибающий момент будет меняться по линейному закону. Соединяем точки, соответствующие значениям изгибающих моментов, найденным в сечениях №1 и №2, наклонной прямой. На втором участке действует распределенная нагрузка постоянной интенсивности. Следовательно, на основании следствия №2 из дифференциальных зависимостей изгибающий момент должен меняться по закону квадратной параболы. При этом на основании следствия №4 выпуклость на эпюре изгибающих моментов должна быть обращена навстречу распределенной нагрузке, т.е. вверх. Соединяем точки, соответствующие значениям изгибающих моментов, найденным в сечениях №3 и №4 параболой, обращенной выпуклостью вверх. На участке №3 распределенная нагрузка так же, как и на участке №1, отсутствует. Следовательно, на основании первого следствия из дифференциальных зависимостей изгибающий момент будет меняться по линейному закону. Поэтому соединяем точки, соответствующие значениям изгибающих моментов, найденных в сечениях №5 и №6 наклонной прямой. Скачков на эпюре изгибающих моментов не наблюдается, так как отсутствуют сосредоточенные моменты, приложенные к балке. Следует обратить внимание, что в сечениях, в которых имеются скачки на эпюре поперечных сил, на эпюре изгибающих моментов должны быть изломы.

Найдем величину максимального изгибающего момента . На втором участке балки поперечная сила меняет знак, пересекая базисную линию. Сечение, в котором поперечная сила равна нулю, также считается“характерным”. В этом сечении изгибающий момент достигает экстремальной величины на рассматриваемом участке. Для рассматриваемой балки изгибающий момент будет максимальным на основании дифференциальной зависимости (2.15), так как интенсивность распределенной нагрузки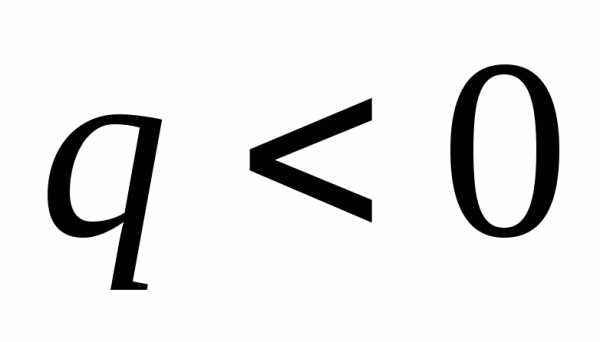

.

Для определения максимального изгибающего момента сначала определим координату сечения, в котором момент максимален. Для этого на эпюре поперечных сил сформируем два треугольника (контур одного из треугольников показан пунктиром). Один из рассматриваемых треугольников имеет неизвестный катет длиной , который и следует определить. Выделенные треугольники подобны по трем углам. Составим пропорцию: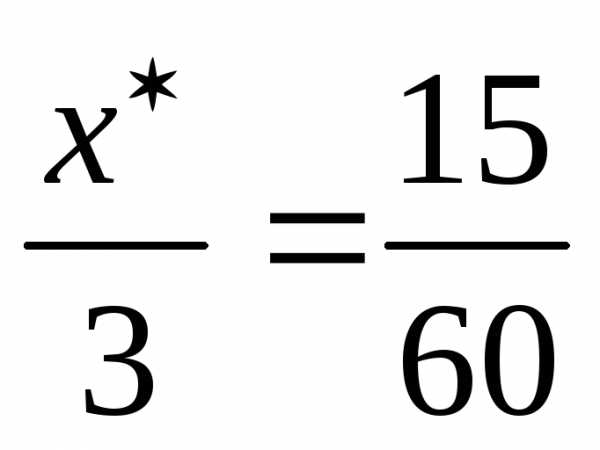, решая которую относительно, получим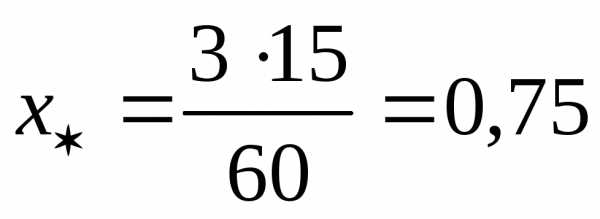

м.

Максимальный изгибающий момент можно определить двумя способами:

1. Помещая начало координат в точке А балки на левом ее конце, вычислим координату сечения, в котором изгибающий момент достигает максимальной величины: м, составляем выражение для изгибающего момента в указанном сечении и подставляем в это выражение координатум. Получим:

кНм.

2. Используя следствие №5 из дифференциальных зависимостей между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом, максимальный изгибающий момент найдем, прибавив к значению изгибающего момента в сечении №3 площадь эпюры поперечной силы на участке длинойм:

кНм.

Последний способ определения изгибающих моментов в некоторых случаях может оказаться предпочтительнее, так как существенно экономит время.

Пример 2.8. Используя метод “характерных” сечений, построить эпюры распределения поперечных[ сил , изгибающих моментов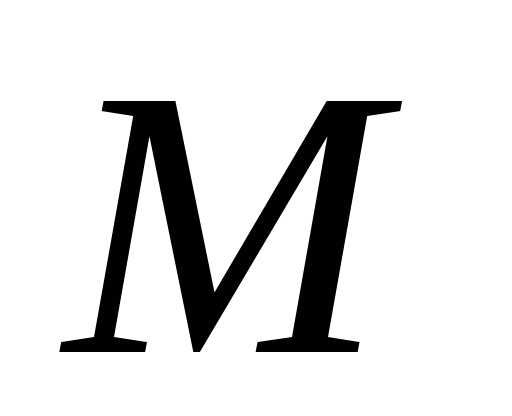и продольных сил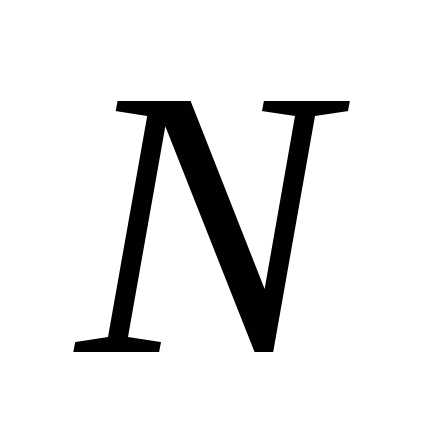для статически определимой рамы, изображенной на рис. 2.17.

Решение:

1.Определяем опорные реакции:

; (а)

; (б)

. (в)

Рис.2.17

Из уравнения (а) находим реакцию :

кН.

Из уравнения (б) находим реакцию :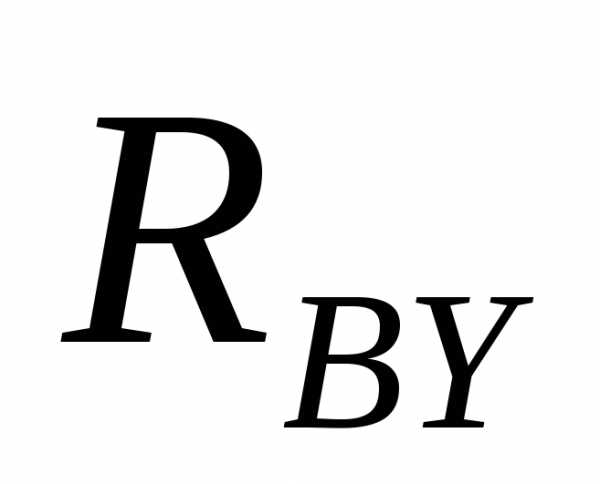

кН.

Из уравнения (в) находим реакцию :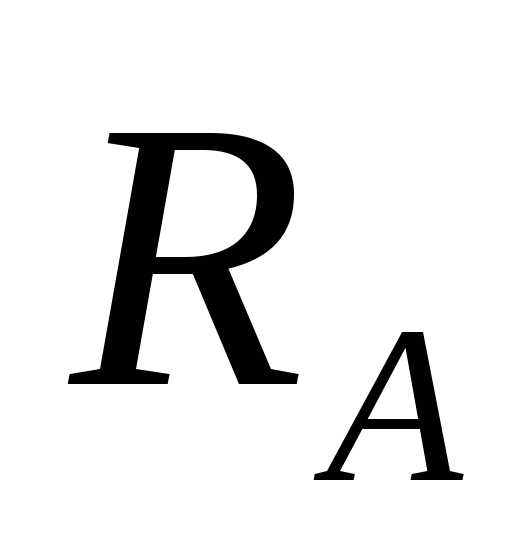

кН.

Реакции получились положительными. Следовательно, их направления выбраны верно.

Выполним проверку. Для этого составим сумму проекций всех сил на ось 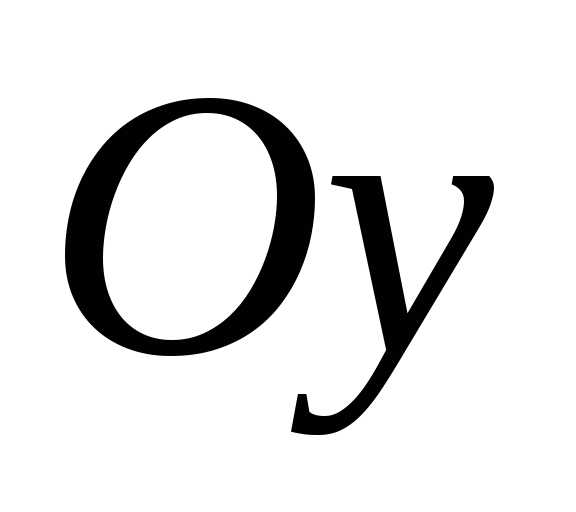. Эта сумма должна тождественно равняться нулю:

.

2. Расставляем реакции, разбиваем раму на участки, выбираем точку наблюдения, расставляем знаки на каждом участке для поперечных сил и изгибающих моментов и расставляем номера “характерных” сечений таким образом, чтобы нумерация сечений производилась слева направо. При этом знак «+» должен находиться над участком, знак «» – под участком.

3. Определяем значения поперечных сил в “характерных” сечениях рамы:

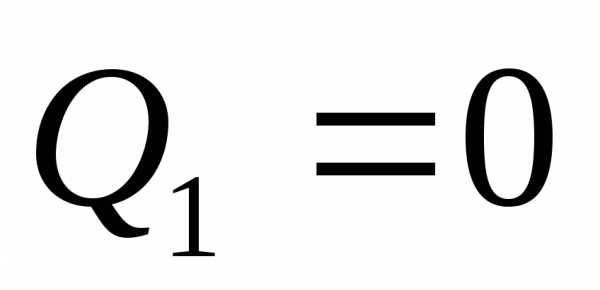; кН; кН;кН;

кН; кН;кН;кН.

Строим эпюру поперечных сил (Рис.2.18):

Рис.2.18

4. Определяем значения для изгибающих моментов в “характерных”сечениях рамы:

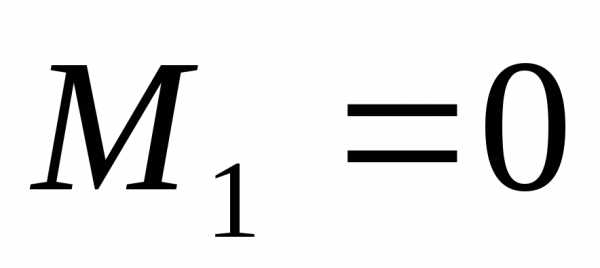;кНм;;кНм;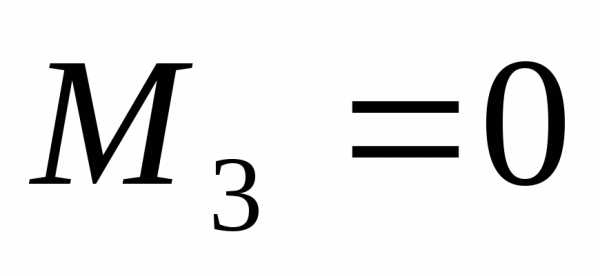

кНм;кНм;

кНм;.

Строим эпюру изгибающего момента (Рис.2.19):

Рис.3.19

5. Выполняем статическую проверку. Статическая проверка состоит а кинематической проверке расновесия узлов рамы. Вырежем сечениями №2, №4 и №5 первый узел С и изобразим его на рис. 2.20,а. Приложим к узлу моменты, характеризующие влияние отброшенной части рамы на узел. Эти моменты численно равны значениям изгибающих моментов соответственно в сечениях №2, №4 и №5. Направление действия этих моментов определяется правилом знаков для изгибающего момента. Значения моментов на рис 2.20 приведены в кНм.

Рис.2.20

Рассматривая равновесие узла С, выделенного из рамы сечениями №2, №4 и №5, составляем уравнение для суммы моментов относительно центра узла. В данном случае следует учитывать, что на узел С действует внешний заданный момент М.

. (а)

Как видно из уравнения (а) узел С находится в равновесии. Выполним проверку узла D, выделенного из рамы сечениями №6 и №7 (Рис.2.20,б). Составим сумму моментов, действующих на узел D:

. (б)

Как видно из уравнения (б) узел Dтакже находится в равновесии.

6. Определяем величину продольной силы в стержнях рамы. Для этого вырежем сечениями №2, №4 и №5 узел Cи изобразим его на рис. 2.21,а. Приложим к узлуC продольные усилияи поперечные силы, характеризующие влияние отброшенной части рамы на узел. Эти усилия численно равны значениям соответственно продольных и поперечных сил в сечениях №2, №4 и №5. Направление действия этих усилий определяется правилом знаков для продолных усилий и поперечных сил. Значения поперечных сил на рис 2.21 приведены в кН.

Составим суммы проекций сил, приложенных к узлу C, на осии: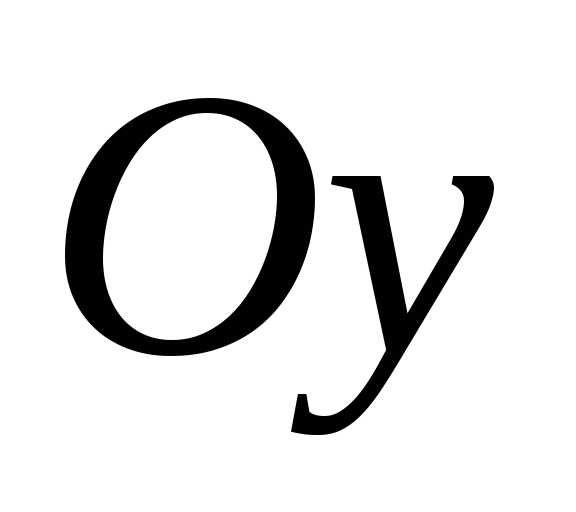

(в)

(г)

Рис.2.21

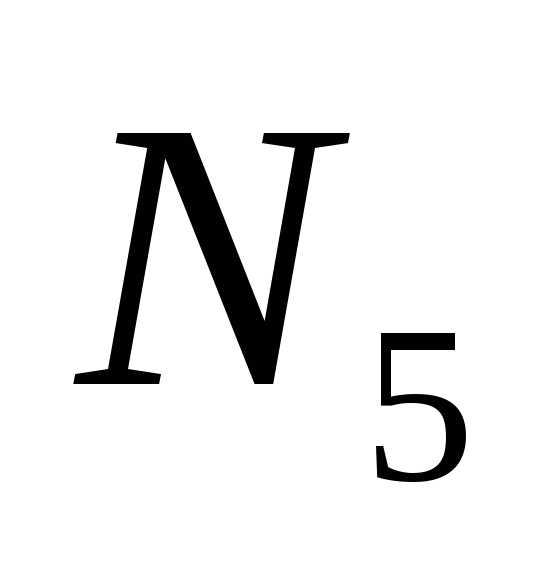Рассматривая уравнение (в), обнаруживаем, что в этом уравнении две неизвестных продольных силы и. Решить это уравнение относительно усилийи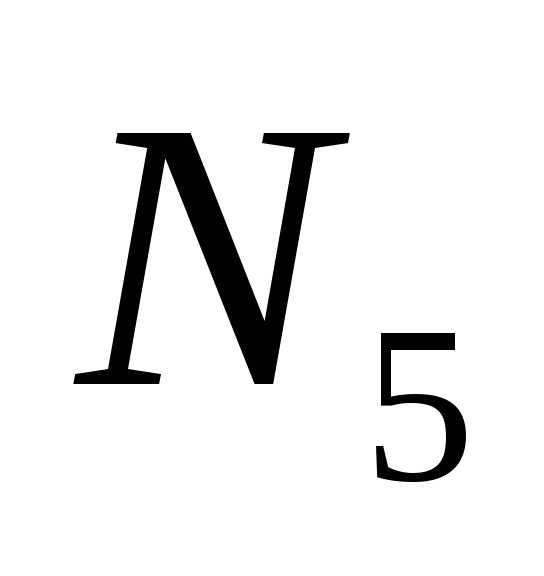невозможно. Найдем сначала усилие, рассмотрев равновесие участка рамы, ограниченного сечениями №3 и №4 (Рис.2.22).

Рис.2.22

Составим для изображенного на рис.2.22 стержня условие равновесия приложенных к стержню сил, на ось :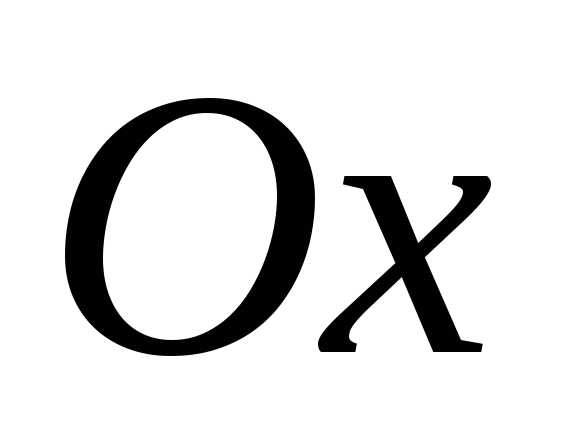

, (д)

откуда .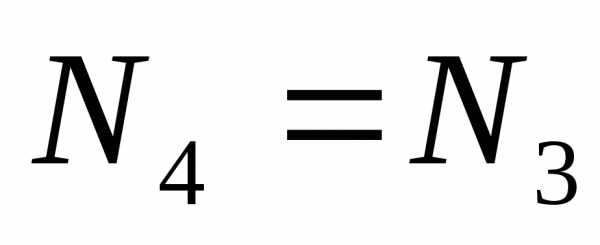

Но усили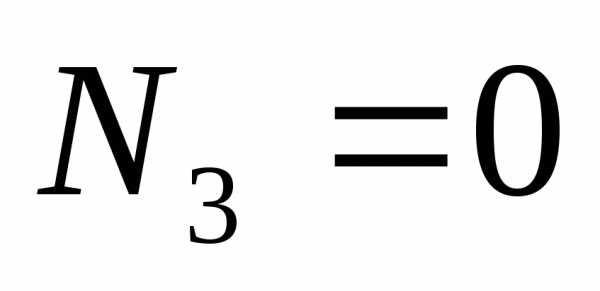е , так как в сечение №3 отсутствуют силы, действующие вдоль участка стержня 3-4 (Рис.2.17). Следовательно,усилие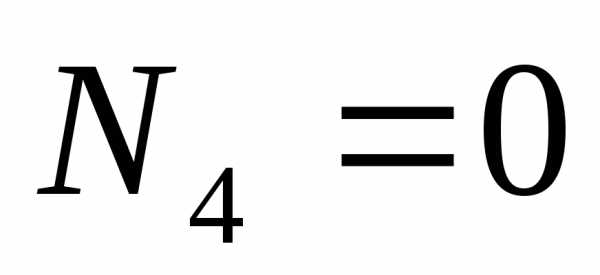. Теперь можно определить остальные продольные усилия, действующие в узле C. Из уравнения (в) находим:

кН.

Из уравнения (г) найдем усилие :

кН.

Найдем продольные усилия в сечениях №6 и №7. Для этого составим уравнения равновесия сил, приложенных к узлу Dна горизонтальную и вертикальную оси координат Х и Y (Рис.2.21,б). При составлении этих уравнений не следует забывать, что к узлуD приложена сосредоточенная сила.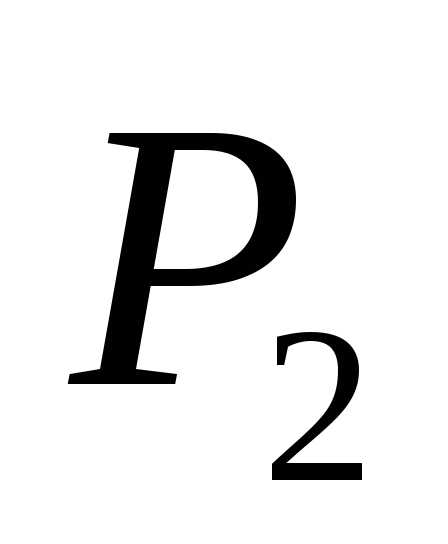

; (е)

. (ж)

Из уравнения (е) находим продольную силу в сечении №6:

кН.

Из уравнения (ж) находим продольную силу в сечении №7:

кН.

Откладываем найденные значения для продольной силы и строим эпюру продольных усилий 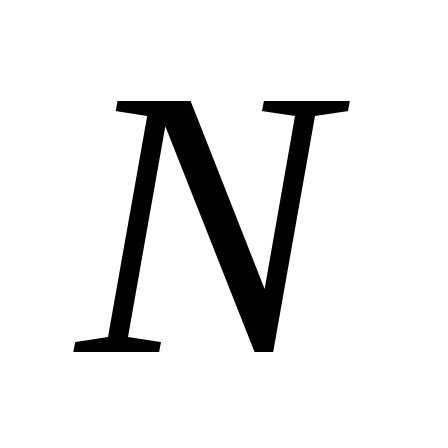(Рис.2.23).

Рис.2.23

Приведенные примеры построения эпюр поперечных сил и изгибающих моментов для балок и эпюр поперечных сил, изгибающих моментов и продольных усилий для рам позволяют получить наглядное представление о преимуществах и недостатках метода “характерных”сечений. К числу преимуществ этого метода можно отнести простоту определения внутренних силовых факторов. К числу недостатков – отсутствие аналитических законов распределения внутренних силовых факторов по длине элементов конструкции. Однако, использования дифференциальных зависимостей между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом для анализа поведения распределения внутренних усилий и следствий из них в значительной мере компенсирует последний недостаток. Сделанный вывод позволяет рекомендовать метод построения эпюр распределения внутренних силовых факторов по“характерным’сечениям в учебную практику.

studfiles.net

Построение эпюр поперечных сил изгибающих моментов: пример (сопромат)

Порядок построения эпюр поперечных сил и изгибающих моментов на примере балки (см. рис. 7.4).

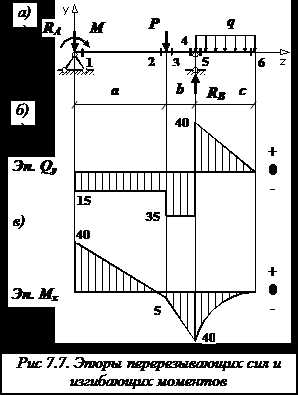
Разобьем балку на 3 отдельных участка (рис. 7.7, а), границами которых являются точки приложения сосредоточенных усилий и точки, соответствующие началу и окончанию действия распределенной нагрузки. По границам выделенных участков наметим шесть поперечных сечений, в которых будем вычислять значения поперечных сил и изгибающих моментов.

Построение эпюр поперечных сил и изгибающих моментов

Определение поперечных сил и изгибающих моментов — сечение 1

Отбросим правую часть балки и заменим ее действие на левую часть поперечной силой и изгибающим моментом . Для удобства вычисления закроем отбрасываемую правую часть балки листком бумаги, совмещая левый край листка с рассматриваемым сечением 1.

Поперечная сила в сечении 1 балки равна алгебраической сумме всех внешних сил, которые видим после закрытия

Видим только реакцию опоры, направленную вниз. Таким образом, поперечная сила равна:

кН.

Знак «минус» нами взят потому, что сила вращает видимую нами часть балки относительно первого сечения против хода часовой стрелки (или потому, что одинаково направлена с направлением поперечной силы по правилу знаков)

Изгибающий момент в сечении 1 балки, равен алгебраической сумме моментов всех усилий, которые мы видим после закрытия отброшенной части балки, относительно рассматриваемого сечения 1.

Видим два усилия: реакцию опоры и момент M. Однако у силы плечо практически равно нулю. Поэтому изгибающий момент равен:

кН·м.

Здесь знак «плюс» нами взят потому, что внешний момент M изгибает видимую нами часть балки выпуклостью вниз. (или потому, что противоположно направлен направлению изгибающего момента по правилу знаков)

Определение поперечных сил и изгибающих моментов — сечение 2

В отличие от первого сечения, у силы реакциипоявилось плечо, равное а.

поперечная сила:

кН;

изгибающий момент:

кН·м.

Определение поперечных сил и изгибающих моментов — сечение 3

поперечная сила:

кН;

изгибающий момент:

кН ·м.

Определение поперечных сил и изгибающих моментов — сечение 4

Теперь удобнее закрывать листком левую часть балки.

поперечная сила:

кН;

изгибающий момент:

кН ·м.

Определение поперечных сил и изгибающих моментов — сечение 5

поперечная сила:

кН;

изгибающий момент:

кН ·м.

Определение поперечных сил и изгибающих моментов — сечение 1

поперечная сила и изгибающий момент:

.

По найденным значениям производим построение эпюры поперечных сил (рис. 7.7, б) и изгибающих моментов (рис. 7.7, в).

Контроль правильности построения эпюр

Убедимся в правильности построения эпюр по внешним признакам, пользуясь правилами построения эпюр.

Проверка эпюры поперечных сил

Убеждаемся: под незагруженными участками эпюра поперечных сил идет параллельно оси балки, а под распределенной нагрузкой q – по наклоненной вниз прямой. На эпюре продольной силы три скачка: под реакцией – вниз на 15 кН, под силой P – вниз на 20 кН и под реакцией – вверх на 75 кН.

Проверка эпюры изгибающих моментов

На эпюре изгибающих моментов видим изломы под сосредоточенной силой P и под опорными реакциями. Углы изломов направлены навстречу этим силам. Под распределенной нагрузкой q эпюра изгибающих моментов изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. В сечении 6 на эпюре изгибающего момента – экстремум, поскольку эпюра поперечной силы в этом месте проходит через нулевое значение.

sopromato.ru

Проверка эпюр изгибающих моментов | Лекции и примеры решения задач механики

Правильность построенных эпюр изгибающих моментов M_x проверяется по “скачкам” и дифференциальной зависимости dM/dz=Q.

Проверим ранее построенную эпюру M_x.

1. Проверка по “скачкам”

В сечениях балки, где приложен изгибающий момент, на эпюре M будет скачок.

Здесь к балке приложено два момента: M в точке A и m в точке B.

Проверим наличие скачков в указанных сечениях:

В точке A изгибающий момент M равен 30кНм.
Скачок значений на эпюре M также равен 30.

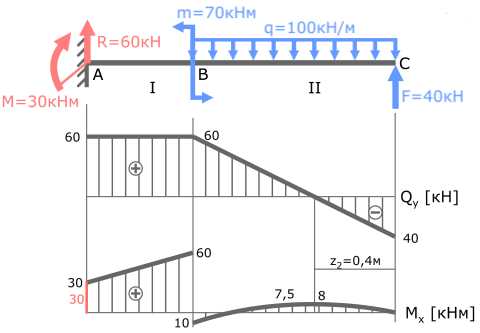
В точке B изгибающий момент m равен 70кНм.
Как видно, скачок значений составляет 70 (от -10 до +60).

2. Проверка дифференциальной зависимости dM/dz=Q

Выполним проверку эпюры по дифференциальной зависимости dM/dz=Q.

На участках балки, где эпюра Q параллельна базовой линии (I с.у.) эпюра M имеет вид прямой наклонной линии.

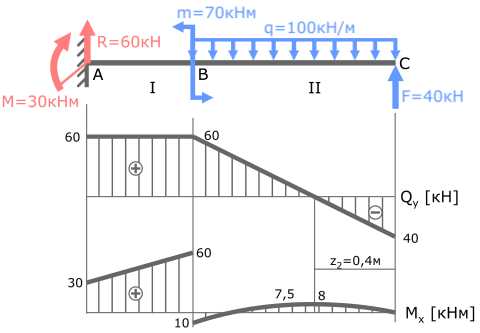
На участках балки с распределенной нагрузкой, где Q≠const (II с.у.) эпюра моментов M имеет вид параболы.

В сечении, где эпюра Q пересекает базовую линию, на эпюре M_xопределяется экстремум.

Все условия выполнены, значит, эпюра M_x построена правильно.

Примеры построения эпюр >
Краткая теория >

isopromat.ru

3.3 Построение эпюр поперечных сил и изгибающих моментов. Расчет на прочность при изгибе

Плоский поперечный изгиб отличается от рассмотренных видов нагружения тем, что в этом случае в поперечных сечениях балки появляется два внутренних силовых фактора: поперечная сила Q и изгибающий момент М, которые определяются методом разрезов.

3.3.1 Построение эпюр поперечных сил и изгибающих моментов

Поперечная сила в рассматриваемом сечении равна алгебраической сумме проекций всех сил на ось y, действующих на балку до рассматриваемого сечения:

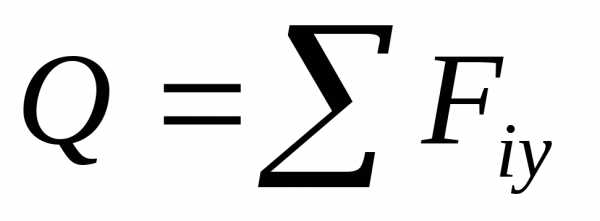(3.7)

Поскольку речь идет об алгебраической сумме, в которой необходимо учитывать знак действующих сил, принимают правило знаков при определении значений поперечной силы в сечении: внешние силы активные и реактивные, лежащие по левую сторону от сечения, считаются положительными, если они направлены вверх, отрицательными – вниз, а по правую сторону – наоборот (рисунок 3.7).

Изгибающий момент в рассматриваемом сечении равен алгебраической сумме моментов относительно этого сечения всех внешних сил и моментов, действующих на балку до рассматриваемого сечения:

(3.8)

Рисунок 3.7 — Правило знаков поперечной силы

Правило знаков при определении значения изгибающего момента: момент, изгибающий балку выпуклостью вниз, считается положительным, а вверх — отрицательным (рисунок 3.8). При изгибе выпуклостью вниз сжатое волокно вверху – момент на эпюре откладывается вверх – плюс. Значение изгибающего момента откладывается в сторону сжатого волокна.

Рисунок 3.8 – Правила знаков изгибающего момента

Между выражениями изгибающего момента М_х, поперечной силы Q_y и интенсивностью распределенной нагрузки q существуют следующие дифференциальные зависимости:

,

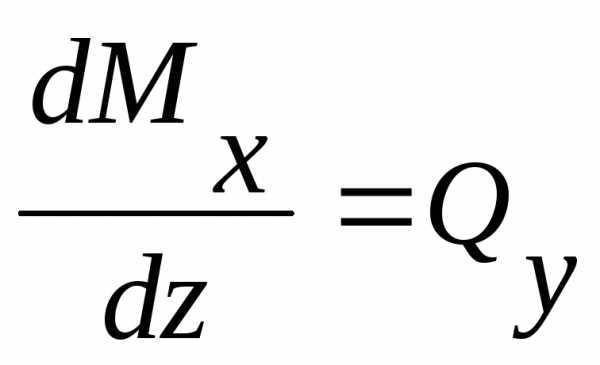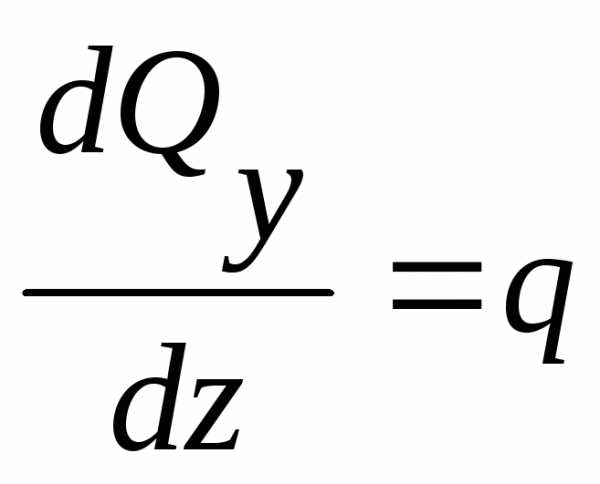
и, следовательно,

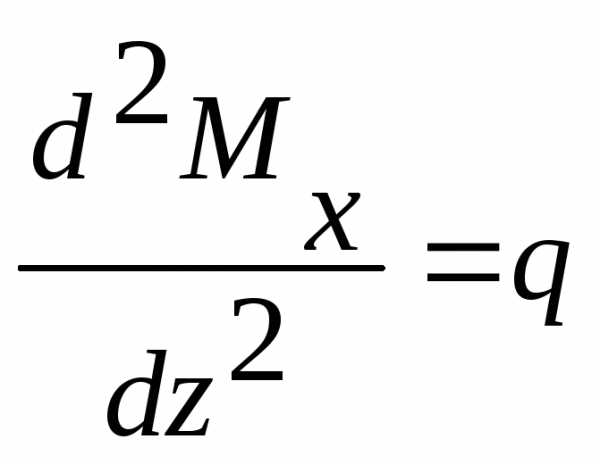. (3.9)

На основе метода сечений и дифференциальных зависимостей можно сделать ряд выводов о характере эпюр Q_y и M_x в зависимости от действующих на балку нагрузок.

Для эпюры поперечных сил:

1) на участке, нагруженном равномерно распределенной нагрузкой, эпюра изображается прямой, наклоненной к оси балки;

2) на участке, свободном от распределенной нагрузки, эпюра изображается прямой, параллельной оси балки;

3) под сечением балки, где приложена сосредоточенная сила, на эпюре поперечных сил имеется скачок, равный по величине приложенной силе;

4) в сечении, где приложена сосредоточенная пара сил, поперечная сила не изменяет своего значения;

5) в концевом сечении балки поперечная сила численно равна сосредоточенной силе (активной или реактивной), приложенной в этом сечении. Если в концевом сечении балки не приложена сосредоточенная сила, то поперечная сила в этом сечении равна нулю.

Для эпюры изгибающих моментов:

1) на участке, нагруженном равномерно распределенной нагрузкой, эпюра моментов изображается квадратной параболой. Выпуклость параболы направлена навстречу действию нагрузки;

2) на участке, свободном от равномерно распределенной нагрузки, эпюра моментов изображается наклонной прямой;

3) под сечением балки, где приложена сосредоточенная пара сил, на эпюре изгибающих моментов имеется скачок, равный величине момента приложенной пары сил;

4) изгибающий момент в концевом сечении балки всегда равен нулю; если в нем не приложена сосредоточенная пара сил. Если же в концевом сечении приложена активная или реактивная пара сил, то изгибающий момент в этом сечении равен по величине моменту приложенной пары;

5) на участке, где поперечная сила равна нулю, балка испытывает чистый изгиб, а эпюра изгибающих моментов – прямая, параллельная оси балки;

6) изгибавший момент принимает экстремальное значение в сечении, где на эпюре сил наклонная прямая пересекает ось.

Для определения экстремальных значений изгибающих моментов дополнительно определяются моменты в сечениях, где поперечные силы равны нулю.

Последовательность построения эпюр поперечных сил и изгибающих моментов

1) Определить опорные реакции и найденные их значения проверить.

2) Балку разделить на участки, границы которых должны совпадать с точками, изменения сечений и приложения силовых факторов.

3) Определить функции эпюр поперечных сил на каждом участке в зависимости от внешней нагрузки.

4) Вычислить поперечные силы в характерных сечениях и построить эпюру.

5) Определить функции эпюр изгибающих моментов на каждом участке в зависимости от внешней нагрузки.

6) Вычислить изгибающие моменты в характерных сечениях и построить эпюру.

Пример 3. Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рисунке 3.9. Подобрать сечение швеллера и сравнить его с прямоугольным.

Дано:

Решение. Определяем опорные реакции:

;

Определим функции внутренних силовых факторов на каждом участке.

I участок: 0 ≤ z ≤ а

при z=0,

при z=а, .

II участок: а ≤ z ≤ 3а

при z=a,

при z=3a,

На участке СД эпюра моментов – парабола. Следовательно, необходимо исследовать на экстремум.

,

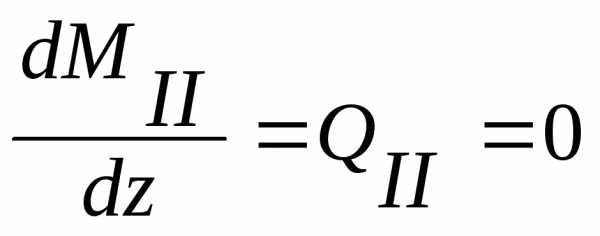
Рисунок 3.9 – Расчетная схема балки

III участок: 3а ≤ z ≤ 4а

;

M_III=;

.

IV участок: 4а ≤ z ≤ 5а

H;

Условие выполняется, что является проверкой правильности построения эпюры ЭQ:

Проверкой правильности последнего уравнения является равенство нулю момента в шарнире В.

studfiles.net

Построение эпюр изгибающих моментов — КиберПедия

Как тонко подметил Архимед, любая сила, приложенная с некоторым плечом относительно рассматриваемой точки, создает вращающий момент. И чем больше плечо, тем больше значение вращающего момента при одном и том же значении приложенной силы.

Это правило рычага действительно и при построении эпюр изгибающих моментов. Вот только моменты называются не вращающими, а изгибающими, но суть от этого не меняется. Так предполагается, что в любом поперечном сечении балки, находящемся на расстоянии х от начала балки (начала координат) могут действовать изгибающие моменты.

Например в нашем случае в начале балки приложена сосредоточенная сила — опорная реакция А = 6 кг, соответственно эта сила будет создавать изгибающий момент Ах, где х — плечо действия силы. При этом равномерно распределенная нагрузка также будет создавать изгибающий момент. А чтобы определить значение этого момента, сначала определяется общее значение нагрузки -qx, что мы и делали при построении эпюры поперечных сил. Общее значение распределенной нагрузки в рассматриваемом сечении можно рассматривать как равнодействующую сосредоточенную силу, а прикладывается эта сила в центре тяжести эпюры нагрузки. Т.е. в этом случае мы рассматриваем эпюру нагрузки, как некое физическое тело, имеющее плотность и соответственно центр тяжести. Впрочем с точки зрения теории сопротивления материалов в этом нет ничего удивительного.

Определить положение центра прямоугольной эпюры нагрузки несложно. Подобными упражнениями мы занимались в школе, когда определяли центр тяжести линейки. И находится этот центр тяжести посредине длины линейки, а в данном случае посредине рассматриваемой части эпюры нагрузки и составляет х/2.Таким образом плечо действия равнодействующей сосредоточенной силы при равномерно распределенной нагрузке составляет х/2. При этом функциональное уравнение изгибающих моментов, необходимое для построения эпюры моментов, будет иметь следующий вид:

M = Ax — qx·x/2 = Ax — qx²/2 (545.5.1)

Примерно такой же результат мы получим, если проинтегрируем уравнение поперечных сил:

M = ∫(A — qx)dx = M₀ + Ax — qx²/2 (545.5.2)

Где М₀ = 0 — это опять же постоянная интегрирования. В данном случае — значение момента на опоре А. Так как мы рассматриваем однопролетную безконсольную балку на шарнирных опорах, то в этом частном случае значение момента на опоре А равно нулю. Кроме того значение момента на опоре В для шарнирной безконсольной балки также равно нулю, так как шарнирные опоры повороту сечений ни как не препятствуют. Эта особенность в частности используется при определении опорных реакций однопролетной безконсольной балки на шарнирных опорах. Другими словами, зная, что момент на опоре В равен нулю, мы можем определить значение опорной реакции А из уравнения (45.5.2):

М_В = 0 = Аl — ql²/2 (545.5.3)

A = (ql²/2)/l = ql/2 (545.5.4)

В общем случае значение момента в начале координат может быть не равно 0.

А теперь рассмотрим еще одну особенность изгибающих моментов: для рассматриваемого сечения не имеет принципиального значения, какой будет знак у момента, положительный или отрицательный, так как при любом знаке в сечении будет как растягиваемая, так и сжимаемая зона сечения. А вот какая именно зона сечения будет растягиваемой, верхняя или нижняя — имеет большое значение, потому что не все материалы имеют равное сопротивление растяжению и сжатию, а кроме того форма сечения далеко не всегда бывает прямоугольной.

В связи с этим при построении эпюр изгибающих моментов принято следующее правило:

Эпюра моментов строится с той стороны, где будет растянутая зона сечения. При этом момент, пытающийся вращать рассматриваемое сечение по часовой стрелке, считается положительным, а против часовой стрелки — отрицательным.

Примечание: это правило не является общепринятым. В некоторых справочниках и учебниках по теории сопротивления материалов положительный момент строится сверху от оси х, что в общем то логично, но при этом получается, что положительный момент там, где сжатая зона сечения. В других он строится с той стороны, где растянутая зона сечения, но при этом может показываться со знаком «-«, если строится снизу от оси х. Но как я уже говорил выше, принципиального значения это не имеет, главное понимать общий смысл изгибающих моментов.

Если мы посмотрим на направление действия опорной реакции А и распределенной нагрузки q (рисунок 545.4), то увидим, что относительно любого из рассматриваемых сечений опорная реакция А пытается вращать это сечение по часовой стрелке, а распределенная нагрузка q — против. Это означает, что функциональное уравнение, описывающее изменение изгибающих моментов по длине балки, составлено у нас правильно.

При этом растянутой будет нижняя зона сечения балки по той причине, что балка прогнется вниз при таком действии нагрузки. Следовательно эпюру моментов в данном случае следует строить снизу от оси координат х.

Теперь у нас есть все данные для построения эпюры изгибающих моментов. Судя по уравнению (545.5.2) это будет квадратная парабола, а максимальное значение изгибающего момента будет посредине балки, так как нагрузка у нас симметричная, и составит М = 6·2 -3·2²/2 = 6 кгм.

Рисунок 545.5.г) эпюра изгибающих моментов, как график функции у = 6х — 3х²/2

В общем случае, когда нагрузка несимметричная, как показано на рисунках 545.2.а) и б) или на балку действуют несколько распределенных нагрузок, то определить сечение в пролете балки, в котором действует максимальный изгибающий момент. можно, воспользовавшись следующим общим правилом:

cyberpedia.su

Построение эпюр изгибающих моментов и поперечных сил в балках — Мегаобучалка

 

Для оценки прочности и жесткости изгибаемых элементов необходимо знать изменение изгибающего момента и поперечной силы по длине балки, а также их экстремальное значение. С этой целью строят эпюры изгибающих моментов и поперечных сил.

Эпюры изгибающих моментов и поперечных сил — представляют собой график, изображающий аналитическую зависимость M_xи Q_y по длине балки. Ординаты на эпюрах откладываются в масштабе или соразмерно их численным значениям.

Для определения M_xи Q_y в пределах каждого участка балки пользуются методом сечений.

Границами участков на балке являются точки приложения сосредоточенных сил и моментов, точки начала и конца действия распределенной нагрузки.

В пределах каждого участка проводим нормальное к оси балки сечение и рассматриваем в равновесии целиком правую или левую часть балки. Действие отброшенной части балки заменяем внутренними силовыми факторами, которые прикладываются в положительном направлении. Для рассматриваемой части составляем уравнения равновесия статики и находим M_xи Q_y, которые при этом считаются внешними силовыми факторами. На основании полученных аналитических зависимостей определяем значение M_xи Q_y в граничных и промежуточных точках, а затем строим эпюры.

На эпюре Q_y положительная ордината откладывается вверх, а на эпюре M_x вниз. Это связано с принятым правилом знаков. Принято говорить, что эпюра M_xстроится со стороны растянутого волокна балки.

Пример 8.2.

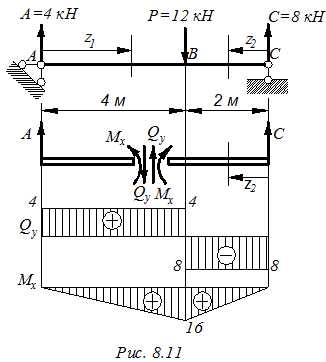
Построить эпюры изгибающих моментов и поперечных сил для балки, нагруженной, как показано на рис. 8.11.

1. Определяем реакции в балке: R_a=4кН, R_c = 8 кН.

2. Балка имеет два участка АВ и ВС_.

3. Участок АВ. На расстоянии z₁ от точки А проводим сечение 1:1 и рассматриваем в равновесии левую часть балки. Сечение может быть проведено в любом месте между точками А и В. Следовательно,

0 ≤ z₁ ≥ 4

ΣF_y = 0 A – Q_y = 0 → Q_y = A = 4 кН

 

Пользуясь принятым правилом знаков, для поперечной силы можно записать

Q_y = A = 4 кН

Сила А приложена слева от сечения и направлена вверх.

ΣM_x = 0 Az – M_x = 0 → M_x = Az

 

В дальнейшем будем рассуждать так: момент в рассматриваемом сечении из условия равновесия левой части равен

M_x = Az.

 

Находим значения изгибающего момента в граничных точках участка:

M₀ = 0, M₄ = 4·4 = 16 кНм

 

Участок ВС. Проводим сечение 2:2 на расстоянии z₂ от точки С и рассматриваем в равновесии правую часть балки.

Q_y = – C = – 8кН, M_x = Cz → M₀ = 0, M₂ = 8·2 = 16 кНм

 

По найденным значениям M_xи Q_y строим соответствующие эпюры.

Пример 8.3.

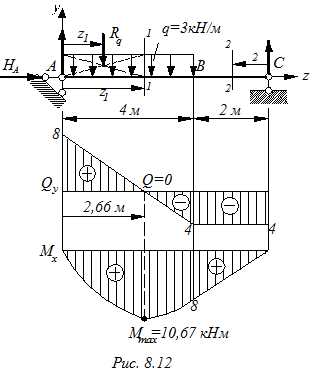Построить эпюры изгибающих моментов и поперечных сил для балки, нагруженной как показано на рис. 8.12.

1. Определяем опорные реакции балки:

ΣF_z = 0 → H = 0

Σm_c = 0, A·6 – q·4·4 = 0 → A = 8 кН

Σm_a = 0, C_c·6 – q·4·2 = 0 → C= 4 кН

ΣF_y = A – q·4 + B = 8 – 12 + 4 = 0

Реакции определены верно.

В дальнейшем будем полагать, что горизонтальная реакция при вертикальной нагрузке равна нулю и соответствующее уравнение для ее нахождения можно не записывать.

2. Балка имеет два участка АВ и ВС.

3. Участок АВ: 0 ≤ z₁ ≥ 4

Q_y = A – q·z₁→ Q₀ = A = 8 кН, Q₄ = 8 – 3·4 = – 4 кН

M_x = A·z₁ – q·z₁· = A·z₁ – → M₀ = 0, M₄ = 8 кНм

= A – q·z₁ =0 → z₁ = =2,66 м, М_2,66 = 10,67 кН

= – q кривая выпуклая

4. Участок ВС: 0 ≤ z₂ ≥ 2

Q_y = – С = – 4 кН

M_x = С·z₂ → M₀ = 0, M₂ = 4·2 = 8 кНм

По найденным значениям M_x и Q_y строим соответствующие эпюры.

Пример 8.4.

Построить эпюры изгибающих моментов и поперечных сил для консольной балки, нагруженной как показано на рис. 8.13.

При построении эпюр в консольной балке реакции в заделке можно не находить. В этом случае рассматривают равновесие части балки, расположенной со стороны ее свободного конца. Балка имеет два участка АВ и ВС.

I. Участок АВ: 0 ≤ z₁ ≥ 3

Q_y = – q·z₁→ Q₀ = 0, Q₃ = – 12 кН

M_x = M – q·z₁· = M – → M₀ = 6 кНм,

М₄ = – 6 кН

II. Участок ВС: 0 ≤ z₂ ≥ 1

Q_y = – q·3 + P = – 2 кН

M_x = M – q·3·(1,5 + z₂) + P·z₂ → M₀ = 12 кНм,

M₁ = – 14 кНм

По найденным значениям M_x и Q_y строим соответствующие эпюры.

 

megaobuchalka.ru

Построение эпюр поперечных сил и изгибающих моментов

Эпюрыпоперечных сил Q_yи изгибающих моментов М_х – это графики изменения их значений вдоль балки. Они позволяют получить максимальные значения сил Q_yмоментов М_х, необходимых для расчёта.

Построение эпюр Q_yи М_х выполняют по значениям поперечных сил Q_yи изгибающих моментов М_х, полученных по грузовым участкам балки. Границами участков являются сечения, в которых приложены сосредоточенные моменты и силы, или имеется начало и конец распределённой нагрузки.

Для каждого участка применяется правило РОЗУ метода сечений:

1) Разрезать балку на 2 части.

2) Отбросить одну из частей.

3) Заменить воздействие отброшенной части на оставленную усилиями Q_yи М_х.

4) Уравновесить внешнюю нагрузку и внутренние усилия Q_yи M_x, составив два уравнения равновесия отсечённой части:

(5.4)

Заметим, что здесь за точку О выбираем центр тяжести текущего сечения, и составляем уравнение моментов относительно этой точки от всех воздействий, действующих на оставленную часть балки.

Разобьём балку на два грузовых участка(рис. 5.4, а) и рассмотрим вычисление усилий Q_yи M_xна каждом.

1-й участок: , где z₁– координата текущего сечения.

Рассмотрим кусок первого участка балки длиной z₁, расположенный по левую сторону от сечения. В сечении возникают изгибающие моменты М_х¹ и поперечные силы Q_y¹, которые предполагаем положительного направления: поперечная сила положительна, если её вектор стремится повернуть рассматриваемую часть по часовой стрелке; изгибающий момент M_xв сечении будем считать положительным, если балка изгибается выпуклой стороной вниз.

 

а б в г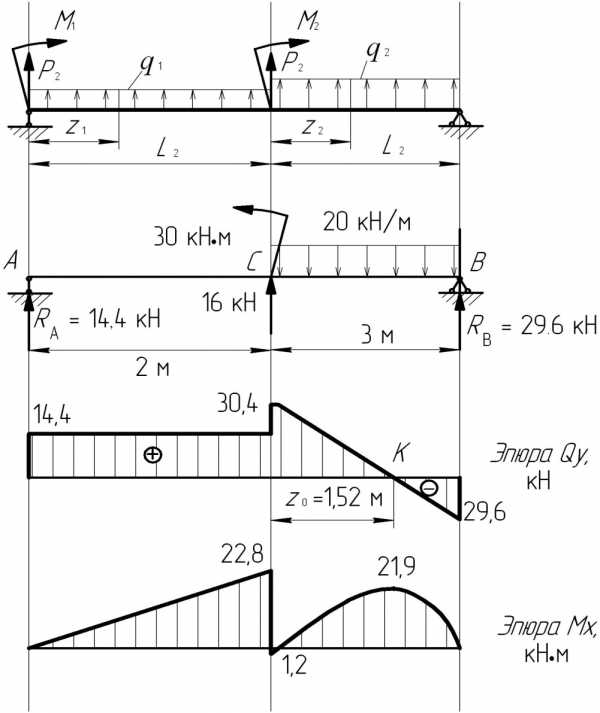

 

Рис. 5.4

 

Слева от сечения расположена только сила R_A(рис. 5.4, б), поэтому записываем:

, .

 

Выражение поперечной силы Q_y¹ не содержит переменных, следовательно, значение Q_yпостоянно и равно 14,4 кН. Отложим вверх от базисной линии это значение в масштабе и построим на 1-м участке эпюры Q_yпрямоугольник (рис. 5.4, в).

Выражение М_х¹ соответствует уравнению прямой. Подсчитаем величины моментов при граничных значениях (z₁= 0 и z₁= l):

При z= 0 ; при м кН∙м.

На базисной линии отложим эти значения и проводим наклонную прямую эпюры M_хна 1-м участке (рис. 5.4, г).

Рассмотрим 2-й участок: . Возьмём участок балки слева от сечения и по (5.2) получаем

 

Подсчитаем и для граничных значений :

при z₂= 0

приz₂= 3 м кН; .

По этим значениям построим эпюры Q_yи M_xна 2-м участке.

Сила изменяется линейно. Отложим в начале участка кН и в конце кН и соединим эти точки наклонной прямой (рис. 5.4, в), прямая пересекла базисную линию в точке К.

Так как функция момента имеет второй порядок по отношению к переменной z₂(это результат наличия распределённой нагрузки на этом участке), то при изображении момента должны изобразить параболу.

Уточним вид этой параболы с помощью эпюры Q_y и выражения (5.1), записанное по теореме Д.И. Журавского об интегрально-дифференциальной зависимости функций Q_y и М_x. Пересечение наклонной линии Q_y с базисной прямой в точке К вносит следующую поправку в изображение параболы: в точке К получается перегиб кривой, т.е. момент получает экстремальное значение .

Необходимо найти этот момент. Для вычисления сначала определим абсциссу этого сечения (рис. 5.4, в), составив уравнение :

.

 

 

Отсюда получаем

м.

Теперь подсчитаем значение экстремального момента . Подставим в выражение момента М₂ вместо z₂ значение 1,52 м:

кН·м.

Отложим полученные значения моментов в начале, в конце участка и в сечении К, построим на эпюре моментов параболу (рис. 5.4, г).

Так как целью построения эпюр является получение максимального (расчётного) значения M_max, то выписываем

M_max=28,8кН·м.

Подбор сечений

Подберём размеры указанных трёх вариантов сечений: двутавровое, кольцевое и коробчатое.

Подбор выполняем, используя условие прочности по допускаемым напряжениям (5.2). Из этого условия при значении момента M_max= 28,8 кН·м и допускаемом напряжении [s]=200 Мпа найдём требуемое значение момента сопротивления сечения W_x:

 

 

Выполним подбордвутаврого сечения балки, длякоторого момент сопротивления поперечного сечения

По таблице ГОСТ 8239-89 (см. табл. П.4 Приложения) выбираем двутавр № 18, для которого

Выполним подбор диаметра кольцевого сечения балки, длякоторого выражение момента сопротивления сечения имеет вид:

,

где имеем согласно рисунку задаваемого сечения (рис. 5.2) отношение внутреннего диаметра к внешнему

= 0,6.

Так как момент сопротивления W_x≥ 144 см³, то требуемый диаметр кольцевого сечения

≈

Принимаем диаметр кольцевого сечения d= 12см.

Коробчатое сечениедолжно иметь то же значение момента сопротивления W_x≥ 144 см³.

Запишем выражение момента сопротивления коробчатого сечения используя (5.3). Сечение состоит из двух прямоугольников размерами b 2bи 0,6b 1,2b.

Тогда

где ̶ моменты инерции прямоугольников, вычисляемые по формуле .

Из полученного выражения момента сопротивления W_xнайдём требуемое значение b:

= .

Принимаем b= 6,5 см.

Сравним расход материала по площади поперечного сечения.

Для двутавра № 18 площадь сечения по таблице ГОСТ 8239-89 (см. табл. П.4)

Для кольцевого сечения диаметром d= 12см площадь сечения

=

Для коробчатого сечения с b= 6,5 см площадь сечения

=

Двутавровое сечение, как сечение с меньшей площадью, принимаем за более экономичное.

Таблица 5.1. Исходные значения к задаче 5

Номер вари­анта	Длина участков, м	Интенсивность нагрузки, кН/м	Сила, кН	Сосредоточенный момент, кН∙м
l1	l2	q1,	q2,	P1	P2	М1	М2
	2,8	2,2						-32
	2,0	2,6		-12	-22
	3,0	1,8
	1,9	2,8				-13	-20
	2,8	2,0
	2,5	3,0	-17			-25
	3,0	2,0
	2,2	2,8		-15	-26			-28
	2,5	2,5					-26
	2,0	2,5	-18
	2,5	2,6				-20	-24
	2,2	3,0
	2,5	2,2		-28
	2,3	2,8			-14
	1,8	3,0	-26				-33
	3,0	1,5			-27			-40
	1,5	2,5	-30		-12
	2,5	1,2	-12	-24
	1,2	3,0		-12				-32
	3,0	1,7	-10
	1,6	2,4						-25
	2,4	1,9		-20	-10
	1,8	2,6	-15	-25
	2,6	1,9	-30					-32
	1,8	2,8		-10			-42
	2,7	2,5			-15
	2,2	2,8	-45			-20		-13
	2,8	2,5		-15				-36
	3,0	1,5			-18
	2,3	1,8	-19				-16

Задача 6
Подбор диаметра вала при изгибе с кручением

Условие задачи

Стальной вал, схемы которого занесены в табл. 6.1, передаёт заданную мощность при известной угловой скорости ω. Исходные значения мощности N, угловой скорости ω, длины l, диаметра D₁ даны в табл. 6.2.

Требуется:

Используя IV теорию прочности, подобрать диаметр вала, приняв допускаемое напряжение [σ] = 180 МПа.

Значение диаметра вала должно быть принятым из стандартного ряда по ГОСТ 6636-60:

10; 10,5; 11; 11,5; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 24; 25; 26; 28; 30; 32; 33; 34; 36; 38; 40; 42; 45; 48; 50; 52; 55; 60; 63; 65; 70; 75; 80; 85; 90; 95; 100; 105; 110; 120; 125; 130 мм и далее через 10 мм.

Рекомендуемые страницы:

lektsia.com