Техническая механика — Тема 2.2. Растяжение и сжатие
Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.
Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений.
Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 1.
Рис. 1. Растяжение стержня
Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис.
1, а, б) оказывается единой (рис. 1, в) согласно принципу Сен – Венана.
Если воспользоваться методом сечений (рис. 2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы Nz, равные силе F (рис. 2, б).
Сжатие отличается от растяжения, формально говоря, только знаком силы Nz. При растяжении нормальная сила Nz направлена от сечения (рис. 2, б), а при сжатии – к сечению.
Рис. 2. Нормальная сила N
Растягивающие продольные силы принято считать положительными (рис. 3, а), а сжимающие – отрицательными (рис. 3, б).
Рис. 3. Знак продольной силы N
При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от Nz), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки.
Продольные силы (Nz), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений.
График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп. Nz). Он дает наглядное представление о законе изменения продольной силы.
Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.
Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти Nmax при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.
Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный.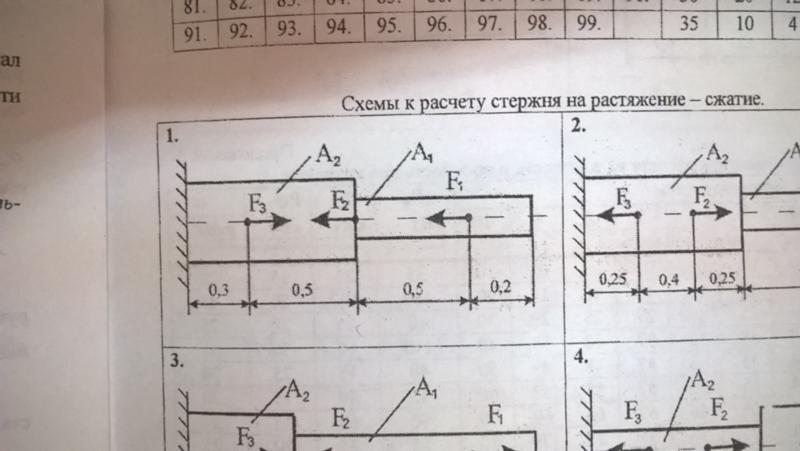
Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня.
Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса.
На основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось.
Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает.
§2. Напряжение в поперечных сечениях стержня
При растяжении или сжатии осевыми силами стержней из однородного материала поперечные сечения, достаточно удаленные от точек приложения внешних сил ,остаются плоскими и перемещаются поступательно в направлении деформации.
Это положение называют — гипотезой плоских сечений. На основании указанного можно заключить, что все точки какого-либо поперечного сечения стержня находятся в одинаковых условиях и, следовательно, напряжения распределяются по сечению равномерно. Эти напряжения перпендикулярны поперечному сечению, а значит, являются нормальными напряжениями. Их значения найдем, разделив продольную силу N на площадь А: σ=N/A
Продольная сила N с помощью метода сечений всегда может быть выражена через внешние силы. В формулe следует подставлять алгебраическое значение N т.е со знаком плюс в случае растяжения и со знаком минус в случае сжатия
§3. Расчеты на прочность и жесткость при растяжении-сжатии
Прочность стержня при осевом растяжении и сжатии обеспечена, если для каждого его поперечного сечения наибольшее расчетное (рабочее) напряжение σ не превосходит допускаемого [σ] : σ=N/A≤ [σ],
где N — абсолютное продольной силы в сечении;
А — площадь поперечного сечения;
[σ] — допускаемое напряжение пр растяжении или сжатии для материала стержня.
Данное выражение определяет условие прочности при растяжении или сжатии.
С помощью этой формулы решается три вида зада (выполняется три вида расчета):
1. Проверка прочности (проверочный расчет). При заданных продольной силы N и площади поперечного сечения А определяют рабочее (расчетное) напряжение и сравнивают его с допускаемым [σ].
Превышение рабочего (расчетного) напряжения не должно быть больше 5% , иначе прочность рассчитываемой детали считается недостаточной.
В случаях, когда рабочее напряжения значительно ниже допускаемых σ<<[σ], получаются неэкономичные конструкции чрезмерным необоснованным расходом материала. Такие решения являются нерациональными. Следует стремится к максимальному использованию прочности материала и снижения материалоемкости конструкций.
2. Подбор сечения (проектный расчет). Исходя из условия прочности можно определить необходимые размеры сечения, зная продольную силу N и допускаемое напряжение [σ]:
A≥N/[σ]
3.
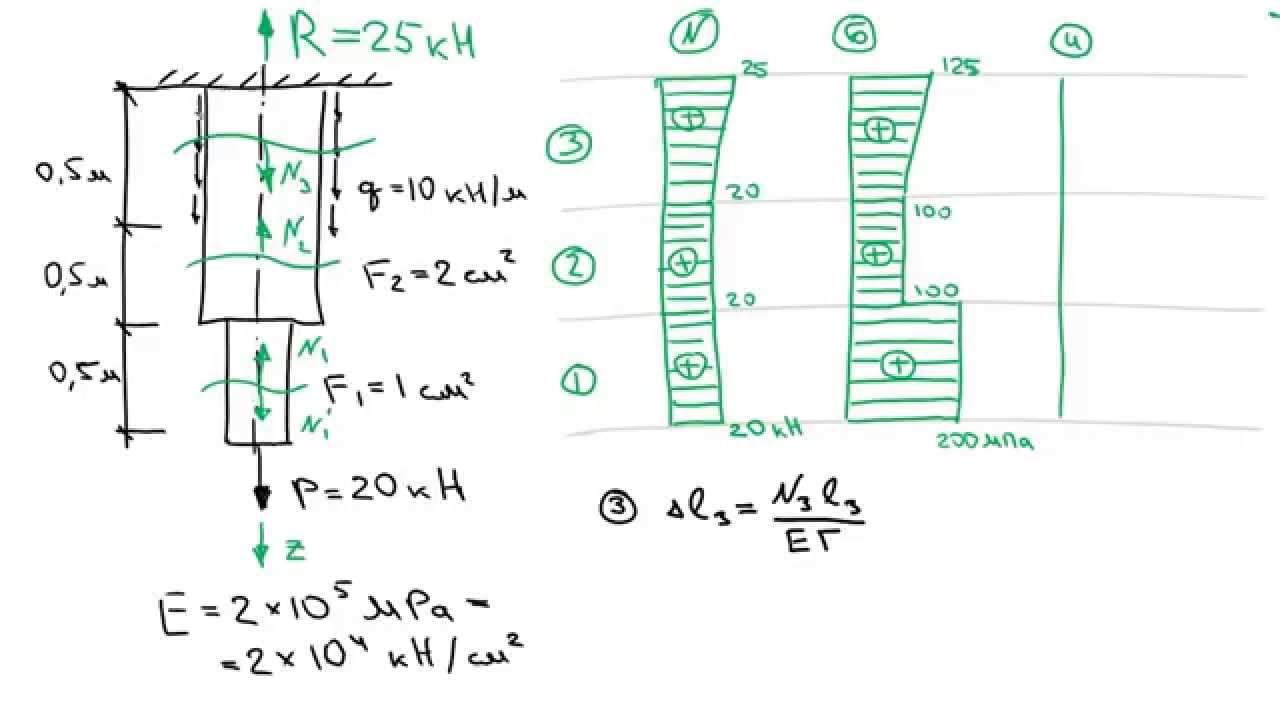Определение допускаемой продольной силы. Допускаемое значение продольной силы в поперечном сечении стержня можно найти по формуле: [N]≤ [σ]·A
Значения допускаемых напряжение для некоторых материалов приведены в табл. 1.
Допускаемые напряжения назначаются на основе результатов механических испытаний образцов соответствующих материалов.
§4. Деформации и перемещения. Закон Гука
Рассмотрим однородный стержень с одним концом, жестко заделанным, и другим — свободным, к которому приложена центральная продольная сила Р (рис. 4). До нагружения стержня его длина равнялась l — после нагружения она стала равной
(рис. 4). Величину называют абсолютной продольной деформацией (абсолютным удлинением) стержня. В большинстве случаев оно мало по сравнению с его первоначальной длиной l (∆l<<l).
Рис. 4. Абсолютное удлинение стержня
Если в нагруженном стержне напряженное состояние является однородным, т.
е. все участки стержня находятся в одинаковых условиях, деформация
остается одной и той же по длине стержня и равной ε = Δl/l
Величина ε называется относительной продольной деформацией.
В пределах малых деформаций при простом растяжении или сжатии закон Гука записывается в следующем виде (нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформации
): σ=Eε
Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости материала первого рода (модуль продольной упругости). Его величина постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки. Так как величина ε безразмерная, то E — измеряется в тех же единицах измерения то и напряжение, т.
е. в Паскалях (Па). Значения модуля упругости E для некоторых конструкционных материалов приведены в табл. 2.
Δl=Nl/EA
Выведенное соотношение показывает, что удлинение (укорочение) при растяжении (сжатии) зависит от величины продольной силы N, поперечного сечения А стержня, его длины l и модуля продольной упругости Е. Произведение ЕА называется жесткостью сечения стержня при растяжении (сжатии).
При растяжении и сжатии изменяются и поперечные размеры стержня. Поперечный размер, первоначально равный a , уменьшается до a1. Изменение поперечно размера Δ a= a- a1, а поперечная деформация равна ε┴= Δ a/ a.
Экспериментально установлено что отношение поперечной деформации к продольной при упругом растяжении или сжатии есть величина постоянная и обозначается µ: µ= ε┴/ ε
Следует учитывать, что продольные и поперечные деформации всегда противоположны по знаку.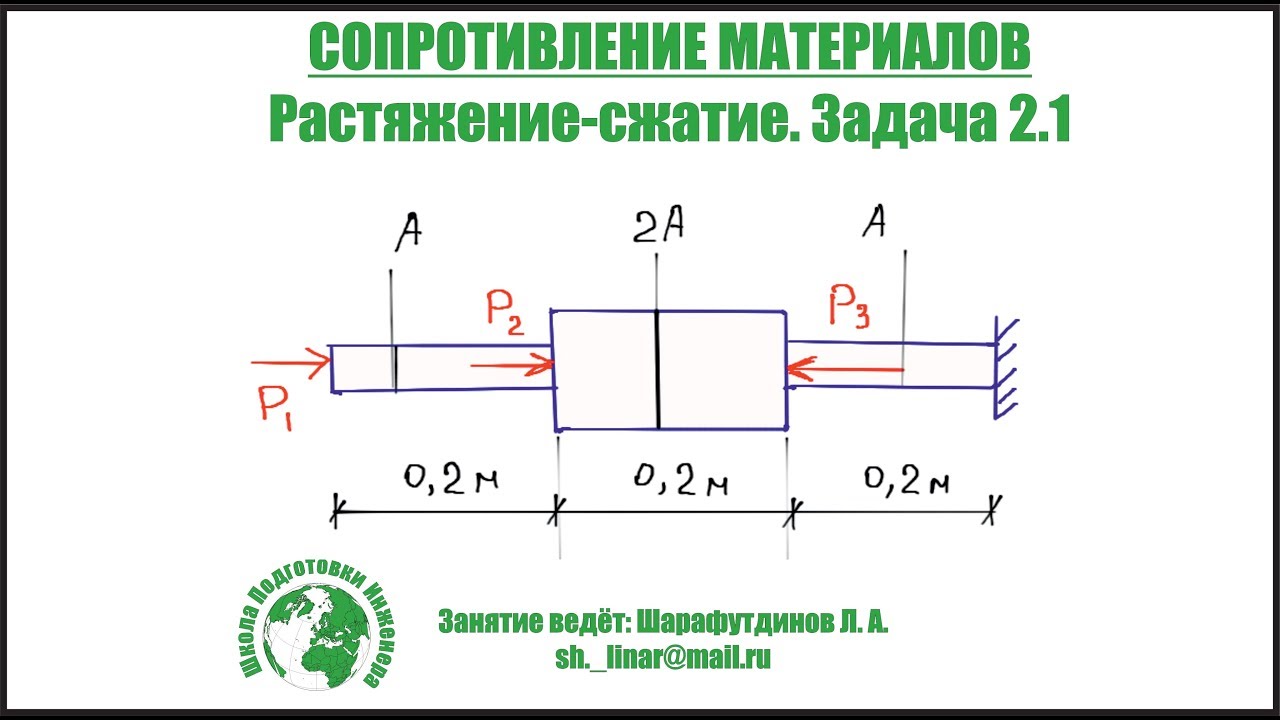
Иными словами, при растяжении, когда продольный размер стержня увеличивается, его поперечный размер уменьшается, и, наоборот , при сжатии продольный размер уменьшается, а поперечный –увеличивается .
Величина µ называется коэффициентом поперечной деформации, или коэффициентом Пуассона. Коэффициент поперечной деформации для некоторых материалов имеет следующие значения:
сталь ….024-032,
медь….031-035,
бронза..032-035,
резина , каучук…047.
Диаграмма взаимодействия — связанный железобетон … / диаграмма взаимодействия-связанный железобетон.pdf / PDF4PRO
1 (Используя CSA) Версия: июнь-6- 2017 Взаимодействие Диаграмма — Связанный Армированный Бетон Колонна Разработка Взаимодействие Диаграмма для квадратной связанной колонны Бетон , показанная на рисунок ниже относительно оси x с использованием положений CSA.
Определите шесть контрольных точек на Взаимодействие Диаграмма и сравнение рассчитанных значений в Справочнике и с точными значениями из полного Взаимодействие Диаграмма , сгенерированная инженерной программой spColumn от StructurePoint. Рис. 1 Армированный Бетонный Поперечное сечение колонны Версия: 6 июня 2017 г. Содержание 1. Чистое сжатие.
3 9 5. Чистый изгиб.. 10 в, а и деформации в арматуре.. 10 Силы в бетоне и 10 Pr и Mr.
. 11 6. Чистая 12 Прочность при чистом осевом растяжении (Prt).. 12 Соответствующий момент (Mrt).. 12 7. Столбец Взаимодействие Диаграмма — Программное обеспечение spColumn.. 13 8. Резюме и сравнение результатов проектирования .. 19 9. Выводы и наблюдения .. 20 1 Проектирование норм Бетонные конструкции (CSA) Ссылка Армированные Бетонные Механика и дизайн, 1-е канадское издание, 2000 г., Джеймс МакГрегор и Фред Майкл Братлетт , Prentice Hall Canada Inc. Расчетные данные fc = 35 МПа fy = 400 МПа Крышка = 55 мм до центра арматуры Колонна 400 мм x 400 мм Верхняя арматура = 4 №
4 30 Нижняя арматура = 4 № 30 Решение Используйте традиционный подход ручных расчетов для создания диаграммы взаимодействия для секции колонны Бетон , показанной выше, путем определения следующих шести контрольных точек: Точка 1: Точка чистого сжатия 2: Напряжение стержня вблизи напряженной поверхности стержня равно нулю, ( fs = 0 ) Точка 3: Напряжение стержня вблизи напряженной поверхности стержня равно fy ( fs = — fy ) Точка 4: Напряжение стержня вблизи напряженной поверхности стержня равно fy ( fs = — fy ) Точка 5: Чистый изгиб Точка 6: Чистое растяжение 2 Рисунок 2 Контрольные точки 3 1.
5 CSA ( ) CSA ( ) Максимальное факторное сопротивление осевой нагрузке , maxroPP CSA (уравнение 10-9) , 4004490 4490 кН 4490 3592 кНr maxroPP ,3592 кНr maxP 4 2. Напряжение стержня вблизи растянутой поверхности элемента равно нулю, ( s = fs = 0 ) Рис. 3. Деформации, силы и плечи моментов ( t = fs = 0) Деформация s равна нулю в крайнем слое растянутой стали. Этот случай учитывается при расчете Взаимодействие Диаграмма , потому что он отмечает переход от соединений внахлестку, разрешенных на всех продольных стержнях, к более жестким требованиям к соединениям внахлестку на растяжение.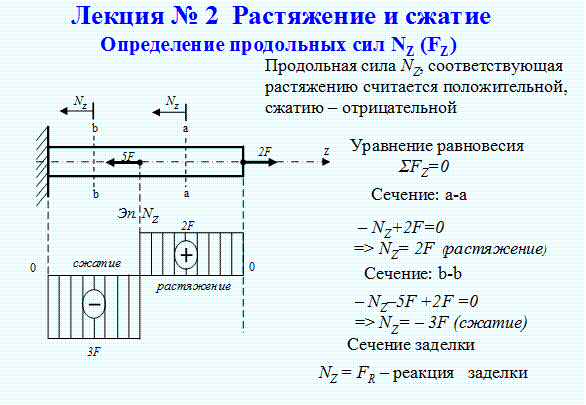
CSA ( и 16) с, а и напряжения в арматуре 1345 мм кд, где с — расстояние от предельно сжатого волокна до нейтральной оси.
6 CSA ( ) 345 304 mmac CSA ( ) Где: a = глубина эквивалентного прямоугольного блока напряжений CSA ( ) ‘ 35 CSA (уравнение 10-2) 0s CSA ( ) CSA ( ) CSA ( ) ‘ ()(345 55 ) (Сжатие) > , 000ycusysFcdcE Силы в бетоне и стали ‘ 35 304 400 2040 kNrcccCfa b CSA ( ) 5 10 kNT0 kNsrssssffA ‘Поскольку > арматура на сжатие выдержала sy ‘400 MPasyff Площадь армирования в этом слое был включен в области (ab), используемой для вычисления Cc. В результате перед вычислением Crs необходимо вычесть 1 cfc из sfs: » 400 352800 905 kNrsssccsffA Pr и Mr 2040 905 0 2945kNrrcrsrsPCCT 212222rrcrsrshahhMCCdTd 400 3044004002040905550345229 6 3.
7 Напряжение в стержнях, близкое к растяжению, на поверхности элемента Равно fy , ( fs = — fy ) Рис. 4 Деформации, силы и плечо момента (fs = — fy) c, a и напряжения в арматуре , 000yysFE арматура не уступила 22ysy CSA ( ) CSA ( ) CSA ( ) 268 Где c — глубина нейтральной оси, измеренная от сжатой кромки сечения колонны.
CSA ( ) 268 237 mmac CSA ( ) Где: a = Глубина эквивалентного прямоугольного блока напряжения CSA ( ) ‘ 35 CSA (Уравнение 10-2) ‘ ()(268 55) (Сжатие) > 268cusycdc Силы в Бетон и сталь ‘ 35 237 400 1586 kNrcccCfa b CSA ( ) 7 200, 000 200 MPassfE 200 2800 476 kNrssssfA ‘Поскольку > арматура на сжатие выдержала sy ‘400 MPasyff Площадь арматуры в этом слое была включена в площадь ( ab) используется для вычисления Cc.
8 В результате перед вычислением Crs: » 400 352800 905 kNrsssccsffA Pr and Mr 1586 905 476 2015kNrrcrsrsPCCT 212222rrcrsrshahhMCCdTd 400 23 необходимо из sfs вычесть 1 cfc 7400400158690555476345330 8 4. Напряжение стержня вблизи растянутой поверхности элемента, равное fy, ( fs = — fy ) Рис. 5 Деформации, силы и плечо момента (fs = — fy) Такое распределение деформации называется случаем сбалансированного разрушения и пределом деформации, контролируемым сжатием. Он отмечает переход от разрушения при сжатии, возникающего в результате разрушения сжимаемой поверхности сечения, к разрушению при растяжении, вызванному текучестью продольной арматуры.
9 C, a и напряжения в арматуре , 000yysFE арматура имеет текучестьsy CSA ( ) CSA ( ) CSA ( ) 220 Где c – глубина нейтральной оси, измеренная от сжатой кромки сечения колонны. CSA ( ) 220 194 mmac CSA ( ) Где: a = глубина эквивалентного прямоугольного блока напряжений CSA ( ) ‘ 35 CSA (уравнение 10-2) ‘ ()(220 55) (сжатие) >
10 В результате перед вычислением Crs: » 400 352800 905 kNrsssccsffA Pr и Mr 1406 901 952 1355kNrrcrsrsPCCT 212222rrcrsrshahhMCCdTd 400 10 необходимо из sfs вычесть 1 cfc 5. Чистый изгиб. Рис. 6. Деформации, силы и плечи моментов ( Чистый момент) Это соответствует случаю, когда учитываемое сопротивление осевой нагрузке Pr равно нулю. Итерационная процедура используется для определения факторизованного сопротивления моменту следующим образом: c, a и напряжения в арматуре Try mmc Где c — глубина нейтральной оси, измеренная от сжатой кромки сечения колонны.