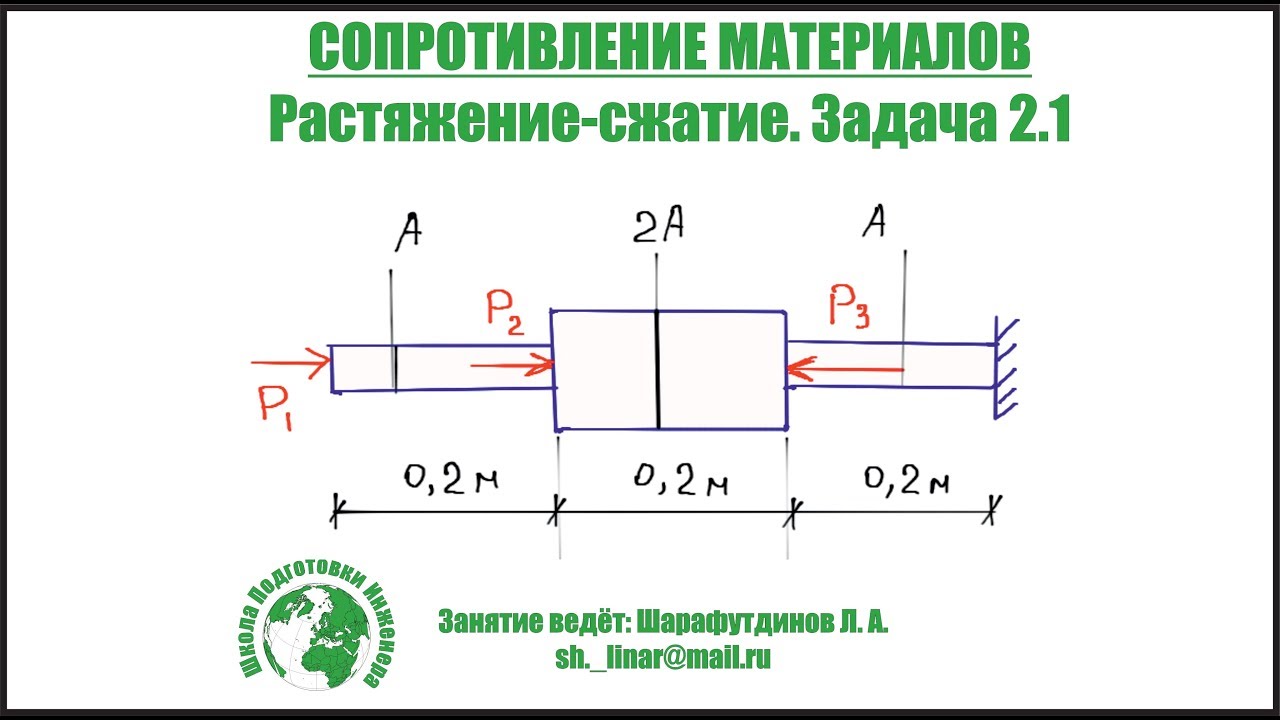
Задание №1. Задачи
- Магазин готовых работ
- Поиск по учебному заведению
- Санкт-Петербургский Государственный Архитектурно-Строительный Университет. СПбГАСУ
- Сопротивление материалов
- Задание №1. Задачи
Задача № 2. Определение напряжений и перемещений в стержне при растяжении-сжатии с учетом собственного веса.
Задача № 3. Определение грузоподъемности статически определимой конструкции, работающей на растяжение-сжатие.
Задача № 4. Расчет статически неопределимого составного стержня, работающего на растяжение-сжатие.
Задача № 5. Расчет статически неопределимой стержневой конструкции, работающей на растяжение-сжатие.
Задача № 6. Определение грузоподъемности статически неопределимой шарнирно-стержневой конструкции.Тема: Исследование плоского напряженного состояния. Проверка прочности для сложного напряженного
 Исследование плоского напряженного состояния по заданным напряжениям на произвольных площадках. Проверка прочности.
Исследование плоского напряженного состояния по заданным напряжениям на произвольных площадках. Проверка прочности.Задача № 8. Исследование плоского напряженного состояния по заданным напряжениям на главных площадках. Проверка прочности.
Задача № 9. Расчет длинной тонкостенной трубы, подверженной действию внутреннего давления, продольной силы и крутящего момента.Тема: Кручение Задача № 10. Подбор сечения составного стержня (вала), работающего на кручение.
Задача № 11. Расчет статически неопределимого вала при кручении.Тема: Изгиб Задачи № 12–15. Определение внутренних усилий в балках при плоском поперечном изгибе.
Задача № 16 (16а). Подбор сечения деревянной (стальной) балки, работающей в условиях плоского поперечного изгиба.
Задача № 17. Подбор сечения стальной двутавровой балки, работающей в условиях плоского поперечного изгиба.
Задача № 18 (18а). Определение грузоподъемности деревянной (стальной) балки, работающей в условиях плоского поперечного изгиба.

Задача № 19. Определение грузоподъемности чугунной балки моносимметричного сечения, работающей в условиях плоского изгиба.
Задача № 20. Подбор сечения и определение перемещений двутавровой балки при плоском изгибе.
Задачи № 21, 22. Определение перемещений в рамах.
Задачи № 23, 24. Расчет статически неопределимой балки (рамы).
Задача № 25. Расчет статически неопределимой рамы с шарнирами с учетом симметрии.
Задача № 26. Расчет плоского трубопровода на температурное воздействие и внутреннее давление.
Задача № 27. Определение напряжений и деформаций в криволинейном стержне.Тема: Сложное сопротивление Задача № 28. Расчет балки, подверженной косому или пространственному изгибу.
Задача № 30. Определение грузоподъемности внецентренно-сжатого призматического стержня массивного несимметричного сечения.

Задача № 31. Определение грузоподъемности внецентренно-сжатого стержня несимметричного сечения из прокатных профилей.
Задача № 32. Расчет стержня в общем случае сложного сопротивления.
Задача № 33. Расчет коленчатого вала на изгиб с кручением.Тема: Устойчивость Задача № 34. Определение грузоподъемности центрально-сжатого стержня.
Задача № 35. Подбор сечения центрально-сжатого стержня.
Задача № 36. Расчет гибкого сжато-изогнутого стержня. Тема: Расчет на динамическую нагрузку Задача № 37. Вынужденные колебания системы с одной степенью свободы.
Задача № 38. Расчет рамы (балки) на ударную нагрузку.
Посмотреть методичку
- Задача № 1. Подбор сечения стержня, подверженного растяжению-сжатию.
- Задача № 1(1). Подбор сечения стержня, подверженного растяжению-сжатию.
- Задача № 2. Определение напряжений и перемещений в стержне при растяжении-сжатии с учетом собственного веса.

- Задача № 3. Определение грузоподъемности статически определимой конструкции, работающей на растяжение-сжатие.
- Задача № 3(1). Определение грузоподъемности статически определимой конструкции, работающей на растяжение-сжатие.
- Задача № 4. Расчет статически неопределимого составного стержня, работающего на растяжение-сжатие.
- Задача №5. Расчет статически неопределимой стержневой конструкции, работающей на растяжение-сжатие.
- Задача № 6. Определение грузоподъемности статически неопределимой шарнирно-стержневой конструкции.
- Задача №7. Исследование плоского напряженного состояния по заданным напряжениям на произвольных площадках. Проверка прочности.
- Задача № 8. Исследование плоского напряженного состояния по заданным напряжениям на главных площадках. Проверка прочности.
- Задача № 10. Подбор сечения составного стержня (вала), работающего на кручение.
- Задача № 13. Определение внутренних усилий в балках при плоском поперечном изгибе
- Задача № 14.
 Определение внутренних усилий в балках при плоском поперечном изгибе.
Определение внутренних усилий в балках при плоском поперечном изгибе. - Задача № 15(1). Определение внутренних усилий в балках при плоском поперечном изгибе.
- Задача №15. Определение внутренних усилий в балках при плоском поперечном изгибе.
- Задача 16. Подбор сечения деревянной балки, работающей в условиях плоского поперечного изгиба.
- Задача № 16(1). Подбор сечения деревянной балки, работающей в условиях плоского поперечного изгиба.
- Задача № 17(1). Подбор сечения стальной двутавровой балки, работающей в условиях плоского поперечного изгиба.
- Задача №17. Подбор сечения стальной двутавровой балки, работающей в условиях плоского поперечного изгиба.
- Задача № 18. Определение грузоподъемности деревянной балки, работающей в условиях плоского поперечного изгиба.
- Задача № 19. Определение грузоподъемности чугунной балки моносимметричного сечения, работающей в условиях плоского изгиба.
- Задача № 20.
 Подбор сечения и определение перемещений двутавровой балки при плоском изгибе.
Подбор сечения и определение перемещений двутавровой балки при плоском изгибе. - Задача № 20(1). Подбор сечения и определение перемещений двутавровой балки при плоском изгибе.
- Задача № 21. Определение перемещений в раме
- Задача № 21(1). Определение перемещений в раме
- Задача № 23. Расчет статически неопределимой балки.
- Задача № 27. Определение напряжений и деформаций в криволинейном стержне.
- Задача № 28. Расчет балки, подверженной косому или пространственному изгибу.
- Задача № 28(1). Расчет балки, подверженной косому или пространственному изгибу.
- Задача №29. Определение грузоподъемности внецентренно-сжатого чугунного стержня большой жесткости.
- Задача № 30(1). Определение грузоподъемности внецентренно-сжатого призматического стержня массивного несимметричного сечения.
- Задача № 31. Определение грузоподъемности внецентренно-сжатого стержня несимметричного сечения из прокатных профилей
- Задача № 32(1).
 Расчет стержня в общем случае сложного сопротивления.
Расчет стержня в общем случае сложного сопротивления. - Задача № 34. Определение грузоподъемности центрально-сжатого стержня.
- Задача № 35. Подбор сечения центрально-сжатого стержня.
- Задача № 35(1). Подбор сечения центрально-сжатого стержня.
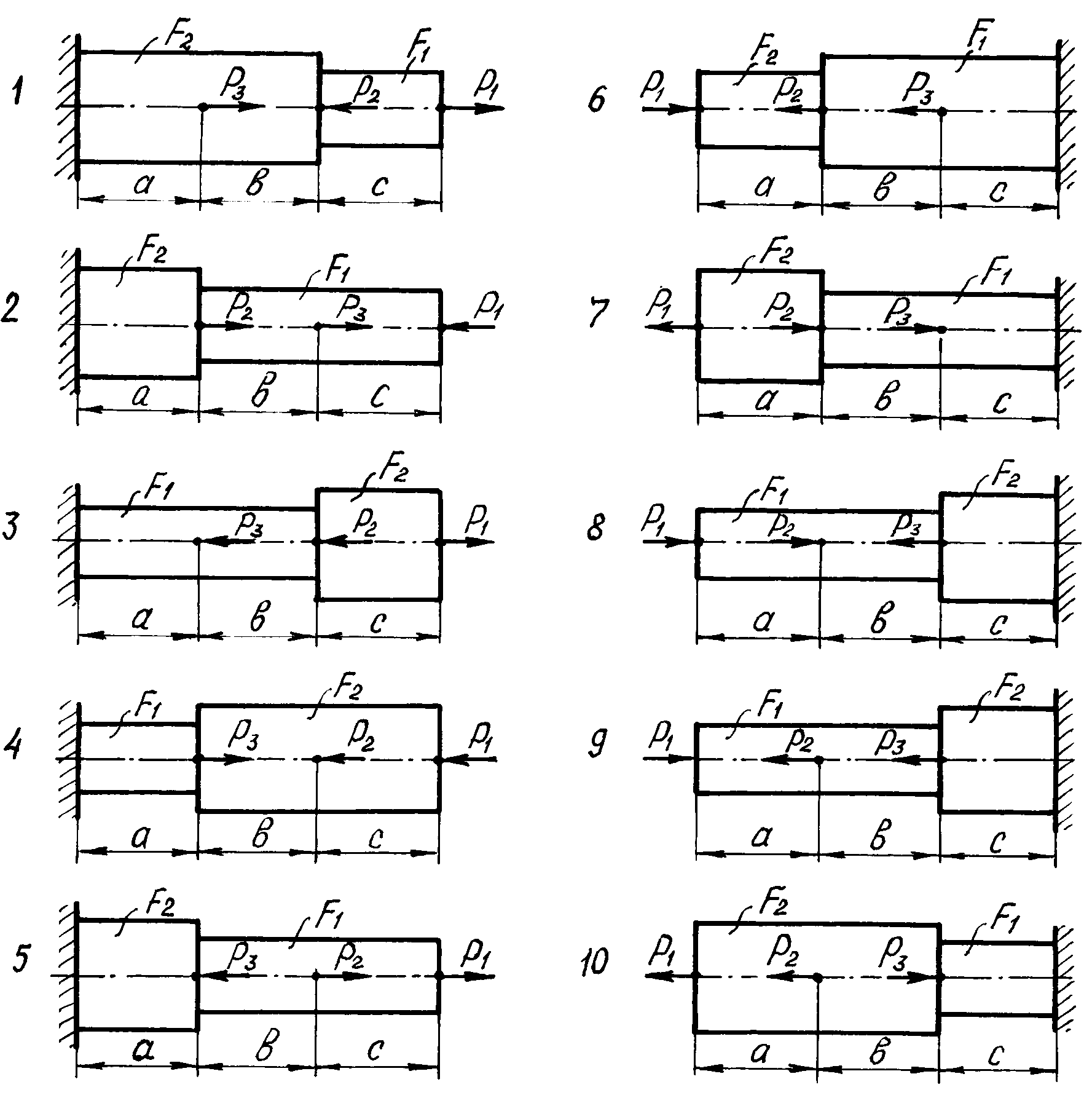
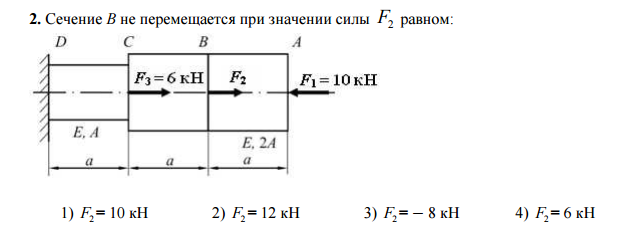
Расчет ступенчатого бруса на растяжение сжатие
Выбери предмет
Технические
Авиационная и ракетно-космическая техника
Автоматизация технологических процессов
Автоматика и управление
Архитектура и строительство
Базы данных
Военное дело
Высшая математика
Геометрия
Гидравлика
Горное дело
Детали машин
Железнодорожный транспорт
Инженерные сети и оборудование
Информатика
Информационная безопасность
Информационные технологии
Искусственный интеллект
Материаловедение
Машиностроение
Металлургия
Метрология
Механика
Микропроцессорная техника
Начертательная геометрия
Пожарная безопасность
Приборостроение и оптотехника
Программирование
Процессы и аппараты
Сварка и сварочное производство
Сопротивление материалов
Судостроение
Текстильная промышленность
Теоретическая механика
Теория вероятностей
Теория игр
Теория машин и механизмов
Теплоэнергетика и теплотехника
Технологические машины и оборудование
Технология продовольственных продуктов и товаров
Транспортные средства
Физика
Черчение
Школьная математика
Электроника, электротехника, радиотехника
Энергетическое машиностроение
Ядерные физика и технологии
Другое
Естественные
Агрохимия и агропочвоведение
Анатомия
Астрономия
Безопасность жизнедеятельности
Биология
Ветеринария
Водные биоресурсы и аквакультура
География
Геодезия
Геология
Естествознание
Землеустройство и кадастр
Медицина
Нефтегазовое дело
Садоводство
Стоматология
Фармация
Химия
Хирургия
Экология
Гуманитарные
Актерское мастерство
Английский язык
Библиотечно-информационная деятельность
Дефектология
Дизайн
Документоведение и архивоведение
Дошкольное образование
Журналистика
Искусство
История
Китайский язык
Конфликтология
Краеведение
Криминалистика
Кулинария
Культурология
Лингвистика
Литература
Логика
Международные отношения
Методика преподавания
Музыка
Немецкий язык
Обществознание
Охрана труда
Парикмахерское искусство
Педагогика
Политология
Право и юриспруденция
Проектная деятельность
Психология
Режиссура
Реклама и PR
Религия
Русский язык
Связи с общественностью
Социальная работа
Социология
Физическая культура
Философия
Французский язык
Эстетика
Этика
Языки (переводы)
Языкознание и филология
Экономические
Анализ хозяйственной деятельности
Антикризисное управление
Банковское дело
Бизнес-планирование
Бухгалтерский учет и аудит
Внешнеэкономическая деятельность
Гостиничное дело
Государственное и муниципальное управление
Деньги
Инвестиции
Инновационный менеджмент
Кредит
Логистика
Маркетинг
Менеджмент
Менеджмент организации
Микро-, макроэкономика
Налоги
Организационное развитие
Производственный маркетинг и менеджмент
Рынок ценных бумаг
Стандартизация
Статистика
Стратегический менеджмент
Страхование
Таможенное дело
Теория управления
Товароведение
Торговое дело
Туризм
Управление качеством
Управление персоналом
Управление проектами
Финансовый менеджмент
Финансы
Ценообразование и оценка бизнеса
Эконометрика
Экономика
Экономика предприятия
Экономика труда
Экономическая теория
Экономический анализ
EVIEWS
SPSS
STATA
Резюме — Гиперучебник по физике
[закрыть]- Обобщенный закон Гука
- стресс
- Напряжение представляет собой силу или комбинацию сил, распределенных по всему объекту, которые деформируют его.

- Напряжения принимают общую форму силы, деленной на площадь ( F / A ).
- Единицей напряжения в системе СИ является паскалей или ньютонов на квадратный метр [Па = Н/м 2 ]
- Напряжение представляет собой силу или комбинацию сил, распределенных по всему объекту, которые деформируют его.
- штамм
- Деформация – это любая деформация объекта, измеренная геометрически как часть некоторого исходного значения.
- Деформации принимают общую форму изменения одной геометрической величины, деленной на первоначальное значение этой величины или аналогичной величины с той же единицей измерения (∆ℓ/ℓ 0 , ∆ В / В 0 и т. д.).
- Деформации всегда являются безразмерными или безразмерными отношениями [м/м, м 3 /м 3 и т.д.]
- модуль (множественное число, модули)
- Напряжение прямо пропорционально деформации.
- Модуль упругости представляет собой отношение некоторого напряжения к деформации, вызванной этим напряжением.
- Единицей СИ всех модулей упругости является паскалей или ньютонов на квадратный метр [Па = Н/м 2 ], но гигапаскалей [1 ГПа = 10 9 Па] чаще используется.
- Модули упругости — это свойства материалов, а не объектов, сделанных из этих материалов.
- стресс
- Напряжение и сжатие
- стресс
- Напряжение растяжения — это нормальная сила на единицу площади (σ = F / A ), которая вызывает увеличение длины объекта.
- Напряжение сжатия — это нормальная сила на единицу площади (σ = F / A ), которая вызывает уменьшение длины объекта.
- штамм
- Деформация растяжения – это относительное увеличение длины объекта (ε = ∆ℓ/ℓ 0 ) из-за напряжения растяжения.
- Деформация сжатия — это частичное уменьшение длины объекта (ε = ∆ℓ/ℓ 0 ) из-за напряжения сжатия.

- модуль
- Модуль Юнга или Модуль упругости представляет собой отношение напряжения растяжения к деформации растяжения или напряжения сжатия к деформации сжатия.
- Символ модуля Юнга: E (для élasticité ) или Y (для молодых).
F = E ∆ℓ 9014 4 А ℓ 0 σ = E ε
- Коэффициент Пуассона
- Осевая деформация в одном направлении обычно сопровождается поперечной деформацией в противоположном направлении.
- Напряжение растяжения делает объекты длиннее и тоньше.
- Напряжение сжатия делает объекты короче и толще.
- Отрицательное отношение поперечной деформации (∆ y / y 0 или ∆ z / z 0 ) к осевой деформации (∆ 900 14 х / х 0 ) называется коэффициентом Пуассона .
- Символ отношения Поссиона: ν (nu).
ν = — ∆ г / г 0 = − ∆ z / z 0 ∆ x / x 0 ∆ х / х 0
- Символ отношения Поссиона: ν (nu).
- Осевая деформация в одном направлении обычно сопровождается поперечной деформацией в противоположном направлении.
- стресс
- Сдвиг
- стресс
- Касательное напряжение — это тангенциальная сила на единицу площади (τ = F / A ), которая заставляет одну грань объекта смещаться параллельно противоположной грани.
- Напряжение сдвига превращает прямоугольники в параллелограммы.
- Касательное напряжение — это тангенциальная сила на единицу площади (τ = F / A ), которая заставляет одну грань объекта смещаться параллельно противоположной грани.
- штамм
- Деформация сдвига — это частичное тангенциальное смещение относительно нормального расстояния между противоположными параллельными гранями (γ = ∆ x / y ), вызванное напряжением сдвига.
- Деформация сдвига представляет собой тангенс угла сдвига.

- Деформация сдвига представляет собой тангенс угла сдвига.
- Деформация сдвига — это частичное тангенциальное смещение относительно нормального расстояния между противоположными параллельными гранями (γ = ∆ x / y ), вызванное напряжением сдвига.
- модуль
- Модуль сдвига или модуль жесткости — отношение напряжения сдвига к деформации сдвига.
- Обозначение модуля сдвига G (для скольжения ) или S (для сдвига)
F = G ∆ x А у τ = G γ
- Обозначение модуля сдвига G (для скольжения ) или S (для сдвига)
- Модуль сдвига или модуль жесткости — отношение напряжения сдвига к деформации сдвига.
- стресс
- оптом
- стресс
- Давление — сжимающее напряжение ( P = F /A), равномерно приложенное ко всем поверхностям объекта.
- Равномерное сжатие или распаковка изменяет объем объектов, но не их форму.
- Давление — сжимающее напряжение ( P = F /A), равномерно приложенное ко всем поверхностям объекта.
- штамм
- Объемная деформация — это частичное изменение объема объекта (θ = ∆ V / V 0 ) из-за изменения давления.

- Объемная деформация — это частичное изменение объема объекта (θ = ∆ V / V 0 ) из-за изменения давления.
- модуль
- Модуль объемного сжатия или модуль сжатия представляет собой отношение увеличения давления к относительному уменьшению объема.
- Символ объемного модуля K (для сжатие ) или B (для объемного).
F = К ∆ В А В 0 P = Κ θ
- Символ объемного модуля K (для сжатие ) или B (для объемного).
- Величина, обратная объемному модулю, называется сжимаемостью .
- Символом сжимаемости является β (бета) или κ (каппа).
β = 1 К - Единицей сжимаемости в системе СИ является обратный паскаль [Па −1 ].
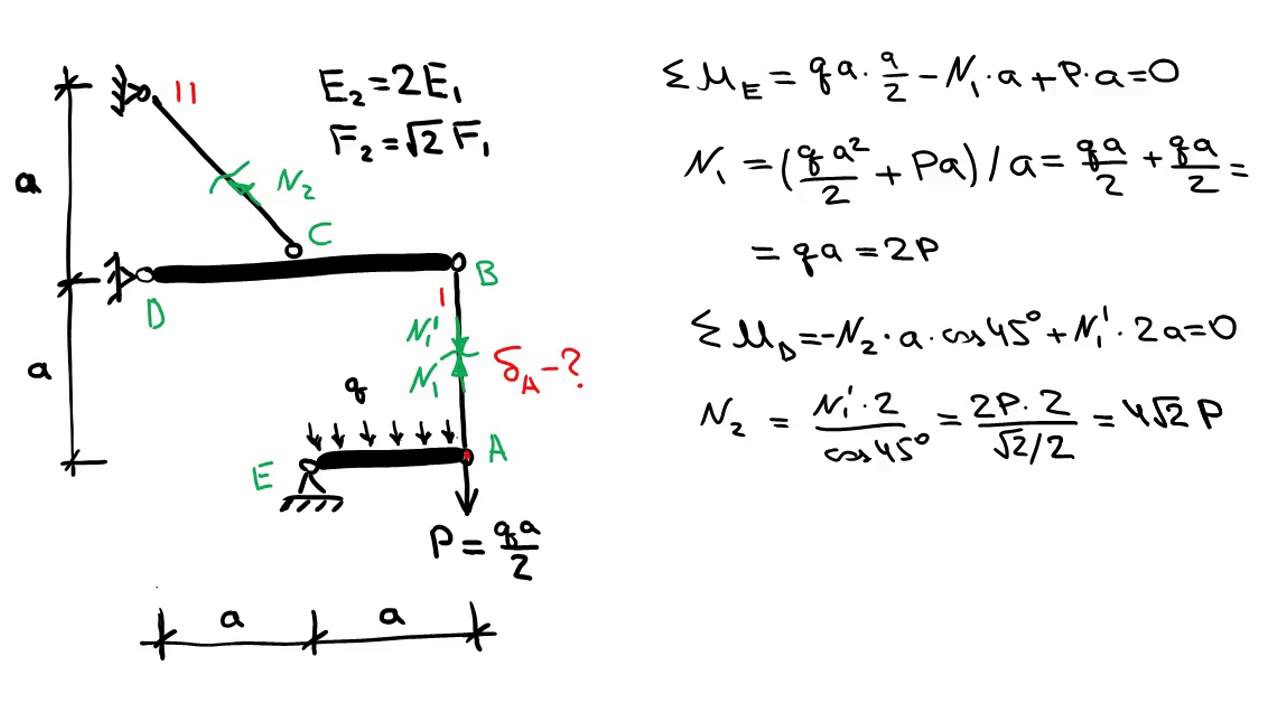
- Символом сжимаемости является β (бета) или κ (каппа).
- Модуль объемного сжатия или модуль сжатия представляет собой отношение увеличения давления к относительному уменьшению объема.
- стресс
Напряжение сжатия: определение, единица измерения, формула и пример
Когда внешняя сила прикладывается таким образом, что сжимает или сжимает объект, это вызывает тип напряжения, называемый сжимающим напряжением. Сжимающее напряжение заставляло атомы в материале пытаться двигаться ближе друг к другу, чем позволяют кристаллическая структура и межатомные силы. Атомы проскальзывают друг относительно друга на более слабых плоскостях кристалла, а также в дефектах и пустотах, вызывая коробление и, в конечном итоге, разрушение. Напряжение сжатия является ключевым принципом в технике и материаловедении, поскольку оно влияет на прочность и долговечность конструкций и материалов. Обычно напряжение сжатия выражается в паскалях (Па) или фунтах на квадратный дюйм (psi). Напряжение сжатия можно рассчитать, разделив силу, приложенную к объекту, на площадь поперечного сечения, перпендикулярную силе.
Прочность на сжатие — это максимальное напряжение, которое материал может выдержать до разрушения при сжатии.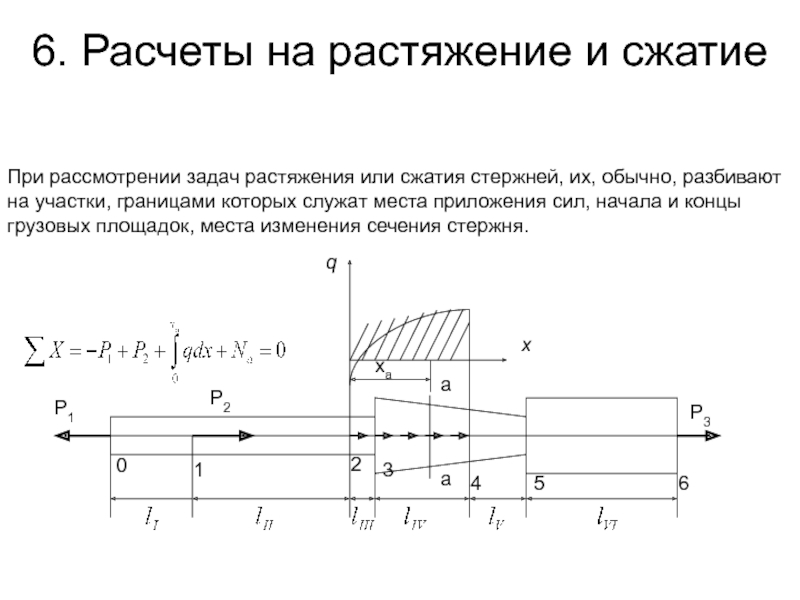 Это важный параметр в области материаловедения, поскольку он определяет, подходит ли материал для данного применения. В этой статье будет обсуждаться напряжение сжатия, как оно рассчитывается, когда оно возникает, и приводятся примеры.
Это важный параметр в области материаловедения, поскольку он определяет, подходит ли материал для данного применения. В этой статье будет обсуждаться напряжение сжатия, как оно рассчитывается, когда оно возникает, и приводятся примеры.
Что такое напряжение сжатия?
Напряжение сжатия представляет собой механическую силу, при которой объект сжимается. Молекулы материала сближаются друг с другом в результате этого особого вида напряжения, что приводит к деформации или разрушению объекта. Понимание реакции материалов на сжимающее напряжение является важной частью инженерии и материаловедения, поскольку оно влияет на прочность, безопасность и долговечность конструкций и искусственных объектов, как больших, так и малых. Роберт Гук — математик и физик 17 века — первым предложил закон Гука. Этот закон описывает взаимосвязь между напряжением и деформацией материала, подвергаемого сжимающим или растягивающим усилиям. С тех пор новые подходы и методы для расчета и анализа сжимающих напряжений были разработаны в различных приложениях в результате развития материаловедения и инженерии.
Когда возникают сжимающие напряжения?
Напряжения сжатия возникают, когда к объекту прикладывается сила, вызывающая его сжатие. Это может произойти в нескольких случаях, например, когда что-то зажато между двумя объектами или когда материал подвергается сильному давлению. Поскольку конструкции и материалы часто подвергаются сжимающим нагрузкам, возникновение сжимающих напряжений в инженерных конструкциях является обычным явлением.
Что такое единица СИ для напряжения сжатия?
Единицей СИ для напряжения сжатия является Паскаль (Па), названный в честь французского физика Блеза Паскаля. Один паскаль равен одному ньютону на квадратный метр (Н/м2). Поскольку большинство материалов очень прочные, напряжение сжатия часто измеряется в килопаскалях (кПа) или мегапаскалях (МПа) в инженерии и материаловедении. Хотя атмосферы (атм) и фунты на квадратный дюйм (фунты на квадратный дюйм) также используются для выражения напряжения сжатия, в научных и инженерных приложениях в основном используется единица СИ, паскаль.
Что такое формула напряжения сжатия?
Формула напряжения сжатия рассчитывается как сила, приложенная к объекту, деленная на площадь его поперечного сечения. В математике это записывается так:
Напряжение сжатия = Сила ÷ Площадь
Когда сила выражается в ньютонах (Н), а площадь выражается в квадратных метрах (м2), результирующей единицей напряжения сжатия является паскаль (Па). Из-за высоких сжимающих усилий, присутствующих во многих приложениях, сжимающее напряжение обычно выражается в килопаскалях (кПа) или мегапаскалях (МПа) в инженерии и материаловедении. 9-2
Анализ размерностей — это математический метод, используемый для изучения размеров или единиц измерения различных физических величин с целью анализа и понимания взаимосвязей между ними. Физические величины, участвующие в задаче, выражаются в терминах их основных размеров, таких как: длина, время, масса и температура. Анализ размерностей может помочь в обеспечении точности и согласованности расчетов и формул, а также в упрощении преобразования единиц за счет отслеживания размеров и единиц измерения этих величин. По сравнению с другими системами единиц измерения, метрическая система или обычные единицы СИ с основанием 10 упрощают преобразование между различными размерными единицами. 9-2
По сравнению с другими системами единиц измерения, метрическая система или обычные единицы СИ с основанием 10 упрощают преобразование между различными размерными единицами. 9-2
Что означает высокое сжимающее напряжение?
Высокое сжимающее напряжение означает, что сжимающие усилия превышают то, что вещество или конструкция может выдержать без деформации или разрушения. Верхний предел высокого напряжения сжатия зависит от конкретного рассматриваемого материала или конструкции, а также от условий использования. Материал или конструкция могут деформироваться, коробиться или ломаться, когда они подвергаются высоким сжимающим напряжениям. В инженерии и материаловедении высокое сжимающее напряжение считается серьезной проблемой, поскольку оно может привести к разрушению конструкции и рискам для безопасности в различных приложениях.
Что является примером напряжения сжатия?
Напряжения сжатия можно наблюдать в строительстве, где бетон используется для возведения конструкций. Бетон известен своей прочностью на сжатие, типичная прочность которой составляет 10 000 фунтов на квадратный дюйм. Примером сжимающего напряжения может быть нагрузка, приложенная к бетонной плите. Приложение внешней сжимающей силы создает равную и противоположную силу внутри бетона, поскольку атомы, составляющие структуру бетона, пытаются сохранить свои первоначальные межатомные расстояния.
Бетон известен своей прочностью на сжатие, типичная прочность которой составляет 10 000 фунтов на квадратный дюйм. Примером сжимающего напряжения может быть нагрузка, приложенная к бетонной плите. Приложение внешней сжимающей силы создает равную и противоположную силу внутри бетона, поскольку атомы, составляющие структуру бетона, пытаются сохранить свои первоначальные межатомные расстояния.
Сталь обычно используется для армирования бетонных конструкций. Это увеличивает прочность материала на растяжение, а также увеличивает напряжение сжатия. Строительные проекты также могут выиграть от прорезиненного бетона. Прорезиненный бетон обычно имеет более низкое напряжение сжатия, чем обычный бетон. Добавление частиц каучука в бетонную смесь снижает общую плотность материала и влияет на сцепление частиц цемента. Прорезиненный бетон обладает дополнительными преимуществами повышенной прочности, долговечности и ударопрочности, при этом демонстрируя достаточное сжимающее напряжение для многих применений.
Какой материал имеет более высокое напряжение сжатия?
Сталь имеет более высокую прочность на сжатие, чем такие материалы, как алюминий, латунь или медь, благодаря более высокому модулю упругости. Модуль упругости является мерой способности материала сопротивляться упругой деформации под нагрузкой. Более высокий модуль означает, что большее напряжение может быть приложено до начала пластической деформации при сжатии и последующего разрушения. Сталь также имеет высокую степень пластичности. Это свойство позволяет ему изгибаться и деформироваться без образования трещин даже при воздействии мощных сжимающих усилий.
Какой материал имеет более низкое напряжение сжатия?
По сравнению с другими материалами бетон имеет низкое напряжение сжатия. Его прочность на сжатие составляет около 10 000 фунтов на квадратный дюйм, что ниже, чем у латуни, меди и стали. Более низкая прочность бетона на сжатие объясняется его составом. Это композитный материал, состоящий из песка, гравия, цемента и воды. Большая часть прочности материала обеспечивается песчано-гравийным заполнителем. Цемент служит связующим веществом, удерживающим частицы заполнителя вместе. Однако из-за своей пористости бетон более склонен к разрушению или растрескиванию под действием сжимающих усилий.
Большая часть прочности материала обеспечивается песчано-гравийным заполнителем. Цемент служит связующим веществом, удерживающим частицы заполнителя вместе. Однако из-за своей пористости бетон более склонен к разрушению или растрескиванию под действием сжимающих усилий.
Как проверить напряжение сжатия?
Ниже приводится обзор того, как определить прочность на сжатие:
- Подготовка проб : Подготовьте пробу вещества для испытания. В зависимости от метода испытаний и типа испытуемого материала это может потребовать резки, сверления или формования материала определенной формы или размера.
- Тестовая установка : Поместите образец между двумя пластинами на испытательном устройстве как часть тестовой установки. Пластины, которые обычно изготавливаются из стали, предназначены для равномерного распределения сжимающей силы по поверхности образца.
- Нагрузка : С помощью испытательного устройства, такого как универсальная испытательная машина, к образцу непрерывно прикладывается сжимающая нагрузка.
 В методе испытаний обычно указывается скорость нагружения, которая может меняться в зависимости от типа испытуемого материала.
В методе испытаний обычно указывается скорость нагружения, которая может меняться в зависимости от типа испытуемого материала. - Измерение нагрузки и деформации : Прибор для испытаний измеряет величину прилагаемой силы, а также деформацию или смещение образца при воздействии на него сжимающей нагрузки. Эти измерения используются для расчета мгновенных сжимающих напряжений и деформаций материала.
- Разрушение и анализ данных : Возрастающая нагрузка прикладывается до тех пор, пока образец не выйдет из строя или не достигнет заданного предела нагрузки или деформации. Прочность материала на сжатие затем определяется путем анализа данных испытаний.
Для получения дополнительной информации см. наше руководство по проверке сжатия.
Как рассчитать напряжение сжатия?
Формула для расчета напряжения сжатия представлена ниже:
Напряжение сжатия = сила / площадь
Где:
- Напряжение сжатия: Напряжение, которое испытывает материал в результате действия силы сжатия.
- Сила: Обычно выражается в фунтах или ньютонах и представляет собой величину давления, оказываемого на материал.
- Площадь: Обычно выражается в квадратных дюймах или квадратных метрах и представляет собой площадь поперечного сечения материала, перпендикулярного направлению силы.
Чтобы рассчитать сжимающее напряжение по формуле, просто разделите сжимающее усилие на площадь поперечного сечения материала. Результирующее сжимающее напряжение принято измерять в фунтах на квадратный дюйм (psi) или в ньютонах на квадратный метр (Н/м2).
Что является основной причиной напряжения сжатия?
Основным источником напряжения сжатия является приложение внешней силы, которая сжимает или сжимает материал, что приводит к уменьшению его объема. Конструкция или объект, давит на материал, или приложение гидравлической или механической силы — вот лишь несколько способов, которыми это может произойти.
Каковы возможные последствия напряжения сжатия?
Напряжение сжатия может вызвать коробление, деформацию или разрыв материала. Материал испытывает сжимающее напряжение, когда к нему приложена сила. Это напряжение может привести к короблению, смятию или уплотнению материала. В зависимости от прочности и упругости материала сжимающие напряжения могут вызвать необратимую деформацию или разрушение компонента или конструкции.
Материал испытывает сжимающее напряжение, когда к нему приложена сила. Это напряжение может привести к короблению, смятию или уплотнению материала. В зависимости от прочности и упругости материала сжимающие напряжения могут вызвать необратимую деформацию или разрушение компонента или конструкции.
Можно ли предотвратить напряжение сжатия?
Нет, напряжения сжатия нельзя полностью избежать. Когда объект сжимается или нажимается, возникает сжимающее напряжение. Это нормальный результат многих физических процессов. Благодаря тщательным инженерным и дизайнерским решениям, таким как использование материалов, более устойчивых к сжатию, или созданию конструкций, которые равномерно распределяют нагрузку, можно уменьшить или контролировать сжимающую нагрузку.
В чем разница между напряжением растяжения и напряжением сжатия?
Напряжение сжатия возникает, когда материал сжимается или сжимается, тогда как напряжение растяжения возникает, когда материал растягивается или растягивается. Основное различие между ними заключается в том, что растягивающее напряжение раздвигает атомы материала, тогда как сжимающее напряжение сталкивает материал вместе. В машиностроении и строительстве, где материалы необходимо выбирать и проектировать на основе их способности противостоять определенным типам сил, крайне важно понимать различие между этими двумя типами нагрузки.
Основное различие между ними заключается в том, что растягивающее напряжение раздвигает атомы материала, тогда как сжимающее напряжение сталкивает материал вместе. В машиностроении и строительстве, где материалы необходимо выбирать и проектировать на основе их способности противостоять определенным типам сил, крайне важно понимать различие между этими двумя типами нагрузки.
Резюме
В этой статье представлено напряжение сжатия, объяснено, что это такое, и обсуждены различные формулы, необходимые для его определения. Чтобы узнать больше о сжимающем напряжении, свяжитесь с представителем Xometry.
Xometry предоставляет широкий спектр производственных возможностей, включая 3D-печать и другие дополнительные услуги для всех ваших потребностей в прототипировании и производстве. Посетите наш веб-сайт, чтобы узнать больше или запросить бесплатное предложение без каких-либо обязательств.
Отказ от ответственности
Контент, отображаемый на этой веб-странице, предназначен только для информационных целей.