Условия равновесия: первое, второе. Виды равновесия: устойчивое, неустойчивое, безразличное, опрокидывание. Формулы, примеры
Тестирование онлайн
Равновесие
Состояние тела, которое не изменяется со временем. Например, тело длительно находится в покое или движется равномерно, или длительно вращается.
Первое условие равновесия
Векторная сумма всех действующих на тело сил равна нулю.
Рассмотрим на примере первое условие равновесия
Предмет будет находиться в равновесии, если векторная сумма всех сил (Fтр1, Fтр2, N1, N2, mg) равна нулю. То есть
Второе условие равновесия
Векторная сумма моментов сил равна нулю
Точку О выберем в точке пересечения Fтр2 и N2. Плечи этих сил равны нулю, значит и моменты этих сил равны нулю.
Определяем плечи сил Fтр1, N1 и mg и направление моментов сил (положительное или отрицательное).
Равновесие бывает устойчивым (тело возвращается в свое первоначальное положение), неустойчивым (тело не возвращается в свое первоначальное состояние), безразличное (тело остается в равновесии, несмотря на то, что на него подействовали (например переложили книгу из одного места на столе в другое). Тело стремится занять такое состояние, при котором его потенциальная энергия будет минимальной, центр масс стремиться быть ниже.
1 — безразличное равновесие, 2 — неустойчивое равновесие, 3 — устойчивое равновесие
На рисунке изображено условие опрокидывания тела.
Тело слева возвращается в исходное состояние. Тело справа опрокидывается.
Тело, имеющее площадь опоры, находится в состоянии устойчивого равновесия, если вертикаль, проведенная через центр масс этого тела, не выходит за рамки контура, ограниченного точками соприкосновения тела с опорой. Если же эта вертикаль проходит вне указанного контура, тело опрокидывается.
Урок 14. статика.
 равновесие абсолютно твердых тел — Физика — 10 класс
равновесие абсолютно твердых тел — Физика — 10 классФизика, 10 класс
Урок 14. Статика. Равновесие абсолютно твёрдых тел
Перечень вопросов, рассматриваемых на уроке:
1.Условия равновесия тела
2.Момент силы
3.Плечо силы
4. Центр тяжести
Глоссарий по теме
Статика – раздел механики, в котором изучается равновесие абсолютно твердых тел, называется статикой
Абсолютно твердое тело – модельное понятие классической механики, обозначающее совокупность точек, расстояния между текущими положениями которых не изменяются.
Центр тяжести – центром тяжести тела называют точку, через которую при любом положении тела в пространстве проходит равнодействующая сил тяжести, действующих на все частицы тела.
Плечо силы — это длина перпендикуляра, опущенного от оси вращения на линию действия силы.
Момент силы — это физическая величина, равная произведению модуля силы на ее плечо.
Устойчивое равновесие — это равновесие, при котором тело, выведенное из состояния устойчивого равновесия, стремится вернуться в начальное положение.
Неустойчивое равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, будет еще больше отклоняться от положения равновесия.
Безразличное равновесие системы — равновесие, при котором после устранения причин, вызвавших малые отклонения, система остается в покое в этом отклоненном состоянии
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017.– С. 165 – 169.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2009.
Степанова Г.Н. Сборник задач по физике. 10-11 класс. — М.: Просвещение. 1999 г. С.48- 50.
Теоретический материал для самостоятельного изучения
Равновесие – это состояние покоя, т.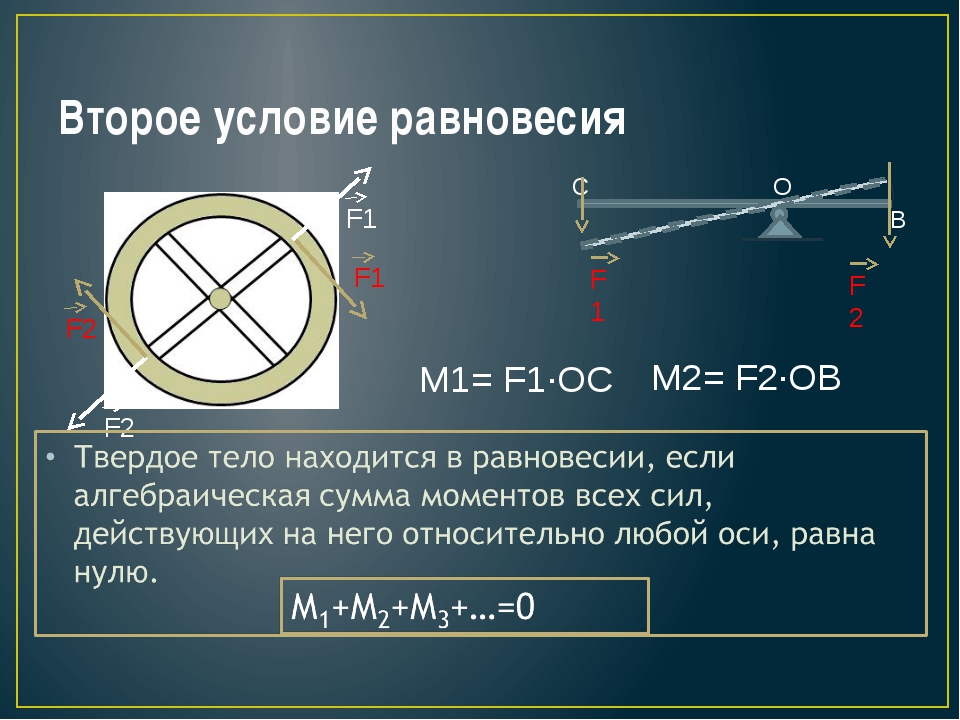
Раздел механики, в котором изучается равновесие абсолютно твердых тел, называется статикой. Статика является частным случаем динамики. В статике твердое тело рассматривается как абсолютно твердое, т.е. недеформируемое тело. Это означает, что деформация так мала, что её можно не учитывать.
Центр тяжести существует у любого тела. Эта точка может находиться и вне тела. Как же подвесить или подпереть тело, чтобы оно находилось в равновесии.
Подобную задачу в свое время решил Архимед. Им же были введены понятие плеча силы и момента силы.
Плечо силы — это длина перпендикуляра, опущенного от оси вращения на линию действия силы.
Момент силы — это физическая величина, равная произведению модуля силы на ее плечо.
После своих исследований Архимед сформулировал условие равновесия рычага и вывел формулу:
Это правило является следствием 2-го закона Ньютона.
Первое условие равновесия
Для равновесия тела необходимо, чтобы сумма всех сил, приложенных к телу была равна нулю.
формула должна быть в векторном виде и стоять знак суммы
Второе условие равновесия
При равновесии твердого тела сумма моментов вcех внешних сил, действующих на него относительно любой оси, равна нулю.
Не менее важен случай, когда тело имеет площадь опоры. Тело, имеющее площадь опоры, находится в равновесии, когда вертикальная прямая, проходящая через центр тяжести тела, не выходит за пределы площади опоры этого тела. Известно, что в городе Пизе в Италии существует наклонная башня. Несмотря на то, что башня наклонена, она не опрокидывается, хотя ее часто называют падающей.
В практике большую роль играет не только выполнение условия равновесия тел, но и качественная характеристика равновесия, называемая устойчивостью.
Различают 3 вида равновесия: устойчивое, неустойчивое, безразличное.
Если при отклонении тела от положения равновесия, возникают силы или моменты сил, стремящиеся вернуть тело в положение равновесия, то такое равновесие называется устойчивым.
Неустойчивое равновесие — это противоположный случай. При отклонении тела от положения равновесия, возникают силы или моменты сил, которые стремятся увеличить это отклонение.
Наконец, если при малом отклонении от положения равновесия тело все равно остается в равновесии, то такое равновесие называется безразличным.
Чаще всего необходимо, чтобы равновесие было устойчивым. Когда равновесие нарушается, то сооружение становится опасным, если его размеры велики.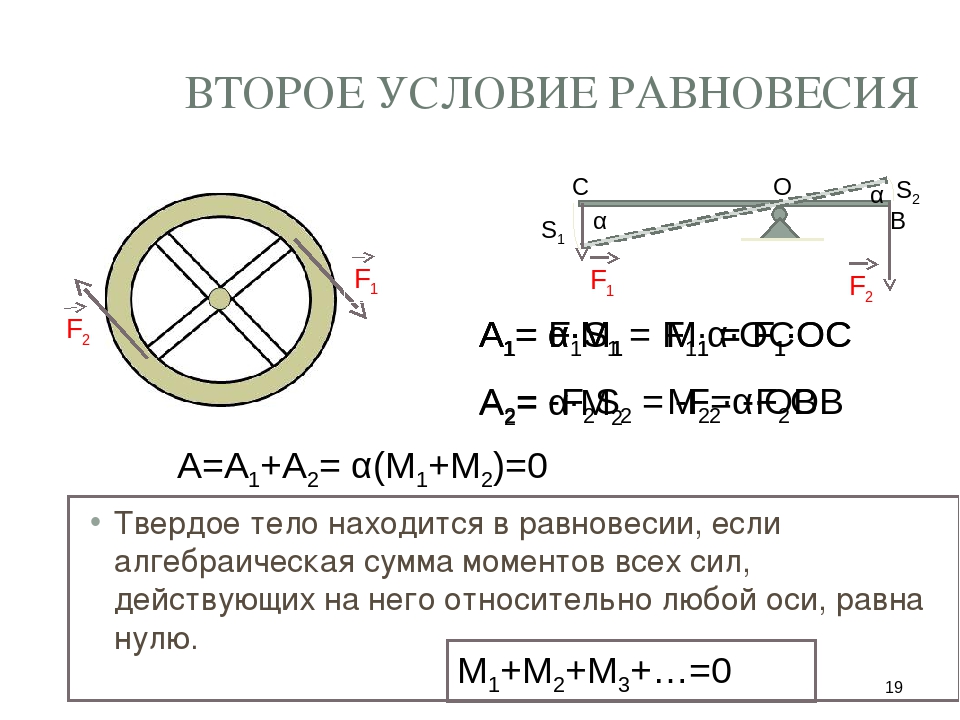
Примеры и разбор решения заданий
1. Чему равен момент силы тяжести груза массой 40 кг, подвешенного на кронштейне АВС, относительно оси, проходящей через точку В, если АВ=0,5 м и угол α=450
Решение:
Момент силы – это величина равная произведению модуля силы на её плечо.
Сначала найдём плечо силы, для этого нам надо опустить перпендикуляр из точки опоры на линию действия силы. Плечо силы тяжести равно расстоянию АС. Так как угол равен 45°, то мы видим, что АС=АВ
Модуль силы тяжести находим по формуле:
После подстановки числовых значений величин мы получим:
F=40×9,8 =400 Н, М= 400 ×0,5=200 Н м.
Ответ: М=200 Н м.
2. Приложив вертикальную силу F, груз массой М — 100 кг удерживают на месте с помощью рычага (см. рис.). Рычаг состоит из шарнира без трения и однородного массивного стержня длиной L=8 м. Расстояние от оси шарнира до точки подвеса груза равно b=2 м. Чему равен модуль силы F, если масса рычага равна 40 кг.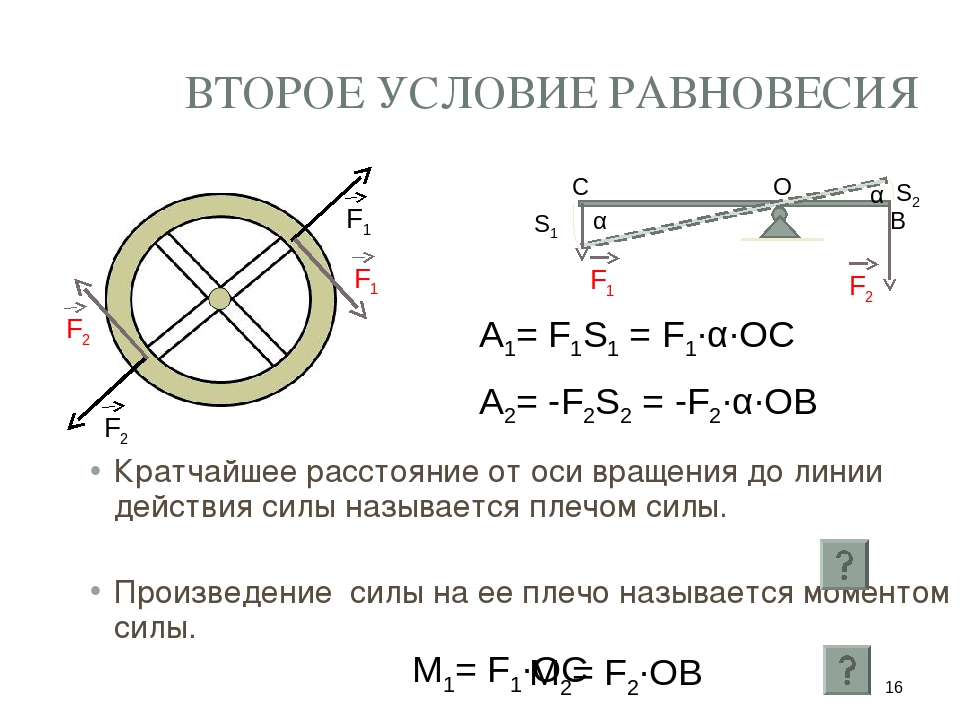
Решение:
По условию задачи рычаг находится в равновесии. Напишем второе условие равновесия для рычага:
.
После подстановки числовых значений величин получим
F= (100×9,8 ×2 + 0,5×40×9,8×8)/8=450 Н
Ответ: 450 Н.
Два условия равновесия тел в физике. Пример решения задачи на равновесие
Раздел физики, который изучает покоящиеся тела с точки зрения механики, называется статикой. Ключевыми моментами статики являются понимание условий равновесия тел в системе и умение применять эти условия для решения практических задач.
Действующие силы
Причиной вращения, поступательного перемещения или сложного движения тел по кривым траекториям является действие внешней ненулевой силы на эти тела. В физике силой называется величина, которая, воздействуя на тело, способна придать ему ускорение, то есть изменить количество движения. Изучают эту величину с давних времен, тем не менее, законы статики и динамики окончательно оформились в стройную физическую теорию только с приходом нового времени. Большую роль в становлении механики движения сыграли работы Исаака Ньютона, в честь которого сейчас называют единицу измерения силы ньютоном.
Большую роль в становлении механики движения сыграли работы Исаака Ньютона, в честь которого сейчас называют единицу измерения силы ньютоном.
При рассмотрении условий равновесия тел в физике важно знать несколько параметров действующих сил. К ним относятся следующие:
- направление действия;
- абсолютное значение;
- точка приложения;
- угол между рассматриваемой силой и другими приложенными к системе силами.
Совокупность перечисленных параметров позволяет однозначно сказать, будет данная система двигаться или покоиться.
Первое условие равновесия системы
Когда система твердых тел не будет поступательно перемещаться в пространстве? Ответ на этот вопрос станет понятен, если вспомнить второй ньютоновский закон. Согласно ему, система не будет совершать поступательного перемещения тогда и только тогда, когда сумма внешних по отношению к системе сил равна нулю. То есть первое условие равновесия твердых тел математически выглядит так:
∑i=1nFi¯ = 0.
Здесь n — число внешних сил в системе. Приведенное выражение предполагает векторное суммирование сил.
Рассмотрим простой случай. Предположим, что на тело действуют две силы одинаковые по величине, но направленные в разные стороны. В итоге одна из них будет стремиться придать ускорение телу вдоль положительного направления произвольно выбранной оси, а другая — вдоль отрицательного. Результатом их действия будет покоящееся тело. Векторная сумма этих двух сил будет равна нулю. Справедливости ради отметим, что описанный пример приведет к появлению растягивающих напряжений в теле, но к теме статьи этот факт не относится.
Для облегчения проверки записанного условия равновесия тел можно воспользоваться геометрическим изображением всех сил в системе. Если их векторы расположить так, чтобы каждая последующая сила начиналась из конца предыдущей, тогда записанное равенство будет выполняться, когда начало первой силы совпадет с концом последней. Геометрически это выглядит в виде замкнутого контура из векторов сил.
Момент силы
Прежде чем переходить к описанию следующего условия равновесия твердого тела, необходимо ввести важное физическое понятие статики — момент силы. Говоря простым языком, скалярная величина момента силы — это произведение модуля самой силы на радиус-вектор от оси вращения до точки приложения силы. Иными словами, момент силы имеет смысл рассматривать только относительно какой-либо оси вращения системы. Скалярная математическая форма записи момента силы выглядит так:
M = F*d.
Где d — плечо силы.
Из записанного выражения следует, что если сила F приложена к любой точке оси вращения под любым углом к ней, то ее момент силы будет равен нулю.
Физический смысл величины M заключается в способности силы F совершать поворот. Эта способность возрастает с увеличением расстояния между точкой приложения силы и осью вращения.
Второе условие равновесия системы
Как можно догадаться, второе условие равновесия тел с моментом силы связано. Сначала приведем соответствующую математическую формулу, а затем разберем ее подробнее. Итак, условие отсутствия вращения в системе записывается так:
Сначала приведем соответствующую математическую формулу, а затем разберем ее подробнее. Итак, условие отсутствия вращения в системе записывается так:
∑i=1nMi = 0.
То есть сумма моментов всех сил должна быть равна нулю относительно каждой оси вращения в системе.
Момент силы является векторной величиной, однако для определения вращательного равновесия важно знать лишь знак данного момента Mi. Следует запомнить, что если сила стремится совершить вращение по ходу стрелки часов, значит, она создает отрицательный момент. Наоборот, вращение против хода стрелки приводит к появлению положительного момента Mi.
Методика определения равновесия системы
Выше были приведены два условия равновесия тел. Очевидно, что для того чтобы тело не двигалось и находилось в покое, необходимо одновременное выполнение обоих условий.
При решении задач на равновесие следует рассматривать систему из записанных двух уравнений. Решение этой системы даст ответ на любую задачу по статике.
Решение этой системы даст ответ на любую задачу по статике.
Иногда первое условие, отражающее отсутствие поступательного движения, может не давать никакой полезной информации, тогда решение задачи сводится к анализу условия моментов.
При рассмотрении проблем статики на условия равновесия тел центр тяжести тела играет важную роль, поскольку именно через него проходит ось вращения. Если сумма моментов сил относительно центра тяжести будет равна нулю, тогда вращение системы наблюдаться не будет.
Пример решения задачи
Известно, что на концы невесомой доски положили два груза. Масса правого груза в два раза больше, чем масса левого. Необходимо определить положение опоры под доской, при которой данная система находилась бы в равновесии.
Обозначим длину доски буквой l, а расстояние от ее левого конца до опоры — буквой x. Ясно, что данная система не испытывает никакого поступательного движения, поэтому первое условие для решения задачи применять не нужно.
Вес каждого груза создает момент силы относительно опоры, причем оба момента имеют разный знак. В выбранных нами обозначениях, второе условие равновесия будет иметь вид:
В выбранных нами обозначениях, второе условие равновесия будет иметь вид:
P1*x = P2*(L-x).
Здесь P1 и P2 — веса левого и правого грузов, соответственно. Разделив на P1 обе части равенства, и используя условие задачи, получаем:
x = P2/P1*(L-x) =>
x = 2*L — 2*x =>
x = 2/3*L.
Таким образом, чтобы система находилась в равновесии, опора должна располагаться на 2/3 длины доски от левого ее конца (на 1/3 от правого конца).
Статика. Условия равновесия. Момент силы. Правило моментов
1. Статика
10 класс© Кузьмина Л.А., шк.№65 г.Санкт-Петербург,
1
2. Содержание
СтатикаМомент силы
Второе условие равновесия
Виды равновесия
Равновесие тел имеющих площадь
опоры
2
3. Статика
Раздел механики, в котором изучаетсяравновесие абсолютно твердых тел,
называется статикой.

Равновесие тела – это состояние покоя
или равномерного и прямолинейного
движения тела.
Абсолютно твердое тело – тело, у
которого деформации, возникающие под
действием приложенных к нему сил,
пренебрежимо малы.
3
4. Первое условие равновесия
F1F1,2
1
F1,3
3
F3,1
F2,1 2 F2
F2,3
F3,2
F1
+
+
F1,2 + F1,3 +…=0
F2 + F2,1 + F2,3 +…=0
F3 + F3,1 + F3,2 +…=0
…….
F3
F1 + F1,2+ F1,3 + F2 + F2,1+ F2,3+ F3+ F3,1+ F3,2+ …=0
F1 + F2 +F3+ …=0
Твердое тело находится в равновесии, если
геометрическая сумма всех сил, приложенных
к нему, равна нулю.
1
2
3 4
4
Момент силы
Правило моментов
10 класс
© Кузьмина Л.А., шк.№65 г.Санкт-Петербург,
14
Что такое равновесие?
Как читается условие равновесия
абсолютно твердого тела?
15
Второе условие равновесия
С
F1
F1
S1
О
α
F1
α S2
В
F2
A1= F1S1 = F1∙α∙OC
F2
F2
A2= -F2S2 = -F2∙α∙OB
Кратчайшее расстояние от оси вращения до
линии действия силы называется плечом силы.

Произведение силы на ее плечо называется
моментом силы. M = F ∙OC
1
1 M2= F2∙OB
16
Второе условие равновесия
С
S1
F1
F2
О
α S2
В
α
F1
F2
A1= α∙М
F1S1 = М
F11∙α∙OC
= F1∙OC
-F2S22 =М-F2=
-F2ОВ
A2= α∙М
2∙α∙OB
А=A1+А2= α(М1+М2)=0
Твердое тело находится в равновесии, если
действующих на него относительно любой оси,
равна нулю.
М1+М2+М3+…=0
19
Условия равновесия
Твердое тело находится в равновесии,
если геометрическая сумма всех сил,
приложенных к нему, равна нулю.
F1 + F2 +F3+ …=0
Твердое тело находится в равновесии,
если алгебраическая сумма моментов всех
сил, действующих на него относительно
любой оси, равна нулю.
М1+М2+М3+…=0
1
2
20
Виды равновесия
10 класс
© Кузьмина Л.А., шк.№65 г.Санкт-Петербург,
25
Что такое равновесие?
При каком условии твердое тело
будет находиться в состоянии
равновесия?
При каком условии твердое тело
способное вращаться будет
находиться в состоянии
равновесия?
26
Виды равновесия
27
Виды равновесия
d
Fт
N
О
Fт
N
О
Fт
Fт
Fт
N d
О
устойчивое
неустойчивое
безразличное
28
14.
 Момент силы Правило моментов Условия устойчивости равновесия
Момент силы Правило моментов Условия устойчивости равновесияТела находятся в состоянии устойчивого
равновесия, если при малейшем отклонении от
положения равновесия возникает сила или
момент силы, возвращающие тело в положение
равновесия.
Тела находятся в состоянии неустойчивого
равновесия, если при малейшем отклонении от
положения равновесия возникает сила или
момент силы, удаляющие тело от положения
равновесия.
Тела находятся в состоянии безразличного
равновесия, если при малейшем отклонении от
положения равновесия не возникает ни сила, ни
момент силы, изменяющие положение тела.
29
Условия устойчивости равновесия
30
16. Второе условие равновесия
Равновесие тел на опорахℓ
ℓ
Fт
Fт
Fт
Fт
Тело, имеющее площадь опоры, будет
находиться в равновесии до тех пор, пока
линия действия силы тяжести будет
проходить через площадь опоры.
31
17.
 Плечо силы Равновесие тел на опорах
Плечо силы Равновесие тел на опорах32
18. Момент силы
Устойчивость транспорта33
Момент силы. Условия равновесия твердого тела
Данная тема посвящена моменту силы и условиям равновесия твердого тела.
Известно, что основным признаком взаимодействия тел в динамике является возникновение ускорений. Однако часто бывает нужно знать, при каких условиях тело, на которое действует несколько сил, не движется с ускорением, а покоится или же движется равномерно и прямолинейно.
Раздел механики, в котором изучаются условия равновесия материальной точки и абсолютно твердого тела, называется статикой.
Абсолютно твердое тело — это тело, размеры и форму которого можно считать неизменной.
Все опытные факты убеждают в том, что любое тело покоится
или движется равномерно и прямолинейно, если равнодействующая всех
сил, действующих на него, равна нулю.
Таким образом первое условие равновесия звучит так: векторная сумма приложенных к телу сил должна быть равна нулю.
Из этого условия следует, что и сумма проекций всех сил на любое направление тоже должна быть равна нулю.
Фактически последние три равенства эквивалентны одному векторному равенству, но с их помощью достаточно просто решать задачи, поскольку проекции сил — это скалярные величины.
В повседневной жизни приходится часто сталкиваться с телами, которые не могут двигаться поступательно, но могут вращаться вокруг оси. Примерами таких тел могут служить двери и окна, качели, колеса машин и так далее.
Рассмотрим однородное тело в форме диска, которое может свободно вращаться вокруг закрепленной оси, проходящей через его центр.
Если к этому телу приложить силу в некоторой точке А,
находящейся под осью вращения, то диск останется в равновесии. Действительно, в
этом случае в диске возникнет сила упругости со стороны оси вращения,
которая и будет компенсировать воздействие внешней силы.
Действительно, в
этом случае в диске возникнет сила упругости со стороны оси вращения,
которая и будет компенсировать воздействие внешней силы.
Если подвесить тело в точке B, находящейся выше или ниже точки «А», то равновесие тоже не нарушится. Отсюда можно сделать вывод, что точку приложения силы можно переносить вдоль линии ее действия. При этом, как видно из рисунка, внешняя сила и сила упругости лежат на одной прямой.
Если же прямая, на которой лежит вектор внешней силы, не проходит через ось вращения, то эта сила не может быть скомпенсирована действием силы упругости оси, и тело начнет поворачивается.
А что произойдет, если к диску приложить не одну, а несколько сил, направленные в разные стороны, например, так, как это показано на рисунке?
Сила F1 будет
стремиться повернуть тело по ходу часовой стрелки, а сила F2
— против хода часовой стрелки. Так вот, в зависимости от соотношения модулей
действующих сил и кратчайших расстояний от оси вращения до линии действия сил,
тело повернется в ту или иную сторону.
Так вот, в зависимости от соотношения модулей
действующих сил и кратчайших расстояний от оси вращения до линии действия сил,
тело повернется в ту или иную сторону.
Если же отношение действующих сил обратно пропорционально этим кратчайшим расстояниям, то тело будет находиться в равновесии.
Данная формула известна из курса физики 7 класса, как условие равновесия рычага.
Кратчайшее расстояние от оси вращения до линии действия силы называется плечом силы. А произведение модуля силы на ее плечо называется моментом силы.
Из определения момента силы следует, что единицей его измерения в системе СИ является
Исходя из условия равновесия рычага и определения момента
силы, можно сформулировать второе условие равновесия тел. И так, тело
находится в равновесии, если алгебраическая сумма моментов всех сил,
приложенных к телу, относительно любой оси равна нулю.
Данное условие равновесия является следствием одной из теорем механики — теоремы Вариньона.
Следует напомнить о том, что при использовании правила моментов необходимо учитывать знаки действующих сил. Так обычно считают, что момент силы, которая вызывает вращение тела по ходу часовой стрелки, положителен. И наоборот, если сила пытается повернуть тело против хода часовой стрелки, то момент этой силы считают отрицательным. Однако можно считать и наоборот.
В механике часто возникает необходимость ответить на вопрос: в
каких случаях тело может сколь угодно долго оставаться в покое, если оно
находилось в покое в начальный момент? Естественно, что должны выполняться
условия равновесия. Но практически не во всяком положении равновесия, тело,
находящееся в начальный момент в покое, будет оставаться в покое и в
последующие моменты времени. Дело в том, что в реальных условиях, помимо
учитываемых сил (сила тяжести, сила реакции подвеса или опоры, силы трения и так
далее), тело испытывает и не учитываемые случайные воздействия. Это могут быть,
например, небольшие сотрясения, колебания воздуха и тому подобное. Под
действием таких сил тело хотя бы немного, но будет отклоняться от положения
равновесия, а в этом случае дальнейшее поведение тела может быть различным.
Это могут быть,
например, небольшие сотрясения, колебания воздуха и тому подобное. Под
действием таких сил тело хотя бы немного, но будет отклоняться от положения
равновесия, а в этом случае дальнейшее поведение тела может быть различным.
Поэтому, для того, чтобы судить о поведении тела в реальных условиях необходимо уметь оценивать равновесие. Различают три вида равновесия — это устойчивое равновесие, неустойчивое равновесие и равновесие безразличное.
Равновесие тела называют устойчивым, если при отклонении тела от положения равновесия возникают силы, возвращающие тело в положение равновесия.
Примером устойчивого равновесия может служить шарик,
находящийся на вогнутой поверхности. Если отклонить шарик от положения
равновесия, то спустя некоторое временя он вернется в первоначальное положение.
Это объясняется тем, что равнодействующая сила в любой точке траектории
шарика (за исключением исходной) направлена к положению равновесия.
В устойчивом положении равновесия центр тяжести тела занимает наинизшее из всех близких положений. Тогда очевидно, что такое равновесие тела связано с минимумом его потенциальной энергии.
Если же равнодействующая сила не возвращает тело в первоначальное положение равновесия, а вызывает его дальнейшее отклонение от него, то такое равновесие называется неустойчивым.
В таком положении, например, находится шарик на выпуклой подставке. При отклонении равнодействующая сила направлена от положения равновесия. В положении неустойчивого равновесия высота центра тяжести тела максимальна. Следовательно, такое равновесие связано с максимумом потенциальной энергии тела.
Если смещения тела в любом направлении не вызывает изменение
действующих на него сил (то есть равнодействующая всех сил, приложенных к телу,
остается равной нулю), то такое положение равновесия называется безразличным.
В таком положении находится шарик на горизонтальной плоскости. Безразличное равновесие связано с неизменной потенциальной энергией, а высота центра тяжести тела одинакова во всех достаточно близких положениях.
Другим примером равновесий может быть равновесие тела, имеющего ось вращения. В качестве примера рассмотрим однородное тело прямоугольной формы (например, линейку), которое может вращаться вокруг оси, проходящей через точку О.
Линейка будет находиться в устойчивом равновесии, если ее
центр тяжести (точка C) находится ниже оси
вращения (то есть ниже точки O). При отклонении
от положения равновесия возникает момент силы тяжести, который возвращает линейку
в положение равновесия. Очевидно, что в отклоненном положении потенциальная
энергия линейки больше, чем в положении равновесия. Таким образом, тело,
имеющее ось вращения, будет находиться и устойчивом равновесии, если центр
тяжести тела находится на вертикальной прямой, проходящей через ось вращения, ниже
оси вращения.
Если же центр тяжести находится на вертикальной прямой, проходящей через ось вращения, расположен выше оси вращения, то равновесие будет неустойчивым. В этом случае при отклонении момент силы тяжести отклоняет тело еще дальше от первоначального положения равновесия. При этом потенциальная энергия тела уменьшается.
Если центр тяжести тела и ось вращения будут совпадать, то при любом положении тела момент силы тяжести равен нулю, поскольку равно нулю плечо этой силы. Иными словами, мы с вами будем наблюдать безразличное равновесие. Что касается потенциальной энергии тела, то она будет оставаться неизменной.
Рассмотрим теперь условия устойчивости тела, опирающегося не
на одну точку, как в ранее рассмотренных случаях, а на несколько точек
(например, стол) или имеющее площадь опоры (например, ящик). В этих случаях для
устойчивого равновесия тела необходимо, чтобы вертикаль, проведенная через
центр тяжести, проходила внутри площади опоры тела, то есть внутри контура,
образованного линиями, соединяющими точки опоры, или внутри площадки, на
которую опирается тело.
Если наклонять стол или ящик, то их центр тяжести будет подниматься. Но момент силы тяжести относительно оси вращения будет стремиться вернуть его в первоначальное положение до тех пор, пока линия действия силы тяжести проходит через площадь опоры.
Однако, если их наклонить так, что линия действия силы тяжести выйдет за пределы площади опоры, то тела опрокинутся вследствие действия момента силы тяжести. Очевидно, что имеется предельный угол наклона, то есть угол между прямой, соединяющей центр тяжести тела и крайнюю точку соприкосновения площади опоры с горизонтальной плоскостью, после которого первоначальное равновесие уже не восстанавливается и тело опрокидывается. Этот предельный угол будет тем меньше, чем выше расположен центр тяжести тела при данной площади опоры.
Основные выводы:
Рассмотрены два условия равновесия тел и основные виды равновесия.
Решаем задания по статике
Статикой называется раздел механики, изучающий равновесие механических систем при воздействии сил и моментов. В статье разберем законы статики, приведем основные формулы.
В статье разберем законы статики, приведем основные формулы.
Условия равновесия
Статика в физике рассматривает абсолютно твердые тела — тела с постоянным расстоянием между любыми двумя точками. В природе они невозможны, однако для упрощения статика сводится к изучению исключительно данных объектов. Статика изучает равновесие тела, то есть состояние механической системы, сохраняющей неподвижность относительно выбранной системы отсчета.
Первое условие равновесия: твердое тело приобретает состояние покоя, состояние равномерного прямолинейного движения, если геометрическая сумма сил, приложенных к объекту, равна нулю. Рассмотрим рисунок. На объект действуют F1, F2, F3, их можно разложить на дополнительные равнодействующие силы. Условие равновесия следующее:
F1 + F12 + F13 + F2 + F21 + F23 + F3 + F31 + F32 = 0
F1 + F2 + F3 = 0
Второе условие равновесия: тело приобретает состояние покоя, состояние равномерного прямолинейного движения, когда сумма моментов сил, влияющих на тело по выбранной оси, равна нулю.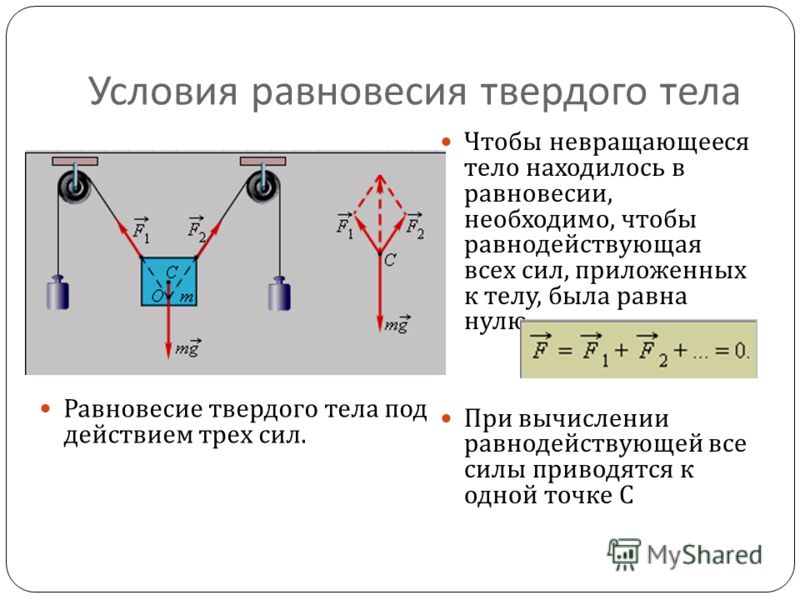 Момент — модуль силы, умноженный на плечо. Плечом называют наиболее короткое расстояние, проведенное от оси вращения до линии действия. Например, рисунок отражает момент F1, равный F1 • OC, момент F2, равный F2 • OB. Момент обозначается буквой M, закон записывается M1 + M2 + M3 +… = 0.
Момент — модуль силы, умноженный на плечо. Плечом называют наиболее короткое расстояние, проведенное от оси вращения до линии действия. Например, рисунок отражает момент F1, равный F1 • OC, момент F2, равный F2 • OB. Момент обозначается буквой M, закон записывается M1 + M2 + M3 +… = 0.
Последний закон статики: объект, обладающий площадью опоры, сохраняет покой, когда линия действия силы тяжести проходит через площадь опоры. Левый рисунок отражает данную ситуацию, тело приобрело состояние покоя. На правом наблюдается расстояние между линией опоры и линией действия силы тяжести — объект приходит во вращение.
Задача
Решим задачу на статику из ЕГЭ по физике.
Условие. Груз, подвешенный на треугольном кронштейне АВС, весит 40 кг. АВ = 0,5 м, угол между АВ и ВС равен 45°. Чему равен момент силы тяжести, проходящий через точку В?
Решение. Помним, момент — показатель, равный произведению модуля на плечо. Внимательно изучим рисунок.
Внимательно изучим рисунок.
Сила тяжести направлена вниз. Плечо — расстояние от точки до линии действия. Получается, им является сторона АС. Поскольку по рисунку один угол прямой, а другой равен 45°, понимаем: треугольник равнобедренный, АС = АВ.
Модуль определяем, используя формулу F = mg = 40 • 10 = 400 Н. Далее ищем момент: M = F • AC = 400 • 0,5 = 200 Н.
Ответ: 200 Н.
Разобрали тему «Статика» по физике, примеры решения задач. Дополнительно выполнять задания можно на курсах «Уникум» Российского университета дружбы народов. Их преимущества:
- возможность посещать онлайн-вебинары;
- доступ к учебному порталу Unikum с полезными материалами, тестами;
- скидка на первый год обучения поступающим на коммерческое отделение.
Содержание данной статьи носит ознакомительный характер. Для подготовки к сдаче ЕГЭ пользуйтесь дополнительными источниками информации!
Статика (материалы для учителя)
Хочу предложить вашему внимания авторскую презентацию по теме «Статика». Презентация рассматривает общие условия равновесия тел; равновесие тел, имеющих площадь опоры; равновесие тел на плоскости. К каждому разделу прилагаются задания для закрепления темы. В дополнение к презентации предлагаю план распределения слайдов презентации по урокам темы, описание слайдов. Презентация «Статика»
Презентация рассматривает общие условия равновесия тел; равновесие тел, имеющих площадь опоры; равновесие тел на плоскости. К каждому разделу прилагаются задания для закрепления темы. В дополнение к презентации предлагаю план распределения слайдов презентации по урокам темы, описание слайдов. Презентация «Статика»
Описание презентации
Ι. Равновесие телСлайд 3
- Раздел механики, в котором изучается равновесие абсолютно твердых тел, называется статикой.
- Равновесие тела – это состояние покоя этого тела.
Вокруг нас нет ни одного тела, на которое не действовали бы силы. Под действием этих сил тела деформируются.
При выяснении условий равновесия деформированных тел необходимо учитывать величину и характер деформации, что усложняет выдвинутую задачу. Поэтому для выяснения основных законов равновесия удобно ввести понятие абсолютно твердого тела.
- Абсолютно твердое тело – тело, у которого деформации, возникающие под действием приложенных к нему сил, пренебрежимо малы.
Рассмотрим условия равновесия абсолютно твердых тел.
Слайд 4
(вывод первого условия равновесия с динамическим рисунком)
Все элементы тела взаимодействуют между собой. Силы, с которыми они действуют друг на друга, называются внутренними. В соответствии с первым законом Ньютона сумма внешних и внутренних сил, действующих на каждый элемент, равна нулю. Сложим все силы, действующие на все элементы тела. По третьему закону Ньютона силы, с которыми два элемента действуют друг на друга, равны по величине и противоположно направлены, а, следовательно их сумма будет равна нулю. После преобразования выражения приходим к выводу, что… .
- Твердое тело находится в равновесии, если геометрическая сумма всех сил, приложенных к нему, равна нулю.
(переход на скрытые слайды – задачи на применение первого условия равновесия)
Задача 1
Электрическая лампа подвешена на шнуре на кронштейне. Найти силы упругости в балках кронштейна, если масса лампы равна 1 кг, а угол α = 60°.
Найти силы упругости в балках кронштейна, если масса лампы равна 1 кг, а угол α = 60°.
Задача 2
К концу двухметрового стержня АС, укрепленного шарнирно одним концом к стене, а с другого конца поддерживаемого тросом ВС длиной 2,5 м, подвешен груз массой 120 кг. Найти силы, действующие на трос и стержень.
Задача 3
На бельевой веревке длиной 10м висит костюм, вес которого 20 Н. Вешалка расположена посередине веревки, и эта точка провисает на 10 см ниже горизонтали, проведенной через точки закрепления веревки. Чему равна сила натяжения веревки?
Задача 4
Найти силы, действующие на подкос ВС и тягу АС, если АВ = 1,5 м, АС = 3 м, ВС = 4 м, а масса груза 200 кг.
В этом состоит первое условие равновесия. Это условие необходимо, но недостаточно.
ΙΙ. Момент силы. Правило моментов.Слайд 14
Вспомним основные понятия равновесия.
Слайд 15
- Что такое равновесие?
- Как читается условие равновесия абсолютно твердого тела?
Данное условие равновесия необходимо, но недостаточно. Рассмотрим условия равновесия тел, способных вращаться вокруг некоторой оси.
Рассмотрим условия равновесия тел, способных вращаться вокруг некоторой оси.
Слайд16
(второе условие равновесия с динамическим рисунком)
Рассмотрим пример с колесом. Если силы, действующие на колесо равны, противоположно направлены и действуют по одной прямой, то равнодействующая сил будет равна нулю и колесо будет в покое. Если те же самые силы будут действовать в противоположных направлениях, но не вдоль одной прямой, то колесо будет поворачиваться.
Найдем условие равновесия стержня способного поворачиваться вокруг некоторой оси.
Каждая из сил, действующих на стержень, стремится повернуть его в свою сторону.
Определим работу, которую совершают внешние силы при повороте рычага на малый угол.
Для вывода второго условия равновесия необходимо ввести два новых понятия: плечо силы, момент силы.
Кратчайшее расстояние от оси вращения до линии действия силы называется плечом силы. (ссылка на слайд 17)
Слайд 17
(скрытый – задачи на определение плеча силы)
- Однородный куб опирается одним ребром о пол, другим – о вертикальную стену.
 Плечо силы трения относительно т.О равно… (см рис.)
Плечо силы трения относительно т.О равно… (см рис.) - На рисунке схематически изображена лестница АВ, опирающаяся на стену. Определите плечо…
а) силы трения относительно точек А, О, В, D.
б) силы реакции опоры относительно точек А, О, В, D.
б) силы тяжести относительно точек А, О, В, D.
Работа силы зависит от произведения силы на ее плечо. (возврат на слайд 17)
Произведение силы на ее плечо называется моментом силы.
Слайд 18
(скрытый – определение момента силы)
- Чему равен момент силы F1 относительно точки О? (см. рис.)
- Наклонная плоскость длиной 0,6м составляет 600 с поверхностью стола. Чему равен момент силы тяжести бруска массой 0,1 кг, находящегося на середине наклонной плоскости относительно точки О?
Вернемся ко второму условию равновесия.
Слайд 19
(вывод второго условия равновесия)
Следовательно, работа каждой силы пропорциональна моменту данной силы. Полная работа всех сил определяется суммой моментов.
Если рычаг находится в равновесии, то работа всех сил равна нулю, и, соответственно, сумма моментов всех сил равна нулю.
Таким образом, второе условие равновесия можно сформулировать так:
- Твердое тело находится в равновесии, если алгебраическая сумма моментов всех сил, действующих на него относительно любой оси, равна нулю.
При этом договорились считать моменты сил, поворачивающих тело по часовой стрелке, положительными, а моменты сил, поворачивающих тело против часовой стрелки, отрицательными.
Подведем итог.
Слайд 20
(объединение условий равновесия)
- Твердое тело находится в равновесии, если геометрическая сумма всех сил, приложенных к нему, равна нулю.
- Твердое тело находится в равновесии, если алгебраическая сумма моментов всех сил, действующих на него относительно любой оси, равна нулю.

Слайд 21
(слайды 11-12 – скрытые – задачи на применение правила моментов сил)
Задача 1
Электрическая лампа подвешена на шнуре на кронштейне. Найти силы упругости в балках кронштейна, если масса лампы равна 1 кг, а угол α = 60°.
(3-ий способ – решение – слайд 23)
Слайд 22
Задача 2
К балке массой 200кг и длиной 5м подвешен груз массой 250кг на расстоянии 3м от одного из концов. Балка своими концами лежит на опорах. Каковы силы давления на каждую из опор?
(решение – слайд 24)
Равновесие бывает разным.
ΙΙΙ. Виды равновесия.Слайд 25
Прежде, чем будем рассматривать виды равновесия, ответьте на вопросы…
Слайд 26
- Что такое равновесие?
- При каком условии твердое тело будет находиться в состоянии равновесия?
- При каком условии твердое тело способное вращаться будет находиться в состоянии равновесия?
Слайд 27
(виды равновесия – рисунки)
Рассмотрим условия различных видов равновесия тел, находящихся на плоскости. Тело находится в состоянии устойчивого равновесия, если при малейшем отклонении тела от положения равновесия возникает сила, возвращающая тело в положение равновесия.
Тело находится в состоянии устойчивого равновесия, если при малейшем отклонении тела от положения равновесия возникает сила, возвращающая тело в положение равновесия.
Тело находится в состоянии неустойчивого равновесия, если при малейшем отклонении тела от положения равновесия возникает сила, удаляющая тело от положения равновесия.
Тело находится в состоянии безразличного равновесия, если при малейшем отклонении тела от положения равновесия не возникает сил, изменяющих положение тела.
Рассмотрим условия различных видов равновесия тел, имеющих ось вращения.
Слайд 28
(виды равновесия тел, имеющих ось вращения – динамические рисунки)
Тело находится в состоянии устойчивого равновесия, если при малейшем отклонении тела от положения равновесия возникает момент сил, возвращающих тело в положение равновесия.
Тело находится в состоянии безразличного равновесия, если при малейшем отклонении тела от положения равновесия не возникает момента сил, изменяющих положение тела.
Тело находится в состоянии неустойчивого равновесия, если при малейшем отклонении тела от положения равновесия возникает момент сил, удаляющих тело от положения равновесия.
Обобщим условия устойчивости равновесия.
Слайд 29
(обобщение условий равновесия)
- Тела находятся в состоянии устойчивого равновесия, если при малейшем отклонении от положения равновесия возникает сила или момент силы, возвращающие тело в положение равновесия.
- Тела находятся в состоянии неустойчивого равновесия, если при малейшем отклонении от положения равновесия возникает сила или момент силы, удаляющие тело от положения равновесия.
- Тела находятся в состоянии безразличного равновесия, если при малейшем отклонении от положения равновесия не возникает ни сила, ни момент силы, изменяющие положение тела.
Условия устойчивого равновесия широко используются в игрушках, в устройствах, которые должны возвращаться в состояние равновесия при отклонениях.
Слайд 30
(рисунки игрушек, шахматных фигурок и т.д.)
Для тел, имеющих площадь опоры, существует дополнительное условие равновесия.
Слайд 31
(динамические рисунки равновесия тел, имеющих площадь опоры)
Рассмотрим, как изменяется положение линии действия силы тяжести по отношению к оси вращения тела при наклоне тела имеющего площадь опоры.
- Тело, имеющее площадь опоры, будет находиться в равновесии до тех пор, пока линия действия силы тяжести будет проходить через площадь опоры.
Кроме того, обратите внимание, что при повороте тела положение центра тяжести изменяется. А любая система всегда стремится к понижению положения центра тяжести. Так наклоненные тела будут находиться в состоянии устойчивого равновесия, пока линия действия силы тяжести будет проходить через площадь опоры.
Слайд 32
(наклонная башня, телебашня, движение человека)
Покачивание или наклон тела человека при ходьбе также объясняется стремлением сохранить устойчивое положение. Площадь опоры определяется площадью внутри линии, проведенной вокруг крайних точек касания телом опоры. когда человек стоит. Линия действия силы тяжести проходит через опору. Когда человек поднимает ногу, то, чтобы сохранить равновесие, он наклоняется перенося линию действия силы тяжести в новое положение таким образом, чтобы она вновь проходила через площадь опоры.
Площадь опоры определяется площадью внутри линии, проведенной вокруг крайних точек касания телом опоры. когда человек стоит. Линия действия силы тяжести проходит через опору. Когда человек поднимает ногу, то, чтобы сохранить равновесие, он наклоняется перенося линию действия силы тяжести в новое положение таким образом, чтобы она вновь проходила через площадь опоры.
Для устойчивости различных сооружений увеличивают площадь опоры или понижают положение центра тяжести сооружения, изготавливая мощную опору, или и увеличивают площадь опоры и, одновременно, понижают центр тяжести сооружения.
Устойчивость транспорта определяется теми же условиями.
Слайд 33
(наклон машины и автобуса)
Так, из двух видов транспорта автомобиля и автобуса на наклонной дороге более устойчив автомобиль.
При одинаковом наклоне данных видов транспорта у автобуса линия силы тяжести проходит ближе к краю площади опоры.
Приложение 1
9.
 2 Второе условие равновесия – College Physics главы 1-17
2 Второе условие равновесия – College Physics главы 1-17Резюме
- Укажите второе условие, необходимое для достижения равновесия.
- Объясните крутящий момент и факторы, от которых он зависит.
- Описать роль крутящего момента в механике вращения
КРУТЯЩИЙ МОМЕНТ
Второе условие, необходимое для достижения равновесия, заключается в избегании ускоренного вращения (поддержании постоянной угловой скорости.Вращающееся тело или система могут находиться в равновесии, если скорость их вращения постоянна и не изменяется под действием действующих на них сил. Чтобы понять, какие факторы влияют на поворот, давайте подумаем, что происходит, когда вы открываете обычную дверь, вращая ее на петлях.
Несколько известных факторов определяют, насколько эффективно вы открываете дверь. См. рис. 1. Прежде всего, чем больше сила, тем эффективнее она открывает дверь — очевидно, чем сильнее вы нажимаете, тем быстрее открывается дверь. Кроме того, точка, в которую вы нажимаете, имеет решающее значение. Если вы приложите силу слишком близко к петлям, дверь откроется медленно, если вообще откроется. Большинство людей были смущены, совершив эту ошибку и наткнувшись на дверь, которая не открылась так быстро, как ожидалось. Наконец, направление, в котором вы продвигаетесь, также важно. Самое эффективное направление — перпендикулярно двери — мы толкаем в этом направлении почти инстинктивно.
Кроме того, точка, в которую вы нажимаете, имеет решающее значение. Если вы приложите силу слишком близко к петлям, дверь откроется медленно, если вообще откроется. Большинство людей были смущены, совершив эту ошибку и наткнувшись на дверь, которая не открылась так быстро, как ожидалось. Наконец, направление, в котором вы продвигаетесь, также важно. Самое эффективное направление — перпендикулярно двери — мы толкаем в этом направлении почти инстинктивно.
 (c) Та же сила, что и в (a), создает меньший крутящий момент против часовой стрелки, когда она приложена на меньшем расстоянии от шарниров.(г) Та же сила, что и в (а), но действующая в противоположном направлении, создает крутящий момент по часовой стрелке. (e) Меньший крутящий момент против часовой стрелки создается силой той же величины, действующей в той же точке, но в другом направлении. Здесь θ меньше, чем 90º . (f) Крутящий момент здесь равен нулю, так как сила просто тянет шарниры, не производя вращения. В этом случае θ = 0º .
(c) Та же сила, что и в (a), создает меньший крутящий момент против часовой стрелки, когда она приложена на меньшем расстоянии от шарниров.(г) Та же сила, что и в (а), но действующая в противоположном направлении, создает крутящий момент по часовой стрелке. (e) Меньший крутящий момент против часовой стрелки создается силой той же величины, действующей в той же точке, но в другом направлении. Здесь θ меньше, чем 90º . (f) Крутящий момент здесь равен нулю, так как сила просто тянет шарниры, не производя вращения. В этом случае θ = 0º .Величина, направление и точка приложения силы включены в определение физической величины, называемой крутящим моментом. Крутящий момент — вращательный эквивалент силы. Это мера эффективности силы в изменении или ускорении вращения (изменение угловой скорости в течение определенного периода времени). В форме уравнения величина крутящего момента определяется как
[латекс]\boldsymbol{\tau=rF\:\sin\:\theta}[/латекс]
, где[латекс]\boldsymbol{\tau}[/латекс](греческая буква тау) — это символ крутящего момента,[латекс]\жирныйсимвол{r}[/латекс] — это расстояние от точки вращения до точки, где приложена сила,[latex]\boldsymbol{F}[/latex]является величиной силы, а[latex]\boldsymbol{\theta}[/latex]является углом между силой и вектором, направленным из точка приложения к точке поворота, как показано на рисунке 1 и рисунке 2.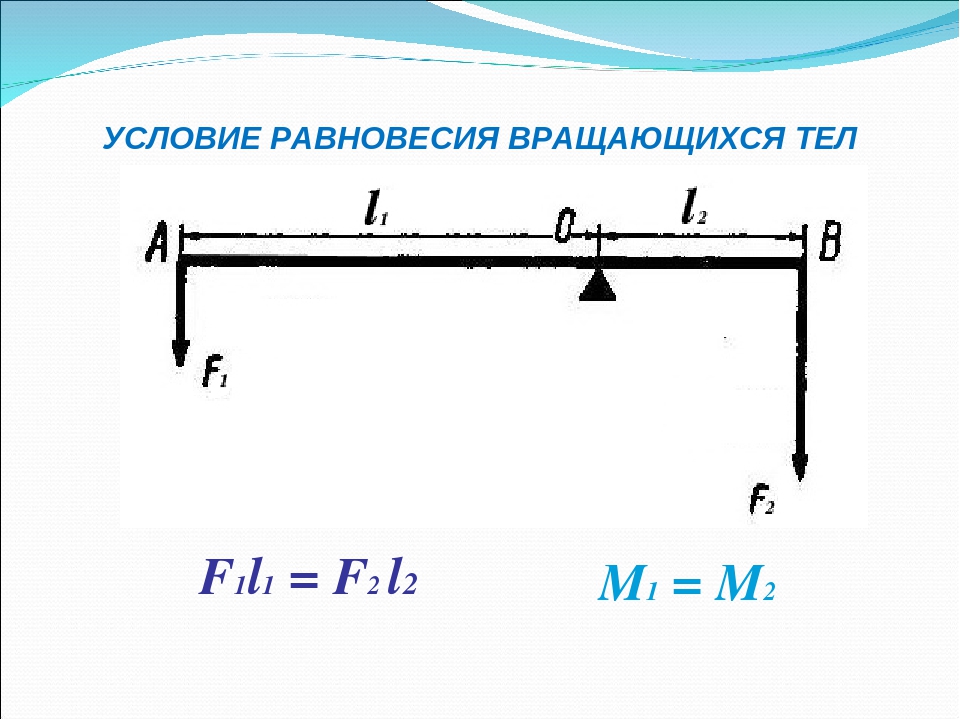 Альтернативное выражение для крутящего момента дается через перпендикулярное плечо рычага [латекс]\boldsymbol{r_{\perp}}[/латекс], как показано на рис. 1 и рис. 2, которое определяется как
Альтернативное выражение для крутящего момента дается через перпендикулярное плечо рычага [латекс]\boldsymbol{r_{\perp}}[/латекс], как показано на рис. 1 и рис. 2, которое определяется как
[латекс]\boldsymbol{r_{\perp}=r\:\sin\:\theta}[/латекс]
так что
[латекс]\boldsymbol{\tau=r_{\perp}F.}[/латекс]
Рисунок 2. Сила, приложенная к объекту, может создавать крутящий момент, который зависит от положения точки вращения. (a) Здесь показаны три фактора r , F и θ для точки вращения A на теле: r — это расстояние от выбранной точки вращения до точки вращения. точка приложения силы F , а θ — угол между F и вектором, направленным от точки приложения к точке вращения.Если объект может вращаться вокруг точки А, он будет вращаться против часовой стрелки. Это означает, что крутящий момент направлен против часовой стрелки относительно точки вращения A. (b) В этом случае точка B является точкой вращения. Крутящий момент от приложенной силы вызовет вращение по часовой стрелке вокруг точки B, и, таким образом, это крутящий момент по часовой стрелке относительно B. расстояние от точки опоры до линии, вдоль которой действует[latex]\textbf{F}[/latex]; он показан пунктирной линией на рис. 1 и рис. 2.Обратите внимание, что отрезок, определяющий расстояние[latex]\boldsymbol{r_{\perp}}[/latex], перпендикулярен [latex]\textbf{F},[/latex], как следует из его названия. Иногда легче найти или визуализировать [латекс]\boldsymbol{r_{\perp}}[/latex], чем найти и [латекс]\boldsymbol{r}[/латекс], и [латекс]\boldsymbol{\theta} .[/latex]В таких случаях может быть удобнее использовать[latex]\boldsymbol{\tau=r_{\perp}F}[/latex],а не [latex]\boldsymbol{tau=rF\:\ sin\:\theta}[/latex] для крутящего момента, но оба они одинаково действительны.0)}[/latex]относительно петель.
Это означает, что крутящий момент направлен против часовой стрелки относительно точки вращения A. (b) В этом случае точка B является точкой вращения. Крутящий момент от приложенной силы вызовет вращение по часовой стрелке вокруг точки B, и, таким образом, это крутящий момент по часовой стрелке относительно B. расстояние от точки опоры до линии, вдоль которой действует[latex]\textbf{F}[/latex]; он показан пунктирной линией на рис. 1 и рис. 2.Обратите внимание, что отрезок, определяющий расстояние[latex]\boldsymbol{r_{\perp}}[/latex], перпендикулярен [latex]\textbf{F},[/latex], как следует из его названия. Иногда легче найти или визуализировать [латекс]\boldsymbol{r_{\perp}}[/latex], чем найти и [латекс]\boldsymbol{r}[/латекс], и [латекс]\boldsymbol{\theta} .[/latex]В таких случаях может быть удобнее использовать[latex]\boldsymbol{\tau=r_{\perp}F}[/latex],а не [latex]\boldsymbol{tau=rF\:\ sin\:\theta}[/latex] для крутящего момента, но оба они одинаково действительны.0)}[/latex]относительно петель.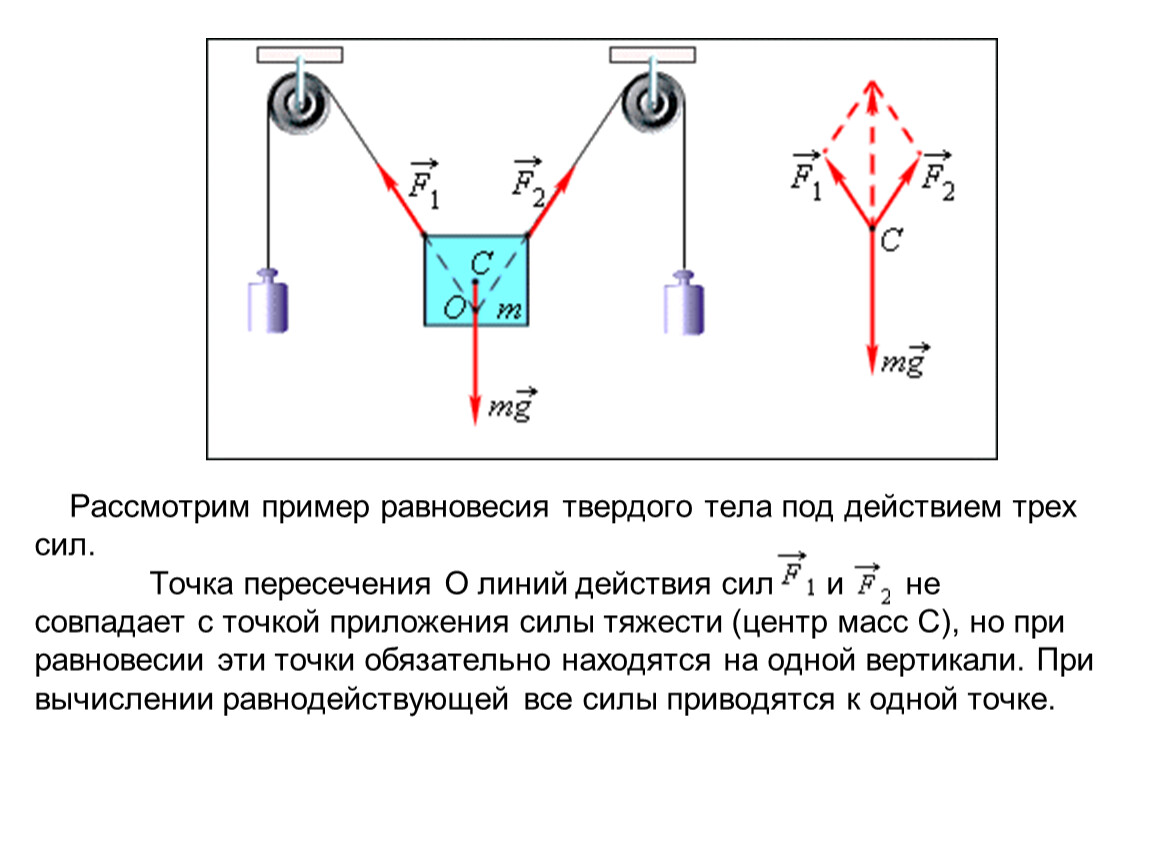 Если вы уменьшите силу до 20 Н, крутящий момент уменьшится до [латекс]\boldsymbol{16\textbf{ Н}\cdotp\textbf{м}},[/латекс]и так далее.
Если вы уменьшите силу до 20 Н, крутящий момент уменьшится до [латекс]\boldsymbol{16\textbf{ Н}\cdotp\textbf{м}},[/латекс]и так далее.Крутящий момент всегда рассчитывается относительно некоторой выбранной точки поворота. Для одной и той же приложенной силы другой выбор положения оси даст другое значение крутящего момента, поскольку как [латекс]\жирныйсимвол{r}[/латекс], так и [латекс]\жирныйсимвол{\тета}[ /latex] зависят от расположения точки опоры. Любая точка любого объекта может быть выбрана для расчета крутящего момента относительно этой точки.Объект может фактически не поворачиваться вокруг выбранной «точки вращения».
Обратите внимание, что при вращении в плоскости крутящий момент имеет два возможных направления. Крутящий момент либо по часовой стрелке, либо против часовой стрелки относительно выбранной точки поворота, как показано для точек B и A соответственно на рисунке 2. Если объект может вращаться вокруг точки A, он будет вращаться против часовой стрелки, что означает, что крутящий момент для силы равен показано как против часовой стрелки относительно точки A. Но если объект может вращаться вокруг точки B, он будет вращаться по часовой стрелке, что означает, что крутящий момент для показанной силы направлен по часовой стрелке относительно точки B.Кроме того, величина крутящего момента больше, когда плечо рычага длиннее.
Но если объект может вращаться вокруг точки B, он будет вращаться по часовой стрелке, что означает, что крутящий момент для показанной силы направлен по часовой стрелке относительно точки B.Кроме того, величина крутящего момента больше, когда плечо рычага длиннее.
Итак, второе условие, необходимое для достижения равновесия , состоит в том, что чистый внешний крутящий момент в системе должен быть равен нулю . Внешний крутящий момент создается внешней силой. Вы можете выбрать точку, вокруг которой рассчитывается крутящий момент. Точка может быть физической точкой вращения системы или любой другой точкой в пространстве, но она должна быть одной и той же точкой для всех крутящих моментов. Если второе условие (чистый внешний крутящий момент в системе равен нулю) выполняется для одного выбора опорной точки, оно также будет выполняться для любого другого выбора опорной точки внутри или вне интересующей системы.(Это верно только в инерциальной системе отсчета.) Второе условие, необходимое для достижения равновесия, сформулировано в форме уравнения как
.
[латекс] \boldsymbol{\textbf{net}\tau=0}[/латекс]
, где чистый означает общий. Моментам, действующим в противоположных направлениях, присваиваются противоположные знаки. Обычно принято называть крутящие моменты против часовой стрелки (ccw) положительными, а крутящие моменты по часовой стрелке (cw) — отрицательными.
Когда двое детей балансируют на качелях, как показано на рисунке 3, они удовлетворяют двум условиям равновесия.Большинство людей имеют прекрасное представление о качелях, зная, что более легкий ребенок должен сидеть дальше от оси вращения и что более тяжелый ребенок может удерживать более легкого на неопределенное время.
Рис. 3. Двое детей, балансирующих на качелях, удовлетворяют обоим условиям равновесия. Более легкий ребенок сидит дальше от оси вращения, чтобы создать крутящий момент, равный по величине крутящему моменту более тяжелого ребенка.Пример 1: Она увидела крутящие моменты на качелях
Двое детей, показанных на рисунке 3, балансируют на качелях незначительной массы. (Это предположение сделано для простоты примера — далее последуют более сложные примеры.) Первый ребенок имеет массу 26,0 кг и сидит на расстоянии 1,60 м от оси вращения. (a) Если второй ребенок имеет массу 32,0 кг, как далеко она от стержня? (b) Какова [латекс]\boldsymbol{F_{\textbf{p}}},[/latex]поддерживающая сила, действующая на шарнир?
(Это предположение сделано для простоты примера — далее последуют более сложные примеры.) Первый ребенок имеет массу 26,0 кг и сидит на расстоянии 1,60 м от оси вращения. (a) Если второй ребенок имеет массу 32,0 кг, как далеко она от стержня? (b) Какова [латекс]\boldsymbol{F_{\textbf{p}}},[/latex]поддерживающая сила, действующая на шарнир?
Стратегия
Должны выполняться оба условия равновесия. В части (а) нас просят указать расстояние; таким образом, необходимо использовать второе условие (относительно крутящих моментов), поскольку в первом (относительно только сил) нет расстояний.Чтобы применить второе условие равновесия, мы сначала идентифицируем интересующую нас систему как качели плюс два потомка. Примем опорную точку за точку, относительно которой вычисляются крутящие моменты. Затем мы определяем все внешние силы, действующие на систему.
Раствор (а)
Три внешние силы, действующие на систему, — это вес двух дочерних элементов и поддерживающая сила стержня. Давайте рассмотрим крутящий момент, создаваемый каждым из них. Крутящий момент определяется как
Давайте рассмотрим крутящий момент, создаваемый каждым из них. Крутящий момент определяется как
[латекс]\boldsymbol{\tau=rF\:\sin\:\theta}.0},[/latex]так что[latex]\boldsymbol{\sin\theta=1}[/latex]для всех трех сил. Это означает [латекс]\жирный символ{r_{\perp}=r}[/латекс]для всех трех. Моменты, создаваемые тремя силами, равны
.[латекс]\boldsymbol{\tau_1=r_1\:w_1}[/латекс]
секунд,
[латекс]\boldsymbol{\tau_2=-r_2\:w_2}[/латекс]
и третий,
[латекс]\begin{array}{lcl} \boldsymbol{\tau _{\textbf{p}}} & \boldsymbol{=} & \boldsymbol{r _{\textbf{p}}F_{\textbf{p} }} \\ {} & \boldsymbol{=} & \boldsymbol{0\:\cdotp\:F_{\textbf{p}}} \\ {} & \boldsymbol{=} & \boldsymbol{0.} \end{массив}[/латекс]
Обратите внимание, что во второе уравнение добавлен знак минус, потому что этот крутящий момент направлен по часовой стрелке и, следовательно, по соглашению является отрицательным. Поскольку [latex]\boldsymbol{F_{\textbf{p}}}[/latex]воздействует непосредственно на точку вращения, расстояние[latex]\boldsymbol{r_{\textbf{p}}}[/latex] равно нулю . Сила, действующая на шарнир, не может вызвать вращение, точно так же, как прямое нажатие на петли двери не заставит ее вращаться. Теперь второе условие равновесия состоит в том, что сумма крутящих моментов обоих потомков равна нулю.Поэтому
Сила, действующая на шарнир, не может вызвать вращение, точно так же, как прямое нажатие на петли двери не заставит ее вращаться. Теперь второе условие равновесия состоит в том, что сумма крутящих моментов обоих потомков равна нулю.Поэтому
[латекс]\boldsymbol{\tau_2=-\tau_1},[/латекс]
или
[латекс]\boldsymbol{r_2\:w_2=r_1\:w_1}.[/латекс]
Вес равен массе, умноженной на ускорение свободного падения. Вводя[latex]\boldsymbol{mg}[/latex]для[latex]\boldsymbol{w},[/latex] получаем
[латекс]\boldsymbol{r_2m_2g=r_1m_1g}.[/латекс]
Решите это для неизвестного[латекс]\жирныйсимвол{r_2}:[/латекс]
[латекс]\boldsymbol{r_2=\:r_1}[/латекс][латекс]\boldsymbol{\frac{m_1}{m_2}}.[/латекс]
Величины в правой части уравнения известны; таким образом, [латекс]\boldsymbol{r_2}[/латекс]равно
[латекс]\boldsymbol{r_2=\:(1,60\textbf{м})}[/латекс][латекс]\boldsymbol{\frac{26,0\textbf{кг}}{32,0\textbf{кг}}}[ /латекс][латекс]\жирныйсимвол{\:=1.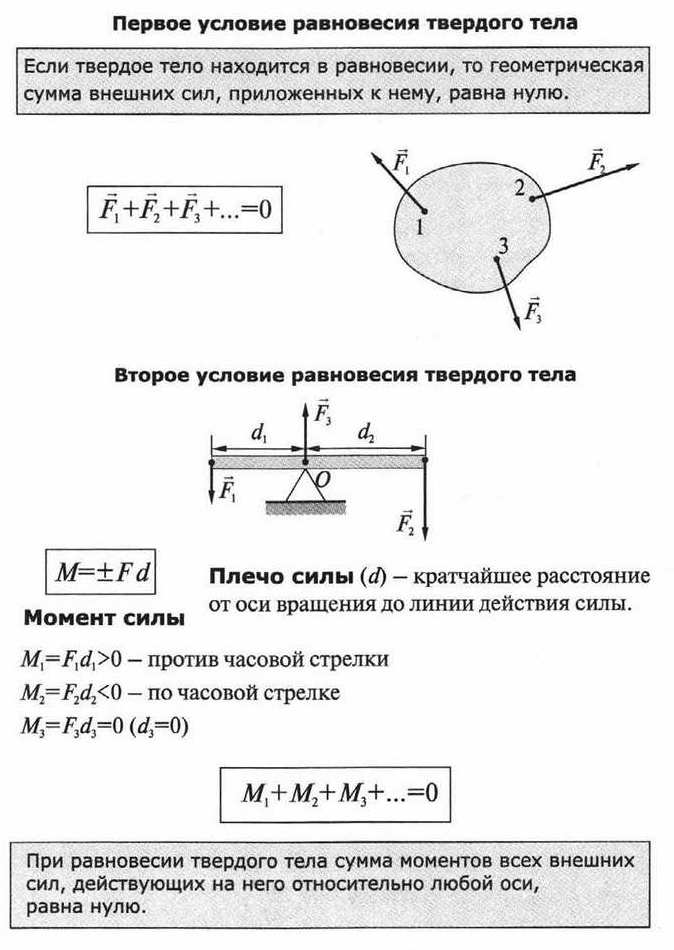 30\textbf{м}}.[/латекс]
30\textbf{м}}.[/латекс]
Как и ожидалось, более тяжелый ребенок должен сидеть ближе к оси вращения (1,30 м против 1,60 м), чтобы уравновесить качели.
Раствор (б)
Эта часть запрашивает силу[латекс]\жирныйсимвол{F_{\textbf{p}}}.[/latex]Самый простой способ найти его — использовать первое условие равновесия, которое равно
.[латекс]\boldsymbol{\textbf{net}F=0}.[/латекс]
Все силы вертикальны, так что мы имеем дело с одномерной задачей вдоль вертикальной оси; следовательно, условие можно записать как
[латекс] \boldsymbol{\textbf{net}F_y=0}[/латекс]
, где мы снова называем вертикальную ось осью и . Выбрав положительное направление вверх и используя знаки плюс и минус для указания направления сил, мы видим, что
[латекс]\boldsymbol{F_{\textbf{p}}-w_1-w_2=0}.[/латекс]
Это уравнение дает то, о чем можно было догадаться вначале:
[латекс]\boldsymbol{F_{\textbf{p}}=w_1+w_2}.[/latex]
Итак, шарнир создает поддерживающую силу, равную общему весу системы:
[латекс]\boldsymbol{F_{\textbf{p}}=m_1g+m_2g}. 2)+(32.2)} \\ {} & \boldsymbol{=} & \boldsymbol{568\textbf{N.}} \end{массив}[/latex]
2)+(32.2)} \\ {} & \boldsymbol{=} & \boldsymbol{568\textbf{N.}} \end{массив}[/latex]
Обсуждение
Два результата интуитивно понятны. Более тяжелый ребенок сидит ближе к оси. Шарнир поддерживает вес двух детей. Часть (b) также может быть решена с использованием второго условия равновесия, поскольку оба расстояния известны, но только в том случае, если точка поворота выбрана не в том месте, где находится фактическая точка поворота качелей!
Несколько аспектов предыдущего примера имеют широкие последствия.Во-первых, выбор точки вращения в качестве точки, вокруг которой рассчитываются крутящие моменты, упростил задачу. Поскольку [латекс]\жирныйсимвол{F_{\textbf{p}}}[/латекс] воздействует на точку вращения, его плечо рычага равно нулю. Следовательно, крутящий момент, создаваемый поддерживающей силой[латекс]\boldsymbol{F_{\textbf{p}}}[/латекс], равен нулю относительно этой точки поворота. Второе условие равновесия выполняется при любом выборе опорной точки, поэтому мы выбираем опорную точку, чтобы упростить решение задачи.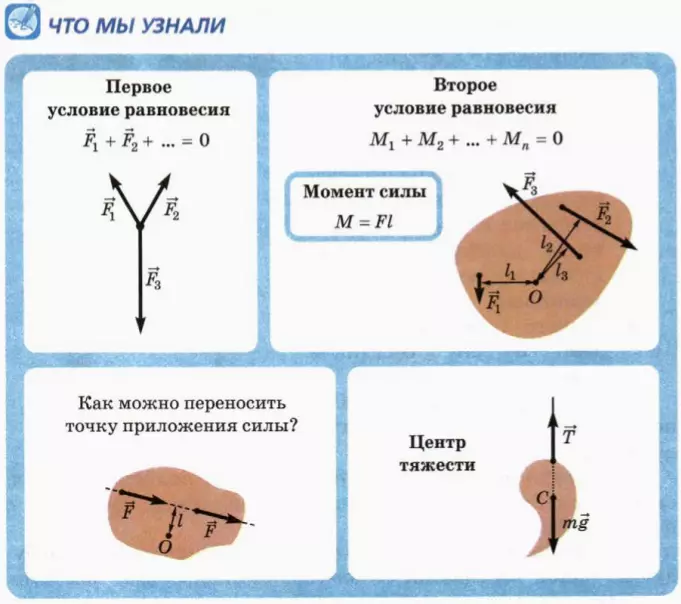
Во-вторых, ускорение свободного падения в этой задаче отменилось, и мы остались с отношением масс. Так будет не всегда . Всегда вводите правильные силы — не забегайте вперед, вводя какое-то отношение масс.
В-третьих, вес каждого ребенка распределяется по площади качелей, однако мы рассматривали веса так, как если бы каждая сила прикладывалась к одной точке. Это не приближение — расстояния[latex]\boldsymbol{r_1}[/latex]и[latex]\boldsymbol{r_2}[/latex]являются расстояниями до точек непосредственно под центром тяжести каждого ребенка. Как мы увидим в следующем разделе, масса и вес системы могут действовать так, как если бы они находились в одной точке.
Наконец, обратите внимание, что концепция крутящего момента имеет значение помимо статического равновесия. Крутящий момент играет ту же роль во вращательном движении, что и сила в прямолинейном движении. Мы рассмотрим это в следующей главе.
ЭКСПЕРИМЕНТ ДЛЯ ДОМАШНИХ
Возьмите кусок глины для лепки и положите его на стол, затем вдавите в него цилиндр так, чтобы линейка могла балансировать на круглой стороне цилиндра, пока все остается неподвижным. Положите монетку на расстоянии 8 см от оси.Куда вам нужно положить две копейки, чтобы сбалансировать? Три пенни?
Положите монетку на расстоянии 8 см от оси.Куда вам нужно положить две копейки, чтобы сбалансировать? Три пенни?
- Второе условие гарантирует, что эти крутящие моменты также сбалансированы. Крутящий момент является вращательным эквивалентом силы, производящей вращение, и определяется как
[латекс]\boldsymbol{\tau=rF\:\sin\:\theta}[/латекс]
где [латекс]\boldsymbol{\tau}[/латекс]это крутящий момент,[латекс]\boldsymbol{r}[/латекс]это расстояние от точки вращения до точки приложения силы,[латекс]\ boldsymbol{F}[/latex] — величина силы, а [latex]\boldsymbol{\theta}[/latex] — угол между [latex]\boldsymbol{F}[/latex] и вектором, направленным из точка, где сила действует на точку опоры.Перпендикулярное плечо рычага[латекс]\boldsymbol{r_{\perp}}[/латекс]определено как
[латекс]\boldsymbol{r_{\perp}=r\:\sin\:\theta}[/латекс]
так что
[латекс]\boldsymbol{\tau=r_{\perp}F}.[/латекс]
- Перпендикулярное плечо рычага[latex]\boldsymbol{r_{\perp}}[/latex]является кратчайшим расстоянием от точки вращения до линии, вдоль которой действует[latex]\boldsymbol{F}[/latex].
 Единицей СИ для крутящего момента является ньютон-метр[латекс]\boldsymbol{(\textbf{N}\cdotp\textbf{м})}.[/latex]Второе условие, необходимое для достижения равновесия, заключается в том, что чистый внешний крутящий момент в системе должен быть равен нулю:
Единицей СИ для крутящего момента является ньютон-метр[латекс]\boldsymbol{(\textbf{N}\cdotp\textbf{м})}.[/latex]Второе условие, необходимое для достижения равновесия, заключается в том, что чистый внешний крутящий момент в системе должен быть равен нулю:[латекс] \boldsymbol{\textbf{net}\tau=0}[/латекс]
По соглашению, крутящий момент против часовой стрелки является положительным, а крутящий момент по часовой стрелке отрицательным.
Концептуальные вопросы
1: Какие три фактора влияют на крутящий момент, создаваемый силой относительно определенной точки поворота?
2: Разрушительный шар используется для разрушения здания.Одна высокая неподдерживаемая бетонная стена осталась стоять. Если разрушающий шар ударится о стену ближе к вершине, стена, скорее всего, упадет, вращаясь у основания, или упадет прямо вниз? Поясните свой ответ. Как вероятнее всего он упадет, если ударить его по основанию с такой же силой? Обратите внимание, что это зависит от того, насколько прочно стена прикреплена к своему основанию.
3: Механики иногда надевают кусок трубы на рукоятку гаечного ключа, когда пытаются открутить очень туго затянутый болт.Как это помогает? (Это также опасно, так как может сломать болт.)
Задачи и упражнения
1: (а) Открывая дверь, вы толкаете ее перпендикулярно с силой 55,0 Н на расстоянии 0,850 м от петель. Какой крутящий момент вы прикладываете к петлям? (b) Имеет ли значение, если вы нажмете на той же высоте, что и петли?
2: При затяжке болта нажимайте перпендикулярно на ключ с усилием 165 Н на расстоянии 0.140 м от центра болта. (a) Какой крутящий момент вы прилагаете в ньютонах × метрах (относительно центра болта)? (b) Переведите этот крутящий момент в футо-фунты.
3: Двое детей во время игры толкают противоположные стороны двери. Оба нажимают горизонтально и перпендикулярно двери. Один ребенок толкает с силой 17,5 Н на расстоянии 0,600 м от шарниров, а второй ребенок толкает на расстоянии 0,450 м. Какую силу должен приложить второй ребенок, чтобы дверь не двигалась? Предположим, что трением можно пренебречь.
Какую силу должен приложить второй ребенок, чтобы дверь не двигалась? Предположим, что трением можно пренебречь.
4: Используйте второе условие равновесия[латекс]\boldsymbol{(\textbf{net}\tau=0)}[/latex]для вычисления[латекс]\boldsymbol{F _{\textbf{p}}} [/latex] в примере 1, используя любые данные, полученные или решенные в части (а) примера.
5: Повторите задачу о качелях из примера 1 с центром масс качелей на 0,160 м левее оси вращения (со стороны более легкого ребенка) и массой качелей 12,0 кг. Остальные данные, приведенные в примере, остаются без изменений.Подробно покажите, как вы следуете шагам стратегии решения проблем для статического равновесия.
Глоссарий
- крутящий момент
- эффективность силы при повороте или скручивании
- перпендикулярный рычаг
- кратчайшее расстояние от точки разворота до линии, вдоль которой лежит FF
- Единицы крутящего момента в системе СИ
- ньютона на метр, обычно записывается как Н·м
- центр тяжести
- точка, в которой предполагается сосредоточение всего веса тела
Задачи и упражнения
1:
а)[латекс]\boldsymbol{46. 8\textbf{N}\cdotp\textbf{m}}[/латекс]
8\textbf{N}\cdotp\textbf{m}}[/латекс]
б) Неважно, на какую высоту вы толкаете. Крутящий момент зависит только от величины приложенной силы и перпендикулярного расстояния приложения силы от шарниров. (Детям не сложнее открыть дверь, потому что они толкают ниже, чем взрослые, им сложнее, потому что они недостаточно далеко от петель.)
3:
23,3 Н
5:
Дано:
[латекс]\begin{array}{lcl} \boldsymbol{m_1} & \boldsymbol{=} & \boldsymbol{26.0\textbf{кг},\:m_2=32.0\textbf{кг},\:m_s=12.0\textbf{кг},} \\ \boldsymbol{r_1} & \boldsymbol{=} & \boldsymbol{1.60\textbf { m},\:r_s=0,160\textbf{ m},\textbf{найти (a)}r_2,\textbf{(b)}F_{\textbf{p}}} \end{массив}[/latex]
а) Так как дети балансируют:
[латекс]\boldsymbol{\textbf{net}\tau_{\textbf{cw}}=-\textbf{net}\tau_{\textbf{ccw}}}[/latex]
[латекс]\boldsymbol{\Rightarrow{w_1r_1}+m_{\textbf{s}}gr_{\textbf{s}}=w_2r_2}[/latex]
Таким образом, решение для [латекс]\boldsymbol{r_2}[/латекс] дает:
[латекс]\begin{array}{lcl} \boldsymbol{r_2} & \boldsymbol{=} & \boldsymbol{\frac{w_1r_1+m _{\textbf{s}}gr_{\textbf{s}}}{ w_2} = \ frac {m_1gr_1 + m _ {\ textbf {s}} gr _ {\ textbf {s}}} {m_2g} = \ frac {m_1r_1 + m _ {\ textbf {s}} r _ {\ textbf {s}} }{m_2}} \\ {} & \boldsymbol{=} & \boldsymbol{\frac{(26. 0\textbf{кг})(1,60\textbf{м})+(12,0\textbf{кг})(0,160\textbf{м})}{32,0\textbf{кг}}} \\ {} & \boldsymbol{ =} & \boldsymbol{1.36\textbf{ m}} \end{массив}[/latex]
0\textbf{кг})(1,60\textbf{м})+(12,0\textbf{кг})(0,160\textbf{м})}{32,0\textbf{кг}}} \\ {} & \boldsymbol{ =} & \boldsymbol{1.36\textbf{ m}} \end{массив}[/latex]
б) Поскольку дети не двигаются:
[латекс] \boldsymbol{\textbf{net F}=0=F_{\textbf{p}}-w_1-w_2-w_s}[/latex]
[латекс] \boldsymbol{\Rightarrow{F}_{\textbf{p}}=w_1+w_2+w_{\textbf{s}}}[/latex]
Так что
[латекс]\begin{array}{lcl} \boldsymbol{F_{\textbf{p}}} & \boldsymbol{=} & \boldsymbol{(26.2)} \\ {} & \boldsymbol{=} & \boldsymbol{686\textbf{N}} \end{массив}[/latex]
5.3: Второе условие равновесия
Цели обучения
К концу этого раздела вы сможете:
- Укажите второе условие, необходимое для достижения равновесия.
- Объясните крутящий момент и факторы, от которых он зависит.
- Описать роль крутящего момента в механике вращения.
Определение: Крутящий момент
Второе условие, необходимое для достижения равновесия, заключается в избегании ускоренного вращения (поддержании постоянной угловой скорости. Вращающееся тело или система могут находиться в равновесии, если скорость их вращения постоянна и не изменяется под действием действующих на них сил. Чтобы понять, какие факторы влияют на поворот, давайте подумаем, что происходит, когда вы открываете обычную дверь, вращая ее на петлях.
Вращающееся тело или система могут находиться в равновесии, если скорость их вращения постоянна и не изменяется под действием действующих на них сил. Чтобы понять, какие факторы влияют на поворот, давайте подумаем, что происходит, когда вы открываете обычную дверь, вращая ее на петлях.
Несколько известных факторов определяют, насколько эффективно вы открываете дверь (рис. \(\PageIndex{1}\)). Прежде всего, чем больше сила, тем эффективнее она открывает дверь — очевидно, чем сильнее вы давите, тем быстрее открывается дверь.Кроме того, точка, в которую вы нажимаете, имеет решающее значение. Если вы приложите силу слишком близко к петлям, дверь откроется медленно, если вообще откроется. Большинство людей были смущены, совершив эту ошибку и наткнувшись на дверь, которая не открылась так быстро, как ожидалось. Наконец, направление, в котором вы продвигаетесь, также важно. Самое эффективное направление — перпендикулярно двери — мы толкаем в этом направлении почти инстинктивно.
Величина, направление и точка приложения силы включены в определение физической величины, называемой крутящим моментом. Крутящий момент является вращательным эквивалентом силы. Это мера эффективности силы в изменении или ускорении вращения (изменение угловой скорости в течение определенного периода времени). Для сил, приложенных строго под прямым углом, мы можем выразить величину крутящего момента в виде уравнения как
Крутящий момент является вращательным эквивалентом силы. Это мера эффективности силы в изменении или ускорении вращения (изменение угловой скорости в течение определенного периода времени). Для сил, приложенных строго под прямым углом, мы можем выразить величину крутящего момента в виде уравнения как
\[\тау = r_{\perp}F \]
, где \(\tau\) (греческая буква tau) – символ крутящего момента, \(r_{\perp}\) – перпендикулярное плечо рычага, а \(F\) – величина силы.
Перпендикулярное плечо рычага \(r_{\perp}\) — это кратчайшее расстояние от точки вращения до линии, вдоль которой действует \(F\). Обратите внимание, что отрезок, определяющий расстояние \(r_{\perp}\), перпендикулярен \(F\), как следует из его названия.
Единицей крутящего момента в СИ является ньютон, умноженный на метр, обычно записывается как Н\(\cdot\)м. Например, если вы толкаете перпендикулярно двери с силой 40 Н на расстоянии 0,800 м от петель, вы прикладываете крутящий момент 32 Н\(\cdot\)м (0. 800 м \(\раз\) 40 Н) относительно шарниров. Если уменьшить силу до 20 Н, крутящий момент уменьшится до 16 Н\(\cdot\)м и так далее.
800 м \(\раз\) 40 Н) относительно шарниров. Если уменьшить силу до 20 Н, крутящий момент уменьшится до 16 Н\(\cdot\)м и так далее.
Крутящий момент всегда рассчитывается относительно некоторой выбранной точки поворота. Для одной и той же приложенной силы другой выбор положения оси вращения даст другое значение крутящего момента. Любая точка любого объекта может быть выбрана для расчета крутящего момента относительно этой точки. Объект может фактически не поворачиваться вокруг выбранной «точки вращения».
Обратите внимание, что при вращении в плоскости крутящий момент имеет два возможных направления.Крутящий момент либо по часовой стрелке, либо против часовой стрелки относительно выбранной точки поворота.
Итак, второе условие, необходимое для достижения равновесия , состоит в том, что чистый внешний крутящий момент в системе должен быть равен нулю . Внешний крутящий момент создается внешней силой. Вы можете выбрать точку, вокруг которой рассчитывается крутящий момент. Точка может быть физической точкой вращения системы или любой другой точкой в пространстве, но она должна быть одной и той же точкой для всех крутящих моментов. Если второе условие (чистый внешний крутящий момент в системе равен нулю) выполняется для одного выбора опорной точки, оно также будет выполняться для любого другого выбора опорной точки внутри или вне интересующей системы.Второе условие, необходимое для достижения равновесия, формулируется в форме уравнения как
Точка может быть физической точкой вращения системы или любой другой точкой в пространстве, но она должна быть одной и той же точкой для всех крутящих моментов. Если второе условие (чистый внешний крутящий момент в системе равен нулю) выполняется для одного выбора опорной точки, оно также будет выполняться для любого другого выбора опорной точки внутри или вне интересующей системы.Второе условие, необходимое для достижения равновесия, формулируется в форме уравнения как
\[чистая \, \тау = 0\]
, где чистый означает общий. Моментам, действующим в противоположных направлениях, присваиваются противоположные знаки. Обычно принято называть крутящие моменты против часовой стрелки (ccw) положительными, а крутящие моменты по часовой стрелке (cw) — отрицательными.
Когда двое детей балансируют на качелях, как показано на рисунке \(\PageIndex{3}\), они удовлетворяют двум условиям равновесия. Большинство людей имеют прекрасное представление о качелях, зная, что более легкий ребенок должен сидеть дальше от оси вращения и что более тяжелый ребенок может удерживать более легкого на неопределенное время.
Пример \(\PageIndex{1}\): Она увидела крутящий момент на качелях
Два дочерних элемента, показанные на рисунке \(\PageIndex{3}\), балансируют на качелях незначительной массы. (Это предположение сделано для простоты примера — далее последуют более сложные примеры.) Масса первого потомка равна 26.0 кг и находится на расстоянии 1,60 м от оси.
- Если второй ребенок имеет массу 32,0 кг, как далеко он находится от оси вращения?
- Что такое \(F_p\), поддерживающая сила, действующая на шарнир?
Стратегия
Должны выполняться оба условия равновесия. В части (а) нас просят указать расстояние; таким образом, необходимо использовать второе условие (относительно крутящих моментов), поскольку в первом (относительно только сил) нет расстояний. Чтобы применить второе условие равновесия, мы сначала идентифицируем интересующую нас систему как качели плюс два потомка.Примем опорную точку за точку, относительно которой вычисляются крутящие моменты. Затем мы определяем все внешние силы, действующие на систему.
Чтобы применить второе условие равновесия, мы сначала идентифицируем интересующую нас систему как качели плюс два потомка.Примем опорную точку за точку, относительно которой вычисляются крутящие моменты. Затем мы определяем все внешние силы, действующие на систему.
Раствор (а)
Три внешние силы, действующие на систему, — это вес двух дочерних элементов и поддерживающая сила стержня. Давайте рассмотрим крутящий момент, создаваемый каждым из них. Крутящий момент определяется как
\[\тау = r_{\perp}F\номер\]
Крутящие моменты, создаваемые тремя силами, являются первыми,
\[\tau_1 = r_1w_1\номер\]
секунд,
\[\tau_2 = -r_2w_2\номер\]
и третий,
\[ \begin{align*} \tau_p &= r_pF_p \\[5pt] &= 0 \cdot F_p \\[5pt] &= 0.\конец{выравнивание*}\]
Обратите внимание, что во второе уравнение добавлен знак минус, потому что этот крутящий момент направлен по часовой стрелке и, следовательно, по соглашению является отрицательным. Поскольку \(F_p\) действует непосредственно на точку вращения, расстояние \(r_p\) равно нулю. Сила, действующая на шарнир, не может вызвать вращение, точно так же, как прямое нажатие на петли двери не заставит ее вращаться. Теперь второе условие равновесия состоит в том, что сумма крутящих моментов обоих потомков равна нулю. Поэтому
Поскольку \(F_p\) действует непосредственно на точку вращения, расстояние \(r_p\) равно нулю. Сила, действующая на шарнир, не может вызвать вращение, точно так же, как прямое нажатие на петли двери не заставит ее вращаться. Теперь второе условие равновесия состоит в том, что сумма крутящих моментов обоих потомков равна нулю. Поэтому
\[\tau_2 = -\tau_1,\номер\]
или
\[r_2w_2 = r_1w_1.\номер\]
Вес равен массе, умноженной на ускорение свободного падения. Вводя \(mg\) вместо \(w\), получаем
\[r_2m_2g = r_1w_1g.\номер\]
Решите это для неизвестного \(r_2\):
\[r_2 = r_1\dfrac{m_1}{m_2}.\номер\]
Величины в правой части уравнения известны; таким образом, \(r_2\) равно
\[ \begin{align*} r_2 &= (1,60 \, м)\dfrac{26,0 \, кг}{32,0 \, кг} \\[5pt] &= 1,30 \, м \end{align*}\ ]
Как и ожидалось, более тяжелый ребенок должен сидеть ближе к оси вращения (1.30 м против 1,60 м) для балансировки качелей.
Раствор (б)
Эта часть запрашивает силу \(F_p\). Самый простой способ найти его — использовать первое условие равновесия, которое равно
.\[чистая \, F = 0.\номер\]
Все силы вертикальны, так что мы имеем дело с одномерной задачей вдоль вертикальной оси; следовательно, условие можно записать как
\[сеть \, F_y = 0 \не число\]
, где мы снова называем вертикальную ось осью и .Выбрав положительное направление вверх и используя знаки плюс и минус для указания направления сил, мы видим, что
\[F_p — w_1 — w_2 = 0.\номер\]
Это уравнение дает то, о чем можно было догадаться вначале:
\[F_p = w_1 + w_2. \номер\]
Итак, шарнир создает поддерживающую силу, равную общему весу системы:
\[F_p = m_1g + m_2g. \номер\]
Ввод известных значений дает
\[ \begin{align*} F_p &= (26.2) \\[5pt] &= 568 \, N. \end{align*}\]
Обсуждение
Два результата интуитивно понятны. Более тяжелый ребенок сидит ближе к оси. Шарнир поддерживает вес двух детей. Часть (b) также может быть решена с использованием второго условия равновесия, поскольку оба расстояния известны, но только в том случае, если точка поворота выбрана не в том месте, где находится фактическая точка поворота качелей!
Более тяжелый ребенок сидит ближе к оси. Шарнир поддерживает вес двух детей. Часть (b) также может быть решена с использованием второго условия равновесия, поскольку оба расстояния известны, но только в том случае, если точка поворота выбрана не в том месте, где находится фактическая точка поворота качелей!
Несколько аспектов предыдущего примера имеют широкие последствия.Во-первых, выбор точки вращения в качестве точки, вокруг которой рассчитываются крутящие моменты, упростил задачу. Так как \(F_p\) воздействует на точку вращения, его плечо рычага равно нулю. Следовательно, крутящий момент, создаваемый поддерживающей силой \(F_p\), равен нулю относительно этой точки поворота. Второе условие равновесия выполняется при любом выборе опорной точки, поэтому мы выбираем опорную точку, чтобы упростить решение задачи.
Во-вторых, ускорение свободного падения в этой задаче отменилось, и мы остались с отношением масс. Так будет не всегда . Всегда вводите правильные силы — не забегайте вперед, вводя какое-то отношение масс.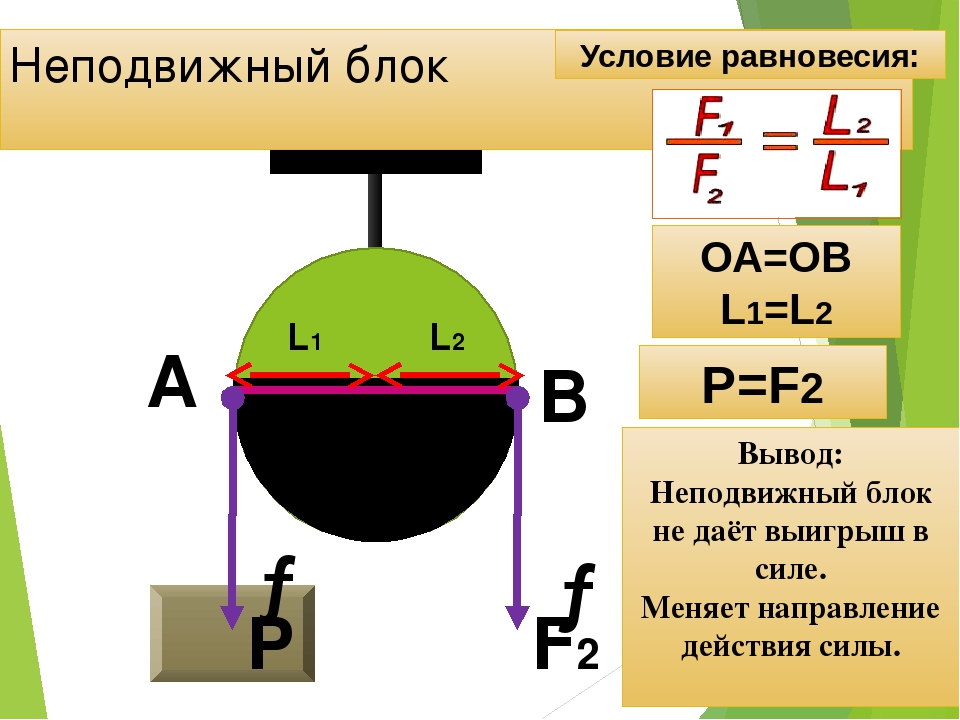
В-третьих, вес каждого ребенка распределяется по площади качелей, однако мы рассматривали веса так, как если бы каждая сила прикладывалась к одной точке. Это не приближение — расстояния \(r_{\perp}\) и \(r_2\) — это расстояния до точек, находящихся непосредственно под центром тяжести каждого ребенка. Как мы увидим в следующем разделе, масса и вес системы могут действовать так, как если бы они находились в одной точке.
Наконец, обратите внимание, что концепция крутящего момента имеет значение помимо статического равновесия. Крутящий момент играет ту же роль во вращательном движении, что и сила в прямолинейном движении. Мы рассмотрим это в следующей главе.
Эксперимент на вынос
- Возьмите кусок пластилина и положите его на стол, затем вдавите в него цилиндр так, чтобы линейка могла балансировать на круглой стороне цилиндра, пока все остается неподвижным. Положите монетку на расстоянии 8 см от оси.Куда вам нужно положить две копейки, чтобы сбалансировать? Три пенни?
Резюме
- Второе условие гарантирует, что эти крутящие моменты также сбалансированы.
 Крутящий момент представляет собой вращательный эквивалент силы, вызывающей вращение, и определяется как \[\tau = r_{\perp}F \nonumber\], где \(\tau\) — крутящий момент, \(r_{\perp}\ ) — расстояние по перпендикуляру от точки поворота до линии, содержащей точку приложения силы, а \(F\) — величина силы.
Крутящий момент представляет собой вращательный эквивалент силы, вызывающей вращение, и определяется как \[\tau = r_{\perp}F \nonumber\], где \(\tau\) — крутящий момент, \(r_{\perp}\ ) — расстояние по перпендикуляру от точки поворота до линии, содержащей точку приложения силы, а \(F\) — величина силы. - Перпендикулярное плечо рычага \(r_{\perp}\) — это кратчайшее расстояние от точки вращения до линии, вдоль которой действует \(F\).Единицей СИ для крутящего момента является ньютон-метр Н\(\cdot\)м. Второе условие, необходимое для достижения равновесия, состоит в том, что чистый внешний крутящий момент в системе должен быть равен нулю: \[ net \, \tau = 0 \nonnumber\] По соглашению крутящие моменты против часовой стрелки положительны, а крутящие моменты по часовой стрелке отрицательны.
Глоссарий
- крутящий момент
- эффективность силы при повороте или скручивании
- перпендикулярный рычаг
- кратчайшее расстояние от точки вращения до линии, вдоль которой лежит \(F\)
- Единицы крутящего момента в системе СИ
- ньютона на метр, обычно записывается как Н·м
- центр тяжести
- точка, в которой предполагается сосредоточение всего веса тела
Авторы и авторство
Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрикс (Государственный университет Нью-Йорка, Колледж в Освего) с соавторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет).
 Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
| ||||
| Этот текст предназначен для обсуждения в классе. Это еще не все, что нужно знать об основах крутящего момента и двух условиях равновесия.Он задуман как подготовка к уроку. Более подробные примечания и примеры приведены в конспектах занятий, презентациях и демонстрациях (нажмите здесь). | ||||
| 2 Условия механического равновесия | ||||
| Когда тело находится в механическом равновесии, | ||||
| ||||
Если выполняются оба этих условия, то ученые и инженеры говорят: «Тело находится в механическом равновесии». Существуют две другие формы равновесия, называемые статическим и динамическим равновесием. Статическое равновесие означает, что тело движется с постоянной скоростью. Механическое равновесие является подмножеством статического равновесия. Динамическое равновесие – это когда тело одновременно ускоряется и движется с постоянной скоростью. Примером этого является мяч, который вращается, но не движется прямолинейно.Каждый вращающийся объект испытывает центростремительное ускорение. В примере объект вращается, но не испытывает никакого поступательного движения.
| ||||
Этот блок занимается только механическим равновесием.
| ||||
| Собираем все вместе | ||||
Когда вы решали задачи со свободным телом, в предыдущем разделе вы применяли одно из условий механического и динамического равновесия, суммируя силы. Это называется первым условием равновесия. Выглядело это так… | ||||
Второе условие равновесия гласит, что тело не вращается.Математически это формулируется так: «Сумма крутящих моментов относительно любой точки равна нулю». Это означает, что у вас есть инструмент, который можно использовать при решении проблем. Выглядит так… | ||||
Вот видео, описывающее смысл приведенного выше математического предложения. | ||||
| Это видео YouTube находится здесь, http://youtu.be/PhOCrlQqI3A | ||||
| Стратегии решения | ||||
Когда используется суммирование крутящих моментов техника ?
| ||||
| Пример #2 Балка Вопрос и решение | ||||
Это видео YouTube можно найти по адресу http://youtu.be/e_T0s-gpjnE .
| ||||
| Пример #3 Балансировка | ||||
| Пример №4 («Задача о лестнице») | ||||
| ||||
Равновесие объекта рассматриваем как турник. В лаборатории это будет метровая палка. Равновесие означает, что оно не имеет поступательного движения (движения, при котором все точки тела движутся с одинаковой векторной скоростью) или вращения. Мы можем определить вращение, выбрав любую точку на теле, назвав эту точку «осью» и учитывая вращение вокруг этой оси.
В лаборатории это будет метровая палка. Равновесие означает, что оно не имеет поступательного движения (движения, при котором все точки тела движутся с одинаковой векторной скоростью) или вращения. Мы можем определить вращение, выбрав любую точку на теле, назвав эту точку «осью» и учитывая вращение вокруг этой оси.
На тело может действовать несколько сил, и каждая сила действует в определенной точке. На диаграмме F 1 действует в точке P 1 и F 2 действует в точке P 2 ; А — ось.
Мы рассматриваем только силы, действующие вверх или вниз. Расстояние от точки действия силы до оси называется плечом момента , d 1 и d 2 на диаграмме. Произведение силы, умноженной на плечо момента, называется крутящим моментом (также называемым моментом ) и обозначается греческой буквой тау: t.
Крутящий момент также имеет знак: он положителен (по соглашению), если он имеет тенденцию вращать объект против часовой стрелки вокруг оси. Он отрицателен, если имеет тенденцию вращать объект по часовой стрелке вокруг оси. На диаграмме крутящий момент от F 2 положительный, а крутящий момент от F 1 отрицательный. Сами силы имеют знаки. Мы можем считать силы положительными, если они направлены вверх, и отрицательными вниз.
Он отрицателен, если имеет тенденцию вращать объект по часовой стрелке вокруг оси. На диаграмме крутящий момент от F 2 положительный, а крутящий момент от F 1 отрицательный. Сами силы имеют знаки. Мы можем считать силы положительными, если они направлены вверх, и отрицательными вниз.
Тогда условия равновесия формулируются просто: сумма всех сил должна быть равна нулю, и сумма всех крутящих моментов должна быть равна нулю.
Ст и = 0СФ и = 0
Здесь «i» — метка, меняющаяся по всем силам, i = 1, 2, 3 и т. д.
Одна конкретная сила требует дальнейшего рассмотрения: вес стержня. Вес (сила земного притяжения) действует не в точке, а во всех точках вдоль объекта. Однако для целей определения равновесия можно считать, что вес сосредоточен в одной точке, называемой центром масс . Таким образом, бар, поддерживаемый двумя направленными вверх силами и удерживаемый в равновесии, выглядит так, как показано на рисунке ниже.
Поскольку ось для решения задач может быть выбрана в любом месте вдоль стержня, ее удобно выбирать в точке действия одной из сил.Тогда плечо момента для этой силы будет равно нулю, и эта сила не войдет в уравнение момента. Например, мы можем выбрать ось в центре масс.
На этой диаграмме предположим, что F 1 = 2,0 Н, d 1 = 0,4 м, d 2 = 0,5 м, а F 2 неизвестно. W также неизвестен, но d W = 0, и поэтому крутящий момент, обусловленный весом, t W = 0. Таким образом, уравнение крутящего момента принимает вид
T 1 = -F 1 D 1 = -2,0 x 0,4 = -0,8,
т 2 = + F 2 = F 2 = F 2 x 0.5 и SO
0,5F 2 — 0,8 = 0,
F 2 = 1,6 Н.
Обратите внимание, что вес не указан и не определен в обсуждении выше. Чтобы найти вес, мы должны использовать второе условие равновесия, что сумма всех сил = 0. Поскольку F 1 и F 2 вверх, а W вниз, мы имеем
Поскольку F 1 и F 2 вверх, а W вниз, мы имеем
Ш = 3,6 Н.
Для многих объектов с простыми геометрическими формами можно определить центр масс по симметрии. Например, центр масс однородного стержня находится в его геометрическом центре. Для метровой палки она находится на отметке 50 см. Из-за износа центр масс может немного отличаться от этой точки. Один из способов определить положение центра масс — сбалансировать штангу, удерживая ее в одной точке снизу.Точка, в которой он уравновешивается, является центром масс.
Какие условия необходимы для равновесия? – Restaurantnorman.com
Какие условия необходимы для равновесия?
Условия равновесия требуют, чтобы сумма всех внешних сил, действующих на тело, была равна нулю (первое условие равновесия), а сумма всех внешних моментов от внешних сил равнялась нулю (второе условие равновесия). Эти два условия должны одновременно выполняться в равновесии.
Каковы условия механического равновесия?
Чтобы объект находился в равновесии, он не должен испытывать никакого ускорения. Это означает, что и чистая сила, и чистый крутящий момент на объекте должны быть равны нулю.
Для чего существуют два состояния и равновесие?
Сумма или равнодействующая всех внешних сил, действующих на тело, должна быть равна нулю. Сумма или равнодействующая всех внешних крутящих моментов от внешних сил, действующих на объект, должна быть равна нулю.
Какое условие равновесия выполняется, когда вентилятор вращается с постоянной скоростью?
чистый крутящий момент
Удовлетворяет ли вентилятор второму условию равновесия?
Условие равновесия не зависит от скорости. Сначала должно быть статическое равновесие, иначе одна сторона вентилятора провиснет, а когда вентилятор начнет вращаться, это вызовет серьезную вибрацию и сломает вентилятор.
Является ли вентилятор равновесием?
Если тело находится в состоянии покоя, результирующая сила равна нулю. Если тело движется равномерно, то результирующая сила равна нулю. Точно так же вращающийся потолочный вентилятор находится в равновесии, поскольку действующий на него чистый крутящий момент равен нулю.
Если тело движется равномерно, то результирующая сила равна нулю. Точно так же вращающийся потолочный вентилятор находится в равновесии, поскольку действующий на него чистый крутящий момент равен нулю.
Какое условие равновесия неверно?
Катализатор не влияет на состояние равновесия. Реакция никогда не прекращается при равновесии, потому что равновесие по своей природе динамическое.
Что всегда верно для тела, находящегося в равновесии?
Тело находится в равновесии только тогда, когда на него не действует результирующая внешняя сила.Другими словами, сумма всех сил, действующих на тело, должна быть равна нулю, чтобы тело находилось в равновесии.
Что такое G в свободном падении?
значение g составляет 9,8 метра в секунду в квадрате на поверхности земли. Ускорение свободного падения g уменьшается пропорционально квадрату расстояния от центра Земли. О предмете, который движется только за счет действия силы тяжести, говорят, что он свободно падает.
Что такое примеры свободного падения?
Некоторые примеры объектов, находящихся в свободном падении, включают: Космический корабль на непрерывной орбите.Свободное падение закончится, как только включатся двигательные установки. Камень упал в пустой колодец.
Что подразумевается под классом свободного падения 9?
Когда объект падает с определенной высоты, он начинает падать к поверхности Земли под действием гравитационной силы. Такое движение объекта называется свободным падением.
Как вы находите время падать?
Выберите продолжительность падения объекта. В этом примере мы будем использовать время 8 секунд. Рассчитайте конечную скорость свободного падения (непосредственно перед ударом о землю) по формуле v = v₀ + gt = 0 + 9.80665 * 8 = 78,45 м/с. Найдите расстояние свободного падения, используя уравнение s = (1/2)gt² = 0,5 * 9,80665 * 8² = 313,8 м.
Зачем нужно второе условие равновесия, если тело удовлетворяет первому условию равновесия? — Ответы на все
Зачем нужно второе условие равновесия, если тело удовлетворяет первому условию равновесия?
Зачем нужно второе условие равновесия, если тело удовлетворяет первому условию равновесия? Две равные, но противоположные силы, действующие по разным направлениям, вращают тело, хотя первое условие выполнено полностью, но тело продолжает двигаться. Таким образом, нам нужно еще одно условие равновесия.
Таким образом, нам нужно еще одно условие равновесия.
Что понимают под состоянием равновесия два условия равновесия тела?
Два условия равновесия тела: (i) равнодействующая всех сил, действующих на тело, должна быть равна нулю. (ii) Результирующий момент всех сил, действующих на тело относительно точки, должен быть равен нулю. Концепция: Сила – Силы в равновесии. Глава 1: Сила, работа, мощность и энергия – подробные ответы.
При выполнении второго условия равновесия тело не имеет?
По Первому условию равновесия сумма сил, действующих на тело, равна нулю ( ∑ F =0 ), А по второму условию равновесия сумма моментов, действующих на тело, равна нулю ( ∑ τ = 0 ).
Почему важно условие равновесия и где мы можем его применить?
Согласно первому закону Ньютона, в условиях равновесия объект, находящийся в состоянии покоя, останется в покое или объект, находящийся в движении, не изменит своей скорости. Если суммарный результат действия всех внешних сил (включая моменты), действующих на объект, отличен от нуля, применяется второй закон Ньютона.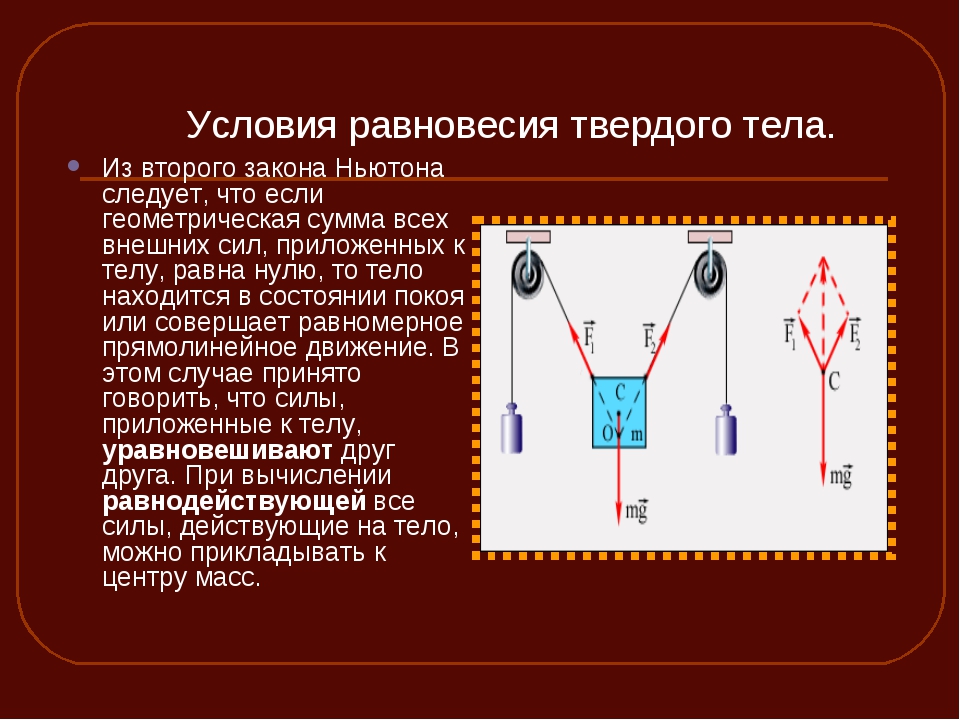
Какова формула второго условия равновесия?
Второе условие, необходимое для достижения равновесия, заключается в избегании ускоренного вращения.Вращающееся тело или система могут находиться в равновесии, если скорость их вращения постоянна и не изменяется под действием действующих на них сил. Величина крутящего момента вокруг оси вращения определяется как τ=rFsinθ.
Какое второе условие равновесия?
Второе условие, необходимое для достижения равновесия, заключается в том, что чистый внешний крутящий момент системы должен быть равен нулю: netτ=0. По соглашению, крутящий момент против часовой стрелки положительный, а крутящий момент по часовой стрелке отрицательный.
При каком условии тело находится в равновесии?
Условия равновесия требуют, чтобы сумма всех внешних сил, действующих на тело, была равна нулю (первое условие равновесия), а сумма всех внешних моментов от внешних сил равнялась нулю (второе условие равновесия).Эти два условия должны одновременно выполняться в равновесии.
Какие три уравнения условий равновесия?
Чтобы система находилась в равновесии, она должна удовлетворять всем трем уравнениям равновесия: Sum Fx = 0, Sum Fy = 0 и Sum M = 0. Начните с суммы уравнений сил. Самый простой способ решить эти системы сил — разбить диагональные силы на составные части.
Что такое 1-е условие равновесия?
Первое условие равновесия состоит в том, что результирующая сила во всех направлениях должна быть равна нулю.
Какое первое условие?
Первое условие состоит в том, что результирующая сила, действующая на объект, должна быть равна нулю, чтобы объект находился в равновесии. Если результирующая сила равна нулю, то результирующая сила в любом направлении равна нулю.
Какое значение имеет равновесие?
Равновесие – это состояние, при котором спрос и предложение на рынке уравновешивают друг друга, в результате чего цены становятся стабильными. Как правило, избыточное предложение товаров или услуг приводит к снижению цен, что приводит к повышению спроса, в то время как недостаточное предложение или нехватка вызывают рост цен, что приводит к снижению спроса.
Что такое 1-е условное выражение?
Значение. Первое условное предложение используется, чтобы говорить о действиях/событиях в будущем, которые, вероятно, произойдут или имеют реальную возможность произойти. Если завтра пойдет дождь, я останусь дома. (Думаю, завтра реальная вероятность дождя. В таком состоянии я останусь дома)
Какое первое условие равновесия? – Firstlawcomic.com
Какое первое условие равновесия?
ноль
Статика изучает силы в равновесии.Два условия должны быть выполнены для достижения равновесия, которое определяется как движение без линейного ускорения или ускорения вращения. Первое условие, необходимое для достижения равновесия, состоит в том, что чистая внешняя сила, действующая на систему, должна быть равна нулю, так что чистая F = 0.
Каковы условия равновесия?
Два условия, важные для равновесия: Сумма или равнодействующая всех внешних сил, действующих на тело, должна быть равна нулю. Сумма или равнодействующая всех внешних крутящих моментов от внешних сил, действующих на объект, должна быть равна нулю.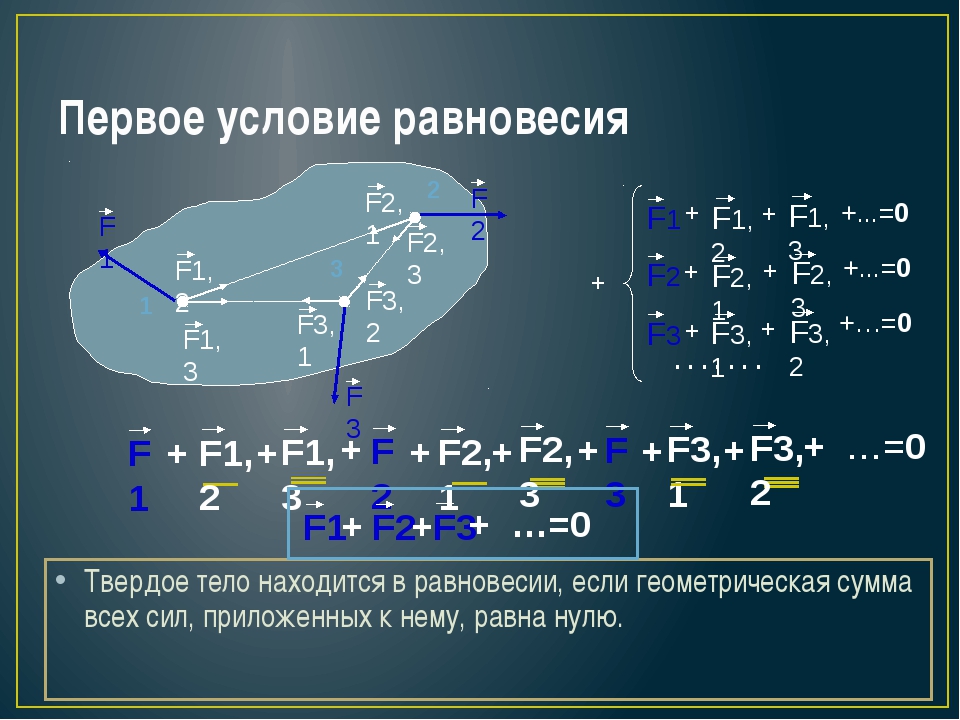
Что такое состояние равновесия одно условие?
Состояние равновесия объекта существует, когда выполняется первый закон Ньютона. Объект находится в равновесии в отсчетной системе координат, когда все действующие на него внешние силы (в том числе и моменты) уравновешены. Это означает, что суммарный результат всех внешних сил и моментов, действующих на этот объект, равен нулю.
Что такое первое и второе условия равновесия?
Условия равновесия требуют, чтобы сумма всех внешних сил, действующих на тело, была равна нулю (первое условие равновесия), а сумма всех внешних моментов от внешних сил равнялась нулю (второе условие равновесия).Эти два условия должны одновременно выполняться в равновесии.
Сколько существует условий равновесия?
Есть два состояния равновесия, первое условие равновесия и второе условие равновесия.
Какое второе условие равновесия?
Второе условие, необходимое для достижения равновесия, заключается в избегании ускоренного вращения (поддержании постоянной угловой скорости). Вращающееся тело или система могут находиться в равновесии, если скорость их вращения постоянна и не изменяется под действием действующих на них сил.
Вращающееся тело или система могут находиться в равновесии, если скорость их вращения постоянна и не изменяется под действием действующих на них сил.
Какие три условия равновесия?
Твердое тело, на которое действуют три силы, линии действия которых не параллельны, находится в равновесии, если выполняются три следующих условия: Линии действия компланарны (в одной плоскости) Линии действия сходятся (пересекаются в одной точке). ) Векторная сумма этих сил равна нулевому вектору.
Зачем нужно второе условие равновесия, если тело удовлетворяет первому условию равновесия?
Второе условие, необходимое для достижения равновесия, заключается в избегании ускоренного вращения (поддержании постоянной угловой скорости.Вращающееся тело или система могут находиться в равновесии, если скорость их вращения постоянна и не изменяется под действием действующих на них сил.
Что является наиболее важным условием равновесия фирмы?
Фирма не хотела бы изменять объем выпуска только тогда, когда она получает максимальную денежную прибыль.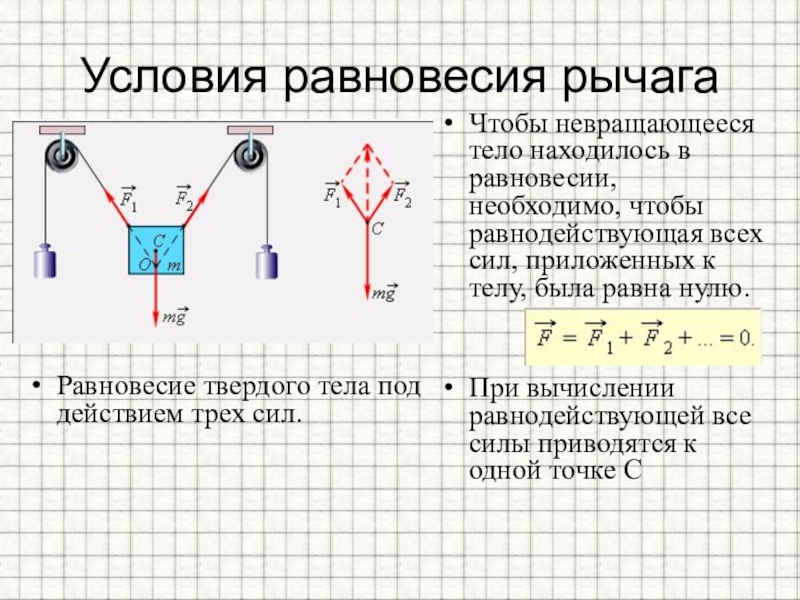 Следовательно, получение максимальной прибыли или минимальные убытки являются важным условием равновесия фирмы.
Следовательно, получение максимальной прибыли или минимальные убытки являются важным условием равновесия фирмы.
Когда выполняется второе условие равновесия, говорят, что тело находится в равновесии?
Второе условие статического равновесия гласит, что чистый крутящий момент, действующий на объект, должен быть равен нулю.
Какие два условия должны быть выполнены, чтобы объект находился в равновесии?
Чтобы объект оставался в равновесии, должны быть выполнены два условия: и чистая сила, и чистый крутящий момент должны быть равны нулю. Примером объекта, находящегося в равновесии, является стержень, который может свободно вращаться вокруг шарнира на одном конце.
Какие два условия равновесия фирмы?
Фирма находится в равновесии, когда она получает максимальную прибыль как разницу между ее общим доходом и общими затратами.Для этого необходимо, чтобы она удовлетворяла двум условиям: (1) МС = MR, и (2) кривая МС должна пересекать кривую MR снизу в точке равенства, а затем подниматься вверх.

 .
.
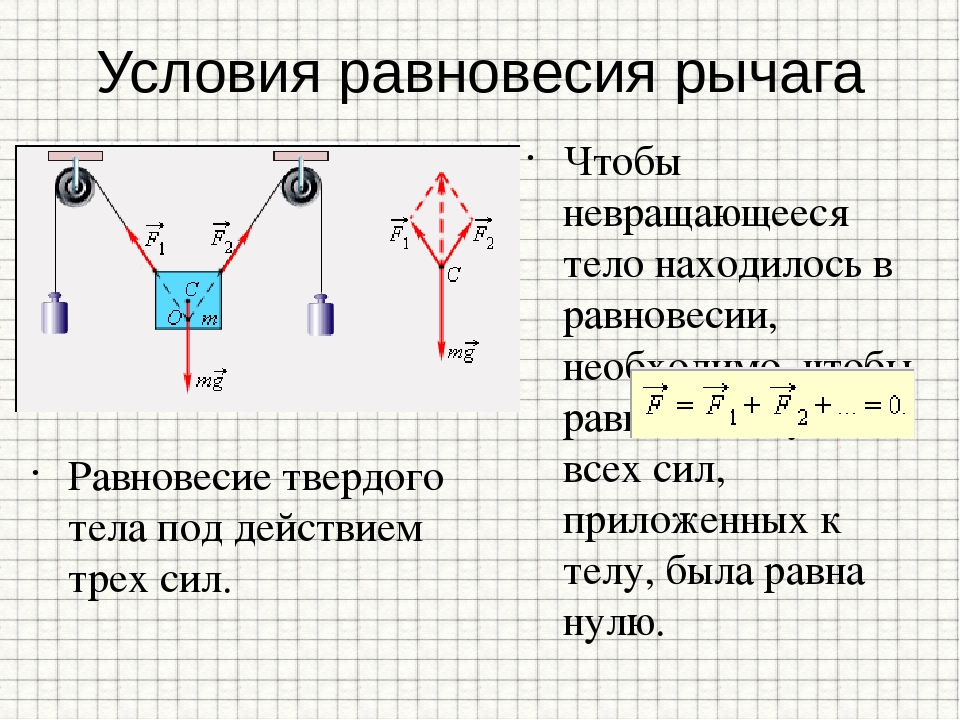 »
»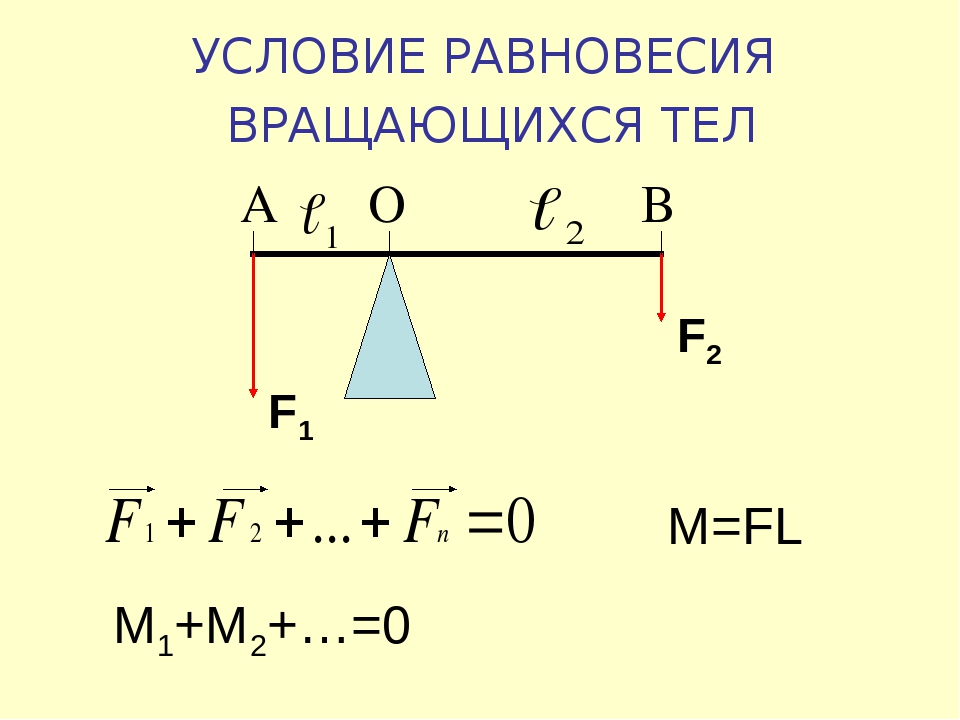 Напишите математическое предложение, суммирующее все крутящие моменты.
Напишите математическое предложение, суммирующее все крутящие моменты.
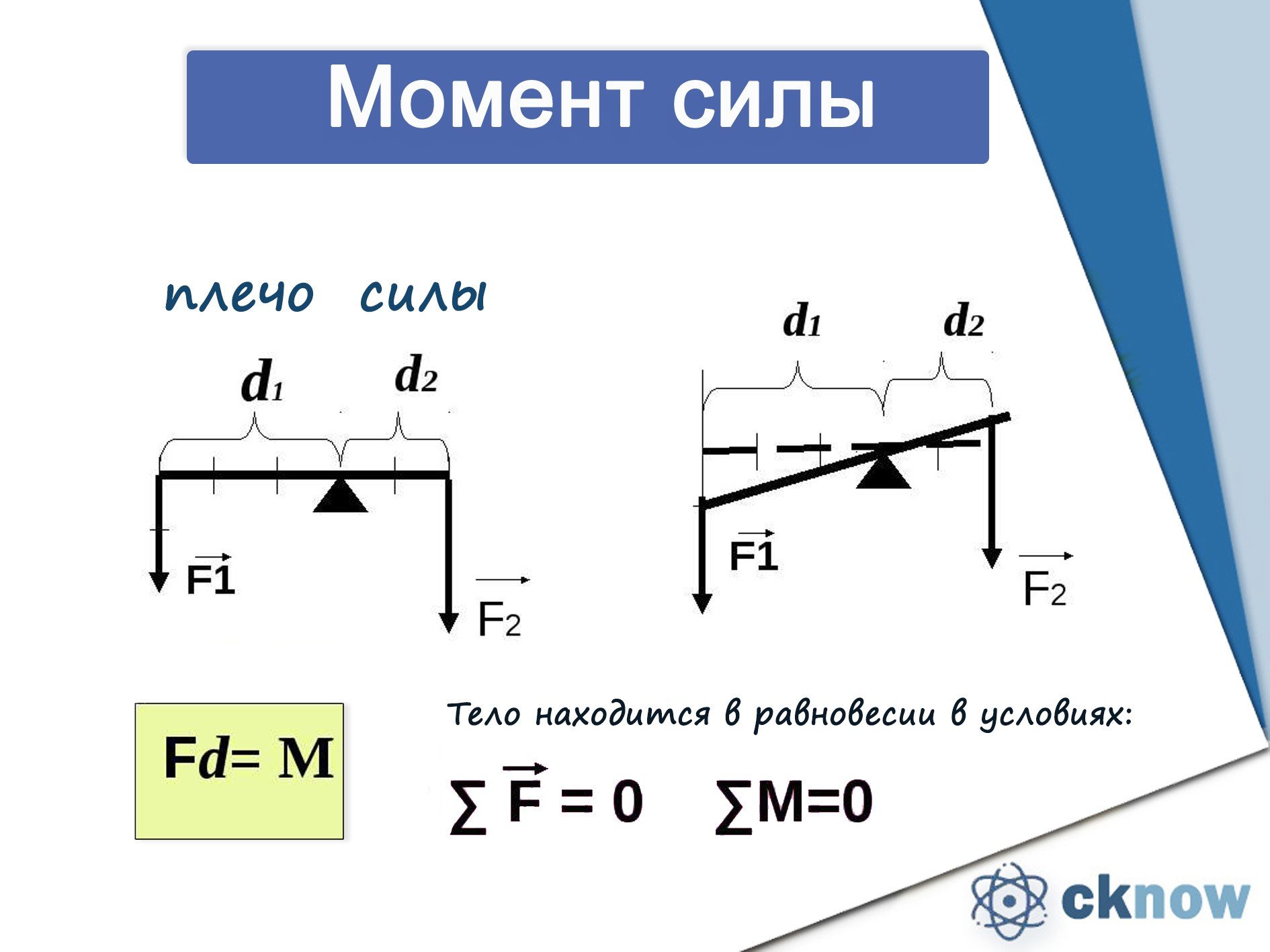 00 м, 200,0 Н, длинная лестница упирается в стену. Центр масс лестницы находится на расстоянии 3,00 м от низа лестницы вдоль лестницы. Трения о стену нет, а по земле коэффициент трения 0,300. На какое расстояние по лестнице может подняться над землей 750. N человек?
00 м, 200,0 Н, длинная лестница упирается в стену. Центр масс лестницы находится на расстоянии 3,00 м от низа лестницы вдоль лестницы. Трения о стену нет, а по земле коэффициент трения 0,300. На какое расстояние по лестнице может подняться над землей 750. N человек?