Второе условие равновесия: Ошибка 403

Содержание

Условия равновесия твердого тела – виды, формулы, примеры кратко

4.7

Средняя оценка: 4.7

Всего получено оценок: 120.

4.7

Средняя оценка: 4.7

Всего получено оценок: 120.

Статика — это раздел механики, который изучает причины отсутствия движения. При отсутствии движения говорят, что «система находится в равновесии». Рассмотрим условия равновесия твердого тела.

Равновесие тела

Равновесием называется такое состояние тела, когда любая из его точек находится в покое, иначе говоря, имеет нулевую мгновенную скорость и нулевое ускорение.

Рис. 1. Равновесие тела.

Как и в случае прямолинейного равномерного движения, о равновесии тела можно говорить лишь применительно к конкретной инерциальной системе отсчета. Это прямо следует из первого закона Ньютона, который говорит о существовании систем отсчета, в которых тело, на которое не действуют силы, либо покоится, либо движется прямолинейно и равномерно. Условия равновесия тела всегда рассматриваются именно в такой инерциальной системе отсчета.

Условия равновесия

Первое условие

Первое условие равновесия прямо следует из определения равновесия. Поскольку мгновенная скорость всех точек тела равна нулю, то и мгновенная скорость всего тела также будет равна нулю. Кроме того, учитывая, что причиной ускорения тела всегда является действие механической силы, выходит, что для тела, находящегося в равновесии, и равнодействующая всех сил, действующих на тело, равна нулю:

$$\overrightarrow v= 0$$

$$\overrightarrow F_{равнод}= 0$$

Второе условие

Второе условие равновесия менее очевидно. Что будет, если приложить к разным концам тела равные по величине противоположно направленные силы?

Равнодействующая таких сил равна нулю. Центр отрезка между точками приложения сил останется в покое. Однако тело начнет вращательное движение.

Отсутствие равновесия в данном случае определяется тем, что приложенные силы создают вращательный момент. Он и поворачивает тело.

Следовательно, вторым условием равновесия тела являются нулевые вращательные моменты относительно любой оси:

$$M_1+M_2+…+M_n= 0$$

Рис.

2. Условия равновесия твердого тела.

Твердые и деформируемые тела

Необходимо отметить, что указанные условия равновесия применимы только к абсолютно твердому телу, то есть к телу, расстояние между любыми двумя его точками не изменяется.

В самом деле, если взять деформируемое тело, например, резиновый жгут, и начать его растягивать, то как равнодействующая, так и сумма моментов будут равны нулю. А жгут не будет в равновесии.

Условия равновесия деформируемого тела должны учитывать упругие свойства тела. Такая задача выходит за рамки школьного курса и решается в вузовском курсе сопротивления материалов. Еще сложнее задача равновесия жидкостей, она решается в курсе гидродинамики.

В рамках школьного курса статики изучается только равновесие твердых тел.

Рис. 3. Абсолютно твердое тело.

Что мы узнали?

Для того чтобы твердое тело находилось в равновесии, необходимо принять систему отсчета, в которой начальная скорость тела равна нулю, и учесть два условия: должна быть равна нулю равнодействующая всех сил, приложенных к телу, и сумма вращательных моментов тела относительно любых осей.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.7

Средняя оценка: 4.7

Всего получено оценок: 120.

А какая ваша оценка?

Условие равновесия тела, теория и онлайн калькуляторы

Если тело покоится относительно инерциальной системы отсчета, то считают, что оно находится в состоянии равновесия. Исследование условий равновесия тел имеет большое прикладное значение для конструирования зданий, сооружений, машин и механизмов.

Условия равновесия изучает такой раздел физики как статика.

Первое условие равновесия тел

Первое условие равновесия сформулируем, опираясь на второй закон Ньютона, который говорит о том, что в инерциальной системе отсчета тело движется равномерно и прямолинейно или покоится, если равнодействующая всех сил, приложенных к этому телу (материальной точке) равна нулю.

N_{i=1}{{\overline{F}}_i=0\left(1\right).}\]

Формула (1) говорит о том, что для того чтобы тело находилось в состоянии равновесия, необходимо равенство нулю суммы, действующих на него сил.

Второе условие равновесия тела

Если тело нельзя принять за материальную точку, то первого условия равновесия будет недостаточно. Так, если на стержень действуют две равный по величине, но противоположные по направлению силы (${\overline{F}}_1\ и{\ \overline{F}}_2\ $) рис.1, то стержень может поворачиваться вокруг своей оси, что означает: он не находится равновесии.

Для формулировки второго условия равновесия следует обратиться к такой физической величине, как момент силы ($\overline{M}$):

\[\overline{M}=\overline{r}\times \overline{F\ }\left(2\right),\]

где $\overline{r}\times \overline{F\ }$ — векторное произведение; $\left|\overline{M}\right|=\left|\overline{r}\right|\cdot \left|\overline{F\ }\right|{\sin \widehat{\overline{r},\overline{F\ }}\ }$; $\widehat{\overline{r},\overline{F\ }}$ — угол между вектором силы и радиус-вектором ($\overline{r}$), который проведен от точки вращения к точке приложения силы. N_{i=1}{{\overline{M}}_i=0\left(3\right).}\]

Второе условие равновесия называют правилом моментов сил.

Условия равновесия тел дают возможность определить, какой выигрыш в силе получается при использовании простых механизмов, которые применялись еще в древние времена, например, рычага. Рычаг является элементом многих орудий труда: ножниц, стрелы подъемного крана, ручного тормоза и т.д. Из второго условия равновесия рычага можно получить выражение:

\[\frac{F_1}{F_2}=\frac{d_2}{d_1}\left(4\right),\]

где $d_1$; $d_2$ — плечи рычага; $F_1$; $F_2$ — силы, действующие на плечи рычага. Из выражения (4) очевидно, что рычаг может обеспечить выигрыш в силе в $\frac{d_2}{d_1}$ раз.

Примеры задач с решением

Пример 1

Задание: Балка массой $m$, имеющая длину $l$ лежит на двух опорах (рис.2). Какая сила давления действует на каждую из опор? Считать, что расстояние $l_1$ известно.

Решение: Рассмотрим рис.2. Обозначим силы, которые действуют на балку. Это сила тяжести ($m\overline{g}$), силы реакции опор ${\overline{N}}_1$ и ${\overline{N}}_2$. Балка находится в состоянии равновесия, следовательно, из первого условия равновесия имеем:

\[m\overline{g}+{\overline{N}}_1+{\overline{N}}_2=0\ \left(1.1\right).\]

В проекции на ось Y уравнение (1.1):

\[N_1+N_2-mg=0\ \left(1.2\right).\]

Для записи второго условия равновесия балки выберем в качестве оси вращения, ось, проходящую через первую опору. Моменты сил проектируем на ось X, перпендикулярную плоскости рисунка (рис.2). Тогда моменты сил равны:

\[{\overline{M}}_1={\overline{r}}_1\times {\overline{N}}_1=0\ \left(1.3\right),\]

так как расстояние от точки вращения до точки приложения силы ($\left|{\overline{r}}_1\right|=0$) равно нулю.

\[{\overline{M}}_2={\overline{r}}_2\times {\overline{N}}_2;;\ M_{x2}=\left(l-l_1\right)N_{2\ }\left(1. 4\right),\]

где угол между ${\overline{r}}_2и\ {\overline{N}}_2$ равен 900; $\left|{\overline{r}}_2\right|=l-l_1$.

Сила тяжести приложена к центру тяжести балки, если она однородна, то цент тяжести находится на середине длины балки, получаем:

\[{\overline{M}}_3={\overline{r}}_3\times m\overline{g};;\ M_{x3}=-mg\left(\frac{l}{2}-l_1\right)\left(1.5\right),\]

Моменты сил направлены вдоль оси X. По второму условию равновесия имеем:

\[M_{x2}+M_{x3}=0\to \left(l-l_1\right)N_{2\ }-mg\left(\frac{l}{2}-l_1\right)=0\ \left(1.6\right).\]

Из выражения (1.6) найдем $N_{2\ }$:

\[N_{2\ }=\frac{mg\left(l-2l_1\right)}{2\left(l-l_1\right)}\left(1.7\right).\]

Подставим (1.7) в формулу (1.2), выразим $N_{1\ }$:

\[N_1+\frac{mg\left(l-2l_1\right)}{2\left(l-l_1\right)}-mg=0\to N_1=\frac{mgl}{2\left(l-l_1\right)}.\]

По третьему закону Ньютона силы давления на опоры равны по величине реакциям соответствующих опор:

\[F_1=N_1=\frac{mgl}{2\left(l-l_1\right)};;\ F_2=N_2=\frac{mg\left(l-2l_1\right)}{2\left(l-l_1\right)}.

Ответ: $F_1=\frac{mgl}{2\left(l-l_1\right)};;\ F_2=\frac{mg\left(l-2l_1\right)}{2\left(l-l_1\right)}$

Пример 2

Задание: В каком месте следует толкать тяжелую дверь, чтобы прикладывать минимум усилий для ее открытия?

Решение: Тяжелую дверь лучше толкать около ручки, так мы применяем условие рычага:

\[\frac{F_1}{F_2}=\frac{d_2}{d_1}\left(2.1\right),\]

где $d_1$; $d_2$ — плечи рычага; $F_1$; $F_2$ — силы, действующие на плечи рычага. Из формулы (2.1) следует, что рычаг может обеспечить выигрыш в силе в $\frac{d_2}{d_1}$ раз.

Читать дальше: центр тяжести тела.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

9.

2 Второе условие равновесия — Колледж физики 2e

Цели обучения

К концу этого раздела вы сможете:

Укажите второе условие, необходимое для достижения равновесия.
Объясните крутящий момент и факторы, от которых он зависит.
Описать роль крутящего момента в механике вращения.

Крутящий момент

Второе условие, необходимое для достижения равновесия, заключается в избегании ускоренного вращения (поддержании постоянной угловой скорости). Вращающееся тело или система могут находиться в равновесии, если скорость их вращения постоянна и не изменяется под действием действующих на них сил. Чтобы понять, какие факторы влияют на поворот, давайте подумаем, что происходит, когда вы открываете обычную дверь, вращая ее на петлях.

Несколько известных факторов определяют, насколько эффективно вы открываете дверь. См. рисунок 9.6. Прежде всего, чем больше сила, тем эффективнее она открывает дверь — очевидно, чем сильнее вы давите, тем быстрее открывается дверь. Кроме того, точка, в которую вы нажимаете, имеет решающее значение. Если вы приложите силу слишком близко к петлям, дверь откроется медленно, если вообще откроется. Большинство людей были смущены, совершив эту ошибку и наткнувшись на дверь, которая не открылась так быстро, как ожидалось. Наконец, направление, в котором вы продвигаетесь, также важно. Самое эффективное направление — перпендикулярно двери — мы толкаем в этом направлении почти инстинктивно.

Рисунок 9,6 Крутящий момент — это эффективность силы при повороте или скручивании, показанная здесь для вращения двери на петлях (если смотреть сверху). Крутящий момент имеет как величину, так и направление. (a) Эта сила создает крутящий момент против часовой стрелки, что означает, что дверь будет вращаться против часовой стрелки из-за FF. Обратите внимание, что r⊥ r⊥ — это перпендикулярное расстояние от оси вращения до линии действия силы. (b) Меньший крутящий момент против часовой стрелки создается меньшей силой F’F’, действующей на том же расстоянии от шарниров (точки поворота). (c) Та же сила, что и в (a), создает меньший крутящий момент против часовой стрелки, когда она приложена на меньшем расстоянии от шарниров. (г) Та же сила, что и в (а), но действующая в противоположном направлении, создает крутящий момент по часовой стрелке. (e) Меньший крутящий момент против часовой стрелки создается силой той же величины, действующей в той же точке, но в другом направлении. Здесь θθ меньше 90º90º. (f) Крутящий момент здесь равен нулю, так как сила просто тянет шарниры, не производя вращения. В этом случае θ=0ºθ=0º.

Величина, направление и точка приложения силы включены в определение физической величины, называемой крутящим моментом. Крутящий момент является вращательным эквивалентом силы. Это мера эффективности силы в изменении или ускорении вращения (изменение угловой скорости в течение определенного периода времени). В форме уравнения величина крутящего момента определяется как

τ=rFsinθτ=rFsinθ

9.3

где ττ (греческая буква тау) — символ крутящего момента, rr — расстояние от точки вращения до точки приложения силы, FF — величина силы, а θθ — угол между силой и вектором, направленным от точки приложения к точке поворота, как показано на рис. 9.6 и рис. 9.7. Альтернативное выражение для крутящего момента дается через перпендикулярное плечо рычага r⊥r⊥, как показано на рис. 9.6 и рис. 9..7, который определяется как

r⊥=rsinθr⊥=rsinθ

9,4

, так что

τ=r⊥F.τ=r⊥F.

9,5

Рисунок 9,7 Сила, приложенная к объекту, может создавать крутящий момент, который зависит от положения точки вращения. (a) Здесь показаны три фактора rr, FF и θθ для точки поворота A на теле: rr — это расстояние от выбранной точки поворота до точки приложения силы FF, а θθ — угол между FF и вектор, направленный из точки приложения в точку вращения. Если объект может вращаться вокруг точки А, он будет вращаться против часовой стрелки. Это означает, что крутящий момент направлен против часовой стрелки относительно точки вращения A. (b) В этом случае точка B является точкой вращения. Крутящий момент от приложенной силы вызовет вращение по часовой стрелке вокруг точки B, и, таким образом, это крутящий момент по часовой стрелке относительно B.

Перпендикулярное плечо рычага r⊥r⊥ — это кратчайшее расстояние от точки поворота до линии, вдоль которой ФФ действует; он показан пунктирной линией на рисунках 9.6 и 9.7. Обратите внимание, что отрезок, определяющий расстояние r⊥r⊥ перпендикулярно FF, как следует из названия. Иногда легче найти или визуализировать r⊥r⊥, чем найти оба рр и θθ. В таких случаях удобнее использовать τ=r⊥Fτ=r⊥F, а не τ=rFsinθτ=rFsinθ для крутящего момента, но оба варианта одинаково действительны.

Единицей крутящего момента в системе СИ является ньютон, умноженный на метр, обычно записывается как Н·мН·м. Например, если вы толкаете перпендикулярно двери с силой 40 Н на расстоянии 0,800 м от петель, вы прилагаете крутящий момент 32 Н·м (0,800 м × 40 Н × sin 90º) относительно петель. Если уменьшить усилие до 20 Н, крутящий момент уменьшится до 16 Н·м16 Н·м и так далее.

Крутящий момент всегда рассчитывается относительно некоторой выбранной точки поворота. Для одной и той же приложенной силы другой выбор местоположения оси вращения даст вам другое значение крутящего момента, поскольку и rr, и θθ зависят от местоположения точки вращения. Любая точка любого объекта может быть выбрана для расчета крутящего момента относительно этой точки. Объект может фактически не поворачиваться вокруг выбранной «точки вращения».

Обратите внимание, что при вращении в плоскости крутящий момент имеет два возможных направления. Крутящий момент либо по часовой стрелке, либо против часовой стрелки относительно выбранной точки поворота, как показано для точек B и A соответственно на рис. 9.7. Если объект может вращаться вокруг точки А, он будет вращаться против часовой стрелки, что означает, что крутящий момент для силы показан против часовой стрелки относительно точки А. Но если объект может вращаться вокруг точки В, он будет вращаться по часовой стрелке, что означает крутящий момент для показанная сила направлена по часовой стрелке относительно B. Кроме того, величина крутящего момента больше, когда плечо рычага длиннее.

Итак, второе условие, необходимое для достижения равновесия состоит в том, что чистый внешний крутящий момент в системе должен быть равен нулю .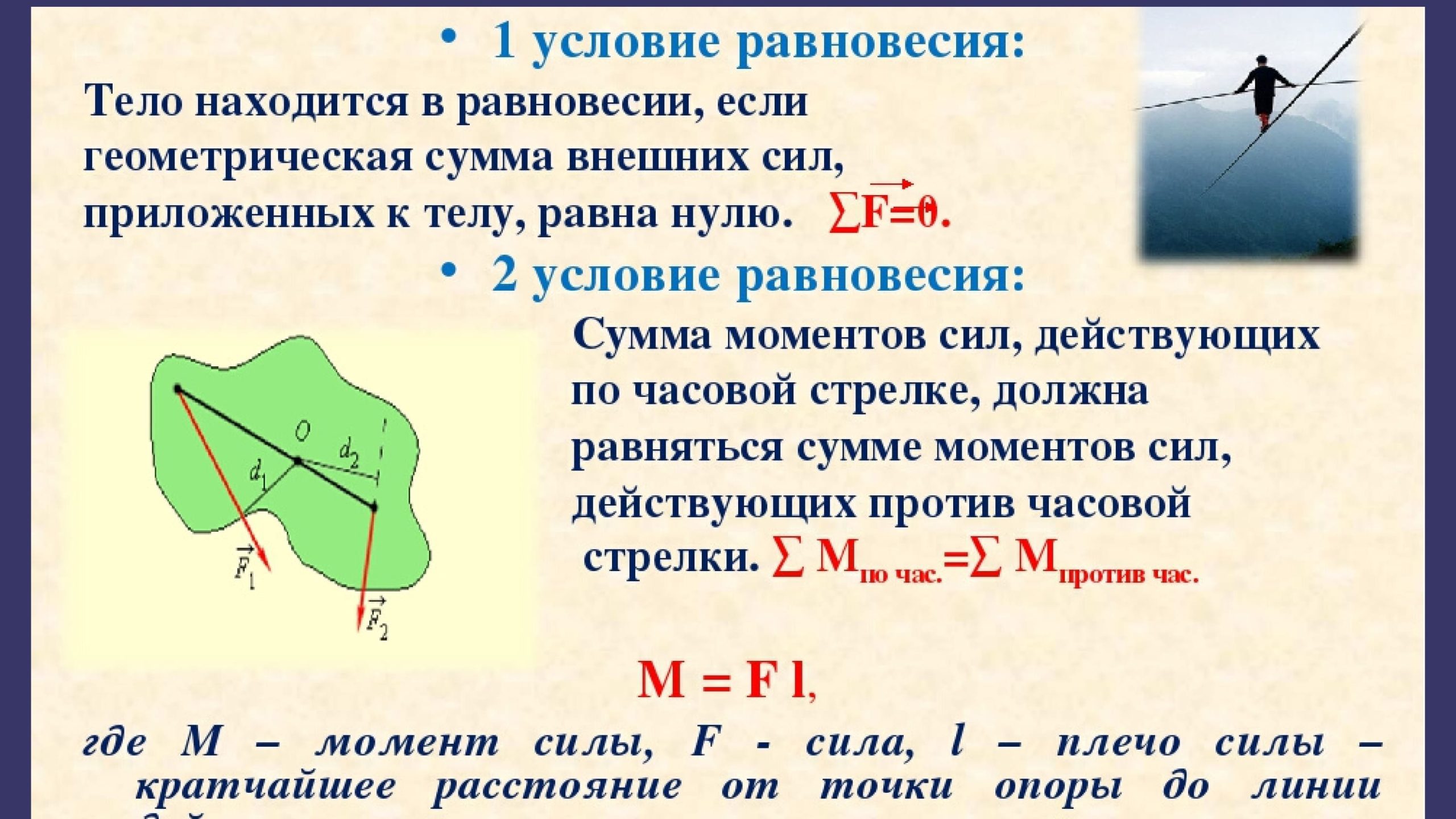 Внешний крутящий момент создается внешней силой. Вы можете выбрать точку, вокруг которой рассчитывается крутящий момент. Точка может быть физической точкой вращения системы или любой другой точкой в пространстве, но она должна быть одной и той же точкой для всех крутящих моментов. Если второе условие (чистый внешний крутящий момент в системе равен нулю) выполняется для одного выбора опорной точки, оно также будет выполняться для любого другого выбора опорной точки внутри или вне интересующей системы. (Это верно только в инерциальной системе отсчета.) Второе условие, необходимое для достижения равновесия, сформулировано в форме уравнения как

netτ=0netτ=0

9,6

где net означает итог. Моментам, действующим в противоположных направлениях, присваиваются противоположные знаки. Обычно принято называть крутящие моменты против часовой стрелки (ccw) положительными, а крутящие моменты по часовой стрелке (cw) — отрицательными.

Когда двое детей балансируют на качелях, как показано на рис. 9.8, они удовлетворяют двум условиям равновесия. Большинство людей имеют прекрасное представление о качелях, зная, что более легкий ребенок должен сидеть дальше от оси вращения и что более тяжелый ребенок может удерживать более легкого на неопределенное время.

Рисунок 9,8 Двое детей, балансирующих на качелях, удовлетворяют обоим условиям равновесия. Более легкий ребенок сидит дальше от оси вращения, чтобы создать крутящий момент, равный по величине крутящему моменту более тяжелого ребенка.

Пример 9.1

Она видела крутящий момент на качелях

Двое детей, изображенных на рис. 9.8, балансируют на качелях незначительной массы. (Это предположение сделано для простоты примера — далее последуют более сложные примеры.) Первый ребенок имеет массу 26,0 кг и сидит на расстоянии 1,60 м от оси вращения. (a) Если второй ребенок имеет массу 32,0 кг, как далеко она от стержня? (b) Что такое FpFp, поддерживающая сила, действующая на точку опоры?

Стратегия

Должны выполняться оба условия равновесия. В части (а) нас просят указать расстояние; таким образом, необходимо использовать второе условие (относительно крутящих моментов), поскольку в первом (относительно только сил) нет расстояний. Чтобы применить второе условие равновесия, мы сначала идентифицируем интересующую нас систему как качели плюс два потомка. Примем опорную точку за точку, относительно которой вычисляются крутящие моменты. Затем мы определяем все внешние силы, действующие на систему.

Решение (a)

Три внешние силы, действующие на систему, — это вес двух дочерних элементов и поддерживающая сила шарнира. Давайте рассмотрим крутящий момент, создаваемый каждым из них. Крутящий момент определяется как

τ=rFsinθ.τ=rFsinθ.

9,7

Здесь θ=90ºθ=90º, так что sinθ=1sinθ=1 для всех трех сил. Это означает, что r⊥=rr⊥=r для всех трех. Крутящие моменты, создаваемые тремя силами, во-первых,

τ1=r1w1τ1=r1w1

9,8

во-вторых,

τ2=–r2w2τ2=–r2w2

9,9

и в-третьих,

τp=rpFp=0⋅Fp=0. τp=rpFp=0⋅Fp=0.

9.10

Обратите внимание, что во второе уравнение вставлен знак минус, потому что этот крутящий момент направлен по часовой стрелке и, следовательно, по соглашению является отрицательным. Поскольку FpFp действует непосредственно на точку вращения, расстояние rprp равно нулю. Сила, действующая на шарнир, не может вызвать вращение, точно так же, как прямое нажатие на петли двери не заставит ее вращаться. Теперь второе условие равновесия состоит в том, что сумма крутящих моментов обоих потомков равна нулю. Поэтому

τ2=–τ1,τ2=–τ1,

9.11

или

r2w2=r1w1.r2w2=r1w1.

9.12

Вес равен массе, умноженной на ускорение свободного падения. Введя mgmg для ww, получим

r2m2g=r1m1g.r2m2g=r1m1g.

9.13

Решите это для неизвестного r2r2 :

r2=r1m1m2. r2=r1m1m2.

9.14

Величины в правой части уравнения известны; таким образом, r2r2 равно

r2=1,60 м26,0 кг32,0 кг=1,30 м. r2=1,60 м26,0 кг32,0 кг=1,30 м.

9.15

Как и ожидалось, более тяжелый ребенок должен сидеть ближе к оси (1,30 м против 1,60 м), чтобы уравновесить качели.

Решение (b)

Эта часть запрашивает силу FpFp. Самый простой способ найти его — использовать первое условие равновесия, которое равно

netF=0.netF=0.

9.16

Все силы вертикальны, так что мы имеем дело с одномерной задачей вдоль вертикальной оси; следовательно, условие можно записать как

net Fy=0net Fy=0

9.17

, где мы снова называем вертикальную ось осью y . Выбрав положительное направление вверх и используя знаки плюс и минус для указания направления сил, мы видим, что

Fp–w1–w2=0. Fp–w1–w2=0.

9.18

Это уравнение дает то, о чем можно было догадаться вначале:

Fp=w1+w2.Fp=w1+w2.

9,19

Итак, шарнир создает поддерживающую силу, равную общему весу системы:

Fp=m1g+m2g.Fp=m1g+m2g.

9,20

Ввод известных значений дает

Fp=26,0 кг9,80 м/с2+32,0 кг9,80 м/с2=568 N.Fp=26,0 кг9,80 м/с2+32,0 кг9,80 м/с2= 568 N.

9.21

Обсуждение

Два результата интуитивно понятны. Более тяжелый ребенок сидит ближе к оси. Шарнир поддерживает вес двух детей. Часть (b) также может быть решена с использованием второго условия равновесия, поскольку оба расстояния известны, но только в том случае, если точка поворота выбрана не в том месте, где находится фактическая точка поворота качелей!

Несколько аспектов предыдущего примера имеют широкие последствия. Во-первых, выбор точки вращения в качестве точки, вокруг которой рассчитываются крутящие моменты, упростил задачу. Поскольку FpFp воздействует на точку вращения, его плечо рычага равно нулю. Следовательно, крутящий момент, создаваемый поддерживающей силой FpFp, равен нулю относительно этой точки поворота. Второе условие равновесия выполняется при любом выборе опорной точки, поэтому мы выбираем опорную точку, чтобы упростить решение задачи.

Во-вторых, ускорение свободного падения в этой задаче отменилось, и мы остались с отношением масс. Так будет не всегда . Всегда вводите правильные силы — не забегайте вперед, вводя какое-то отношение масс.

В-третьих, вес каждого ребенка распределяется по площади качелей, но мы рассматривали веса так, как если бы каждая сила прикладывалась к одной точке. Это не приближение — расстояния r1r1 и r2r2 — это расстояния до точек, находящихся непосредственно под центром тяжести каждого ребенка. Как мы увидим в следующем разделе, масса и вес системы могут действовать так, как если бы они находились в одной точке.

Наконец, обратите внимание, что концепция крутящего момента важна не только для статического равновесия. Крутящий момент играет ту же роль во вращательном движении, что и сила в прямолинейном движении. Мы рассмотрим это в следующей главе.

Домашний эксперимент

Возьмите кусок пластилина и положите его на стол, затем вдавите в него цилиндр так, чтобы линейка могла балансировать на круглой стороне цилиндра, пока все остается неподвижным. Положите монетку на расстоянии 8 см от оси. Куда вам нужно положить две копейки, чтобы сбалансировать? Три пенни?

9.2 Второе условие равновесия – Колледж физики, главы 1-17

9 Статика и крутящий момент

Резюме

Укажите второе условие, необходимое для достижения равновесия.
Объясните крутящий момент и факторы, от которых он зависит.
Описать роль крутящего момента в механике вращения

КРУТЯЩИЙ МОМЕНТ

Второе условие, необходимое для достижения равновесия, предполагает избегание ускоренного вращения (поддержание постоянной угловой скорости. Вращающееся тело или система могут находиться в равновесии, если скорость их вращения постоянна и остается неизменной под действием действующих на них сил. Понять какие факторы влияют на поворот, давайте подумаем, что происходит, когда вы открываете обычную дверь, вращая ее на петлях.0005

Несколько известных факторов определяют, насколько эффективно вы открываете дверь. См. рис. 1. Прежде всего, чем больше сила, тем эффективнее она открывает дверь — очевидно, чем сильнее вы нажимаете, тем быстрее открывается дверь. Кроме того, точка, в которую вы нажимаете, имеет решающее значение. Если вы приложите силу слишком близко к петлям, дверь откроется медленно, если вообще откроется. Большинство людей были смущены, совершив эту ошибку и наткнувшись на дверь, которая не открылась так быстро, как ожидалось. Наконец, направление, в котором вы продвигаетесь, также важно. Самое эффективное направление — перпендикулярно двери — мы толкаем в этом направлении почти инстинктивно.

Рис. 1. Крутящий момент — это вращающая или скручивающая эффективность силы, показанная здесь для вращения двери на петлях (если смотреть сверху). Крутящий момент имеет как величину, так и направление. (a) Эта сила создает крутящий момент против часовой стрелки, что означает, что дверь будет вращаться против часовой стрелки из-за F . Обратите внимание, что r _⊥ — это расстояние по перпендикуляру от оси вращения до линии действия силы. (b) Меньший крутящий момент против часовой стрелки создается меньшей силой F′ , действующие на одинаковом расстоянии от шарниров (точки поворота). (c) Та же сила, что и в (a), создает меньший крутящий момент против часовой стрелки, когда она приложена на меньшем расстоянии от шарниров. (г) Та же сила, что и в (а), но действующая в противоположном направлении, создает крутящий момент по часовой стрелке. (e) Меньший крутящий момент против часовой стрелки создается силой той же величины, действующей в той же точке, но в другом направлении.

Здесь θ меньше, чем 90º . (f) Крутящий момент здесь равен нулю, так как сила просто тянет шарниры, не производя вращения. В этом случае θ = 0º .

Величина, направление и точка приложения силы включены в определение физической величины, называемой крутящим моментом. Крутящий момент — вращательный эквивалент силы. Это мера эффективности силы в изменении или ускорении вращения (изменение угловой скорости в течение определенного периода времени). В форме уравнения величина крутящего момента определяется как

[латекс]\boldsymbol{\tau=rF\:\sin\:\theta}[/латекс]

, где [латекс]\boldsymbol{\tau}[/латекс](греческая буква тау) — обозначение крутящего момента,[латекс]\жирныйсимвол{r}[/латекс] — расстояние от точки вращения до точки, где приложена сила,[latex]\boldsymbol{F}[/latex]является величиной силы, а[latex]\boldsymbol{\theta}[/latex]является углом между силой и вектором, направленным из точка приложения к точке поворота, как показано на рис. 1 и рис. 2. Альтернативное выражение для крутящего момента дается через перпендикулярный рычаг [латекс]\boldsymbol{r_{\perp}}[/латекс], как показано на Рисунке 1 и Рисунке 2, который определяется как

[латекс]\boldsymbol{r_{\perp}=r\:\sin\:\theta}[/латекс]

так что

[латекс]\boldsymbol{\tau=r_{\perp}F.}[/латекс]

Рис. 2. Сила, приложенная к объекту, может создавать крутящий момент, который зависит от положения точки вращения. (a) Три фактора r , F и θ для точки вращения A на теле показаны здесь — r — расстояние от выбранной точки вращения до точки приложения силы F , и θ угол между F и вектором, направленным от точки приложения к точке поворота. Если объект может вращаться вокруг точки А, он будет вращаться против часовой стрелки.

Это означает, что крутящий момент направлен против часовой стрелки относительно точки вращения A. (b) В этом случае точка B является точкой вращения. Крутящий момент от приложенной силы вызовет вращение по часовой стрелке вокруг точки B, и, таким образом, это крутящий момент по часовой стрелке относительно B.

Перпендикулярное плечо рычага[latex]\boldsymbol{r_{\perp}}[/latex]является кратчайшим расстоянием от точки вращения до линии, вдоль которой действует[latex]\textbf{F}[/latex]; она показана пунктирной линией на рисунках 1 и 2. Обратите внимание, что отрезок, определяющий расстояние[latex]\boldsymbol{r_{\perp}}[/latex], перпендикулярен [latex]\textbf{F} ,[/latex], как следует из названия. Иногда легче найти или визуализировать [латекс]\boldsymbol{r_{\perp}}[/latex], чем найти и [латекс]\boldsymbol{r}[/латекс], и [латекс]\boldsymbol{\theta} .[/latex]В таких случаях может быть удобнее использовать[latex]\boldsymbol{\tau=r_{\perp}F}[/latex],а не [latex]\boldsymbol{tau=rF\:\ sin\:\theta}[/latex] для крутящего момента, но оба они одинаково действительны. 90)}[/latex]относительно петель. Если вы уменьшите силу до 20 Н, крутящий момент уменьшится до [латекс]\boldsymbol{16\textbf{ Н}\cdotp\textbf{м}},[/латекс]и так далее.

Крутящий момент всегда рассчитывается относительно некоторой выбранной точки поворота. Для одной и той же приложенной силы другой выбор положения оси даст другое значение крутящего момента, поскольку как [латекс]\жирныйсимвол{r}[/латекс], так и [латекс]\жирныйсимвол{\тета}[ /latex] зависят от расположения точки опоры. Любая точка любого объекта может быть выбрана для расчета крутящего момента относительно этой точки. Объект может фактически не поворачиваться вокруг выбранной «точки вращения».

Обратите внимание, что при вращении в плоскости крутящий момент имеет два возможных направления. Крутящий момент либо по часовой стрелке, либо против часовой стрелки относительно выбранной точки поворота, как показано для точек B и A соответственно на рисунке 2. Если объект может вращаться вокруг точки A, он будет вращаться против часовой стрелки, что означает, что крутящий момент для силы равен показано как против часовой стрелки относительно точки A. Но если объект может вращаться вокруг точки B, он будет вращаться по часовой стрелке, что означает, что крутящий момент для показанной силы направлен по часовой стрелке относительно B. Кроме того, величина крутящего момента больше, когда плечо рычага дольше.

Итак, второе условие, необходимое для достижения равновесия , заключается в том, что чистый внешний крутящий момент в системе должен быть равен нулю . Внешний крутящий момент создается внешней силой. Вы можете выбрать точку, вокруг которой рассчитывается крутящий момент. Точка может быть физической точкой вращения системы или любой другой точкой в пространстве, но она должна быть одной и той же точкой для всех крутящих моментов. Если второе условие (чистый внешний крутящий момент в системе равен нулю) выполняется для одного выбора опорной точки, оно также будет выполняться для любого другого выбора опорной точки внутри или вне интересующей системы. (Это верно только в инерциальной системе отсчета.) Второе условие, необходимое для достижения равновесия, сформулировано в форме уравнения как

[латекс] \boldsymbol{\textbf{net}\tau=0}[/латекс]

, где чистый означает общий. Моментам, действующим в противоположных направлениях, присваиваются противоположные знаки. Обычно принято называть крутящие моменты против часовой стрелки (ccw) положительными, а крутящие моменты по часовой стрелке (cw) — отрицательными.

Когда двое детей балансируют на качелях, как показано на рисунке 3, они удовлетворяют двум условиям равновесия. Большинство людей имеют прекрасное представление о качелях, зная, что более легкий ребенок должен сидеть дальше от оси вращения и что более тяжелый ребенок может удерживать более легкого на неопределенное время.

Рис. 3. Двое детей, балансирующих на качелях, удовлетворяют обоим условиям равновесия. Более легкий ребенок сидит дальше от оси вращения, чтобы создать крутящий момент, равный по величине крутящему моменту более тяжелого ребенка.

Пример 1: Она увидела крутящий момент на качелях

Двое детей, изображенных на рисунке 3, балансируют на качелях незначительной массы. (Это предположение сделано для простоты примера — далее последуют более сложные примеры. ) Первый ребенок имеет массу 26,0 кг и сидит на расстоянии 1,60 м от оси вращения. (a) Если второй ребенок имеет массу 32,0 кг, как далеко она от стержня? (b) Какова [латекс]\boldsymbol{F_{\textbf{p}}},[/latex]поддерживающая сила, действующая на шарнир?

Стратегия

[латекс]\boldsymbol{\tau_1=r_1\:w_1}[/latex]

второму,

[латексу]\boldsymbol{\tau_2=-r_2\:w_2 }[/latex]

и третий,

[латекс]\begin{array}{lcl} \boldsymbol{\tau _{\textbf{p}}} & \boldsymbol{=} & \boldsymbol{r _{\textbf {p}}F_{\textbf{p}}} \\ {} & \boldsymbol{=} & \boldsymbol{0\:\cdotp\:F_{\textbf{p}}} \\ {} & \boldsymbol {=} & \boldsymbol{0.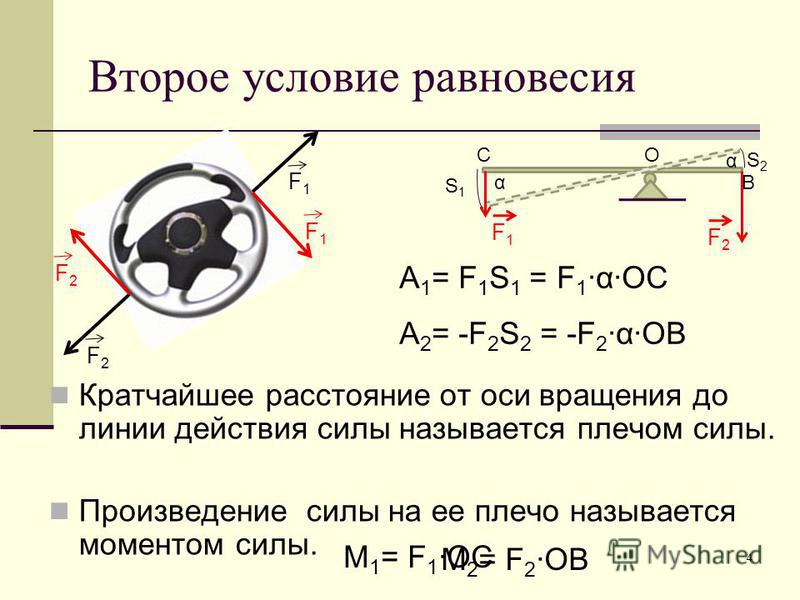 } \end{массив}[/latex]

Обратите внимание, что во второе уравнение добавлен знак минус, потому что этот крутящий момент направлен по часовой стрелке и, следовательно, по соглашению является отрицательным. Поскольку [latex]\boldsymbol{F_{\textbf{p}}}[/latex]воздействует непосредственно на точку вращения, расстояние[latex]\boldsymbol{r_{\textbf{p}}}[/latex] равно нулю . Сила, действующая на шарнир, не может вызвать вращение, точно так же, как прямое нажатие на петли двери не заставит ее вращаться. Теперь второе условие равновесия состоит в том, что сумма крутящих моментов обоих потомков равна нулю. Поэтому

[латекс]\boldsymbol{\tau_2=-\tau_1},[/latex]

или

[латекс]\boldsymbol{r_2\:w_2=r_1\:w_1}.[/latex]

Вес масса, умноженная на ускорение свободного падения. Введя[latex]\boldsymbol{mg}[/latex]для[latex]\boldsymbol{w},[/latex] получаем

[latex]\boldsymbol{r_2m_2g=r_1m_1g}.[/latex]

Решаем это для неизвестного [латекс]\boldsymbol{r_2}:[/latex]

[латекс]\boldsymbol{r_2=\:r_1}[/latex][латекс]\boldsymbol{\frac{m_1}{m_2}}. [/латекс]

Величины в правой части уравнения известны; таким образом, [латекс]\boldsymbol{r_2}[/латекс] равно

[латекс]\boldsymbol{r_2=\:(1,60\textbf{m})}[/латекс][латекс]\boldsymbol{\frac{26,0 \textbf{ кг}}{32,0\textbf{ кг}}}[/latex][latex]\boldsymbol{\:=1,30\textbf{ м}}.[/latex]

Как и ожидалось, более тяжелый ребенок должен сидеть ближе к оси (1,30 м против 1,60 м), чтобы сбалансировать качели.

Решение (b)

В этой части запрашивается сила[latex]\boldsymbol{F_{\textbf{p}}}.[/latex]Самый простой способ найти ее — использовать первое условие равновесия , то есть

[латекс]\boldsymbol{\textbf{net}F=0}.[/латекс]

[латекс]\boldsymbol{\textbf{net}F_y=0}[/латекс]

, где мы снова называем вертикальную ось y -осью. Выбирая положительное направление вверх и используя знаки плюс и минус для указания направлений сил, мы видим, что

[латекс]\boldsymbol{F_{\textbf{p}}-w_1-w_2=0}. [ /латекс] 92)} \\ {} & \boldsymbol{=} & \boldsymbol{568\textbf{ N.}} \end{array}[/latex]

Обсуждение

Несколько аспектов предыдущего примера имеют широкие последствия. Во-первых, выбор точки вращения в качестве точки, вокруг которой рассчитываются крутящие моменты, упростил задачу. Поскольку [латекс]\жирныйсимвол{F_{\textbf{p}}}[/латекс] воздействует на точку вращения, его плечо рычага равно нулю. Следовательно, крутящий момент, создаваемый поддерживающей силой[латекс]\boldsymbol{F_{\textbf{p}}}[/латекс], равен нулю относительно этой точки поворота. Второе условие равновесия выполняется при любом выборе опорной точки, поэтому мы выбираем опорную точку, чтобы упростить решение задачи.

В-третьих, вес каждого ребенка распределяется по площади качелей, однако мы рассматривали веса так, как если бы каждая сила прикладывалась к одной точке. Это не приближение — расстояния[latex]\boldsymbol{r_1}[/latex]и[latex]\boldsymbol{r_2}[/latex]являются расстояниями до точек непосредственно под 9 точками.0218 центр тяжести каждого ребенка. Как мы увидим в следующем разделе, масса и вес системы могут действовать так, как если бы они находились в одной точке.

Наконец, обратите внимание, что концепция крутящего момента имеет значение помимо статического равновесия. Крутящий момент играет ту же роль во вращательном движении, что и сила в прямолинейном движении. Мы рассмотрим это в следующей главе.

ДОМАШНИЙ ЭКСПЕРИМЕНТ

Второе условие гарантирует, что эти крутящие моменты также сбалансированы. Крутящий момент является вращательным эквивалентом силы, производящей вращение, и определяется как
[латекс]\boldsymbol{\tau=rF\:\sin\:\theta}[/латекс]
, где [латекс]\boldsymbol{\tau}[/латекс]это крутящий момент,[латекс]\boldsymbol{r}[/латекс]это расстояние от точки вращения до точки приложения силы,[латекс]\ boldsymbol{F}[/latex] — величина силы, а [latex]\boldsymbol{\theta}[/latex] — угол между [latex]\boldsymbol{F}[/latex] и вектором, направленным из точка, где сила действует на точку опоры. Перпендикулярное плечо рычага[латекс]\boldsymbol{r_{\perp}}[/латекс] определяется равным
[латекс]\boldsymbol{r_{\perp}=r\:\sin\:\theta}[/латекс]
так что
[латекс]\boldsymbol{\tau=r_{\perp}F}.[/латекс]
Перпендикулярное плечо рычага[latex]\boldsymbol{r_{\perp}}[/latex]является кратчайшим расстоянием от точки вращения до линии, вдоль которой действует[latex]\boldsymbol{F}[/latex].