Внешние и внутренние силы в сопромате.

В сопромате силы, приложенные к телу в результате взаимодействия тел, называются внешними. Внешние силы бывают объемными (например, собственный вес) и поверхностными. Поверхностные силы делятся на сосредоточенные (теоретически действующие в точке), и на распределенные (приложенные по длине или на площади). Величина распределенной нагрузки, приходящейся на единицу длины или площади, называется интенсивностью нагрузки. Сопротивление материалов изучает не только статические , но и динамические нагрузки.  По времени действия нагрузки делятся на постоянные и временные. По характеру действия нагрузки подразделяются на статические и динамические. Статические нагрузки прилагаются постепенно, они не меняются, или меняются незначительно. Динамические нагрузки меняют величину в течение короткого промежутка времени. Под действием внешних сил в материале возникают внутренние силы, сопровождающие деформацию.

Для определения внутренних сил, возникающих в брусе от действия внешних сил, в сопромате применяется метод сечений.

 

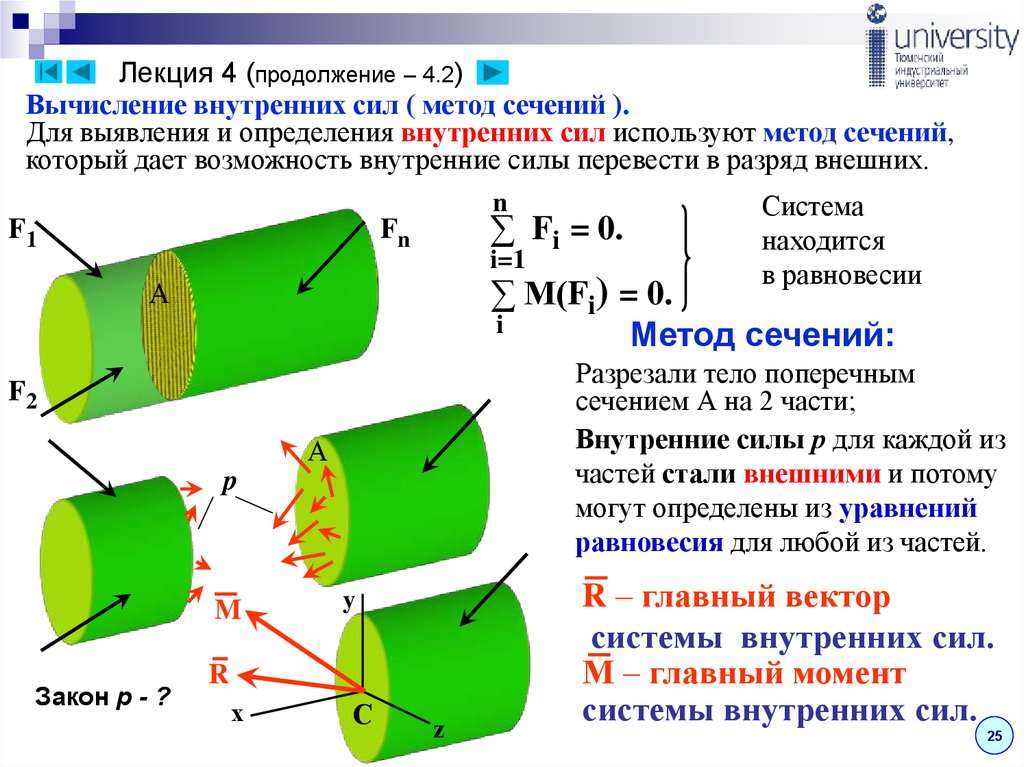
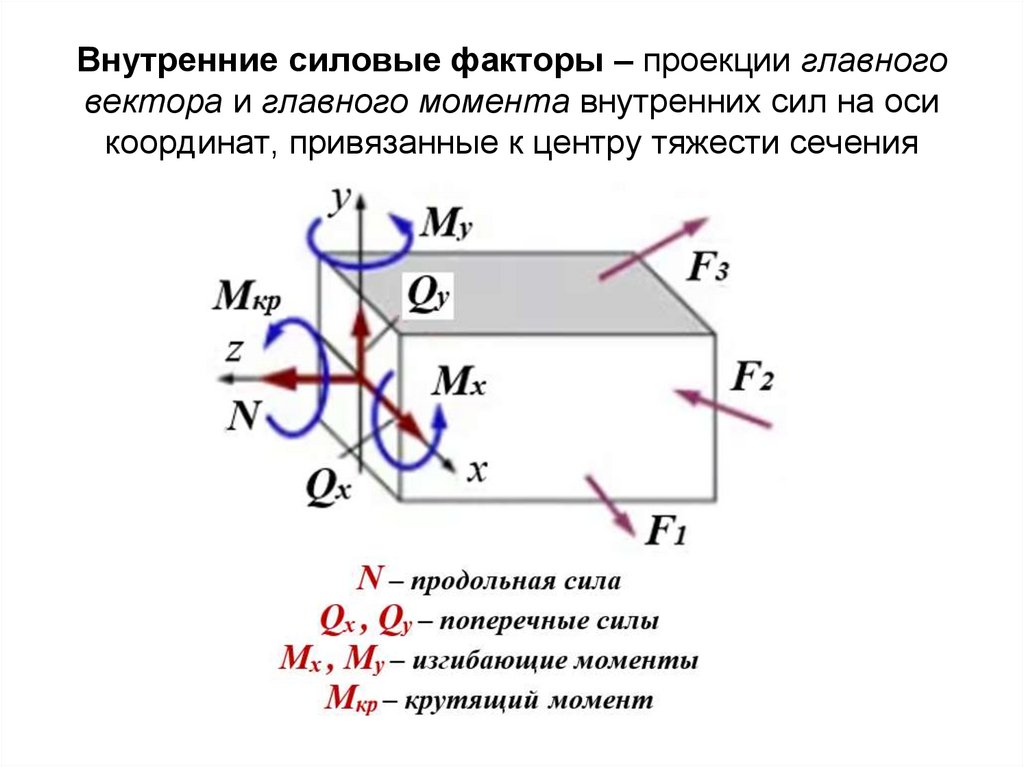
  Изучаемый брус мысленно рассекаем плоскостью на две части. Предполагаем, что каждая из частей находится в равновесии под действием внешних сил, приложенных к этой части, и внутренних сил, возникающих в сечении и представляющих собой силы взаимодействия между оставшейся и отброшенной частями. Равнодействующая внутренних сил в сечении называется внутренним усилием. Рассмотрим пространственный брус, находящийся в равновесии под действием внешних сил (рис. 1).

  Если брус рассечь плоскостью (использование метода сечений), перпендикулярной оси, т.е. поперечным сечением (рис. 1) и разложить главный вектор и главный момент внутренних сил по осям x,y,z, то на каждой стороне сечения получим шесть внутренних силовых факторов: три силы (N, Qx, Qy) и три момента (Mx, My, Mz).

 

 Эти шесть усилий, совместно с внешними силами, действующими на отсеченную часть бруса, должны обеспечить равновесия этой части. Таким образом, для каждой части бруса должны быть выполнены шесть условий равновесия: сумма моментов сил относительно осей координат, сумма проекций сил на оси координат равна нулю.

В этом и есть суть метода сечений сопромата.

 Усилия, возникающие в сечении бруса, имеют в сопромате следующие наименования: 

 

N — продольная сила; Qу, Qх — поперечные силы;

Мz — крутящий момент; Мх, Му — изгибающие моменты.

 

  Внутренняя сила (Nz, Qу , Qх) численно равна алгебраической сумме проекций на соответствующую ось бруса всех внешних сил, расположенных по одну сторону от сечения.

 

  Момент (Мz Мx Мy) в любом сечении численно равен алгебраической сумме моментов относительно соответствующей оси бруса от всех внешних сил, расположенных по одну сторону от сечения.

 

  Графики, показывающие как изменяются внутренние усилия при переходе от сечения к сечению, в сопромате называются эпюрами.

  Интенсивность внутренних сил, приходящихся на единицу площади, в сопротивление материалов называется напряжением.

  Допустим, что около некоторой точки поперечного сечения бруса, выделена элементарная площадка dА (рис.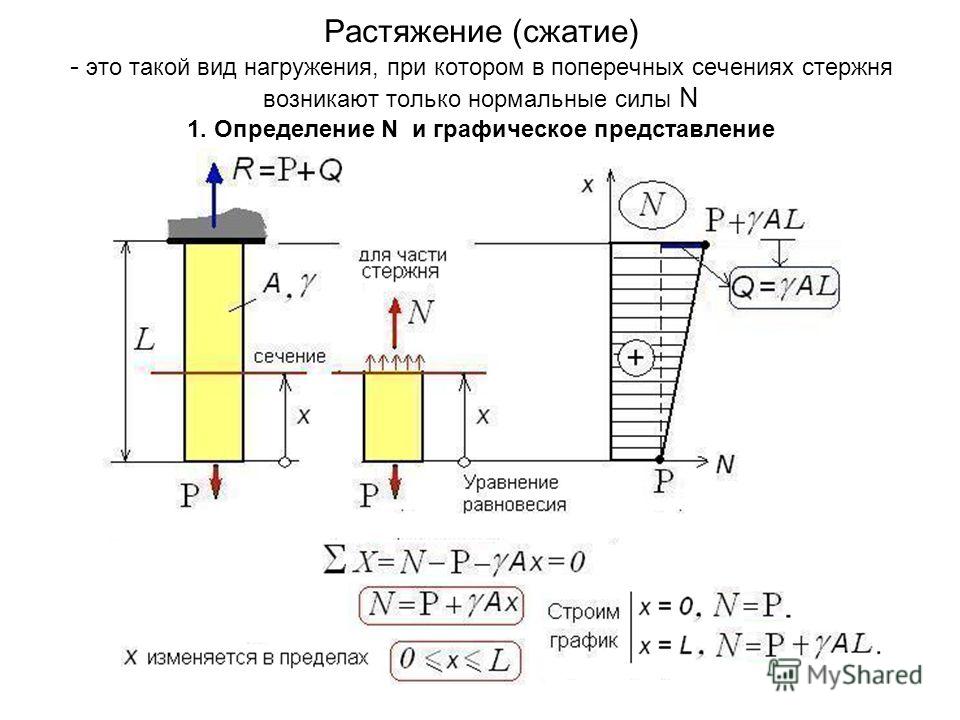 2). Равнодействующая внутренней силы, действующая на данной площадке, равна dR.. Проекциями dR на оси будут dN, dQy и dQx.

Разделив величины dN, dQy и dQx на площадь dA, получим величины продольных и попе-

речных сил, приходящихся на единицу площади: 

 

 

 

 

 Их измеряют в единицах напряжения — паскалях (Па) и кратных ему — (кПа и мПа)

Полное напряжение в данной точке рассматриваемого сечения:

Сила — величина векторная, следовательно, и напряжение – вектор того же направления.

Между напряжениями и деформациями существует зависимость. В случае упругой деформации эта зависимость выражается законом Гука.

 

 Закон Гука при линейной деформации (растяжение или сжатие) выражает прямолинейную зависимость между нормальными напряжениями и относительными деформациями.

 

 

При угловой деформации (сдвиг) существует прямолинейная зависимость между касательными напряжениями и углами сдвига:   т = уе.

В этих выражениях Е и G — коэффициенты пропорциональности,

характеризующие упругие свойства материалов:

Е — модуль нормальной упругости или модуль Юнга;

G — модуль упругости при сдвиге или модуль сдвига;

е — относительная продольная деформация;

у — относительная угловая деформация.

 

Внутренняя сила — глоссарий технических терминов

Внутренняя сила (ВС) – один из двух (наряду с внутренним моментом) силовых факторов возникающих в поперечном сечении бруса под действием внешних нагрузок.

Рассмотрим некоторый брус, находящийся под воздействием произвольной системы внешних сил.

Оговоримся, что эти нагрузки удерживают брус в состоянии равновесия.

Для расчета внутренних сил применяется метод сечений.

Если данный брус мысленно рассечь в любом месте и рассмотреть одну из частей, то для обеспечения ее неподвижности отброшенная часть заменяется действием внутренней силы R и внутреннего момента M.

Другими словами, внутренняя сила это некоторое усилие, с которым обе части бруса «удерживают» друг друга.

В общем случае нагружения внутренняя сила может располагаться под любым углом к поперечному сечению рассматриваемого бруса. Поэтому для некоторого упрощения расчетов её раскладывают на составляющие, проецируя на соответствующие оси координат.

Всего может быть три составляющие полной внутренней силы: продольная сила N и две поперечные силы Q_x и Q_y.

Величина и направление внутренних сил определяется из условия статичности отсеченных частей бруса. Для этого записываются необходимые уравнения статики: суммы проекций всех внешних и внутренних сил приложенных к рассматриваемой части приравниваются к нулю

откуда

При растяжении-сжатии внутренняя сила в поперечном сечении направлена вдоль оси стержня (продольная сила N).

При кручении ВС равна нулю (имеет место только внутренний скручивающий момент).

При поперечном изгибе ВС направлена поперек продольной оси балки (поперечная сила Q).

Знак внутренних сил зависит от направления и расположения по отношению к рассматриваемой части бруса и принимается согласно соответствующих правил.

Практически все прочностные расчеты в механике начинаются с определения внутренних усилий в элементах конструкций.

В случаях, когда внутренние усилия меняют величину и знак по длине бруса для наглядности строят их эпюры.

Пример эпюры внутренних продольных сил при растяжении-сжатии

Расчет внутренних сил >>
Другие примеры решения задач >>

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.

---

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Сохранить или поделиться с друзьями

---

Заказать решение

---

Поиск формул и решений задач

6.1 Типы внутренних сил – инженерная механика: статика

Глава 6: Внутренние силы

Когда вы делаете разрез в объекте, аналогично фиксированной реакции, мы описываем, что происходит в этой точке, используя одну горизонтальную силу (называемую нормальной силой), одну вертикальную силу (называемую поперечной силой) и изгибающий момент.

Взято из источника: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/6_internal_forces/6-2_internal_forces_равновесие/internal_forces_равновесие.html

Существует 3 типа внутренних сил (и моментов):

• нормальная сила (Н) – горизонтальная сила, которую мы рассчитали для ферм в предыдущей главе
• поперечная сила (В) – вертикальная сила, которая изменяется в зависимости от приложенных нагрузок
• изгибающий момент (М) – изменения в зависимости от приложенных нагрузок и приложенных моментов

Нормальная сила обозначается буквой «Н».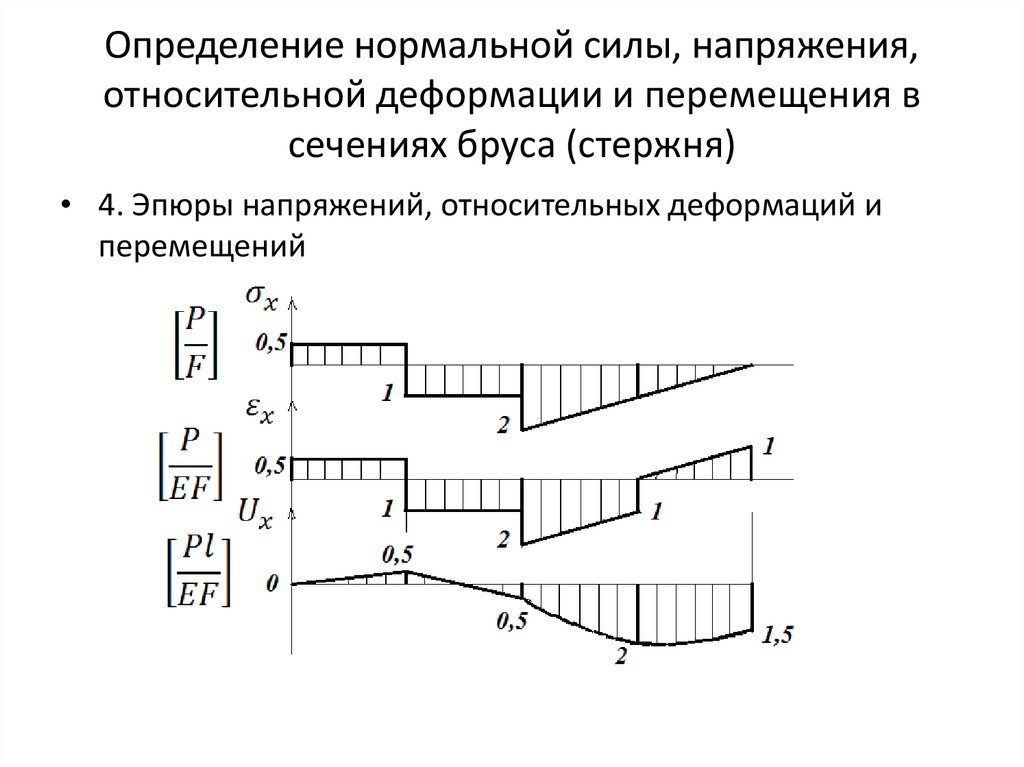 Сила сдвига, вертикальная сила представлена ​​буквой «V». Изгибающий момент «М». Нормальный и поперечный имеют единицы Н или фунты, а изгибающий момент имеет единицы Нм или фут-фунт. В следующей таблице обобщена информация о внутренних силах (и моментах).

Сила/момент	Сокращение	Блок	Направление горизонтального луча
Нормальная сила	Н	Н или фунт	горизонтальный
Сила сдвига	В	Н или фунт	вертикальный
Момент	М	Нм или фут-фунт	вращение

Обратите внимание, что для вертикальной колонны нормальная сила будет вертикальной. По этой причине нормальную силу часто называют «осевой», например: вдоль оси. Сила сдвига для колонны будет горизонтальной и иногда называется «поперечной».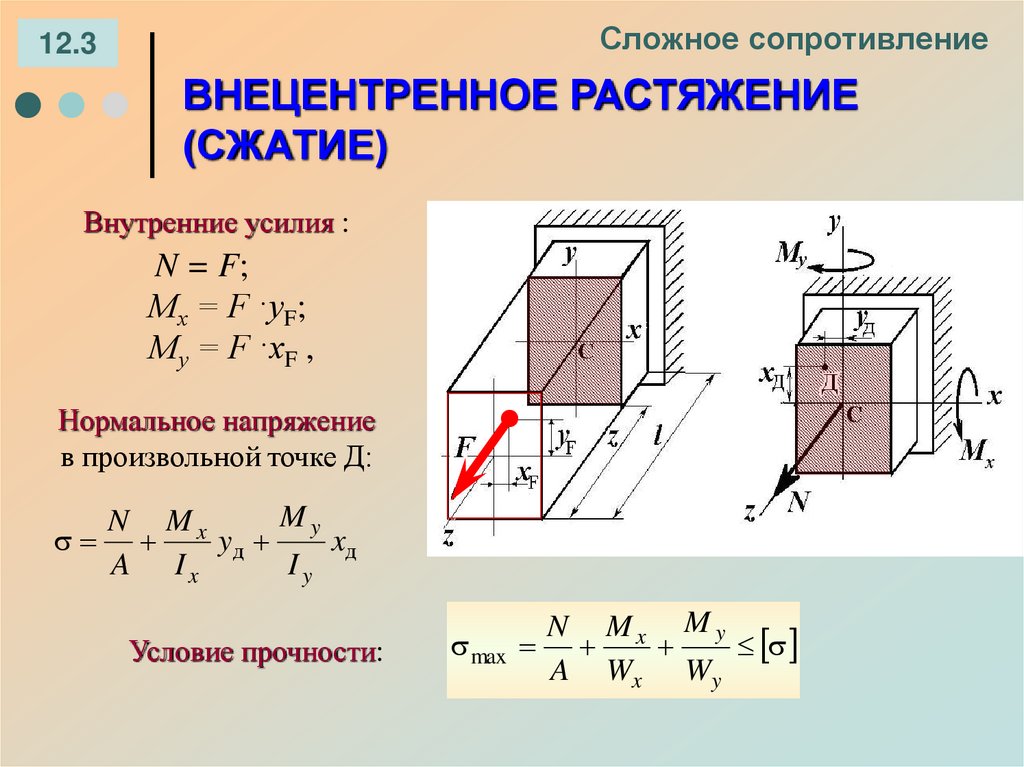

Это для двухмерного анализа балки при условии незначительной нагрузки в третьем измерении.

 

Когда балка или рама подвергаются поперечным нагрузкам, возникают три возможные внутренние силы: нормальная или осевая сила, сила сдвига и изгибающий момент, как показано в разделе 9.0087 k консоли на рисунке ниже. Чтобы предсказать поведение конструкций, необходимо знать величины этих сил. В этой главе учащиеся узнают, как определить величину поперечной силы и изгибающего момента в любом сечении балки или рамы и как представить вычисленные значения в графической форме, которая называется «поперечной силой». и «диаграммы изгибающих моментов». Диаграммы изгибающего момента и силы сдвига оказывают неоценимую помощь при проектировании, поскольку они показывают максимальные изгибающие моменты и силы сдвига, необходимые для определения размеров элементов конструкции.

Нормальная сила

Нормальная сила в любом сечении конструкции определяется как алгебраическая сумма осевых сил, действующих с обеих сторон сечения.

Сила сдвига

Сила сдвига (SF) определяется как алгебраическая сумма всех поперечных сил, действующих по обе стороны сечения балки или рамы. Фраза «с любой стороны» важна, так как подразумевает, что в каждом конкретном случае поперечную силу можно получить, суммируя поперечные силы с левой или с правой стороны сечения.

Изгибающий момент

Изгибающий момент (BM) определяется как алгебраическая сумма моментов всех сил, действующих по обе стороны сечения балки или рамы.

Источник: Внутренние силы в балках и рамах, Либретексты. https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.04%3A_Internal_Forces_in_Beams_and_Frames

 

В 3-х измерениях есть:

• 1 нормальное усилие (Н)
• 2 усилия сдвига (V ₁ и V ₂ ) и
• 3 изгибающих момента (M ₁ , M ₂ , & T – кручение).

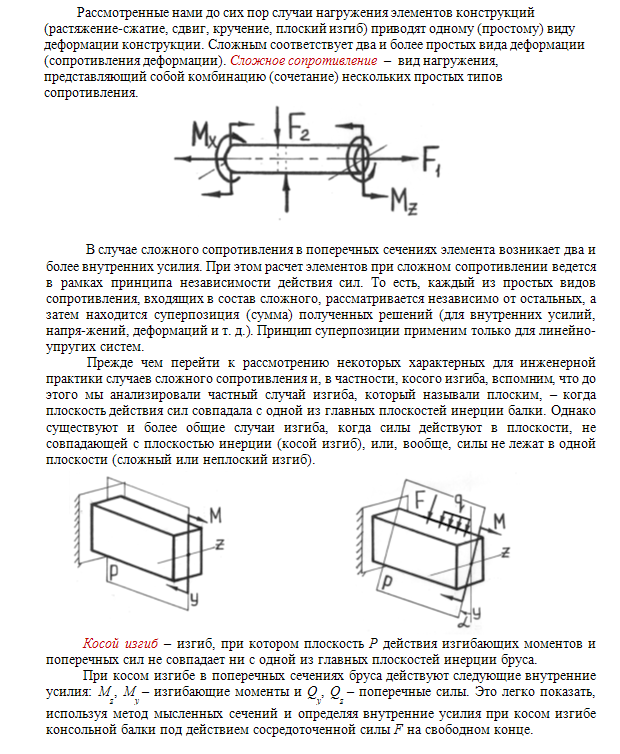Источник: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/6_internal_forces/6-2_internal_forces_равновесие/internal_forces_равновесие.html

Чтобы в отрасли существовал стандарт, необходимо соглашение о знаках, чтобы мы договорились о том, что является положительным, а что отрицательным. Справа для сдвига – положительная. Обратите внимание, что на обоих следующих рисунках показано одинаковое соглашение о знаках.

Соглашение о положительном знаке адаптировано из источника: https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.04%3A_Internal_Forces_in_Beams_and_Frames

Когда вы смотрите на балку в целом (на рисунке ниже ), положительный сдвиг правой стороной вниз. Когда вы разрезаете балку, чтобы она находилась в статическом равновесии, положительный сдвиг должен быть направлен вверх справа, чтобы быть равным и противоположным общему движению.

 

 

Осевая (нормальная) сила

Осевая сила считается положительной, если она стремится сместить элемент в рассматриваемом сечении. Такая сила считается растягивающей, а элемент подвергается осевому растяжению. С другой стороны, осевая сила считается отрицательной, если она стремится раздавить элемент в рассматриваемом сечении. Такая сила считается сжимающей, а элемент находится в осевом сжатии.

Сила сдвига

Сила сдвига, стремящаяся сместить левую часть секции вверх или правую сторону секции вниз, считается положительной. Точно так же поперечная сила, имеющая тенденцию перемещать левую сторону сечения вниз или правую сторону вверх, будет считаться отрицательной поперечной силой.

Изгибающий момент

Изгибающий момент считается положительным, если он стремится вызвать вогнутость вверх (провисание). Если изгибающий момент имеет тенденцию вызывать вогнутость вниз (заклинивание), это будет считаться отрицательным изгибающим моментом.

Источник: Внутренние силы в балках и рамах, Либретексты. https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.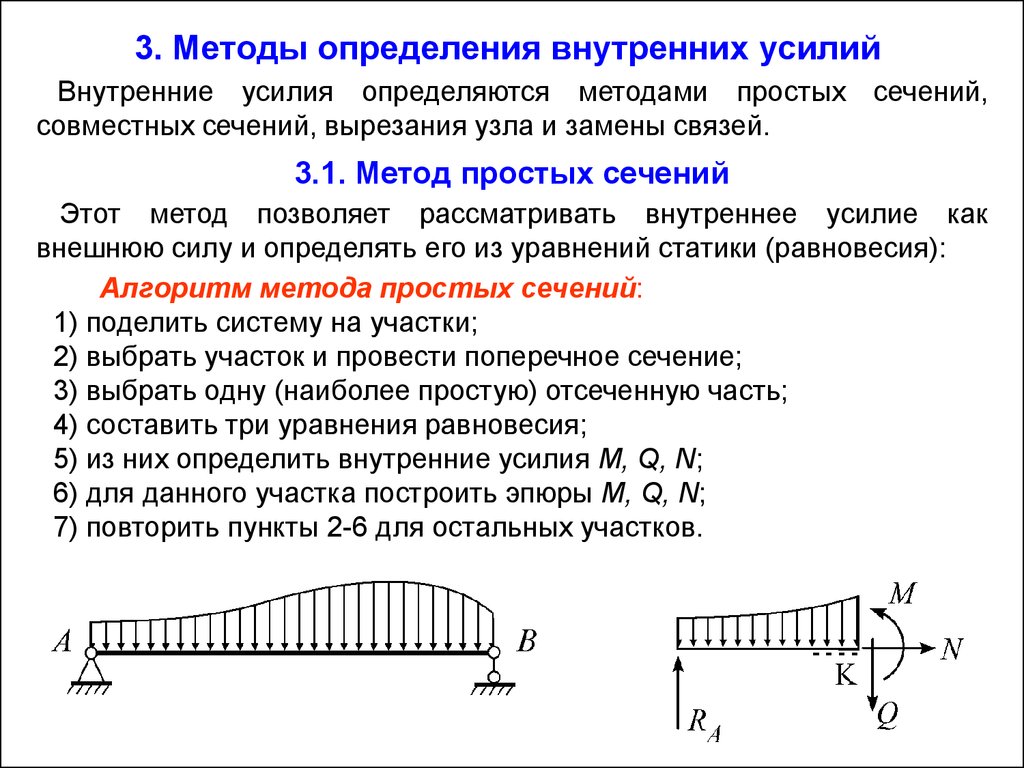 04%3A_Internal_Forces_in_Beams_and_Frames

Для решения внутренних сил в определенной точке балки,

Соглашение о положительном знаке адаптировано из https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.04%3A_Internal_Forces_in_Beams_and_Frames

 

1. Найти внешние силы и силы реакции
2. Сделайте надрез.
3. В FBD одной стороны разреза добавьте внутренние силы (и моменты), используя положительный знак.
4. Используйте уравнения равновесия для решения неизвестных внутренних сил и моментов.

 

 

Пример: Для следующей распределенной нагрузки: а) что такое силы реакции? б) каковы внутренние силы в средней точке б) между силами реакции?

Адаптировано из: Источник: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/6_internal_forces/6-3_axial_torque_diagrams/axial_torque_diagrams.html

1. Решите внешние силы:

Адаптировано из: Источник: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/6_internal_forces/6-3_axial_torque_diagrams/axial_torque_diagrams.html

[латекс]\сумма F_{X}=A_{x}=0[/латекс]
[латекс]\сумма F_{ y}=A_{y}+C-\omega L=0[/latex]
[латекс]\sum M_{A}=-(\omega L)\left(\frac{L}{2}\right) +d_{A C} C=0[/латекс] 92}{2 * (4 фута)} = 612,5 фунтов \text{ (+j направление)} $$
$$A_y = \omega*L- C = (100 \frac{lb}{ft})*(7 футов ) – 612,5 фунта = 87,5 фунта \text{ (направление +j) }$$
$$\underline{A_x = 0 \qquad A_y = 87,5 \text{ (+j )} \qquad C = 612,5 фунта \text{ ( +j )} }$$

2. Сделать разрез по В.

3. В FBD одной стороны разреза добавьте внутренние силы (и моменты), используя положительный знак.

4. Используйте уравнения равновесия для решения неизвестных внутренних сил и моментов.

Только для этой части сила интенсивности равна: F _w = ( 100 фунтов/фут ) * ( 2 фута) = 200 фунтов и действует на расстоянии 1 фут слева, поэтому момент силы равен: M _w = w * 2 фута * 1 фут = F _w * 1 фут = (100 фунтов/фут) * (2 фута) * (1 фут)  = 200 фут-фунт

$$\sum F_y = 87,5 фунта – 200 фунтов – V = 0 \\ V = -112,5 фунтов \text{ (- означает движение вверх, а не вниз)} $$

 

$$ \sum M_A = – (w * 2 фута) * (1 фут) – V * (2 фута) + M = 0 \\ M = (100 \frac{lb}{ft}) * 2 ft^2 + (-112,5 фунта) * (2 фута) \\ M = 200 футов \cdot lb – 225 футов \cdot lb \\ M = -25 ft \cdot lb \text{ (- указывает на движение в обратном направлении)} $$

 

$$\underline{N = 0 \qquad V = -112,5 фунтов \text{ (+j )} \qquad M = -25 футов \cdot lb \text{ (по часовой стрелке)} }$$

 

В основном : Внутренние силы (и моменты) для двумерной балки: поперечный, нормальный и изгибающий момент.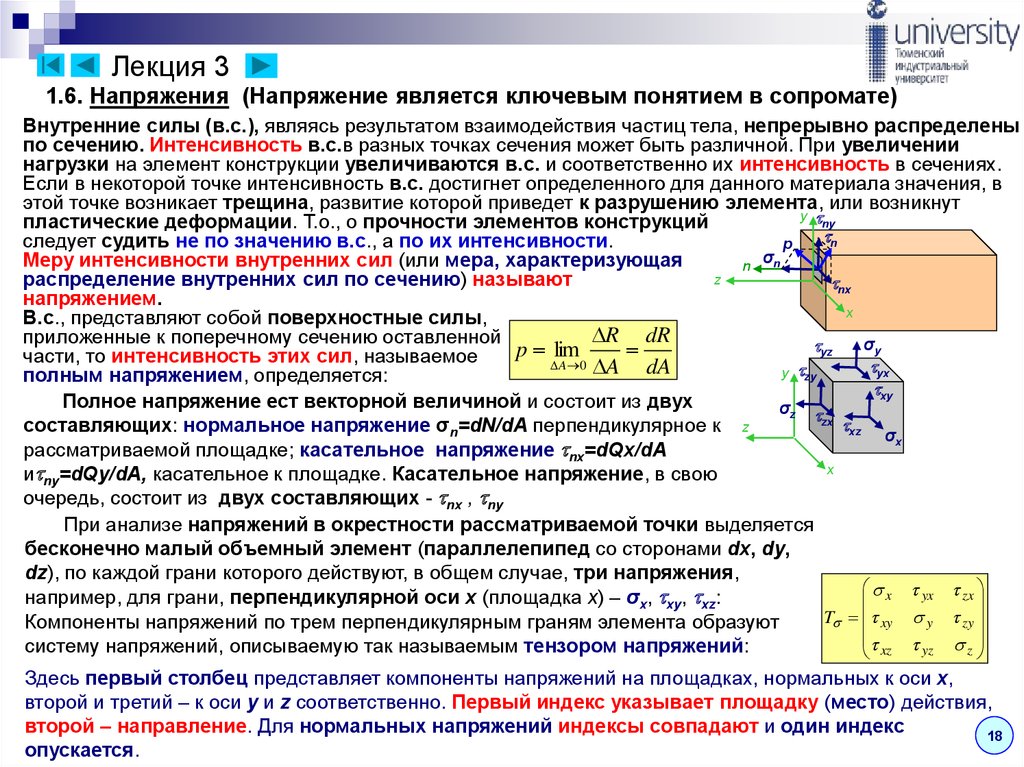 При выполнении разреза вдоль балки для определения внутренних сил следует использовать положительный знак: слева: сдвиг вниз, нормаль наружу, момент вверх.

Применение : Мост, на который воздействуют различные нагрузки (от автомобилей, грузовиков, фонарных столбов и т. д.). Используйте этот метод для расчета внутренних нагрузок в конкретной интересующей точке.

Заглядывая вперед : В следующем разделе мы рассмотрим, как рассчитать внутреннюю силу по всей балке и отобразить результаты графически.

 

Внутренние силы — значение, типы, примеры, факторы наша повседневная жизнь. Силы можно разделить на две категории: внутренние и внешние силы. Когда определенные виды сил присутствуют и участвуют в воздействии на объекты, общая механическая энергия объекта изменяется. С другой стороны, какая-то сила никогда не может повлиять на полную механическую энергию объекта, а может только сместить энергию объекта с потенциальной на кинетическую или наоборот.

Они называются внутренними силами и внешними силами. Внутренние силы могут изменить KE на PE. Суммарная работа внутренних сил всегда равна нулю.

При действии на тело внешних сил внутри тела возникает система внутренних сил и внутренних моментов, противодействующих внешним силам. Внутренние силы и моменты необходимо понимать, чтобы понять, как тело будет деформироваться и не сломается ли оно под нагрузкой. В этой статье мы подробно изучим внутренние силы, факторы, от которых зависят внутренние силы, и различные примеры, с которыми мы сталкиваемся в нашей повседневной жизни.

Загрузить полные примечания к формуле расчета конструкций в формате PDF

Содержание

• 1. Что такое внутренние силы?
• 2. Типы внутренних сил
• 3. Внутренние силы Пример 
• 4. Факторы, от которых зависят внутренние силы
• 5. Как действует внутренняя сила на систему?

Читать полностью

Что такое внутренние силы?

Внутренние силы — это силы, которыми обмениваются тела в системе.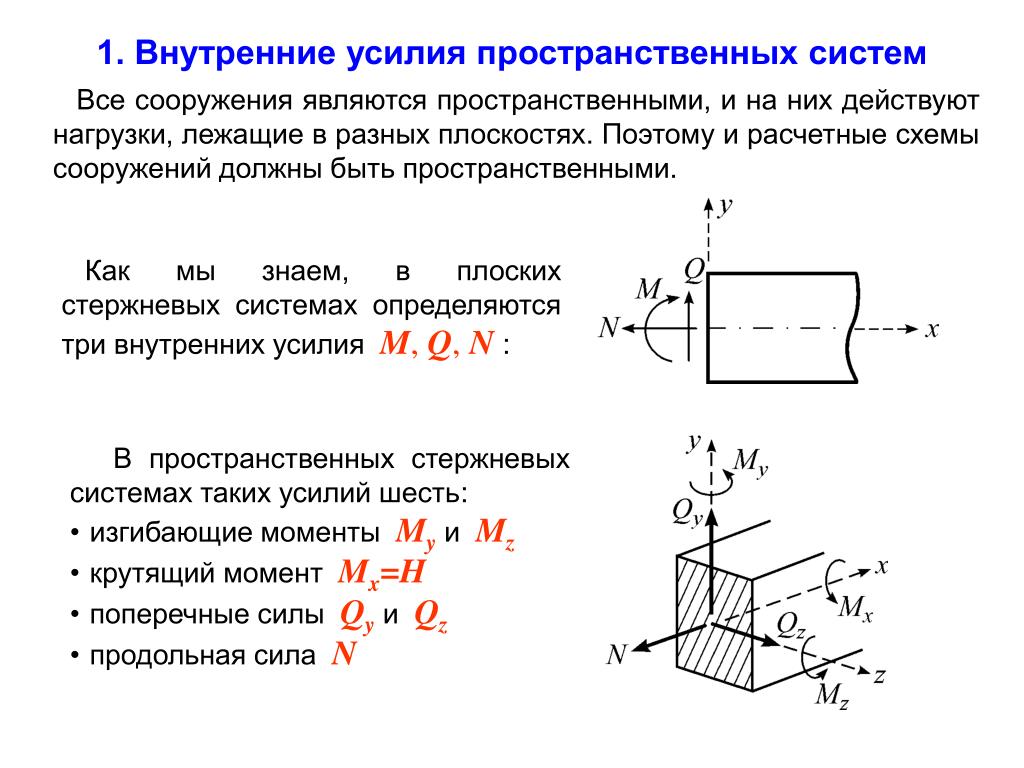 Внутренние силы могут вызывать ускорение в различных областях системы, но не могут вызывать ускорение в центре масс системы.

Внутренние силы Значение

Внутренние силы могут изменить энергию системы. Внутренние силы — это силы, удерживающие частицы тела вместе. Суммарная работа, совершаемая внутренними силами, не влияет на работу, совершаемую системой, так как всегда остается равной нулю.

Внутренние силы, действующие внутри объекта, не вызывают ускорение тела в состоянии покоя, но внутренние силы приводят к изменению энергии системы. Потенциальная или кинетическая энергия объекта преобразуется в механическую энергию за счет внутренней деятельности. Поскольку ускорение объекта из-за внутренних сил равно нулю, у объекта нет импульса; следовательно, работа, совершаемая системой, всегда равна нулю, и механическая энергия сохраняется. В результате внутренняя сила консервативна.

Типы внутренних сил

Сила, действующая изнутри тела, называется внутренней силой. Внутреннюю силу можно разделить на 4 типа в зависимости от реакции, происходящей внутри тела в системе:

1. Сжатие: Сжатие — это сила сжатия, приложенная к материалу. Этот штамм часто укорачивает материалы. Например, сожмите в руке губку. Вы создаете сжатие.
2. Напряжение: Напряжение — это сила, которая заставляет вещество растягиваться. Этот штамм часто удлиняет материалы. Например, возьмите в каждую руку по одному концу резинки. Начните разводить руки. Вы растягиваете эластичную ленту, создавая напряжение.
3. Кручение: Кручение — это сила, которая скручивает или поворачивает. Например, крутящая сила кручения используется для отжима влажной тряпки для мытья посуды. Чтобы вытеснить воду, вы берете мочалку двумя руками и крутите ее в разные стороны.
4. Гибка: Гибка — это процесс сгибания прямого материала в изогнутую форму. Одна сторона материала прижимается к другой (компрессия). Другая сторона расправляется (напряжение).
5. Сдвиг: Две близлежащие силы толкают или тянут друг друга, но не противостоят друг другу напрямую. Раздвигая молекулы объекта в стороны, напряжение сдвига разрезает или разрывает его (например, ножницы, разрезающие ветку, резак для бумаги, разрезающий бумагу — ветка и бумага «подвергаются нагрузке сдвига»).

Пример внутренних сил 

Когда ветер дует на дерево, оно раскачивается вперед и назад. Поскольку он исходит извне, сила ветра, действующая на дерево, считается внешней силой. С другой стороны, внутренняя сила удерживает дерево на месте и не дает ему упасть. Другой пример — когда края шкалы изгибаются при приложении к ним мышечной силы. В этом масштабе существует значительное напряжение и сжатие. Мышечная сила, действующая на весы, является внешней силой. Величина этой силы достаточно велика, чтобы согнуть, но не разрушить шкалу. Это потому, что он удерживается вместе внутренней силой, которая предотвращает его разрушение.

Когда автобус толкают изнутри, пока внутри находятся пассажиры, он не двигается. С другой стороны, автобус имеет тенденцию двигаться, когда пассажиры выходят и прикладывают усилие снаружи. Внешняя сила, которую прикладывают пассажиры, вызывает движение в автобусе. Толкающая сила пассажиров, сидящих внутри автобуса, не помогает транспортному средству двигаться, потому что пассажиры стали частью системы. Внутренняя сила – это сила, удерживающая систему от движения.

Когда к пружине прикладывается усилие для ее растяжения, пружина смещается. Внешняя сила – это сила, которая приводит в движение пружину. Внутренняя сила – это сила, стремящаяся сжать пружину и восстановить ее первоначальную форму. Внутренняя сила противодействует подвижности и любому изменению формы и диаметрально противоположна внешней силе.

Факторы, от которых зависят внутренние силы

Величина силы, воздействующей на тело, а также внутренние и внешние переменные являются факторами, от которых зависят как внутренние силы, так и внешние силы.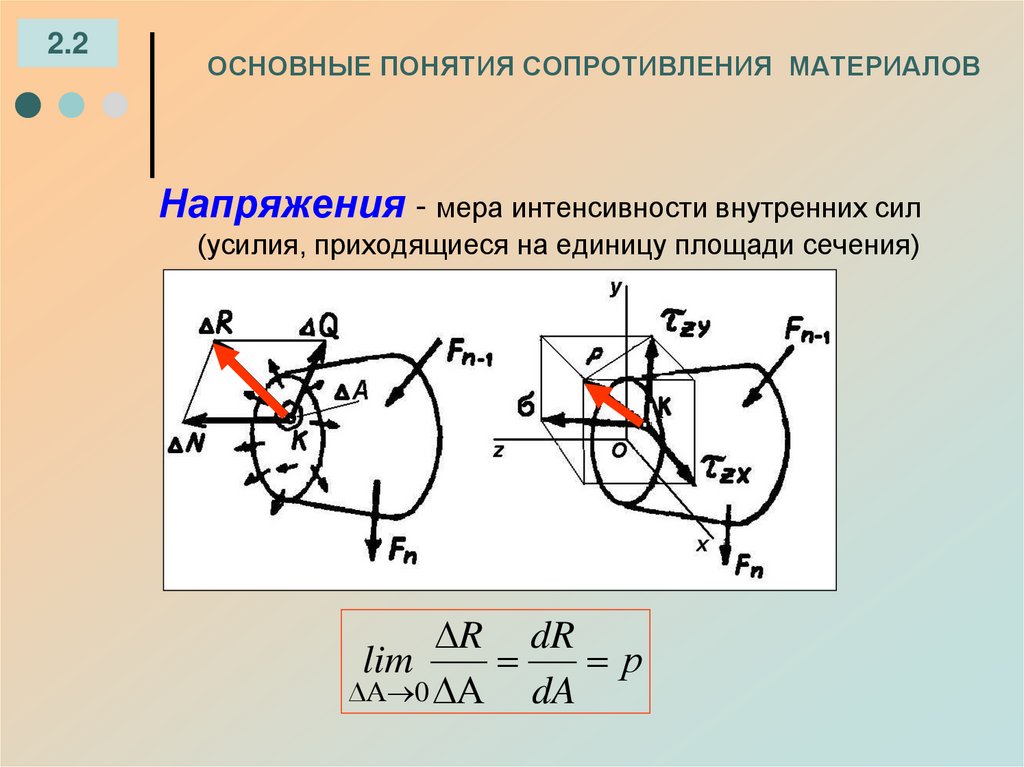 Важно знать, что чистая работа, выполняемая внутренними силами, инвариантна относительно системы отсчета, что означает, что она не изменится, даже если система отсчета изменится.

Дипольные моменты, внутреннее тепло системы, излучательная способность, температура системы и ее окружения, состав, вес, плотность, расстояние между молекулами, составляющими систему, движение частиц в системе, геометрия системы, молекулярный состав, ковалентные связи между атомами, количество свободных частиц и другие факторы влияют на внутренние силы в системе.

Как внутренняя сила действует на систему?

Внутренние силы в системе действуют противоположно, компенсируя друг друга и приводя к нулевому выходу. Внутренние силы, по-видимому, в первую очередь противодействуют изменениям, вызванным внешними силами или в ответ на внешние факторы, такие как взаимодействие электрического поля, магнитного поля или изменение температуры.

Когда на проводник воздействует электрическое поле, заряженная частица движется по спирали, но не вызывает никаких внешних изменений предмета и не вызывает ускорения центра масс. Из-за вращения электрической частицы магнитное поле создается движением заряженной частицы. Когда материал с магнитными свойствами помещается в магнитное поле, диполи располагаются в направлении поля. Линии внутреннего магнитного потока заставляют магнитные спиновые диполи выравниваться вслед за полем.

Часто задаваемые вопросы о внутренних войсках

• Что вы подразумеваете под внутренними силами?

  Внутренние силы — это силы, испытываемые или прикладываемые телом внутри системы. Внутренние силы не изменяют ускорение системы. Внутренние силы консервативны по своей природе.

• Как найти внутреннюю силу?

  Чтобы рассчитать внутренние силы, сначала нарисуйте диаграмму свободного тела всей системы, найдите опорные реакции (внешние силы) и оставьте все нагрузки в их исходных положениях. В точке, где должны быть определены внутренние нагрузки, разрежьте элемент перпендикулярно его оси. Затем строится диаграмма свободного тела разреза для определения внутренних сил с использованием уравнений статического равновесия.

• Различают внутренние и внешние силы?

  В случае внутренних сил, поскольку в системе нет движения, центр масс системы неподвижен. В то время как для внешних сил по мере того, как система набирает обороты из-за внешних воздействий, центр тяжести массы изменяется с течением времени. Энергия переносится в виде механической энергии во внутренних силах, но преобразуется в потенциальную или кинетическую энергию в случае внешних сил. Внутренние силы, действующие внутри системы, действуют в противоположных направлениях, компенсируя друг друга и приводя к тому, что в системе не совершается чистая работа. Внешние силы действуют в направлении приложенной силы, и совершается работа.

• Каковы 5 основных типов внутренних сил?

  5 важных типов внутренних сил:

  • Сдвиг
  • Изгиб
  • Скручивание
  • Сжатие
  • Растяжение.

• Почему внутренние силы всегда уравновешены?

  Если внутренние силы в системе не уравновешены, они вызовут деформацию тела.