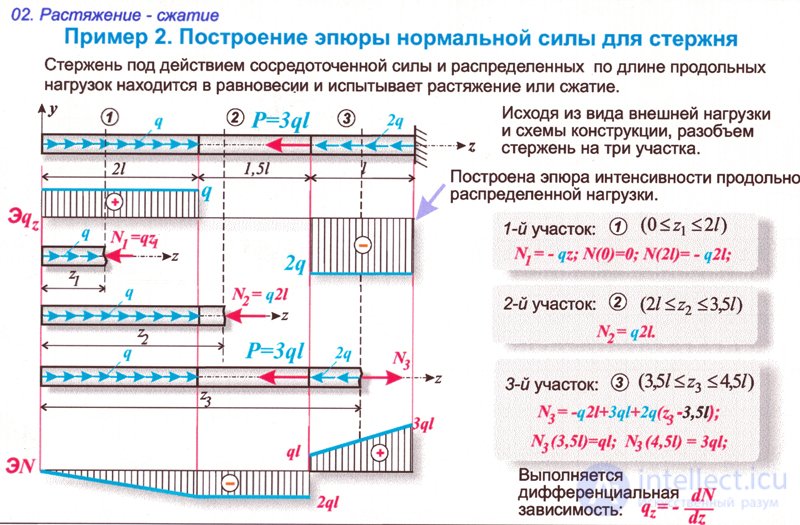
Внутренние силовые факторы при растяжении и сжатии: Внутренние силовые факторы

Внутренние силовые факторы

Внутренние силовые факторы (усилия) возникают в результате деформации бруса, когда под действием внешних нагрузок происходит изменение взаимного расположения элементарных частиц тела.

По своей природе внутренние силовые факторы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций. Для определения этих усилий применяют метод сечений:

надо мысленно рассечь брус, находящийся в равновесии, на две части

и рассмотреть равновесие одной из них.

Действие усилий отброшенной части бруса заменим уравновешивающими рассматриваемую часть внутренней силой R и внутренним моментом M.

Для упрощения расчетов силу R и момент M принято раскладывать на составляющие усилия относительно осей координат x, y и z.

Таким образом, под действием внешних нагрузок в поперечном сечении бруса могут возникать следующие внутренние силовые факторы:

  • Nz = N — продольная растягивающая (сжимающая) сила;
  • Mz = T — крутящий (скручивающий) момент;
  • Qx (Qy) = Q — поперечные силы;
  • Mx (My) = M — изгибающие моменты.

Каждый внутренний силовой фактор определяется из соответствующего уравнения равновесия оставшейся после рассечения бруса части (уравнения статики):

Наш видеоурок построения эпюр внутренних силовых факторов для балки:


Другие видео

Правила знаков для внутренних силовых факторов

Для определения знаков внутренних усилий, возникающих в брусе при различных способах его нагружения, приняты следующие правила:

  • при растяжении/сжатии — положительными являются растягивающие усилия;
  • при кручении — положительны моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки;
  • при изгибе — положительны моменты сжимающие верхний слой балки.

Эпюры внутренних силовых факторов

В инженерной практике особое место занимает умение ясно представить взаимодействие усилий в конструкции, а также связь между внешними и внутренними силами в элементах конструкции, для этого графически изображают внутренние силовые факторы в функции осевой координаты и называют эти графики — эпюрами.

Примеры решения задач >
Основные виды нагружения и деформаций >

Сохранить или поделиться с друзьями


Вы находитесь тут:


На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее


Здесь можно узнать стоимость и заказать решение
задач и выполнение учебных работ для студентов

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Сохранить или поделиться с друзьями


Заказать решение

Поиск формул и решений задач

    Поддержать сайт

    1. Внутренние силовые факторы. Понятие о напряжениях.

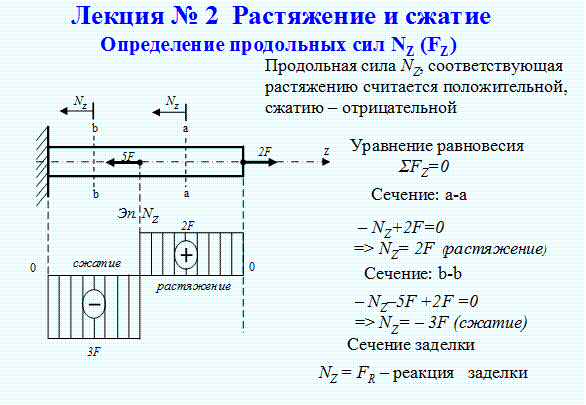
    В сопротивлении материалов под внутренними силами понимают силы взаимодействия между частицами элемента, вызванные действием внешних сил. Для определения внутренних сил используют метод сечений: мысленно разрезают нагруженное тело на две части и рассматривают равновесие одной из отсеченных частей. Со стороны отброшенной части на оставшуюся действуют внутренние силы, которые уравновешивают действие сил, проложенных к оставшейся части тела. Все внутренние силы приводятся к главному вектору R и главному моменту М. Главный вектор R можно разложить по осям координат и получить Qx, Qy, называемые поперечными или перерезывающими силами, и N

    z— продольную силу. Главный момент М при разложении по осям координат дает два изгибающих момента Mx и My и крутящий момент Мz. Эти шесть величин и представляют собой компоненты внутренних силовых факторов.

    Для их определения в случае пространственной системы сил можно составить шесть уравнений равновесия, а в случае плоской – три.

    Под напряжениями следует понимать силы взаимодействия между частицами элемента, приходящиеся на единицу площади.

    На площадках перпендикулярных оси стержня будут возникать нормальные σ и касательные τ напряжения. Нормальные напряжения всегда действуют перпендикулярно рассматриваемой площадке, а касательные – в плоскости это площадки:

    , , где А – площадь сечения стержня.

    Напряжение представляет собой интенсивность распределения внутренних сил по площади поперечного сечения. Напряжение всегда служит точной оценкой напряженного состояния любого нагруженного элемента конструкции в отличии от нагрузок F. Размерность у напряжений: [ , МПа]

    Центральное растяжение – сжатие – такой вид нагружения, когда в поперечных сечениях бруса возникают только нормальные (продольные) силы. Рассмотрим две схемы, подвергающиеся растяжению – сжатию (рис.2.1).

    При центральном растяжении – сжатии действующие нагрузки приложены по оси стержня. Для определения продольных сил в любом сечении используется метод сечений. Нормальная сила в сечении численно равна алгебраической сумме проекций всех внешних сил на ось стержня, расположенную по одну сторону от сечения. Проведем сечение 1 –1 (рис.2.1) и рассмотрим равновесие отсеченной части (рис.2.2).

    1

    1

    F

    F

    F

    F

    а ) б)

    1

    1

    Рис. 2.1 – Деформация стержня: а) сжатие; б) растяжение

    1

    N

    F

    z

    F

    ℓ

    5,2

    N

    1

    z

    1

    а) б)

    Рис.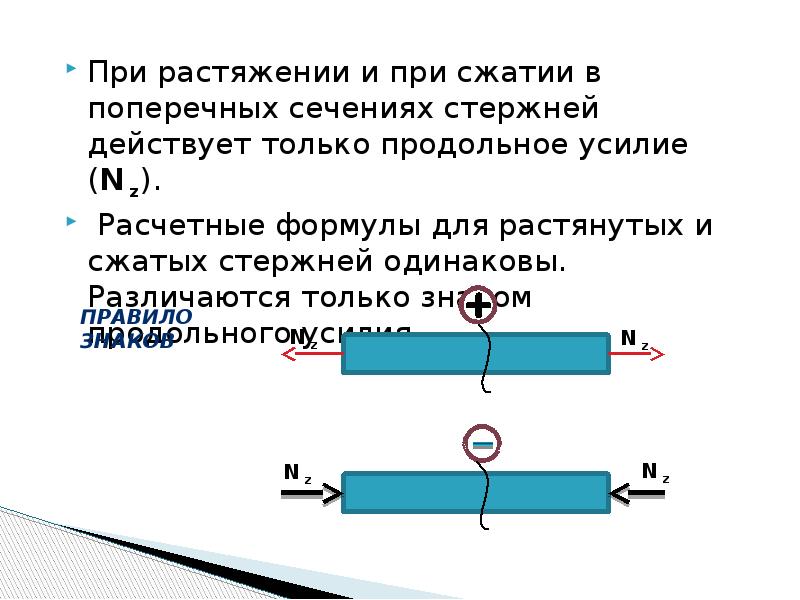 2.2– Продольные силы в сечении:

    а) сжимающая (отрицательная) продольная сила;

    б) растягивание (положительная) продольная сила

    Продольная сила в сечении считается положительной, если она растягивает отсеченную часть (рис.2.2,б) и отрицательной, если сжимает отсеченную часть (рис.2.2,а). Спроектируем все силы на ось z: ∑Z = 0; F – N = 0; N = -F, то есть сила N сжимающая и отрицательная.

    Эксперименты показывают, что при центральном растяжении – сжатии сечения в средней части стержня остаются плоскими после нагружения и поступательно перемещаются вдоль оси стержня. Следовательно, все продольные волокна испытывают одинаковое удлинение и укорочение. Действующие по сечению напряжения будут постоянны. В сечениях 1 –1 (рис.2.2) будут действовать только нормальные напряжения σ, определяемые по формуле (2.1): (2.

    1)

    Условие прочности при центральном растяжении-сжатии записывается так:

    ≤ R, (2.2)

    где R – расчетное сопротивление данного материала.

    Экспериментально установлена зависимость между нагрузкой, приложенной к стержню, и перемещениями сечений, к которым эта нагрузка приложена: , (2.3)

    где ∆ℓ – абсолютное удлинение стержня, ℓ – длина этого стержня, А – площадь сечения стержня , Е – модуль упругости первого рода (модуль Юнга), характеризует упругие свойства материала, то есть способность материала сопротивляться действию внешних сил. Размерность Е -[МПа]. Для каждого из материалов величина модуля упругости имеет свое значение: сталь, Е = 2.105 МПа, медь, Е = 1.

    105 МПа, алюминий, Е = 0,7. 105 МПа. Значение модуля упругости устанавливается экспериментально. Произведение ЕА – называется жесткостью стержня при растяжении – сжатии.

    Учитывая, что N/А = σ, выражение (2.3) можно записать так:

    . (2.4)

    Выражение : (2.5)

    получило название относительной продольной деформации, тогда в выражении (2.3), разделив на ℓ, имеем

    . (2.6)

    Выражение (2.6) носит название закона Гука при растяжении – сжатии. Этот закон был предложен в 1660 г. английским физиком Гуком.

    Пример 1. Ступенчатый стержень закреплен одним концом и нагружен сосредоточенными силами. Длины участков бруса равны ℓ1, ℓ2, ℓ3 площади их поперечных сечений А1, А2, А3. Материал бруса – сталь с расчетным сопротивлением R=210 МПа .

    Требуется: Построить эпюры внутренних сил N, напряжений σ и основных перемещений ∆ℓ, оценить прочность стержня.

    Решение:

    1) Определим продольные силы: Для этого разбиваем стержень на участки. Границами участков служат: точки приложения сил, места изменения поперечного сечения. На каждом участке мысленно проводим сечение и рассматриваем равновесие любой из отсеченных частей, приложив вместо отброшенной части неизвестную силу N в положительном направлении (от сечения). Рассматриваем сумму проекций на горизонтальную ось Z всех сил, расположенных в отсеченной части. Так как в начале задачи мы не определили реакцию в опоре, то идем от «свободного конца» и отсеченную часть рассматриваем всегда левую.

    I участок: ∑Z = 0; N1 – 24=0; N1=24 кH.

    II участок: ∑Z = 0; – N2 – 24 + 38,4 =0; N2=14,4 кH.

    III участок: ∑Z = 0; N3 – 24 + 38,4 – 28,8 =0; N3= 14,4 кH.

    Полученные значения откладываем на графике (эпюре) в виде прямоугольников, поло-жительные значения свер-ху, отрицательные снизу.

    2) Определим на-пряжения на всех участ-ках: Напряжение при растяжении — сжатии определяются по фор-муле: , где N –внутренняя продольная сила на участке, А – площадь поперечного сечения на данном участке.

    По полученным данным строим эпюру напря-жений.

    Рис.2.3

    3) Строим эпюру перемещений: Перемещения точек определяем на границах участков (нарастающим итогом, начиная от опоры). Используем формулу для абсолютной деформации по закону Гука: , где N – продольная сила на участке, ℓ — длина участка, А – площадь поперечного сечения на участке, Е –модуль упругости (модуль Юнга) материала стержня.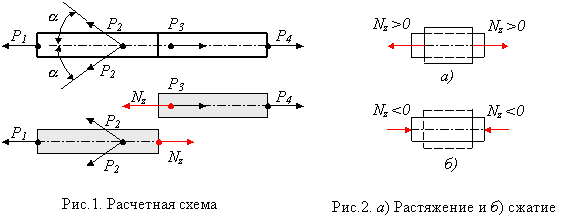 В данном примере материал – сталь с Е= 2*105 МПа

    Эпюра перемещений строится в виде ломаных линий, начиная от опоры справа, где значение перемещения равно нулю.

    4) Оцениваем прочность стрежня. Условие прочности при растяжении или сжатии записывается так: .

    С эпюры напряжений (σ) берем самое большое значение напряжения (по модулю) и сравниваем с расчетным сопротивлением. В нашем примере , т.е прочность обеспечена. Если прочность будет не обеспечена, необходимо дать рекомендации по обеспечению прочности: уменьшить нагрузку, увеличить площадь поперечного сечения.

    1.4: Внутренние силы в балках и рамах

    1. Последнее обновление
    2. Сохранить как PDF
  • Идентификатор страницы
    17610
    • Феликс Удойо
    • Университет Темпл

    Глава 4

    Внутренние силы в балках и рамах

    4. 1 Введение

    Когда балка или рама подвергаются поперечным нагрузкам, возникают три возможные внутренние силы: нормальная или осевая сила, сила сдвига и изгибающий момент, как показано в сечении k кантилевера на рис. 4.1. Чтобы предсказать поведение конструкций, необходимо знать величины этих сил. В этой главе учащиеся узнают, как определить величину поперечной силы и изгибающего момента в любом сечении балки или рамы и как представить вычисленные значения в графической форме, которая называется «поперечной силой». и «диаграммы изгибающих моментов». Диаграммы изгибающего момента и силы сдвига оказывают неоценимую помощь при проектировании, поскольку они показывают максимальные изгибающие моменты и силы сдвига, необходимые для определения размеров элементов конструкции.

    Рис. 4.1. Внутренние силы в балке.

    4.2 Основные определения

    4.2.1 Нормальная сила

    Нормальная сила в любом сечении конструкции определяется как алгебраическая сумма осевых сил, действующих с обеих сторон сечения.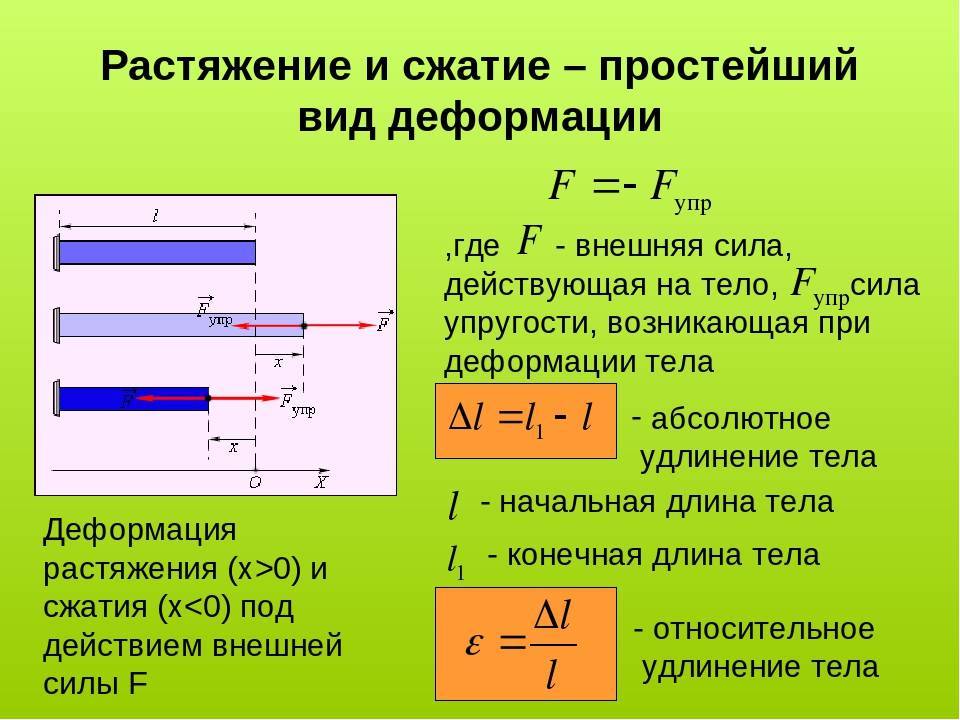

    4.2.2 Сила сдвига

    Сила сдвига (SF) определяется как алгебраическая сумма всех поперечных сил, действующих по обе стороны сечения балки или рамы. Фраза «с любой стороны» важна, так как подразумевает, что в каждом конкретном случае поперечную силу можно получить, суммируя поперечные силы с левой или с правой стороны сечения.

    4.2.3 Изгибающий момент

    Изгибающий момент (BM) определяется как алгебраическая сумма моментов всех сил, действующих по обе стороны сечения балки или рамы.

    4.2.4 Диаграмма силы сдвига

    Это графическое изображение изменения силы сдвига на части или по всей длине балки или рамы. По соглашению, диаграмма поперечной силы может быть нарисована выше или ниже x — центральной оси конструкции, но это должно быть указано, является ли это положительной или отрицательной поперечной силой.

    4.2.5 Диаграмма изгибающего момента

    Это графическое изображение изменения изгибающего момента на сегменте или по всей длине балки или рамы. По соглашению положительные изгибающие моменты изображаются над центральной осью конструкции с размерами x , а отрицательные изгибающие моменты изображаются под осью.

    4.3 Соглашение о знаках

    4.3.1 Осевая сила

    Осевая сила считается положительной, если она стремится сместить элемент в рассматриваемом сечении. Такая сила считается растягивающей, а элемент подвергается осевому растяжению. С другой стороны, осевая сила считается отрицательной, если она стремится раздавить элемент в рассматриваемом сечении. Такая сила считается сжимающей, а элемент находится в осевом сжатии (см. рис. 4.2а и рис. 4.2б).

    4.3.2 Сила сдвига

    Сила сдвига, стремящаяся сместить левую часть секции вверх или правую сторону секции вниз, считается положительной. Точно так же поперечная сила, имеющая тенденцию перемещать левую сторону сечения вниз или правую сторону вверх, будет считаться отрицательной поперечной силой (см. рис. 4.2c и рис. 4.2d).

    4.3.3 Изгибающий момент

    Изгибающий момент считается положительным, если он стремится вызвать вогнутость вверх (провисание). Если изгибающий момент имеет тенденцию вызывать вогнутость вниз (заклинивание), он будет считаться отрицательным изгибающим моментом (см. рис. 4.2e и рис. 4.2f).

    Рис. 4.2. Условные обозначения для осевой силы, поперечной силы и изгибающего момента.

    4.4 Взаимосвязь между распределенной нагрузкой, поперечной силой и изгибающим моментом

    Для получения соотношений между w, V и M рассмотрим свободно опертую балку, на которую действует равномерно распределенная нагрузка по всей ее длине, как показано на рис. 4.3. Пусть поперечная сила и изгибающий момент на участке, расположенном на расстоянии х от левой опоры, равны В и М соответственно, а на участке х + dx быть В + dV и М + dM 9003 9 соответственно. Полная нагрузка, действующая через центр бесконечно малой длины, равна wdx .

    Рис. 4.3. Просто поддерживаемая балка.

    Чтобы вычислить изгибающий момент в сечении x + d x , используйте следующее:

    Из уравнения 4. 1 следует, что первая производная изгибающего момента по расстоянию равна поперечной силе. Уравнение также предполагает, что наклон диаграммы моментов в конкретной точке равен поперечной силе в той же точке. Уравнение 4.1 предлагает следующее выражение:

    Уравнение 4.2 утверждает, что изменение момента равно площади под диаграммой сдвига. Аналогично, сила сдвига в сечении x + d x равна:

    В x + dx = В – wdx

    В + dV = В – wdx

    или

    Из уравнения 4.3 следует, что первая производная силы сдвига по расстоянию равна интенсивности распределенной нагрузки. Уравнение 4.3 предлагает следующее выражение:

    Уравнение 4.4 утверждает, что изменение силы сдвига равно площади под диаграммой нагрузки. Уравнения 4.1 и 4.3 предполагают следующее:

    Из уравнения 4.5 следует, что вторая производная изгибающего момента по расстоянию равна интенсивности распределенной нагрузки.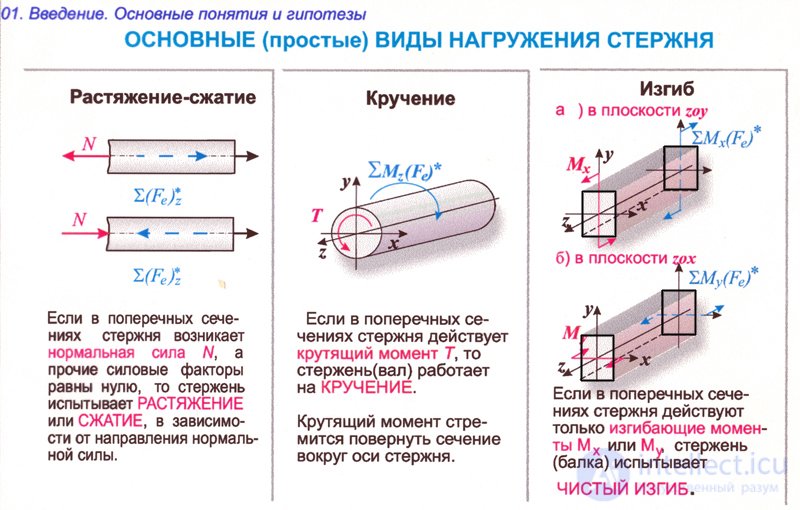

    Процедура расчета внутренних сил

    • Нарисуйте схему конструкции в свободном пространстве.

    •Проверить устойчивость и определенность конструкции. Если структура устойчива и детерминирована, переходите к следующему этапу анализа.

    •Определить неизвестные реакции, применяя условия равновесия.

    • Проведите воображаемое сечение перпендикулярно нейтральной оси конструкции в точке, где должны быть определены внутренние силы. Пройденный участок делит конструкцию на две части. Рассмотрим любую часть конструкции для расчета желаемых внутренних сил.

    •Для расчета осевой силы определите сумму осевых сил на рассматриваемой для анализа детали.

    • Для расчета поперечной силы и изгибающего момента сначала напишите функциональное выражение для этих внутренних сил для сегмента, в котором находится сечение, относительно расстояния x от начала координат.

    •Вычислите основные значения поперечной силы и изгибающего момента на участке, где находится сечение.

    • Начертите диаграмму осевой силы, поперечной силы и изгибающего момента для конструкции, обращая внимание на условные знаки, рассмотренные в разделе 4.3.

    •Для консольных конструкций третий этап можно пропустить, рассматривая свободный конец конструкции в качестве исходной точки расчета.

    Пример 4.1

    Нарисуйте диаграммы поперечной силы и изгибающего момента для консольной балки, несущей сосредоточенную нагрузку на свободном конце, как показано на рис. 4.4а.

    Рис. 4.4. Консольная балка.

    Решение

    Реакции поддержки. Сначала вычислите реакции на опоре. Так как поддержка в B зафиксирован, на этой опоре будет три реакции, а именно B y , B x и M B , как показано на диаграмме свободного тела на рисунке 4.4б . Применение условий равновесия предполагает следующее:

    Перерезывающая сила (SF).

    Функция поперечной силы. Пусть х — расстояние произвольного сечения от свободного конца консольной балки (рис. 4.4б). Перерезывающая сила в этом сечении из-за поперечных сил, действующих на сегмент балки слева от сечения (см. рис. 4.4д), равна В = –5 кОм.

    Знак минус указывает на отрицательное усилие сдвига. Это связано с тем, что правило знаков для силы сдвига гласит, что поперечная сила, направленная вниз слева от рассматриваемого сечения, вызовет отрицательную силу сдвига на этом сечении.

    Диаграмма силы сдвига. Обратите внимание, что поскольку сила сдвига является постоянной величиной, она должна быть одинаковой в любой точке балки. Условно диаграмму поперечных сил наносят выше или ниже линии, соответствующей нейтральной оси балки, но при этом должен быть указан знак «плюс», если это положительная поперечная сила, и знак «минус», если это положительная поперечная сила. отрицательное усилие сдвига, как показано на рис. 4.4c.

    Изгибающий момент (ВМ).

    Функция изгибающего момента. По определению изгибающий момент в сечении представляет собой сумму моментов всех сил, действующих по обе стороны сечения. Таким образом, выражение для изгибающего момента силы 5 к на сечении на расстоянии х от свободного конца консольной балки выглядит следующим образом: сегмент балки на левой стороне сечения имеет вогнутость вверх, что соответствует отрицательному изгибающему моменту в соответствии с соглашением о знаках для изгибающего момента.

    Диаграмма изгибающего момента. Поскольку функция изгибающего момента линейна, диаграмма изгибающего момента представляет собой прямую линию. Таким образом, достаточно использовать два главных значения изгибающих моментов, определенных при х = 0 футов и при х = 3 фута, чтобы построить диаграмму изгибающих моментов. По соглашению диаграммы отрицательных изгибающих моментов наносятся ниже нейтральной оси балки, а диаграммы положительных изгибающих моментов строятся над осью балки, как показано на рис. 4.4d.

    Пример 4.2

    Нарисуйте диаграммы поперечной силы и изгибающего момента для консольной балки, подверженной равномерно распределенной нагрузке по всей ее длине, как показано на рис.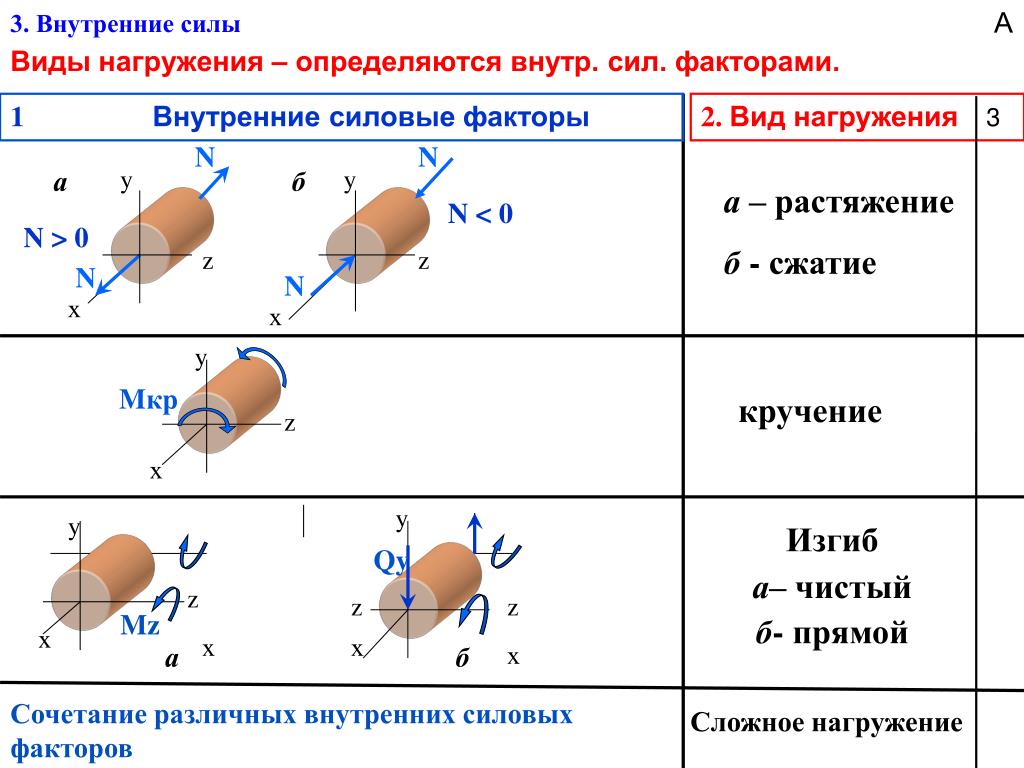 4.5а.

    Рис. 4.5. Консольная балка.

    Решение

    Реакции поддержки. Сначала вычислите реакции на опоре. Поскольку опора B фиксирована, возможно, на этой опоре будет три реакции, а именно B y , B x и M B , как показано на диаграмме свободного тела на рис. 4.4b. Применение условий равновесия предполагает следующее:

    Перерезывающая сила (SF).

    Функция поперечной силы. Пусть x будет расстоянием произвольного сечения от свободного конца консольной балки, как показано на рис. 4.5б. Перерезывающая сила всех сил, действующих на отрезок балки слева от сечения, как показано на рис. 4.5д, определяется следующим образом:

    Полученное выражение справедливо для всей балки. Знак минус указывает на отрицательную силу сдвига, которая была установлена ​​из правила знаков для силы сдвига. Выражение также показывает, что сила сдвига линейно зависит от длины балки.

    Диаграмма силы сдвига. Обратите внимание, что поскольку выражение для поперечной силы является линейным, его диаграмма будет состоять из прямых линий. Сила сдвига при х = 0 м и х = 5 м были определены и использованы для построения диаграммы поперечной силы, как показано на рисунке 4.5c. Как показано на диаграмме, перерезывающая сила изменяется от нуля на свободном конце балки до 100 кН на закрепленном конце. Расчетная вертикальная реакция B y на опоре может рассматриваться как проверка правильности расчета и диаграммы.

    Изгибающий момент (ВМ).

    Выражение изгибающего момента. Выражение для изгибающего момента на отрезке расстояния x от свободного конца консольной балки: соответствует отрицательному изгибающему моменту в соответствии с соглашением о знаках для изгибающего момента.

    Диаграмма изгибающего момента. Поскольку функция изгибающего момента параболическая, диаграмма изгибающего момента представляет собой кривую. В дополнение к двум основным значениям изгибающего момента при х = 0 м и при х = 5 м следует определить моменты в других промежуточных точках, чтобы правильно построить диаграмму изгибающих моментов. Диаграмма изгибающего момента балки показана на рис. 4.5d.

    Пример 4.3

    Нарисуйте диаграммы поперечной силы и изгибающего момента для консольной балки, подверженной нагрузкам, показанным на рис. 4.6а.

    Рис. 4.6. Консольная балка.

    Решение

    Реакции поддержки. Диаграмма свободного тела балки показана на рисунке 4.6b. Сначала вычисляем реакции на опоре Б . Применение условий равновесия предполагает следующее:

    Функции поперечной силы и изгибающего момента. Из-за разрыва распределенной нагрузки в точке B и наличия сосредоточенной нагрузки в точке C три области описывают функции сдвига и момента для консольной балки. Функции и значения поперечной силы ( V ) и изгибающего момента ( M ) на сечениях в трех областях на расстоянии x от свободного конца балки:

    Сегмент AB 0 < x < 2 футов

    В = −3 x

    Когда x = 0, V = 0

    Когда x = 1, V = −3 тысячи фунтов

    Когда x = 2 фута, V = −6 тысяч фунтов

    9 0032

    Когда x = 0, M = 0

    Когда x = 1 фут, M = −1,5 тысячи фунтов стерлингов. футов

    Когда x = 2 фута, M = −6 тысяч фунтов. фут

    Сегмент BC 2 фута < x < 3 фута

    V = −3(2) = −6 тысяч фунтов

    Когда x = 2 фута, M = −6 тысяч фунтов . футов

    Когда x = 3 фута, M = −12 тысяч фунтов. фут

    Сегмент CD 3 фута < x < 4 фута

    V = −(3)(2) − 10 = −16 тысяч фунтов

    M = -(3)(2)( x — 1) — 10( x — 3)

    Когда x = 3 фута, M = -12 тысяч фунтов. футов

    Когда x = 4 фута, M = −28 тысяч фунтов. футов

    Рисунок 4.6б.

    Диаграммы поперечной силы и изгибающего момента. Расчетные значения силы сдвига и изгибающего момента представлены на рис. 4.6c и рис. 4.6d. Важно помнить, что всегда будет внезапное изменение диаграммы поперечной силы там, где в балке сосредоточена нагрузка. Числовое значение изменения должно быть равно значению сосредоточенной нагрузки.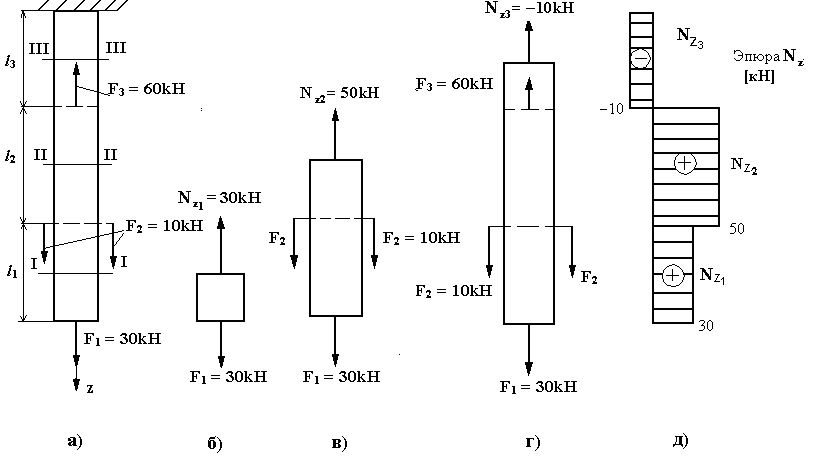 Например, в точке C , где сосредоточенная нагрузка 10 тысяч фунтов находится в балке, изменение поперечной силы на диаграмме поперечной силы составляет 16 k — 6k = 10 тысяч фунтов. Диаграмма изгибающего момента представляет собой кривую на участке AB и прямую линию на участках BC и CD .

    Пример 4.4

    Начертите диаграммы поперечной силы и изгибающего момента для балки с выступом, подверженной нагрузкам, показанным на рис. 4.7а.

    Рис. 4.7. Балка с навесом.

    Решение

    Реакции поддержки. Реакции на опорах показаны на диаграмме свободного тела балки на рис. 4.7b. Они вычисляются путем применения следующих условий равновесия:

    Функции сдвига и изгибающего момента. Из-за сосредоточенной нагрузки в точке B и выступающей части CD рассматриваются три области для описания функций поперечной силы и изгибающего момента для выступающей балки. Выражение для этих функций на участках внутри каждой области и главные значения в конечных точках каждой области следующие:

    0 < x < 3

    В = 25 − 8 x

    Когда x = 0, В = 25 тысяч фунтов

    Когда x = 3, В = 1 KIP

    Когда x = 0, M = 0

    Когда x = 3, M = 39 KIP. ft

    3 < x < 6

    V = 25 − 14 − 8 x

    При x = 3, В = −13 тысяч фунтов

    Когда x = 6, В = −37 тысяч фунтов

    M =

    Когда 900 38 х = 3, М = 39 к. футов

    Когда x = 6, M = −36 тысяч фунтов. ft

    0 < x < 2

    V = 10 + 8 x

    Когда x = 0, 9 0038 В = 10 тысяч фунтов

    Когда x = 2, В = 26 тысяч фунтов 9 M = 0 0039 = −36 тысяч фунтов стерлингов. ft

    Диаграмма поперечной силы и изгибающего момента. Определенная диаграмма поперечной силы и момента в конечных точках каждой области представлена ​​на рис. 4.7c и рис. 4.7d. Для точного построения кривой изгибающего момента иногда необходимо определить некоторые значения изгибающего момента в промежуточных точках путем подстановки некоторых расстояний внутри области в полученную функцию для этой области. Обратите внимание, что в местах сосредоточенных нагрузок и на опорах численные значения изменения перерезывающей силы равны сосредоточенной нагрузке или реакции.

    Пример 4.5

    Начертите диаграммы поперечной силы и изгибающего момента для балки с выступом, подверженной нагрузкам, показанным на рис. 4.8а. Определить положение и величину максимального изгибающего момента.

    Рис. 4.8. Балка с навесом.

    Решение

    Реакции поддержки. Реакции на опорах балки показаны на диаграмме свободного тела на рис. 4.8б. Реакции рассчитываются с применением следующих уравнений равновесия:

    Функции сдвига и изгибающего момента. Из-за разрыва оттенков распределенных нагрузок на опоре B для описания и функций моментов рассматриваются две области x , как показано ниже:

    0 < x < 4

    V =

    Когда x = 0, В = 6,10 кН

    Когда x = 2, В = 1,1 кН

    Когда x = 4, В = −13,9 кН

    M =

    Когда x = 0, M = 0

    Когда x = 2, М = 8,87 кН. м

    Когда x = 4, M = −2,3 кН. м

    0 < x < 1,5

    В = 2 x

    Когда x = 0, 9003 8 В = 0

    Когда x = 1,5, В = 3 кН

    М = -(2)( x )

    Когда x = 0, M = 0

    Когда x = 1,5 м, M = -2. 3 кН. м

    Рисунок 4.8d. Обратите внимание, что значения поперечной силы на опорах равны значениям опорных реакций. Также обратите внимание на диаграмму, что сдвиг в области AB является кривой, а сдвиг в области BC является прямой, что соответствует параболической и линейной функциям, соответственно полученным для областей. Диаграммы изгибающих моментов для обеих областей криволинейны. Кривая для 9Область 0038 AB глубже, чем область BC . Это связано с тем, что полученная функция для области AB является кубической, а для области BC — параболической.

    Положение и величина максимального изгибающего момента.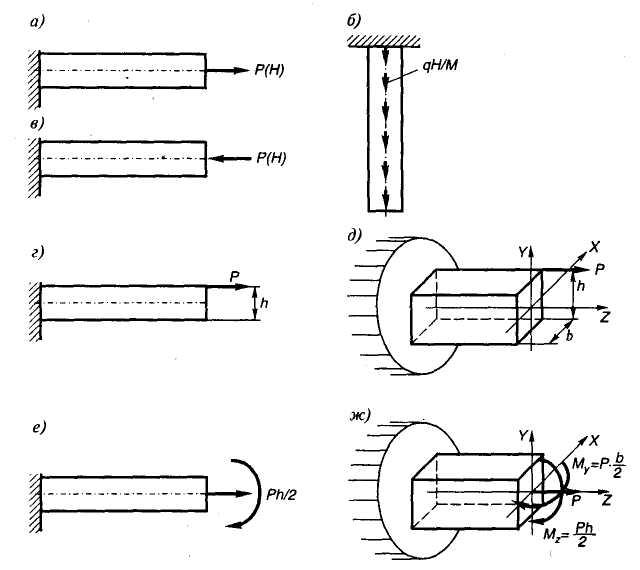 Максимальный изгибающий момент возникает там, где сила сдвига равна нулю. Как показано на диаграмме усилия сдвига, максимальный изгибающий момент возникает на участке -АВ . Приравнивание выражения для силы сдвига для этой части к нулю предполагает следующее:

    Величину максимального изгибающего момента можно определить, подставив x = 2,21 м в выражение для изгибающего момента для участка AB . Таким образом,

    Пример 4.6

    Нарисуйте диаграммы поперечной силы и изгибающего момента для составной балки, подверженной нагрузкам, показанным на рис. 4.9а.

    Рис. 4.9. Составной луч.

    Решение

    Схема свободного тела. Диаграмма свободного тела балки показана на рисунке 4.9.б.

    Классификация строения. Составная балка имеет r = 4, м = 2 и f i = 2. Поскольку 4 + 2 = 3(2), конструкция является статически определимой.

    Идентификация основной и дополнительной конструкции.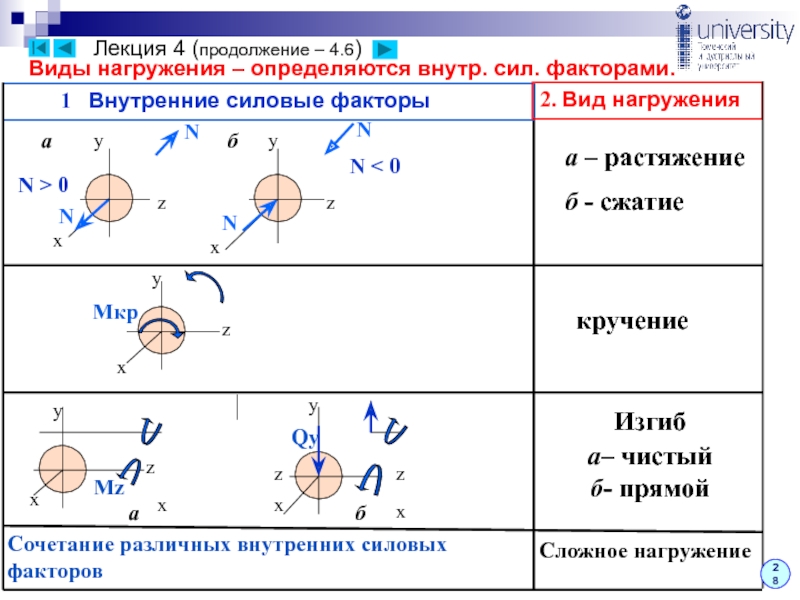 Схематическая диаграмма взаимодействия стержня для балки показана на рис. 4.9c. Часть AC является основной структурой, а часть CD — дополнительной структурой.

    Анализ дополнительной структуры.

    Реакция поддержки.

    C y = D y = 25 кН, из-за симметрии нагрузки.

    Сила сдвига и изгибающий момент.

    0 < x < 0,5

    V = 25 кН

    M = 25 x

    При 90 038 х = 0, М = 0

    При х = 0,5, М = 12,5 кН. м

    Анализ основной конструкции.

    Реакции поддержки.

    Отрицательное значение подразумевает реакцию на A действует вниз.

    Функции поперечной силы и изгибающего момента.

    0 < x < 1

    В = 25 + 14 x

    Когда x = 0, В = 25 кН

    Когда x = 1, В = 39 кН

    M =

    Когда x = 0, M = 0

    Когда x = 1, M = −32 кН.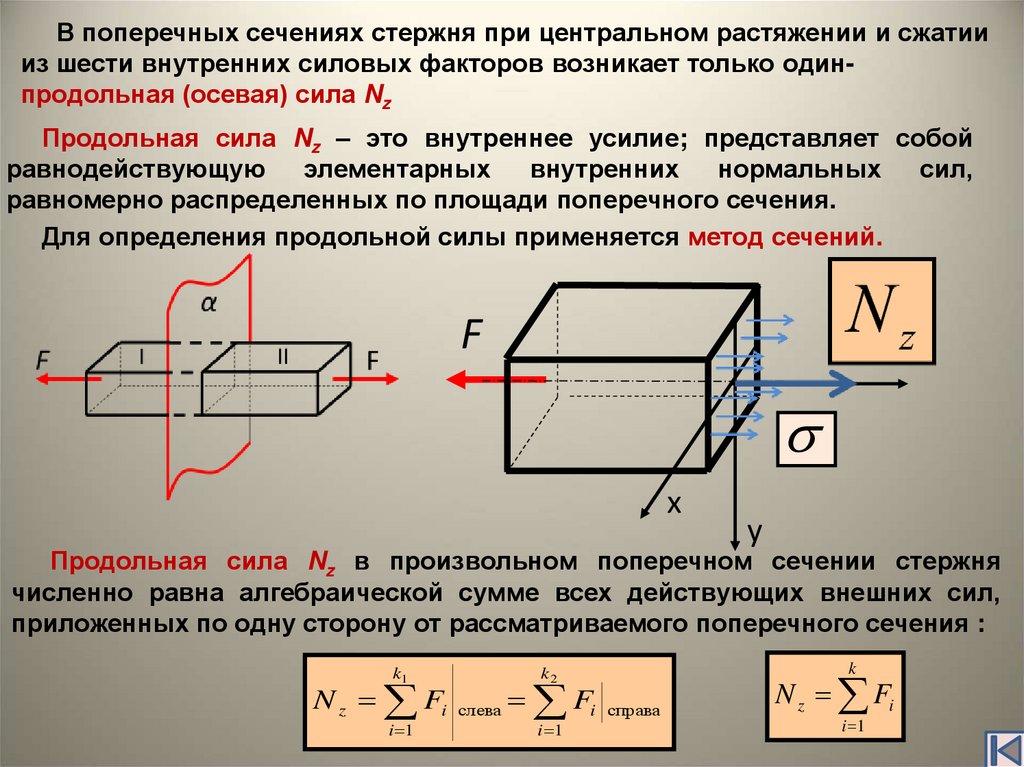 м

    0 < x < 2

    В = −2 − 14 x

    При x = 0, В = − 2 кН

    Когда x = 2, В = −30 кН

    M =

    Когда x = 0, M = 0

    Когда x = 2, M = −32 кН. м

    Рисунок 4.9д.

    Пример 4.7

    Начертите диаграммы поперечной силы и изгибающего момента для рамы, подверженной нагрузкам, показанным на рис. 4.10а.

    Рис. 4.10. Рамка.

    Решение

    Схема свободного тела. Диаграмма свободного тела балки показана на рисунке 4.10a.

    Реакции поддержки. Реакции на опоре балки можно рассчитать следующим образом при рассмотрении диаграммы свободного тела и использовании уравнений равновесия:

    Функции поперечной силы и изгибающего момента балки г. до н.э.

    0 < x 1 < 3

    В = 0

    М = 0

    3 < x 2 < 6

    В = 20 кН

    M = −20 ( x − 3)

    Когда x = 3, M = 0

    Когда x = 6, M = −60 кН. м

    Обратите внимание, что расстояние x до сечения в выражениях указано от правого конца балки.

    Функции поперечной силы и изгибающего момента колонны AB.

    0 < x 3 < 10

    В

    Когда x = 0, В = 0

    Когда x = 10, В = 50 кН

    M =

    Когда x = 0, M = −60 кН. м

    Когда x = 10, M = −226,67 кН. м

    Обратите внимание, что расстояние x до секции на колонне находится от вершины колонны и что аналогичный треугольник использовался для определения интенсивности треугольной нагрузки на секцию в колонне следующим образом:

    Сила сдвига и диаграммы изгибающих моментов. Расчетные значения поперечной силы и изгибающего момента для рамы нанесены на график, как показано на рис. 4.10c и рис. 4.10d.

    Пример 4.8

    Нарисуйте диаграммы поперечной силы и изгибающего момента для рамы, подверженной нагрузкам, показанным на рис. 4.11а.

    Рис. 4.11. Рамка.

    Решение

    Схема свободного тела. Диаграмма свободного тела балки показана на рисунке 4.11b.

    Реакции поддержки. Реакции на опорах рамы можно рассчитать, рассмотрев диаграмму свободного тела всей рамы и части рамы. Вертикальные реакции опор в точках A и E вычисляются с учетом равновесия всей рамы следующим образом:

    Знак минус указывает, что A y действует вниз, а не вверх, как предполагалось изначально.

    С учетом равновесия части CDE рамы горизонтальная реакция опоры в точке E определяется следующим образом: можно рассчитать следующим образом:

    Сдвиг и изгибающий момент колонн рамы.

    Перерезывающая сила и изгибающий момент в колонке АБ.

    0 < x 1 < 10 футов

    V = 13 − 2 x

    При x 90 039 = 0, В = 13 тысяч фунтов

    Когда x = 10 футов , В = −7 тысяч фунтов

    M =

    Когда x = 0, M = 0

    Когда x = 1 0 футов, M = 30 тысяч фун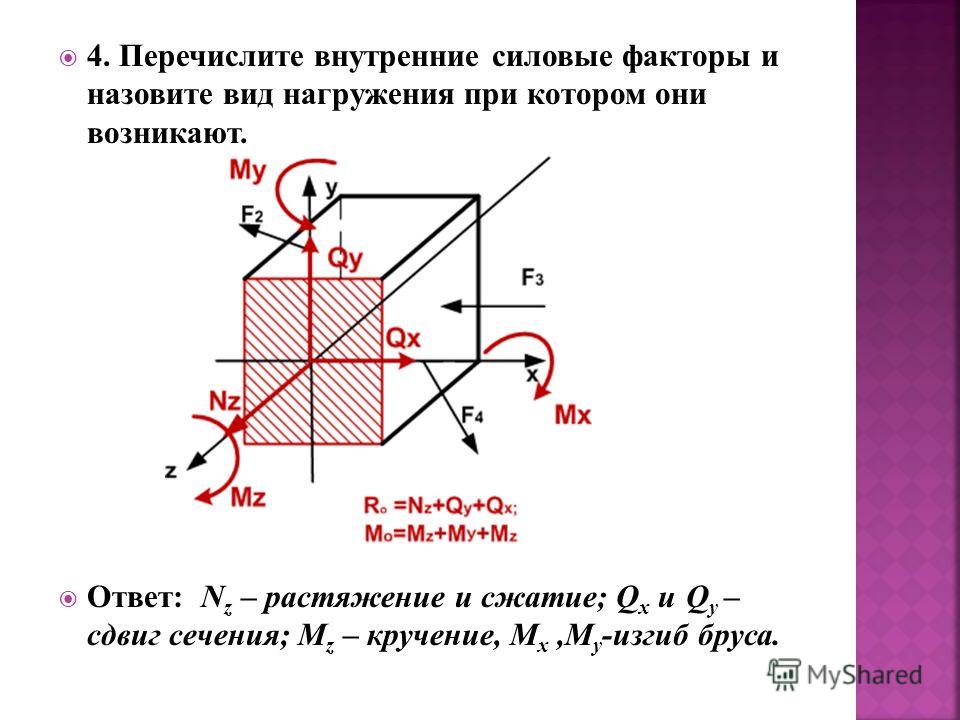тов. футов

    Когда x = 5 футов, M = 30 тысяч фунтов. футов

    Перерезывающая сила и изгибающий момент в колонне ЕД.

    0 < x 2 < 10 футов

    V = 7 тысяч фунтов

    M = 7 x 9 0039

    Когда x = 0, M = 0

    Когда x = 10 футов, M = 70 тысяч фунтов. ft

    Сдвиг и изгибающий момент балки рамы.

    Перерезывающая сила и изгибающий момент в балке BC .

    0 < х 3 < 4 футов

    V = −7,5 тысяч фунтов

    M = −7,5 x + 13(10) − 2(10)

    Когда x = 0, M = 30 тысяч фунтов на фут

    Когда x = 4 фута, M = 0

    Перерезывающая сила и изгибающий момент в балке CD .

    0 < x 4 < 4 футов

    V = −17,5 тысяч фунтов

    M = 17,5 x 90 039 − 7(10)

    Когда x = 0, M = −70 тысяч фунтов на фут

    Когда x = 4 фута, M = 0

    Расчетные значения силы сдвига и изгиба момент для кадра нанесены на рисунке 4. 11c и рисунке 4.11d.

    Резюме главы

    Внутренние силы в балках и рамах: Когда на балку или раму действуют внешние поперечные силы и моменты, в элементе возникают три внутренние силы, а именно нормальная сила ( Н ), поперечная сила ( В ) и изгибающий момент ( М ). Они показаны на следующем рисунке.

    Нормальная сила : Нормальная сила в любом сечении балки может быть определена путем сложения горизонтальных нормальных сил, действующих с обеих сторон сечения. Если равнодействующая нормальной силы стремится двигаться к сечению, это рассматривается как сжатие и обозначается как отрицательное. Однако, если оно имеет тенденцию удаляться от сечения, это расценивается как напряжение и обозначается как положительное.

    Поперечное усилие : Поперечное усилие в любом сечении балки определяется как сумма всех поперечных сил, действующих с обеих сторон сечения. Соглашение о знаках, принятое для поперечной силы, приведено ниже. Диаграмма, показывающая изменение поперечной силы вдоль балки, называется диаграммой поперечной силы.

    Изгибающий момент : Изгибающий момент в сечении балки можно определить путем суммирования моментов всех сил, действующих по обе стороны сечения. Правила знаков для изгибающих моментов показаны ниже. Графическое представление изгибающего момента, действующего на балку, называется диаграммой изгибающего момента.

    Взаимосвязь между распределенной нагрузкой, поперечной силой и изгибающим моментом: Между распределенной нагрузкой, поперечной силой и изгибающим моментом существует следующая взаимосвязь.

    Практические задачи

    4.1. Нарисуйте диаграммы поперечной силы и изгибающего момента для балок, показанных на рис. P4.1–рис. P4.11.

    Рис. П4.1. Луч.Рис. P4.2. Луч.Рис. P4.3. Луч.Рис. P4.4. Луч.Рис. P4.5. Луч.Рис. P4.6. Луч.Рис. P4.7. Луч.Рис. P4.8. Луч.Рис. P4.9. Луч.Рис. P4.10. Луч.Рис. P4.11. Луч.

    4. 2. Начертите диаграммы поперечной силы и изгибающего момента для рам, показанных на рис. P4.12–рис. P4.19.

    Рис. П4.12. Рамка.Рис. P4.13. Рамка.Рис. P4.14. Рамка.Рис. P4.15. Рамка.Рис. P4.16. Рамка.Рис. P4.17. Рамка.Рис. P4.18. Рамка.Рис. P4.19. Рамка.

    Эта страница под названием 1.4: Внутренние силы в балках и рамах распространяется под лицензией CC BY-NC-ND 4.0 и была создана, изменена и/или курирована Феликсом Удоэйо посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформа LibreTexts; подробная история редактирования доступна по запросу.

    1. Наверх
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или Страница
        Автор
        Феликс Удоэйо
        Лицензия
        CC BY-NC-ND
        Версия лицензии
        4,0
      2. Теги
        1. источник@https://temple. manifoldapp.org/projects/structural-analysis

      Инженерное дело на курсах Альберты » Типы внутренних сил

      Внутренние силы между частицами (молекулами/атомами) тела поддерживают целостность тела. Внутренние силы внутри тела напрямую зависят от (внешних) нагрузок, действующих на тело. Следовательно, проектирование тела, способного должным образом противостоять внешним нагрузкам и сохранять свою целостность, требует полного знания внутренних сил внутри тела.

      Внутренние силы в теле можно исследовать или определить путем (воображаемого) плоского сечения или разрезания FBD тела. Разрезание тела на срезы снаружи обнажает внутренние силы в поперечном сечении. Воздействующие внутренние силы, являясь фактически непрерывным распределением сил по поперечному сечению, могут быть представлены равнодействующими силами и парными моментами на воображаемой границе или поперечном сечении (глава 4).

      Результирующие силы и момент пары (рис. 7.1а) обычно изображаются тремя ортогональными осями (т. е. в декартовой системе координат), одна из которых перпендикулярна плоскости поперечного сечения, как показано на рис. 7.1б. Составляющие внутренних сил и момент пары вдоль этих осей показаны на рис. 7.1в. Эти компоненты классифицируются и объясняются следующим образом.

      1- Нормальная сила. Обозначаемая , нормальная сила представляет собой составляющую внутренней силы, которая перпендикулярна поперечному сечению (рис. 7.1d).

      2- Сила сдвига. Сила сдвига – это составляющая внутренней силы, касательная к поперечному сечению. Сила сдвига может иметь две прямоугольные составляющие, как показано на рис. 7.1d.

      3- Изгибающий момент. Изгибающий момент — это внутренний момент пары (вектор), который касается поперечного сечения. Изгибающий момент может иметь две составляющие, как показано на рис. 7.1d.

      4- Крутящий момент. Крутящий или крутящий момент представляет собой внутреннюю составляющую момента, которая перпендикулярна поперечному сечению. Компонент момента на рис. 7.1d представляет собой крутящий момент.

      Рис. 7.1 (а) Плоское сечение или сечение тела, (б) результирующая внутренняя сила и момент пары в поперечном сечении, (в) три ортогональные оси, определенные в поперечном сечении, (г) составляющие результирующей силы и пара момент на поперечном сечении.

      Классификация внутренних сил и парных моментов основана на деформациях (физических воздействиях), которые они вызывают на тело. Чтобы иметь представление о деформациях, вызываемых внутренними силами и парными моментами, рассмотрим следующий пример.

      1- Деформация, вызванная нормальной силой, представляет собой удлинение или сжатие тела. Это можно наблюдать, прикладывая тянущее или толкающее усилие к кончику и вдоль оси стержня, как показано на рис. 7.2а.

      2-Деформация, вызванная силой сдвига, представляет собой сдвиг или скольжение слоев тела относительно друг друга. Это можно наблюдать, приложив касательную силу к поверхности блока (например, спичечного коробка), как показано на рис.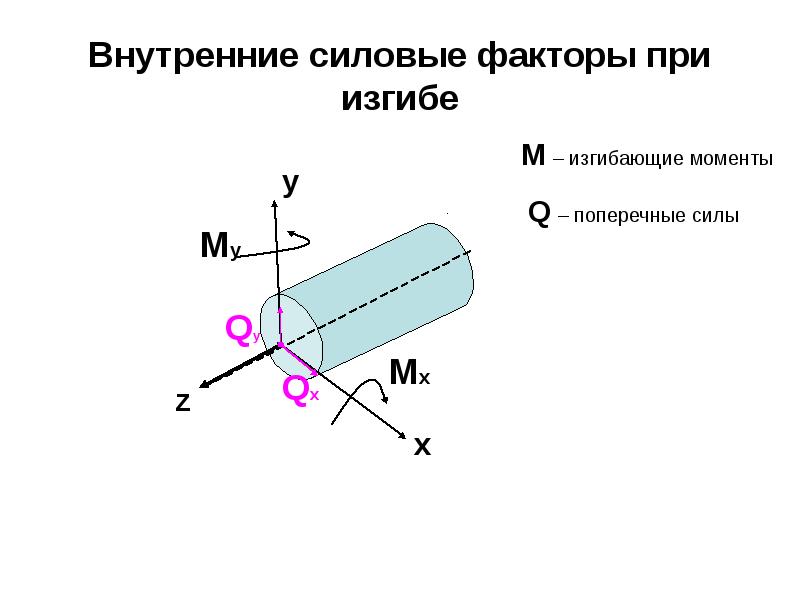 7.2b. Обратите внимание, как верхняя часть блока смещена в одном направлении.

      3- Изгибающий момент изгибает тело в плоскости момента. Эту деформацию можно испытать, вращая кончик стержня, не перемещая кончик в каком-либо направлении, как показано на рис. 7.2c.

      4- Крутящий момент вращает сечения тела вокруг оси, перпендикулярной сечениям. Деформация, создаваемая крутящим моментом на стержне, показана на рис. 7.2d. Наглядный пример — скручивание полотенца.

      Рис. 7.2 Деформации, создаваемые (а) нормальной силой, (б) поперечной силой, (в) изгибающим моментом и (г) крутящим моментом.

      В этом курсе мы сосредоточимся на внутренних силах и парном моменте двумерных балок. Балка представляет собой длинный конструктивный элемент, основная нагрузка которого перпендикулярна длинной оси элемента. Некоторые примеры балок показаны на рис. 7.3.

      Рис. 7.3 Балки.

      Двумерная балка — это балка, внешние и внутренние силы (или их равнодействующие) можно идеализировать так, чтобы они были копланарны оси балки. Кроме того, внешний и внутренний парные моменты перпендикулярны плоскости сил. В этом случае распределенные нагрузки (на единицу площади) упрощаются до распределенных нагрузок вдоль оси (на единицу длины) балки (см. раздел 3.5). Например, на рис. 7.4 показаны условия, при которых луч считается двумерным.

      Рис. 7.4 Пример условий, при которых балка рассматривается как двумерная балка.

      Внутренние силы (нагруженной) балки можно выявить методом сечения. Рассмотрим балку, показанную на рис. 7.5а. Для выявления внутренних сил и моментов пары в точке чертят FBD балки (рис. 7.5b) и делают воображаемый разрез, перпендикулярный оси балки (рис. 7.5b). Разделение балки приводит к двум сегментам. (Результирующие) внутренние силы и моменты в воображаемом сечении в каждом FBD показаны на рис. 7.5c. Обратите внимание, что действующие внутренние силы и момент проявляются в виде пар действия и противодействия с каждой стороны поперечного сечения.

      Рис. 7.5 (a) Нагруженная балка, (b) FBD балки и воображаемое сечение в точке A , (c) внешние и внутренние силы на каждом сегменте балки.

      Примечание: Поперечное сечение балки перпендикулярно оси балки (в этом курсе).

      Внутренние силы и момент пары (рис. 7.5c) в (двумерной) балке подразделяются на три типа:

      1- Осевая сила или нормальная сила ( Н ). Нормальная сила направлена ​​вдоль оси балки и перпендикулярна поперечному сечению балки. Нормальная сила в точке либо растягивающая, либо сжимающая (рис. 7.6а).

      2- Сила сдвига ( В ). Перерезывающая сила перпендикулярна оси балки или касается плоскости поперечного сечения. Когда мы имеем дело с горизонтальными балками с вертикальными разрезами, поперечные силы будут направлены «вверх» и «вниз» (рис. 7.6б).

      3- Изгибающий момент ( M ). Изгибающий момент — это парный момент, заставляющий балку изгибаться и отклоняться в плоскости, т. е. в двух измерениях (рис. 7.6в).

      Рис. 7.6 Внутренние силы и парный момент в двумерной балке.

      Подписать Конвенцию для внутренних войск

      Знаковое соглашение, дополненное силой, должно выражать физическую природу или тип силы. Возьмем, к примеру, усилия на стержни в фермах, сила растяжения или растяжения стержня положительна, а сжатие отрицательна. Важно различать знак силы, присваиваемый для указания типа силы, и знаковое правило силы (составляющей), основанное на направлении силы. Таким образом, есть два преобразования знака для силы:

      1- Соглашение о знаке точки.  Согласование знаков для написания уравнений равновесия. Это соглашение о знаках основано на используемой системе координат и присваивает положительные и отрицательные знаки компонентам сил, участвующих в уравнениях равновесия. Условное обозначение точки, используемое в этой книге, показано на рис. 7.7

      . Рис. 7.7 Условное обозначение точки, используемое в этой главе.

      Соглашение о знаке элемента (балки). Соглашение о знаках, предназначенное для присвоения знаков (внутренним) силам стержня в соответствии с их физическими эффектами, аналогично силам стержней ферм.

      Для балки внутренние силы и момент сопряжения имеют следующие правила знаков:

      1- Нормальная сила называется положительной, если она представляет собой силу растяжения, т. е. силу, стремящуюся растянуть элемент. Тогда сжимающая сила является отрицательной силой. На рис. 7.8 показаны положительные и отрицательные нормальные силы, действующие на свободные сегменты балки.

      Рис.7.8 Условные обозначения для положительных и отрицательных нормальных сил.

      2- Сила сдвига называется положительной, если она создает вращение по часовой стрелке сегмента, на который действует. Сила сдвига тогда отрицательна, если она стремится повернуть сегмент против часовой стрелки. Рисунок 7.9показывает положительные и отрицательные поперечные силы, действующие на свободные сегменты и сечения балки.

      Рис. 7.9. Условные обозначения для положительных и отрицательных поперечных сил.

      3- Изгибающий момент на сегменте считается положительным, если он стремится согнуть сегмент вогнутой стороной вверх. Отрицательный изгибающий момент изгибает сегмент вогнутой стороной вниз. На рис. 7.10 показаны положительные и отрицательные изгибающие моменты, действующие на свободные сегменты и секции балки.

      Рис. 7.10 Условные обозначения положительных и отрицательных изгибающих моментов.
      Контекст: Внутренние силы
      • До сих пор мы предполагали, что нагрузки передаются на опоры, но игнорировали вопрос «как?» Исключение: метод узлов и метод сечений позволил найти нормальные (они же осевые) усилия в фермах.
      • Инженерам при проектировании конструкции необходимо учитывать, как сила передается из одного места (например, из места приложения силы) в другое (например, из земли). Например, если вы читаете это прямо сейчас внутри здания, ваш вес должен дойти до земли через плиты, балки, стены и/или колонны здания.
      • Внутренние силы передают элементы с по между внешними нагрузками и опорами (т. е. это силы, которые элемент «чувствует»).
      • Внутренние силы являются наиболее важным фактором, который необходимо учитывать инженерам при проектировании конструкций несущих элементов. Величина и направление внутренних сил влияют на форму, материал и размеры элемента.
      Применение: Почему важны внутренние силы?

      Оглядевшись вокруг, вы можете найти свидетельства того, как внутренние силы влияют на конструкцию конструкции. Мостовые балки часто имеют глубину более метра, поскольку они должны выдерживать тяжелые нагрузки на длинном пролете, в то время как балки перекрытия в доме обычно имеют глубину ~ 150 мм, поскольку они несут легкие нагрузки на коротком пролете.

      Изгибающие моменты вызывают растяжение с одной стороны балки и сжатие с другой стороны (вспомните пары сил в разделе 3.3 этой книги). Бетон прочен на сжатие, но слаб на растяжение. Чтобы компенсировать эту слабость, бетон часто армируют (обычно стальными арматурными стержнями, также известными как «арматура») материалами, прочными на растяжение. Инженеры указывают арматуру в областях, которые, как ожидается, будут выдерживать растяжение при расчетных нагрузках. Чем больше ожидаемые силы натяжения, тем больше арматуры требуется, чтобы противостоять этим силам.

      Нет ничего непобедимого. Если внутренние силы станут слишком большими, элемент выйдет из строя. Исследователи структурной инженерии используют разрушающие испытания, чтобы сравнить реальную реакцию конструкций на компьютерное моделирование и упрощенные расчетные уравнения, чтобы оптимизировать инженерную практику и сделать наши конструкции более безопасными и эффективными. Бетонная балка на рис. 7.11а вышла из строя, потому что изгибающий момент, вызванный большим гидравлическим прессом, вызвал разрушение бетона в верхней части балки. Армирование, сосредоточенное в нижней части балки (рис. 7.11б), предотвратило перелом балки пополам при очень небольшом усилии (что произошло бы, если бы арматуры там не было). Хотя балка вышла из строя, она смогла выдержать нагрузки, намного превышающие те, на которые она была бы рассчитана в реальном мире.

      Рис. 7.11 Бетонные балки, испытанные в Университете Альберты для оценки их способности противостоять внутренним силам (а) балка, которая разрушилась из-за чрезмерного момента, вызванного гидравлическим прессом, который приложил большую силу к середине балки (б) поперечное сечение той же бетонная балка с арматурой (обведена красным), сосредоточенной в нижней части балки, где ожидается растяжение под действием расчетных изгибающих моментов.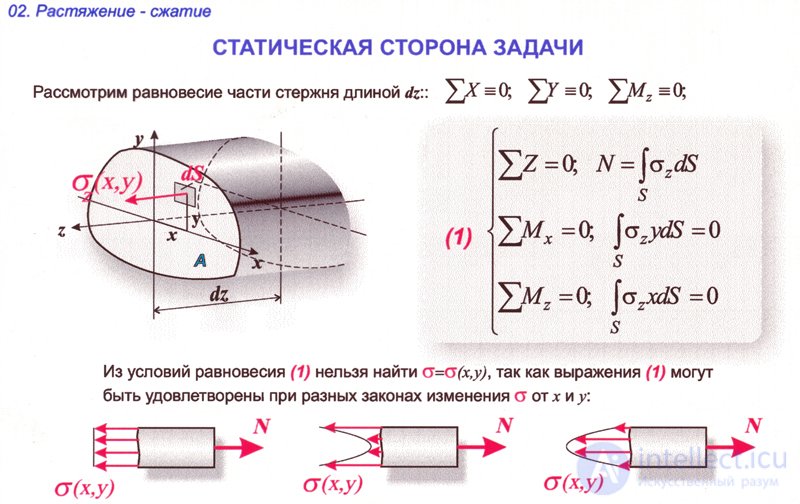 Большие пустоты в балке делают ее легче при сохранении высокого момента инерции (обсуждается в главе 10 этой книги) конец балки. (фото Д. Томлинсона).

      Если силы приложены к концу балки, поперечные силы будут высокими, а изгибающие моменты будут низкими (обсуждается в разделе 7.2 этой книги). Разрушения бетона при сдвиге могут быть внезапными и катастрофическими. Например, авария путепровода Де Ла Конкорд возле Монреаля в 2006 году побудила к серьезным исследованиям в области проектирования и обслуживания канадских мостов. Чтобы противостоять сдвигу, бетонные балки часто армируют вертикальной арматурой (называемой «хомутами»), которая предотвращает расщепление балок под нагрузкой (рис. 7.11c). Хомуты сосредоточены в областях, где поперечные силы, как ожидается, будут большими. Разрушение бетона при сдвиге легко распознать по наличию диагональных трещин (в отличие от вертикальных или горизонтальных трещин, наблюдаемых в других случаях). Причина, по которой трещины при сдвиге являются диагональными, объясняется в будущих курсах.

      Процедура анализа внутренних сил

      Внутренние силы можно определить методом сечения (разрезать элемент, чтобы выявить внутренние силы). Для двумерных балок это двумерная задача о равновесии твердого тела, удовлетворяющая трем уравнениям равновесия (см. раздел 5.2),

         

      Реализация метода сечения для определения внутренних сил требует следующих шагов.

      1. Начертите ФБР всей конструкции (балки) для получения опорных реакций (не требуется, если реакции не участвуют в уравнениях равновесия сегмента).
      2. Разрежьте или разделите свободное тело на две части в том месте, где требуются внутренние силы.
      3. Выберите одну секцию, начертите и обозначьте открытые неизвестные внутренние силы (примите положительное направление в соответствии с соглашением о знаках луча).
      4. Применить уравнения равновесия (со знаком точки).
      5. Решите внутренние силы.

      Обратите внимание, что для обозначения сил и парных моментов в двумерных задачах нежирные заглавные буквы обозначают величины сил и парных моментов. Пример показан на рис. 7.12.

      Рис. 7.12 Обозначение опорных реакций и внутренних сил в FBD балки.
      ПРИМЕР 7.1.1

      Определите внутренние силы и момент пары в точке балки, показанной на рисунке. Выполните пять шагов метода раздела.

      РЕШЕНИЕ

      1- Нарисуйте FBD балки, чтобы определить опорные реакции. Предположим, что неизвестные направления соответствуют соглашению о знаках точек (рис. 7.7).

      Опорные реакции:

         

      2- Разрежьте или разделите свободное тело на две части в том месте, где требуются внутренние силы.

      3- Выберите одну секцию, начертите и обозначьте открытые неизвестные внутренние силы (примите положительное направление в соответствии с соглашением о знаках луча).

      Чтобы показать, что выбор любого из сегментов (или сечения на сегменте) приводит к одинаковым внутренним силам и изгибающим моментам, мы находим внутренние силы и моменты на обоих сегментах.

      Выбор сегмента или секции с левой стороны

      4- Примените уравнения равновесия (со знаком точки) и

      5- Решите внутренние силы.

         

      Следовательно, – положительная поперечная сила, а – отрицательный изгибающий момент. Внутренняя сила и момент показаны как:

      Выбор сегмента или секции с правой стороны

      4- Примените уравнения равновесия (соглашение о знаках точки) и

      5- Решите для внутренних сил.

         

      Следовательно, – положительная поперечная сила, а – отрицательный изгибающий момент. Внутренняя сила и момент показаны как,

      Как видно, выбор любого из сегментов (или секций) приводил к одному и тому же результату. Для этой конкретной задачи выбор правого участка для определения внутренних сил и момента не требует предварительного решения опорных реакций.

      Секции вблизи сосредоточенной нагрузки

      Возникает вопрос о нахождении внутренних сил и парных моментов балки точно в точке приложения сосредоточенной нагрузки (силы или парного момента) (рис. 7.13а). На самом деле сосредоточенная нагрузка по-прежнему действует на площадь (длину).