1.3. Пластичность металлов

Пластичность– свойство металла пластически деформироваться, не разрушаясь под действием внешних сил. Это одно из важных механических

свойств металла, которое в сочетании с высокой прочностью делает его основным конструкционным материалом. Для определения пластичности образцы и оборудование не требуются. Показатели (характеристики) пластичности – относительные удлинение (дельта) и сужение(кси).

Относительным удлинениемназывается отношение абсолютного удлинения, т. е. приращение расчетной длины образца после разрыва, к его первоначальной расчетной длине,мм, выраженное в процентах:

%

(2)

где – длина образца после разрыва, мм.

Относительным сужениемназывается отношение абсолютного сужения, т.

е. уменьшение площади поперечного сечения образца после разрыва, к первоначальной площади его поперечного сечения мм²,выраженное в процентах:

%,

(3)

где – площадь поперечного сечения образца после разрыва,мм²_.

Твердость– свойство металла сопротивляться внедрению в него другого более твердого тела. Для определения твердости не требуется изготовления специальных образцов, испытания проводятся без разрушения металла.

Твердость металла определяют прямыми и косвенными методами: вдавливанием, царапанием, упругой отдачей, магнитным.

При прямых методах в металл вдавливают твердый наконечник (индентор) различной формы (шарик, конус, пирамида) из закаленной стали, алмаза или твердого сплава.

После снятия нагрузки на индентор в металле остается отпечаток, который и характеризует твердость.

Метод Бринелля. В плоскую поверхность металла вдавливается стальной закаленный шарик диаметра 10 мм (рис. 2). После снятия нагрузки в металле остается отпечаток (лунка). Диаметр отпечатка d измеряют специальным микроскопом с точностью 0,05 мм. На практике пользуются специальной таблицей, в которой диаметру отпечатка d соответствует определенное число твердости НВ.

Диаметр шарика Dи нагрузкуPустанавливают в зависимости от твердости и толщины испытуемого металла. Например, для стали и чугуна нагрузкаР= 3000 кг;D= 10 мм. Твердость технически чистого железа по Бринеллю равна 80 – 90 единиц.

а б

Рис. 2. Схема испытания твердости:

а – по Бринеллю; б – по Роквеллу

Метод Бринелля не рекомендуется применять для металлов с твердостью более НВ 450, так как шарик может деформироваться и в результате получится искаженный результат. Этот метод используется в основном для измерения твердости заготовок и полуфабрикатов из неупрочненного металла.

Метод Роквелла. Твердость определяют по глубине отпечатка. Индентором служит стальной закаленный шарик диаметра 1,58 мм для мягких металлов или алмазный конус с углом при вершине 120ºдля твердых и сверхтвердых (болееHRC70) металлов (рис. 2, б).

Шарик и конус вдавливаются в металл под действием двух нагрузок – предварительной и основной. Общая нагрузка равна их сумме. Предварительная нагрузка принимается одинаковой для всех металлов (10 кг). Перед началом испытания большая стрелка твердомера выставляется на «0» шкалы индикатора, и затем включается основная нагрузка – большая стрелка перемещается по шкале индикатора и показывает значение твердости.

При вдавливании стального шарика нагрузка составляет 100 кг, отсчет твердости производится по внутренней (красной) шкале индикатора, твердость обозначают НRВ. При вдавливании алмазного конуса твердость определяется по показанию стрелки по внешней (черной) шкале индикатора. Для твердых металлов основная нагрузка составляет 150 кг. Это основной метод измерения твердости закаленных сталей. Обозначение твердости – НRC.

Для очень твердых, а также тонких материалов нагрузка принимается равной 60 кг. Обозначение твердости – НRА.

Метод определения твердости по Роквеллу позволяет испытывать мягкие и твердые металлы, при этом отпечатки от шарика или конуса очень малы, поэтому этим методом можно измерять твердость и готовых деталей. Поверхность для испытания должна быть шлифованной. Измерения выполняются быстро (в течение 30 – 60 с), не требуется никаких вычислений, так как значение твердости снимается по шкале индикатора твердомера.

Метод Виккерса. В испытуемую поверхность (шлифованную или полированную) вдавливается четырехгранная алмазная пирамида под нагрузкой 5, 10, 20, 30, 50 или 100 кг. В металле остается квадратный отпечаток. Специальным микроскопом твердомера измеряют диагональ отпечатка (рис. 3).

Рис. 3. Схема испытания твердости по Виккерсу

Зная нагрузку на пирамиду и диагональ отпечатка, по таблицам определяют твердость металла НV. Метод универсальный. Его можно использовать для определения твердости деталей малой толщины и тонких поверхностных слоев большой твердости (после азотирования, нитроциментации и т. п.).

Чем тоньше металл, тем меньше должна быть нагрузка на пирамиду, однако при большой нагрузке результат получается точнее.

ПЛАСТИЧНОСТЬ | Энциклопедия Кругосвет

ПЛАСТИЧНОСТЬ – свойство твердых тел изменять форму и размеры под влиянием внешних нагрузок и сохранять ее, когда нагрузки перестают действовать (после снятия нагрузок).

Первое представление о свойстве материала, называемом пластичностью, дает комок пластилина, который под давлением пальцев легко меняет форму, и сохраняет новую форму после действия на него (в отличие о растянутой пружинки, которая опять сожмется, если ее отпустить В этом смысле говорят, что пружинка упруга, а пластилин пластичен. Пластилин и пластичность – слова одного корня, от греческого слова пластика, что значит лепка, от глагола «лепить» (из глины).

Чтобы получить более точное представление о свойстве пластичности, можно сделать (или представить себе) простой опыт. Пусть есть вытянутый параллелепипед (стержень) из пластилина, длинное ребро которого составляет приблизительно 10 см, а малая грань представляет собой квадрат 1 см × 1 см. Пусть этот стержень опирается концами на две опоры («мостик»). Если на средину стержня класть металлические грузики (например, монеты), то пока нагрузка невелика, изменение формы стержня на глаз незаметно. При дальнейшем нагружении обнаруживается, что в некоторый момент стержень прогибается и становится криволинейным. Если убрать все грузики, криволинейная форма все равно сохранится.

Этот опыт показывает, что стержень из материала, обладающего свойством пластичности, сопротивляется действию нагрузок, почти не изменяя свою форму, до тех пор, пока нагрузка не превысит некоторый порог, после чего происходит заметное изменение формы, сохраняющееся и после снятия нагрузки. В этом суть пластичности, но не вся – изменение формы (деформирование) зависит только от приложенной нагрузки и не изменяется само по себе с течением времени. Если деформирование при неизменной нагрузке все же происходит, то материал называют не пластическим, а вязкопластическим или вязкоупругим (см. РЕОЛОГИЯ; ПОЛЗУЧЕСТЬ). Конечно, пластилин – это знакомый и наглядный пример пластического материала. Важно то, что свойство пластичности присуще очень многим конструкционным материалам. В первую очередь, это – металлы и сплавы – сталь, железо, медь, алюминий и другие, но представление о пластическом деформировании оказывается очень полезным и для понимания процессов деформирования композиционных материалов, в том числе металлокерамических, углеродных и полимерных.

Пластичность материала как бы противопоставлена упругости: пластическое тело сохраняет приданную ему форму, а упругое – восстанавливает первоначальную. Но пластичность противопоставляется еще и хрупкости: пластическое тело отвечает на увеличение нагрузки заметным изменением формы, а хрупкое (например, стекло) – появлением трещин и разрушением.

Изучение пластичности развивается по двум направлениям: одно из них связано, в первую очередь, с проблемами техники и цель его – ответ на вопрос: если конструкция подвергается воздействию внешних сил известной величины, каково при этом меняется форма – т.е. как она деформируется? Это важно знать конструктору, но есть и еще одно важное обстоятельство: обычно пластичность предшествует разрушению, так что изучение пластических деформаций является основой прогноза прочности и долговечности конструкции.

Второе направление изучения пластичности – это исследование того, что происходит в материале, как говорят, на микроуровне, т.е., что происходит внутри материала, например, при пластическом изгибе балки. Можно, по аналогии с опытом на изгиб стержня, сделать опыт на его растяжение: верхний конец стержня (его обычно называют образцом) закрепляют, а к нижнему прикладывают нагрузку. В этом случае заметить на глаз изменение длины образца трудно, но если измерять деформации специальными приборами, то обнаруживается, что процесс деформирования оказывается похожим на тот, что и в опыте с изгибом: при постепенном возрастании растягивающей нагрузки сначала проявляются очень малые упругие деформации, когда же нагрузка достигает порогового значения, то деформации (теперь уже, в основном, пластические) становятся, во-первых, более существенными, а, во-вторых, необратимыми (т.е. не исчезают после снятия нагрузки).

При этом обнаруживаются интересные явления. Если в опыте на растяжение использовать стальной образец в виде длинной пластинки с полированной (зеркальной) поверхностью, то в процессе пластического деформирования на этой поверхности появляется много близких тонких параллельных прямых линий, ориентированных под углом 45° к оси образца (ось образца – здесь прямая линия, проходящая посредине пластинки, параллельно ее длинным сторонам). Эти линии называются линиями Людерса – Чернова (по фамилиям открывших их ученых).

Микроскопический анализ этих линий показывает, что они появляются в результате того, что в материале пластинки происходит сдвиг, т.е. один тонкий слой как бы сдвигается относительно второго, второй – относительно третьего и т.д., как карты в колоде. Можно сказать, что линии Людерса – Чернова и есть границы сдвигающихся слоев. На рис.1 схематически изображена картина такого деформирования. Эта схема позволяет понять, как такие сдвиги приводят к пластическому удлинению образца и почему после снятия нагрузки пластические деформации не исчезают. Более сложные и точные опыты показали, что пластические деформации металлов и сплавов всегда вызываются сдвигами внутри материала. Кроме того, в пористых материалах происходят деформации, по внешним проявлениям очень сходные с пластическими, но связанные с уменьшением пор. Наиболее знакомым пористым материалом является пенопласт; в технике пористые материалы создает порошковая металлургия, где детали прессуются из металлического порошка.

Можно довольно точно описать картину деформирования, считая, что упругие деформации тела – это результат изменения расстояния между атомами, из которых оно состоит, а пластические деформации – результат сдвигов.

Итак, пластичность – результат сдвигов. А как происходят сами сдвиги? На этот вопрос (и на многие другие) отвечают разделы физики: физика твердого тела, теория дислокаций, физика металлов и т.д.

Таковы два направления, по которым исследуется пластичности, первое называется феноменологическим – оно изучает феномен пластичности так, как его можно наблюдать в опытах с образцами и нагрузками, и не опирается на результаты микроскопических опытов. Феноменологическое изучение пластичности металлов начинается с классического опыта на растяжение. Его результаты представляются в виде графиков (рис. 2), где по вертикальной оси откладывается напряжение s, равное растягивающей силе P, отнесенной к площади сечения образца F, т.е.

s = P/F

а по горизонтали – деформация образца e, равная удлинению dl образца (под действием силы P), отнесенному к его первоначальной длине l.

e = dl/l

На рис. 2 изображен график, который называется «кривой растяжения»; материал – одна из марок стали. В начале нагружения (на графике от точки O до точки A) напряжение и деформация оказываются пропорциональными, т.е. имеет место закон Гука. Коэффициент пропорциональности называется модулем упругости (или модулем Юнга) E. Точка A на графике называется пределом упругости – после нее пропорциональность, свойственная упругости, сменяется криволинейной зависимостью, причем теперь деформация растет значительно быстрее, чем напряжение. Если в некоторой точке B мы начнем уменьшать напряжение (это называется разгрузкой), то на графике получится кривая, мало отличающаяся от прямой – BC со стрелкой вниз. Если, доведя напряжение до нуля, снова его увеличивать, на графике получится кривая CB1 (со стрелкой вверх), причем далее эта кривая плавно перейдет в кривую B1D, которая получилась бы при деформировании образца без разгрузки. Для простоты обычно обе кривые, BC и CB1, заменяют отрезком прямой B2C, который параллелен отрезку OA.

Есть несколько вариантов теории пластичности, которые отличаются, с одной стороны, тем, насколько точно они учитывают реальные особенности процесса деформирования упруго-пластического материала, и, с другой стороны, используемым математическим аппаратом. Одни теории являются менее точными, но более простыми и удобными для расчетов, что очень важно, так как расчет пластических деформаций в телах сложной формы представляет собой очень трудную задачу даже при использовании современных компьютеров. Другие теории могли бы обеспечить высокую точность, но приводят к очень большим трудностям, как математическим, так и экспериментальным. По-видимому, создание «идеальной» теории, сочетающей физическую наглядность, математическую простоту и в то же время обеспечивающей адекватное описание процессов пластического деформирования, является делом будущего. Но даже «простые» теории пластичности на самом деле достаточно сложны, так как требуют знания и понимания многих экспериментальных результатов и серьезной математической подготовки. В качестве примера можно рассмотреть идею самой простой теории пластичности.

В самом простом случае опыта на растяжение образца процесс упругого деформирования описывается законом Гука

s = E/e

За пределом упругости пропорциональности нет, но экспериментальную кривую растяжения можно описать, если считать, что модуль упругости E при этом перестает быть постоянной величиной и становится функцией деформации, т.е.

В этих формулах появляется новая функция w = w(e), которая называется функцией пластичности и должна быть найдена из экспериментальных данных.

Видно, что функция w(e) тождественно равна нулю при упругих деформациях и возрастает при пластических. Тогда ясно, что и упругие, и пластические деформации описываются уравнением, обобщающим закон Гука

s = E[1 – w (e)]e

Это уравнение описывает кривую деформирования, из которой оно, по существу, и получено и это так, пока речь идет только об опыте на растяжение. Но теория пластичности должна «уметь» описывать любые процессы деформирования – например, и кручение, и изгиб, и их совместное проявление, а для этого формулу необходимо существенно обобщить и сформулировать аналогичные по сути, но неизмеримо более сложные соотношения, которые связывали бы шесть компонент тензора деформаций с шестью компонентами тензора напряжений. Здесь и начинаются сложности.

Классическая деформационная теория называется «теорией малых упругопластических деформаций». Эта теория основана на трех экспериментальных фактах:

1. При различных упругопластических деформациях в каждой точке тела существует универсальная функциональная зависимость между среднеквадратичным значением сдвиговых деформаций и аналогичным среднеквадратичным значением сдвиговых напряжений.

2. При упругопластическом деформировании материала изменение объема всегда происходит упруго.

3. Первые два утверждения справедливы только при условии, что все внешние силы, действующие на тело, возрастают пропорционально друг другу (точнее – пропорционально одному параметру, например, времени). Это так называемое «простое» или «пропорциональное» нагружение.

Чтобы правильно понять эти три утверждения, нужно принять во внимание следующее:

Теория пластичности, как и все эмпирические теории, по своему существу является теорией приближенной. Это означает, что при известных условиях, когда она может описывать физическую реальность («условия применимости»), эмпирическая теория эту реальность описывает с относительно небольшой, но всегда присутствующей погрешностью (проще говоря, с небольшой ошибкой).

Теория пластичности, о которой идет речь, может дать ответ с погрешностью, близкой к 10%. И почти всегда такая погрешность оказывается вполне приемлемой – говорят, что «теория хорошо работает».

Математическая формулировка теории: пусть есть тензор деформации e ij и тензор напряжений sij. Требуется написать формулы (соотношения), которые связывают эти тензоры при малых упругопластических деформациях, подобно тому, как закон Гука связывает их при упругих деформациях.

Учитывая различные закономерности объемного и сдвигового деформирования, можно разделить тензоры на объемную (шаровую) и сдвиговую (девиаторную) части:

e ij = 1/3 Q dij + e_ij

sij = sdij + s_ij

(см. ДЕФОРМАЦИЯ;)

Следующий шаг – установление связи сдвиговых напряжений с деформацииями, поскольку пластичность – это сдвиги.

Для девиатора деформаций среднеквадратичный сдвиг в данной точке определяется формулой

Аналогично, среднеквадратичное сдвиговое напряжение определяется:

(величины и часто называют «интенсивностями» напряжений и деформаций). Теперь можно математически записать первый постулат:

Это и есть универсальная функциональная зависимость между и , а универсальна она в том смысле, что имеет место в любой точке тела и при любом виде деформаций (изгиб, кручение, их комбинация и т.д.). Функция считается известной, а фактически должна быть найдена из обработки результатов эксперимента. Так как в силу универсальности она одинакова всегда, в частности, в любом опыте, то удобно использовать опыт на кручение трубки, из которого эта функция определяется особенно легко.

В пределах упругости, и зависимость между и превращается в закон Гука. В теории пластичности считается, что в любой точке тела пластические деформации появляются тогда, когда величина достигает некоторого значения e_s. Это значение находится из эксперимента и называется пределом текучести по деформациям. Таким образом, условие появления первых пластических деформаций запишется в виде

Это условие называется условием пластичности Хубера – Мизеса. Таким образом, можно окончательно записать

если

если

Второй постулат записывается в виде: s = KQ

где s – среднее нормальное напряжение (давление) в данной точке, а Q – относительное изменение объема малой частицы, окружающей эту точку. Число K > 0 называется объемным модулем упругости. Таким образом, относительное изменение объема малой частицы пропорционально среднему нормальному напряжению в этой частице.

Теперь можно записать определяющие соотношения теории малых упругопластических деформаций:

Девиаторы напряжений и деформаций связаны пропорциональной зависимостью

Коэффициент пропорциональности за пределами упругости перестает быть постоянным и становится переменной величиной:

Функция становится отличной от нуля при выполнении неравенства, связанного с условиями пластичности Хубера–Мизеса

Шаровые тензоры напряжений деформаций всегда пропорциональны

s·dij = KQ·dij

или, что эквивалентно,

s = KQ

Все это справедливо только при пропорциональном нагружении, которое иногда называют простым, так как сложное нагружение – это непропорциональное нагружение. Оказывается, что в опыте, когда трубка подвергается растяжению силой P и кручению моментом M, деформации будут различными, в зависимости от того, как прикладываются нагрузки: сразу обе, сначала M, потом P, или наоборот.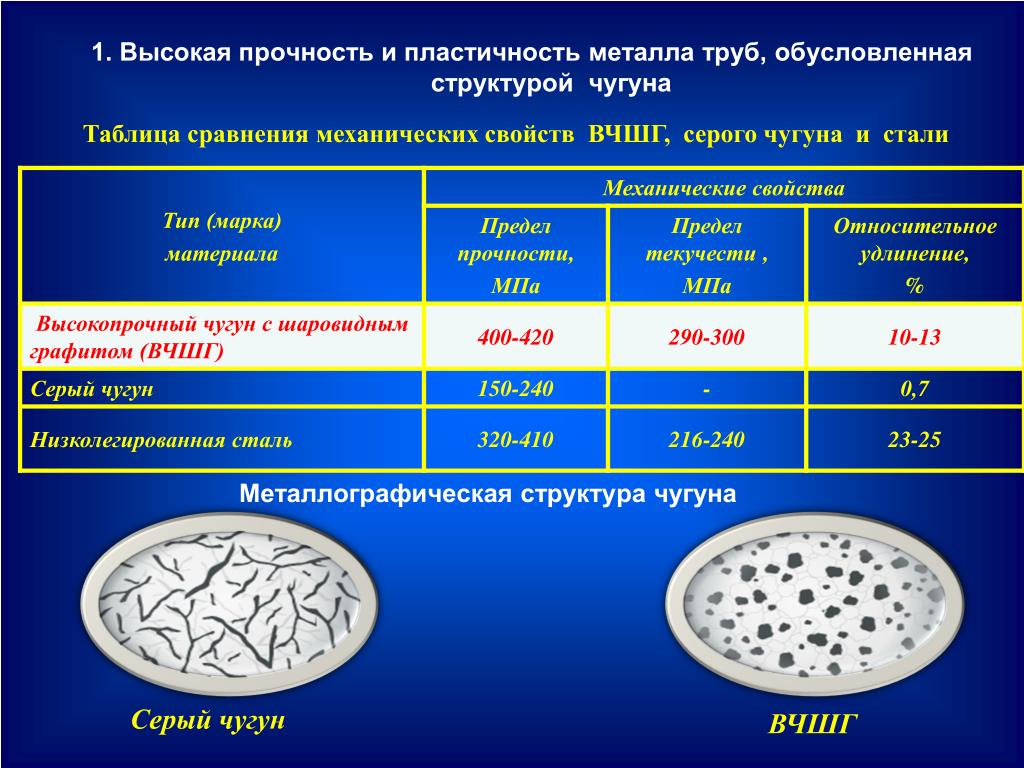 Это обстоятельство приводит к тому, что теорию пластичности при сложном нагружении уже нельзя построить по аналогии с теорией упругости.

Приведенная теория была разработана, экспериментально и теоретически обоснована и внедрена в инженерную практику работами А.Ильюшина, который опирался на работы своих предшественников – в первую очередь, Х.Хенки и Р.фон Мизеса.

Владимир Кузнецов

Различные методы измерения пластичности керамического материала

Пластичность – это характерное поведение керамического материала, при котором он необратимо деформируется после приложения внешней силы. Это свойство является наиболее характерным для глин, и есть несколько факторов, влияющих на пластичность, и их следует учитывать при измерении пластичности:

• Физические характеристики воды, такие как вязкость, поверхностное натяжение…
• Гранулометрический состав твердого образца и его удельная поверхность
• Химический и минералогический состав проб
• Влияние добавок, добавленных в систему глина/вода
• Температура образца
• Способ подготовки образца, особенно энергия, используемая для смешивания и обработки глины, воды и добавок

Пластичность определяется как способность деформироваться без разрушения. Существует множество методов его измерения, и они подразделяются на две группы: прямые и косвенные методы.

Таблица1. Методы прямой и непрямой пластики.

	Имя	Описание
Прямой	Мур (сжатие)	Дает хорошие результаты благодаря низкой чувствительности к малым скоростным изменениям и независимости от содержания влаги. Он определяется как отношение между давлениями для деформации цилиндрического зонда до 10% и 50% от его первоначальной высоты.
	Экструзия	Процесс в режиме реального времени в масштабе пилотной установки, в котором записываются многие параметры, такие как сила тока, давление, производительность, консистенция, температура…
	Деформация-деформация	Сжатие, тракция, сгибание, кручение.
Косвенный	Аттерберг	Определяет диапазон влажности, в котором можно работать с образцами, и определяется как разница между пределами жидкости и пластика. Предел жидкости — это максимальная влажность, при которой глина становится пригодной для обработки, а предел пластичности — это минимальная влажность, при которой глина пригодна для формования.
	Пфефферкорн	Определяет количество воды, необходимое для достижения 30-процентного сжатия по отношению к начальной высоте испытуемого тела под действием стандартной массы. Результаты обычно представляют в виде графиков, показывающих уменьшение высоты в зависимости от содержания влаги. Измерение пластичности основано на принципе ударной деформации с использованием образца определенного диаметра и высоты, деформируемого свободно падающей пластиной заданной массы.
	Барна	Определяется как соотношение между водой, ответственной за усадку плитки, и общей водой; Кривые Биго показывают эту информацию.
	Механическая прочность	Этот метод вычисляет Модули разрыва маленькой плитки, разбивая ее.

Прямые методы определяют пластическое поведение, измеряя влияние влаги на соотношение между напряжением и деформацией. Таким образом, прямые методы обеспечивают более надежное измерение пластического поведения, чем косвенные методы. Ограничения прямых методов связаны со стоимостью оборудования и временем, необходимым для подготовки образца и запуска метода. Эти ограничения делают прямые методы непрактичными, когда важно получить быстрые результаты.

Косвенные методы оценивают другие свойства, связанные с пластичностью, такие как содержание влаги, консистенция глины, механическая прочность и т. д. Косвенные методы обычно используются для контроля качества в керамической промышленности из-за их низкой стоимости и практичности. Аттерберг и Пфефферкорн являются двумя примерами этих методов.

Одна из основных проблем, наблюдаемых в непрямых методах, заключается в том, что качество упаковки оказывает сильное влияние на результаты пластичности. Чем ниже класс упаковки, тем выше влажность, необходимая для получения заданной пластичности, поскольку объем пор должен быть покрыт водой. Метод Пфефферкорна сильно зависит от упаковки, в то время как метод Аттерберга менее зависим от этой переменной, поскольку этот эффект модифицирует оба предела, жидкости и пластика, и исчезает после вычисления разницы между ними (индекс Аттерберга).

Как прямой, так и непрямой методы могут предоставить полезную информацию о пластичности глины и о том, как она изменяется при введении в глину добавок. Однако очень важно понимать основы и ограничения каждого метода, чтобы избежать неправильного толкования результатов пластичности.

Индекс пластичности, рассчитанный для пяти образцов с использованием трех различных методов, показан на рисунке ниже. Этот случай иллюстрирует, как разные методы могут привести к совершенно разным результатам при оценке пластичности образца глины.

Рис. 1. Индекс пластичности, рассчитанный разными методами.

 

Возможно, лучшим решением может быть работа с комбинацией прямых и косвенных методов для установления экспериментальной корреляции между ними. Непрямой метод может затем использоваться для целей контроля качества, поскольку он обеспечивает быстрые результаты. Затем эти результаты можно использовать для прогнозирования пластичности глины на промышленном предприятии. При таком подходе важно пересматривать соотношение между прямыми и непрямыми методами каждый раз, когда в процесс вносятся существенные изменения (например, новое глиняное сырье, новые добавки, другой размер частиц глины и т. д.).

Использование биополимеров может помочь согласовать поведение глины при изменении производственных процессов или даже при изменении свойств сырья.

Измерение пластичности мягких твердых пищевых продуктов

Пластичность это свойство проявляют многие материалы, такие как полимеры, металлы и большинство пищевых продуктов. Это способность материала подвергаться постоянному деформация.

Если вы нажимаете пальцем на пружину, она возвращается в исходную форму. Если вы сделали эту пружину из сыра, она не отскочила бы так далеко — он останется раздавленным. При растяжении образца видна пластичность на графике сила-расстояние как изменение градиента после начального линейный участок (прямой). Точка изменения градиента известный как «сила текучести». Если эта точка достигнута и больше силы применяется, образец будет постоянно изменен. До этого момента поведение упругое и пружинистое.

Пластичность вызвано «пластическим течением». Это может означать разные вещи в зависимости по рассматриваемому материалу. В полимере длинные молекулы могут двигаться мимо друг друга. В металле действует механизм, называемый дислокацией. позволяет атомам металла двигаться вдоль своего ряда в металлической решетке. Пищевые материалы могут иметь самые разнообразные структуры, поэтому механизм будет зависеть от рассматриваемой пищи. Однако эффект всегда очень похожий.

Если вы осторожно надавите пальцем на образец еду и уберите ее, если остался отпечаток пальца, произошла пластическая деформация. Например, если бы вы сделали это на поверхности среза толстого ломтика хлеба легкое нажатие не оставить отпечаток – хлеб отскочил бы назад. Более сильный толчок был бы, и это связано с пластическим течением.

Это Эффект можно измерить разными способами с помощью анализатора текстуры. Во-первых, некоторые удлиненные образцы подходят для испытаний на растяжение. Для Например, если на текстуру натянут длинный кусок лакрицы. Анализатор, он будет растягиваться, пока не сломается. Хорошая мера пластичности может быть расстоянием, на которое захваты переместились между усилием текучести и разрыв, разделенный начальным отрывом захвата. Это известно как пластическая деформация до разрушения. Более пластичная лакрица показала бы большую ценить. Если образец хранился в морозильной камере в течение ночи и тестировался замороженный, он может показать очень низкую пластическую деформацию до разрушения. Вы можете чувствовать этот эффект, потянув его между руками — было бы более вероятно чтобы показать хрупкий щелчок, чем образец комнатной температуры. испытание на изгиб покажет очень похожие результаты.
 
Во-вторых, тестирование на вдавливание может быть быстрым и простым. Если коническая, сферическая или Зонд Виккерса воткнули в плоскую поверхность баночки с маргарином. график может выглядеть примерно так:

Если индентор каждый раз вдавливался в поверхность на одну и ту же глубину (т.е. 5 мм), более пластичный образец покажет более глубокую вмятину, когда зонд удаляется, и соответственно большая пластическая глубина. Если образец с была измерена очень низкая пластичность (например, резина), может быть почти не остается вмятин, и, следовательно, почти нулевая пластическая глубина.

Использование кондитерского маргарина, например, метод, называемый «пальцевым методом». часто используется для определения пластичности образца. Это предполагает использование пальцы, чтобы манипулировать образцом. Если образец очень «короткий», это может ощущаться растрескиванием и невозможностью формовать его. это наоборот из «пластика». Хороший пластиковый маргарин можно согнуть, не ломая и не ломая. пластичность оценивается повторной ручной обработкой для проверки стабильности, твердость и жирность. В этом контексте пластичность является общее описание продукта, но приведенный выше тест на вдавливание по-прежнему дают ценную информацию о его истинной пластичности, и это скорее всего, коррелирует с более «пластичным» образцом, по ощущениям пальцевый метод.

Как со всеми тестами, выполненными человеком, а не машиной, хотя тест может повторяться, если его каждый раз проводит один и тот же человек, это не практично. Гораздо эффективнее и точнее использовать инструментальное испытательное оборудование, такое как анализатор текстуры. Результаты хранятся в виде чисел в электронной таблице для суждения о будущем партии или для разработки нового вида продукции как основы сравнение.

Есть представляет собой тест анализа текстуры практически для любого физического свойства. Свяжитесь со Stable Micro Systems сегодня, чтобы узнать больше о нашем полном ассортименте решения.