6. 4. Уравнения равновесия плоской произвольной системы сил

47

две силы R′ и R1 уравновешиваются, так как R′ = — R1 , и рассматриваемая система сил приводится только к одной силе R, равной главному вектору R′ и приложенной в точке А. Эта сила является равнодействующей заданной системе сил (рис. 6. 3, в).

Таким образом, если силы, произвольно расположенные на плоскости, не уравновешиваются, то их можно привести или к одной силе или к паре сил.

Для равновесия любой плоской системы сил необходимо и достаточно, чтобы одновременно выполнялись условия:

			R′ = 0;		М0 = 0		(6. 1)
Эти условия можно получить в трех различных формах.
1. Основная форма уравнений равновесия.
Величины		′ и М0 определяются равенствами:
	R
____________
		R′ = √ (Rх′)2 + (Rу′)2				;	М0 = ∑ М0 (	Рi) = 0 ,

где Rх′ = ∑ Хi , R у′ = ∑ Уi . Но R′ может равняться нулю только тогда, когда одновременно Rх′ = 0 и Rу′= 0. Следовательно, условия (6. 1) будут выполнены, если:

∑ Хi = 0 ;	∑ Уi = 0 ;	∑ М0 (Рi) = 0			(6. 2)
Таким образом,	для равновесия	плоской системы			сил необходимо и

достаточно, чтобы сумма проекций всех сил на каждую из двух координатных осей в плоскости их действия и сумма моментов всех сил относительно любой точки на плоскости равнялись нулю. Так как оси прямоугольных координат выбираются произвольно и точка О – любая точка плоскости, то для полученной системы уравнений равновесия (6. 1) ограничения отсутствуют. Поэтому такая система уравнений равновесия является основной.

2. Вторая форма уравнений равновесия.

Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма моментов всех этих сил относительно любых двух точек А, В на плоскости и сумма их проекций на ось ОХ, не перпендикулярную к прямой АВ, были равны нулю:

∑ МА (Рi		) = 0 ; ∑ МВ (Рi) = 0 ; ∑ Хi = 0			(6. 3)

3. Третья форма уравнений равновесия.

Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно любых трех точек А, В, С на плоскости, не лежащих на одной прямой, были равны нулю:

∑ МА (Рi) = 0 ; ∑ МВ (Рi) = 0 ; ∑ МС (Рi) = 0							(6. 4)

48

a.		б.
0		A
M0			d	_
	_			R1
	R			O
_
R’				_
				R’

в.

	A
_	d
R	O

	Рис.6.3.
_	_
P1	P2
	A2
	A1

_

R1

A

O

C

An

_

Pn

X

B

Рис. 6.4

49

Докажем справедливость уравнений равновесия (6. 2), (6. 3), (6. 4). Рассмотрим систему уравнений (6. 3).

Если имеет место уравнение ∑ МА (Рi) = 0, то главный момент системы сил, когда за центр приведения выбрана точка А, равен нулю и система сил или находится в равновесии или приводится к равнодействующей R′, линия действия которой должна проходить через точку А.

Из уравнения ∑ МА (Рi) = 0 следует, что главный момент системы сил равен нулю, а если равнодействующая R′ отлична от нуля, то ее линия действия должна проходить через центр приведения – точку В.

При выполнении двух первых уравнений системы следует, что система сил или находится в равновесии, или приводится к равнодействующей, причем ее линия действия должна проходить по прямой АВ.

Из третьего уравнения системы ∑Хi = 0 следует, что проекция равнодействующей Rх′ = 0, и если ось Х не перпендикулярна АВ, то это возможно лишь только в том случае, когда равнодействующая R′ = 0.

Таким образом, система уравнений является системой уравнений равновесия.

Рассмотрим систему уравнений (6. 4).

При выполнении двух первых уравнений системы (как было показано) следует, что система сил или находится в равновесии или приводится к равнодействующей R′, линия действия которой совпадает с прямой АВ. Из третьего уравнения системы ∑МС(Рi) = 0 следует, что момент равнодействующей R′ относительно точки С должен равняться нулю.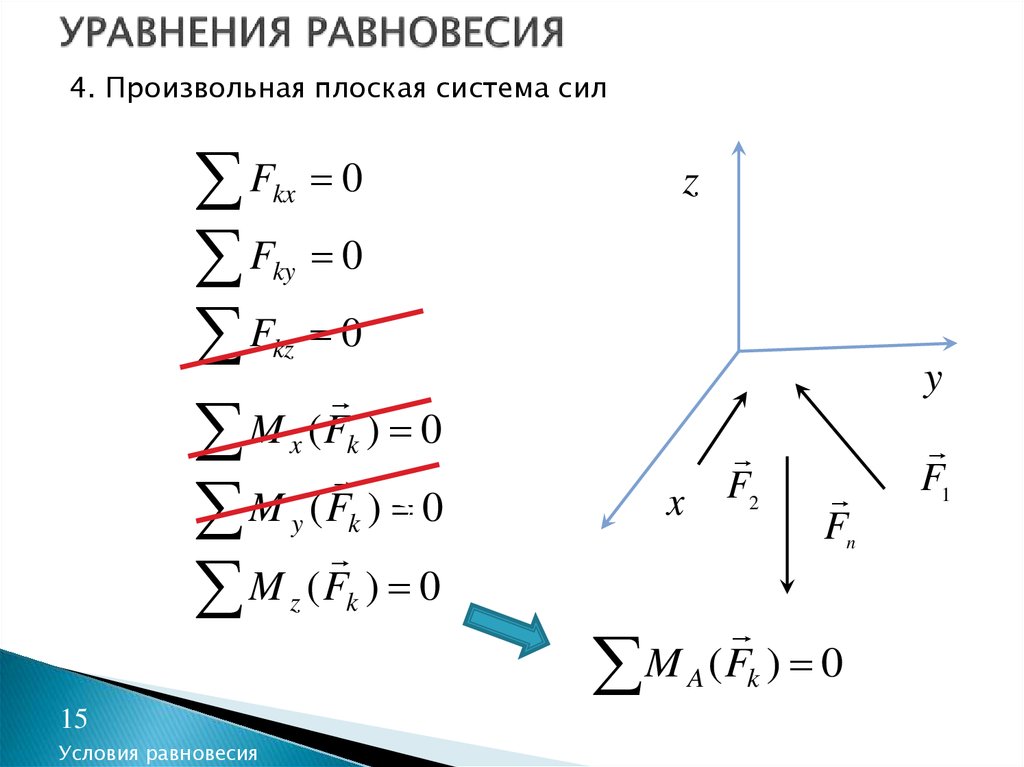 Это возможно лишь в том случае, когда равнодействующая R′ = 0 (мы предположили, что точка С не должна лежать на прямой АВ).

Таким образом, полученные выражения являются системой уравнений равновесия для сил, произвольно расположенных на плоскости (при принятом ограничении выбора моментных точек).

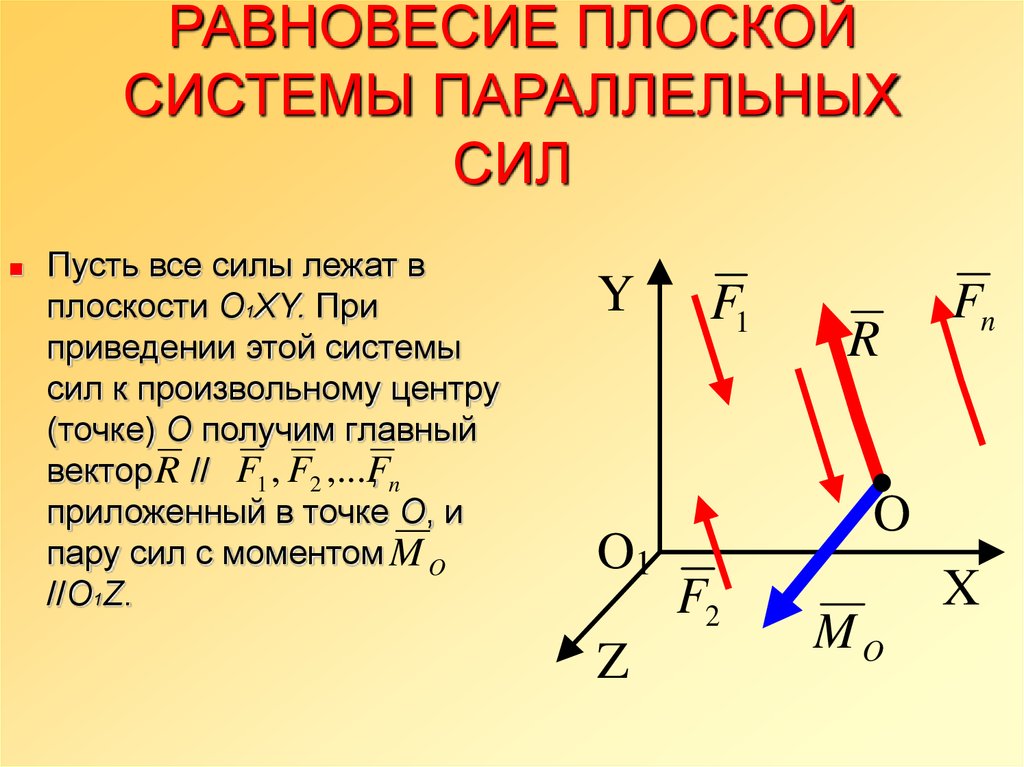
6. 5. Уравнения равновесия плоской системы параллельных сил

Систему n параллельных сил (Р1, Р2, … Рn), лежащих в одной плоскости, можно рассматривать как частный случай плоской произвольной системы сил. Выбрав одну из осей прямоугольных координат (например, ось у) параллельной линии действия сил рассматриваемой системы, из уравнений равновесия (6. 2) получаем только два уравнения равновесия:

∑ Уi = 0 ;			∑ МС (			(6. 5)
				Рi) = 0 .
Другой вид уравнений равновесия системы параллельных сил на
плоскости:
∑ МА (Рi) = 0 ;			∑ МВ (Рi) = 0			(6. 6)

причем прямая АВ не должна быть параллельна линии действия сил.

50

6.6. Теорема Вариньона о моменте равнодействующей плоской системы сил

Докажем, что если плоская система сил приводится к равнодействующей, то момент равнодействующей относительно любой точки, лежащей в плоскости действия данных сил, равен алгебраической сумме моментов составляющих сил относительно той же точки.

Определим момент равнодействующей силы R′, приложенной в точке А, относительно произвольно выбранного центра приведения О (рис. 6. 3, в).

М0

	М0 (Ri) = R . d , но R = R′			и d = ——
			М0			R′
Тогда	М0	(R)	= R′ . —— = М0 =	∑ М0 (Рi)
			R′

Из этой теоремы следует, что главный момент плоской системы сил относительно любой точки, лежащей на линии действия ее равнодействующей, равен нулю.

6. 7. Статически определимые и статически неопределимые задачи

Различают задачи статически определимые, которые можно решать методами статики твердого тела, и задачи статически неопределимые, которые могут быть решены, если принять во внимание упругие свойства тела и возникающие в нем деформации. Но так как решение последних задач выходит за пределы статики абсолютно твердого тела, то эти задачи рассматриваются в курсах сопротивления материалов и строительной механики.

Статически определимыми будем называть задачи, в которых число неизвестных не превышает числа уравнений равновесия статики для данной системы сил.

При равновесии плоской системы произвольно расположенных сил, приложенных к твердому телу, можно составить три уравнения равновесия, а для уравновешенной системы параллельных сил только два уравнения равновесия. В первом случае задача будет статически определимой, если число неизвестных не превышает трех, во втором случае число неизвестных задачи не должно быть больше двух.

В противном случае задача становится статически неопределимой, так как число уравнений равновесия статики окажется меньше числа неизвестных.

Балка (рис. 6. 5, а) имеет связь в виде жесткой заделки. Реакции заделки представляют собой силы, которые приводятся к силе RА (препятствующей перемещению балки) и реактивной паре сил с моментом МА (препятствующей вращению балки вокруг закрепленного конца). Так как неизвестна RА, то ее заменяем составляющими ХА и УА. Таким образом, неизвестными,

51

подлежащими определению, являются ХА , УА и МА. Для определения неизвестных имеем 3 уравнения равновесия статики. Число неизвестных равно числу уравнений равновесия, следовательно, задача является статически определимой.

Ферма (рис. 6.5, б) имеет шарнирно неподвижную связь А. Линия действия RА неизвестна. Поэтому при решении задачи ее заменяем двумя взаимно перпендикулярными составляющими ХА и УА. Связь В выполнена шарнирно подвижной. Линия действия реакции RВ известна, она пройдет перпендикулярно плоскости катания.

Таким образом, число неизвестных, подлежащих определению, равно трем (ХА, УА и RВ), что соответствует числу уравнений равновесия статики. Следовательно, задача является статически определимой.

Балка, показанная на рис. 6. 5, в, также является статически определимой на основании рассуждений, приведенных для фермы (рис. 6. 5, б).

Балка (рис. 6. 5, г) имеет шарнирно неподвижные опорные связи А и В. Так как линия действия реакций RА и RВ заранее неизвестны, то их заменяем

составляющими ХА , УА и ХВ, УВ. Число уравнений равновесия статики равно трем. Так как число неизвестных превышает число уравнений равновесия, задача является статически неопределимой.

Балка (рис. 6. 5, д) имеет три шарнирно неподвижные связи. На балку действует система параллельных сил. Поэтому горизонтальные составляющие опорных реакций ХА , ХВ и ХС будут заведомо равны нулю. Неизвестными

будут только вертикальные составляющие УА = RА, УВ = RВ, УС = RС . Таким образом, число неизвестных, подлежащих определению, равно трем. Для системы параллельных сил имеем два уравнения равновесия статики. Число неизвестных превышает число уравнений равновесия, следовательно, задача является статически неопределимой.

Балка (рис. 6. 5, е) имеет шарнирно неподвижную связь А. Так как линия действия реакции RА неизвестна, то ее заменяем двумя составляющими ХА и УА. В точке В и С балка закреплена двумя стержнями. Стержень шарнирно закреплен с балкой и основанием. Линия действия реакции таких связей проходит по линии, соединяющей шарниры. Таким образом, число неизвестных, подлежащих определению, равно четырем (ХА , УА и Т1, Т2). Число уравнений равновесия для определения неизвестных равно трем.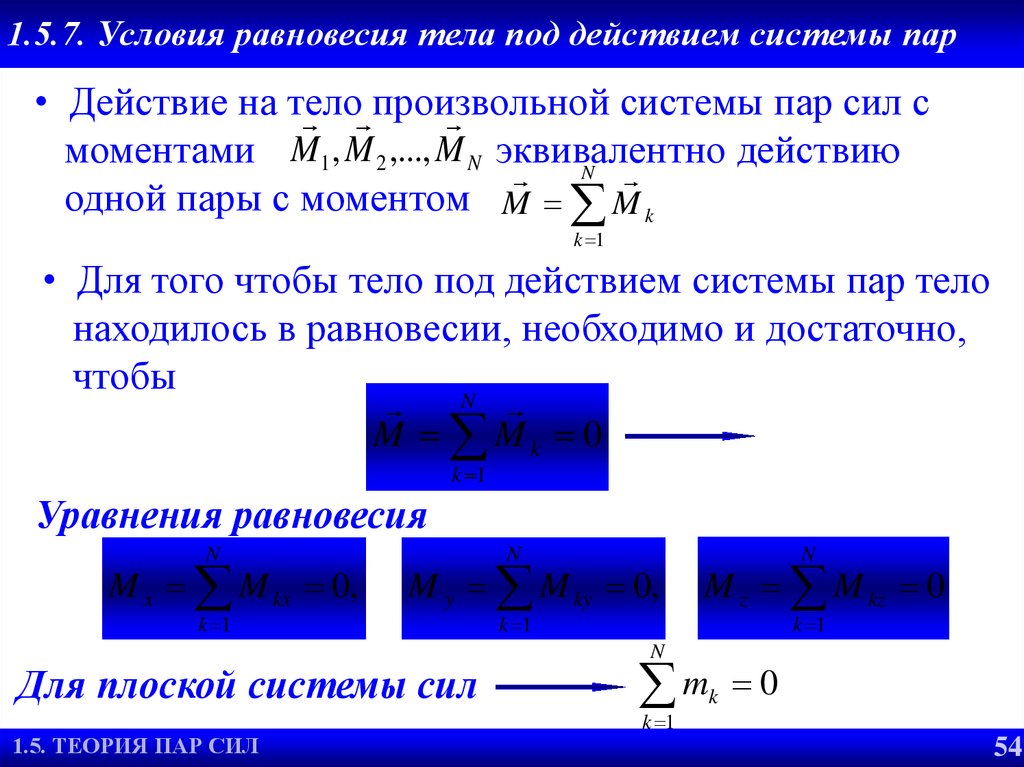 Число неизвестных превышает число уравнений равновесия статики, следовательно, задача является статически неопределимой.

52

а.	_
	yA		_
	_		P		_
A	xA				P1
				M
	MA
б.					_
					P2
_
P1					_
_	_
					B
yA					R
	xA				B
A			_
			P3
в.		_		q
_					_
		P
yA	_
					B
	xA				R
A
					B
					M
г. _		_	q		_
yA	_	P			yB _
A	xA				xB
					B
д.				_
_		_	_		_
RA		1	RB	P2 q	RC
		P
A			B		C
е.
_			_		_
yA	_			_
			1		2
	xA		T	P2	T

A_

P1

Рис.6.5

Краткий курс теоретической механики

Краткий курс теоретической механики

Тарг С. М. Краткий курс теоретической механики: Учеб. для втузов.— 10-е изд., перераб. и доп. — М.: Высш. шк., 1986.— 416 с. В книге изложены основы механики материальной точки, системы материальных точек и твердого тела в объеме, соответствующем программам технических вузов. Приведено много примеров и задач, решения которых сопровождаются соответствующими методическими указаниями. В 10-м издании (9-е — 1974 г.) значительно изменены и более компактно изложены вопросы статики; в разделе «Динамика» дополнительно рассмотрены приложения общих теорем к изучению движения жидкости, малые колебания системы и некоторые другие вопросы. Для студентов очных и заочных технических вузов. Оглавление ПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮ ВВЕДЕНИЕ Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ § 3. СВЯЗИ И ИХ РЕАКЦИИ Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ) § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ § 10. ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ И О СЛОЖЕНИИ ПАР Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ Глава V. ПЛОСКАЯ СИСТЕМА СИЛ § 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ § 17. РЕШЕНИЕ ЗАДАЧ § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ) § 20. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ § 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ Глава VI. ТРЕНИЕ § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ § 27. ТРЕНИЕ КАЧЕНИЯ Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ Глава VIII. ЦЕНТР ТЯЖЕСТИ § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ § 32. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА § 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ § 38. ВЕКТОР СКОРОСТИ ТОЧКИ § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ § 43. КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ § 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ § 46. РЕШЕНИЕ ЗАДАЧ § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ § 50. РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ § 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 52. УРАВНЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ (ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ). РАЗЛОЖЕНИЕ ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ § 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ § 57. РЕШЕНИЕ ЗАДАЧ § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА § 62. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ТЕЛА § 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ § 64. ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ § 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА) § 67. РЕШЕНИЕ ЗАДАЧ Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ Раздел третий. ДИНАМИКА ТОЧКИ Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ § 75. СИСТЕМЫ ЕДИНИЦ § 76. ОСНОВНЫЕ ВИДЫ СИЛ Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ) § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ § 80. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ § 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ) § 82. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ § 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ) § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ § 87. РАБОТА СИЛЫ. МОЩНОСТЬ § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ § 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ § 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ § 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ) § 96. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС Глава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА § 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ § 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ § 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС § 109. РЕШЕНИЕ ЗАДАЧ Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ § 110. КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ § 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ § 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ) § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ § 118. РЕШЕНИЕ ЗАДАЧ § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ § 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ § 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ § 124. РЕШЕНИЕ ЗАДАЧ § 125. СМЕШАННЫЕ ЗАДАЧИ § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ Глава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА Глава XXVII. ПРИНЦИП ДАЛАМБЕРА § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ § 135. РЕШЕНИЕ ЗАДАЧ § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ § 140. РЕШЕНИЕ ЗАДАЧ § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ Глава XXIX. УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ § 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ § 143. ОБОБЩЕННЫЕ СИЛЫ § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ § 145. УРАВНЕНИЯ ЛАГРАНЖА § 146. РЕШЕНИЕ ЗАДАЧ Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ) § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ. ЦЕНТР УДАРА

5.4: 2D-равновесие твердого тела

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

70236

• Дэниел У. Бейкер и Уильям Хейнс
• Университет штата Колорадо через Engineeringstatics

Двумерные твердые тела имеют три степени свободы, поэтому для их решения требуется всего три независимых уравнения равновесия. Шесть скалярных уравнений (5.3.3) можно легко свести к трем, исключив уравнения, относящиеся к неиспользуемой размерности \(z\). Для объектов в плоскости \(xy\) нет сил, действующих в направлении \(z\) и создающих моменты относительно осей \(x\) или \(y\), поэтому сокращенная система из трех уравнений равна

.

\begin{align*} \{1\} \amp = \begin{cases} \sum F_x \amp =0 \\ \sum F_y \amp =0 \\ \sum M_A \amp =0 \end{cases} \text{.} \end{выравнивание*}

, где нижний индекс \(z\) заменен буквой для обозначения произвольного центра момента в плоскости \(xy\) вместо перпендикулярной оси \(z\).

Это не единственная возможная система уравнений равновесия. Любое уравнение силы можно заменить линейно независимым уравнением момента относительно выбранной вами точки ¹ Метки \(A\text{,}\) \(B\) и \(C\) в этих уравнениях являются репрезентативными. Они не обязательно должны соответствовать точкам \(A\text{,}\) \(B\) и \(C\) в вашей задаче, поэтому других возможных наборов 9.0032

\begin{align*} \{2\} \amp = \begin{cases} \sum F_x \amp =0 \\ \sum M_B \amp =0 \\ \sum M_A \amp =0 \end{cases} \amp \{3\} \amp = \begin{cases} \sum M_C \amp =0 \\ \sum F_y \amp =0 \\ \sum M_A \amp =0 \end{cases} \amp \{4 \} \amp = \begin{cases} \sum M_C \amp =0 \\ \sum M_B \amp =0 \\ \sum M_A \amp =0 \end{cases}\text{.} \end{align* }

Для набора четыре центры моментов \(A\text{,}\) \(B\text{,}\) и \(C\) должны образовывать треугольник, чтобы три уравнения были линейно независимыми.

Вы обладаете большой гибкостью при решении задач равновесия твердого тела. Помимо выбора используемого набора уравнений, вы также можете поворачивать систему координат в любую ориентацию по своему усмотрению, выбирать разные точки для центров моментов и решать уравнения в любом порядке или одновременно.

Эта свобода вызывает несколько вопросов. Какой набор уравнений выбрать? Является ли один вариант «лучше» другого? Зачем заморачиваться с вращающимися системами координат? Как выбрать центры моментов? Студенты хотят знать, «как решить задачу», хотя на самом деле есть много способов сделать это.

Актуальная задача — выбрать эффективный подход и осуществить его. Эффективное решение — это то, которое позволяет избежать математических сложностей и упрощает решение проблемы. Усложнения включают неприятную геометрию, ненужную алгебру и, в частности, одновременные уравнения, которые интенсивно используют алгебру и подвержены ошибкам.

Так как же настроить эффективный подход? Во-первых, остановитесь, подумайте и ищите возможности сделать решение более эффективным. Вот несколько рекомендаций.

1. Первый набор уравнений обычно является хорошим выбором, и его следует рассматривать в первую очередь.
2. Проверьте свою диаграмму свободного тела и определите неизвестные значения в задаче. Это могут быть величины, направления, углы или размеры.
3. Совместите систему координат хотя бы с одной неизвестной силой.
4. Возьмите моменты относительно точки, где пересекаются линии действия двух неизвестных сил, что исключает их из уравнения.
5. Сначала решить уравнения с одним неизвестным.

Пример 5.4.1. Штифт и ролик.

L-образное тело поддерживается роликом в точке \(B\) и штифтом без трения в точке \(A\text{.}\) Тело воспринимает вертикальную силу \(\lb{100}\) в точке \ (C\) и парный момент \(\ftlb{500}\) в точках \(D\text{.}\) Определить реакции в точках \(A\) и \(B\text{.}\)

Эта задача будет решена тремя различными способами, чтобы продемонстрировать преимущества и недостатки различных подходов.

Решение 1

Решения всегда начинаются с диаграммы свободного тела, показывающей все силы и моменты, действующие на объект. Здесь известные нагрузки \(C = \lb{250}\) (вниз) и \(D= \ftlb{500}\) (против часовой стрелки) выделены красным цветом, а неизвестные реакции \(A_x\text{,}\ ) \(A_y\) и \(B\) синие.

Сила в точке \(B\) проведена вдоль ее известной линии действия перпендикулярно поверхности ролика и направлена ​​вверх и вправо, поскольку это будет противодействовать вращению рамы вокруг A, вызванному нагрузкой C и моментом D. Сила в точке \(A\) представлена ​​неизвестными компонентами \(A_x\) и \(A_y\text{.}\). Смысл этих компонентов неизвестен, поэтому мы произвольно назначили стрелки, указывающие влево и вверх.

Мы выбрали стандартную систему координат с положительным \(x\) вправо и положительным \(y\) направленным вверх, и разложили силу \(A\) на составляющие в \(x\) и \(y\) ) направления.

Величина силы \(B\) неизвестна, но известно ее направление, поэтому компоненты \(x\) и \(y\) силы B могут быть выражены как

\begin{align*} B_x \amp= B \sin \ang{60} \amp B_y \amp = B \cos \ang{60} \text{.} \end{align*}

Мы решили решить набор уравнений \(\{A\}\text{,}\) и решили взять моменты относительно точки \(A,\), потому что неизвестные \(A_x\) и \(A_y\) пересекаются в ней. Подстановка переменных в уравнение и решение неизвестных дает

\begin{align*} \sum F_x \amp = 0 \\ B_x — A_x \amp = 0\\ A_x \amp = B\ \sin \ang{60} \amp \amp (1)\\ \\ \ сумма F_y \amp = 0\\ B_y — C + A_y \amp= 0\\ A_y \amp= C — B\ \cos \ang{60}\amp \amp (2)\\ \\ \sum M_A \amp = 0 \\ -B_x( 3) -B_y(7)+C(4) + D \amp = 0\\ 3 B \cos \ang{60} + 7 B \sin \ang{60} \amp = 4 C + D \\ B (3 \sin \ang{60} + 7 \cos \ang{60})\amp = 4 C + D \\ B \amp = \frac{4 C + D}{6,098} \ усилитель \amp (3) \end{align*}

Из этих трех уравнений только третье можно вычислить сразу, потому что мы знаем \(C\) и \(D\text{. }\) В уравнениях \((1)\) и \((2)\) неизвестные \(A_x\) и \(A_y\) не могут быть найдены, пока не известно \(B\). Вставка известных значений в \((3)\) и решение для \(B\) дает

\begin{align*} B \amp = \frac{4 (250) + 500} {6.098} \\ \amp = \frac{\ftlb{1500}}{\ft{6.098}} \\ \amp = \lb{246.0} \end{align*}

Теперь, зная величину \(B\), \(A_x\) и \(A_y\) можно найти с помощью \((1)\) и \((2)\text{.}\)

\begin{align*} A_x \amp = B \sin \ang{60} \\ \amp = 246.0 \sin \ang{60} \\ \amp = \lb{213.0}\\ \\ A_y \amp= C — B \cos \ang{60}\\ \amp= 250 — 246.0 \cos \ang{60}\\ \amp= \lb{127.0} \end{align*}

Положительные знаки этих значений указывают на то, что направления, принятые на диаграмме свободного тела, были правильными. 9{-1} \слева | \frac{ A_y}{A_x} \right | = \ang{30.8} \end{собрать*}

Окончательный ответ для \(\vec{A}\) и \(\vec{B}\text{,}\) с углами, измеренными против часовой стрелки от положительной оси \(x\), равен

\[ \vec{A} = \lb{248,0}\ \измеренный угол\ \ang{149,2}, \номер\]

\[ \vec{B} = \lb{246,0}\ \измеренный угол \ 60° \текст{. } \номер\]

Это решение демонстрирует довольно стандартный подход, подходящий для многих задач статики, и его следует учитывать всякий раз, когда диаграмма свободного тела содержит штифт без трения. Начните с моментов там.

Решение 2

В этом решении мы повернули систему координат \(\ang{30}\), чтобы выровнять ее по силе \(\vec{B}\), а также выбрали компоненты силы \(\vec{A}\) для согласования с новой системой координат.

Этот подход не имеет особого преимущества перед первым, но с двумя неизвестными силами, ориентированными в направлении \(x’\), \(A_{y’}\) можно найти сразу после разрывной силы \(C\ ) на компоненты.

\begin{align*} \sum F_{x’} \amp = 0 \\ B — C_{x’} + A_{x’} \amp = 0\\ A_{x’} \amp = -B + C \sin \ang{30} \amp \amp (1)\\ \\ \sum F_{y’} \amp = 0\\ C_{y’} + A_{y’} \amp= 0\\ A_ {y’} \amp= C \cos \ang{30} \amp \amp (2)\\ \\ \sum M_A \amp = 0 \\ -B_x( 3) -B_y(7)+C(4) + D \amp = 0\\ 3 B \cos \ang{60} + 7 B \sin \ang{60} \amp = 4 C + D \\ B (3 \cos \ang{60} + 7 \sin \ang{60})\amp = 4 C + D \\ B \amp = \frac{4 C + D}{7. 56} \amp \amp (3) \end{align*}

Решение уравнения (2) дает

\[ A_{y’} = \lb{216.5}\text{.} \nonnumber \]

Решение уравнения (3) дает тот же результат, что и ранее

\[ B = \lb{246.0}\text{.} \номер\]

Подстановка \(B\) и \(C\) в уравнение (1) дает

\begin{align*} A_{x’} \amp = -B + C \sin \ang{30} \\ \amp = — 246.0 + 250 \sin \ang{30} \\ \amp = -\lb {121.0} \end{выравнивание*}

Знак минус в этом результате указывает на то, что наше предполагаемое направление для \(A_{x’}\) было неправильным, и что сила фактически указывает \(\ang{180}\) на предполагаемое направление. 9{-1} \слева | \frac{ A_y}{A_x} \right | = \ang{60.8}\\ \alpha = \ang{180} — (\theta — \ang{30}) = \ang{149.2} \end{gather*}

Опять же, окончательный ответ для \(\vec{A}\) и \(\vec{B}\text{,}\) с углами, измеренными против часовой стрелки от положительной оси \(x\), равен

\[ \vec{A} = \lb{248,0}\ \измеренный угол\ \ang{149,2}, \номер\]

\[ \vec{B} = \lb{246,0}\ \измеренный угол \ 60° \не число \]

Этот подход был немного сложнее, чем решение 1, из-за дополнительной тригонометрии, необходимой для поиска компонентов в повернутой системе координат.

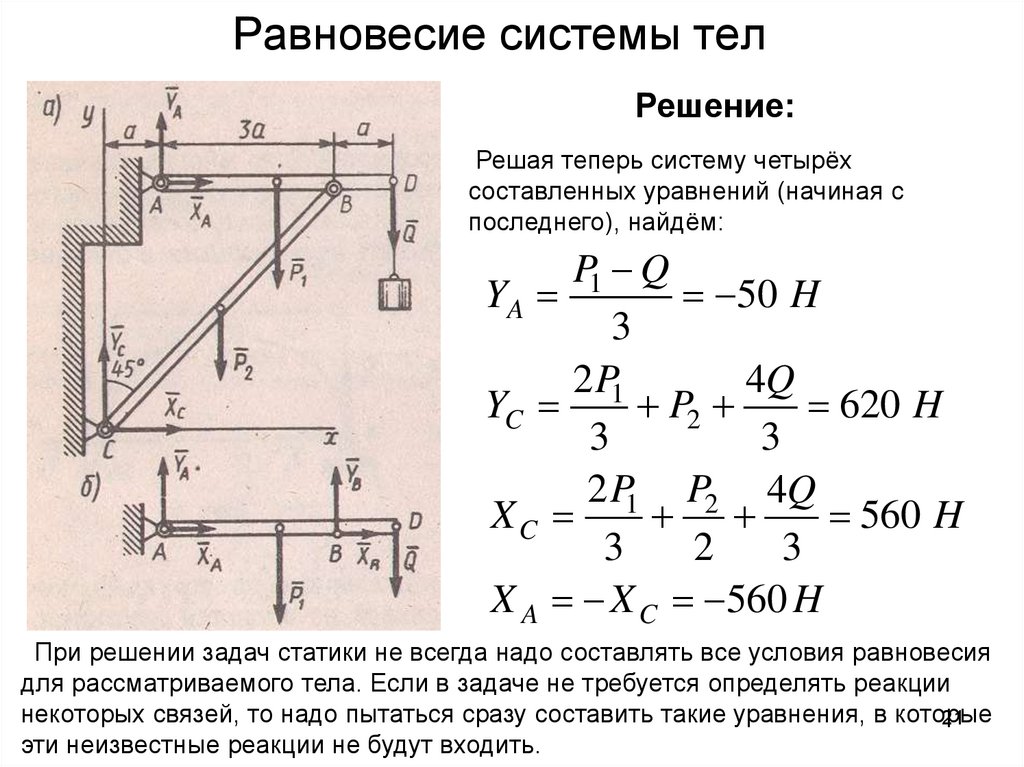
Решение 3

Для этого решения мы будем использовать ту же диаграмму свободного тела, что и первое решение, но будем использовать три уравнения моментов относительно точек \(B\text{,}\) \(C\) и \(D\text{. }\)

\begin{align*} \sum M_B \amp = 0 \\ — A_x(3) + A_y(7) — C(3) + D \amp = 0 \\ — 3 A_x + 7 A_y \amp = 250 \ amp \amp (1)\\ \\ \sum M_C \amp = 0\\ -A_x(3) + A_y(4) — B_y(3) + D \amp= 0\\ -3A_x + 4 A_y — 3 B \cos \ang{60} \amp= -D \\ 3A_x — 4 A_y + 1,5 B \amp = 500 \amp \amp (2)\\ \\ \sum M_D \amp = 0 \\ — A_x(1.5) -B_x( 1.5 ) -B_y(7) + C(4) + D \amp = 0\\ 1,5 A_x + 1,5 B \sin \ang{60} + 7 B \cos \ang{60} \amp = 4 C + Д \ 1,5 А_х + 4,799 B \amp = 1500 \amp \amp (3) \end{align*}

Эту систему из трех уравнений и трех неизвестных можно решить с помощью алгебры.

Сложение (1) и (2) дает

\begin{align*} 3 A_y + 1,5 B \amp = 750 \amp \amp (4) \end{align*}

Разделение уравнения (2) на 2 и вычитание его из (3) дает

\begin{align*} 2 A_y + 4,049 B = 1250 \amp \amp (5) \end{align*}

Умножение (4) на 2/3 и вычитание из (5) исключает \(A_y\) и дает

\начать{собрать*} 3,049 Б = 750 \конец{собрать*}

\begin{gather*} B = \lb{246. 0}\text{,} \end{gather*}

тот же результат, что и раньше.

Подстановка \(B\) в (3) дает \(A_x = \lb{213.0}\text{,}\), а подстановка этого в (1) дает \(A_y = \lb{127.0}\text{,} \) снова тот же результат, что и раньше.

Альтернативный подход состоит в том, чтобы подготовить эти три уравнения для матричного решения и использовать технологию для выполнения алгебры, как это сделано здесь с Sage.

\[ \begin{bmatrix} -3 \amp 7 \amp 0 \\ 3 \amp -4 \amp 1.5 \\ 1.5 \amp 0 \amp 4.799 \end{bmatrix} \begin{bmatrix} A_x \\ A_y \ \ B \end{bmatrix} = \begin{bmatrix} 250 \\ 500 \\ 1500 \end{bmatrix} \nonumber \]

Это хороший пример неэффективного решения из-за всей алгебры. Проблема здесь заключалась в неправильном выборе \(B\text{,}\) \(C\) и \(D\) в качестве центров моментов. Когда это возможно, вы должны брать моменты относительно точки, где линии действия двух неизвестных пересекаются, как это было сделано в решении 1. Это дает уравнение моментов, которое можно решить немедленно для третьего неизвестного.

---

Эта страница под названием 5.4: 2D Rigid Body Equilibrium распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Дэниелом У. Бейкером и Уильямом Хейнсом (Engineeringstatics) посредством исходного содержимого, которое было отредактировано. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Дэниел В. Бейкер и Уильям Хейнс

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. источник@https://engineeringstatics. org

BME 332: Стресс

I. Обзор

         Стресс является критическим концепция для понимания в качестве основы для дальнейшего понимания континуума и впоследствии, механика тканей. Напряжение возникает, когда к телу прикладывают силы, ограниченный. Другими словами, если тело не движется как твердое тело, часть тела будет растянута или сжата, и возникнут стрессы внутри тела. Таким образом, напряжение является мерой интенсивности внутренней силы. развивается внутри тела в ответ на внешние силы, как определено в этом класс, не обязательно то, что вы чувствуете, когда у вас есть два домашних задания а завтра тест.

         Стресс, как уже упоминалось, является фундаментальным компонентом механики сплошных сред и механики биотвердых тел. Действительно, уравнения равновесия, описывающие баланс сил внутри тела написаны под ударением. Кроме того, многие теории разрушения материалов на самом деле основаны на уровне стресса в организме. Цель этого раздел должен описать и определить напряжение как тензор второго порядка, и вывести основные уравнения равновесия для механики сплошной среды. Примечание в этой главе предполагается, что у вас есть практические знания об индексах обозначения и математические понятия из главы 1. Таким образом, вы изучите следующие понятия в этом разделе:

1. Определение сил, действующих на тело
2. Определение тензора напряжений Коши
3. Вывод уравнения равновесия напряжений из баланса линейных импульса
4. Вывод симметрии тензора напряжений Коши из баланса угловых импульс
5. Инварианты тензора напряжений
6. Определение неопределенности из уравнений равновесия напряжений

II. Силы, действующие на тело

         Есть два основных типы сил, которые могут действовать на тело, будь то ткань или искусственная компонент.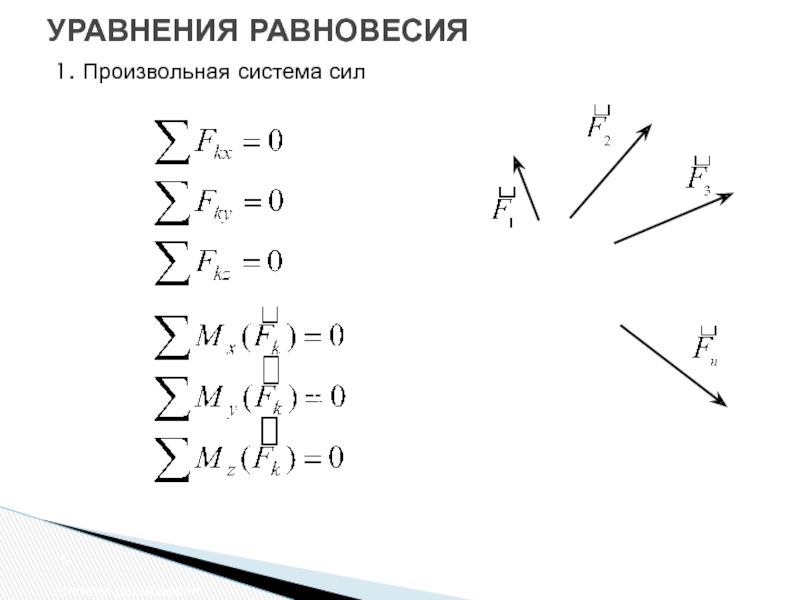

Объемная сила действует на элемент массы или объема внутри тела. Примеры объемных сил включают силы тяжести и электромагнитные силы. Тело силы записывают или считают на единицу массы или на единицу объема. Таким образом, чтобы найти полную объемную силу, действующую на тело, нам нужно проинтегрировать силу умноженная на плотность массы (если объемная сила считается на массу) за объем:

где V — объем, r — массовая плотность, bi — компоненты вектора объемной силы, отнесенные к единице массы.

Вторая и на самом деле более распространенная сила, с которой мы имеем дело в биологических твердых телах механика надводная сила . Поверхностные силы обычно возникают из-за для контакта между двумя телами или из-за давления жидкости на твердое тело. В механике биотвердых тел мы видим, как поверхностные силы развиваются на поверхностях скелетных суставов. из-за соприкосновения двух суставов. Мы также видим, что напряжения развиваются в скелете. ткани из-за мышечных сил, которые передаются костям через сухожилия. Мышцы являются уникальной тканью, поскольку они могут активно генерировать силы. Однако на микроструктурном уровне механизм генерации силы собственно контакт между двумя мышечными белками, актином и миозином. Поверхность силы на артерии и в легочных альвеолах развиваются за счет кровяной жидкости и давления газа соответственно на эти ткани. Наконец, поверхностные силы на тканях также может развиваться при контакте тела человека с внешними объекты, как это происходит в различных видах спорта и в автомобильных авариях. Поверхностные силы исчисляются или записываются на единицу площади. Поэтому для определения общего поверхностную силу интегрируем по площади:

где S — площадь поверхности, а ti — компоненты поверхностной силы. вектор.

III. Определение тензора напряжений Коши

      При приложении внешних сил к тела, мы знаем из 1-го закона Ньютона, что внутренние силы должны развиваться внутри тело уравновешивать внешние силы, иначе тело не может находиться в равновесие. Рассмотрим теперь, какую форму могут принимать эти внутренние силы. Поскольку тело является трехмерным объектом, внутренние силы внутри тело может быть визуализировано на кубе материала. Поэтому мы можем считать, что вектор силы тяги действует внутри и в произвольном направлении на каждая из трех граней куба:

Каждый вектор тяги в 3D будет состоять из трех компонентов. Эти три компонента могут быть показаны ниже на кубе:

Обратите внимание, что, поскольку мы имеем дело с механикой сплошной среды, мы предполагаем, что объем куба можно последовательно уменьшить до точки, если объем однородный. В действительности это, как правило, не так, особенно в биологических тканях. Однако понятие стресса, определенное таким образом, все еще очень полезен для инженерного анализа механики тканей. Более продвинутые концепции многомасштабного континуального анализа рассматриваются в продвинутом курсе BME 456.

Когда показанный выше куб материала сжимается до бесконечно малой точки, то по три составляющие каждой из тяг векторы на грани куба становятся девятью компонентами напряжения второго порядка тензор . Важно отметить, что этот тензор напряжений всегда определяется в деформированном состоянии материала и известен как Коши тензор напряжений . Это определение станет важным, когда мы будем иметь дело с механика малых и больших деформаций. Тензор напряжений Коши 2-го порядка может быть записано в матричной форме как:

IV. Связь тензора напряжений Коши с приложенными силами

      Естественный вопрос заключается в том, как Тензор напряжения относится к приложенным силам. Чтобы ответить на этот вопрос, мы можем обратимся к анализу, впервые проведенному А. Л. Коши, известному как стресс Коши. тетраэдр. Рассмотрим тетраэдр с произвольно вырезанной наибольшей гранью. внутри интересующего тела:

Из тетраэдрической геометрии мы можем вывести тот факт, что три компонента вектора нормали n лежат вдоль осей x1, x2 и x3. Эти компоненты можно записать так:

Мы также можем видеть, что высота тетраэдра ON с длиной h, катет каждого из трех прямоугольных треугольников ANO, BNO и CNO с гипотенузами ОА, ОБ, ОС. Таким образом, длину h также можно записать как:

Мы также знаем из базовой геометрии, что объем тетраэдра равен единице. третий базовый раз. Если мы сначала рассмотрим высоту как h, мы можем написать тетраэдрический объем как:

Если мы далее рассмотрим высоту как OA и основание S1, мы получим:

Следуя той же цепочке рассуждений для OB и OC, мы получаем:

h к каждой из нормальных компонент, которые у нас есть:

Аналогично, мы можем написать отношения:

Эти геометрические соотношения будут полезны для установления баланса сил, как описано далее.

Произвольно ориентированный вектор тяги на наибольшей грани, которая уравновешивается векторами тяги на трех ортогональных гранях:

Известно, что каждая из сил тяги, с, с1, с2 и с3 have — это векторы, компоненты которых могут быть отображены вдоль трех ортогональных оси. Тогда мы можем, согласно 1-му закону физики Ньютона, записать баланс сил с точки зрения каждой из этих составляющих. Так как поверхностные силы считаются на единицу площади, мы должны умножить каждую составляющую поверхностного сцепления по площади поверхности, на которую он воздействует. Кроме того, поскольку массовые силы считаются на единицу массы, мы должны умножить силы тела на массу. Таким образом, мы можем запишите баланс сил в направлении x1 как:

мы можем записать баланс сил в направлениях x2 и x3 как:

 

мы получили из тетраэдрической геометрии, мы получаем:

Поскольку дельта S теперь умножает все члены, мы можем разделить дельту S из оставшиеся уравнения:

Теперь, поскольку мы работаем в предположении континуума, мы предположим что мы можем сжать тетраэдр в точку и что материал содержит внутри тетраэдра останется однородным. Кроме того, поскольку тяга векторы s и t представляют собой средние силы по площадям лица, здесь средние будет сходиться к одному значению по мере уменьшения объема тетраэдра до нуля. Таким образом, в пределе площади основания и высота тетраэдра приблизится к нулю. Любые члены, умноженные на высоту или площадь основания, будут становится нулем в пределе. В приведенных выше уравнениях условия объемной силы становятся ноль, когда мы сжимаем тетраэдр. Остается следующее:

Здесь мы отмечаем, что три компонента вектора тяги на ортогональных поверхностях существенно эквивалентен тензору напряжений 2-го порядка при сжатии тетраэдра до точки. Таким образом, мы можем записать три составляющие трех тяг векторы как компоненты девяти элементов Тензор напряжений 2-го порядка и переписать уравнения баланса сил как (помещая компоненты тензора напряжений в правую часть уравнения):

Поскольку грань n является произвольной плоскостью, мы можем опустить верхний индекс n и просто напишите:

Если мы рассмотрим приведенное выше векторное уравнение тягового напряжения, мы увидим, что оно может быть непосредственно записана в виде индекса:

. поскольку N на исходном тетраэдре может естественным образом встречаться на внешнем поверхность тела. В этом состоянии мы признаем, что вектор тяги представляет собой приложенное поверхностное сцепление, поэтому уравнение связывая вектор тяги с внутренним напряжением и нормаль к поверхность может связать поверхностное сцепление с внутренним напряженным состоянием. Позже мы увидим, что это соответствует граничному условию для уравнение равновесия напряжений в частных производных.

V. Вывод основных уравнений равновесия и симметрии тензор напряжения Коши

    Теперь, когда у нас есть понимание тензора Коши тензора напряжений, получим основное уравнение равновесия напряжений. Для начала давайте сначала снова рассмотрим небольшой куб материала внутри тело. Если учесть, что на тело действуют напряжения, то начертим куб материала и посмотрите сначала на баланс сил в направлении x. Сюда относятся силы напряжения, возникающие на единицу площади, умноженные на площадь грани куба и приложенная сила тела:

где s11 — нормальное напряжение на плоскости перпендикулярно оси x1, s21 — сдвиг напряжение в плоскости, перпендикулярной оси x2, действующее в направлении x1, s31 — касательное напряжение в плоскости, перпендикулярной к оси x3, действующей в направлении x1. В общем, сид представляет собой напряжение, действующее на плоскость, перпендикулярную оси xi в направление оси xj. Таким образом, действует s11. на плоскости, перпендикулярной оси x1 в направлении x1. В списке выше b — общая объемная сила. Только b1 составляющая объемной силы входит в баланс сил в направлении х. Теперь мы можем написать баланс сил в направлении х с учетом двух фактов. Во-первых, стресс определяется как сила на единицу площади, поэтому, чтобы получить силу, мы должны умножить напряжение на площадь плоскости, на которую он действует. Таким образом, площадь плоскости, перпендикулярной к оси x1 равно , площадь плоскости, перпендикулярной x2, равна , а плоскость, перпендикулярная x3, имеет площадь . Далее мы отмечаем положительные и отрицательные силы в одном и том же направлении. разделены , , или . с11 действует по месту нахождения. Если мы сложим все действующие силы, включая компонент x1 силы объемная сила b получаем:

            

, где важно отметить, что представлено все умножение членов звездочкой *. Затем мы разделим приведенное выше уравнение на величину **, объем получаемого бесконечно малого куба:

                                  

Далее, поскольку мы используем принципы механики сплошных сред, пусть размер инкрементного куба в пределе уменьшается до нуля . Обратите внимание, что объем куба не становится нулем , а приближается к нулю. В этом случае величины с участием сил, действующих в разных направлениях оказываются частными производными напряжений по направлению знаменателя. Например,

           

Точно так же мы можем определить производную для других членов как:

Используя это определение для всех членов, мы получаем уравнение равновесия в x1: направление как:

                          

Теперь рассмотрим баланс сил в направлении x2:

пусть объем куба стремится к нулю, мы имеем:

              

Наконец, если мы посмотрим на баланс сил в направлении x3, мы получим:

             

Мы можем записать уравнение баланса сил в направлении x3 в виде:

              

Снова делим на бесконечно малый объем и приближаем объем нуля, чтобы получить:

                  

Таким образом, мы можем видеть, что если мы уравновешиваем внутренние силы на бесконечно малой кусок материала внутри тела, мы получаем три уравнения, которые определяют напряженное состояние, предполагая, что у нас есть активная объемная сила:

                  

                  

                   

и в первом индексе три уравнения. Следовательно, мы можем написать приведенные выше три уравнения в обозначении индекса как:

                  

Симметрия напряжений:

     Помимо баланса сил, первый закон также гласит, что любой момент на бесконечно малом кубе должен уравновеситься. Позволять рассмотрим баланс моментов, обусловленный компонентами тензора напряжений относительно каждого трех ортогональных осей, также называемых балансом углового момента. Мы сначала рассмотрим момент относительно оси x1:

Теперь запишем момент, создаваемый напряжением s32. s32 действует на грань, площадь которой равна delta x1*delta x2, поэтому общая сила, действующая на s32 это:

Плечо момента — это расстояние до середины куба, деленное на 3 дельты на 2. Таким образом, общий момент равен:

Нормальные напряжения не вызывают момент, так как они имеют плечо момента нуля. Если мы запишем баланс моментов для четырех касательных напряжений, получаем:

Далее рассмотрим моменты, возникающие на плоскостях, перпендикулярных оси x1 и x3:

                        

Суммарный момент, связанный с напряжением s13 составляет:

                                        

, где первые два дельта-х члена представляют собой площадь плоскости, а последний термин — это плечо момента. Теперь мы можем сбалансировать моменты в плоскости x2 из-за этим касательным напряжениям. Важно отметить, что на бесконечно малом куба нет внешних приложенных моментов (существуют континуальные теории предполагающие моменты на этом уровне, но они не получили широкого распространения и выходит за рамки этих заметок). Таким образом, баланс моментов в x2 направление ведет к:

                 

Вероятно, у вас уже есть идея, поэтому мы пропустим момент баланса о ось х3. Суть в том, что баланс углового момента дает нам получается, что тензор напряжений симметричен:

                   

VI. Инварианты стресса и что они означают

    Теперь, когда мы определили стресс как второй порядок тензор и уравнения равновесия, управляющие напряжением, мы кратко рассмотрим при инвариантах тензора напряжений. Напомним, что тензоры второго порядка, такие как тензор напряжения Коши изменит значение при обращении к другому системы координат. Инварианты — это скалярные функции тензоров, которые по определению имеют одно и то же значение независимо от системы координат, к которой они относятся. Важно понимать инварианты напряжения, поскольку они будут играть роль в разработке определяющих уравнений, особенно для мягких тканей, которые часто считается несжимаемым. Напомним из раздела 1 общее определение инвариантов для тензора второго порядка. Если мы просто заменим обозначение A для тензора второго порядка с s для тензора напряжений Коши имеем:

      

Как уже упоминалось, инварианты тензора напряжений имеют физический смысл. Первый инвариантом является гидростатическое напряжение или давление. Это играет важную роль в тканях, которые считаются несжимаемыми. несжимаемость означает, что каким бы высоким ни было гидростатическое давление, оно не вызовет объемная деформация. Второй инвариант связан с напряжением сдвига. Фактически октаэдрическое касательное напряжение вычисляется из второго инварианта как:

             

VII. Резюме

    В этом разделе мы разработали 2-й порядок Тензор напряжений Коши и выведенные уравнения равновесия напряжений и напряжения симметрия. Важно резюмировать, что уравнения равновесия напряжений иметь в виду. Во-первых, заметим, что мы не делали никаких предположений о характере материала, когда мы вывели уравнения равновесия напряжений. Поэтому, эти уравнения справедливы для любого материала, включая любую биологическую ткань. Во-вторых, мы не указывали величину деформации при выводе Коши. напряжения или уравнения равновесия напряжений. Таким образом, эти уравнения справедливы для Любая деформация. Однако важно помнить, что оба тензор напряжений Коши, и уравнения равновесия напряжений должны быть решены в деформированном состоянии материала. Мы узнаем позже в следующем разделе номенклатура деформированных и недеформированных, а также мелких и крупных деформация. Мы увидим, что в действительности для решения больших задач деформации которые являются нормой для механики мягких тканей, нам нужно будет получить больше тензоры напряжений и изменить уравнения равновесия напряжений. Наконец, это важно учитывать уравнения равновесия напряжений, показанные ниже. и что они означают. В компактном обозначении индекса равновесие трех напряжений уравнения для 3D (было бы два уравнения для 2D) записываются как:

Имеется три уравнения, так как i является независимым индексом и принимает значения от 1 до 3. Обратите внимание, что с учетом нашего определение оператора дивергенции, приведенные выше уравнения можно записать Символически как:

, которые могут быть расширены по мере:

Со следующим границей тяги:

.0032

Теперь давайте посмотрим, сколько неизвестных в приведенном выше уравнении. По сути, наша цель при анализе напряжения ткани состоит в том, чтобы решить проблему стресса. уравнение равновесия для тела, на которое действует данная объемная сила b и поверхностное сцепление т. Следовательно, оба b (если есть) и t должно быть дано для того, чтобы у нас был хотя бы шанс теоретически решить проблема. Когда мы пытаемся решить полномасштабную 3D-задачу, мы немедленно видим, что даже с учетом симметрии напряжений остается шесть неизвестных (три нормальное и три напряжения сдвига), а только три уравнения. Учитывая, что число уравнений меньше числа неизвестных, имеем неопределенное проблема, а это значит, что решение, если мы его вообще найдем, не будет быть уникальный. То есть будет более одного решения, которое удовлетворит задача равновесия напряжений в 3D. Таким образом, мы, очевидно, не можем найти истинное решение, если мы не сделаем одну из трех вещей:

1. Мы можем упростить проблему на основе разумных предположений (или это догадки?) так что количество неизвестных сводится к равному количество уравнений. По этой причине проводятся испытания материалов. с образцами простой геометрии, так что мы можем упростить напряженное состояние к одноосным (одно напряжение) или двухосным (2-3 напряжения). Очевидно, будет будет много случаев, в которых этот подход не будет работать.

2. Мы можем дополнить уравнения равновесия напряжений с дополнительными уравнения и дополнительные неизвестные, пока мы не сможем сбалансировать количество уравнений и неизвестные.

3. Мы можем оптимизировать , в котором мы признаем, что более одного решения существует, но мы определяем критерии, по которым выбираем лучшее решение .

Получается для механики деформируемого тела, номер варианта выбираем 2. При выборе варианта № 2 дополняем напряжения как неизвестные деформации и смещения, которые являются кинематическими переменными. Мы найдем, что вариант №3 используется, когда нет возможности добавить дополнительные переменные и неизвестные.