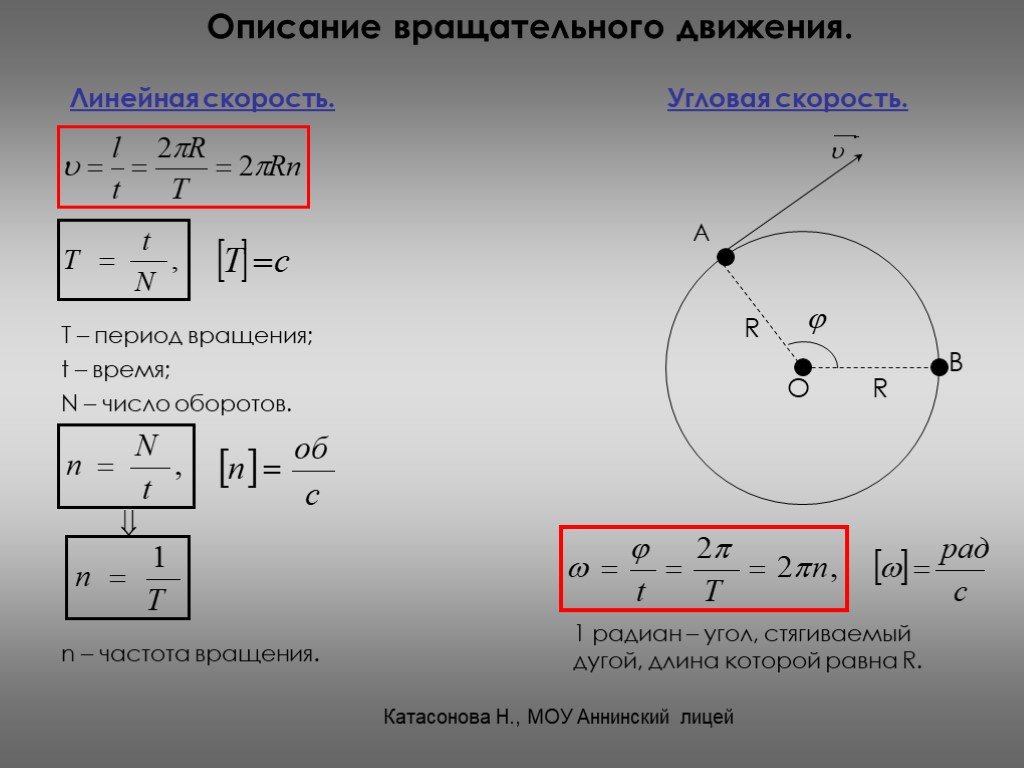
Определить угол поворота и прогиб сечения В консольной балки
Пример задачи 5.15
Определить угол поворота и прогиб сечения В консольной балки (в долях от жесткости сечения ), рис. 5.28.
Решение
Эпюра изгибающих моментов от заданной нагрузки (грузовая эпюра ) показана на рис. 5.28, а.
Для определения прогиба в сечении В к свободной от заданной нагрузки балке (вспомогательное состояние) в названном сечении прикладывается вспомогательная единичная сосредоточенная сила (F = 1) и строится эпюра изгибающих моментов — единичная эпюра (рис. 5.28, б). Единичная сила направляется произвольно, т. е. в положительном или отрицательном направлении оси У.
Аналогичная операция производится для определения угла поворота сечения. Только в качестве вспомогательной единичной силы выступает единичный вспомогательный момент ( Эпюра от единичного момента показана на рис. 5.28, в.
Эпюра от единичного момента показана на рис. 5.28, в.
На рис. 5.28, б и в схема балки и единичные эпюры совмещены. Заметим, что балка имеет один расчетный участок как для ,
так для и что единичные эпюры прямолинейны и имеют вид треугольника или прямоугольника, а грузовая — криволинейна и имеет сложное очертание.
Для определения перемещений по способу Верещагина используются эпюры изгибающих моментов (грузовые и единичные). От одних из них берутся площади эпюр (), из других — ординаты (у) под центром тяжести первых. Поскольку грузовая эпюра имеет криволинейное очертание, площадь должна браться с этой эпюры.
Для проведения расчета эпюра сложного очертания делится на простые фигуры: прямоугольник (от момента М) площадью
и параболический треугольник (от нагрузки q) площадью
На выделенных простых фигурах отмечаются их центры тяжести (см. табл. 5.1).
табл. 5.1).
На единичных эпюрах отмечаются ординаты у, лежащие под центром тяжести составляющих частей грузовой эпюры . В данном примере ордината определяется как
Для определения углов поворота сечений ординаты берутся из единичной эпюры :
Прогиб в сечении В по формуле (5.12):
Все слагаемые в выражении прогибов положительны, так как площади и ординаты у лежат по одну сторону от оси эпюры. Положительные значения означают, что прогиб происходит в направлении единичной силы, т. е. вниз.
Угол поворота сечения В
В полученном выражении слагаемые отрицательны, так как площади и ординаты  5.28, г).
5.28, г).
Эпюра прогибов показана на рис. 5.28, г.
Таким образом, перемещения на свободном конце балки (в долях от жесткости сечения) (по ходу часовой стрелки), (вниз).
Этот пример решения задачи взят со страницы решения задач с примерами по всем темам предмета «Сопротивление материалов»:
Примеры решения задач по сопротивлению материалов
Дополнительные задачи которые вам будут полезны:
Определение угла поворота на шарнирной опоре балки с жестким защемлением на второй опоре
Для статически неопределимых балок, например для однопролетной балки с одной шарнирной опорой и второй опорой — жестким защемлением, я при составлении таблиц с расчетными схемами углы поворота на шарнирных опорах не указывал. Впрочем, определить такой угол наклона не сложно, для этого достаточно воспользоваться уравнением начальных параметров:
θх = — θA + МАх/EI + Ax2/2EI — qx3/6ЕI (173.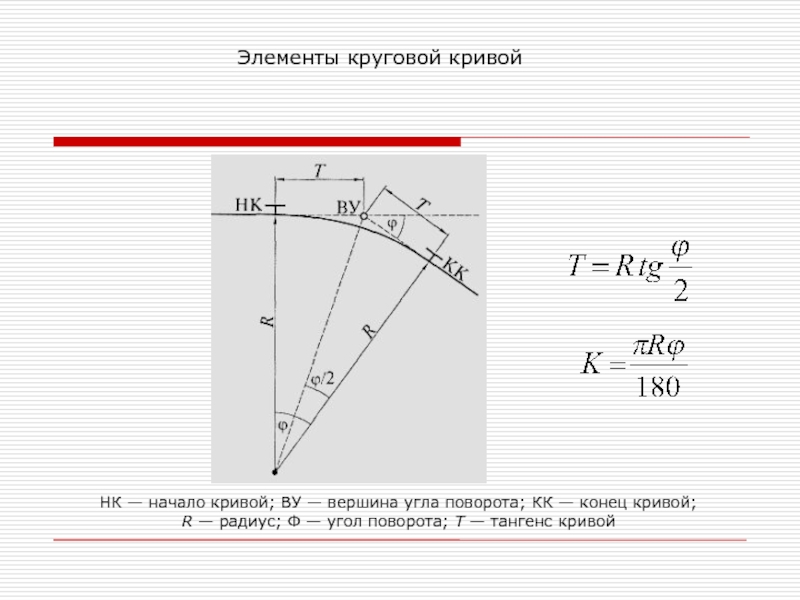 1)
1)
Так если у балки жесткое защемление на опоре А (соответственно θА = 0), а на шарнирной опоре В приложен только изгибающий момент М и больше никаких нагрузок не действует, то уравнение начальных параметров в точке В будет иметь вид:
θВ = МАl/EI + Al2/2EI (492.1)
Согласно таблицы 2, расчетная схема 3.1: МА = М/2, -А = 3М/2l, то
θВ = Мl/2EI — 3Мl2/(2l(2EI)) = -Ml/4EI (492.2)
В данном случае знак «-» означает, что если момент М на опоре В будет отрицательным, т.е. направлен так, как показано на расчетной схеме 3.1, то сечение в точке В будет повернуто по часовой стрелке относительно оси z и будет отрицательным, как ни странно это звучит. Другими словами, отрицательный момент на опоре В в итоге дает отрицательное значение угла поворота на этой же опоре.
Если момент на опоре В будет положительным, то значения момента на опоре А и опорной реакции следует подставлять с обратными знаками. В итоге сечение в точке В будет повернуто против часовой стрелки относительно оси z и будет положительным. Т.е. положительное значение момента на опоре В означает положительное значение угла поворота на этой же опоре.
В итоге сечение в точке В будет повернуто против часовой стрелки относительно оси z и будет положительным. Т.е. положительное значение момента на опоре В означает положительное значение угла поворота на этой же опоре.
Как видим, самое сложное в подобном расчете — это правильно разобраться со знаками.
Если же на рассматриваемую балку кроме изгибающего момента действуют другие нагрузки, то можно воспользоваться принципом суперпозиции, т.е. определить по соответствующей расчетной схеме все необходимые данные, затем определить угол наклона для выбранного типа загружения, а затем полученные значения углов наклона сложить с учетом знаков.
Например, если на рассматриваемую балку кроме изгибающего момента на опоре В будет действовать равномерно распределенная нагрузка по всему пролету l. Для такой балки согласно расчетной схеме 2.1: А = 5ql/8, МА = -ql2/8. Тогда
θВ = -ql3/8EI + 5ql3/16EI — ql3/6ЕI = ql3(-6 + 3·5 — 8)/48EI = ql3/48EI (492. 3)
3)
В данном случае положительное значение угла наклона в точке В означает. что поперечное сечение будет повернуто против часовой стрелки относительно оси z.
В итоге, если значение момента на опоре В имеет некоторое вполне определенное значение, например, МВ = -ql
ΣθВ = -ql3/(16·4EI) + ql3/48EI = ql3(-3 + 4)/192EI = ql3/192EI (492.4)
Если на рассматриваемую балку действуют еще какие-либо нагрузки, то определить суммарный угол поворота на опоре В можно, воспользовавшись выше приведенными предпосылками.
Как правильно выбрать датчик угла поворота
Датчик угла поворота марки BaumerИнкрементальный энкодер измеряет угловое перемещение относительно опорной позиции. После сбоя питания система обработки данных должна дождаться, пока энкодер отправит информацию, соответствующую изначальной позиции, чтобы иметь возможность правильно использовать информацию, связанную с угловым смещением.
Инкрементальные энкодеры разработаны с использованием различных технологий, каждая из которых имеет свои преимущества и недостатки. Наиболее используемые технологии :
• Магнитные инкрементальные энкодеры: импульсы испускаются магнитами. Эта технология также широко распространена в промышленности, потому что магнитные энкодеры менее подвержены риску загрязнения.
Независимо от принципа работы энкодера, выходной сигнал представляет собой последовательность импульсов, которая представляет собой двоичное кодирование, то есть последовательность 1 и 0, которая соответствует угловому смещению, в зависимости от разрешения энкодера.
В случае инкрементальных энкодеров вы можете подключить провода энкодера к входам автомата. Входы, которые будут использоваться, определяются рабочей частотой энкодера. Эта частота пропорциональна скорости вращения оси и разрешению энкодера. В случае повышенной частоты сигнал, соответствующий изначальной позиции, позволяет исправить ошибки в подсчетах некоторых импульсов.
Как правило, датчик угла поворота оснащен 5-12 выходами (проводами или клеммами разъема), которые должны быть подключены к счетчику. В случае энкодера с 5 выходами два провода используются для электропитания, а три других — для отправки сигналов, соответствующих угловому смещению.
Вращательное движение
Вращательное движение является периодическим движением.
Период обозначается буквой T.
Чтобы найти период обращения, надо время вращения разделить на число оборотов:
|
Частота вращения обозначается буквой n.
Чтобы найти частоту вращения, надо число оборотов разделить на время, в течение которого эти обороты совершены:
Частота вращения и период обращения связаны друг с другом как взаимообратные величины: Период измеряется в секундах: [T] = 1 с.
Единица частоты – секунда в минус первой степени: [n] = 1 с–1.
Эта единица имеет собственное название – 1 герц (1 Гц).
Проведем аналогию между вращательным и поступательным движениями.
Поступательно движущееся тело изменяет свое положение в пространстве относительно других тел.
Тела, совершающие вращательное движение поворачиваются на некоторый угол.
Если за любые равные промежутки времени поступательно движущееся тело совершает равные перемещения, движение называется равномерным.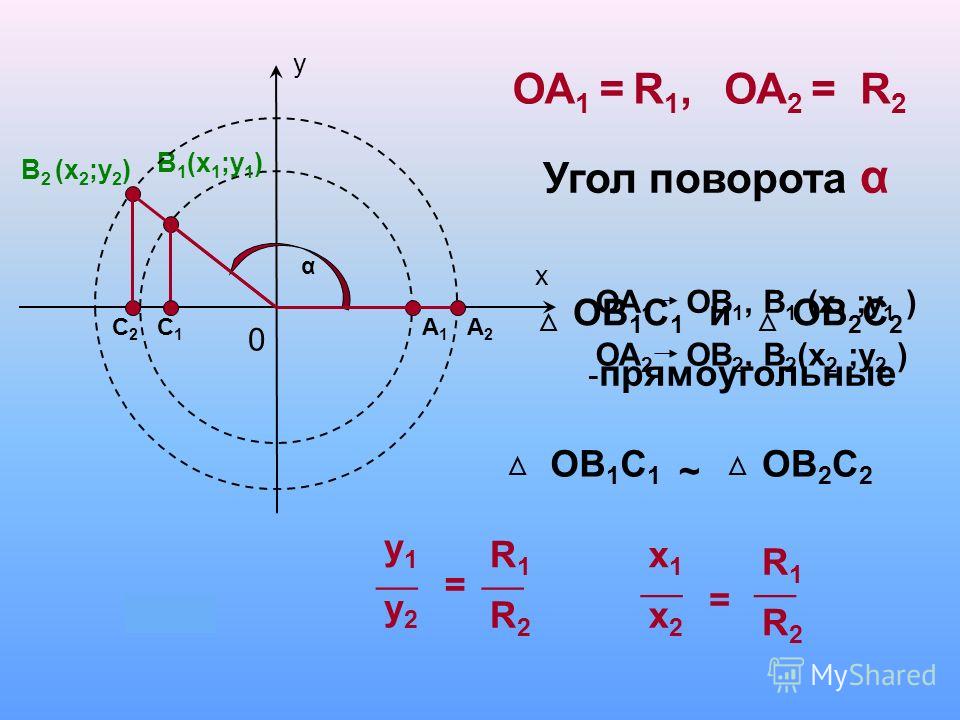
Если за любые равные промежутки времени вращающееся тело поворачивается на один и тот же угол, то такое вращение называется равномерным. Характеристикой равномерного поступательного движения служит скорость Соответствующей характеристикой вращательного движения служит угловая скорость:
Угловая скорость – это физическая величина, равная отношению угла поворота тела ко времени, в течение которого этот поворот совершен.
Угловая скорость показывает, на какой угол поворачивается тело за единицу времени.
Чтобы получить единицу угловой скорости, нужно в ее определяющую формулу подставить единицу – 1 радиан, и времени – 1 с. Получаем: [ω] = 1
Аналогично можно ввести характеристику неравномерного вращения. Если видом неравномерного поступательного движения является равнопеременное движение, то для вращательного движения можно ввести понятие равнопеременного вращения.
Характеристикой равнопеременного поступательного движения является ускорение:
|
Продолжая аналогию дальше, запишем уравнение для перемещения при прямолинейном равноускоренном движении
Так как при вращении перемещению тела соответствует угол вращения, линейной скорости – угловая скорость, линейному ускорению – угловое ускорение, то аналогичное уравнение для вращательного движения будет иметь вид:
Другому уравнению для поступательного движения будет соответствовать уравнение для вращательного движения:
Метод, который использовался в данном случае, называется методом аналогий.
Точки тела, совершающего вращательное движение, поворачиваются относительно оси вращения на некоторые углы и движутся по дугам окружностей, проходя определенные пути. Таким образом, характеристиками вращательного движения являются и угловая, и линейная скорости.
Линейная скорость точки направлена по касательной к окружности, по которой она движется.
Об этом свидетельствует слетающая с колес автомобиля грязь или искры, летящие от металлического предмета, прижатого к наждачному кругу.
Чем дальше от оси вращения находится точка, тем больше ее линейная скорость. Угловая же скорость точек, лежащих на одном радиусе, одинакова. Следовательно, линейная скорость точки прямо пропорциональна радиусу окружности, по которой она вращается.
За время, равное периоду, точка проходит путь, равный длине окружности. Её линейная скорость при этом равна Отношение же угла поворота ко времени поворота на этот угол равно угловой скорости
Таким образом, линейная скорость вращающейся точки связана с ее угловой скоростью соотношением:
При равномерном вращении скорость меняется по направлению, но не изменяется по величине.
|
Пусть вращающееся тело в начальный момент времени находится в точке A и скорость его направлена по касательной. В следующий момент времени тело находится в точке B. При этом скорость его изменилось только по направлению и направлена по касательной к окружности.
Найдем вектор разности скоростей, воспользовавшись правилом действия с векторами. Из чертежа видно, что вектор разности направлен в сторону близкую к центру окружности. Чем меньше угол поворота, тем ближе направлен вектор скорости
к направлению на центр вращения.
При малом времени движения изменение положения тела незначительно. Поэтому можно считать, что вектор скорости характеризующий изменение скорости по направлению, направлен на центр. Отсюда и происходит название центростремительного ускорения.
Угловое же ускорение, характеризующее изменение скорости по величине, называют еще касательным или тангенциальным ускорением (при неравномерном вращении).
Получим выражение для центростремительного ускорения. Будем считать, что угол поворота очень мал. Соединим точки A и B. Угол MAN = φ по построению.
Мы имеем два равнобедренных треугольника. Треугольник OAB, ребра которого R и AB, и треугольник MAN, ребра которого и
Так как треугольники подобны (по двум сторонам и углу между ними), то можно записать:
Дуга окружности и хорда практически равны из-за малости угла поворота. Поэтому дуга Следовательно, Получим
Разделив правую и левую части последнего уравнения на t, получим:
Отсюда Таким образом,
Полученная формула является формулой для расчета центростремительного ускорения.
Центростремительное ускорение, при движении тела по окружности, равно отношению квадрата скорости к радиусу окружности, по которой движется тело:
Углы поворота на опора — Энциклопедия по машиностроению XXL
Углы поворота на опоре прогиб в середине пролета [c.185]Для построения эпюр Q x) w w (x) вычислим углы поворота по концам балки, а также прогиб посредине пролета w l/2) = f. Углы поворота на опорах найдем из уравнения (10.61). При х = 0 получим величину угла поворота на левой опоре [c.295]
Определить прогибы и углы поворота на опорах, посередине балки и в точках приложения сил Р. [c.125]
Задача 7.6 (к 7.13, 7.14). Определить прогиб посредине пролета и углы поворота на опорах для деревянной балки прямоугольного сечения (рис. 7.87). Высота сечения балки равна 20 см, а ширина 12 см. Модуль упругости =10 МПа. [c.333]
Углы поворота на опорах [c.
 86]
86]Требуется определить углы поворота на опорах а ч Ь —обозначаем их 6 4 и (ig, а также в сечениях с (в условной точке приложения силы к зубу шестерни) и близко к условной точке приложения нагрузки к валу от ступицы зубчатого колеса) — обозначим их и Ьр прогибы требуется определить в сечениях с ч d — обозначаем их У(2 и ур. Используем схемы нагружения вала (фиг. 16) в плоскостях XZ и XV. [c.156]
Предельно допустимые перемещения детали определяются условиями работы ее в узле. Для валов, например, предельно допустимые углы поворота на опорах могут определяться перекосом колец подшипников качения [1] и защемлением тел качения углы поворота вала в месте установки зубчатых ко- [c.71]
Таково значение наибольшего угла поворота (на опоре). Подставляем его в уравнение прогиба [c.185]
Деля Лф и Вф на жесткость ЕУ, получаем углы поворота на опорах [c.188]
Углы поворота на опорах простой балки
[c. 214]
214]
Для определения углов поворота на опорах двухопорной статически определимой балки удобно применение графоаналитического метода. [c.214]
Пример 14. Найти прогиб и угол поворота посредине пролета в точке с балки, представленной на рис. 7.58, а, и углы поворота на опорах. [c.216]
Если балку АВ рассматривать как простую балку, то эпюра изгибающих моментов от нагрузки Р изобразится кривой (фиг. 247, б), а от опорных моментов — трапецией М о (фиг. 247, в). Пусть от действия первой нагрузки углы поворота на опорах А и В будут 9д и 0д, а от действия второй — 6д и При защемлении концевых сечений должно быть [c.248]
Обозначив через и У, моменты инерции сечений пролетов, ввА и Оде — углы поворота на опорах В только от нагрузок, действующих в пределах длин пролетов и /г, и учтя формулы (329) и (330), найдем [c.252]
Рис. 48. к определению перемещений при изгибе. Схемы испытываемых балок а — балка с консолями б — простая балка с установленным на ней зеркалом для измерения угла поворота на опоре Л в — консоль. [c.89]
[c.89]
Вычисляем значения углов поворота на опорах и максимальный прогиб [c.442]
Углекислоты пары 513 Углы поворота на опорах 72 [c.795]
Углы поворота на левой и правой опорах найдутся как [c.207]
Определение угла поворота на 1-й опоре при известном М, не представляет никакого труда. Перемножая эпюры (рис. 276), получаем [c.167]
Метод этот при большом числе участков балки приводит к решению системы уравнений с большим числом неизвестных постоянных. Эти постоянные определяются из условий равенства прогибов и углов поворота на границах соседних участков и из условий поведения балки на опорах. Однако, соблюдая некоторые условия и приемы составления и интегрирования уравнений изгибающих моментов по участкам, можно всегда сократить число неизвестных до двух. Это сильно упрощает задачу нахождения упругой линии балки, имеющей несколько участков.
[c. 251]
251]
При малых углах поворота упругую опору, изображенную на рис. 57, б, рассматривают как статически неопределимую симметричную раму (рис. 62), нагруженную весом Q и приложенным моментом М, при этом каждая из пластин будет нагружена моментом Mi = — и сжимающей силой Рх=- — . [c.115]
Пример 3. Требуется составить формулы для угла поворота на ле вой опоре и прогиба в точке С (под си. Юй Р) для ступенчатого свободно опертого вала (фиг. 57, а). [c.99]
Здесь А. и Вф— фиктивные опорные реакции (см. табл. 12), равные умноженным на EJ значениям углов поворота над опорами А п В лля балки при шарнирных опорах с заданной нагрузкой. [c.60]
У равнение, выведенное нами для расчета многоопорных звеньев, оси которых до деформации — прямые линии, будет в силе и для колена с опорами на разных уровнях, имеющего переломы на опорах. Для этого необходимо, чтобы углы поворота над опорами во время деформации щек кривошипа были одинаковы. Шейка кривошипа симметрично нагружена силой Р, вследствие чего перекоса колена не будет, а потому, не изменяя условия работы
[c.95]
Шейка кривошипа симметрично нагружена силой Р, вследствие чего перекоса колена не будет, а потому, не изменяя условия работы
[c.95]
Теорема взаимности перемещений позволяет значительно сократить объем вычислений при решении целого ряда практических задач. Например, можно без вычислений утверждать, что для приведенных на (рис.14.13) двух состояний балки т.е. прогиб под силой Р от действия сосредоточенного момента = 1 численно равен углу поворота на правой опоре от силы .=1- [c.210]
Шаргтрно опертая, по, концам стальная балка длиной 1 м нагружена моментами М [c.79]
Подобрать размеры балки прямоугольного ае чвимя, найти углы поворота на опора , прогиб под нагрузкой, а также наибольший про-гиб я его положение по отношении к левой опоре, если Р 4 кН, а 1 м, [О ]. 8 МПа, Е 10 ГПа, [c.83]
После того как определены опорные моменты, много-пролетная балка расчленяется на систему однопролетных балок, загруженных на опорах опорными моментами. Для получения уравнения частот собственных колебаний записывается значение углов поворота на какой-либо опоре балки для двух смежных пролетов. Приравняв последние, получаем уравнение, определяющее искомую частоту колебаний нераз резиой балки.
[c.88]
Для получения уравнения частот собственных колебаний записывается значение углов поворота на какой-либо опоре балки для двух смежных пролетов. Приравняв последние, получаем уравнение, определяющее искомую частоту колебаний нераз резиой балки.
[c.88]
Пример. 5. Требуется составить формулы для угла поворота на левой опоре и прогиба в точке С (под силой Р)для ступе/1члтого свободно опертого еала (фиг, 121, а). [c.89]
Для указанных на рисунке балок на двух опорах определить величину прогиба в сечении С и угла поворота на правой опоре В. Предварительно подобрать сечение каждой двутавровой балки из условия прочности при допускаемом напряжении 1600 Kzj M или воспользоваться данными о номерах двутавров, указанных в таблице с ответами. Предлагается два варианта загружения балки 1) TjM, Р—Л т, М—6 тм и 2) 9 = 4 rju, P—Q т, М=3тм. Пролет балок 1 — За — 6 м. На какую величину Ау изменится прогиб каждой балки, если учесть ее собственный вес
[c. 208]
208]
| Телефон : | 780-427-5318 | |
| (Composer d’abord le 310-0000 pour obtenir une ligne sans frais) | ||
| Телекопьер: | 780-427-1179 | |
| Курьерский адрес: | cshelpdesk@gov.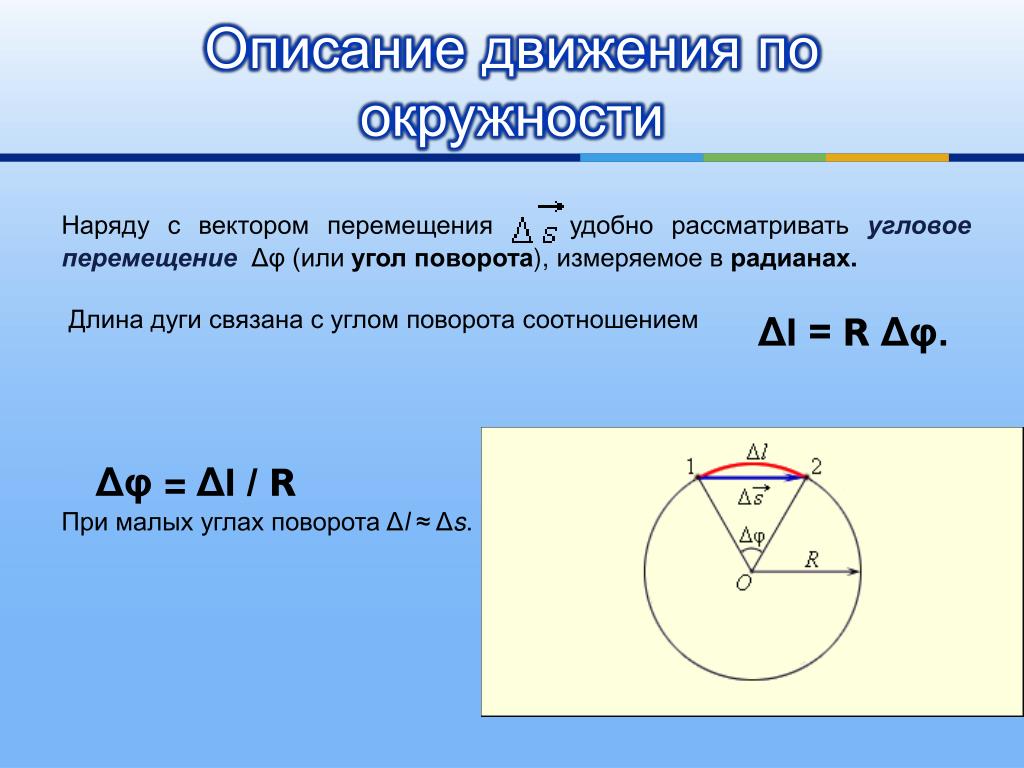 ab.ca ab.ca | |
6.1 Угол поворота и угловая скорость
Угловая скорость
Как быстро вращается объект? Мы можем ответить на этот вопрос, используя понятие угловой скорости. Сначала рассмотрим угловую скорость (ω)(ω) — скорость изменения угла поворота. В форме уравнения угловая скорость равна
6.2ω=ΔθΔt,ω=ΔθΔt,, что означает, что угловой поворот (Δθ)(Δθ) происходит за время ΔtΔt.Если объект поворачивается на больший угол поворота за заданное время, он имеет большую угловую скорость. Единицами угловой скорости являются радианы в секунду (рад/с).
Теперь давайте рассмотрим направление угловой скорости, а значит мы теперь должны называть его угловой скоростью. Направление угловой скорости вдоль оси вращения. Для объекта, вращающегося по часовой стрелке, угловая скорость направлена от вас вдоль оси вращения. Для объекта, вращающегося против часовой стрелки, угловая скорость указывает на вас вдоль оси вращения.
Для объекта, вращающегося против часовой стрелки, угловая скорость указывает на вас вдоль оси вращения.
Угловая скорость (ω) является угловой версией линейной скорости v . Тангенциальная скорость — это мгновенная линейная скорость объекта, находящегося во вращательном движении . Чтобы получить точное соотношение между угловой скоростью и тангенциальной скоростью, снова рассмотрим ямку на вращающемся компакт-диске. Эта яма движется по дуге (Δs)(Δs) за короткое время (Δt)(Δt), поэтому ее тангенциальная скорость равна
Из определения угла поворота Δθ=ΔsrΔθ=Δsr видно, что Δs=rΔθΔs=rΔθ.Подставляя это в выражение для v , получаем
. v=rΔθΔt=rω.v=rΔθΔt=rω. Уравнение v=rωv=rω говорит, что тангенциальная скорость v пропорциональна расстоянию r от центра вращения. Следовательно, тангенциальная скорость больше для точки на внешнем краю компакт-диска (с большими r ), чем для точки ближе к центру компакт-диска (с меньшими r ).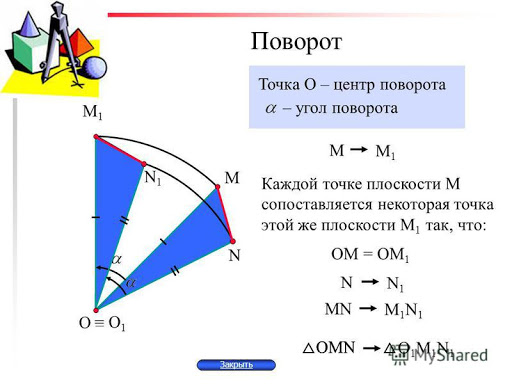 Это имеет смысл, потому что точка, расположенная дальше от центра, должна пройти большую длину дуги за то же время, что и точка, расположенная ближе к центру.Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. Рисунок 6.4.
Это имеет смысл, потому что точка, расположенная дальше от центра, должна пройти большую длину дуги за то же время, что и точка, расположенная ближе к центру.Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. Рисунок 6.4.
Теперь рассмотрим другой пример: шина движущегося автомобиля (см. рис. 6.5). Чем быстрее вращается шина, тем быстрее движется автомобиль — большое ωω означает большое против , потому что v=rωv=rω.Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ωω, создаст для автомобиля большую линейную (тангенциальную) скорость v, . Это связано с тем, что больший радиус означает, что более длинная дуга должна касаться дороги, поэтому автомобиль должен двигаться дальше за то же время.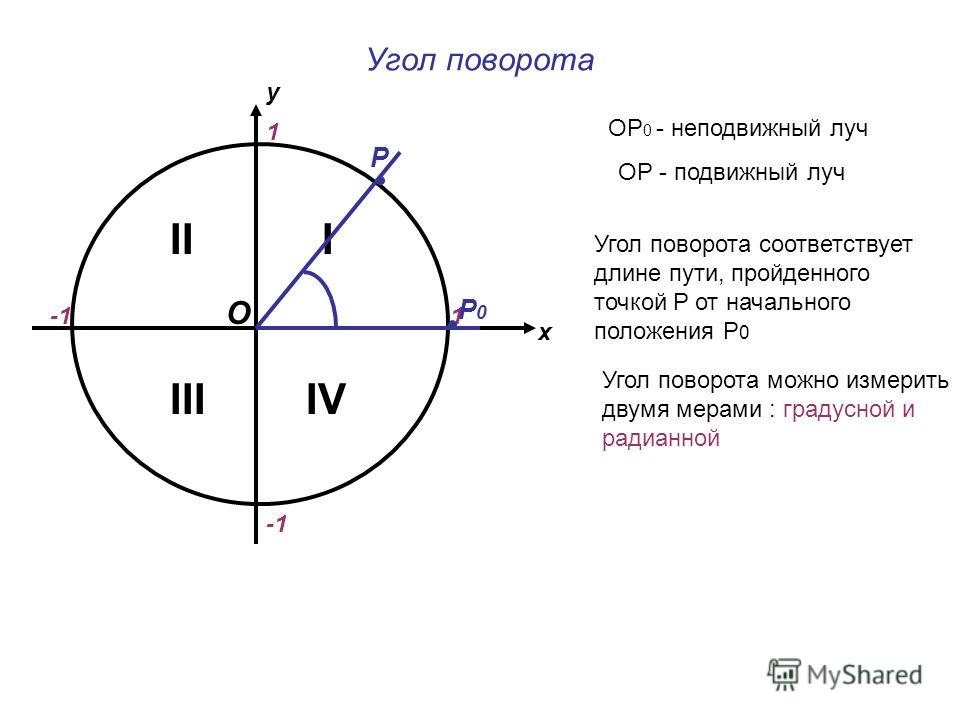
Однако бывают случаи, когда линейная скорость и тангенциальная скорость не эквивалентны, например, когда колеса автомобиля крутятся на льду.В этом случае линейная скорость будет меньше тангенциальной скорости. Из-за отсутствия трения под шинами автомобиля по льду длина дуги, по которой перемещаются протекторы шин, больше, чем линейное расстояние, по которому движется автомобиль.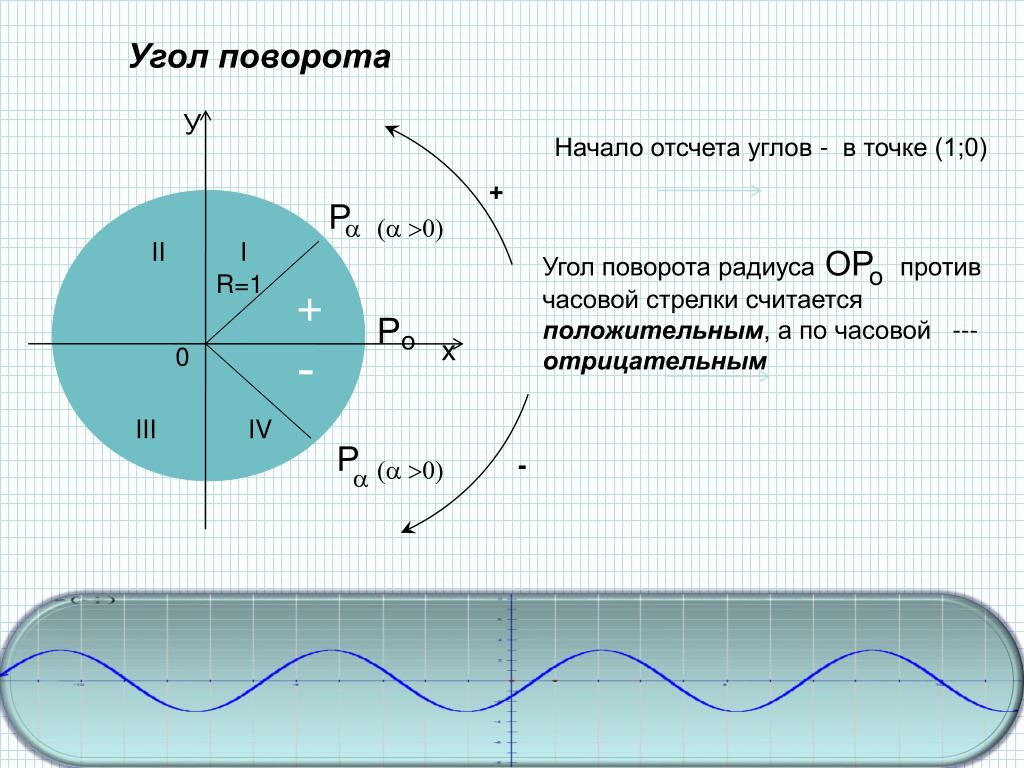 Это похоже на бег на беговой дорожке или вращение педалей на велотренажере; вы буквально никуда не денетесь.
Это похоже на бег на беговой дорожке или вращение педалей на велотренажере; вы буквально никуда не денетесь.
Советы для достижения успеха
Угловая скорость ω и тангенциальная скорость v являются векторами, поэтому мы должны указать величину и направление.Направление угловой скорости находится вдоль оси вращения и указывает от вас для объекта, вращающегося по часовой стрелке, и к вам для объекта, вращающегося против часовой стрелки. В математике это описывается правилом правой руки. Тангенциальная скорость обычно описывается как восходящая, нисходящая, левая, правая, северная, южная, восточная или западная, как показано на рис. 6.6.
Рис. 6.6 Когда муха на краю старой виниловой пластинки движется по кругу, ее мгновенная скорость всегда направлена по касательной к кругу.В этом случае направление угловой скорости находится на странице.
Watch Physics
Взаимосвязь между угловой скоростью и скоростью
В этом видео рассматривается определение и единицы измерения угловой скорости, а также их связь с линейной скоростью. Он также показывает, как конвертировать между оборотами и радианами.
Он также показывает, как конвертировать между оборотами и радианами.
Проверка захвата
Для объекта, движущегося по круговому пути с постоянной скоростью, изменится ли линейная скорость объекта, если радиус пути увеличится?
- Да, потому что тангенциальная скорость не зависит от радиуса.
- Да, потому что тангенциальная скорость зависит от радиуса.
- Нет, так как тангенциальная скорость не зависит от радиуса.
- Нет, потому что тангенциальная скорость зависит от радиуса.
Правила ротации | Обзор геометрии [Видео]
Привет и добро пожаловать в это видео о вращении! В этом видео мы рассмотрим вращение фигуры вокруг точки. Давайте узнаем о ротациях!
Вращения везде, куда ни глянь.Земля — наиболее распространенный пример, вращающийся вокруг оси. Колесо автомобиля или велосипеда вращается вокруг центрального болта. Эти два примера вращаются на 360°. Существуют и другие формы вращения, которые меньше, чем полное вращение на 360 °, например, персонаж или объект, вращающийся в видеоигре. Говоря более формально, вращение — это форма преобразования, при котором фигура поворачивается вокруг точки. Мы называем эту точку центром вращения . Фигура и ее вращение сохраняют ту же форму и размер, но смотрят в другом направлении.Фигуру можно вращать по часовой или против часовой стрелки. Еще один отличный пример вращения в реальной жизни — колесо обозрения, центральная ступица которого является центром вращения.
Эти два примера вращаются на 360°. Существуют и другие формы вращения, которые меньше, чем полное вращение на 360 °, например, персонаж или объект, вращающийся в видеоигре. Говоря более формально, вращение — это форма преобразования, при котором фигура поворачивается вокруг точки. Мы называем эту точку центром вращения . Фигура и ее вращение сохраняют ту же форму и размер, но смотрят в другом направлении.Фигуру можно вращать по часовой или против часовой стрелки. Еще один отличный пример вращения в реальной жизни — колесо обозрения, центральная ступица которого является центром вращения.
Мера, на которую фигура поворачивается вокруг центра вращения, называется углом поворота . Угол поворота обычно измеряется в градусах. Указываем градусную меру и направление вращения. Вот фигура, повернутая на 90° по часовой стрелке и против часовой стрелки вокруг центральной точки.
Отличный математический инструмент, который мы используем для отображения поворотов, — это координатная сетка. Давайте начнем с вращения точки вокруг центра (0,0). Если вы возьмете координатную сетку и нанесете точку, а затем повернете бумагу на 90° или 180° по часовой стрелке или против часовой стрелки вокруг начала координат, вы сможете найти положение повернутой точки. Давайте посмотрим на реальный пример, здесь мы нанесли точку A в (5,6), затем повернули бумагу на 90° по часовой стрелке, чтобы создать точку A’, которая находится в (6,-5).
Давайте начнем с вращения точки вокруг центра (0,0). Если вы возьмете координатную сетку и нанесете точку, а затем повернете бумагу на 90° или 180° по часовой стрелке или против часовой стрелки вокруг начала координат, вы сможете найти положение повернутой точки. Давайте посмотрим на реальный пример, здесь мы нанесли точку A в (5,6), затем повернули бумагу на 90° по часовой стрелке, чтобы создать точку A’, которая находится в (6,-5).
Вот та же точка A в (5,6), повернутая на 180° против часовой стрелки относительно начала координат, чтобы получить A’(-5,-6).
Давайте подробнее рассмотрим два вращения из нашего эксперимента.В нашем первом эксперименте, когда мы поворачивали точку A (5,6) на 90° по часовой стрелке вокруг начала координат, чтобы создать точку A’ (6,-5), значение y точки A стало значением x точки A’ и значение x точки A стало значением y точки A’, но с противоположным знаком.
В нашем втором эксперименте точка A (5,6) поворачивается на 180° против часовой стрелки вокруг начала координат, создавая точку A’ (-5,-6), где значения x и y такие же, как у точки A, но с противоположные знаки.
К счастью для нас, эти эксперименты позволили математикам придумать правила для наиболее распространенных поворотов на координатной сетке, приняв начало координат (0,0) за центр вращения.Вот правила поворота :
- Вращение на 90° по часовой стрелке: (x,y) становится (y,-x)
- Вращение на 90° против часовой стрелки: (x,y) становится (y,x)
- 180° вращение по часовой стрелке и против часовой стрелки: (x, y) становится (-x,-y)
- вращение на 270° по часовой стрелке: (x,y) становится (-y,x)
- вращение на 270° против часовой стрелки: (x,y) становится (y,-x)
Как видите, два наших эксперимента следуют этим правилам.
Примеры вращения
Теперь, когда мы знаем, как вращать точку, давайте рассмотрим вращение фигуры на координатной сетке.Чтобы повернуть треугольник ABC вокруг начала координат на 90° по часовой стрелке, мы должны следовать правилу (x,y) → (y,-x), где значение y исходной точки становится новым значением x, а значение x исходной точки исходная точка становится новым значением y с противоположным знаком. Давайте применим правило к вершинам, чтобы создать новый треугольник A’B’C’:
Давайте применим правило к вершинам, чтобы создать новый треугольник A’B’C’:
- A (-4, 7) станет A’ (7, 4)
- B (-6, 1) станет B’ ( 1, 6)
- C (-2, 1) становится C’ (1, 2)
Давайте посмотрим на другое вращение.Повернем треугольник ABC на 180° вокруг начала координат против часовой стрелки, хотя при вращении фигуры на 180° по часовой стрелке и против часовой стрелки используется то же правило, что (x,y) становится (-x,-y), где координаты вершин повернутый треугольник — это координаты исходного треугольника с противоположным знаком. Применим правило к вершинам, чтобы создать новый треугольник A’B’C’:
- A (2,7) станет A’ (-2,-7)
- B (2,1) станет B’ ( -2,-1)
- C (6,1) становится C’ (-6,-1)
Вот четырехугольник ABCD.Чтобы повернуть четырехугольник ABCD на 90° против часовой стрелки вокруг начала координат, мы воспользуемся правилом (x,y) превращается в (-y,x). Давайте применим правила к вершинам, чтобы создать четырехугольник A’B’C’D’:
- A (-8,-2) становится A’ (2,-8)
- B (-7,-7) становится B’ (7,-7)
- C (-2,-6) становится C’ (6,-2)
- D (-3,-2) становится D’ (2,-3)
Теперь Я хочу, чтобы вы сами попробовали несколько практических задач.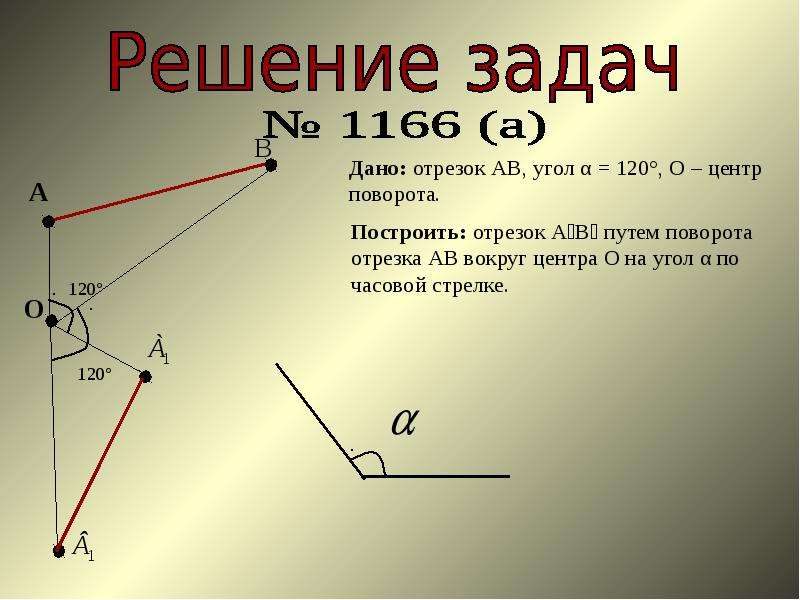 Воздушный змей KLMN показан на координатной сетке. Воздушный змей был повернут вокруг исходной точки, чтобы создать воздушный змей K’L’M’N’.Можете ли вы определить, какое вращение воздушного змея KLMN создало воздушный змей K’L’M’N’?
Воздушный змей KLMN показан на координатной сетке. Воздушный змей был повернут вокруг исходной точки, чтобы создать воздушный змей K’L’M’N’.Можете ли вы определить, какое вращение воздушного змея KLMN создало воздушный змей K’L’M’N’?
Начнем с определения координат вершин воздушного змея KLMN и нашего повернутого воздушного змея:
- K (-8,3) становится K’ (8,-3)
- L (-5,5) становится L ‘ (5,-5)
- M (-2,3) становится M’ (2,-3)
- N (-5,-3) становится N’ (5,3)
Пристальный взгляд на координаты вершин показывают, что координаты K’L’M’N’ такие же, как у исходного змея, но с обратным знаком.Давайте посмотрим на правила, единственное правило, при котором значения x и y не меняются, но меняется их знак, — это поворот на 180°.
- Вращение на 90° по часовой стрелке: (x,y) становится (y,-x)
- Вращение на 90° против часовой стрелки: (x,y) становится (-y,x)
- Вращение на 180° по часовой и против часовой стрелки: (x ,y) становится (-x,-y)
- Вращение на 270° по часовой стрелке: (x,y) становится (-y,x)
- Вращение на 270° против часовой стрелки: (x,y) становится (y,-x)
Таким образом, воздушный змей KLMN был повернут на 180° вокруг исходной точки, чтобы создать воздушный змей K’L’M’N’.
Давайте рассмотрим другую задачу. Пентагон QRSTU показан на координатной сетке. Поверните пятиугольник QRSTU на 90° против часовой стрелки, чтобы создать пятиугольник Q’R’S’T’U’.
Начнем с определения координат вершин нашего исходного пятиугольника. Правило для поворота на 90° против часовой стрелки: (x,y) становится (-y,x), давайте применим правило, чтобы найти вершины нашего нового пятиугольника.
(x,y) становится (-y,x)
- Q (-6,6) становится Q’ (-6,-6)
- R (-4,7) становится R’ (-7, -4)
- S (0,4) становится S’ (-4,0)
- T (-4,1) становится T’ (-1,-4)
- U (-6,2) становится U ‘ (-2,-6)
Теперь нанесем точки на координатную сетку и пометим вершины.
Последнее практическое задание. Трапеция PQRS, где P (-3,-5), Q (3, -5), R (5,-2) и S (-5,-2) повернута на 90° по часовой стрелке вокруг начала координат, образуя трапецию P ‘Вопросы’. Создайте обе трапеции на координатной сетке.
Мы начнем с решения, какое правило использовать для поворота на 90° по часовой стрелке вокруг начала координат. Мы собираемся использовать (x,y) в (y,-x). Теперь применим правило к координатам вершин PQRS.
Мы собираемся использовать (x,y) в (y,-x). Теперь применим правило к координатам вершин PQRS.
- P (-3,-5) становится P’ (-5,3)
- Q (3,-5) становится Q’ (-5,-3)
- R (5,-2) становится R ‘ (-2,-5)
- S (-5,-2) становится S’ (-2,5)
Теперь давайте нанесем точки и создадим трапеции на координатной сетке.
Надеюсь, этот обзор ротации был полезен! Спасибо за просмотр и удачной учебы!
Формула поворота вектора в 2D — Учебные пособия по визуализации, вычислениям и математике
\(\newcommand{L}[1]{\| #1 \|}\newcommand{VL}[1]{\L{ \ vec{#1}}}\newcommand{R}[1]{\operatorname{Re}\,(#1)}\newcommand{I}[1]{\operatorname{Im}\, (#1)}\ )
Допустим, у нас есть точка \((x_1, y_1)\). Точка также определяет вектор \((x_1, y_1)\).
Вектор \((x_1, y_1)\) имеет длину \(L\).
Поворачиваем этот вектор против часовой стрелки вокруг начала координат на \(\beta\) градусов.
Повернутый вектор имеет координаты \((x_2, y_2)\)
Повернутый вектор также должен иметь длину \(L\).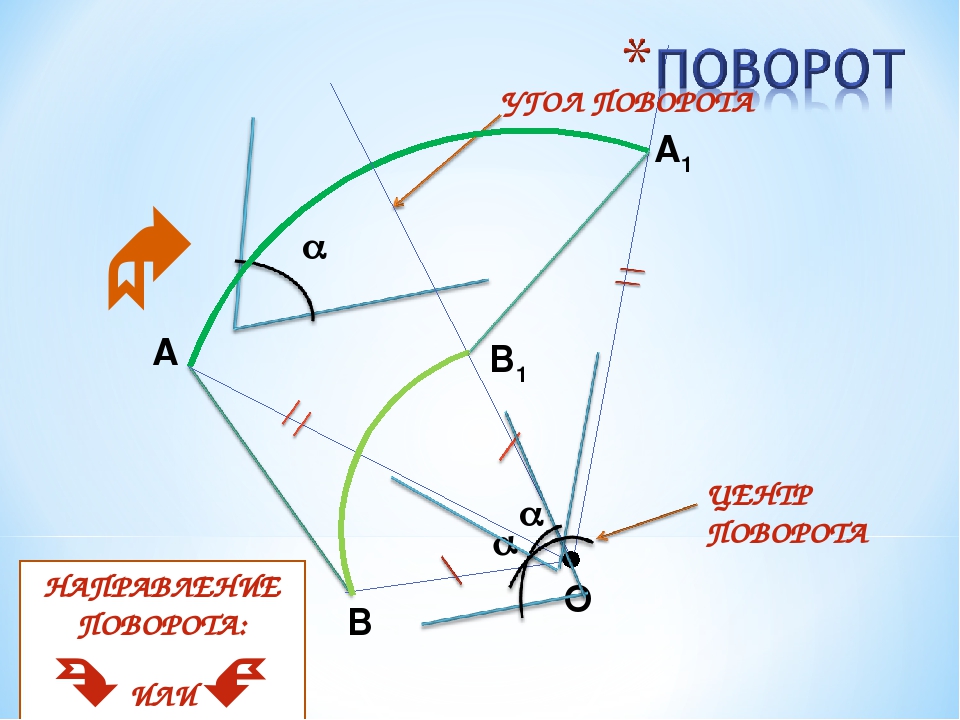
Теорема
\[\begin{split}x_2 = \cos\beta x_1 — \sin\beta y_1 \\ y_2 = \sin\beta x_1 + \cos\beta y_1\end{split}\]
См.: Википедия о матрицах вращения.
Предварительные занятия
Вызовите угол между \((x_1, y_1)\) и осью x: \(\alpha\).Тогда:
(1)\[\begin{split}x_1 = L \cos(\alpha) \\ y_1 = L \sin(\alpha)\end{split}\]Поворачиваем \((x_1, y_1)\) на угол \(\beta\), чтобы получить \((x_2, y_2)\). Таким образом, угол между \((x_2, y_2)\) и осью X равно \(\alpha + \beta\):
(2)\[\begin{split}x_2 = L \cos(\alpha + \beta) \\ y_2 = L \sin(\alpha + \beta)\end{split}\]Доказательство по правилу сумм углов
Если вы довольны доказательством правила суммы углов, то мы почти там.
Правило суммы углов дает нам:
\[\begin{split}\cos(\alpha + \beta) = \cos \alpha \cos \beta — \sin \alpha \sin \beta \\ \sin(\alpha + \beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta\end{split}\]
Итак, подставляя из уравнений (1), (2):
\[\begin{split}L \cos(\alpha + \beta) = L \cos\alpha\cos\beta — L\sin\alpha\sin\beta\подразумевается\\ x_2 = x_1 \cos\beta — y_1\sin\beta\\\end{split}\]
Выполняем соответствующие замены в \(\sin(\alpha + \beta)\), чтобы получить \(y_2\).
\(\черный квадрат\)
Доказательство с помощью длинного варианта доказательства суммы углов
В этом разделе не предполагается правило суммы углов, но используется версия доказательство суммы углов для доказательства формул вращения.
На картинке видно, что:
\[ \begin{align}\begin{aligned}x_2 = r — u\\y_2 = t + s\end{align}\end{align} \]
Мы собираемся использовать некоторую базовую тригонометрию, чтобы получить длины \(r, u, t, с\).
Поскольку сумма углов треугольника равна 180 градусам, \(\phi\) на картинке \(90 — \alpha\) и, следовательно, угол между прямыми \(q, t\) также равен \(\alpha\).
Вспоминая определения \(\cos\) и \(\sin\):
\[ \begin{align}\begin{aligned}\cos\theta = \frac{A}{H} \ подразумевает A = \cos \theta H\\\sin\theta = \frac{O}{H} \ подразумевает O = \sin \theta H\end{aligned}\end{align} \]
Таким образом:
\[ \begin{align}\begin{align}x_1 = \cos \alpha L\\y_1 = \sin \alpha L\\p = \cos \beta L\\q = \sin \beta L\\r = \cos \alpha p = \cos \alpha \cos \beta L = \cos \beta x_1\\s = \sin \alpha p = \sin \alpha \cos \beta L = \cos \beta y_1\\t = \cos \alpha q = \cos \alpha \sin \beta L = \sin \beta x_1\\u = \sin \alpha q = \sin \alpha \sin \beta L = \sin \beta y_1\end{выровнено }\конец{выравнивание} \]
Итак:
\[ \begin{align}\begin{align}x_2 = r — u = \cos \beta x_1 — \sin \beta y_1\\y_2 = t + s = \sin \beta x_1 + \cos \beta y_1\end {выровнено}\конец{выравнивание} \]
\(\черный квадрат\).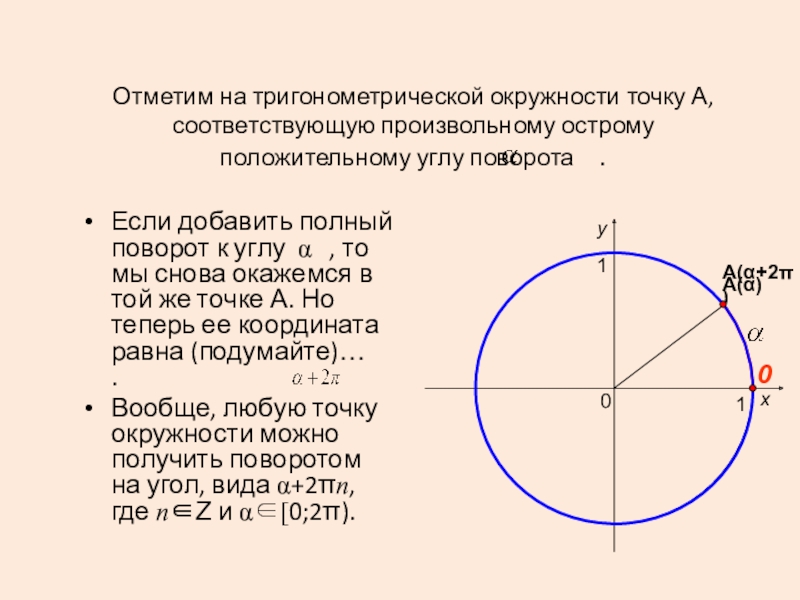
Угол поворота — обзор
Моделирование неправильной нормализации и окклюзии.
В идеале автоматическая система должна сегментировать область лица и нормализовать ее с помощью правильного масштаба, угла поворота и перемещения. Но оценка этих параметров может быть неточной, что приведет к ухудшению характеристик распознавания системы [18, 134, 127]. В совокупности мы называем эти проблемы проблемой неправильной нормализации.
Для решения проблемы неправильной нормализации было предложено несколько методов [18, 134, 111, 140].В [140] основное внимание уделяется тому, как справиться с изменением масштаба при отслеживании; в то время как основной проблемой в [111] является распознавание при изменении масштаба и окклюзии. В [18, 134] предложен метод, основанный на разложении по искаженному собственному пространству , который аналогичен [111], для обработки случаев различного масштаба и неправильной локализации, включая вращение в плоскости, перенос.
В реальности лицо может быть частично закрыто, например, очками. В литературе по распознаванию изображений существуют два традиционных подхода к распознаванию частично закрытых объектов: (1) попытка восстановить закрытые части, (2) распознавание только на основе незакрытых частей.Преимущество первого подхода заключается в использовании полной информации , если восстановление закупоренных частей прошло успешно. С другой стороны, второй подход использует только частичную, но правильную информацию. Проблема окклюзии при распознавании лиц была решена с использованием обоих подходов. В рамках первого подхода собственное представление используется для частичного восстановления закрытых частей для распознавания [80, 111] (рис. 1.5). В [59] статистическая модель, сочетающая ASM и информацию о градациях серого, используется для восстановления всей области лица.Интересно отметить, что алгоритм также удаляет очки, представленные на входных изображениях, на основе ограниченного количества примеров. Позже статистическая модель ASM была дополнена AAM на основе обзора для восстановления всей области лица из повернутого вида, например, профиля, половина лица которого закрыта [83].
Позже статистическая модель ASM была дополнена AAM на основе обзора для восстановления всей области лица из повернутого вида, например, профиля, половина лица которого закрыта [83].
В рамках второго подхода существует множество общих методов распознавания объектов, основанных на локальных частях. В частности, лицо можно разделить на модули глаз, рта и носа, каждый модуль имеет выход, и, наконец, все выходы объединяются для формирования окончательного решения.Например, в контексте распознавания лиц Burl et al. [45] ввел принципиальную основу для представления деформаций объекта с использованием вероятностных моделей формы. Локальные детекторы деталей использовались для определения возможных местоположений частей объекта. Затем эти кандидаты были сгруппированы в объектные гипотезы (да или нет) и оценены на основе пространственного расположения частей. Одним из недостатков этого подхода является то, что алгоритм обнаружения деталей использует стратегию жесткого обнаружения, то есть, если ответ детектора деталей превышает пороговое значение, записывается только положение детали; фактические значения ответа не сохраняются для последующей обработки. В [41] этот полувероятностный (локальный детерминистический и глобальный вероятностный) подход расширен до полного вероятностного подхода, который сочетает в себе как локальную фотометрию (совпадение частей), так и глобальную геометрию (вероятность формы), которая, как было показано, имеет значительное улучшение.
В [41] этот полувероятностный (локальный детерминистический и глобальный вероятностный) подход расширен до полного вероятностного подхода, который сочетает в себе как локальную фотометрию (совпадение частей), так и глобальную геометрию (вероятность формы), которая, как было показано, имеет значительное улучшение.
Недавно был предложен вероятностный метод, который моделирует лицо с шестью частями эллипсоидной формы для распознавания [127]. Для каждой части/области собственное пространство изучается из обучающего набора изображений правильных областей.Далее для моделирования ошибки окклюзии/локализации большой набор синтетических выборок с ошибками проецируется на собственное подпространство малой размерности для оценки параметров предполагаемой гауссианы (или смеси гауссовок) для каждого класса: ковариационной матрицы и среднего вектора. Чтобы выполнить распознавание, область лица сначала преобразуется в ее окончательный массив 120 × 170 пикселей, а затем каждая из ее шести областей проецируется в вычисленное выше собственное пространство для вычисления вероятности правильного совпадения. Наконец, все эти вероятности совпадения на основе частей суммируются, чтобы сформировать окончательную оценку совпадения.
Наконец, все эти вероятности совпадения на основе частей суммируются, чтобы сформировать окончательную оценку совпадения.
Та же идея использования синтетических образцов для оценки вероятности также была применена к распознаванию при неправильной локализации [127]. Единственная разница здесь в том, что все грани являются входными выборками, поэтому строится только одно собственное пространство.
Математика — Вращение вокруг точки
Для двумерных вращений вокруг x,y мы можем представить это с помощью следующей матрицы 3×3:
| р 00 | р 01 | х-р 00 *х-р 01 *у |
| р 10 | р 11 | у-р 10 *х-р 11 *у |
| 0 | 0 | 1 |
То же самое, что и вращение вокруг исходной точки, но со смещением на:
(- r 00 *x — r 01 *y, — r 10 *x — r 11 *y).
Для трехмерных вращений вокруг x,y мы можем представить это с помощью следующей матрицы 4×4:
| р 00 | р 01 | р 02 | x — r 00 *x — r 01 *y — r 02 *z |
| р 10 | р 11 | р 12 | y — r 10 *x — r 11 *y — r 12 *z |
| р 20 | р 21 | р 22 | z — r 20 *x — r 21 *y — r 22 *z |
| 0 | 0 | 0 | 1 |
То же самое, что и вращение вокруг исходной точки, но со смещением на:
(- r 00 *x — r 01 *y — r 02 *z,- r 10 *x — r 11 *y — r 12 * *x — r 21 *y — r 22 *z).
Затем мы покажем, что в двух измерениях верно и обратное. То есть любая комбинация переноса и вращения может быть представлена одним вращением при условии, что мы выбираем правильную точку для вращения.
Комбинированное вращение и перемещение
Чтобы вычислить вращение вокруг любой произвольной точки, нам нужно вычислить его новое вращение и перевод. Другими словами, вращение вокруг точки есть «правильное» преобразование изометрии, что означает, что оно имеет линейную и вращательную составляющую.
Предположим, у нас есть матрица [R0], которая определяет вращение вокруг начала координат:
Теперь мы хотим применить тот же поворот, но относительно произвольной точки P:
Как мы видим, его ориентация такая же, как если бы он вращался вокруг начала, но она была перемещена в другую точку пространства в результате вращения.
Чтобы доказать это и вычислить величину линейного переноса, мы нужно заменить:
- перевести относительно произвольной точки P (Px,Py,Pz).

Со следующими тремя более простыми преобразованиями, которые при выполнении по порядку эквивалентны:
- перевести произвольную точку в начало координат (вычесть P, который переводит по -Px,-Py,-Pz)
- повернуть вокруг начала координат (можно использовать матрицу 3×3 R0)
- потом переведи обратно. (добавьте P, который переводится как +Px,+Py,+Pz)
Итак, если мы используем глобальную систему отсчета (как описано здесь) затем
[результирующее преобразование] = [третье преобразование] * [второе преобразование] * [первое преобразование]
[результирующее преобразование] = [+Px,+Py,+Pz] * [поворот] * [-Px,-Py,-Pz]
Примечание для матричной алгебры, порядок операций важен, поэтому эти переводы не отменять.
Итак, матрица, представляющая вращение вокруг заданной точки:
[R] = [T] -1 * [R0] * [T]
где:
[T] -1 = обратное преобразование = перевод точки в начало координат
| 1 | 0 | 0 | х |
| 0 | 1 | 0 | г |
| 0 | 0 | 1 | г |
| 0 | 0 | 0 | 1 |
[R0] = вращение вокруг начала координат (если это неясно, см. это обсуждение)
это обсуждение)
| р 00 | р 01 | р 02 | 0 |
| р 10 | р 11 | р 12 | 0 |
| р 20 | р 21 | р 22 | 0 |
| 0 | 0 | 0 | 1 |
[T] = перевод происхождения в точку
| 1 | 0 | 0 | -х |
| 0 | 1 | 0 | -у |
| 0 | 0 | 1 | -з |
| 0 | 0 | 0 | 1 |
Перемножение этих матриц даст следующий результат для вращение вокруг x,y,z:
(чтобы увидеть все шаги, см. эту страницу)
эту страницу)
| р 00 | р 01 | р 02 | x — r 00 *x — r 01 *y — r 02 *z |
| р 10 | р 11 | р 12 | y — r 10 *x — r 11 *y — r 12 *z |
| р 20 | р 21 | р 22 | z — r 20 *x — r 21 *y — r 22 *z |
| 0 | 0 | 0 | 1 |
Таким образом, компоненты вращения те же, но вращение перемещает положение центра.
Изометрия в двух измерениях SE(2)
Теперь мы хотим проверить обратное, то есть любую комбинацию переноса и вращения можно представить одним вращением при условии, что мы выбираем правильную точку для вращения.
Представьте, что мы хотим преобразовать твердое тело в точке «А» в твердое тело в точке «В».
Затем мы можем определить точку на A (например, центр масс) и соответствующую точку на B. Затем мы можем объединить два преобразования:
- Выполните линейное перемещение таким образом, чтобы точка на ‘A’ была преобразована в точку на ‘B’.
- Сделайте вращение вокруг точки, чтобы правильно преобразовать твердое тело.
Однако есть второй вариант, мы можем сделать перевод всего за один оборот:
Итак, при условии, что мы можем найти подходящую точку для поворота (в приведенном выше примере показана зеленой точкой), мы можем выполнить перемещение и вращение за одну операцию. Точка, вокруг которой мы вращаемся, должна быть равноудалена от выбранной точки на каждом теле, поэтому она должна лежать на линии, перпендикулярной линии, соединяющей две точки.Так всегда ли мы можем найти точку, которая будет выполнять любую комбинацию переноса и поворота? Чтобы узнать, мы можем принять две крайности:
- Если точка вращения находится точно посередине двух объектов, то объект будет повернут на 180 градусов.

- Если точка вращения находится в бесконечности вдоль биссектрисы, то объект только перемещается, и вращение будет равно нулю.
Поместив точку на некотором расстоянии между ними, мы можем получить любой поворот от 0 до 180 градусов.Мы можем получить отрицательные углы, двигаясь в противоположном направлении вдоль линии.
Поэтому мы можем сделать любой поворот, поступательную комбинацию за один оборот.
Выполнение поворота-перемещения за одну операцию, подобное этой, может упростить некоторые вычисления, и нам не нужно думать, делаем ли мы сначала вращение вокруг исходного положения, а затем перемещение, или сначала выполняем перемещение, а затем вращение вокруг его исходного положения. конечное положение, или сначала выполните перенос в среднюю точку, затем вращение вокруг среднего положения и затем заключительный полуперевод.
Расчет точки вращения
Учитывая сдвиг (заданный двумерным вектором) и поворот (заданный скалярным углом в радианах), как мы вычисляем точку вращения P?
Нам известны точки А и В и угол при Р, который равен тета.
sin(θ/2) = v/(2*r)
г = v/(2*sin(θ/2))
где:
- r = скалярное расстояние P от A и B
- v = скалярное расстояние B от A
- θ = угол поворота
Мы также знаем по Пифагору:
(Px — Ax) 2 + (Py — Ay) 2 = r 2
(Px — Bx) 2 + (Py — By) 2 = r 2
Это становится немного грязно! Можем ли мы найти P в векторных координатах?
Думаю, мне придется отказаться от этого подхода и вместо этого инвертировать матричные уравнения, с которых мы начали:
Из полученной выше матрицы:
| р 00 | р 01 | х-р 00 *х-р 01 *у |
| р 10 | р 11 | у-р 10 *х-р 11 *у |
| 0 | 0 | 1 |
получаем уравнения для смещения:
Смещениеx = x — r 00 *x — r 01 *y
Смещение = y — r 10 *x — r 11 *y
Где:
- Смещение = линейное расстояние, на которое переместилась точка на объекте.

- x, y = координаты точки, вокруг которой мы вращаемся (относительно начального положения объекта).
Мы хотим найти x и y, поэтому возьмем обратное:
дать:
| = |
|
В этом случае матрица вращения:
| соз(θ) | — грех(θ) |
| sin(θ) | соз(θ) |
где
θ = угол поворота
что дает:
| = |
|
|
расширение определителя (и использование sin 2 (θ)+cos 2 (θ)=1) дает:
| = |
|
Чек
Мы можем проверить некоторые особые случаи, чтобы увидеть, получаем ли мы разумные результаты:
, если θ = 0, то:
Если тета = 0, то точка вращения находится в бесконечности.
, если θ = 90°, то:
, так что если смещение равно (1,0), то точка вращения находится на (0,5,0,5)
, если θ = 180°, то:
Итак, мы вращаемся вокруг точки на полпути к B.
Объединение вращений вокруг разных точек
Как применить два таких поворота один за другим, чтобы получить третий эквивалентный поворот?
Итак, представьте, что мы применяем ротацию:
С центром в: (tax,tay,taz) с последующим вращением:
По центру: (tbx,tby,tbz)
Общее вращение является произведением двух матриц вращения:
| = |
Смещение будет:
| налог — ra 00 *налог — ra 01 *tay + tbx — rb 00 *tbx — rb 01 *tby |
| tay — ra 10 *tay — ra 11 *tay + tbx — rb 00 *tbx — rb 01 *tby |
Таким образом, общий центр будет:
В трех измерениях мы также можем представить изометрию как вращение и перемещение. Можем ли мы представить любую изометрию как одно вращение, как в двумерном случае, как описано выше?
Можем ли мы представить любую изометрию как одно вращение, как в двумерном случае, как описано выше?
В трех измерениях есть три степени свободы вращения, но когда мы ищем точки, которые равноудалены от центров объектов до и после преобразования положения. Равноудаленные точки лежат на плоскости, которая имеет только две степени свободы, но есть также возможность вращаться вокруг линии из точки. Поэтому имеется достаточно степеней свободы для представления всех возможных изометрий.
Итак, представьте, что мы хотим перевести из точки A (0,0) в точку B (0,1), мы можем сделать это, вращаясь вокруг любой точки плоскости x=0,5.
Если, например, мы хотим объединить его с поворотом на 90° вокруг оси z, мы можем сделать это, повернув вокруг (0.5,0.5,0):
Если, например, мы хотим объединить его с поворот на 90° вокруг оси y, мы можем сделать это, повернув вокруг (0.5,0,0.5):
Если, например, мы хотим объединить его с поворотом на 90° вокруг оси x, у нас есть проблема !
Нам нужно повернуть его вокруг оси x, чтобы получить желаемое вращение, и нам нужно повернуть вокруг оси y или z, чтобы получить желаемое перемещение, и эти два варианта не кажутся совместимыми?
Таким образом, когда есть компонент оси вращения в том же направлении, что и вектор переноса, они кажутся несовместимыми.
Чтобы представить все возможные перемещения и повороты в одной операции, мы должны разрешить вращение вокруг точки вместе с перемещением вдоль вектора, параллельного оси вращения. Операция представлена линией вокруг внешней стороны цилиндра. Это известно как винт (см. эту страницу, чтобы продолжить эту тему).
На следующих страницах есть код для расчета аффинного перевода при вращении о точке:
Вас могут заинтересовать другие способы представления ориентации и вращения такие величины, как:
Или вас может заинтересовать, как эти величины используются для имитации физических объекты:
Угол поворота для достижения максимального главного напряженного состояния
Это можно сделать на нескольких экзаменах NCEES FE: гражданское право, механика и другие дисциплины.Решение:
Это обычная проблема, с которой вы можете столкнуться на экзамене FE, PE и в школе. Для экзаменов FE вы найдете его в следующих темах:
1.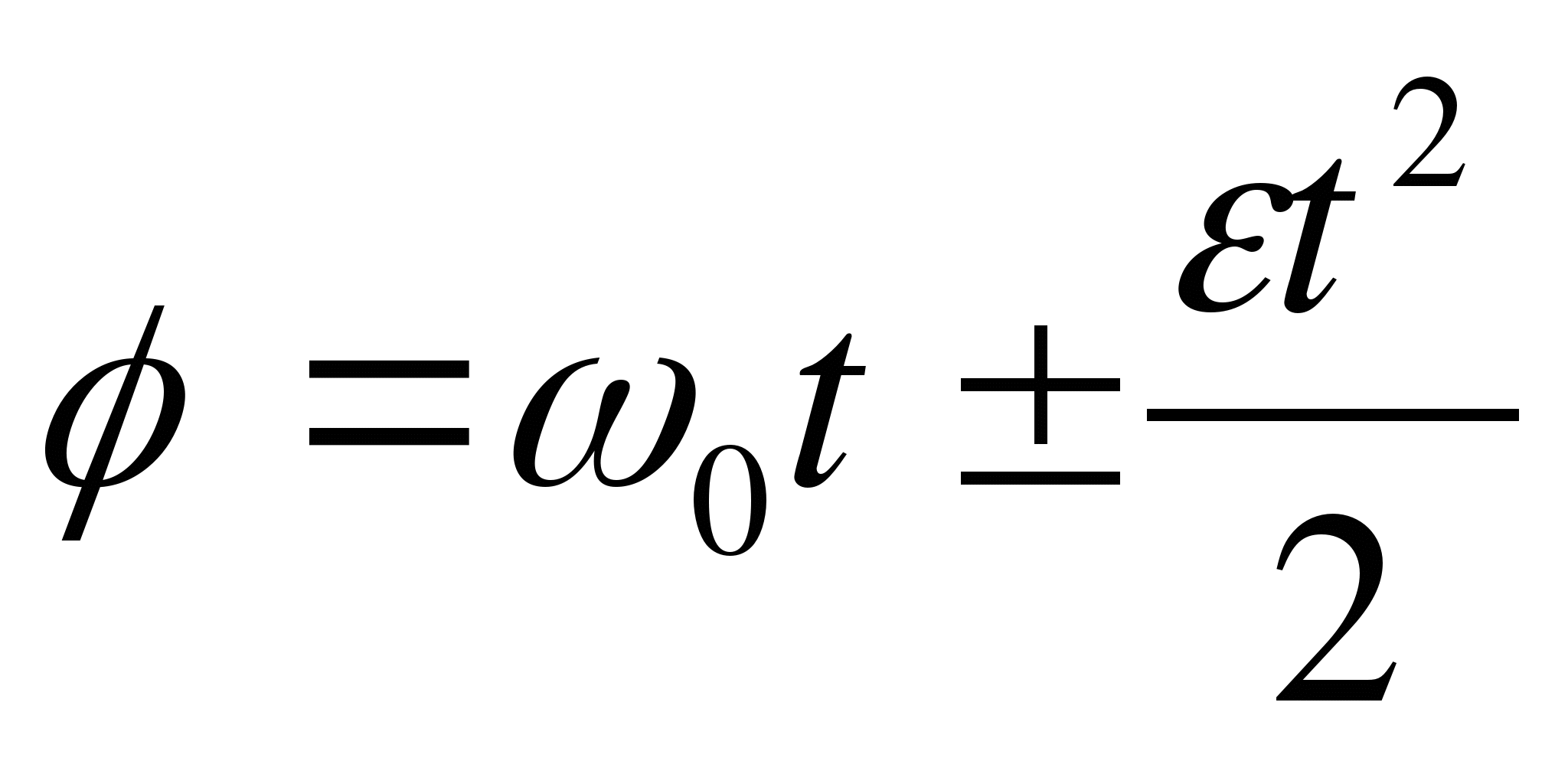 FE Civil — Механика материалов — Комбинированные напряжения, главные напряжения и круг Мора
FE Civil — Механика материалов — Комбинированные напряжения, главные напряжения и круг Мора
2. FE Mechanical — Механика материалов — Преобразование напряжений и круг Мора
3. Прочие дисциплины КЭ — Сопротивление материалов — Трансформация напряжения и основные напряжения, включая критерий текучести и разрушения на основе напряжения (например,г., круг Мора, максимальное нормальное напряжение, Треска, фон Мизес)
В конечном итоге мы должны определить угол поворота, необходимый для приведения напряжённого элемента (напряженного блока) в главное напряженное состояние.
Шаги для определения необходимого угла поворота:
1. Быстро нарисуйте круг Мора на основе того, что показано в элементе напряжения.
2. Начертите прямоугольный треугольник из центра круга Мора в известную точку на этом круге. Определите угол круга Мора между известной точкой и сигма-осью (ось x), где возникает главное напряжение.Это и будет угол поворота круга Мора, необходимый для достижения главного напряженного состояния.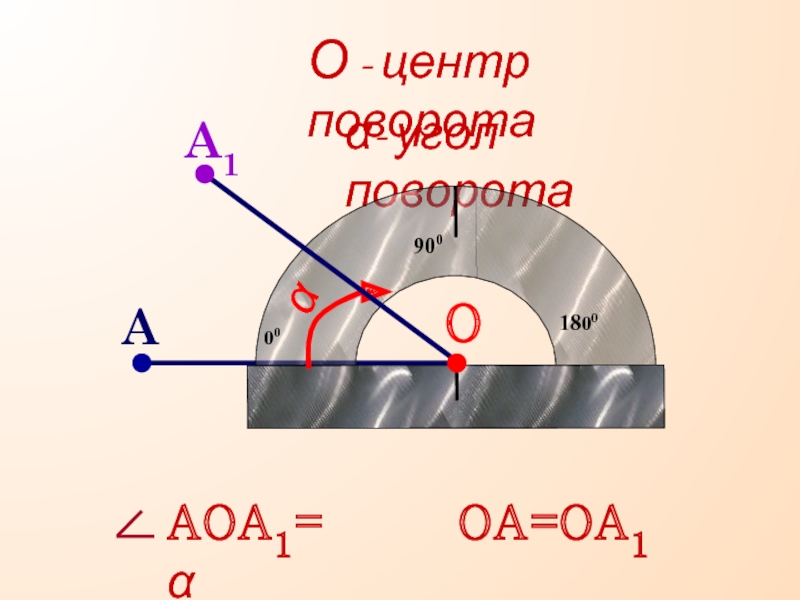
3. Преобразуйте угол поворота круга Мора, необходимый для перехода в состояние главного напряжения, в угол элемента напряжения, необходимый для перехода в состояние главного напряжения.
Шаг 1. Быстро нарисуйте круг Мора на основе того, что показано в элементе напряжения.
Нормальные напряжения (σ x , σ y ) при растяжении (исходящие от элемента напряжения) положительны, а нормальные напряжения сжатия (входящие в элемент напряжения) отрицательны.Касательные напряжения (τ xy ) смотрите на правую часть элемента напряжения. Если правая стрелка сдвига тянет элемент напряжения по часовой стрелке, то сдвиг отрицателен. Если правая стрелка сдвига тянет элемент напряжения против часовой стрелки, то сдвиг положительный. Следовательно,
τ xy = -530 МПа
σ x = 400 МПа
σ y = -550 МПа
Вычислить центр круга Мора.
Имея известную информацию, начертите случайную точку по периметру круга.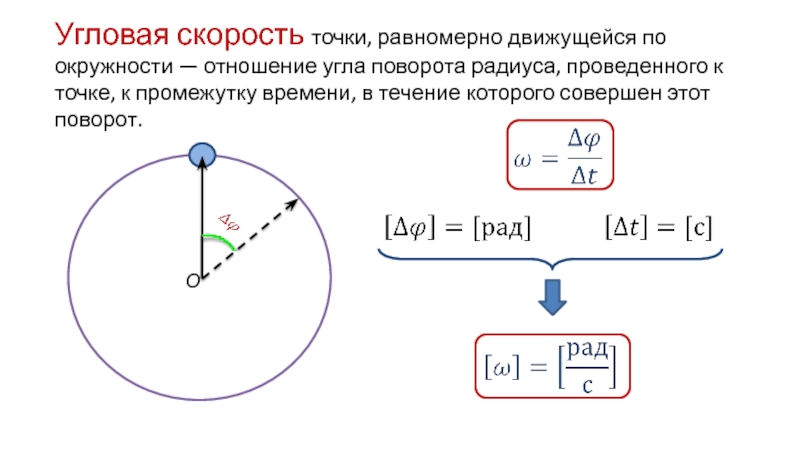
Шаг 2. Постройте прямоугольный треугольник из центра круга Мора в известную точку по периметру круга.
Используйте теорему Пифагора, чтобы найти гипотенузу треугольника, которая также является радиусом окружности.
A 2 + B 2 = Hypotenuse 2
(530 МПа) 2 + (75 + 400 МПа) 2 = гипотенузы 2
Hypotenuse = Radius = 711.7 МПа
Рассчитать угол круга Мора к главному напряженному состоянию. Используйте со-ка-тоа.
Шаг 3. Преобразование угла поворота круга Мора, необходимого для перехода в состояние главного напряжения, в угол элемента напряжения, необходимый для перехода в состояние главного напряжения.
Угол 2θ представляет собой угол круга Мора для достижения основного состояния, это НЕ угол элемента напряжения для достижения основного состояния.