|
Задача № 1. Выполнить построение эпюра точки B(x, y, z), по двум известным проекциям точки построить третью. 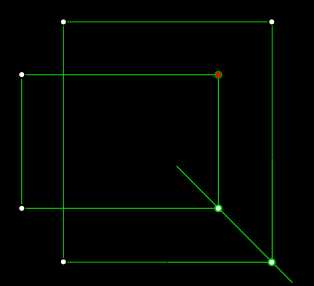 Эпюра точки
Задача №2. Выполнить построение эпюра точки 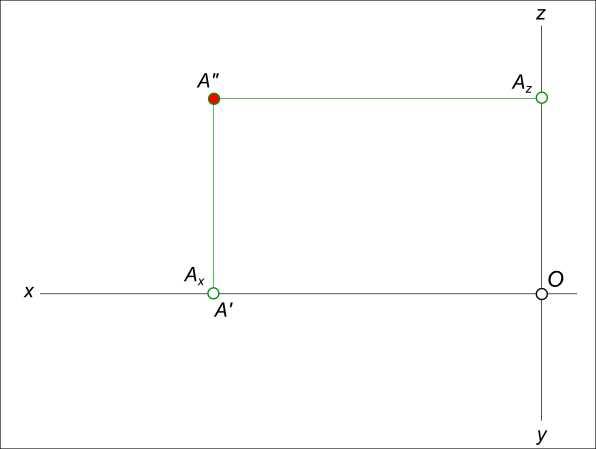 Эпюра точки
Задача №3. Выполнить построение эпюра точки A(x, y, z),принадлежащей только горизонтальной плоскости проекций: z = 0. 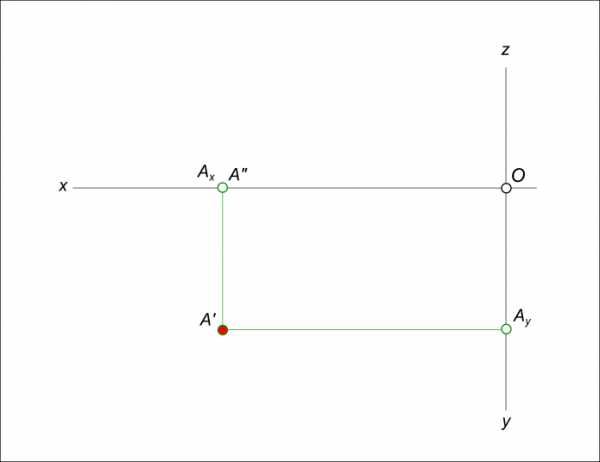 Эпюра точки
Задача №4. Дана горизонтальная прямая h. Выполнить построение эпюра точки A(A`, A»), принадлежащей прямой h. 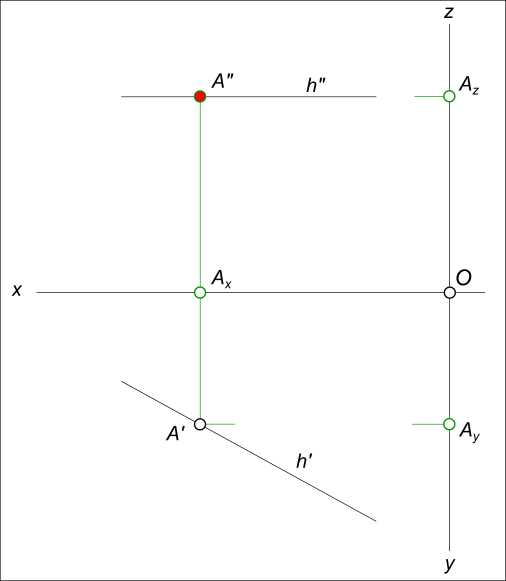 Эпюра точки
Задача №5. Дана фронтальная прямая f. Выполнить построение эпюра точки точки A(A`, A»), принадлежащей фронтальной прямой f.  Эпюра точки
Задача №6. Дан отрезок прямой [AB]. Выполнить построение эпюра точки K(K`, K»), принадлежащей отрезку прямой [AB] и делящей его в отношении [AK]/[KB]=1/2. 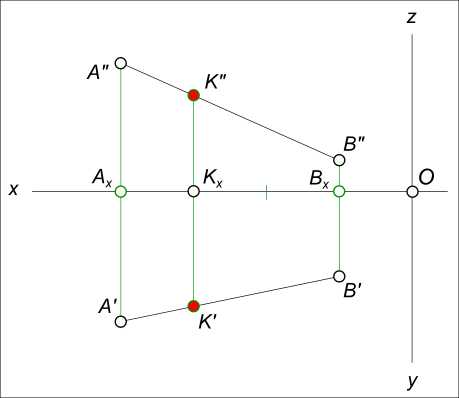 Эпюра точки
Задача №7. Дана фронтальная проекция точки B, принадлежащей плоскости α. Построить недостающую проекцию точки B. 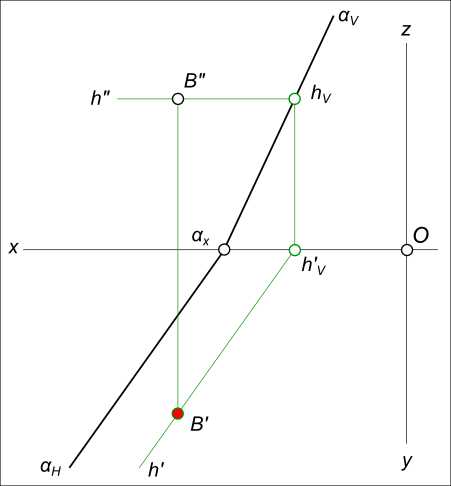 Эпюра точки
Задача № 8. Дана горизонтальная проекция точки A, принадлежащей плоскости α(b ║ c). Построить недостающую проекцию точки A. 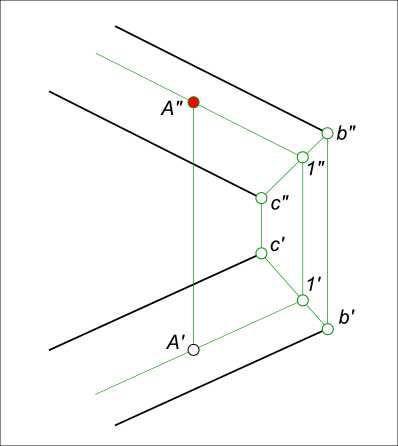 Эпюра точки
+ |
ngeo.fxyz.ru
|
Задача № 1. Даны точки A(93, 15, 38), B(42, 47, 52). Выполнить построение эпюра прямой [AB]. 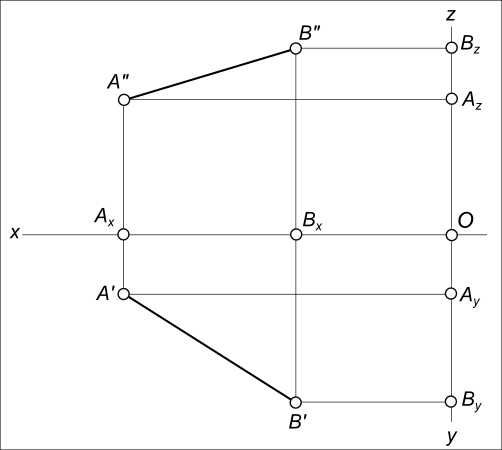 Эпюра прямой
Задача № 2. Даны фронтальная проекция отрезка [BC], принадлежащего плоскости α(A, b). Построить горизонтальную проекцию отрезка [BC].  Эпюра прямой
Задача № 2a. Даны фронтальная проекция отрезка [AB], принадлежащего плоскости . Построить горизонтальную проекцию отрезка [AB].  Эпюра прямой
Задача № 3. Даны проекции отрезка [AB] ([A`], [A»B»]). Построить недостающую проекцию отрезка [A`B`], если действительная величина отрезка [AB] = R и By больше Ay.  Эпюра прямой HTML код таблицы, примеры
Задача № 4. Даны проекция отрезка [AB] (…, [A»B»]). Построить недостающую проекцию отрезка [AB]. 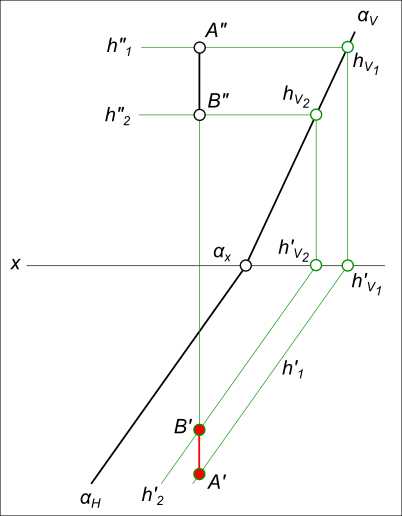 Эпюра прямой
+ |
ngeo.fxyz.ru
Отрицательные значения x, y и z на эпюре Монжа | Начертательная геометрия
Даны координаты точки A (30, -10, 40) или A (Ax, Ay, Az). Необходимо построить проекции A`, A», A»` и определить в каком октанте находится данная точка.
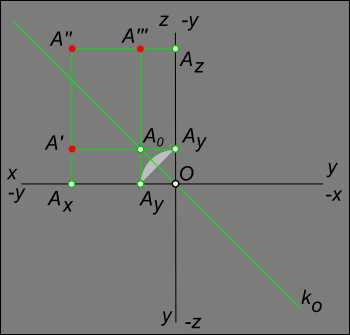
Отрицательные значения x, y и z на эпюре Монжа
Для построения проекций точки по координатам требуется знать где направления x, y, z положительные и где отрицательные значения x, y и z на эпюре Монжа. Значение координаты равное нулю принято относить к положительной полуоси. Эпюры точек и знаки координат точек в октантах левой половины пространственного макета
| Эпюр точки | ||||
| Положение | Октант I | Октант II | Октант III | Октант IV |
| x | + | + | + | + |
| y | + | — | — | + |
| z | + | + | — | — |
Эпюры точек и знаки координат точек в октантах правой половины пространственного макета
| Эпюр точки | ||||
| Положение | Октант V | Октант VI | Октант VII | Октант VIII |
| x | — | — | — | — |
| y | + | — | — | + |
| z | + | + | — | — |
По приведенным эпюрам точек в октантах выводится следующая последовательность построения эпюра точки:
— проводятся оси координат Oxyz;
— откладывается абсцисса точки от оси z;
— проводится линия проекционной связи ⊥ оси x;
— откладывается аппликата точки от оси x;
— откладывается ордината точки от оси x.
Для определения октанта в котором располагается точка A следует знать преобразование пространственного макета Эпюра Монжа путем совмещения плоскостей H и W с фронтальной плоскостью проекций V или воспользоваться таблицей. Положение точки A соответствует в таблице октанту №2.
+
ngeo.fxyz.ru
Копия ЭПЮРЫ, блеать!!! 1-4 / Эпюр 1
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОРБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
«Курский государственный технический университет»
Кафедра начертательной геометрии и инженерной графики
ТОЧКА, ПРЯМАЯ, ПЛОСКОСТЬ. ВЗАИМНОЕ ПОЛОЖЕНИЕ
Методические указания к выполнению эпюра № 1 (для студентов технических специальностей)
2
УДК 621.(076.1)
Составители: Ж.С.Калинина, С.И.Иванова, Ю.А.Попов
Рецензент Кандидат технических наук, доцент А.С.Белозеров
Точка. Прямая. Плоскость: методические указания к выполнению эпюра № 1 / Курск. гос. техн. ун-т; сост.: Ж.С. Калинина, С.И. Иванова, Ю А Попов. Курск, 2008. 41 с.: ил. 39, табл.1, прилож..
Библиогр.: с.4.
Настоящие методические указания написаны с целью оказать помощь студентам в организации самостоятельной работы при выполнении домашнего задания по эпюру №1.
Предназначены для студентов технических специальностей дневной формы обучения.
Текст печатается в авторской редакции.
Подписано в печать | .Формат 60х84 1/16 | |
Усл.печ.л. | .Уч.-изд.л. | . Тираж 150 экз. Заказ. Бесплатно. |
Курский государственный технический университет. Издательско-полиграфический центр Курского государственного технического университета. 305040, Курск, ул.50 лет Октября, 94.
3
ВВЕДЕНИЕ
Настоящие методические указания разработаны в соответствии с рабочей программой по курсам «Начертательная геометрия» и «Инженерная графика».
По мере изучения курса студенты выполняют 4 домашних задания по начертательной геометрии (4 эпюра).
Эпюры выполняются на листах чертежной бумаги формата А3 (297х420 мм) в соответствии с требованиями ГОСТ ЕСКД и должны отличаться выразительностью и опрятностью графического решения поставленных задач.
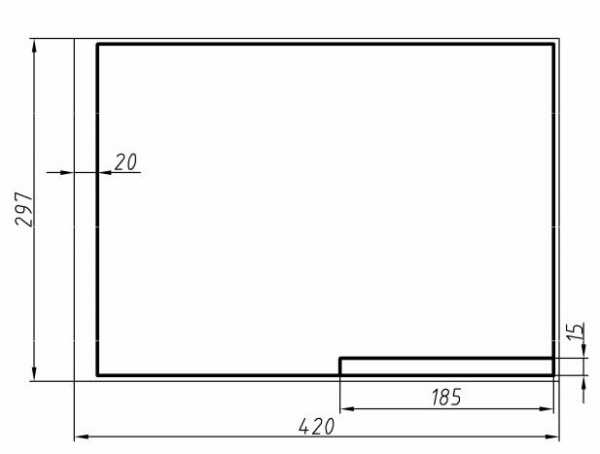
Внутри каждого формата вычерчивается рамка, расстояние от которой до границ формата (внешней рамки) сверху, справа и снизу должно быть равно 5мм, а слева 20мм (ГОСТ 2.301-68 «Форматы»).
В правом нижнем углу надо оставить свободное место размером 15х185мм, очертив его прямыми линиями (рис.1).
4
В этом месте на эпюре должна помещаться основная надпись (рис. 2).
ЭП.01.13 — 01 – номер эпюра 13 – вариант студента
Рис. 2
Все надписи, а также буквенные и цифровые обозначения выполняются стандартным шрифтом в соответствии с ГОСТ 2.304-81 «Шрифты чертёжные».
Чертить следует хорошо заточенным карандашом Т (Н) или ТМ (НВ, F) в зависимости от качества бумаги (на более плотной бумаге следует чертить более твёрдым карандашом). Все линии, независимо от их назначения (линии контура, построений, искомые и т.д.), сначала должны быть тонкими. Их следует проводить с очень лёгким нажимом карандаша на бумагу. Толщина линии обводки ≈ 1мм, тонких линий ≈ 0,3мм (ГОСТ 2.303-68 «Линии чертежа»).
Эпюры выполняются в карандаше, рекомендуется использовать при решении задач цветные карандаши (см. стенды кафедры). Результат обводится красным цветом.
Решение любой задачи должно выполняться в строго определённой последовательности:
1.Осмысление исходных данных и результата, который необходимо получить в ходе решения задачи.
2.Составление алгоритма (плана) решения поставленной задачи. Так как задачи начертательной геометрии пространственные, но выполняемые на эпюре, т.е. на плоскости, алгоритм решения задачи должен состоять из двух частей: первая – решение задачи в пространстве и вторая – осуществление плана решения этой задачи на эпюре. Обе эти части взаимосвязаны.
5
3. Выполнение задачи в соответствии с составленным алгоритмом.
Вариант задания соответствует порядковому номеру студента в групповом журнале.
1. Содержание эпюра №1
Даны координаты точек A, B, C, D, E, F. Координаты точек студент выбирает из таблицы 1 по своему порядковому номеру в журнале группы.
Задачи 1, 2 и 3 выполняются на формате А3. Пример выполнения дан на рисунке 37.
Задача 1
-Построить точку T, симметричную точке А относительно
плоскости проекций π1(для нечётных вариантов) или π2(для четных вариантов).
-Записать координаты точки T и определить её положение в пространстве.
-Построить проекции прямой, заданной двумя точками А и С.
-Определить следы прямой АС, показать её видимость.
-Показать, через какие четверти проходит прямая.
Задача 2
-Определить натуральную величину отрезка АC.
-Показать углы наклона отрезка прямой АС к плоскостям
проекций π1 и π2.
— Отложить на прямой АС отрезок СК длиной 30 мм.
Задача 3
-Построить проекции треугольника АВС.
-Провести горизонталь и фронталь в плоскости ΔАВС.
-Определить угол наклона плоскости ΔАВС к плоскости проекций π1 (для нечётных вариантов) или π2 (для чётных вариантов).
Задача 4 – выполняется на формате А3. Пример выполнения дан на рисунке 38.
6
-Построить линию пересечения двух плоских фигур, заданных ΔАВС и ΔDEF.
-Определить видимость.
-Записать алгоритм решения задачи.
Задачи 5 и 6 выполняются на формате А3. Пример выполнения дан на рисунке 39.
Задача 5
-Определить расстояние от точки D до плоскости ΔАВС.
Задача 6
-Построить плоскость, параллельную ΔАВС и отстоящую от неё на расстоянии 40мм.
Все задачи выполняются в масштабе М 1:1 (натуральная величина).
2. Общие методические указания по выполнению эпюра
Для решения задач эпюра необходимо изучить следующий материал
2.1. Ортогональные проекции точки
Каждая точка, заданная на рисунке, должна определять единственную точку изображаемого объекта. Для построения чертежа применяется метод ортогонального проецирования на две (или три) взаимно перпендикулярные плоскости проекций, который впервые предложил французский учёный Гаспар Монж (1746 – 1818 г.).
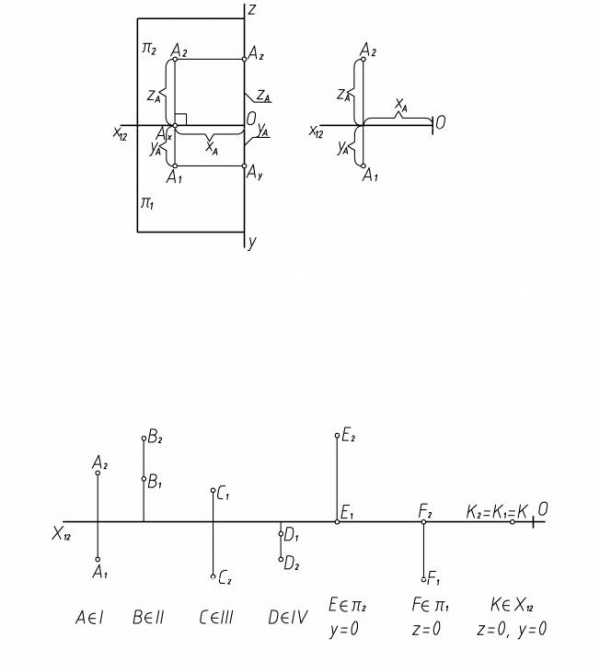
Пусть дана в пространстве точка А и две (или три) взаимно перпендикулярные плоскости проекций π1, π2, π3. Из точки А опускаем перпендикуляры на плоскости проекций. Точки пересечения перпендикуляров с плоскостями проекций А1, А2, А3 – называются
ортогональными проекциями точки А. Длины перпендикуляров определяют расстояния от точки А до плоскостей проекций и задают координаты точки А – x, y, z.
X – расстояние от точки А до профильной плоскости проекций π3, X= |A, π3|.

7
Y – расстояние от точки А до фронтальной плоскости проек-
ций π2, Y= |A, π2|.
Z – расстояние от точки А до горизонтальной плоскости проекций π1, Z= |A, π1|.
Таким образом, точка А в пространстве может быть задана своими координатами – А(x, y, z).
Две плоскости проекций делят пространство на четыре четверти, а три плоскости проекций – на 8 октантов..
Рассмотрим пространственный рисунок (рис.3).
Рис. 3 π1 – горизонтальная плоскость проекций;
π2 — фронтальная плоскость проекций; OX, OY, OZ – оси проекций; π1 π2 ;
OAx=x, AxA1=y, AxA2=z;
A (x, y, z) → A1 (x, y), A2 (x, z)
При переходе к плоскому чертежу (эпюру) передняя пола плоскости π1 опускается вниз и совмещается с нижней полой плоскости π2; задняя пола π1, поднимаясь вверх, совмещается с верхней полой плоскости π2 (рис. 4, а).
Эпюром называется чертеж, составленный из двух или трёх, связанных между собой, ортогональных проекций геометрической фигуры (рис. 4, б).
8
Таким образом, для построения эпюра точки А(x, y, z) нужно от начала координат по оси х12 отложить координату х точки А, затем провести вертикальную линию связи, на которой от оси х12 отложить координату y вниз (если она положительна), а координату z вверх (положительное значение).
Рис. 4
A1A2 — вертикальная линия связи
Эпюры точек, расположенных в разных четвертях пространства.
9
2.2. Построение симметричных точек
Точки, симметричные относительно заданной плоскости, расположены на общем перпендикуляре к плоскости, по разные стороны от плоскости и на одном расстоянии от точки пересечения перпендикуляра с плоскостью.
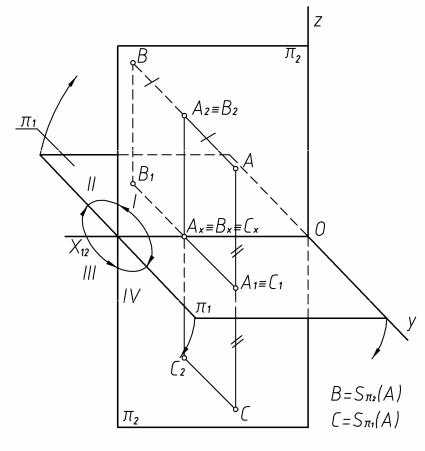
На рисунке 6 показано построение точки В, симметричной точке А относительно плоскости π2, и точки С, симметричной точке А относительно π1.
Рис. 6
Из рисунка 6 видно, что точки А и В, симметричные относительно плоскости π2, расположены на одном перпендикуляре к плоскости π2 (АВ), поэтому фронтальные проекции точек совпадают (А2=В2), а так как расстояние от точки А и точки В до плоскости π2 одинаково, то координаты y точек А и В будут равны по величине, но разными по знаку.
Точка А расположена в I четверти, точка В будет располагаться во II четверти.

10
Точками, симметричными относительно плоскости, называются точки, расположенные на одном перпендикуляре к плоскости, по разные стороны от плоскости, но на одинаковом расстоянии от плоскости.
На рисунке 7 показано построение симметричных точек А и В на эпюре.
Видно, что точка С, симметричная точке А относительно π1 будет расположена в IV четверти, у этих точек совпадают горизонтальные проекции и координата z будет равна по величине, но противоположна по знаку (рис. 6 и 8).
Таким образом, у точек, симметричных относительно плоскости π2, на эпюре совпадают фронтальные проекции, а горизонтальные расположены по разные стороны от оси х12, но на одинаковом расстоянии (рис. 7).
Если точки симметричны относительно π1, то на эпюре совпадают их горизонтальные проекции, а фронтальные располагаются по разные стороны от оси х12, но на одинаковом расстоянии (рис. 8).
studfiles.net
Комплексный чертёж точки. Эпюр Монжа
Количество просмотров публикации Комплексный чертёж точки. Эпюр Монжа — 527
Проецирование точки
Выделим в пространстве две взаимно перпендикулярные плоскости проекций П1 и П2, которые пересекаются по оси, называемой осью проекций или осью координат (рис. 10). Проводя из точки А перпендикулярно плоскостям прямые линии (проецирующие лучи) до их пересечения с плоскостями, определяем две ортогональные проекции точки А – А1иА2. Проецирующие прямые АА1 и АА2 определяют проецирующую плоскость, перпендикулярную к обеим плоскостям проекций и к оси проекций х. Прямые А1АХ и АХА2,являющиеся проекциями проецирующей плоскости на плоскостях проекций П1 и П2, будут перпендикулярны к оси проекций х.
Здесь, как и в случае центрального проецирования, одной точке пространства соответствуют две ее проекции. Аналогичным образом мы можем получить две проекции точек В,С или любой другой точки пространства.
В случае если положение плоскостей фиксировано, то каждой точке пространства соответствует упорядоченная пара точек на плоскостях проекций. Справедливо и обратное утверждение – упорядоченной паре точек на плоскостях проекций соответствует единственная точка пространства.
Эти утверждения являются фундаментальными и составляют основу построения проекционного чертежа.
Плоскости П1и П2при пересечении образуют четыре двугранных угла. Их называют квадрантами или четвертями пространства.
Рис. 10
На практике в ряде построений или при решении задач появляется крайне важно сть вводить в систему плоскостей П1и П2 и другие плоскости проекций. Чертежи машин или их частей часто содержат больше двух изображений. В случае если ввести в систему двух плоскостей проекций П1и П2еще одну плоскость проекций, то имеет смысл расположить ее перпендикулярно двум существующим. На практике третью плоскость проекций располагают так, как показано на рис. 11, и обозначают П3. Так же как и плоскости П1и П2, плоскость П3расположена вертикально. При введении третьей плоскости проекций появляются еще две оси координат – одна вертикальная, другая горизонтальная, которые одновременно являются линиями пересечения трех плоскостей проекций. Принятые обозначения координатных осей: х – ось абсцисс; у – ось ординат; z – ось аппликат. Точка пересечения осей принимается за начало координат и обозначается буквой О.
Условно принята правая система расположения координатных осей. Ось х направлена от начала координат влево, ось у – вперед (к наблюдателю), ось z – вверх. Обратные направления осей считаются отрицательными. Такую систему осей координат и плоскостей проекций называют декартовой системой, по имени французского ученого Р. Декарта (1596–1650), предложившего прямоугольную систему координат для определения положений точек в пространстве. Координатные плоскости, или плоскости проекций, имеют следующие названия:
П1 – горизонтальная плоскость проекций;
П2 – фронтальная плоскость проекций;
П3– профильная плоскость проекций.
Плоскости проекций в своем пересечении образуют восемь трехгранных углов, разделяя пространство на восемь частей – восемь октантов. Расположение октантов и их номера показаны на рис. 12.
Рис. 11 Рис. 12
Сегодня в технической практике получил широкое применение чертеж, составленный из двух или более связанных между собой ортогональных проекций изображаемого предмета. Такой чертеж называют комплексным чертежом в ортогональных проекциях или комплексным чертежом.
Представим точку А в системе трех плоскостей (рис. 13). Проводя из точки А прямые линии, перпендикулярные плоскостям до их пересечения с этими плоскостями, определяем ортогональные проекции точки А. Проекции точки А на плоскостях называют соответственно горизонтальной А1, фронтальной А2 и профильной проекцией А3 точки А. Точка в пространстве удалена от начала координат на расстояние от оси ее фронтальной, горизонтальной и профильной проекций.
Ввиду неудобства пользования пространственным макетом, на чертеже его разворачивают и представляют эпюром – чертежом, составленным из двух или трех связанных между собой ортогональных проекций геометрической фигуры (рис. 14).
Рис. 13 Рис. 14
Развернутый пространственный макет называют эпюром Монжа. На чертеже контуры плоскостей проекций не показывают. Прямые, соединяющие разноименные проекции точки А, называют линиями связи. Две проекции любой точки принадлежат одному перпендикуляру – одной линии связи.
Связь между горизонтальной и профильной проекциями должна быть определена с помощью двух отрезков ОАY и ОАY, которые равны, поскольку принадлежат одной и той же оси. Этой связью пользуются для того, чтобы найти недостающую горизонтальную или профильную проекции точки.
Ортогональный чертеж (эпюр) точки А является полным и метрически определенным. Как видно из эпюра, сочетание двух любых проекций точки дает значение всех трех координат:
А1 (АхАy ),
А2 (Аz Ах ),
А3 (Аz Аy ).
По этой причине положение точки в пространстве вполне определяется положением двух ее ортогональных проекций. Как следствие, по двум заданным проекциям всегда можно построить недостающую третью.
Расстояния точки от плоскости проекций и от осей координат бывают измерены непосредственно, как определенные отрезки на чертеже. Как видно из рис. 13, точка А располагается от горизонтальной проекции на расстоянии, равном отрезку А1 А.Этот отрезокпроецируется на фронтальную и профильную проекции без искажения, следовательно, отрезки Аx А2 и Аy А3 равны отрезку А1 А. По этой причине определить расстояния точки А от горизонтальной плоскости проекций на эпюре (см. рис. 14) можно, измерив отрезки А2 Аx или А3 Аy. Аналогичным образом можно определить по эпюру расстояния точки А и от двух других плоскостей проекций:
от фронтальной плоскости – А2 А = Аx А1 = Аz А3
от профильной плоскости – А3 А = Аz А2 = Аy А1
Чем длиннее будут эти отрезки, тем дальше от соответствующих плоскостей проекций будет расположена точка в пространстве, в связи с этим, зная эти закономерности, можно легко определять по эпюру положение любой точки пространства. В случае если на эпюре будут заданы две или более точек, то, сравнивая длину отрезков каждой точки, можно точно определить, как относительно плоскостей проекций или наблюдателя будут расположены эти точки в пространстве.
При переходе к эпюру утрачивается пространственная картина расположения плоскостей проекций и объектов, но эпюр обеспечивает точность при значительной простоте построений. Чтобы по нему представить пространственную картину объекта͵ требуется лишь работа воображения.
referatwork.ru