Условие равновесия пространственной системы сходящихся сил
Условие равновесия пространственной системы сходящихся сил гласит: необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую из трех координатных осей равнялись нулю.
Пусть на свободное твердое тело действует система сходящихся сил (F1, F2, … FN). Сложив по правилу силового многоугольника N-1 этих сил, приведем данную систему сходящихся сил к системе двух сил (R1, FN).
Но, по первой аксиоме, две силы R1 и FN приложенные к твердому телу, эквивалентны нулю, т.е. находятся в равновесии только в том случае, когда они имеют равные модули и направлены по одной прямой в противоположные стороны, т.е. если их равнодействующая R*= R1 + FN равна нулю.
Следовательно, для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этой системы сил равнялась нулю, т.
R* = ∑ Fk = 0. (6)
Это векторное условие равновесия системы сходящихся сил.
Так как равнодействующая R* изображается вектором, замыкающим силовой многоугольник, то геометрически условие равновесия системы сходящихся сил означает, что силовой многоугольник, построенный на векторах слагаемых сил данной системы, замкнут.
Выразим теперь это условие аналитически. Из предыдущего параграфа известно, что модуль равнодействующей системы сходящихся сил определяется по формуле
Но при равновесии R*= 0, а следовательно равно нулю и подкоренное выражение формулы (2). Поскольку под знаком корня стоит сумма положительных чисел, то R* может равняться нулю только в случае, если каждое из этих слагаемых равно нулю в отдельности, т.е.
∑Fkx = 0, ∑Fky = 0 , ∑Fkz = 0 . (8)
Таким образом, для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую из трех выбранных любым образом координатных осей равнялись нулю.
Имея плоскую систему сходящихся сил, всегда можно плоскость, в которой расположены силы, принять за координатную плоскость хОу. Тогда третье условие в формулах (8) выполняется тождественно, и условия равновесия, в рассматриваемом случае, сведутся к двум следующим условиям:
∑Fkx = 0, ∑Fky = 0. (9)
Т.е., для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую из двух выбранных любым образом координатных осей, лежащих в плоскости действия сил данной системы, равнялись нулю.
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
На нашем сайте можно бесплатно скачать:
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Сохранить или поделиться с друзьями
Заказать решение
Поиск формул и решений задач
«Техническая механика. Система сходящихся сил»
Техническая механика
Система сходящихся сил
Сложение двух сил
Сложение системы сходящихся сил
Аналитический способ сложения сил
Равновесие системы сходящихся сил
Сложение трех сил, не лежащих в одной плоскости
Разложение силы по двум и трем заданным направлениям
Система сходящихся сил
1. Сложение двух сил
Геометрическая сумма R двух сил F 1 и F 2 находится по правилу параллелограмма .
Модуль равнодействующей определяется по теоремам sin и cos.
или
==
Система сходящихся сил
1. Сложение двух сил
Система сходящихся сил
2. Сложение трех сил, не лежащих в одной плоскости
Геометрическая сумма
трех сил ,не лежащих в одной плоскости, изображается диагональю параллелепипеда, построенного на этих силах
Система сходящихся сил
3. Сложение системы сходящихся сил
Рассмотрим систему сходящихся сил, т.е. линии действия пересекаются в одной точке.
Последовательно применяя закон параллелограмма сил, придем к выводу, что система сходящихся сил имеет равнодействующую, равную геометрической сумме этих сил и приложенную в (.) пересечения их линий действия.
Для нахождения равнодействующей пользуются силовым многоугольником.
Система сходящихся сил
3. Сложение системы сходящихся сил
=++…+
=
Система сходящихся сил
4. Разложение силы по двум и трем заданным направлениям
Разложить данную силу на составляющие – значит найти такую систему нескольких сил, для которой данная сила является равнодействующей.
Система сходящихся сил
5. Аналитический способ сложения сил.
Этот метод основывается на понятии о проекции силы на ось. Проекция силы на ось есть алгебраическая величина, равная произведению модуля силы на cos угла между силой и положительным направлением оси.
Для двухмерного: F =
Для трехмерного:
5. Аналитический способ сложения сил.
Система сходящихся сил
6. Равновесие системы сходящихся сил
Для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая (а следовательно и главный вектор)была равна нулю.
Следовательно, для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнут или суммы проекций всех сил на каждую ось равны нулю.
=0
=0
=0
Виды равновесия
Безразличное равновесие
Устойчивое равновесие
Неустойчивое равновесие
Виды равновесия
Равновесие называется устойчивым, если возникшая сила стремится вернуть тело в положение равновесия.
Равновесие называется неустойчивым, если при бесконечно малом отклонении тела от положения равновесия, возникает результирующая сила, которая удаляет тело от положения равновесия.
Равновесие называется безразличным, если оно сохраняется при любом смещении ( или повороте) тела.
Вывод о видах равновесия:
1. Устойчиво то положение тела, в котором его потенциальная энергия имеет минимальное значение.
Устойчиво то положение тела, в котором его потенциальная энергия имеет минимальное значение.
2. Устойчивость равновесия тел на плоской поверхности тем больше, чем больше площадь опоры и ниже центр тяжести.
Благодарю за внимание!
Что такое Равновесие?
Что такое равновесие?
Что такое равновесие?
Архитектурные конструкции, как правило, стационарные. Большинство клиентов, строящих чиновники и дизайнеры предпочитают, чтобы их структуры оставались статичными, а не чем двигаться динамично. Существуют определенные условия нагрузки, которые являются динамическими. нагрузки, но в каждом случае возврат к стабильному и статичному состоянию желательно. Такое состояние называется равновесием.
Различные состояния статического равновесия испытываются на протяжении всей жизни. Подумайте о «качели на качелях» на детской площадке или в игре «перетягивание каната».
 В первом случае
двое или более человек сидят на доске, прикрепленной к точке опоры
который допускает вращение. Если каждая из особей на качелях качается на весу
точно такое же количество и сидеть на точно таком же расстоянии от точки опоры
качалка не будет двигаться. Достигнуто состояние равновесия.
Эти двое будут оставаться в покое, пока какое-либо действие не выведет их из равновесия.
В первом случае
двое или более человек сидят на доске, прикрепленной к точке опоры
который допускает вращение. Если каждая из особей на качелях качается на весу
точно такое же количество и сидеть на точно таком же расстоянии от точки опоры
качалка не будет двигаться. Достигнуто состояние равновесия.
Эти двое будут оставаться в покое, пока какое-либо действие не выведет их из равновесия. Таким действием может быть добавление другого человека в систему
или могло случиться так, что один из первоначальных двух изменит свою позицию
немного. В любом случае качели, скорее всего, качнулись бы в одну сторону.
боком и опираться на землю. Новое состояние равновесия было бы
найденный.
В этом случае другой ребенок забрался перед уже сидящим справа. Чтобы привести систему в равновесие, ребенок слева пришлось двигаться назад по доске, пока она не оказалась далеко. Момент, когда двое детей создали вокруг точки опоры, почти удвоился, когда залез второй ребенок. Девушка знала, что единственный способ, которым она могла увеличить величину созданного ею момента означало бы увеличить плечо момента (плечо рычага).
 Таким образом, она отошла назад, пока не стала примерно в два раза больше.
далеко от точки опоры. В этот момент система вернется в равновесие.
Таким образом, она отошла назад, пока не стала примерно в два раза больше.
далеко от точки опоры. В этот момент система вернется в равновесие.Другой пример состояния равновесия — игра в «перетягивание каната». Веревка натягивается между двумя командами; каждый надеется тянуть хоть с силой что равно силе, приложенной противоположной командой. Предположим, что каждая команда на рисунке тянет с силой 220 фунтов. Система находится в равновесии пока каждая команда поддерживает силу натяжения в 220 фунтов. Если устройство будет вставлен между двумя командами вдоль веревки, чтобы измерить величину силы натяжения внутри веревки, она будет составлять 220 фунтов на каждую и каждой точке веревки. Это будет верно в ЛЮБОЙ точке веревки. Равновесие будет потеряно, если кто-либо из конкурентов внезапно отпустите веревку.
А
структура находится в равновесии , когда все силы или моменты, действующие на
они сбалансированы. Это означает, что всякая сила, действующая на тело,
или часть тела, сопротивляется другой равной и противоположной силе
или набор сил, чистый результат которых равен нулю. Сэр Исаак Ньютон обратился к этому
проблема, когда он заметил, что тело в состоянии покоя будет оставаться в покое, пока не будет действовать
на внешней силой. Каждая структура, которую можно увидеть, остается стоять
ежедневно находится в равновесии; оно покоится, и каждый из его членов,
сочетание его членов или любой части члена, которая поддерживает
нагрузки, также находятся в состоянии покоя. Существует чистый результат нулевой во всех направлениях
для всех приложенных нагрузок и реакций.
Сэр Исаак Ньютон обратился к этому
проблема, когда он заметил, что тело в состоянии покоя будет оставаться в покое, пока не будет действовать
на внешней силой. Каждая структура, которую можно увидеть, остается стоять
ежедневно находится в равновесии; оно покоится, и каждый из его членов,
сочетание его членов или любой части члена, которая поддерживает
нагрузки, также находятся в состоянии покоя. Существует чистый результат нулевой во всех направлениях
для всех приложенных нагрузок и реакций.
Это узел Олимпийского стадиона в Мюнхене, разработанный Фраем Отто. Массивная чугунная форма удерживается на месте растягивающими силами, передаваемыми каждым из кабелей, которые к нему присоединены.
На этом рисунке кусок
расщепленный бамбук держат так, чтобы он находился в равновесии. Точка опоры
находится очень близко к центру длины куска. Это иллюстрирует
система, находящаяся в равновесии под действием собственного веса. Затем добавляются два элемента
к бамбуку; кофейный термос и ножницы.
Расколотая бамбуковая балка остается в состоянии равновесия. ножницы отдыхает
на большом расстоянии от точки опоры, чтобы уравновесить более тяжелый вес
термоса с противоположной стороны. Все силы и моменты должны
быть уравновешены так, чтобы система находилась в устойчивом равновесии.
Есть два типа равновесия; Внешний и Внутренний . Внешнее равновесие включает в себя нагрузки и реакции структурных элементов. система в целом. Внутреннее равновесие описывает различные силы, действуют внутри каждого члена системы. Есть условия равновесия которое должно выполняться для обоих типов. Это:
Сумма всех вертикальных сил (Fy) = 0
Сумма всех горизонтальных сил (Fx) = 0
Сумма всех моментов (Mz) = 0
(Сумма всех сил (Fz) = 0)
(Сумма всех моментов (Мои) = 0)
(Сумма всех моментов (Mx) = 0)
Эти шесть уравнений — все, что можно использовать для определения
каждая из сил, действующих на конструкцию. Их мало,
но очень мощный. Первые три являются наиболее распространенными уравнениями и будут
использоваться во всех задачах, связанных с этим курсом. Другой
три необходимы только при рассмотрении трехмерных силовых систем.
Их мало,
но очень мощный. Первые три являются наиболее распространенными уравнениями и будут
использоваться во всех задачах, связанных с этим курсом. Другой
три необходимы только при рассмотрении трехмерных силовых систем.
Равновесие силовой системы
Вопросы к размышлению
Какие еще игры развили у вас чувство равновесия во время игры в качестве
ребенок? Как поддерживается равновесие большим дубом, когда он должен сопротивляться
натиск сильного ветра? Как поддерживается равновесие высоким
Ель Дугласа, когда она должна противостоять натиску сильного ветра? Как
это равновесие, поддерживаемое зданием, когда оно должно сопротивляться натиску
урагана? Как поддерживается равновесие, когда человек едет на велосипеде?
Проблемы
Associated Readings
Schodek. п. 40
Copyright © 1995 Крис Х. Любкеман и Дональд Peting
Copyright © 1996, 1997, 1998 Крис Х.
 Любкеман
ЛюбкеманРавновесие — инженерная механика — Статика
3.1 Введение
3,2 Свободное тело
3.3 Уравнения равновесия для твердого тела
A: равновесие в 2D
3.4 Уравнение равновесия (2d)
3.4.0003 3,5 Диаграммы свободного тела (2d)
3.6 Специальные системы сил (2d)
3.7 Ограничения и равновесие (2d)
3,8 Проблемы решения (2d)
B: равновесие в 3D
3,9 Уравнение равновесия (3d).
3.10 Диаграммы свободного тела (3d)
3.11 Специальные системы сил (3d)
3.12 Ограничения и равновесие (3d)
3.13 Решающие проблемы (3d)
C: Равновесие специальных членов
9000 3,14.3.15 ТРОЙНЫЕ ЧЛЕНЫ
3.16 РЕЗЮМЕ
3.1 ВВЕДЕНИЕ
3.1.1 Понятие равновесия
Понятие равновесия вводится для описания тела, которое неподвижно или движется с постоянной скоростью. На тело в таком состоянии действуют только уравновешенные силы и уравновешенные пары. На него не действует неуравновешенная сила или неуравновешенная пара. В статике понятие равновесия обычно используется при анализе неподвижного тела или, как говорят, находящегося в состоянии статического равновесия.
На него не действует неуравновешенная сила или неуравновешенная пара. В статике понятие равновесия обычно используется при анализе неподвижного тела или, как говорят, находящегося в состоянии статического равновесия.
Концепция равновесия является самой основной и самой важной концепцией в инженерном анализе. Концепция должна быть действительно понята каждым студентом. Способность понимать механику и многие другие инженерные дисциплины зависит от овладения концепцией равновесия.
3.1.2 Частицы и твердые тела
Частицы. Частица — это тело, размер которого не оказывает никакого влияния на результаты механических анализов над ним и, следовательно, его размерами можно пренебречь. Размер частицы очень мал по сравнению с размером анализируемой системы.
Жесткий корпус. Тело состоит из группы частиц. Размер тела влияет на результаты любого механического анализа на нем. Тело называется жестким , когда взаимное расположение его частиц всегда фиксировано и не изменяется при воздействии на тело какой-либо нагрузки (будь то сила или пара). Большинство тел, встречающихся в инженерных работах, можно считать жесткими с точки зрения механического анализа, поскольку деформациями, происходящими внутри этих тел под действием нагрузок, можно пренебречь по сравнению с другими эффектами, вызываемыми нагрузками. Все тела, которые будут изучаться в этой книге, твердые, кроме 9.0140 пружины . Пружины испытывают деформации, которыми нельзя пренебречь при воздействии на них сил или моментов. При анализе в этой книге рассматриваются только эффекты деформаций пружин на твердое тело, взаимодействующее с пружинами, но сами пружины не будут анализироваться как тело.
Большинство тел, встречающихся в инженерных работах, можно считать жесткими с точки зрения механического анализа, поскольку деформациями, происходящими внутри этих тел под действием нагрузок, можно пренебречь по сравнению с другими эффектами, вызываемыми нагрузками. Все тела, которые будут изучаться в этой книге, твердые, кроме 9.0140 пружины . Пружины испытывают деформации, которыми нельзя пренебречь при воздействии на них сил или моментов. При анализе в этой книге рассматриваются только эффекты деформаций пружин на твердое тело, взаимодействующее с пружинами, но сами пружины не будут анализироваться как тело.
3.1.3 Эффекты действия сил на частицы и твердые тела
В общем, сила, действующая на частицу, стремится заставить частицу перемещаться. Кроме того, сила, действующая на тело, не только стремится заставить тело перемещаться (как в случае с частицей), но также стремится заставить тело вращаться вокруг любой оси, которая не пересекается с линией или не параллельна ей. действия силы. Эта склонность к вращению называется «моментом» и количественно измеряется методами, описанными в главе 2.
действия силы. Эта склонность к вращению называется «моментом» и количественно измеряется методами, описанными в главе 2.
3.2 СВОБОДНОЕ ТЕЛО
Механический анализ конструкции, как правило, начинается с применения закона Ньютона ко всей конструкции или к ее части. Чтобы увидеть, что на самом деле происходит с какой-либо конкретной частью структуры, эту часть нужно изолировать от других частей тела. Концепция выделения детали, которая является целью анализа, является очень важной концепцией в механическом анализе. Изолированная часть называется свободным телом .
В этом разделе мы увидим, как изолируется целевая часть и как графически отображается свободное тело, сформированное в процессе изоляции.
3.2.1 Механическая система
Механическая система определяется как система тел, которая может быть изолирована от других тел. Система может быть образована одним телом, частью тела или группой связанных тел. Тела, образующие систему, могут быть как жесткими, так и нежесткими.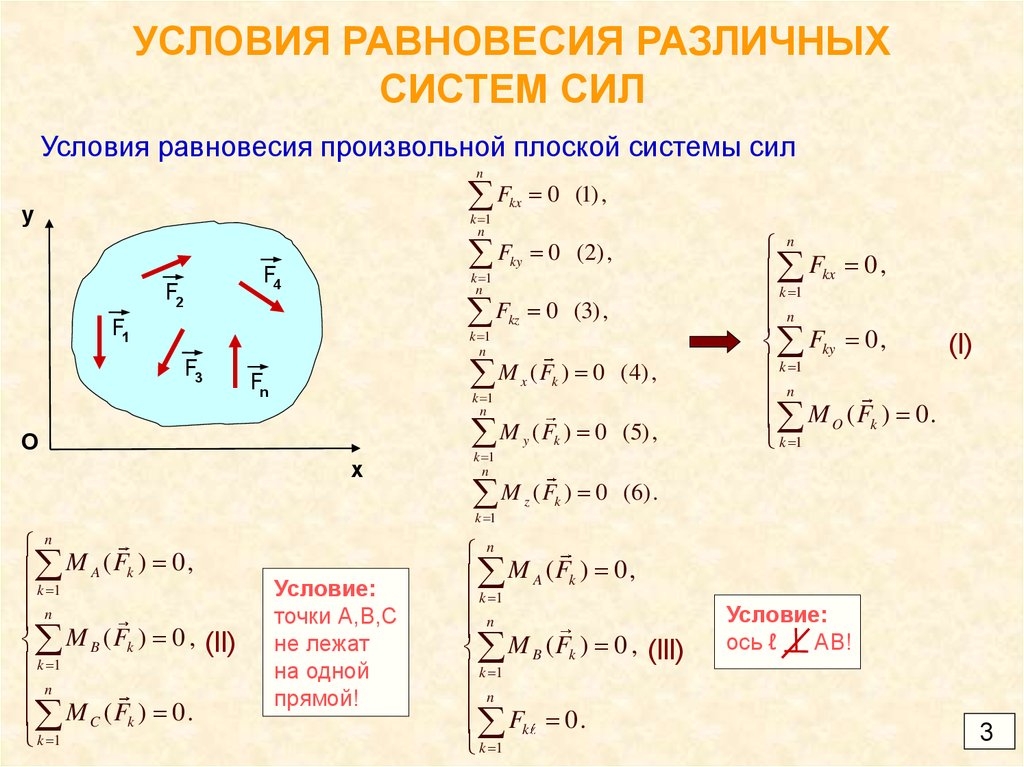 Механическая система может быть твердой, жидкой или даже комбинацией твердого тела и жидкости.
Механическая система может быть твердой, жидкой или даже комбинацией твердого тела и жидкости.
3.2.2 Диаграмма свободного тела (FBD)
Изоляция механической системы достигается путем разрезания и изоляции системы от ее окружения. Изоляция позволяет нам увидеть взаимодействие между изолированной частью и другими частями. Часть, которая была вырезана (воображаемо), образует свободное тело. Диаграмма, которая изображает свободное тело вместе с системой внешних сил, действующих на него за счет его взаимодействия с удаленными частями, называется диаграммой свободного тела (СБТ) изолированной части.
FBD системы тел показывает все нагрузки, действующие на внешнюю границу изолированного тела. К нагрузкам относятся активные силы, действующие на свободное тело удаленными от него частями. Обратите внимание, что внутренние силы, действующие на конструкцию, становятся внешними силами, когда подвергаются воображаемому процессу «разрезания», выполняемому для формирования свободного тела.
В качестве примера рассмотрим конструкцию стрелы погрузчика, рис. 3.1. Предположим, что необходимо провести анализ всей конструкции рычага, когда он несет нагрузку, как показано на рисунке, при этом вес составных частей рычага можно не учитывать по сравнению с весом груза. Предположим также, что все суставы руки не препятствуют вращению вокруг соответствующих суставов, т. е. каждый сустав создает только реактивную силу и не создает никакого реактивного момента. Поскольку направление и смысл каждой реактивной силы неизвестны, следует принять направление и смысл.
Рычаг может быть отделен от кузова погрузчика в точке А, где он прикреплен к кузову грузовика, и в точке С, где на него действует активная сила штока гидравлического поршня. Изолированная рука показана на рис. 3.1(b). На диаграмме FA — сила, создаваемая взаимодействием между точкой A на стреле и кузовом грузовика, FC — сила взаимодействия между точкой C на стреле грузовика и гидравлическим поршнем, м г — вес нагрузки и G — центр тяжести груза. Рисунок 3.1 (b) представляет собой FBD для всей руки для указанных условий.
Рисунок 3.1 (b) представляет собой FBD для всей руки для указанных условий.
Если анализу подлежит только грузовой контейнер, рисуется FBD, показанный на рис. 3.1(c). Если член BC — это то, что нужно проанализировать, FBD показан на рисунке 3.1 (d).
Обратите внимание, что в показанных FBD направление и смысл всех реакций нарисованы произвольно, поскольку предполагается, что они неизвестны. Позже мы научимся определять направление некоторых типов реактивных сил путем наблюдения.
3.2.3 Процедура рисования FBD
FBD рисуется следующим образом:
1. Покажите тело, изолированное от окружающей среды, нарисовав его контур.
2. Покажите на чертеже все нагрузки, действующие на тело. Нагрузки состоят из пар активных сил (вызывающих стремление к движению) и реактивных сил и пар (вызванных какими-либо ограничениями и стремящихся предотвратить движение).
3. Укажите величину и направление каждой нагрузки. Используйте буквы для обозначения неизвестных величин. Для неизвестного направления выберите значение произвольно, но каждая пара взаимодействующих нагрузок должна подчиняться третьему закону Ньютона.
Для неизвестного направления выберите значение произвольно, но каждая пара взаимодействующих нагрузок должна подчиняться третьему закону Ньютона.
4. Показать все размеры, необходимые для расчета моментов.
Здесь следует подчеркнуть, что только правильно построенный FBD даст правильное решение. Самый важный шаг , предпринятый для решения задач в механике, — это рисование FBD.
————————————————————————
ПРИМЕР ЗАДАЧИ
EP3.1 На рис. трактор, который содержит груз массой м и рычажный механизм. Соединение в точке А является штифтовым соединением. Нарисуйте FBD ковша, изолированного от всех остальных элементов механизма ковша.
Обратите внимание, что штифтовое соединение может создавать только реактивную силу, но не может создавать реактивную пару. Предположим, что сила, действующая на гидравлический цилиндр в точке B, действует вдоль линии стержня. Для сил, направление которых неизвестно, их можно представить двумя перпендикулярными составляющими.
Весом совка и весом звеньев пренебречь.
Рисунок MC3.1
Решение
Вес груза действует вниз в центре тяжести Г . Реактивная сила в точке В действует вдоль оси гидроцилиндра. Его смысл неизвестен, но можно предположить, что он действует в любом смысле. Реакция в точке А неизвестна ни по направлению, ни по смыслу. Следовательно, он представлен двумя перпендикулярными компонентами с произвольно заданным смыслом.
FBD показан на рисунке MC3.1(1)
——————— УЧЕБНЫЕ ЗАДАЧИ TP3.1-TP3.5 ———————
3 .3 УРАВНЕНИЯ РАВНОВЕСИЯ ДЛЯ A ЖЕСТКИЙ КОРПУС
Твердое тело, на которое действует любая приложенная нагрузка, будет иметь тенденцию к поступательному перемещению и вращению вокруг определенной оси. Тенденция к перемещению обусловлена действием равнодействующей силы на тело, а тенденция к вращению обусловлена действием равнодействующей пары. На теле наступит равновесие, если равнодействующая сила и равнодействующая пара равны нулю. Математически равновесие определяется условиями:
Математически равновесие определяется условиями:
∑ F = 0
(3.1)
∑ M = 0
, где ∑ F — результирующая сила, а ∑ M — результирующий момент. все силы, действующие на тело, равны нулю. Второе выражение говорит о том, что сумма моментов относительно любой оси должна быть равна нулю. Два условия, представленные уравнением 3.1, являются необходимыми и достаточными для равновесия. Говорят, что это необходимо, потому что выполнение только первого условия приведет к неравновесию с точки зрения вращения. Точно так же, если выполняется только второе условие, возникает неравновесие с точки зрения перевода. Два условия называются достаточными, потому что равновесие имеет место, когда оба условия выполняются без необходимости каких-либо дополнительных условий.
В учебных целях изучение равновесия в этой книге будет разделено на два этапа:
(1) равновесие тел, на которые действуют плоские системы сил, и
(2) равновесие тел, на которые действуют плоские системы сил. общая система пространственных сил.
общая система пространственных сил.
В разделах 3.4-3.8 обсуждается равновесие в двух измерениях (системы плоских сил), а в разделах 3.9-3.11 обсуждается равновесие в трех измерениях (системы пространственных сил).
А: РАВНОВЕСИЕ В 2D
3.4 УРАВНЕНИЯ РАВНОВЕСИЯ (2D)
3.4.1 Общие уравнения
Результирующий вектор силы для плоской системы сил действует на панели исходной системы сил. Результирующий вектор момента действует перпендикулярно этой плоскости. Следовательно, результирующий вектор силы может быть представлен двумя его перпендикулярными компонентами, действующими на плоскости. С другой стороны, результирующий вектор момента может быть представлен круговой стрелкой, которая указывает на его смысл действия. Например, если поверхность этой книги принять за плоскость действия данной системы сил, скажем плоскость х-у, то получаются следующие соотношения:0004
∑ F = ∑ F x + ∑ F y
∑ M O | г × F | = ∑ Fd
, где d — расстояние по перпендикуляру между любым центром момента O и линией действия F .
Второе выражение в этом уравнении дает величину результирующего момента. Направление ∑ M O 9вектор 0093 перпендикулярен этой странице; его направление действия обозначено круговой стрелкой, которая действует по часовой стрелке или против часовой стрелки, в зависимости от направления r и F , рисунок 3.2.
Рис. 3.2
Используя приведенные выше соотношения, уравнение равновесия для двумерного случая можно записать в скалярной форме: 0 (3.2)
∑ M O = 0
Первые два уравнения в уравнении (3.2) утверждают, что сумма компонентов силы в направлениях x и y равна нулю. Третье выражение утверждает, что момент относительно любой точки O (т. е. относительно любой оси, перпендикулярной плоскости x-y и проходящей через O ) равен нулю.
Все три выражения уравнения (3.2) необходимы для равновесия. Кроме того, если тело поддерживается таким образом, что все силы, действующие на тело, могут быть определены с помощью одного лишь уравнения (3.2), то говорят, что этого уравнения достаточно. На этом раннем этапе обучения студенты должны решать только задачи, которые можно решить с помощью уравнения (3.2). Таким образом, уравнение (3.2) необходимо и достаточно для анализа равновесия всех тел в этой книге.
Кроме того, если тело поддерживается таким образом, что все силы, действующие на тело, могут быть определены с помощью одного лишь уравнения (3.2), то говорят, что этого уравнения достаточно. На этом раннем этапе обучения студенты должны решать только задачи, которые можно решить с помощью уравнения (3.2). Таким образом, уравнение (3.2) необходимо и достаточно для анализа равновесия всех тел в этой книге.
Обратите внимание, что для описания равновесия на плоскости существует только три независимых уравнения. Следовательно, можно решить только три неизвестных значения. На начальном этапе обучения студенты часто совершают ошибку, добавляя число к уравнению, принимая во внимание дополнительные моменты. Здесь подчеркивается, что такие усилия бесплодны, поскольку они приведут к уравнениям, которые не являются независимыми и дублируют одно из трех основных уравнений, данных в уравнении (3.2).
В общем случае выражения в уравнении (3.2) должны решаться одновременно.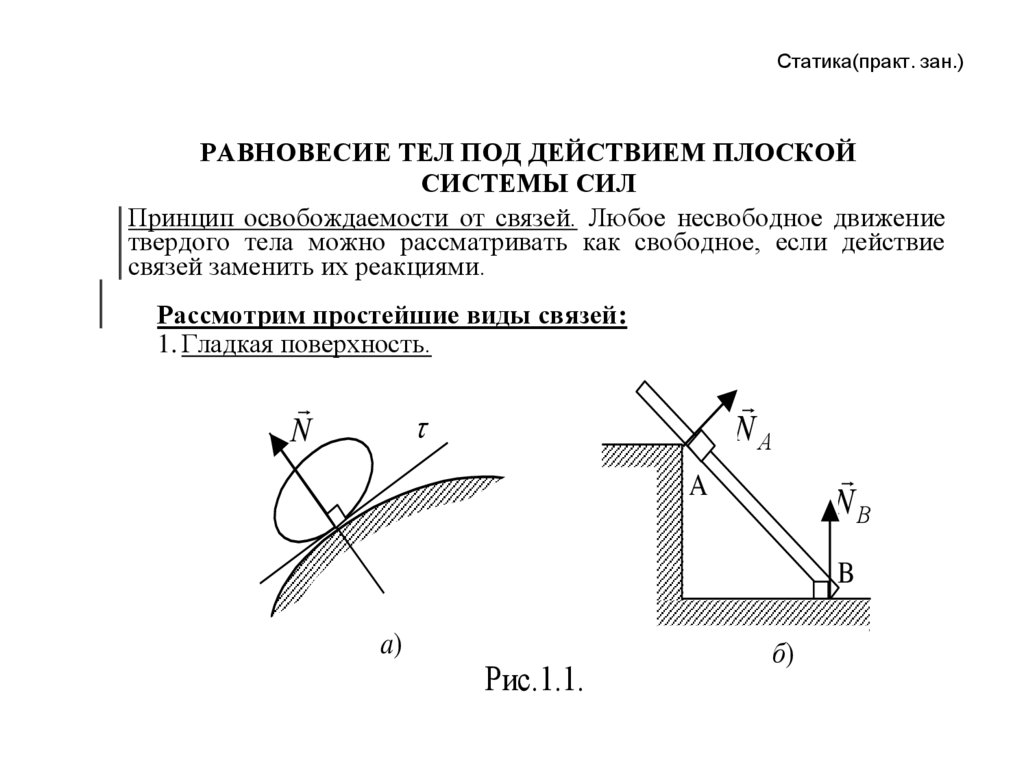 Однако этого можно избежать, приняв за центр момента O точку пересечения двух неизвестных сил. Делая это, третье неизвестное может быть решено напрямую. Кроме того, процесс получения решения можно упростить, задав ориентацию системы осей x-y таким образом, чтобы получить простейшую равнодействующую систему сил в направлении осей.
Однако этого можно избежать, приняв за центр момента O точку пересечения двух неизвестных сил. Делая это, третье неизвестное может быть решено напрямую. Кроме того, процесс получения решения можно упростить, задав ориентацию системы осей x-y таким образом, чтобы получить простейшую равнодействующую систему сил в направлении осей.
3.4.2 Альтернативные уравнения
Уравнение (3.2) является исходным уравнением, наиболее часто используемым для решения задачи о равновесии тел. Однако есть еще две комбинации 90 140 трех 90 141 других выражений, которые можно использовать для представления условий, проявляемых уравнением (3.2). Эти комбинации можно использовать в качестве альтернативы уравнению (3.2).
Первое альтернативное уравнение:
F x = 0 или F Y = 0
M A = 0
M A = 0
0141 (3.3)M B = 0
Это уравнение включает одно выражение для силы и два выражения для момента.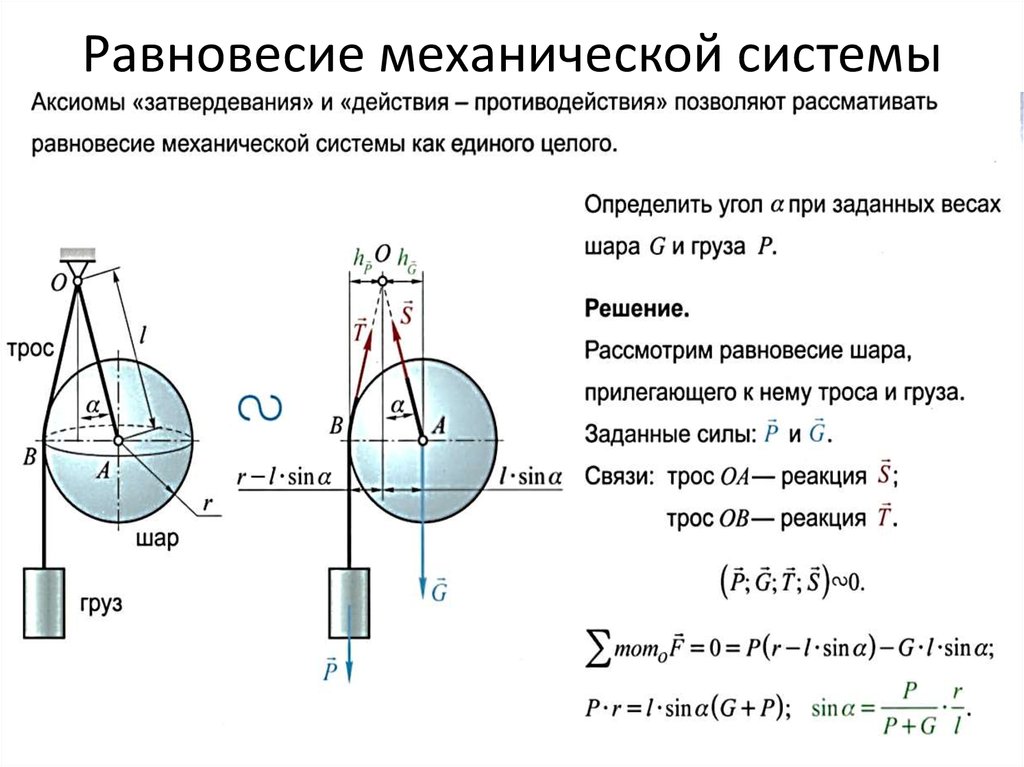 Чтобы использовать это первое альтернативное уравнение, точки A и B не должны лежать на линии, перпендикулярной направлению суммирования сил. (Например, его нельзя использовать для решения механизма на рис. 3.3(а), если для суммирования сил выбрано направление x).
Чтобы использовать это первое альтернативное уравнение, точки A и B не должны лежать на линии, перпендикулярной направлению суммирования сил. (Например, его нельзя использовать для решения механизма на рис. 3.3(а), если для суммирования сил выбрано направление x).
Второе альтернативное уравнение включает выражение момента tiga, т.е.:
∑ M A = 0
∑ M B = 0 (3.4)
∑ M C = 0
Equation (3.4) can be used on condition that points A , B и C не лежат на одной прямой. Его нельзя, например, использовать для решения механизма на рис. 3.3(b).
Можно доказать, что уравнение (3.3) и уравнение (3.4) удовлетворяют тем же условиям, что и уравнение 3.2 при условии соблюдения условий, связанных с их применением. Следовательно, любое из альтернативных уравнений можно использовать в качестве замены уравнения (3. 2). Пока используются три, но не более трех из приведенных выше уравнений области (т. е. два уравнения силы и одно уравнение момента, или одно уравнение силы и два уравнения момента, или три уравнения момента), комбинация формируется из независимых уравнений .
2). Пока используются три, но не более трех из приведенных выше уравнений области (т. е. два уравнения силы и одно уравнение момента, или одно уравнение силы и два уравнения момента, или три уравнения момента), комбинация формируется из независимых уравнений .
Обратите внимание, что
3.5 ДИАГРАММЫ СВОБОДНОГО ТЕЛА (2D)
3.6 Специальные системы сил (2d)
3.7 Ограничения и равновесие (2d)
3.8 Проблемы с решением (2d)
B: равновесие в 3D
3.9 Уравнения равновесия (3D)
3.10. 3d)
3.11 Специальные системы сил (3d)
3.12 Ограничения и равновесие (3d)
3.13 Решающие проблемы (3d)
C: равновесие специальных членов
3.14 Члены Двухформ
3,15 Три-Фор. ЧЛЕНЫ
3.16 РЕЗЮМЕ
В этой главе вводится понятие равновесия . Условия равновесия и уравнения равновесия частиц и твердых тел приведены в скалярной и векторной формах.