Техническая механика сжатие и растяжение: Лекция по технической механике на тему "Растяжение (сжатие)" (СПО)

Содержание

Растяжение и сжатие

Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор -продольная сила.
Продольные силы меняются по длине бруса. При расчётах после определения величин продольных сил по сечениям строится график — эпюра продольных сил.
Условно назначают знак продольной силы Если продольная сила направлена от сечения, то брус растянут. Растяжение считают положительной деформацией.
Если продольная сила направлена к сечению, то брус сжат. Сжатие считают отрицательной деформацией. Примеры построения эпюр

Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплён в стене (закрепление «заделка») (рис. 30.)
Делим брус на участки закрепления.

Участком закрепления считают часть бруса между внешними силами.
На представленном рисунке 3 участка нагружения.

Расчёт начинаем со свободного конца бруса, чтобы не определять величины реакции в опорах.
Участок 1 :

Продольная сила положительна, участок 1 растянут. Участок 2:

=F. Продольная сила положительна, участок 2 растянут.
Участок .’
Продольная сила отрицательна, участок з сжат. Полученное значение равно реакции в заделке.
Под схемой бруса строим эпюру продольной силы (рис.31.).
Эпюра продольной силы строится только под брусом.

Эпюрой продольной силы называется график распределения продольной силы вдоль от бруса.
Ось эпюры параллельна продольной оси. Нулевая линия проводится тонкой линией. Значения чисел откладывают от оси, положительные — вверх, отрицательные вниз.

В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.

Правило контроля: в месте приложения внешней силы на эпюре должен быть скачек на величину приложенной силы.
На эпюре проставляют значения Nz. Величины продольных сил откладывают в заранее выбранном масштабе.
Эпюра по контуру обводится толстой линией и обводится поперёк оси.
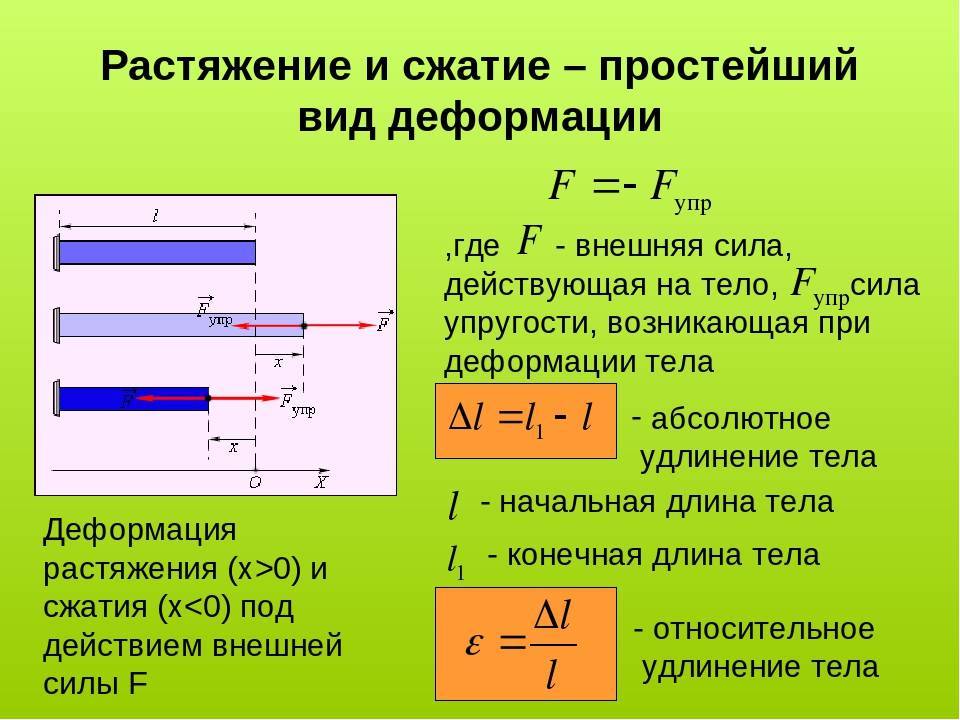
Принцип смягчения граничных условий гласит: в точках тела, удалённых от мест нагрузки, модуль внутренних сил мало зависит от способа закрепления. Поэтому при решении задач не уточняют способ закрепления.

Деформация растяжения-сжатия: характеристики, расчеты, параметры

В машиностроении, строительстве и архитектуре при расчетах прочности и жесткости материалов используется математический аппарат технической механики. Деформация растяжения – одно из ключевых понятий, характеризующее механические процессы, происходящие в материалах при приложении к ним внешних воздействий.

Для наглядности изучаются изменения, происходящие в брусе с постоянным сечением, характерные для упругой деформации при приложении внешних усилий.

Закон Гука (английский физик Р. Гук, 1653-1703) для упругой деформации растяжения/сжатия гласит, что нормальное напряжение находится в линейной зависимости (прямо пропорционально) к относительному удлинению/укорочению. Математический аппарат технической механики описывает эту формулу следующим образом:

Коэффициент пропорциональности E (модуль упругости, модуль Юнга) – величина определяющая жесткость материала, единица измерения – паскаль (ПА).

Его значения были установлены эмпирическим путем для большинства конструкционных материалов, необходимую информацию можно почерпнуть в справочниках по машиностроению. Относительная деформация является отношением изменения длины бруса к его изначальным размерам, это безразмерная величина, которая иногда отражается в процентном соотношении.

При растяжении или сжатии у бруса меняется не только длина, но происходят поперечные деформации: при сжатии образуется утолщение, при растяжении толщина сечения становится меньше. Величины этих изменений находятся в линейной зависимости друг от друга, причем установлено, что коэффициент пропорциональности Пуассона (фр. ученый С. Пуассон, 1781-1840) остается всегда неизменным для исследуемого материала.

Внутренние усилия при растяжении и сжатии

При приложении к брусу с постоянным сечением внешних воздействий, действие которых в любом поперечном разрезе направлено параллельно его центральной оси и перпендикулярно сечению, с ним происходит следующий вид деформации: растяжение или сжатие.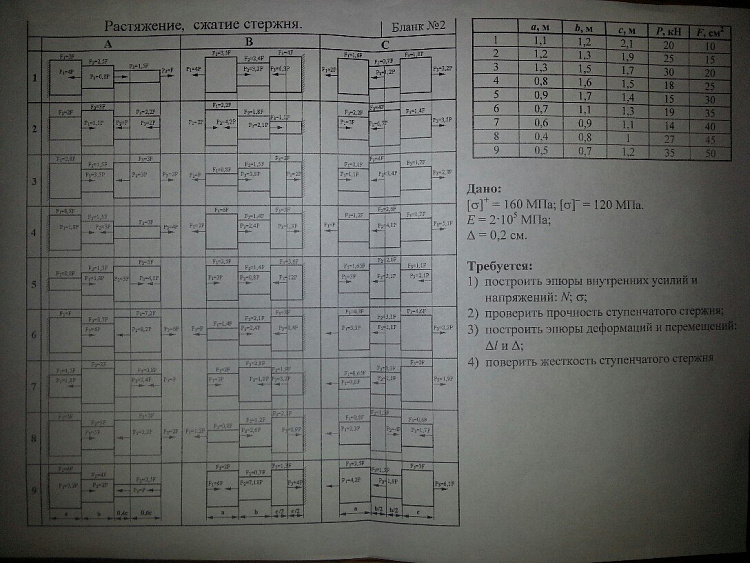 На основе гипотезы о принципе независимости внешнего воздействия для каждого из поперечных разрезов можно рассчитать внутреннее усилие как векторную сумму всех приложенных внешних воздействий. Растягивающие нагрузки в сопромате принято считать положительными, а сжимающие отрицательными.

Рассмотрев произвольный разрез бруса или стержня, можно сказать что внутренние напряжения равны векторной сумме всех внешних сил, сгруппированных по одной из его сторон. Это верно только с учетом принципа Сен-Венана (фр. инженер А. Сен-Венан, 1797-1886) о смягчении граничных условий, т.к. распределение внутренних усилий по поверхности разреза носит сложный характер с нелинейными зависимостями, но в данном случае значением погрешности можно пренебречь как несущественным.

Применяя гипотезу Бернулли (швейцарский математик, И. Бернулли, 1667-1748) о плоских сечениях, для более наглядного представления процессов распределения сил и напряжений по центральной оси бруса можно построить эпюры. Визуальное представление более информативно и в некоторых случаях позволяет получить необходимые величины без сложных расчетов.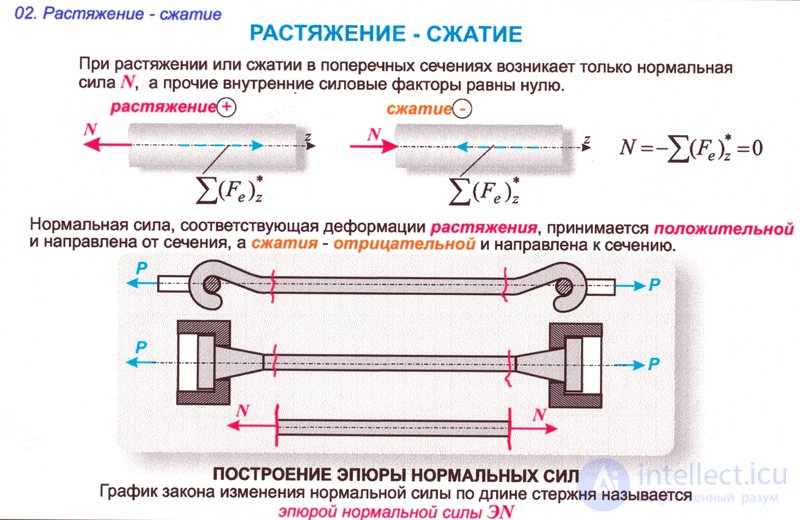 Графическое представление отражает наиболее нагруженные участки стержня, инженер может сразу определить проблемные места и ограничиться расчетами только для критических точек.

Все вышесказанное может быть применимо при квазистатической (система может быть описана статически) нагрузке стержня с постоянным диаметром. Потенциальная энергия системы на примере растяжения стержня определяется по формуле:

U=W=FΔl/2=N²l/(2EA)

Потенциальная энергия растяжения U концентрируется в образце и может быть приравнена к выполнению работы W (незначительное выделение тепловой энергии можно отнести к погрешности), которая была произведена силой F для увеличения длины стержня на значение абсолютного удлинения. Преобразуя формулу, получаем, что вычислить значение величины потенциальной энергии растяжения можно, рассчитав отношение квадрата продольной силы N помноженной на длину стержня l и удвоенного произведения модуля Юнга E материала на величину сечения A.

Как видно из формулы, энергия растяжения всегда носит положительное значение, для нее невозможно применить гипотезу о независимости действия сил, т. к. это не векторная величина. Единица измерения – джоуль (Дж). В нижней части формулы стоит произведение EA – это так называемая жесткость сечения, при неизменном модуле Юнга она растет только за счет увеличения площади. Величина отношения жесткости к длине бруса рассматривается как жесткость бруса целиком.

Напряжения при растяжении сжатии

Используя гипотезу Бернулли для продольной упругой деформации стержня, можно определить продольную силу N как равнодействующую всех рассредоточенных по сечению внутренних усилий. Гипотеза Бернулли совместно с гипотезой о ненадавливании волокон позволяет сказать, что σ в произвольной точке разреза будут постоянны, т. к. реакция продольных волокон одинакова на всем поперечном разрезе. Для определения величины нормального напряжения σ используется следующая формула:

Напряжение для упруго деформированного стержня описывается как отношение внутренней силы N к площади сечения A. Считается положительным при растяжении, при сжатии рассматривается как отрицательное.

Абсолютная деформация зависит от жесткости сечения, величины продольной силы и длины бруса. Зависимость можно описать по следующей формуле:

Δl=Nl/EA

Таким образом, методика расчета величины абсолютного изменения длины такова: необходимо просчитать отношение значения продольной силы N умноженной на длину стержня l и жесткости сечения (произведение модуля Юнга E на площадь сечения A).

В реальных расчетах на брус действует достаточно много разнонаправленных сил, для решения таких задач требуется построение эпюр, которые могут наглядно показать какие напряжения действуют на разных участках, чем обусловлена деформация при растяжении и сжатии.

В рамках такой квазистатической (условно статической) системы, как брус или стержень с переменным сечением или отверстием, потенциальная энергия растяжения может быть рассмотрена как сумма энергий однородных участков. При проведении расчетов важно правильно разделить стержень на участки и смоделировать все участвующие в процессе силы и напряжения.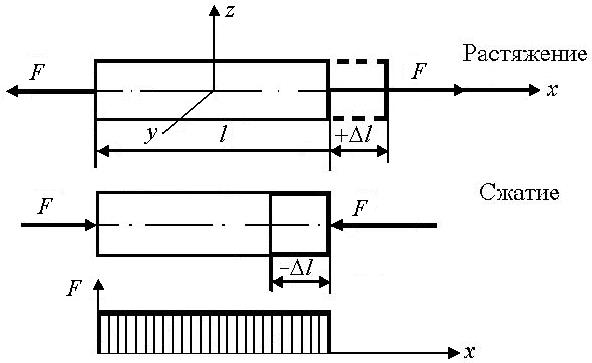 Для реальных расчетов построение эпюр – сложная задача, которая требует от инженера хорошего понимания действующих на деталь нагрузок. Например, вал со шкивами разного диаметра требует сначала определения критических точек и разбивки на соответствующие участки, затем построения графиков по ним.

Деформации при растяжении сжатии

При растяжении/сжатии бруса могут возникать 2 вида деформации. Первый – упругая, второй – пластическая. Для упругой деформации характерно восстановление первоначальных параметров после прекращения воздействия. В случае пластической стадии деформации материала он утрачивает и не восстанавливает форму и размеры. Величина воздействия для перехода одного вида в другой называется пределом текучести.

Для расчета перемещения при растяжении бруса или стержня следует использовать метод разделения на участки, в рамках которых осуществляется приложение внешних воздействий. В точках воздействия силы следует вычислить величину изменения длины, используя формулу: Δl=Nl/EA. Как видно она зависит от жесткости сечения, длины бруса или стержня и величины действующей продольной силы. Итоговым перемещением для бруса целиком будет сумма всех частичных перемещений, рассчитанных для точек приложения силы.

Поперечные деформации бруса (становится более толстым при сжатии и тонким при растяжении) также характеризуются абсолютной и относительной величиной деформации. Первая – разность между размером сечения после и до приложения внешних воздействий, вторая – отношение абсолютной деформации к его исходному размеру. Коэффициент Пуассона, отражающий линейную зависимость продольной и поперечной деформаций, определяет упругие качества материалов и считается неизменным для растяжения и сжатия. Продольные наиболее наглядно отражают процессы, происходящие в брусе или стержне при внешнем воздействии. Зная величину любой из них (продольной или поперечной) и используя коэффициент Пуассона, можно рассчитать значение неизвестной.

Для определения величины деформации пружины при растяжении можно применить закон Гука для пружин:

F=kx

В данном случае х – увеличение длины пружины, k – коэффициент жесткости (единица измерения Н/м), F – сила упругости, направленная в противоположную от смещения сторону. Величина абсолютной деформации будет равна отношению силы упругости к коэффициенту жесткости. Коэффициент жесткости определяет упругие свойства материала, используемого для изготовления, может быть использован для выбора материала изготовления в условиях решения конкретной задачи.

Расчеты на прочность и жесткость

Прочность характеризует способность конструкционного материала сопротивляться внешним воздействиям без разрушений и остаточных изменений. Жесткость находится в линейной зависимости от модуля Юнга и размера сечения. Чем больше площадь, модуль упругости не меняется, тем больше жесткость. В общем случае жесткость подразумевает способность деформироваться без значительных изменений. Коэффициент запаса прочности – безразмерная величина, равная отношению предельного напряжения к допустимому. Запас прочности характеризует штатный режим работы конструкции даже с учетом случайных и не предусмотренных нагрузок. Наименьшим запасом прочности обладают пластические (1.2-2.5) и хрупкие (2-5) материалы.

Применение в расчетах этих коэффициентов позволяет, например, рассчитать опасную толщину для стержня, при которой может возникнуть максимальное нормальное напряжение. Используя коэффициент прочности и возможное предельное напряжение возможно произвести расчет необходимого диаметра вала, который гарантированно обеспечит упругую деформацию и не приведет к пластической. Для инженеров-экономистов важны расчеты наименьших безопасных размеров деталей конструкции по заданным нагрузкам.

Большинство практических расчетов на прочность и жесткость производятся для получения минимальных значений геометрических размеров конструкционных элементов и деталей машин в условиях известных внешних воздействий и необходимого и достаточного запаса прочности. Может решаться обратная задача получения значений предельных нагрузок при условии сохранения геометрических размеров и для конкретного материала.

Сложные конструкции могут быть разделены на элементарные части, для которых будут производиться расчеты, затем полученные результаты интерпретируются в рамках всей системы, для этого удобно строить эпюры распределения внешних воздействий и внутренних напряжений статически определенной системы.

С помощью известной жесткости материала делают расчеты максимально возможной длины балки или стержня (вала) при условии неизменности его сечения. Для ступенчатых валов необходимо строить эпюры воздействия внешних сил и возникающих в точках их приложения внутренних напряжений в критических точках. От правильно построенной теоретической модели будет зависеть насколько эффективно и долго прослужит вал для станка, не разрушится ли он от динамических крутящих моментов. На этапе проектирования можно выявить потенциальные слабые точки и рассчитать необходимые параметры для заданного предела прочности.

С расчетами на прочность связаны такие понятия, как срез и смятие. Срез проявляется в виде разрушения детали соединения в условиях возникновения в ее поперечном сечении перпендикулярной к нему и достаточной силы.

При расчетах соединений используют пределы текучести используемых материалов и коэффициенты запаса прочности, вычисляют максимально возможные напряжения.

Исследования на прочность обычно подразумевают решение нескольких задач: в условиях проведения поверочного расчета на проверку прочности при известных усилиях и площади сечения оценивают фактический коэффициент запаса прочности; подбор оптимального диаметра при заданных нагрузках и допустимом напряжении; вычисляют грузоподъемность или несущую способность с помощью определения внутреннего усилия при известной площади сечения и напряжении.

Прочностные расчеты при разных видах воздействий в рамках условно статических систем сложны, требуют учета многих, иногда не очевидных, факторов, их практическая ценность заключается в вычислении допустимых размеров конструкционных материалов для заданных параметров запаса прочности.

Напряжение и сжатие — разница между растяжением и сжатием

от Civil Lead

Содержание

Растяжение и сжатие

Растяжение и сжатие — две основные силы, действующие на любую конструкцию/здание. Каждый материал может выдерживать определенное напряжение, а также сжатие.

Некоторые материалы обладают отличной способностью выдерживать сжатие, а некоторые материалы легко выдерживают растяжение.

Некоторые материалы могут эффективно выдерживать как растяжение, так и сжатие. Например, если вы потянете веревку, она может выдержать значительное натяжение, а если вы нажмете, она может значительно сопротивляться сжатию, только изгибаться.

Что такое напряжение?

Сила, которая растягивает материал, относится к силе натяжения и пытается растянуть материал.

Когда мы привязываем объект к веревке, вес объекта тянет за веревку и пытается удлинить шнур. Эта сила называется силой натяжения.

Из-за этого натяжения молекулы, образующие струну, отклоняются от своего положения равновесия.

Молекулы пытаются вернуться в свое положение равновесия. При этом они пытаются оттянуть объект, пытаясь удлинить его.

Если силы уравновешиваются, то система становится равновесной. Но тем не менее струна следует за натяжением и, возможно, удлинилась за пределы своей первоначальной длины.

Напряжение на объекте может быть представлено численно как:

T = мг + мА

Где;
T = напряжение в Н (Ньютонах)
m = масса, кг
g = сила тяжести, 9,8 м/с2
A = ускорение, м/с2

Сила растяжения на единицу площади относится к растягивающему напряжению Отношение увеличения длины к исходной длине материала называется деформацией растяжения .

Что такое сжатие?

Сила, сжимающая или укорачивающая материал, относится к силе сжатия и пытается сжать объект.

Например, если мы надавим на пружину, мы приложим к ней сжимающую силу. Если сжимающая сила действует в одном направлении, она относится к одноосной сжимающей силе.

Если сжимающая сила действует в двух или трех направлениях, они называются двухосными и трехосными сжимающими силами.

Сила сжатия обычно измеряется в ньютонах (Н) и представляется как

Н = ма

Где

m = масса в кг

a = ускорение свободного падения в н/мм2

Сила сжатия на единицу сечения относится к сжимающим напряжениям . А отношение уменьшения длины к первоначальной длине обозначается как деформация сжатия .

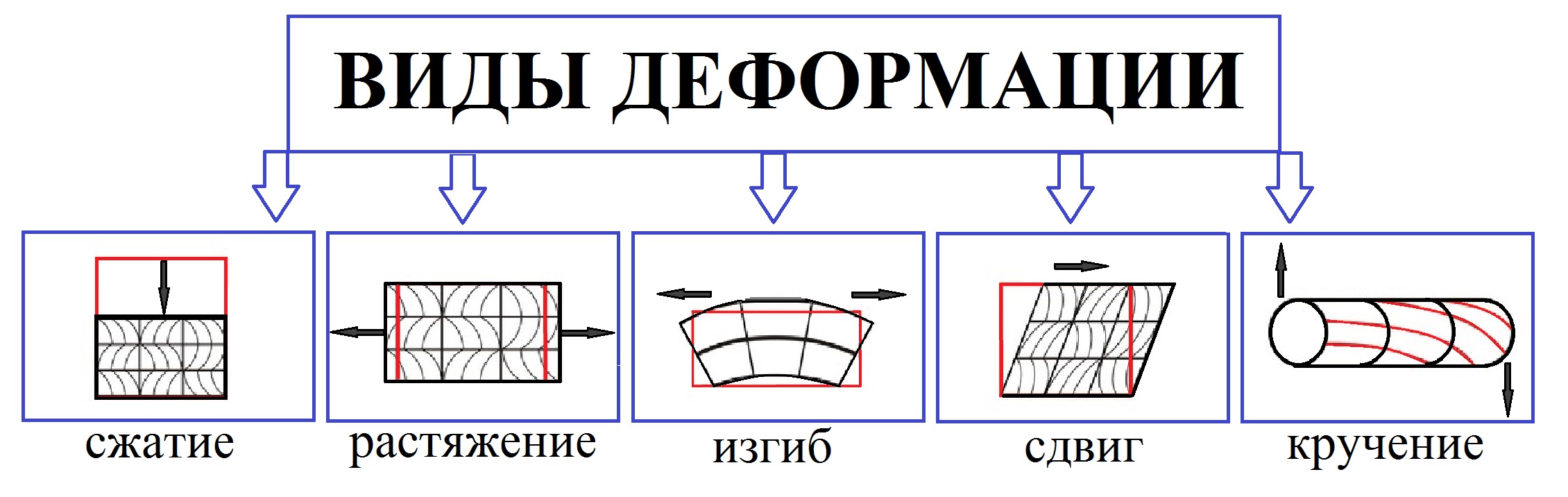
Напряжение изгиба

Когда материал изгибается, он одновременно испытывает растяжение и сжатие.

Например, рассмотрим балку . Когда к балке приложена нагрузка, ее нижняя часть испытывает растяжение, а верхняя — сжатие.

В то время как слой, называемый нейтральной осью, проходит вдоль середины балки, как ни странно, он испытывает нулевые напряжения при изгибе.

Также прочтите – Что такое поперечная сила и изгибающий момент?

Силы растяжения и сжатия необходимо учитывать при проектировании конструкции.

Если мы построили конструкцию из материала, который не выдерживает растягивающих и сжимающих усилий из-за постоянных и временных нагрузок, то конструкция может разрушиться.

Следовательно, все конструкции должны быть спроектированы так, чтобы выдерживать воздействующие на них силы.

Силы растяжения и сжатия существуют во всех конструкциях. Инженер должен спроектировать конструкцию, способную выдерживать эти силы без коробления и поломки.

Изгиб происходит, когда сжимающая сила превышает способность материала выдерживать сжатие, а защелкивание происходит, когда сила натяжения превышает способность материала выдерживать растяжение.

Самый лучший способ управлять этими силами — либо передавать их, либо рассеивать.

Для передачи силы переместите ее из зоны уязвимости в место силы — пространство, предназначенное для обработки силы.

Чтобы рассеять силу, рассредоточьте ее по большой площади, чтобы ни одно место не подверглось воздействию концентрированной силы.

Арочный мост — отличный пример рассеяния, а висячий мост — прекрасный пример передачи.

Разница между растяжением и сжатием

С.№.	Растяжение	Сжатие
1.	Сила растяжения пытается удлинить материал.	Напротив, сжатие пытается укоротить тело.
2.	Растягивает материалы.	Сжимает материал.
3.	При растяжении все силы оттягиваются от объекта.	При сжатии силы, действующие на материал, толкают его к телу.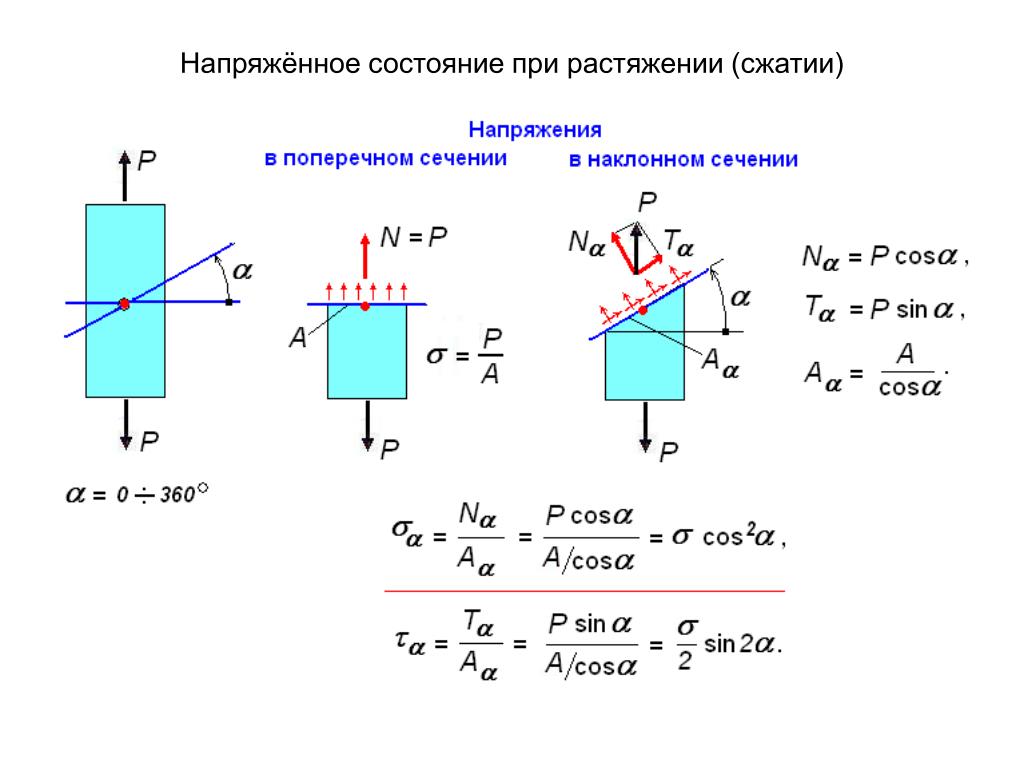
4.	Натяжение может быть связано с натяжением концов материала.	Сжатие может быть связано с толчком краев тела к центру.
5.	Как правило, натяжение относится к струнам.	Можно наносить на любой материал.
6.	Сила растяжения направлена наружу от тела.	При сжатии движение силы, действующей на тело, всегда направлено внутрь тела.

См. также

Двутавровая балка и двутавровая балка – 15 различий между двутавровой и двутавровой балками

Разница между длиной колена и длиной развития

Разница между Уплотнение и уплотнение почвы

Разница между мягкой и нержавеющей сталью

Разница между мрамором и гранитом

Разница между МДФ и ДСП

ньютоновской механики.

Как узнать, находятся ли элементы в растяжении или сжатии при использовании метода сечений?

спросил 4 года 3 месяца назад

Изменено 3 года, 11 месяцев назад

Просмотрено 34к раз

$\begingroup$

Итак, недавно мы начали заниматься структурным анализом в моем инженерном классе и занимаемся фермами. Однако я не совсем уверен, как концептуально работает метод разделов. Я получаю правильные цифры, но я не уверен, как указания в моем FBD связаны с тем, находится ли элемент в растяжении или сжатии. Я нашел на слайде 5 первого результата Google, что

Когда сила стержня направлена на соединение, оно прикреплено к, член находится в сжатии. Если эта сила указывает в сторону от сустава, к которому он прикреплен, член находится в напряжении.

Забираю мой FBD, означает ли это, что силы ML, CL и CD следует рассматривать в напряжении, если это члены, которые я вырезал?

Причина, по которой я запутался, заключается в том, что исходная система выглядит так поэтому ML, CL и CD действуют «сжимающе» по отношению к мосту.

Мой профессор еще не вдавался в подробности об этом в классе, и предоставленные видео не очень помогли, поэтому объяснение/ссылка на объяснение того, как определить «направление» (сжатие/натяжение) членов было бы большим подспорьем.

ньютоновская механика
силы
векторы
диаграмма свободного тела
статика

$\endgroup$

$\begingroup$

Судя по всему, вы вырезаете элементы CD, CL и ML и анализируете оставшуюся часть слева. Далее, я предполагаю, что вы правильно рассчитали силу реакции (100 кН) на штифтовой опоре A. Наконец, я предполагаю, что вы выбрали направления неизвестных сил, действующих на элементы CD, CL и ML, произвольно, как находящиеся под напряжением (от центра тяжести).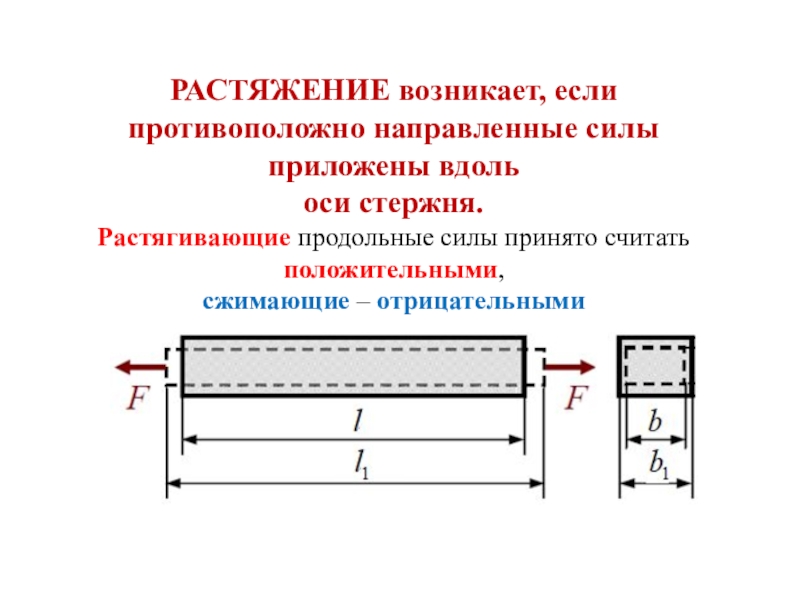

суставы).

Можно предположить направления сил, но чтобы определить, каковы направления на самом деле, вы должны вычислить их фактические значения. Вы делаете это, (1) суммируя вертикальные силы и приравнивая их к нулю, (2) суммируя горизонтальные силы и приравнивая их к нулю и (3) суммируя моменты сил относительно A и приравнивая их к нулю. Если величина расчетной силы положительна и направлена в сторону от сустава, у вас есть напряжение. Если он отрицательный и направлен в сторону от сустава, у вас компрессия.

У вас есть только одна неизвестная вертикальная сила, CL. Его ценность и, следовательно, направление будут очевидны. У вас есть две неизвестные горизонтальные силы, ML и CD. Чтобы их сумма равнялась нулю, один из них должен быть выбран в неправильном направлении. Другими словами, один из них должен быть в сжатом состоянии. CD не вносит никакого вклада в точку A, а ML и CL вносят. Поскольку теперь вы знаете CL, суммирование моментов всех сил относительно A даст вам ML.