Примеры решения задач по строительной механике(расчет составной балки)

                                                                    Задача 32 (300).

    Для балки требуется :

    1. Используя индивидуальный шифр выбрать : расчётную схему балки, её размеры, действующую нагрузку.

    2. Провести кинематический анализ балки, построив её этажную схему.

    3. Рассчитать отдельные простые балки и построить для них эпюры М и Q.

    4. Построить эпюры усилий для исходной составной балки.

    5. Построить линии влияния : двух опорных реакций (по собственному выбору), двух изгибающих моментов Mi, Mk и двух поперечных сил Qi, Qk (номера точек i, k даются в таблице).

    6. Загрузить одну из линий влияния (по выбору) заданной нагрузкой, определить по ней соответствующие усилие и сравнить его со значением, полученным в п. 3.

    Дано :

№ схемы	№ загружения	L1 ,    м	L2 ,    м	L3,     м	а,     м	F1,    кН	F2,    кН	q,  кН/м	i	k
3	0	6	4. 5	5.1	2	50	28	10	3	8

                                                                 Решение.

    1. Составляем расчётную схему балки.

    2. Кинематический анализ схемы, построение её этажной схемы.

    Степень свободы балки по формуле :

                                W=3Д-2Ш-С0

    где Д – число дисков ; Ш – число простых шарниров ; C0 – число опорных связей.

    В нашем случае : Д=3 ; Ш=2 ; C0=5.

    Тогда степень свободы балки :

                                 W=3×3-2×2-5=9-4-5=0

    На рисунке 1 построена поэтажная схема. Составная балка состоит из трёх дисков : DN – основная балка, к которой присоединены второстепенные – AD и NH.

    Таким образом, балка не подвижна, геометрически неизменяема и статически определима.

    3. Рассчитаем отдельные простые балки и построим эпюры М и Q.

    Балка NH. Определим опорные реакции :

             ΣmL=0  ;  — 

             RN= кН

             ΣmN=0  ; 

             RL= кН

    Контроль :

             ΣY=RL+RN-q(2L3/3+a)=11.12+42.88-10×(3.4+2)=0

    Запишем выражения Q и М для каждого участка.

    Участок NL : 0<x1<3.4 м (ход слева)

     Q1=RN-qx1  ;   M1=RNx1-0.5qx12

    Участок LH : 0<x2<2 м (ход справа)

     Q2=qx2  ;  M2=-0.5qx22

    Находим значения Q и М в характерных точках балки.

    Участок NL : при x1=0

       QN=RN=11.12 кН  ;  MN=0

                            при x1=3.4 м

       QLл=RN-3.4q=11.12-3.4×10=-22.88 кН  ; 

       MLл=3.4RN-0.5q·3.42=3.4×11.12-0.5×10×3.42= -20 кН·м

    На участке NL эпюра М ограничена параболой, имеющей экстремум. Найдём абсциссу сечения, где момент имеет экстремум из условия Q1=RN-qx0=0 ; x0=RN/q=11.12/10=1.1 м.

    Значение экстремального момента :

             Mэкс=RNx0-0.5qx02=11.12×1.1-0.5×10×1.12=6.2 кН·м

    Участок LH : при x2=2 м

        QLпр=2q=2×10=20 кН  ;  MLпр=-0.5q·22=-0.5×10×22=-20 кН·м

                            при x2=0

      QH=0  ;  MH=0

    На основании вычислений эпюры Q и М построены на рисунке 2.  

    Балка AD. Определим опорные реакции.

           ΣmD=0  ; 

                            RB= кН

         ΣmB=0  ; 

                            RD= кН

    Контроль :

          ΣY=RB+RD-F1-qa=50+20-50-10×2=0

    Запишем выражения Q и М для каждого участка.

    Участок AB : 0<x1<2 (ход слева).

           Q1= -qx1  ;  M1=-0.5qx12

    Участок BC : 2<x2<4 (ход лева).

           Q2=-qa+RB  ;  M2=-qa(x2-0.5a)+RB(x2-a)

    Участок CD : 0<x3<2 (ход справа).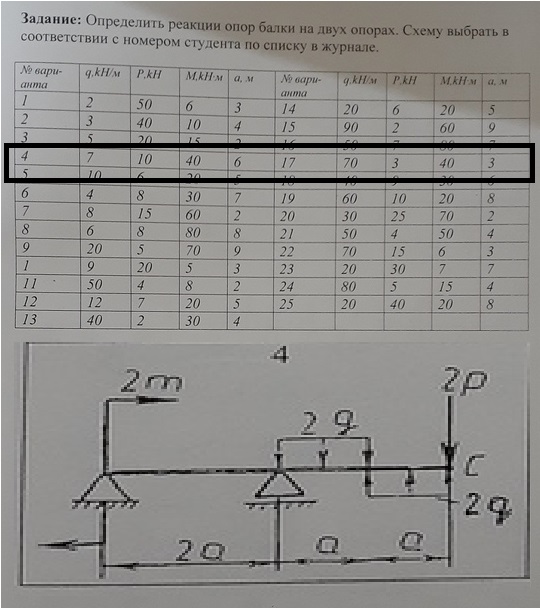

           Q3=-RD  ;  M3=RDx3

    Находим Q и М в характерных точках балки.

    Участок AB : при x1=0

            QA=0  ;  MA=0

                            при x1=2 м

             QBл=-2q=-2×10= -20 кН ; MBл=-0.5q·22=-0.5×10×4= -20 кН·м

    Участок BC : при x2=2

             QBпр=-qa+RB=-10×2+50=30 кН ;

             MBпр=-qa(2-0.5a)+RB(2-a)=-10×2×1=-20 кН·м

                            при x2=4

             QCл=-qa+RB=-10×2+50=30 кН ;

             MCл=-qa(4-0.5a)+RB(4-a)=-10×2×(4-1)+50×(4-2)=40 кН·м

    Участок CD : при x3=2

             QCпр=-RD=-20 кН  ;  MCпр=2RD=2×20=40 кН·м

                            при x3=0

             QD=-RD=-20 кН  ;  MD=0

    Эпюры Q и М построены на рисунке 2.

    Балка DN. Определим опорные реакции.

               ΣmM=0  ;              

      RE=

             кН

               ΣmE=0  ; 

    RM=

          кН

    Контроль :

       ΣY=-RD+RE-F2+RM-1. 7q-RN= -20+40.14-28+35.98-1.7×10-11.12=0

    Запишем выражения Q и М для каждого участка.

    Участок DE : 0<x1<2 (ход слева)

         Q1= -RD  ;  M1=-RDx1

    Участок EF : 2<x2<3.5 (ход слева)

         Q2=-RD+RE  ;  M2=-RDx2+RE(x2-L1/3)

    Участок FM : 1.7<x3<4.7 (ход справа)

         Q3=qL3/3+RN-RM  ;  M3=-RNx3-q(L3/3)(x3-0.5L3/3)+RM(x3-L3/3)

    Участок MN : 0<x4<1.7

          Q4=qx4+RN  ;  M4=-0.5qx42-RNx4

    Находим Q и М в характерных точках балки.

    Участок DE : при x1=0

                   QD=-RD=-20 кН  ;  MD=0

                           при x1=2 м

                   QEл=-RD=-20 кН  ;  MEл=-2RD=-2×20=-40 кН·м

    Участок EF : при x2=2 м

                    QEпр=-RD+RE=-20+40.14=20.14 кН ;

                    MEпр=-2RD+RE(2-2)=-2×20=-40 кН

                           при x2=3.5 м

                    QFл=-RD+RE=-20+40.14=20.14 кН

                    MFл=-3. 5RD+RE(3.5-2)=-3.5×20+40.14×1.5=-9.79 кН·м

    Участок FM : при x3=4.7 м

                     QFпр=qL3/3+RN-RM=10×1.7+11.12-35.98= -7.86 кН

                     MFпр=-4.7RN-q(L3/3)(4.7-0.5L3/3)+RM(4.7-L3/3)=

                             =-4.7×11.12-1.7×10×(4.7-0.5×1.7)+35.98×(4.7-1.7)= -9.77 кН·м

                            при x3=1.7 м

                      QMл=qL3/3+RN-RM=10×1.7+11.12-35.98=-7.86 кН

                      MMл=-1.7RN-q(L3/3)(1.7-0.5L3/3)+RM(1.7-L3/3)=

                             =-1.7×11.12-10×1.7×(1.7-0.5×1.7)= -33.35 кН·м

    Участок MN : при x4=1.7

                       QMпр=1.7q+RN=1.7×10+11.12=28.12 кН

                        MMпр=-0.5q·1.72-1.7RN=-0.5×10×1.72-1.7×11.12=-33.35 кН·м

                             при x4=0

                        QN=RN=11.12 кН

                        MN=0

    Эпюры Q и М построены на рисунке 2.

 

 

 

 

 

 

 

    4. Эпюры Q и М для исходной составной балки.

    Объединяя эпюры Q и М, построенные для каждой простой балки в одну, получим эпюры Q и М для исходной составной балки.

    Эпюры Q и М для составной балки построены на рисунке 3.

    5. Построение линий влияния.

    Построение линии влияния реакции RB.

    Располагаем начало координат в точке B. Пусть сила P=1 движется по балке AD. Тогда уравнение равновесия балки :

                   ΣMD=0 ; -4RB+P(4-x)=0

    Отсюда уравнение линии влияния RB  на участке AD имеет вид :

                   RB==1-x/4

    Строим линию влияния RB по двум точкам :

                   при x=0 (сила P располагается в точке B) – RB=1

                   при x=4 (сила P располагается в точке D) – RB=0

    Найдём ординату линии влияния в точке А :

                    при x=-2 (сила P располагается в точке А) – RB=1.5

    При движении силы P=1 по участкам DN и NH RB=0, так как при положениях груза P=1 на этих участках балка AD не работает. Линия влияния RB построена на рисунке 4.

    Построение линии влияния RE.

    При расположении силы P=1 на участке DN уравнение линии влияния RE найдём из уравнения равновесия балки :

                    ΣMM=0  ;  -4.5RE+P(10.5-x)=0

                                       RE=  

    Эту линию строим по двум точкам :

                     при x=6 (сила P располагается в точке Е) – RE=1 ;

                     при x=10.5 (сила P располагается в точке М) – RE=0

    Определим ординаты линии влияния RE в точках D и N :

                    при x=4 (сила P находится в точке D) – RE=1.4

                    при x=12.2 (сила P находится в точке N) – RE=-0.4

    Линию влияния RE на участке AD строим по двум точкам. В точке D ордината линии влияния участка AD совпадает с ординатой линии влияния участка DN. В точке B – RE=0. Через эти точки проводим линию влияния RE на участке AD.

   Определим ординату линии влияния в точке А.

               RE=1. 4RD, где RD – реакция в точке D. Определим её из уравнения равновесия балки AD :

                         4RD-Px=0  ;  RD=x/4

    Тогда уравнение линии влияния на участке AD имеет вид :

                         RE= ; при x=-2 (сила P располагается в точке А) – RE=-0.7

    Аналогично строим линию влияния на участке NH. В точке N – RE=-0.4 ; в точке L – RE=0. Найдём ординату линии влияния в точке H.

                RE=-0.4RN , где RN – реакция в точке N. Определим её из уравнения равновесия балки NH :

                      -3.4RN+P(15.6-x)=0  ;  RN=  — уравнение линии влияния на участке NH.

                       при x=17.6 (сила P располагается в точке H) – RE= 

    Линия влияния RE построена на рисунке 4.

    Построение линии влияния изгибающего момента в сечении 3 (левее точки Е, бесконечно близко к ней).

    При движении P=1 по участку DE левее точки 3, рассматривая равновесие левой отсечённой части (относительно точки 3) балки DN, имеем :

                      M3=-P(2-x)=-(2-x)

    при x=0 (точка D) – M3=-2 м ; при x=2 м (точка Е) – M3=0.

    По этим точкам строим линию влияния М3 на участке DE.

    При движении P=1 по участку ED правее точки 3, рассматривая равновесие левой отсечённой части балки DN, имеем :

                      M3=0

    При движении P=1 по участку EN балки DN и по балки NH, рассматривая равновесие левой отсечённой части балки DN, также получим : M3=0. Т.е. на участках EN и NH линия влияния совпадает с осью абсцисс.

    При движении P=1 по балке AD М3=-2RD, где RD находим из уравнения равновесия балки AD :

                    ΣmB=0 ; -P(-4-x)-4RD=0  ;  RD= 

    Тогда уравнение линии влияния М3=

    при x=0 (точка D) – M3=-2 м ; при x=-4 м (точка B) – M3=0 ; при x=-6 м (точка А) – М3=1 м.

    Линия влияния М3 построена на рисунке 5.

    Построение линии влияния поперечной силы Q3 в сечении 3 (левее точки Е, бесконечно близко к ней).

    Линия влияния Q3 строится аналогично линии влияния М3.

    При движении P=1 по участку DE левее точки 3, рассматривая равновесие левой отсечённой части (относительно точки 3) балки DN, имеем :

                      Q3=-P=-1

    Т. е. на участке DE линия влияния Q3 параллельна оси абсцисс.

    Для построения л.в. на участке AD поступим следующим образом : ординату точки D (y=-1) соединим с ординатой точки B (y=0) и продолжим до пересечения с ординатой точки А. Ординату точки А найдём из подобия треугольников : yA=2×1/4=0.5

    При движении P=1 по участку DE, правее точки 3, а также по участкам EN и NH, рассматривая равновесие левой отсечённой части балки DN, имеем Q3=0

    Линия влияния Q3 построена на рисунке 5.

    Построение линии влияния изгибающего момента М8 в сечении 8 (левее точки М, бесконечно близко от неё).

    При движении P=1 по участку DM левее точки 8 и по участку AD – М8=0 (линия влияния совпадает с осью абсцисс). Это следует из рассмотрения равновесия правой отсечённой части MN :

                              M8=MM=RM·0=0

    При движении P=1 по участку MN правее точки 8, рассматривая равновесие правой отсечённой части MN балки DN, имеем :

               M8=RM·0-Px=-x

    при x=0 (точка М) – М8=0 ; при x=1. 7 м (точка N) – M8=-1.7 м

    При движении P=1 по участку NH, рассматривая равновесие правой отсечённой части MN балки DN, имеем :

                               M8=-1.7RN

    где RN находим, рассматривая равновесие участка NH.

                          ΣmL=0 ; -3.4RN+P(5.1-x)=0  ;  RN= 

                            M8=

    при x=1.7 (точка N) – M8=-1.7 м ; при x=5.1 (точка L) – M8=0 ; при x=7.1 м (точка H) – M8=1 м.

    Линия влияния М8 построена на рисунке 6.

    Построение линии влияния поперечной силы Q8 в сечении 8 (левее точки М, бесконечно близко к ней).

    Линия влияния Q8 строится аналогично линии влияния М8.

    При движении P=1 по участку DM (с лево от точки 8), рассматривая равновесие правой отсечённой части (MN) балки DN, имеем :

                    Q8=-RM=

    где RM находим из уравнения равновесия, составленного для балки DN :

                   ΣME=0 ; -P(x-2)+4.5RM=0 ; RM=

    при x=0 (точка D) – Q8=0. 4 ; при x=2 м (точка Е) – Q8=0 ; при x=6.5 м (точка M) – Q8=-1 ; при x=8.2 м (точка N) – Q8=-1.4

По полученным данным строим левую прямую л.в. Q8, при движении P=1 по балке DM.

    Для построения л.в., при движении P=1 по балке AD поступаем следующим образом : соединяем ординату точки D (0.4) с ординатой точки B (y=0) и, продолжаем эту прямую до пересечения с ординатой точки А. Ординату точки А находим из подобия треугольников : ; yA=2×0.4/4=0.2. Таким образом, левая прямая л.в. построена.

    При движении P=1 по участку MN (с право от точки 8), рассматривая равновесие левой отсечённой части (DM), балки DN, имеем :

                    Q8=-RE=

    где RE находим из уравнения равновесия, составленного для балки DN :

                     ΣmM=0 ; -P(x-6.5)+4.5RE=0 ; RE=  

    при x=0 (точка D) – Q8=1.4 ; при x=6.5 м (точка М) – Q8=0 ; при x=8.2 м (точка N) –

Q8= -0.4.

    По полученным данным строим правую прямую л.в. Q8, при движении P=1 по участку MN. Для построения л.в., при движении P=1 по балке NH поступаем следующим образом : соединяем ординату точки N (-0.4) с ординатой точки L (y=0) и, продолжаем эту прямую до пересечения с ординатой точки H. Ординату точки H найдём из подобия треугольников :    yH=2×0.4/3.4=0.24. Таким образом, правая прямая л.в. Q8 – построена. Линия влияния Q8 приведена на рисунке 6.

 

  

    6. Определение поперечной силы QE в сечении Е по линии влиянии от заданно нагрузки.

             QE=

    где y – ордината линии влияния под сечением с сосредоточенной нагрузкой P ; ω — площадь участка линии влияния под нагрузкой q ; α – угол наклона линии влияния в месте приложения сосредоточенного момента.

    Тогда (см. рисунок 7) :

             QE= кН

    На эпюре Q, при движении слева : QE=-20 кН

404 Cтраница не найдена

Мы используем файлы cookies для улучшения работы сайта МГТУ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь. Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом ФГБОУ ВО «МГТУ» и согласны с нашими правилами обработки персональных данных.

Размер:

AAA

Изображения Вкл. Выкл.

Обычная версия сайта

К сожалению запрашиваемая страница не найдена.

Но вы можете воспользоваться поиском или картой сайта ниже

Университет Майкопский государственный технологический университет – один из ведущих вузов юга России. История университета Анонсы Объявления Медиа Представителям СМИ Газета «Технолог» О нас пишут Ректорат Структура Филиал Политехнический колледж Медицинский институт Лечебный факультет Педиатрический факультет Фармацевтический факультет Стоматологический факультет Факультет послевузовского профессионального образования Факультеты Кафедры Ученый совет Дополнительное профессиональное образование Бережливый вуз – МГТУ Новости Объявления Лист проблем Лист предложений (Кайдзен) Реализуемые проекты Архив проектов Фабрика процессов Рабочая группа «Бережливый вуз-МГТУ» Вакансии Профсоюз Противодействие терроризму и экстремизму Противодействие коррупции WorldSkills в МГТУ Научная библиотека МГТУ Реквизиты и контакты Автошкола МГТУ Опрос в целях выявления мнения граждан о качестве условий оказания образовательных услуг Управление имущественным комплексом Работа МГТУ в условиях предотвращения COVID-19 Документы, регламентирующие образовательную деятельность Система менеджмента качества университета Региональный центр финансовой грамотности Аккредитационно-симуляционный центр Абитуриентам Подача документов онлайн Абитуриенту 2023 Для поступающих на обучение по программам бакалавриата, специалитета, магистратуры — Прием 2023 Для поступающих на обучение по программам среднего профессионального образования (колледж) Для поступающих на обучение по договорам об оказании платных образовательных услуг Образец договора Образовательный кредит Оплата материнским (семейным) капиталом Банковские реквизиты для оплаты обучения Приказ об установлении стоимости обучения для 1 курса набора 2022-2023 учебного года Для поступающих на обучение по программам ординатуры Для поступающих на обучение по программам аспирантуры Часто задаваемые вопросы (бакалавриат, специалитет, магистратура) Видеоматериалы для постуающих Экран приёма 2022 Иностранным абитуриентам Международная деятельность Общие сведения Кафедры Новости Центр международного образования Академическая мобильность и международное сотрудничество Академическая мобильность и фонды Индивидуальная мобильность студентов и аспирантов Как стать участником программ академической мобильности Дни открытых дверей в МГТУ День открытых дверей online Университетские субботы Дни открытых дверей на факультетах Подготовительные курсы Подготовительное отделение Курсы для выпускников СПО Курсы подготовки к сдаче ОГЭ и ЕГЭ Онлайн-курсы для подготовки к экзаменам Подготовка школьников к участию в олимпиадах Малая технологическая академия Профильный класс Социально-экономический профиль Медико-фармацевтический профиль Инженерно-технологический профиль Эколого-биологический профиль Агротехнологический профиль Индивидуальный проект Кружковое движение юных технологов Олимпиады, конкурсы, фестивали Веб-консультации для абитуриентов и их родителей Веб-консультации для абитуриентов Родительский университет Олимпиады для школьников Отборочный этап Заключительный этап Итоги олимпиад Профориентационная работа Стоимость обучения Студентам Студенческая жизнь Стипендии Организация НИРС в МГТУ Студенческое научное общество Студенческие научные мероприятия Конкурсы Академическая мобильность и международное сотрудничество Образовательные программы Расписание занятий Расписание звонков Онлайн-сервисы Социальная поддержка студентов Общежития Трудоустройство обучающихся и выпускников Вакансии Обеспеченность ПО Инклюзивное образование Условия обучения лиц с ограниченными возможностями Доступная среда Ассоциация выпускников МГТУ Перевод из другого вуза Вакантные места для перевода Студенческое пространство Студенческое пространство Запись на мероприятия Отдел по социально-бытовой и воспитательной работе

Наука и инновации Научная инфраструктура Проректор по научной работе и инновационному развитию Научно-технический совет Управление научной деятельностью Управление послевузовского образования Точка кипения МГТУ О Точке кипения МГТУ Руководитель и сотрудники Документы Контакты Центр коллективного пользования Центр народной дипломатии и межкультурных коммуникаций Студенческое научное общество Научные издания Научный журнал «Новые технологии» Научный журнал «Вестник МГТУ» Научный журнал «Актуальные вопросы науки и образования» Публикационная активность Конкурсы, гранты Научные направления и результаты научно-исследовательской деятельности Основные научные направления университета Отчет о научно-исследовательской деятельности в университете Результативность научных исследований и разработок МГТУ Финансируемые научно-исследовательские работы Объекты интеллектуальной собственности МГТУ Результативность научной деятельности организаций, подведомственных Минобрнауки России (Анкеты по референтным группам) Студенческое научное общество Инновационная инфраструктура Федеральная инновационная площадка Проблемные научно-исследовательские лаборатории Научно-исследовательская лаборатория «Совершенствование системы управления региональной экономикой» Научно-исследовательская лаборатория проблем развития региональной экономики Научно-исследовательская лаборатория организации и технологии защиты информации Научно-исследовательская лаборатория функциональной диагностики (НИЛФД) лечебного факультета медицинского института ФГБОУ ВПО «МГТУ» Научно-исследовательская лаборатория «Инновационных проектов и нанотехнологий» Научно-техническая и опытно-экспериментальная база Центр коллективного пользования Научная библиотека Экспортный контроль Локальный этический комитет Конференции Школа молодого врача Международная научно-практическая конференция «Фундаментальные и прикладные аспекты геологии, геофизики и геоэкологии с использованием современных информационных технологий» Международная научно-практическая конференция «Актуальные вопросы науки и образования» VI Международная научно-практическая онлайн-конференция Наука и университеты Международная деятельность Иностранным студентам Международные партнеры Академические обмены, иностранные преподаватели Академическая мобильность и фонды Индивидуальная мобильность студентов и аспирантов Факультет международного образования Новости факультета Информация о факультете Международная деятельность Кафедры Кафедра русского языка как иностранного Кафедра иностранных языков Центр Международного образования Центр обучения русскому языку иностранных граждан Приказы и распоряжения Курсы русского языка Расписание Академическая мобильность Контактная информация Контактная информация факультета международного образования Сведения об образовательной организации Основные сведения Структура и органы управления образовательной организацией Документы Образование Образовательные стандарты и требования Руководство. Педагогический (научно-педагогический) состав Материально-техническое обеспечение и оснащённость образовательного процесса Стипендии и меры поддержки обучающихся Платные образовательные услуги Финансово-хозяйственная деятельность Вакантные места для приёма (перевода) Международное сотрудничество Доступная среда Организация питания в образовательной организации

Механика материалов III: Изгиб балки

Хотите просмотреть все массовые открытые онлайн-курсы?

Массовые открытые онлайн-курсы

Глобальный учебный центр Технологического института Джорджии и кампус Технологического института Джорджии в Саванне соответствуют требованиям Закона об американцах-инвалидах. Любой человек, которому требуется проживание для участия в любом курсе, предлагаемом GTPE, должен связаться с нами до начала курса.

Курсы, являющиеся частью сертификационных программ, включают обязательную оценку. Критерии прохождения определяются инструктором и предоставляются учащимся в начале курса.

CEU присуждаются участникам, которые посещают не менее 80% запланированного времени занятий.

Управление безопасности исследований и соблюдения нормативных требований Технологического института Джорджии требует сохранения информации о гражданстве для тех, кто участвует в большинстве курсов GTPE. Информация о гражданстве получается непосредственно от учащегося во время регистрации и хранится в Системе студентов Технологического института Джорджии.

Учащиеся, зачисленные на любую из программ профессионального образования Технологического института Джорджии, считаются членами сообщества Технологического института Джорджии и должны соблюдать все правила и процедуры, установленные Институтом, включая Кодекс поведения учащихся и Кодекс академической чести.

Полную информацию о правилах изменения и отмены курса см. в наших Условиях использования.

Участники курсов GTPE должны заполнить онлайн-профиль, соответствующий требованиям безопасности Технологических исследований Джорджии. Собранная информация хранится в системе студентов Технологического института Джорджии. Следующие элементы данных считаются справочной информацией и собираются от каждого участника в рамках процесса регистрации и настройки профиля:

• Полное юридическое имя
• Адрес электронной почты
• Адрес доставки
• Название компании

Эти данные не публикуются в онлайн-справочной системе Технологического института Джорджии и, следовательно, в настоящее время недоступны для широкой публики. Информация об учащемся используется только так, как описано в нашей Политике конфиденциальности. Данные GTPE не продаются и не предоставляются внешним организациям.

Конфиденциальные данные
Следующие элементы данных, если они находятся в системах для студентов Технологического института Джорджии, считаются конфиденциальной информацией и доступны только сотрудникам Технологического института Джорджии, которым это необходимо знать:

• Технический идентификатор Джорджии
• Дата рождения
• Гражданство
• Пол
• Этническая принадлежность
• Религиозные предпочтения
• Номера социального страхования
• Регистрационная информация
• Расписания занятий
• Записи о посещаемости
• Академическая история

В любое время вы можете отозвать свое согласие на получение маркетинговых электронных писем, а также запросить удаление ваших личных данных. Посетите нашу страницу GTPE EU GDPR для получения дополнительной информации.

На занятия и мероприятия, проводимые в Глобальном учебном центре Технологического института Джорджии в Атланте или в кампусе Технологического института Джорджии в Саванне, могут повлиять закрытия или задержки из-за ненастной погоды.

Глобальный учебный центр Технологического института Джорджии будет следовать указаниям главного кампуса Технологического института Джорджии в Атланте. Студенты, гости и преподаватели должны проверить домашнюю страницу Технологического института Джорджии , чтобы получить информацию о закрытии университетов или задержке открытия из-за ненастной погоды. Обратите внимание, что если кампус закрыт по каким-либо причинам, все классные занятия также отменяются.

Студенты, гости и преподаватели, посещающие занятия и мероприятия в Технологическом институте Джорджии, должны проверить домашнюю страницу Технологического института Джорджии, чтобы получить информацию о закрытии или задержке открытия из-за ненастной погоды.

Сертификаты GTPE об окончании программы

состоят из установленного количества обязательных и факультативных курсов, предлагаемых и пройденных в Технологическом институте Джорджии в течение последовательного шестилетнего периода. Исключения, такие как запросы на замену или зачет за предшествующее образование, могут быть запрошены через форму петиции. Исключения не могут быть гарантированы.

Полную информацию о правилах возврата средств см. в наших Условиях использования.

Технологический институт Джорджии — это кампус без табака и курения. Использование сигарет, сигар, трубок, всех форм бездымного табака и любых других курительных устройств, в которых используется табак, строго запрещено. На территории кампуса нет специально отведенных мест для курения.

Курсы, на которые распространяются специальные скидки, будут соответствующим образом отмечены на странице курса. В процессе оформления заказа можно ввести только один код купона, и его нельзя активировать после завершения оформления заказа. Если вы уже зарегистрировались и забыли использовать код купона, вы можете запросить соответствующий возврат средств. GTPE отменит любую транзакцию, в которой купон был использован не по назначению или не соответствовал требованиям. Если вы не уверены, можете ли вы использовать код купона, обратитесь к администратору курса.

В GTPE нет программы для пенсионеров. Тем не менее, Технологический институт Джорджии предлагает программу 62 лет и старше для жителей Джорджии в возрасте 62 лет и старше, которые заинтересованы в прохождении кредитных курсов. Эта программа не оплачивает некредитные курсы профессионального образования. Посетите страницу приема в бакалавриат Технологического института Джорджии, чтобы получить дополнительную информацию о программе бакалавриата, и страницу приема в аспирантуру Технологического института Джорджии, чтобы получить дополнительную информацию о программе магистратуры.

Нет специального процесса или формы для регистрации вашей группы. Все заинтересованные учащиеся должны создавать и управлять своими индивидуальными профилями, учетными записями и регистрациями.
 

1. Заполните профиль GTPE.
2. Купить курс.
3. Добавьте курсы в корзину.*
4. Применить групповой код скидки (если применимо).
5. Укажите приемлемый способ оплаты для завершения заказа (кредитная карта, держатель кредитной карты третьего лица или один принятый платежный документ).
    

*Корзины будут активны в течение 14 дней, но места не удерживаются до тех пор, пока транзакция не будет завершена.

Курсы, предлагающие групповые скидки, будут отображать код скидки на странице курса. Ваши сотрудники будут использовать код в процессе регистрации, и итоговая сумма корзины изменится соответствующим образом. Групповые скидки могут быть использованы только в том случае, если три или более сотрудников компании посещают один и тот же курс, и для каждой корзины можно использовать только один код купона.

Если вы уже зарегистрировались и забыли использовать код купона, вы можете запросить соответствующий возврат средств.

Принятые платежные документы должны быть загружены в процессе регистрации. К ним относятся:

• Заказ на поставку компании (PO или SF182)
• Доверенность на бланке компании
• Заявление/ваучер на корпоративное обучение

• Название компании и фактический адрес
• Имя сотрудника(ов), утвержденного(ых) для обучения
• Номер документа (документы SF-182: раздел C, графа 4)
• Платежный адрес (документы SF-182: раздел C, графа 6)
• Название курса и даты курса
• Максимальная сумма выплаты (сумма счета)
• Срок годности (если применимо)
• Подпись уполномоченного лица
• Условия платежа меньше или равны нетто 30

Сотрудник может распечатать копию своей корзины для подачи, если это требуется для платежных документов. Корзина будет оставаться активной в течение 14 дней, но место не будет удерживаться до завершения регистрации и оплаты.

Регистрация не может быть обработана без оплаты. Если ваш сотрудник боится потерять место в классе из-за внутренних процессов компании, мы предлагаем ему зарегистрироваться и оплатить с помощью личной или корпоративной кредитной карты и потребовать возмещения.

Если вам нужна помощь с регистрацией вашей группы или у вас есть вопросы о том, как начать процесс, пожалуйста, не стесняйтесь обращаться к нам по телефону 404-385-3501 или по электронной почте [email protected].

Большинство аудиторных курсов GTPE проводятся в Глобальном учебном центре Технологического института Джорджии (GLC). Любые курсы, которые проводятся в другом месте, будут четко отмечены на странице курса. Получите информацию о парковке, направлениях и транспорте до GLC.

Мы не предоставляем комнаты для ночлега. Тем не менее, размещение может быть сделано в отеле и конференц-центре Georgia Tech, расположенном рядом с нами. Дополнительные отели можно найти в нескольких минутах ходьбы. Получите больше информации о размещении.

Учащиеся могут перейти на другой курс равной или большей стоимости, если уведомление будет сделано не менее чем за 10 рабочих дней до первоначальной даты начала курса. Курс, на который переводят, должен быть уже запланирован.

Мы рекомендуем вам зарегистрироваться на курсы как можно раньше. Подробная информация о сеансе будет указывать, когда в конкретном сеансе будет доступно менее пяти мест.

 

Обновления вашей компании, адреса, электронной почты, телефона и паролей можно сделать непосредственно на веб-сайте GTPE. Изменения имени и изменения гражданства должны быть представлены в отдел регистрации GTPE.

1. Заполните профиль GTPE.
2. Купить курс.
3. Добавьте курсы в корзину.*
4. Применить специальный код скидки (если применимо).
5. Укажите приемлемый способ оплаты для завершения заказа (кредитная карта, держатель кредитной карты третьего лица или один принятый платежный документ).
    

*Корзины будут активны в течение 14 дней, но места не удерживаются до тех пор, пока транзакция не будет завершена.

Регистрация без предварительной записи принимается при наличии свободных мест, но не гарантируется ни для каких курсов.

Скидки, если они доступны, будут отображаться на странице курса или автоматически применяться в процессе покупки. В процессе оформления заказа следует ввести только один код купона, который будет подтвержден системой, если это применимо к товарам в вашей корзине. Если вы уже зарегистрировались и забыли использовать код купона, вы можете запросить соответствующий возврат средств.

ГТЭП не имеет программы скидок для пенсионеров. Тем не менее, Технологический институт Джорджии предлагает программу 62 лет и старше для жителей Джорджии в возрасте 62 лет и старше, которые заинтересованы в прохождении кредитных курсов. Эта программа не оплачивает некредитные курсы профессионального образования. Посетите страницу приема в бакалавриат Технологического института Джорджии, чтобы получить дополнительную информацию о программе бакалавриата, и страницу приема в аспирантуру Технологического института Джорджии, чтобы получить дополнительную информацию о программе магистратуры.

Следующие программы GTPE имеют право на льготы по обучению ветеранов:

• Программа сертификации по безопасности и гигиене труда (только курсы кампуса в Атланте)
• Сертификационная программа по управлению проектами (только курсы кампуса в Атланте)
• Сертификационная программа по управлению безопасностью и здоровьем (только курсы кампуса в Атланте)

Для получения дополнительной информации см. контрольный список льгот ветерана GTPE по законопроекту о военнослужащих.

В ГТПЭ нет программы для пенсионеров. Тем не менее, Технологический институт Джорджии предлагает программу 62 лет и старше для жителей Джорджии в возрасте 62 лет и старше, которые заинтересованы в прохождении кредитных курсов. Эта программа не оплачивает некредитные курсы профессионального образования. Посетите страницу приема в бакалавриат Технологического института Джорджии для получения дополнительной информации о программе бакалавриата и страницу приема в аспирантуру Технологического института Джорджии для получения дополнительной информации о программе магистратуры.

В случае отмены мы полностью вернем вам деньги или переведем на эквивалентный курс.

Краткосрочные курсы (1-5 дней) и конференции не требуют студенческой визы. Туристической визы B-2 вместе с копией электронного письма с подтверждением регистрации и копией заполненной страницы заказа на веб-регистрацию должно быть достаточно.

Если участие в курсе связано с трудоустройством и немедленным отъездом из США, потребуется временная деловая виза B-1.

Мы рекомендуем вам связаться с вашим консульством или посольством США, чтобы определить, имеете ли вы право на получение визы. Полное возмещение будет предоставлено участникам, которые не смогут получить въездную визу и связаться с нашим офисом до начала курса.

Студенты, изучающие английский как второй язык, должны связаться с Language Institute для получения информации о зачислении и получении визы.

Мы не выдаем приглашения и не можем предоставить иммиграционные документы для оформления студенческой визы. Полное возмещение будет предоставлено участникам, которые не смогут получить въездную визу и связаться с нашим офисом до начала курса.

Если вам нужна помощь с регистрацией вашей группы или у вас есть вопросы о том, как начать процесс, пожалуйста, не стесняйтесь обращаться к нам по телефону 404-385-3501 или по электронной почте peregistration@gatech. edu.

Полная оплата производится во время регистрации. Принимаемые способы оплаты включают:

• Кредитные карты
• Заказы на поставку (компания и правительство)
• Международные электронные платежи*
• Номер рабочего дня Технологического института Джорджии (только для сотрудников Технологического института Джорджии)
• Частные кредиты*
• Пособия по счету GI * (только соответствующие курсы в кампусе Атланты. Курсы за пределами кампуса и онлайн-курсы не имеют права на льготы VA.)
• Чеки компании*

* Требуется загрузка документа или проверка транзакции в процессе оформления заказа.

Документы заказа на поставку должны включать следующее:

• Название компании и физический адрес
• Имя финансового контакта компании и/или адрес электронной почты (кредиторская задолженность)
• Имя сотрудника(ов), утвержденного(ых) для обучения
• Номер документа (документы SF-182: раздел C, графа 4)
• Платежный адрес (документы SF-182: раздел C, графа 6)
• Название курса и даты курса
• Максимальная сумма выплаты (сумма счета)
• Срок годности (если применимо)
• Подпись уполномоченного лица
• Условия платежа меньше или равны нетто 30

Пожалуйста, не указывайте номера социального страхования в документах заказа на покупку.

1. Сделайте свой чек подлежащим оплате «Технологическому институту Джорджии» и укажите номер заказа и имя участника на лицевой стороне чека.
2. Выберите «Заказ компании» в качестве способа оплаты при оформлении заказа и загрузите копию чека в свой заказ.
3. Отправьте чек по адресу:

   GTPE Accounting
   Технологический институт Джорджии
   Global Learning Center
   84 5th St. NW
   Atlanta, GA 30308-1031

Полная оплата производится во время регистрации.

Общественный номер
Оплата производится в момент покупки. Оплата счетов должна соответствовать бизнес-условиям Board of Regent в размере 30.

Сотрудники Технологического института Джорджии
Платежи PeopleSoft обрабатываются во время регистрации. Сотрудники Технологического института Джорджии не могут использовать карты PCard для оплаты регистрации GTPE.

Дополнительные сборы зависят от курса. Обязательно ознакомьтесь с вкладкой «Требования и материалы» на странице курса для получения дополнительной информации.

Да. Вот шаги для получения счета:

1. Заполните профиль GTPE.
2. Купить курс.
3. Добавьте курсы в корзину.
4. Распечатайте свою корзину и отправьте своему работодателю в качестве сметы расходов.
5. Получите копию заказа на поставку вашей компании или документ об утверждении платежа для GTPE для выставления счета.
6. Вернитесь в корзину, пройдите процедуру оформления заказа и загрузите заказ на покупку нашей компании на последнем этапе оплаты.
7. Бизнес-офис GTPE выставит счет за 10 дней до начала курса, после чего вы больше не имеете права снимать деньги со средств.

   Ваша компания должна:

• Соблюдать деловые условия Технологического института Джорджии и Попечительского совета нетто 30.
• Оплатить полную сумму счета Технологического института Джорджии (скидки за досрочную или своевременную оплату не предоставляются).
• Оплатить счет, если сотрудник не отказывается от участия в течение периода возврата и не посещает курс.

Возвраты с кредитной карты обрабатываются на исходную кредитную карту. Эмитент кредитной карты несет ответственность за возврат кредитных остатков держателю карты.

Мы не предлагаем планы оплаты каких-либо наших услуг, конференций или курсов. Оплата должна быть произведена в полном объеме в момент покупки.

ГТПЭ не может выдавать налоговые формы 1098-Т. Если у вас есть история платежей, необходимая для целей налогообложения, мы будем рады предоставить вам квитанции об оплате. Пожалуйста, отправьте свои требования по адресу [email protected]. Обязательно укажите свое полное официальное имя и идентификатор технологического института Джорджии, который можно найти в вашем профиле GTPE.

Полную информацию о наших правилах в отношении изменений в регистрации на курс см. в наших Условиях использования.

GTPE использует CEU в соответствии с принятыми критериями и рекомендациями, установленными Попечительским советом штата Джорджия, которые следуют международным стандартам, таким как Международная ассоциация непрерывного образования и обучения (IACET).

GTPE не выдает стенограммы или сертификаты с часами профессионального развития (PDH) или единицами профессионального развития (PDU), но пешеходный переход здесь приведен для справки.

Один CEU = 10 контактных часов обучения
Один PDH = 1 контактный час обучения (один CEU = 10 PDH)
Один PDU = 1 контактный час обучения (один CEU = 10 PDU)

После успешного завершения большинства курсов GTPE (минимальная посещаемость 80% и проходной балл по курсам, требующим оценивания) вы можете получить сертификат с указанием количества заработанных CEU. Исключения для выдачи сертификатов включают курсы с выдающимися аттестационными организациями (например, OSHA или PADI).

заработанных CEU записываются на имя участника и отображаются в стенограмме GTPE. Все стенограммы должны быть запрошены участником через форму запроса стенограммы. Обычно запросы обрабатываются в течение трех рабочих дней.

Для проверки вашей стенограммы на предмет прогресса в получении сертификата заполните форму запроса на стенограмму. Курсы GTPE не дают академического кредита или кредита на получение степени. Академический кредит или кредит Технологического института Джорджии доступен только для зачисленных студентов, проходящих курсы, соответствующие требованиям степени.

Для получения конкретной информации о лицензировании штата или кредитных требованиях обратитесь в совет штата по лицензированию. Если вы хотите пройти сертификацию через профессиональную ассоциацию, ознакомьтесь с конкретными требованиями этой ассоциации.

Хотите узнать больше об этом курсе?

Связаться с нами

Механика материалов: выпучивание балки » Механика гибких конструкций

---

исследования

человек

курсы

блог

---

Критическая нагрузка на изгиб

На прошлом уроке мы узнали об уравнении кривой упругости и описали прогиб балки в ответ на поперечную нагрузку. В нашем первом уроке о напряжении мы говорили об осевых нагрузках, которые создают растягивающие и сжимающие напряжения в материале, а при изучении деформации мы описали, как конструкция будет сжиматься до более короткой длины под действием осевого сжимающего напряжения. Мы знаем из собственного опыта, что это не единственное, что может случиться. Представьте, что вы толкаете соломинку — если вы нажимаете мягко, на самом деле ничего не происходит, но как только вы толкаете ее с достаточной силой, она изгибается наружу в центре. Это явление известно как выпучивание , и это совершенно другая структурная реакция, чем плоскостное сжатие. При проектировании колонн и балок выпучивание может привести к катастрофическим последствиям — представьте выпучивание вертикальных опор моста. Иногда желательно спроектировать конструкции, которые могут изгибаться, например, рулевое управление в вашем автомобиле спроектировано таким образом, чтобы изгибаться при значительных нагрузках, чтобы предотвратить дальнейшее травмирование водителя в аварии.

Давайте посмотрим на изображение консольной балки (свободной на одном конце и зажатой на другом. В

действует точечная сила0457 x , которая заставляет луч отклоняться в направлении y  . (Поскольку мы предполагаем, что балка однородна и изотропна, изгиб вверх или вниз не является предпочтительным. Если балка имеет круглое поперечное сечение, она может выгибаться вне плоскости в любом направлении.)

Мы можем начать анализ этой структуры, написав дифференциальное уравнение для упругой кривой. На нашей диаграмме свободного тела мы можем заменить момент силой, умноженной на изменение отклонения от плоскости.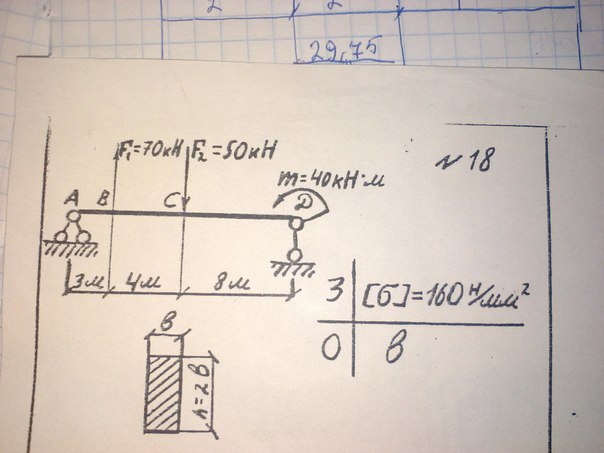

Давайте определим новую переменную  k , чтобы упростить наши следующие вычисления:

. Теперь мы не можем переписать наши уравнения кривой упругости с нашей новой переменной.

Затем мы соберем члены, содержащие и , в одной части уравнения.

Приведенное выше уравнение представляет собой линейное обыкновенное дифференциальное уравнение (ОДУ) второго порядка, известное как уравнение свободных колебаний. Это общее решение для значений позиции k ^{2 (что, конечно же, имеет место для нашего определения k ) задается с двумя неизвестными константами, A и B .}

Итак, теперь у нас есть решение для y , но нам нужно определить, каково значение двух неизвестных. Это краевая задача, и для этого воспользуемся граничными условиями на балке. Луч зафиксирован в точке x=0 , что означает, что луч не может двигаться вверх или вниз в направлении y в этой точке, т. е. y=0 на защемленном ребре. Кроме того, зажатая граница требует, чтобы балка была ортогональна стене, что математически означает, что она должна иметь нулевой наклон при x=0 , а наклон представляет собой изменение y по сравнению с изменением x. Есть третье условие, которое нам нужно будет использовать через мгновение, а именно то, что положение y на свободном краю балки, т. е. x=L , равно отклонению дельта .

Используя эти граничные условия, решая для A и B просты. Начнем с первого граничного условия: добавление x=0 в наше уравнение убивает второй член (поскольку sin(x)=0) и требует, чтобы для y=0 , A = – дельта. Второе граничное условие, дифференцирующее y по x, , превращает первый член в sin(x) (и, как и прежде, уходит), убивает последний член (поскольку дельта не является функция x ), и она превращает второй член в cos(0)=1. Единственный способ  y=0 для B=0 .

Итак, возвращая наши константы в наше общее решение, мы получаем следующее уравнение:

Здесь вступает в действие наше третье граничное условие. Нам нужно решить это уравнение для k , так как это даст нам информацию о нагрузке P . Используя наше третье граничное условие, которое гласит, что при x=L , y=дельта , мы сводим приведенное выше уравнение к следующему:

То, что у нас осталось, может быть равно нулю, только если delta=0 или cos(kL)=0. Первый случай — тривиальный случай, он соответствует отсутствию прогиба и, следовательно, выпучению — он описывает случай, когда аксиально приложенная нагрузка просто сжимает балку в направлении x . Для потери устойчивости балки нас интересует второй случай, то есть cos(kL)=0 . Косинус — периодическая функция, и мы знаем, что cos(x)=0 с интервалами pi/2, 3pi/2 и т. д. Таким образом, приведенное выше уравнение будет равно нулю, когда kL равно следующему (где n — целое число от 1 до бесконечности):

Теперь мы можем заменить k соответствующими переменными нашей задачи, и мы будем использовать n=1 , так как это потребует наименьшего изгиба балки и, следовательно, будет наиболее энергетически выгодным решением:

И, наконец, мы можем изменить приведенное выше уравнение, чтобы найти P , что будет критической нагрузкой, описывающей начало потери устойчивости для балки со свободным концом и защемленным концом.