ПРИМЕР РЕШЕНИЯ ЗАДАЧИ №1 — Мегаобучалка

 

Ступенчатый брус нагружен силами Р₁, Р₂, Р₃, (Рисунок 2,а).

Требуется построить эпюры продольных сил N, нормальных напряжений s, продольных перемещений D и проверить, вы­по­лняется ли условие прочно­с­ти.

Числовые данные к задаче выбираются по табл. 1.

Например: кН, кН, кН, м м, м; .

Для всех вариантов принимается: ; .

 

1. Построение эпюры N.

На брус действуют три си­лы, следовательно, про­­до­льная си­ла по его длине будет изменяться. Разбиваем брус на участки, в пределах которых про­­до­льная сила будет постоянной. В данном случае границами участков являются сечения, в ко­­торых приложены силы. Обозначим сечения буквами А, В, С, D, начиная со свободного конца, в данном случае правого.

 

 

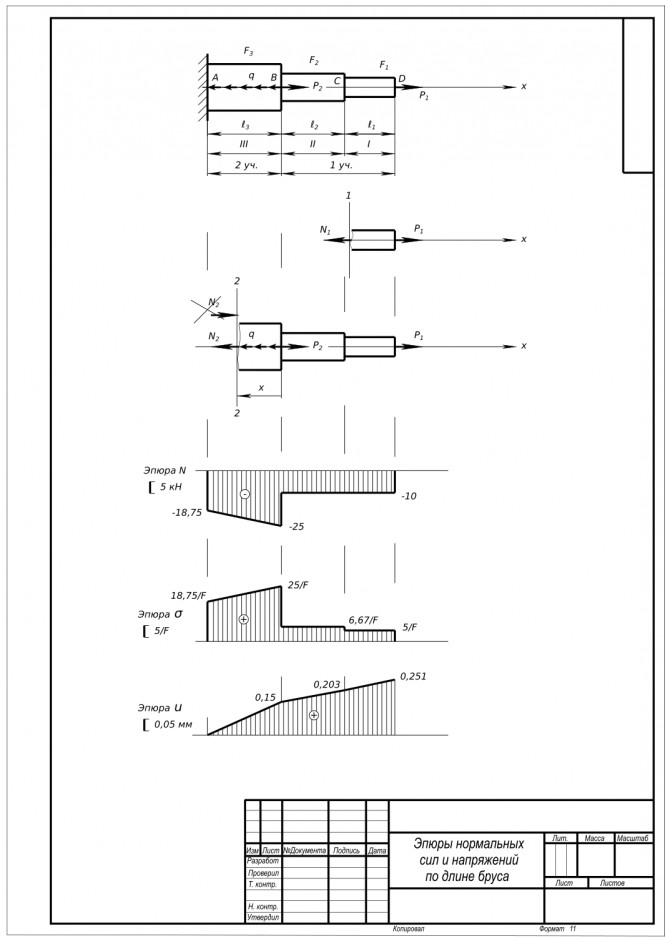
Рисунок 2- Расчетная схема бруса и эпюры: а ‑ расчетная схема; б ‑ эпюра продольных сил; в ‑ эпюра напряжений; г ‑ эпюра продольных перемещений

Для определения продольной силы на каждом участке рассматриваем про­извольное поперечное сечение, сила в котором определяется по пра­вилу, приведенному ранее. Чтобы не определять предварительно реакцию в заделке D, начинаем расчеты со свободного конца бруса А.

Участок АВ, сечение 1-1. Справа от сечения действует растягивающая сила (Рисунок 2, а). В соответствии с упомянутым ранее правилом, по­лу­ча­ем

Участок ВС, сечение 2-2. Справа от него расположены две силы, на­правленные в разные стороны. С учетом правила знаков, получим

Участок СD, сечение 3-3: аналогично получаем

По найденным значениям N в выбранном масштабе строим эпюру, учи­тывая, что в пределах каждого участка продольная сила постоянна (Рисунок 2 б)

Положительные значения

N откладываем вверх от оси эпюры, отри­ца­тель­ные — вниз.

2. Построение эпюры напряжений s.

Вычисляем напряжения в поперечном сечении для каждого участка бруса:

;

;

.

При вычислении нормальных напряжений значения продольных сил N берутся по эпюре с учетом их знаков.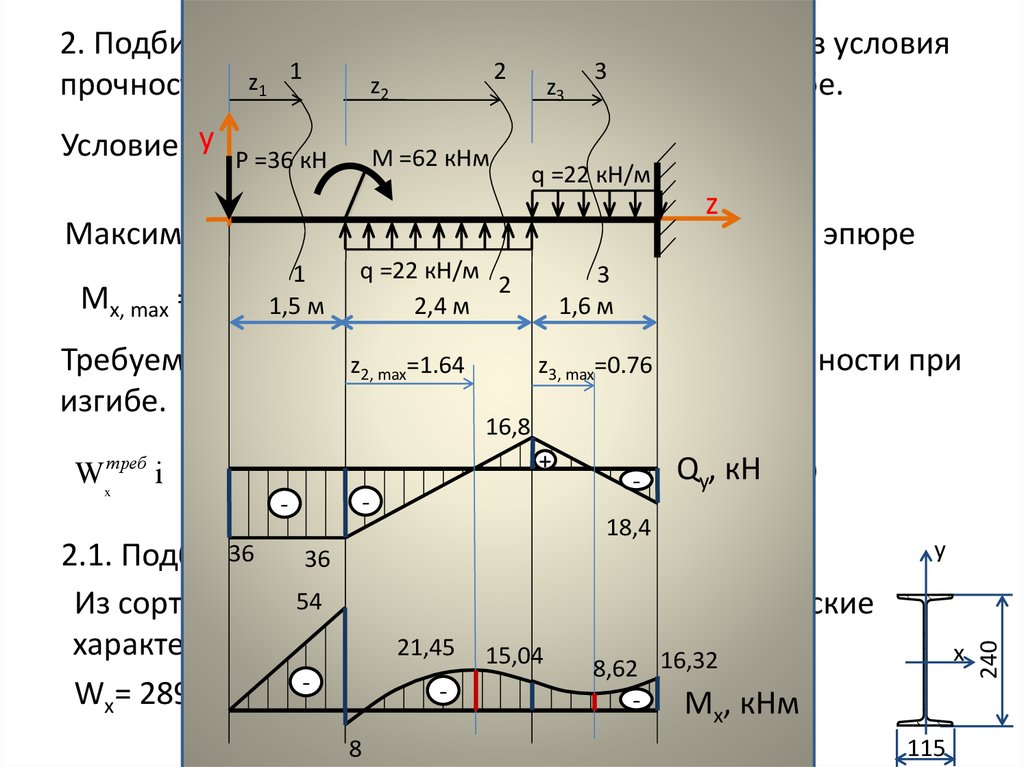 Знак плюс соответствует растя­же­нию, минус — сжатию. Эпюра напряжений показана на Рисунок 2, в.

3. Построение эпюры продольных перемещений.

Для построения эпюры перемещений вычисляем абсолютные удли­нения отдельных участков бруса, используя закон Гука:

;

.

Определяем перемещения сечений, начиная с неподвижного за­кре­плен­ного конца. Сечение D расположено в заделке, оно не может сме­щать­ся и его пере­мещение равно нулю:

Сечение

С переместится в результате изменения длины участка CD. Пе­ремещение сечения С определяется по формуле

.

При отрицательной (сжимающей) силе точка С сместится влево.

Пере­мещение сечения В является результатом изменения длин DC и CB. Скл­а­дывая их удлинения, получаем

.

Рассуждая аналогично, вычисляем перемещение сечения А:

 

.

В выбранном масштабе откладываем от исходной оси значения вычис­лен­ных перемещений. Соединив полученные точки прямыми линиями, стр­о­­­им эпю­ру перемещений (Рисунок 2, г).

4. Проверка прочности бруса.

Условие прочности записывается в следующем виде:

.

Максимальное напряжение находим по эпюре напряжений, выби­рая максимальное по абсолютной величине:

.

Это напряжение действует на участке DC, все сечения которого являются опасным.

Допускаемое напряжение вычисляем по формуле:

.

Сравнивая и , видим, что условие прочности не выполняется, так как максимальное напряжение превышает допускаемое.

 

ЗАДАЧА № 2

Абсолютно жесткий брус АВ опирается на шарнирно-неподвижную опору и прикреплен с помощью шарниров к двум стальным стержням.

Требуется подобрать сечения стержней по условию их прочности, при­няв запас прочности по отношению к пределу текучести .

Соотношение площадей поперечных сечений стержней указано на рас­четных схемах, модуль упругости стали для всех вариантов

Числовые данные берутся из таблицы 2, расчетные схемы — по рисунку 3.

Таблица 2—Числовые данные к задаче № 2

 

Номер строки	Номер расчет. схемы по	Размер, м	Сила, кН	Марка стали	Предел текучести, МПа
	рисунку 3	а	b	с
		1,2	1,6	1,0
		1,2	1,5	0,8
		1,4	1,4	1,0
		1,4	1,6	0,9
		1,4	1,5	0,7
		1,3	1,4	0,8
		1,5	1,2	1,0		40Х
		1,5	1,1	0,9
		1,2	1,5	1,0
		1. 2	1.6	1,0		40Х

 

 

Пример решения задачи

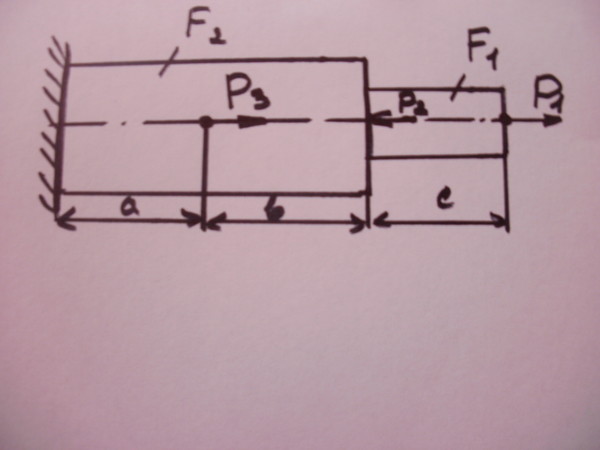
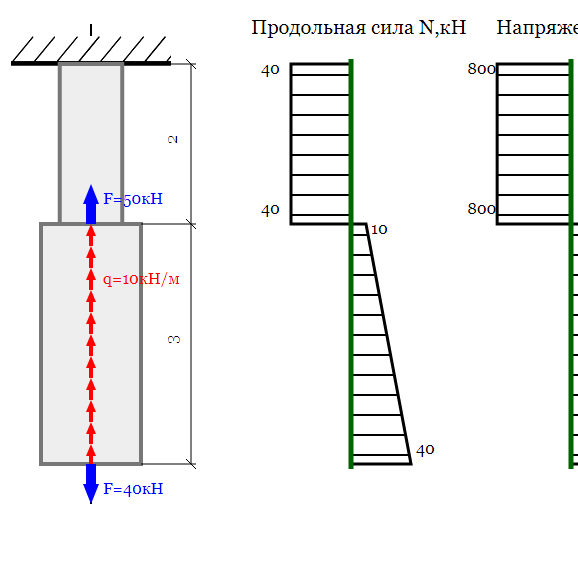
Ступенчатый брус нагружен вдоль оси двумя силами. Брус защемлён с левой стороны (рис. 35) пренебрегая весом бруса, построить эпюры продольных сил и нормальных напряжений.

Рис. 35.

1. Определяем участки напряжения, их два.

2. Определяем продольную силу в сечениях 1 и 2.

3. Строим эпюру.

1. Рассчитываем величины нормальных напряжений и строим эпюру нормальных напряжений в собственном произвольном масштабе.

1. Определяем продольные силы.

2. Определяем нормальное напряжение

Сопоставляем участки нагружения с границами изменения площади, видим, что образуется 4 участка напряжений.

Нормальные напряжения в сечениях по участкам:

Откладываем значения напряжений вверх от оси, т.к. значения их положительны (растяжение). Масштаб эпюр продольной силы и нормальных напряжений выбирается отдельно в зависимости от порядка цифр и имеющегося на листе места.

Задачи для самостоятельного решения Задача № 10

Выбрать соответствующую эпюру продольных сил в поперечных сечениях бруса

Задача № 11

Определить нормальное напряжение в сечении С — С из задачи №10.

Контрольные вопросы

1. Какие внутренние силовые факторы возникают в сечении бруса при сжатии и растяжении?

2. Как распределяются по сечению силы упругости при растяжении и сжатии? (Использовать гипотезу плоских сечений)

3. Какого характера напряжения возникают в поперечном сечении при сжатии и растяжении: нормальные или касательные?

4. Как распределены напряжения по сечению при сжатии и растяжении?

5. Запишите формулу для расчёта нормальных напряжений при сжатии и растяжении?

6. Как назначаются знаки продольной силы и нормального напряжения?

7. Что показывает эпюра продольной силы?

8. Как изменится величина напряжений, если площадь поперечного сечения возрастет в 4 раза?

9. В каких единицах измеряется напряжение?

Продольные и поперечные деформации

■

Рассмотрим деформацию бруса под действием

продольной силы F (рис. 37.). Начальные размеры бруса : 1о — начальная длинна; а₀ — начальная ширена.

Брус удлиняется на величину

абсолютное удлинение. При растяжении поперечные размеры уменьшаются, ∆а -абсолютное сужение;

В сопротивлении материалов принято рассчитывать дефромации в относительных единицах:

относительное удлинение; — относительное сужение.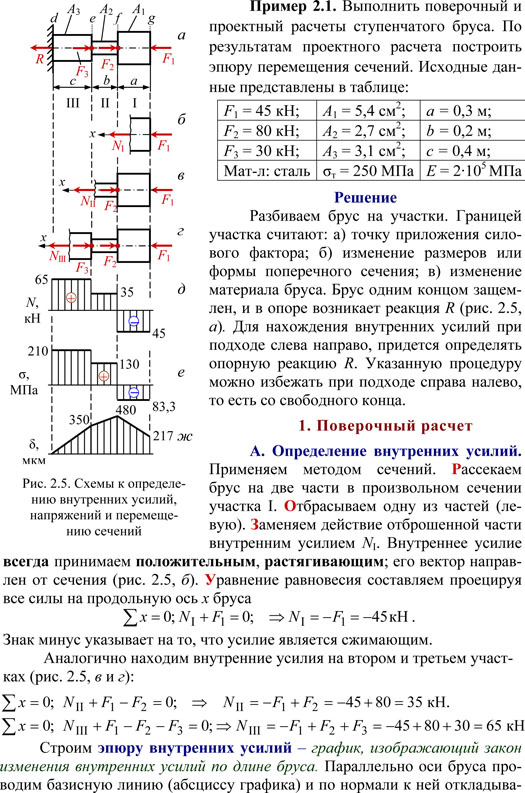

Между продольной и поперечной деформациями существует зависимость

где— коэффициент поперечной деформации, или коэффициент Пуассона, — характеристика пластичности материала.

Закон Гука

По закону Гука деформации

прямопропорциональны напряжению:

Формулы для расчета перемещений поперечных

сечений бруса при растяжении и сжатие

Используем известные формулы.

В результате получим зависимость между нагрузкой, размерами бруса и возникающей деформацией:

Пример решения задачи

Дана схема нагружения и размеры бруса до деформации (рис. 38.). Брус защемлён, определить перемещение свободного конца.

Решение

1. Брус ступенчатый, поэтому следует построить эпюры продольных сил и нормальных напряжении.

Делим брус на участки нагружения, определяем продольные силы, строим эпюр; продольных сил.

2. Определяем величину нормальных напряжений по сечениям с учётом изменений площади поперечного сечения.

Строим эпюру нормальны напряжений.

З.На каждом участке определяем абсолютное удлинение. Результаты алгебраически суммируем.

Примечание. Балка защемлена, в заделке возникает неизвестная реакция в опоре, поэтому расчёт начинаем со свободного конца (справа).

4. Суммарное удлинение бруса (перемещение свободного конца).

Д1 = Ah + Al₂ + A/₃; Al = 0,125 + 0,05 — 0,07 = 0,105 мм

Задача для самостоятельного решения Задача № 12

Стальной стержень длинной 1,5 м вытянулся под нагрузкой на Змм. Чему равно относительное удлинение? Чему равно относительное сужение? (ц=0,25).

Контрольные вопросы

1. Что характеризует коэффициент поперечной деформации?

3. Что характеризует модуль жёсткости

материала? Какая единица модуля упругости?

4. Запишите формулы для определения удлинения бруса. Что характеризует произведение АЕ и как оно называется?

5. Как определяется абсолютное удлинение ступенчатого бруса, нагруженного несколькими силами?

Расчёты на прочности при растяжении и сжатии

Расчёты на прочность ведутся по условиям прочности — неравенствам, выполнение которых гарантирует прочность детали при данных условиях.

Для обеспечения прочности расчётное напряжение не должно превышать допускаемое напряжение:

Расчётное напряжение зависит от нагрузки и размеров поперечного сечения, допускаемого только от материала детали и условий работы.

Существует три правила для расчёта на прочность.

1. Проектировочный расчёт — заданная расчётная схема и нагрузки; материал или размеры детали подбираются.

по величине можно подобрать марку материала.

2. Проверочный расчёт — известны нагрузки, материал, размеры детали; необходимо проверить, обеспечена ли прочность.

Проверяется неравенство

Пример решения задачи.

Прямой брус растянут силой 150 кН (рис. 39.), материал — сталь =570 МПа, а_в =720 МПа, запас прочности [s] = 1,5. определить размеры поперечного сечения бруса.

3.Допускаемое напряжение для материала рассчитывается из данных механических характеристик. Наличие предела текучести означает, что материал -пластичный.

4.Определяем величину потребной площади поперечного сечения бруса и подбираем размеры для двух случаев.

Сечение — круг, определяем диаметр.

Полученную величину округляем в большую сторону d=25MM, А=4,91см .

Сечение — равнополочный уголок № 5 по ГОСТ 8509-86.

Ближайшая площадь поперечного сечения уголка -А=4,29см²(d=5мм). 4,91>4,29.

Статика: распределенные нагрузки

Ключевые вопросы

• Что такое распределенная нагрузка?

• Учитывая распределенную нагрузку, как мы можем найти величину эквивалентной сосредоточенной силы?

• Учитывая распределенную нагрузку, как мы можем найти местоположение эквивалентной сосредоточенной силы?

Распределенные нагрузки — это силы, распределенные по длине, площади или объему. Большинство реальных нагрузок распределены, включая вес строительных материалов и силу ветра, воды или земли, воздействующую на поверхность. Давление, нагрузка, плотность веса и напряжение — все это названия, обычно используемые для распределенных нагрузок. Распределенная нагрузка — это сила на единицу длины или сила на единицу площади, изображенная рядом векторов силы, соединенных вместе вверху, и будет обозначаться как \(w(x)\), чтобы указать, что распределенная нагрузка является функцией \ (х\текст{. }\)

Например, хотя полку с книгами можно рассматривать как совокупность отдельных сил, более распространено и удобно представлять вес книг как равномерно распределенную нагрузку . Равномерно распределенная нагрузка — это нагрузка, имеющая везде одинаковое значение, т. е. \(w(x) = C\text{,}\) — константа.

(а) Полка с книгами разного веса. (b) Каждая книга представлена ​​как отдельный вес (c) Все книги представлены как распределенная нагрузка. Рисунок 7.8.1.

Мы можем использовать вычислительные инструменты, обсуждавшиеся в предыдущих главах, для обработки распределенных нагрузок, если мы сначала преобразуем их в эквивалентные точечные силы. Эта эквивалентная замена должна быть результатом распределенной нагрузки, как описано в Разделе 4.8. Напомним, что эта результирующая сила оказывает такое же внешнее воздействие на объект, как и исходная система сил.

Чтобы быть эквивалентной, точечная сила должна иметь:

• Величину, равную площади или объему под функцией распределенной нагрузки.

• Линия действия, проходящая через центроид распределения распределенной нагрузки.

В следующих двух разделах мы рассмотрим, как найти величину и местоположение эквивалентной точечной силы для распределенной нагрузки.

Подраздел 7.8.1 Эквивалентная величина

Величина распределенной нагрузки книг равна общему весу книг, деленному на длину полки

\begin{equation*} w (x) = \ гидроразрыва {\ Sigma W_i} {\ ell} \end{уравнение*}

. Он представляет собой средний вес книг на единицу длины. Точно так же общий вес книг равен произведению распределенной нагрузки на длину полки или

\begin{align*} Вт \amp = w(x) \ell\\ \text{общий вес} \amp = \frac{\text{вес}}{\text{длина}} \times\ \text{длина полки} \конец{выравнивание*}

Эта общая нагрузка представляет собой просто площадь под кривой \(w(x)\text{,}\) и выражается в единицах силы. Если функция загрузки неравномерна, может потребоваться интегрирование для нахождения площади.

Пример 7.8.2. Книжная полка.

Обычная мягкая обложка имеет толщину около \(\cm{3}\) и весит примерно \(\N{3}\text{.}\)

Какова функция загрузки \(w(x)\) для Полка полна книг в мягкой обложке, и каков общий вес книг в мягкой обложке на \(\m{6}\) полке?

Ответ.

\begin{выравнивание*} w(x) \amp = \Nperm{100}\\ Вт \амп = \N{600} \end{align*}

Решение.

Вес одной книги в мягкой обложке по отношению к ее толщине равен интенсивности нагрузки \(w(x)\text{,}\), поэтому

\begin{уравнение*} w(x) = \frac{\N{3}}{\cm{3}}= \Nperm{100} \end{уравнение*}

.

Общий вес – это площадь под диаграммой интенсивности нагрузки, которая в данном случае представляет собой прямоугольник. Таким образом, \(\m{6}\) книжная полка, покрытая книгами в мягкой обложке, должна поддерживать

\begin{equation*} W = w(x) \ell = (\Nperm{100})(\m{6}) = \N{600} \end{уравнение*}

.

Линия действия этой эквивалентной нагрузки проходит через центр тяжести прямоугольной нагрузки, поэтому она действует в точке \(x = \m{3}\text{.}\)

Подраздел 7.8.2 Эквивалентное местоположение

Чтобы использовать распределенную нагрузку в задаче на равновесие, вы должны знать эквивалентную величину для суммирования сил, а также знать положение или линию действия для суммирования моментов.

Линия действия эквивалентной силы проходит через центр тяжести площади под кривой интенсивности нагрузки. Для прямоугольной нагрузки центр тяжести находится в центре. Нам известны вертикальная и горизонтальная координаты этого центроида, но поскольку линия действия эквивалентной точечной силы вертикальна, и мы можем перемещать силу вдоль ее линии действия, вертикальная координата центроида в данном контексте не важна.

Аналогично, для треугольной распределенной нагрузки — также называемой равномерно изменяющейся нагрузкой — величина эквивалентной силы равна площади треугольника \(bh/2\), а линия действия проходит через центр тяжести треугольника .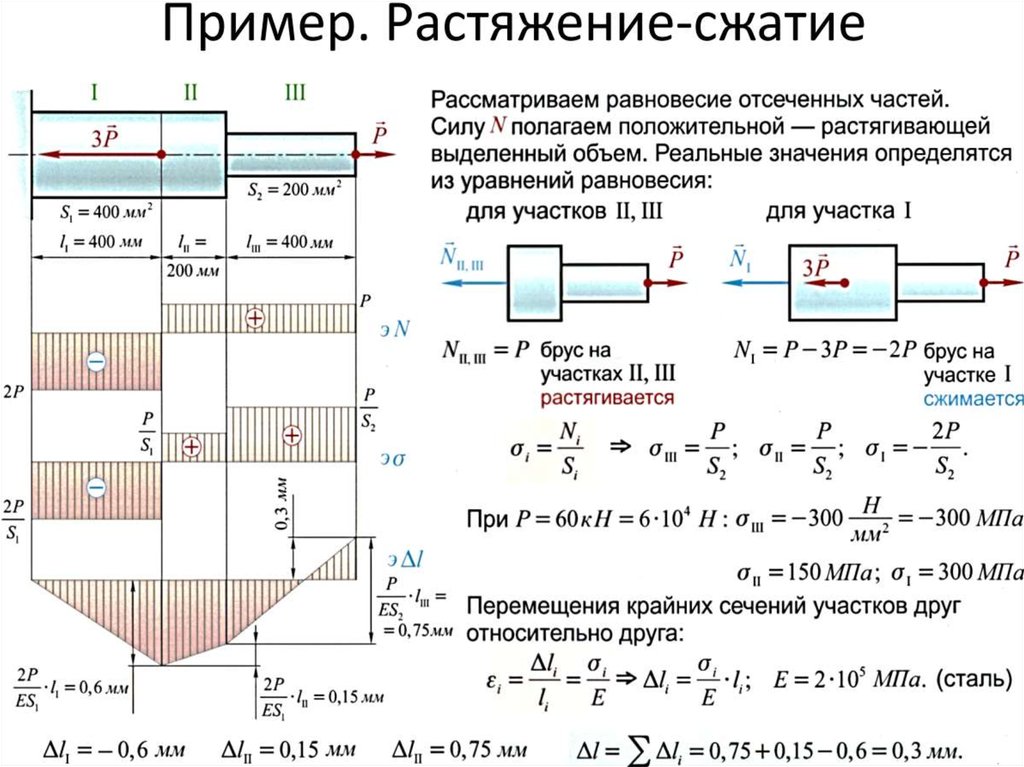 Расстояние по горизонтали от большего конца треугольника до центра тяжести равно \(\bar{x} = b/3\text{.}\)

По сути, мы находим точку равновесия, чтобы момент силы слева от центроида был таким же, как момент силы справа.

Приведенные ниже примеры иллюстрируют, как можно комбинировать вычисление как величины, так и местоположения эквивалентной точечной силы для ряда распределенных нагрузок.

Пример 7.8.3. Равномерно изменяющаяся нагрузка.

Найдите эквивалентную точечную силу и ее точку приложения для показанной распределенной нагрузки.

Ответ.

Эквивалентная нагрузка равна \(\lb{30}\) направленной вниз силе, действующей \(\ft{4}\) с левого конца.

Раствор 1.

Эквивалентная нагрузка представляет собой «площадь» под треугольной кривой интенсивности нагрузки и действует прямо вниз в центре треугольника. Эта треугольная нагрузка имеет основание \(\ft{6}\) и высоту\(\lbperft{10}\), поэтому

\begin{equation*} W = \frac{1}{2} b h =\frac{1}{2}(\ft{6})(\lbperft{10}) =\lb{30}. \end{equation*}

, а центроид расположен \(2/3\) пути от левого конца, поэтому

\begin{equation*} \ бар {х} = \ футов {4} \end{уравнение*}

.

Решение 2.

Распределенные нагрузки могут иметь любую геометрическую форму или определяться математической функцией. Если нагрузка представляет собой комбинацию обычных форм, используйте свойства форм, чтобы найти величину и местоположение эквивалентной точечной силы, используя методы, описанные в разделе 7.5. Если распределенная нагрузка определяется математической функцией, проинтегрируйте, чтобы найти их площадь, используя методы раздела 7.7.

Несколько замечаний:

• Вы можете включить распределенную нагрузку или эквивалентную сосредоточенную силу на диаграмме свободного тела, , но не оба !

• Поскольку вы вычисляете площадь, вы можете разделить площадь на любые удобные формы. Итак, если вы не помните площадь трапеции с макушки, разбейте ее на прямоугольник и треугольник.

Подраздел 7.8.3 Приложения с распределенной нагрузкой

Как только вы преобразуете распределенные нагрузки в результирующую точечную силу, вы можете решить задачу так же, как и другие задачи в предыдущих главах этой книги. Обратите внимание, что хотя результирующие силы равны внешне эквивалентны распределенным нагрузкам, они не внутренне эквивалентны , как будет показано в главе 8.

Пример 7.8.4. Консольная балка.

Найти реакции при фиксированном соединении в \(A\text{.}\)

Ответ.

\begin{выравнивание*} А_х\ампер = 0\\ A_y \amp = \N{16}\\ М \амп = \Nm{64} \end{align*}

Решение.

Нарисуйте диаграмму свободного тела, заменив распределенную нагрузку эквивалентной сосредоточенной нагрузкой, затем примените уравнения равновесия.

\begin{выравнивание*} \Sigma F_x \amp = 0 \amp \amp \rightarrow \amp A_x \amp = 0\\ \Sigma F_y \amp = 0 \amp \amp \rightarrow \amp A_y \amp = \N{16}\\ \Sigma M_A \amp = 0 \amp \amp \rightarrow \amp M_A \amp = (\N{16})(\m{4}) \\ \amp \amp \amp \amp \amp = \Nm{64} \end{выравнивание*}

Пример 7.

8.5. Лучевые реакции.

Найдите реакции в опорах показанной балки.

Ответ.

\begin{уравнение*} A_y = \lb{196,7}, A_x = \lb{0}, B_y = \lb{393,3} \end{уравнение*}

Раствор.

Начните с рисования диаграммы свободного тела балки с двумя распределенными нагрузками, замененными эквивалентными сосредоточенными нагрузками. Две распределенные нагрузки равны \((\inch{10}) (\lbperin{12}) = \lb{120}\) каждая.

Затем применим уравнения равновесия.

\begin{выравнивание*} \сумма M_A \ампер = 0\\ +(\lbperin{12})(\дюйм{10}) (\дюйм{5}) -(\lb{100}) (\дюйм{6})\\ -(\фунт{150})(\дюйм{12}) -(\фунт{100}) ( \дюйм{18})\\ +(B_y) (\дюйм{18}) — (\lbperin{12}) (\дюйм{10}) (\дюйм{29)})\amp = 0 \rightarrow \amp B_y \amp= \lb{393.3}\\ \\ \сумма F_y\амп = 0\\ -(\lbperin{12}) (\дюйм{10}) + B_y — \lb{100} — \lb{150} \\ — \lb{100} +B_y — (\lbperin{12})( \inch{10})\amp = 0 \rightarrow \amp B_y\amp= \lb{196,7}\\ \\ \sum F_x \amp = 0 \rightarrow \amp A_x \amp = 0 \end{align*}

Как рассчитать железобетонную балку на сдвиг? Пример включен

🕑 Время чтения: 1 минута

Расчет железобетонной (ЖБ) балки на сдвиг включает определение расстояния между хомутами. Слово «сдвиг» используется для обозначения сил, действующих перпендикулярно продольной оси железобетонной балки. Обычно поперечные усилия максимальны на опорах балок и уменьшаются к середине пролета балки.

Трещины железобетонных балок при изгибе из-за главных растягивающих напряжений, которые горизонтальны в середине пролета балки. Эти главные напряжения меняют направление от горизонтального в продольной арматуре до 45 градусов на нейтральной оси и вертикального в месте максимального напряжения сжатия.

Таким образом, сдвиговая арматура или хомуты ограничивают трещины при сдвиге и выдерживают касательные напряжения в сочетании с сопротивлением сдвигу бетона. Таким образом, способность железобетонной балки к сдвигу представляет собой комбинацию прочности на сдвиг бетона и прочности на сдвиг арматуры в соответствии с нормами ACI.

Рисунок-1: Типы трещин в железобетонных балках из-за главных растягивающих напряжений

Содержание:

• Виды разрушения при сдвиге
• Армирование при сдвиге
  • Функции хомутов
• Расчет критического сечения 90 Расположение критического сечения 90 005 Код АСИ Положение о расчете ж/б балки на сдвиг
  • 1. Прочность на сдвиг железобетонной балки
  • 2. Минимальная арматура на сдвиг
  • 3. Минимальное расстояние между хомутами
  • 4. Максимальное расстояние между хомутами
• Процедура расчета на сдвиг железобетонной балки
• Пример
  • Решение:
• Часто задаваемые вопросы 0226
• Разрушение при изгибе трещины которых преимущественно вертикальные в средней трети пролета балки.
• Разрушение по диагонали при растяжении, когда прочность балки при диагональном растяжении ниже, чем ее прочность при изгибе.
• Разрушение при сжатии при сдвиге, когда балка имеет небольшое отношение пролета к глубине сдвига, составляющее 1–2,5 для сосредоточенной нагрузки и менее 5 для распределенной нагрузки.

Когда поперечное сечение бетона имеет недостаточную площадь для поддержания касательных напряжений ниже допустимых значений, дополнительное сопротивление сдвигу может быть обеспечено двумя способами. Одна из поперечной арматуры, состоящей из обручей или хомутов, которые могут располагаться вертикально или наклоняться под некоторым углом к ​​горизонтали.

Другой вариант представляет собой армирование полотна, которое может состоять из гибкого армирования, которое можно изогнуть по диагонали вверх (где сопротивление изгибу больше не требуется) для усиления полотна.

Рис. 2: Арматура, работающая на сдвиг

Функции хомутов

Арматура на сдвиг выполняет четыре основные функции:

1. Переносит часть поперечной силы, учитываемой при изгибе.
2. Ограничивает рост диагональных трещин.
3. Удерживает на месте продольные арматурные стержни.
4. Обеспечивает некоторое удержание бетона в зоне сжатия, если хомуты выполнены в виде закрытых связей.

Расположение критического сечения для расчета на сдвиг определяется исходя из условий на опорах. Место критического сдвига находится на расстоянии эффективной глубины (d) для условий (a, b и c) на рисунке 3, тогда как критическое сечение для расчетного сдвига находится на поверхности опор для условий (e, f и г) на рисунке-3.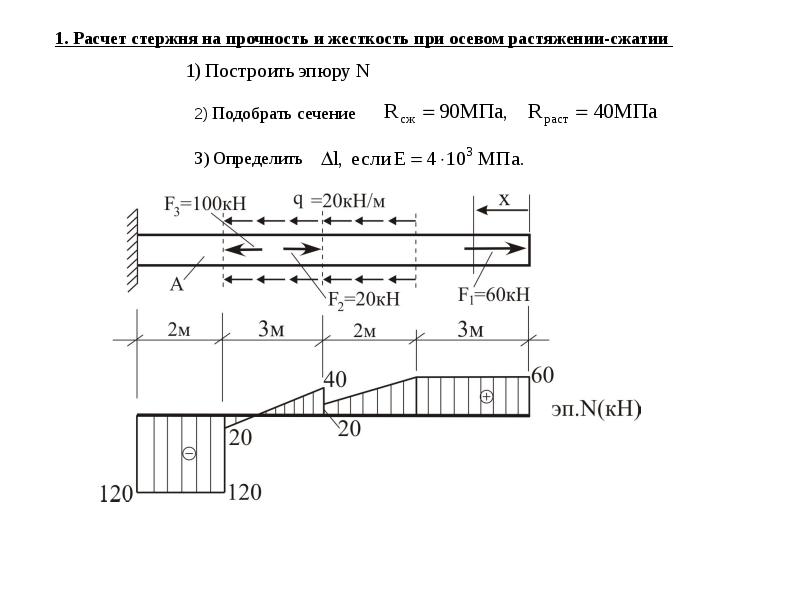

а- Концевая балка

b- Балка, опирающаяся на колонны

c- Сосредоточенная нагрузка на расстоянии d от поверхности опоры

d- Элемент, нагруженный внизу глубина

f- Балка, опирающаяся на монолитный вертикальный элемент

0007

V _u = n

где:

V _u : общая поперечная сила, приложенная к любому сечению балки из-за факторизованных нагрузок, кН

: коэффициент снижения прочности, равный 0,7 .

V _n : прочность балки на сдвиг, которая равна сумме вклада бетона и хомута, кН

Прочность балки на сдвиг можно рассчитать по следующей формуле: с +V _s Уравнение 1

Прочность бетона на сдвиг и прочность хомутов на сдвиг можно рассчитать, используя уравнения 2 и 3 соответственно:

Примечание:

1. Код ACI указывает, что площадь, используемая для расчета Vc в уравнении 2, представляет собой произведение диаметра и эффективной глубины. Последний можно принять равным 0,8 диаметра элемента.
2. Уравнение 2 становится менее точным при прогнозировании вклада бетона в прочность бетона выше 42 МПа, по этой причине Кодекс ACI устанавливает верхний предел 8,3 МПа для √(fc′). Однако значения √(fc′) более 8,3 МПа могут использоваться при расчете Vc, если используется минимальное количество армирующей сетки.

Уравнение 3, используемое для расчета прочности на сдвиг вертикальных хомутов. Если хомуты наклонены, для расчета прочности на сдвиг следует использовать уравнение 4:

2. Минимальное армирование на сдвиг

Если Vu, сила сдвига при факторизованной нагрузке, не превышает (∅Vc), то теоретически армирование стенки не требуется. . Однако даже в таком случае Кодекс ACI требует обеспечения минимальной площади армирования стенки, равной:

3. Минимальное расстояние между хомутами

Нежелательно размещать вертикальные скобы ближе, чем на 100 мм. Размер стремян следует выбирать таким образом, чтобы избежать более близкого расстояния.

4. Максимальное расстояние между хомутами

Максимальное расстояние между хомутами наименьшее из следующего при условии, что (V _s <0,33(fc') ^0,5 b _w d):

Для продольных стержней, изогнутых в 45 градусов, второе вышеприведенное уравнение заменяется на S _max =3d/4

Ни в коем случае, согласно Кодексу ACI, Vs не должно превышать (0,66√(fc′) b _w d) независимо от количества используемой стальной стенки, в противном случае необходимо увеличить размер балки.

Процедура расчета на сдвиг железобетонной балки

Расчет на сдвиг включает оценку расстояния между хомутами для поддержки предельного сдвига. Обычно часть бетона сопротивляется сдвигающей силе, а та часть, которая не поддерживается бетоном, удерживается поперечной арматурой.

1. Во-первых, рассчитайте предельное усилие сдвига.
2. Во-вторых, оцените проектную прочность бетона на сдвиг, используя уравнение, умноженное на коэффициент снижения прочности в 2 раза.
3. Армирование на сдвиг не требуется, если Vu< 0,5Vc.
4. Если 0,5Vc>Vu< Vc , то используйте только арматуру с минимальным сдвигом.
5. Обеспечить поперечную арматуру, когда Vu> Vc.
6. Если шаг 5 выполнен, рассчитайте поперечную силу (V _s ), которой должны сопротивляться хомуты, используя уравнение 1. .
7. Умножьте площадь поперечной арматуры на количество опор хомута, чтобы вычислить площадь поперечной арматуры. 90,5bwd, то это максимальное расстояние должно быть уменьшено вдвое.
8. Наконец, начертите расчетную балку с продольной и поперечной арматурой.

Где:

Пример

Свободно опертая прямоугольная балка шириной 400 мм и эффективной глубиной 550 мм выдержала суммарную факторизованную нагрузку 137 кН/м на 6-метровом пролете. Он укреплен 4914 м ² из растянутой стали, которая прерывается в опорах. Спроектируйте балку на сдвиг с помощью вертикальных U-образных хомутов.

Свойства материала: fc′=28 МПа и fyt=420 МПа

Решение:

Рассчитайте поперечную силу на балке с помощью уравнения или начертите диаграмму сдвига:

поддержки составляет 411 кН. Однако для свободно опертой балки расположение критического сечения для расчета на сдвиг находится на расстоянии (d), где (d) — эффективная глубина. Итак, поперечная сила в критическом сечении балки вычисляется следующим образом:

V _{u, на расстоянии (d)} = (411*(3-0,55))/(3)= 335,65 кН

Рассчитать расчетную прочность бетона на сдвиг:

V _c =0,75*0,17*(28) ^(1/2) *400*550*10 ^-3 = 148,426 кН

С В _{u, на расстоянии (d)} =335,65 кН > В _c

4 = 16 КН 256 , Поэтому требуется поперечная арматура. .

V _{с, необходимое} = V _{u, на расстоянии (d)} -V _c = 335,65-148,426= 187,22 кН , Хомуты должны быть спроектированы таким образом, чтобы выдерживать такое усилие сдвига, которое превышает прочность бетона на сдвиг.

В _{с, требуется} =187,22 кН<0,66*(28) ^(1/2) *400*550*10 ^-3 =288,12 кН , Следовательно, размер балки удовлетворяет требованиям к сдвигу.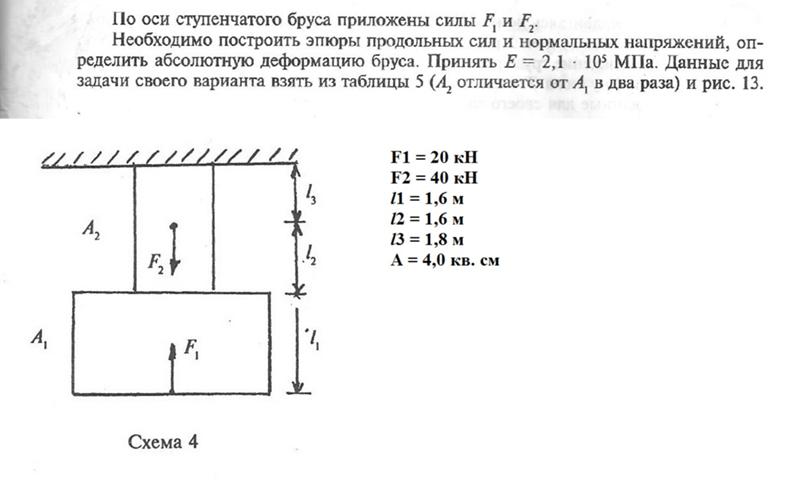

Предположим, диаметр стремени и вычислить его площадь:

Предположим, что стремени НЕТ. 1

A _v =(PI/4)*(10) ² *2= 157,079 мм ²

Рассчитайте необходимое расстояние между скобами, используя уравнение 3:

S=(0,75*157,079*420*550)/(187,22*10 ³ )= 145,35 мм для 1, округляем это значение до 145,35 мм 9026. просто работа по размещению.

Значение ( 145,35 мм ) больше минимального расстояния (100 мм). Однако он также не должен превышать максимальный интервал.

Определите максимальную арматуру между хомутами, используя уравнение 6:

S _макс. =((157,079*420)/(0,062*(28) ^(1/2) *400))=<((157,079*420)/(0,35*400))

S _max =502,73= <471.237

S _макс. =d/2= 550/2= 275 мм

S _макс. = 600 мм

Наименьшее значение 225 мм, поэтому

макс. > требуемое расстояние 140 мм

Теперь распределите хомуты в соответствии с требованиями кода ACI:

Теоретически, если расчетная прочность бетона на сдвиг больше силы сдвига, то хомуты не требуются. Однако код ACI указывает, что для такой области должно быть предусмотрено минимальное армирование (т.е. максимальное расстояние).

В нормах ACI также указано, что поперечная арматура не требуется, если поперечная сила составляет менее половины расчетной прочности бетона на сдвиг. Определим эти места и наложим на диаграмму сдвига балки. Половина луча будет принята во внимание, поскольку луч является симметричным.

Исходя из геометрии диаграммы сдвига, расстояние (x), за пределами которого хомуты не требуются, составляет:

(411/3)=((411-74,213)/x), x=2,458 м какое минимальное армирование (максимальное расстояние необходимо:

(411/3)=((411-148,426)/x), x=1,916 м

Таким образом, требуемый шаг (140 мм) следует использовать на расстоянии 1,916 м от поверхности крепи.

Рисунок-5: Распределение хомутов в соответствии с кодом ACI

Хомуты могут быть распределены по следующей схеме. Первый хомут устанавливается на расстоянии (шаг/2) от торца опоры:

1 хомут на s/2=140/2= 70 мм

13 хомутов на расстоянии 140 мм, 13*140= 1820 мм

3 хомута на расстоянии 275 мм, 3*275= 825 мм

Общее расстояние = 70+1820+825= 2715 мм

Часто задаваемые вопросы

Как рассчитать прочность на сдвиг железобетонной балки?

Прочность на сдвиг железобетонной балки представляет собой сочетание прочности бетона на сдвиг и прочности на сдвиг, обеспечиваемой армированием стенок.

Прочен ли бетон на сдвиг?

Бетон не выдерживает поперечной силы.

Каковы режимы разрушения при сдвиге железобетонных балок?

1. Разрушение при изгибе, при котором трещины преимущественно вертикальные в средней трети пролета балки.
2. Разрушение при диагональном растяжении, это разрушение происходит, если прочность балки при диагональном растяжении ниже, чем ее прочность при изгибе.
3. Разрушение при сжатии при сдвиге. В этом случае балка имеет небольшое отношение пролет/глубина сдвига величиной 1-2,5 для сосредоточенной нагрузки и менее 5 для распределенной нагрузки.

Что такое арматура на сдвиг?

Арматура на сдвиг предназначена для сопротивления сдвиговым усилиям, превышающим предел прочности бетона на сдвиг. Они представлены в виде вертикальных или наклонных хомутов или продольной арматуры, изогнутой под углом 45 градусов, в местах, где они больше не нужны для сопротивления изгибу.

Почему в ж/б балке предусмотрены хомуты?

1. Выдерживает часть поперечной силы изгиба.
2. Ограничить рост диагональных трещин.
3. Удерживайте продольные арматурные стержни на месте.