Способ верещагина

Содержание

Правило А.К. Верещагина «перемножения эпюр»

⇐ ПредыдущаяСтр 2 из 2

В 1924 г. студент Московского института инженеров транспорта Андрей Константинович Верещагин (1896–1959), ставший впоследствии инженером-полковником, заметил, что, если для стержня с постоянной жесткостью в формуле Мора одна из функций, стоящих в числителе, является линейной, вычисление интеграла можно упростить и вместо функциональных зависимостей M_F(х) и использовать эпюры соответствующих моментов. Поэтому способ, полученный А.К. Верещагиным для вычисления интеграла от произведения двух функций, называют способом «перемножения эпюр». Слова «перемножение эпюр», поставлены в заголовке в кавычки, поскольку правило относится не к вычислению произведения эпюр, входящих в формулу Мора, а к интегралу от этого произведения. В случае стержневой системы, состоящей из прямолинейных стержней, единичная эпюра всегда является линейной, и поэтому способ А.К. Верещагина применяется достаточно часто.

Для случая преобразуем формулу (9.2) к виду:

(9.3)

Покажем, как вычисление интеграла в формуле (9.3) сводится к использованию геометрических параметров соответствующих эпюр.

На рис. 9.4 показана грузовая эпюра моментов М_F от внешних нагрузок, предполагаемая произвольной,и единичная эпюра , которая предполагается линейной.

Рис. 9.4. К выводу правила Верещагина А.К.

Уравнение для линейной эпюры запишем в виде:

Интеграл, входящий в (9.3), будет равен:

Первый интеграл, стоящий в правой части равенства, является площадью эпюры М_F, которую обозначим w_F. Учитывая, что второй интеграл, равный представляет собой статический момент площади w

_F относительно оси у, который равен:

где х_С – расстояние от оси у до центра тяжести площади w_F. В итоге приходим к равенству

Из рис. 9.4 нетрудно установить, что сумма, стоящая в скобках, равна

где: у_С – ордината единичной эпюры, находящаяся под центром тяжести грузовой эпюры. Таким образом, для интеграла Мора получим окончательное выражение, называемое способом или правилом А.К. Верещагина:

(9.4)

Правило Верещагина.

Интеграл от произведения грузовой и единичной эпюр равен площади грузовой эпюры, умноженной на ординату единичной эпюры под центром тяжести грузовой эпюры.

В случае, когда грузовая эпюра также линейная, в формуле (9.4) можно брать площадь любой из двух эпюр (грузовой или единичной).

Произведение w_F и у_С следует брать с учетом знака. Оно может быть положительное или отрицательное. Для балок, где знаки на эпюрах моментов ставят (вверху «минус», снизу «плюс»), вычисление знака этого произведения не представляет трудности. В рамах принято знак момента не ставить, а эпюры строить со стороны растянутого волокна. Считают, что если эпюра М_F и ордината эпюры лежат с одной стороны от оси, то их произведение будет положительным, в противоположном случае – отрицательным.

Для балки, состоящей из нескольких участков, и для рам следует вычислять интегралы Мора по каждому из участков конструкции. Во многих случаях площадь грузовой эпюры, и особенно ее центр тяжести, найти затруднительно, поэтому рассмотрим способы разбиения сложных эпюр на простейшие.

Ограничиваясь рассмотрением грузовых эпюр М_F, имеющих вид квадратной параболы, приведем способ разбиения сложных эпюр на более простые, указав площади и положения центров тяжести отдельных частей.

На рис. 9.5 показан способ разбиения «равнозначной» трапеции, у которой основания имеют одинаковый знак (рис. 9.5, а), «разнозначной» трапеции (рис. 9.5, б) и квадратной параболы (рис. 9.5, в).

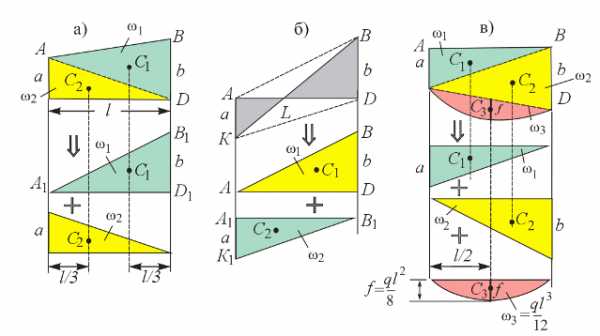
Рис. 9.5. Способы разбиения эпюр

Буквами обозначены площади отдельных частей эпюры. На первый взгляд, трапецию логично разбить на прямоугольник и треугольник, но на самом деле удобнее представить трапецию как сумму двух треугольников, что позволяет ввести единообразие в использование правила А.К. Верещагина. На рис. 9.5, а треугольники ABD и A₁B₁D

₁ отличаются по форме, но их можно считать эквивалентными, поскольку, эти треугольники, имеющие одинаковое основание (b) и высоту (l), имеют равную площадь ( bl/2), и их центры тяжести находятся на одинаковом расстоянии (l/3) от основания. Показанная на рис. 9.5, б разнозначная трапеция разбивается на два треугольника, один из которых расположен выше базовой линии, а другой ниже. Если к балке приложена равномерно распределенная нагрузка q, то на соответствующем участке эпюра моментов представляется квадратной параболой (рис. 9.5, в). В этом случае суммарная эпюра разбивается на трапецию, которая рассмотрена выше, и «чистую» квадратную параболу (значения которой на концах участка равны нулю).

Для определения площади параболы можно проинтегрировать функцию M(x) для балки на двух опорах, загруженной равномерно распределенной нагрузкой q.

На расстоянии х от левой опоры для этой балки:

(9.5)

где: f = ql²/8 – максимальное значение изгибающего момента посередине балки (эту величину часто называют «стрелкой параболы»), l – длина участка. Центр тяжести лежит посредине параболы.

При разбиении сложных эпюр на более простые формула (9.4) будет иметь вид:

(9.6)

где: – площади простейших фигур, составляющих грузовую эпюру, а у_i – ординаты единичной эпюры под центрами тяжести соответствующих площадей .

В случае, когда обе эпюры (грузовая и единичная) имеют вид трапеций (рис. 9.6), для вычисления интеграла от произведения этих эпюр существует формула «перемножения трапеций», вывод которой приведен ниже.

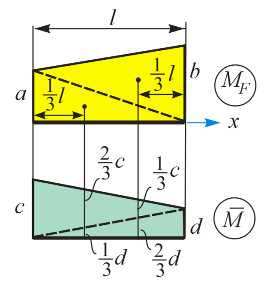
Рис. 9.6. К формуле «перемножения трапеций»

Значения a, b, c, и d в формуле (9.7) следует брать с учетом знака (выше – ниже оси). Надо разделить длину участка на шесть, а затем перемножить дважды левые ординаты, дважды правые ординаты и, далее, перемножить друг на друга ординаты, расположенные «крест на крест».

Пример 9.2.Вычислим, используя правило Верещагина А.К. прогиб и угол поворота на левом конце балки, рассмотренной в примере 9.1.

На рис. 9.7 показаны грузовая эпюра , а также две единичные эпюры: (от вертикальной единичной силы в т. A) и (от единичного момента в т. А).

Грузовая эпюра разбита на треугольник, площадь которого равна и «чистую» квадратную параболу площадью

Для удобства рассуждений стрелками показано положение частей грузовой эпюры относительно оси (сверху, снизу).

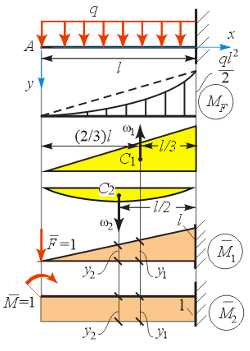
Рис. 9.7. К примеру 9.2

Ординаты единичных эпюр под центрами тяжести треугольника и параболы будут равны:

— для эпюры

;

— для эпюры

Подставляя полученные значения и у_iв (9.6), находим:

Знак «плюс» при перемножении площади на соответствующую ординату получают при условии, что грузовая эпюра и ордината единичной эпюры находятся с одной стороны от базовой линии, а знак «минус» – когда грузовая эпюра и ордината единичной эпюры находятся по разные стороны от базовой линии.

Знак окончательного результата «перемножения» эпюр имеет следующее значение. Положительный результат свидетельствует о том, что перемещение происходит по направлению единичного воздействия, а отрицательный – против. Так, например, знак «минус» в результате дляφ

_А указывает на то, что направление угла поворота сечения балки в т. А противоположно направлению единичного момента, приложенного к балке.

Метод Мора удобен при вычислении перемещений в рамах, поскольку позволяет вычислять не только вертикальные перемещения и углы поворота, но и горизонтальные перемещения.

⇐ Предыдущая12

stydopedya.ru

Верещагина способ определения — Энциклопедия по машиностроению XXL

Верещагина способ определения перемещений 124 Взаимозаменяемость резьбовых соединений 287 [c.953]

Рассмотрим некоторые примеры применения способа Верещагина для определения перемещений в различных стержневых си- [c.382]

При использовании способа Верещагина для определения указанных выше перемещений необходимо построить эпюры моментов от действия внешних нагрузок (рис. 6.16, а, в) и отдельно эпюры моментов от каждой единичной силы (рис. 6.16, г, д, е, ж, 3, и).

[c.75]

В качестве примера рассмотрим применение способа Верещагина для определения прогиба точки С (под силой Р ) балки, изображен ной ла рис. 16. 1Т,а при этом учтем действие изгибающих моментов и поперечных сил. [c.509]

Способ Верещагина. При определении перемещений поперечных сечений прямых брусьев постоянного сечения методом единичной нагрузки интеграл Мора (93) удобно вычислять, пользуясь графо-аналитическиы способом Верещагина. Согласно этому способу перемещение (угловое или линейное) определяется по формуле [c.124]

Для определения второй и третьей характеристик, строим эпюры х и у, т. е. законы изменения расстояний точек контура от осей у и х (рис. 380, б и в). Затем производим перемножение эпюры а на эпюры х и у но способу Верещагина. Так как эпюра х всюду положительна, а ш при переходе через ось симметрии х меняет знак, получаем

[c.332]

Рис. 3i. к определению прогиба способом Верещагина [c.219]

Для определения единичного 6л и грузового А,р перемещений строим эпюры моментов в основной системе от единичного неизвестного = 1 и от заданной нагрузки (рис. в и г). По формуле Мора, используя способ Верещагина, найдем перемещения [c.178]

Указание. Центр изгиба сечения находится на оси симметрии х. При его-определении геометрические характеристики сечения не могут быть вычислены по способу Верещагина [c.221]

Определение перемещений по способу Верещагина [c.75]

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В РАМЕ ПО СПОСОБУ ВЕРЕЩАГИНА [c.78]

Результаты определения перемещений сечений рамы (рис. 6.16) по способу Верещагина представлены в табл, 6.2. [c.79]

Следует отметить, что при определении перемещений по способу Верещагина при числе слагаемых при суммировании три и более вычисления во избежание ошибок целесообразно проводить в табличной форме. [c.79]

Говорят и так Определим прогиб по правилу Верещагина . Но ведь правило Верещагина—это не способ для определения перемещения, а ра-фо-аналитический прием вычисления интеграла Мора, а значит, и говорить надо Определим прогиб методом Мора, применив правило Верещагина . Конечно, такая формулировка излишне многословна, поэтому можно просто сказать Определим прогиб по методу Мора , не упоминая о правиле Верещагина, тем более, что в техникумах (да и в вузах) почти не встречается задач, в которых требовалось бы вычислять этот интеграл аналитическим способом. Такая сокращенная формулировка все же правильнее, чем приведенная выше. [c.13]

Правило Верещагина. Это правило не следует трактовать как метод определения перемещений, это способ вычисления интеграла Мора. Вывод правила Верещагина рекомендуем давать в плане чисто математическом, как графо-аналитический способ вычисления интеграла от произведения двух функций, из которых одна произвольная, а вторая линейная. [c.214]

Для определения перемещения по способу Верещагина необходимо знать площадь эпюры моментов от внешней нагрузки и найти [c.218]

Для решения системы уравнений (а) необходимо определить коэффициенты б и А. Для их определения используем способ Верещагина. [c.278]

Для определения перемещений 6,t, Д,р рассматриваем основную систему, отдельно нагруженную заданной нагрузкой и каждой единичной силой 1 = 1, А2=1 (рис. 411, а). Так как стержни прямолинейные, то удобно применить для определения перемещений способ Верещагина. Эпюры изгибающих моментов Мр, М , М2 показаны иа рис. 411, б. [c.430]

В этих случаях рекомендуется пользоваться энергетическим методом определения перемещений — частными формулами (интегралом) Мора или способом Верещагина. [c.45]

Для определения прогиба способом Верещагина необходимо построить эпюры изгибающих моментов [c.57]

Существуют методы расчета [26, 52], в которых моменты определяют графоаналитическим способом, а для определения прогибов используют правило Верещагина и интеграл Максвелла—Мора, которые приводят также к весьма сложным выражениям и подсчетам, но оптимальный зазор при этом определяется однозначно. [c.126]

Он сводится к определению линейных и угловых перемещений и сравнению их с допускаемыми. Перемещения целесообразно определять, используя интеграл Мора и способ Верещагина (см. гл. 19). Величина допускаемых упругих перемещений зависит от конкретных требований к конструкции, и устанавливают ее в каждом отдельном случае. [c.318]

Определение способом Верещагина 328, 329, 331 —Таблицы 317—325 [c.973]

В балках и рамах для определения коэффициентов и свободных членов канонических уравнений удобно пользоваться способом Верещагина, т.е. [c.219]

В 1924 г. А. Н. Верещагин предложил правило вычисления интеграла Мора графо-аналитическим способом для определения перемещений (прогиба и угла поворота сечений) балки постоянной по всей длине жесткости BJ. Достоинство правила Верещагина состоит в том, что все расчеты заменяются простейшими геометрическими вычислениями, производимыми над эпюрами изгибающих моментов. Строятся две эпюры одна—от заданной нагрузки (нагрузок), другая—от единичной нагрузки, приложенной по направлению искомого перемещения. Единичная нагрузка может быть или сосредоточенной силой (при определении прогиба), или сосредоточенным моментом (при определении угла поворота сечения). Единичная сила прикладывается в том сечении балки, в котором определяют прогиб, а единичный момент — в сечении балки, в котором определяют угол поворота сечения. Прогиб и угол поворота сечения балки определяют по формулам [c.200]

Способ Верещагина может применяться не только при определении перемещений, но и при определении потенциальной энергии. [c.512]

Г, в, г). Определение перемещений производим по формуле (24.11). Для этого перемножаем по способу Верещагина эпюры Мр и М1, а затем эпюры Мр и Мц [c.513]

Определение по способу Верещагина 124, 126 [c.964]

Эпюры — Определение 5 — Расслоение при определении перемещения по способу Верещагина 126 [c.974]

Для определения вертикальных смещений точек приложения сил Р при искривлении рамы составляем уравнение угловых перемещений (углов поворота) стойки. Приложим к статически определимой основной системе единичный момент (фиг. 610) и построим соответствующую эпюру изгибающих моментов. Перемножая эпюры на фнг. 609 и 610 по способу Верещагина, имеем [c.813]

Способ перемножения эяюр — правило Верещагина. Если жесткость поперечного сечения стержня на участке постоянна, то каждый интеграл формулы Максвелла — Мора (185) можно подсчитывать через произведение площади ю эпюры усилия от заданных сил (рис. 167) на координату эпюры такого же усилия от единичной фиктизной обобщенной силы (обязательно прямолинейной), приходящейся против центра тяжести первой эпюры. Практически это тавило Верещагина применяют для определения линейных и угловых перемещелий в балочно-рамных системах от действия изгибающих [c.252]

Для вычисления коэффициентов и свободных членов уравнений перемещений используем энергетический метод определения перемещений и графо-аналитический способ интегрирования (по Верещагину). С этой целью строим эпюры изгибающих моментов и нормальных сил от единичных нагрузок Х — кг, = I кг и Хз= 1 кгсм (фиг. 367, г, д, е. ж, 3, и) и производим соответствующее перемножение [c.435]

Расчет на прочность В этом случае связан с необходимостью определения прогиба. При продольно-поперечном изгибе прннцип сложения действия сил неприменим, поэтому прогибы нельзя определять с помощью интеграла Мора и способом Верещагина. Перемещения при продольно-поперечном изгибе бпределяюг интегрированием дифферен- циального уравнения упругой линии. [c.254]

mash-xxl.info

Верещагина способ определения перемещений — Энциклопедия по машиностроению XXL

Верещагина способ определения перемещений 124 Взаимозаменяемость резьбовых соединений 287 [c.953]

Определение перемещений по способу Верещагина [c.75]

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В РАМЕ ПО СПОСОБУ ВЕРЕЩАГИНА [c.78]

Результаты определения перемещений сечений рамы (рис. 6.16) по способу Верещагина представлены в табл, 6.2. [c.79]

Эпюры — Определение 5 — Расслоение при определении перемещения по способу Верещагина 126 [c.974]

mash-xxl.info

Эпюра — Перемножение способом Верещагина

Эпюра — Перемножение способом Верещагина 217 [c.768]

Эпюра — Перемножение способом Верещагина 1.217 [c.665]

Моменты изгибающие 170, 208 — Расчет 171 — Эпюры 208—217, 250 — Эпюры — Перемножение способом Верещагина 224, 226, 228, 229 — Эпюры для балок статически неопределимых 236—239, 242 [c.784]

Рнс. 29. Перемножение эпюр способом Верещагина [c.217]

Определяем коэффициенты канонического уравнения. Для этого в основной системе строим эпюры Mf от приложения единичной неизвестной Х 1 (рис. 1.3, в, г) и от заданной внешней нагрузки Mf (рис. 1.3, д, е). Для удобства перемножения эпюр по способу Верещагина эпюру Мрш первом пролете разбиваем на две эпюру от распределенной нагрузки, приложенной к консоли, и эпюру от распределенной нагрузки, приложенной собственно в первом пролете. [c.18]

Чтобы определить перемещения, применим способ Верещагина. На рис. 414 показаны эпюры изгибающих моментов для основной системы от заданной нагрузку от единичных обобщенных сил 1 = 1, 2=1, А з=1- Отметим, что эпюры Ml и Мз симметричные, а эпюра М2 — кососимметричная. Как указывалось, побочные коэффициенты, определяющиеся перемножением симметричной эпюры на кососимметричную, равны нулю. В силу этого 612 = = 621=0 623 = 632=0. [c.432]

Таким образом, по способу Верещагина операция интегрирования заменяется перемножением площади первой эпюры на ординату второй (линейной) эпюры под центром тяжести первой. [c.244]

Способ перемножения эпюр предложен в 1925 г. студентом Московского института инженеров железнодорожного транспорта А. К. Верещагиным, а потому он называется правилом (или способом) Верещагина. [c.441]

Такой способ вычисления интегралов предложил в 1924 году Верещагин А.Н., будучи студентом 3-го курса Московского железнодорожного института. Поэтому в литературе он называется способом Верещагина, или способом перемножения эпюр по Верещагину, что символически можно записать так [c.203]

Приведенное решение носит имя русского ученого Верещагина, впервые его получившего. Таким образом, по способу Верещагина операция интефирования выражения (6.4) в случае линейности хотя бы одной из подынтегральных функций существенно упрощается и сводится к перемножению площади криволинейной эпюры на ординату второй (линейной) функции под центром тяжести криволинейной. [c.140]

В рассмотренных выше примерах учитывалось только влияние изгибающих моментов на величину перемещения. В действительности, на перемещение влияют также сдвиги, вызванные действием поперечных сил. Для учета этого влияния можно использовать второй член формулы (143), вычисляя его тем же способом Верещагина, т. е. способом перемножения эпюр . [c.203]

По формуле (24.11), используя, способ Верещагина при перемножении эпюр, находим [c.511]

Вычисления производят методом перемножения эпюр по способу Верещагина (см. ТСЖ, том 2, стр. 146). [c.231]

Путем перемножения соответствующих эпюр способом Верещагина вычисляем единичные перемещения [c.70]

Вычисляем единичные перемещения путем перемножения соответствующих эпюр по способу Верещагина [c.72]

Способ перемножения эпюр по Верещагину широко применяют при расчете рамных конструкций (конструкций, у которых уг/ы в месте сопряжения отдельных стержней, жесткие до деформации, остаются жесткими после нее). [c.382]

Вместо непосредственного вычисления интеграла Мора (УП.40) можно пользоваться графоаналитическим приемом способом перемножения эпюр , или правилом Верещагина. [c.186]

Способ перемножения эпюр — правило Верещагина [c.308]

Способ вычисления интегралов от произведения функций, из которых одна линейна, иногда называют способом перемножения эпюр. Его предложил в 1925 г. студент Московского института инженеров транспорта А. Верещагин. Этот способ получил широкое распространение и известен сейчас каждому инженеру, изучившему курс сопротивления материалов. [c.101]

Вычисление интеграла Мора по правилу Верещагина часто называют способом перемножения эпюр. При этом эпюру Мр обычно называют г р у з о в о й , а эпюру Мх — един и ч-н о й . [c.298]

Способ перемножения эпюр — правило Верещагина. Если жесткость поперечного сечения стержня на участке постоянна, то каждый интеграл формулы Максвелла —Мора (9.3) можно подсчитывать через произведение площади со эпюры снлы от заданных сил на координату Ё эпюры такого же усилия от единичной фиктивной обобщенной силы (обязательно прямолинейной), приходящейся против центра тяжести первой эпюры (рис. 9.5). [c.205]

Чтобы определить перемещения, применим способ Верещагина. На рис. 410 показаны эпю ш изгибающих моментов для осношюн системы от заданной нагрузки от единичных обобщенных сил Xj = 1, = I, Л»з = 1. Отметим, что Енюры Ml и Л1з симметричные, а эпюра Mj— кососимметричная. Как указывалось, побочные коэффициенты, определяюн1иеся перемножением симметричной эпюры на кососимметричную, равны нулю. В силу этого Ьц = = 0 6aj = =- бз2 = О, [c.408]

Графоаналитический прием вычиеления интеграла Мора называется способом Верещагина и сводится к перемножению эпюр изгибак1щих моментов Мд (от заданной нагрузки) и /Я (от единичной нагрузки) по формуле [c.46]

В каждый из интегралов Мора (5.8) входит произведение функций MxpMxi, Му рМ х и т.д. Способ Верещагина применим к любому из шести интегралов, и перемножение эпюр проводится одинаково, независимо от того, построены эти эпюры для изгибающих и крутящих моментов и нормальных и поперечных сил. Разница заключается лишь в том, что результат перемножения делится не на жесткость EJ, как при изгибе, а на жесткость iJJ, если речь идет о кручении, или на EF или GF — при растяжении и сдвиге. [c.245]

Вычисление йнтепрала Мора, записанного в такой форме, удобнее всего выполнять графо-аналитическим методом, называемым правилом Верещагина или способом перемножения эпюр. Этим правилом можно пользоваться в тех случаях, когда хотя бы одна из эпюр (Мо или Ml) ограничена прямой линией на участке в пределах интегрирования. [c.258]

Способ вычисления интегралов в формуле Мора с помощью формулы (10.14) называется правилом А. К. Верещагина или правилом перемножения эпюр. Согласно формуле (10.14) результат перемножения двух эпюр равен произведению площади нелинейной эпюры на ординату под ее центром тяжести в линейной эпюре. Если обе эпюры на рассмаа риваемом участке являются линейными, то при перемножении можно брать площадь любой из них. Результат перемножения однозначных эпюр является положительным, а разнозначных — отрицательным. [c.213]

Д, я сечений с прямолинейными участками при вычислении и уДобно применять способ перемножения эпюр по правилу Верещагина, используя для этого построенные эпюры линййных координат (г и у) средней линии сечения и эпюру секториальных координат ш [c.228]

mash-xxl.info

Метод Верещагина.

Количество просмотров публикации Метод Верещагина. — 153

Способ Максвелла — Мора в значительной степени вытеснил на практике непосредственное применение теоремы Кастильяно. В справочниках обычно приводятся таблицы интегралов для наиболее часто встречающихся типов нагрузки.

Наш соотечественник А. Н. Верещагин в 1924 ᴦ. предложил упрощение вычислений. Так как единичной нагрузкой бывает обычно либо сосредоточенная сила, либо пара сил, то эпюра оказывается ограниченной прямыми линиями. Тогда вычисление при любом очертании эпюры М можно произвести следующим образом. Пусть эпюра М (Рис.3) имеет криволинейное очертание, а эпюра — прямолинейное. Произведение Mdx можно рассматривать, как элемент площади эпюры М, заштрихованный на чертеже.

Так как ордината равна , то произведение , а весь интеграл представляет собой статический момент площади эпюры М относительно точки А, умноженный на .

Рис.3. Расчетная модель метода Верещагина.

Но данный статический момент равен всей площади эпюры М, умноженной на расстояние от ее центра тяжести до точки А. Таким образом,

но величина равна ординате эпюры под центром тяжести эпюры М. Отсюда

и искомое перемещение равно

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, для определения перемещения нужно вычислить — площадь эпюры М, умножить ее на ординату эпюры от единичной нагрузки под центром тяжести площади и разделить на жесткость балки.

Определим этим способом угол поворота сечения D балки, изображенной на Рис.4, а; Балка загружена моментом М, приложенным в сечении В к консоли АВ. Эпюра М показана на Рис.4, б. Прикладываем в сечении D единичную пару, выбирая ее направление произвольно (Рис.4, в). Эпюра моментов от единичной нагрузки показана на рис.4, г. Так как М на участках DC и СВ равен нулю, то остается лишь один интеграл для участка АВ.

а) расчетная схема б)грузовая эпюра в)фиктивное состояние г) эпюра моментов от единичного момента

Рис.4. Иллюстрация метода Верещагина:

Площадь равна ; ордината эпюры под центром тяжести площади равна отсюда искомый угол поворота равен

Знак плюс показывает, что вращение происходит по направлению единичной пары, т. е. по часовой стрелке.

Лекция № 35. Расчет статически неопределимых балок. Способ сравнения деформаций.

referatwork.ru

Метод Верещагина — Энциклопедия по машиностроению XXL

Пользуясь методом Верещагина, определить величину прогиба сечения С и угла поворота сечения D балок, показанных на [c.200]

Для вычисления перемещений, перечисленных в канонических уравнениях, применим метод Верещагина. [c.251]

Удлинение от изгиба можно определить по методу Верещагина [c.52]

Определение ср. Для определения ср надо вычислить единичный прогиб 8 . Используя метод Верещагина, перемножаем эпюру (фиг. 448) самое на себя [c.550]

При вычислении главных и грузовых коэффициентов канонических уравнений метода сил для упрощения расчета учитываются только изгибающие моменты. Значения коэффициентов вычисляются по методу Верещагина. [c.159]

Расчет коэффициентов податливости, необходимый для вычисления коэффициентов о, 6 и с, производят методом Верещагина. Для этого рассматривают схему ротора и в центрах масс прикладывают единичные силы, а к дискам — единичные изгибающие моменты. Для каждой единичной нагрузки строят на сжатых волокнах вала эпюры изгибающих моментов. Затем определяют сумму произведений элементов площади эпюры I на ординаты эпюры 5, находящиеся против центра тяжести элемента площади -й эпюры. Разделив эту сумму на жесткость вала EJ, определяют коэффициент податливости а,-5. [c.185]

Поскольку эпюры изгибающих моментов от единичной силы Хх= 1 и Мр от внешних сил прямолинейные, то интеграл Мора определяют по методу Верещагина, т. е. искомый интеграл получают умножением площади эпюры М1 на расположенную под ее центром тяжести ординату прямолинейной эпюры Мр. Интеграл Мора положительный, если знаки М1 и Мр одинаковы и отрицательный — если знаки М1 и Мр различны. [c.111]

Определив по методу Верещагина интегралы Мора и подставив их значения в уравнение (38), получим окончательно [c.113]

Перемещения Д/р и б,, входящие в канонические уравнения, чаще всего определяют по методу Мора или по способу Верещагина. При этом для балок и рам влиянием поперечных и продольных сил обычно пренебрегают и учитывают лишь изгибающие моменты. Однако, определяя перемещения в балках прямоугольного поперечного сечения, для которых отношение высоты сечения к длине [c.401]

Статически неопределимые системы, содержащие криволинейные стержни, рассчитывают по методу сил в такой же последовательности, как и системы, рассмотренные в предыдущих параграфах. В этих случаях, однако, перемещения, входящие в канонические уравнения, нельзя вычислять по способу Верещагина. Для этой цели рекомендуется применять метод Мора. [c.422]

Для определения перемещений применяется метод Мора — Верещагина (перемножаем эпюры). [c.205]

Вычисление интеграла Мора по правилу Верещагина обычно называют методом перемножения эпюр. Эпюра М р называется грузовой эпюрой, а эпюра — единичной. [c.225]

Перемещения v и в = v, которые обозначим одной буквой б, могут быть определены универсальным методом единичной нагрузки с помощью интеграла Мора или способом Верещагина. [c.216]

Вычисление интеграла Мора целесообразно выполнять графоаналитическим методом, называемым правилом Верещагина. [c.269]

Как показывают полученные значения перемещений, аналитический метод Мора и графо — аналитический способ Верещагина дают одинаковые результаты. [c.79]

Выполняется деформативная (кинематическая) проверка. Физический смысл ее заключается в равенстве нулю перемещений по направлению любой из связей, наложенных на систему. Перемещения определяются любым известным методом, например, по способу Верещагина. [c.10]

Возможны доклады обзорного характера, скажем, сопоставление нескольких методов графо-аналитического вычисления интеграла Мора (правило Верещагина, метод Попова). [c.42]

Какой из методов определения перемещений — обобщенное (или универсальное) уравнение упругой линии, графо-аналитический метод (фиктивных нагрузок) или интеграл Мора и правило Верещагина — наиболее рационален По нашему мнению, ответ однозначен — интеграл Мора и правило Верещагина. Этот метод наиболее универсален, так как применим не только к балкам, но и к любым стержневым системам и криволинейным брусьям. Он наименее формален, так как имеет четкую физическую основу, а его применение всегда требует построения эпюр, что дает дополнительные возможности для развития у учащихся соответствующих навыков. Затрата времени на определение перемещений меньше, чем при применении любого другого метода. Неоднократно проводившийся хронометра) [c.209]

Наименее рациона.аен метод фиктивных нагрузок. Мы считаем нужным особо подчеркнуть это обстоятельство, так как по традиции в строительных техникумах им до сих пор продолжают пользоваться. Доводы приверженцев этого метода сводятся примерно к следующему. Во-первых, при простых нагрузках он достаточно прост и быстро приводит к цели во-вторых, интеграл Мора и правило Верещагина неизбежно применяются в статике сооружений, там их и следует рассматривать. [c.210]

Определение перемещений производится методом Мора (с использованием, там где это возможно, правила Верещагина), поэтому оказывается удобным выразить перемещения Дхх,. Дхл, и т. д. через перемещения Зц, 0 2 и т. д. от единичных сил, приложенных взамен лиш- [c.161]

Пользуясь методом Мора, по правилу Верещагина получаем величины единичных и грузовых перемещений [c.170]

Определять перемещения соответствующих точек основной системы можно любым способом, однако лучше всего общими методами — методом Мора или способом Верещагина. [c.420]

Перемещения А,р и 6,, входящие в канонические уравнения, чаще всего определяют по методу Мора или по способу Верещагина. При этом для балок и рам влиянием поперечных и продольных сил обычно пренебрегают и учитывают лишь изгибающие моменты. Однако, определяя перемещения в балках прямоугольного поперечного сечения, для которых отношение высоты сечения к длине пролета /г// 1 /5, поперечные силы учитывать обязательно. При расчете статически неопределимых рам с большими значениями указанного отношения (h/l> 1 /5) ошибка, вызванная неучетом интегралов продольных и поперечных сил, также становится существенной, особенно для высокой рамы. Следует иметь в виду, что в реальных [c.425]

При расчете статически неопределимых балок и рам вначале отбрасываются «лишние» связи и их действие заменяется неизвестными усилиями. Заданная система таким образом превращается в статически определимую, называемую основной системой. Основная система должна быть геометрически неизменяемой. Для вычисления лишних неизвестных составляются уравнения деформации, смысл которых заключается в том, что основная система под действием заданной нагрузки и липших неизвестных деформируется так же, как и заданная статически неопределимая система. Число уравнений деформации равно степени статической неопределимости. Для составления уравнений деформаций могут быть использованы известные из предыдущего раздела методы вычисления перемещений (метод начальных параметров, интеграл Мора, правило Верещагина и др.). [c.60]

На первый взгляд может показаться, что способ Верещагина не дает существенных упрощений. Для его применения необходимо вычислять площадь эпюры моментов и положение ее центра тяжести, что при сложных эпюрах все равно потребует интегрирования, как и в методе Мора. Однако встречающиеся на практике эпюры изгибающих моментов могут быть, как правило, разбиты на простейшие фигуры прямоугольник, треугольник и параболический треугольник (рис. 5.19), для которых площадь П и положение центра тяжести известны. При кручении, растяжении и сдвиге эпюры оказываются еще более простыми они, как правило, линейные и состоят из прямоугольников и треугольников в различных комбинациях. [c.245]

Применение метода единичной нагрузки (Максвелла—Мора) с использованием правила Верещагина или формулы Симпсона. [c.309]

Решение. Задача может быть решёна при помощи теоремы Кастильяно, при помощи интегралов Максвелла—Мора или методом Верещагина. Применим метод Верещагина. От заданной нагрузки (схема й) построим эпюры изгибающего момента (схема б). Покажем положения центров тяжести площадей [c.200]

Так как центр изгиба должен находиться на оси симметрии г, то для определения его положения достаточно вычислить один момент инерции /г- Для этого на контуре сечения (рис. 10.9, а) строим эпкзру ординат у и используем метод Верещагина [c.237]

Величину Д можно также вВ1числить по методу Верещагина или пользуясь имеющимися готовыми таблицами. В табл. 20 14 приводятся формулы для определения значения О, при некоторых наиболее часто применяющихся видах загружения. [c.456]

Определяются единичные и грузовые коэффициенты (свободные члены) канонических уравненнй метода сил. для этого в- основной системе стопятся. эпюры изгибающих моментов M ot единичных неизвестных X и от заданной нагрузки М,-, Ееличины коэффициентов опоеделяются по способу Верещагина [c.68]

Определяются единичные и грузовые коэффициенты (свободные члены) канонических уравнений метода сил. Для этого в основной системе строятся эпюры изгибающих моментов Mf от единичных неизвестных х, и от задар(ной нагрузки Mf. Величины коэффициентов определяются, как правило, по способу Верещагина [c.9]

Многократно приходилось выслушивать от преподавателей техникумов мнение, что тот или иной вопрос программы излишне труден для учащихся. Скажем, они не могут освоить метод Мора и правило Верещагина. Не говоря уже о личном опыте, который показывает, что это не так, возиикает вопрос В чем заключаются трудности Здесь мнения тех, кто считает тему трудной, расходятся одни приписывают затруднения математической стороне вопроса (при применении интеграла Мора без правила Верещагина), другие связывают эти трудности со сложностью определения ординат эпюр, третьи просто разводят руками, будучи не в силах сформулировать причины затруднений. Определенные трудности, конечно, есть, и их характер зависит от ряда причин, связанных с общей подготовкой учащихся, но они преодолимы. Не надо нагромождать математические выкладки там, где в них нет необходимости, или сопровождать изложение частностями, если общий метод позволит учащимся самостоятельно разобраться в этих частных случаях. [c.9]

Некоторые вопросы теории. Обязательная часть программы не предусматривает изучения какого-либо из методов определения перемещений. Поэтому вопросы об интегрировании дифференциального уравнения упругой линии или об интеграле Мора и правиле Верещагина могут рассматриваться лишь за счет времени, отводимого на допо1лнительные вопросы программы. [c.135]

При простых нагрузках прост любой метод, и графо-аналитический не обнаруживает никаких преимуществ по сравнению, скажем, с применением правила Верещагина, а при мало-мальски сложной нагрузке вычисление статических моментов площадей эпюр оказывается весьма трудоемкой задачей. По поводу второго аргумента скажем следующее. Нужно ли, чтобы учащийся техникума владел несколькими методами определения перемещений Совершенно очевидно, что не нужно. Важно добиться твердого освоения одного метода, и метод надо выбрать такой, который в равной мере был бы удобен и в сопротивлении материалов, и в статике сооружений, а это — интеграл Мора. [c.210]

В атучаях, когда ось бруса прямолинейна и жесткость поперечного сечения в пределах отдельных участков постоянна, интеграл Мора целесообразно вычислять графоаналитическим методом, применяя правило Верещагина. [c.138]

Определение единичного (3 ) и грузового (Д р) перемещений будем вести методом Мора с применением правила Верещагина. Основная система с заданной нагрузкой показана на рис. 7-32, а и на рис. 7-32, б дана соответствуювтая эпюра моментов Мр. Основная система, нагруженная единичной силой, приложенной взамен лишней неизвестной Х, представлена на рис. 7-32, в, а на рис. 7-Ъ2,г дана эпюра [c.164]

mash-xxl.info

ПРАВИЛО (СПОСОБ, МЕТОД) ВЕРЕЩАГИНА

Недостатком метода Мора является необходимость получать значения внутренних силовых факторов, входящих в подинтегральные выражения формул (2.18) и (2.19), в общем виде, как функций от z, что становится достаточно трудоемким уже при двух – трех участках разбиения в балках и особенно – в рамах.Оказывается, что от этого недостатка можно уйти, если непосредственное интегрирование в формулах Мора заменить так называемым перемножением эпюр. Такая замена возможна в тех случаях, когда хотя бы одна из перемножаемых эпюр является прямолинейной. Этому условию соответствуют все системы, состоящие из прямолинейных стержней. Действительно, в таких системах эпюра, построенная от обобщенной единичной силы, всегда будет прямолинейной.Способ вычисления интеграла Мора путем замены непосредственного интегрирования перемножением соответствующих эпюр называется способом (или правилом) Верещагина и заключается в следующем: чтобы перемножить две эпюры, из которых хотя бы одна является прямолинейной, нужно площадь одной эпюры (если есть криволинейная эпюра, то обязательно ее площадь) умножить на ординату другой эпюры, расположенную под центром тяжести первой.
Докажем справедливость этого правила. Рассмотрим две эпюры (рис.28). Пусть одна из них (Mn) является грузовой и имеет криволинейное очертание, а вторая соответствует единичной нагрузке и является линейной.Из рис.28 следует, что Подставим значения в выражение

где — дифференциал площади эпюры Mn.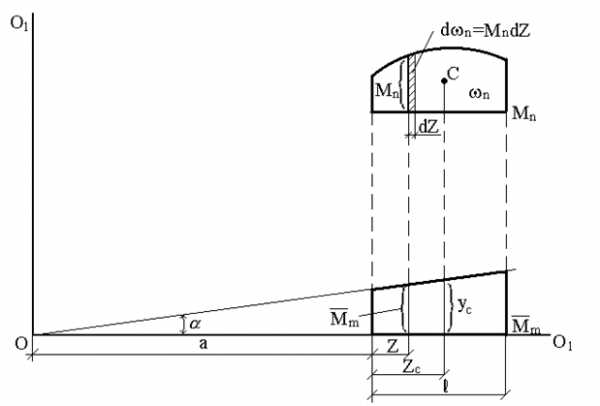
Рис. 28

Интеграл представляет собой статический момент площади относительно оси О – О1, при этом:

где zc – абсцисса центра тяжести площади , тогда:

Учитывая, что получим:
(2.20)
Выражение (2.20) определяет результат перемножения двух эпюр, а не перемещения. Чтобы получить перемещение, этот результат нужно разделить на жесткость, соответствующую внутренним силовым факторам, стоящим под знаком интеграла.

23. Статически неопределимой называют такую систему, которая не может быть рассчитана по методу сечений с использованием лишь одних условий равновесия, так как она обладает лишними связями. В качестве лишних следует принимать те связи, которые необходимо отбросить из состава заданной, чтобы превратить ее в статически определимую и геометрически неизменяемую систему.

Главной особенностью статически неопределимых систем является наличие лишних связей в их структуре. Лишние связи сооружений можно удалять, не нарушая их геометрической неизменяемости. Например, удалением опорных вертикальных связей Ви С неразрезная балка преобразуется в консольный стержень, введением цилиндрических шарниров K и L – в статически определимую двухпролётную составную балку (рис. 6.1,а). Удалив из статически неопределимой фермы стержень 14 или 34, получим два варианта статически определимой шарнирно-стержневой системы с простой структурой (рис. 6.1,б). Статически неопределимая двухшарнирная рама после удаления горизонтальной связи опоры В превращается в ломаный стержень, прикреплённый к диску «земля» шарниром А и вертикальной связью, ось которой не проходит через шарнир А. Введением цилиндрического шарнира С эта же рама преобразуется в статически определимую трёхшарнирную раму (рис. 6.1,в).

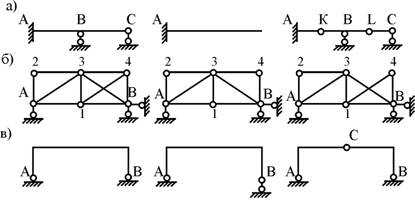
Рис.6.1

Особенностью всех лишних связей, удалённых из статически неопределимых систем, показанных слева на рис. 6.1, является то, что реакции в них от внешних воздействий с помощью уравнений статики определить нельзя. Эти связи называются условно необходимыми. Вместе с тем, в составе рассмотренных сооружений имеются связи, усилия в которых определяются из условий равновесия: горизонтальная связь опоры А неразрывной балки (рис. 6.1,а), стержни А_2,23, А₁, А₃ фермы (рис. 6.1,б), вертикальные связи пятовых шарниров А и В рамы (рис. 6.1,в). Такие связи называются абсолютно необходимыми. Их удаление превращает заданное сооружение в геометрически изменяющую или мгновенно изменяемую систему.

Следует различать внешне статически неопределимые и внутренне статически неопределимые системы.

Внешне статически неопределимой называют такую систему, которая имеет только лишние внешние связи, т.е. лишние опорные закрепления. Примером внешне статически неопределимой плоской системы является трехпролетная рама (рис.6.2).

Рис.6.2

Степень статической неопределимости системы С легко установить путем вычитания из общего числа опорных стержней m число стержней, необходимых для сохранения геометрически неизменяемого прикрепления системы (одно — для одномерных; три — для плоских и шесть — для пространственных систем).

Для плоской рамы, изображенной на рис.6.2, учитывая, что защемление эквивалентно трем опорным стержням, получаем:

m = 3 + 2×2 +1 = 8; C = m — 3 = 8-3 = 5,

т.е. данная система 5 раз статически неопределима.

Внутренне статически неопределимой называют систему, обладающую лишними связями, введенными для взаимного соединения частей системы.

24. Статически неопределимые системы обладают рядом характерных особенностей:

1. Статически неопределимыеконструкции являются более жесткими, чем соответствующиестатически определимые, так как имеют дополнительные связи.
2. В статически неопределимыхсистемах возникают меньшие внутренние усилия, что определяет их экономичность по сравнению со статически определимымисистемами при одинаковых внешних нагрузках.
3. Нарушение лишних связей в статически неопределимойсистеме не всегда приводит к разрушению, в то время как потеря связи в статически определимой системе делает ее геометрически изменяемой.
4. Для расчета статически неопределимых систем необходимо предварительно задаваться геометрическими характеристиками поперечных сечений элементов, т.е. фактически их формой и размерами, так как их изменение приводит к изменению усилий в связях и новому распределению усилий во всех элементах системы.
5. При расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости.
6. В статически неопределимых системах температурное воздействие, осадка опор, неточности изготовления и монтажа вызывают появление дополнительных усилий.
Основными методами расчетастатически неопределимых систем являются:

1.Метод сил.Здесь в качестве неизвестных рассматриваются усилия – силы и моменты.
2.Метод перемещений. Неизвестными являются деформационные факторы – углы поворотов и линейные смещения.
3.Смешанный метод. Здесь часть неизвестных представляет собой усилия, а другая часть – перемещения.
4. Комбинированный метод. Используется при расчете симметричных систем на несимметричные нагрузки. Оказывается, что на симметричную составляющую заданной нагрузки систему целесообразно рассчитывать методом перемещений, а на обратносимметричную составляющую – методом сил.
Помимо указанных аналитичеких методов при расчете особо сложных систем используются различные численные методы.

Сущность метода сил

Существует несколько методов расчета статически неопределимых систем, но все они базируются на двух основных методах расчета: методе сил и методе перемещений. Метод сил является наиболее универсальным, применяемым в настоящее время. Для определения усилий в статически неопределимых системах необходимо дополнительно к уравнениям статики составлять уравнения совместности деформаций, т. е. уравнения, выражающие связь между деформациями отдельных элементов системы. При этом число дополнительных уравнений должно всегда быть равно числу лишних связей системы, или, что то же, степени ее статической неопределимости.

При расчете статически неопределимых систем методом сил основными неизвестными в уравнениях совместности деформаций являются силы (внешние или внутренние), а известными — перемещения в направлении .этих сил, что и обусловило само название данного метода расчета.

Решение статически неопределимых систем по методу сил производится в строго определенном порядке:

— выявляются лишние связи и устанавливается степень статической неопределимости системы;

— выбирается для расчета основная, система;

— основная система загружается заданной внешней нагрузкой и реакциями или усилиями отброшенных лишних связей;

— составляются уравнения, выражающие условия эквивалентности основной системы, загруженной заданной внешней нагрузкой и неизвестными усилиями, приложенными вместо отброшенных связей, и заданной системы. Эти уравнения составляются по единому правилу и называются каноническими;

— определяются коэффициенты при неизвестных усилиях в канонических уравнениях;

— решается система канонических уравнений и после определения неизвестных усилий строятся эпюры внутренних сил.

27.Канонические уравнения метода сил, их физические свойства и особенности

stydopedia.ru