Сопротивление материалов — Южно-Уральский государственный университет
Размер шрифта
Межбуквенный интервал
Семейство шрифтов
- Образование
- Учебный план 20.03.01, 2019, (4.0), Техносферная безопасность
- Сопротивление материалов
Программа дисциплины
- Цели и задачи дисциплины
- Цели изучения дисциплины «Сопротивление материалов» ‒ ознакомить студентов с основами расчета на прочность и жесткость стержневых конструкций и простейших соединений при силовых воздействиях, а также сформировать представление о технологических мероприятиях, направленных на повышение статической прочности элементов конструкций. Задачи изучения дисциплины ‒ научить студентов анализировать внутренние силы в типовых расчетных схемах элементов конструкций; проводить расчеты на прочность и жесткость стержней и стержневых систем, работающих в условиях растяжения-сжатия, кручения, изгиба, а также проводить расчет на прочность элементов простейших соединений типа заклепочного, шпоночного, штифтового и других.
- Краткое содержание дисциплины
- Введение. Проблема прочности в технике и основные направления ее решения. Объекты расчета и их расчетные схемы. Геометрическая модель объекта, модель нагружения, модель материала. Внутренние силы. Метод сечений. Внутренние силовые факторы. Понятие о напряжении и деформациях в точке тела. Основные принципы сопротивления материалов. Растяжение-сжатие. Напряжения в поперечном сечении. Продольная и поперечная деформации стержня. Закон Гука при растяжении-сжатии. Свойства материалов при растяжении и сжатии. Механические характеристики металлов и конструкционных материалов. Расчеты на прочность и жесткость при растяжении-сжатии. Коэффициент запаса прочности, допускаемые напряжения. Сдвиг и кручение. Напряженное состояние, механические свойства материалов при чистом сдвиге, закон Гука. Кручение. Определение касательных напряжений и угловых перемещений при кручении прямого стержня круглого поперечного сечения. Кручение стержней некруглого (прямоугольного и трубчатого) поперечных сечений. Расчеты на прочность и жесткость при кручении. Геометрические характеристики поперечного сечения стержня. Главные оси и главные моменты инерции сечения. Изгиб. Классификация видов изгиба. Определение кривизны изогнутой оси и нормальных напряжений в поперечном сечении стержня при прямом чистом изгибе. Касательные напряжения при поперечном изгибе. Условие прочности при прямом изгибе. Определение напряжений и расчет на прочность при косом изгибе и изгиб с растяжением или сжатием. Условные расчеты на прочность, область их применимости. Основные допущения. Расчет простейших соединений на прочность: заклёпочных, штифтовых, шпоночных и др.
- Компетенции обучающегося, формируемые в результате освоения дисциплины
- Выпускник должен обладать:
- ПК-1 способностью принимать участие в инженерных разработках среднего уровня сложности в составе коллектива
- ПК-4 способностью использовать методы расчетов элементов технологического оборудования по критериям работоспособности и надежности
Расчеты на прочность и жесткость при кручении. Геометрические характеристики поперечного сечения стержня. Главные оси и главные моменты инерции сечения. Изгиб. Классификация видов изгиба. Определение кривизны изогнутой оси и нормальных напряжений в поперечном сечении стержня при прямом чистом изгибе. Касательные напряжения при поперечном изгибе. Условие прочности при прямом изгибе. Определение напряжений и расчет на прочность при косом изгибе и изгиб с растяжением или сжатием. Условные расчеты на прочность, область их применимости. Основные допущения. Расчет простейших соединений на прочность: заклёпочных, штифтовых, шпоночных и др.Вы нашли ошибку в тексте:
Просто нажмите кнопку «Сообщить об ошибке» — этого достаточно.
Также вы можете добавить комментарий.
404 Cтраница не найдена
Мы используем файлы cookies для улучшения работы сайта МГТУ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь. Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом ФГБОУ ВО «МГТУ» и согласны с нашими правилами обработки персональных данных.
Размер:
AAA
Изображения Вкл. Выкл.
Обычная версия сайта
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Педагогический (научно-педагогический) составМеханические свойства материалов | МеханиКальк
База данных
ПРИМЕЧАНИЕ.
Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
Механические свойства материала влияют на его поведение при нагрузке. Модуль упругости материала влияет на то, насколько он прогибается под нагрузкой, а прочность материала определяет напряжения, которые он может выдержать до разрушения. Пластичность материала также играет важную роль в определении того, когда материал сломается, когда он нагружен сверх своего предела упругости. Поскольку каждая механическая система подвергается нагрузкам во время работы, важно понимать, как ведут себя материалы, из которых состоят эти механические системы.
На этой странице описываются механические свойства материалов, которые имеют отношение к проектированию и анализу механических систем.
Содержимое
Стресс и деформация
Соотношение между напряжением и деформацией в материале определяется путем испытания образца материала на растяжение или сжатие.
В этом испытании к испытательному образцу прикладывается постоянно возрастающая осевая сила, и по мере увеличения нагрузки измеряется прогиб. Эти значения можно изобразить в виде кривой нагрузки-прогиба. Прогиб образца для испытаний зависит как от модуля упругости материала, так и от геометрии образца (площадь и длина). Поскольку нас интересует поведение материала без учета геометрии, полезно обобщить данные, чтобы убрать влияние геометрии. Это делается путем преобразования значений нагрузки в значения напряжения и преобразования значений прогиба в значения деформации:
| Стресс: | |
| Штамм: |
В уравнении для напряжения P — это нагрузка, а A 0 — первоначальная площадь поперечного сечения испытуемого образца. В уравнении деформации L — текущая длина образца, а L 0 — исходная длина.
Кривая напряжения-деформации
Значения напряжения и деформации, определенные в результате испытания на растяжение, могут быть нанесены на график в виде кривая напряжения-деформации , как показано ниже:
На приведенной выше диаграмме есть несколько интересных моментов:
- P: Это предел пропорциональности , который представляет максимальное значение напряжения, при котором кривая напряжения-деформации является линейной.
- E: Это предел упругости , который представляет собой максимальное значение напряжения, при котором не происходит остаточная деформация. Несмотря на то, что кривая между пределом пропорциональности и пределом упругости нелинейна, материал все еще остается упругим в этой области, и если снять нагрузку в этой точке или ниже, образец вернется к своей первоначальной длине.
- Y: Это предел текучести , который представляет собой значение напряжения, выше которого деформация начнет быстро увеличиваться. Напряжение в пределе текучести называется пределом текучести , S ty . Для материалов без четко определенного предела текучести он обычно определяется с использованием метода смещения 0,2% , в котором проводится линия, параллельная линейной части кривой, которая пересекает ось x при значении деформации 0,002. Точка, в которой линия пересекает кривую напряжения-деформации, обозначается как точка текучести.
- U: Эта точка соответствует пределу прочности , S tu , что является максимальным значением напряжения на диаграмме напряжение-деформация. Предел прочности также называют пределом прочности при растяжении . После достижения предельного напряжения образцы из пластичных материалов будут иметь сужение , при котором площадь поперечного сечения в локализованной области образца значительно уменьшается.
- F: Это точка перелома или точка разрыва , которая является точкой, в которой материал разрушается и разделяется на две части.
Предел прочности также называют пределом прочности при растяжении . После достижения предельного напряжения образцы из пластичных материалов будут иметь сужение , при котором площадь поперечного сечения в локализованной области образца значительно уменьшается.Кривые напряжения-деформации обычно необходимы при анализе инженерного компонента. Однако данные о напряжении-деформации не всегда могут быть легко доступны. В этом случае довольно просто аппроксимировать кривую напряжения-деформации материала с помощью уравнения Рамберга-Осгуда.
Истинное напряжение и напряжение
Инженеры обычно работают с инженерное напряжение , которое представляет собой усилие, деленное на исходную площадь образца перед нагружением: σ = P/A 0 . Однако по мере загрузки материала площадь уменьшается.
Истинное напряжение , , представляет собой значение напряжения в материале с учетом фактической площади образца. Поскольку площадь уменьшается по мере нагружения материала, истинное напряжение выше инженерного напряжения.
На рисунке ниже показана инженерная кривая напряжения-деформации по сравнению с истинной кривой напряжение-деформация. Поскольку инженерное напряжение рассчитывается как сила, деленная на исходную площадь (которая является постоянной), инженерная кривая напряжения-деформации имеет ту же форму, что и кривая нагрузка-прогиб. Кривая инженерного напряжения-деформации падает после достижения предела прочности, потому что сила, которую может выдержать материал, падает, когда он начинает сужаться. Однако значение напряжения на истинной кривой напряжение-деформация всегда увеличивается по мере увеличения деформации. Это связано с тем, что при расчете истинного напряжения используется мгновенное значение площади. Даже когда сила, поддерживаемая материалом, падает, уменьшение площади образца перевешивает уменьшение силы, и напряжение продолжает расти.
Следует отметить, что инженерное напряжение и истинное напряжение практически одинаковы в линейно-упругой области кривой напряжения-деформации. Поскольку инженеры обычно работают в этой линейно-упругой области (необычно проектировать конструкцию, которая предназначена для работы за пределами предела упругости), допустимо работать с инженерным напряжением, а не с истинным напряжением.
Инженерная деформация – это изменение длины, деленное на исходную длину: ε = ΔL/L 0 . Вместо того, чтобы просто вычислять одно значение ΔL, учтите, что изменение длины делится на множество небольших приращений, ΔL j . Деформация также рассчитывается в малых приращениях: ε j = ΔL j /L j , где ΔL j — изменение длины при приращении, а L j — длина в начале приращение. Поскольку эти приращения становятся бесконечно малыми, сумма деформаций приближается к истинной деформации:
Если предположить, что объем постоянен на всем протяжении прогиба, то истинное напряжение и деформация могут быть рассчитаны как:
| Истинное напряжение: | |
| Истинная деформация: |
где и — истинные напряжения и деформации, а σ и ε — инженерные напряжения и деформации.
Закон Гука
Ниже предела пропорциональности кривой напряжение-деформация зависимость между напряжением и деформацией является линейной. Наклон этой линейной части кривой напряжения-деформации составляет модуль упругости , E, также называемый модулем Юнга и модулем упругости . Закон Гука выражает связь между модулем упругости, напряжением и деформацией материала в линейной области:
σ = E ε
, где σ — значение напряжения, а ε — значение деформации.
Закон Гука в сдвиге
Закон Гука также имеет форму, касающуюся касательных напряжений и деформаций:
τ = G γ
где τ — значение напряжения сдвига, γ — значение деформации сдвига, а G — модуль упругости при сдвиге. Модуль упругости и модуль сдвига связаны соотношением:
где ν — коэффициент Пуассона.
Более подробную информацию о законе Гука можно найти здесь.
Коэффициент Пуассона
Когда к материалу прикладывается нагрузка, он удлиняется, а площадь поперечного сечения уменьшается.
Это уменьшение площади поперечного сечения называется боковая деформация , и она связана с осевой деформацией коэффициентом Пуассона , ν. Для круглого образца это уменьшение площади реализуется как уменьшение диаметра, а коэффициент Пуассона рассчитывается как:
Коэффициент Пуассона применяется только в пределах упругой области кривой напряжения-деформации и обычно составляет около 0,3 для большинства металлов. Теоретический максимальный предел коэффициента Пуассона равен 0,5.
Деформационное упрочнение
После текучести материал начинает испытывать высокую скорость пластической деформации. Как только материал становится пластичным, он начинает деформационно твердеть, что увеличивает прочность материала. На приведенных ниже кривых напряжение-деформация видно, что прочность материала увеличивается между точкой текучести Y и пределом прочности в точке U. Это увеличение прочности является результатом деформационного упрочнения.
Пластичный материал на рисунке ниже все еще способен выдерживать нагрузку даже после достижения предельной прочности. Однако после достижения предела прочности в точке U увеличение прочности за счет деформационного упрочнения опережает снижение несущей способности из-за уменьшения площади поперечного сечения. Между пределом прочности в точке U и точкой разрушения F техническая прочность материала снижается и возникает образование шейки.
На приведенной ниже кривой напряжение-деформация для хрупкого материала показана очень небольшая область деформационного упрочнения между пределом текучести Y и пределом прочности U. Обратите внимание, однако, что хрупкий материал может на самом деле вообще не проявлять каких-либо свойств текучести или деформационного упрочнения. — в этом случае материал выйдет из строя на линейной части кривой. Это чаще встречается в таких материалах, как керамика или бетон.
Поскольку область деформационного упрочнения возникает между пределом текучести и пределом текучести, отношение предела прочности к пределу текучести иногда используется как мера степени деформационного упрочнения материала.
Это соотношение равно 9.0014 Коэффициент деформационного упрочнения :
= S tu / S ty
Согласно Доулингу, типичные значения коэффициента деформационного упрочнения металлов находятся в диапазоне примерно от 1,2 до 1,4.
Если материал нагружен сверх предела упругости, он будет подвергаться остаточной деформации. После разгрузки материала упругая деформация восстановится (вернется к нулю), но пластическая деформация останется.
На рисунке ниже показана кривая напряжение-деформация материала, который был нагружен выше предела текучести Y. При первом нагружении материала напряжение и деформация следовали кривой O-Y-Y’, а затем нагрузка была снята после того, как напряжение достигло точки Y’. Поскольку материал был нагружен сверх предела упругости, восстанавливается только упругая часть деформации — теперь в материале есть некоторая постоянная деформация. Если бы материал загружался снова, он следовал бы по линии O’-Y’-F, где O’-Y’ — предыдущая линия разгрузки.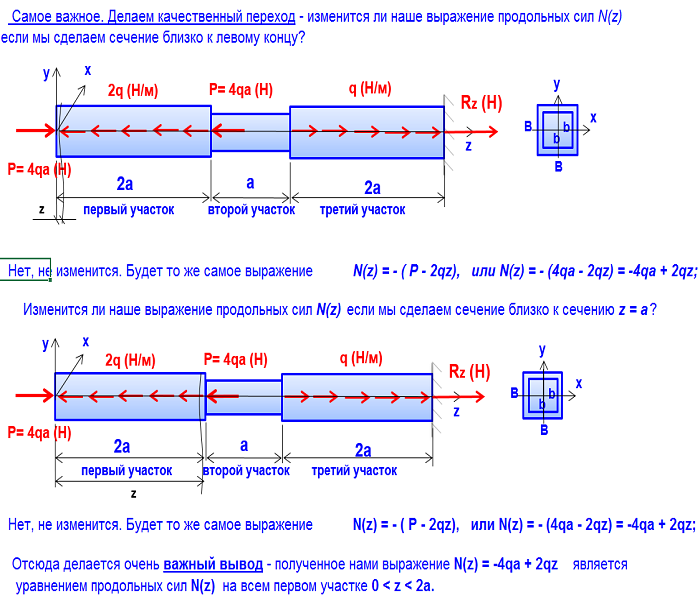
Точка Y’ является новой точкой текучести. Обратите внимание, что линия O’-Y’ является линейной с наклоном, равным модулю упругости, а точка Y’ имеет более высокое значение напряжения, чем точка Y. Следовательно, материал теперь имеет более высокий предел текучести, чем раньше, что является результатом деформационного упрочнения, которое произошло при нагрузке материала сверх предела упругости.
За счет деформационного упрочнения материала теперь он имеет большую область упругости и более высокий предел текучести, но его пластичность была снижена (деформация между точками Y’-F меньше, чем деформация между точками Y-F).
Эластичная и пластическая деформация
Вплоть до предела упругости деформация в материале также является упругой и будет восстанавливаться при снятии нагрузки, так что материал возвращается к своей первоначальной длине. Однако, если материал нагружен сверх предела упругости, в материале возникнет остаточная деформация, которую также называют пластической деформацией.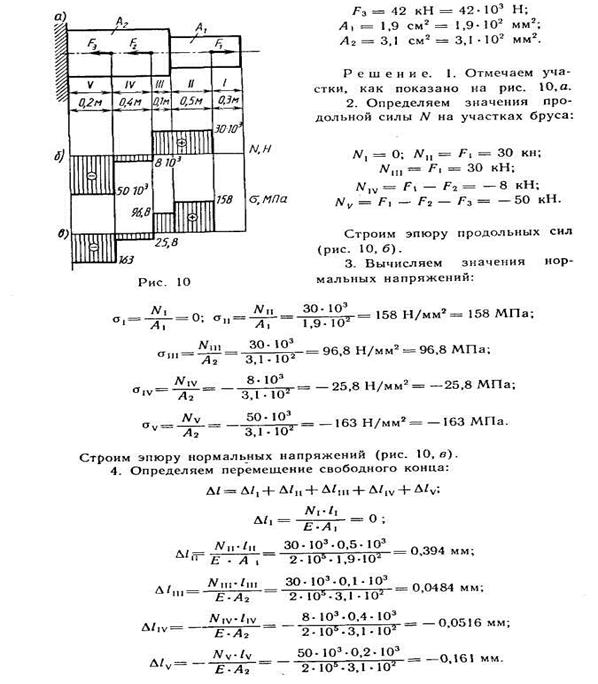
На рисунке выше в материале существуют как упругие, так и пластические деформации. Если снять нагрузку в указанной точке (σ, ε), напряжение и деформация в материале будут следовать линии разгрузки, как показано. Упругая деформация и пластическая деформация указаны на рисунке и рассчитываются как:
| Упругая деформация: | ε e = σ/E |
| Пластиковая деформация: | ε p = ε − ε е |
где σ — напряжение в указанной точке, ε — деформация в указанной точке, E — модуль упругости.
Пластичность
Пластичность — это показатель того, какую пластическую деформацию может выдержать материал, прежде чем он сломается. Пластичный материал может выдерживать большие деформации даже после того, как он начал поддаваться. Общие показатели пластичности включают удлинение на %, и сокращение на на площади 9.0015 , как описано в этом разделе.
После разрыва образца во время испытания на растяжение измеряется окончательная длина образца и рассчитывается пластическая деформация при разрушении, также известная как деформация при разрыве :
где L f — конечная длина образца после разрыва, а L o — начальная длина образца.
Важно отметить, что после разрушения образца восстанавливается упругая деформация, существовавшая во время нахождения образца под нагрузкой, поэтому измеренная разница между конечной и начальной длинами дает пластическая деформация при разрушении. Это показано на рисунке ниже:
На рисунке видно, что пластическая деформация при разрушении ε f представляет собой деформацию, оставшуюся в материале после восстановления упругой деформации. Предельная деформация, ε u , является полной деформацией при разрушении (пластическая деформация плюс упругая деформация).
Удлинение процентов рассчитывается по пластической деформации при разрушении по формуле:
Процентное удлинение является обычно предоставляемым свойством материала, поэтому пластическая деформация при разрушении обычно рассчитывается на основе процентного удлинения:
ε f = eL / 100%
Предельная деформация учитывает как пластическую, так и упругую деформацию при разрушении:
ε u = ε f + С ту /Е
Еще одним важным свойством материала, которое можно измерить во время испытания на растяжение, является уменьшение площади , которое рассчитывается по формуле:
Помните, что процентное удлинение и уменьшение площади составляют пластиковых компонентов осевой деформации и поперечной деформации соответственно.
Пластичные и хрупкие материалы
Пластичный материал может выдерживать большие деформации даже после того, как он начал поддаваться деформации, тогда как хрупкий материал может выдерживать небольшую пластическую деформацию или вообще не выдерживать ее. На рисунке ниже показаны репрезентативные кривые напряжения-деформации для пластичного материала и хрупкого материала.
На приведенном выше рисунке видно, что пластичный материал значительно деформируется перед точкой разрушения F. Между пределом текучести в точке Y и пределом прочности в точке U, где материал деформационно упрочняется, существует длинная область. Существует также длинная область между пределом прочности в точке U и точкой разрушения F, в которой площадь поперечного сечения материала быстро уменьшается и происходит образование шейки.
Можно видеть, что хрупкий материал на рисунке выше разрушается вскоре после достижения предела текучести. Кроме того, предел прочности совпадает с точкой разрушения.
В этом случае шейки не происходит.
Поскольку площадь под кривой напряжения-деформации для пластичного материала выше, чем площадь под кривой напряжения-деформации для хрупкого материала, пластичный материал имеет более высокий модуль ударной вязкости — он может поглотить гораздо больше энергии деформации, прежде чем перерывы. Кроме того, из-за того, что пластичный материал очень сильно деформируется перед тем, как сломаться, его прогибы перед разрушением будут очень большими. Таким образом, будет визуально очевидно, что сбой неизбежен, и можно будет предпринять действия для разрешения ситуации до того, как произойдет бедствие.
Репрезентативная кривая напряжения-деформации для хрупкого материала показана ниже. Эта кривая показывает напряжение и деформацию как для растягивающей, так и для сжимающей нагрузки. Обратите внимание, что материал гораздо более устойчив к сжатию, чем к растяжению, как с точки зрения нагрузки, которую он может выдержать, так и с точки зрения деформации перед разрушением.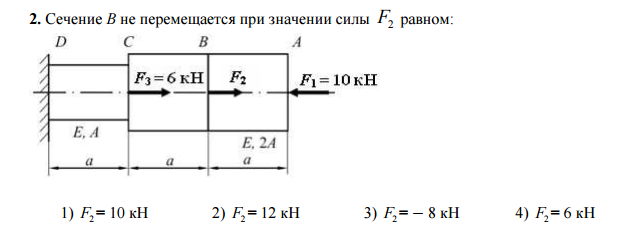
Это характерно для хрупкого материала.
Энергия напряжения
Когда к материалу прикладывается сила, он деформируется и накапливает потенциальную энергию, как пружина. энергия деформации (т.е. количество потенциальной энергии, накопленной в результате деформации) равна работе, затраченной на деформацию материала. Полная энергия деформации соответствует площади под кривой отклонения нагрузки и выражается в дюймо-фунтах в обычных единицах США и Н-м в единицах СИ. Энергия упругой деформации может быть восстановлена, поэтому, если деформация остается в пределах предела упругости, то вся энергия деформации может быть восстановлена.
Энергия деформации рассчитывается как:
| Общая форма: | U = Работа = ∫ F дл | (площадь под кривой нагрузки-прогиба) |
| В пределах эластичности: | (площадь под кривой нагрузки-прогиба) | |
| (потенциальная энергия пружины) |
Обратите внимание, что есть два уравнения для энергии деформации в пределе упругости.
Первое уравнение основано на площади под кривой отклонения нагрузки. Второе уравнение основано на уравнении потенциальной энергии, запасенной в пружине. Оба уравнения дают один и тот же результат, просто они выводятся несколько по-разному.
Плотность энергии деформации
Иногда удобнее работать с плотностью энергии деформации , которая представляет собой энергию деформации на единицу объема. Это равно площади под диаграммой напряжения-деформации:
где пределы в приведенном выше интеграле находятся в пределах от деформации от 0 до ε app , которая представляет собой деформацию, существующую в нагруженном материале.
Обратите внимание, что единицами плотности энергии деформации являются фунты на квадратный дюйм в обычных единицах США и Па в единицах СИ.
Модуль упругости
Модуль упругости представляет собой количество энергии деформации на единицу объема (т. е. плотность энергии деформации), которую материал может поглотить без возникновения остаточной деформации.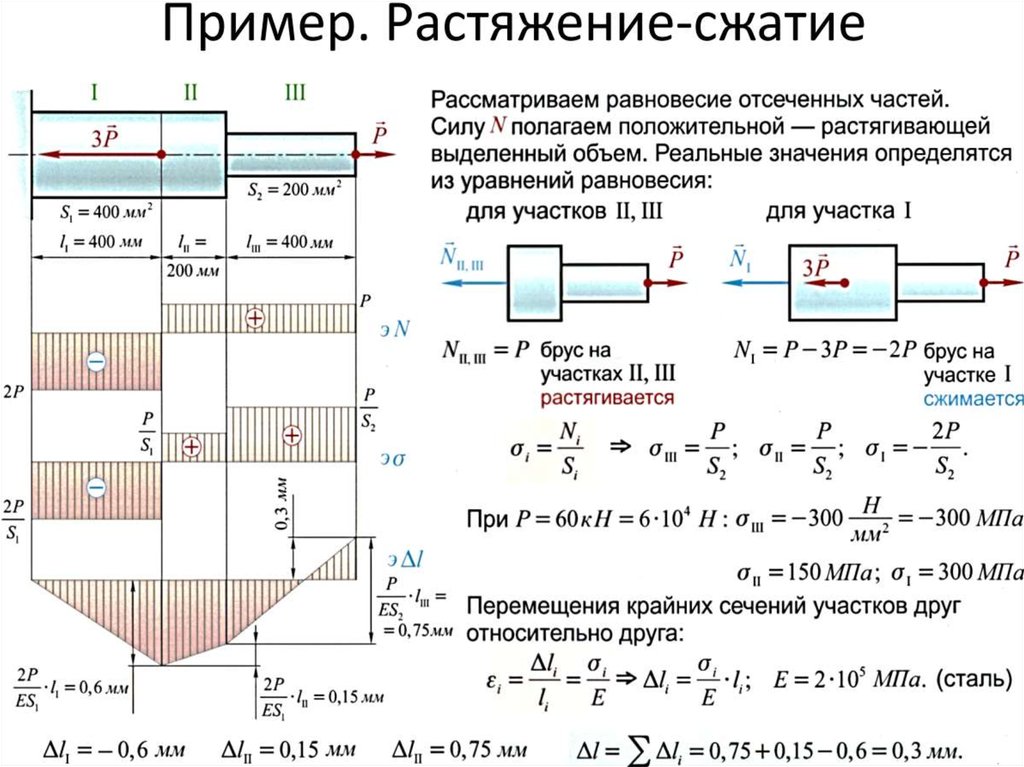
Модуль упругости рассчитывается как площадь под кривой напряжения-деформации до предела упругости. Однако, поскольку предел упругости и предел текучести обычно очень близки, упругость можно аппроксимировать как площадь под кривой напряжения-деформации до предела текучести. Поскольку кривая напряжения-деформации почти линейна вплоть до предела упругости, эта область имеет треугольную форму.
Модуль упругости рассчитывается как:
| общая форма | |
| треугольной формы |
где σ el и ε el — напряжение и деформация на пределе упругости, S ty — предел текучести при растяжении, а E — модуль упругости.
Обратите внимание, что единицы модуля упругости такие же, как единицы плотности энергии деформации, которые являются фунтами на квадратный дюйм в обычных единицах США и Па в единицах СИ.
Модуль прочности
Модуль ударной вязкости — это количество энергии деформации на единицу объема (т.
е. плотность энергии деформации), которую материал может поглотить непосредственно перед разрушением. Модуль ударной вязкости рассчитывается как площадь под кривой напряжения-деформации до точки разрушения.
В некоторой степени требуется точный расчет общей площади под кривой напряжения-деформации для определения модуля ударной вязкости. Однако грубое приближение можно сделать, разделив кривую напряжения-деформации на треугольную и прямоугольную части, как показано на рисунке ниже. Высота участков равна среднему значению предела текучести и предела прочности.
Модуль жесткости может быть аппроксимирован как:
где S ty — предел текучести при растяжении, S tu — предел прочности при растяжении, ε y — деформация при текучести, ε u — предельная деформация (полная деформация при разрушении), а E — предел прочности при растяжении. модуль упругости.
Более точный расчет модуля ударной вязкости можно выполнить, используя уравнение Рамберга-Осгуда для аппроксимации кривой напряжение-деформация, а затем интегрируя площадь под кривой.
Следует отметить, какой большой вклад в ударную вязкость материала вносит площадь под пластической областью кривой напряжения-деформации (т. е. прямоугольная часть). Поскольку пластичный материал может выдерживать гораздо большую пластическую деформацию, чем хрупкий материал, пластичный материал будет иметь более высокий модуль ударной вязкости, чем хрупкий материал с таким же пределом текучести. Несмотря на то, что конструкции обычно предназначены для удержания напряжений в области упругости, пластичный материал с более высоким модулем ударной вязкости лучше подходит для применений, в которых может возникнуть случайная перегрузка.
Обратите внимание, что единицы модуля ударной вязкости такие же, как единицы плотности энергии деформации, которые являются фунтами на квадратный дюйм в обычных единицах США и Па в единицах СИ.
Приближение кривой напряжения-деформации
Обычно требуются кривые напряжения-деформации для материалов; однако без репрезентативных данных испытаний необходимо получить аппроксимацию кривой.
Уравнение Рамберга-Осгуда можно использовать для аппроксимации кривой напряжения-деформации для материала, зная только предел текучести, предел прочности, модуль упругости и процентное удлинение материала (все это общие и легкодоступные свойства).
Уравнение Рамберга-Осгуда для полной деформации (упругой и пластической) как функции напряжения:
где σ — значение напряжения, E — модуль упругости материала, S ty — предел текучести материала при растяжении, а n — показатель деформационного упрочнения материала, который можно рассчитать на основе известных свойств материала как показано далее в этом разделе. (Примечание 1)
Объяснение вывода уравнения Рамберга-Осгуда дается в следующих разделах.
Уравнение Рамберга-Осгуда
Соотношение было предложено Рамбергом и Осгудом, которое часто используется для аппроксимации кривой напряжения-деформации материала. Эта зависимость является экспоненциальной и используется для описания пластической деформации в материале.
Кривая напряжение-деформация в пластической области может быть аппроксимирована следующим образом:
| σ = H ε p n | ⟹ |
где в приведенном выше уравнении ε p — пластическая деформация, H — коэффициент прочности в тех же единицах, что и напряжение, а n — показатель деформационного упрочнения , безразмерный.
Упругая деформация в материале линейно пропорциональна напряжению:
| σ = E ε e | ⟹ | ε e = σ/E |
где в приведенном выше уравнении ε e — упругая деформация, E — модуль упругости.
Полная деформация материала представляет собой сумму упругой деформации и пластической деформации:
| ε = ε e + е р | ⟹ |
Определение констант Рамберга-Осгуда
Чтобы уравнение Рамберга-Осгуда было полезным, должны быть известны значения констант n и H.
Здесь дается обсуждение того, как определить константы для показательного уравнения.
Константы находятся:
где в приведенных выше уравнениях (σ 1 , ε 1 ) и (σ 2 , ε 2 ) соответствуют двум точкам в пластической области кривой напряжения-деформации. Тогда задача состоит в том, чтобы найти эти две точки, чтобы можно было вычислить константы.
Если предел текучести (S ty ), предел прочности (S tu ), модуль упругости (E) и пластическая деформация при разрушении (ε f ) для материала известны, то можно определить две точки в области пластичности (точки текучести и предельной прочности), и по этим точкам можно рассчитать кривую области пластичности. Помните, что пластическую деформацию при разрушении можно рассчитать по процентному удлинению, eL, по формуле ε f = eL/100%. К счастью, все эти свойства материала общеизвестны.
Важно отметить, что уравнение для кривой пластической области σ = H ε p n , зависит от пластической деформации, поэтому нам необходимо определить значения пластической деформации для двух точек интереса.
Пластическая деформация может быть рассчитана по общей деформации с использованием:
ε p = ε − ε e = ε − σ/E
где в приведенном выше уравнении ε — полная деформация, а ε e — упругая деформация.
Таблица ниже используется для определения предела текучести и предела текучести:
| Напряжение, σ | Общая деформация, ε | Упругая деформация, ε e | Пластиковая деформация, ε p | |
|---|---|---|---|---|
| Предел текучести: | С ти | S ty /E + 0,002 | S ти /Е | 0,002 |
| Конечная точка: | С ту | S ту /E + ε ф | С ту /Е | е ж |
Отметим, что при определении деформации в пределе текучести принималась пластическая деформация 0,002. Это согласуется с методом смещения 0,2%, как описано ранее.
Это допущение необходимо для того, чтобы поместить точку текучести в пластическую область кривой. Из приведенной выше таблицы видно, что предел текучести и предел прочности в пластической области даются:
| • | Предел текучести: | (С ти , 0,002) |
| • | Конечная точка: | (S ту , ε ф ) |
По двум точкам пластической области кривой можно рассчитать константы n и H для уравнения Рамберга-Осгуда. Показатель деформационного упрочнения n рассчитывается как: (Примечание 1)
Значение H рассчитывается с использованием точки текучести (S ty , 0,002) в качестве точки отсчета, хотя подойдет любая точка:
Теперь, когда константы n и H определены, уравнение для полной деформации как функции напряжения известно:
Приведенное выше уравнение можно упростить, подставив выражение для H. Окончательное уравнение для полной деформации как функции напряжения:
PDH Classroom предлагает курс повышения квалификации, основанный на этой справочной странице по механическим свойствам материалов.
Этот курс можно использовать для выполнения кредитных требований PDH для поддержания вашей лицензии PE.
Теперь, когда вы прочитали эту справочную страницу, заработайте за это признание!
Просмотреть курс сейчас:
Просмотреть курс
Примечания
Примечание 1. Показатель деформационного упрочнения в уравнении Рамберга-Осгуда
Показатель деформационного упрочнения, обозначаемый n, не следует путать с параметром Рамберга-Осгуда, который также обозначается n. Эти два параметра являются обратными друг другу, что только добавляет путаницы. Мы используем показатель деформационного упрочнения в уравнении Рамберга-Осгуда, а не параметр Рамберга-Осгуда. Причина, по которой мы используем показатель деформационного упрочнения, заключается в том, что это общее свойство материала, полезное вне контекста уравнения Рамберга-Осгуда.
Каталожные номера
Общие каталожные номера:
- Будинас-Нисбетт, «Машиностроение Шигли», 8-е изд.
- Доулинг, Норман Э., «Механическое поведение материалов: инженерные методы деформации, разрушения и усталости», 3-е изд.
- Гир, Джеймс М., «Механика материалов», 6-е изд.
- Хиббелер, Рассел К., «Механика материалов», 10-е изд.
- Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена PE», 13-е изд.
Технические характеристики и стандарты:
- ASTM E8, «Стандартные методы испытаний металлических материалов на растяжение», Американское общество испытаний и материалов, 2011 г.
Оценка испытаний на растяжение, сжатие, кручение, поперечное и ударное воздействие и корреляция результатов для хрупких керметов
%PDF-1.4 % 308 0 объект > эндообъект 303 0 объект >поток приложение/pdf
Тем не менее, обратите особое внимание на отдельные работы, чтобы убедиться, что не указаны ограничения авторского права. Для отдельных произведений может потребоваться получение других разрешений от первоначального правообладателя.