Решение задач Построение 📝 Эпюр Сопротивление материалов
1. Сколько стоит помощь?
Цена, как известно, зависит от объёма, сложности и срочности. Особенностью «Всё сдал!» является то, что все заказчики работают со экспертами напрямую (без посредников). Поэтому цены в 2-3 раза ниже.
2. Каковы сроки?
Специалистам под силу выполнить как срочный заказ, так и сложный, требующий существенных временных затрат. Для каждой работы определяются оптимальные сроки. Например, помощь с курсовой работой – 5-7 дней. Сообщите нам ваши сроки, и мы выполним работу не позднее указанной даты. P.S.: наши эксперты всегда стараются выполнить работу раньше срока.
 Выполняете ли вы срочные заказы?
Выполняете ли вы срочные заказы?Да, у нас большой опыт выполнения срочных заказов.
4. Если потребуется доработка или дополнительная консультация, это бесплатно?
Да, доработки и консультации в рамках заказа бесплатны, и выполняются в максимально короткие сроки.
5. Я разместил заказ. Могу ли я не платить, если меня не устроит стоимость?
Да, конечно — оценка стоимости бесплатна и ни к чему вас не обязывает.
6. Каким способом можно произвести оплату? Работу можно оплатить множеством способом: картой Visa / MasterCard, с баланса мобильного, в терминале, в салонах Евросеть / Связной, через Сбербанк и т. д.
д.
7. Предоставляете ли вы гарантии на услуги?
На все виды услуг мы даем гарантию. Если эксперт не справится — мы вернём 100% суммы.
8. Какой у вас режим работы?
Мы принимаем заявки 7 дней в неделю, 24 часа в сутки.
Построение эпюр изгибающих моментов и поперечных сил
из «Сопротивление материалов »
Пример. Построить эпюры моментов и поперечных сил для балки, лежащей на двух опорах и нагруженной силой Р (рис. 137). [c.199]Для вычисления Л1 и Q в любом сечении этой балки прежде всего необходимо отыскать реакции.
 На рис. 137 намечено предполагаемое направление этих реакций А, Яд и В.
[c.199]
На рис. 137 намечено предполагаемое направление этих реакций А, Яд и В.
[c.199]
Этот результат можно было предвидеть заранее, так как нагрузки перпендикулярны к оси балки. [c.200]
Для получения выражений, дающих нам величины поперечной силы и изгибающего момента в любом сечении балки, возьмем какое-либо сечение 1—1 между точками Л и С на расстоянии Xi от конца Л. Заметим, что выражение взять сечение требует не только обозначить это сечение на чертеже, но и обязательно отметить его расстояние от выбранного начала координат. Центр тяжести проведенного сечения обозначен через 0 . [c.200]
Поперечная сила в сечении с абсциссой Xi не зависит от этого расстояния. Таким образом, пока Xi меняется в пределах от О да а, поперечная сила остается постоянной, и ее эпюра на этом участке изобразится прямой FJDi, параллельной оси абсцисс Л2В2 (рис. 137). [c.201]
Выражение (10.
Чтобы найти величину поперечной силы на втором участке, придется взять еще одно сечение между точками В и С с центром тяжести Оз. Расстояние его будем отсчитывать от правой опоры В. В этом случае нам будет выгоднее рассматривать правую часть балки, так как на нее действует лишь сила В. [c.201]
Выражение (10.7) пригодно при любом значении х ., не выходящем за пределы участка ВС, т. е. при О Хз Ь, и показывает, что Q2 от Ха не зависит. [c.201]
Такое очертание эпюры поперечных сил (рис. 137) есть следствие того, что мы при расчете считаем сосредоточенную силу Р приложенной в одной точке С.
 В действительности передача давления Р на балку происходит через очень малую площадку, имеющую некоторую длину вдоль балки (рис. 138). Поэтому на самом деле поперечная сила на протяжении этой длрны постепенно изменяется от величины +РЬ/1 до —Ра/1, переходя через нуль.
[c.202]
В действительности передача давления Р на балку происходит через очень малую площадку, имеющую некоторую длину вдоль балки (рис. 138). Поэтому на самом деле поперечная сила на протяжении этой длрны постепенно изменяется от величины +РЬ/1 до —Ра/1, переходя через нуль.
[c.202]
Опасными в отношении касательных напряжений будут все сечения участка балки СВ. [c.202]
Для построения эпюры изгибающих моментов воспользуемся теми же сечениями 1—1 (с началом координат в точке А) для левой части балки и 2—2 (с началом координат в точке В) для правой части балки. [c.202]
Как только Xi станет больше а, на левую часть балки попадут уже две силы Л и Р, и формула (10.8) окажется непригодной. Так как этот график — прямая линия, то х достаточно дать лишь два значения для получения двух точек эпюры моментов. При Xi=0 получаем Mi=Q— это ордината под точкой А. Точно так же при x =a получим Mi=- -Pabll—ордината под сечением С.
 [c.202]
[c.202]
Построим эпюры моментов и поперечных сил для балки, изображенной на рис. 139, нагруженной сплошной равномерно распределенной нагрузкой интенсивности q (выражае.мой в кГ/м, TjM, н1м и т. п.). [c.203]
Здесь необходимо начать с определения опорных реакций. [c.203]
Возьмем сечение О на расстоянии х от левого конца балки. Оставим для вычисления Q и М левую часть. На нее действуют реакция А и равномерно распределенная по длине х нагрузка q. [c.203]
Эпюра моментов получает вид, показанный на рис. 139. [c.204]
Наибольший изгибающий момент имеет место посредине пролета, т. е. в том сечении, где Q=0, что является следствием установленной выше ( 57) зависимости между М х) и Q x). [c.204]
Вернуться к основной статье
«Построение эпюр поперечных сил и изгибающих моментов для балки на двух опорах» по дисциплине «Сопротивление материалов»
Министерство образования и науки РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«КРЫМСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ ИМЕНИ в. И. вЕРНАДСКОГО»
И. вЕРНАДСКОГО»
(фгаоу во «кфу им. В.И. ВЕРНАДСКОГО»)
«Бахчисарайский колледж строительства, архитектуры и дизайна»
Утверждаю
Директор Бахчисарайского колледжа строительства, архитектуры и дизайна (филиал) ФГАОУ ВО «КФУ им. В.И. Вернадского»
_____________ Г.П. Пехарь
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по выполнению расчетно-графической работы № 3 по
На тему: «Построение эпюр поперечных сил и изгибающих моментов
для балки на двух опорах»
Бахчисарай — 2016
Теоретические сведения.
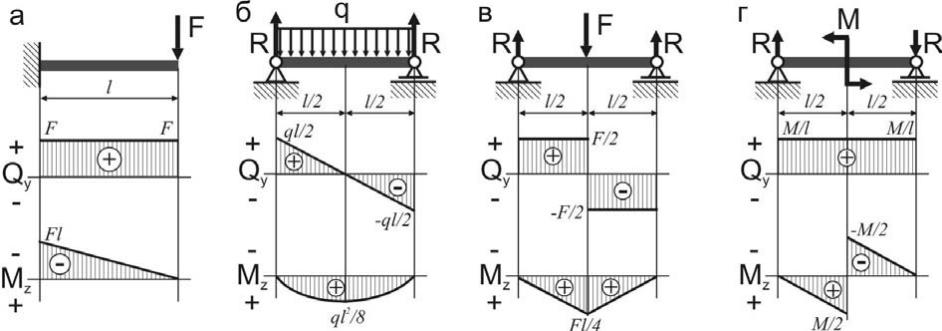
Для наглядного представления о законах изменения поперечной силы и изгибающего момента по длине балки удобно изображать их в виде графиков, ординаты которых соответствуют значениям поперечных сил или изгибающих моментов в любом ее сечении балки.
Графики, выражающие закон изменения поперечных сил или изгибающих моментов по длине балки, называются эпюрами Q или М.
Построение эпюр производится следующим образом.
Линию, параллельную оси балки, принимают за ось абсцисс, от которой в произвольном масштабе откладывают ординаты, соответствующие значениям С2 или М, действующим в различных сечениях балки. Соединяя концы отложенных ординат, получаем эпюру Q или М.
Ординаты, выражающие величины положительных поперечных сил, принято откладывать вверх от оси, а отрицательных —вниз. Ординаты, выражающие положительные изгибающие моменты, откладывают по-разному: выше или ниже оси, т. е. эпюру М строят или от сжатого волокна балки, или от растянутого. У строителей принято изображать эпюру изгибающих моментов со стороны растянутого волокна, так как это удобнее при использовании эпюры в расчетах и конструировании изгибаемых элементов некоторых строительных конструкций. Дело в том, что на рабочих чертежах, например железобетонных балок, строят совмещенную с эпюрой М так называемую эпюру материалов, способы построения которой изучаются в курсе «Строительные конструкции». Эпюра материалов показывает расположение стержней, работающих в растянутых зонах балок, их рабочую длину, места отгибов и т. д. Благодаря такому совмещению эпюр создается удобство наглядной и быстрой проверки прочности железобетонной балки на изгиб в любом ее сечении и правильности установки в ней растянутых стержней арматуры.
Эпюра материалов показывает расположение стержней, работающих в растянутых зонах балок, их рабочую длину, места отгибов и т. д. Благодаря такому совмещению эпюр создается удобство наглядной и быстрой проверки прочности железобетонной балки на изгиб в любом ее сечении и правильности установки в ней растянутых стержней арматуры.
Штриховать эпюры Q и М следует только вертикальными линиями, поскольку каждая линия штриховки в принятом масштабе выражает величину Q или М в данном сечении.
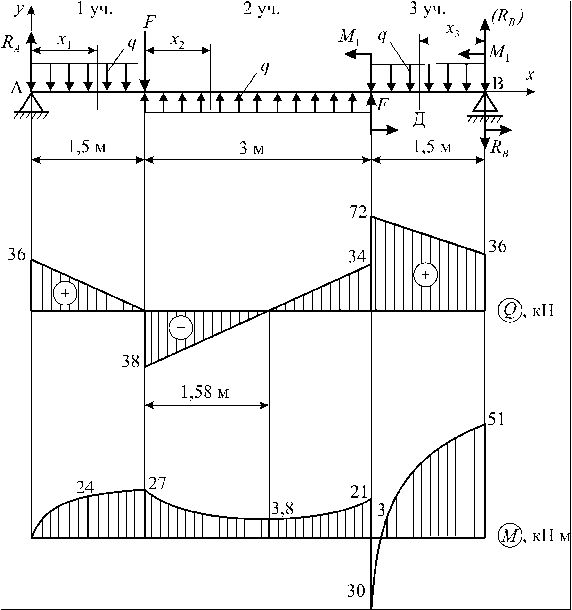
Порядок выполнения работы:
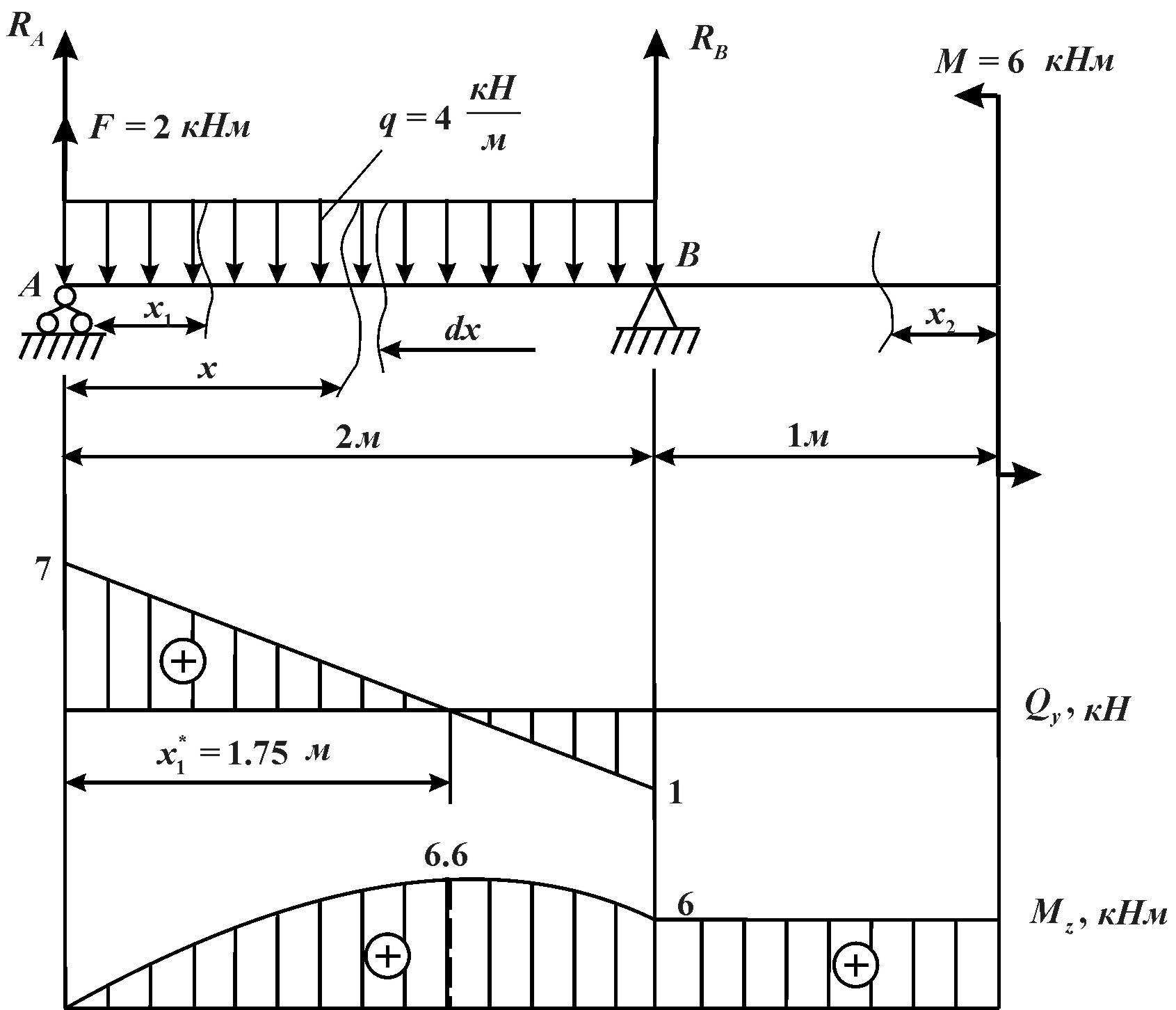
1. Определяют опорные реакции балки.
2. Обозначают характерные сечения (точки) балки. Ими являются концевые сечения балки, опоры, точки приложения сосредоточенных сил и моментов, начало и конец распределенной нагрузки.
3.Строим эпюру поперечных сил С>х. Для этого определяют значения поперечных сил в характерных точках. Напомним, что поперечная сила в сечении равна сумме проекций всех сил, расположенных только слева или только справа от рассматриваемого сечения на ось, перпендикулярную к оси элемента. Сила, расположенная слева от рассматриваемого сечения и направленная вверх, принимается со знаком «плюс», а сила, направленная вниз, — со знаком «минус», а для правой части балки наоборот.
Сила, расположенная слева от рассматриваемого сечения и направленная вверх, принимается со знаком «плюс», а сила, направленная вниз, — со знаком «минус», а для правой части балки наоборот.
В сечениях, соответствующих точкам приложения сосредоточенных сил, в том числе в точках приложения опорных реакций, необходимо определить два значения поперечной силы: чуть левее рассматриваемой точки и чуть правее ее. Поперечные силы в этих сечениях обозначаются соответственно
Qлев и Qправ
Найденные значения поперечных сил в характерных точках отложим в некотором масштабе от нулевой линии. Эти значения соединяем прямыми линиями, руководствуясь следующими правилами:
а) если на участке балки нет нагрузки (распределенной), то под этим участком значение поперечных сил соединяем прямой линией, параллельной нулевой линии;
б) если на участке балки приложена распределенная нагрузка, то под этим участком значения поперечных сил соединяем прямой, наклонной к нулевой линии.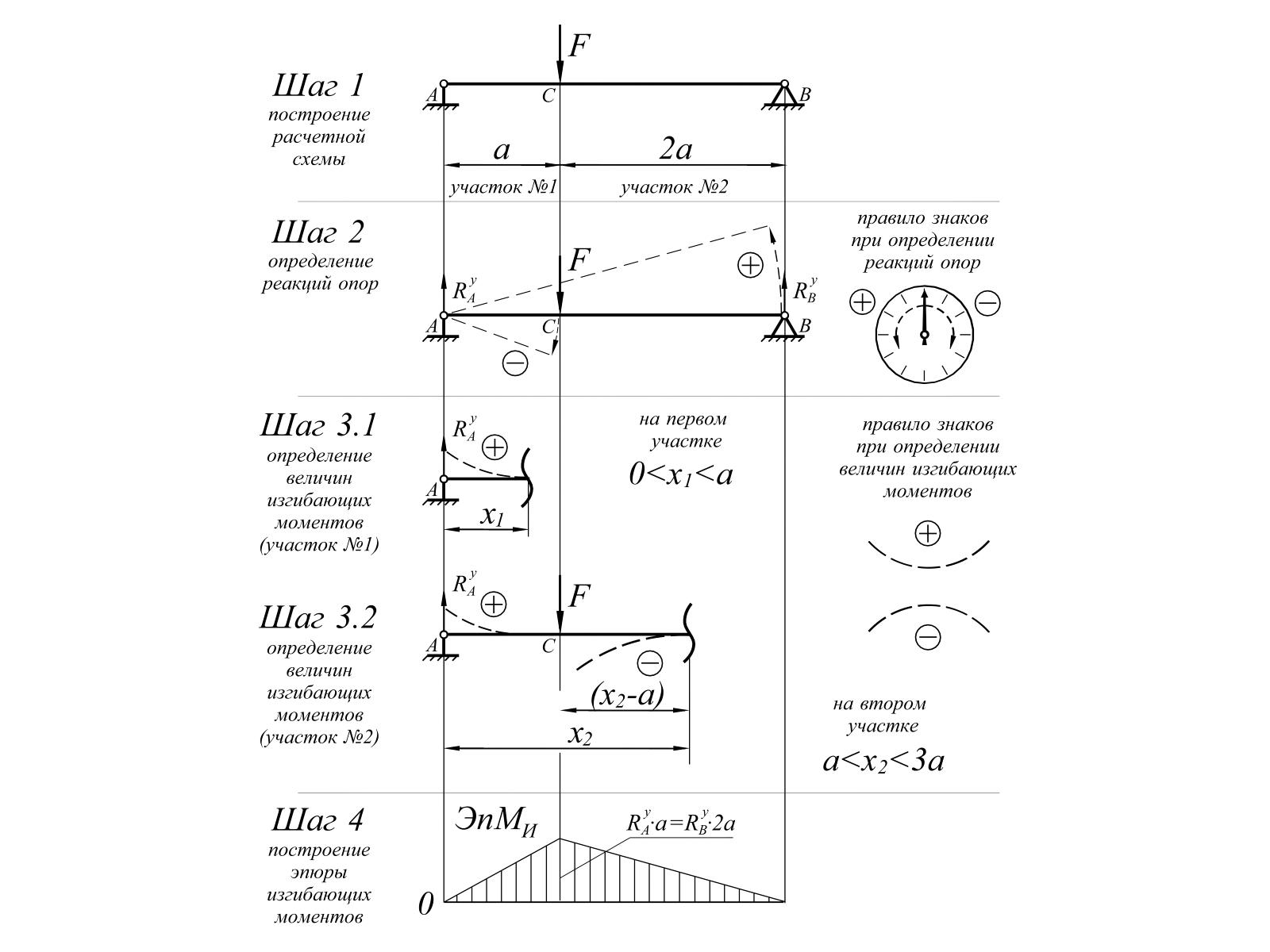 Она может пересекать или не пересекать нулевую линию.
Она может пересекать или не пересекать нулевую линию.
Соединив все значения поперечных сил по указанным правилам, получим график изменения поперечных сил по длине балки. Такой график называется эпюрой Qх.
4. Строим эпюру изгибающих моментов Мх. Для этого определяем изгибающие моменты в характерных сечениях. Напомним, что изгибающий момент в рассматриваемом сечении равен сумме моментов всех сил (распределенных, сосредоточенных, в том числе и опорных акций, а также внешних сосредоточенных моментов), расположенных только слева или только справа от этого сечения. Если любое из перечисленных силовых воздействий стремится повернуть левую часть балки по часовой стрелке, то они сообщают изгибающему моменту знак «плюс», а если против — знак «минус». Для правой части — наоборот.
В сечении, соответствующем точкам приложения сосредоточенных моментов, необходимо определить два значения изгибающего момента чуть левее рассматриваемого сечения Млев и чуть правее его Мправ.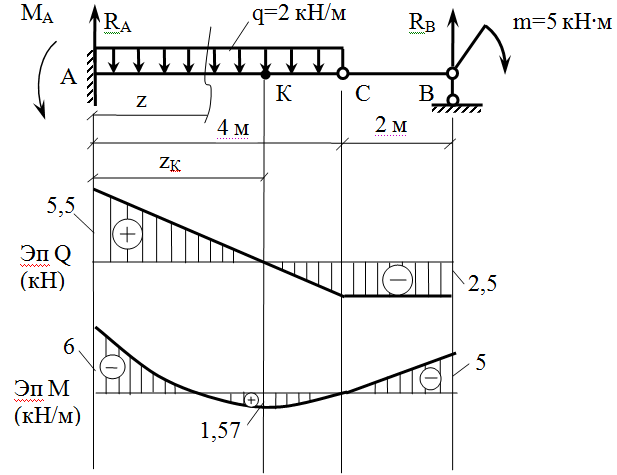 В точках приложения сил определяется одно значение изгибающего момента.
В точках приложения сил определяется одно значение изгибающего момента.
Полученные значения откладывают в некотором масштабе от нулевой линии. Соединяют концы отложенных ординат, руководствуясь следующими правилами:
а) если на участке балки нет нагрузки (распределенной), то под этим участком балки концы отложенных ординат соединяются прямой линией;
б) если на участке, балки приложена распределенная нагрузка, то под этим участком концы отложенных ординат соединяются по параболе. Парабола имеет выпуклость в сторону действия нагрузки (при действии нагрузки сверху вниз парабола обращена выпуклостью вниз). При этом, если эпюра Qх на рассматриваемом участке не пересекает нулевую линию, то эпюра Мх (она является параболой) может быть построена по двум точкам, так как все значения изгибающих моментов в промежуточных сечениях находятся между значениями в характерных сучениях. Если эпюра Qх пересекает нулевую линию, то под этим сечением эпюра Мх будет иметь экстремальное (максимальное или минимальное) значение или вершину параболы. Положение этого сечения находят по эпюре Qх из подобия треугольников. Затем находят значение изгибающего момента в этом сечении и строят эпюру Мх на участке с распределенной нагрузкой по трем точкам. Соединив все полученные точки по указанным выше правилам, получают график изменения изгибающих моментов по длине балки. Этот график называется эпюрой Мх.
Положение этого сечения находят по эпюре Qх из подобия треугольников. Затем находят значение изгибающего момента в этом сечении и строят эпюру Мх на участке с распределенной нагрузкой по трем точкам. Соединив все полученные точки по указанным выше правилам, получают график изменения изгибающих моментов по длине балки. Этот график называется эпюрой Мх.
Существует несколько способов проверки правильности построения эпюр. Наиболее простой способ заключается в том, что суммы моментов всех левых и всех правых сил, взятые отдельно, в любом сечении балки должны быть равны между собой.
Приведенный способ построения эпюр Qх и Мх назовем способом построения по характерным сечениям.
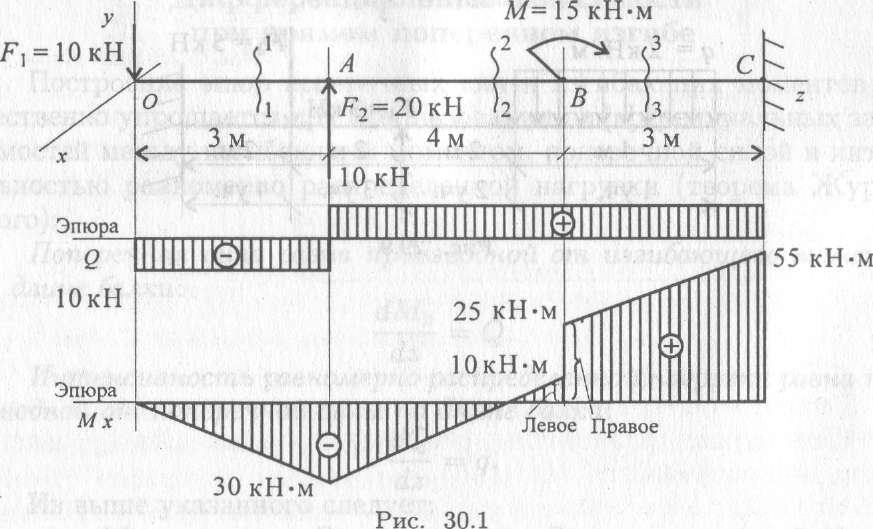
Пример решения задачи
Построить эпюры Q и М для балки, изображенной на рисунке.
Решение: определяем опорные реакции балки:
,
Откуда
Откуда
Проверка:
Построение эпюры Q:
QA=VA=19,25КН QC(ПР)=VA-P=19,25-6,0=13,25КН
QC(ЛЕВ)=VA=19,25КН
Поперечная сила в точке D своего значения не изменяет, так как проекция пары сил на любую ось равна нулю,
Строим эпюру Q, откладывая положительные значения ординат вверх от оси, а отрицательные — вниз (рис. б).
б).
Построение эпюры М. Изгибающие моменты в сечениях балки на опорах МА и Мв равны нулю,
Мс = УАа1 = 19,25 • 1,0 = 19,25 кн • м;
Значение максимального изгибающего момента на участке балки ВЕ выразится ординатой, соответствующей значению поперечной силы (3=0.
Из подобия треугольников, образовавшихся на четвертом участке эпюры Q длиной 5 м, определим расстояние ъ от правой опоры до сечения, в котором Q = 0
26,75 _ 13,25
2 5-z
откуда z = 3,34 м
Mmax = = 26,75 • 3,34 — 8 • 3,34 • 1,67 = 44,7кн • м.
Оказалось, что наибольшее значение изгибающего момента на участке ВЕ является также Мтах и для всей балки. Однако при других значениях сосредоточенных силы и пары и их абсцисс Мтах может быть в сечении под силой или парой. Объясняется это тем, что в точке приложения сосредоточенной силы или пары непрерывность функции нарушается.
Величину абсциссы ъ можно определить и другим способом. Для этого необходимо составить уравнение, выражающее равенство нулю суммы проекций всех сил на ось у справа или слева от точки О:
,
откуда
Строим эпюру М, откладывая в произвольно выбранном масштабе значения М в сечениях С, D, Е и К. Здесь также нужно обратить внимание на то, что на эпюре М, где ордината соответствует точке Э приложения сосредоточенной пары, образуется скачок на полную величину момента пары (в данном случае на т = 12 кн • м), и так как момент пары отрицателен, то скачок получился направленным вверх; в случае положительного момента пары скачок был бы направлен вниз.
Контрольные вопросы
1. Какой изгиб называется плоским изгибом?
2. Какой изгиб называется чистым изгибом?
3. Что происходит с продольными волокнами материала при изгибе?
4. Какой слой волокон балки называется нейтральным?
5. Что называется нейтральной осью?
Что называется нейтральной осью?
6. На какие три типа делятся опоры балок?
7. Какие реакции возникают в каждом из трех типов опорных устройств балок при действии изгибающих сил, направленных перпендикулярно к оси балки?
8. Что называется интенсивностью равномерно распределенной нагрузки? Ее размерность?
9. Что называется изгибающим моментом и поперечной силой в данном сечении?
Ю.Как определяется знак изгибающего момента и поперечной силы?
11 .Какая существует связь между изгибающим моментом, поперечной силой и интенсивностью нагрузки? 12.Для чего строятся эпюры изгибающих моментов и поперечных сил?
Новогоднее обращение Министра науки и высшего образования РФ Валерия Фалькова Дорогие друзья! Совсем скоро наступит самый волшебный, теплый, семейный праздник — Новый год. И у каждого из нас есть заветные планы и мечты. Все мы хотим, чтобы родные были здоровы, в семье царило согласие, дети радовали, и все в нашей жизни менялось только к лучшему.
Под бой курантов мы, как в детстве, загадываем желания. Но уже точно знаем, что чудо не случается само по себе. Его можно совершить только личными достижениями, слаженной работой и стремлением реализовать самые смелые планы.
В преддверии Нового года каждый вспоминает самые важные для него события, встречи, слова и поступки. И у каждого из нас есть заветные планы и мечты. Все мы хотим, чтобы родные были здоровы, в семье царило согласие, дети радовали, и все в нашей жизни менялось только к лучшему.
Под бой курантов мы, как в детстве, загадываем желания. Но уже точно знаем, что чудо не случается само по себе. Его можно совершить только личными достижениями, слаженной работой и стремлением реализовать самые смелые планы.
В преддверии Нового года каждый вспоминает самые важные для него события, встречи, слова и поступки. |
Поздравление ректора НГАСУ (Сибстрин) Юрия Сколубовича с наступающим Новым годом! Дорогие преподаватели и сотрудники, студенты и аспиранты, выпускники, ветераны и партнеры Новосибирского государственного архитектурно-строительного университета (Сибстрин)! Примите самые теплые и сердечные поздравления с наступающим Новым годом и Рождеством! Провожая 2021 год, прежде всего, хочу выразить благодарность всему коллективу университета за хорошую работу и учебу, за успехи и достижения, за понимание и доверие. В уходящем году мы доказали, что НГАСУ (Сибстрин) – эффективный вуз, укрепили свои позиции в регионе, открыли новые образовательные программы, продолжили развивать науку, сетевое взаимодействие и международную деятельность, вместе с Попечительским советом – улучшать материально-техническую базу. Наши умные и талантливые студенты стали победителями и лауреатами конкурсов в различных областях, международных и всероссийских конференций, обладателями стипендий и грантов. В уходящем году мы доказали, что НГАСУ (Сибстрин) – эффективный вуз, укрепили свои позиции в регионе, открыли новые образовательные программы, продолжили развивать науку, сетевое взаимодействие и международную деятельность, вместе с Попечительским советом – улучшать материально-техническую базу. Наши умные и талантливые студенты стали победителями и лауреатами конкурсов в различных областях, международных и всероссийских конференций, обладателями стипендий и грантов. |
График работы университета в новогодние праздники Для студентов, профессорско-преподавательского состава и сотрудников университета в соответствии с приказами ректора НГАСУ (Сибстрин) № 177-о от 16.11.2020 г., № 170-о от 23.11.2021 г. устанавливаются выходные и праздничные дни с 31.12.2021 г. по 09.01.2022 г. Поздравляем коллектив НГАСУ (Сибстрин) с наступающим Новым годом! |
50 новогодних подарков от студентов и сотрудников университета было передано детям из малообеспеченных семей Октябрьского района 28 декабря 2021 года в университете завершилась ежегодная акция «Сотвори новогоднее чудо!» по сбору подарков для детей из малообеспеченных семей Октябрьского района Новосибирска. На ее призыв активно откликнулись студенты, магистранты, сотрудники и преподаватели НГАСУ (Сибстрин). Не остались в стороне творческие коллективы и студенческие объединения. Приятно удивили первокурсники своим массовым участием!
Выражаем всем огромную благодарность за принесенные сладости, школьные принадлежности, оригинальные развивающие игры, мягкие игрушки, а главное, за отзывчивость и небезразличие к детям из семей, попавшим в трудную ситуацию. Большое спасибо организаторам акции: Волонтерскому штабу НГАСУ (Сибстрин), Профкому студентов нашего университета и студенческому объединению «Сибстрин-ТВ».
На ее призыв активно откликнулись студенты, магистранты, сотрудники и преподаватели НГАСУ (Сибстрин). Не остались в стороне творческие коллективы и студенческие объединения. Приятно удивили первокурсники своим массовым участием!
Выражаем всем огромную благодарность за принесенные сладости, школьные принадлежности, оригинальные развивающие игры, мягкие игрушки, а главное, за отзывчивость и небезразличие к детям из семей, попавшим в трудную ситуацию. Большое спасибо организаторам акции: Волонтерскому штабу НГАСУ (Сибстрин), Профкому студентов нашего университета и студенческому объединению «Сибстрин-ТВ». |
В эксперименте строится график сопротивления материала класс 12 по физике CBSE
Подсказка: Давайте определим некоторые значения температуры и сопротивления, которые помогут нам в наших расчетах. Также мы можем увидеть некоторые дополнительные термины или переменные, используемые в параметрах. проверьте, для какого из них мы получаем отрицательный наклон и положительную константу. {2}}} $ и Ось у представляет собой функцию сопротивления R, т.е.{2}}} \ right)}}
{2}}} $ и Ось у представляет собой функцию сопротивления R, т.е.{2}}} \ right)}}$ Итак, правильный ответ — «Вариант В».
Примечание:
Обратите внимание, что константа, которую мы определили, и константы, используемые в параметрах, не совпадают. Следовательно, не обязательно, чтобы уравнение в решении и вариант были одинаковыми.
Также можно проверить правильный вариант по логу с основанием е с обеих сторон каждой и записать в виде уравнения прямой. Затем проверьте, для какого из них мы получаем отрицательный наклон и положительную константу.
Таблица выбора материалов — обзор
Решение
Укажите функцию, цель, ограничения и свободные переменные.
Функция в этом случае: стяжка несет растягивающую силу.
Цель: Сведение к минимуму массы.
Ограничения: Должен быть установлен указанный груз.
Свободные переменные: Площадь поперечного сечения стяжки, обычно это геометрические размеры.
Функция объекта описывается формулой
m = Alρ (уравнение для цели)
, где A — площадь поперечного сечения, l — длина, а ρ — плотность.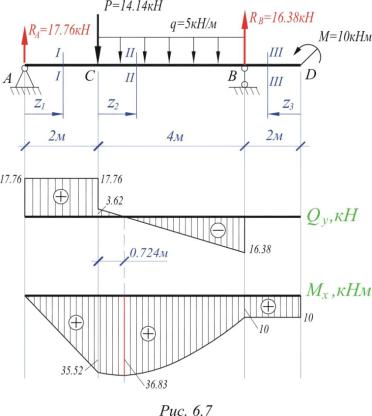
Длина ( l ) указана и не должна выходить из строя под нагрузкой F (ограничение). Площадь поперечного сечения ( A ) свободна (переменная произвольная). Подводя итог, функция: рулевая тяга. Цель: минимизировать ограничение массы. Длина указана, не должен разрушаться под нагрузкой F (адекватная вязкость разрушения).
F / A <σy (уравнение для ограничения)
Формула для массы стяжки следующая: плотность ( ρ ) × площадь ( A ) × длина ( l )
Следовательно, площадь (свободная переменная):
(9.4) A = F (Сила) σy (предел текучести)
Более прочные материалы, такие как нержавеющая сталь, требуют небольшой площади поперечного сечения, тогда как более слабые материалы, такие как полимеры, требуют больших площадей поперечного сечения, чтобы выдерживать ту же нагрузку. В этой конструкции могут использоваться как малые, так и большие площади поперечного сечения, поскольку они не являются ограничением.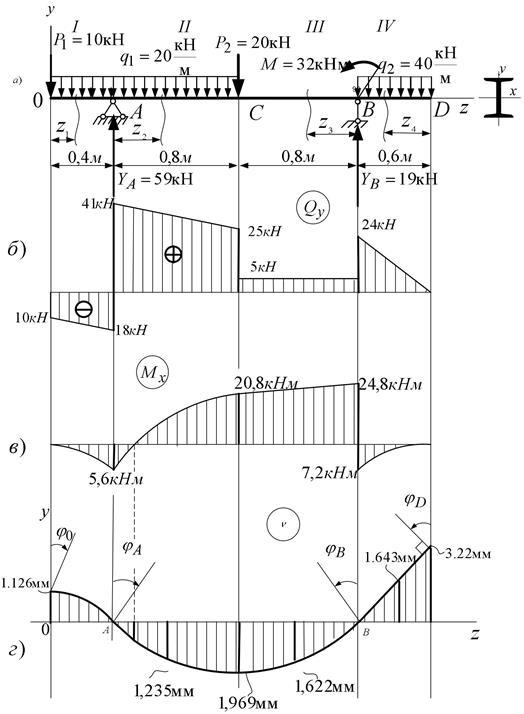 Важный вопрос — какой материал даст наименьшую массу для легкого и жесткого луча. Это можно определить как: создать м в терминах F, G, M .Определим m в терминах любой комбинации F, G, M. Показано, что m = A × l × p. Отсутствующий параметр: F. Определите F в приведенном выше уравнении, F / A = σ y , исключив область.
Важный вопрос — какой материал даст наименьшую массу для легкого и жесткого луча. Это можно определить как: создать м в терминах F, G, M .Определим m в терминах любой комбинации F, G, M. Показано, что m = A × l × p. Отсутствующий параметр: F. Определите F в приведенном выше уравнении, F / A = σ y , исключив область.
Следовательно, индекс эффективности для легкой прочной стяжки составляет
Выберите материал с меньшим размером l .
Первый и второй кронштейны содержат указанную нагрузку и указанную длину. Свойство материала, представленное ( ρ / σ y ) в последней скобке, предполагает, что самая легкая стяжная шпилька, которая будет выдерживать указанную нагрузку F , — это материал с наименьшим значением ρ / σ y. . Чтобы максимизировать производительность, член свойств материала ( ρ / σ y ) инвертирован.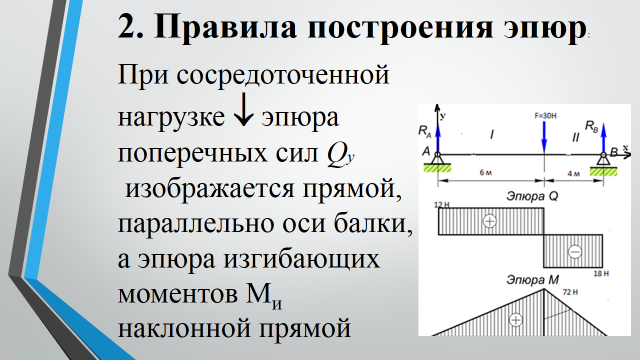 Свойство материала определяется индексом M. В приведенном выше случае M = σ y / ρ. Самая легкая стяжка будет нести нагрузку F будет с наибольшим значением M.
Свойство материала определяется индексом M. В приведенном выше случае M = σ y / ρ. Самая легкая стяжка будет нести нагрузку F будет с наибольшим значением M.
Аналогично для легкой сильной балки индекс материала M составляет
M = σf3 / 2ρ
и масса минимизируется за счет выбора материала с наибольшим значением индекса.В приведенном выше примере ограничениями были l и f .
Типичные примеры показателей материалов приведены в таблице 9.3.
Таблица 9.3. Индексы материалов [16]
| Функции, цели и ограничения | Максимальный показатель эффективности |
|---|---|
| 1. Стяжки — минимальный вес, предписанная жесткость | Eρ |
| 2. Балка — минимальный вес , предписанная прочность | σy2 / 3ρ |
| 3.Балка — минимальная стоимость, предписанная жесткость | σy2 / 3Cmρ |
4. Теплоизоляция — минимальная стоимость, предписанный тепловой поток Теплоизоляция — минимальная стоимость, предписанный тепловой поток | 1λCmρ |
Производительность зависит от двух или более свойств материала, которые представлены на графике. механическое свойство или математическая комбинация свойств на каждой оси диаграммы материалов. Один из способов рассмотреть материалы для определенного свойства или индекса материала — использовать таблицу выбора материалов.Таблица выбора материала (ρ по сравнению с E ) показана на рис. 9.3. Он показывает модуль растяжения материалов на четыре декады от 0,1 ГПа до 1000 ГПа. Масштаб журнала позволяет отображать большую информацию на небольшом пространстве. Данные для ряда материалов определенного класса сгруппированы и заключены в конверт (жирная линия). Пузырьки в конверте представляют собой подмножество материалов. Например, на рис. 9.3 оболочка инженерных композитов содержит KFRP (полимер, армированный волокном Кельвера), GFRP (полимер, армированный графитовым волокном) и CFRP (полимер, армированный углеродным волокном) в качестве подмножеств материалов в пузыре. Конверт включает в себя всех членов класса и пузырьковые элементы подклассов. В таблицу включен ряд материалов. Эти диаграммы отображают данные для важных свойств, которые представляют наибольший интерес для характеристики материалов и инженерного проектирования. Эти свойства включают плотность, модуль, прочность, ударную вязкость, теплопроводность, коэффициент диффузии и расширение.
Конверт включает в себя всех членов класса и пузырьковые элементы подклассов. В таблицу включен ряд материалов. Эти диаграммы отображают данные для важных свойств, которые представляют наибольший интерес для характеристики материалов и инженерного проектирования. Эти свойства включают плотность, модуль, прочность, ударную вязкость, теплопроводность, коэффициент диффузии и расширение.
Рисунок 9.3. Материалы для весел. Углепластик лучше дерева, потому что структурой можно управлять. (От Эшби, М.Ф. (1999). Выбор материалов в механическом проектировании , Баттерворт. С любезного разрешения Butterworth Publication)
На основе информации, представленной в таблицах, найдено подмножество материалов, которые максимизируют производительность компонентов после устранения основных ограничений. Устойчивость к коррозии, модуль, прочность и плотность — все это основные ограничения, которые необходимо соблюдать. Ограничения могут исключить несколько классов материалов. Ограничения задаются следующим образом:
P> Pcritical
, где P — свойство, а P критическое значение — критическое значение, которое нельзя превышать.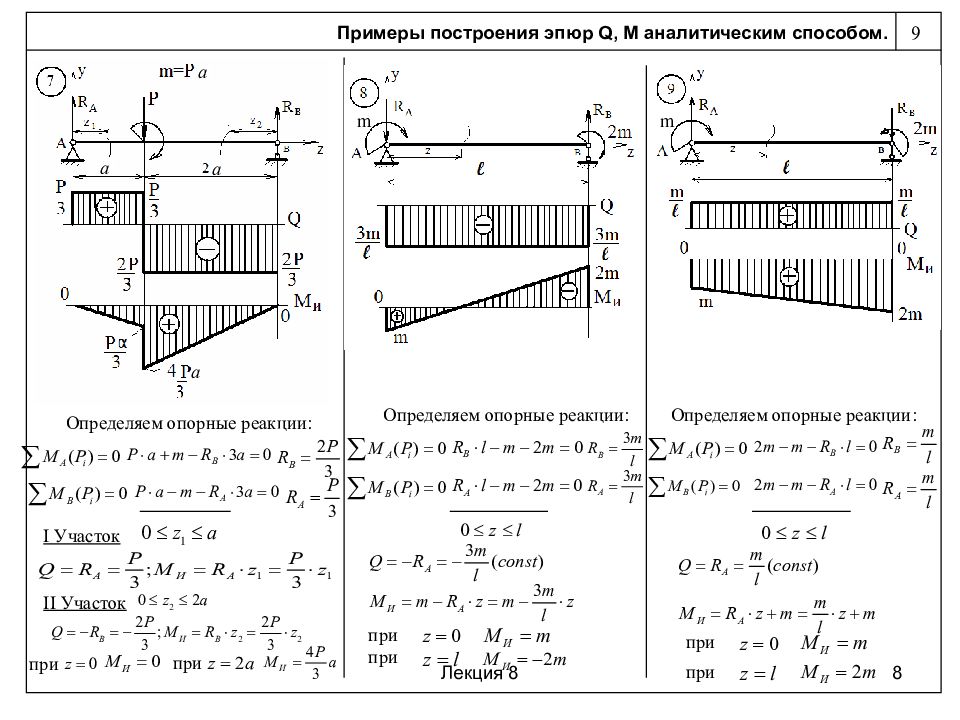
Например, если присутствует коррозия, скорость коррозии не должна превышать предписанное критическое значение. Основные ограничения отображаются в виде горизонтальных или вертикальных линий на диаграмме выбора материала. Например, если ограничение E > 10 ГПа и ρ = 3 мг / м 3 , пересечение линий даст область поиска для выбора подходящих материалов.
Из информации, представленной в таблице свойств материалов, материалы, которые обеспечивают максимальную производительность, выбираются из подмножеств, которые соответствуют пределам свойств с использованием индексов материалов.
Например, выберите материалы с модулем упругости всего 10 ГПа, при этом значении будет проведена линия (рис. 9.4). Все материалы над линией будут показывать набор материалов кандидатов. Если требуемая плотность меньше 2,0 мг / м 3 , на указанном значении плотности проводится линия. Подмножество материалов, отвечающих обоим критериям, можно найти в верхнем левом квадранте.
Рисунок 9.4. Таблица свойств
Индексы материалов Eρ, E1 / 2ρ, E1 / 3ρ для легких и жестких компонентов могут быть нанесены на диаграмму (Рис.9.5).
Рисунок 9.5а. Нормы для E 1/2 / ρ максимальное
Рассмотрим, например, максимизирующий коэффициент для легкой жесткой балки и присвоим ему значение
Взятие бревен с обеих сторон, log E = log ρ + log C, которое представляет собой уравнение прямой линии с наклоном 1. Значение C получается, когда ρ = 1 и равно E , и определяет значение нормативов. Материалы, указанные в нормативных документах, имеют одинаковое значение для E / ρ (удельный модуль).
Для условия:
C = E1 / 2ρ logC = 12logE − logρ logE = 2logρ + 2logC
Таким образом, мы получаем семейство прямых (рис. 9.5a). Другие линии в семействе будут параллельными линиями с градиентом 2.
Аналогичным образом, для условия:
E1 / 3ρ = C
мы получили бы другой набор линий с наклоном 3. На рис. 9.5b показаны направляющие и Подмножество материала. В рекомендациях показаны наклоны семейства параллельных линий для определенного индекса производительности.
На рис. 9.5b показаны направляющие и Подмножество материала. В рекомендациях показаны наклоны семейства параллельных линий для определенного индекса производительности.
Рисунок 9.5b. Линия для E / ρ = 1000
Рассмотрите возможность выбора материала со значениями E / ρ больше, чем, приблизительно, 1000.
log E − log ρ = log 1000log E = log ρ + 3 [log E − log ρ = log C]
Это дало бы линию с наклоном, равным единице, и точкой пересечения, равной 3, на оси бревна E . Материалы, пересекаемые нормативными требованиями, имеют одинаковое значение E / ρ (удельный модуль). Материалы выше этой линии имеют значения выше C , а материалы ниже имеют более низкие значения и не подходят.Схематическая диаграмма E – ρ , показывающая рекомендации по трем показателям материалов для жесткой и легкой конструкции, показана на рис. 9.6.
Рисунок 9.6. Схема E — ρ , показывающая рекомендации по трем показателям материалов для жесткой и легкой конструкции.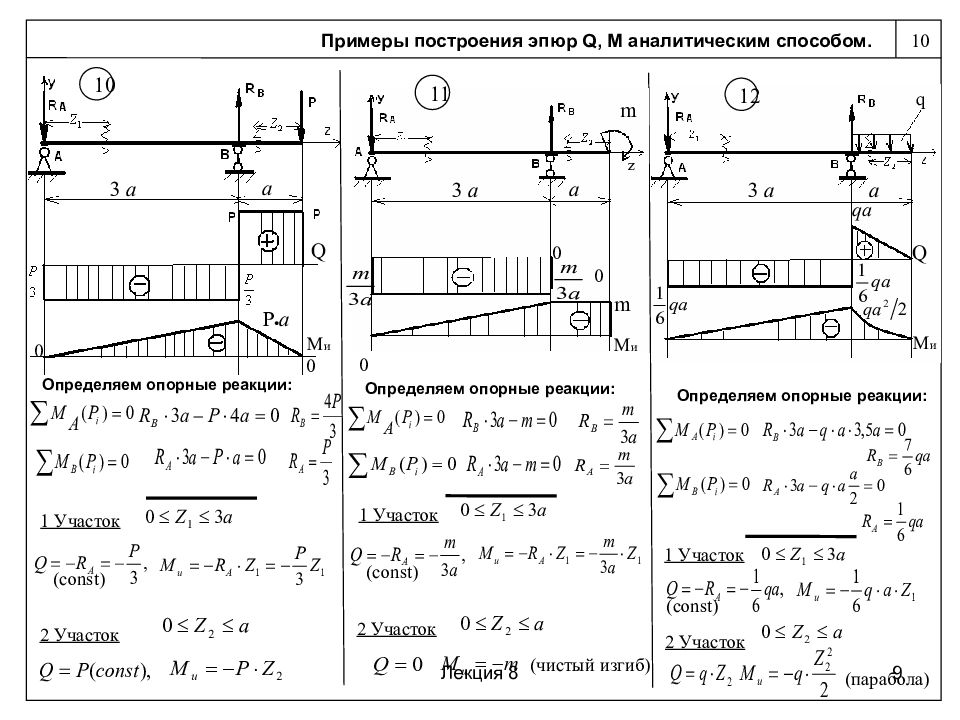 (Из Эшби, М.Ф. (1999). Выбор материалов в механическом проектировании , Баттерворт)
(Из Эшби, М.Ф. (1999). Выбор материалов в механическом проектировании , Баттерворт)
Предел текучести — прочность (механика) материалов
Предел текучести — прочность (механика) материалов
Прочность / Механика материалов
Ряд терминов был определен с целью определения напряжения, при котором начинается пластическая деформация.Чаще всего для этой цели используется предел текучести. Предел текучести определяется как напряжение, при котором возникает заданная величина остаточной деформации. Графическая часть ранних стадий испытания на растяжение используется для оценки предела текучести. Для определения предела текучести заданная величина остаточной деформации устанавливается вдоль оси деформации графика справа от начала координат (ноль). Это обозначено на Рисунке 5 как Точка (D).
Предел текучести, модуль упругости, предел прочности выбранных материалов
Прямая линия проведена через точку (D) с тем же наклоном, что и начальная часть кривой напряжения-деформации. Точка пересечения новой линии и кривой деформации проецируется на ось напряжений. Значение напряжения в фунтах на квадратный дюйм — это предел текучести. Это обозначено на рисунке 5 как точка 3. Этот метод построения графика выполняется с целью вычитания упругой деформации из общей деформации, оставляя предварительно определенное «постоянное смещение» в качестве остатка. Когда указывается предел текучести, следует указывать величину смещения, использованную при определении. Например, «Предел текучести (при
Точка пересечения новой линии и кривой деформации проецируется на ось напряжений. Значение напряжения в фунтах на квадратный дюйм — это предел текучести. Это обозначено на рисунке 5 как точка 3. Этот метод построения графика выполняется с целью вычитания упругой деформации из общей деформации, оставляя предварительно определенное «постоянное смещение» в качестве остатка. Когда указывается предел текучести, следует указывать величину смещения, использованную при определении. Например, «Предел текучести (при
Модуль Юнга общих технических материалов
Ниже приведены некоторые примеры предела текучести металлов.
Нажмите на картинку для увеличения
Типичная кривая напряжения-деформации пластмасс
Вместо предела текучести иногда используются альтернативные значения. Некоторые из них кратко описаны ниже.
Некоторые из них кратко описаны ниже.
Предел текучести , определяемый методом делителя, включает в себя наблюдателя с парой разделителей, наблюдающего за видимым удлинением между двумя метками на образце.Когда происходит видимое растяжение, нагрузка в этот момент записывается, и рассчитывается напряжение, соответствующее этой нагрузке.
Мягкая сталь при испытании на растяжение часто демонстрирует особую характеристику, известную как предел текучести. Если построена кривая напряжения-деформации, наблюдается падение нагрузки (или иногда постоянная нагрузка), хотя деформация продолжает увеличиваться. В итоге за счет деформации металл упрочняется, и при дальнейшем деформировании нагрузка возрастает.Верхняя точка на S-образной части кривой, где начинается текучесть, известна как верхний предел текучести, а точка минимума — это нижний предел текучести. Это явление очень неприятно при некоторых операциях глубокой вытяжки листовой стали. Сталь продолжает удлиняться и становиться тоньше в тех местах, где начинается пластическая деформация, оставляя неприглядные углубления, называемые растяжными деформациями или «червями».
Сталь продолжает удлиняться и становиться тоньше в тех местах, где начинается пластическая деформация, оставляя неприглядные углубления, называемые растяжными деформациями или «червями».
Предел пропорциональности определяется как напряжение, при котором кривая напряжения-деформации сначала отклоняется от прямой линии.Ниже этого предельного значения напряжения отношение напряжения к деформации является постоянным, и говорят, что материал подчиняется закону Гука (напряжение пропорционально деформации). Пропорциональный предел обычно не используется в спецификациях, потому что отклонение начинается настолько постепенно, что наверняка возникнут разногласия относительно точного напряжения, при котором линия начинает изгибаться.
Предел упругости ранее определялся как напряжение, при котором начинается пластическая деформация. Этот предел не может быть определен из кривой напряжения-деформации. Метод определения предела должен включать последовательность слегка увеличивающихся нагрузок с промежуточной полной разгрузкой для обнаружения первой пластической деформации или «остаточного схватывания». Как и пропорциональный предел, его определение вызвало бы споры. Однако предел упругости используется как описательный, качественный термин.
Этот предел не может быть определен из кривой напряжения-деформации. Метод определения предела должен включать последовательность слегка увеличивающихся нагрузок с промежуточной полной разгрузкой для обнаружения первой пластической деформации или «остаточного схватывания». Как и пропорциональный предел, его определение вызвало бы споры. Однако предел упругости используется как описательный, качественный термин.
Графический закон Ома: ток vs.Возможная разница — видео и стенограмма урока
Закон Ома
Помните, что Закон Ома говорит вам о взаимосвязи между тремя важными величинами в электрической цепи: током, разностью потенциалов и сопротивлением. Закон Ома гласит, что разность потенциалов ( В, ) на резисторе, таком как лампочка Аарона, равна току ( I ) через резистор, умноженному на его сопротивление ( R ).
На графике Аарона разность потенциалов нанесена на оси y , а ток нанесен на ось x , так что у нас уже есть две величины, представленные в законе Ома.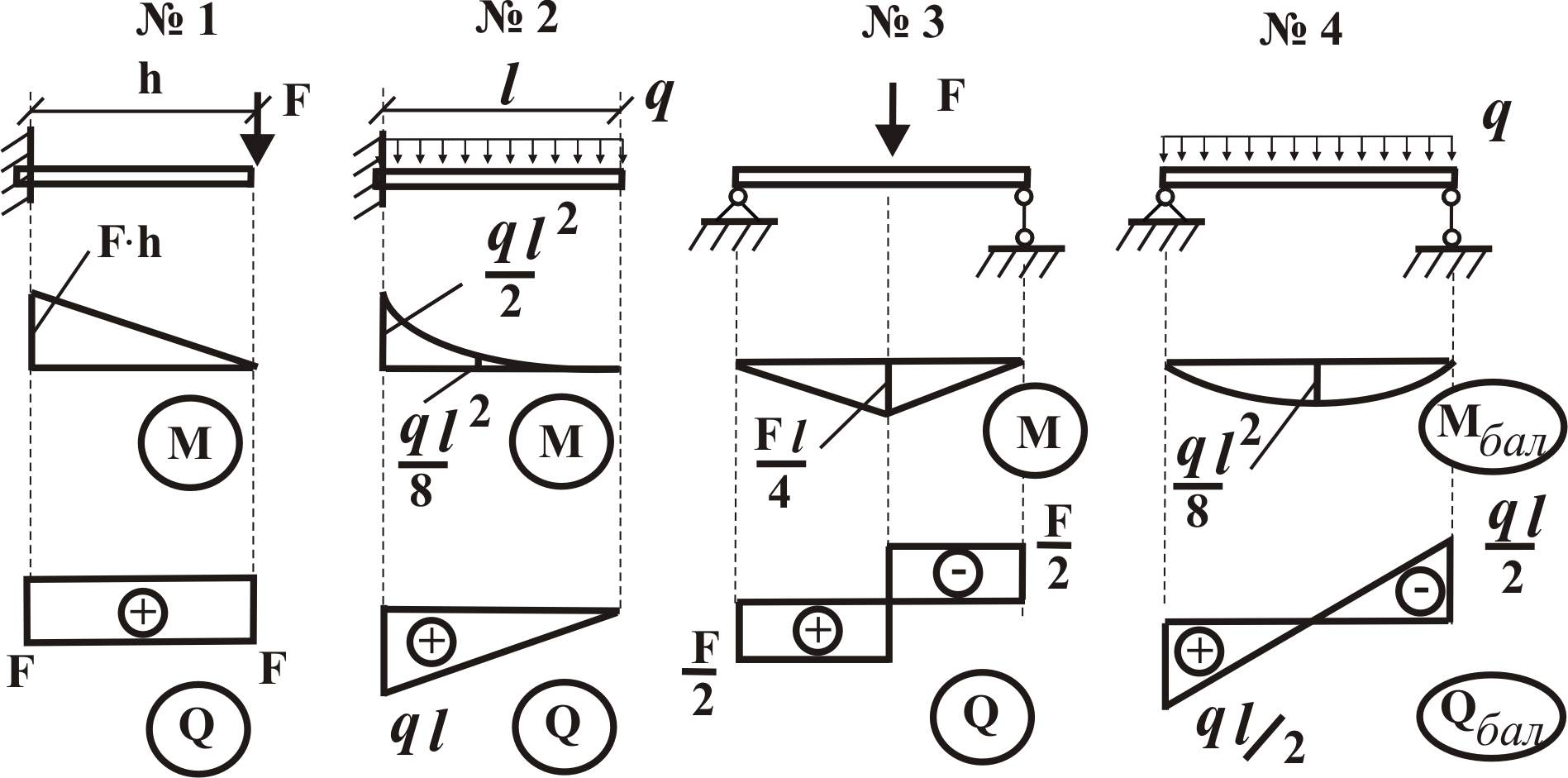 Не хватает только сопротивления.
Не хватает только сопротивления.
Обратите внимание на сходство между законом Ома и основным уравнением для прямой: y = mx + b , где m — наклон прямой.
Ток I соответствует x , а разность потенциалов V соответствует y . Таким образом, наклон этого графика соответствует сопротивлению, R .
Итак, Аарон обнаружил сопротивление своей лампочки! Он равен наклону графика зависимости тока от разности потенциалов, который в данном случае составляет 10 Ом.
Омические и неомические материалы
В случае Аарона, когда ток и разность потенциалов были нанесены на график, график образовывал прямую линию, а наклон линии был равен сопротивлению. Это означает, что электрическая лампочка Аарона имела Ом , что означает, что это материал, соответствующий закону Ома. Таким образом, если ток и разность потенциалов прямо пропорциональны, то резистор считается омическим.
Не все материалы подчиняются закону Ома.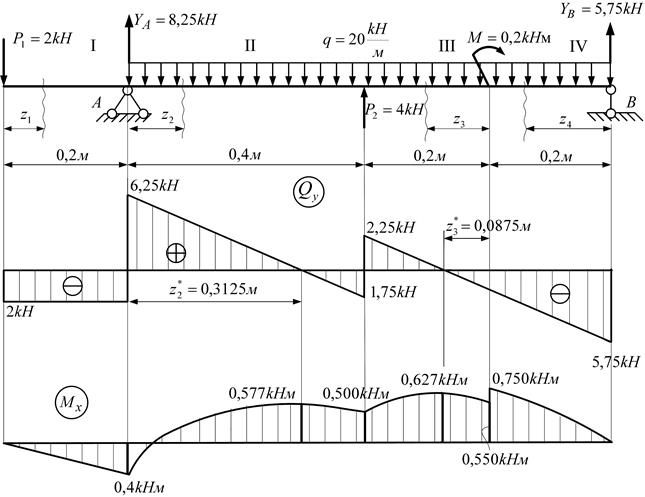 В некоторых случаях, когда вы строите график зависимости тока от разности потенциалов, он не будет образовывать прямую линию. В такой ситуации мы бы сказали, что этот материал неомический или материал, который не подчиняется закону Ома.
В некоторых случаях, когда вы строите график зависимости тока от разности потенциалов, он не будет образовывать прямую линию. В такой ситуации мы бы сказали, что этот материал неомический или материал, который не подчиняется закону Ома.
Краткое содержание урока
Омические материалы соответствуют закону Ома. Это означает, что если вы построите график разности потенциалов между ними в зависимости от тока через них, вы получите прямую линию. Если резистор омический, наклон линии наилучшего соответствия на графике зависимости тока от разности потенциалов будет равен сопротивлению.
Напротив, неомические материалы не демонстрируют этой прямой зависимости между током и напряжением и не подчиняются закону Ома. График зависимости тока от разности потенциалов для неомического материала не будет образовывать прямую линию, а вместо этого будет изогнутым.
11,2 Закон Ома | Электрические цепи
11,2 Закон Ома (ESBQ6)
временный текст Основными для электрических цепей являются три величины: ток, напряжение (потенциал
разница) и сопротивление .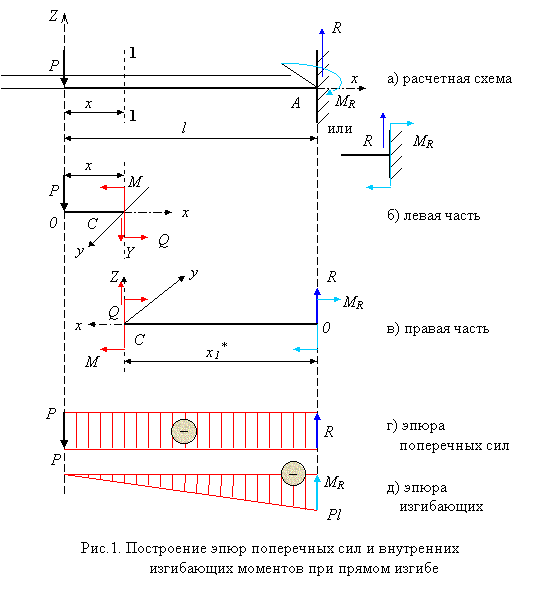 Напомним:
Напомним:
Электрический ток, \ (I \), определяется как скорость прохождения заряда через цепь.
Разность потенциалов или напряжение \ (В \) — это количество энергии на единицу заряда, необходимое для перемещения этого заряд между двумя точками в цепи.
Сопротивление, \ (R \), является мерой того, насколько «сложно» протолкнуть ток через элемент схемы.
Теперь посмотрим, как эти три величины связаны друг с другом в электрических цепях.
Георг обнаружил важную взаимосвязь между током, напряжением и сопротивлением в цепи. Саймона Ома и называется он законом Ома .
- Закон Ома
Количество электрического тока, проходящего через металлический проводник при постоянной температуре в цепи, составляет пропорциональна напряжению на проводнике и может быть описана как
\ (I = \ frac {V} {R} \)где \ (I \) — ток через проводник, \ (V \) — напряжение через проводник, а \ (R \) сопротивление проводника.
 Другими словами, при постоянной температуре сопротивление
проводник является постоянным, независимо от приложенного к нему напряжения или проходящего через него тока.
Другими словами, при постоянной температуре сопротивление
проводник является постоянным, независимо от приложенного к нему напряжения или проходящего через него тока.
Закон Ома говорит нам, что если проводник имеет постоянную температуру, ток, протекающий через проводник прямо пропорционален напряжению на нем. Это означает, что если мы нанесем напряжение на По оси X графика и тока по оси Y графика мы получим прямую.
Наклон прямолинейного графика связан с сопротивлением проводника как \ [\ frac {I} {V} = \ frac {1} {R} \] Это можно изменить с точки зрения постоянного сопротивления как: \ [R = \ frac {V} {I} \]
временный текстЗакон Ома
Цель
Для определения взаимосвязи между током, протекающим через резистор, и потенциалом
разность (напряжение) на одном и том же резисторе.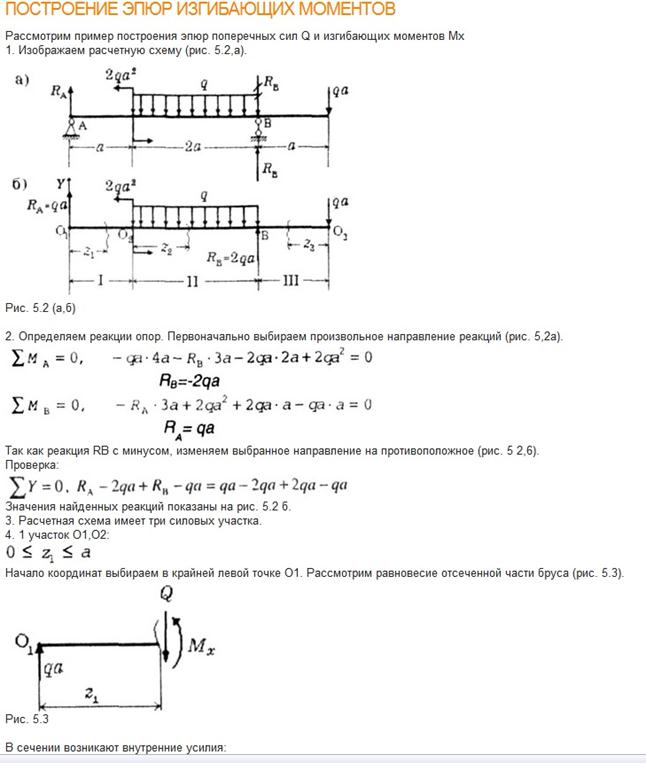
Аппарат
4 ячейки, 4 резистора, амперметр, вольтметр, соединительные провода
Метод
Этот эксперимент состоит из двух частей. В первой части мы будем изменять приложенное напряжение на резисторе. и измерить результирующий ток в цепи. Во второй части мы будем варьировать ток в цепи и измерьте полученное напряжение на резисторе.После получения обоих наборов измерения, мы рассмотрим взаимосвязь между током и напряжением на резистор.
Изменение напряжения:
Установите схему в соответствии со схемой 1), начиная с одной ячейки.
Нарисуйте следующую таблицу в своем лабораторном журнале.

Кол-во ячеек
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
\ (\ text {1} \)
\ (\ text {2} \)
\ (\ text {3} \)
\ (\ text {4} \)
Попросите учителя проверить электрическую цепь перед включением питания.
Измерьте напряжение на резисторе с помощью вольтметра, а ток в схему с помощью амперметра.
Добавьте в схему еще одну ячейку \ (\ text {1,5} \) \ (\ text {V} \) и повторите измерения.
Повторяйте, пока не получите четыре ячейки и не заполните таблицу.
Изменение тока:
Установите схему в соответствии со схемой 2), начиная только с 1 резистора в схема.
Нарисуйте следующую таблицу в своем лабораторном журнале.
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
Попросите учителя проверить вашу схему перед включением питания.

Измерьте ток и напряжение на единственном резисторе.
Теперь добавьте еще один резистор последовательно в цепь и измерьте ток и напряжение снова только на исходном резисторе. Продолжайте добавлять резисторы, пока не получите четыре последовательно, но не забывайте измерять напряжение только на исходном резистор каждый раз.Введите измеренные вами значения в таблицу.
Анализ и результаты
Используя данные, записанные в первой таблице, постройте график зависимости тока от напряжения. С напряжение — это переменная, которую мы изменяем напрямую, это независимая переменная.
 и будет нанесен на ось \ (x \).Текущий является зависимой переменной и должен быть
отложено по оси \ (y \).
и будет нанесен на ось \ (x \).Текущий является зависимой переменной и должен быть
отложено по оси \ (y \).Используя данные, записанные во второй таблице, постройте график зависимости напряжения от тока. В этом в случае, если независимая переменная — это ток, который должен быть нанесен на ось \ (x \), и напряжение является зависимой переменной и должно быть отложено по оси \ (y \).
Выводы
Изучите график, который вы построили из первой таблицы. Что происходит с током через резистор при увеличении напряжения на нем? т.е. увеличивается или уменьшается?
Изучите график, который вы построили на основе второй таблицы.
 Что происходит с напряжением на
резистор при увеличении тока через резистор? я.е. Увеличивается или уменьшается?
Что происходит с напряжением на
резистор при увеличении тока через резистор? я.е. Увеличивается или уменьшается?Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.
Вопросы и обсуждение
- Для каждого из ваших графиков вычислите градиент и по нему определите сопротивление оригинальный резистор. Получаете ли вы одно и то же значение, вычисляя его для каждого из ваших графиков?
Как бы вы попытались определить сопротивление неизвестного резистора, используя только мощность? блок питания, вольтметр и известный резистор \ (R_0 \)?
Закон Ома
Учебное упражнение 11. 1
1Постройте график напряжения (по оси X) и тока (по оси Y).
Какой тип графика вы получите (прямой, парабола, другая кривая)
прямая линия
Рассчитайте градиент графика.
Градиент графика (\ (m \)) — это изменение тока, деленное на изменение напряжение:
\ begin {align *} m & = \ frac {\ Delta I} {\ Delta V} \\ & = \ frac {(\ text {1,6}) — (\ text {0,4})} {(\ text {12}) — (\ text {3})} \\ & = \ текст {0,13} \ end {выровнять *} Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.
Да. График с прямой линией получается, когда мы строим график зависимости напряжения от тока.
Как бы вы попытались определить сопротивление неизвестного резистора, используя только мощность? питание, вольтметр и известный резистор \ (R_ {0} \)?
Вы начинаете с подключения известного резистора в цепь с источником питания.Теперь ваша очередь Считайте напряжение источника питания и запишите это.
Затем вы последовательно подключаете два резистора. Теперь вы можете проводить измерения напряжения. для каждого из резисторов.
Итак, мы можем найти напряжения для двух резисторов.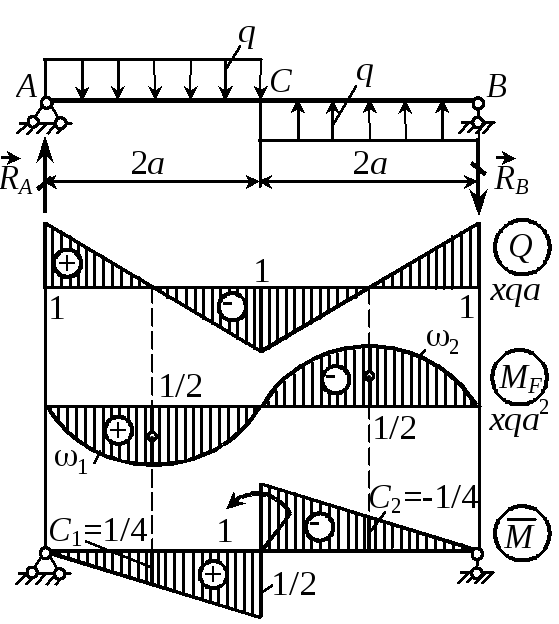 Теперь отметим, что:
Теперь отметим, что:
Итак, используя это и тот факт, что для резисторов, включенных последовательно, ток такой же везде в цепи мы можем найти неизвестное сопротивление.
\ begin {align *} V_ {0} & = IR_ {0} \\ I & = \ frac {V_ {0}} {R_ {0}} \\ V_ {U} & = IR_ {U} \\ I & = \ frac {V_ {U}} {R_ {U}} \\ \ frac {V_ {U}} {R_ {U}} & = \ frac {V_ {0}} {R_ {0}} \\ \ поэтому R_ {U} & = \ frac {V_ {U} R_ {0}} {V_ {0}} \ end {выровнять *}Омические и неомические проводники (ESBQ7)
Проводники, подчиняющиеся закону Ома, имеют постоянное сопротивление при изменении напряжения на них или
ток через них увеличивается. Эти проводники называются омическими проводниками . График
ток в зависимости от напряжения на этих проводниках будет прямолинейным. Некоторые примеры омических
жилы — резисторы цепи и нихромовая проволока.
Эти проводники называются омическими проводниками . График
ток в зависимости от напряжения на этих проводниках будет прямолинейным. Некоторые примеры омических
жилы — резисторы цепи и нихромовая проволока.
Как вы видели, когда мы говорим о законе Ома, есть упоминание о постоянной температуре . Этот происходит потому, что сопротивление некоторых проводников изменяется при изменении их температуры. Эти типы проводники называются неомическими проводниками , потому что они не подчиняются закону Ома.Лампочка распространенный пример неомического проводника. Другими примерами неомических проводников являются диоды и транзисторы.
В лампочке сопротивление нити накала резко возрастает по мере того, как она нагревается из комнаты.
температура до рабочей температуры. Если мы увеличим напряжение питания в реальной цепи лампы,
в результате увеличение тока вызывает повышение температуры нити, что увеличивает ее
сопротивление.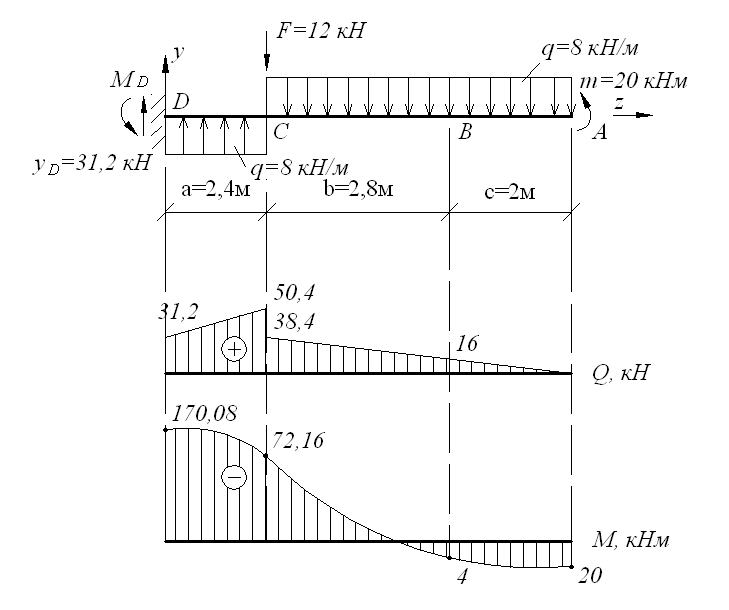 Это эффективно ограничивает увеличение тока. В этом случае напряжение и ток не изменяются.
подчиняться закону Ома.
Это эффективно ограничивает увеличение тока. В этом случае напряжение и ток не изменяются.
подчиняться закону Ома.
Явление изменения сопротивления при изменении температуры присуще почти всем металлам, из которых сделано большинство проводов. Для большинства приложений эти изменения сопротивления достаточно малы, чтобы их можно было игнорируется. При применении металлических ламп накаливания, температура которых сильно повышается (примерно до \ (\ text {1 000} \) \ (\ text {℃} \), и начиная с комнатной температуры) изменение довольно велико.
В общем, для неомических проводов график зависимости напряжения от тока не будет прямолинейным, указывает на то, что сопротивление не является постоянным для всех значений напряжения и тока.
Включен рекомендуемый эксперимент для неформальной оценки. В этом эксперименте учащиеся получат
данные о токе и напряжении для резистора и лампочки и определяют, какой из них подчиняется закону Ома. Ты будешь
нужны лампочки, резисторы, соединительные провода, источник питания, амперметр и вольтметр.Учащимся следует
обнаружите, что резистор подчиняется закону Ома, а лампочка — нет.
Ты будешь
нужны лампочки, резисторы, соединительные провода, источник питания, амперметр и вольтметр.Учащимся следует
обнаружите, что резистор подчиняется закону Ома, а лампочка — нет.
Проводники омические и неомические
Цель
Чтобы определить, подчиняются ли два элемента схемы (резистор и лампочка) закону Ома
Аппарат
4 ячейки, резистор, лампочка, провода соединительные, вольтметр, амперметр
Метод
Две схемы, показанные на схемах выше, одинаковы, за исключением того, что в первой резистор, а во втором — лампочка.Настройте обе схемы, указанные выше, начиная с 1 клетка. Для каждой цепи:
Измерьте напряжение на элементе схемы (резисторе или лампочке), используя вольтметр.

Измерить ток в цепи с помощью амперметра.
Добавьте еще одну ячейку и повторяйте измерения, пока в вашей цепи не будет 4 ячейки.
Результаты
Нарисуйте в своей книге две таблицы, которые выглядят следующим образом. У вас должна быть одна таблица для измерения первой цепи с резистором и еще одна таблица для второй схемы измерения с помощью лампочки.
Кол-во ячеек | Напряжение, В (\ (\ text {V} \)) | Ток, I (\ (\ text {A} \)) |
\ (\ text {1} \) | ||
\ (\ text {2} \) | ||
\ (\ text {3} \) | ||
\ (\ text {4} \) |
Анализ
Используя данные в ваших таблицах, нарисуйте два графика \ (I \) (\ (y \) — ось) vs. \ (V \) (\ (x \) — ось), одна
для резистора и один для лампочки.
\ (V \) (\ (x \) — ось), одна
для резистора и один для лампочки.
Вопросы и обсуждение
Внимательно изучите свои графики и ответьте на следующие вопросы:
Как должен выглядеть график зависимости \ (I \) от \ (V \) для проводника, подчиняющегося закону Ома?
Один или оба ваших графика выглядят так?
Какой можно сделать вывод о том, подчиняются ли резистор и / или лампочка резистору Ома? Закон?
Имеет ли лампочка омический или неомический провод?
Использование закона Ома (ESBQ8)
Теперь мы готовы увидеть, как закон Ома используется для анализа схем.
Рассмотрим схему с ячейкой и омическим резистором R. Если сопротивление резистора равно \ (\ text {5} \) \ (\ text {Ω} \) и напряжение на резисторе \ (\ text {5} \) \ (\ text {V} \), тогда мы можем использовать сопротивление Ома. Закон для расчета тока, протекающего через резистор. Наша первая задача — нарисовать схему диаграмма. При решении любой проблемы с электрическими цепями очень важно составить схему схему перед выполнением любых расчетов.Принципиальная схема этой проблемы выглядит следующим образом:
Уравнение закона Ома: \ [R = \ frac {V} {I} \]
, который можно преобразовать в: \ [I = \ frac {V} {R} \]
Ток, протекающий через резистор:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {5} \ text {V}} {\ text {5} \ Omega} \\ & = \ текст {1} \ текст {А} \ end {align *}
временный текстРабочий пример 1: Закон Ома
Изучите электрическую схему ниже:
Сопротивление резистора равно \ (\ text {10} \) \ (\ text {Ω} \), а ток, проходящий через
резистор — \ (\ text {4} \) \ (\ text {A} \). Какова разность потенциалов (напряжение) на
резистор?
Какова разность потенциалов (напряжение) на
резистор?
Определите, как подойти к проблеме
Нам задают сопротивление резистора и ток, проходящий через него, и просят рассчитать напряжение на нем. Мы можем применить закон Ома к этой проблеме, используя: \ [R = \ frac {V} {I}. \]
Решить проблему
Измените приведенное выше уравнение и замените известные значения на \ (R \) и \ (I \), чтобы найти \ (V \).\ begin {align *} R & = \ frac {V} {I} \\ R \ times I & = \ frac {V} {I} \ times I \\ V & = I \ раз R \\ & = \ текст {10} \ times \ text {4} \\ & = \ текст {40} \ текст {V} \ end {align *}
Напишите окончательный ответ
Напряжение на резисторе равно \ (\ text {40} \) \ (\ text {V} \).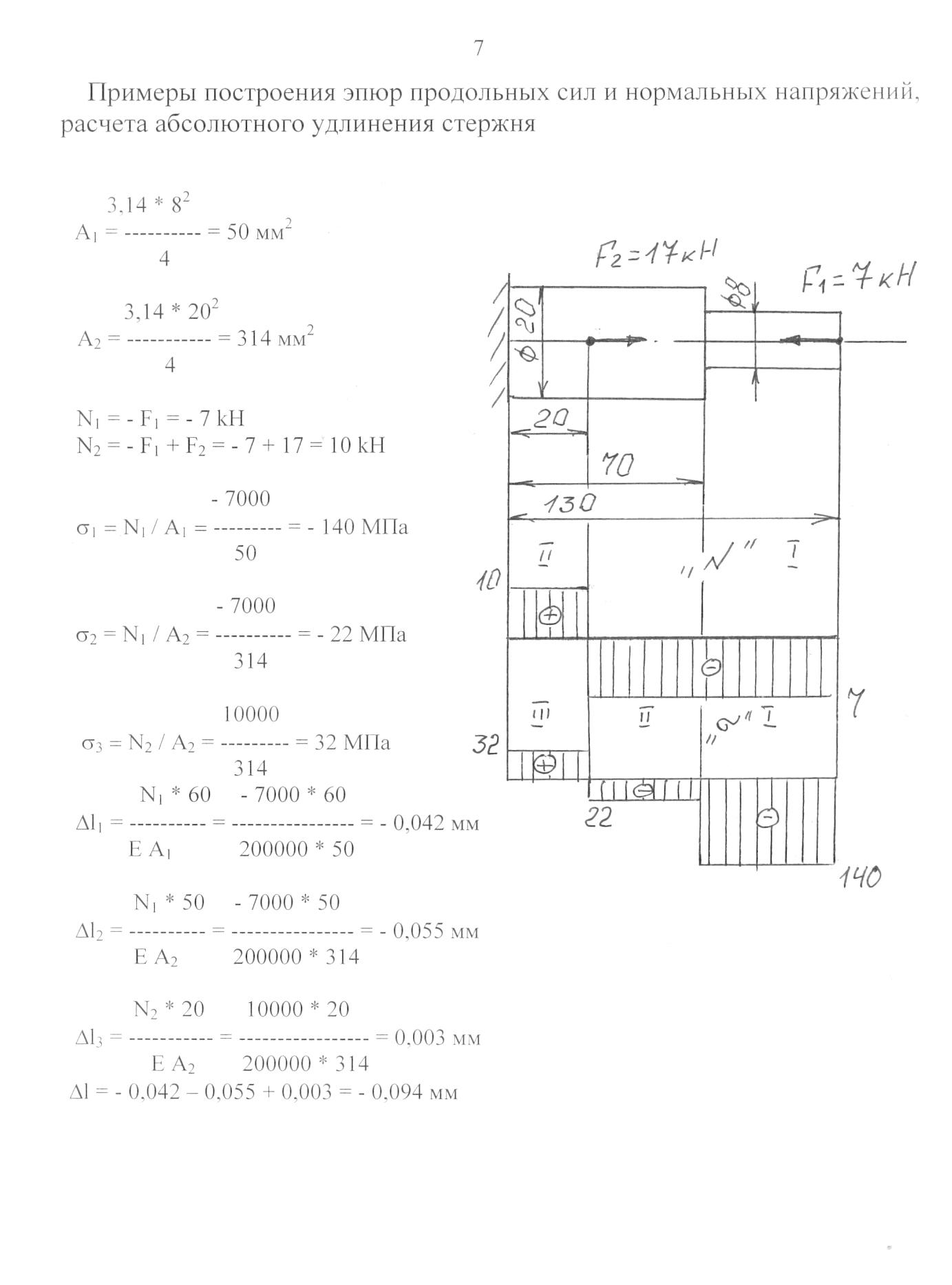
Закон Ома
Учебное упражнение 11.2Вычислите сопротивление резистора с разностью потенциалов \ (\ text {8} \) \ (\ text {V} \) через него, когда через него протекает ток \ (\ text {2} \) \ (\ text {A} \). Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {8} {2} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *} Какой ток будет протекать через резистор \ (\ text {6} \) \ (\ text {Ω} \) при наличии
разность потенциалов \ (\ text {18} \) \ (\ text {V} \) на концах? Нарисуйте схему
диаграмму перед расчетом.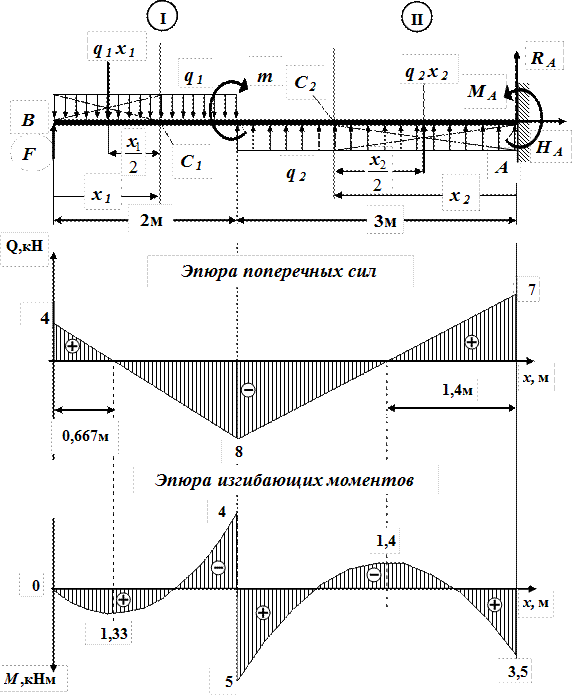
Сопротивление неизвестного резистора составляет:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {18} {6} \\ & = \ текст {3} \ текст {А} \ end {выровнять *}Какое напряжение на резисторе \ (\ text {10} \) \ (\ text {Ω} \), когда ток \ (\ text {1,5} \) \ (\ text {A} \) течет через него? Прежде чем приступить к работе, нарисуйте принципиальную схему. расчет.
Сопротивление неизвестного резистора составляет:
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {1,5}) (10) \\ & = \ текст {15} \ текст {V} \ end {выровнять *}Переплет резисторов последовательно и параллельно (ESBQ9)
В 10 классе вы узнали о резисторах и познакомились со схемами, в которых резисторы подключены в
последовательно и параллельно.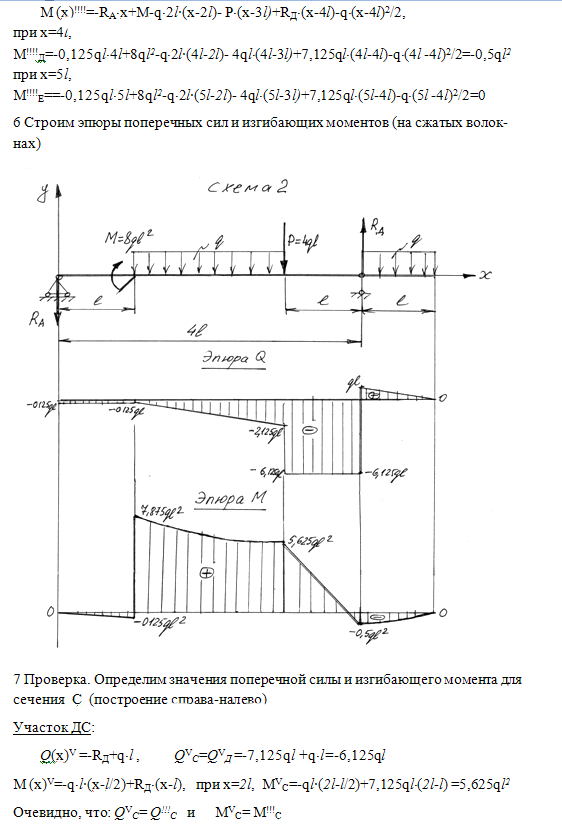 В последовательной цепи есть один путь, по которому течет ток. Параллельно
В цепи есть несколько путей, по которым течет ток.
В последовательной цепи есть один путь, по которому течет ток. Параллельно
В цепи есть несколько путей, по которым течет ток.
Когда в цепи более одного резистора, мы обычно можем рассчитать общую суммарную сопротивление всех резисторов. Это известно как сопротивление , эквивалентное .
Эквивалентное последовательное сопротивление
В цепи, в которой резисторы включены последовательно, эквивалентное сопротивление равно сумме сопротивлений всех резисторов.
- Эквивалентное сопротивление в последовательной цепи,
Для резисторов, включенных последовательно, эквивалентное сопротивление составляет:
\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + \ ldots + R_ {n} \]
Применим это к следующей схеме.
Резисторы включены последовательно, следовательно:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {3} \ text {Ω} + \ text {10} \ text {Ω} + \ text {5} \ text {Ω} \\ & = \ текст {18} \ текст {Ω} \ end {выровнять *}Эквивалентное параллельное сопротивление
В цепи, в которой резисторы включены параллельно, эквивалентное сопротивление определяется как
следующее определение.
- Эквивалентное сопротивление в параллельной цепи
Для резисторов \ (n \), включенных параллельно, эквивалентное сопротивление составляет:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ ldots + \ frac {1} {R_ {n}} \]
Применим эту формулу к следующей схеме.
Какое полное (эквивалентное) сопротивление в цепи?
\ begin {align *} \ frac {1} {R_ {p}} & = \ left (\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}) } \правильно) \\ & = \ left (\ frac {1} {\ text {10} \ text {Ω}} + \ frac {1} {\ text {2} \ text {Ω}} + \ frac {1} {\ text {1} \ text {Ω}} \ right) \\ & = \ left (\ frac {\ text {1} \ text {Ω} + \ text {5} \ text {Ω} + \ text {10} \ text { Ω}} {\ text {10} \ text {Ω}} \ right) \\ & = \ left (\ frac {\ text {16} \ text {Ω}} {\ text {10} \ text {Ω}} \ right) \\ R_ {p} & = \ text {0,625} \ text {Ω} \ end {выровнять *}Последовательное и параллельное сопротивление
Учебное упражнение 11.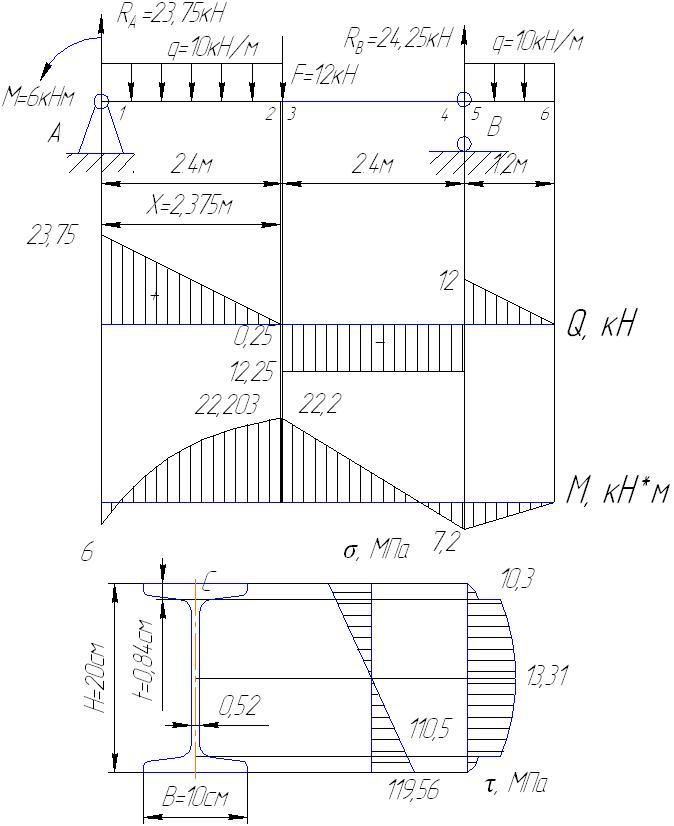 3
3Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) соединены последовательно. Рассчитать эквивалентное сопротивление.
Поскольку резисторы включены последовательно, можно использовать:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {10} \ text {kΩ} + \ text {10} \ text {kΩ} \\ & = \ текст {20} \ текст {кОм} \ end {выровнять *} Два резистора соединены последовательно.Эквивалентное сопротивление \ (\ text {100} \)
\ (\ текст {Ω} \). Если один резистор \ (\ text {10} \) \ (\ text {Ω} \), рассчитайте
номинал второго резистора.
Если один резистор \ (\ text {10} \) \ (\ text {Ω} \), рассчитайте
номинал второго резистора.
Поскольку резисторы включены последовательно, можно использовать:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ R_ {2} & = R_ {s} — R_ {1} \\ & = \ text {100} \ text {Ω} — \ text {10} \ text {Ω} \\ & = \ текст {90} \ текст {Ω} \ end {выровнять *} Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) подключены параллельно.Рассчитать
эквивалентное сопротивление.
Поскольку резисторы включены параллельно, можно использовать:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {100}} + \ frac {1} {\ text {10}} \\ & = \ frac {1 + 10} {\ text {100}} \\ & = \ frac {11} {\ text {100}} \\ R_ {p} & = \ text {9,09} \ text {kΩ} \ end {выровнять *} Два резистора подключены параллельно.Эквивалентное сопротивление \ (\ text {3,75} \)
\ (\ текст {Ω} \). Если один резистор имеет сопротивление \ (\ text {10} \) \ (\ text {Ω} \),
какое сопротивление у второго резистора?
Если один резистор имеет сопротивление \ (\ text {10} \) \ (\ text {Ω} \),
какое сопротивление у второго резистора?
Поскольку резисторы включены параллельно, можно использовать:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ \ frac {1} {R_ {2}} & = \ frac {1} {R_ {p}} — \ frac {1} {R_ {1}} \\ & = \ frac {1} {\ text {3,75}} — \ frac {1} {\ text {10}} \\ & = \ frac {\ text {10} — \ text {3,75}} {\ text {37,5}} \\ & = \ frac {\ text {6,25}} {\ text {37,5}} \\ R_ {2} & = \ текст {6} \ текст {Ω} \ end {выровнять *}Вычислите эквивалентное сопротивление в каждой из следующих цепей:
a) Резисторы включены параллельно, поэтому мы используем:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {3}} + \ frac {1} {\ text {2}} \\ & = \ frac {\ text {2} + \ text {3}} {\ text {6}} \\ & = \ frac {\ text {5}} {\ text {6}} \\ R & = \ текст {1,2} \ текст {Ω} \ end {выровнять *}b) Резисторы включены параллельно, поэтому мы используем:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \\ & = \ frac {1} {\ text {2}} + \ frac {1} {\ text {3}} + \ frac {1} {\ text {4}} + \ frac {1} {\ text { 1}} \\ & = \ frac {\ text {6} + \ text {4} + \ text {3} + \ text {12}} {\ text {12}} \\ & = \ frac {\ text {25}} {\ text {12}} \\ R & = \ text {0,48} \ text {Ω} \ end {выровнять *}c) Резисторы включены последовательно, поэтому мы используем:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}d) Резисторы включены последовательно, поэтому мы используем:
\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + R_ {4} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} + \ text {4} \ text {Ω} + \ текст {1} \ текст {Ω} \\ & = \ текст {10} \ текст {Ω} \ end {выровнять *}Использование закона Ома в последовательных и параллельных цепях (ESBQB)
Используя определения эквивалентного сопротивления для резисторов, включенных последовательно или параллельно, мы можем проанализировать
некоторые схемы с этими настройками.
Цепи серии
Рассмотрим схему, состоящую из трех резисторов и одного одиночная ячейка соединена последовательно.
Первый принцип, который нужно понять в отношении последовательных цепей, заключается в том, что величина тока одинакова. через любой компонент в цепи. Это потому, что существует только один путь для движения электронов. в последовательной цепи. По способу подключения аккумулятора мы можем сказать, в каком направлении ток будет течь.Мы знаем, что ток по условию течет от положительного к отрицательному. Общепринятый ток в этой цепи будет течь по часовой стрелке от точки A к B, от C к D и обратно к А.
Мы знаем, что в последовательной цепи ток должен быть одинаковым во всех компонентах. Итак, мы можем написать:
\ [I = I_ {1} = I_ {2} = I_ {3}. \]
\]Мы также знаем, что полное напряжение цепи должно быть равно сумме напряжений по всем три резистора.Итак, мы можем написать:
\ [V = V_ {1} + V_ {2} + V_ {3} \]Используя эту информацию и то, что мы знаем о вычислении эквивалентного сопротивления резисторов в серии, мы можем подойти к некоторым проблемам схемы.
Рабочий пример 2: Закон Ома, последовательная цепь
Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.
Определите, что требуется
Нам необходимо рассчитать ток, протекающий в цепи.
Определите, как подойти к проблеме
Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома.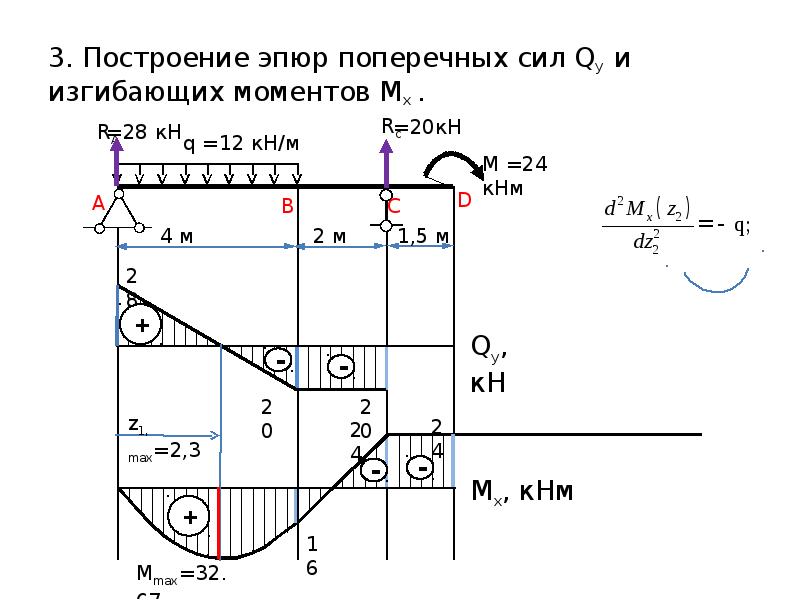 Однако есть два
резисторы в цепи и нам нужно найти общее сопротивление.
Однако есть два
резисторы в цепи и нам нужно найти общее сопротивление.
Найти полное сопротивление в цепи
Поскольку резисторы включены последовательно, общее (эквивалентное) сопротивление R составляет:
\ [R = R_ {1} + R_ {2} \]Следовательно,
\ begin {align *} R & = \ текст {2} + \ текст {4} \\ & = \ текст {6} \ текст {Ω} \ end {выровнять *}Применить закон Ома
\ begin {align *} R & = \ frac {V} {I} \\ R \ times \ frac {I} {R} & = \ frac {V} {I} \ times \ frac {I} {R} \\ I & = \ frac {V} {R} \\ & = \ frac {12} {6} \\ & = \ текст {2} \ текст {А} \ end {align *}
Напишите окончательный ответ
В цепи протекает ток \ (\ text {2} \) \ (\ text {A} \).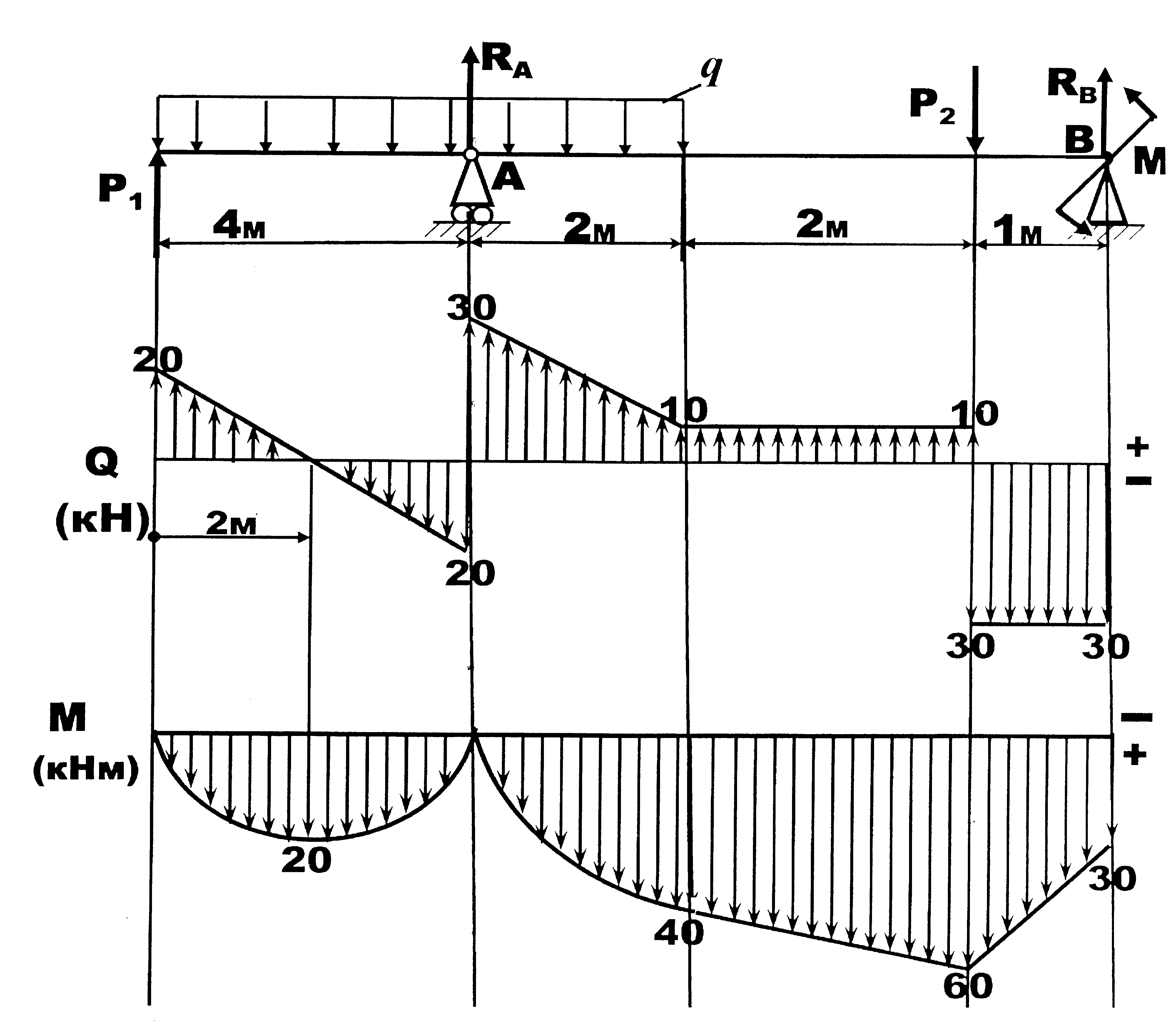
Рабочий пример 3: Закон Ома, последовательная цепь
Два омических резистора (\ (R_ {1} \) и \ (R_ {2} \)) соединены последовательно с ячейкой. Найди сопротивление \ (R_ {2} \), учитывая, что ток, протекающий через \ (R_ {1} \) и \ (R_ {2} \), равен \ (\ text {0,25} \) \ (\ text {A} \) и что напряжение на ячейке равно \ (\ text {1,5} \) \ (\ текст {V} \).\ (R_ {1} \) = \ (\ text {1} \) \ (\ text {Ω} \).
Нарисуйте схему и введите все известные значения.
Определите, как подойти к проблеме.
Мы можем использовать закон Ома, чтобы найти полное сопротивление R в цепи, а затем вычислить неизвестное сопротивление с использованием:
\ [R = R_ {1} + R_ {2} \], потому что он находится в последовательной цепи.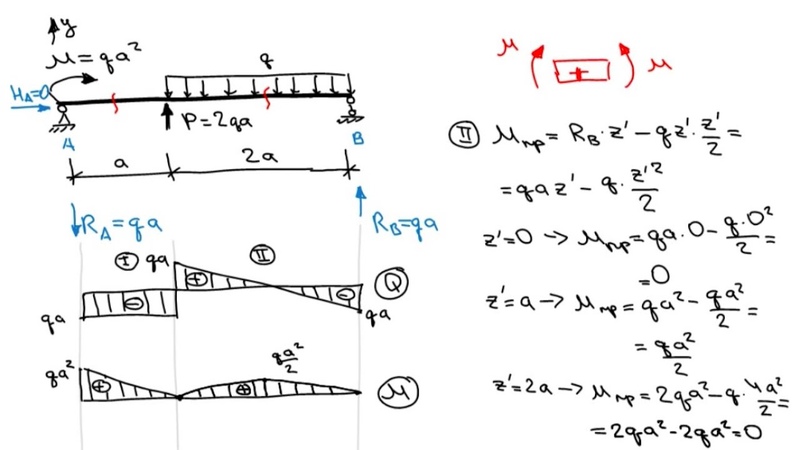
Найдите полное сопротивление
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {\ text {1,5}} {\ text {0,25}} \\ & = \ текст {6} \ текст {Ω} \ end {выровнять *}Найдите неизвестное сопротивление
Мы знаем, что:
\ [R = \ text {6} \ text {Ω} \]и что
\ [R_ {1} = \ text {1} \ text {Ω} \]с
\ [R = R_ {1} + R_ {2} \] \ [R_ {2} = R — R_ {1} \]Следовательно,
\ [R_ {1} = \ text {5} \ text {Ω} \]Рабочий пример 4: Закон Ома, последовательная цепь
Для следующей схемы рассчитайте:
падение напряжения \ (V_1 \), \ (V_2 \) и \ (V_3 \) на резисторах \ (R_1 \), \ (R_2 \), и \ (R_3 \)
сопротивление \ (R_3 \).
Определите, как подойти к проблеме
Нам даны напряжение на ячейке и ток в цепи, а также сопротивления двух из трех резисторов. Мы можем использовать закон Ома для расчета напряжения падение через известные резисторы. Поскольку резисторы включены в последовательную цепь, напряжение равно \ (V = V_1 + V_2 + V_3 \), и мы можем вычислить \ (V_3 \).Теперь мы можем использовать эту информацию для найти напряжение на неизвестном резисторе \ (R_3 \).
Рассчитать падение напряжения на \ (R_1 \)
Используя закон Ома: \ begin {align *} R_1 & = \ frac {V_1} {I} \\ I \ cdot R_1 & = I \ cdot \ frac {V_1} {I} \\ V_1 & = {I} \ cdot {R_1} \\ & = 2 \ cdot 1 \\ V_1 & = \ текст {2} \ текст {V} \ end {align *}
Рассчитать падение напряжения на \ (R_2 \)
Снова используя закон Ома: \ begin {align *} R_2 & = \ frac {V_2} {I} \\ I \ cdot R_2 & = I \ cdot \ frac {V_2} {I} \\ V_2 & = {I} \ cdot {R_2} \\ & = 2 \ cdot 3 \\ V_2 & = \ текст {6} \ текст {V} \ end {align *}
Рассчитать падение напряжения на \ (R_3 \)
Так как падение напряжения на всех резисторах вместе должно быть таким же, как и падение напряжения через ячейку в последовательной цепи, мы можем найти \ (V_3 \), используя: \ begin {align *} V & = V_1 + V_2 + V_3 \\ V_3 & = V — V_1 — V_2 \\ & = 18-2-6 \\ V_3 & = \ текст {10} \ текст {V} \ end {align *}
Найдите сопротивление \ (R_3 \)
Мы знаем напряжение на \ (R_3 \) и ток через него, поэтому мы можем использовать закон Ома, чтобы рассчитать значение сопротивления: \ begin {align *} R_3 & = \ frac {V_3} {I} \\ & = \ frac {10} {2} \\ R_3 & = \ text {5} \ Omega \ end {align *}
Напишите окончательный ответ
\ (V_1 = \ text {2} \ text {V} \)
\ (V_2 = \ text {6} \ text {V} \)
\ (V_3 = \ text {10} \ text {V} \)
\ (R_1 = \ text {5} \ Omega \)
временный текстПараллельные цепи
Рассмотрим схему, состоящую из одной ячейки и трех резисторов, соединенных параллельно.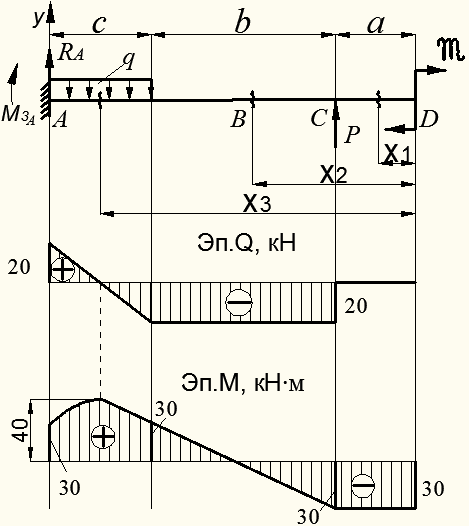
Первый принцип, который нужно понять в отношении параллельных цепей, заключается в том, что напряжение одинаково на всех компонентах в цепи. Это потому, что есть только два набора электрически общие точки в параллельной цепи и напряжение, измеренное между наборами общих точек всегда должны быть одинаковыми в любой момент времени. Итак, для показанной схемы верно следующее:
\ [V = V_ {1} = V_ {2} = V_ {3}.\]Второй принцип параллельной схемы состоит в том, что все токи, проходящие через каждый резистор, должны складываться. до полного тока в цепи:
\ [I = I_ {1} + I_ {2} + I_ {3}. \]Используя эти принципы и наши знания о том, как рассчитать эквивалентное сопротивление параллельной резисторов, теперь мы можем подойти к некоторым схемам, связанным с параллельными резисторами.
Рабочий пример 5: Закон Ома, параллельная цепь
Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.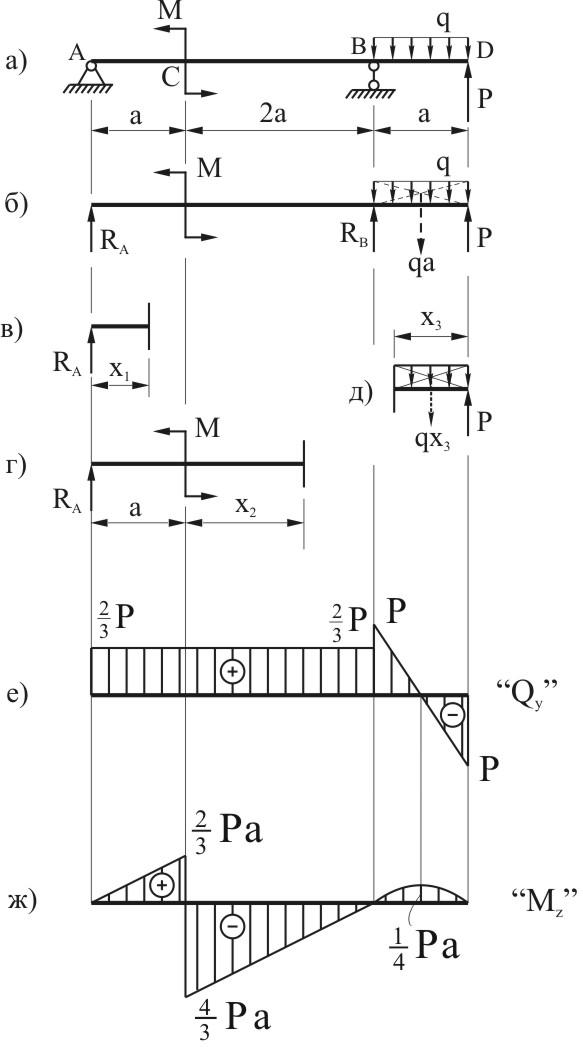
Определите, что требуется
Нам необходимо рассчитать ток, протекающий в цепи.
Определите, как подойти к проблеме
Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома. Однако есть два резисторы в цепи и нам нужно найти общее сопротивление.
Найдите эквивалентное сопротивление в цепи
Поскольку резисторы включены параллельно, общее (эквивалентное) сопротивление R составляет:
\ [\ frac {1} {R} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}}. \] \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\ & = \ frac {1} {2} + \ frac {1} {4} \\ & = \ frac {2 + 1} {4} \\ & = \ frac {3} {4} \\ \ text {Следовательно,} R & = \ text {1,33} \ Omega \ end {выровнять *}Применить закон Ома
\ begin {align *} R & = \ frac {V} {I} \\ R \ cdot \ frac {I} {R} & = \ frac {V} {I} \ cdot \ frac {I} {R} \\ I & = \ frac {V} {R} \\ I & = V \ cdot \ frac {1} {R} \\ & = (12) \ left (\ frac {3} {4} \ right) \\ & = \ текст {9} \ текст {А} \ end {выровнять *}Напишите окончательный ответ
В цепи протекает ток \ (\ text {9} \) \ (\ text {A} \).
Рабочий пример 6: Закон Ома, параллельная цепь
Два омических резистора (\ (R_1 \) и \ (R_2 \)) подключены параллельно ячейке. Найди сопротивление \ (R_2 \), учитывая, что ток, протекающий через ячейку, равен \ (\ text {4,8} \) \ (\ text {A} \) и что напряжение на ячейке равно \ (\ text {9} \) \ (\ text {V} \).
Определите, что требуется
Нам нужно рассчитать сопротивление \ (R_2 \).
Определите, как подойти к проблеме
Так как резисторы омические и нам даны напряжение на ячейке и ток через ячейку мы можем использовать закон Ома, чтобы найти эквивалентное сопротивление в цепи. \ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {9} {\ text {4,8}} \\ & = \ text {1,875} \ \ Omega \ end {align *}
Вычислить значение для \ (R_2 \)
Поскольку мы знаем эквивалентное сопротивление и сопротивление \ (R_1 \), мы можем использовать формулу
для резисторов, включенных параллельно, найти сопротивление \ (R_2 \).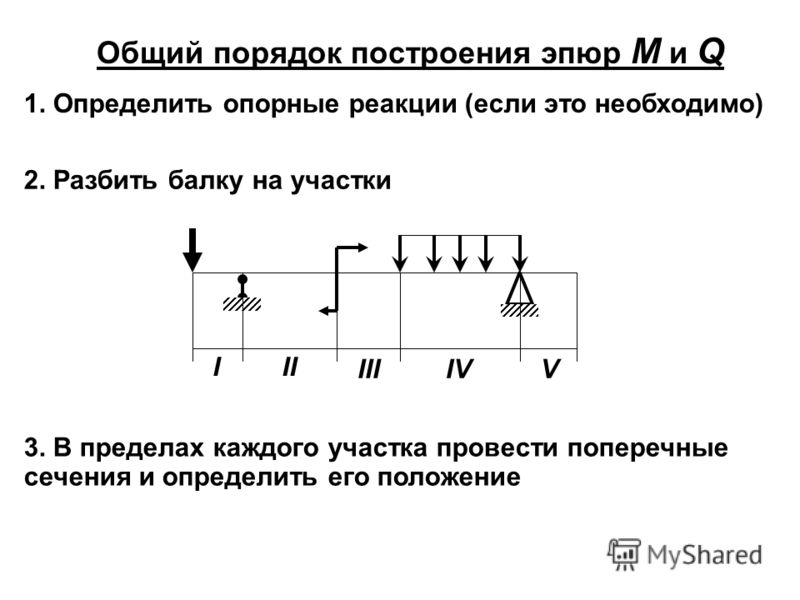 \ begin {align *}
\ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2}
\ end {выровнять *}
Переставляем решение для \ (R_2 \):
\ begin {align *}
\ frac {1} {R_2} & = \ frac {1} {R} — \ frac {1} {R_1} \\
& = \ frac {1} {\ text {1,875}} — \ frac {1} {3} \\
& = \ текст {0,2} \\
R_2 & = \ frac {1} {\ text {0,2}} \\
& = \ текст {5} \ \ Omega
\ end {align *}
\ begin {align *}
\ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2}
\ end {выровнять *}
Переставляем решение для \ (R_2 \):
\ begin {align *}
\ frac {1} {R_2} & = \ frac {1} {R} — \ frac {1} {R_1} \\
& = \ frac {1} {\ text {1,875}} — \ frac {1} {3} \\
& = \ текст {0,2} \\
R_2 & = \ frac {1} {\ text {0,2}} \\
& = \ текст {5} \ \ Omega
\ end {align *}
Напишите окончательный ответ
Сопротивление \ (R_2 \) равно \ (\ text {5} \) \ (\ Omega \)
temp textРабочий пример 7: Закон Ома, параллельная цепь
Ячейка 18 В подключена к двум параллельным резисторам \ (\ text {4} \) \ (\ Omega \) и
\ (\ text {12} \) \ (\ Omega \) соответственно. Рассчитайте ток через ячейку и через
каждый из резисторов.
Рассчитайте ток через ячейку и через
каждый из резисторов.
Сначала нарисуйте схему перед выполнением любых расчетов
Определите, как подойти к проблеме
Нам нужно определить ток через ячейку и каждый из параллельных резисторов. У нас есть задана разность потенциалов в ячейке и сопротивления резисторов, поэтому мы можем использовать закон Ома для расчета силы тока.
Рассчитать ток через ячейку
Чтобы рассчитать ток через ячейку, нам сначала нужно определить эквивалент сопротивление остальной части цепи. Резисторы включены параллельно и поэтому: \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\ & = \ frac {1} {4} + \ frac {1} {12} \\ & = \ frac {3 + 1} {12} \\ & = \ frac {4} {12} \\ R & = \ frac {12} {4} = \ text {3} \ \ Omega \ end {выровнять *} Теперь, используя закон Ома, чтобы найти ток через ячейку: \ begin {align *} R & = \ frac {V} {I} \\ I & = \ frac {V} {R} \\ & = \ frac {18} {3} \\ I & = \ text {6} \ text {A} \ end {align *}
Теперь определите ток через один из параллельных резисторов
Мы знаем, что для чисто параллельной схемы напряжение на ячейке такое же, как
напряжение на каждом из параллельных резисторов. Для этой схемы:
\ begin {align *}
V & = V_1 = V_2 = \ text {18} \ text {V}
\ end {выровнять *}
Начнем с расчета тока через \ (R_1 \) по закону Ома:
\ begin {align *}
R_1 & = \ frac {V_1} {I_1} \\
I_1 & = \ frac {V_1} {R_1} \\
& = \ frac {18} {4} \\
I_1 & = \ text {4,5} \ text {A}
\ end {align *}
Для этой схемы:
\ begin {align *}
V & = V_1 = V_2 = \ text {18} \ text {V}
\ end {выровнять *}
Начнем с расчета тока через \ (R_1 \) по закону Ома:
\ begin {align *}
R_1 & = \ frac {V_1} {I_1} \\
I_1 & = \ frac {V_1} {R_1} \\
& = \ frac {18} {4} \\
I_1 & = \ text {4,5} \ text {A}
\ end {align *}
Рассчитайте ток через другой параллельный резистор
Мы можем снова использовать закон Ома, чтобы найти ток в \ (R_2 \):
\ begin {align *}
R_2 & = \ frac {V_2} {I_2} \\
I_2 & = \ frac {V_2} {R_2} \\
& = \ frac {18} {12} \\
I_2 & = \ text {1,5} \ text {A}
\ end {выровнять *} Альтернативный метод вычисления \ (I_2 \) заключался бы в использовании того факта, что
токи через каждый из параллельных резисторов должны суммироваться с общим током через
клетка: \ begin {align *}
I & = I_1 + I_2 \\
I_2 & = I — I_1 \\
& = 6 — 4. 5 \\
I_2 & = \ text {1,5} \ text {A}
\ end {align *}
5 \\
I_2 & = \ text {1,5} \ text {A}
\ end {align *}
Напишите окончательный ответ
Ток через ячейку равен \ (\ text {6} \) \ (\ text {A} \).
Ток через резистор \ (\ text {4} \) \ (\ Omega \) равен \ (\ text {4,5} \) \ (\ text {A} \).
Ток через резистор \ (\ text {12} \) \ (\ Omega \) равен \ (\ text {1,5} \) \ (\ text {A} \).
Закон Ома в последовательной и параллельной цепях
Учебное упражнение 11.4Рассчитать номинал неизвестного резистора в цепи:
Сначала мы используем закон Ома для вычисления полного последовательного сопротивления:
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {9} {1} \\ & = \ текст {9} \ текст {Ω} \ end {выровнять *}Теперь мы можем найти неизвестное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ R_ {4} & = R_ {s} — R_ {1} — R_ {2} — R_ {3} \\ & = 9 — 3 — 3 — 1 \\ & = \ текст {2} \ текст {Ω} \ end {выровнять *}Рассчитайте значение тока в следующей цепи:
Сначала находим общее сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {1} + \ text {2,5} + \ text {1,5} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать ток:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {9} {5} \\ & = \ текст {1,8} \ текст {А} \ end {выровнять *} Три резистора с сопротивлением \ (\ text {1} \) \ (\ text {Ω} \), \ (\ text {5} \)
\ (\ text {Ω} \) и \ (\ text {10} \) \ (\ text {Ω} \) соответственно соединены в
серия с \ (\ text {12} \) \ (\ text {V} \) батареей.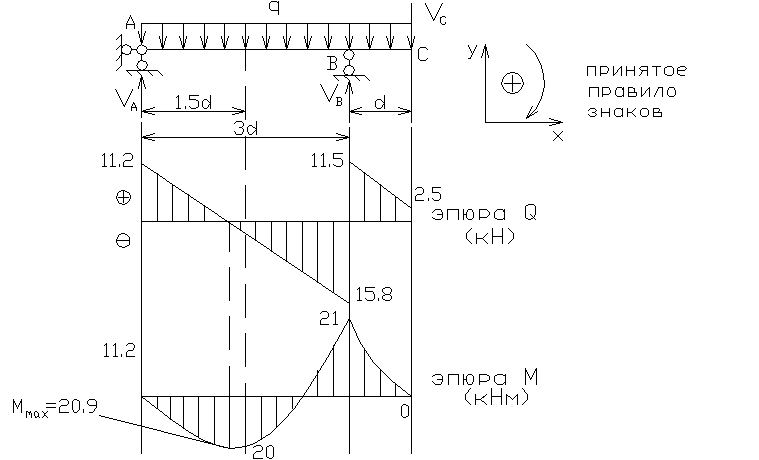 Рассчитайте значение тока в
схема.
Рассчитайте значение тока в
схема.
Рисуем принципиальную схему:
Теперь мы находим полное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ текст {1} + \ текст {5} + \ текст {10} \\ & = \ текст {16} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать ток:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {12} {16} \\ & = \ текст {0,75} \ текст {А} \ end {выровнять *} Рассчитайте ток через ячейку, если оба резистора омические по своей природе.
Сначала находим общее сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {1}} + \ frac {1} {\ text {3}} \\ & = \ frac {3 + 1} {\ text {3}} \\ & = \ frac {4} {\ text {3}} \\ & = \ текст {0,75} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать ток:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {9} {\ text {0,75}} \\ & = \ текст {12} \ текст {А} \ end {выровнять *}Вычислить номинал неизвестного резистора \ (R_ {4} \) в цепи:
Сначала находим общее сопротивление:
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {24} {\ text {2}} \\ & = \ текст {12} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать неизвестное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \\ \ frac {1} {R_ {4}} & = \ frac {1} {R_ {p}} — \ frac {1} {R_ {1}} — \ frac {1} {R_ {2}} — \ frac {1} {R_ {3}} \\ & = \ frac {1} {\ text {12}} — \ frac {1} {\ text {120}} — \ frac {1} {\ text {40}} — \ frac {1} {\ text {60}} \\ & = \ frac {10 — 1 — 3 — 2} {\ text {120}} \\ & = \ frac {4} {\ text {120}} \\ & = \ текст {30} \ текст {Ω} \ end {выровнять *}значение тока через АКБ
Рисуем принципиальную схему:
Чтобы вычислить значение тока через аккумулятор, нам сначала нужно вычислить эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {\ text {1}} + \ frac {1} {\ text {5}} + \ frac {1} {\ text {10}} \\ & = \ frac {10 + 2 + 1} {\ text {10}} \\ & = \ frac {13} {\ text {10}} \\ & = \ текст {0,77} \ текст {Ω} \ end {выровнять *}Теперь можем посчитать ток через батарею:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {0,77}} \\ & = \ текст {26} \ текст {А} \ end {выровнять *} значение тока в каждом из трех резисторов.
Для параллельной схемы напряжение на ячейке такое же, как и напряжение на каждой резисторов. Для этой схемы:
\ [V = V_ {1} = V_ {2} = V_ {3} = \ text {20} \ text {V} \]Теперь мы можем рассчитать ток через каждый резистор. Начнем с \ (R_ {1} \):
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {1}} \\ & = \ текст {20} \ текст {А} \ end {выровнять *}Затем мы вычисляем ток через \ (R_ {2} \):
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {5}} \\ & = \ текст {4} \ текст {А} \ end {выровнять *}И наконец вычисляем ток через \ (R_ {3} \):
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {10}} \\ & = \ текст {2} \ текст {А} \ end {выровнять *} Вы можете проверить, что они в сумме составляют общий ток.
Последовательные и параллельные сети резисторов (ESBQC)
Теперь, когда вы знаете, как работать с простыми последовательными и параллельными цепями, вы готовы к работе со схемами. которые объединяют эти две схемы, например, следующую схему:
Рисунок 11.1: Пример последовательно-параллельной сети. Пунктирными прямоугольниками обозначены параллельные участки цепи. Проработать такие схемы относительно легко, потому что вы используете все, что у вас уже есть.
узнал о последовательных и параллельных цепях. Единственная разница в том, что вы делаете это поэтапно. На рисунке 11.1 схема состоит из двух параллельных частей.
которые затем последовательно с ячейкой. Чтобы вычислить эквивалентное сопротивление для схемы, вы начнете с
вычисление общего сопротивления каждой из параллельных частей, а затем сложение этих сопротивлений в
ряд.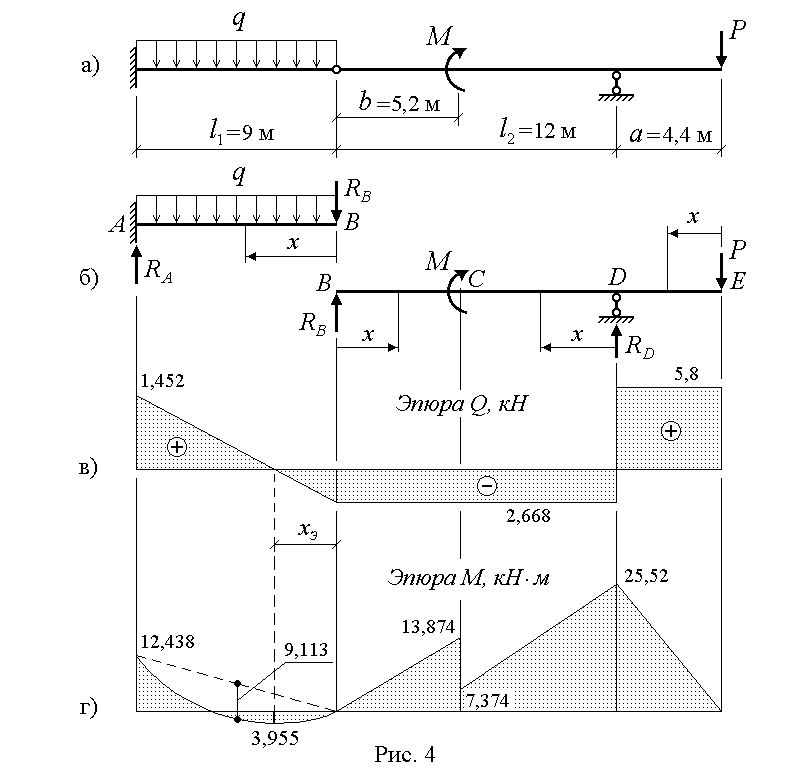 {- 1} \\
& = \ текст {5} \, \ Omega
\ end {align *}
{- 1} \\
& = \ текст {5} \, \ Omega
\ end {align *}
Теперь вы можете рассматривать схему как простую последовательную схему следующим образом:
Следовательно, эквивалентное сопротивление: \ begin {align *} R & = R_ {p1} + R_ {p2} \\ & = 5 + 5 \\ & = 10 \, \ Omega \ end {align *}
Эквивалентное сопротивление цепи на Рисунке 11.1 это \ (\ текст {10} \) \ (\ текст {Ω} \).
временный текстПоследовательные и параллельные сети
Учебное упражнение 11.5Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {4} + \ frac {1} {2} \\ & = \ frac {3} {4} \\ R_ {p} & = \ text {1,33} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\ begin {align *} R_ {s} & = R_ {3} + R_ {p} \\ & = \ текст {2} + \ текст {1,33} \\ & = \ текст {3,33} \ текст {Ω} \ end {выровнять *}Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {1} + \ frac {1} {2} \\ & = \ frac {3} {2} \\ R_ {p} & = \ text {0,67} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с тремя последовательно включенными резисторами, поэтому мы можем рассчитать эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {3} + R_ {4} + R_ {p} \\ & = \ текст {4} + \ текст {6} + \ текст {0,67} \\ & = \ текст {10,67} \ текст {Ω} \ end {выровнять *}Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,652} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ & = \ текст {2} + \ текст {0,652} \\ & = \ текст {2,652} \ текст {Ω} \ end {выровнять *} ток \ (I \) через ячейку.
Чтобы найти ток \ (I \), нам сначала нужно найти эквивалентное сопротивление. Мы начинаем путем вычисления эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,652} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ & = \ текст {2} + \ текст {0,652} \\ & = \ текст {2,652} \ текст {Ω} \ end {выровнять *}Значит, ток через ячейку:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {12}} {\ text {2,652}} \\ & = \ текст {4,52} \ текст {А} \ end {выровнять *} ток через резистор \ (\ text {5} \) \ (\ text {Ω} \).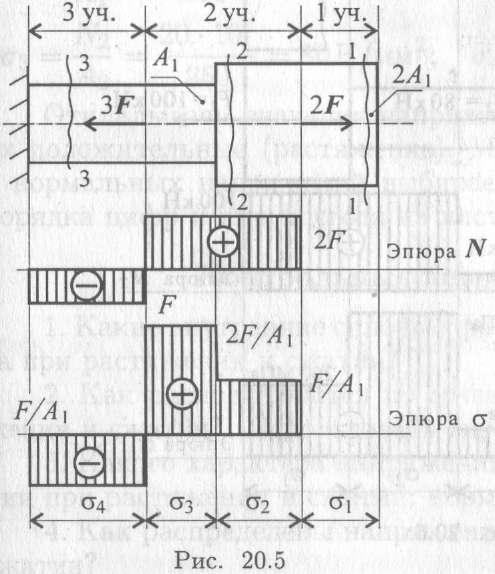
Ток через параллельную комбинацию резисторов равен \ (\ text {4,52} \) \ (\ текст {A} \). (Сила тока одинакова при последовательной комбинации резисторов и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение через параллельную комбинацию резисторов. (не забудьте использовать эквивалентное параллельное сопротивление, а не эквивалентное сопротивление цепи):
\ begin {align *} V & = I \ cdot R \\ & = (\ text {4,52}) (\ text {0,652}) \\ & = \ текст {2,95} \ текст {V} \ end {выровнять *} Поскольку напряжение на каждом резисторе в параллельной комбинации одинаковое, это
также является напряжением на резисторе \ (\ text {5} \) \ (\ text {Ω} \).
Итак, теперь мы можем рассчитать ток через резистор:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {2,95}} {\ text {5}} \\ & = \ текст {0,59} \ текст {А} \ end {выровнять *}Если ток, протекающий через ячейку, равен \ (\ text {2} \) \ (\ text {A} \), и все резисторы являются омическими, рассчитайте напряжение на ячейке и на каждом из резисторов \ (R_1 \), \ (R_2 \) и \ (R_3 \) соответственно.
Чтобы найти напряжение, нам сначала нужно найти эквивалентное сопротивление.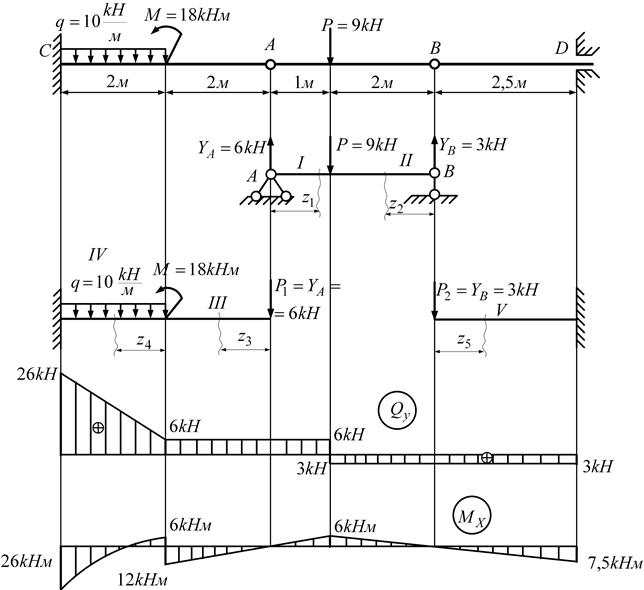 Мы начинаем с
расчет эквивалентного сопротивления параллельной комбинации:
Мы начинаем с
расчет эквивалентного сопротивления параллельной комбинации:
Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {p} \\ & = \ text {4,66} + \ text {1,33} \\ & = \ текст {5,99} \ текст {Ω} \ end {выровнять *}Значит, напряжение на ячейке:
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {5,99}) \\ & = \ текст {12} \ текст {V} \ end {выровнять *} Ток через параллельную комбинацию резисторов равен \ (\ text {2} \) \ (\ text {A} \). (Ток одинаков при последовательной комбинации резисторов, и мы можем рассмотреть
весь параллельный набор резисторов как один последовательный резистор.)
(Ток одинаков при последовательной комбинации резисторов, и мы можем рассмотреть
весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение на каждом из резисторов. Начнем с поиска напряжение на \ (R_ {1} \):
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {4,66}) \\ & = \ текст {9,32} \ текст {V} \ end {выровнять *}Теперь находим напряжение на параллельной комбинации:
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {1,33}) \\ & = \ текст {2,66} \ текст {V} \ end {выровнять *} Поскольку напряжение на каждом резисторе в параллельной комбинации одинаково, это
также напряжение на резисторах \ (R_ {2} \) и \ (R_ {3} \).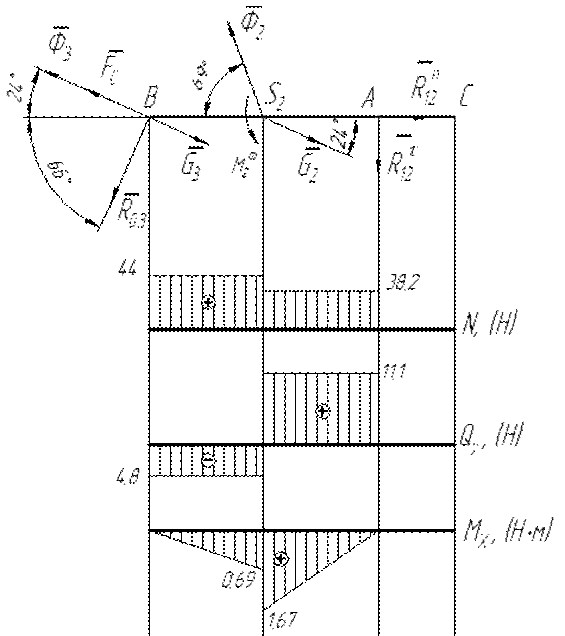
ток через ячейку
Чтобы найти ток, нам сначала нужно найти эквивалентное сопротивление. Мы начинаем с расчет эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {1} + \ frac {1} {1} \\ & = 2 \\ R_ {p} & = \ text {0,5} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {4} + R_ {p} \\ & = \ text {2} + \ text {1,5} + \ text {0,5} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}Значит, ток через ячейку:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {10}} {\ text {4}} \\ & = \ текст {2,5} \ текст {А} \ end {выровнять *}падение напряжения на \ (R_4 \)
Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).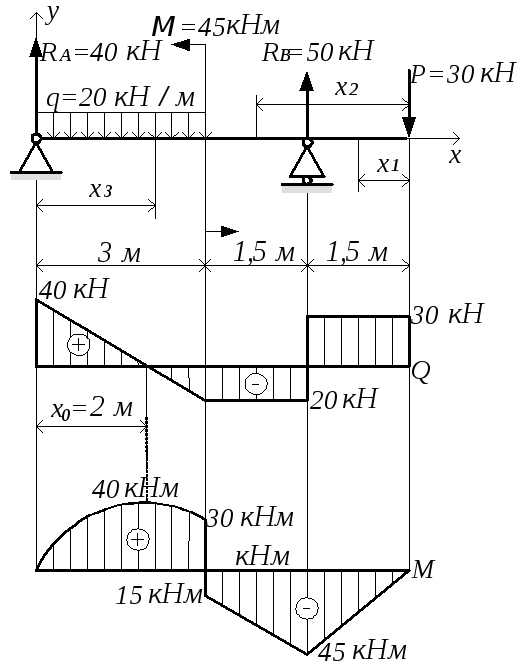 (Текущий
то же самое через последовательные комбинации резисторов, и мы можем рассмотреть все
параллельный набор резисторов как один последовательный резистор.)
(Текущий
то же самое через последовательные комбинации резисторов, и мы можем рассмотреть все
параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение через \ (R_ {4} \):
\ begin {align *} V & = I \ cdot R \\ & = (\ text {2,5}) (\ text {1,5}) \\ & = \ текст {3,75} \ текст {V} \ end {выровнять *}ток через \ (R_2 \)
Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Текущий
то же самое через последовательные комбинации резисторов, и мы можем рассмотреть все
параллельный набор резисторов как один последовательный резистор. )
)
Используя это, мы можем найти ток через \ (R_ {2} \).
Сначала нам нужно найти напряжение на параллельной комбинации:
\ begin {align *} V & = I \ cdot R \\ & = (\ text {2,5}) (\ text {0,5}) \\ & = \ текст {1,25} \ текст {V} \ end {выровнять *}Теперь мы можем найти ток через \ (R_ {2} \), используя тот факт, что напряжение равно то же самое на каждом резисторе в параллельной комбинации:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {1,25}} {\ text {1}} \\ & = \ текст {1,25} \ текст {А} \ end {выровнять *}Учебное пособие по физике: электрическое сопротивление
Электрон, движущийся по проводам и нагрузкам внешней цепи, встречает сопротивление. Сопротивление — помеха прохождению заряда. Для электрона путешествие от терминала к терминалу не является прямым маршрутом. Скорее, это зигзагообразный путь, который возникает в результате бесчисленных столкновений с неподвижными атомами в проводящем материале. Электроны сталкиваются с сопротивлением — препятствием для их движения. В то время как разность электрических потенциалов, установленная между двумя выводами , способствует перемещению заряда , а препятствует перемещению заряда .Скорость, с которой заряд проходит от терминала к терминалу, является результатом совместного действия этих двух величин.
Сопротивление — помеха прохождению заряда. Для электрона путешествие от терминала к терминалу не является прямым маршрутом. Скорее, это зигзагообразный путь, который возникает в результате бесчисленных столкновений с неподвижными атомами в проводящем материале. Электроны сталкиваются с сопротивлением — препятствием для их движения. В то время как разность электрических потенциалов, установленная между двумя выводами , способствует перемещению заряда , а препятствует перемещению заряда .Скорость, с которой заряд проходит от терминала к терминалу, является результатом совместного действия этих двух величин.
Поток заряда по проводам часто сравнивают с потоком воды по трубам. Сопротивление потоку заряда в электрической цепи аналогично эффектам трения между водой и поверхностями трубы, а также сопротивлению, создаваемому препятствиями, присутствующими на ее пути. Именно это сопротивление препятствует потоку воды и снижает как ее расход, так и скорость дрейфа . Подобно сопротивлению потоку воды, общее сопротивление потоку заряда в проводе электрической цепи зависит от некоторых четко идентифицируемых переменных.
Именно это сопротивление препятствует потоку воды и снижает как ее расход, так и скорость дрейфа . Подобно сопротивлению потоку воды, общее сопротивление потоку заряда в проводе электрической цепи зависит от некоторых четко идентифицируемых переменных.
Во-первых, общая длина проводов влияет на величину сопротивления. Чем длиннее провод, тем большее сопротивление будет. Существует прямая зависимость между величиной сопротивления, с которым сталкивается заряд, и длиной провода, который он должен пройти.В конце концов, если сопротивление возникает в результате столкновений между носителями заряда и атомами провода, то, вероятно, столкновений будет больше в более длинном проводе. Больше столкновений означает большее сопротивление.
Во-вторых, на величину сопротивления влияет площадь поперечного сечения проводов. Более широкие провода имеют большую площадь поперечного сечения. Вода будет течь по более широкой трубе с большей скоростью, чем по узкой. Это можно объяснить меньшим сопротивлением, которое присутствует в более широкой трубе. Таким же образом, чем шире провод, тем меньше будет сопротивление прохождению электрического заряда. Когда все другие переменные одинаковы, заряд будет проходить с большей скоростью через более широкие провода с большей площадью поперечного сечения, чем через более тонкие провода.
Таким же образом, чем шире провод, тем меньше будет сопротивление прохождению электрического заряда. Когда все другие переменные одинаковы, заряд будет проходить с большей скоростью через более широкие провода с большей площадью поперечного сечения, чем через более тонкие провода.
Третья переменная, которая, как известно, влияет на сопротивление потоку заряда, — это материал, из которого сделан провод. Не все материалы одинаковы с точки зрения их проводящей способности. Некоторые материалы являются лучшими проводниками, чем другие, и обладают меньшим сопротивлением потоку заряда.Серебро — один из лучших проводников, но никогда не используется в проводах бытовых цепей из-за своей стоимости. Медь и алюминий являются одними из наименее дорогих материалов с подходящей проводящей способностью, позволяющей использовать их в проводах бытовых цепей. На проводящую способность материала часто указывает его удельное сопротивление . Удельное сопротивление материала зависит от электронной структуры материала и его температуры.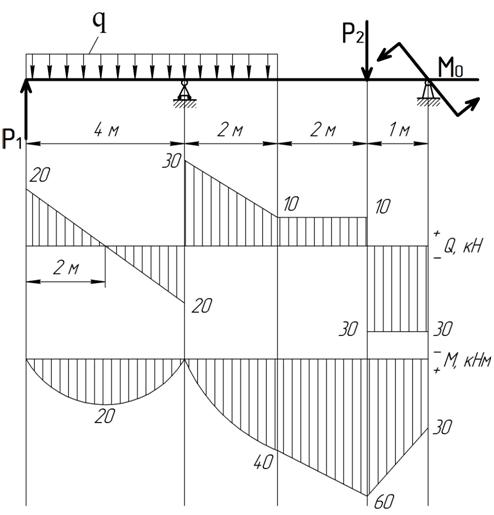 Для большинства (но не для всех) материалов удельное сопротивление увеличивается с повышением температуры.В таблице ниже приведены значения удельного сопротивления для различных материалов при температуре 20 градусов Цельсия.
Для большинства (но не для всех) материалов удельное сопротивление увеличивается с повышением температуры.В таблице ниже приведены значения удельного сопротивления для различных материалов при температуре 20 градусов Цельсия.
Материал | Удельное сопротивление (Ом • метр) |
Серебро | 1,59 х 10 -8 |
Медь | 1.7 х 10 -8 |
Золото | 2,2 х 10 -8 |
Алюминий | 2,8 х 10 -8 |
Вольфрам | 5,6 х 10 -8 |
Утюг | 10 х 10 -8 |
Платина | 11 х 10 -8 |
Свинец | 22 х 10 -8 |
Нихром | 150 х 10 902 10-8 |
Углерод | 3. 5 х 10 -5 5 х 10 -5 |
Полистирол | 10 7 — 10 11 |
Полиэтилен | 10 8 — 10 9 |
Стекло | 10 10 — 10 14 |
Твердая резина | 10 13 |
Как видно из таблицы, существует широкий диапазон значений удельного сопротивления для различных материалов.Материалы с более низким удельным сопротивлением обладают меньшим сопротивлением потоку заряда; они лучшие дирижеры. Материалы, показанные в последних четырех строках вышеприведенной таблицы, обладают таким высоким удельным сопротивлением, что их даже нельзя рассматривать как проводники.
Посмотри! Используйте виджет Resistivity of a Material , чтобы найти удельное сопротивление данного материала. Введите название материала и нажмите кнопку Submit , чтобы узнать его удельное сопротивление. Математическая природа сопротивления
Введите название материала и нажмите кнопку Submit , чтобы узнать его удельное сопротивление. Математическая природа сопротивления Сопротивление — это числовая величина, которую можно измерить и выразить математически. Стандартной метрической единицей измерения сопротивления является ом, представленный греческой буквой омега -. Электрическое устройство с сопротивлением 5 Ом будет представлено как R = 5 . Уравнение, представляющее зависимость сопротивления ( R ) проводника цилиндрической формы (например,, провод) от влияющих на него переменных составляет
, где L представляет длину провода (в метрах), A представляет площадь поперечного сечения провода (в метрах 2 ) и представляет удельное сопротивление материала (в Ом • метр). В соответствии с приведенным выше обсуждением это уравнение показывает, что сопротивление провода прямо пропорционально длине провода и обратно пропорционально площади поперечного сечения провода. Как показано в уравнении, знание длины, площади поперечного сечения и материала, из которого изготовлен провод (и, следовательно, его удельного сопротивления), позволяет определить сопротивление провода.
Как показано в уравнении, знание длины, площади поперечного сечения и материала, из которого изготовлен провод (и, следовательно, его удельного сопротивления), позволяет определить сопротивление провода.
— один из наиболее распространенных компонентов в электрических цепях. На большинстве резисторов нанесены цветные полосы или полосы. Цвета отображают информацию о значении сопротивления.Возможно, вы работаете в лаборатории и вам нужно знать сопротивление резистора, используемого в лаборатории. Используйте виджет ниже, чтобы определить значение сопротивления по цветным полосам.
1. В бытовых цепях часто используются провода двух разной ширины: 12-го и 14-го калибра. Проволока 12-го калибра имеет диаметр 1/12 дюйма, а проволока 14-го калибра — 1/14 дюйма.Таким образом, провод 12-го калибра имеет более широкое сечение, чем провод 14-го калибра. Схема на 20 ампер, используемая для настенных розеток, должна быть подключена с использованием провода 12-го калибра, а цепь на 15 ампер, используемая для цепей освещения и вентиляторов, должна быть подключена с помощью провода 14-го калибра. Объясните физику, лежащую в основе такого электрического кода.
Схема на 20 ампер, используемая для настенных розеток, должна быть подключена с использованием провода 12-го калибра, а цепь на 15 ампер, используемая для цепей освещения и вентиляторов, должна быть подключена с помощью провода 14-го калибра. Объясните физику, лежащую в основе такого электрического кода.
2. Основываясь на информации, изложенной в предыдущем вопросе, объясните риск, связанный с использованием провода 14-го калибра в цепи, которая будет использоваться для питания 16-амперной пилы.
3. Определите сопротивление медного провода 12 калибра длиной 1 милю. Дано: 1 миля = 1609 метров и диаметр = 0,2117 см.
4. Два провода — A и B — круглого сечения, имеют одинаковую длину и изготовлены из одного материала. Тем не менее, сопротивление провода A в четыре раза больше, чем у провода B.Во сколько раз диаметр проволоки B больше диаметра проволоки A?
ДЛЯ ОПРЕДЕЛЕНИЯ СОПРОТИВЛЕНИЯ НА СМ ДАННОГО ПРОВОДА Путем построения графика потенциальной разницы от тока
Необходимые материалы: Провод сопротивления, вольтметр, амперметр, батарея, реостат, шкала измерителя, односторонний ключ, соединительные провода и т. Д.
Д.
Теория: Если I — ток, текущий через проводник, а V — разность потенциалов на его концах, то согласно закону Ома
V∝I или
В = RI
Где, R — коэффициент пропорциональности.Это известно как сопротивление проводника.
В / I = R
R зависит от материала, температуры и размеров проводника.
Процедура:
1. Очистите концы соединительных проводов наждачной бумагой, чтобы удалить с них изоляционное покрытие. Подключите различные компоненты — сопротивление, реостат, аккумулятор, ключ, вольтметр и амперметр
3. Отметьте, совпадают ли стрелки миллиамперметра и вольтметра с нулевой отметкой на шкале измерения.Если это не так, отрегулируйте указатель так, чтобы он совпал с нулевой меткой, отрегулировав винт, расположенный рядом с основанием иглы, с помощью отвертки.
4. Отметьте диапазон и наименьшее значение счетчика данных вольтметра и миллиамперметра.
5. Вставьте ключ K и сдвиньте контакт реостата к одному из его крайних концов, чтобы ток, проходящий через резистивный провод, был минимальным.