Задачи на растяжение-сжатие | ПроСопромат.ру

Стальной ступенчатый брус нагревается на 50˚. Построить эпюры N, σ, δ и проверить прочность при [σ]=160МПа.

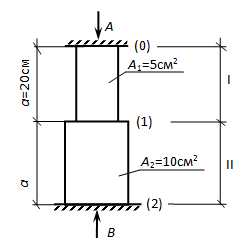
В процессе нагрева брус стремится к увеличению своей длины, но опоры этому препятствуют. Поэтому естественно предположить возникновение опорных реакций, направленных навстречу друг другу (см. схему). Для их определения имеем одно-единственное уравнение статики:

∑ у= — A+ В = 0.                                   (1)

Здесь два неизвестных, поэтому задача статически неопределима, и для получения дополнительного уравнения нужно сформулировать условие совместности деформаций двух участков бруса. Очевидно, что в условиях двух жёстко закрепленных концов длина бруса измениться не может и, следовательно,

абсолютная деформация его должна равняться нулю:

∆ℓ=∆ℓ_I+∆ℓ_II=0.

Известно, что в статически неопределимых системах, испытывающих температурное воздействие, абсолютная деформация складывается из силовой части и температурной, то есть

В нашем случае:

В частности, ℓ₁=ℓ₂=а, α₁=α₂=α и Е₁=Е₂=Е.

С учетом этих соотношений подстановка в условие совместности деформаций даст:

откуда после сокращений имеем:

Это и есть (2) второе (дополнительное уравнение).

Далее методом сечений выразим неизвестные внутренние силы N₁ и  N₂ через неизвестные опорные реакции (лучше через одну из них):

 

∑

у = — A— N₁ = 0, откуда: N₁ = — А.

∑у = — A— N₂ = 0, откуда: N₂ = — А.

С учетом этих соотношений уравнение (2) примет вид:

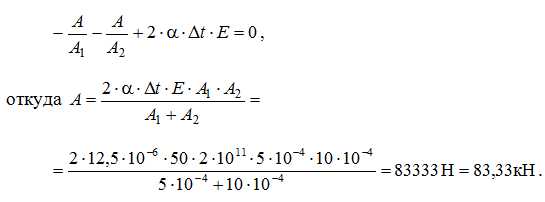
Тогда N₁= N₂=-83,33кН (сжатие).

Напряжения:

Таким образом, верхняя часть бруса испытывает перенапряжение на

а в нижней части условие прочности выполняется.

Перемещение защемленного верхнего сечения (0) равно нулю: δ(0)=0.

Перемещение границы участков (1) определяется абсолютной деформацией верхнего участка бруса:

Перемещение нижнего сечения (2) определяется ради контроля:

Результаты расчета представляются в виде эпюр:

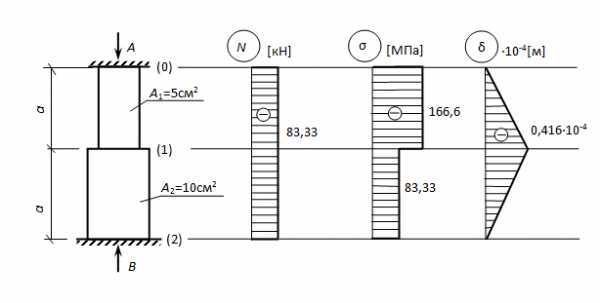
prosopromat.ru

Задачи на растяжение-сжатие | ПроСопромат.ру

Ступенчатый брус защемлен  обоими концами. Проверить прочность  бруса, если [σ]_стали=160МПа, [σ]_меди=120МПа, Е_стали=2·10¹¹Па, Е_меди=1·10¹¹Па.

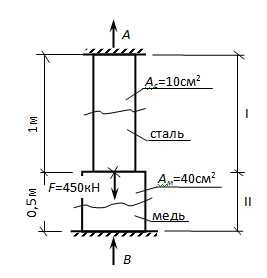
В каждой из двух опор возможно возникновение опорных реакций. Направления их нам неизвестны. Поэтому принимаем произвольные, но обязательно показываем эти принятые направления реакций на схеме

(А и В).

Далее «разбиваем» брус на участки. В дополнение к вышесказанному, за границы участков, кроме точек приложения внешних сил и мест резкого изменения размеров сечений, следует принимать и места, где изменяется вид материала.

В данном случае все эти три признака совпали в одном месте, и поэтому число участков два (на схеме Ι и ΙΙ).

При расчёте брусьев начинать следует с определения опорных реакций, для чего составляется уравнение статики:

∑у = A– F+ B= 0.                                                                                          (1)

В этом одном уравнении две неизвестных силы: А и В. Потребуется дополнительное уравнение, выражающее мысль о совместности деформаций участков бруса I и II. А условие совместности деформаций при наличии двух защемлений по концам состоит в невозможности изменения общей длины бруса (или в отсутствии удлинения): ∆

ℓ=0.

Полное удлинение ∆ℓ складывается из удлинений участков: ∆ℓ=∆ℓ_I+∆ℓ_II.

Если учесть, что участки I и II отличаются и длиной, и размером поперечных сечений, и даже видом материала, то:

Это и есть дополнительное (геометрическое) уравнение (2).

Правда, если судить формально, то уравнения (1) и (2) не образуют системы совместных уравнений, поскольку включают в себя разные неизвестные: в уравнении (1) это реакции А и В, а в уравнении (2) – усилия N₁ и N₂. Чтобы исключить это несоответствие, следует воспользоваться методом сечений и выразить неизвестные усилия через неизвестные опорные реакции.

Так, мысленно разрезав брус в произвольном сечении I участка и рассматривая равновесие

верхней части, найдем:

∑у = A— N₁ = 0, откуда N₁ = А

А разрезав брус в произвольном сечении II участка и рассмотрев равновесие опять же верхней части, будем иметь:

∑у = A– F— N₂ = 0,

откуда N₂ = А — F

Если подставить найденные выражения в уравнение (2), то из него сразу найдем значение реакции «А», а из записанных выше соотношений  узнаем величины усилий N₁ и N₂.

Итак:

Тогда:

Прежде чем подставить исходные данные, полезно отметить важнейшие особенности

расчета и свойства статически неопределимых конструкций:

1. Невозможно определить численные значения усилий в элементах (участках) статически неопределимых систем, если заранее не задаваться соотношениями жесткостей этих элементов и размеров, т.е.

2. В статически неопределимых системах «более жесткий» элемент «принимает на себя» большую долю общей нагрузки. И происходит это автоматически. Если, например, нам хочется «облегчить» работу какому-то элементу конструкции, то достаточно сделать его менее жестким (уменьшить модуль упругости или площадь сечения…)

Возвращаясь к задаче, подставляем исходные данные и находим:

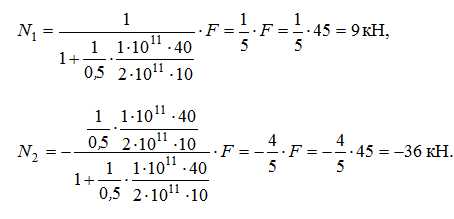
Для проверки прочности вычисляем напряжения и сравниваем их с допускаемыми для каждого материала:

Оба условия прочности выполняются.

 

 

prosopromat.ru

Задачи на растяжение-сжатие | ПроСопромат.ру

Определить грузоподъемность (допускаемую нагрузку [F]) шарнирно-стержневой системы для двух случаев:

1. Если материал стержней пластичный (сталь – 3, [σ]=160 МПа),
2. Если материал стержней хрупкий (чугун — [σ_р]=20 МПа, [σ_с]=80МПа).

Сначала необходимо найти усилия в стержнях, оставляя нагрузку в общем (буквенном) виде. Начинаем с использования метода сечений: делаем сквозной (замкнутый) разрез и рассматриваем равновесие средней части (неизвестные усилия при этом предполагаем положительными, т.е. растягивающими):

∑х =

Н = 0,       (1)

∑у = R+N₁— F—N₂=0,    (2)

∑М(А)= N₁·1 — F·2 – N₂·3=0, (3)

В этих трёх уравнениях статики содержатся 4 неизвестных, следовательно, задача один раз статически неопределима. Для раскрытия статической неопределимости придётся составить одно дополнительное уравнение, но уже не статическое, а геометрическое, которое выражало бы условие совместности деформаций всех упругих элементов системы. С этой целью следует рассмотреть систему в деформированном состоянии с тем, чтобы «связать» друг с другом абсолютные деформации первого и второго стержней. Картина возможной деформации системы:

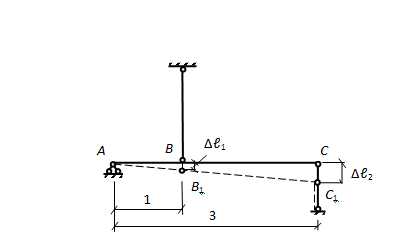
Очевидно, что ВВ₁ – удлинение первого стержня (∆ℓ₁), а СС₁ – укорочение второго (∆ℓ₂). Из подобия треугольников

или

По формуле Гука:

(знак «плюс» соответствует деформации удлинения), а

(знак «минус» соответствует деформации укорочения). После подстановки получим необходимое нам дополнительное уравнение:

      (4)

Т.к. ℓ₁=2ℓ, ℓ₂=ℓ, А₁= 2см², А₂= 4см², то

,

откуда N₂=-12N₁. Подставляя это соотношение в уравнение (3), имеем: N₁·1- F·2 — (-12N₁

) 3=0, откуда

(растяжение), и тогда

(сжатие).

Напряжения в стержнях будут:

Для определения допускаемой нагрузки используем условия прочности при растяжении-сжатии.

Случай 1. Оба стержня из пластичного материала, который одинаково сопротивляется как растяжению, так и сжатию. Для него достаточно одного условия прочности:

|_maxσ| ≤ [σ].

Наибольшим по абсолютной величине оказывается напряжение во втором стержне. Его и вводим в условие прочности. Допускаемая нагрузка (или грузоподъёмность) – это такая величина нагрузки, при которой напряжение в точности равно допускаемому значению (т.е. в условии прочности необходимо оставить знак равенства)

Случай 2. Оба стержня из хрупкого материала. В этом случае требуется выполнение двух условий прочности: а) по растяжению: _maxσ_р ≤ [σ_р],

б) по сжатию |_maxσ_с| ≤ [σ_с].

Начинать можно с любого из них. Например, из первого условия:

найдём одно значение допускаемой нагрузки (по растяжению):

Если принять это значение за допускаемую нагрузку, то во втором стержне возникает напряжение

Это напряжение превышает допускаемое значение по сжатию: |σ_II| =120МПа > [σ_р]=80МПа, следовательно, нагрузка [F_р] не является допускаемой для всей конструкции. Поэтому будем определять допускаемую нагрузку из второго условия прочности: Остается лишь убедиться, что при такой нагрузке в первом стержне условие прочности будет выполнено.

что меньше допускаемого по растяжению напряжения [σ_р]=20МПа. Итак, для варианта стержней из хрупкого материала допускаемая нагрузка [F]=49,333 кН.

 

prosopromat.ru

Внецентренное сжатие-растяжение | ПроСопромат.ру

Задача :

Чугунная опора круглого сечения подвергается действию сжимающей силы в точке К. Требуется:1) определить допускаемое (безопасное) значение сжимающей силы [F], если [σc]=120МПа, [σр]=120МПа, 2) сравнить эту нагрузку с допускаемой при центральном сжатии опоры.

Решение:

Это определены моменты инерции и квадраты радиусов инерции сечения

1)                 Чтобы составить условие прочности, надо знать положение нулевой линии в сечении. Поэтому вычисляем отрезки, которые она отсекает от главных центральных осей х и у:

Следовательно, Н.Л. параллельна оси у. Так как нулевая пересекает сечения, то в нем образуется две зоны: сжимающая (в данном случае располагается справа от Н.Л.) и растягивающая (слева от Н.Л.), как это и показано на эпюре напряжений.

 

Наиболее удаленной от нулевой линии в сжатой зоне сечения оказывается точка А, где и возникает наибольшее сжимающее напряжение, а наиболее удаленной от нулевой линии в растянутой зоне оказывается точка В, где возникает наибольшее растягивающее напряжение.

Что понимать под допускаемым значением нагрузки? По физическому смыслу это такое значение нагрузки, при котором в наиболее опасной точке напряжение в точности равно допускаемой величине, и во всех других точках условие прочности выполняется.

Поскольку при внецентренном нагружении возможны напряжения разных знаков, то приходится допускаемую нагрузку вычислить дважды: один раз из условия прочности по сжатию, а затем из условия прочности по растяжению. Из этих двух значений действительно допускаемой (безопасной) нагрузкой является меньшая по величине. Итак, первое значение [Fc] найдем из условия прочности по сжатию:

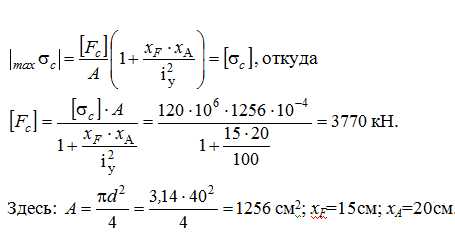
Второе значение [Fр]= — из условия прочности по растяжению:

Здесь: xВ=-20cм.

Из двух значений принимаем меньшее. При таком значении нагрузки ни в одной точке сечения напряжения не превысят допускаемых значений (ни в сжатой, ни в растянутой зоне). Итак, допускаемое (безопасное) значение сжимающей нагрузки [F]=2512кН.

2)                 Найдем, какова величина допускаемой нагрузки для той же самой опоры в случае ее центрального нагружения. В этом случае следует использовать условие прочности для центрального сжатия:

Это в  раз  больше, чем при внецентренном нагружении.

 

prosopromat.ru

Сопромат задачи на растяжение сжатие примеры решения

В треугольнике ABC AC=BC, AD высота, угол BAD равен 28. Найдите угол C. Решение: AC=BC треугольник ABC равнобедренный, углы A и B равны. Найдем угол B из прямоугольного треугольника ABD 90-28=62 180-62-62=56. Ответ: 56. Отправить по электронной почтеНаписать об этом в.

Примеры решения задач по сопромату

Приветствую тебя, читатель сайта — sopromats. ru, на котором размещено много полезной и интересной информации о сопромате и не только. Сегодня я решил написать большую статью о примерах решения задач по сопромату, которые размещены на этом ресурсе. Все примеры было решено классифицировать на три категории: по виду деформации, по виду рассчитываемого объекта и по типу расчета. Эти категории имеют три уровня вложенности. Например, в категории — по виду деформации входят задачи, связанные с изгибом, кручением, растяжением (сжатием) и сложным сопротивлением. В свою очередь, решения на изгиб классифицируются на статически определимые и неопределимые. Для того, чтобы найти нужную категорию перемещайтесь по указанным ссылкам на страничках. Также хотелось бы отметить, что на данный момент на сайте преобладают рукописные примеры решения. Но наша команда, активно работает над добавлением электронных материалов: с качественными схемами и набранными в цифровом виде расчетами. По мере развития сайта, все рукописные записи, планируется заменить цифровыми. Ну что же перейдем непосредственно к нашим примерам.

Классификация по виду деформации

Как уже говорилось выше, здесь все примеры отсортированы по виду деформации: растяжению и сжатию, кручению, изгибу и сложному сопротивлению. В категорию задач на сложное сопротивление попадают такие популярные решения на такие темы как изгиб с кручением, внецентренное растяжение (сжатие), косой изгиб. Теперь давайте перейдем непосредственно к категориям и не забывайте переходить по ссылкам на интересующую вас подкатегории.

Что можно найти в данной категории задач?

определение реакций в опорах из уравнений равновесия статики; расчет ВСФ методом сечений; вычисление продольной и поперечной силы; расчет изгибающего момента; расчет нормальных и касательных напряжений; вычисление перемещений поперечных сечений; раскрытие статической неопределимости с использованием уравнения совместности деформации.

Растяжение и сжатие

статически определимые брусья; статически неопределимые брусья; статически определимые стержневые системы; статически неопределимые стержневые системы.

Примеры задач на кручение распределены по 2 основным категориям:

статически определимое кручение; статически неопределимое кручение.

Задачи на изгиб подразделяются по тем же признакам:

статически определимый изгиб; статически неопределимый изгиб.

Классификация по типу рассчитываемого объекта

В этом разделе все решения распределены по типу рассчитываемого объекта: на балки, рамы, фермы и т. д. Каждая представленная здесь категория имеет укрупненную классификацию, которую можно изучить, перейдя по соответствующим ссылкам.

Решения, связанные с балками, можно разделить на две основные подкатегории:

статически определимые балки; статически неопределимые балки.

статически определимые валы; статически неопределимые валы.

статически определимые рамы; статически неопределимые рамы.

Все примеры решения задач, связанные с расчетом ферм, решено было поместить в одну большую категорию. В этой категории можно встретить задачи на:

определение реакций в опорах фермы; определение продольных усилий в стержнях методом вырезания узлов, либо методом Риттера; построение линий влияния.

В разделе про сечения, связанные с расчетом геометрических характеристик, принята следующая классификация:

симметричные и несимметричные сечения, состоящие из геометрических примитивов; симметричные и несимметричные сечения, состоящие из металлопрокатных профилей.

Классификация по типу расчета

В этом разделе материалы разделены по типу расчета. Сюда попали расчеты на прочность, жесткость и устойчивость. Здесь же находятся задачи, связанные с расчетом напряжений, эпюр внутренних силовых факторов и другие.

В этой категории находятся задачи, связанные с расчетом прочности, при различных видах деформации: изгибе, кручении, растяжении (сжатии) и сложном сопротивлении. Здесь можно встретить как проверочные, так и проектировочные расчета. Найти расчеты на грузоподъемность какой-либо системы.

В расчетах на жесткость, можно найти задачах, в которых исследуются различные элементы конструкций: балки, рамы, валы и другие. Во всех задачах проверяется жесткость, путем сравнения расчетных значений перемещений с допустимыми значениями.

Устойчивость

В примерах на устойчивость, можно найти задачи, связанные с подбором сечения стоек из условия устойчивости, либо расчетом грузоподъемности.

Данная категория, связанна с расчетом эпюр внутренних силовых факторов, при различных видах деформации: растяжении и сжатии, кручении, изгибе и сложном сопротивлении. Есть эпюры, которые откладываются со стороны растянутых волокон (строителям) и сжатых волокон (машиностроителям).

Сопромат задачи на растяжение сжатие примеры решения

Растяжение и сжатие. Усилия в поперечном сечении стержня.

Центральным растяжением или сжатием в сопромате называется такой вид деформации, при

poiskvstavropole.ru

Расчеты на прочность при осевом растяжении (сжатии). Типы задач при расчете на прочность

Условие прочности при растяжении (сжатии):,где

 —площадь поперечного сечения; — максимальная продольная сила;

 —максимальное нормальное напряжение;  или — допускаемое напряжение   

Если расчет ведется по методу предельных состояний,то  в расчет вместо допускаемого напряжения вводится расчетное сопротивление материала R.

Три типа задач при расчете на прочность при растяжении (сжатии)

1. Проверочный расчет 

2. Проектный расчет или подбор сечения

3. Определение допускаемой нагрузки 

Запись опубликована 19.04.2015 автором admin в рубрике Растяжение — Сжатие.

prosopromat.ru

Задачи по сопромату на растяжение-сжатие с решением

Площадь боковой поверхности усеченной пирамиды можно найти, зная апофему (высоту грани) – то есть высоту трапеции в данном случае, и стороны оснований – пирамиды и трапеции одновременно. Имея эти данные, мы найдем площадь одной грани по формуле площади трапеции и умножим на.

Примеры решения задач по сопромату

Приветствую тебя, читатель сайта — sopromats. ru, на котором размещено много полезной и интересной информации о сопромате и не только. Сегодня я решил написать большую статью о примерах решения задач по сопромату, которые размещены на этом ресурсе. Все примеры было решено классифицировать на три категории: по виду деформации, по виду рассчитываемого объекта и по типу расчета. Эти категории имеют три уровня вложенности. Например, в категории — по виду деформации входят задачи, связанные с изгибом, кручением, растяжением (сжатием) и сложным сопротивлением. В свою очередь, решения на изгиб классифицируются на статически определимые и неопределимые. Для того, чтобы найти нужную категорию перемещайтесь по указанным ссылкам на страничках. Также хотелось бы отметить, что на данный момент на сайте преобладают рукописные примеры решения. Но наша команда, активно работает над добавлением электронных материалов: с качественными схемами и набранными в цифровом виде расчетами. По мере развития сайта, все рукописные записи, планируется заменить цифровыми. Ну что же перейдем непосредственно к нашим примерам.

Классификация по виду деформации

Как уже говорилось выше, здесь все примеры отсортированы по виду деформации: растяжению и сжатию, кручению, изгибу и сложному сопротивлению. В категорию задач на сложное сопротивление попадают такие популярные решения на такие темы как изгиб с кручением, внецентренное растяжение (сжатие), косой изгиб. Теперь давайте перейдем непосредственно к категориям и не забывайте переходить по ссылкам на интересующую вас подкатегории.

Что можно найти в данной категории задач?

определение реакций в опорах из уравнений равновесия статики; расчет ВСФ методом сечений; вычисление продольной и поперечной силы; расчет изгибающего момента; расчет нормальных и касательных напряжений; вычисление перемещений поперечных сечений; раскрытие статической неопределимости с использованием уравнения совместности деформации.

Растяжение и сжатие

статически определимые брусья; статически неопределимые брусья; статически определимые стержневые системы; статически неопределимые стержневые системы.

Примеры задач на кручение распределены по 2 основным категориям:

статически определимое кручение; статически неопределимое кручение.

Задачи на изгиб подразделяются по тем же признакам:

статически определимый изгиб; статически неопределимый изгиб.

Классификация по типу рассчитываемого объекта

В этом разделе все решения распределены по типу рассчитываемого объекта: на балки, рамы, фермы и т. д. Каждая представленная здесь категория имеет укрупненную классификацию, которую можно изучить, перейдя по соответствующим ссылкам.

Решения, связанные с балками, можно разделить на две основные подкатегории:

статически определимые балки; статически неопределимые балки.

статически определимые валы; статически неопределимые валы.

статически определимые рамы; статически неопределимые рамы.

Все примеры решения задач, связанные с расчетом ферм, решено было поместить в одну большую категорию. В этой категории можно встретить задачи на:

определение реакций в опорах фермы; определение продольных усилий в стержнях методом вырезания узлов, либо методом Риттера; построение линий влияния.

В разделе про сечения, связанные с расчетом геометрических характеристик, принята следующая классификация:

симметричные и несимметричные сечения, состоящие из геометрических примитивов; симметричные и несимметричные сечения, состоящие из металлопрокатных профилей.

Классификация по типу расчета

В этом разделе материалы разделены по типу расчета. Сюда попали расчеты на прочность, жесткость и устойчивость. Здесь же находятся задачи, связанные с расчетом напряжений, эпюр внутренних силовых факторов и другие.

В этой категории находятся задачи, связанные с расчетом прочности, при различных видах деформации: изгибе, кручении, растяжении (сжатии) и сложном сопротивлении. Здесь можно встретить как проверочные, так и проектировочные расчета. Найти расчеты на грузоподъемность какой-либо системы.

В расчетах на жесткость, можно найти задачах, в которых исследуются различные элементы конструкций: балки, рамы, валы и другие. Во всех задачах проверяется жесткость, путем сравнения расчетных значений перемещений с допустимыми значениями.

Устойчивость

В примерах на устойчивость, можно найти задачи, связанные с подбором сечения стоек из условия устойчивости, либо расчетом грузоподъемности.

Данная катег

poiskvstavropole.ru