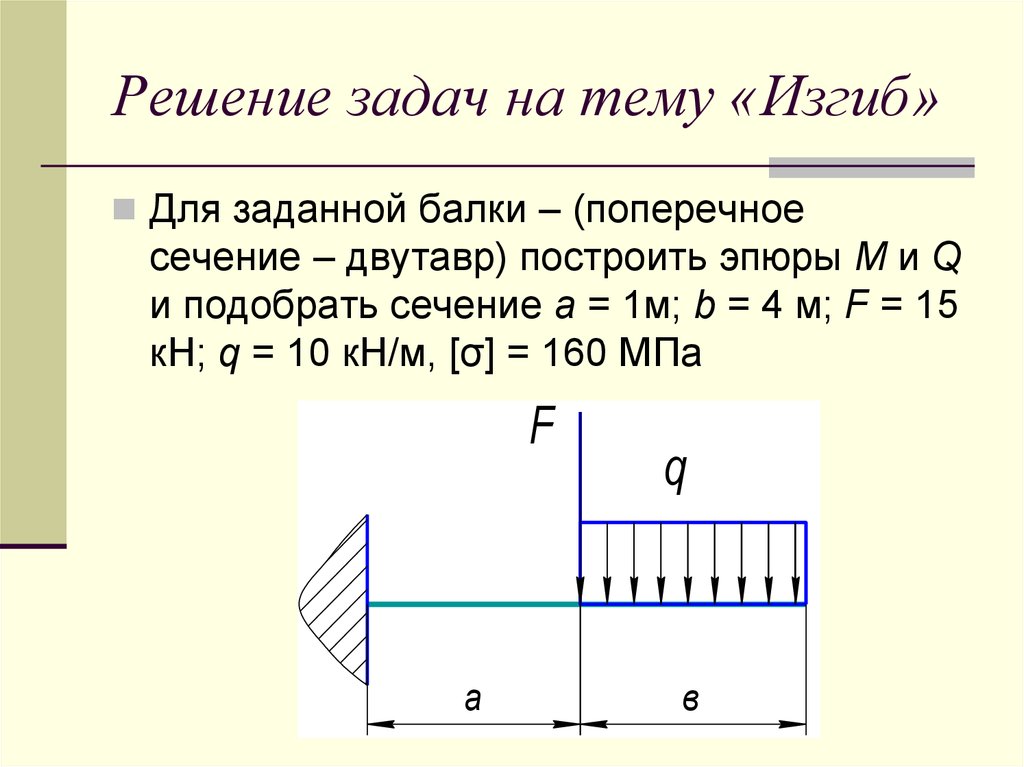
Задачи на изгиб по сопромату примеры и решения
Содержание:
- Алгоритм расчета на прочность при продольно-поперечном изгибе заключается в следующем.
- Пример решения задачи 11.1.
- Пример решения задачи 11.2.
- Пример решения задачи 11.3.
Определение 11.1. Продольно-поперечным изгибом стержня (балки) называется такой изгиб, при котором продольные силы оказывают влияние на упругую линию, и напряжения в любом его поперечном сечении распределены так, что векторы внутренних силовых имеют вид
Справедливы условия, аналогичные приведенным в утверждении 5.1.
Утверждение 11.1 (условия продольно-поперечного изгиба). Необходимым условием продольно-поперечного изгиба балки при силовом нагружении является следующий вид векторов внешних сосредоточенных и распределенных сил и моментов:
Изгиб стержня под действием продольной силы также рассматривается в рамках внецентренного растяжения сжатия.
Далее в рамках определения 5.3 будем рассматривать только прямой продольно-поперечный изгиб в плоскости полагая, что оси системы координат являются главными центральными для любого поперечного сечения.
Пусть на стержень кроме нагрузок, обеспечивающих прямой поперечный изгиб, действуют в положительном направлении оси продольные погонная нагрузка и сосредоточенная сила приложенная в точке с координатой Эта продольная нагрузка для недеформированного состояния приведена на рис. 11.1 а (здесь опоры не указаны). Она, очевидно, соответствуст сжимающему продольному усилию.
Если при деформации направление внешних сил не меняется, то полный изгибающий
момент имеет вид, рис. 11.1 б:
где — изгибающие моменты от поперечной и продольной нагрузок, — ордината точки приложения силы в деформированном состоянии, а — единичная функция Хевисайда, определяемая так:
Формула для очевидным образом может быть обобщена на случай конечного числа сосредоточенных сил. Кроме того, возможен такой вариант продольной нагрузки, когда ее направление в деформированном состоянии зависит от угла поворота поперечного сечения (рис. 11.2):
Кроме того, возможен такой вариант продольной нагрузки, когда ее направление в деформированном состоянии зависит от угла поворота поперечного сечения (рис. 11.2):При нагрузка называется следящей. Формулы (11.3) соответствуют Далее везде ограничимся этим вариантом.
Возможно вам будут полезны данные страницы:
Расчётная схема: определение и пример с решением |
Метод сил: определение и расчёт |
Задачи на косой изгиб по сопромату примеры и решения |
Поперечный изгиб решение задач по сопромату |
Подстановка равенств (11.3) в уравнения (5.15) или (5.20) приводит к уравнению упругой линии при продольно-поперечном изгибе, к которым должны быть добавлены соответствующие граничные условия (5.24) (5.26).
Далее будем рассматривать только линейный вариант, полагая, как правило, что погонная продольная нагрузка отсутствует а единственная сосредоточенная сила приложена на конце стержня:
Уравнение (11. 5) аналогично (5.22) и (5.23) может быть также представлено так:
5) аналогично (5.22) и (5.23) может быть также представлено так:
Как правило, при решении задач применяются следующие формы уравнений, вытекающие из (11.5) и (11.7) при учете (5.20):
где верхний знак соответствует сжимающим а нижний растягивающим усилиям
Отметим, что (11.5), (11.6) и первое уравнение в (11.8) могут использоваться только в СО задачах, а второе уравнение в (11.8) — в задачах с силовыми граничными условиями (5.24).
Таким образом первый шаг при исследовании продольно-поперечного изгиба заключается в определении упругой линии с помощью решения соответствующих краевых задач (см. также § 5.2). При некоторых значениях продольных сил (они совпадают с критическими силами, определенными в §11.2) эти решения обращаются в бесконечность, что связано с линеаризацией уравнений.
Если использовать нелинейные уравнения типа (5.14), то в окрестностях указанных значений сил прогибы будут большими, но конечными. Однако эти вопросы обычно в сопротивлении материалов не рассматриваются.
Подход, связанный с решением краевых задач, при переменных характеристиках стержня и разрывной нагрузке становится достаточно сложным. Приближенный способ определения упругой линии, позволяющий избежать решения краевой задачи.
Алгоритм расчета на прочность при продольно-поперечном изгибе заключается в следующем.
1. Вычисляется полный изгибающий момент если это возможно, по решению краевой задачи для второго уравнения в (11.8), либо по найденной упругой линии с помощью соотношений (11.3).
В первом случае используются указанные в (5.27) в скобках силовые условия стыковки участков:
где — внешние сосредоточенные момент и сила в сечении
2. Проводится расчет на прочность так же, как и при внецен-тренном растяжении сжатии (см. § 5.2). При этом нормальные напряжения в сечении вычисляются по вытекающей из (6.9) формуле:
Однако проектировочный расчет здесь осложняется тем, что упругая линия как решение краевой задачи и, соответственно, и нормальные напряжения зависят от геометрических параметров сечения сложным нелинейным образом.
Поэтому обычно ограничиваются поверочным расчетом (определяют запас прочности см. определение П.18). При этом возможны три варианта расчетов: а) считается неизменной продольная нагрузка; б) полагается фиксированной поперечная нагрузка; в) поперечная и продольная нагрузки изменяются пропорционально. В последних двух вариантах задача сводится к уравнению типа которое, как правило, является сложным нелинейным и решается с использованием какого-либо численного метода.
Пример решения задачи 11.1.
Для балки постоянной жесткости, изображенной на рис. 11.3, определить полный изгибающий момент
и упругую линию.
- Решение:
Нумерация характерных сечений балки указана на рисунке.
Поскольку в данном случае раничные условия являются силовыми (см. (5.24)):
то для решения используем второе дифференциальное уравнение в (11.8), где следует положить Его общие решения для участков 1-2 и 2-3 имеют вид
Константы определяются из указанных выше граничных условий и условий стыковки участков (см. (11.9), на обоих участках использована одна и та же система координат):
(11.9), на обоих участках использована одна и та же система координат):
Тогда приходим к системе линейных алгебраических уравнений
решение которой таково:
Следовательно, изгибающие моменты на каждом участке определяются выражениями:
Далее, вычисляя изгибающие моменты от продольной нагрузки
с помощью уравнения (11.5)по участкам находим упругую линию балки
Пример решения задачи 11.2.
Для балки постоянной жесткости, изображенной на рис. 11.4, определить полный изгибающий момент и упругую линию. Поперечная сила приложена в середине балки
- Решение:
Нумерация характерных сечений балки указана на рисунке. Решение задачи с использованием кинематических граничных условий (см. (5.25)):
приводит к громоздким уравнениям, поэтому воспользуемся симметрией задачи и рассмотрим участок 1-2. Для решения используем дифференциальное уравнение в форме (11.7), где следует положить Его общее решение для рассматриваемого участка имеет вид
Константы определяются из следующих граничных условий:
Тогда приходим к системе линейных алгебраических уравнений
Решая ее, получаем
Тогда изгибающие моменты и прогибы на участке определяются выражениями:
Пример решения задачи 11.
 3.
3.Выполнить поверочный расчет на прочность изображенной на рис. 11.3 балки прямоугольного поперечного сечения с основанием и высотой считая, что продольная сила остается постоянной. В расчетах принять:
- Решение:
Вычисляем площадь, момент инерции и момент сопротивления изгибу сечения балки (см. табл. П.б):
Находим параметры (см. (11.8)),
и с учетом результатов примера определяем изгибающие моменты:
Исследуя эти функции, убеждаемся, что изгибающий момент достигает наибольшего значения при Поскольку изгибающий момент пропорционален поперечной силе а продольная сила но условию задачи считается неизменной, то уравнение для запаса прочности (см. п. 2 алгоритма) является линейным
Отсюда находим
Изгиб и кручение пространственного стержня
Ниже приведено условие и решение задачи. Закачка решения в формате doc начнется автоматически через 10 секунд.
Для заданного на рис. 10 пространственного стержня постоянного поперечного сечения диаметром d требуется :
10 пространственного стержня постоянного поперечного сечения диаметром d требуется :
1. Построить эпюры изгибающих и крутящих моментов ;
2. На каждом участке стержня выявить опасное сечение и составить условие прочности по третьей гипотезе прочности ;
3. Определить диаметр стержня при R=210 МПа.
Дано : F=20 кН ; q=1 кН/м ; a=51 см ; b=60 см ; c=40 см.
Решение.
1. Построим эпюры изгибающих и крутящих моментов.
Чтобы построить эпюры изгибающих моментов М и крутящих моментов Т, будем рассматривать участки стержня со стороны свободного конца. В этом случае не требуется определять опорные реакции в защемлении. Эпюра изгибающих моментов строится со стороны растянутых волокон.
На участке AB стержня сосредоточенная сила F приложена перпендикулярно продольной оси стержня и подвергает его плоскому изгибу. В сечении А изгибающий момент МА=0, в сечении B изгибающий момент MB=bF=0.
На участке CD стержня равномерно распределённая нагрузка q приложена вдоль продольной оси и подвергает его изгибу в вертикальной плоскости. Изгибающие моменты MC=0 ; MD=q(0.5a)2=1×(0.5×0.51)2=0.065 кН·м. Этот участок стержня изгибается так, что растянуты верхние волокна. Поэтому ординаты эпюры М откладываем вверх. Крутящий момент на этом участке Т=0.
На участке DE стержня равномерно распределённая нагрузка q приложена перпендикулярно продольной оси и подвергает его плоскому изгибу в вертикальной плоскости. Изгибающие моменты : MD=q(0.5a)2=1×(0.5×0.51)2=0.065 кН·м ; ME=0. Этот участок стержня изгибается так, что растянуты верхние волокна. Поэтому ординаты эпюры М откладываем вверх. Крутящий момент T=0.
На участке DB стержня сосредоточенная сила qa=1×0.51=0.51 кН приложена перпендикулярно продольной оси и подвергает его плоскому изгибу в вертикальной плоскости. Изгибающие моменты : MD=0 ; MB=qac=0.51×0.4=0.204 кН·м. Этот участок стержня изгибается так, что растянуты верхние волокна. Поэтому ординаты эпюры М откладываем вверх. Крутящий момент Т=0.
Изгибающие моменты : MD=0 ; MB=qac=0.51×0.4=0.204 кН·м. Этот участок стержня изгибается так, что растянуты верхние волокна. Поэтому ординаты эпюры М откладываем вверх. Крутящий момент Т=0.
На участке BG изгибающий момент : MB=Fb=20×0.6=12 кН·м ; MG=F(a+b)-qa2=
=20×(0.51+0.6)-1×0.512=21.94 кН·м. Этот участок стержня изгибается так, что растянуты нижние волокна. Поэтому, ординаты эпюры М откладываем вниз. Крутящий момент Т=qac=1×0.51×0.4=0.204 кН·м.
Эпюры показаны на рисунке.
На каждом участке стержня выявим опасное сечение и составим условие прочности по третей теории прочности.
На участке AB опасным сечением является сечение B, где изгибающий момент максимален. Условие прочности по третьей гипотезе прочности имеет вид :
где M3 – приведённый момент по третьей гипотезе прочности ; W – осевой момент сопротивления (для круглого сечения W=0.1d3).
M3= кН·м
где Мy – изгибающий момент в плоскости xz ; Mz – изгибающий момент в плоскости xy ; T – крутящий момент.
На участке BG опасным сечением является сечение G, где изгибающий момент наибольший :
M3= кН·м
На участке BD опасным сечением является сечение B, где изгибающий момент наибольший :
M3= кН·м.
На участке CE опасным сечением является сечение D :
M3= кН·м
Определим диаметр стержня. Для наиболее нагруженного сечения G :
0.1d3=
Отсюда диаметр стержня : d= м=101 мм.
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке
4.2: Общие свойства управляющего уравнения балки – общие и частные решения
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 21491
- Томаш Вежбицкий 92}{2} + C_3x + C_4 \метка{4.
 2.2}\]
2.2}\]Частное решение \(w_p\) уравнения прогиба балки, уравнение (4.1.11) зависит от нагрузки, но не от граничных условий. Для равномерно нагруженной балки частным решением является первый член уравнения (4.1.27-4.1.28). В качестве иллюстрации рассмотрим ту же балку с опорой на штифт, нагруженную треугольной линейной нагрузкой
.\[q(x) = q_0 \frac{2x}{l} \; , \; 0 < х < \frac{l}{2}\]
где \(q_0\) — интенсивность нагрузки в середине пролета \(x = l/2\). Частное решение этой задачи, удовлетворяющее основному уравнению, равно 95}{60EIl}\]
Тогда полное решение равно \(w(x) = w_g + w_p\).
Балка, нагруженная сосредоточенными силами (или моментами), требует специального рассмотрения.
Внезапное изменение поперечного сечения балки или нагрузки может привести к прерывистому решению. Какие величины могут испытывать скачок, а какие должны быть непрерывными?
Рисунок \(\PageIndex{1}\): В балках не допускаются разрывы смещения и уклона.В механике разрыв данной функции обозначается квадратной скобкой 9—1) обозначают значения аргумента справа и слева от разрыва.
 В квазистатической теории балки
В квазистатической теории балки\[[w] = 0 \label{4.2.6}\]
\[\left[\frac{dw}{dx}\right] = 0\]
Прерывистость в вертикальном смещении означает разделение, поэтому, конечно, этого может не произойти. Почему же тогда уклоны должны быть непрерывными для упругих балок? Это просто. Изменение наклона называется искривлением. Скачок наклона дает бесконечную кривизну и, следовательно, бесконечные изгибающие моменты. Такая ситуация невозможна, так как поперечное сечение балки перейдет в область пластичности, и балка перестанет оставаться упругой. Величины, которые могут быть прерывистыми, равны
\[\text{Изгибаемые элементы } \quad [M] = \bar{M} \]
\[\text{Сдвиговое усилие } \quad [V] = \bar{V} \label{4.2.9 }\]
В качестве иллюстрации рассмотрим балку с опорой на штифт, нагруженную в середине пролета точечной силой \(P\).
Как упоминалось ранее, точечная нагрузка может рассматриваться как предельный случай непрерывной линейной нагрузки с помощью дельта-функции Дирака
\[q(x) = P \delta(x − \frac{l}{ 2}), \quad \text{ где } \int \delta(x − \frac{l}{2})dx = 1 \]
Несмотря на то, что были разработаны методы работы с функциями сингулярности для лучей, они требуют использования аппарата математической теории распределения.
 2}{16EI}, \; С_4 = 0 \] 93}{48EI}\]
2}{16EI}, \; С_4 = 0 \] 93}{48EI}\]График распределения изгибающего момента и поперечных усилий по длине балки, определяемый по расчетной линии прогиба, показан на рисунке (\(\PageIndex{3}\)).
Обратите внимание, что скачок внутренней поперечной силы равен приложенной силе
\[[V ] = V_{\text{right}}(x = \frac{l}{2}) − V_{\text {left}}(x = \frac{l}{2}) = P\]
Рисунок \(\PageIndex{3}\): Изгибающий момент непрерывен в середине пролета, а поперечная сила – нет.Если точечная нагрузка приложена не в середине пролета, а на произвольном расстоянии \(x = a\), балка должна быть разделена на две части \(0 < x < a\), \(a < x < l\), и каждую часть нужно решать независимо. 92}{2} + C_7x + C_8\]
Это дает восемь постоянных интегрирования, по четыре на каждую сторону. Достаточно ли условий для определения этих констант? Ответ ДА. Имеются два граничных условия при \(x = 0\), четыре условия непрерывности при \(x = a\), заданные уравнениями \ref{4.2.6}-\ref{4.2.9}, и снова два граничных условия условия при \(х = 1\).
 Итого
Итого\[\begin{array}{l|l|l}
\mathrm{BC}, x = 0 & \text { Непрерывность, } x = a & \mathrm{BC}, x = l \\
\hline w = 0 & {[w] = 0} & w = 0 \\
M = 0 & {\left[ \frac{d w}{d x} \right] = 0} & M=0 \\
& {[M] = 0} \\
& {[V] = P}
\end{array}\]Обратите внимание, что сосредоточенный изгибающий момент не приложен \(\bar{M} = 0\), поэтому что поле изгибающих моментов непрерывно через \(x = a\). Сосредоточенная сила вызывает скачок в распределении поперечных сил, поэтому \(\bar{V} = P\).
Мы предоставляем читателю применить вышеуказанное условие и решить проблему. Подробнее об этой проблеме можно узнать в двух разделах этих заметок: «Наборы задач» и «Рецитации».
Метод суперпозиции гласит, что прогибы и наклоны балки, подвергаемой системе нагрузок, равны сумме этих величин, вызванных отдельными нагрузками. Другими словами, отдельные результаты могут быть наложены друг на друга для определения комбинированного ответа, отсюда и термин «метод наложения».