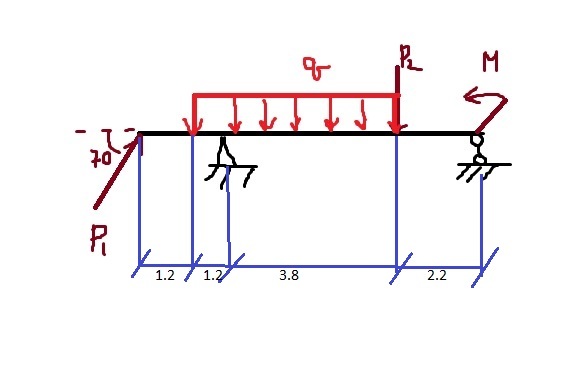
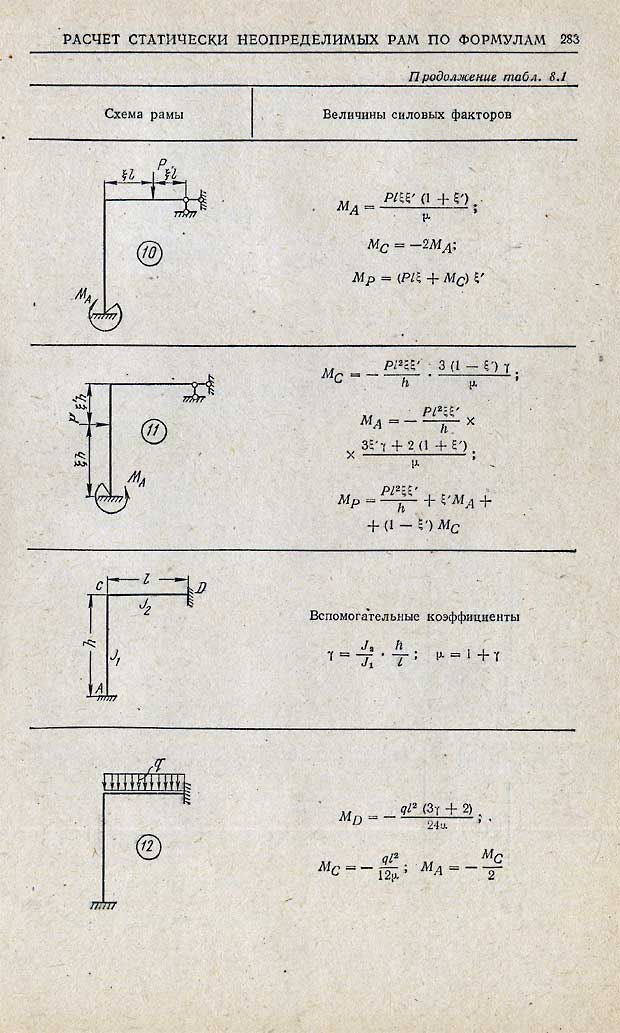
Подбор сечения ломаного пространственного стержня
Дан ломаный пространственный стержень (брус) Для пространственного стержня круглого поперечного сечения с ломаной осью подобрать размеры поперечного сечения (круглого), если дано F=20кН, q=30кН/м, М=25кНм, ℓ1=2м, ℓ2=1,5м, допускаемое напряжение σadm=250МПа. Расчет произвести по гипотезе наибольших касательных напряжений.
Отнесем каждый из элементов пространственного стержня к системе координат xyz, при этом продольная ось каждого элемента обозначается символом z.
Определим значения внутренних усилий в характерных сечениях элементов. Определяем внутренние силовые факторы методом характерных точек.
Участок LК:
Продольные силы ( растягивает –плюс, сжимает – минус)
Поперечные силы (по часовой – плюс, против – минус)
Крутящие моменты
Участок КD:
Продольные силы
Поперечные силы
Изгибающие моменты
Крутящие моменты
Далее, участок DC:
Участок СВ:
Определяем экстремальное значение Мх на участке КD
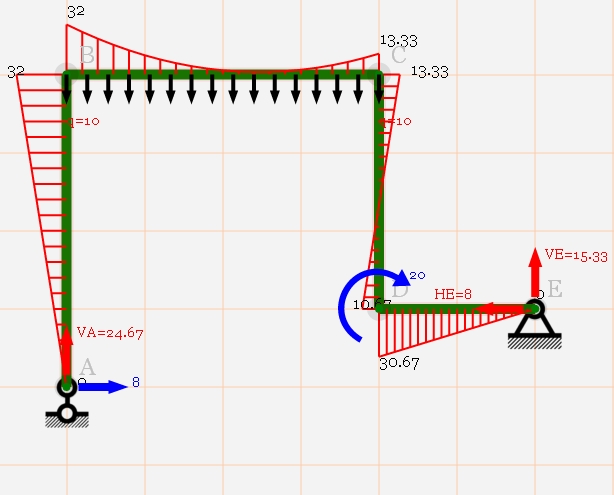
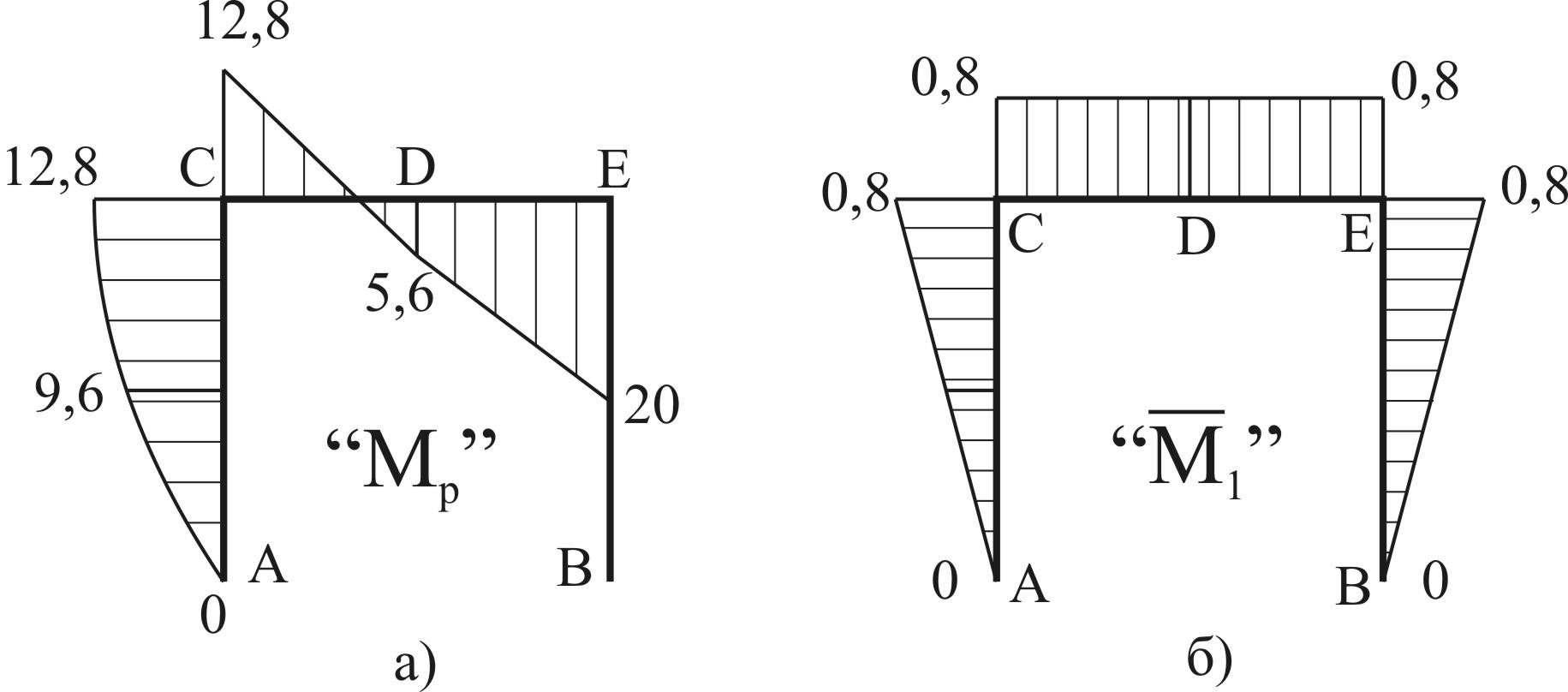
Строим эпюры внутренних усилий
Наиболее опасным является сечение В
Условие прочности по третьей теории прочности (наибольших касательных напряжений) имеет вид:
В опасных точках сечения В:
После подстановки численных значений:
В результате получим значение диаметра:
Принимаем D=185 мм.
Sopromatguru / СОПРОМАТ ГУРУ. Расчет балки онлайн. Построение эпюр
Sopromatguru / СОПРОМАТ ГУРУ. Расчет балки онлайн. Построение эпюр| Sopromatguru.ru Valuation | |
|---|---|
| US$37,698 | Sopromatguru.ru has a global Alexa ranking of 627,075 and ranked 132,759th in Russia. The global rank declined 50,773 positions versus the previous 3 months. Sopromatguru.ru estimated website worth is US$37,698 (based on the daily revenue potential of the website over a 12 month period). Sopromatguru.ru possibly receives an estimated 1,671 unique visitors every day. The website server is using IP address 81.177.49.49 and is hosted in , Russia. |
| Traffic & Worth Estimations | |
| Purchase/Sale Value | US$37,698 |
| Daily Ads Revenue | US$6 |
| Monthly Ads Revenue | US$191 |
| Yearly Ads Revenue | US$2,303 |
| Daily Unique Visitors | 1,671 |
| Monthly Unique Visitors | 50,798 |
| Yearly Unique Visitors | 610,332 |
Note: All traffic and earnings values are estimates only. | |
| Alexa Traffic Ranks | |
|---|---|
| Global Rank | 627,075 |
| Delta | 50,773 |
| Reach Rank | 614,638 |
| Country | Russia |
| Rank in Country | 132759 |
| global rank trend of the past year | |
| Search Traffic Percentage Trend | |
| Last updated on 2018-08-11 00:00:48(UTC) | |
| Http Header |
|---|
| HTTP/1.1 200 OK Date: Thu, 04 Oct 2018 18:27:26 GMT Server: Apache X-Powered-By: PHP/5.5.38 Vary: Accept-Encoding Content-Type: text/html; charset=utf-8 Transfer-Encoding: chunked |
| Sopromatguru.ru Whois Infomation |
|---|
| N/A |
| Robots.txt Information | ||
|---|---|---|
/robots. txt | ✔Found | |
| Robot | Path | Permission |
| GoogleBot | / | ✔ |
| BingBot | / | ✔ |
| YandexBot | / | ✔ |
| CuterCounterBot | / | ✔ |
| Meta Tags | |
|---|---|
| Title | СОПРОМАТ ГУРУ. Расчет балки онлайн. Построение эпюр |
| Description | Решение задач по сопромату и теоретической механике онлайн. Определение реакций опор, построение эпюр изгибающих моментов, эпюр поперечных сил бесплатно. Расчет статически определимой, статически неопределимой балки, рамы, фермы с решением |
| Keywords | расчет балки,онлайн,решение,реакция опоры,эпюры онлайн,построение эпюр |
| Server Information | |
|---|---|
| WebSite | www.sopromatguru.ru |
| Host IP | 81.177.49.49 |
| Location | , Russia |
Шалфей — что это такое? Определение, значение, перевод
Шалфей (ударение на «е») это род цветковых растений семейства яснотковые, дальних родственников мяты и мелиссы.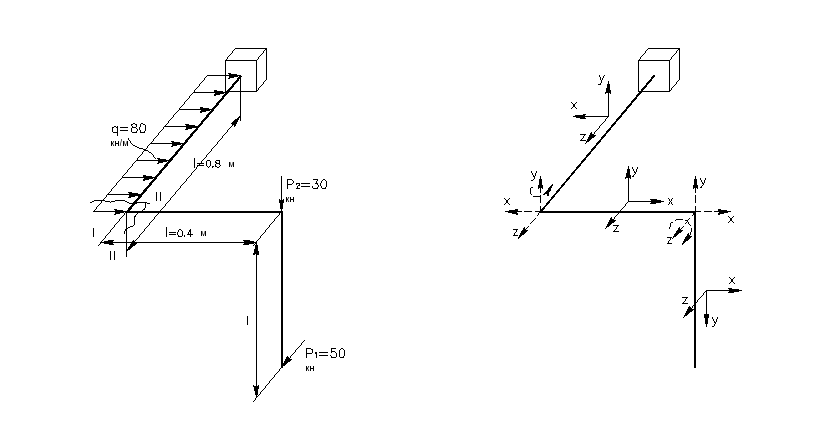
Цветы шалфея имеют, как правило, фиолетовую окраску, но иногда и ярко-красную. Шалфей применяется как лекарственное растение, богатое эфирными маслами. Немцы используют шалфей в виноделии для вкусовых ублажений. Жиры, которые содержатся в цветках шалфея, применяются при производстве эмалей и красок. Но это всё не так интересно, как психоделические свойства шалфея, о которых тебе, малыш, ещё рано знать, если тебе не исполнилось дохренадцать лет. Употребление шалфея может вызвать не только радужные галлюцинации, дружок мой, но и наряд полиции, который увезёт тебя в ближайший СИЗО. Так что полегче, студент, с этими веществами, договорились? Лучше выпей стакан зелёного чая с мелиссой и иди учить сопромат. Вы узнали, откуда произошло слово Шалфей, его объяснение простыми словами, перевод, происхождение и смысл.
Пожалуйста, поделитесь ссылкой «Что такое Шалфей?» с друзьями:
И не забудьте подписаться на самый интересный паблик ВКонтакте!
Шалфей (ударение на «е») это род цветковых растений семейства яснотковые, дальних родственников мяты и мелиссы.
Шалфей применяется как лекарственное растение, богатое эфирными маслами. Немцы используют шалфей в виноделии для вкусовых ублажений. Жиры, которые содержатся в цветках шалфея, применяются при производстве эмалей и красок. Но это всё не так интересно, как психоделические свойства шалфея, о которых тебе, малыш, ещё рано знать, если тебе не исполнилось дохренадцать лет. Употребление шалфея может вызвать не только радужные галлюцинации, дружок мой, но и наряд полиции, который увезёт тебя в ближайший СИЗО. Так что полегче, студент, с этими веществами, договорились? Лучше выпей стакан зелёного чая с мелиссой и иди учить сопромат.
KingRoon KP3S + Marlin + BTT TMC 2209 + Bltouch + UART + Новая голова = Достойный принтер?
Приветствую тебя читатель и тот у кого «руки не для скуки»
Сегодня будем готовить принтер Kingroon KP3S на медленном огне с хорошей прожаркой:)
Почему на медленном? — Так потому что информация собиралась очень долго и все это переваривалось в одну субстанцию на протяжении 4х месяцев (Логистика, изучение и все остальное)
В первую очередь хочу предупредить что все это делаете на свой страх и риск — ответственность никакую не несу)
1) Голова — головушка
Как только я получил принтер и увидя массивную конструкцию головы, дошли до меня мысли что там явно не легко.
Действительно. Голова в сборе весила 560гр!!!! Первое что я сделал — отпили кусок крепления и поставил Titan+ Short e3dv6
Похудели но не достаточно.
Был заказан блинчик.
Начал думать на счет крепление всего добра в одно целое. По быстрому открыл «Paint для моделирования» (использую продукт ANSYS) и сообразил голову.
К конструкции попрошу без придирок и сопромата. ВСЕ БУДЕТ ПЕРЕДЕЛЫВАТЬСЯ. P.s. Обдув тоже)
Собрал я значит все это в единое целое и на весы.
Норм, можно жить. Плюс обдув, Bltouch что-то в районе 260гр.
Итого путем использования диеты удалось сбросить вес почти в 2 раза!!
Встал вопрос как будет нажиматься концевик???! Долго не думал, выбор пал на использование принтера без них.
2)Marlin + BTT TMC2209 + BLtouch+ Sensorless Homing+ UART + управление подсветкой стола + включение/отключение вентилятора охлаждения хотенда выше/ниже 100 градусов
Этот пункт в рецепте заслуживает отдельного «слова» ибо пришлось изучить всю документацию марлина и наработки пользователей вдоль и поперек.
Компания Kingroon заказала кастом плату Robin Nano 1.2 у MKS убрав слот wifi и еще кучу всего.
Наткнувшись на плату принтера «FlyingBear» и инструкцию от уважаемого Sergey1560 https://sergey1560.github.io/fb4s_howto/tmc_uart/ было принято решение мучить себя и плату.
Выше на картинке можете наблюдать всю цепочку подключений. Надеюсь все доступно и понятно. Цвет каждой буквы- совпадает с цветом кабеля.
Управление вентилятором хотенда(соблюдать полярность!) — HЕ1 пин (полярность на плате)
Управление посветкой(соблюдать полярность!) — PB2
Bltouch — J16 ( черный и белый подключается в пин Z-)
UART XYZ — ПОСЛЕДОВАТЕЛЬНО в 4е пина под драйвером E1.
UART E — в 5ый если отсчитывать как на фото пин TC (см на фото) Пин находится рядом с BLtouch
Сигнальный от драйвера X — в «S-сигнальный» пин контактов концевика X
Сигнальный от драйвера Y — в «S-сигнальный» пин контактов концевика Y
Родные драйвера TMC2225 со всеми джамперами(черные заглушки под драйвером) извлек из платы.
Драйвера приобретались Btt ибо там сразу есть выводы к которым не надо подпаивать провода.
К Драйверам XYZE в пин uart подключается кабель ( белый, синий, оранжевый, красный цвет проводов на картинки)
К драйверам XY подключается кабель в пин рядом с потенциометром для управления Sensorless Homing (желтый и фиолетовый цвет провода на картинки).
Я не стал заморачиваться с пайкой сопротивлений на 1К, все заработало.
Начал собирать прошивку. Решил сразу включить управление кулера хотенда и подсветку из меню.
За два вечера заставил работать принтер без концевиков.
Скинул на Sd прошивку вставил в принтер и он мне пишет «KP3S READY» Радости полные штаны!!
В меню появились новые пункты:
1) Управление подсветкой стола
2) Дополнительная команда для настройки BLtouch «G0Z0» чтобы не доставать пк
3) Заветное меню TMC Drivers
«Под капот» принтера для настройки токов больше не придется лазить)
Теперь принтер готов к бою и дальнейшим настройкам.
Сразу пишу что настройки были все под стоковое состояние принтера с его тяжелой головой. Попрошу не писать про эхо, воблинг и остальное. Статья не про качество печати.
К сожалению тут не очень удобно выкладывать информации по прошивкам и каждые изменения. Да и не многословен я в написании статей) Приглашаю в тематический чат по принтерам KP3/KP3S https://t.me/kingroonkp3_chat (не реклама)
Прошивка марлин под стоковые драйвера — https://github.com/nehilo/KP3S
Маунт дисплея — https://www.thingiverse.com/thing:4578390
Крепление Bltouch — https://www.thingiverse.com/thing:4636399
Спасибо за уделенное время.
Всем хорошей печати!)
Аналитическая геометрия в пространстве (Лекция №19)
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Рассмотрим две плоскости α1 и α2, заданные соответственно уравнениями:
Под углом
между двумя плоскостями будем понимать один из двугранных углов, образованных
этими плоскостями.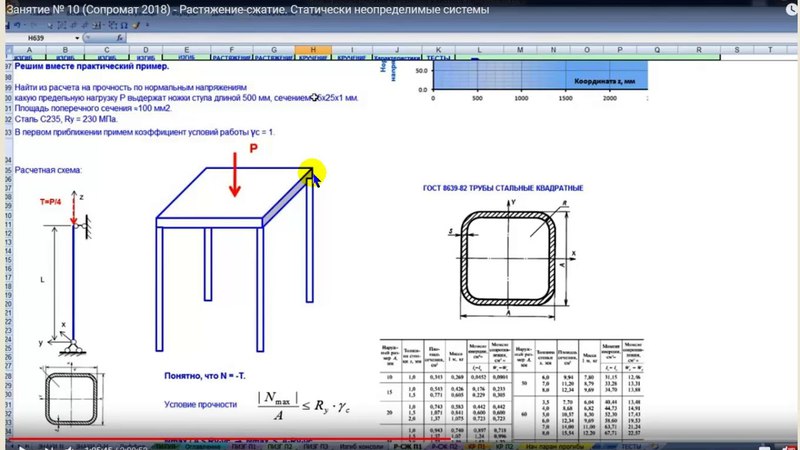
Очевидно, что угол между нормальными векторами и плоскостей α1
и α2 равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то
.
Пример. Определить угол между плоскостями x+2y-3z+4=0 и 2x+3y+z+8=0.
Условие параллельности двух плоскостей.
Две плоскости α1 и α2 параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .
Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:
или
Условие перпендикулярности плоскостей.
Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .
Таким образом, .
Примеры.
- Составить уравнение плоскости, проходящей через точку
M(-2; 1; 4) параллельно плоскости 3x+2y-7z+8=0.
Уравнение плоскости будем искать в виде Ax+By+Cz+D=0. Из условия параллельности плоскостей следует, что: . Поэтому можно положить A=3, B=2, C=-7. Поэтому уравнение плоскости принимает вид3x+2y-7z+D=0.
Кроме того, так какMÎ α, то-6+2-28+D=0, D=32.
Итак, искомое уравнение 3x+2y-7z+32=0.
- Составить уравнение
плоскости, проходящей через точки M1(1;
1; 1), M2(0;
1; –1) перпендикулярно плоскости x+y+z=0.
Так как M1Î α, то используя уравнение плоскости, проходящей через заданную точку, будем иметь A(x-1)+B(y-1)+C(z-1)=0.
Далее, так как M2Î α, то подставив координаты точки в выписанное уравнение, получим равенство -A-2C=0 или A+2C=0.
Учтем, что заданная плоскость перпендикулярна искомой.
Поэтому A+B+C=0.Выразим коэффициенты Aи Bчерез C: A=-2C, B=C и подставим их в исходное уравнение: -2C(x-1)+C(y-1)+C(z-1)=0.
Окончательно получаем -2x+y+z=0.
- Составить уравнение
плоскости, проходящей через точку M(-2; 3; 6) перпендикулярно
плоскостям 2x+3y-2z-4=0 и 3x+5y+z=0.
Так как MÎ α, то A(x+2)+B(x-3)+C(z-6)=0.
По условию задачи , поэтому
Итак уравнение плоскости принимает вид 13(x+2)-8(y-3)+z-6=0 или 13x-8y+z+44=0.
Поэтому A+B+C=0.ПРЯМАЯ В ПРОСТРАНСТВЕ.
ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.
ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
Положение прямой в пространстве вполне определяется заданием какой-либо её
фиксированной точки М1 и вектора , параллельного этой прямой.
Вектор , параллельный прямой, называется направляющим вектором этой прямой.
Итак, пусть прямая l проходит через точку М1(x1, y1, z1), лежащую на прямой параллельно вектору .
Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что .
Векторы и коллинеарны, поэтому найдётся такое число t, что , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М1 и М соответственно через и , получаем . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М, лежащей на прямой.
Запишем это уравнение в координатной форме. Заметим, что , и отсюда
Полученные уравнения называются параметрическими
уравнениями прямой.
При изменении параметра t изменяются координаты x, y и z и точка М перемещается по прямой.
КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
Пусть М1(x1, y1, z1) – точка, лежащая на прямой l, и – её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .
Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,
– канонические уравнения прямой.
Замечание 1. Заметим, что канонические уравнения прямой можно было получить из параметрических,исключив параметр t. Действительно, из параметрических уравнений получаем или .
Пример. Записать уравнение прямой в параметрическом виде.
Обозначим ,
отсюда x = 2 + 3t, y = –1 + 2t, z = 1 –t.
Замечание 2. Пусть прямая перпендикулярна одной из координатных осей, например оси Ox. Тогда направляющий вектор прямой перпендикулярен Ox, следовательно, m=0. Следовательно, параметрические уравнения прямой примут вид
Исключая из уравнений параметр t, получим уравнения прямой в виде
Однако и в этом случае условимся формально записывать канонические уравнения прямой в виде. Таким образом, еслив знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Аналогично, каноническим уравнениям соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz.
Примеры.
- Составить канонические и параметрические уравнения прямой,
проходящей через точку М1(1;0;-2) параллельно вектору .
Канонические уравнения: .
Параметрические уравнения:
- Составить уравнения прямой,
проходящей через две точки М1(-2;1;3), М2(-1;3;0).
Составим канонические уравнения прямой. Для этого найдем направляющий вектор . Тогда l: .
ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ
Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.
Вообще любые две не параллельные плоскости, заданные общими уравнениями
определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.
Примеры.
Построить прямую, заданную уравнениями
Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z= 0:
Решив эту систему, найдем точку M1(1;2;0).
Аналогично, полагая y= 0, получим точку пересечения прямой с плоскостью xOz:
От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М1 на прямой и направляющий вектор прямой.
Координаты точки М1 получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к обоим нормальным векторам и . Поэтому за направляющий вектор прямой l можно взять векторное произведение нормальных векторов:
.
Пример. Привести общие уравнения прямой к каноническому виду.
Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y= 0 и решим систему уравнений:
Нормальные векторы плоскостей, определяющих прямую имеют координаты Поэтому направляющий вектор прямой будет
.
Следовательно, l: .
УГОЛ МЕЖДУ ПРЯМЫМИ
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
Пусть в пространстве заданы две прямые:
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим
.
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов и :
Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l1 параллельна l2 тогда и только тогда, когда параллелен .
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна
нулю: .
Примеры.
- Найти угол между прямыми и .
- Найти уравнения прямой проходящей через точку М1(1;2;3) параллельно прямой l1:
Поскольку искомая прямая l параллельна l1, то в качестве направляющего вектора искомой прямой l можно взять направляющий вектор прямой l1.
- Составить уравнения прямой,
проходящей через точку М1(-4;0;2) и перпендикулярной прямым: и .
Направляющий вектор прямой l можно найти как векторное произведение векторов и :
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями
Рассмотрим векторы и .
Если угол между ними острый, то он будет ,
где φ – угол между прямой и плоскостью. Тогда .
Если угол между векторами и тупой, то он равен . Следовательно . Поэтому в любом случае . Вспомнив формулу вычисления косинуса угла между векторами, получим .
Условие перпендикулярности прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой и нормальный вектор плоскости коллинеарны, т.е. .
Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы и перпендикулярны.
Примеры.
- Написать уравнение плоскости, проходящей через точку М1(2;-3;4) параллельно прямым и .
Так как M1Î α, то уравнение плоскости будем искать в виде
.
Применяя условие параллельности прямой и плоскости, получим систему линейных уравнений
Отсюда
Итак, или .
- Найти угол между прямой и плоскостью .
Направляющий вектор прямой . Нормальный вектор плоскости . Следовательно,
- Найдите точку, симметричную данной М(0;-3;-2) относительно прямой .
Составим уравнение плоскости α перпендикулярной l. MÎ α, . Следовательно, или .
Найдём точку пересечения прямой l и α:
Итак, N(0.5;-0.5;0.5). Пусть искомая точка М1 имеет координаты М1(x,y,z). Тогда очевидно равенство векторов , т.е. (0,5;2,5;2,5)=(х-0.5;у+0.5;z-0.5). Откуда x=1, y=2, z=3 или М1(1;2;3)..
| Заголовок страницы | Waiting for the redirectiron. ..Длина : 31 Замечательно, Ваш заголовок страницы содержит от 10 до 70 символов. | |||||||||||||
| Описание страницы | Joomla! Длина : 7 В идеале, Ваше описание страницы должено содержать от 70 до 160 символов (вместе с пробелами). Используйте этот бесплатный инструмент для подсчета длины символов в тексте. | |||||||||||||
| Ключевые слова | joomla, Joomla, joomla 1.5, wordpress 2.5, Drupal Хорошо, Ваш веб-сайт содержит ключевые слова. | |||||||||||||
| Og Meta Properties | Вы не используете преимущества Og Properties. Эти мета-тэги помогают социальным роботам лучше структурировать Ваш сайт. Используйте бесплатный генератор og properties, чтобы создать их. | |||||||||||||
| Заголовки |
| |||||||||||||
| Картинки | Мы нашли 0 картинок на этом веб-сайте. Хорошо. Все (или почти все) картинки на вашем сайте имеют alt атрибут. | |||||||||||||
| Соотношение Контент/HTML | Соотношение : 10% Соотношение текста в коде HTML у этой страницы меньше чем 15 процентов, это означает, что Вашем веб-сайту требуется больше контента. | |||||||||||||
| Flash | Замечательно, мы не нашли Flash контента на странице. | |||||||||||||
| Iframe | Замечательно, мы не зафиксировали Iframe’ов на Вашей странице. |
ЭИОС ТГУ (Тамбов). 🔥 Поможем закрыть сессию. Жми!!!
ЭИОС ТГУ (Тамбов) – цифровой образовательный портал для обучения в дистанционном формате www.tsutmb.ru. Сервисы и функционал web-платформы максимально адаптированы под все категории студентов: очного и заочного, удаленного и очно-заочного направлений.
В СДО электронного Moodle-университета предложены самые перспективные и технологичные образовательные программы, изучение которых не требует временного переезда и проживания в Тамбове.
LMS-система ЭИОС ТГУ удобна и для вчерашних школьников, и для опытных слушателей, получающих второе ВО или осваивающих смежные профессии sdoinfo.tsutmb.ru. Используя ПК, смартфон, планшет или ноутбук, можно читать онлайн-учебники и участвовать в вебинарах, отсылать на проверку контрольные, курсовые и практические работы, сдавать зачеты и тесты, консультироваться в чатах и на форумах. Всем пользователям доступна помощь преподавателей, кураторов и администрации.
Тамбовский государственный университет имени Г. Р. Державина – один из крупнейших образовательных центров, обучающих студентов по десяткам направлений, стратегически приоритетных для развития региона. Вуз развивает партнерские связи с учебными и научными учреждениями США, Европы и Китая. Слушатели университета стажируются и проходят практику в ведущих международных институтах.
Если вы учитесь дистанционно у вас нет лишнего времени на изучение лекционного материала, чтобы выполнять непростые домашние задания, или не хватает сил решить тест, зачет, экзамен.
Мы поможем закрыть сессию «под ключ».
Вход в ЭИОС ТГУ (Тамбов)
Чтобы попасть в личный кабинет, необходимо перейти на moodle.tsutmb.ru, активировать кнопку «Вход», выбрать блок для студентов-дистанционщиков или очников-заочников.
Ссылка auth.tsutmb.ru/authorize?response_type=code&client_id=moodle&state=xyz на доступ к персональному аккаунту. В качестве логина используют телефон или электронный адрес, пароль запрашивают в режиме онлайн у администратора сайта.
spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + www.datebest.xyz +% f0% 9f% aa % 80% e2% 9d% a4% ef% b8% 8f + best + дейтинг + сайт% ef% b8% 8f +% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8 % 8f + spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f% aa% 80% e2 % 9d% a4% ef% b8% 8f% ef% b8% 8f + spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef % b8% 8f + spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f +% f0% 9f% aa% 80 % e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + www.
datebest.xyz +% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f + best + dating + site% ef% b8% 8f +% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + | Alliance for Zero Extinction spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + www.datebest.xyz +% f0 % 9f% aa% 80% e2% 9d% a4% ef% b8% 8f + best + dating + site% ef% b8% 8f +% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f % ef% b8% 8f + spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f% aa % 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f% aa% 80% e2% 9d% a4% ef% b8 % 8f% ef% b8% 8f + spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f +% f0% 9f % aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + www.datebest.
xyz +% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f + best + dating + site% ef% b8% 8f +% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + | Alliance for Zero Extinction Результаты поиска по запросу «spri + 3 + in + 1 + сопротивление + tube ++% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + www.datebest.xyz + % f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f + best + dating + site% ef% b8% 8f +% f0% 9f% aa% 80% e2% 9d% a4% ef% b8 % 8f% ef% b8% 8f + spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f % aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f% aa% 80% e2% 9d% a4% ef % b8% 8f% ef% b8% 8f + spri + 3 + in + 1 + сопротивление + трубка ++% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f +% f0 % 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + www.
datebest.xyz +% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f + best + dating + site% ef% b8% 8f +% f0% 9f% aa% 80% e2% 9d% a4% ef% b8% 8f% ef% b8% 8f + »- Альянс за нулевое вымирание| Административный менеджер | Джефферсон-Сити, Миссури, США, 65109 | 24 мая 2021 г. | |
| Аналитик программы инфраструктурных активов | Джефферсон-Сити, Миссури, США, 65102 | 22 мая 2021 г. | |
| Техник цеха оборудования | Eminence, Миссури, США, 654669714 | 21 мая 2021 г. | |
| Техник по рыболовству I | Салем, штат Миссури, США, 65560 | 20 мая 2021 г. | |
| ГИС техник | Джефферсон-Сити, Миссури, США, 65102 | 13 мая 2021 г. | |
| Инженер-электрик | Джефферсон-Сити, Миссури, США, 65109 | 8 мая 2021 г. | |
| Инженер-механик | Джефферсон-Сити, Миссури, США, 65109 | 8 мая 2021 г. | |
| Техник по управлению ресурсами — (19 мест) | 19 населенных пунктов по всему штату, Миссури, США, N / A | 5 мая 2021 г. | |
| Руководитель программ дикой природы | Джефферсон-Сити, Миссури, США, 65102 | 4 мая 2021 г. | |
| Специалист по инфраструктурной сети | Джефферсон-Сити, Миссури, США, 65102 | 4 мая 2021 г. | |
| Начальник Секции услуг ИТ-поддержки | Джефферсон-Сити, Миссури, США, 65109 | 29 апреля 2021 г. | |
| Руководитель по обслуживанию региональной инфраструктуры — (2 офиса) | Сент-Чарльз, Миссури, США, 633042215 | 27 апреля 2021 г. |
| Административный менеджер | Джефферсон-Сити, Миссури, США, 65109 | 24 мая 2021 г. | |
| Аналитик программы инфраструктурных активов | Джефферсон-Сити, Миссури, США, 65102 | 22 мая 2021 г. | |
| Техник цеха оборудования | Eminence, Миссури, США, 654669714 | 21 мая 2021 г. | |
| Техник по рыболовству I | Салем, Миссури, США, 65560 | 20 мая 2021 г. | |
| ГИС техник | Джефферсон-Сити, Миссури, США, 65102 | 13 мая 2021 г. | |
| Инженер-электрик | Джефферсон-Сити, Миссури, США, 65109 | 8 мая 2021 г. | |
| Инженер-механик | Джефферсон-Сити, Миссури, США, 65109 | 8 мая 2021 г. | |
| Техник по управлению ресурсами — (19 мест) | 19 населенных пунктов по всему штату, Миссури, США, N / A | 5 мая 2021 г. | |
| Руководитель программ дикой природы | Джефферсон-Сити, Миссури, США, 65102 | 4 мая 2021 г. | |
| Специалист по инфраструктурной сети | Джефферсон-Сити, Миссури, США, 65102 | 4 мая 2021 г. | |
| Начальник Секции услуг ИТ-поддержки | Джефферсон-Сити, Миссури, США, 65109 | 29 апреля 2021 г. | |
| Руководитель по обслуживанию региональной инфраструктуры — (2 офиса) | Сент-Чарльз, Миссури, США, 633042215 | 27 апреля 2021 г. |
| Сцена — Помощник шеф-повара проекта CRM — L’Occitane en Provence H / F | Иль-де-Франс, Франция | 27 мая 2021 г. | Этап | Маркетинг | |
| CDI — Responsable des Opérations Retail H / F — L’Occitane en Provence | Иль-де-Франс, Франция | 27 мая 2021 г. | Durée indéterminée (CDI) | Розничная торговля / Ventes | |
| CDI — Formateur Merchandiseur H / F — Secteur Aquitaine | Овернь-Рона-Альпы, Франция | 27 мая 2021 г. | Durée indéterminée (CDI) | Оптовая | |
| Методы вмешательства поверенного за координацию H / F | Маноск, Прованс-Альпы-Лазурный берег (PACA), FR | 27 мая 2021 г. | Durée indéterminée (CDI) | Autres | |
| Conseiller de vente H / F — CDD 13h — Belle Epine | Иль-де-Франс, Франция | 27 мая 2021 г. | A durée déterminée (CDD) | Розничная торговля / Ventes | |
| Галерея инноваций Technicien Formulation — H / F | Маноск, Прованс-Альпы-Лазурный берег (PACA), FR | 27 мая 2021 г. | Durée indéterminée (CDI) | Recherche et Développement | |
| Уровень 6 mois — Сервисные клиенты — Groupe L’OCCITANE: Melvita et Erborian H / F | Иль-де-Франс, Франция | 26 мая 2021 г. | Этап | Розничная торговля / Ventes | |
| Verkäuferin (м / ж / д) в Teilzeit — Köln Weiden | Северный Рейн-Вестфалия, DE | 26 мая 2021 г. | Festangestellt | Розничная торговля / Веркауф | |
| Apprenti Transposition H / F | Овернь-Рона-Альпы, Франция | 26 мая 2021 г. | A durée déterminée (CDD) | Производство | |
| Поверенный за новое планирование — H / F | Прованс-Альпы-Лазурный берег (PACA), FR | 26 мая 2021 г. | Durée indéterminée (CDI) | Цепочка поставок | |
| Контроллер промышленного управления Usine H / F | Маноск, Прованс-Альпы-Лазурный берег (PACA), FR | 26 мая 2021 г. | A durée déterminée (CDD) | Финансы | |
| Финансовый контролер | Лондон, Великобритания | 26 мая 2021 г. | Постоянный | Розничные продажи | |
| Logisticien Cariste — H / F | Маноск, Прованс-Альпы-Лазурный берег (PACA), FR | 26 мая 2021 г. | A durée déterminée (CDD) | Цепочка поставок | |
| Technicien comptabilité fournisseurs H / F | Маноск, Прованс-Альпы-Лазурный берег (PACA), FR | 25 мая 2021 г. | Durée indéterminée (CDI) | Финансы | |
| Сотрудник отдела продаж Liffey St (Temp) -16 часов в неделю | Ленстер, IE | 25 мая 2021 г. | Контракт с фиксированными условиями | Розничные продажи |
| Ученик | Гургаон, IN | MG Road и близлежащие магазины_Gurgaon | |
| Ученик | Гургаон, IN | Sohna Road и поле для гольфа Road_Gurgaon | |
| Ученик | Бангалор, IN | MG Road | |
| Ученик | Лакхнау, IN | Лакхнау | |
| Ученик | Дели, IN | Намасте Мидуэй, Мансурпур | |
| Ученик | Нойда, IN | Нойда и экспресс | |
| Ученик | Ченнаи, IN | Нуггамбакан | |
| Ученик | Хайдарабад, Индиана | Юбилейные холмы | |
| Ученик | Бангалор, IN | Кочи | |
| Ученик | Ченнаи, IN | Velachery | |
| Ученик | Бангалор, IN | Белое поле | |
| Ученик | Бангалор, IN | БИАЛ Ехланка | |
| Ученик | Бангалор, IN | Маллешварам | |
| Ученик | Хайдарабад, Индиана | Шамшабад аэропорт | |
| Ученик | Ченнаи, IN | Аннанагар | |
| Ученик | Хайдарабад, Индиана | Hitech City | |
| Начальник смены | Дели, IN | Центральный и Западный Дели | |
| Начальник смены | Хайдарабад, Индиана | Hitech City | |
| Начальник смены | Нойда, IN | Нойда и экспресс | |
| Начальник смены | Калькутта, IN | Калькутта | |
| Начальник смены | Гургаон, IN | MG Road и близлежащие магазины_Gurgaon | |
| Бариста | Нойда, IN | Нойда и экспресс | |
| Бариста | Бангалор, IN | Белое поле | |
| Бариста | Мумбаи, Индиана | Южный Мумбаи | |
| Бариста | Гургаон, IN | MG Road и близлежащие магазины_Gurgaon |
Джон Адамс: Внутренние дела | Миллер Центр
Стиль президента Адамса заключался в том, чтобы оставить внутренние дела Конгрессу и самому контролировать внешнюю политику.Мало того, что Конституция возлагает на президента ответственность за внешнюю политику, но, возможно, ни один другой американец не имел такого дипломатического опыта, как Адамс. В результате его мировоззрения большая часть его внутренней политики была переплетена с его внешней политикой, поскольку дипломатические вопросы часто вызывали внутреннюю реакцию, которая поглощала президента и нацию.
Вслед за «делом XYZ» (см. Раздел «Международные отношения») появилось много негативных настроений по отношению к французам. Почувствовав это настроение среди граждан и определив возможность сокрушить профранцузскую Демократическую республиканскую партию Томаса Джефферсона, Конгресс, в котором доминируют федералисты, подготовил и принял законы об иностранцах и подстрекательстве весной и летом 1798 года.Адамс подписал закон. Эти акты состояли из четырех законодательных актов, которые стали самым ожесточенным внутренним вопросом во время президентства Адамса.
Якобы созданные как средство предотвращения помощи и подстрекательства Франции в Соединенных Штатах и препятствования американской внешней политике, законы на самом деле имели внутриполитический подтекст. Три закона были направлены на иммигрантов, большинство из которых, как правило, голосовали за кандидатов от демократов-республиканцев.Закон о натурализации увеличил срок проживания, необходимый для получения гражданства, с пяти до четырнадцати лет. Закон об иностранцах, единственный из четырех актов, принятых при поддержке обеих партий, разрешал задержание вражеских иностранцев во время войны без суда или защиты. Закон об инопланетных врагах уполномочил президента депортировать иностранцев, которых он считал опасными для безопасности страны. Четвертый закон, Закон о подстрекательстве, объявил заговор с целью воспрепятствовать исполнению федеральных законов и наказал подрывные выступления — штрафами и тюремным заключением.За последние полтора года правления Адамса было вынесено пятнадцать обвинительных заключений и десять обвинительных приговоров в соответствии с Законом о подстрекательстве к делу. Ни один иностранец не был депортирован или арестован, хотя сотни иммигрантов бежали из страны в 1798 и 1799 годах.
Чтобы оплатить военные меры, принятые во время кризиса XYZ, Конгресс федералистов ввел новые высокие гербовые сборы и налоги на жилье. Фермеры в восточной Пенсильвании взбунтовались и напали на федеральных сборщиков налогов в инциденте, позже названном Восстанием Фрайса.Они считали, что новые налоги были разработаны для поддержки большой постоянной армии и флота, против чего они выступали. Некоторые из их лидеров были арестованы и приговорены к смертной казни за государственную измену. Однако накануне выборов 1800 года Адамс помиловал всех заключенных.
В ответ на драконовское использование федералистами федеральной власти республиканцы-демократы Томас Джефферсон и Джеймс Мэдисон тайно составили ряд резолюций. Эти резолюции были внесены в законодательные органы Кентукки и Вирджинии осенью 1798 года.Джефферсон и Мэдисон утверждали, что, поскольку Конституция была создана соглашением между штатами, люди, выступая в законодательных собраниях своих штатов, имели право судить о законности федеральных действий. Следовательно, они объявили законы об иностранцах и подстрекательстве недействительными. (Подробнее о политических последствиях этих действий и реакций см. В разделе «Кампания и выборы 1800 года».)
Хотя никакие другие штаты формально не поддержали резолюции, они сплотили мнение республиканцев и демократов в стране.Что наиболее важно, они поместили Джефферсоновских республиканцев в рамки революционной традиции сопротивления тирании. Резолюции также подняли вопрос о правах штатов и конституционный вопрос о том, как конфликт между двумя властями будет разрешен, кроме отделения или войны.
ЗаписьOMIM — # 145650
Адамс, М., Мэтьюз, К., Коллингвуд, Т. Н., Тон, Ю., Бек-Пекко, П., Чаттерджи, К. К. Генетический анализ 29 родственников с генерализованной и гипофизарной резистентностью к гормону щитовидной железы: выявление тринадцати новых мутаций в гене рецептора гормона щитовидной железы бета. J. Clin. Вкладывать деньги. 94: 506-515, 1994. [PubMed: 8040303] [Полный текст: https: // doi.org / 10.1172 / JCI117362]
Агилар Диосдадо, М., Эскобар-Хименес, Л., Фернандес Сото, М. Л., Гарсия Куриэль, А., Эскобар-Хименес, Ф. Гипертиреоз, вызванный семейной резистентностью гипофиза к тироидным гормонам: успешный контроль с помощью 3,5,3-прайм-трийодтироуксусной кислоты, связанной с пропранололом. J. Endocr. Вкладывать деньги. 14: 663-668, 1991. [PubMed: 1774450] [Полный текст: https: // ссылка.springer.com/article/10.1007/BF03347890]
Геффнер, М. Э., Су, Ф., Росс, Н. С., Хершман, Дж. М., Ван Доп, К., Менке, Дж.Б., Хао, Э., Станзак, Р. К., Итон, Т., Сэмюэлс, Х. Х., Усала, С. Дж. Мутация аргинина в гистидин в кодоне 311 гена C-erbA-beta приводит к появлению мутантного рецептора тироидного гормона, который не опосредует доминантно-негативный фенотип. J. Clin. Вкладывать деньги. 91: 538-546, 1993. [PubMed: 8381821] [Полный текст: https: // doi.org / 10.1172 / JCI116233]
Гершенгорн, М.С., Вайнтрауб, Б.Д. Тиреотропин-индуцированный гипертиреоз, вызванный избирательной резистентностью гипофиза к гормону щитовидной железы: новый синдром «несоответствующей секреции ТТГ». J. Clin. Вкладывать деньги. 56: 633-642, 1975. [PubMed: 1159077] [Полный текст: https://doi.org/10.1172/JCI108133]
Хамон, П., Bovier-Lapierre, M., Robert, M., Peynaud, D., Pugeat, M., Orgiazzi, J. Гипертиреоз из-за избирательной резистентности гипофиза к гормонам щитовидной железы у 15-месячного мальчика: эффективность терапии D-тироксином. J. Clin. Endocr. Метаб. 67: 1089-1093, 1988. [PubMed: 3182960] [Полный текст: https: // Acade.oup.com/jcem/article-lookup/doi/10.1210/jcem-67-5-1089]
Миксон, А.Дж., Рено, Дж. К., Рэнсом, С., Боденнер, Д. Л., Вайнтрауб, Б.Д. Идентификация новой мутации в гене, кодирующем рецептор бета-трийодтиронина, у пациента с очевидной селективной резистентностью гипофиза к гормону щитовидной железы. Clin. Endocr. 38: 227-234, 1993. [PubMed: 8384535] [Полный текст: https: // onlinelibrary.wiley.com/resolve/openurl?genre=article&sid=nlm:pubmed&issn=0300-0664&date=1993&volume=38&issue=3&spage=227]
Рослер, А., Литвин, Ю., Хаге, К., Гросс, Дж., Серази, Э. Семейный гипертиреоз, вызванный несоответствующей секрецией тиреотропина, успешно лечится трийодтиронином. J. Clin. Endocr. Метаб. 54: 76-82, 1982. [PubMed: 6798060] [Полный текст: https: // Acade.oup.com/jcem/article-lookup/doi/10.1210/jcem-54-1-76]
Сасаки, С., Накамура, Х., Тагами, Т., Миёси, Ю., Ногимори, Т., Мицума, Т., Имура, Х. Устойчивость гипофиза к гормону щитовидной железы, связанная с мутацией основания в гормон-связывающем домене человеческого 3,5,3-прайм-трийодтиронинового рецептора-бета. J. Clin. Endocr. Метаб. 76: 1254-1258, 1993. [PubMed: 8496318] [Полный текст: https: // Acade.oup.com/jcem/article-lookup/doi/10.1210/jcem.76.5.8496318]
Спанхеймер, Р. Г., Бар, Р. С., Хейфорд, Дж. К. Гипертиреоз, вызванный несоответствующей гиперсекрецией тиреотропина: исследования на пациентах с избирательной резистентностью гипофиза к гормону щитовидной железы. Arch. Междунар. Med. 142: 1283-1286, 1982. [PubMed: 7092445] [Полный текст: https://jamanetwork.com/journals/jamainternalmedicine/fullarticle/vol/142/pg/1283]