Сложное сопротивление | ПроСопромат.ру
Хрупкие материалы, в отличие от пластичных, плохо работают на растяжение. Однако строительные конструкции, некоторые части машин и механизмов делают из хрупких материалов. Для того, чтобы при внецентренном приложении нагрузки в материале не возникало растягивающих напряжений, определяют ядро сечения.
Ядро сечения — это область, расположенная вокруг центра тяжести сечения, в пределах которой должна находиться точка приложения продольной сжимающей или растягивающей силы, чтобы напряжения в сечении были одного знака, а нулевая линия при этом не пересекала сечения или касалась бы его контура.
Ядро сечения определяется координатами по формулам:
где х0, у0 – координаты точек, принадлежащих касательным к контуру поперечного сечения.
При расчете бруса круглого поперечного сечения при сочетании изгиба и кручения потребуются формулы для расчета эквивалентных напряжений.
Эквивалентное напряжение по гипотезе максимальных касательных напряжений (третья теория прочности):
, где σ — это расчетное нормальное напряжение, τ — расчетное касательное напряжение.
Эквивалентное напряжение по гипотезе энергии формоизменения (четвертая теория прочности):
Нормальное и касательное напряжения определяются по формулам:
где МК – крутящий момент, МИ — изгибающий момент, Wρ – полярный момент сопротивления сечения, WХ — осевой момент сопротивления сечения.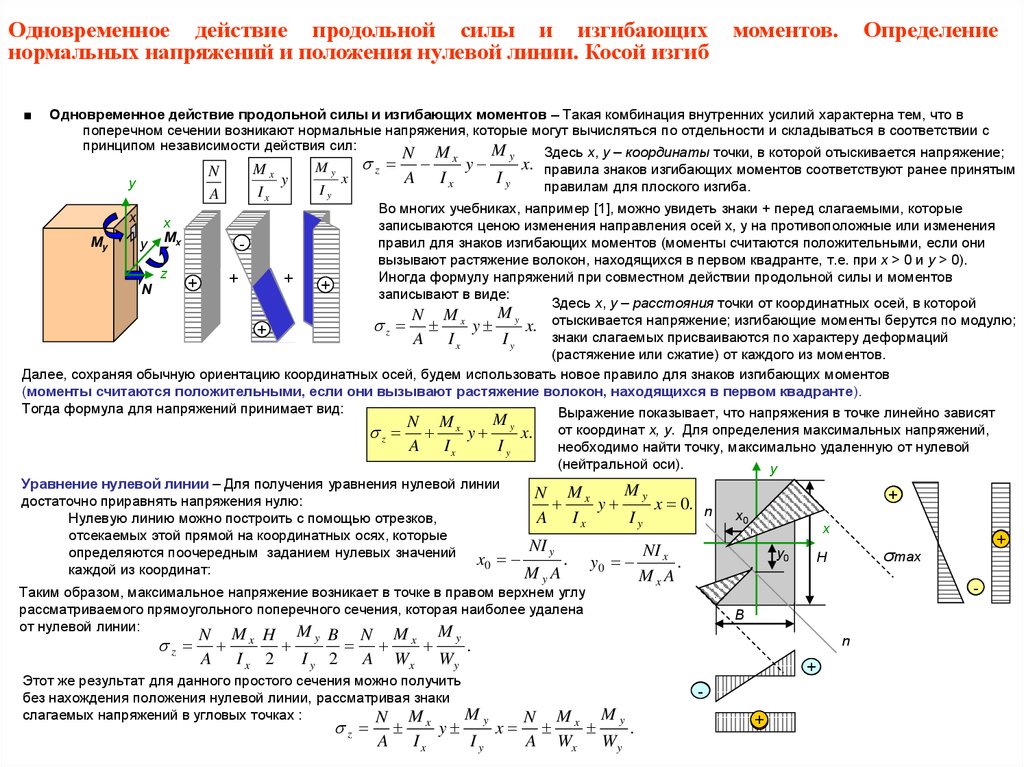
Условие прочности при совместном действии изгиба и кручения:
где Мэкв– эквивалентный момент.
Эквивалентный момент по гипотезе максимальных касательных напряжений:
Эквивалентный момент по гипотезе энергии формоизменения:
Особенность расчета валов
Большинство валов испытывают сочетание деформаций изгиба и кручения. Обычно валы – прямые брусья с круглым или кольцевым сечением. При расчете валов касательные напряжения от действия поперечных сил
Расчеты проводят по опасным поперечным сечениям. При пространственном нагружении вала пользуются гипотезой независимости действия сил, и изгибающие моменты рассматривают в двух взаимно перпендикулярных плоскостях, а суммарный изгибающий момент определяют геометрическим суммированием.
Такие части машин, как валы редко работают на чистое скручивание. Прямой вал при работе изгибается под действием собственного веса, веса шкивов, натяжений ремней и усилий, возникающих в различных зацеплениях различных передач. Таким образом, большинство скручиваемых элементов машин работают на совместное действие изгиба и кручения. К числу подобных элементов относятся и коленчатые валы.
При расчете элементов, работающих на изгиб и кручение необходимо знать расчетные значения изгибающих моментов Ми и крутящего момента Т, где Q – вес шкивов, t – натяжение ремней, Р – окружная сила.
Затем строятся эпюры изгибающих моментов от сил, лежащих в горизонтальной Мг и вертикальной Мв плоскостях и суммарный изгибающий момент Мс по формуле:
Схема действующих моментов:
Определяется расчетный (эквивалентный) момент по одной из теорий прочности.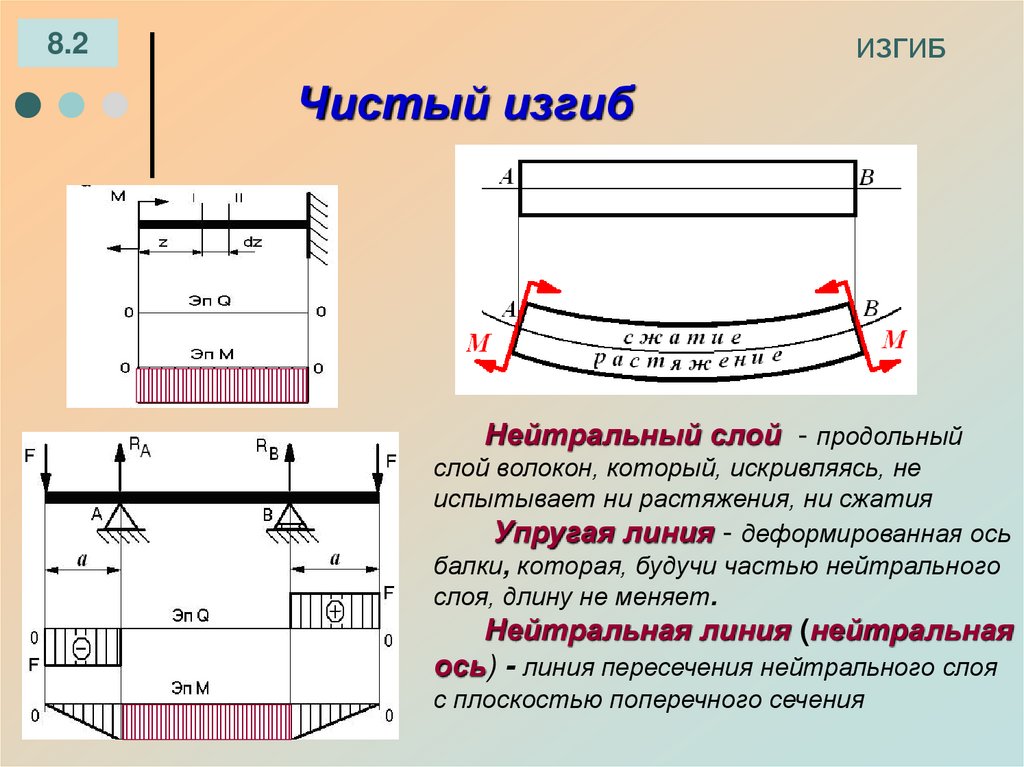
Напряженное состояние в условиях изгиба с кручением
При расчетах валов, изготовленных из конструкционных сталей, используются третья и четвертая теории прочности, согласно которым расчетные (эквивалентные) напряжения определяются так: (1)
где напряжения рассчитывают по известным формулам:
где W – момент сопротивления при изгибе, W=0,1d3;
2W=Wp – момент сопротивления при кручении, WP=0,2d3 =2W.
Подставим эти значения в (1), получим:
Расчетный момент по третьей и четвертой теории прочности:
Условие прочности:
В случае если на вал действует осевая сила N, условие прочности имеет вид:
где А – площадь кругового вала, А=0,785d2.
Напряженное состояние в условиях изгиба и кручения:
Запись опубликована автором admin в рубрике Сложное сопротивление.
Рассмотрим важный частный случай изгиба с растяжением или сжатием. Этот вид деформации получится, если к стержню будут приложены две равные и противоположно направленные силы Р, линия действия которых не будет совпадать с центральной осью стержня, а будет ей параллельна.
Эксцентриситет (е) линии действия силы:
В результате переноса получаем три силовых фактора: нормальная сила
Нормальные напряжения будут определяться по формуле:
перепишем эти формулы в другом виде
Если площадь А вынести за скобки
(1)
По этим формулам можно вычислить напряжения в любой точке сечения.
Положение нулевой (нейтральной) линии определим, приравнивая (1) к нулю:
По этому уравнению можно определить отрезки, отсекаемые нулевой линией на осях координат. Обозначим эти отрезки через ахи а у. Положим ах=0, получим:
(2)
Нейтральная линия не проходит через ту четверть, где приложена сила Р, так как здесь знаки компоненты нормального напряжения одинаковы.
Очевидно, что если точка приложения силы будет передвигаться по прямой, параллельной одной из главных осей инерции, то нейтральная линия будет поворачиваться вокруг некоторой точки, лежащей на другой оси.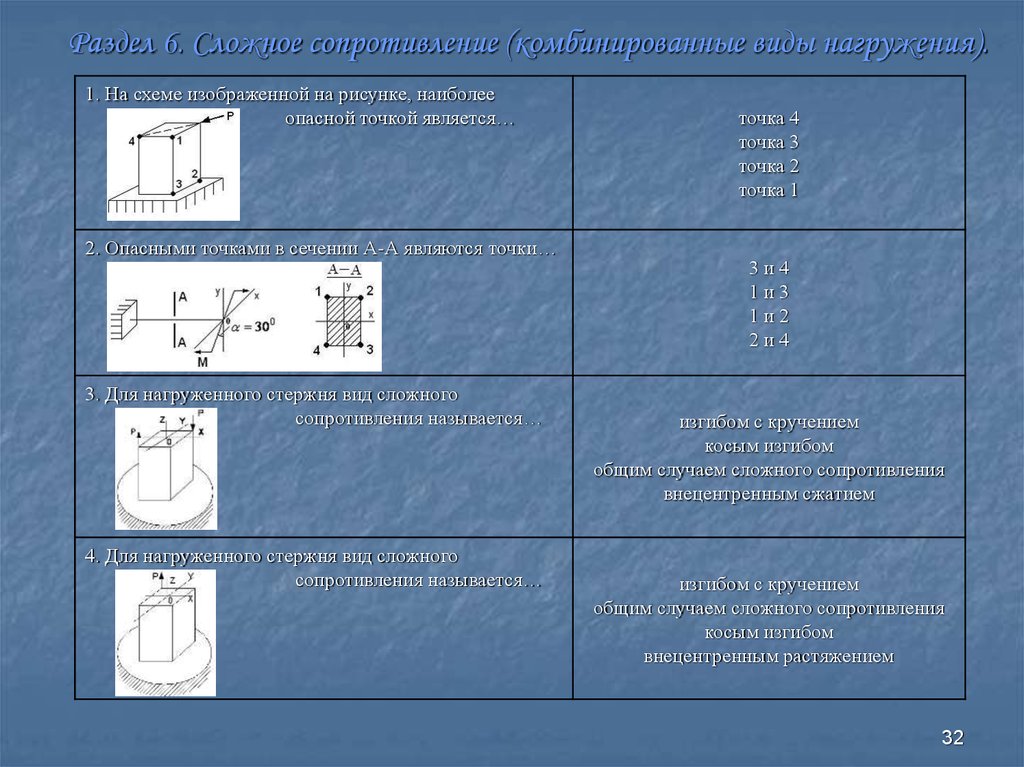
Если координата ур=const, а ахменяется, то нейтральная линия, меняя своё положение в сечении, все время проходит через точку Д на оси Y. Когда хр=0 (точка 1 на оси у), то нейтральная линия параллельна оси Х.
Если точка приложения силы будет перемещаться по
Нейтральная линия проходит через точку Н и поворачивается вокруг неё.
Ядро сечения
Из формул (2) видно, что с уменьшением координат точки приложения силы расстояния ауи ах увеличиваются, то есть точки пересечения нейтральной линии с осями координат удаляются от центра.
При некоторых значениях ури хр нейтральная линия окажется за пределами сечения,
Хрупкие материалы, как известно, плохо работают на растяжение. Между тем, части сооружений подвергаются действию сжимающей нагрузки, нередко их делают из хрупких материалов. Для того, чтобы и при внецентренном приложении сжимающей нагрузки в материале не возникало растягивающих напряжений, нужно ограничить величину эксцентриситета нагрузки, не выводить точку приложения за пределы некоторой области в сечении.
Область, расположенная вокруг центра сечения, в пределах которой должна находиться точка приложения продольной сжимающей или растягивающей силы, чтобы напряжения в сечении были одного знака, называется ядром сечения:
Границы ядра сечения определяются из (2).
Запись опубликована автором admin в рубрике Сложное сопротивление.
Косым изгибом называется такой случай изгиба, при котором плоскость действия нагрузки не совпадает ни с одной из главных осей инерции сечения. Рассмотрим случай, когда к сечению бруса под некоторым углом приложена сила P.
При решении таких задач силу Р раскладывают на составляющие Рх и Ру и затем пользуются принципом независимости действия сил:
Изгибающие моменты в сечении 1-1:
Нормальные напряжения в общем случае:
(1)
Очевидно, что можно найти такую линию, на которой суммарные напряжения равны нулю. Такая линия называется нейтральной (или нулевой), текущие координаты x и y:
(2)
Так как (3)
Из этих формул следует, что нейтральная линия в сечении, в общем случае, не перпендикулярна следу плоскости действия в том же сечении результирующего изгибающего момента.
Эти линии будут перпендикулярны при условии равенства углов α и φ. А это возможно в следующих случаях:
,т.е.когда — угол между силовой и нулевой линией прямой, а это значит, что любая центральная ось сечения является главной осью ,значит ,изгиб будет прямым.
Для таких сечений, у которых центральные оси главные (квадрат ,круг и т.п.), косой изгиб невозможен.
Нейтральная линия делит поперечное сечение на две области: растянутую и сжатую. Проводя линии, параллельные нейтральной и касательной к контуру поперечного сечения, находим в той и другой области наиболее удалённые от нейтральной линии точки О1 и О2 с наибольшими растягивающими и сжимающими напряжениями:
Определим напряжение в одной из точек
(4)
Определим прогибы при косом изгибе.
Прогибы определяются отдельно от составляющих Рх и Ру, затем определяется общее перемещение:
(5)
Определим направление суммарного перемещения:
(6)
Если проанализировать формулы (6) и (3), то можно отметить ,что направление прогибов перпендикулярно к нулевой линии и вместе с тем направление прогибов не совпадает с направлением действующей силы. Если нагрузка представляет плоскую систему сил, то ось изогнутого бруса лежит в плоскости, которая не совпадает с плоскостью действующих сил. Поэтому изгиб и называется косым.
В случае действия пространственной системы сил ось изогнутого стержня представляет пространственную кривую.
Запись опубликована автором admin в рубрике Сложное сопротивление.
Осевое растяжение или сжатие, кручение, плоский изгиб — это простые деформации, которые могут испытывать элементы конструкций. На практике детали машин и сооружений подвергаются действию сил, вызывающих одновременно несколько простых деформаций. Такие случаи работы элементов конструкций называются сложным сопротивлением.
При расчётах на сложное сопротивление обычно используется принцип независимости действия сил, что значительно упрощает решение задач сложного сопротивления. Для рассмотрения силовых факторов при сложном нагружении применим пространственную систему координат, ось Z проведём перпендикулярно сечению стержня, оси Х и Y совместим с главными центральными осями инерции сечения.
Рассмотрим действие силы Р, приложенной в точке А на консольный брус, заделанный одним концом.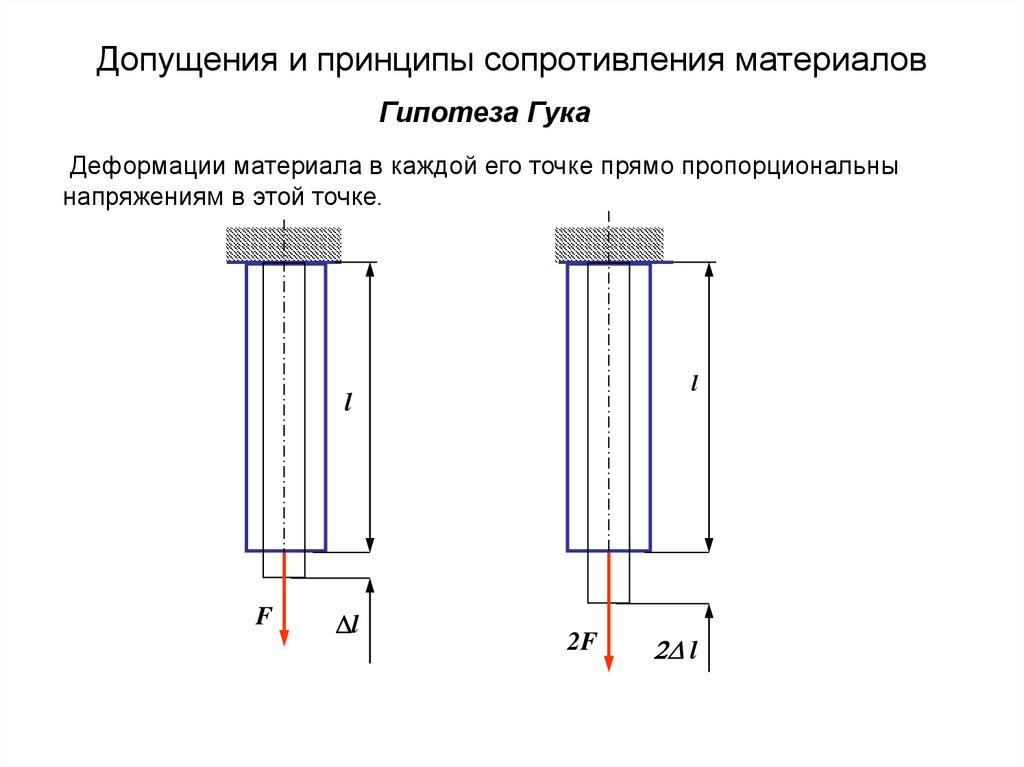
Силовые факторы: — продольная сила
Поперечная сила:
Изгибающие и крутящий моменты:
Нормальная сила и изгибающие моменты вызывают в точках поперечного сечения нормальные напряжения. От поперечных сил и крутящего момента возникают касательные напряжения.
Для определения величины и знака нормальных напряжений пользуются следующим методом. От каждого силового фактора устанавливают знаки напряжений в опасном сечении BCDE (в заделке) и суммируют их с учётом знаков.
Очевидно, что наиболее нагруженной будет точка В, где знаки напряжений от всех составляющих силовых факторов совпадают. Тогда нормальное напряжение:
Покажем положение нейтральной линии (напряжения в ней равны нулю) на рисунке:
Кроме того, от поперечных сил Qx, Qy и крутящего момента в поперечных сечениях возникают касательные напряжения.
Касательные напряжения от поперечных сил определяются по формуле Журавского:
Суммарное касательное напряжение от поперечных сил определяется так:
Рассмотрим, как определяются касательные напряжения от крутящего момента в прямоугольных сечениях (брус имеет прямоугольное сечение).
Для оценки напряжённого состояния при кручении стержней прямоугольного сечения используется гидродинамическая аналогия. Согласно этой теории распределение касательных напряжений по высоте и ширине сечения подобно скорости движения жидкости в трубке круглого сечения, согнутой в виде прямоугольника. Очевидно, что наибольшей скорости разгона жидкость будет достигать в середине длинных сторон прямоугольника и будет равна нулю в углах, где направление скорости изменяется на девяносто градусов. Аналогично, наибольшие касательные напряжения будут в серединах длинных сторон прямоугольника.
Формулы для определения касательных напряжений для прямоугольного сечения находятся в рубрике «Кручение» Для того, чтобы определить касательные напряжения в серединах узких сторон, следует полученные касательные напряжения умножить на коэффициент η. (определяется по таблице вместе с коэффициентами α, β в зависимости от величины отношения h/b).
Эпюра распределения касательных напряжений при кручении стержней прямоугольного сечения:
Рассмотрим данную схему распределения касательных напряжений от поперечных сил и кручения. Очевидно, что наиболее опасной точкой по касательным напряжениям будет точка К, где касательные напряжения будут равны:
Напряжённое состояние в точке К:
Для точной оценки напряжённого состояния в точке К следует определить главные напряжения в точке К по формуле:
Условие прочности имеет вид:
Запись опубликована автором admin в рубрике Сложное сопротивление.
8. Сложное сопротивление бруса
Ранее рассматривались простейшие виды деформации бруса, при которых от действия определённых нагрузок в поперечных сечениях бруса возникали отдельные внутренние силовые факторы: растяжение и сжатие (N), кручение ( M к), прямой изгиб ( M и Q). Однако в других случаях нагружения в поперечных сечениях бруса могут возникать различные сочетания внутренних силовых факторов (в общем случае — все шесть). Такая сложная деформация бруса называется
сложным сопротивлением. Используя принцип суперпозиции, слож-
ное сопротивление бруса может быть представлено как сумма простых видов деформации. Особо оговаривается лишь случай бруса относительно большой жёсткости при действии сжимающей силы, чтобы исключить возможность потери устойчивости бруса (см. часть II). Чаще всего рассматривают специальные случаи сложного сопротивления бруса: косой изгиб, косой изгиб с растяжением (сжатием), внецентренное растяжение (сжатие), изгиб с кручением.
Косой изгиб возникает в случае действия поперечной нагрузки (P, M, q) в плоскости, проходящей через ось бруса и не совпадающей ни с одной из главных плоскостей инерции. Плоскость действия на-
грузки называется силовой плоскостью. Главной плоскостью инерции
называется плоскость, в которой расположены соответствующие главные оси инерции всех поперечных сечений бруса. В общем случае таких плоскостей две. Например, для призматического консольного бруса (рис. 8.1,а) — вертикальная (Оyz) и горизонтальная (Оxz) плоскости.
Примечание. Исключение составляет брус, имеющий сечение в виде круга или правильного многоугольника. Для такого бруса никогда не будет косого изгиба.
Рассмотрим особенности косого изгиба на примере консольной призматической балки, нагруженной силой P в торцевом сечении под углом α к оси y (см. рис. 8.1,а). Разложим силу P на составляющие Px и Py по осям:
Px = P sinα ; Py = P cosα . | (8. |
1)Каждая из этих сил действует в одной из главных плоскостей инерции и вызывает прямой изгиб. Используя принцип суперпозиции, представим косой изгиб как сумму двух прямых изгибов. Опасное сечение — в заделке, где расчётные значения изгибающих моментов от сил Px и Py равны:
M x=Pyl = Pl cosα =M cosα ; M y=Pxl= Pl sinα =M sinα ; M =Pl. (8.2)
Рис. 8.1
Напряжения при косом изгибе
Запишем выражения для нормальных напряжений в произвольной точке А(x,y) сечения балки (рис. 8.1,б), рассматривая их как сумму напряжений для каждого прямого изгиба (см. формулу (6.7)):
σ (x,y) = | M | x | y+ | M y | x. | (8.3) |
|
| Jy | ||||
| Jx |
|
| |||
Для вычисления максимальных напряжений необходимо знать положение нейтральной линии сечения.
Согласно определению нейтральная линия представляет геометрическое место точек, где нормальные напряжения равны нулю:
σ (x,y)= 0 èëè | M x | y+ | M y | x = 0. |
|
| |||
| Jx | Jy | ||
Откуда, учитывая соотношения (8.2), получаем уравнение нейтральной линии при косом изгибе:
y= −− | M | y |
|
| J | x | x | èëè y= −− ( | J | x | tgα )x. | (8.4) |
M x |
|
|
|
|
| |||||||
|
|
| Jy |
| Jy |
| ||||||
Нейтральная линия проходит через центр сечения и расположена в квадрантах, противоположных тем, где расположена линия силовой плоскости (рис.
8.1,б). Из условия Jx≠Jy следует, что нейтральная ли-
ния не перпендикулярна силовой плоскости. При этом нейтральная линия повёрнута от направления, перпендикулярного силовой плоскости, в сторону главной оси минимального момента инерции. Соответственно, при Jx=Jy невозможен косой изгиб, т.к. все центральные оси сечения являются главными (всегда имеет место прямой изгиб).
Зная положение нейтральной линии, можно построить эпюру нормальных напряжений в сечении (эп.σ на рис. 8.1,б). Максимальные напряжения возникают в точках, наиболее удалённых от нейтральной линии (xm, ym — координаты такой точки):
σ | m ax | = | M | x | y | + | M y | x . | (8.5) |
|
|
| |||||||
|
|
|
| m |
| Jy | m |
| |
|
|
| Jx |
|
|
| |||
Для сечения произвольной формы координаты xm, ym обычно определяются графическим образом для точек касания контура сечения линиями, параллельными нейтральной линии (рис.
8.1,в). Для сечений, имеющих наружные угловые точки и две плоскости симметрии (прямоугольник, двутавр и т.д.) xm=xmax, ym=ymax, максимальные напряжения определяются согласно формул (8.5) и (6.8) наиболее просто, используя моменты сопротивления сечения относительно осей x, y
(Wx=Jx/ymax, Wy=Jy/xmax):
σ m ax = | M | x | + | M y | . | (8.6) |
|
| W y | ||||
| W x |
|
| |||
Из формулы (8.6) видно, что при косом изгибе могут значительно увеличиваться нормальные напряжения в балках, имеющих сечения с существенно различными моментами сопротивления (например, двутавр, швеллер, для которых Wx >> Wy).
Касательные напряжения при косом изгибе играют такую же второстепенную роль, как и при прямом изгибе.
При косом изгибе величина полных касательных напряжений в определённой точке сечения находится как геометрическая сумма компонент τ x и τ y:
τ = ττ 2x++ ττ 2y .
Напряжения τ x и τ y вычисляются по формуле (6.11) для каждого прямого изгиба, используя соответствующие значения поперечных сил
Qx и Qy.
Перемещения при косом изгибе
При определении перемещений также применяется принцип суперпозиции. Например, компоненты линейного перемещения центра сечения δ x и δ y в главных плоскостях инерции вычисляются с использованием какого-нибудь метода, а полное перемещение δ (по величине и направлению) определяется как геометрическая сумма этих компонент (рис. 8.1,г):
δ = δ x2+δ y2 ; | tgβ = | δ | x , | (8.7) | ||||
|
|
|
| δ | y |
| ||
где β — угол между вектором |
|
| и осью Оy. |
| ||||
δ |
| |||||||
При косом изгибе β ≠ α , a вектор |
|
| полного перемещения пер- | |||||
δ | ||||||||
пендикулярен нейтральной линии (см. рис. 8.1,г).
8.2. Косой изгиб с растяжением (сжатием)
В этом случае имеет место сложная деформация бруса, включающая изгиб и осевое растяжение или сжатие (рис. 8.2,а). Кроме изгибающих моментов ( M x и M y), определяемых для опасного сечения по формулам (8.2), учитывается и нормальная сила N= ± Pо (знак «+» соответствует растягивающей силе Pо, знак «-» — сжимающей силе). Используя принцип суперпозиции, по аналогии с выражением (8.3) суммарные напряжения записываются следующим образом:
σ (x,y)= | N | + | M | x | y+ | M y | x. | (8.8) |
F |
|
| Jy | |||||
|
| Jx |
|
| ||||
Уравнение нейтральной линии в сечении из условия σ (x,y)=0
принимает вид:
y = ax + b, a = — | M | y |
| J | x | , | b = — | N | J | x | . (8.9) |
M x |
|
| M x |
| F | ||||||
|
| Jy |
|
| |||||||
Заказать задание по сопротивлению материалов.
Контрольные бумаги на заказ.ГлавнаяСопротивление материалов. Задания на сопротивление материалов.
4 дня назад
Studik.kiev.ua
Помощь студентам
ПОМОЩЬ В РЕШЕНИИ ТЕСТИРОВАНИЯ НА СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ! Где заказать решение задач на сопротивление материалов?Заказать задания на сопротивление материалов просто! Есть специальные агентства, в которых есть авторы, умеющие решать такие задачи. Учителя часто дают ученикам домашнее задание, которое они должны сделать самостоятельно. Учащийся сам решает, заказывать ли задания на материальное сопротивление в агентстве или выполнять их самостоятельно. Естественно, что студентам предлагаются учебники, написанные преподавателями, но, как правило, они включают решение только одной задачи, и это общий случай.
А ученику сложно разобраться в своих проблемах, потому что решение проблемы зависит от многих факторов, которые нужно учитывать.
Комплекс решения задач охватывает разные науки: механику (статика, кинематика, динамика), математику (геометрия, алгебра, тригонометрия), материаловедение и др.
Изучение дисциплины «сопротивление материалов» в техникумах представляет определенные трудности для студентов. Это связано с недостатками изучения физики и математики в школьных программах. Программа института требует глубоких начальных знаний и понимания физических процессов наряду со знанием математических правил расчетов и преобразований.
Большинство формул в науке о сопротивлении материалов сложны и основаны на использовании специальных функций. Предлагаем отличный вариант в таких ситуациях – заказать курсовую работу по сопротивлению материалов у нас. Для этого просто заполните форму заказа на нашем сайте и мы тут же найдем автора для вашего теста.
Заказать решения задач по сопротивлению материалов можно здесь⇓
Нашим исполнителям не составит труда решить даже самые сложные задачи по сопротивлению материалов.
Ведь многие из них преподают в вузах и хорошо разбираются в своем предмете. Для автора это будет явно не первая контрольная работа по сопротивлению материалов на заказ. Поэтому вы можете не сомневаться в качестве наших услуг.
Доверьте решение испытательной работы на стойкость материалов нашей компании Studik. А о такой дисциплине, как «сопротивление материалов», можно и не думать. Большим подспорьем ученику в обучении и поиске правильного решения является заказ задачи на сопротивление материалов у людей, достаточно хорошо разбирающихся в этих вопросах.
Готовое решение может помочь, как разобраться в вопросах решения именно той задачи, которая задана, так и проверить свое индивидуальное решение и найти ошибку. Во многих случаях при сдаче курсовой или самостоятельной работы преподавателю могут быть заданы провокационные вопросы о ходе решения, источниках тех или иных данных, сопровождающих решение задачи. А студент, не разбирающийся в технической стороне вопроса – ответить не сможет.
Метод решения задачи будет подробно описан применительно к этой задаче и с небольшим усилием, так сказать, просто прочитав или переписав решение, учащийся по большей части запомнит ход решение. Преобладающее большинство технических задач, решаемых методами сопротивления материалов, требуют длительных расчетов.
В расчетах используются различные физические величины, имеющие свою размерность – ньютоны, метры, паскали, градусы, градусы Цельсия, радианы, килограммы и т. д. Будущему инженеру или технику сложно учесть все эти факторы и готовое решение поможет. Часто расчеты не дают правдоподобных ответов, а после ночи расчетов нет положительных результатов. Наличие готового решения позволит вам сравнить ход решения, найти несоответствия и понять причину ошибки.
Зачем заказывать курсовую работу по сопротивлению материалов? Да, потому что упругость материалов имеет ту же физическую основу, но подходы к решению совершенно разные. Техническому специалисту, инженеру необходимо знать основные понятия.
Сопротивление материала является исходной и первой инженерной основой для расчета последующих проектов. Знание работы материалов под действием различных сил позволяет создавать и понимать работу всех механизмов на основе законов механики.
Разыскивается в качестве предостережения, что заказ заданий по сопротивлению материалов (курсовых или контрольных), сдача его учителю не гарантирует 100% успеха, т.к. опять же, возможно, придется отвечать на вопросы, поэтому следует ознакомиться с решением обработайте и пройдитесь по пунктам расчета.
Процесс обучения строится из запоминания способов решения, общих принципов формул, с какой стороны начинать расчеты, просмотра готовых решений. Затем, когда багаж знаний получен, в памяти приходит понимание принципов строения под действием внутренних и внешних сил.
Большой опыт работы со студентами ВУЗов г. Киева таких как: Университет экономики и права «КРОК», Национальная академия внутренних дел (НИАИ), Академия адвокатуры Украины (ААУ), Институт интеллектуальной собственности НУ «Одесская юридическая академия» », Киевский кооперативный институт бизнеса и права (ККИБП), Киевский международный университет (КИМУ), Киевский национальный торгово-экономический университет (КНТЭУ), Киевский национальный университет им.
Киевский национальный торгово-экономический университет (КНУ), Киевская национальная академия туризма, экономики и права (КУТЭП), Национальная академия Службы безопасности Украины, Национальный авиационный университет (НАУ), Национальный университет Киево-Могилянская академия (НаУКМА), Национальный университет «Киево-Могилянская академия» (НаУКМА). (НаУКМА), Национальный педагогический университет имени М. П. Драгоманова (НПУ)
Помимо киевских вузов мы пишем тесты на прочность материалов для других учебных заведений Украины.
Выполняем контрольные работы по сопротивлению материалов на заказ в Украине и России:
Вы можете заказать задания по сопротивлению материалов не только по Украине, но и в таких городах как Киев, Днепр, Кривой Рог, Запорожье, Херсон, Винница, Одесса, Харьков, Кировоград, Луцк, Сумы, Полтава, Чернигов, Житомир, Черкассы, Львов, Ивано-Франковск, Хмельницкий, Тернополь, Ровно, Черновцы, Николаев, Симферополь.
Купить тесты Сопромат в России: Москва, Санкт-Петербург, Новосибирск, Екатеринбург, Нижний Новгород, Казань, Самара, Омск, Челябинск, Ростов-на-Дону, Уфа, Волгоград, Красноярск, Пермь, Воронеж, Саратов, Краснодар, Тольятти, Барнаул, Тюмень, Ижевск, Ульяновск, Иркутск, Владивосток, Ярославль, Хабаровск, Махачкала, Оренбург, Новокузнецк, Томск, Кемерово, Рязань, Астрахань, Пенза, Набережные Челны, Липецк, Тула, Киров, Чебоксары, Калининград, Курск, Улан-Удэ , Ставрополь, Магнитогорск, Брянск, Иваново, Тверь, Белгород, Сочи, Нижний Тагил.
Срок выполнения
Написание курсовых работ и тестов определяется индивидуально, исходя из сложности задания обычно на данный вид работ наши сотрудники тратят от 3 до 7 дней.
Курсовую работу по сопротивлению материалов заказать здесь⇓
500 — ВНУТРЕННЯЯ ОШИБКА СЕРВЕРА
Почему я вижу эту страницу? Ошибки
500 обычно означают, что сервер столкнулся с непредвиденной ситуацией, которая помешала ему выполнить запрос, сделанный клиентом. Это общий класс ошибок, возвращаемый веб-сервером, когда он сталкивается с проблемой, в которой сам сервер не может более конкретно указать состояние ошибки в своем ответе клиенту.
Во многих случаях это указывает не на реальную проблему с самим сервером, а скорее на проблему с информацией, к которой серверу было приказано обратиться или вернуть в результате запроса. Эта ошибка часто вызвана проблемой на вашем сайте, которая может потребовать дополнительной проверки вашим веб-хостом.
Для получения дополнительной помощи обратитесь к своему веб-хостингу.
Могу ли я что-нибудь сделать?
Существует несколько распространенных причин появления этого кода ошибки, включая проблемы с отдельными сценариями, которые могут выполняться по запросу. Некоторые из них легче обнаружить и исправить, чем другие.
Владение файлами и каталогамиСервер, на котором вы находитесь, в большинстве случаев запускает приложения очень специфическим образом. Обычно сервер ожидает, что файлы и каталоги принадлежат вашему конкретному пользователю cPanel user . Если вы внесли изменения в владельца файла самостоятельно через SSH, сбросьте владельца и группу соответствующим образом.
Права доступа к файлам и каталогам Сервер, на котором вы находитесь, в большинстве случаев запускает приложения очень специфическим образом. Сервер обычно ожидает, что файлы, такие как HTML, изображения и другие медиафайлы, будут иметь режим разрешений 9.
0011 644 . Сервер также ожидает, что режим разрешений для каталогов в большинстве случаев будет установлен на 755 .
(См. раздел «Разрешения для файловой системы»).
Если вы хотите проверить определенное правило в вашем файле .htaccess, вы можете прокомментировать эту конкретную строку в .htaccess, добавив # в начало строки. Вы должны всегда делать резервную копию этого файла, прежде чем начать вносить изменения.
Например, если .htaccess выглядит как
DirectoryIndex default.html
AddType application/x-httpd-php5 php
Тогда попробуйте что-то вроде этого
DirectoryIndex default.html
#AddType application/x-httpd-php5 php
Примечание: Из-за того, как настроены серверные среды, вы не можете использовать аргументы php_value в файле .htaccess.
Превышен лимит процессов Возможно, эта ошибка вызвана слишком большим количеством процессов в очереди сервера для вашей отдельной учетной записи.
Каждая учетная запись на нашем сервере может иметь только 25 одновременных активных процессов в любой момент времени, независимо от того, связаны ли они с вашим сайтом или другими процессами, принадлежащими вашему пользователю, такими как почта.
ps faux
Или введите это, чтобы просмотреть учетную запись определенного пользователя (не забудьте заменить имя пользователя на фактическое имя пользователя):
ps faux |grep имя пользователя
Если у вас есть идентификатор процесса («pid» ), введите это, чтобы убить конкретный процесс (обязательно замените pid фактическим идентификатором процесса):
kill pid
Ваш веб-хостинг сможет посоветовать вам, как избежать этой ошибки, если она вызванные технологическими ограничениями. Пожалуйста, свяжитесь с вашим веб-хостингом. Обязательно укажите шаги, необходимые для появления ошибки 500 на вашем сайте.
Понимание разрешений файловой системы
Символическое представление Первый символ указывает тип файла и не связан с разрешениями.
Остальные девять символов находятся в трех наборах, каждый из которых представляет класс разрешений в виде трех символов. Первый набор представляет класс пользователя. Второй набор представляет групповой класс. Третий набор представляет остальные классы.
Каждый из трех символов представляет права на чтение, запись и выполнение:
- r , если чтение разрешено, — , если нет.
- w если запись разрешена, — если нет.
- x , если выполнение разрешено, — , если нет.
Ниже приведены некоторые примеры символической записи:
- -rwxr-xr-x обычный файл, пользовательский класс которого имеет полные разрешения, а группа и другие классы имеют только разрешения на чтение и выполнение.
- crw-rw-r— специальный символьный файл, чьи пользовательские и групповые классы имеют права на чтение и запись, а остальные классы имеют только права на чтение.
- dr-x—— каталог, чей пользовательский класс имеет права на чтение и выполнение, а группа и другие классы не имеют разрешений.
Другим методом представления разрешений является восьмеричная запись (с основанием 8), как показано. Это обозначение состоит как минимум из трех цифр. Каждая из трех крайних правых цифр представляет отдельный компонент разрешений: пользователь , группа и другие .
Каждая из этих цифр представляет собой сумму составляющих ее битов. В результате определенные биты добавляются к сумме, представленной числом:
- Бит чтения добавляет 4 к ее сумме (в двоичном формате 100),
- Бит записи добавляет к своему общему количеству 2 (в двоичном формате 010) и
- Бит выполнения добавляет 1 к своей сумме (в двоичном формате 001).
Эти значения никогда не создают неоднозначных комбинаций.
каждая сумма представляет определенный набор разрешений. С технической точки зрения, это восьмеричное представление битового поля — каждый бит ссылается на отдельное разрешение, и группировка по 3 бита за раз в восьмеричной форме соответствует группировке этих разрешений по 9.0011 пользователь , группа и другие .
Режим разрешений 0755
- 4+2+1=7
- Чтение, запись, выполнение
- 4+1=5
- Чтение, выполнение
- 4+1=5
- Чтение, выполнение
Режим разрешений 0644
- 4+2=6
- Чтение, запись
- 4
- Читать
- 4
- Читать
Как изменить файл .htaccess
Файл .htaccess содержит директивы (инструкции), которые сообщают серверу, как вести себя в определенных сценариях, и напрямую влияют на работу вашего веб-сайта.
Перенаправление и переписывание URL — это две очень распространенные директивы, находящиеся в файле .htaccess, и многие сценарии, такие как WordPress, Drupal, Joomla и Magento, добавляют директивы в .htaccess, чтобы эти сценарии могли работать.
Возможно, вам потребуется отредактировать файл .htaccess в какой-то момент по разным причинам. В этом разделе рассматривается, как редактировать файл в cPanel, но не то, что может потребоваться изменить. статьи и ресурсы для этой информации.)
Существует множество способов редактирования файла .htaccess- Отредактируйте файл на своем компьютере и загрузите его на сервер через FTP
- Использовать режим редактирования программы FTP
- Используйте SSH и текстовый редактор
- Использование файлового менеджера в cPanel
Самый простой способ отредактировать файл .htaccess для большинства людей — через диспетчер файлов в cPanel.
Как редактировать файлы .
htaccess в файловом менеджере cPanel Прежде чем что-либо делать, рекомендуется сделать резервную копию вашего веб-сайта, чтобы вы могли вернуться к предыдущей версии, если что-то пойдет не так.
Открыть файловый менеджер- Войдите в cPanel.
- В разделе «Файлы» щелкните значок File Manager .
- Установите флажок для Корень документа для и выберите доменное имя, к которому вы хотите получить доступ, из раскрывающегося меню.
- Убедитесь, что установлен флажок Показать скрытые файлы (dotfiles) «.
- Нажмите Перейти . Файловый менеджер откроется в новой вкладке или окне.
- Найдите файл .htaccess в списке файлов. Возможно, вам придется прокрутить, чтобы найти его.
- Щелкните правой кнопкой мыши файл .htaccess и выберите Редактировать код в меню.
Кроме того, вы можете щелкнуть значок файла .htaccess, а затем щелкнуть значок Code Editor в верхней части страницы. - Может появиться диалоговое окно с вопросом о кодировании. Просто нажмите Изменить , чтобы продолжить. Редактор откроется в новом окне.
- Отредактируйте файл по мере необходимости.
- Когда закончите, нажмите Сохранить изменения в правом верхнем углу. Изменения будут сохранены.
- Протестируйте свой веб-сайт, чтобы убедиться, что ваши изменения были успешно сохранены. Если нет, исправьте ошибку или вернитесь к предыдущей версии, пока ваш сайт снова не заработает.
- После завершения нажмите Закрыть , чтобы закрыть окно диспетчера файлов.
Как изменить права доступа к файлам и каталогам
Права доступа к файлу или каталогу сообщают серверу, каким образом он должен иметь возможность взаимодействовать с файлом или каталогом.
В этом разделе рассказывается, как изменить права доступа к файлу в cPanel, но не о том, что может потребоваться изменить.
(Дополнительную информацию см. В разделе о том, что вы можете сделать.)
- Использовать программу FTP
- Используйте SSH и текстовый редактор
- Используйте файловый менеджер в cPanel
Самый простой способ изменить права доступа к файлам для большинства людей — через диспетчер файлов в cPanel.
Как изменить права доступа к файлам в файловом менеджере cPanelПрежде чем что-либо делать, рекомендуется сделать резервную копию вашего веб-сайта, чтобы вы могли вернуться к предыдущей версии, если что-то пойдет не так.
Откройте файловый менеджер- Войдите в cPanel.
- В разделе «Файлы» нажмите значок Значок файлового менеджера .
- Установите флажок для Корень документа для и выберите доменное имя, к которому вы хотите получить доступ, из раскрывающегося меню.
