Сопромат решение задач метод сечений: Метод сечений (РОЗУ)

Метод сечений решение задач по сопромату

Содержание:

  1. Рассмотрим общий прием определения внутренних усилий, называемый методом сечений.

Метод сечений (см. рис. 2) состоит в том, что брус, находящийся в равновесии под действием системы внешних сил, мысленно рассекают на две части (рис. 2, а), и рассматривают равновесие одной из них, заменяя действие отброшенной части бруса системой внутренних сил, распределенных по сечению (рис. 2, б).

Заметим, что внутренние силы для бруса в целом, становятся внешними для одной из его частей. Причем во всех случаях внутренние усилия уравновешивают внешние силы, действующие на отсеченную часть бруса.

В соответствии с правилом параллельного переноса сил статики приведем все распределенные внутренние силы к центру тяжести сечения. В результате получим их главный вектор и главный момент системы внутренних сил (рис. 2, в).

  • Выбрав систему координат так, чтобы ось являлась продольной осью бруса и проецируя главный вектор и главный момент внутренних сил на оси, получим шесть внутренних силовых факторов (ВСФ) в сечении бруса: продольную силу поперечные силы изгибающие моменты а также крутящий момент

По виду внутренних силовых факторов можно определить характер на-гружения бруса. Если в поперечных сечениях бруса возникает только продольная сила а другие силовые факторы отсутствуют, то имеет место «растяжение» или «сжатие» бруса (в зависимости от направления силы Если в сечениях действуют только поперечная сила — это случай «чистого сдвига». При «кручении» в сечениях бруса действуют только крутящие моменты При «чистом изгибе» — только изгибающие моменты Возможны также комбинированные виды нагружения (изгиб с растяжением, кручение с изгибом и др.) — это случаи «сложного сопротивления».

Для наглядного представления характера изменения внутренних силовых факторов вдоль оси бруса строят их графики, называемые эпюрами.

Эпюры позволяют определить наиболее нагруженные участки бруса и установить опасные сечения.

Внутри любого материала имеются внутренние межатомные силы, наличие которых определяет способность тела воспринимать действующие на него внешние силы, сопротивляться разрушению, изменению формы и размеров. Приложение к телу внешней нагрузки вызывает изменение (увеличение или уменьшение) внутренних сил, т. е. появление дополнительных внутренних сил.

В сопротивлении материалов изучаются дополнительные внутренние силы. Поэтому под внутренними силами (или внутренними усилиями) в сопротивлении материалов понимают силы взаимодействия между отдельными элементами сооружения или между отдельными частями элемента, возникающие под действием внешних сил. Это понятие равносильно допущению об отсутствии в теле внутренних сил до приложения к нему внешних нагрузок. Поэтому иногда считают, что в сопротивлении материалов принимается гипотеза о ненапряженном начальном состоянии тела.

Рассмотрим элемент конструкции, на который действует система внешних сил, находящихся в равновесии (рис. 4.1,а). Напоминаем, что в число внешних сил входят как заданные активные силы, так и реакции связей. Мысленно рассечем элемент плоскостью Силы воздействия отсеченной правой части элемента на его левую часть (на правый ее торец) являются по отношению к ней внешними; для всего же элемента в целом они являются внутренними силами.

Этим силам (на основании известного закона механики: действие равно противодействию) равны по величине и противоположны по направлению внутренние силы воздействия левой части элемента на правую.

В общем случае пространственной задачи взаимодействие между левой и правой частями элемента можно представить некоторой силой приложенной в произвольно выбранной точке сечения и моментом относительно некоторой оси, проходящей через эту точку (рис. 4.1,6, в).

Возможно вам будут полезны данные страницы:

Двухопорная балка по сопромату задачи с примерами и решениями

Решение статически неопределимых задач

Сопромат готовые задачи с решением

Сила является главным вектором, а момент —главным моментом системы внутренних сил, действующих по проведенному сечению.

Определение внутренних сил, возникающих в брусе, обычно производится для сечений, перпендикулярных к его продольной оси, т. е. для поперечных сечений бруса. Точка принимается расположенной на оси бруса, т. е. совпадающей с центром тяжести его поперечного сечения.

Главный вектор раскладывается на две составляющие силы: силу направленную вдоль оси бруса и называемую продольной силой, и силу действующую в плоскости поперечного сечения и называемую поперечной силой (рис. 5.1,а). Момент раскладывается на два составляющих момента: момент действующий в плоскости поперечного сечения и называемый крутящим моментом, и момент действующий в плоскости, перпендикулярной к поперечному сечению, и называемый изгибающим моментом (рис. 5.1,6).

Каждому из внутренних усилий соответствует определенный вид деформации бруса. Продольной силе соответствует растяжение (или сжатие), поперечной силе —сдвиг, крутящему моменту —кручение, а изгибающему моменту — изгиб. Различные их сочетания, например сжатие с изгибом, изгиб с кручением и т. п., представляют собой сложные сопротивления.

Внутренние усилия характеризуются каждое одним параметром—величиной усилия.

Поперечная сила характеризуется двумя параметрами, например, величиной этой силы и ее направлением (в плоскости поперечного сечения бруса). Более удобно силу определять через составляющие ее поперечные силы параллельные двум взаимно перпендикулярным осям, расположенным в плоскости поперечного сечения бруса (рис. 5.1, а). Изгибающий момент также характеризуется двумя параметрами; его обычно раскладывают на два составляющих изгибающих момента относительно осей

Таким образом, взаимодействие любых двух частей конструкции характеризуется тремя составляющими главного вектора и тремя составляющими главного момента внутренних сил, возникающих в рассматриваемом поперечном сечении. Эти составляющие называются внутренними силовыми факторами, или внутренними усилиями.

Рассмотрим общий прием определения внутренних усилий, называемый методом сечений.

Рассечем стержень (рис. 6.1, а) плоскостью совпадающей с поперечным сечением стержня. В полученном поперечном сечении в общем случае действует шесть внутренних усилий: (рис.

6.1, б, в).

Правая часть стержня (рис. 6.1,в) находится в равновесии; значит, внешние силы приложенные к ней, уравновешиваются внутренними усилиями, действующими на правую часть. Но те же внешние силы уравновешиваются и нагрузками, приложенными к левой части стержня (силами так как весь стержень в целом (рис. 6.1,а) также находится в равновесии. Следовательно, нагрузки, приложенные к левой части стержня (силы и внутренние усилия, действующие на правую часть, статически эквивалентны друг другу.

Таким образом, проекция на какую-либо ось внутренних усилий в сечении, действующих со стороны левой части стержня на правую, равна проекции на эту ось всех внешних сил, приложенных к левой части.

Аналогично, момент относительно какой-либо оси внутренних усилий в сечении, действующих со стороны левой части стержня на правую, равен моменту всех внешних сил, приложенных к левой части относительно этой оси.

Из шести внутренних усилий, действующих в поперечном сечении стержня, проекции пяти усилий на каждую из осей равны нулю. Аналогично равны нулю и моменты пяти внутренних усилий относительно каждой из указанных осей. Это позволяет легко определять внутренние усилия в стержне, проектируя на ось или или все внутренние усилия, действующие на правую часть стержня (рис. 6.1, б), и все внешние силы, приложенные к левой части (рис. 6.1,6), или определяя их моменты относительно одной из указанных осей.

Определим, например, величину продольной силы в поперечном сечении показанном на рис. 6.1, а. Как следует из рис. 6.1, в, проекция на ось х всех внутренних усилий, действующих на правую часть стержня, равна если для проекции положительным считать направление справа налево. Поэтому сила равна сумме проекций на ось всех внешних сил, действующих на левую часть стержня (т. е. сил рис. 6.1,6). Аналогично значение, например, крутящего момента в поперечном сечении стержня равно сумме моментов сил относительно

оси если положительными считать моменты, направленные по часовой стрелке (при взгляде с левого конца оси на правый), и т. д.

Внутренние силы, действующие в сечении со стороны левой части на правую, можно определить по внешним силам, приложенным не к левой, а к правой части. В этом случае полученные направления проекций внешних сил на выбранные оси и моментов относительно этих осей необходимо изменять на противоположные.

Внутренние усилия в каком-либо сечении обычно определяют по внешним силам, приложенным к той части конструкции (расположенной по одну сторону от рассматриваемого сечения), на которую действует меньше сил.

В теоретической механике, в разделе статики, широко применяется замена системы сил их равнодействующей и перенос силы по линии ее действия. В сопротивлении материалов это не всегда возможно, так как может приводить к неправильным результатам. Например, совершенно очевидно, что при определении внутренних сил в сечении (рис. 6.1, а) замена нескольких сил, приложенных к телу по разные стороны от этого сечения, их равнодействующей недопустима, так как она приведет к изменению величин внутренних сил. По этой же причине недопустим перенос какой-либо силы, приложенной левее сечения по линии ее действия, в точку, расположенную правее этого сечения.

Примеры решения задач

Рис. 5.28. К решению задачи № 32:

а – схема стержня с нагрузками;

б – местные системы координат на участках стержня

Задан стержень пространственного очертания, загруженный нагрузками (рис. 5.28, а). Для заданного материала стержня требуется подобрать размеры поперечного сечения наиболее опасного участка для двух вариантов сечения: круглого и прямоугольного.

Решение

Определим внутренние усилия, используя метод сечений и правила знаков для усилий, справедливые для всех задач сложного сопротивления (см. рис. 5.1). На каждом участке введем местные системы координат, показанные на рис. 5.28, б. Ось х всегда направлена вдоль оси стержня12, оси – главные центральные оси инерции сечения. Чтобы не определять опорные реакции, будем рассматривать все силы со свободного конца стержня и найдем усилия в сечениях 0–5 (см. рис. 5.28,б).

; ;;

; ;;

; ;;;

; ;;

; ;

; ;;

; ;

; ;.

В соответствии с полученными результатами построим эпюры внутренних усилий (рис. 5.29). В рассматриваемом примере опасным является участок длиной , где действуют все усилия. На этом участке опасным будем считать сечение 5 (хотя при определенном сочетании величин нагрузок и размеров может быть опасным и сечение 4). Считая, что материал стержня – чугун (,,) подберем размеры поперечного сечения стержня, приняв следующие исходные данные:;;;;;. Для этих данных в опасном сечении 5 действуют такие усилия:,,,,,.

Рассмотрим первый вариант – стержень круглого поперечного сечения.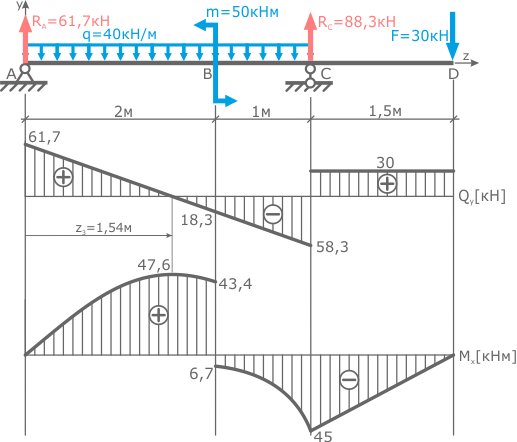 Подбор радиуса сечения производим без учета продольной и поперечных сил в соответствии с заданным материалом из условия прочности по теории Мора (5.36). В формуле (5.36)

, ,.

Из условия (5.36) найдем необходимый момент сопротивления

см3,

откуда, вспомнив, что , найдем радиус сечения

см.

Округляя радиус в большую сторону, примем см.

Рис. 5.29. Эпюры внутренних усилий в стержне

Далее необходимо построить эпюры распределения напряжений в круглом поперечном сечении так, как описано во вступительной части разд. 5.3. Для рассматриваемого примера эти эпюры показаны на рис. 5.30. Напряжения определены по формулам (5.33)–(5.35). Сделаем проверку прочности для найденного размера с учетом продольной силы. Для чугунного стержня опасной является точка, в которой действуют растягивающие нормальные напряжения, т. е. точка 1 на рис. 5.30. В этой точке

кН/см2;

кН/см2.

Подставим найденные напряжения в условие прочности по теории Мора (5.30):

кН/см2 < кН/см2.

Рис. 5.30. Эпюры напряжений (в кН/см2) в стержне

круглого сечения

Таким образом, найденный радиус см удовлетворяет условию прочности с учетом продольной силы и является окончательным.

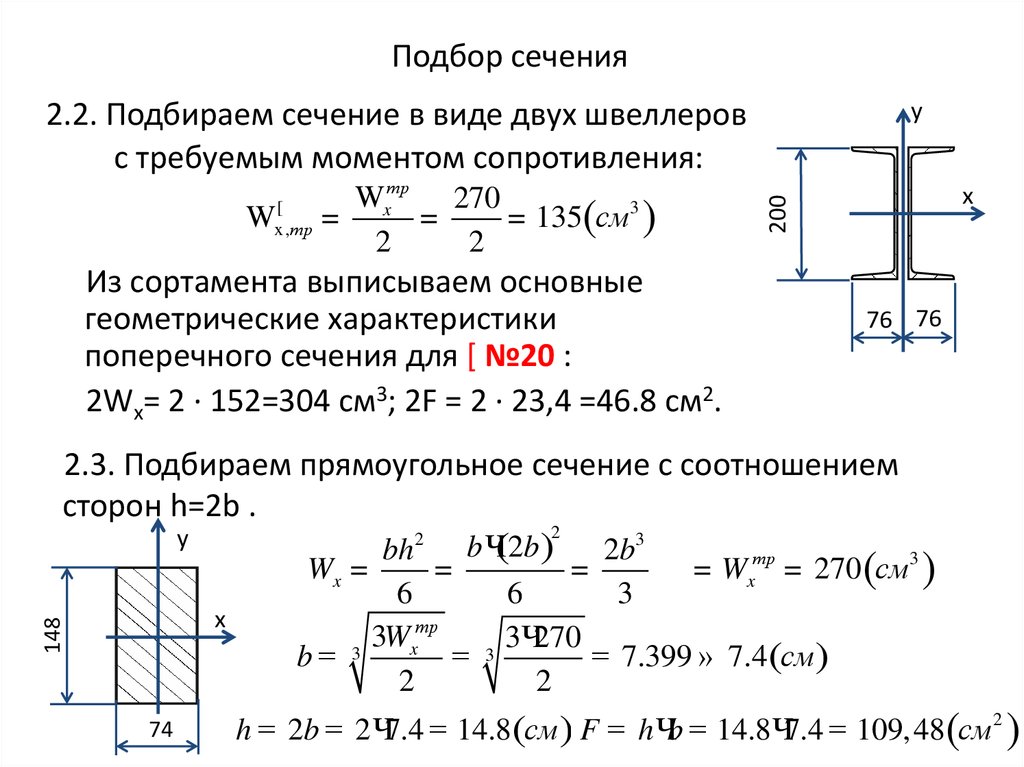
Теперь рассмотрим второй вариант – стержень прямоугольного сечения с отношением . Подбор сечения производим из условия прочности (5.50) в угловой точке сечения. Поскольку в рассматриваемом примере, то располагаем сечение выгодным образом, т.е. так, чтобы осьрасполагалась по середине длинной стороныпрямоугольника. Тогдаи условие (5.50) для чугуна перепишем в таком виде:

.

Отсюда получим необходимый момент сопротивления

см3

и, учтя, что , найдем высоту сечения

см см.

Построим эпюры распределения напряжений в прямоугольном сечении от всех видов внутренних усилий так, как описано во вступительной части разд. 5.3, и проверим прочность во всех опасных точках. Эпюры напряжений и опасные точки для рассматриваемого примера показаны на рис. 5.31. Напряжения найдены по формулам (5.44)–(5.49). Опасными для хрупкого материала являются точки, в которых действуют растягивающие напряжения, т. е. точки 1, 2 и 3 (см. рис. 5.31). Суммируем напряжения в опасных точках с учетом их направлений. В точке 1

кН/см2 <кН/см2,

то есть условие прочности выполняется.

В точке 2

кН/см2,

кН/см2

и условие прочности (5. 30) по теории Мора

<кН/см2

выполняется.

Наконец, в точке 3 действуют напряжения

кН/см2,

кН/см2.

Условие прочности (5.30) в этой точке

<кН/см2

Рис. 5.31. Эпюры напряжений (в кН/см2) в стержне

прямоугольного сечения

тоже выполняется. Таким образом, найденные размеры поперечного сечения иудовлетворяют условиям прочности во всех опасных точках.

5.3 Метод сечений – инженерная механика: статика

Перейти к содержанию

Глава 5: Фермы

Метод сечений использует анализ твердого тела для расчета одного или двух конкретных элементов. Вместо того, чтобы смотреть на каждый стык, вы делаете разрез в ферме, превращая элементы вдоль этой линии во внутренние силы (предположим, что они натянуты). Затем вы решаете твердое тело, используя уравнения равновесия для твердого тела: [латекс]\сумма F_x=0\;\сумма F_y=0\;\сумма M_z=0[/латекс]

Ферма:

 

Источник: Инженерная механика, Джейкоб Мур и др. http://mechanicsmap.psu.edu/websites/5_structures/5-5_method_of_sections/methodofsections.html

разбивается на две части, чтобы найти F E .

Источник: Инженерная механика, Джейкоб Мур и др. http://mechanicsmap.psu.edu/websites/5_structures/5-5_method_of_sections/methodofsections.html

В этом примере можно выбрать правую или левую половину. Для некоторых проблем необходима стратегия, в противном случае вам придется делать несколько сокращений. В этой задаче сначала нужно было найти силы реакции, но это не всегда так, поскольку иногда можно просто сделать разрез (см. пример 2 ниже).

 

Вот еще примеры того, как сделать разрез и показать соглашение об именах:

 

 

Источник: Внутренние силы в балках и рамах, Либретексты. https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.05%3A_Internal_Forces_in_Plane_Trusses

 

 

Вот подробное объяснение:

Метод разделов — это процесс, используемый для расчета неизвестных сил, действующих на элементы фермы . Метод включает в себя разбиение фермы на отдельные секции и анализ каждой секции как отдельного жесткого тела. Метод сечений обычно является самым быстрым и простым способом определения неизвестных сил, действующих в конкретном элементе фермы.

Использование этого метода:

Процесс, используемый в методе секций, описан ниже:

  1. В начале обычно полезно маркировать элементы фермы. Это поможет вам сохранить все организованным и последовательным в последующем анализе. В этой книге члены будут помечены буквами.
  2. Рассматривая всю ферменную конструкцию как твердое тело, нарисуйте диаграмму свободного тела, запишите уравнения равновесия и найдите внешние реактивные силы, действующие на ферменную конструкцию. Этот анализ не должен отличаться от анализа отдельного твердого тела.
  3. Теперь вы можете представить себе, как вы разрезаете свою ферму на две отдельные секции. Разрез должен проходить через элемент, в котором вы пытаетесь вычислить силы, и должен проходить через как можно меньше элементов (разрез не обязательно должен быть прямой линией).
  4. Далее вы нарисуете свободную диаграмму тела для одной или обеих секций, которые вы создали. Обязательно учитывайте все силы, действующие на каждую секцию.
    • Любая внешняя реакция или силы нагрузки, которые могут действовать на секцию.
    • Внутреннее усилие в каждом элементе, которое было разрезано при разделении фермы на секции. Помните, что для элемента с двумя силами сила будет действовать вдоль линии между двумя точками соединения на элементе. Нам также нужно будет угадать, будет ли это растягивающая или сжимающая сила. Неверное предположение сейчас просто приведет к отрицательному решению позже. Тогда общая стратегия состоит в том, чтобы предположить, что все силы являются растягивающими, тогда позже в решении любые положительные силы будут растягивающими, а любые отрицательные силы будут сжимающими.
    • Обозначьте каждую силу на диаграмме. Включите любые известные величины и направления и укажите имена переменных для каждого неизвестного.
  5. Запишите уравнения равновесия для каждой секции, для которой вы нарисовали диаграмму свободного тела. Это будут протяженные тела, поэтому вам нужно будет написать уравнения силы и момента.
    • У вас будет три возможных уравнения для каждой секции, два уравнения силы и одно уравнение момента. $$\sum\vec F=0\; \; \sum\vec M=0\\\sum F_x=0\; \; \сумма F_y=0\; \; \сумма M_z=0$$
  6. Наконец, решите уравнения равновесия для неизвестных. Вы можете сделать это алгебраически, решая по одной переменной за раз, или вы можете использовать матричные уравнения для решения всех сразу. Если вы предполагали, что раньше все силы были растягивающими, то помните, что отрицательные ответы указывают на сжимающие силы в стержнях.

Источник: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap. psu.edu/websites/5_structures/5-5_method_of_sections/methodofsections.html

 

Дополнительные примеры с веб-страницы Engineering Mechanics:

Пример 1:

Найдите силы, действующие на элементы BD и CE. Обязательно укажите, являются ли силы растягивающими или сжимающими.

 

Источник: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/5_structures/5-5_method_of_sections/pdf/MethodOfSections_WorkedExample1.pdf

 

Пример 2:

Найдите силы, действующие на элементы AC, BC и BD фермы. Обязательно укажите, являются ли силы растягивающими или сжимающими.

 

 

Если мы делаем разрез в верхней части, нам не нужно вычислять силы реакции.

 

Источник: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/5_structures/5-5_method_of_sections/pdf/MethodOfSections_WorkedExample2. pdf

 

Еще больше примеров доступно по адресу: https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.05%3A_Internal_Forces_in_Plane_Trusses

 

Итого:

 

 

В основном : Метод сечений — это метод анализа для определения усилий в некоторых элементах фермы. Он разделяет ферму на две секции, а затем использует уравнения равновесия твердого тела.

Приложение : Для расчета нагрузок на мосты и крыши, особенно если вам нужно знать только один или два элемента.

Взгляд в будущее : В следующем разделе исследуется трюк, который ускоряет решение, особенно для метода соединений.

 

Лицензия

Инженерная механика: Статика Либби (Элизабет) Осгуд; Гейла Кэмерон; Эмма Кристенсен; Аналия Бенни; и Мэтью Хатчисон находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.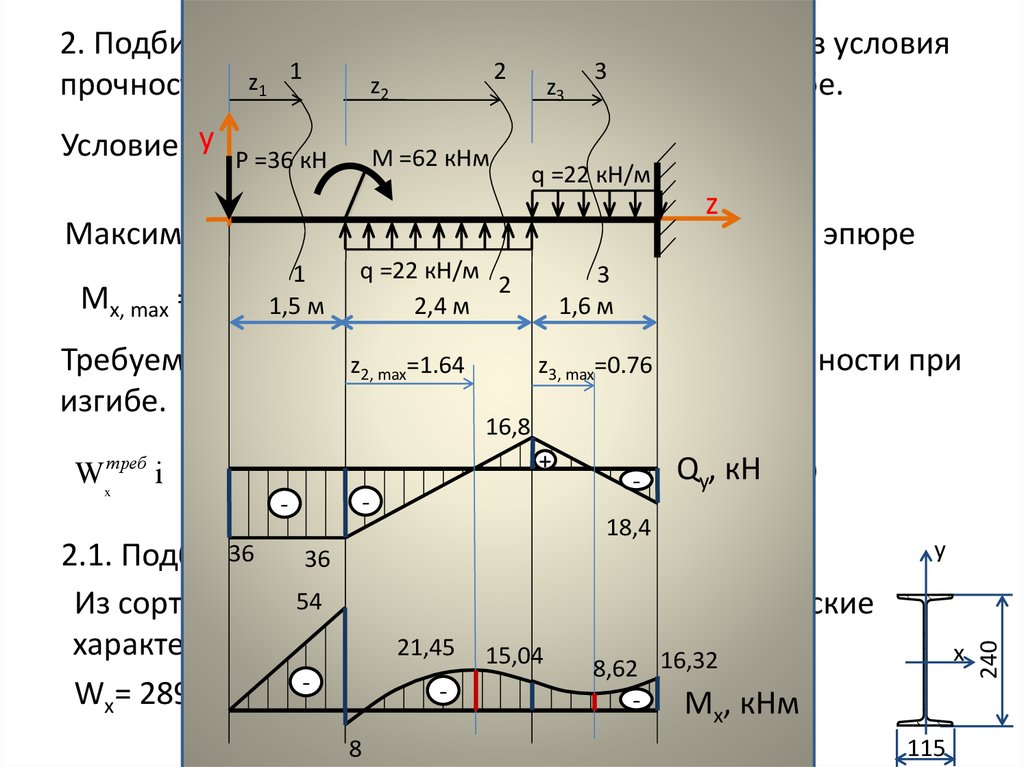 0 International License, если не указано иное.

Поделиться этой книгой

Поделиться в Твиттере

5.5: Метод сечений — Engineering LibreTexts

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    52781
    • Джейкоб Мур и участники
    • Пенсильванский государственный университет Мон-Альто через карту механики

    Метод сечений — это процесс, используемый для расчета неизвестных сил, действующих на элементы фермы . Метод включает в себя разбиение фермы на отдельные секции и анализ каждой секции как отдельного жесткого тела. Метод сечений обычно является самым быстрым и простым способом определения неизвестных сил, действующих в конкретном элементе фермы.

    Процесс, используемый в методе секций, описан ниже.

    1. Вначале обычно бывает полезно пометить элементы фермы. Это поможет вам сохранить все организованным и последовательным в последующем анализе. В этой книге члены будут помечены буквами.

      Рисунок \(\PageIndex{1}\): Первый шаг в методе разделов — маркировка каждого члена.

    2. Рассматривая всю ферменную конструкцию как твердое тело, нарисуйте диаграмму свободного тела, запишите уравнения равновесия и найдите внешние реактивные силы, действующие на ферменную конструкцию. Этот анализ не должен отличаться от анализа отдельного твердого тела.

      Рисунок \(\PageIndex{2}\): Рассматривайте всю ферму как твердое тело и определите силы реакции, поддерживающие конструкцию фермы.

    3. Теперь представьте себе, что вы разрезаете свою ферму на две отдельные секции. Разрез должен проходить через член, в котором вы пытаетесь определить силы, и должен проходить через как можно меньше членов. Срез не обязательно должен быть прямой линией. Рисунок \(\PageIndex{3}\): Далее вы представите, что ферма разрезается на две части. Если вы хотите найти силы в конкретном члене, обязательно прорежьте этот член. Это также упрощает задачу, если вы сокращаете как можно меньше участников.
    4. Далее вы нарисуете свободную диаграмму тела для одной или обеих секций, которые вы создали. Обязательно учитывайте все силы, действующие на каждую секцию.
    5. Запишите уравнения равновесия для каждой секции, для которой вы нарисовали диаграмму свободного тела. Это будут протяженные тела, поэтому вам нужно будет написать уравнения силы и момента.
      • Для 2D-задач у вас будет три возможных уравнения для каждой секции: два уравнения силы и одно уравнение момента. \[ \sum \vec{F} = 0 \quad\quad\quad\quad \sum \vec{M} = 0 \] \[ \sum F_x = 0 \, ; \,\,\, \сумма F_y = 0 \, ; \,\,\, \сумма M_z = 0 \]
      • Для трехмерных задач у вас будет шесть возможных уравнений для каждой секции: три уравнения силы и три уравнения момента. \[ \sum \vec{F} = 0 \] \[ \sum F_x = 0 \, ; \,\,\, \сумма F_y = 0 \, ; \,\,\, \sum F_z = 0 \] \[ \sum \vec{M} = 0 \] \[ \sum M_x = 0 \, ; \,\,\, \сумма M_y = 0 \, ; \,\,\, \сумма M_z = 0 \]
    6. Наконец, решите уравнения равновесия для неизвестных. Вы можете сделать это алгебраически, решая по одной переменной за раз, или вы можете использовать матричные уравнения для решения всех сразу. Если вы предполагали, что раньше все силы были растягивающими, то помните, что отрицательные ответы указывают на сжимающие силы в стержнях.
    Видеолекция по этому разделу, прочитанная доктором Джейкобом Муром. Источник YouTube: https://youtu.be/XcRn776w22Q.

    Пример \(\PageIndex{1}\)

    Найдите силы, действующие на стержни BD и CE. Обязательно укажите, являются ли силы растягивающими или сжимающими.

    Рисунок \(\PageIndex{5}\): схема проблемы для примера \(\PageIndex{1}\). Двумерное представление ферменного моста со стандартной ориентацией \(xy\)-системы координат.
    Решение
    Видео \(\PageIndex{2}\): рабочее решение примера проблемы \(\PageIndex{1}\), предоставленное доктором Джейкобом Муром. Источник на YouTube: https://youtu.be/9xxmHpLB1uU.

    Пример \(\PageIndex{2}\)

    Найдите силы, действующие на элементы AC, BC и BD фермы. Обязательно укажите, являются ли силы растягивающими или сжимающими.

    Рисунок \(\PageIndex{6}\): Диаграмма проблемы для примера \(\PageIndex{2}\). Двухмерное изображение башни, состоящей из ферм, расположенных в виде высокого прямоугольника, состоящего из прямоугольных элементов с трапециевидным верхом.
    Решение
    Видео \(\PageIndex{3}\): рабочее решение примера проблемы \(\PageIndex{2}\), предоставленное доктором Джейкобом Муром.