Сопромат. Заочники. | Решебник. Контрольные курсовые работы Ижевск. Решение задач.
<в каталог
Задача 1. Растяжение сжатие стержней
Задача 2. Статически неопределимая стержневая конструкция.
Задача 3. Изгиб балок
Задача 4. Изгиб рам.
Задача 5. Кручение валов
Задача 6. Косой изгиб.
Задача 7. Совместное действие изгиба и кручения.
Задача 8. Расчет сжатых стержней на устойчивость.
Таблица с готовыми вариантами
Пример выполненной работы
Задача 1.
Для стержня (рис. 1) постоянного сечения следует:
№ строки | № схемы | Р, кН | а, м | Е, МПа |
1 | I | 30 | 1,1 | 1,2∙105 |
2 | II | 20 | 1,2 | 1,4∙105 |
3 | III | 25 | 1,3 | 1,5∙105 |
4 | IV | 30 | 1,4 | 1,6∙105 |
5 | V | 40 | 1,5 | 1,7∙105 |
6 | VI | 48 | 1,6 | 1,8∙105 |
7 | VII | 64 | 1,7 | 1,9∙105 |
8 | VIII | 80 | 1,8 | 2,0∙105 |
9 | IX | 90 | 1,9 | 2,1∙105 |
0 | X | 60 | 2,0 | 2,2∙105 |
| в | а | б | а |
1.
2. Выписать выражение наибольшего по модулю нормального напряжения σmax и из условия прочности определить необходимую площадь сечения F, приняв [σ]=160 МПа.
3. Определить перемещение сечения I-I.
4. Составить раскрытые выражения потенциальной энергии U в брусе.
Данные взять из таблицы 1.
Задача 2
Статически неопределимая стержневая конструкция.
Для системы, состоящей из абсолютно жесткого бруса и упругих стержней, требуется:
1. Определить усилия в стержнях, поддерживающих абсолютно жесткую балку (см. рисунок 2), от нагрузки Р.
2. Вычислить напряжения в стержнях от нагрузки Р.
3. Из условия прочности, определить необходимую площадь F поперечного сечения стержней, приняв [
Материал стержней – сталь. Данные взять из таблицы
№ строки | № схемы | а, м | в, м | ℓ, м | Р, кН |
1 | I | 2,1 | 1,1 | 1,8 | 21 |
2 | II | 2,2 | 1,2 | 1,7 | 22 |
3 | III | 2,3 | 1,3 | 1,6 | 23 |
4 | IV | 2,4 | 1,4 | 1,5 | 24 |
5 | V | 2,5 | 1,5 | 1,4 | 25 |
6 | VI | 2,6 | 1,6 | 1,3 | 26 |
7 | VII | 2,7 | 1,7 | 1,2 | 27 |
8 | VIII | 2,8 | 1,8 | 1,1 | 28 |
9 | IX | 2,9 | 1,9 | 1,0 | 29 |
0 | X | 2,0 | 1,0 | 1,9 | 20 |
| в | а | б | в | в |
Задача 3
На рисунке 3 приведены схемы балок.
Требуется:
1. Построить эпюры изгибающих моментов и поперечных сил.
2. Подобрать сечение в виде прямоугольника (h=2b), приняв [σ]=160 МПа.
3. Построить эпюру нормальных напряжений в опасном сечении.
Данные взять из таблицы 3.
Принять интенсивность равномерно распределенной нагрузки q=6 кН/м.
№ строки | № схемы | а, м | Р, кН | М, кН∙м |
1 | I | 1,5 | 10 | 150 |
2 | II | 2,0 | 15 | 200 |
3 | III | 2,5 | 20 | 120 |
4 | IV | 3,0 | 25 | 100 |
5 | V | 3,5 | 30 | 300 |
6 | VI | 4,0 | 35 | 180 |
7 | VII | 4,5 | 40 | 60 |
8 | VIII | 5,0 | 45 | 240 |
9 | IX | 5,5 | 50 | 220 |
0 | X | 6,0 | 60 | 160 |
| в | а | б | в |
Задача 4
Изгиб рам.
Для схемы рамы требуется:
1. Составить аналитические выражения изменения продольной силы Nx, поперечной силы Qy, изгибающего момента Mz.
2. Построить эпюры внутренних силовых факторов (э Nx, э Qy, э Mz).
3. По опасному сечению подобрать диаметр d поперечного сечения.
Исходные данные взять из таблицы.
№ строки | № схемы | с/a | P/qa | m/qa2 | a,м | q, кН/м |
1 | 1 | 1,2 | 0,6 | 0,2 | 0,5 | 6 |
2 | 2 | 1,4 | 0,5 | 0,4 | 1,0 | 8 |
3 | 3 | 1,6 | 0,8 | 0,6 | 1,5 | 10 |
4 | 4 | 1,8 | 1,2 | 0,8 | 2,0 | 12 |
5 | 5 | 2,0 | 1,5 | 1,0 | 2,5 | 14 |
6 | 6 | 1,2 | 1,6 | 0,2 | 1,5 | 16 |
7 | 7 | 1,4 | 1,0 | 0,4 | 2,0 | 12 |
8 | 8 | 1,6 | 1,8 | 0,6 | 1,0 | 10 |
9 | 9 | 1,8 | 2,4 | 0,8 | 2,5 | 8 |
0 | 0 | 2,0 | 2,0 | 1,0 | 0,5 | 6 |
| в | а | б | в | б | а |
Задача 5
Кручение валов.
На приводном валу (см. рис. 4) установлен ведущий шкив В и два рабочих 1 и 2, от которых последовательно берутся мощности: N1, N2 кВт. Требуется:
1. Построить эпюру крутящих моментов.
2. По заданным [τ] и [φ] определить необходимый диаметр сплошного вала и округлить его до ближайшей величины, соответственно равной 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 180, 200 (мм).
3. Построить эпюру углов закручивания вала.
Данные взять из таблицы 4.
№ строки | № схемы | а, м | в, м | с, м | N1, кВт | N2, кВт | n0, об/мин | [φ], град | [τ], МПа |
1 | I | 1,0 | 1,5 | 2,0 | 40 | 130 | 600 | 2 | 100 |
2 | 1,2 | 1,6 | 1,8 | 50 | 120 | 900 | 3 | 120 | |
3 | III | 1,4 | 1,7 | 1,6 | 60 | 110 | 1200 | 4 | 140 |
4 | IV | 1,6 | 1,8 | 1,4 | 70 | 100 | 1500 | 3 | 160 |
5 | V | 1,8 | 2,0 | 1,2 | 80 | 90 | 1200 | 2 | 180 |
6 | VI | 2,0 | 1,8 | 1,4 | 90 | 80 | 900 | 3 | 200 |
7 | VII | 1,8 | 1,7 | 1,6 | 100 | 70 | 600 | 4 | 180 |
8 | VIII | 1,6 | 1,6 | 1,8 | 110 | 60 | 900 | 3 | 160 |
9 | IX | 1,4 | 1,5 | 2,0 | 120 | 50 | 1200 | 2 | 140 |
0 | X | 1,2 | 1,4 | 2,2 | 130 | 40 | 1500 | 4 | 120 |
| в | б | а | в | а | в | б | а | в |
Задача 6.
Косой изгиб.
Балка двутаврового профиля, повернутая на угол α относительно вертикали, загружена равномерно распределенной вертикальной нагрузкой q (рис. 6). Требуется:
1. Определить положение нулевой линии в опасном сечении.
2. Определить величину наибольшего нормального напряжения.
3. Вычертить опасное сечение балки и показать на нем нулевую линию, эпюру нормальных напряжений.
Данные взять из таблицы.
№ строки | q, кН/м | ℓ, м | α, град | № двутавра |
1 | 5,0 | 1,6 | 4 | 32 |
2 | 4,5 | 2,0 | 5 | 30 |
3 | 4,0 | 2,4 | 6 | 28 |
4 | 3,5 | 3,2 | 8 | 26 |
5 | 3,0 | 4,0 | 10 | 24 |
6 | 2,5 | 4,8 | 12 | 22 |
7 | 2,0 | 5,6 | 15 | 20 |
8 | 1,5 | 6,4 | 16 | 18 |
9 | 1,0 | 7,2 | 18 | 16 |
0 | 0,5 | 8,0 | 20 | 14 |
| в | б | в | а |
Задача 7.
Совместное действие изгиба и кручения.
На валу насажены зубчатые колеса. К колесам приложены окружные усилия Р1, Р2, Р3. Требуется:
1. Из условия равновесия ∑Мх=0 определить величину Р1 или Р3.
2. Определить крутящие моменты и построить эпюру крутящих моментов.
3. Определить силы, изгибающие вал в вертикальной и горизонтальной плоскости.
4. Построить эпюры изгибающих моментов от горизонтальных сил Му, и от вертикальных сил Мz.
5. При помощи эпюр найти опасное сечение и определить величину максимального расчетного момента.
6. Подобрать диаметр вала по III теории прочности – теории наибольших касательных напряжений.
Данные взять из таблицы.
№ строки | № схемы | Р1, кН | Р2, кН | Р3, кН | [σ], кН/см2 | а, см | b, см | Диаметры зубчатых колес, см | ||
D1 | D2 | D3 | ||||||||
1 | I | — | 6 | 10 | 10 | 40 | 50 | 40 | 40 | 20 |
2 | II | 8 | 5 | — | 9 | 50 | 40 | 50 | 40 | 20 |
3 | III | — | 7 | 9 | 10 | 40 | 30 | 40 | 30 | 30 |
4 | IV | 6 | 8 | — | 10 | 50 | 40 | 60 | 30 | 20 |
5 | V | — | 6 | 11 | 10 | 30 | 50 | 50 | 50 | 30 |
6 | VI | 5 | 8 | — | 9 | 20 | 30 | 30 | 30 | 20 |
7 | VII | — | 5 | 10 | 9 | 30 | 40 | 40 | 20 | 10 |
8 | VIII | 4 | 7 | — | 11 | 50 | 20 | 20 | 20 | 10 |
9 | IX | — | 6 | 11 | 10 | 30 | 50 | 30 | 30 | 20 |
0 | X | 8 | 6 | — | 9 | 40 | 30 | 50 | 20 | 10 |
| в | б | б | б | а | в | б | б | а | а |
Задача 8.
Расчет сжатых стержней на устойчивость.
Стальной стержень длиной ℓ сжимается силой Р.
Требуется:
1. Найти размеры поперечного сечения при допускаемом напряжении на простое сжатие [σ]=160 МПа (расчет производить последовательным приближением, предварительно задавшись величиной коэффициента φ=0,5).
2. Найти величину критической силы и коэффициент запаса устойчивости.
Данные взять из таблицы.
Значение коэффициента продольного изгиба j в зависимости от гибкости λ
l | 0 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 |
j | 1,00 | 0,96 | 0,92 | 0,86 | 0,75 | 0,60 | 0,45 | 0,36 | 0,29 | 0,23 | 0,19 |
Таблица с готовыми вариантами
SOPROMAT, Ltd.
Информация о компании, технический стек и конкурентыКомпании / ООО «СОПРОМАТ»
Последнее обновление : 26 мая 2022
Компания ООО «Сопромат» была основана в 2013 году как исследовательский, инжиниринговый и консалтинговый офис в Риге, Латвия. Наша цель состоит в том, чтобы повысить качество и снизить затраты на разработку и производство продукции за счет использования самых современных методов численного моделирования. Компания была основана высококвалифицированными инженерами и разработчиками программного обеспечения, имеющими большой опыт в области численного моделирования. Знания в области проектирования и разработки программного обеспечения позволяют нам использовать и создавать удобный интерфейс для программного обеспечения с открытым исходным кодом для промышленных приложений. Мы также используем коммерческое программное обеспечение для решения сложных инженерных задач. Основатели компании имеют ученую степень кандидата наук.
Наши программные инструменты подтверждены экспериментальными результатами.
Подробнее
SOPROMAT, Ltd. Стек технологий
Найдите потенциальных клиентов по технологиям, которые они используют. Используйте этот раздел, чтобы узнать подробнее о ключевых технологиях и инструментах, используемых ООО «СОПРОМАТ», и о том, как они влияют на взаимодействие пользователей и взаимодействие с компанией. Изучите 0 технологий по 0 категориям, используемым СОПРОМАТ, ООО
Подробнее технологии
Профиль сотрудника
Вы ищете лиц, принимающих решения в ООО «СОПРОМАТ»?
Получите их адрес электронной почты, номера телефонов и другую информацию от Linkedin или любого веб-сайта.
Установите и откройте информацию о сотрудниках ООО «СОПРОМАТ» менее чем за 30 секунд.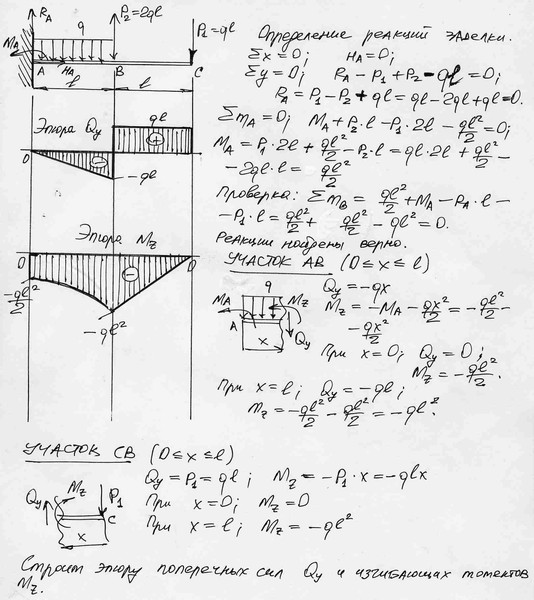
Зарегистрируйтесь в 6sense Revenue AI™ for Sales
Чтобы найти электронные письма, прямой набор и многое другое для потенциальных клиентов в Интернете.
Часто задаваемые вопросы
Ознакомьтесь с часто задаваемыми вопросами о деятельности SOPROMAT, Ltd., включая сведения об основании, информация о стеке технологий, отраслевом списке и другие подробности.
Что такое официальный сайт ООО «СОПРОМАТ»?
Официальный сайт ООО «СОПРОМАТ» — sopromat.lv Вы можете найти их контактный номер, адрес электронной почты и штаб-квартиру по адресу нажмите здесь.
Сколько сотрудников работает в ООО «СОПРОМАТ»?
6sense отслеживает 0–9 сотрудников, которые
работают в ООО «СОПРОМАТ».
Вы можете узнать больше об их сотрудниках через LinkedIn или их веб-сайт, используя
Расширение 6sense для Chrome.
Кроме того, ознакомьтесь с категорией вакансий и найма в компании SOPROMAT, Ltd., упомянутой ранее на этой странице, чтобы определить
в каком секторе развивается компания.
В какой отрасли работает ООО «СОПРОМАТ»?
ООО «СОПРОМАТ» занимается производством Исследовать.
Что такое технический стек SOPROMAT, Ltd.?
Лучшие технологии, используемые ООО «СОПРОМАТ»: . Вы также можете изучить 0 технологий в 0 категорий, используемых ООО «СОПРОМАТ», упомянутых ранее на этой странице.
Где находится штаб-квартира ООО «СОПРОМАТ»?
Штаб-квартира ООО «СОПРОМАТ» находится по адресу
Рига, Рига, Латвия.
Чтобы узнать точный адрес разблокировки сейчас.
Недостаточно материалов для SOPROMAT, Ltd. Связанные компании.
У нас недостаточно контента для SOPROMAT, Ltd. Связанные компании.
Прогиб предварительно натянутого гибкого тяжелого каната, закрепленного в двух произвольных точках | Кравчука
Главная > Том 5, № 4 (2017) > Кравчук
Прогиб предварительно натянутого гибкого тяжеловесного каната, закрепленного в двух произвольных точках
Кравчук А.С., Тарасюк И.А. дифференциальное уравнение провисания гибкого тяжелого каната, натянутого под произвольным углом к горизонту, и его решение в случае малых прогибов. Показано, что максимальный прогиб всегда достигается в середине выступа каната и его величина не зависит от положения опор. Впервые при постановке задачи предполагается, что растяжение каната происходит под действием двух независимых факторов: деформации предварительного напряжения и деформации силы тяжести, причем каждый из факторов может не учитываться.
Рассмотрен случай деформации каната в однородном температурном поле и установлено, что представленная модель становится некорректной в случае малого предварительного натяжения по сравнению с термической деформацией. Для случаев отсутствия предварительного растяжения и равенства температурной деформации и предварительного растяжения представлены решения задачи для линейно-упругого и реологически активного материалов. Отмечены методические особенности решения задачи для разных стадий ползучести с использованием уравнения Кельвина-Фойгта. Приведены решения для совместного использования модели Кельвина-Фойгта и линейной наследственной вязкоупругости для первичной и вторичной стадий ползучести соответственно. Рассмотрены проблемы моделирования сушки и восстановления биологического филамента.
Полный текст:
PDFСписок литературы
Скворцов А.В. Расчетные модели гибкой нити применимо к висячим мостам и вантово-балочным системам: дис. … канд. техн.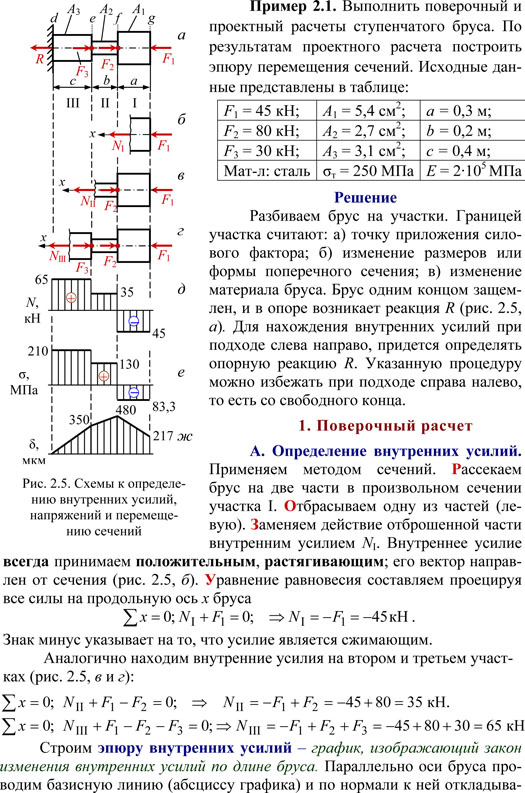
Наук Расчетные модели гибкой нити применяются для висячих мостов и вантово-балочных систем. кандидатская диссертация. Москва, 2005. 248 с. (на рус.)
Решение задач и выполнение письменных работ по ТОЕ (Теоретические основы электротехники), высшей математике, физике, программированию, термеху… высшая математика, физика, программирование, термеху…] Режим доступа: http://www.toehelp.ru/theory/sopromat/15.html (дата обращения: 17 сентября 2017 г.). (на русск.)
Виноградов Г.Г. Расчет строительных пространственных конструкций. Л.: Стройиздат, 1990. 264 с. (на рус.)
Меркин Д.Р. Введение в механику гибкой нити. М.: Наука, 1980. 240 с. (на рус.)
Кравчук А.С., Кравчук А.И. Малые поперечные прогибы весовой горизонтальной тяги под действием силы тяжести // Малые поперечные прогибы весовой горизонтальной натянутой нити под действием силы тяжести. Серия: Естественные и технические науки [APRIORI. Серия: Естественные и технические науки, 2015, №2 (доступно по: http://apriori-journal.