Реакции опоры

Опорными называют реакции связей возникающие под действием внешних нагрузок в опорах и удерживающие рассматриваемый элемент или конструкцию в равновесии.

Замена опор их реакциями

При расчете элементов конструкций реакции опор также выступают в качестве внешних усилий приложенных к рассматриваемому телу.

Вопрос определения опорных реакций подробно рассматривается в курсе теоретической механики, но на практике часто применяется и при решении задач сопротивления материалов.

При этом некоторые задачи в сопромате можно решить без их определения. Это возможно в случаях, когда за расчетную схему принимается брус, закрепленный в жесткой опоре (заделке) без дополнительных опор, например, статически определимые консольные балки, стержни либо стержневые системы.

Определение реакций

Количество и направление реакций зависит как от вида опор, так и от способа нагружения бруса и для статически определимых систем определяются из уравнений равновесия конструкции или ее элементов.

Для общего случая нагружения (пространственных систем), при котором может возникать до 6 реакций опор, требуется соответствующее количество уравнений.

Например, из условия, что заданная система относительно опор не перемещается в пространстве (вправо-влево, вверх-вниз, и вперед-назад) можем приравнять к нулю сумму проекций всех сил на оси x, y и z.

∑F(x)=0;
∑F(y)=0;
∑F(z)=0.

Из условия, что система не вращается, приравниваем к нулю суммы моментов всех нагрузок относительно соответствующих осей.

∑m(x)=0;
∑m(y)=0;
∑m(z)=0.

Совместное решение системы полученных уравнений позволяет определить величину и направление реакций в опорах.

Для плоской системы нагружения можно составить максимум три уравнения равновесия для определения до трех искомых усилий в опорах.

Линейно нагруженные элементы позволяют записать лишь одно уравнение равновесия.

Для расчета реакций опор статически неопределимых систем помимо уравнений статики требуются дополнительные зависимости, связывающие усилия с соответствующими им деформациями.

В некоторых случаях опорные реакции могут быть равны нулю. Это говорит лишь о том, что внешние нагрузки и остальные реакции взаимно уравновешены таким образом, что система может оставаться статичной и без соответствующего усилия в данной точке.

Примеры определения опорных реакций >
Внутренние силовые факторы >

isopromat.ru

Определение опорных реакций двухопорной балки

Условие задачи

Для заданной двухопорной балки с консольной частью, нагруженной комплексом нагрузок: силой F, моментом m и распределенной нагрузкой q, определить величину и направление опорных реакций.

Расчетная схема балки показана на рис.1

рис.1

Длина пролета балки 3м. Длина консольной части – 1,5м.

Пример решения

Рекомендуем посмотреть наш видеоурок по расчету опорных реакций балки. В нем мы постарались подробно показать порядок расчета реакций в опорах балки.

Не забудьте подписаться на наш канал 🙂

Для решения задачи, обозначим характерные точки (сечения) балки (точки A, B, C и D) и определим положение системы координат y-z, выбрав ее начало например в т. A (рис.2)

рис.2

Обе опоры балки являются шарнирными, поэтому в каждой из них будет возникать только сила, обозначим их соответственно R_A и R_C

Еще один видеоурок определения реакций опор, но уже для консольной балки:

Так как все заданные нагрузки раположены исключительно в вертикальной плоскости (плоский поперечный изгиб) и не дают проекций на ось z, то опорные реакции будут тоже только вертикальными.

Вообще говоря, реакции в опорах являются такими силами, которые необходимы для удержания балки с приложенными к ней нагрузками, в статичном (неподвижном) состоянии. В данном случае эти силы не позволяют ей вращаться и перемещаться в вертикальной плоскости.

Данная балка является статически определимой, т.к. уравнений равновесия достаточно для определения неизвестных усилий в опорах балки.

Для составления уравнений статики, опорные реакции R_A и R_C предварительно направляются произвольно, например, вверх (рис.3).

рис.3

Для определения двух неизвестных реакций потребуется два уравнения.

Запишем уравнения статики:

1. Балка не перемещается по вертикали, т.е. сумма проекций всех сил на ось y равна нулю:
2. Тот факт, что балка не вращается, говорит о том, что сумма моментов относительно любой ее точки тоже равна нулю, т.е.: В данном уравнении, согласно правила знаков для моментов, сосредоточенные силы, моменты и распределенные нагрузки стремящиеся повернуть балку против хода часовой стрелки относительно рассматриваемой точки A записываются положительными и наоборот.
   Как записывается момент распределенной нагрузки показано здесь.
   Сила приложенная в точке относительно которой рассматривается сумма моментов в уравнении не участвует, так как плечо момента для нее равно нулю.

Все правила знаков для сил и моментов (плейлист)

Здесь сумму моментов лучше записывать относительно точки расположенной на опоре (например, A), т.к. в этом случае соответствующая реакция R

A в уравнении не участвует.

Из выражения (2) определяем R_C:

и подставив его в выражение (1) находим R_A:

Направление и величина реакций, как правило, необходимы для дальнейших расчетов балки на прочность и жесткость, поэтому во избежание возможных ошибок рекомендуется выполнять проверку найденных значений.

Проверка опорных реакций балки >
Построение эпюр Q и M для балки >
Другие примеры решения задач >

isopromat.ru

Расчет реакций опор составной конструкции

Задача

Конструкция, состоящая из двух частей, соединенных в точке С шарниром (рисунок 4), удерживается двумя неподвижными шарнирными опорами в точках A и B.

Конструкция нагружена сосредоточенными силами P₁

=5 кН, P₂=7 кН, парой сил с моментом M=22 кН∙м и равномерно распределенной нагрузкой интенсивностью q=2 кН/м; α=60^o. Определить реакции опор A и B, а также шарнира C.

Пример решения

Освобождаем конструкцию от связей, т.е. убираем опоры, заменяя их действие неизвестными силами в точках A и B, распределенную нагрузку заменяем сосредоточенной силой Q (рисунок 5).

Рисунки 4 и 5

Составим уравнение равновесия моментов сил относительно точки B. Для упрощения вычисления момента силы P₁ разложим ее на вертикальную и горизонтальную составляющие (рисунок 5):

где Q=q∙4=2∙4=8 кН.

После подстановки данных и вычислений уравнение (1.1) получает вид

X_A-5Y_A=-24,74 кН.     (2.1′)

Второе уравнение с неизвестными X_A и Y_A получим, рассмотрев систему уравновешивающихся сил, приложенных к части конструкции, расположенной левее шарнира

C (рисунок 6, а):

∑M_iC=0; P₁»∙6 + Q∙2 — Y_A∙3 + X_A∙4=0,

или после вычислений

4X_A — 5Y_A = -41,98 кН.     (2.2)

Решая систему уравнений (2.1′) и (2.2), находим: X_A=7,97 кН, Y_A=3,36 кН.

Рисунок 6

Модуль реакции опоры

Направление реакции R_A определяется по направляющим косинусам:

cos(R_A,Ox) = X_A/R_A,
cos(R_A,Oy) = Y_A/R_A.

Запишем условия равновесия для сил, действующих на всю конструкцию (рисунок 5):

∑X_i=0; -P₁‘ + Q + X_A — P₂cosβ + X_B=0;

отсюда X_B=15,07 кН;

∑Y_i=0; -P’₁» + Y_A — P₂sinβ + Y

B=0;

отсюда Y_B=9,37 кН.

Модуль реакции опоры B

Направление реакции R_B определяется по направляющим косинусам:

cos(R_B,Ox) = X_B/R_B,
cos(R_B,Oy) = Y_B/R_B.

Запишем условия равновесия для части конструкции, расположенной правее шарнира C (рисунок 6, б):

∑X_i=0; -P₁‘ + Q + X_A + X_C=0;

отсюда X_C=2,47 кН;

∑Y_i=0; -P₁» + Y_A + Y_C=0;

отсюда Y_C=0,97 кН.

Модуль реакции шарнира C

Направление реакции R_C определяется по направляющим косинусам:

cos(R_C,Ox) = X_C/R_C,
cos(R_C,Oy) = Y_C/R_C.

Результаты расчетов приведены в таблице: 

Другие примеры решения задач >>

isopromat.ru

Определение реакции опор с моментом. Определение опорных реакций. Решение задач

Балки предназначены для восприятия поперечных нагрузок. По способу приложения нагрузки делятся на сосредоточенные (действуют на точку) и распределенные (действуют на значительную площадь или длину).

q — интенсивность нагрузки, кн/м

G = q L – равнодействующая распределенной нагрузки

Балки имеют опорные устройства для сопряжения их с другими элементами и передачи на них усилий. Применяются следующие виды опор:

· Шарнирно-подвижная

Эта опора допускает поворот вокруг оси и линейное перемещение параллельно опорной плоскости. Реакция направлена перпендикулярно опорной поверхности.

· Шарнирно-неподвижная

Эта опора допускает поворот вокруг оси, но не допускает никаких линейных перемещений. Направление и значение опорной реакции неизвестно, поэтому заменяется двумя составляющими R A у и R A х вдоль осей координат.

· Жесткая заделка (защемление)

Опора не допускает перемещений и поворотов. Неизвестны не только направление и значение опорной реакции, но и точка её приложения. Поэтому заделку заменяют двумя составляющими R A у, R A х и моментом М А. Для определения этих неизвестных удобно использовать систему уравнений.

∑ m А (F к)= 0

Для контроля правильности решения используется дополнительное уравнение моментов относительно любой точки на консольной балке, например точка В ∑ m В (F к)= 0

Пример. Определить опорные реакции жесткой заделки консольной балки длиной 8 метров, на конце которой подвешен груз Р = 1 кн. Сила тяжести балки G = 0,4 кн приложена посередине балки.

Освобождаем балку от связей, т.е отбрасываем заделку и заменяем её действие реакциями. Выбираем координатные оси и составляем уравнения равновесия.

∑ F kx = 0 R A х = 0

∑ F k у = 0 R A у – G – P = 0

∑ m А (F к)= 0 — M A + G L / 2 + P L = 0

Решая уравнения, получим R A у = G + P = 0,4 + 1 = 1,4 кн

M A = G L / 2 + P L = 0,4 . 4 + 1 . 8 = 9,6 кн. м

Проверяем полученные значения реакций:

∑ m в (F к)= 0 — M A + R A у L — G L / 2 = 0

— 9,6 + 1,4 . 8 – 0,4 . 4 = 0

— 11,2 + 11,2 = 0 реакции найдены верно.

Для балок расположенных на двух шарнирных опорах удобнее определять опорные реакции по 2 системе уравнений, поскольку момент силы на опоре равен нулю и в уравнении остается одна неизвестная сила.

∑ m А (F к)= 0

∑ m В (F k)= 0

Для контроля правильности решения используется дополнительное уравнение ∑ F k у = 0

1) Освобождаем балку от опор, а их действие заменяем опорными реакциями;

2) Заменяем распределенную нагрузку на равнодействующую G = q . L;

3) Выбираем координатные оси;

4) Составляем уравнения равновесия.

∑ F kx = 0 R Вх = 0

∑ m А (F к)= 0 G . L/2 + m — R Ву (L + B)= 0

R Ву = /(L + B) = (6+6) = 2,08 кн

∑ m В (F k)= 0 R A у. (L + B) — Q . (L/2 + B) + m = 0

R A у = / (L + B) = / (6 + 6) = 2,92 кн

Если испытываете трудности в написании , оформите заявку и Вы узнаете сроки и стоимость работы.


3. Изгиб. Определение напряжений.

3.3. Определение опорных реакций.

Рассмотрим несколько примеров.

Пример 3.1. Определить опорные реакции консольной балки (рис. 3.3).

Решение. Реакцию заделки представляем в виде двух сил Az и Ay , направленных, как указано на чертеже, и реактивного момента MA .

Составляем уравнение равновесия балки.

1. Приравняем нулю сумму проекций на ось z всех сил, действующих на балку. Получаем Az = 0. При отсутствии горизонтальной нагрузки горизонтальная составляющая реакции равна нулю.

2. То же, на ось y: сумма сил равна нулю. Равномерно распределенную нагрузку q заменяем равнодействующей qaз , приложенной посредине участка aз :

Ay — F1 — qaз = 0,

Откуда

Ay = F1 + qaз .

Вертикальная составляющая реакции в консольной балке равна сумме сил, приложенных к балке.

3. Составляем третье уравнение равновесия. Приравняем нулю сумму моментов всех сил относительно какой-нибудь точки, например относительно точки А:

Откуда

Знак минус показывает, что принятое вначале направление реактивного момента следует изменить на обратное. Итак, реактивный момент в заделке равен сумме моментов внешних сил относительно заделки.

Пример 3.2. Определить опорные реакции двухопорной балки (рис. 3.4). Такие балки обычно называют простыми.

Решение. Так как горизонтальная нагрузка отсутствует, то Az = 0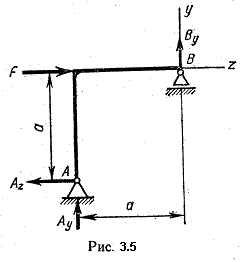

Вместо второго уравнения можно было использовать условие того, что сумма сил по оси Y равна нулю, которое ы данном случае следует применить для проверки решения:
25 — 40 — 40 + 55 = 0, т.е. тождество.

Пример 3.3. Определить реакции опор балки ломаного очертания (рис. 3.5).

Решение.

т.е. реакция Ay направлена не вверх, а вниз. Для проверки правильности решения можно использовать, например, условие того, что сумма моментов относительно точ

mirhat.ru

Опорные реакции — Сопромат — Каталог статей

Для решения многих задач в сопромате необходимо найти опорные реакции. Для их нахождения мы пользуемся правилами из термеха, но если вы пропускали пары или просто не усвоили материал – эта статья для вас.

Для начала разберемся что такое опорные реакции и с чем их едят:  Реакциями опор называют усилия, возникающие в опорах и удерживающие элемент находящийся под действием внешних нагрузок в состоянии статического равновесия.

Это определение, но если сказать проще, то опорные реакции это силы и моменты.

Нужно разобраться где и какие возникают силы. Для начала рассмотрим опоры, которые будут нам нужны:

1. Неподвижный шарнир

2. Подвижный шарнир

Такой  или такой  отличаются они только видом.

3. Жесткая заделка

 

Еще встречается промежуточный шарнир, но о нем поговорим позже, т.к. в нем нет ничего сложного.

Теперь нужно разобраться, какие силы возникают в каждой из этих опор.

1. И так, неподвижный шарнир, что нам нужно о нем знать, а знать нам нужно то, что в этом шарнире возникает две силы Ra и Ha

Они могут быть направленны в противоположные стороны, это не влияет на ход решения, а просто зависит от вашего оформления.

 

2. Подвижный шарнир. Они бывают двух видов. Отличия лишь в изображении. Что в том, что в другом возникает только одна сила

 

В первом типе она перпендикулярна площадке 

во втором – она идет как продолжение стержня 

Нужно учесть то, что мы можем направить их вниз, а ни вверх, как на рисунке, и это тоже будет правильно. Просто при нахождении они могут оказаться отрицательными, что означает их действие в противоположном направлении.

 

3. Жесткая заделка. Пожалуй самая сложная из этих опор. Дело в том, что в ней возникают три силы, кроме Ra и Ha добавляется момент Ма.

Здесь тоже решение не зависит от вашего оформления, вы можете направить не только силы в противоположные стороны, но и момент. Можете направить его по часовой стрелке, а не против, как на рисунке, это повлияет только на знак, а ответ останется тем же.

Еще стоит отметить обозначения. Это тоже ваше личное дело, как обозначать возникающие силы, у нас это R, Н и М. Буква «а» это что-то вроде принадлежности к данному шарниру или заделке, т.е. на схеме шарнир может быть обозначен буквой «В» , тогда и силы будут соответственно Rв, Нв и Мв.

 

tehnaryk.my1.ru