Сопромат пространственная рама: Пространственные рамы. — Сопротивление материалов.

Сопротивление материалов (Феодосьев В.И.)

Сопротивление материалов (Феодосьев В.И.)
  

Феодосьев В.И. Сопротивление материалов. Учеб. для вузов. – 10-е изд., перераб. и доп. – М.: Изд-во МГТУ, 2000. – 592 с.

В книге изложены основные разделы курса сопротивления материалов: растяжение, кручение, изгиб, статически неопределимые системы, теория напряженного состояния, теория прочности, толстостенные трубы, пластины и оболочки, прочность при переменных напряжениях, расчеты при пластических деформациях, устойчивость и методы испытаний. Для лучшего усвоения теоретического материала сопротивления материалов даны примеры задач по сопромату с решениями. По сравнению с предыдущими изданиями опущены параграфы и главы, не получившие широкого практического применения, внесены дополнения и уточнения с учетом современных тенденций развития механики и прочности конструкций.

Содержание учебника по сопромату соответствует программе и курсу лекций, читаемому в МГТУ им. Баумана. Для студентов машиностроительных вузов и технических университетов. Может быть полезен аспирантам и преподавателям, а также специалистам, деятельность которых связана с вопросами прочности, жесткости, устойчивости и надежности элементов конструкций, машин и приборов.



Оглавление

Предисловие
Введение
В2. Реальный объект и расчетная схема
В3. Силы внешние и внутренние. Уравнения равновесия стержня
В4. Напряжения
В5. Перемещения и деформации
В6. Закон Гука и принцип независимости действия сил
В7. Общие принципы расчета элементов конструкции
Глава 1. РАСТЯЖЕНИЕ И СЖАТИЕ
1.1. Внутренние силы и напряжения, возникающие в поперечных сечениях стержня при растяжении – сжатии
1.2. Удлинения стержня и закон Гука. Уравнения равновесия
1.3. Потенциальная энергия деформации при растяжении – сжатии стержня
1. 4. Статически определимые и статически неопределимые стержневые системы
1.5. Напряженное и деформированное состояния при растяжении — сжатии
1.6. Испытание материалов на растяжение – сжатие
1.7. Диаграмма растяжения
1.8. Механизм образования деформации
1.9. Основные механические характеристики материала
1.10. Пластичность и хрупкость. Твердость
1.11. Влияние температуры и фактора времени на механические характеристики материала
1.12. Коэффициент запаса
Глава 2. КРУЧЕНИЕ
2.1. Чистый сдвиг и его особенности
2.2. Кручение стержня с круглым поперечным сечением. Уравнения равновесия
2.3. Кручение стержня с некруглым поперечным сечением
2.4. Краткие сведения о пленочной (мембранной) аналогии
2.5. Кручение тонкостенного стержня
Глава 3. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙ СТЕРЖНЯ
3.2. Моменты инерции сечения
3.3. Главные оси и главные моменты инерции
Глава 4. ИЗГИБ СТЕРЖНЕЙ
4.1. Внутренние силовые факторы, возникающие в поперечных сечениях стержня при изгибе
4. 2. Напряжения при чистом изгибе
4.3. Напряжения при поперечном изгибе
4.4. Касательные напряжения при поперечном изгибе тонкостенных стержней
4.5. Центр изгиба
4.6. Дифференциальные уравнения равновесия стержня. Перемещения при изгибе
4.7. Стержень на упругом основании
4.8. Косой изгиб
4.9. Внецентренное растяжение – сжатие
4.10. Изгиб бруса большой кривизны
Глава 5. ПЕРЕМЕЩЕНИЯ В СТЕРЖНЕВОЙ СИСТЕМЕ ПРИ ПРОИЗВОЛЬНОЙ НАГРУЗКЕ
5.2. Теорема Кастилиано
5.3. Интеграл Мора
5.4. Способ Верещагина
5.5. Определение перемещений и напряжений в витых пружинах
5.6. Теорема взаимности работ
Глава 6. РАСКРЫТИЕ СТАТИЧЕСКОЙ НЕОПРЕДЕЛИМОСТИ СТЕРЖНЕВЫХ СИСТЕМ МЕТОДОМ СИЛ
6.2. Метод сил. Выбор основной системы
6.3. Канонические уравнения метода сил
6.4. Использование свойств симметрии при раскрытии статической неопределимости
6.5. Плоскопространственные и пространственные системы
6.6. Определение перемещений в статически неопределимых системах
6. 7. О методе перемещений
Глава 7. ОСНОВЫ ТЕОРИИ НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЙ
7.2. Определение напряжений в произвольно ориентированной площадке
7.3. Главные оси и главные напряжения
7.4. Круговая диаграмма напряженного состояния
7.5. Обзор различных типов напряженных состояний
7.6. Деформированное состояние
7.7. Обобщенный закон Гука и потенциальная энергия деформации в общем случае напряженного состояния
7.8. Анизотропия
Глава 8. КРИТЕРИИ ПЛАСТИЧНОСТИ И РАЗРУШЕНИЯ
8.2. Гипотезы (критерии) появления пластических деформаций
8.3. Теория Мора и ее применение
8.4. О хрупком разрушении и вязкости
8.5. О новых материалах
Глава 9. ТОЛСТОСТЕННЫЕ ТРУБЫ
9.2. Определение перемещений и напряжений в толстостенном цилиндре
9.3. Определение напряжений в составных трубах
Глава 10. ПЛАСТИНЫ И ОБОЛОЧКИ
10.1. Основные особенности пластин и оболочек
10.2. Определение напряжений в симметричных оболочках по беэмоментной теории
10. 3. Изгиб круглых симметрично нагруженных пластин
10.4. Определение напряжений и перемещений в круглых пластинах
10.5. Изгиб прямоугольных пластин
10.6. Изгиб цилиндрической оболочки при симметричном нагружении
Глава 11. ОСНОВЫ РАСЧЕТА ЭЛЕМЕНТОВ КОНСТРУКЦИЙ, РАБОТАЮЩИХ ЗА ПРЕДЕЛАМИ УПРУГОСТИ
11.2. Напряжения и перемещения в простейших стержневых системах при наличии пластических деформаций
11.3. Упругопластический изгиб стержня
11.4. Кручение стержня круглого поперечного сечения при наличии пластических деформаций
11.5. Основы расчета по предельным нагрузкам
11.6. Основы теории пластичности
Глава 12. ПРОЧНОСТЬ ПРИ ЦИКЛИЧЕСКИ ИЗМЕНЯЮЩИХСЯ НАПРЯЖЕНИЯХ
12.2. Основные характеристики цикла и предел выносливости
12.3. Влияние концентрации напряжений на прочность при циклическом нагружении
12.4. Масштабный эффект
12.5. Влияние качества обработки поверхности
12.6. Коэффициент запаса при циклическом нагружении и его определение
Глава 13. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ДЕФОРМИРУЕМЫХ СИСТЕМ
13.2. Определение критических нагрузок
13.3. Задача Эйлера
13.4. Зависимость критической силы от условий закрепления стержня
13.5. Устойчивость плоской формы изгиба прямолинейного стержня
13.6. Энергетический метод определения критических нагрузок
13.7. Продольно-поперечный изгиб
Глава 14. МЕТОДЫ ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ ДЕФОРМИРОВАННОГО И НАПРЯЖЕННОГО СОСТОЯНИЙ
14.2. Определение деформаций при помощи механических тензометров
14.3. Применение датчиков сопротивления
14.4. Оптический метод определения напряжений при помощи прозрачных моделей
ПРИЛОЖЕНИЕ

Краткий курс сопротивления материалов

Краткий курс сопротивления материалов
  

Заславский Б. В. Краткий курс сопротивления материалов. Учебник для авиационных специальностей вузов. М.: Машиностроение, 1986. — 328 с.

Изложены основные термины и определения теории сопротивления материалов. Рассмотрены растяжение, сжатие, сдвиг, кручение, изгиб, удар, колебания, устойчивость элементов и систем, статически определимые и неопределимые системы. Приведены методы расчетов: на прочность, за пределами упругости и др. Даны примеры расчетов. Материал изложен в соответствии с учебной программой авиационных специальностей вузов.



Оглавление

ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ и ОПРЕДЕЛЕНИЯ
1.3. КЛАССИФИКАЦИЯ ВНЕШНИХ СИЛ
1.4, ФОРМЫ ТЕЛ, РАССМАТРИВАЕМЫХ В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
1.5. ОПОРНЫЕ УСТРОЙСТВА. ОПОРНЫЕ РЕАКЦИИ
1.6. ОСНОВНЫЕ ГИПОТЕЗЫ О СВОЙСТВАХ МАТЕРИАЛА
1.7. ПОНЯТИЕ О РАСЧЕТНОЙ СХЕМЕ
1.8. ВНУТРЕННИЕ СИЛЫ. МЕТОД СЕЧЕНИЙ
1.9. НАПРЯЖЕНИЕ. ПОНЯТИЕ О НАПРЯЖЕННОМ СОСТОЯНИИ
1.10. НОРМАЛЬНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ
1.
11. ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ В БРУСЕ
1.12. ВИДЫ ДЕФОРМАЦИЙ БРУСА
ГЛАВА 2. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ И СЖАТИЕ ПРЯМОГО БРУСА
2.2. ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ДЕФОРМАЦИИ БРУСА
2.3. КОЭФФИЦИЕНТ ПОПЕРЕЧНОЙ ДЕФОРМАЦИИ (КОЭФФИЦИЕНТ ПУАССОНА)
2.4. НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ
2.5. НАПРЯЖЕНИЯ В НАКЛОННЫХ СЕЧЕНИЯХ
2.6. ЗАКОН ГУКА ПРИ ОДНООСНОМ РАСТЯЖЕНИИ. ПРИНЦИП НЕЗАВИСИМОСТИ ДЕЙСТВИЯ СИЛ
2.7. УДЛИНЕНИЯ И ПЕРЕМЕЩЕНИЯ
2.8. ОПРЕДЕЛЕНИЕ МЕХАНИЧЕСКИХ СВОЙСТВ МАТЕРИАЛА ПРИ РАСТЯЖЕНИИ
2.9. ДИАГРАММЫ УСЛОВНЫХ И ИСТИННЫХ НАПРЯЖЕНИЙ
2.10. МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛА
2.11. ЗАКОН РАЗГРУЗКИ И ПОВТОРНОГО НАГРУЖЕНИЯ
2.12. ПЛАСТИЧНЫЕ И ХРУПКИЕ МАТЕРИАЛЫ
2.13. МЕХАНИЧЕСКИЕ СВОЙСТВА ПРИ СЖАТИИ
2.14. ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
2.15. ПОЛЗУЧЕСТЬ. ПОСЛЕДЕЙСТВИЕ И РЕЛАКСАЦИЯ
2.16. ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
2.17. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
2.18. О РАСЧЕТЕ НА ПРОЧНОСТЬ
2.19. ДВА ТИПА РАСЧЕТОВ НА ПРОЧНОСТЬ
2. 20. ЭПЮРЫ НОРМАЛЬНЫХ СИЛ, НОРМАЛЬНЫХ НАПРЯЖЕНИЙ И ПЕРЕМЕЩЕНИЙ
2.21. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ
2.22. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
2.23. МОНТАЖНЫЕ УСИЛИЯ
2.24. НАПРЯЖЕНИЯ ПРИ ДВУХОСНОМ РАСТЯЖЕНИИ И СЖАТИИ
2.25. ЗАКОН ГУКА ПРИ ДВУХОСНОМ И ТРЕХОСНОМ РАСТЯЖЕНИИ
2.26. ИЗМЕНЕНИЕ ОБЪЕМА ПРИ ТРЕХОСНОМ РАСТЯЖЕНИИ
2.27. УДЕЛЬНАЯ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ТРЕХОСНОМ РАСТЯЖЕНИИ И СЖАТИИ
2.28. ЗАКОН ПАРНОСТИ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
ГЛАВА 3. СДВИГ
3.2. ЧИСТЫЙ СДВИГ
3.3. СВЯЗЬ МЕЖДУ УПРУГИМИ ПОСТОЯННЫМИ Е, G И «МЮ» ДЛЯ ИЗОТРОПНОГО ТЕЛА
3.4. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ СДВИГЕ
ГЛАВА 4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
4.2. ЦЕНТР ТЯЖЕСТИ СЕЧЕНИЯ
4.3. ЗАВИСИМОСТЬ МЕЖДУ МОМЕНТАМИ ИНЕРЦИИ ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ
4.4. МОМЕНТЫ ИНЕРЦИИ ПРОСТЕЙШИХ ФИГУР
4.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЛОЖНЫХ ФИГУР
4.6. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ КООРДИНАТ
4.7. ГЛАВНЫЕ ОСИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ
4. 8. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ГЛАВНЫХ ОСЕЙ
ГЛАВА 5. КРУЧЕНИЕ
5.2. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ ЦИЛИНДРИЧЕСКОГО БРУСА КРУГЛОГО СЕЧЕНИЯ
5.3. НАПРЯЖЕНИЯ В РАЗЛИЧНО ОРИЕНТИРОВАННЫХ СЕЧЕНИЯХ И ХАРАКТЕР РАЗРУШЕНИЯ ПРИ КРУЧЕНИИ БРУСА КРУГЛОГО СЕЧЕНИЯ
5.4. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ
5.5. О НАПРАВЛЕНИИ ВЕКТОРА КАСАТЕЛЬНОГО НАПРЯЖЕНИЯ В КОНТУРНЫХ ТОЧКАХ СЕЧЕНИЯ ЦИЛИНДРИЧЕСКОГО БРУСА
5.6. КРУЧЕНИЕ ТОНКОСТЕННОГО БРУСА ЗАМКНУТОГО ПРОФИЛЯ
5.7. КРУЧЕНИЕ БРУСА ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
5.8. КРУЧЕНИЕ ТОНКОСТЕННОГО БРУСА ОТКРЫТОГО ПРОФИЛЯ
5.9. ОБОБЩЕНИЕ РАСЧЕТНЫХ УРАВНЕНИЙ ДЛЯ БРУСЬЕВ РАЗЛИЧНЫХ СЕЧЕНИЙ
5.10. ЭПЮРЫ КРУТЯЩИХ МОМЕНТОВ, НАПРЯЖЕНИЙ И УГЛОВ ЗАКРУЧИВАНИЯ
5.11. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ КРУЧЕНИИ
5.12. ЦИЛИНДРИЧЕСКИЕ ВИНТОВЫЕ ПРУЖИНЫ МАЛОГО ШАГА
5.13. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ КРУЧЕНИИ
ГЛАВА 6. ИЗГИБ
6.2. ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ ПРИ ИЗГИБЕ БРУСА
6.3. ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ ПРИ ИЗГИБЕ
6.4. ЭПЮРЫ ПЕРЕРЕЗЫВАЮЩИХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ
6. 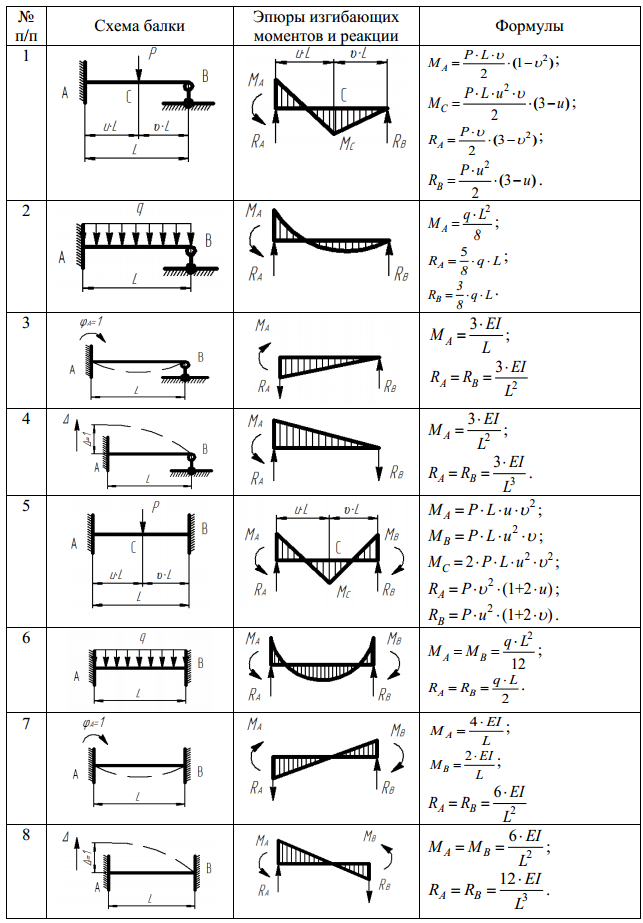5. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ЧИСТОМ ИЗГИБЕ
6.6. НОРМАЛЬНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ. ФОРМУЛА ЖУРАВСКОГО
6.7. НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ ТОНКОСТЕННЫХ БАЛОК
6.8. ЦЕНТР ИЗГИБА
6.9. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ
6.10. РАЦИОНАЛЬНЫЕ ФОРМЫ ПОПЕРЕЧНЫХ СЕЧЕНИЙ
6.11. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ИЗГИБЕ
6.12. ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ УПРУГОЙ ЛИНИИ И ЕГО ИНТЕГРИРОВАНИЕ
6.13. ЭНЕРГЕТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ СЕЧЕНИЙ БАЛОК. ИНТЕГРАЛ МОРА
6.14. СПОСОБ ВЕРЕЩАГИНА
6.15. БАЛКИ ПЕРЕМЕННОГО СЕЧЕНИЯ
ГЛАВА 7. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ СТЕРЖНЕВЫЕ СИСТЕМЫ
7.2. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ПРОСТРАНСТВЕННОМ БРУСЕ МАЛОЙ КРИВИЗНЫ. ИНТЕГРАЛ МОРА
7.3. ПЛОСКИЕ РАМЫ
7.4. ПРОСТРАНСТВЕННЫЕ РАМЫ
7.5. ПЛОСКОПРОСТРАНСТВЕННЫЕ РАМЫ
7.6. ФЕРМЫ
7.7. СМЕШАННЫЕ СИСТЕМЫ
7.8. ОТНОСИТЕЛЬНЫЕ ПЕРЕМЕЩЕНИЯ СЕЧЕНИЙ СТЕРЖНЕВОЙ СИСТЕМЫ
ГЛАВА 8. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СТЕРЖНЕВЫЕ СИСТЕМЫ
8.2. 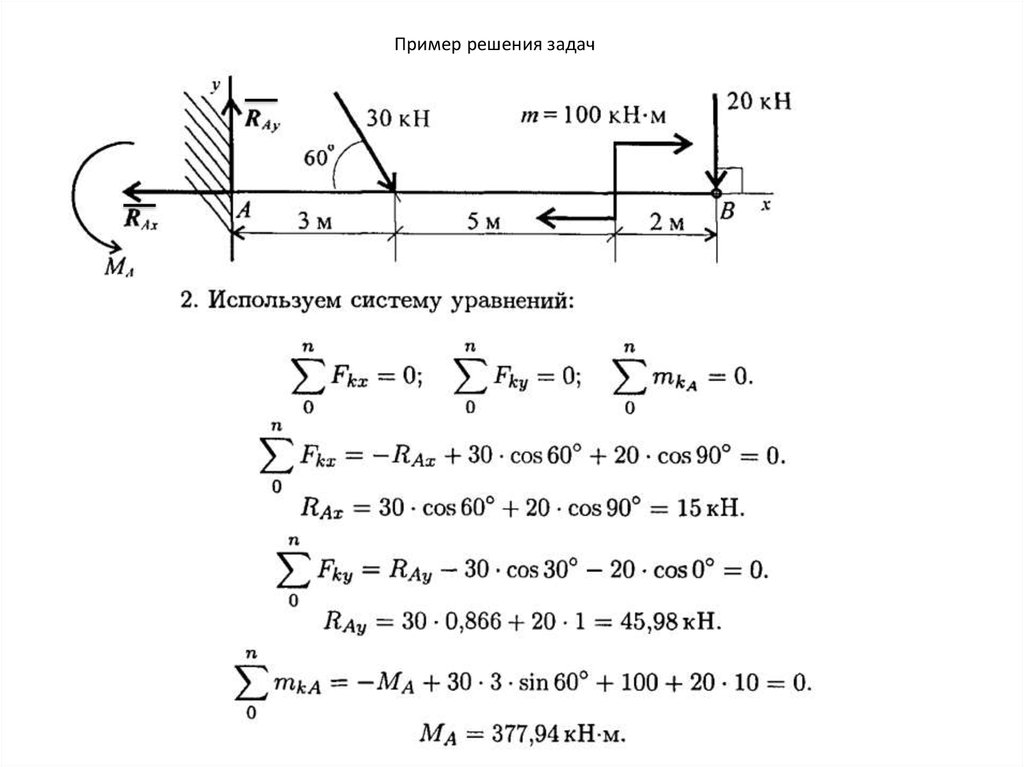ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ КАНОНИЧЕСКИХ УРАВНЕНИЙ
8.3. ПОСЛЕДОВАТЕЛЬНОСТЬ РЕШЕНИЯ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ЗАДАЧ
8.4. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ СЕЧЕНИЙ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
8.5. О РАЦИОНАЛЬНОМ ВЫБОРЕ ОСНОВНОЙ СИСТЕМЫ. ИСПОЛЬЗОВАНИЕ ПРЯМОЙ И ОБРАТНОЙ СИММЕТРИИ
ГЛАВА 9. КОСОЙ ИЗГИБ. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ И СЖАТИЕ
9.2. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ И СЖАТИЕ
ГЛАВА 10. ОСНОВЫ НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ В ТОЧКЕ ТЕЛА
10.3. НАПРЯЖЕНИЯ НА ПРОИЗВОЛЬНО НАКЛОНЕННОЙ К ОСЯМ КООРДИНАТ ПЛОЩАДКЕ
10.4. НОРМАЛЬНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ НА НАКЛОННОЙ ПЛОЩАДКЕ
10.5. ГЛАВНЫЕ ПЛОЩАДКИ И ГЛАВНЫЕ НАПРЯЖЕНИЯ. ИНВАРИАНТЫ НАПРЯЖЕННОГО СОСТОЯНИЯ
10.6. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ГЛАВНЫХ ПЛОЩАДОК
10.7. ЭЛЛИПСОИД НАПРЯЖЕНИЙ
10.8. ЭКСТРЕМАЛЬНЫЕ ЗНАЧЕНИЯ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ И ПЛОЩАДКИ ИХ ДЕЙСТВИЯ
10.9. КРУГОВАЯ ДИАГРАММА НАПРЯЖЕНИЙ (КРУГИ МОРА)
10.10. НАПРЯЖЕНИЯ НА ПЛОЩАДКАХ, РАВНОНАКЛОННЫХ К ГЛАВНЫМ (ОКТАЭДРИЧЕСКИЕ НАПРЯЖЕНИЯ)
10.11. ПОНЯТИЕ О ШАРОВОМ ТЕНЗОРЕ И ДЕВИАТОРЕ НАПРЯЖЕНИЙ
10. 12. КЛАССИФИКАЦИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ В ТОЧКЕ ТЕЛА
10.13. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
10.14. ГЛАВНЫЕ НАПРЯЖЕНИЯ И ГЛАВНЫЕ ПЛОЩАДКИ В БРУСЕ
10.15. ДЕФОРМИРОВАННОЕ СССТОЯНИЕ В ТОЧКЕ ТЕЛА. АНАЛОГИЯ МЕЖДУ ЗАВИСИМОСТЯМИ ТЕОРИИ НАПРЯЖЕНИЙ И ТЕОРИИ ДЕФОРМАЦИЙ
10.16. ОБОБЩЕННЫЙ ЗАКОН ГУКА ДЛЯ ИЗОТРОПНОГО ТЕЛА
10.17. УДЕЛЬНАЯ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ И ЕЕ ДЕЛЕНИЕ НА УДЕЛЬНУЮ ЭНЕРГИЮ ИЗМЕНЕНИЯ ОБЪЕМА И УДЕЛЬНУЮ ЭНЕРГИЮ ИЗМЕНЕНИЯ ФОРМЫ
10.18. ОПРЕДЕЛЕНИЕ ГЛАВНЫХ НАПРЯЖЕНИЙ И ГЛАВНЫХ ДЕФОРМАЦИЙ ПО РЕЗУЛЬТАТАМ ЭКСПЕРИМЕНТА
ГЛАВА 11. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ
11.2. НАЗНАЧЕНИЕ ТЕОРИЙ ПРЕДЕЛЬНОГО СОСТОЯНИЯ
11.3. ТЕОРИЯ НАИБОЛЬШИХ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ
11.4. ТЕОРИЯ НАИБОЛЬШИХ ОТНОСИТЕЛЬНЫХ УДЛИНЕНИЙ
11.5. ТЕОРИЯ НАИБОЛЬШИХ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ
11.6. ТЕОРИЯ УДЕЛЬНОЙ ЭНЕРГИИ ИЗМЕНЕНИЯ ФОРМЫ
11.7. ТЕОРИЯ МОРА
11.8. СООТНОШЕНИЯ МЕЖДУ ПРЕДЕЛАМИ ТЕКУЧЕСТИ ПРИ ПРОСТОМ РАСТЯЖЕНИИ И ЧИСТОМ СДВИГЕ ПО РАЗЛИЧНЫМ ТЕОРИЯМ
11. 9. НЕКОТОРЫЕ ЗАМЕЧАНИЯ О ВЫБОРЕ ТЕОРИИ ПРЕДЕЛЬНЫХ СОСТОЯНИЙ ПРИ РАСЧЕТАХ
11.10. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ЕЕ ВЛИЯНИЕ НА ПРОЧНОСТЬ ПРИ ПОСТОЯННЫХ ВО ВРЕМЕНИ НАПРЯЖЕНИЯХ
11.11. О МЕХАНИКЕ ХРУПКОГО РАЗРУШЕНИЯ
ГЛАВА 12. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ НАПРЯЖЕНИЯХ, ПЕРЕМЕННЫХ ВО ВРЕМЕНИ
12.2. МЕХАНИЗМ УСТАЛОСТНОГО РАЗРУШЕНИЯ
12.3. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
12.4. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ПРЕДЕЛА ВЫНОСЛИВОСТИ. ПРЕДЕЛ ОГРАНИЧЕННОЙ ВЫНОСЛИВОСТИ
12.5. ЗАВИСИМОСТЬ ПРЕДЕЛА ВЫНОСЛИВОСТИ ОТ СТЕПЕНИ АСИММЕТРИИ ЦИКЛА. ДИАГРАММА ПРЕДЕЛЬНЫХ АМПЛИТУД
12.6. ВЕРОЯТНОСТНЫЙ ХАРАКТЕР ЯВЛЕНИЯ УСТАЛОСТИ
12.7. МАЛОЦИКЛОВАЯ УСТАЛОСТЬ
12.8. ФАКТОРЫ, ВЛИЯЮЩИЕ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ
12.9. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ОДНООСНОМ НАПРЯЖЕННОМ СОСТОЯНИИ И ЧИСТОМ СДВИГЕ (ИЗГИБЕ, РАСТЯЖЕНИИ И КРУЧЕНИИ)
12.10. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ СЛОЖНОЕ НАПРЯЖЕННОМ СОСТОЯНИИ
12.11. СОПРОТИВЛЕНИЕ УСТАЛОСТИ ПРИ НЕСТАЦИОНАРНЫХ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
ГЛАВА 13. РАСЧЕТЫ ЗА ПРЕДЕЛАМИ УПРУГОСТИ
13. 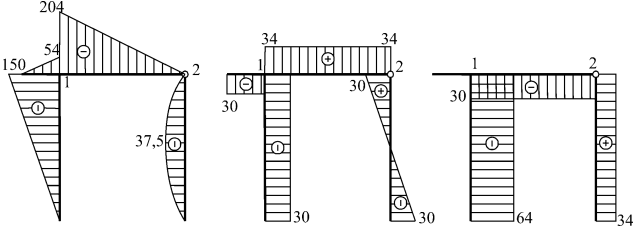2. СХЕМАТИЗАЦИЯ ДИАГРАММ РАСТЯЖЕНИЯ
13.3. РАСЧЕТ ПО НАГРУЗКАМ, ИСЧЕРПЫВАЮЩИМ НЕСУЩУЮ СПОСОБНОСТЬ
13.4. РАСЧЕТ БАЛОК ПО НАГРУЗКАМ, ИСЧЕРПЫВАЮЩИМ НЕСУЩУЮ СПОСОБНОСТЬ
13.5. НЕСУЩАЯ СПОСОБНОСТЬ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК И РАМ
13.6. ЧИСТЫЙ УПРУГОПЛАСТИЧЕСКИЙ ИЗГИБ ПРЯМОГО БРУСА
13.7. РАЗГРУЗКА И ОСТАТОЧНЫЕ НАПРЯЖЕНИЯ
ГЛАВА 14. РАСЧЕТ ПРОСТЕЙШИХ ОСЕСИММЕТРИЧНО НАГРУЖЕННЫХ ТОНКОСТЕННЫХ ОБОЛОЧЕК ВРАЩЕНИЯ
14.2. УРАВНЕНИЯ РАВНОВЕСИЯ ЭЛЕМЕНТА СИММЕТРИЧНОЙ БЕЗМОМЕНТНОЙ ОБОЛОЧКИ
14.3. ТЕОРЕМА О ДАВЛЕНИИ НА КРИВОЛИНЕЙНУЮ СТЕНКУ
14.4. РАСЧЕТ СФЕРИЧЕСКИХ И ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК НА НОРМАЛЬНОЕ ДАВЛЕНИЕ ПО БЕЗМОМЕНТНОЙ ТЕОРИИ
ГЛАВА 15. РАСЧЕТ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ, ДВИЖУЩИХСЯ С УСКОРЕНИЕМ
15.2. РАСЧЕТ ПОСТУПАТЕЛЬНО ДВИЖУЩИХСЯ СИСТЕМ
15.3. НАПРЯЖЕНИЯ В ТОНКОСТЕННОМ ВРАЩАЮЩЕМСЯ КОЛЬЦЕ
15.4. РАСЧЕТ РАВНОМЕРНО ВРАЩАЮЩЕГОСЯ ПРЯМОГО БРУСА
15.5. ВРАЩАЮЩИЕСЯ РАМЫ
ГЛАВА 16. УДАР
16.2. УДАР ПАДАЮЩЕГО ГРУЗА ПО УПРУГОЙ СИСТЕМЕ, МАССА КОТОРОЙ МАЛА ПО СРАВНЕНИЮ С МАССОЙ ГРУЗА
16. 3. ПРИВЕДЕННАЯ МАССА. КОЭФФИЦИЕНТ ПРИВЕДЕНИЯ
16.4. УДАР ПО СИСТЕМЕ, МАССА КОТОРОЙ СОИЗМЕРИМА С МАССОЙ УДАРЯЮЩЕГО ГРУЗА
ГЛАВА 17. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ. ПРОДОЛЬНЫЙ ИЗГИБ
17.2. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ СИЛЫ МЕТОДОМ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ УПРУГОЙ ЛИНИИ СТЕРЖНЯ. ФОРМУЛА ЭЙЛЕРА
17.3. ПРЕДЕЛЫ ПРИМЕНИМОСТИ ФОРМУЛЫ ЭЙЛЕРА
17.4. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ЗА ПРЕДЕЛАМИ ПРОПОРЦИОНАЛЬНОСТИ. ГРАФИК КРИТИЧЕСКИХ НАПРЯЖЕНИЙ
17.5. ПРАКТИЧЕСКИЕ СПОСОБЫ РАСЧЕТА НА ПРОДОЛЬНЫЙ ИЗГИБ
17.6. ЭНЕРГЕТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОЙ НАГРУЗКИ
17.7. ДИНАМИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОЙ НАГРУЗКИ
ГЛАВА 18. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ
18.3. ПРИБЛИЖЕННАЯ ФОРМУЛА ДЛЯ ОПРЕДЕЛЕНИЯ ПРОГИБА БАЛКИ ПРИ ПРОДОЛЬНО-ПОПЕРЕЧНОМ ИЗГИБЕ
18.4. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ДЛЯ ИЗГИБАЮЩИХ МОМЕНТОВ
18.5. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПРОДОЛЬНО-ПОПЕРЕЧНОМ ИЗГИБЕ

Крыша с пространственным каркасом • параметрический дизайн

В этом уроке мы создадим типичную крышу с пространственным каркасом и продолжим получать знаком с Кузнечиком.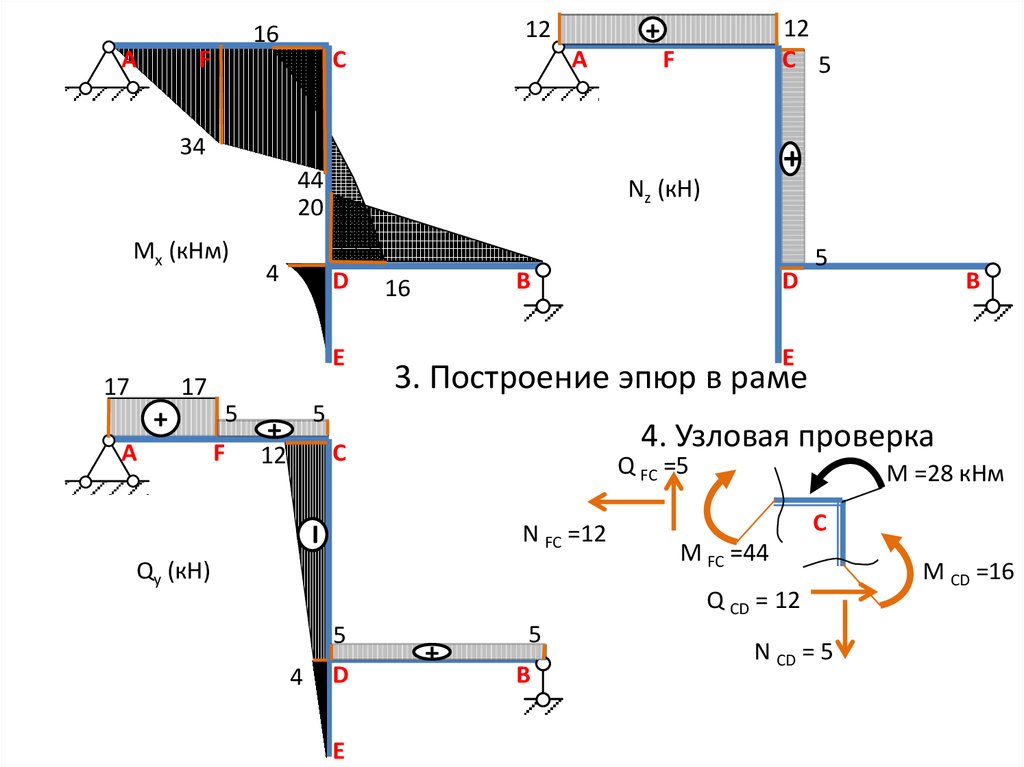 Подробнее о структурной идее пространства можно прочитать кадров на этой странице

Эта страница еще не завершена.

.

Планарные пространственные рамы обычно создаются путем комбинирования различных типов многогранники. Для следующего В упражнении мы выбираем комбинацию двух платоновых тел: полуоктаэдра и тетраэдр (см. рисунок ниже). В качестве альтернативы мы можем представить пространственную рамку как две параллельные, взаимно сдвинутые квадратные сетки, которые отделены друг от друга на расстояние $h$ и узлы которого соединены пространственными диагоналями.

Тетраэдр

Полуоктаэдр

$h$

$a$

Пространственная рама, созданная из различных многогранников.

В этом уроке мы установили базовую длину $a = 1$ и, таким образом, расстояние равно $h = 1. / 2 \cdot \sqrt 2 = 0,707$.

Grasshopper

1
Создание верхней сетки

Первое, что нужно сделать, это создать сетку. Мы делаем это, размещая компонент Square

Square (SqGrid)

Vector  >  Grid  >  Square

2D-сетка с квадратными ячейками

042
Inputs
Plane (P) Base plane for grid
Size (S) Size of grid cells
Extent X (Ex) Number of
Протяженность Y (Ey) Количество ячеек сетки в направлении y базовой плоскости
Выходы
Контуры ячеек сетки
Точки (P) Точки в углах сетки
на холсте. Мы могли бы использовать ввод S для определения размер ячейки, но этот компонент уже использует желаемое значение 1 по умолчанию ценить.

Мы можем увидеть предустановленное значение, наведя курсор на ручку ввода с помощью курсора мыши.

Мы можем увидеть предустановленное значение, наведя курсор на ручку ввода с помощью курсора мыши.

Входы Ex и Ey определяют количество ячеек, которые генерируются в соответствующее направление квадратной сетки. Если мы напечатаем "10 в поиск холста, получаем панель

Panel

Params  >  Input  >  Panel

Панель для пользовательских заметок и текстовых значений

со значением 10 . После подключения этой панели к на входы Ex и Ey будет создана сетка с 10 × 10 квадратами.

Вход Р использует строительную плоскость в качестве входных данных. Здесь значение по умолчанию — World XY , что это плоскость, которая определена в направлениях x и y и начало которой имеет начало координаты 0,0,0 . Мы получим тот же результат, если соединим плоскость XY

. Плоскость XY (XY)

Вектор  >  Плоскость  >  Плоскость XY

Мировая плоскость XY.

Входы
Начало (O) Начало плоскости
Выходы
Плоскость (P) Мировая плоскость XY
на вход P .

2
Определить начало нижней сетки

Теперь, когда мы создали одну сетку, мы создадим вторую, смещенную к первая сетка. Для этого создадим вспомогательную плоскость с новой точкой источник; компонент Construct Point

Точка построения (Pt)

Вектор  >  Точка  >  Точка построения

Построить точку по координатам {xyz}.

9006 создаст эту точку с координаты, заданные на трех входах.

Горизонтальное смещение сетки составляет половину размера ячейки. Поэтому создаем Панель

Panel

Params  >  Input  >  Panel

Панель для пользовательских заметок и текстовых значений

со значением 0.5 и подключить ее к входам X и Y Точка построения . Вертикальное смещение составляет $h = 0,707$, а вторая сетка должна быть ниже первого. Соответственно создаем еще одну панель

Панель

Параметры  >  Ввод  >  Панель

Панель для пользовательских заметок и текстовых значений

с -0,707 и подключить его ко входу Z .

Десятичный разделитель в Grasshopper — точка; запятая используется для разделения координаты. Начальный ноль для десятичных значений является необязательным. Итак, еще один способ определить предыдущий пункт будет использовать панель

Panel

Params  >  Input  >  Panel

Панель для пользовательских заметок и текстовых значений

и установите ее содержание до .5,.5,-.707
3
Создать нижнюю сетку

Вторая сетка также создается с помощью компонента Квадрат

Square (SqGrid)

Vector  >  Grid  >  Square

2D grid with square cells

Входы
x Координата (x) {x} Координата
Y координата (Y) {y {y {y {y {y {y {y {y {y {y {y {y}39136 3 3 3. {z} координата
Выходы
Точка (Pt) Координата точки
Inputs
Plane (P) Base plane for grid
Size (S) Размер ячеек сетки
Протяженность X (Ex) Количество ячеек сетки в базовой плоскости x направлении
Extent Y (Ey) Number of grid cells in base plane y direction
Outputs
Cells (C) Grid cell outlines
Points (P ) Точки на углах сетки
. Как упоминалось выше, вход P принимает плоскость построения. Что осталось сделать Теперь нужно соединить только что созданную точку с вводом P .

Вы могли заметить, что мы подключили точку к входу, который на самом деле запрашивает самолет. Кузнечик иногда сообразителен и угадывает недостающую информацию. В этом случае он взял значение по умолчанию World XY и изменил исходную точку на мы подключились. Если нам нужен самолет в других направлениях, то XY , мы должны Сначала создайте самолет, а затем подключите его.

Вы могли заметить, что мы подключили точку к входу, который на самом деле запрашивает самолет. Кузнечик иногда сообразителен и угадывает недостающую информацию. В этом случае, он взял по умолчанию World XY и изменил точку происхождения на ту, мы подключились. Если нам нужен самолет в других направлениях, то XY , мы должны Сначала создайте самолет, а затем подключите его.

Если мы посмотрим на окно просмотра Rhino, мы обратите внимание, что симметрия сеток была потеряна из-за смещения. Для нашего пространственная каркасная крыша, мы хотим, чтобы нижняя сетка была на одну ячейку меньше в каждом направлении. В этом случае искомое количество ячеек равно 9. Но мы должны решить это в гибким образом: на единицу меньше исходного количества ячеек. В кузнечике, это означает использование вычитания

Subtraction (A-B)

Maths  >  Operators  >  Subtraction

Mathematical subtraction

компонента 900 начальное значение для ввода А . На входе B нам нужна панель с 1 (используйте Поиск холста с "1 ). Теперь мы соединяем выход R из Вычитание с входами Ex и Ey второй сетки. Square (SqGrid)

Vector  >  Grid  >  Square

2D-сетка с квадратными ячейками

Inputs
A (A) First operand for subtraction
B (B) Second operand для вычитания
Выходы
Результат (R) Результат вычитания
Входы
Plane (P) Base plane for grid
Size (S) Size of grid cells
Extent X (Ex) Number of grid cells in base plane x direction
Extent Y (Ey) Number of grid cells in base plane y direction
Outputs
Cells (C) Grid cell outlines
Точки (P) Точки в углах сетки
имеет два выхода: На S мы получаем очертания ячеек, в данном случае квадраты, а на P получаем точки на углы сетки. Данные расположены в древовидной структуре данных

Эта страница еще не завершена.

: Каждая ветвь представляет строку сетки и содержит список квадратов или точек.

Создаем диагонали пространственного каркаса, соединяя точки верхней сетки с таковыми из нижней сетки. Такое соединение может быть создано с помощью компонент Строка

Линия (Ln)

Кривая  >  Примитив  >  Линия

Создайте линию между двумя точками.

Входы
Начальная точка (A) Начальная точка
Конечная точка (B) Линейная точка
. Линия (L) Сегмент линии
. Большой вопрос, как сортировать точки для входов A и B для создания нужных соединений. Давайте подумаем полуоктаэдр (который является пирамидой) в изоляции: он имеет квадратное основание и вершина. Наклонные ребра соединяют вершины основания с вершиной. ребра представляют диагонали, которые мы ищем. Итак, помним: есть четыре вершины, противостоящие одной вершине.

Края основания представляют собой контуры ячеек сетки на выходе C из Квадрат . Мы можно использовать компонент Discontinuity

Разрыв (Диск)

Кривая  >  Анализ  >  Разрыв

Найти все разрывы вдоль кривой.

. )
Входы
Кривая (C) Кривая для анализа
(L)
Выходы
Точки (P) Точки на разрывах
Параметры (t) Параметры кривой на разрывах
для создания точек на всех изломах очертаний; соедините выход C с входом C . Теперь у нас есть четыре вершины для основания. Если мы внимательно посмотрим на вывод P , то заметим, что точки сортируются как дерево данных, последние разветвления которого содержат 4 вершины каждой ячейки сетки в виде списка.

Теперь у нас есть четыре базовые вершины, но двойник, вершина, все еще отсутствующий. Важно, чтобы вершина находилась в одном дереве данных. структуру в качестве наших базовых вершин: последнее разветвление должно содержать список с только одна вершина. В этом случае нам нужно использовать компонент Graft Tree

Привить дерево (Привить)

Наборы  >  Дерево  >  Привить дерево

Привить дерево данных, добавив дополнительную ветвь для каждого элемента.

Inputs
Tree (T) Data tree to graft
Outputs
Tree (T) Grafted data tree
в сочетании с углами сетки нижней сетки: запустите провод от выхода P сетки нижней на ввод T которая прививка наша дерево данных. Затем мы соединяем оба дерева данных с компонентом Line

. Линия (Ln)

Кривая  >  Примитив  >  Линия

Создайте линию между двумя точками.

Inputs
Start Point (A) Line start point
End Point (B) Line end point
Выходы
Линия (L) Сегмент линии
для создания диагоналей нашего пространственного фрейма.

5
Создание труб

Последний шаг — превратить оси в трубы. Для этого мы разделяем контуры наши клетки (квадраты) на отдельные строки; компонент Взорвать

Explode (Расчленить)

Curve  >  Util  >  Explode

Разбить кривую на более мелкие сегменты.

Inputs
Curve (C) Curve to explode
Recursive (R) Recursive decomposition until all segments are atomic
Outputs
Сегменты (S) Разнесенные сегменты, составляющие базовую кривую
Вершины (V) Вершины разнесенных сегментов
сделает это за нас. Кроме того, давайте не будем возражать против двойных строк, которые вызваны по соседним ячейкам. На выходе S of Explode находим разделенные строки и соедините их между собой диагоналями к входу C Трубы

Труба (труба)

Поверхность  >  Произвольная форма  >  Труба

Создайте поверхность трубы вокруг кривой рельса.

Входы
Кривая (C) Базовая кривая
Radius (R) Pipe radius
Caps (E) Specifies the type of caps (0=None, 1=Flat, 2=Round)
Outputs
Труба (P) Результирующая труба
компонент.

Для подключения нескольких проводов к одному входу удерживайте Сдвиг при подключении проводов.

Для подключения нескольких проводов к одному входу удерживайте Сдвиг при подключении проводов. Чтобы определить радиус для труб, мы используем панель

Panel

Params  >  Input  >  Panel

Панель для пользовательских заметок и текстовых значений

с 0,05 и подключить ее к ввод R . Это придаст нашей пространственной каркасной крыше некоторый объем для лучшего визуализация.

Получить результаты

Информация о версии

  • Rhino 6.30
  • Grasshopper 1.0.0007

Проверь свои навыки

Как это часто бывает с алгоритмами написания, есть несколько способов получить такое же решение. В этом случае вместо использования двух квадратных сеток и соединяя их вершины, крыша пространственного каркаса также может быть сгенерирована создание соответствующих многогранников и использование их ребер для пространственного каркаса. Теперь это ваша задача! (Помните ссылку на пирамиду?)

Подсказка 1

Найдите подходящий многогранник

Многогранник, который мы представляет собой полуоктаэдр, который также можно описать как пирамиду. В отличие от Rhino, мы не можем создавать их напрямую в Grasshopper (по крайней мере, без внешнего плагина). Либо импортируем нужную геометрию из Rhino в Grasshopper

Эта страница еще не завершена.

или используем компонент Extrude Point

Точка выдавливания (Extr)

Поверхность  >  Произвольная форма  >  Точка выдавливания

Выдавливание кривых и поверхностей в точку.

Входы
Основание (B) Кривая профиля или поверхность
.
Экструзия (E) Результат экструзии
в сочетании с квадратом. Давайте тогда разложим квадрат.

Подсказка 2

Сгенерировать квадраты

Квадраты созданы с помощью компонент Квадрат

Square (SqGrid)

Vector  >  Grid  >  Square

2D-сетка с квадратными ячейками

0042
Размер (S) Размер ячеек сетки
Протяженность X (Ex) Количество ячеек сетки в базовой плоскости x направлении
Протяженность 9 дюймов сетки Y (Ey2) Базовая плоскость Y Направление
Выходы
Клетки (C) Сетки. 0086 , как и в основном упражнении. Чтобы для точки выдавливания

Точка выдавливания (Extr)

Поверхность  >  Произвольная форма  >  Точка выдавливания

Выдавливание кривых и поверхностей в точку.

Inputs
Base (B) Profile curve or surface
Point (P) Extrusion tip
Outputs
Extrusion (Э) Результат экструзии
для работы нам еще нужны вершины пирамиды.

Подсказка 3

Создание вершин

Для вершин мы используем компонент Район

Area (Площадь)

Surface  >  Analysis  >  Area

Решите свойства площади для брепсов, сеток и плоских замкнутых кривых.

Входы
Геометрия (G) Бреп, сетка или плоская замкнутая кривая для вычисления площади
Выходы
Область (A) Область геометрии
Centroid (C). затем используем Move

Переместить (Переместить)

Преобразовать  > Евклидово  >  Переместить

Переместить (переместить) объект вдоль вектора.

Входы
Geometry (G) Base geometry
Motion (T) Translation vector
Outputs
Geometry (G) Translated geometry
Transform ( X) Преобразование данных
для перемещения их на другую плоскость. Move требует перевода вектор, который мы получаем с компонентом Unit Z

Блок Z (Z)

Вектор  >  Вектор  >  Единица Z

Единичный вектор, параллельный мировой оси {z}.

Inputs
Factor (F) Unit multiplication
Outputs
Unit vector (V) World {z} vector
. Теперь у нас есть пирамиды ( Брепс ) и не хватает только осей для трубок.

Подсказка 4

Найти все линии пространственного каркаса

Компонент Brep Wireframe

Каркас брепа (проволоки)

Поверхность  > Анализ  > Каркас брипа

Извлеките кривые каркаса брепа.

Inputs
Brep (B) Base Brep
Density (D) Wireframe isocurve density
Outputs
Каркас (W) Кривые каркаса
экспортирует верхнюю сетку и диагонали из экструдированный Брепс . Для нижней сетки мы должны сделать небольшой крюк через PolyLine

. PolyLine (PLLine)

Curve  >  Spline  >  PolyLine

Создайте ломаную линию, соединяющую несколько точек.

Входы
Вершины (V) Точки вершин полилинии
Закрыто (C) Close Polyline
Выходы
Polyline (PL). Поскольку это дает нам только одно направление нижней сетки, используем PolyLine

PolyLine (PLLine)

Curve  >  Spline  >  PolyLine

Создайте ломаную линию, соединяющую несколько точек.

Inputs
Vertices (V) Polyline vertex points
Closed (C) Close polyline
Outputs
Polyline (Pl) Результирующая полилиния
снова, но это время мы размещаем Flip Matrix

Flip Matrix (Flip)

Наборы  >  Tree  >  Flip Matrix

Отразить матричное дерево данных, поменяв местами строки и столбцы.

Inputs
Data (D) Data matrix to flip
Outputs
Data (D) Flipped data matrix
Компонент перед ним.

Альтернативное решение для создания каркасной крыши.

Получить результаты

Получить результаты

Получить результаты

Информация о версии

  • Rhino 6.30
  • Grasshopper 1.0.0007

Космические каркасы – гражданское строительство X

Это один из наиболее эффективных способов использования конструкционных материалов. Пространственные каркасы представляют собой трехмерные структуры
решетчатого типа, которые простираются более чем в одном направлении. Общепринятой практикой является применение обозначения пространственного каркаса к конструкциям, которые точнее было бы классифицировать как пространственные фермы, то есть сборки элементов, соединенных штифтами в соединениях или узлах.
В дополнение к высокой жесткости и присущей избыточности пространственные рамы могут экономично охватывать большие площади, обеспечивая исключительную гибкость использования внутри конструкции за счет исключения внутренних колонн. Космические рамы обладают разнообразием форм и форм. Они могут использовать стандартный модуль для создания плоских сеток, бочкообразных сводов, куполов и произвольных форм.
Наиболее распространенным примером пространственной фермы является двухслойная сетка, состоящая из верхнего и нижнего слоев пояса, соединенных стержнями. Можно использовать различные типы ориентации сетки. Элементы верхнего и нижнего пояса могут быть параллельны или наклонены к краям конструкции, а также могут быть параллельны или наклонены друг к другу (см. рис. 8.29). Одним из преимуществ наклона верхнего и нижнего поясов относительно друг друга является то, что элементы верхнего пояса имеют более короткую длину, что приводит к более экономичной конструкции для сжимающих усилий. Кроме того, более длинные нижние пояса имеют меньше деталей и соединений.
Пространственные рамы, охватывающие большие площади без колонн, обычно поддерживаются по периметру или по углам. Свесы используются там, где это возможно, для обеспечения некоторого противодействия напряжениям для уменьшения сил внутреннего пояса и для обеспечения большего количества активных диагональных элементов стенки для распределения реакций на опорах в пространственной раме. В случаях, когда реакции очень велики, элементы пространственного каркаса у опор иногда продлевают под нижний пояс в виде перевернутых пирамид до верха колонн. Это эффективно создает капитель колонны, которая облегчает распределение сил в пространственной раме.
Глубина пространственной рамы обычно составляет от 4 до 8% ее пролета. Для эффективного использования двустороннего охвата пространственной рамы соотношение сторон (длины к ширине) обычно не должно превышать 1,5:1,0. При соотношении 1,5:1,0 около 70% гравитационных нагрузок приходится на короткий пролет.
Типы элементов, используемых для пространственных каркасов, могут представлять собой горячекатаные профили из конструкционной стали, круглые или прямоугольные трубы или холодногнутые стальные профили. Многие пространственные рамы могут использовать два или более различных типов элементов.
Для некоторых конструкций крыши с пространственным каркасом верхние пояса также действуют как прогоны для непосредственной поддержки кровельной системы. В этих случаях верхние пояса должны быть рассчитаны на сочетание осевых и изгибающих напряжений. Для других конструкций кровли для кровельной системы используется отдельная подкаркасная система, а сопряжение с пространственным каркасом предусмотрено в верхних
узлах пояса. В этих случаях кровельная система не передает напряжения изгиба на элементы верхнего пояса.
Вне зависимости от типа пространственного каркаса, сутью любой такой системы является ее узел. Большинство систем пространственного каркаса имеют концентрические узлы; то есть центральные оси всех элементов, образующих узел, проецируются на общую рабочую точку в центре узла.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

2019 © Все права защищены.