Перемещения при изгибе
Как отмечалось ранее, деформацией при изгибе является искривление продольной оси балки.
Вследствие этого искривления, точки и поперечные сечения балки получают линейные и угловые перемещения.
Рассмотрим на примере простой консольной балки.
Линейные перемещения
Отметим в произвольном месте балки точку K и приложим к свободному концу консоли сосредоточенную силу F.
Под действием этой силы балка изогнется, и точка K переместится в новое положение K’.
Очевидно, что перемещение точки K произойдет, не строго вертикально, поэтому разложим его на две составляющие:
вертикальное перемещение по оси y, называемое прогибом балки в т. K (yK)
и горизонтальное (осевое) смещение точки вдоль горизонтальной оси — zK
Практические расчеты показывают, что осевые смещения как правило, несоизмеримо меньше вертикальных перемещений (например, в данном случае zKK), поэтому ими пренебрегают, ограничиваясь вычислением прогибов.
Линейные перемещения (прогибы балки) измеряются в метрах или кратных единицах измерения (миллиметрах и сантиметрах).
Прогибы, при которых сечение в результате деформации балки перемещается вверх принимаются положительными.
Именно по величине прогибов определяется жесткость балки.
Угловые перемещения
Кроме линейных, сечения балки при изгибе получают и угловые перемещения.
Проведем касательные к продольной оси балки в точках K и K’.
В первом случае линия касательной совпадает с прямой осью балки, во втором – располагается под углом θ.
Угол между касательными очевидно равен углу между нормалями к оси балки в этих точках.
Этот угол θK называется углом наклона сечения K в результате деформации балки.
Вычисляется в радианах, с последующим переводом в градусы.
Между линейными и угловыми перемещениями при изгибе существует дифференциальная зависимость.
Например, в сечениях, углы наклона которых равны нулю следует ожидать экстремума изогнутой линии балки на данном участке.
Методы расчета перемещений
Существует несколько способов расчета линейных y и угловых θ перемещений при изгибе:
Метод начальных параметров (МНП)
Перемещения рассчитываются по уравнениям МНП
Считается относительно простым методом расчета перемещений в прямых балках с постоянной жесткостью сечения.
Данный способ не применим для расчета прогибов и углов наклона в балках переменного сечения, с изогнутой или ломаной осью и в рамах.
Подробнее >>
Интеграл Мора
Интеграл Мора относится к энергетическим методам расчета перемещений.
В отличие от МНП позволяет определять линейные и угловые перемещения для любых систем.
Подробнее >>
Способ Верещагина
Данный способ расчета перемещений представляет собой графическую интерпретацию интеграла Мора, особенностью которой является «перемножение эпюр» грузовой и единичных схем.
Подробнее >>
Метод интегрирования дифференциального уравнения упругой линии балки
Непосредственное интегрирование дифференциального уравнения упругой линии
является одним из наиболее универсальных способов расчета перемещений в балках. Может применяться без ограничений к балкам любой формы.
По результатам расчета перемещений сечений балки строится линия изогнутой оси балки (либо эпюра прогибов), с указанием числовых значений прогибов и углов наклона в характерных сечениях.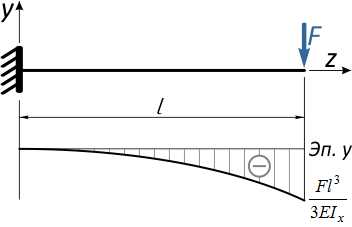
Эти вычисления и построения необходимы для проверки балок на жесткость.
Примеры решения задач >
Лекции по сопромату >
isopromat.ru
Определение перемещений | ПроСопромат.ру
Виды перемещений. Дифференциальное уравнение упругой линии балки
При плоском изгибе балки её упругая линия, лежащая в плоскости действия внешних сил, искривляется
, точки этой линии получают некоторые перемещения.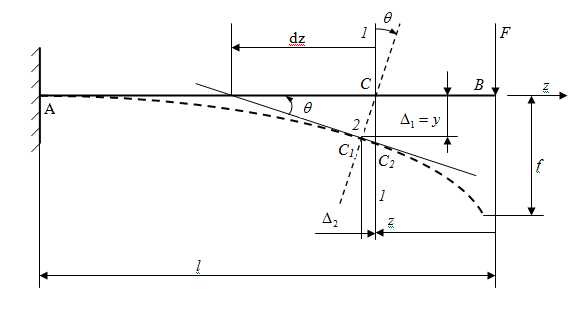
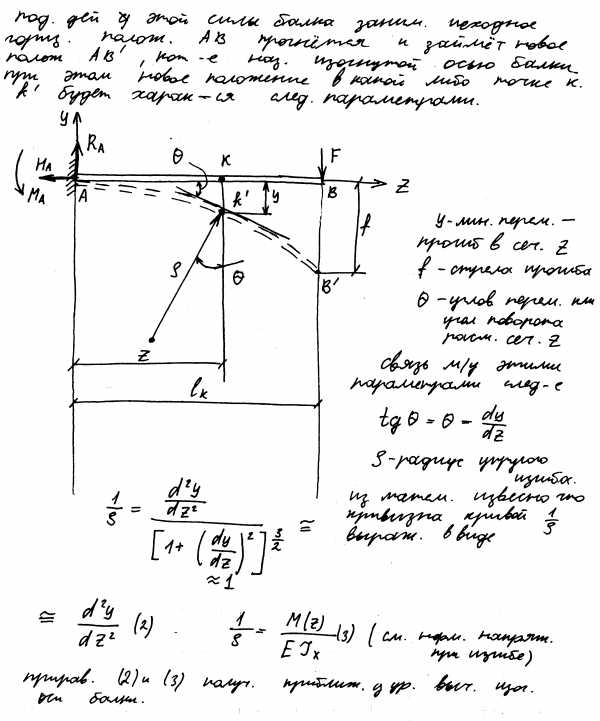
Произвольно выбранная точка С перемещается как в направлении, перпендикулярном АВ, так и вдоль этой линии на величину . Наибольший практический интерес представляет перемещение , которое называется прогибом балки. Угол между направлениями 1-1 и 2-2 называется углом поворота сечения балки. Таким образом , перемещения бывают линейные и угловые.
Наряду с расчётом балки на прочность необходимо производить и расчёт на жёсткость, то есть определять прогибы и углы поворота балки. Существует несколько способов решения задачи о деформациях балок. Рассмотрим аналитический способ. Установим зависимость координаты – уравнение упругой линии.
Из рисунка видно ,что Но! В упругой стадии работы материала углы поворота настолько малы ,что
Правила знаков для перемещений, знаки перемещений
Угол считается положительным, если сечение поворачивается против хода часовой стрелки и наоборот. Прогиб считают положительным согласно принятому направлению осей координат. Если ось координат направлена вверх, то положительным будет прогиб вверх, а отрицательным — вниз.
Для нахождения зависимости y=f(z) используем известное соотношение между кривизной оси с изгибающим моментом и жесткостью сечения балки
При постоянных моменте, кривизне и жесткости балка изгибается по окружности.
Из математики известно, что кривизна кривой может быть выражена так:
Пренебрегая получим приближённое дифференциальное уравнение изогнутой оси балки:
Или
При приближённом дифференциальном уравнении изогнутой оси балки пользуются принципом малости перемещений, а если перемещения очень большие, то используют точное дифференциальное уравнение. В технике допускаемая величина прогиба , где — длина пролёта балки. Уравнение представляет собой линейное дифференциальное уравнение второго порядка с разделяющимися переменными и может быть проинтегрировано в общем виде:
где v- линейное перемещение (прогиб), θ – угловое перемещение, С1 и С2 – постоянные интегрирования.
С1– угол поворота в начале координат, умноженной на величину ЕI;
С2 – прогиб балки в начале координат, умноженный на EI.
Значения этих постоянных определяют из граничных условий ,т.е. условий опирания балки и условий на границах смежных участков. Вот эти условия:
— у свободно лежащей балки прогибы на обеих опорах равны нулю. При симметричном нагружении у такой балки угол поворота в середине пролета также равен нулю;
— у консольной балки в заделке и прогиб и угол поворота равны нулю;
— на границе смежных участков балки прогиб и угол поворота одинаковы как для левого, так и для правого участка.
Определение перемещений по методу начальных параметров (или по универсальным формулам прогибов и углов поворота сечений)
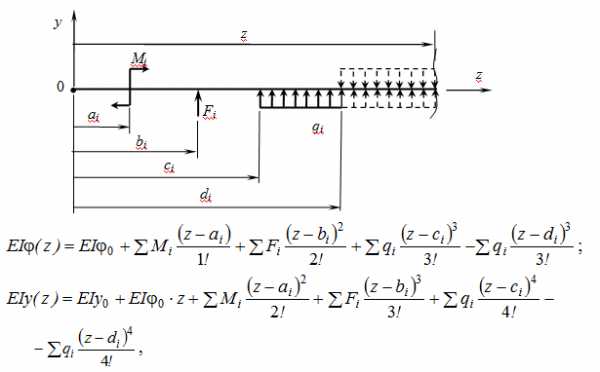
где у0 и φ0 – начальные параметры, то есть прогиб и угол поворота в начале координат, которые определяются из условий закрепления балки:
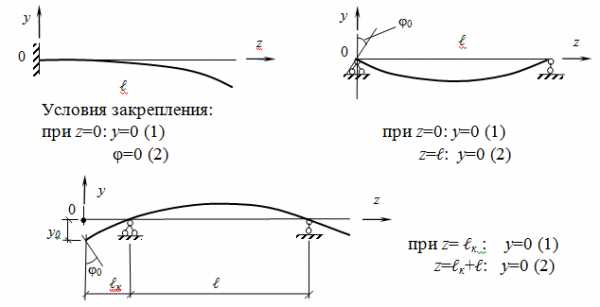
Порядок определения перемещений по универсальным формулам:
- Определить все опорные реакции.
- Поместить начало координат обязательно в крайнее сечение балки (левое или правое).
- Ось у направить вверх, ось z — вдоль балки.
- Найти начальные параметры из условий закрепления балки (возможные случаи показаны выше).
- Зная начальные параметры у0 и φ0, по универсальным формулам определить интересующие нас перемещения.
При использовании универсальных формул
а) В универсальные формулы включать только те внешние силы, которые действуют между началом координат (т.0) и сечением, в котором определяются перемещения. Следует помнить, что опорные реакции – тоже внешние силы.
б) Каждая внешняя сила (Мi, Fi, qi) вводится со знаком изгибающего момента, который эта сила вызывает в сечении, где определяется перемещение.
prosopromat.ru
3.5. Деформации участков стержня и перемещения сечений. Условия жесткости
При осевом растяжении или сжатии до предела пропорциональности σpr справедлив закон Гука, т.е. закон о прямо пропорциональной зависимости между нормальными напряжениями
и продольными относительными деформациями
: 
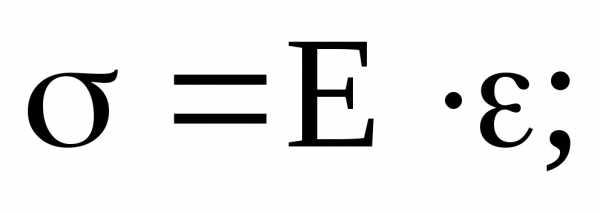(3.10)
или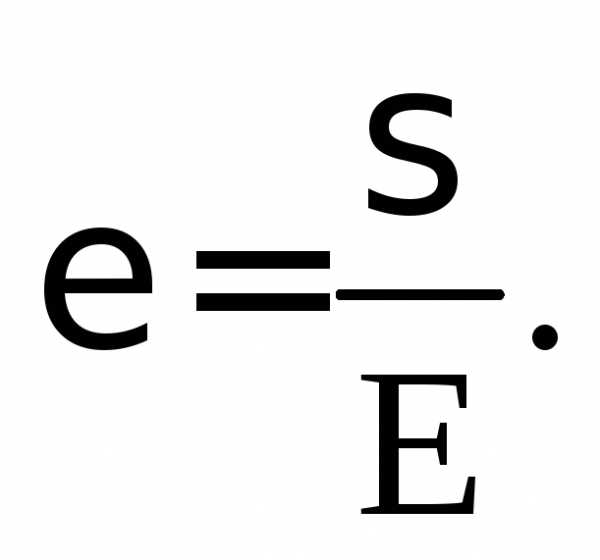 
(3.11)
Здесь Е – коэффициент пропорциональности в законе Гука имеет размерность напряжения и называется модулем упругости первого рода, характеризующим упругие свойства материала, илимодулем Юнга.
О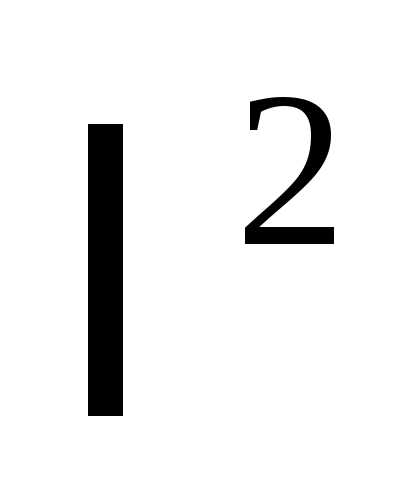
тносительной
продольной деформацией
называется отношение абсолютной
продольной деформации участка
стержня к длине этого участка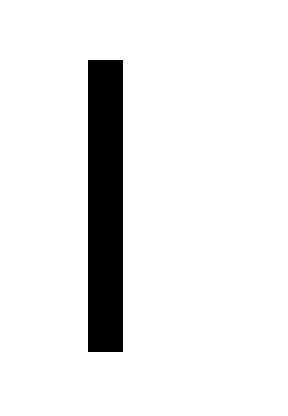 
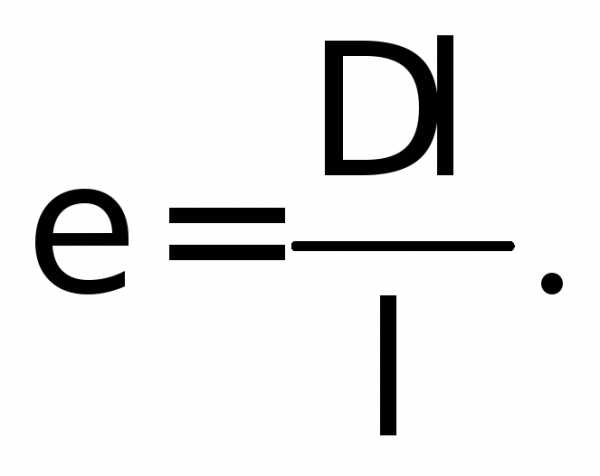(3.12)
Относительная поперечная деформация будет равна: ’ = = b/b, гдеb=b1–b.
Отношение относительной поперечной деформации ’ к относительной продольной деформации, взятое по модулю, есть для каждого материала величина постоянная и называется коэффициентом Пуассона:
Определение абсолютной деформации участка бруса
В формулу (3.11) вместо 
и
подставим выражения (3.1) и (3.12):
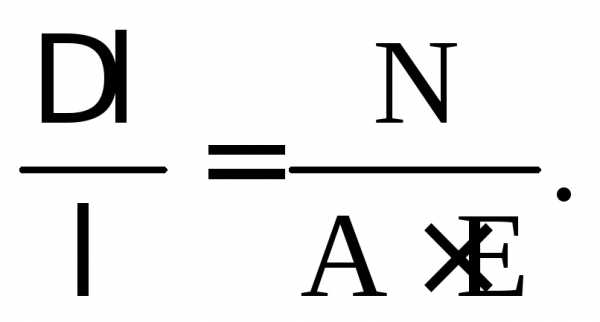
Отсюда получим формулу для определения
абсолютного удлинения (или укорочения)
участка стержня длиной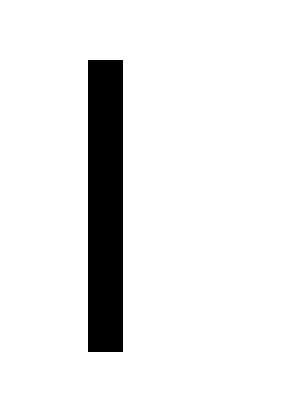 
:
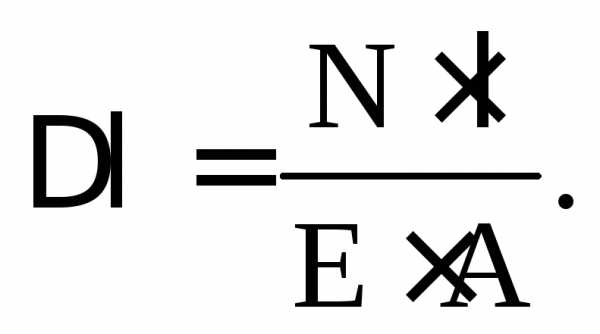
(3.13)
В формуле (3.13) произведение ЕА называетсяжесткостью бруса при растяжении или сжатии,которая измеряется в кН, или в МН.
По этой формуле определяется абсолютная
деформация 
,
если на участке продольная сила постоянна.
В случае, когда на участке продольная
сила переменна, она определяется по
формуле:
(3.14)
где N(х) – функция продольной силы по длине участка.
В частности, по этой же формуле вычисляется абсолютная деформация при учете собственного веса для вертикального бруса, когда вес одного погонного метра бруса входит в выражение для N(х) как интенсивность распределенной нагрузки, направленной вниз, параллельно оси бруса:
,
где 
– плотность материала бруса, кН/м3,
Н/м3; А – площадь поперечного
сечения бруса, м2.
Определение перемещений сечений бруса
Определим горизонтальное перемещение
точки аоси бруса (рис. 3.5) –ua:
оно равно абсолютной деформации части
брусааd, заключенной
между заделкой и сечением, проведенным
через точку, т.е.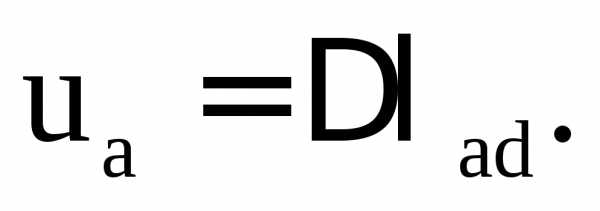 
В свою очередь удлинение участка аdсостоит из удлинений отдельных грузовых участков 1, 2 и 3:
(3.15)
Продольные силы на рассматриваемых участках:
Следовательно,
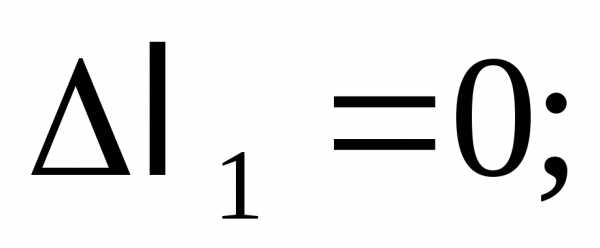
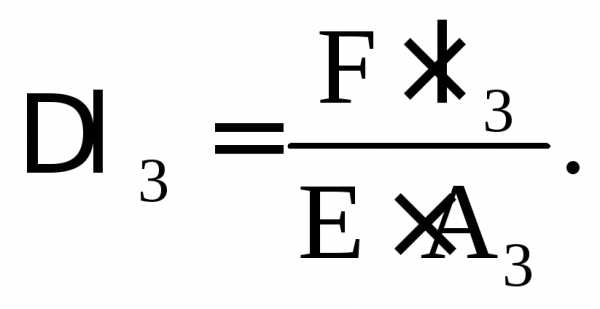
Тогда
Аналогично можно определить перемещение любого сечения бруса и сформулировать следующее правило:
перемещение любого сечения j стержня при растяжении–сжатии определяется как сумма абсолютных деформаций n грузовых участков, заключенных между рассматриваемым и неподвижным (закрепленным) сечениями, т.е.
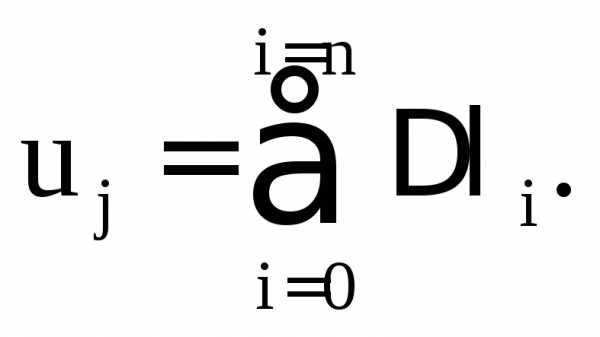(3.16)
Условие жесткости бруса запишется в следующем виде:
,
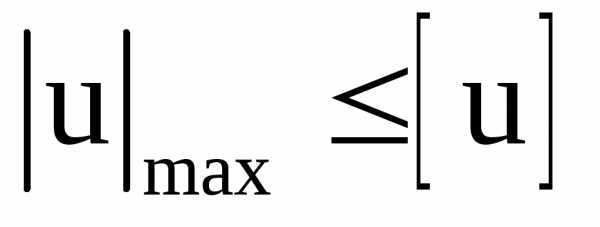(3.17)
где 
–
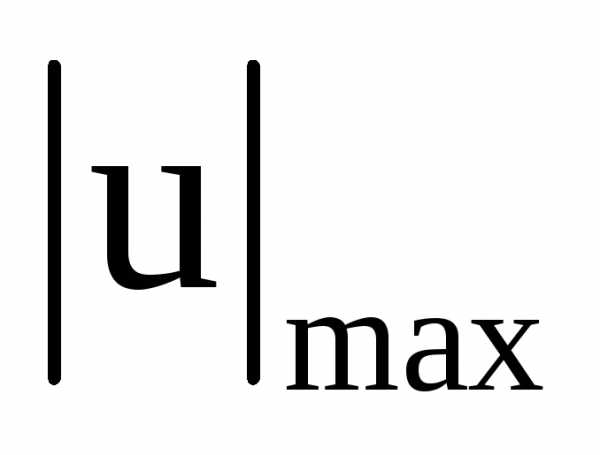наибольшее значение перемещения сечения,
взятое по модулю из эпюры перемещений;u– допускаемое значение перемещения
сечения для данной конструкции или ее
элемента, устанавливаемое в нормах.
ПРИМЕР 3.2
Требуется построить эпюру N для бруса, изображенного на рис. 3.6а и подобрать площадь сечения А и размер сторон квадратного сечения из условия жесткости при
Е = 0,27105 МПа,u= 2 мм = 210–3 м.
РЕШЕНИЕ
1. В данной задаче, как и в предыдущей, нет необходимости определять реакцию заделки, так как один конец бруса свободный.
2. Разбиваем брус на грузовые участки 1, 2, 3.
3. В пределах каждого грузового участка проводим сечения на расстоянии xiот начала участка, т.е. используем местную систему координат.
4. Используя рабочее правило и принятое правило знаков, в каждом сечении записываем функцию продольной силы Ni(хi) (в таком случае рекомендуется рукой или бумагой закрывать отбрасываемую часть бруса, чтобы не делать дополнительных рисунков). При этом рассматриваем свободную часть бруса.
При
При
При
При
5. По вычисленным результатам строим эпюру N (рис. 3.3б).
Анализ построенной эпюры N позволяет выделить следующие особенности:
– в сечении, где приложена
сосредоточенная сила F,
параллельная оси бруса, имеется скачок,
равный этой силе;
– на грузовых участках, где действуют равномерно распределенные нагрузки интенсивностью q, на эпюре N имеются наклонные прямые, тангенсы углов между этими прямыми и осью бруса равны интенсивности распределенной по длине нагрузки q;
– на тех грузовых участках, где отсутствует распределенная нагрузка, эпюра N постоянна.
6. Определим перемещения характерных сечений и построим эпюру перемещений при А = const:
uA= 0 (так как здесь защемление, препятствующее вертикальным перемещениям).
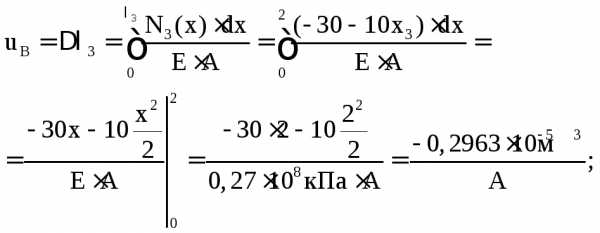
Используя полученные результаты, строим
эпюру перемещений сечений (см. рис. 3.3в),
из которой видим, что
Используя равенство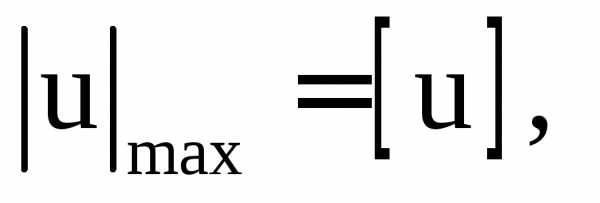
получаем
Отсюда А =
При А = сторона квадратного поперечного сечения будет равна а =
ПРИМЕР 3.3
Для бруса, изображенного на рис. 3.7а требуется:
– построить эпюру Nбез учета собственного веса;
– подобрать площади поперечных сечений из условий прочности;
– построить эпюры продольных сил N, нормальных напряжений и перемещений сечений u с учетом собственного веса бруса и проверить прочность и жесткость при следующих данных:
Rt= 0,9 МПа = 0,9103кПа.
;= 25 кН/м3;u= 0,510–3м.
РЕШЕНИЕ
1. Как и в предыдущем примере, опорную реакцию не определяем, так как один конец бруса свободен.
2. Выделяем грузовые участки стержня 1, 2, 3.
3. В этом примере эпюру N будем строить, записывая их функции на каждом грузовом участке, используя рабочее правило, приведенное в конце примера 3.1 (с. 17).
Расчет без учета собственного веса бруса
x2 = 0, N2(0) = 40 кН;
х2 = 1,2 м, N2(1,2) = 16 кН;
N3(x3) = – F3 + F2–F1 – qn )1,2 + x3) =
= –100 +140 – 120 – 20(1,2 +x3) = –104 – 20x3.
x3 = 0,N3(0) = –104 кН;
х3= 1,2 м, N3(1,2) = –144 кН.
По вычисленным значениям строим эпюру продольных сил N (рис. 3.7б).
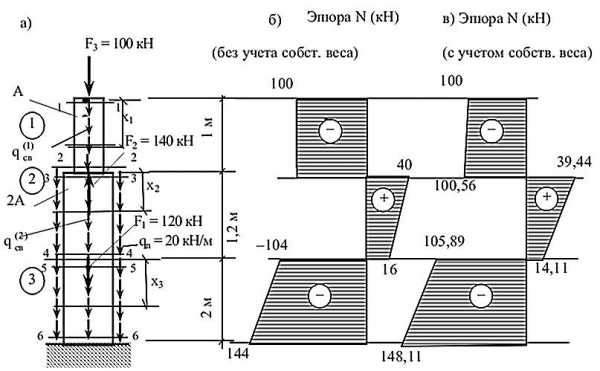
Рис. 3.7
4. Из условий прочности (3.3), используя эпюру N, построенную без учета собственного веса, определяем требуемую площадь поперечного сечения бруса, соблюдая заданное соотношение площадей на отдельных участках (рис. 3.7а). По условию задачи на участках 2 и 3 (нижняя ступень) площади сечения одинаковы и равны 2А. Для этих участков из эпюры N имеем:
В условиях прочности (3.3) приравняем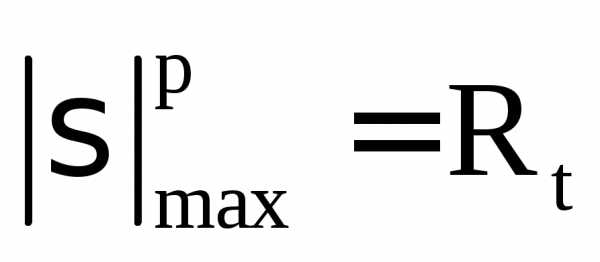 
и получаем:
На участке 1 (верхняя ступень) площадь сечения по условию задачи должна быть равна А. Из эпюры N для этого участка имеем:
.
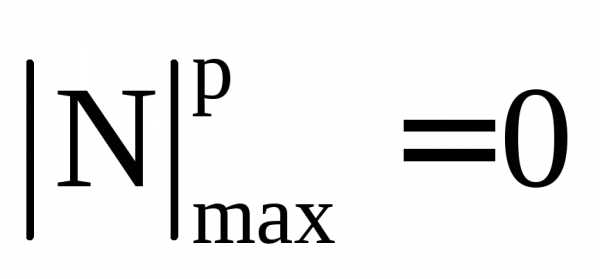Площадь поперечного сечения будет равна:
Из трех найденных значений А выбираем большую:
, 2А = 44,4410–3м2.
studfiles.net
ПОНЯТИЕ О НАПРЯЖЕНИЯХ, ДЕФОРМАЦИЯХ И ПЕРЕМЕЩЕНИЯХ. — КиберПедия
Рабочие гипотезы СОПРОМАТА
ОТВЕТ: В отличие от термеха, базирующегося на модели абс. твердого тела, в сопромате принята своя расчетная модель-модель идеализированного деформируемого тела. А для упрощения расчетов принимаются следующие допущения или гипотезы: 1) Материал тела имеет сплошное строение. 2) материал однороден, т.е. во всех точках свойства одинаковы. 3) материал изотропен, т.е. по всем направлениям свойства одинаковы. 4) до приложения внешних сил начальные напряжения в материале отсутствуют. 5) при решении реальных задач целесообразно использовать принцип суперпозиции, или принцип независимости действия сил, т.е. воздействие на конструкцию группы сил равно сумме воздействий от каждой силы в отдельности и не зависит от последовательности приложения этих сил.
ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ И МЕТОД ИХ ОПРЕДЕЛЕНИЯ.
ОТВЕТ: Под действием внешних сил на брус возникают внутренние силы или внутренние силовые факторы, для определения которых в сопромате принят единый расчетный метод – метод сечений. 1) разрезаем мысленно брус в исследуемом сечении на 2 части I и II. 2) Отбрасываем одну из частей. 3) Заменяем действие отбрасываемой части II на часть I внутренними силовыми факторами(в общем случае их 6). Qx Qy – поперечные силы, Nz – продольная сила, Mx My – изгибающие моменты, Mz – крутящий момент. 4) Уравновешиваем оставшуюся часть бруса и с помощью уравнений равновесия термеха находим искомые силовые факторы.
ПОНЯТИЕ О НАПРЯЖЕНИЯХ, ДЕФОРМАЦИЯХ И ПЕРЕМЕЩЕНИЯХ.
ОТВЕТ: Мерой интенсивности действия внутренних сил в окрестности точки рассматриваемого поперечного сечения являются напряжения, определяемые отношением силы к единице площади [Па]. Если в поп. сечении выделить элемент DА, к которому будет приложена сила DР, то DР/DА=рm – среднее полное напряжение в рассматриваемой точке поперечного сечения. — полное истинное напряжение. Вектор раскладывают на и . — нормальное напряжение – вызывает разрушения путем отрыва. — касательное напряжение – вызывает разрушение путем сдвига. Перемещения и деформации – понятия, характеризующие изменение размеров и формы исследуемого тела. При этом перемещения являются следствием деформации.
Напряжения и деформации при кручении вала круглого поперечного сечения.
Определение деформаций.
При кручении как было отмечено выше лин. деформаций не происходит,и под действием касат. напряжений происходит перенос сетки(квадраты становятся ромбами, при этом max величины переноса — абсолютный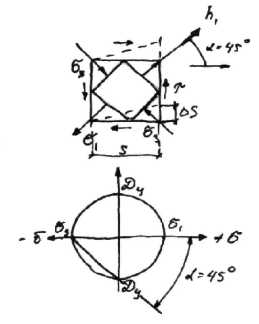 
сдвиг, а отношение — относит. 
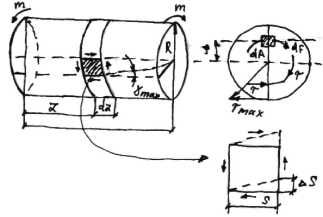сдвиг.
По аналогии с растяжением сжатием:
( ) З-Н Гука применительно к кручению: (1) G – модуль упругости II рода
Связь м/у модулями II рода: , для стали
Определение перемещений при изгибе. Условие жесткости. Дифференциальное уравнение изогнутой оси балки.
Варианты расчета простых статически неопределимых балок
Существует несколько способов расчета простых балок:
1.Сравнение линейных перемещений.
ΔВ=ΔВq+ΔBRB=0(1) доп. уравнение деформаций
Слагаемые в(1) могут быть найдены исп-я готовые таблицы или универсальные уравнения. Применительно к рас-му предмету:
ΔBq=-qe4/8EIx; ΔBRB=RBe3 /3EIx;
ΔB=-qe4/8EIx +RBe3/3EIx =0 =>RB=3qe/8
2. Сравнение угловых перемещений.
Можно отбросить связь, препятствующая повороту опорного сечения А и записать
ΔA=ΔAq+ΔAMA=0(2)
Также ур-е деформации слагаемое означает углы поворота.
3.Составление замкнутой системы ур-я.
3 ур-я статики+ унивес. ур-е
yB=0.
43. Метод сил для расчета сложных СНС.
Метод при котором за неизвестное принимаются сосредоточенные моменты наз-ся методом сил. Он явл-ся наиболее распространенным и ис-ся для любых упругих систем (балки, рамы,эстакады итд.).
Например:
К трем ур-ям статики для решения данной СНС добавится 3 уравнения, выражающие рав-во 0 перемещений по направлениям всех отброшенных связей т.е. опорное сечение и не перемещаются им в горизонтальном или в вертикальном перемещениях и не переворачиваются.
X1 Δ1=0
X2 Δ2=0 (1)
X3 Δ3=0
Каждое уравнение системы(1) можно записать в развернутом виде:
Δ1=Δ11+Δ12+Δ13+Δ1f=0 (2)
Первый символ указывает направление; 2-й воз-е.
Δ1f-перемещение опорного сечения А в направлении действия X, вызванное внешней нагрузкой
(2) можно выразить через единичные перемещения и искомое неизвестное (это первые три слагаемых)
Δ11=δ11-x1 и тогда система примет закончен. вид.
δ11 x1+ δ12 x2+ δ13 x3+ Δ1f=0
δ21 x1+ δ22 x2+ δ23 x3+ Δ2f=0 (3)-система кумс.
δ31 x1+ δ32 x2+ δ33 x3+ Δ3f=0
Канонические ур-я метода сил-КУМС.
Число ур-й равно степени статической неопределимости.
Рабочие гипотезы СОПРОМАТА
ОТВЕТ: В отличие от термеха, базирующегося на модели абс. твердого тела, в сопромате принята своя расчетная модель-модель идеализированного деформируемого тела. А для упрощения расчетов принимаются следующие допущения или гипотезы: 1) Материал тела имеет сплошное строение. 2) материал однороден, т.е. во всех точках свойства одинаковы. 3) материал изотропен, т.е. по всем направлениям свойства одинаковы. 4) до приложения внешних сил начальные напряжения в материале отсутствуют. 5) при решении реальных задач целесообразно использовать принцип суперпозиции, или принцип независимости действия сил, т.е. воздействие на конструкцию группы сил равно сумме воздействий от каждой силы в отдельности и не зависит от последовательности приложения этих сил.
ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ И МЕТОД ИХ ОПРЕДЕЛЕНИЯ.
ОТВЕТ: Под действием внешних сил на брус возникают внутренние силы или внутренние силовые факторы, для определения которых в сопромате принят единый расчетный метод – метод сечений. 1) разрезаем мысленно брус в исследуемом сечении на 2 части I и II. 2) Отбрасываем одну из частей. 3) Заменяем действие отбрасываемой части II на часть I внутренними силовыми факторами(в общем случае их 6). Qx Qy – поперечные силы, Nz – продольная сила, Mx My – изгибающие моменты, Mz – крутящий момент. 4) Уравновешиваем оставшуюся часть бруса и с помощью уравнений равновесия термеха находим искомые силовые факторы.
ПОНЯТИЕ О НАПРЯЖЕНИЯХ, ДЕФОРМАЦИЯХ И ПЕРЕМЕЩЕНИЯХ.
ОТВЕТ: Мерой интенсивности действия внутренних сил в окрестности точки рассматриваемого поперечного сечения являются напряжения, определяемые отношением силы к единице площади [Па]. Если в поп. сечении выделить элемент DА, к которому будет приложена сила DР, то DР/DА=рm – среднее полное напряжение в рассматриваемой точке поперечного сечения. — полное истинное напряжение. Вектор раскладывают на и . — нормальное напряжение – вызывает разрушения путем отрыва. — касательное напряжение – вызывает разрушение путем сдвига. Перемещения и деформации – понятия, характеризующие изменение размеров и формы исследуемого тела. При этом перемещения являются следствием деформации.
cyberpedia.su
Построение эпюры перемещений при растяжении-сжатии
Задача
Рассчитать перемещения характерных сечений стержня постоянного сечения и построить их эпюру.
Пример решения
Предыдущие пункты решения задачи:
- Расчет опорной реакции стержня,
- Расчет внутренних сил с построением эпюры,
- Подбор размеров поперечного сечения,
- Построение эпюры напряжений,
- Расчет деформаций участков стержня.
Под действием внешних сил стержень деформируется, вследствие чего его поперечные сечения перемещаются (в данном случае влево либо вправо).
Для расчета величины и направления перемещений воспользуемся соответствующей формулой:
где δi – перемещение рассматриваемого сечения,
δi-1 – перемещение предыдущего сечения,
Δli – деформация участка расположенного между указанными сечениями (рассчитаны ранее).
По расчетной схеме видно, что сечение, расположенное в заделке (сечение B) перемещаться не может, следовательно, его перемещение равно нулю, т.е.
Перемещение остальных сечений рассчитывается последовательно от него.
Следующим рассматриваем сечение C.
Его перемещение δC будет складываться из двух составляющих:
- изменения дины участка BC,
- перемещения предыдущего сечения B с которым связан их общий участок.
Так как сечение В неподвижно, сечение C переместится ровно на ту величину, на которую растянется III участок BC.
Перемещения остальных сечений рассчитываются аналогично:
По этим данным строится эпюра перемещений δ. Для этого рассчитанные значения в выбранном масштабе откладываются от базовой линии под соответствующим сечением стержня.
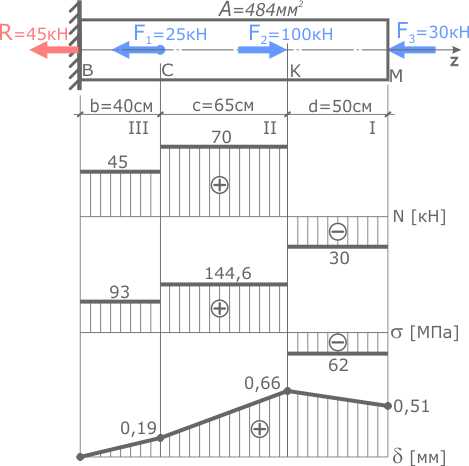
Эпюра наглядно показывает, что в результате деформации стержня наибольшее перемещение получило сечение K, которое переместилось вправо на 0,66 мм, а общая длина всего стержня увеличилась на 0,51 мм.
На участках, где нормальные напряжения положительны линия эпюры перемещений идет на возрастание (при условии, что заделка слева) и, наоборот. При этом, чем больше величина напряжений, тем больше угол наклона линии эпюры δ к базовой линии.
Другие примеры решения задач >
isopromat.ru
Понятие о напряжениях и деформациях (Лекция №5)
Как отмечалось выше, внутренние силы, действующие в некотором сечении со стороны отброшенной части тела, можно привести к главному вектору и главному моменту. Зафиксируем точку М в рассматриваемом сечении с единичным вектором нормали n. В окрестности этой точки выделим малую площадку F. Главный вектор внутренних сил, действующих на этой площадке, обозначим через P (рис. 1 а). При уменьшении размеров площадки соответственно
Рис.1. Композиция вектора напряжения.
а) вектор полного напряжения б) вектор нормального и касательного напряжений
уменьшаются главный вектор и главный момент внутренних сил, причем главный момент уменьшается в большей степени. В пределе при получим
Аналогичный предел для главного момента равен нулю. Введенный таким образом вектор рn называется вектором напряжений в точке. Этот вектор зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки F, характеризуемой вектором п. Совокупность всех векторов напряжений в точке М для всевозможных направлений вектора п определяет напряженное состояние в этой точке.
В общем случае направление вектора напряжений рn не совпадает с направлением вектора нормали п. Проекция вектора рnна направление вектора п называется нормальным напряжением , а проекция на плоскость, проходящую через точку М и ортогональную вектору n, касательным напряжением (рис. 1 б).
Размерность напряжений равна отношению размерности силы к размерности площади. В международной системе единиц СИ напряжения измеряются в паскалях: 1 Па=1 Н/м2.
При действии внешних сил наряду с возникновением напряжений происходит изменение объема тела и его формы, т. е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела.
Отнесем недеформированное тело к декартовой системекоординат Oxyz (рис. 2). Положение некоторой точки М в этой системе координат определяется радиус-вектором r(х, у, z). В деформированном состоянии точка М займет новое положение М/ , характеризуемое радиус-вектором r‘ (х, у, z). Вектор u=r’r называется вектором, перемещений точки М. Проекции вектора u на координатные оси определяют компоненты вектора перемещений и(х, у, z), v(х, у, z), w(х, у, z), равные разности декартовых координат точки тела после и до деформации.
Перемещение, при котором взаимное расположение точек тела не меняется, не сопровождается деформациями. В этом случае говорят, что тело перемещается как жесткоецелое (линейное перемещение в пространстве или поворот относительно некоторой точки). С другой стороны, деформация, связанная с изменением формы тела и его объема, невозможна без перемещения его точек.
Рис.2. Композиция вектора перемещения
Деформации тела характеризуются изменением взаимного расположения точек тела до и после деформации. Рассмотрим, например, точку М и близкую к ней точку N, расстояние между которыми в недеформированном состоянии вдоль направления вектора s обозначим через (рис. 2). В деформированном состоянии точки М и N переместятся в новое положение (точки М’ и N), расстояние между которыми обозначим через s’. Предел отношения
называется относительной линейной деформацией в точке М в направлении вектора s, рис.3. Рассматривая три взаимно перпендикулярных направления, например, вдоль координатных осей Ох, Оу и Oz, получим три компоненты относительных линейных деформаций характеризующих изменение объема тела в процессе деформации.
Для описания деформаций, связанных с изменением формы тела, рассмотрим точку М и две близкие к ней точки N и Р, расположенные в недеформированном состоянии в направлении двух взаимно ортогональных векторов s1 и s2. Расстояния между точками обозначим через и (рис. 4). В деформированном состоянии положение точек обозначим через М’, N’ и Р’. Угол между отрезками M’N’ и М’Р’ в общем случае будет отличным от прямого. При , изменение угла между двумя ортогональными до деформации направлениями называется угловой деформацией. Как видно из рис. 4, угловая деформация складывается из двух углов и , связанных с поворотами отрезков MN’ и М’Р’ ‘в.плоскости, образованной векторами s1 и s2, относительно этих векторов. Если заданы три взаимно ортогональных вектора, направленных вдоль координатных осей, то имеются три угловые деформации , и , которые вместе с тремя линейными деформациями , и полностью определяют деформированное состояние в точке.
Рис.3. Композиция линейной деформации
Рис. 4. Композиция угловой деформации
НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ. ТЕНЗОР НАПРЯЖЕНИЙ
Вектор напряжений pn является физическим объектом, имеющим длину, направление и точку приложения. В этом смысле он обладает векторными свойствами. Однако этому объекту присущи некоторые свойства, не характерные для векторов. В частности, величина и направление вектора напряжений зависят от ориентации вектора n нормали бесконечно малого элемента поверхности dF. Совокупность всех возможных пар векторов п, рn в точке определяет напряженное состояние в данной точке. Однако для полного описания напряженного состояния в точке нет необходимости задавать бесконечное множество направлений вектора n, достаточно определить векторы напряжений на трех взаимно перпендикулярных элементарных площадках. Напряжения на произвольно ориентированных площадках могут быть выражены через эти три вектора напряжений. В дальнейшем лектор умышленно меняет ориентацию координат. Так, что ось Z продольная ось бруса, а X и Y координаты любой точки его поперечного сечения.
Проведем через точку М три взаимно перпендикулярных плоскости с векторами нормалей, направления которых совпадают с направлениями координатных осей. Элементарные площадки образуем дополнительными сечениями, параллельными исходным плоскостям и отстоящими от них на бесконечно малые расстояния dx, dy, dz. В результате в окрестности точки М получим бесконечно малый параллелепипед, поверхность которого образована элементарными площадками dFх=dydz, dFн==dxdz, dFя=dxdy. Векторы напряжений px, py, pz, действующие на элементарных площадках, показаны на рис. 5.
Разложим каждый вектор напряжений на составляющие вдоль координатных осей (рис. 6). На каждой площадке действует одно нормальное напряжение , , , где индекс обозначает направление вектора нормали к площадке и два касательных напряжения с двумя индексами, из которых первый указывает направление действия компоненты напряжения, второйнаправление вектора нормали к площадке.
Рис. 5. Равновесное состояние бесконечно-малого параллелепипеда
Рис.6. Компоненты тензора напряженного состояния
Совокупность девяти компонент напряжений (по три на каждой из трех взаимно перпендикулярных площадок) представляет собой некоторый физический объект, называемый тензором напряжений в точке. Тензор можно представить в виде матрицы, соответствующим образом упорядочив девять компонент:
Для компонент тензора напряжений общепринятым является следующее правило знаков: компонента считается положительной, если на площадке с положительной внешней нормалью (т. е. направленной вдоль одной из координатных осей) эта компонента направлена в сторону положительного направления соответствующей оси. На рис. 6 все компоненты тензора напряжений изображены положительными. На площадках с отрицательной внешней нормалью (грани параллелепипеда, не видимые на рис. 5 и 6) положительная компонента направлена в противоположном направлении. Напряжения на трех взаимно ортогональных площадках с отрицательными направлениями нормалей также характеризуют напряженное состояние в точке. Эти напряжения, являющиеся компонентами тензора напряжений, определяются аналогично напряжениям на площадках с положительной нормалью. Они обозначаются теми же символами и имеют положительное направление, обратное изображенному на рис. 6.
Дальше…toehelp.ru
MYsopromat.ru: Определение деформаций и перемещений
Опыты показывают, что при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются, при сжатии наоборот (Рис. 4.2 б).
Для многих материалов при нагружении до определенных пределов опыты показывают следующую зависимость между относительным удлинением стержня ε и напряжением σ:
|
, |
(4.4) |
где ε = Δl/l — относительное удлинение стержня; Δl = (l1-l) — абсолютное удлинение стержня; l — длина образца до деформации; l1 — то же, после деформации.
Эта зависимость, как отмечалось выше, носит название закона Гука и формулируется следующим образом: линейные деформации прямо пропорциональны нормальным напряжениям.
В формуле (4.4) Е — коэффициент, зависящий от материала и называемый модулем продольной упругости или модулем упругости первого рода, а также модулем Юнга. Он характеризует жесткость материала, т. е. его способность сопротивляться деформированию. Поскольку ε — безразмерная величина, то из формулы (4.4) видно, что единица Е та же, что и σ, т. е. Паскаль (Па). В Табл. 4.1 даны средние значения E для некоторых материалов.
Табл.4.1. Значения модуля продольной упругости для разных материалов
| Материал | E, МПа |
| Сталь | 2·105– 2.2·105 |
| Медь | 1·105 |
| Дерево | 1·104 |
| Алюминий | 0.675·105 |
| Чугун | 0.75·105 – 1.6·105 |
| Стеклопластики | 0.18·105 – 0.4·105 |
Для других материалов значение Е можно найти в справочниках. Имея в виду, что для стержня постоянного сечения ε = Δl/l, а σ = N/F, из формулы (4.4) можно получить формулу для определения полного (абсолютного) удлинения (укорочения) стержня
|
. |
(4.5) |
Между продольной ε и поперечной ε/ деформациями существует установленная экспериментально зависимость
|
. |
(4.6) |
Здесь μ — коэффициент поперечной деформации (коэффициент Пуассона), характеризующий способность материала к поперечным деформациям. При пользовании приведенной формулой удлинение считается положительным, укорочение — отрицательным. Значение μ для всех материалов колеблется в пределах 0<μ<0.5, а для большинства материалов — от 0.25 до 0.35 (Табл. 4.2).
Для стали при упругих деформациях можно принимать μ ≈ 0.3. Зная ε/, можно определить полное поперечное сужение или расширение стержня Δb:
,
где b первоначальный поперечный размер стержня; b1 — поперечный размер стержня после деформации.
Табл. 4.2 Значения коэффициента Пуассона для разных материалов
| Материал | μ |
| Сталь | 0.25-0.33 |
| Медь | 0.31-0.34 |
| Бронза | 0.32-0.35 |
| Чугун | 0.23-0.27 |
| Стекло | 0.25 |
| Бетон | 0.08-0.18 |
| Пробка | 0.00 |
| Целлулоид | 0.39 |
| Свинец | 0.45 |
| Латунь | 0.32-0.42 |
| Алюминий | 0.32-0.36 |
| Цинк | 0.21 |
| Камень | 0.16-0.34 |
| Каучук | 0.47 |
| Фанера | 0.07 |
mysopromat.ru