Сопромат.in.ua: Напряжения
Напряжением называется интенсивность действия внутренних сил в точке тела, то есть, напряжение — это внутреннее усилие, приходящееся на единицу площади. По своей природе напряжение — это поверхностная нагрузка, возникающая на внутренних поверхностях соприкасания частей тела. Напряжение, так же как и интенсивность внешней поверхностной нагрузки, выражается в единицах силы, отнесенных к единице площади:Па=Н/м2 (МПа = 106 Н/м2, кгс/см2=98 066 Па ≈ 105Па, тс/м2 и т. д.).
 Рассечем тело произвольным сечением Выделим небольшую площадку ∆A. Внутреннее усилие, действующее на нее, обозначим [math]∆\vec{R}[/math]. Полное среднее напряжение на этой площадке [math]\vec{р} = ∆\vec{R}/∆A [/math]. Найдем предел этого отношения при [math]∆A \to 0[/math] . Это и будет полным напряжение на данной площадке (точке) тела.
Рассечем тело произвольным сечением Выделим небольшую площадку ∆A. Внутреннее усилие, действующее на нее, обозначим [math]∆\vec{R}[/math]. Полное среднее напряжение на этой площадке [math]\vec{р} = ∆\vec{R}/∆A [/math]. Найдем предел этого отношения при [math]∆A \to 0[/math] . Это и будет полным напряжение на данной площадке (точке) тела.Полное напряжение [math]\vec p[/math], как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σn и касательное к площадке – касательное напряжение [math]\tau_n[/math]. Здесь n – нормаль к выделенной площадке.
Касательное напряжение, в свою очередь, может быть разложено на две составляющие, параллельные координатным осям x, y, связанным с поперечным сечением – [math]\tau_{nx}, \tau_{ny}[/math]. В названии касательного напряжения первый индекс указывает нормаль к площадке,второй индекс — направление касательного напряжения.
$$\vec{p} = \left[\matrix{\sigma _n \\ \tau _{nx} \\ \tau _{nx}} \right]$$
Отметим, что в дальнейшем будем иметь дело главным образом не с полным напряжением [math]\vec p [/math], а с его составляющими [math]σ_x,\tau _{xy}, \tau _{xz} [/math] . В общем случае на площадке могут возникать два вида напряжений: нормальное σ и касательное τ.
Тензор напряжений
При анализе напряжений в окрестности рассматриваемой точки выделяется бесконечно малый объемный элемент (параллелепипед со сторонами dx, dy, dz), по каждой грани которого действуют, в общем случае, три напряжения, например, для грани, перпендикулярной оси x (площадка x) – [math]σ_x,\tau _{xy}, \tau _{xz} [/math]Компоненты напряжений по трем перпендикулярным граням элемента образуют систему напряжений, описываемую специальной матрицей – тензором напряжений
$$ T _\sigma = \left[\matrix{
\sigma _x & \tau _{yx} & \tau _{zx} \\
\tau _{xy} & \sigma _y & \tau _{zy} \\
\tau _{xz} & \tau _{yz} & \sigma _z
}\right]$$
Здесь первый столбец представляет компоненты напряжений на площадках,
При повороте осей координат, совпадающих с нормалями к граням выделенного
элемента, компоненты напряжений изменяются. Вращая выделенный элемент вокруг осей координат, можно найти такое положение элемента, при котором все касательные напряжения на гранях элемента равны нулю.
Площадка, на которой касательные напряжения равны нулю, называется главной площадкой.
Нормальное напряжение на главной площадке называется главным напряжением
Нормаль к главной площадке называется главной осью напряжений .
В каждой точке можно провести три взаимно-перпендикулярных главных площадки.
При повороте осей координат изменяются компоненты напряжений, но не меняется напряженно-деформированное состояние тела (НДС).
Связь внутренних усилий и напряжений
Внутренние усилия есть результат приведения к центру поперечного сечения внутренних сил, приложенных к элементарным площадкам. Напряжения – мера, характеризующая распределение внутренних сил по сечению.
Предположим, что нам известно напряжение в каждой элементарной площадке. Тогда можно записать:Продольное усилие на площадке dA: dN = σzdA
Поперечная сила вдоль оси х: dQ x = [math]\tau {zx}[/math] dA
Поперечная сила вдоль оси y: dQ y = [math]\tau {zy}[/math] dA
Элементарные моменты вокруг осей x,y,z: $$\begin{array}{lcr}
dM _x = σ _z dA \cdot y \\
dM _y = σ _z dA \cdot x \\
dM _z = dM _k = \tau _{zy} dA \cdot x — \tau _{zx} dA \cdot y
\end{array}$$
Выполнив интегрирование по площади поперечного сечения получим:

То есть, каждое внутренне усилие есть суммарный результат действия напряжений по всему поперечному сечению тела.
Связанные статьи
метки: напряжения
sopromat.in.ua
Формулы для расчетов на растяжение-сжатие
Обозначения в формулах:
σ — нормальные напряжения,
N – внутренняя продольная сила,
A – площадь поперечного сечения,
[σ] – допустимые напряжения,
E – модуль продольной упругости,
ε — относительные деформации.
Закон Гука:
Формула для расчета напряжений в поперечном сечении стержня
Условие прочности (проверочный расчет) при растяжении-сжатии
Расчет минимальной площади поперечного сечения бруса
Расчет допустимой величины внешней растягивающей/сжимающей силы (определение грузоподъемности)
Формула для расчета абсолютных деформаций
Расчет перемещения сечений
Здесь: δi — перемещение рассматриваемого сечения,
δi-1 — перемещение предыдущего сечения,
Δli — деформация участка между указанными сечениями.
Напряжения в наклонных сечениях
Здесь α — угол отклонения сечения от поперечного.
Другие формулы >
Примеры решения задач >
Краткая теория >
isopromat.ru
Касательные напряжения при изгибе.Формула Д.И. Журавского
Для определения касательных напряжений рассмотрим балку, нагруженную силами.
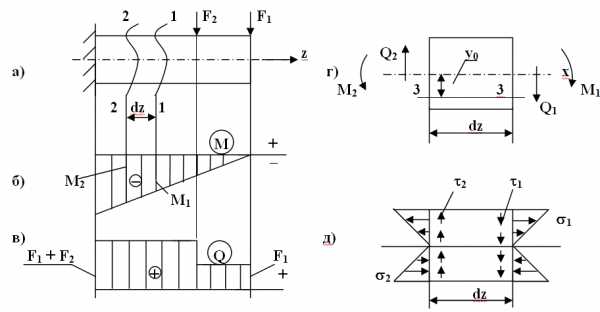
Схема для вывода формулы касательных напряжений: а) схема нагружения; б) эпюра изгибающих моментов; в) эпюра поперечных сил; г) и д) – схема напряженного состояния
Задача по определению напряжений всегда статически неопределима и требует привлечения геометрических и физических
Двумя бесконечно близкими поперечными сечениями 1-1 и 2-2 выделим элемент dz, изобразим его в крупном масштабе, затем проведем продольное сечение 3-3.
В сечениях 1–1 и 2–2 возникают нормальные σ1, σ2 напряжения, которые определяются по известным формулам:
где М — изгибающий момент в поперечном сечении , dМ — приращение изгибающего момента на длине dz
Поперечная сила в сечениях 1–1 и 2–2 направлена вдоль главной центральной оси Y и, очевидно, представляет сумму вертикальных составляющих внутренних касательных напряжений, распределенных по сечению. В сопротивлении материалов обычно принимается допущение о равномерном их распределении по ширине сечения.
Для определения величины касательных напряжений в какой-либо точке поперечного сечения, расположенного на расстоянии у0от нейтральной оси Х, проведем через эту точку плоскость, параллельную нейтральному слою (3-3), и вынесем отсеченный элемент. Будем определять напряжение, действующее по площадке АВСД. 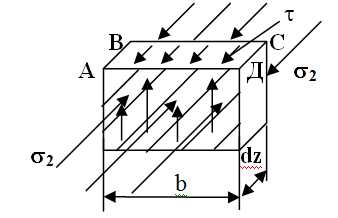
Спроецируем все силы на ось Z
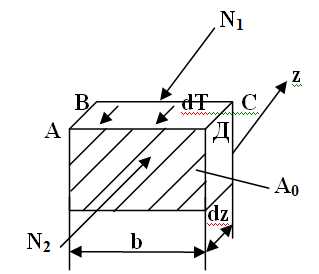
Равнодействующая внутренних продольных сил по правой грани будет равна:
где А0 – площадь фасадной грани, Sx0 – статический момент отсеченной части относительно оси Х. Аналогично на левой грани:
Обе равнодействующие направлены навстречу друг другу, поскольку элемент находится в
Предположим, что касательные напряжения τ распределены по ширине поперечного сечения балки b равномерно. Такое допущение тем вероятнее, чем меньше ширина по сравнению с высотой сечения. Тогда равнодействующая касательных сил dT равна значению напряжений, умноженному на площадь грани:
Составим теперь уравнение равновесия Σz=0:
или, откуда
Вспомним дифференциальные зависимости, согласно которым Тогда получаем формулу:
Эта формула получила название формулы Д. И. Журавского. Эта формула получена в 1855 г. Здесь Sx0 – статический момент части поперечного сечения, расположенной по одну сторону от слоя, в котором определяются касательные напряжения, Ix – момент инерции всего поперечного сечения, b – ширина сечения в том месте, где определяется касательное напряжение, Q -поперечная сила в сечении.
prosopromat.ru
Формула Журавского (сопромат)
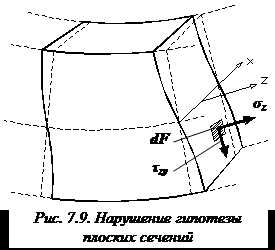 Формула Журавского позволяет определить касательные напряжения при изгибе, возникающие в точках поперечного сечении балки, находящиеся на расстоянии от нейтральной оси x.
Формула Журавского позволяет определить касательные напряжения при изгибе, возникающие в точках поперечного сечении балки, находящиеся на расстоянии от нейтральной оси x.
Вывод формулы Журавского
Вырежем из балки прямоугольного поперечного сечения (рис. 7.10, а) элемент длиной и дополнительным продольным сечением рассечем на две части (рис. 7.10, б).
Рассмотрим равновесие верхней части: из-за отличия изгибающих моментов возникают разные сжимающие напряжения. Чтобы эта часть балки находилась в равновесии () в ее продольном сечении должна возникнуть касательная сила . Уравнение равновесия части балки:
Отсюда
,
где интегрирование ведется только по отсеченной части площади поперечного сечения балки (на рис. 7.10, в заштрихована), – статический момент инерции отсеченной (заштрихованной) части площади поперечного сечения относительно нейтральной оси x.
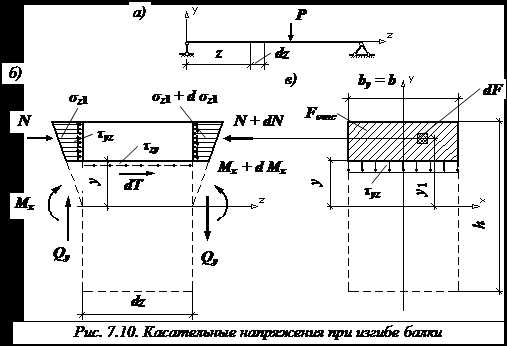
Предположим: касательные напряжения (), возникающие в продольном сечении балки, равномерно распределены по ее ширине () в месте сечения:
Получим выражение для касательных напряжений:
, а , тогда формула касательных напряжений (), возникающих в точках поперечного сечения балки, находящихся на расстоянии y от нейтральной оси x:
— формула Журавского
Формула Журавского получена в 1855 г. Д.И. Журавским, поэтому носит его имя.
sopromato.ru
действительные ответы на вопросы по сопромату
Какие усилия возникают в поперечном сечении стержня при изгибе?
При плоском поперечном изгибе в поперечных сечениях стержня возникают два усилия :изгибающий момент Mz и поперечная сила Qy. Если присутствуют осевые нагрузки в поперечных сечениях балки , то присутствует ещё продольная сила N.
Какие напряжения возникают в поперечном сечении стержня при поперечном изгибе? Как они направлены?
При поперечном изгибе возникает нормальное напряжение, направленное вдоль оси x . При этом если напряжение имеет положительное значение, то оно работает на растяжение (вектор напряжения направлен наружу) если отрицательное , то работает на сжатие( вектор направлен во внутрь).
Так же при поперечном изгибе возникает касательное напряжение ,которое можно разложить на касательное напряжение параллельное оси икс и касательное напряжение параллельное оси игрек( эти напряжения действуют на поверхности элементарного параллелепипеда). Если внешняя нормаль к площадке элементарного параллелепипеда совпадает с направлением одной из осей координат , то положительное касательное напряжение направлено вдоль соответствующей оси .В противоположном случае положительное касательное напряжение имеет противоположное направление.
Запишите формулу для определения нормальных напряжений в любой точке поперечного сечения. По какому закону нормальные напряжения изменяются по высоте поперечного сечения стержня. Приведите примеры эпюр нормальных напряжений для сечений различной формы.
Формула для определения нормального напряжения :
Нормальные напряжения изменяются по высоте поперечного сечения стержня по линейному закону.
Примеры эпюр нормальных напряжений для сечений различной формы:
По какой формуле определяются максимальные напряжения в поперечном сечении стержня?
где hн = hв = h/2 и Wн = Wв = W = Jz/0,5h
-для сечений симметричных относительно нейтральной оси.
где Wнм – наименьший момент сопротивления из
Для сечений которые не симметричны относительно нейтральной оси.
По какой формуле определяются касательные напряжения в поперечном сечении стержня? По какому закону изменяются касательные напряжения в сечении стержня? Приведите примеры эпюр касательных напряжений для сечений различной формы.
формула для определения касательных напряжений.
Для сечений прямоугольной формы касательные напряжения изменяются по закону квадратной параболы.
Примените закон парности касательных напряжений для поперечного изгиба и на рисунке балки покажите направления совпадающих по модулю касательных напряжений.
7.Что такое главные площадки напряжений и главные напряжения?
Главные площадки – площадки на которых отсутствует касательное напряжение , а нормальное напряжение принимает экстремальные значения . Главные напряжения –экстремальные напряжения действующие на главных площадках.
8.Запишите формулу для определения главных напряжений.
;
9. Укажите формулы для определения положения главных площадок.
.
10. Что называется предельным состоянием конструкции? Какие группы предельных состояний различают?
Предельное состояние – такое состояние конструкции , при котором невозможна её дальнейшая эксплуатация.
1 и 2 группа.
1 группа :Более опасная .сюда относится потеря прочности (исчерпание несущей способности),потеря устойчивости.
2 группа: Сюда относятся развитие чрезмерных перемещений ,деформаций, колебаний. Раскрытие трещин в железобетонных конструкциях, если для таких конструкций раскрытие трещин нормами не допускается или чрезмерное раскрытие трещин в железобетонных конструкциях.
Укажите 3 варианта постановки задачи расчёта на прочность.
1 вариант: задача подбора сечения конструкции .Известна : расчётная схема (нагрузка, условия опирания конструкции),материал конструкции. Нужно подобрать сечение.
2 вариант: Проверка конструкции на прочность. Известно всё .Требуется проверить условия прочности.
3 вариант: Определение грузоподъёмности конструкции, то есть максимальную нагрузку ,которую может нести данная конструкция.
Какие коэффициенты используются в методе расчёта по предельным состояниям? Вспомните смысл коэффициентов.
Коэффициент надёжности по нагрузке. Учитывает возможное увеличение нагрузки по сравнению с её нормативным значением.
Коэффициент условий работы. Учитывает возможные изменения прочности материала конструкции в зависимости от условий её эксплуатации.
Коэффициент надёжности по материалу. Учитывает возможные изменения прочности материала конструкции по сравнению с прочностью стандартных образцов материала.
Запишите условие прочности при изгибе по нормальным и касательным напряжениям.
нб ≤ сR , (1) условие прочности по нормальным напряжениям.
Для хрупких материалов расчётное сопротивление при растяжении Rр существенно меньше, чем при сжатии Rс . В этом случае должны выполняться условия прочности по наибольшим растягивающим и наибольшим сжимающим напряжениям
, (2),(3)
В случае расчёта на прочность по методу допускаемых напряжений в формулах (1), (2), (3) величины в правых частях необходимо заменить соответственно на [], [р] и [с].
Для балок из материала, одинаково сопротивляющегося растяжению и сжатию, с поперечным сечением, симметричным относительно нейтральной оси, условие прочности записывается в виде
нб = ≤ сR . где W= Wн = Wв = Jz/0,5h .
(4.13)
Для сечений, несимметричных относительно нейтральной оси (типа тавра и др.)
нб = ≤ сR .
-условие прочности по касательным напряжениям.
studfiles.net
Напряжения и прочность при изгибе
Важнейшим критерием оценки прочности балок при изгибе являются напряжения.
Расчет напряжений
Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент Mx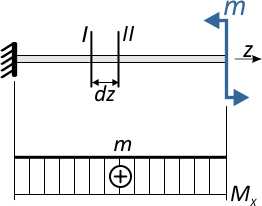
представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения.
Закон распределения нормальных напряжений по высоте сечения выражается формулой:
где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
Ix — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.
Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.
По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.
Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.
Например, для симметричного относительно нейтральной оси сечения, где y1=y2=h/2:
Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку.
Для несимметричного сечения
напряжения определяются отдельно для нижней точки 1 и верхней точки 2:
где:
WX — осевой момент сопротивления симметричного сечения;
WX(1) и WX(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.
Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.
Условия прочности при изгибе
Прочность по нормальным напряжениям
Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.
В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.
Здесь:
Mmax — максимальное значение изгибающего момента, определяемого по эпюре Mx;
[σ], [σ]р, [σ]с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).
Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [σ]с>[σ]р.
В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.
При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:
- Проверка прочности
- Подбор сечений
- Определение максимально допустимой нагрузки
Прочность по касательным напряжениям
В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.
Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского
где
Sx отс — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
by — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.
Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Qmax:
где [τ] – допустимое значение касательных напряжений для материала балки.
Полная проверка прочности
Полную проверку прочности балки производят в следующей последовательности:
- По максимальным нормальным напряжениям для сечения, в котором возникает наибольший по абсолютному значению изгибающий момент M.
- По максимальным касательным напряжениям для сечения, в котором возникает наибольшая по абсолютному значению поперечная сила Q.
- По главным напряжениям для сечения, в котором изгибающий момент и поперечная сила одновременно достигают значительных величин (или когда Mmax и Qmax действуют в одном и том же сечении балки).
При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид:
так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.
Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений:
Деформации при изгибе >
Угловые и линейные перемещения в балках >
Примеры решения задач >
Лекции по сопромату >
isopromat.ru
Как определить нормальное напряжение?
Сегодня будем говорить о том, как определить нормальное напряжение при растяжении (сжатии). Долго говорить не придется, так как определяется оно элементарно.
Формула для нахождения нормального напряжения следующая:
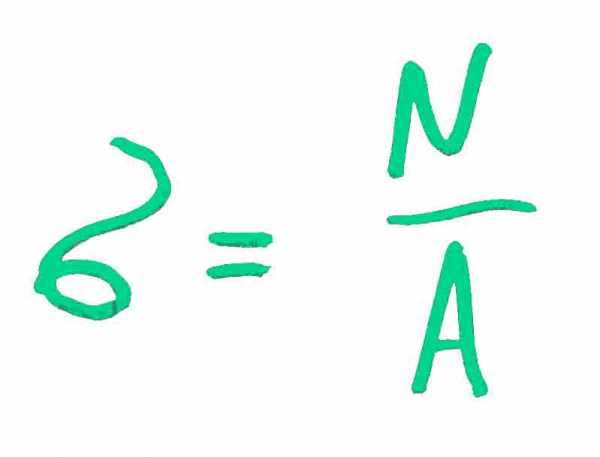
То есть это отношение продольной силы (N) к площади поперечного сечения (A), на которой действует эта сила.
Пример определение нормальных напряжений
Посмотрим, как на практике пользоваться этой формулой. Например, возьмем брус с постоянным поперечным сечением, на который действует кучка внешних сил. Вас просят найти максимальное нормальное напряжение, возникающее в поперечных сечениях бруса.
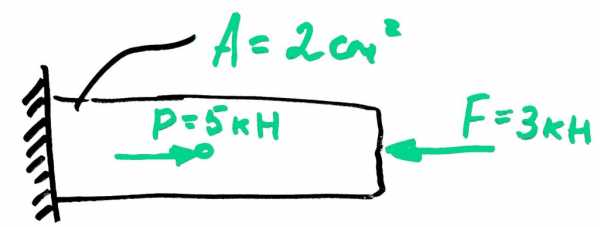
Ваша тактика будет такой: Сначала нужно определить продольные силы и по-хорошему построить эпюру, чтобы видеть наиболее опасное сечение, то есть сечение, в котором внутренняя сила максимальная.
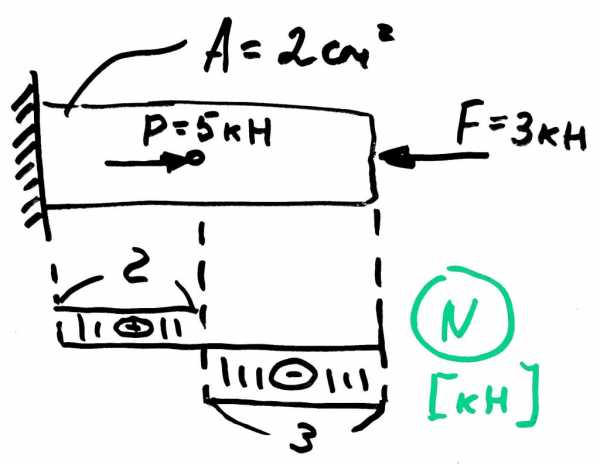
В нашем случае продольную силу берем равной трем килоньютонам и делим на площадь поперечного сечения:
Итого получили максимальное напряжение равное 15 мегапаскалям, что для стального бруса совсем пустяк.
ssopromat.ru