Задачи на кручение стержня круглого сечения (задачи по сопромату)
Пример решения задачи на кручение стержня круглого сечения
Кручение стержня круглого сечения – условие задачи
К стальному валу постоянного поперечного сечения (рис. 3.8) приложены четыре внешних скручивающих момента: кН·м; кН·м; кН·м; кН·м. Длины участков стержня: м; м, м, м. Требуется: построить эпюру крутящих моментов, определить диаметр вала при кН/см2 и построить эпюру углов закручивания поперечных сечений стержня.
Кручение стержня круглого сечения – расчетная схема
Рис. 3.8
Решение задачи кручение стержня круглого сечения
Определяем реактивный момент, возникающий в жесткой заделке
Обозначим момент в заделке и направим его, например, против хода часовой стрелки (при взгляде навстречу оси z).
Запишем уравнение равновесия вала. При этом будем пользоваться следующим правилом знаков: внешние скручивающие моменты (активные моменты, а также реактивный момент в заделке), вращающие вал против хода часовой стрелки (при взгляде на него навстречу оси z), считаем положительными.
Тогда
кН·м.
Знак «плюс» в полученном нами выражении говорит о том, что мы угадали направление реактивного момента , возникающего в заделке.
Строим эпюру крутящих моментов
Напомним, что внутренний крутящий момент , возникающий в некотором поперечном сечении стержня, равен алгебраической сумме внешних скручивающих моментов, приложенных к любой из рассматриваемых частей стержня (то есть действующих левее или правее сделанного сечения). При этом внешний скручивающий момент, вращающий рассматриваемую часть стержня против хода часовой стрелки (при взгляде на поперечное сечение), входит в эту алгебраическую сумму со знаком «плюс», а по ходу – со знаком «минус».
Соответственно, положительный внутренний крутящий момент, противодействующий внешним скручивающим моментам, направлен по ходу часовой стрелки (при взгляде на поперечное сечение), а отрицательный – против ее хода.
Разбиваем длину стержня на четыре участка (рис. 3.8, а). Границами участков являются те сечения, в которых приложены внешние моменты.
Делаем по одному сечению в произвольном месте каждого из четырех участков стержня.
Cечение 1 – 1. Мысленно отбросим (или закроем листком бумаги) левую часть стержня. Чтобы уравновесить скручивающий момент кН·м, в поперечном сечении стержня должен возникнуть равный ему и противоположно направленный крутящий момент . С учетом упомянутого выше правила знаков
кН·м.
Сечения 2 – 2 и 3 – 3:
кН·м;
кН·м.
Сечение 4 – 4. Чтобы определить крутящий момент, в сечении 4 – 4 отбросим правую часть стержня. Тогда
кН·м.
Легко убедиться в том, что полученный результат не изменится, если мы отбросим теперь не правую, а левую часть стержня. Получим
кН·м.
Для построения эпюры крутящих моментов проводим тонкой линией ось, параллельную оси стержня z (рис. 3.8, б). Вычисленные значения крутящих моментов в выбранном масштабе и с учетом их знака откладываем от этой оси. В пределах каждого из участков стержня крутящий момент постоянен, поэтому мы как бы «заштриховываем» вертикальными линиями соответствующий участок. Напомним, что каждый отрезок «штриховки» (ордината эпюры) дает в принятом масштабе значение крутящего момента в соответствующем поперечном сечении стержня. Полученную эпюру обводим жирной линией.
Напомним, что каждый отрезок «штриховки» (ордината эпюры) дает в принятом масштабе значение крутящего момента в соответствующем поперечном сечении стержня. Полученную эпюру обводим жирной линией.
Отметим, что в местах приложения внешних скручивающих моментов на эпюре мы получили скачкообразное изменение внутреннего крутящего момента на величину соответствующего внешнего момента.
Определяем диаметр вала из условия прочности
Условие прочности при кручении имеет вид
,
где – полярный момент сопротивления (момент сопротивления при кручении).
Наибольший по абсолютному значению крутящий момент возникает на втором участке вала: кН·см.
Тогда требуемый диаметр вала определяется по формуле
см.
Округляя полученное значение до стандартного, принимаем диаметр вала равным мм.
Определяем углы закручивания поперечных сечений A, B, C, D и E и строим эпюру углов закручивания
Сначала вычисляем крутильную жесткость стержня , где G – модуль сдвига, а – полярный момент инерции. Получим
Получим
кН·см2.
Углы закручивания на отдельных участках стержня равны:
рад;
рад;
рад;
рад.
Угол закручивания в заделки равен нулю, то есть . Тогда
рад;
рад;
рад;
рад.
Эпюра углов закручивания показана на рис. 3.8, в. Отметим, что в пределах длины каждого из участков вала угол закручивания изменяется по линейному закону.
Пример задачи на кручение «круглого» стержня для самостоятельного решения
Условие задачи на кручение «круглого» стержня
Жестко защемленный одним концом стальной стержень (модуль сдвига кН/см2) круглого поперечного сечения скручивается четырьмя моментами (рис. 3.7).
Требуется:
· построить эпюру крутящих моментов;
· при заданном допускаемом касательном напряжении кН/см2 из условия прочности определить диаметр вала, округлив его до ближайшего из следующих значений 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 мм;
· построить эпюру углов закручивания поперечных сечений стержня.
Варианты расчетных схем к задаче на кручение стержня круглого сечения для самостоятельного решения
Рис. 3.7
Пример задачи на кручение круглого стержня – исходные условия для самостоятельного решения
Номер схемы | М1, кН·м | М2, кН·м | М3, кН·м | М4, кН·м | a, м | b, м | c, м | d, м |
1 | 1,0 | 2,0 | 1,0 | 1,0 | 1,0 | 1,2 | 1,4 | 1,6 |
2 | 1,0 | 2,0 | 1,0 | 0,8 | 1,2 | 1,4 | 1,6 | 1,9 |
3 | 2,0 | 4,0 | 1,0 | 1,0 | 1,4 | 1,6 | 1,0 | 1,2 |
4 | 3,0 | 5,0 | 1,6 | 1,4 | 1,6 | 1,0 | 1,2 | 1,4 |
5 | 4,0 | 6,0 | 1,8 | 1,4 | 1,1 | 1,1 | 1,8 | 1,5 |
6 | 2,0 | 4,0 | 1,2 | 1,2 | 1,3 | 1,3 | 1,5 | 1,1 |
7 | 2,0 | 3,0 | 1,2 | 1,0 | 1,5 | 1,5 | 1,3 | 1,3 |
8 | 3,0 | 4,0 | 1,0 | 1,0 | 1,7 | 1,7 | 1,5 | 1,4 |
9 | 4,0 | 5,0 | 1,8 | 1,6 | 1,9 | 1,9 | 1,7 | 1,3 |
0 | 5,0 | 6,0 | 2,0 | 1,6 | 1,2 | 1,4 | 1,4 | 1,2 |
Задачи на кручение по сопромату примеры и решения
Содержание:
- Пример решения задачи 78.

- Вычисление моментов, передаваемых на вал. построение эпюр крутящих моментов для валов
- Пример решения задачи 79.
- Пример решения задачи 80.
- Напряжения и перемещения при кручении брусьев круглого поперечного сечения
- Пример решения задачи 81.
- Пример решения задачи 82.
- Пример решения задачи 83.
- Пример решения задачи 84.
- Пример решения задачи 85.
- Пример решения задачи 86.
- Пример решения задачи 87.
- Пример решения задачи 88.
- Пример решения задачи 89.
- Пример решения задачи 90.
- Статически неопределимые задачи кручения
- Пример решения задачи 93.
- Пример решения задачи 94.
- Кручение стержней прямоугольного поперечного сечения
- Пример решения задачи 95.
- Пример решения задачи 96.
Под кручением понимается такой вид иагруження бруса, при котором в его поперечных сечениях возникают только крутящие моменты.
Кручение имеет место при действии па брус внешних пар сил, плоскости которых перпендикулярны к оси стержня.
Моменты этих внешних пар, являющиеся нагрузкой для бруса, называют внешними, вращающими или скручивающими моментами.
Простейший случай кручения показан на рис. 79: брус находится под действием двух равных и противоположных скручивающих моментов, приложенных по концам. Моменты пар, приложенных к брусу, должны удовлетворять условию равновесия
В общем случае на брус может действовать несколько скручивающих моментов, приложенных в различных сечениях и взаимно уравновешивающихся. Для случая, представленного па рис. 80,
При действии на брус скручивающих моментов в его поперечных сечениях возникают крутящие моменты (рис. 81). Чтобы определить крутящий момент в каком-либо произвольном сечении бруса, необходимо мысленно разрезать его по этому сечению, отбросить одну
из его частей, а к оставшейся части приложить уравновешивающий крутящий момент и найти его величину из условия равновесия. Крутящий момент в любом сечении численно равен алгебраической сумме внешних моментов, приложенных по одну сторону от сечения, и направлен в противоположную сторону п-о отношению к результирующему моменту.
Крутящий момент, действующий на одну часть бруса (левую), равен Рис. 82 и противоположно направлен крутящему моменту, действующему в том же сечении на его другую часть (правую) (рис. 82).
Возможно вам будут полезны данные страницы:
Расчет рамы по сопромату примеры и решения |
Задачи на сжатие и растяжение по сопромату примеры и решения |
Расчёт балки задачи по сопромату примеры и решения |
Задачи на эпюры по сопромату построение примеры и решения |
В простейшем случае, когда брус нагружен по концам двумя равными и противоположно направленными скручивающими моментами (см. рис. 79), крутящий момент в любом поперечном сечении бруса имеет одинаковую величину:
Если к брусу приложено несколько скручивающих моментов, то крутящий момент будет оставаться постоянным в пределах каждого участка между местами приложения скручивающих моментов и меняется скачком на границах участков.
Пример решения задачи 78.
Для бруса изображенного на .рис. 83, а, определить реактивный момент в заделке, а также
величины крутящих моментов в поперечных сечениях участков построить эпюру крутящих моментов, если
Решение:
Определим реактивный момент в заделке, составив уравнение равновесия бруса
откуда
Знак «плюс» указывает, что направление момента в заделке предварительно было выбрано правильно.
Для определения крутящих моментов и построения эпюры применим метод сечений для каждого из трех участков бруса. Проведем сечение на участке Часть бруса, расположенная слева от сечения, будет находиться в равновесии под действием скручивающего момента (реакции заделки) и момента приложенного в сечении и заменяющего действие отброшенной правой части (рис. 83, б). Значение найдем из условия равновесия:
или
Если взять сечение (на участке ), то крутящий момент (рис.
83, в), возникающий в этом сечении, должен уравновешивать сумму скручивающих моментов действующих на отсеченную левую часть, т. е.
откуда
Ту же величину крутящего момента для сечения получим, если будем рассматривать равновесие правой отсеченной части, па которую действуют скручивающие моменты В этом случае
Но из условия равновесия
Знак крутящего момента физического смысла не имеет. Условимся считать крутящий момент положительным, если он при взгляде на сечение со стороны отброшенной части направлен по часовой стрелке.
Для левой части бруса, отсеченной любой плоскостью в пределах участка
откуда
По найденным данным строим эпюру крутящих моментов (рис. 83, г). Для этого проводим ось абсцисс параллельно оси бруса. Точки соответствуют сечениям, в которых приложены скручивающие моменты. В точке отложим ординату величина которой в выбранном масштабе соответствует крутящему моменту — Так как на участке крутящий момент постоянен, то проведем прямую линию параллельную оси
Далее, от точки отложим отрезок величина которого в выбранном масштабе будет соответствовать крутящему моменту Крутящий момент на участке постоянен. Поэтому из точки проведем линию параллельную Заметим, что в тех сечениях, где приложены скручивающие моменты, ординаты эпюры изменяются скачком на величину, равную значению приложенного момента. Аналогично строится эпюра и на участке (ординаты отложены вниз от оси, так как отрицателен).
Поэтому из точки проведем линию параллельную Заметим, что в тех сечениях, где приложены скручивающие моменты, ординаты эпюры изменяются скачком на величину, равную значению приложенного момента. Аналогично строится эпюра и на участке (ординаты отложены вниз от оси, так как отрицателен).
Следует обратить внимание на то, что наибольший крутящий момент равен 1,4 кн-м, в то время как наибольший скручивающий момент равен 1,6 кн-м. Это общее положение — лишь в частных случаях величины наибольшего крутящего момента и наибольшего скручивающего момента совпадают. В дальнейшем следует учесть, что .расчет бруса на прочность и на жесткость ведут по наибольшему крутящему моменту.
Вычисление моментов, передаваемых на вал. построение эпюр крутящих моментов для валов
На практике обычно известны не моменты, действующие на вал, а передаваемая валом мощность и его угловая скорость. В СИ единицей мощности является ватт (вт) — работа в один джоуль, совершенная в одну секунду Угловая скорость в этой системе измеряется в радианах в секунду
Как известно из теоретической механики, между моментом, мощностью и угловой скоростью существует зависимость
где — в -ваттах, — в радианах в секунду, — в ньютоно-метрах.
Пример решения задачи 79.
Изображенный на рис. 84 трансмиссионный вал .получает движение при помощи ременной передачи от шкива, насаженного на валу двигателя (на
рисунке не показан), к шкиву на валу. В свою очередь шкивы сидящие на этом валу, также через ременные передачи приводят в движение рабочие машины. Эти шкивы передают мощности Вал вращается с угловой скоростью
Построить эпюру крутящих моментов без учета трения в подшипниках.
Решение:
Машина, соединенная ременной передачей со шкивом потребляет мощность так что скручивающий момент, передаваемый от вала машине,
Скручивающий момент, передаваемый через шкив
Через шкив передается скручивающий момент
Скручивающий момент, передаваемый валу двигателем через шкив
На участках вала между шкивами будут действовать крутящие моменты следующей величины: момент в любом поперечном сечении на участке определим из условия равновесия части вала, расположенной левее сечения
отсюда
Аналогично для сечения на участке
откуда
для сечения
откуда
Для построения эпюры крутящих моментов проведем ось абсцисс, параллельную оси вала. От точки отложим ординату соответствующую крутящему моменту Этот момент на участке не изменяется, поэтому эпюра на этом участке представляет собой прямую (рис. 84, б). Крутящему моменту соответствует ордината эпюры.
От точки отложим ординату соответствующую крутящему моменту Этот момент на участке не изменяется, поэтому эпюра на этом участке представляет собой прямую (рис. 84, б). Крутящему моменту соответствует ордината эпюры.
На участке крутящий момент постоянен. Наконец, от точки отложим ординату равную в выбранном масштабе Момент, представленный на эпюре ординатой постоянен на всем участке вала.
Из уравнения равновесия
следует, что за шкивом и перед шкивом крутящие моменты равны нулю. Эпюра крутящих моментов вала будет ограничена линией Из эпюры видно, что наиболее нагруженным участком вала является участок между шкивами в поперечных сечениях которого возникают наибольшие крутящие моменты.
Пример решения задачи 80.
Сохраняя данные предыдущего примера, построить эпюру крутящих моментов для вала с расположением шкивов, показанном на рис. 85, а.
Решение:
Применим метод сечений к каждому участку вала в отдельности. На участке вала слева от шкива крутящий момент равен нулю. В любом сечении участка крутящий момент { уравновешивает скручивающий момент приложенный слева от сечения (правую часть отбрасываем), т. е.
На участке вала слева от шкива крутящий момент равен нулю. В любом сечении участка крутящий момент { уравновешивает скручивающий момент приложенный слева от сечения (правую часть отбрасываем), т. е.
Этот момент на рис. 85, б представлен в масштабе ординатой отложенной вверх от оси абсцисс. В любом сечении участка вала крутящий момент равен алгебраической сумме скручивающих моментов, расположенных слева от сечения:
Этот момент представлен на эпюре ординатой
Крутящий момент определим как алгебраическую сумму скручивающих моментов, приложенных слева от сечения
Знак «минус» показывает, что крутящий момент отрицателен, а следовательно, ординату надо отложить вниз от оси абсцисс. Правее сечения крутящий момент равен нулю. Ломаная линия представляет собой эпюру крутящих моментов (рис. 85,6).
Сравнивая эпюры, представленные на рис. 84, б и 85, б, видим, что наибольший крутящий момент в первом случае равен 2781 а во втором случае — 1625 Отсюда следует, что величина наибольшего крутящего момента зависит от порядка расположения шкивов и в особенности от положения шкива получающего скручивающий момент от двигателя. Далее будет установлено, что рациональным расположением шкивов па валу можно получить экономию в материале, гак как уменьшение максимального крутящего момента ведет,’конечно, и к уменьшению требуемого диаметра вала.
Далее будет установлено, что рациональным расположением шкивов па валу можно получить экономию в материале, гак как уменьшение максимального крутящего момента ведет,’конечно, и к уменьшению требуемого диаметра вала.
Напряжения и перемещения при кручении брусьев круглого поперечного сечения
При кручении брусьев круглого (сплошного и кольцевого) поперечного сечения:
а) поперечные сечения, плоские до деформации бруса, остаются плоскими и перпендикулярными к оси бруса и после деформации;
б) диаметр бруса не изменяется; не изменяется также и его длина и расстояния между поперечными сечениями;
в) образующие цилиндра из прямых линий превращаются в винтовые.
Угол поворота торцового поперечного сечения бруса по отношению к защемленному сечению (рис. 85) называют полным углом закручивания бруса.
•Взаимный угол поворота двух бесконечно близких сечений — угол закручивания элемента длиной связан (как видно из рис. 86) с углом сдвига зависимостью
где — относительный угол закручивания. Касательное напряжение, возникающее в любой точке поперечного сечения (рис. 87), определяется по формуле
Касательное напряжение, возникающее в любой точке поперечного сечения (рис. 87), определяется по формуле
где (или — крутящий момент в рассматриваемом сечении;
— полярный момент инерции сечения.
Для круга
для кольца
где отношение внутреннего диаметра кольца к наружному. В точках контура поперечного сечения касательные напряжения будут иметь наибольшее значение, определяемое по формуле
где -полярный момент сопротивления.
Для сплошного круглого сечения
для кольцевого сечения
Угол закручивания бруса постоянного диаметра при одинаковом во всех поперечных сечениях крутящем моменте
Произведение условно называют жесткостью сечения бруса при кручении.
Пример решения задачи 81.
Стальной брус диаметром и длиной жестко заделан одним концом, а другой конец нагружен скручивающим моментом. При закручивании точка (см. рис. 86), взятая на окружности концевого сечения, перемещается в положение проходя дугу длиной 3 мм. Определить: угол сдвига «а поверхности бруса; относительный угол закручивания полный угол закручивания наибольшее
Определить: угол сдвига «а поверхности бруса; относительный угол закручивания полный угол закручивания наибольшее
касательное напряжение крутящий момент в поперечных сечениях бруса;
Решение:
Угол сдвига, как видно из чертежа, равен отношению длины дуги к длине бруса:
Зная величину угла сдвига найдем относительный угол закручивания:
Полный угол закручивания
Наибольшее касательное напряжение определим на основании закона Гука:
Крутящий момент в любом поперечном сечении бруса
Пример решения задачи 82.
Стальной вал диаметром скручивается моментом Определить наибольшее напряжение угол сдвига на поверхности вала и относительный угол закручивания
Решение:
Наибольшее касательное напряжение определим по формуле
где а следовательно,
Зная определяем угол сдвига
Тогда относительный угол закручивания
Пример решения задачи 83.
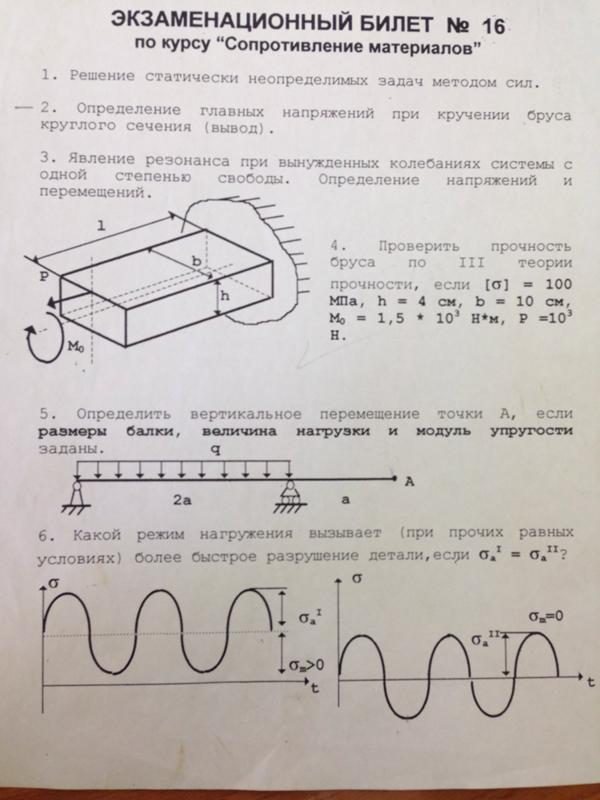
Круглый дюралевым стержень длиной одним концом заделан жестко, а на другом конце нагружен скручивающим моментом. Определить величину момента и диаметр стержня, если наибольшее касательное напряжение а полный угол закручивания рад, модуль сдвига
Решение:
Наибольшее касательное напряжение определяют по формуле
Из этой формулы можно было бы определить стержня, если найти величину или отношение
Нетрудно видеть, что величину этого отношения легко определить из формулы
откуда Следовательно, откуда
Крутящий момент в любом поперечном сечении вала
Пример решения задачи 84.
Для определения модуля сдвига материала испытывают на кручение образец круглого поперечного сечения и производят с помощью зеркальных приборов измерения углов поворота двух его сечении. Вычислить модуль упругости, если приращению кр\гяшего момента соответствуют углы
поворота Расстояние между сечениями диаметр образца
Решение:
Приращение угла закручивания на длине соответствующее . изменению крутящего момента будет
изменению крутящего момента будет
Полярный момент инерции сечения
Модуль упругости определим из формулы для угла закручивания:
Пример решения задачи 85.
Стальная проволока длиной и диаметром одним концом закреплена в зажиме, а другой конец нагружен закручивающей парой сил. При каком угле закручивания наибольшие касательные напряжения достигнут если модуль сдвига
Решение:
Зная величину наибольшего касательного напряжения а также модуль упругости можно определить угол сдвига на наружной поверхности проволоки:
Угол закручивания определим по формуле
Эту задачу можно решить иначе, а именно: определим крутящий момент:
Тогда угол закручивания
РАСЧЕТЫ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ КРУЧЕНИИ
Условие прочности при кручении бруса круглого поперечного сечения имеет вид
где — допускаемое напряжение. Величину допускаемого .напряжения при кручении принимают равной от допускаемого напряжения при растяжении.
Зная диаметр бруса и допускаемое напряжение для его материала при данных условиях работы, можно определить максимальный допускаемый крутящий момент:
При проектном расчете требуемый «полярный момент сопротивления поперечного сечения бруса определяется но формуле
Во многих случаях расчет валов должен быть выполнен не только на прочность, но и на жесткость. Условие жесткости
здесь —допускаемый относительный угол закручивания.
Если величина задана в то величина должна быть подставлена в либо можно перевести значение в и тогда
При определении диаметра вала из условия жесткости («гири проектном ‘расчете) находят требуемую величину полярного момента инерции:
Допускаемый по условию жесткости крутящий момент определяется но формуле
Пример решения задачи 86.
При проверить прочность вала, имеющего диаметр Вал передает мощность 150 квт и вращается с угловой скоростью
Решение:
Определяем крутящий момент, равный моменту, передаваемому валу Полярный момент сопротивления поперечного сечения вала
Наибольшее напряжение
Пример решения задачи 87.
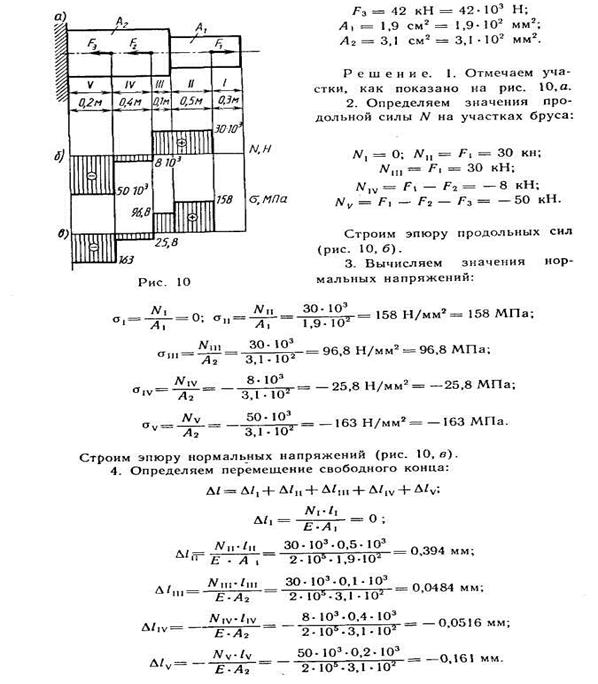
Ступенчатый стальной брус круглого сечения нагружен, как показано на рис. 88, а, скручивающими моментами
Требуется определить максимальные касательные’напряжения в сечениях вала, если Определить коэффициент запаса, если для материала бруса предел текучести при чистом сдвиге
Решение:
Составив уравнение равновесия, определим-реактивный момент в заделке:
откуда
Крутящий момент в произвольном сечении участка
Крутящий момент в произвольном сечении участка
Крутящий момент в произвольном сечении участка
Строим эпюру крутящих моментов (рис. 88, б). Определим полярные моменты сопротивления поперечных сечений бруса: на участке
на участке
на участке
Искомые напряжения:
Коэффициент запаса определяем для наиболее нагруженного участка бруса
Пример решения задачи 88.
Проверить ‘прочность валов зубчатой передачи от электродвигателя к станку (рис. 89), приняв допускаемое напряжение Передаваемая мощность Угловая скорость вала электродвигателя Коэффициент полезного действия передачи
89), приняв допускаемое напряжение Передаваемая мощность Угловая скорость вала электродвигателя Коэффициент полезного действия передачи
Решение:
Угловая скорость ведущего вала
Вычислим вращающий момент на валу
Крутящий момент в любом (расположенном левее шестерни поперечном сечении вала
(на рис. 89 изображена эпюра крутящих моментов для вала
Проверяем прочность этого вала
Определим вращающий момент па валу 2:
Крутящий момент в любом (расположенном между зубчатыми колесами) поперечном сечении вала 2
Проверим прочность вала 2:
Пример решения задачи 89.
Определить диаметр вала, передающего мощность Угловая скорость вала
Допускаемое напряжение допускаемый относительный угол закручивания
Решение:
Крутящий момент, возникающий в любом -поперечном сечении вала, равен передаваемому валом вращающему моменту:
Из условия прочности следует
Из условия жесткости
следует
(здесь
Окончательно принимаем
Пример решения задачи 90.
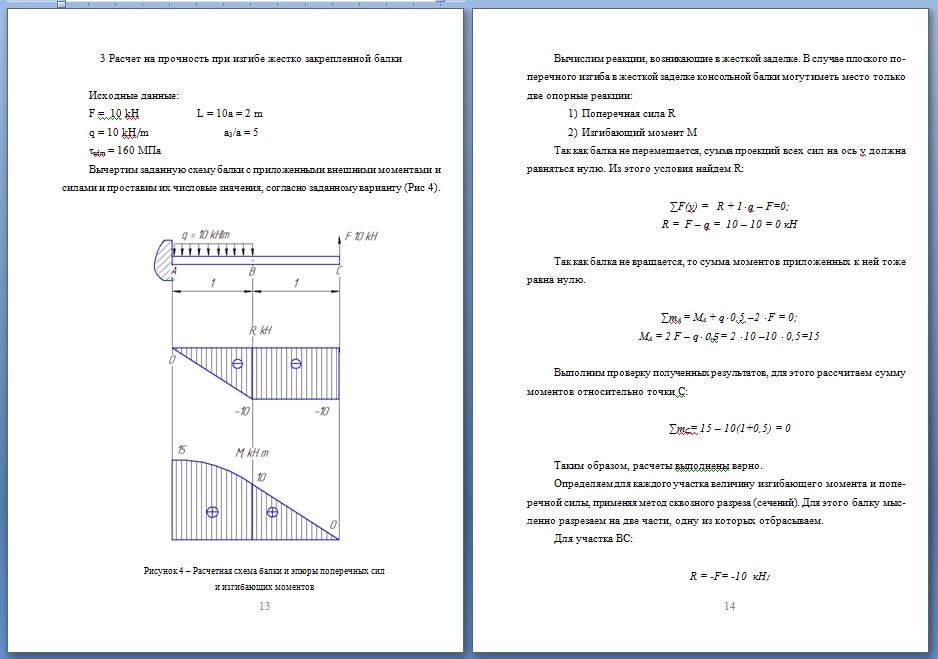
На валу насажены три шкива, из которых шкив соединен со шкивом двигателя при помощи ремня и -получает мощность а шкивы и эту мощность отдают станкам, соответственно (рис. 90, а). Определить диаметры вала если допускаемое напряжение а угловая скорость вала Определить угол поворота сечения, совпадающего с серединой шкива по отношению к сечению если
Решение:
В этой задаче вал имеет ступенчатую форму. Чтобы определить диаметры вала необходимо найти величины скручивающих моментов, передаваемых шкивами, после чего определить крутящие
моменты в сечениях на участках вала. Скручивающий момент, действующий на шкив
Скручивающие моменты, действующие на шкивы
Крутящий момент в любом сечении участка вала
Крутящий момент в любом сечении участка вала
Строим эпюру крутящих моментов (рис. 90, б). Зная величины крутящих моментов, а также величину допускаемого напряжения определим диаметры вала на участках
тогда
тогда откуда
принимаем
Для определения углов закручивания будем руководствоваться правилом: угол закручивания отсчитывает ся от сечения вала в месте расположения главного шкива
Определим угол поворота сечения относительно сечения
Так как вал вращается, то неподвижных сечений здесь нет. Но пас интересуют .не повороты сечений вообще, а углы поворота отдельных сечений, получающиеся в результате деформации вала. «Поэтому, приняв условно сечение за неподвижное, вычислим значения углов поворота отдельных сечений относительно сечения
Но пас интересуют .не повороты сечений вообще, а углы поворота отдельных сечений, получающиеся в результате деформации вала. «Поэтому, приняв условно сечение за неподвижное, вычислим значения углов поворота отдельных сечений относительно сечения
На участке угол поворота сечения, расположенного на расстоянии от сечения будет где угол поворота сечения относительно сечения
— крутящий момент на участке
При
т. е. угол поворота сечения относительно сечения составляет
На участке угол поворота сечения, расположенного -на расстоянии от сечения равен алгебраической сумме углов закручивания участков и части участка длиной т. е.
Эпюра углов закручивания показана на рис. 90, в
Статически неопределимые задачи кручения
т. е. на основе применения лишь метода сечении. Так же как и при решении .статически неопределимых задач на растяжение (сжатие), дополнительно к уравнениям статики должны быть составлены уравнения перемещении.
Пример решения задачи 93.
В сечении бруса круглого поперечного сечения приложен скручивающий момент Концы -бруса жестко заделаны (рис. 93, а). Определить реактивные моменты в заделках; построить эпюру крутящих моментов н найти требуемый диаметр бруса, если допускаемое напряжение
Решение:
В заделках бруса возникают реактивные моменты которые связаны с заданным моментом уравнением равновесия
Неизвестных величии две, а уравнение статики можно составить лишь одно и, следовательно, задача статически неопределима.
Составим второе уравнение, т. е. уравнение перемещений. При этом учтем, что угол поворота сечения одинаков как по отношению к левому, так и к правому концу
где
После подстановки значений получим
Решая совместно уравнения (1) и (2), найдем
откуда
Взяв произвольное поперечное сечение на расстоянии от левой опоры, найдем, что крутящий момент в этом сечении
В произвольном поперечном -сечении вала на расстоянии от левой опоры крутящий момент
Эпюра крутящих моментов показана на рис. 93, б. Диаметр бруса определим по наибольшему крутящему моменту из формулы
93, б. Диаметр бруса определим по наибольшему крутящему моменту из формулы
откуда
Пример решения задачи 94.
Стальной валик и дюралевая трубка жестко заделаны на одном конце, а на другом скреплены с диском, к которому приложен скручивающий момент (рис. 94). Определить (в долях ) крутящие моменты, возникающие в поперечных сечениях трубки и валика.
Модули сдвига: стали дюраля
Решение:
В поперечных сечениях валика возникает крутящий момент а трубки — Сумма этих моментов равна скручивающему моменту, приложенному к диску.
Задача статически неопределима, так как уравнение статики можно составить только одно, а неизвестных моментов два.
Угол поворота диска, к которому приложен -скручивающий момент, равен углу закручивания валика. Точно так же можно утверждать, что угол поворота диска равен углу закручивания трубки. Следовательно, углы закручивания валика и трубки одинаковы:
Используя формулу для угла закручивания, получаем
или
где
После несложных преобразований получаем
или
Используя уравнение статики, получаемм
откуда
и
Кручение стержней прямоугольного поперечного сечения
Задачу об определении касательных-напряжений при кручении стержней ‘прямоугольного поперечного сечения Методами сопротивления материалов решить нельзя. Это связано с тем, что в данном случае ‘первоначально плоские поперечные сечения искривляются, как это видно из рис. 95, а. По степени перекашивания сетки квадратиков, нанесенных на боковых гранях стержня, можно судить о величине касательных напряжений в различных точках. Квадратики, лежащие у ребер стержня, не перекашиваются — в этом месте касательные напряжения равны нулю. Наибольшее искажение квадратиков возникает в средних точках -боковых граней бруса— здесь касательные напряжения достигают своего наибольшего значения. На рис. 95, б представлено поперечное сечение бруса. Наибольшие касательные напряжения возникают в точках т. е. в серединах ‘длинных-сторон прямоугольника. Величина этих ‘напряжений определяется по формуле
Это связано с тем, что в данном случае ‘первоначально плоские поперечные сечения искривляются, как это видно из рис. 95, а. По степени перекашивания сетки квадратиков, нанесенных на боковых гранях стержня, можно судить о величине касательных напряжений в различных точках. Квадратики, лежащие у ребер стержня, не перекашиваются — в этом месте касательные напряжения равны нулю. Наибольшее искажение квадратиков возникает в средних точках -боковых граней бруса— здесь касательные напряжения достигают своего наибольшего значения. На рис. 95, б представлено поперечное сечение бруса. Наибольшие касательные напряжения возникают в точках т. е. в серединах ‘длинных-сторон прямоугольника. Величина этих ‘напряжений определяется по формуле
где — соответственно меньшая и большая «стороны поперечного сечения; —числовой коэффициент, зависящий от отношения
Величины этого коэффициента приведены в табл. 5.
Таблица 5
Наибольшее .напряжение в середине малой стороны поперечного сечения определяют-по формуле
где — табличная величина, зависящая также от отношения (см. табл. 5).
табл. 5).
Угол закручивания
где —численный коэффициент, зависящий от отношения (см. табл. 5), а величина — геометрическая характеристика крутильной жесткости для бруса прямоугольного сечения.
Пример решения задачи 95.
Определить максимальное напряжение, возникающее в поперечном сечении стального стержня и его угол закручивания. Поперечное сечение — прямоугольник со сторонами и скручивающий момент Длина стержня
Решение:
Выбор коэффициентов производим по отношению
Такого значения в табл. 5 нет. Поэтому определим а интерполированием по значениям, соответствующим
После этого определим по формуле
Угол закручивания
Значение коэффициента ( определим интерполированием по значениям при
Пример решения задачи 96.
Определить размеры прямоугольного сечения стержня с отношением сторон -нагруженного моментом Допускаемое напряжение допускаемый относительный угол закручивания
Решение:
Из условия прочности
найдем
где (взято из табл. 5).
5).
Но откуда
Найдем значения из условия жесткости:
откуда
-где (взято по табл. 5), подставлено Учитывая, что имеем
Из последнего выражения
Тогда
Принимаем размеры, полученные из условия жесткости.
Введение в кручение с рабочими примерами
Серия «Фундаментальная инженерная механика». Часть 3
д-ра Шона Кэрролла
|
Опубликовано: 15 сентября 2022 г.
|
Учебник
Добро пожаловать в третью часть серии руководств по фундаментальной инженерной механике. В этой части основное внимание будет уделено кручению в круглых валах, а также напряжениям и деформациям, которые оно вызывает. Предыдущий выпуск серии здесь.
В предыдущем уроке этой серии мы рассмотрели диаграммы свободного тела и способы расчета сил реакции. Может показаться, что изучение скручивания в части 3 — это большой скачок. Это связано с тем, что перед скручиванием я обычно предлагаю рассмотреть анализ фермы, поперечную силу и анализ изгибающего момента для балок и рам. Но я уже рассмотрел их в нескольких уроках, так что нет необходимости рассказывать о них снова в рамках этой серии. Не стесняйтесь рассказать о них, прежде чем погрузиться в Torsion со мной здесь.
Но я уже рассмотрел их в нескольких уроках, так что нет необходимости рассказывать о них снова в рамках этой серии. Не стесняйтесь рассказать о них, прежде чем погрузиться в Torsion со мной здесь.
Помните, что вы можете получить доступ к любому видео и загружаемым версиям заметок, присоединившись к соответствующему курсу ниже.
1.0 Знакомство с кручением
Как упоминалось выше, в предыдущих уроках мы обсуждали фермы и заметили, что элементы, составляющие ферму, испытывают только осевую нагрузку. Можно сказать, что действие , которое испытывают эти члены, является осевой силой. Мы также обсудили конструктивные элементы, основными действиями которых были поперечные силы и изгибающие моменты (балки и рамы).
Здесь следует пояснить, что осевая сила отличается от силы сдвига просто осью, вдоль которой действует сила. Осевые силы имеют линию действия, параллельную продольной оси элемента, а поперечные силы имеют линию действия, перпендикулярную этой оси.
При обсуждении изгибающих моментов, применяемых к 2D-конструкциям в плоскости x-y, мы не обращали внимание на момент времени, но все рассматриваемые моменты относились к оси, перпендикулярной плоскости x-y (страница или экран) – оси z , см. рис. 1 ниже.
Рис. 1. Балка, на которую действуют поперечные силы (синий), осевая сила (зеленый) и изгибающий момент (розовый). Все эти действия обсуждались в предыдущих уроках.В этом уроке мы вводим еще одно действие — кручение. Это просто изгибающий момент, приложенный вокруг другой оси – продольной оси, рис. 2. Скручивание вызовет скручивание вокруг продольной оси, и это очень распространенная форма нагрузки, которую нам нужно уметь анализировать. Мы часто называем крутящие моменты крутящими моментами (мы можем использовать термины крутящий момент и крутящий момент взаимозаменяемы).
Рис. 2. Балка, на которую действует крутящий момент относительно продольной оси x. Мы можем изобразить кручение (или любой другой момент) изогнутой стрелкой, с которой вы знакомы из предыдущих руководств, или двунаправленной прямой стрелкой.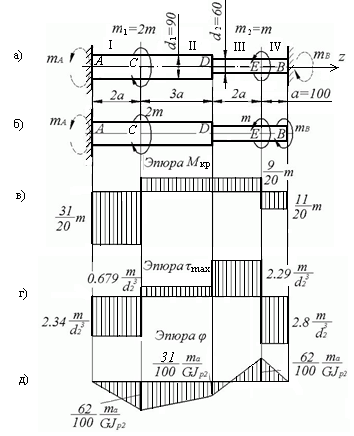 Двунаправленная стрелка обычно более удобна для представления кручения, примененного к 2D-структурам. Чтобы определить направление вращения, указанное двунаправленной стрелкой, мы используем правило правого винта 9.0024 .
Двунаправленная стрелка обычно более удобна для представления кручения, примененного к 2D-структурам. Чтобы определить направление вращения, указанное двунаправленной стрелкой, мы используем правило правого винта 9.0024 .
В соответствии с этим соглашением о знаках, если вы направите большой палец или правую руку в направлении двунаправленной стрелки и сожмете кулак, ваши пальцы согнутся и укажут в направлении положительного направления вращения для крутящего момента . Это важное соглашение, которое нужно понять и запомнить.
2.0 Деформация при кручении
Нашей отправной точкой здесь будет изучение концепции деформации применительно к круглым стержням и получение уравнения, которое связывает деформацию с углом закручивания стержня. Во-первых, давайте сформулируем некоторые предположения, которые применимы к нашему обсуждению:
- стержень или стержень имеет круглое поперечное сечение и призматическую форму, что означает, что он имеет одинаковую форму поперечного сечения по всей своей длине.

- угол закручивания между обоими концами стержня, который мы обозначим как , остается небольшим.
- приложенный крутящий момент постоянен по всей длине стержня, поэтому мы говорим, что стержень находится в состоянии чистого кручения.
- углов закручивания измеряются в радианах, напомним, что .
Рассмотрим стержень с радиусом поперечного сечения и длиной , изображенный ниже. Он зафиксирован от торсионного вращения на конце. Приложенный крутящий момент при , вызывает угол закручивания таким образом, что точка поворачивается вокруг точки на свободном конце стержня. Заметим также, что угол закрутки изменяется линейно между и .
Рис. 3. Призматический круглый стержень, подверженный крутящему моменту, показывающий результирующую угловую деформацию Как и все хорошие инженерные решения, теперь мы рассмотрим небольшой сегмент стержня длиной , изображенный ниже. Заметим, что правое сечение поворачивается относительно левого сечения на величину . В результате исходный элемент становится с поворотом на и поворотом на .
В результате исходный элемент становится с поворотом на и поворотом на .
Поскольку мы сделали исходное предположение, что угол поворота между концами стержня мал, можно сказать, что длины сторон и остаются неизменными. Отсюда можно сделать вывод, что деформация элемента полностью определяется уменьшением угла . Мы признаем это деформацией сдвига и заключаем, что элемент находится в состоянии чистого сдвига, что означает, что он испытывает только деформацию сдвига, в отличие от нормальных деформаций, которые могут быть вызваны осевыми силами или изгибающими моментами.
Рис. 4. (а) Призматический круглый стержень в состоянии чистого кручения. (b) Подучасток, испытывающий угол закручивания, вызывающий деформацию сдвига на внешней поверхности стержня.Из рис. 4(а) выше видно, что величина деформации сдвига определяется как
Величина представляет собой скорость скручивания или скручивания на единицу длины и заменяется на ,
(3)
В результате получаем уравнение для деформации сдвига на радиусе ,
(4)
Отметим, что для элементов длины, испытывающих чистое кручение (постоянная величина крутящего момента по всему стержню), и для чистое кручение только мы имеем,
(5)
Из предыдущих уравнений видно, что для любого данного поперечного сечения деформация сдвига изменяется линейно с радиусом. Например, для полых круглых труб мы можем получить величину деформации сдвига на внутренней и внешней стенках, просто подставив соответствующее значение радиуса (см. ниже). Следовательно, max в нижнем индексе относится к тому факту, что эта деформация сдвига была оценена для внешней поверхности стержня, где радиус и, следовательно, деформация сдвига являются максимальными.
Например, для полых круглых труб мы можем получить величину деформации сдвига на внутренней и внешней стенках, просто подставив соответствующее значение радиуса (см. ниже). Следовательно, max в нижнем индексе относится к тому факту, что эта деформация сдвига была оценена для внешней поверхности стержня, где радиус и, следовательно, деформация сдвига являются максимальными.
3.0 Кручение в линейно-упругих круглых стержнях
Итак, на данный момент у нас есть уравнение, связывающее угол кручения с соответствующей деформацией сдвига. Затем мы хотели бы связать это с напряжением сдвига, . Если стержень изготовлен из линейно упругого материала, мы знаем, что напряжение сдвига будет линейно пропорционально деформации сдвига. В случае сдвига (в отличие от растяжения и сжатия) напряжение и деформация связаны модулем упругости сдвига, ,
(6)
Таким образом, мы можем определить напряжение сдвига на радиусе как
(7)
Если мы хотим определить напряжение сдвига на некотором внутреннем радиусе , мы можем сделать это следующим образом:
( 8)
где – максимальное касательное напряжение на наружной поверхности.
На рис. 6(а) ниже показан стержень при чистом кручении и увеличенный элемент напряжения с указанием направлений результирующих касательных напряжений на поверхности. На изображении (b) мы можем видеть касательное напряжение и соответствующую сдвиговую деформацию элемента. Мы снова видим на изображении (с), что напряжение сдвига линейно зависит от радиуса.
Рис. 6. (а) Стержень при чистом кручении, (б) результирующие напряжения и деформации, отраженные от элемента, взятого из стержня, (в) поперечное сечение стержня, показывающее линейное изменение напряжения сдвига с радиусом. 3.1 Связь напряжения сдвига с крутящим моментом Теперь мы получим формулу кручения , которая связывает приложенный крутящий момент с индуцированным напряжением сдвига, . Начнем с рассмотрения напряженного сечения и элемента площади внутри этого сечения (см. рис. 7 ниже). Эта бесконечно малая область расположена на радиусе и испытывает касательное напряжение . Поэтому мы можем рассчитать силу, которую испытывает as . Эта сила создает момент относительно оси стержня, .
Поэтому мы можем рассчитать силу, которую испытывает as . Эта сила создает момент относительно оси стержня, .
(9)
Замена полученным ранее выражением дает
(10)
Обратите внимание, что сумма всех моментов , действующих на все элементы площади , равна приложенному крутящему моменту, . Мы можем выполнить это суммирование путем интегрирования по всей площади поперечного сечения,
(11)
Теперь мы определим полярный момент инерции кругового поперечного сечения, ,
(12)
Это свойство формы поперечного сечения (аналог второго момента площади , с которым мы сталкиваемся при рассмотрении жесткости на изгиб, при изгибе). Для круга диаметром , полярный момент инерции определяется как,
(13)
Следовательно, имеем
(14)
Переставляя, получаем формулу кручения скручивающее напряжение.
Если мы вспомним наше выражение выше, где была скорость скручивания или скручивания на единицу длины, мы можем объединить это с формулой кручения, чтобы получить
(16)
В приведенном выше уравнении величина известна как жесткость на кручение и аналогична жесткости на изгиб при изгибе.
Ограничения
В наших обсуждениях и выводах до сих пор предполагалось, что материал остается линейно упругим, и приложенный крутящий момент ни при каких обстоятельствах не превышает пропорциональный предел для материала. Наши выводы также действительны только при отсутствии концентраций напряжений, возникающих из-за неоднородностей в геометрии или в точках приложения нагрузки. Далее мы можем рассмотреть некоторые численные примеры, чтобы продемонстрировать эти уравнения в действии.
3.2 Пример 1Рассмотрим сплошной стальной стержень с круглым поперечным сечением. Стержень подвержен приложенному крутящему моменту и имеет следующие значения параметров:
- диаметр
- длина
- модуль сдвига
Используйте эту информацию, чтобы:
- Определить максимальное касательное напряжение, возникающее в стержне
- Определить угол скручивания между концами стержня
- Если максимально допустимое напряжение сдвига и максимально допустимый угол закручивания , каков максимально допустимый крутящий момент?
Решение
(1) Максимальное напряжение сдвига получается с использованием,
Мы будем использовать простой Python для выполнения вычислений, но вы можете легко решить это с ручкой и бумагой, если хотите.
1 2 3 4 5 6 7 8 10 110005 12 13 | 92
phi_radians = T*L/(G*Ip) #(rads) phi_deg = phi_radians*180/math.pi #(deg) print(f’Угол закручивания между концами {round( phi_radians,3)} радианы или {round(phi_deg,2)} градусов’)
|
-> Угол скручивания между концами составляет 0,035 радиана или 1,99 градуса
(3) Сначала предположим, что крутящий момент ограничен максимально допустимым напряжением сдвига, . В этом случае мы можем найти максимальный крутящий момент, изменив формулу кручения следующим образом: 92)
T_max_1 = (tau_max*10**6)*Ip/r
print(f’Максимальный крутящий момент, ограниченный напряжением сдвига, равен {round(T_max_1,1)} Нм’)
-> Максимальный крутящий момент, ограниченный напряжением сдвига, составляет 859,0 Нм
Теперь мы можем проверить, каким был бы максимальный крутящий момент, если бы угол закручивания был ограничивающим критерием, используя
1 2 3 4 5 6 |
phi_max_deg = 1,75 #(градусы) phi_max_rad = phi_max_deg*math. T_max_2 = phi_max_rad*G*Ip/L крутки {раунд(T_max_2,1)} Нм’)
|
-> Максимальный крутящий момент, ограниченный углом закручивания, составляет 702,8 Нм
Мы видим, что максимально допустимый крутящий момент ограничивается заданным допустимым углом закручивания. Однако, придерживаясь здесь темы Python и чтобы у нас был повторно используемый код, который дает окончательный ответ без нашего вмешательства в конце, мы напишем некоторый код для вывода окончательного вывода.
1 2 3 4 5 6 7 8 9 |
#Программно проверьте, что является ограничивающим фактором if(T_max_1 print(f'(c) Максимально допустимый крутящий момент равен {round(T_max_1,1)} Нм, ограничен напряжением сдвига’ ) elif(T_max_1>T_max_2): print(f'(c) Максимально допустимый крутящий момент {round(T_max_2,1)} Нм, ограничен углом закручивания’) иначе: print(f'(c) Допустимый крутящий момент {round(T_max_1,1)} Нм и одновременно ограничен напряжением сдвига и углом закручивания’) |
-> Максимально допустимый крутящий момент составляет 702,8 Нм, ограничен углом закручивания
3.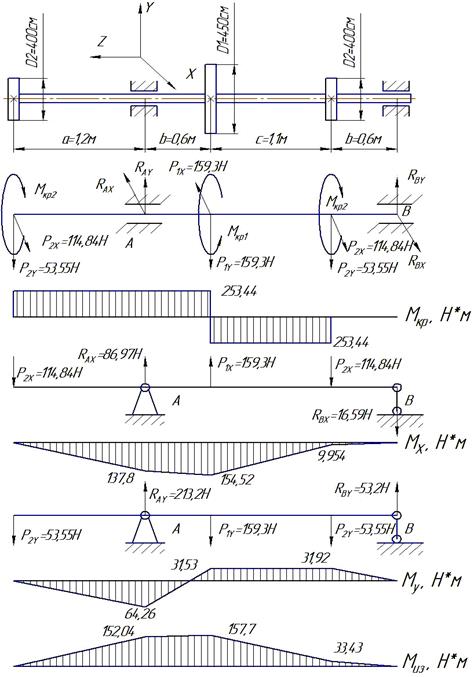 3 Пример 2
3 Пример 2 Рассмотрим два вала, один полый и один сплошной. Оба имеют внешний диаметр, в то время как полый вал имеет внутренний диаметр. Оба вала испытывают крутящий момент. Наша задача — проанализировать относительную эффективность каждого вала при передаче крутящего момента. Сделаем это, установив соотношение следующих свойств для каждого вала:
- напряжение сдвига
- угол закручивания
- вес
Решение
(a) Если крутящий момент и внешний радиус одинаковы, напряжение сдвига пропорционально . Поэтому нам просто нужно сравнить соотношение значений, чтобы получить отношение напряжения сдвига для валов. Для сплошного вала,
Для полого вала,
1 2 3 4 5 6 7 8 9 10 11 | D_OUTER = 1 #Value, представляющий внешний диаметр D_RATIO = 0,75 #ratio of Diamers, D_INNER/D_OUTER IP_SOLID = (MATH. . math.pi*(D_ratio*D_outer)**4)/2
tau_ratio = (1/Ip_hollow)/(1/Ip_solid) print(f'(a) Отношение максимального напряжения сдвига в полости на сплошном валу равно {round(tau_ratio,2)}’) print(f’Другими словами, полый вал испытывает на {круглое(100*(tau_ratio-1))}% большее максимальное напряжение при том же приложенном крутящем моменте’)
|
-> (a) Отношение максимального напряжения сдвига в полом валу к напряжению на сплошном валу составляет 1,46
-> (b) Другими словами, полый вал испытывает на 46 % большее максимальное напряжение для одинаковый прилагаемый крутящий момент
(b) Поскольку оба вала имеют одинаковую длину и сделаны из одного и того же материала, углы закручивания также обратно пропорциональны полярному моменту инерции, поэтому…
print(f'(b) Отношение угла закручивания полого вала к углу закручивания сплошного вала также {round(tau_ratio,2)}’) print(f’Опять же, полый вал испытывает на {round(100*(tau_ratio-1))}% больше вращения при том же приложенном крутящем моменте’)
|
-> (b) Отношение угла закручивания полого вала к углу закручивания сплошного вала также равно 1,46
-> Опять же, полый вал вращается на 46 % больше при том же приложенном крутящем моменте
(c) Вес валов пропорционален площади их поперечного сечения.
1 2 3 4 5 6 7 |
A_solid = math.pi*D_outer**2 A_hollow = A_solid — math.pi*(D_ratio*D_outer)**2 weight_ratio = A_hollow/A_solid print(f'(c) Отношение веса полого вала к весу сплошного вала составляет {weight_ratio}’) print(f’Полый вал {круглый(100*(1-weight_ratio))}% легче сплошного вала эквивалентного диаметра’)
|
-> (c) Отношение веса полого вала к весу сплошного вала составляет 0,4375
-> Полый вал на 56% легче сплошного вала эквивалентного диаметра
Из этого анализа, мы можем видеть внутреннюю эффективность, предлагаемую полым валом. Хотя он развивает напряжение сдвига большей величины при том же приложенном крутящем моменте и большем вращении, он значительно легче. Таким образом, если материал, из которого изготовлен вал, может выдержать большую нагрузку и если можно выдержать больший угол закручивания, имеет смысл выбрать полый вал.
Мы можем лучше понять, как меняются эти отношения, нанеся графики отношений для различных значений отношения диаметров. Поскольку мы уже написали код для выполнения вычисления для одного соотношения диаметров, все, что нам нужно сделать, это заключить его в цикл for и сохранить значения, рассчитанные на каждой итерации.
1 2 3 4 5 6 7 8 10 11 12 13 14 15 16 17 18 19 20 21 22 |
#Значения внешнего диаметра являются постоянными D_outer = 1 Ip_solid = (math.pi*D_outer**4)/2 A_solid = math.pi*D_outer**2 # контейнеров сохранить наши рассчитанные отношения tr = np.array([]) wr = np.array([]) r = np.arange (0,1,0,81,0,01) #a Выбор коэффициентов диаметра для r in r: d_ratio = r #ratio of diamters, d_inner/d_outer ip_hollow = ip_solid -(D_Inner/d_outer = IP_SOLID -(D_INNER/D_OUTER . A_hollow = A_solid — math.pi*(D_ratio*D_outer)**2
tau_ratio = (1/Ip_hollow)/(1/Ip_solid) # Отношение напряжения сдвига tr = np.append(tr, tau_ratio) #Сохранить на потом
weight_ratio = A_hollow/A_solid #Соотношение весов wr = np.append(wr, weight_ratio) #Сохранить на потом
|
Теперь, когда у нас есть все рассчитанные и сохраненные значения, мы можем нанести их на график, чтобы более четко увидеть поведение.
1 2 3 4 5 6 7 8 10 110005 12 13 10 12 13 0005 14 15 16 17 |
import matplotlib.pyplot as plt # Функции построения графиков
fig, ax1 = plt.subplots(figsize=(12,6)) ax2 = ax1. 45 ax1. tr,’b’)ax2.plot(R,wr,’r’)
#Housekeeping ax1.set_xlabel(‘Отношение диаметров (Di/Do)’) ax1.set_ylabel(‘Стресс ratio’, color=’b’) ax2.set_ylabel(‘Весовое соотношение’,color=’r’) ax1.set_title(‘Отношение диаметра к соотношению напряжения и веса’) ax1.set_xlim([0.1,1]) plt.grid() plt.show()
|
Синяя линия показывает нам, как полая труба создает большее напряжение по сравнению со сплошной трубой, поскольку внутренний диаметр приближается к внешнему диаметру, а стенки трубы становятся тоньше. В то же время по красной линии видно, как постепенно уменьшается вес полой трубы. Обратите внимание, что точка пересечения здесь не имеет особого значения, поскольку у нас есть две разные шкалы y.
3.4 Пример 3 Круглый стальной вал должен передавать крутящий момент без превышения допустимого напряжения сдвига или допустимой скорости скручивания . Модуль упругости при сдвиге равен . Можно использовать полый или сплошной вал. Для оценки пригодности каждого варианта:
Модуль упругости при сдвиге равен . Можно использовать полый или сплошной вал. Для оценки пригодности каждого варианта:
- определить необходимый диаметр сплошного вала,
- определить требуемый наружный диаметр полого вала, если толщина стенки соответствует наружному диаметру
- определить соотношение диаметров между валами и соотношение веса полого и сплошного валов
Решение
Для сплошного и полого вала диаметр может быть ограничен либо допустимым напряжением сдвига, либо допустимой скоростью кручения. Нам нужно определить диаметры на основе обоих критериев и выбрать наибольший в качестве минимального диаметра для каждого вала. Для оценки диаметра, ограниченного допустимым напряжением, мы будем использовать
Для оценки диаметра, ограниченного допустимой скоростью скручивания, мы будем использовать
(17)
В обоих случаях мы можем изменить порядок и решить, чтобы определить диаметр.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 192)
#ЦЕЛЬНЫЙ ВАЛ — ОГРАНИЧЕНО ДОПУСТИМЫМ НАПРЯЖЕНИЕМ НА СДВИГ r = ((2*T)/(math.pi*tau_max))**(1/3) d_solid_1 = 2*r #( m) Сплошной диаметр ограничен напряжением сдвига
#СТАЛЬНОЙ ВАЛ — ОГРАНИЧЕН ДОПУСТИМОЙ СКОРОСТЬЮ КРУТЕНИЯ r = ((2*T)/(math.pi*G*theta_max_rad))**(1/4) d_solid_2 = 2*r #(m) Диаметр тела, ограниченный скоростью кручения
#Определить, какое условие управляет if(d_solid_1>d_solid_2): d_solid = d_solid_1 print(f'(a). Требуемый диаметр сплошного вала {round(d_solid_1,3)} м, ограничен допустимым напряжением сдвига’) elif(d_solid_1 print(f'(a). |
-> (а). Треб. диам. сплошного вала 0,096 м, ограничена допустимой скоростью крутки
Для полого вала отметим внутренний диаметр, . Следовательно,
1 2 3 4 5 6 7 8 10 110005 12 13 14 000 9000 9000 0005 16 17 18 |
#ПОЛЫЙ ВАЛ — ОГРАНИЧЕН ДОПУСКАЕМЫМ НАПРЯЖЕНИЕМ СДВИГАНИЯ d_hollow_1 = ((0,5*T)/(0,058*tau_max))**(1/3) #(м) Внешний диаметр полого отверстия ограничен напряжением сдвига #ПОЛЫЙ ВАЛ — ОГРАНИЧЕН ДОПУСТИМОЙ СКОРОСТЬЮ КРУТЕНИЯ ): d_hollow = d_hollow_1 print(f'(b). Требуемый наружный диаметр полого вала {round(d_hollow_1,3)} м, ограничен допустимым напряжением сдвига’) elif(d_solid_1 weight_ratio = A_полый/A_твердый # Отношение веса (=отношение площади) print(f’c. Отношение диаметра полого вала к сплошному равно {round(diam_ratio,2) } в то время как отношение веса {round(weight_ratio,2)}’)
|
-> Диам. соотношение полых и сплошных валов равно 1,14, а весовое отношение равно 0,47.
4.0 Резюме
Давайте быстро повторим то, что мы установили в этом руководстве:
- Крутящий момент или кручение — это просто изгибающий момент относительно продольной оси
- Установлена связь между деформацией сдвига на поверхности круглого вала , и углом закручивания на единицу длины ,
- Мы вывели формулу кручения, которая связывает напряжение сдвига на поверхности круглого вала с приложенным крутящим моментом, , радиусом вала, и полярным моментом инерции, ,
- Мы вывели уравнение, которое связывает скорость кручения на единицу длины, , с приложенным крутящим моментом и жесткостью при кручении, .
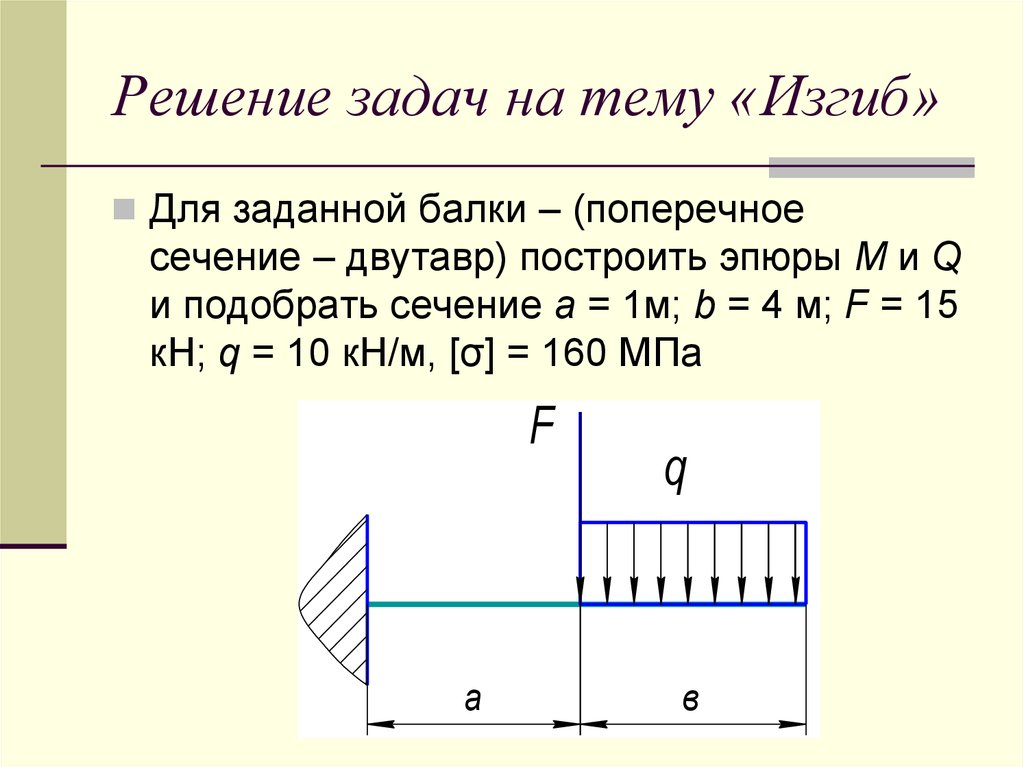
Все, что мы обсуждали, предполагало, что:
- Мы имели дело с призматическими круглыми валами
- Материал вала остается линейно-эластичным
- Валы были в чистом кручении
- Вращательная деформация вала осталась небольшой
В следующем уроке этой серии мы расширим обсуждение кручения и рассмотрим неравномерное кручение в круглых валах. Если вы хотите получать уведомления о публикации следующей части, присоединяйтесь к бесплатному курсу «Основы механики», зарегистрировавшись по ссылке в верхней части этого руководства.
Линкедин Твиттер YouTube
Автор
Д-р Шон Кэрролл
Бакалавр искусств (с отличием), MSc, PhD, CEng MIEI, FHEA
Привет, я Шон, основатель DegreeTutors.com. Я надеюсь, что вы нашли этот урок полезным. Проработав 10 лет в качестве преподавателя в университете по проектированию конструкций, я создала DegreeTutors.com, чтобы помочь большему количеству людей понять инженерное дело и получить от его изучения такое же удовольствие, как и я. Не стесняйтесь связаться или подписаться на DegreeTutors в любой из социальных сетей.
Не стесняйтесь связаться или подписаться на DegreeTutors в любой из социальных сетей.
Если вам нужен полный доступ ко всей библиотеке курсов DegreeTutors (и коду!) за небольшую ежегодную плату, рассмотрите возможность подписки на Полный доступ к DegreeTutors . Вы можете прочитать больше о преимуществах членства здесь или просмотреть заголовки и подписаться непосредственно ниже. Если вы учитесь в колледже или университете, станьте участником программы DegreeTutors, чтобы совершенно бесплатно получить доступ к ряду премиальных курсов.
Доступ ко всем курсам и инструментам
$ 279 / Год
(меньше кофе в неделю ☕ ☕)
Гарантия цен — избегайте будущего повышения цен, когда мы выращиваем
Более 740 лет и более 140 часов видеоконтента HD
. Неограниченный доступ к инструментам онлайн-анализа. 🛠️
Упакованный план разработки курсов и инструментов 🏗️
Доступ к хабу участников DegreeTutors:Labs 🧪
Неограниченная потоковая передача всех текущих и будущих курсов
Ранний доступ к новым курсам
Доступ ко всем загрузкам, руководствам в формате pdf и кодам Python
Сертификаты об окончании курса
Приоритетная поддержка вопросов и ответов
Подпишитесь на обновления новых руководств и курсов
© 2023 DegreeTutors & Mind Map Media Ltd. Все права защищены
Все права защищены
Сила кручения – определение, формула, эффект и примеры
Что такое сила кручения?
Сила кручения — это сила, приложенная крутящим моментом. Сила кручения — это нагрузка, приложенная к материалу через крутящий момент. Приложенный крутящий момент создает напряжение сдвига. Если сила кручения достаточно велика, она может заставить материал превратиться в скручивающее движение во время упругой и пластической деформации.
Сила кручения, приложенная к телу, влияет на его вращательное движение и вызывает скручивание тела. Это имеет тенденцию вызывать скручивающее напряжение в теле. Торсионная способность сечения будет зависеть от полярного момента инерции поперечного сечения и радиального расстояния от центра.
Блок силы кручения
Как мы знаем, сила кручения также является силой, вызывающей скручивание поперечного сечения. Значит, единицей этой силы также является Ньютон (Н). Хотя крутящий момент является крутящим моментом для поперечного сечения, он имеет ту же единицу, что и единица момента, Н-м. Сила скручивания индуцирует напряжения кручения, то есть напряжение, поэтому единицей напряжения кручения будет Н/м 2 или паскаль.
Сила скручивания индуцирует напряжения кручения, то есть напряжение, поэтому единицей напряжения кручения будет Н/м 2 или паскаль.
- Единица крутящего момента в СИ: Ньютон (Н)
- Единица крутящего момента в СИ: Н-м
- Единица крутящего момента в СИ: Н/м 2 или паскаль
Крутящий момент создается скручивающей силой, действующей на тело. Крутящий момент – это способность тела сопротивляться его крутящему движению. Крутящий момент может быть выражен скручивающей силой, умноженной на плечо рычага.
Крутящий момент – это момент, создаваемый скручивающей силой, приложенной к телу вдоль поперечной оси тела. В то время как силы вдоль оси создают равномерное напряжение по поперечному сечению тела, сила кручения создает напряжение кручения по поперечному сечению, имеющему треугольную форму.
Влияние кручения в балке
Кручение в балках появляется из-за действия поперечной нагрузки (т.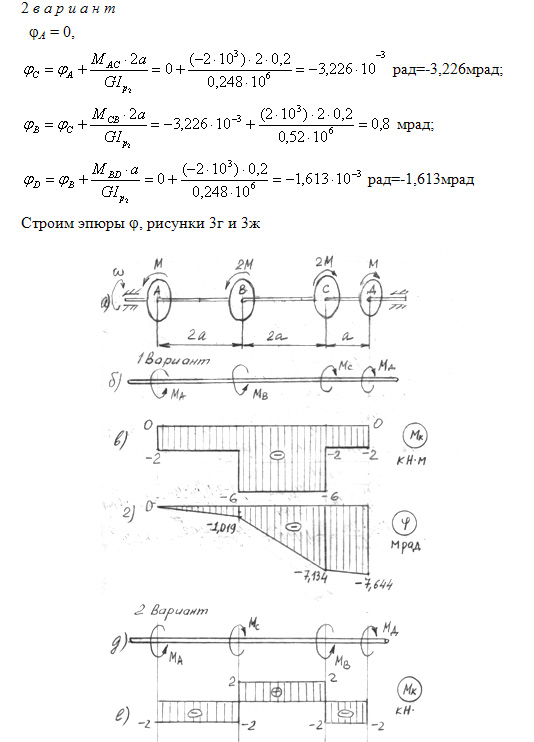 е. поперечной силы) в балке. снижает прочность балки; следовательно, при проектировании балки необходимо учитывать безопасный расчетный эффект кручения. В балках действие кручения учитывается в виде поперечной силы и изгибающего момента.
е. поперечной силы) в балке. снижает прочность балки; следовательно, при проектировании балки необходимо учитывать безопасный расчетный эффект кручения. В балках действие кручения учитывается в виде поперечной силы и изгибающего момента.
Как известно, кручение является важным параметром при проектировании строительных конструкций. В случае проектирования балки в расчет включается некоторый эффект кручения для изгибающего момента, а также учитывается некоторый эффект наряду с поперечной силой.
Разница между кручением и изгибом
Кручение и изгиб представляют собой допустимый момент сечения. Но кручение — это крутящий момент, а изгибающий момент — продольный момент. Одни и те же единицы используются как для изгибающего момента, так и для крутящего момента. Изгибающий момент заставляет секцию изгибаться, а крутящий момент заставляет секцию скручиваться.
Скручивание — это момент, действующий относительно поперечной оси тела, а изгиб — это момент, действующий относительно продольной оси тела.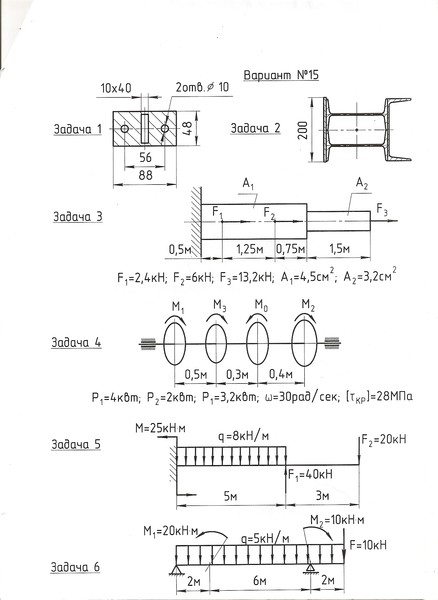
 pi/180 #(рад)
pi/180 #(рад) PI*D_OUter ** 4)/2
PI*D_OUter ** 4)/2 .pi*(D_ratio*D_outer)**4)/2
.pi*(D_ratio*D_outer)**4)/2 twinx()
twinx() Требуемый диаметр сплошного вала {round(d_solid_1,3)} м, одновременно ограниченный допустимым напряжением сдвига и скоростью кручения’)
Требуемый диаметр сплошного вала {round(d_solid_1,3)} м, одновременно ограниченный допустимым напряжением сдвига и скоростью кручения’)