Меню сайтаРасчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции — теория, практика, задачи… Примеры решения задач
Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Форум сопромата и механики Книги — разная литература по теме. Заказать задачу Друзья сайта (ссылки) WIKIbetta Разработчикам (сотрудничество) Веб-мастерам (партнёрка) О проекте, контакты Подпроекты |
Базовый курс лекций по сопромату, теория, практика, задачи.::Оглавление:: 1. Геометрические характеристики сечений 1.1. Статический момент сечения Статические моменты сечения Sx и Sy используются главным образом для определения положения центра площади сечения и центральных осей. Рассмотрим изменение статических моментов при параллельном переносе осей (рис.
Учитывая соотношения x1 = x — a и y1 = y — b получим: или Sx1 = Sx — bF; Sy1 = Sy — aF; (1.1) Оси x1, y1 можно выбрать таким образом, чтобы выполнились условия: Sx1 = 0, Sy1 = 0. Оси, относительно которых статические моменты сечения равны нулю, называются центральнми. Точка пересечения центральных осей называется центром тяжести сечения. Принимая S
Соответственно, если площадь F и положение центра площади сечения (координаты xc, yc) в системе координат 0xy известны, то статические моменты сечения относительно осей x, y можно определить из выражений (1.2): Sx = F yc; Sy = F xc. (1.3) Можно показать, что статический момент относительно любой оси, проходящей через центр площади сечения, равен нулю. При определении центра площади сложного сечения применяется следующая процедура:1) сечение разбивается на n частей, площади (Fi) и положение центров (Ci) площади которых известны; 2) задается вспомогательная система координат, в которой определяются координаты центров площадей (xci, yci) этих частей; 3) вычисляются координаты составного сечения по формулам:
Примеры Пример 1. ::Старый вариант этой лекции:: ::Оглавление:: |
СообществоВходРешение задачРасчет редукторовДля Android (рекомендую)Программа для расчета балок на прочность на Вашем Android устройстве… Java 2 ME |
Сопромат. Расчеты на устойчивость при продольном изгибе.
Сопротивление материалов
Расчеты на устойчивость при продольном изгибе
Понятие продольного изгиба
Продольным изгибом называется изгиб первоначально прямолинейного стержня вследствие потери устойчивости под действием центрально приложенных продольных сжимающих сил. Продольный изгиб возникает при достижении сжимающими силами и напряжениями критического значения.
Продольный изгиб возникает при достижении сжимающими силами и напряжениями критического значения.
Расчеты на прочность и жесткость, выполняемые для большинства видов деформаций основываются на предположении, что между внешними нагрузками и вызываемыми ими внутренними силами существует устойчивая форма равновесия, при которой малым возмущающим воздействиям соответствуют малые отклонения конструкции от первоначальной формы.
Нагрузки, при превышении которых происходит потеря устойчивости (критическое состояние), называют критическими нагрузками.
Примером явления продольного изгиба может послужить длинная школьная линейка, к одному из концов которой приложена сжимающая сила. Сначала материал линейки сопротивляется нагрузке, и линейка работает, как обычный сжимаемый брус. Затем, по достижении определенной нагрузки, линейка начинает прогрессирующе изгибаться без существенного увеличения сжимающей силы и теряет устойчивость (т. е. гнется без заметных усилий вплоть до поломки).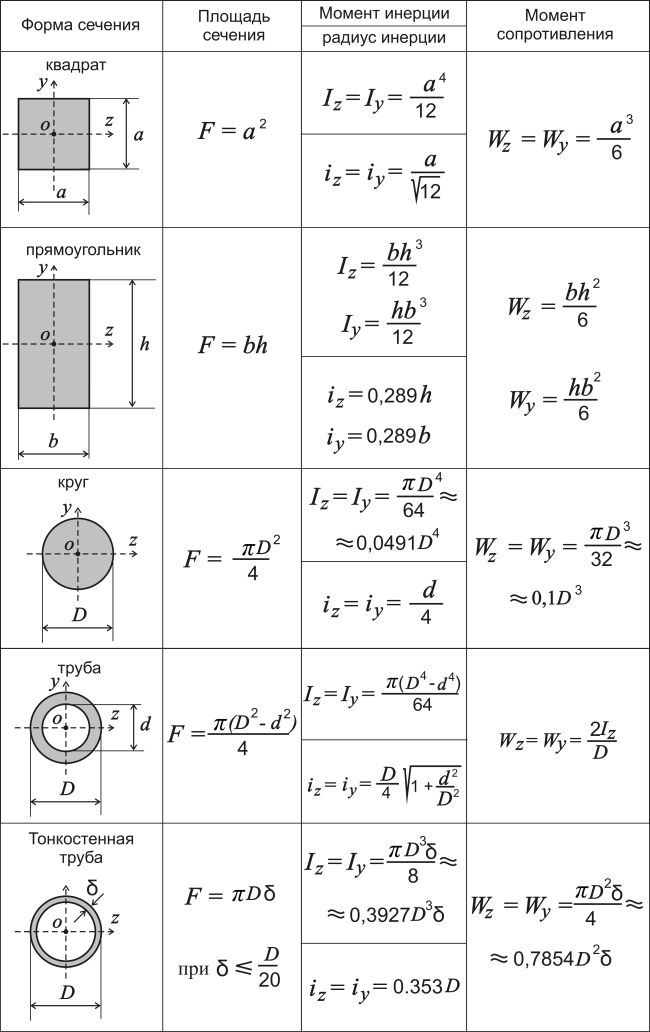
Явление продольного изгиба можно объяснить тем, что к реальному стержню практически невозможно применить основные гипотезы и допущения сопромата — об однородности, изотропности и непрерывности материала. Поэтому при продольном сжатии стержня, даже если сжимающая сила приложена идеально вдоль его оси (что тоже на практике нереально), отдельные волокна этого стержня неодинаково сопротивляются сжатию (из-за неоднородности и анизотропии материала, из которого он изготовлен). В результате, при достижении сжимающей силой критической величины, стержень начинает изгибаться в сторону наименьшего сопротивления волокон.
В конечном итоге стержень теряет устойчивость, что чаще всего сопровождается его поломкой или неупругой деформацией (безвозратной потерей прямолинейности или начальной формы).
Если предположить, что материал стержня идеально соответствует принимаемым в сопромате допущениям и гипотезам, а сжимающая сила приложена строго к центру тяжести сечения вдоль оси стержня, то такой стержень будет работать на простое сжатие, и разрушится не из-за потери устойчивости, а из-за превышения предельных прочностных характеристик для сжатия. Если же стержень имеет сечение в виде сложной фигуры, то решающую роль при потере устойчивости играет отклонение продольной нагрузки от главной центральной оси этой фигуры.
Опасность потери устойчивости особенно велика для тонкостенных конструкций, стержней, пластинок и оболочек.
Рассмотрим тонкий стальной стержень, длина которого значительно больше поперечных размеров, сжимаемый силой F, немного большей критической силы Fкр (см. рисунок 1).
рисунок 1).
Применяя метод сечений, убеждаемся, что в результате искривления оси в поперечных сечениях стержня возникают два внутренних силовых фактора – продольная сила N = F и изгибающий момент Ми.
Таким образом, искривленный стержень испытывает сочетание деформаций центрального сжатия и изгиба.
При сжимающих силах, даже немного превышающих критическую силу, напряжения изгиба могут непосредственно угрожать прочности конструкции. Поэтому критическое состояние конструкции считается недопустимым.
Для обеспечения устойчивости необходимо, чтобы действующая на стержень сжимающая сила F была меньше критической Fкр. Обозначим допускаемую сжимающую силу [F], тогда:
[F] = Fкр/[sy],
где: [sy] – допускаемый коэффициент запаса устойчивости.
Очевидно, что устойчивость стержня обеспечена, если [sy] > 1.
Значение коэффициента запаса устойчивости зависит от назначения стержня и его материала.
***
Формулы Эйлера и Ясинского для расчетов стержней на устойчивость
Первые исследования устойчивости сжатых стержней были проведены академиком Петербургской Академии наук Леонардом Эйлером (1707-1783 г.г.). В дальнейшем большая работа в области теоретического и экспериментального следования вопросов устойчивости была проведена русским ученым, профессором Петербургского института инженеров путей сообщения Ф. С. Ясинским (1856-1899 г.г.), опубликовавшим в 1893 году научную работу «Опыт развития продольного изгиба».
Леонард Эйлер (Leonhard Euler, 1707 — 1783) — выдающийся ученый, которого в разных источниках называют швейцарским, немецким и российским. Математик, физик, астроном и механик, внёсший фундаментальный вклад в развитие этих и ряда других прикладных наук.
Эйлер — автор более чем 850 научных работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и другим областям.
Академик Петербургской, Берлинской, Туринской, Лиссабонской и Базельской академий наук, иностранный член Парижской академии наук.
Л. Эйлер почти полжизни провёл в России, где внёс существенный вклад в становление российской науки. С 1726 по 1741, а также с 1766 года и до конца жизни был академиком Петербургской академии наук. С 1741 по 1766 год работал в Берлине (оставаясь одновременно почётным членом Петербургской академии).
Превосходно знал русский язык и часть своих сочинений (особенно учебники) публиковал на русском.
Некоторые из потомков Л. Эйлера до сих пор живут в России.
Л. Эйлером была предложена формула для определения величины критической силы Fкр, которая приводится здесь без вывода:
Fкр = π2ЕImin / lп2,
где: Е – модуль упругости первого рода; Imin — наименьший из осевых моментов инерции сечения, поскольку искривление происходит в плоскости наименьшей жесткости; lп – приведенная длина стержня, которая может быть определена по формуле:
lп = μl,
где: l – длина стержня; μ – коэффициент приведения длины, зависящий от способа закрепления концов стержня.
Наиболее часто встречающиеся способы закрепления концов стержня и соответствующие им значения коэффициента приведения длины представлены на рисунке 2.
Вывод формулы Эйлера основан на известном законе Гука, который справедлив лишь до предела пропорциональности. Поэтому формулой Эйлера можно пользоваться не всегда.
Для определения пределов применимости формулы Эйлера определим критическое напряжение σкр, т. е. напряжение, которое возникает в поперечном сечении площадью А стержня при достижении критической силы:
σкр =Fкр / А = π2ЕImin /[(μl2)A].
Определим наименьший радиус инерции imin поперечного сечения стержня:
imin = √(Imin / A) (здесь √ — знак квадратного корня).
Перепишем формулу для σкр так:
σкр = π2Е / (μl / imin2).
Введем понятие гибкости стержня: λ = μl / imin. Это безразмерная величина, характеризующая размеры стержня и способ закрепления его концов. Окончательно получим:
σкр = π2Е / λ2.
Формулу Эйлера можно применять только при выполнении условия:
σкр = π2Е / λ2 ≤ σпц,
где: σпц – предел пропорциональности материала стержня. Следовательно, должно быть
λ ≥ √( π2Е / σпц) = λпред (здесь √ — знак квадратного корня).
Величину, стоящую в правой части неравенства, называют предельной гибкостью. Предельная гибкость зависит только от физико-механических свойств материала стержня.
Условие применимости формулы Эйлера можно записать так: λ ≥ λпред, т. е. формула Эйлера применима лишь в тех случаях, когда гибкость стержня больше или равна предельной гибкости. Так, для стержней из низкоуглеродистой стали формула Эйлера применима, если их гибкость λ ≥ 100.
Так, для стержней из низкоуглеродистой стали формула Эйлера применима, если их гибкость λ ≥ 100.
В тех случаях, когда гибкость стержней меньше предельной, формула Эйлера становится неприменимой и при расчетах пользуются эмпирической формулой Ясинского:
σкр = a – bλ,
где: а и b – коэффициенты, зависящие от материала и определяемые по таблицам справочников.
Если стержень имеет гибкость λ ≤ 40, то его можно рассчитывать на простое сжатие по формуле σс = F / А.
***
Расчеты прямолинейных стержней на устойчивость
Существует три вида расчетов на устойчивость прямолинейных стержней – проектный, проверочный и силовой.
Проектный расчет заключается в определении минимального осевого момента инерции поперечного сечения стержня по формуле:
Imin = F[sy](μl)2 / (π2E),
где: F — действующая нагрузка; [sy] – допускаемый коэффициент запаса устойчивости; μ – коэффициент приведения длины стержня; l – длина стержня; Е – модуль продольной упругости.
Далее находят гибкость стержня по формуле: λ = μl / imin,
где: imin = √(Imin / A), (А – площадь сечения стержня).
Полученную гибкость сравнивают с предельной для данного материала.
Проверочный расчет заключается в определении действительного коэффициента запаса устойчивости sy и сравнении его с допускаемым:
sy = Fкр / F ≥ [sy].
Силовой расчет заключается в определении допускаемой нагрузки [F] по формуле:
[F] = Fкр / [sy].
Расчет сжатых стержней на устойчивость можно свести к расчету на простое сжатие. При расчете применяют следующую формулу:
[F] = φ[σс]A,
где: [σс] – допускаемое напряжение на сжатие; φ – коэффициент продольного изгиба (справочная величина, определяемая по таблицам).
Расчеты показывают, что при продольном изгибе наиболее выгодными являются кольцевые и коробочные тонкостенные сечения, имеющие относительно большой момент инерции.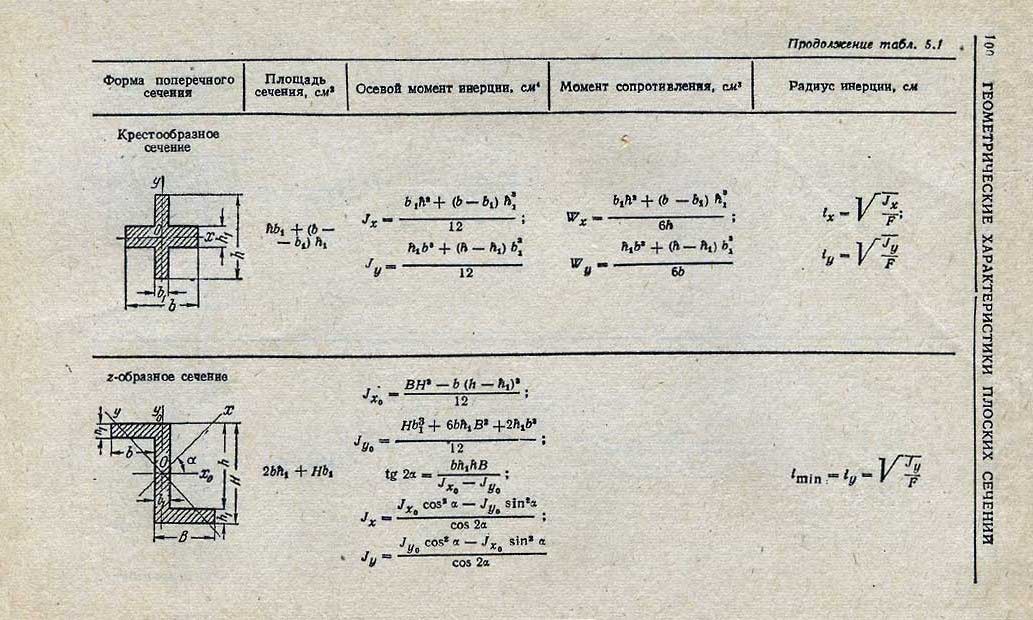
***
Растяжение и сжатие
Главная страница
Дистанционное образование
Специальности
Учебные дисциплины
Олимпиады и тесты
Определение критической силы. Формула Эйлера
Впервые проблема устойчивости сжатых стержней была поставлена Леонардом Эйлером. Эйлер вывел расчетную формулу для критической силы и показал, что ее величина существенно зависит от способа закрепления стержня. Идея метода Эйлера заключается в установлении условий, при которых кроме прямолинейной возможна и смежная (т.е. сколь угодно близкая к исходной) криволинейная форма равновесия стержня при постоянной нагрузке.
Предположим, что шарнирно закрепленный по концам прямой стержень, сжатый силой P=Pk, был выведен некоторой горизонтальной силой из состояния прямолинейного равновесия и остался изогнутым после устранения горизонтальной силы (рис. 13.4). Если прогибы стержня малы, то приближенное дифференциальное уравнение его оси будет иметь такой же вид, как и при поперечном изгибе бруса:
13.4). Если прогибы стержня малы, то приближенное дифференциальное уравнение его оси будет иметь такой же вид, как и при поперечном изгибе бруса:
|
. |
(13.2) |
Рис. 13.4.
Совмещая начало координат с центром нижнего сечения, направим ось у в сторону прогибов стержня, а ось х — по оси стержня.
В теории продольного изгиба принято сжимающую силу считать положительной. Поэтому, определяя изгибающий момент в текущем сечении рассматриваемого стержня, получаем
.
Но, как следует из рис. 13.4, при выбранном направлении осей у//<0, поэтому знаки левой и правой частей уравнения (17.2) будут одинаковыми, если в правой части сохранить знак минус. Если изменить направление оси у на противоположное, то одновременно изменятся знаки у и у// и знак минус в правой части уравнения (13.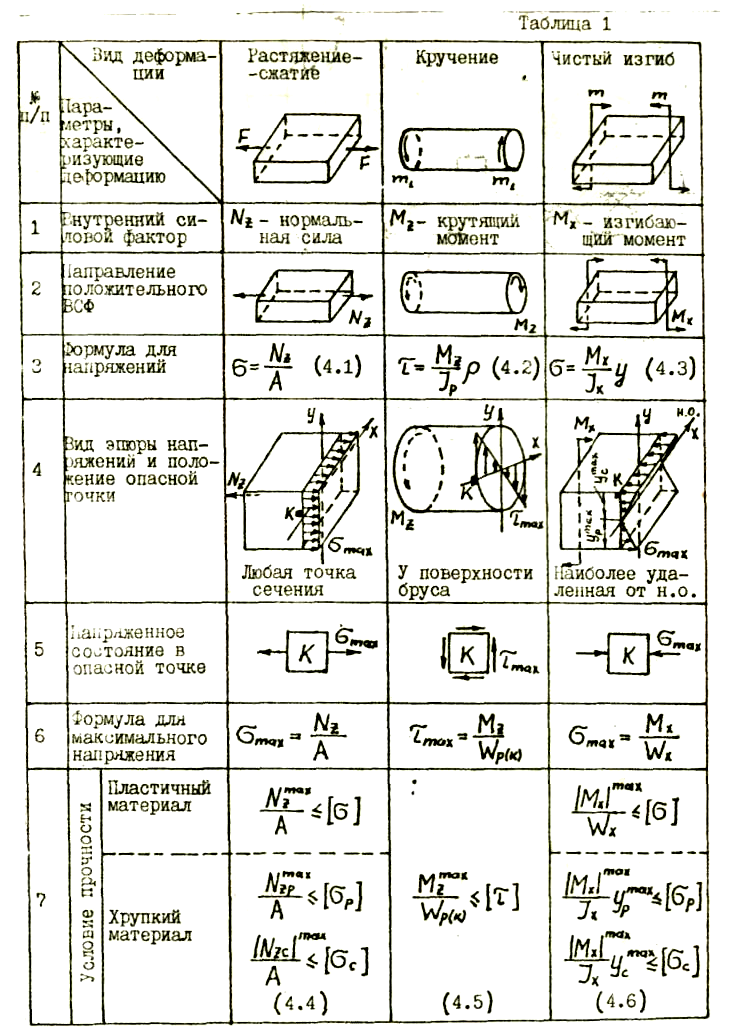 2) сохранится.
2) сохранится.
Следовательно, уравнение упругой линии стержня имеет вид
.
Полагая α2=Рк/EI, получаем линейное однородное дифференциальное уравнение
|
, |
(13.3) |
общий интеграл которого
.
Здесь A и B — постоянные интегрирования, определяемые из условий закрепления стержня, так называемых граничных или краевых условий.
Горизонтальное смещение нижнего конца стержня, как видно из рис. 13.4, равно нулю, т. е. при х=0 прогиб у=0. Это условие будет выполнено, если B=0. Следовательно, изогнутая ось стержня является синусоидой
|
. |
(13.4) |
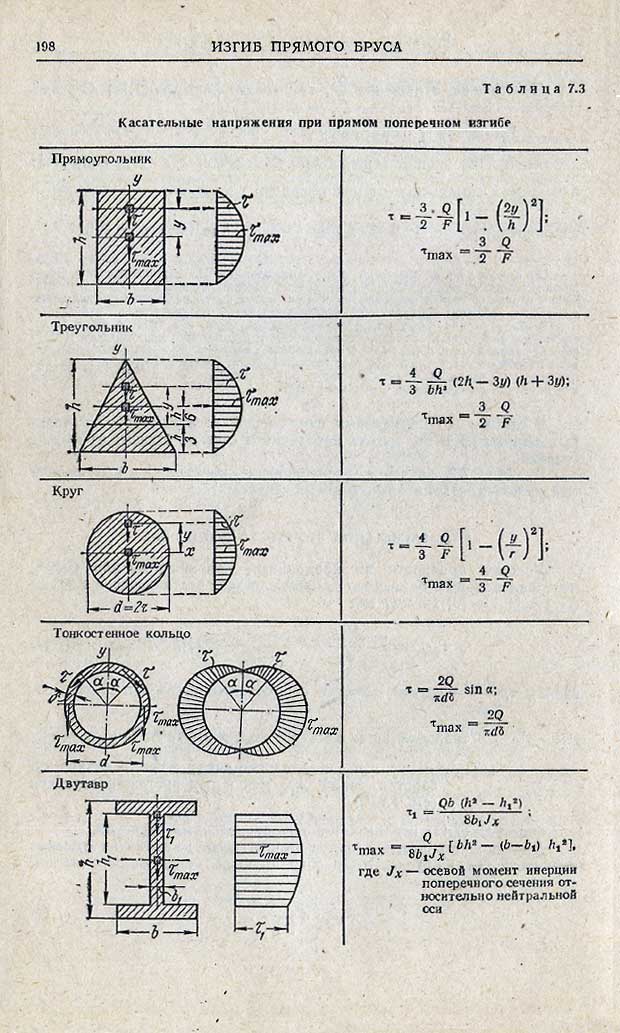
Горизонтальное смещение верхнего конца стержня также равно нулю, поэтому
.
Константа A, представляющая собой наибольший прогиб стержня, не может быть равна нулю, так как при A=0 возможна только прямолинейная форма равновесия, а мы ищем условие, при котором возможна и криволинейная форма равновесия. Поэтому должно быть sinαl=0. Отсюда следует, что криволинейные формы равновесия стержня могут существовать, если αl принимает значения π,2π,.nπ. Величина αl не может быть равна нулю, так как это решение соответствует случаю
или .
Приравнивая αl = nπ и подставляя
,
получаем
|
. |
(13.5) |
Выражение (13.5) называется формулой Эйлера. По ней можно вычислить критическую силу Рк при выпучивании стержня в одной из двух главных его плоскостей, так как только при этом условии справедливо уравнение (13. 2), а следовательно и формула (13.5).
2), а следовательно и формула (13.5).
Выпучивание стержня происходит в сторону наименьшей жесткости, если нет специальных устройств, препятствующих изгибу стержня в этом направлении. Поэтому в формулу Эйлера надо подставлять Imin — меньшей из главных центральных моментов инерции поперечного сечения стержня.
Величина наибольшего прогиба стержня A в приведенном решении остается неопределенной, она принята произвольной, но предполагается малой.
Величина критической силы, определяемая формулой (13.5), зависит от коэффициента n. Выясним геометрический смысл этого коэффициента.
Выше мы установили, что изогнутая ось стержня является синусоидой, уравнение которой после подстановки α=πn/l в выражение (13.4) принимает вид
|
. |
(13.6) |
Синусоиды для n=1, n=2 изображены на рис. 13.5. Нетрудно заметить, что величина n представляет собой число полуволн синусоиды, по которой изогнется стержень. Очевидно, стержень всегда изогнется по наименьшему числу полуволн, допускаемому его опорными устройствами, так как согласно (13.5) наименьшему n соответствует наименьшая критическая сила. Только эта первая критическая сила и имеет реальный физический смысл.
13.5. Нетрудно заметить, что величина n представляет собой число полуволн синусоиды, по которой изогнется стержень. Очевидно, стержень всегда изогнется по наименьшему числу полуволн, допускаемому его опорными устройствами, так как согласно (13.5) наименьшему n соответствует наименьшая критическая сила. Только эта первая критическая сила и имеет реальный физический смысл.
Рис. 13.5.
Например, стержень с шарнирно опертыми концами изогнется, как только будет достигнуто наименьшее значение критической силы, соответствующее n=1, так как опорные устройства этого стержня допускают изгиб его по одной полуволне синусоиды. Критические силы, соответствующие n=2, n=3, и более, могут быть достигнуты только при наличии промежуточных опор (рис. 13.6). Для стержня с шарнирными концевыми опорами без промежуточных закреплений реальный смысл имеет первая критическая сила
|
. |
(13.7) |
Формула (13.5), как следует из ее вывода, справедлива не только для стержня с шарнирно закрепленными концами, но и для любого стержня, который изогнется при выпучивании по целому числу полуволн. Применим эту формулу, например, при определении критической силы для стержня, опорные устройства которого допускают только продольные смещения его концов (стойка с заделанными концами). Как видно из рисунка 13.7, число полуволн изогнутой оси в этом случае n=2 и, следовательно, критическая сила для стержня при данных опорных устройствах
.
Эту формулу можно записать в виде
|
. |
(13.8) |
Рассмотрим далее пример, чтобы показать, какой вид имеет выражение для критической силы в случаях, когда стойка выпучивается не по целому числу полуволн синусоиды.
Предположим, что стойка с одним защемленным и другим свободным концом (рис. 13.8) сжата силой Р.
Если сила P=Pk, то кроме прямолинейной может существовать также и криволинейная форма равновесия стойки (пунктир на рис. 13.8).
Дифференциальное уравнение изогнутой оси стойки в изображенной на рис. 13.8 системе координатных осей имеет прежний вид.
Общее решение этого уравнения:
.
Подчиняя это решение очевидным граничным условиям: y=0 при x=0 и y/=0 при x=l, получаем B=0, Aαcosαl=0.
Мы предположили, что стойка изогнута, поэтому величина A не может быть равна нулю. Следовательно, cosαl=0. Наименьший отличный от нуля, корень этого уравнения αl=π/2 определяет первую критическую силу
|
, |
(13. |
которой соответствует изгиб стержня по синусоиде
.
Значениям αl=3π/2, αl=5π/2 и т.д, как было показано выше, соответствуют большие величины Pk и более сложные формы изогнутой оси стойки, которые могут практически существовать лишь при наличии промежуточных опор.
В качестве второго примера рассмотрим стойку с одним защемленным и вторым шарнирно опертым концом (рис. 13.9). Вследствие искривления оси стержня при P=Pk со стороны шарнирной опоры возникает горизонтальная реактивная сила R. Поэтому изгибающий момент в текущем сечении стержня
.
Дифференциальное уравнение упругой линии
или
.
Общее решение этого уравнения имеет вид
.
Используя условия на концах стержня, выразим постоянные A и B через R.
При x=0 прогиб у=0, следовательно, B=0.
При x=l угол поворота сечения равен нулю, поэтому y/(l)=0. Из этого условия получаем
.
Итак, имеем следующее уравнение упругой линии стержня:
.
Условие y(l)=0 будет выполнено, если
.
Отсюда получаем следующее трансцендентное разрешающее уравнение для определения величины α:
.
Наименьший корень этого уравнения определяет первую критическую силу. Это уравнение решается методом подбора. Нетрудно поверить, что наименьший, отличный от нуля, корень этого уравнения αl=4.493=1.43π.
Принимая αl=1.43π, получаем следующее выражение для критической силы:
|
. |
(13.10) |
Сопоставляя формулы (13. 7), (13.8), (13.9) и (13.10), нетрудно заметить, что все они имеют одинаковое строение, и их можно обобщить на случай любых опорных устройств стойки, если записать формулу Эйлера в виде
7), (13.8), (13.9) и (13.10), нетрудно заметить, что все они имеют одинаковое строение, и их можно обобщить на случай любых опорных устройств стойки, если записать формулу Эйлера в виде
|
. |
(13.11) |
Здесь μ=1/n — величина, обратная числу полуволн n синусоиды, по которой изогнется стержень. Постоянная μ называется коэффициентом приведения длины, а произведение μl — приведенной длиной стержня. Приведенная длина есть длина полуволны синусоиды, по которой изгибается этот стержень.
Случай шарнирного закрепления концов стержня называется основным. Из сказанного выше следует, что критическая сила для любого случая закрепления стержня может быть вычислена по формуле для основного случая при замене в ней действительной длины стержня его приведенной длиной μl.
Коэффициенты приведения μ для некоторых стоек даны на рис. 17.10.
17.10.
Рис. 13.10.
прогиб предварительно натянутого гибкого тяжелого каната, закрепленного в двух точках произвольной формы | Кравчук
Скворцов А.В. Расчетные модели гибкой нити применительно к висячим мостам и вантово-балочным системам: дис. … Канд. техн. Расчетные модели гибкой нити применяются для подвесных мостов и вантово-балочных систем. Кандидатская диссертация, Москва, 2005, 248 с.
Решение задач и выполнение письменных работ по ТОЭ, высшей математике, физике, программированию, термху… , термеху…] Доступно по адресу: http://www.toehelp.ru/theory/sopromat/15.html (по состоянию на 17 сентября 2017 г.).
Виноградов Г.Г. Расчет строительных пространственных конструкций. Л .: Стройиздат, 1990. 264 с.
Меркин Д.Р. Введение в механику гибкой резьбы. М .: Наука, 1980. 240 с.
Кравчук А.С., Кравчук А.И. Малые поперечные прогибы груза горизонтально натянутым под действием силы тяжести // АПРИОРИ. Серия: Естественные и технические науки [АПРИОРИ. Серия: Естественные и технические науки], 2015, №2 (доступно по адресу: http://apriori-journal.ru/seria2/2-2015/Kravchuk-Kravchuk.pdf).
Серия: Естественные и технические науки [АПРИОРИ. Серия: Естественные и технические науки], 2015, №2 (доступно по адресу: http://apriori-journal.ru/seria2/2-2015/Kravchuk-Kravchuk.pdf).
Лукаш П.А. Основы нелинейной строительной механики. Лукаш] М .: Стройиздат, 1978, 204 с.
Кравчук А.С., Кравчук А.И. Моделирование ползучести по наследственной теории в простой модели деформируемого покрытия постоянной толщины // АПРИОРИ.Серия: Естественные и технические науки [АПРИОРИ. Серия: Естественные и технические науки], 2014, №2 (доступно по адресу: http://apriori-journal.ru/seria2/2-2014/Kravchuk-Kravchuk.pdf).
Кравчук А.С., Чигарев А.В. Механика контактного взаимодействия тел с круговыми границами. Минск: Технопринт, 2000. 196 с.
Ржаницын А.Р. Теория использования. М .: Стройиздат, 1968. 418 с.
Малинин Н.Н. Прикладная теория пластичности и ползучести. М .: Машиностроение, 1975. 400 с.
(PDF) Способ повышения точности контроля маневрирования судна за счет оценки абсцисс центра тяжести
Бумага поступила 10. 09.20; Принята к публикации 24.09.20.
09.20; Принята к публикации 24.09.20.
Аннотация. В статье представлен алгоритм, позволяющий быстро определить центр тяжести судна.При рассмотрении вопросов управления маневрированием
судно рассматривается как точка, масса которой сосредоточена в центре тяжести. Начало координат
помещается в точку пересечения диаметральной плоскости и середины кадра. Погрешность определения местоположения составляет
, что соизмеримо со значением абсциссы центра тяжести, а иногда и намного меньше. Точное определение координат центра тяжести уменьшит ошибку при определении местоположения корабля.
Ключевые слова: абсцисса центра тяжести, статический момент перемещения судна; оценка посадки корабля; смещение; ma-
невозможность.
Вопрос, связанный с определением масс
и координат центра тяжести (ЦТ) судна
, является одним из важнейших вопросов при проектировании судна
, поскольку многие важные качества Судно де-
на нем: мореходные качества. В процессе проектирования необходимо определить массу и координаты
В процессе проектирования необходимо определить массу и координаты
ЦТ корабля
. Наибольшую трудность для конструктора представляет
определение массы и координат ЦТ
пустого корабля [1].
Краткий обзор публикаций по теме. В публикации
[2] был разработан алгоритм и блок-схема
навигационного устройства для расчета поправок координат антенны
для пересчета на центр тяжести
судна.Для более точной работы блок-схемы
в данной статье представлен алгоритм вычисления CG
.
В статье [3] авторы разработали алгоритм для
определения точки поворота с использованием доплеровского запаздывания. Для того, чтобы
точно определял расстояние точки поворота
от ЦТ, вам также необходимо знать точные координаты
центра тяжести.
Назначение: 1) повышение точности определения положения судна
; 2) доработка расчета
методом определения абсцисс точки поворота.
При рассмотрении управленческих вопросов маневрирование
считается точкой. Масса которого
сосредоточена в центре тяжести. Начало координат
расположено в точке пересечения диаметральной плоскости
и середины кадра.
Ошибка определения местоположения соизмерима
со значением абсциссы ЦТ, а иногда
намного меньше.
Материалы и методы.На начальных этапах определения знака
могут быть использованы эмпирические зависимости для определения легкости корабля
, которые получены статистической обработкой
данных о массовой загрузке построенных и спроектированных
кораблей [1] .
Координата ЦТ любого объекта относительно любой выбранной базовой плоскости — это отношение сумм статистических моментов
отдельных элементов, на которые делится рассматриваемый объект
, на сумму весов
всех элементов, то есть к весу всего объекта
[4].Для определения абсцисс ЦТ (
) судна
необходимо статический момент перемещения судна
относительно миделя (
) разделить на
полного водоизмещения (
. ( 1)
( 1)
Статический момент смещения корабля относительно
относительно миделя (
) состоит из суммы моментов, созданных светом корабля (
), как указано в формуле (2).
. (2)
Чтобы определить применимость ЦТ (
) загруженного судна
, необходимо разделить статический момент
нагрузок относительно основной плоскости (
) на общее смещение
. (
). Однако необходимо учитывать
с учетом наличия свободной поверхности жидкости в
резервуарах и цистернах.Для этого вводятся корректирующие моменты (
)
. Скорректированная аппликата ЦТ приведена в формуле 3
.
(3)
Статический момент нагрузок относительно основной плоскости (
) находится как сумма моментов от массы —
es от легкий корабль (
58
Наука и образование в новом измерении. Естественные и технические науки, VIII (29), выпуск: 238, сентябрь 2020 г.www.seanewdim.com
Способ повышения точности контроля маневрирования судна за счет определения оси абсцисс центра тяжести
Введение. Любое морское судно представляет собой сложную конструкцию, конструкция которой
Любое морское судно представляет собой сложную конструкцию, конструкция которой
требует решения множества и
очень разных вопросов, возникающих на пути развития проекта
от самой общей концепции до создания набора из
чертежей, переданных в судостроительное предприятие.Практика
показала, что весь этот путь нельзя пройти сразу,
за один шаг, поэтому для принятия полноценного и
обоснованного решения необходимо преодолевать его
постепенно, шаг за шагом. шаг за шагом, проверка и анализ
результатов, полученных на каждом этапе, а затем уточнение
и их корректировка при переходе к следующему этапу.
Национальный университет «Одесская морская академия», Одесса, Украина
Автор, ответственный за переписку.E-mail: [email protected]
Суринов И.Л.
https://doi.org/10.31174/SEND-NT2020-238VIII29-14
Сила сдвига и изгибающий момент
Понятие силы сдвига и изгибающего момента в балках:
Когда балка нагружается произвольным образом, внутренние силы и моменты развиваются, а термины поперечная сила и изгибающие моменты появляются на рисунках, которые полезны для дальнейшего анализа балок. Определим эти термины
Определим эти термины
Рис 1
Теперь давайте рассмотрим балку, показанную на рис. 1 (a), которая поддерживает нагрузки P 1 , P 2 , P 3 и просто поддерживается в двух точках, создавая реакции R 1 и R 2 соответственно.Теперь предположим, что балка должна быть разделена на две части или предположительно разрезана на две части в сечении AA. Теперь предположим, что равнодействующая нагрузок и реакций слева от AA равна �F ‘вертикально вверх, и, поскольку вся балка должна оставаться в равновесии, следовательно, равнодействующая сил справа от AA также должна быть F, действуя вниз. Эта сила �F ’действует как сила сдвига. Сила сдвига в любом x-сечении балки представляет собой тенденцию части балки с одной стороны сечения к скольжению или сдвигу в поперечном направлении относительно другой части.
Таким образом, теперь мы можем определить поперечную силу �F ’следующим образом:
В любом x-сечении балки поперечная сила �F ’представляет собой алгебраическую сумму всех боковых составляющих сил, действующих по обе стороны от x-сечения.
Соглашение о знаках для поперечной силы:
Обычные условные обозначения, которым необходимо следовать для поперечных сил, показаны на рисунках 2 и 3.
Рис. 2: Положительное поперечное усилие
Рис. 3: Отрицательная сила сдвига
Изгибающий момент:
Рис. 4
Давайте снова рассмотрим балку, которая просто поддерживается на двух отпечатках, несущая нагрузки P 1 , P 2 и P 3 и имеющая реакции R 1 и R 2 на опорах Рис. .Теперь представим, что луч разрезан на две части в x-сечении AA. Подобным образом, как это сделано для случая поперечной силы, если мы скажем, что результирующий момент относительно сечения AA всех нагрузок и реакций слева от x-сечения в AA равен M в направлении CW, тогда момент силы справа от x-секции AA должны быть �M ‘против часовой стрелки. Тогда �M ’называется изгибающим моментом и обозначается аббревиатурой B. M. Теперь можно определить изгибающий момент просто как , алгебраическую сумму моментов относительно x-сечения всех сил, действующих по обе стороны от сечения
M. Теперь можно определить изгибающий момент просто как , алгебраическую сумму моментов относительно x-сечения всех сил, действующих по обе стороны от сечения
Условные обозначения для изгибающего момента:
Для изгибающего момента могут быть приняты следующие условные обозначения, как показано на Рис. 5 и Рис. 6.
Рис.5: Положительный изгибающий момент
Рис.6: Отрицательный изгибающий момент
Иногда термины «провисание» и «проседание» обычно используются для обозначения положительного и отрицательного изгибающих моментов соответственно.
Диаграммы изгибающего момента и поперечной силы:
Диаграммы, которые иллюстрируют изменения значений B.M и S.F по длине балки для любых фиксированных условий нагружения, будут полезны для дальнейшего анализа балки.
Таким образом, диаграмма поперечной силы представляет собой графический график, который показывает, как внутренняя поперечная сила �F ’изменяется по длине балки.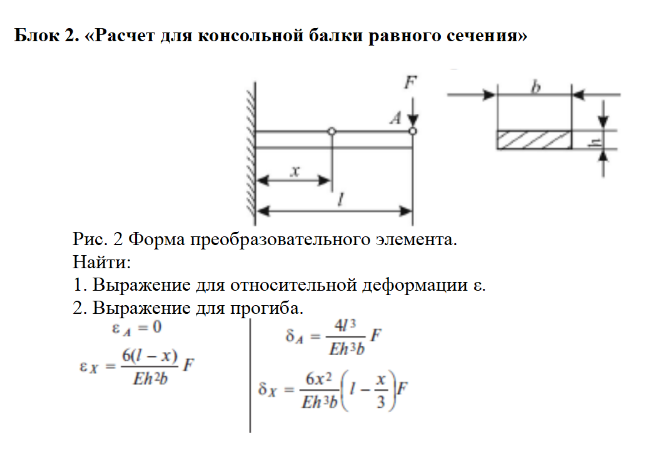 Если x определяет длину балки, то F является функцией x, то есть F (x).
Если x определяет длину балки, то F является функцией x, то есть F (x).
Аналогичным образом диаграмма изгибающего момента представляет собой графический график, который показывает, как внутренний изгибающий момент �M ’изменяется по длине балки. Снова M — это функция x, то есть M (x).
Основная взаимосвязь между скоростью нагрузки, поперечной силой и изгибающим моментом:
Построение диаграммы поперечных сил и диаграмм изгибающего момента значительно упрощается, если установлена взаимосвязь между нагрузкой, поперечной силой и изгибающим моментом.
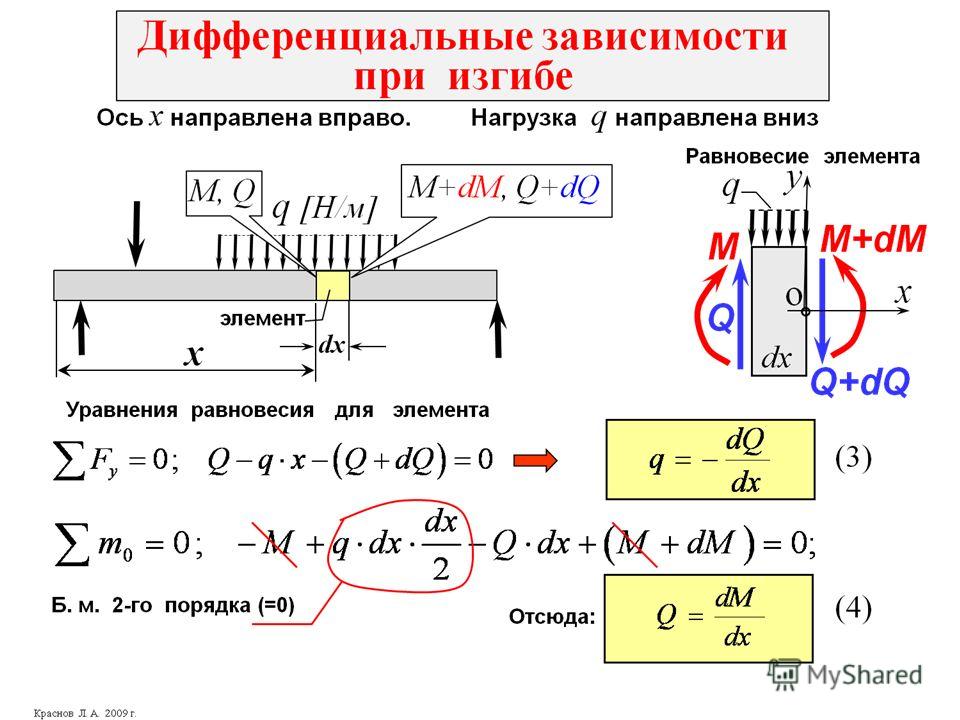
Рассмотрим свободно опертую балку АВ, несущую равномерно распределенную нагрузку по длине. Представим себе, что вы разрезаете короткий кусок длиной dx, вырезанный из этой нагруженной балки на расстоянии x ’от начала координат �0 ′.
Отделим эту часть балки и нарисуем схему ее свободного тела.
Силы, действующие на диаграмму свободного тела оторванной части этой нагруженной балки, следующие:
• Сила сдвига F и F + dF в сечении x и x + dx соответственно.
• Изгибающий момент на участках x и x + dx равен M и M + dM соответственно.
• Сила из-за внешней нагрузки, если �w ’- средняя скорость нагрузки на единицу длины, то общая нагрузка на этот отрезок длины dx равна w. dx, который приблизительно действует через центр �c ’. Если предполагается, что нагрузка распределена равномерно, то она будет проходить точно через центр �c ’.
Этот маленький элемент должен находиться в равновесии под действием этих сил и пар.
Теперь давайте возьмем моменты в точке �c ’. Такой, что
Выводы: Из приведенных выше соотношений можно сделать следующие важные выводы
• Из уравнения (1) площадь диаграммы поперечных сил между любыми двумя точками, из основных расчетов — диаграмма изгибающего момента
• Наклон диаграммы изгибающего момента — это поперечная сила, поэтому
Таким образом, если F = 0; наклон диаграммы изгибающего момента равен нулю, и поэтому изгибающий момент постоянен. ’
’
• Максимальный или минимальный изгибающий момент возникает там, где
Наклон диаграммы поперечной силы равен величине интенсивности распределенной нагрузки в любом месте вдоль балки. Знак �ve является следствием нашего особого выбора условных обозначений
Нравится:
Нравится Загрузка …
СвязанныеNapon smicanja — Напряжение сдвига
Komponenta napona koplanarnog presjeka materijala
Na vrh pravokutnika primjenjuje se sila smicanja dok se dno drži na mjestu.Rezultirajuće naprezanje posmika, τ, deformira pravokutnik u paralelogram. Uključeno područje bilo bi vrh paralelograma. Napon smicanja , esto označena sa τ (grčki: tau), komponenta je stres koplanarna s presjekom materijala. Чтобы произвести из sila smicanja, компонент sila vektor paralelno prema presjek materijala. Uobičajeni stres, s druge strane, proizlazi iz komponente vektora sil okomita do presjeka materijala na koji djeluje.
Općenito posmično naprezanje
Formula za izračunavanje prosječnog smičućeg naprezanja je sila po jedinici površine.: [1]
- τ = FA, {displaystyle tau = {F preko A},}
gdje:
- τ = posmični napon;
- F = primijenjena sila;
- A = površina presjeka materijala s površinom paralelnom primijenjenomvektoru force.
Ostali oblici
Čist
Čisto smicanje stres je povezan s čistim smičuće naprezanje, označeno γ, sljedećom jednadžbom: 000 [2]
gamma = gamma = gamma = = γ Je modul smicanja od izotropna materijal, dao- G = E2 (1 + ν).{displaystyle G = {frac {E} {2 (1+ nu)}}.}
Ovdje E je Youngov modul i v je Poissonov omjer.
Smicanje grede
Smicanje snopa Definira se kao unutarnje posmično naprezanje grede uzrokovano posmičnom silom koja se primjenjuje na gredu.
- τ = fPJab, {displaystyle tau = {fQ over Ib},}
gdje
- f = ukupna sila smicanja na predmetnom mjestu;
- P = statični trenutak površine;
- b = debljina (širina) u materijalu okomito na smicanje;
- Ja = Trenutak tromosti cijelog područja presjeka.

Формула smicanja snopa poznata JE я као Журавский формула posmičnog naprezanja Nakon Dmitrij Ivanović Žuravski Кодзи га JE izveo 1855. [3] [4]
Polumonokonske SKAREPosmična naprezanja unutar polumonoka Konstrukcija се może izračunati idealiziranjem presjeka konstrukcije u niz struna (koje Nose Samo aksijalna opterećenja) и mreža (Samo Noise) smicanje teče). Podijelom posmičnog toka s debljinom zadanog dijela polumonokoke structure dobiva se posmični napon.Dakle, najveće smičuće naprezanje pojavit çe se или u mreži maksimalnog posmičnog protoka or minimalne debljine
Također konstrukcije u tlu mogu propasti zbog smicanja; npr., težina zemlje ispunjene brana или nasip može uzrokovati urušavanje podzemlja, poput malog klizište.
Udarni smicanje
Максимально возможное значение напряжения у чврстой округлой шипки повышенной прочности для данного случая:
- τ = 2UGV2 9039, {display oversize 9039 9039, {display over the 2UGV2 9039] U = promjena kinetičke energije;
- G = modul smicanja;
- V = объем шипке;
i
- U = U rotacioni + U primijenjena ;
- U rotacioni = 1/2 Iω 2 ;
- U primijenjena = Tθ raseljeni ;
- Ja = момент тромости масс;
- ω = kutna brzina.

Napon smicanja u tekućinama
Bilo kakav stvaran tekućine (tekućine i plinovi uključeni) kretanje duž čvrste granice na toj će granici izazvati posmični napon. Станция proklizavanja [5] nalaže da je brzina fluida na granici (u odnosu na granicu) jednaka nuli; iako na nekoj visini od granice brzina protoka mora biti jednaka brzini protoka. Подручное изменение на двух точках называния с границами слоя. Za sve Newtonove tekućine u ламинарный ток, smičući napon proporcionalan je brzina naprezanja u tekućini, gdje je viskoznost konstanta proporcionalnosti.Za ne-njutnovske tekućine, viskoznost nije konstanta. Posmični napon prenosi se na granicu kao rezultat gubitka brzine.
Za Newtonovu tekućinu, smičući napon na površinskom elementu paralelnom s ravnom pločom u točki g daje:
- τ (g) = μ∂u∂g {displaystyle tau (y) = mu {domi učnoel {djno}) }}}
gdje
- μ je dinamička viskoznost protoka;
- у Je brzina protoka uz granicu;
- g je visina iznad granice.
Konkretno, naprezanje smicanja zida Definira se kao:
- τw≡τ (g = 0) = μ∂u∂g | g = 0. {Displaystyle tau _ {mathrm {w}} Equiv tau (y = 0 ) = му льево. {frac {djelomično u} {djelomično y}} desno | _ {y = 0} около je njen gradijent tenzor otherog reda):
- τ (u →) = μ∇u → {displaystyle mathbf {tau} ({vec {u}}) = mu nabla {vec {u}}}
a imenuje se konstanta proporcionalnosti dinamička viskoznost .За изотропни Ньютонов ток на скалар, док за анизотропни Ньютонов ток може бити и тензор другог реда. Temeljni aspekt je da je za Newtonovu tekućinu dinamička viskoznost neovisna o brzini protoka (tj. Konstitutivni zakon smičućeg naprezanja je linearno ), dok ne-newtonovski tokovi to nije , dok ne-newtonovski tokovi to nije → τ =
- = 9393 = 9393 = 9393 = 9393 = 9393 → μ (u →) ∇u → {displaystyle mathbf {tau} ({vec {u}}) = mu ({vec {u}}) nabla {vec {u}}}
Формула Горня više nije Newtonov zakon, već generički tenzorski identity: uvijek se može naći izraz viskoznosti u funkciji brzine protoka s obzirom na bilo koji izraz posmičnog naprezanja u ovisnosti o brzini protoka.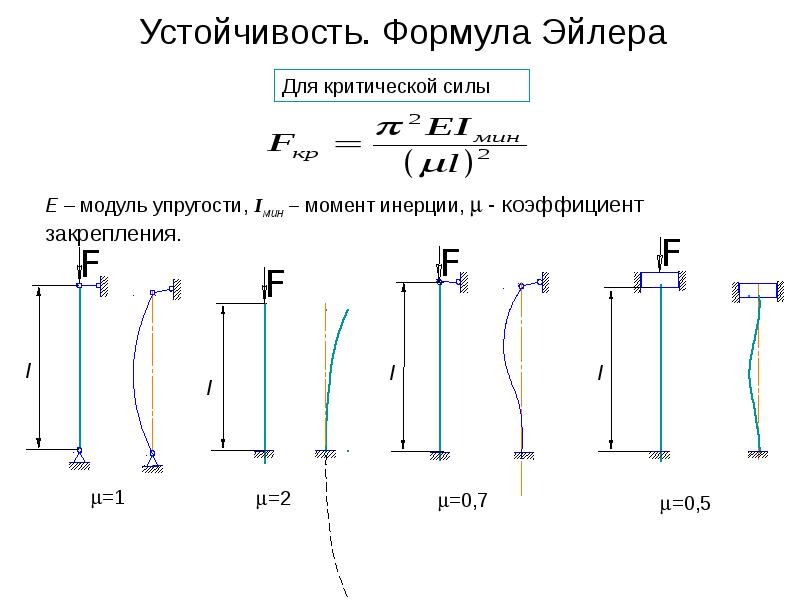 S druge strane, s obzirom na posmični napon kao funkciju brzine protoka, on prestavlja Newtonov tok samo ako se može izraziti kao konstanta za gradijent brzine protoka. Konstanta koju u ovom slučaju nalazimo je dinamička viskoznost protoka.
S druge strane, s obzirom na posmični napon kao funkciju brzine protoka, on prestavlja Newtonov tok samo ako se može izraziti kao konstanta za gradijent brzine protoka. Konstanta koju u ovom slučaju nalazimo je dinamička viskoznost protoka.
Primjer
Uzimajući u obzir 2D prostor u kartezijanskim koordinatama (x, y) (komponente brzine protoka su (u, v)), matrica posmičnog naprezanja dana je:
- (xxxτxg) t∂v∂g) {displaystyle {begin {pmatrix} tau _ {xx} & tau _ {xy} tau _ {yx} & tau _ {yy} end {pmatrix}} = {begin {pmatrix} x {frac { djelomično u} {djelomično x}} & 0 0 & -t {frac {djelomično v} {djelomično y}} kraj {pmatrix}}}
представляет Newtonov tok, zapravo se može izraziti kaogg: 9000τ = (x00 − t) ⋅ (∂u∂x∂u∂g∂v∂x∂v∂g) {displaystyle {begin {pmatrix} tau _ {xx} & tau _ {xy} tau _ {yx} & tau _ {yy} end {pmatrix}} = {begin {pmatrix} x & 0 0 & -t end {pmatrix}} cdot {begin {pmatrix} {frac {djelomično u} {djelomično x}} & {frac {djelomično u } {djelomično y}} {frac {djelomično v} {djelomično x}} & {frac {djelomično v} {djelomično y}} kraj {pmatrix}}},
tj. анизотропный ток с тензором вискозности:
анизотропный ток с тензором вискозности:
- (μxxμxgμgxμgg) = (x00 − t) {displaystyle {begin {pmatrix} mu _ {xx} & mu _ {xy} mu _ {yx} & mu _ {yy} end {pmatrix }} = {begin {pmatrix} x & 0 0 & -t end {pmatrix}}}
koja nije neujednačena (ovisi o koordinatama prostora) и раньше, ali bitno je neovisna o brzini protoka:
- μ (x , t) = (x00 − t) {displaystyle mathbf {mu} (x, t) = {početak {pmatrix} x & 0 0 & -t end {pmatrix}}}
Taj je tok stoga newtonovski.S druge strane, protok u kojem je viskoznost bila:
- (μxxμxgμgxμgg) = (1u001u) {displaystyle {begin {pmatrix} mu _ {xx} & mu _ {xy} mu _ {yx} & mu _ {yy} end {pmatrix}} = {begin {pmatrix} {frac {1} {u}} & 0 0 & {frac {1} {u}} end {pmatrix}}}
je nonnewtonov jer viskoznost ovisi o brzini protoka . Taj je nonwtonov protok izotropan (matrica je proporcionalna matrici identiteta), pa je viskoznost jednostavno skalarna:
- μ (u) = 1u {displaystyle mu (u) = {frac {1} {u}}}
or M
Senzor naprezanja smicanja s rubnim rubom
Taj se oneos može iskoristiti za mjerenje naprezanja posmičnog zida. Kad bi senzor mogao izravno izmjeriti gradijent profila brzine na zidu, pomnoženje s dinamičkom viskoznošću dalo bi posmični napon. Такав сенсор демонстрации су А. А. Накви и В. К. Рейнольдса. [6] Узорак сметни родовой слэнджем снопа света кроз два паралельна прореза твори мрежу линейно разилазечих рубова коди као да потечу из равнине двию прореза (виды экспериментов с движением). Како честица у текучини пролази кроз рубове, приямник открытие одраз узорка руба. Signal se može obraditi, a znajući rubni kut, visina i brzina čestice mogu se ekstrapolirati.Izmjerena vrijednost gradijenta brzine stjenke neovisna je o svojstvima fluida и kao результат toga ne zahtijeva kalibraciju. Новые предложения у технологии микрооптики израда омогуцио е употребляемый интегрираног дифрактивный оптический элемент за израду дивергентных осьетника смичуцег на руб. у зраку я текучини. [7]
Kad bi senzor mogao izravno izmjeriti gradijent profila brzine na zidu, pomnoženje s dinamičkom viskoznošću dalo bi posmični napon. Такав сенсор демонстрации су А. А. Накви и В. К. Рейнольдса. [6] Узорак сметни родовой слэнджем снопа света кроз два паралельна прореза твори мрежу линейно разилазечих рубова коди као да потечу из равнине двию прореза (виды экспериментов с движением). Како честица у текучини пролази кроз рубове, приямник открытие одраз узорка руба. Signal se može obraditi, a znajući rubni kut, visina i brzina čestice mogu se ekstrapolirati.Izmjerena vrijednost gradijenta brzine stjenke neovisna je o svojstvima fluida и kao результат toga ne zahtijeva kalibraciju. Новые предложения у технологии микрооптики израда омогуцио е употребляемый интегрираног дифрактивный оптический элемент за израду дивергентных осьетника смичуцег на руб. у зраку я текучини. [7]
Датчик запрещен при срабатывании микро-ступа
Дальняя техника мёрения она витких зидних микро ступова изображены од флексибильного полимера PDMS, у которого есть кожа, которая проявляет себя. Große, S .; Schröder, W. (2008), «Динамическая мера напр. При пос. Зиду у турбулентного протока с помощью микро-ступенчатого сенсора MPS 3 «, Međunarodni časopis za protok3 30, 8-800-29-482, 9022–210, 9022–210, 9022–210 , doi: 10.1016 / j.ijheatfluidflow.2008.01.008
Große, S .; Schröder, W. (2008), «Динамическая мера напр. При пос. Зиду у турбулентного протока с помощью микро-ступенчатого сенсора MPS 3 «, Međunarodni časopis za protok3 30, 8-800-29-482, 9022–210, 9022–210, 9022–210 , doi: 10.1016 / j.ijheatfluidflow.2008.01.008
Строительный журнал
1.02 -8172Журнал гражданского строительства14520141-120CHRRUS5-50000-0003-2533-9732SamarinOlegНациональные исследования Московский государственный строительный университетsamarin-olegsamarin-oleg.ruИтоги 5-го Международного научно-технического форума «Теоретические основы тепло-, газоснабжения и вентиляции» Представлена информация 5-го Форума «Теоретические основы HVAC». В документе изложена структура конференции и тематика наиболее важных презентаций; отмечает роль форума в развитии науки о вентиляции и кондиционировании воздуха. 10.5862 / MCE.45.1forumheatgas supply and Ventilationenergyungenergy Competitiony молодых исследователей https://engstroy. spbstu.ru/article/2014.45.1 / 01.pdfRARRUS6-11IevzerovIsaakLLC PRAYM [email protected] Задачи устойчивости стержней и пластин Рассмотрены задачи устойчивости стержней и пластин. Для задач устойчивости используются вариационные формулировки. Исследована положительная определенность функционала потенциальной энергии. Осуществлен переход от задачи трехмерной устойчивости к соответствующим задачам для стержней и пластин. Представления о перемещениях по сечению стержня и толщине пластины используются для геометрически нелинейных задач.Эти концепции основаны на предположении об исчезновении деформации через плоскость поперечного сечения стержня или толщину пластины. Рассчитаны вторые вариации нелинейных деформаций. Интегрирование по поперечному сечению стержня и толщине пластины было выполнено с использованием известных формул для усилий и уравнения равновесия. Получены функционалы устойчивости стержней и пластин. Проведено сравнение с известными ранее результатами. Дано решение тестовой задачи для сжатой по центру консольной балки с поперечным сечением Pi, моделированной пластинами.
spbstu.ru/article/2014.45.1 / 01.pdfRARRUS6-11IevzerovIsaakLLC PRAYM [email protected] Задачи устойчивости стержней и пластин Рассмотрены задачи устойчивости стержней и пластин. Для задач устойчивости используются вариационные формулировки. Исследована положительная определенность функционала потенциальной энергии. Осуществлен переход от задачи трехмерной устойчивости к соответствующим задачам для стержней и пластин. Представления о перемещениях по сечению стержня и толщине пластины используются для геометрически нелинейных задач.Эти концепции основаны на предположении об исчезновении деформации через плоскость поперечного сечения стержня или толщину пластины. Рассчитаны вторые вариации нелинейных деформаций. Интегрирование по поперечному сечению стержня и толщине пластины было выполнено с использованием известных формул для усилий и уравнения равновесия. Получены функционалы устойчивости стержней и пластин. Проведено сравнение с известными ранее результатами. Дано решение тестовой задачи для сжатой по центру консольной балки с поперечным сечением Pi, моделированной пластинами. 10.5862 / MCE.45.2 Проблемы устойчивости планок и пластин вариации формулировок https://engstroy.spbstu.ru/article/2014.45.2/02.pdfRARRUS12-22ЧернухаНикитаАО «АТОМПРОЕКТ» [email protected] ул. Савушкина, 82А, Санкт-Петербург , 197183, Россия Структурный анализ зданий при взрывных воздействиях в SCAD В статье рассматриваются методы расчета конструкций зданий и сооружений при взрывных воздействиях. Во введении дается обзор видов взрывов и особенностей их воздействия на конструкции.В теоретической части исследования основной задачей было представить различные методы расчета конструкций зданий при взрывах. Представлено определение волновых параметров и процесс дифракции волн. Описано импульсное нагружение строительных конструкций в SCAD. В статье также показано, как модуль «Прямое интегрирование уравнений движения» в SCAD может быть использован для решения задач динамики взрыва. В эмпирической части исследования основной задачей было сравнение напряженно-деформированного состояния строительных конструкций при взрывах с использованием различных методов структурного анализа.
10.5862 / MCE.45.2 Проблемы устойчивости планок и пластин вариации формулировок https://engstroy.spbstu.ru/article/2014.45.2/02.pdfRARRUS12-22ЧернухаНикитаАО «АТОМПРОЕКТ» [email protected] ул. Савушкина, 82А, Санкт-Петербург , 197183, Россия Структурный анализ зданий при взрывных воздействиях в SCAD В статье рассматриваются методы расчета конструкций зданий и сооружений при взрывных воздействиях. Во введении дается обзор видов взрывов и особенностей их воздействия на конструкции.В теоретической части исследования основной задачей было представить различные методы расчета конструкций зданий при взрывах. Представлено определение волновых параметров и процесс дифракции волн. Описано импульсное нагружение строительных конструкций в SCAD. В статье также показано, как модуль «Прямое интегрирование уравнений движения» в SCAD может быть использован для решения задач динамики взрыва. В эмпирической части исследования основной задачей было сравнение напряженно-деформированного состояния строительных конструкций при взрывах с использованием различных методов структурного анализа. Автоматический анализ был выполнен в SCAD, который реализует метод конечных элементов (FEM). Результаты исследования демонстрируют достоинства и недостатки описанных методов, а также функциональные возможности SCAD при решении задач динамики взрыва. 10.5862 / MCE.45.3 Типы взрывов структурная динамикаквазистатический методимпульсное воздействиепрямая интеграциядифракция волнFEMSCADhttps: // engstroy .spbstu.ru / article / 2014.45.3 / 03.pdfRARRUS23-40БенинАндрейПетербургский государственный университет путей сообщенияБенин[email protected]СеменовАртемДрезденский технологический университет[email protected]СеменовСергей Петра Великого Санкт-Петербургский политехнический университет[email protected] Политехническая улица, 29 67017517050000-0002-7889-1996БорисМельников Санкт-Петербургский политехнический университет Петра Великого[email protected] Политехническая улица, 29 Моделирование разрушения связи между арматурными стержнями и бетоном.
Автоматический анализ был выполнен в SCAD, который реализует метод конечных элементов (FEM). Результаты исследования демонстрируют достоинства и недостатки описанных методов, а также функциональные возможности SCAD при решении задач динамики взрыва. 10.5862 / MCE.45.3 Типы взрывов структурная динамикаквазистатический методимпульсное воздействиепрямая интеграциядифракция волнFEMSCADhttps: // engstroy .spbstu.ru / article / 2014.45.3 / 03.pdfRARRUS23-40БенинАндрейПетербургский государственный университет путей сообщенияБенин[email protected]СеменовАртемДрезденский технологический университет[email protected]СеменовСергей Петра Великого Санкт-Петербургский политехнический университет[email protected] Политехническая улица, 29 67017517050000-0002-7889-1996БорисМельников Санкт-Петербургский политехнический университет Петра Великого[email protected] Политехническая улица, 29 Моделирование разрушения связи между арматурными стержнями и бетоном. Часть 2. Модели без учета разрыва связи Для повышения точности оценки прочности действующих железобетонных конструкций рационально использовать модель с дискретным расположением арматурных стержней с фактическими характеристиками сцепления с арматурой бетона.Проблема вытягивания арматурного стержня из бетонного блока актуальна для практики, так как представляет собой наиболее распространенный метод экспериментальной оценки характеристик сцепления железобетона. Разрушение связки при вытягивании арматуры из бетона — сложный многоступенчатый процесс, характеризующийся наличием неоднородной и неупругой деформации, разрывом адгезионных связей, зарождением и распространением трещин различной формы и ориентации, наличием контактных и трибологических явления.Нелинейные конечно-элементные решения вытягивания арматурного стержня из задачи о бетонном блоке были получены с использованием различных моделей поведения сцепления и растрескивания бетона. Приведено и обсуждено сравнение полученных численных результатов с экспериментальными данными.
Часть 2. Модели без учета разрыва связи Для повышения точности оценки прочности действующих железобетонных конструкций рационально использовать модель с дискретным расположением арматурных стержней с фактическими характеристиками сцепления с арматурой бетона.Проблема вытягивания арматурного стержня из бетонного блока актуальна для практики, так как представляет собой наиболее распространенный метод экспериментальной оценки характеристик сцепления железобетона. Разрушение связки при вытягивании арматуры из бетона — сложный многоступенчатый процесс, характеризующийся наличием неоднородной и неупругой деформации, разрывом адгезионных связей, зарождением и распространением трещин различной формы и ориентации, наличием контактных и трибологических явления.Нелинейные конечно-элементные решения вытягивания арматурного стержня из задачи о бетонном блоке были получены с использованием различных моделей поведения сцепления и растрескивания бетона. Приведено и обсуждено сравнение полученных численных результатов с экспериментальными данными. Первая часть статьи посвящена моделям с учетом разрывности связи. Вторая часть касается моделей без явного учета разрывов.10.5862 / MCE.45.4 деградация железобетонной связиматематические моделиимоделирование конечных элементовиспытание на вытяжку трещины повреждениеотказ https://engstroy.spbstu.ru/article/2014.45.4/04.pdfRARRUS41-52SelyaevVladimirOgarev Mordovia State University [email protected] Мордовский государственный университет[email protected] Мордовский государственный университет газообразная среда) грузоподъемность и жесткость при эксплуатации снижаются.В статье рассматриваются проблемы оценки остаточного ресурса и долговечности бетонных конструкций. Проведены экспериментальные исследования взаимодействия образцов бетона с агрессивной сульфатной средой. Измеряя микротвердость, изохроны разрушения, что позволяет экспериментам определять скорость продвижения фронта разрушения вглубь продукта; получены интенсивные изменения прочностных свойств поверхности материала и другие характеристики, характеризующие процесс деградации.
Первая часть статьи посвящена моделям с учетом разрывности связи. Вторая часть касается моделей без явного учета разрывов.10.5862 / MCE.45.4 деградация железобетонной связиматематические моделиимоделирование конечных элементовиспытание на вытяжку трещины повреждениеотказ https://engstroy.spbstu.ru/article/2014.45.4/04.pdfRARRUS41-52SelyaevVladimirOgarev Mordovia State University [email protected] Мордовский государственный университет[email protected] Мордовский государственный университет газообразная среда) грузоподъемность и жесткость при эксплуатации снижаются.В статье рассматриваются проблемы оценки остаточного ресурса и долговечности бетонных конструкций. Проведены экспериментальные исследования взаимодействия образцов бетона с агрессивной сульфатной средой. Измеряя микротвердость, изохроны разрушения, что позволяет экспериментам определять скорость продвижения фронта разрушения вглубь продукта; получены интенсивные изменения прочностных свойств поверхности материала и другие характеристики, характеризующие процесс деградации. В статье исследуются механизмы коррозионных процессов в железобетоне в условиях сульфатной коррозии. В статье предлагается расчетная модель и метод, прогнозирующий долговечность бетонных конструкций. 10.5862 / MCE.45.5 Durabilitysulfate коррозия бетонаразрушение функции деградации цемента. Университет в Кошицемохамаде[email protected] Технический университет в Кошицемичале[email protected]Анализ сопротивления тонкостенных холодногнутых сжатых стальных стержня с замкнутым поперечным сечением. Часть 2 В части 1 статьи представлена фундаментальная информация об экспериментальных и теоретических исследованиях, направленных на определение сопротивления тонкостенных холодногнутых сжатых стальных элементов с замкнутым поперечным сечением [1]. Исследуемые элементы были изготовлены из однородного материала. Теоретический анализ был направлен на определение сопротивления упомянутых элементов в соответствии с европейскими и словацкими стандартами, в то время как экспериментальное исследование было направлено на проверку теоретических результатов и изучение поведения упомянутых выше элементов во время процесса нагружения [2].
В статье исследуются механизмы коррозионных процессов в железобетоне в условиях сульфатной коррозии. В статье предлагается расчетная модель и метод, прогнозирующий долговечность бетонных конструкций. 10.5862 / MCE.45.5 Durabilitysulfate коррозия бетонаразрушение функции деградации цемента. Университет в Кошицемохамаде[email protected] Технический университет в Кошицемичале[email protected]Анализ сопротивления тонкостенных холодногнутых сжатых стальных стержня с замкнутым поперечным сечением. Часть 2 В части 1 статьи представлена фундаментальная информация об экспериментальных и теоретических исследованиях, направленных на определение сопротивления тонкостенных холодногнутых сжатых стальных элементов с замкнутым поперечным сечением [1]. Исследуемые элементы были изготовлены из однородного материала. Теоретический анализ был направлен на определение сопротивления упомянутых элементов в соответствии с европейскими и словацкими стандартами, в то время как экспериментальное исследование было направлено на проверку теоретических результатов и изучение поведения упомянутых выше элементов во время процесса нагружения [2]. Часть 2 посвящена численному анализу достигнутых результатов, а также 3D-моделированию и моделированию экспериментальных испытаний. 10.5862 / MCE.45.6 Тонкостенные профили холодного формования начальные дефекты https://engstroy.spbstu.ru/article/ 2014.45.6 / 06.pdfRARRUS59-70ЭйгенсонСанкт-Петербургский политехнический университет им. Сергея Петра Великого[email protected] 195251, Россия, , Санкт-Петербург, ул. Политехническая, 29
Корихин Николай Санкт-Петербургский политехнический университет Петра ВеликогоKor440 @ mail333.com Россия , 195251, Санкт-Петербург, ул. Политехническая, 29
Головин Александр Петра Великого Санкт-Петербургский политехнический университет [email protected] 195251, Россия, , Санкт-Петербург, ул. Политехническая, 29
Экспериментальное исследование напряженного состояния некоторых принципиальных конструкций крупных гидроэнергетических зданий В статье проводится экспериментальное исследование напряженного состояния принципиальных конструкций гидроэнергетических зданий: напорной «вилки» магистрального гидроагрегата и упруго закрепленных тяжелых арок, ослабленных круглым сечением.
Часть 2 посвящена численному анализу достигнутых результатов, а также 3D-моделированию и моделированию экспериментальных испытаний. 10.5862 / MCE.45.6 Тонкостенные профили холодного формования начальные дефекты https://engstroy.spbstu.ru/article/ 2014.45.6 / 06.pdfRARRUS59-70ЭйгенсонСанкт-Петербургский политехнический университет им. Сергея Петра Великого[email protected] 195251, Россия, , Санкт-Петербург, ул. Политехническая, 29
Корихин Николай Санкт-Петербургский политехнический университет Петра ВеликогоKor440 @ mail333.com Россия , 195251, Санкт-Петербург, ул. Политехническая, 29
Головин Александр Петра Великого Санкт-Петербургский политехнический университет [email protected] 195251, Россия, , Санкт-Петербург, ул. Политехническая, 29
Экспериментальное исследование напряженного состояния некоторых принципиальных конструкций крупных гидроэнергетических зданий В статье проводится экспериментальное исследование напряженного состояния принципиальных конструкций гидроэнергетических зданий: напорной «вилки» магистрального гидроагрегата и упруго закрепленных тяжелых арок, ослабленных круглым сечением. дыры.Точное знание напряженно-деформированного состояния (НДС) конструкции на этапе проектирования имеет важное значение для долговечности конструкции. Аналитические методы расчетов, в том числе численные (например, метод конечных элементов — МКЭ), развиваются и совершенствуются. Экспериментальные методы исследования напряженно-деформированного состояния конструкций на моделях дополняют аналитические расчеты и эффективно сочетаются с ними. Исследования проводились методом «замораживания» деформаций фотоупругости с использованием способности эпоксидных полимеров сохранять постоянную оптическую анизотропию, возникающую при нагружении модели, после разгрузки.Полученные результаты позволили уточнить распределение напряжений в значимых критических сечениях конструкции, оценить достоверность оценок концентраций напряжений по отверстиям в арках, выполненных методом конечных элементов. «Замораживающая» напряженная концентрация государственного напряжения https://engstroy.spbstu.ru/article/2014.
дыры.Точное знание напряженно-деформированного состояния (НДС) конструкции на этапе проектирования имеет важное значение для долговечности конструкции. Аналитические методы расчетов, в том числе численные (например, метод конечных элементов — МКЭ), развиваются и совершенствуются. Экспериментальные методы исследования напряженно-деформированного состояния конструкций на моделях дополняют аналитические расчеты и эффективно сочетаются с ними. Исследования проводились методом «замораживания» деформаций фотоупругости с использованием способности эпоксидных полимеров сохранять постоянную оптическую анизотропию, возникающую при нагружении модели, после разгрузки.Полученные результаты позволили уточнить распределение напряжений в значимых критических сечениях конструкции, оценить достоверность оценок концентраций напряжений по отверстиям в арках, выполненных методом конечных элементов. «Замораживающая» напряженная концентрация государственного напряжения https://engstroy.spbstu.ru/article/2014. 45.7/07.pdfRARRUS71-79LiangLiСанкт-Петербургский политехнический университет Петра Великогоhitliliang @ gmail.com Политехническая, 29 ШхинекКарлПетра Великого Санкт-Петербургский политехнический университет [email protected] Политехническая, 29 В данной статье исследуется динамическое взаимодействие льда и наклонной конструкции Действие льда на наклонные конструкции. Ранее эта задача рассматривалась много раз, но, как правило, учитывались только квазистатические и двумерные решения. В частности, эти предположения предложены в широко используемом решении Кроасдейла для наклонных конструкций.Некоторые улучшения 2D-решения, предложенные Croasdale, не могут учесть всех особенностей 3D-явления. В статье используется численное исследование задачи на основе программы ANSYS. Рассмотрены следующие темы: а) в чем разница максимальных ледовых нагрузок в 3D и 2D решениях; б) как динамика процесса взаимодействия льда и конструкции влияет на нагрузки; в) как ледовая нагрузка зависит от основных факторов — прочности льда, толщины льда и угла наклона конструкции.
45.7/07.pdfRARRUS71-79LiangLiСанкт-Петербургский политехнический университет Петра Великогоhitliliang @ gmail.com Политехническая, 29 ШхинекКарлПетра Великого Санкт-Петербургский политехнический университет [email protected] Политехническая, 29 В данной статье исследуется динамическое взаимодействие льда и наклонной конструкции Действие льда на наклонные конструкции. Ранее эта задача рассматривалась много раз, но, как правило, учитывались только квазистатические и двумерные решения. В частности, эти предположения предложены в широко используемом решении Кроасдейла для наклонных конструкций.Некоторые улучшения 2D-решения, предложенные Croasdale, не могут учесть всех особенностей 3D-явления. В статье используется численное исследование задачи на основе программы ANSYS. Рассмотрены следующие темы: а) в чем разница максимальных ледовых нагрузок в 3D и 2D решениях; б) как динамика процесса взаимодействия льда и конструкции влияет на нагрузки; в) как ледовая нагрузка зависит от основных факторов — прочности льда, толщины льда и угла наклона конструкции. 10.5862 / MCE.45.8 ширина конструкции ледяная нагрузка сваи наклонная гидротехника ANSYShttps: //engstroy.spbstu.ru/article/2014.45.8/08.pdfRARRUS80-89555867100000000-0002-6498-5043SultanovTakhirjonT Ташкентский институт ирригации и механизации сельского хозяйства [email protected] Ташкент, Республика Узбекистан ХоджаевДадаханТашкентский институт ирригации и механизации сельского хозяйстваru Узбекистан, 100000 , ул. Кори Ниезий, 39, Ташкент
Оценка динамического поведения гетерогенных систем с учетом нелинейных вязкоупругих свойств грунта В статье подробно рассматривается современное состояние задачи расчета нелинейных реологических свойств грунта при оценке напряженно-деформированного состояния грунтовых конструкций. . Приведены математическая постановка, методы и алгоритмы оценки динамического поведения земляных конструкций с учетом неоднородных особенностей конструкции, линейных, нелинейно-упругих, нелинейно-вязкоупругих свойств грунта при различных динамических воздействиях.
10.5862 / MCE.45.8 ширина конструкции ледяная нагрузка сваи наклонная гидротехника ANSYShttps: //engstroy.spbstu.ru/article/2014.45.8/08.pdfRARRUS80-89555867100000000-0002-6498-5043SultanovTakhirjonT Ташкентский институт ирригации и механизации сельского хозяйства [email protected] Ташкент, Республика Узбекистан ХоджаевДадаханТашкентский институт ирригации и механизации сельского хозяйстваru Узбекистан, 100000 , ул. Кори Ниезий, 39, Ташкент
Оценка динамического поведения гетерогенных систем с учетом нелинейных вязкоупругих свойств грунта В статье подробно рассматривается современное состояние задачи расчета нелинейных реологических свойств грунта при оценке напряженно-деформированного состояния грунтовых конструкций. . Приведены математическая постановка, методы и алгоритмы оценки динамического поведения земляных конструкций с учетом неоднородных особенностей конструкции, линейных, нелинейно-упругих, нелинейно-вязкоупругих свойств грунта при различных динамических воздействиях. Результатом динамического расчета является исследование нестационарных вынужденных колебаний ряда земляных плотин с учетом нелинейных вязкоупругих свойств грунта и неоднородных особенностей конструкции. Полученные результаты позволяют выявить ряд механических эффектов, имеющих теоретическое и практическое значение. Выявлено, что при высокочастотном интенсивном воздействии характер колебаний конструкций, имеющих низкочастотный спектр, имеет три ярко выраженных стадии: начальную, характеризующуюся малыми амплитудами, переходную, когда происходит раскачивание конструкции; и стадия свободных колебаний с реализованной амплитудой и частотой собственных колебаний.Несмотря на высокую интенсивность высокочастотного воздействия, вызывающего большие напряжения в теле обсуждаемых плотин, расчет нелинейной деформации материала не сильно искажает картину линейно-упругой конструкции. 10.5862 / MCE.45.9 реология плотины, неоднородность, нелинейность, вязкоупругость, ускорение, гидростатическое давление, кинематический эффект https://engstroy.
Результатом динамического расчета является исследование нестационарных вынужденных колебаний ряда земляных плотин с учетом нелинейных вязкоупругих свойств грунта и неоднородных особенностей конструкции. Полученные результаты позволяют выявить ряд механических эффектов, имеющих теоретическое и практическое значение. Выявлено, что при высокочастотном интенсивном воздействии характер колебаний конструкций, имеющих низкочастотный спектр, имеет три ярко выраженных стадии: начальную, характеризующуюся малыми амплитудами, переходную, когда происходит раскачивание конструкции; и стадия свободных колебаний с реализованной амплитудой и частотой собственных колебаний.Несмотря на высокую интенсивность высокочастотного воздействия, вызывающего большие напряжения в теле обсуждаемых плотин, расчет нелинейной деформации материала не сильно искажает картину линейно-упругой конструкции. 10.5862 / MCE.45.9 реология плотины, неоднородность, нелинейность, вязкоупругость, ускорение, гидростатическое давление, кинематический эффект https://engstroy. spbstu.ru/article/2014.45.9/09.pdf
Расчет надежности основания фундамента по несущей способности (смещению) при эксплуатации Предложены новые методы расчета надежности фундамента по критерию смещения при воздействии на основание горизонтальных (смещающих) сил.Исходная статистическая информация ограничена. Случайные величины в расчетной модели описываются функциями распределения возможностей (из теории возможностей), функциями распределения, полученными из неравенства Чебышева; сочетание функций. Объем измерений контролируемых параметров (статистической информации) для расчета надежности на практике невелик и иногда не позволяет провести их статистический анализ с использованием вероятностно-статистических методов расчета надежности фундаментов.Значительное снижение надежности основания фундамента вызывает увлажнение почвы, как, например, сейчас на Дальнем Востоке Российской Федерации. При недостатке времени на сбор информации для оценки безопасности зданий и сооружений можно использовать разработанные методики.
spbstu.ru/article/2014.45.9/09.pdf
Расчет надежности основания фундамента по несущей способности (смещению) при эксплуатации Предложены новые методы расчета надежности фундамента по критерию смещения при воздействии на основание горизонтальных (смещающих) сил.Исходная статистическая информация ограничена. Случайные величины в расчетной модели описываются функциями распределения возможностей (из теории возможностей), функциями распределения, полученными из неравенства Чебышева; сочетание функций. Объем измерений контролируемых параметров (статистической информации) для расчета надежности на практике невелик и иногда не позволяет провести их статистический анализ с использованием вероятностно-статистических методов расчета надежности фундаментов.Значительное снижение надежности основания фундамента вызывает увлажнение почвы, как, например, сейчас на Дальнем Востоке Российской Федерации. При недостатке времени на сбор информации для оценки безопасности зданий и сооружений можно использовать разработанные методики. В данной работе такая ситуация иллюстрируется примером.ru / article / 2014.45.10 / 10.pdf
В данной работе такая ситуация иллюстрируется примером.ru / article / 2014.45.10 / 10.pdfЭкспонатов
11.12 Галерея в Центре современного искусства Винзавод:
Из Сибири с любовью: картины и арт-объекты Дамира Муратова, до 30 июня. Адрес: 4-й Сыромятнический переулок, дом 1, корп. 6. М. Чкаловская, Курская. С полудня до 20:00, выходной — пн. 495-940-6471, www.11-12.ru
Литературный музей ХХ века:
Сказки Великого Шелкового Пути: современные иллюстрации к народным сказкам, к 30 июня.Адрес: Трубниковский переулок, 17. М. Баррикадная. Касса работает с 11:00 до 17:30, чт. С 13 до 19:30, выходной — пн. и последний день месяца. 495-695-4618, www.goslitmuz.ru/ru/ostroukhov-museum
Академия художеств:
Владимир Мочалов: карикатуристические портреты в графике и живописи, Вс. Адрес: Пречистенка, 21. М. Кропоткинская. С полудня до 20:00, вс. с полудня до 19:00, выходной — пн. 495-637-4771, www. rah.ru
rah.ru
Минералогический музей Александра Ферсмана:
MT PICK Постоянная экспозиция: собрание минералов со всего мира.Адрес: Ленинский проспект, 18, корп. 2. М. Октябрьская, Ленинский проспект, далее любым автобусом до Больницы Святителя Алексия. С 11.00 до 16.00, выходной — пн. и вт. 495-954-3900, www.fmm.ru
Музей-квартира Александра Гольденвейзера:
Мемориальная квартира выдающегося русского пианиста и композитора, постоянная экспозиция. Адрес: ул. Тверская, 17, кв. 110. М. Тверская. Открыто ср. с полудня до 16:00 Экскурсии по предварительной записи. 495-629-2929, www.glinka.museum/about/apartment_museum_goldenweiser/
Дом-музей Александра Герцена:
Небольшой особняк, где находится русский публицист и философ Александр Герцен (1812-70), наиболее известный своей автобиографической книгой «Мое прошлое и мысли» и социальным романом «Кто виноват?» жили до отъезда из России.Адрес: Сивцев Вражек, 27. М. Кропоткинская, Смоленская. Касса работает с 11:00 до 17:30, чт. С 14 до 19:30, выходной — пн. и последний день месяца. 499-241-5859, www.goslitmuz.ru/ru/herzen-museum
М. Кропоткинская, Смоленская. Касса работает с 11:00 до 17:30, чт. С 14 до 19:30, выходной — пн. и последний день месяца. 499-241-5859, www.goslitmuz.ru/ru/herzen-museum
Дом-музей Александра Островского:
Постоянная экспозиция о жизни и творчестве русского драматурга XIX века, который практически в одиночку создавал русский национальный репертуар. Адрес: Малая Ордынка, 9, корп. 1. М. Полянка, Третьяковская.Касса работает с полудня до 18:30, чт. С 13 до 20:30, выходной — пн, вт. и последний пт. месяца. 495-953-8684, www.bakhrushin.theatre.ru/branches/dmo
Музейно-выставочный зал-квартира Александра Пушкина:
Пушкин и Москва: постоянная экспозиция. Адрес: Арбат, 55/32, вход со стороны Денежного переулка. М. Смоленская. Касса работает с 10.00 до 17.30, чт. с полудня до 20:30, выходной — пн, вт. и последняя пятница месяца. 499-241-9295, www.pushkinmuseum.ru
ГМИИ А.С.Пушкина:
Открытое хранилище редких книг, картин, графики, фарфора, бронзы, керамики, генеалогических материалов и частных коллекций.
Пушкин и его эпоха (Пушкин и его эпоха): постоянная экспозиция.
Пушкин и семья Романовых (Пушкин и Семья Романовых): экспонат из музейных собраний и архивов, до 14 июля.
Сказки Пушкина (Сказки Пушкина): постоянная экспозиция.
Vita Nova: A New Life of Old Legends (Новая Жизнь Старых Легенд): иллюстрации к европейским средневековым эпосам Игоря Ганзенко и Бориса Забирохина, к 30 июля.
Искусство Западной Европы: живопись, графика и скульптура из собрания музея, до 1 июля. Адрес: ул. Пречистенка. М. Кропоткинская. Касса работает с 10.00 до 17.30, чт. с полудня до 20:30, выходной — пн. и последний пт. месяца. 495-637-5674, www.pushkinmuseum.ru
Мемориальный кабинет Анатолия Луначарского:
Постоянная экспозиция: выставка, посвященная Анатолию Луначарскому (1875-1933) — русскому писателю, переводчику, публицисту, искусствоведу, политику, первому советскому комиссару просвещения, ответственному за культуру и образование. Адрес: Денежный переулок, 9/5, кв. 1. М. Смоленская. По предварительной записи 499-241-8873, www.goslitmuz.ru/ru/lunacharsky-museum
Адрес: Денежный переулок, 9/5, кв. 1. М. Смоленская. По предварительной записи 499-241-8873, www.goslitmuz.ru/ru/lunacharsky-museum
Музей-квартира Андрея Белого:
Постоянная экспозиция: личные вещи, портреты и редкие архивные материалы известного поэта и писателя Серебряного века. Адрес: Арбат, 55. М. Смоленская. Касса работает с 10.00 до 17.30, чт. с полудня до 20:30, выходной — пн, вт. и последняя пятница месяца. 499-241-9295, www.pushkinmuseum.ru, kvartira-belogo.guru.ru
Музей древнерусской культуры и искусства имени Андрея Рублева:
Постоянная экспозиция: иконы, настенная живопись, предметы декоративно-прикладного искусства, рукописи и книги на черных буквах в отреставрированных зданиях бывшего Спасо-Андроникова монастыря. Адрес: Андроньевская площадь, 10. М. Римская, Площадь Ильича. Касса работает с 11:00 до 17:15, закрыта в среду. и последняя пятница месяца. 495-678-1467, www.rublev-museum.ru
Музейно-общественный центр Андрея Сахарова:
Постоянная экспозиция, посвященная наследию этого правозащитника и физика, представляет хронику политических репрессий против советских граждан с 1917 по 1980-е годы с фотографиями и документальными материалами. Адрес: Земляной Вал, 57, корп. 6. М. Курская. Касса работает с 11.00 до 19.00, закрыта пн. 495-623-4401 / 4420, www.sakharov-center.ru
Адрес: Земляной Вал, 57, корп. 6. М. Курская. Касса работает с 11.00 до 19.00, закрыта пн. 495-623-4401 / 4420, www.sakharov-center.ru
Школа акварели Андрияки:
NEW Страницы истории Дома Романовых: живопись, графика, фарфор и уникальные документы из редких собраний, пт. до 21 июня. Расположен по адресу Гороховский переулок, 17/1. М. Курская. С 11.00 до 19.00, выходной — пн. и вт.499-267-5435, www.andriaka.ru
Музей-студия Анны Голубкиной:
Коллекция скульптур этого выдающегося мастера художественной культуры Серебряного века, постоянная экспозиция. Адрес: Большой Левшинский переулок, 12. М. Парк Культуры, Смоленская. Ср., Чт. и пт. с полудня до 18:00, сб. и вс. 10.00 — 16.00, выходной — пн. и последняя пятница месяца. 495-637-2564 / 5682, www.tretyakovgallery.ru/ru/museum/branch/museum_studio_golubkina
Дом-музей Антона Чехова:
Постоянная экспозиция: московская квартира писателя с небольшой экспозицией фотографий и рукописей. Адрес: ул. Садовая-Кудринская, 6. М. Баррикадная. Вт, чт, сб. С 11.00 до 18.00, ср, пт. С 14 до 20, выходной — пн. и последний день месяца. 495-691-6154 / 3837, www.goslitmuz.ru/ru/chekhov-museum
Адрес: ул. Садовая-Кудринская, 6. М. Баррикадная. Вт, чт, сб. С 11.00 до 18.00, ср, пт. С 14 до 20, выходной — пн. и последний день месяца. 495-691-6154 / 3837, www.goslitmuz.ru/ru/chekhov-museum
Мемориальный музей А.П. Чехова в Мелихово:
Постоянная экспозиция: дом обставлен более или менее так, как он был, когда писатель жил в нем с 1892 по 1899 год и написал знаменитую пьесу «Чайка».
Анатомия постановки (Анатомия Спектакля): Эта выставка иллюстрирует процесс постановки Константином Станиславским пьес Чехова в МХАТе в течение августа.Находится в Мелихово, от Курского вокзала до Чехова, далее автобус 25. 10-17, выходной — пн. и последняя пятница месяца. 499-270-7991, www.chekhov-melikhovo.com
Аптекарский огородский сад:
В садах (В Садах): инсталляция Ивана Горшкова, Ильи Романова и Ксении Сорокиной к 14 июля. Расположена на проспекте Мира, 26. М. Проспект Мира. Касса открыта с 10:00 до 21:30. 495-680-5880 / 6765/7222, hortus. ru
ru
Музей-усадьба Архангельское:
Дворцово-парковый ансамбль XVIII века (Дворцово-Парковый Ансамбль 18 Века) представляет произведения из собрания графа Юсупова, постоянную экспозицию.Расположен в поселке Архангельское, на 5-м километре Ильинского шоссе. М. Тушинская, далее автобусом 549 до Архангельского или автобусом 151 до Санатория. Парк открыт с 10:00 до 18:00. Выставки открыты с 10 до 17, сб, вс. и праздничные дни с 10.00 до 18.00, выходной — пн, вт. и последняя ср. месяца. 495-797-5409, www.arhangelskoe.su
Art4.ru:
Современное русское искусство собрано Игорем Маркиным и хранится в частном музее. Адрес: Хлыновский тупик, 4.М. Тверская. По приложению 499-136-5656, art4.ru
Центр дизайна ArtPlay:
Mech Mat (Сопромат): выставка произведений искусства из необычных материалов, до 18 июня.
NEW Студенческий художественный бал: работы московских студентов-художников с 14 июня по 14 июля.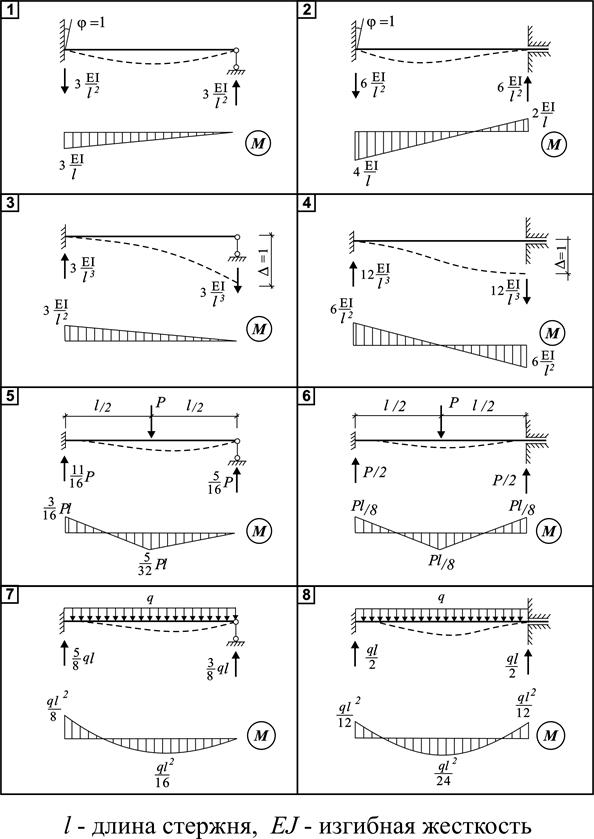 Адрес: Нижняя Сыромятническая ул., 10, корп. 7. М Курская. С полудня до 20:00. 8-926-619-2889, 495-620-0882, www.artplay.ru
Адрес: Нижняя Сыромятническая ул., 10, корп. 7. М Курская. С полудня до 20:00. 8-926-619-2889, 495-620-0882, www.artplay.ru
Театральный музей имени А.А. Бахрушина:
Золотой век русского театра (Золотой Век Русского Театра): афиши, фотографии, костюмы и другие памятные вещи известных русских актеров и режиссеров последних двух веков, постоянная экспозиция.Адрес: 31/12 Ul. Бахрушина. М. Павелецкая. Касса работает с полудня до 18:30, чт. С 13 до 20:30, выходной — пн, вт. и последний пт. месяца 495-953-4470 / 4848, www.gctm.ru/museum
Музей Бориса Пастернака:
Постоянная экспозиция: Знаменитый дачный дом, где автор «Доктора Живаго» выдержал нападения после присуждения Нобелевской премии по литературе 1958 года. Расположены в Переделкино, 3 Ул. Павленко. От Киевского вокзала до Переделкино. Касса открыта 11 а.м. до 17:30, чт. С 13 до 19:30, выходной — пн. и последний день месяца. 495-934-5175, www.pasternakmuseum.ru/index_angl.html
Центр фотографии имени братьев Люмьер:
MT PICK Игорь Пальмин показывает архитектурные фотографии из серии «Свет» до 30 июня.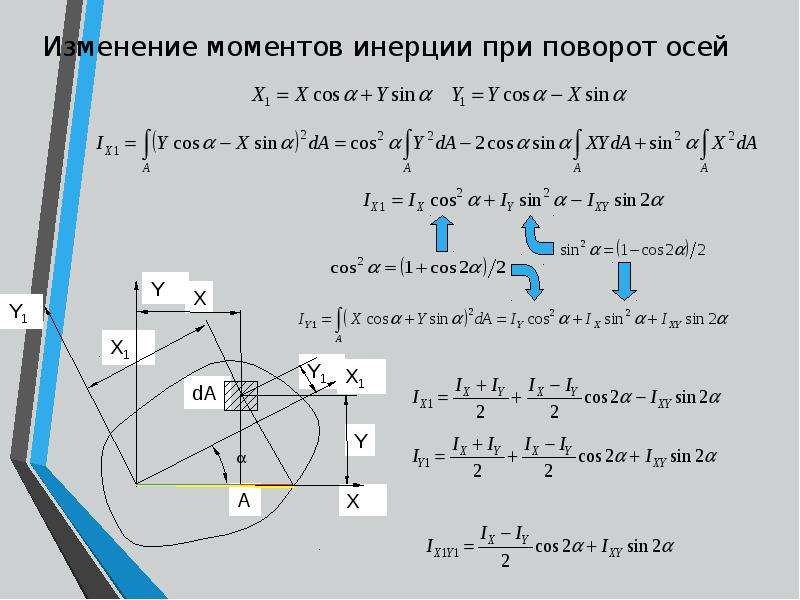
MT PICK Лив Ульманн и Ингмар Бергман: фотографии, до 30 июня. Расположены по адресу: Болотная набережная, 3, корп. 1. М. Кропоткинская. С полудня до 21:00, сб.и вс. С 11.00 до 21.00, выходной — пн. 495-228-9878, www.lumiere.ru
Булгаков Дом:
Odd Flat: Коммунальная квартира, в которой Михаил Булгаков жил с 1921 по 1924 год, и которая стала прообразом «Странной квартиры», где Воланд поселился со своим двором. Постоянные экспозиции, спектакли, выставки и экскурсии, посвященные жизни и творчеству Михаила Булгакова и его роману «Мастер и Маргарита». Адрес: ул. Большая Садовая, 10. через арку, кв.50. М. Маяковская. 13 до 23 часов, пт. и сб. 13:00 до часу ночи вход свободный. 495-970-01619, www.dombulgakova.ru
Музей Храма Христа Спасителя:
История Храма Христа Спасителя: постоянная экспозиция. Адрес: 15 Ul. Волхонка. М. Кропоткинская. С 10:00 до 18:00, выходной — последний понедельник месяца. 495-637-1276, 495-924-8058 / 8490, www. xxc.ru/complex/museum/index.htm, www.xxc.ru/english/index.htm
Галерея классической фотографии:
Eurasian Ways (Со стороны Евразии): фотографии из Италии и Южной Кореи, до 30 июня.Адрес: Саввинская набережная, 23, корп. 1. ср. к вс. с полудня до 21:00, выходной — пн. и вт. 495-510-7713 / 14, classic-gallery.ru
Галерея Connaisseur:
NEW Отгоо Бадаам: портреты, пейзажи и жанровые сцены маслом монгольского художника до 5 июля. Адрес: ул. Мясницкая, 22, корп. 1. М. Чистые пруды. Пн. по чт. 11.00-19.00, пт. и сб. с полудня до 19:00, выходной — вс. 495-623-1029, www.connaisseur.ru
Дарвиновский музей:
Botanic Art Book: международная интерактивная выставка до 23 июня.
Dreams (Снай): Александр Авалов показывает фотографии спящих животных, до 17 августа.
«Пройдите путь эволюции»: новая интерактивная мультимедийная выставка, постоянная экспозиция.
Постоянные экспозиции: «Макроэволюция», «Микроэволюция», «Зоогеография», «Разнообразие жизни на Земле», «Живая выставка» и другие.
NEW Сто и одна профессия овчарок (Сто и одна профессия овчарки): скульптура, живопись и фотография, пт.по 25 августа. Адрес: 57 Ul. Вавилова. М. Академическая. Касса работает с 10.00 до 18.00, чт. С 13:00 до 21:00 закрыто пн. и последний пт. месяца. 499-134-6124, 783-2253, www.darwin.museum.ru/eng
Дом Иконы На Спиридоновке:
Иконы и другие произведения христианского искусства из частной коллекции, постоянная экспозиция.
Russian Moderne (Русский модерн): произведения русских художников рубежа ХХ веков до ноября.
Романовы.Падение династии (Романовы. Падения династий): личные вещи, произведения искусства и архивные документы до 19 декабря. Находится на ул. Спиридоновка. М. Арбатская, Тверская. С полудня до 22:00. 495-690-5474 / 2660, www.dom-ikony.ru
Музей английского двора:
Русско-английские торговые отношения (Русско-английские торговые отношения): это здание, культурный и торговый центр английской общины в Москве 16-17 веков, отражает развитие русско-английских отношений на протяжении веков, постоянная экспозиция.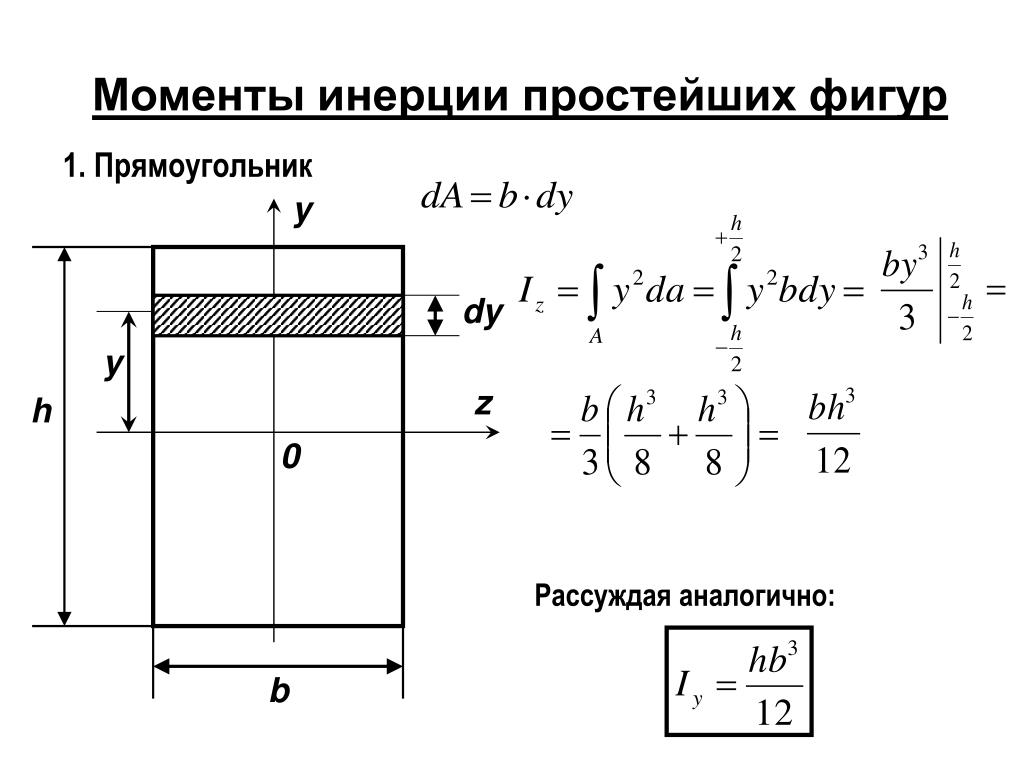 Адрес: ул. Варварка, 4А. М. Китай-город. Касса работает с 10.00 до 17.30, чт. С 13 до 20:30, выходной — пн. и последняя пятница месяца. 495-698-3952, www.mosmuseum.ru/museum-menu-english-dvor.html
Адрес: ул. Варварка, 4А. М. Китай-город. Касса работает с 10.00 до 17.30, чт. С 13 до 20:30, выходной — пн. и последняя пятница месяца. 495-698-3952, www.mosmuseum.ru/museum-menu-english-dvor.html
Выставочный зал Федерального архива:
Русские Императрицы: Мода и Стиль (Русские Императрицы: Мода и Стиль): костюмы, украшения, аксессуары, картины, гравюры, рисунки, фотографии и другие предметы, Вс. Адрес: Большая Пироговская ул., 17.М. Фрунзенская. Кассы открыты с полудня до 17:15, закрыты пн. и вт. 495-580-8825, 499-245-1925, www.rusarchives.ru/evants/exhibitions/index.shtml
Изобразительное искусство:
«Личное Пространство»: картины Дмитрия Шорина, до 20 июня. Находится по адресу: Большая Садовая ул., Д. 3, корп. 10, во дворе ресторана «Пекин». М. Маяковская. С 11.00 до 18.00, сб. с полудня до 18:00, выходной — вс. 499-251-7649, www.galleryfineart.ru
Музей народной графики:
Русский лубок: постоянная экспозиция. Адрес: Малый Головин переулок, 10. М. Сухаревская, Тургеневская, Сретенский бульвар. Вт, ср. Пт. 10.00 — 18.00, чт. С 14 до 21, сб, вс. с полудня до 17:00, выходной — пн. 495-5608-5182, www.russianlubok.ru
Адрес: Малый Головин переулок, 10. М. Сухаревская, Тургеневская, Сретенский бульвар. Вт, ср. Пт. 10.00 — 18.00, чт. С 14 до 21, сб, вс. с полудня до 17:00, выходной — пн. 495-5608-5182, www.russianlubok.ru
Дом-музей Федора Шаляпина:
Постоянная экспозиция: небольшой экспонат, посвященный великому русскому басу. Адрес: Новинский бульвар, 25. М. Баррикадная. Касса открыта вт. и сб. 10.00-17.00, ср. и чт. С 11:30 до 18:00.м., вс. 10.00-15.30, выходной — пн, пт. и последний день месяца. 495-605-6236, 252-2530, www.shalyapin-museum.org
Музей-квартира Федора Достоевского:
Постоянная экспозиция: небольшая выставка, посвященная автору «Преступление и наказание» и «Братья Карамазовы» в доме, где он родился. Адрес: 2 Ul. Достоевского. М. Новослободская. Касса работает с 11.00 до 17.30, ср. и чт. С 13 до 19:30, выходной — пн. и последний день месяца.495-681-1085, www.goslitmuz.ru/ru/dostoyevsky-museum
Дом Гоголя:
Мемориальный музей и научная библиотека в этом московском доме-усадьбе, где Николай Гоголь провел свои четыре последних года. Адрес: Никитский бульвар, 7А. М. Арбатская. Пн., Ср., Пт. с полудня до 19:00, чт. С 14 до 21, сб. и вс. с полудня до 17:00, вторник выходной. и последний день месяца. 495-9256, www.domgogolya.ru
Адрес: Никитский бульвар, 7А. М. Арбатская. Пн., Ср., Пт. с полудня до 19:00, чт. С 14 до 21, сб. и вс. с полудня до 17:00, вторник выходной. и последний день месяца. 495-9256, www.domgogolya.ru
Усадьба Голицыных:
NEW Визуальный очерк: абстракции Марины Колотвиной, Валерия Колотвина, Константина Егорова и Михаила Медведева, до 28 июня.Адрес: Козицкий переулок, 5. М. Пушкинская. С 11.00 до 19.00, выходной — сб. и вс. 495-694-0371, sias.ru
Исторический музей:
Бронзовый век (Эпоха бронзы): постоянная экспозиция.
История России с древнейших времен до начала ХХ века (История России с древнеиших времен до начала 20 века): постоянная экспозиция.
Отечественная война 1812 года (Отечественная война 1812 года): дополнение к постоянной экспозиции.
Филиал Исторического музея:
Романовские палаты в Зарядье: аутентичные интерьеры русского боярского дома XVII века, постоянная экспозиция.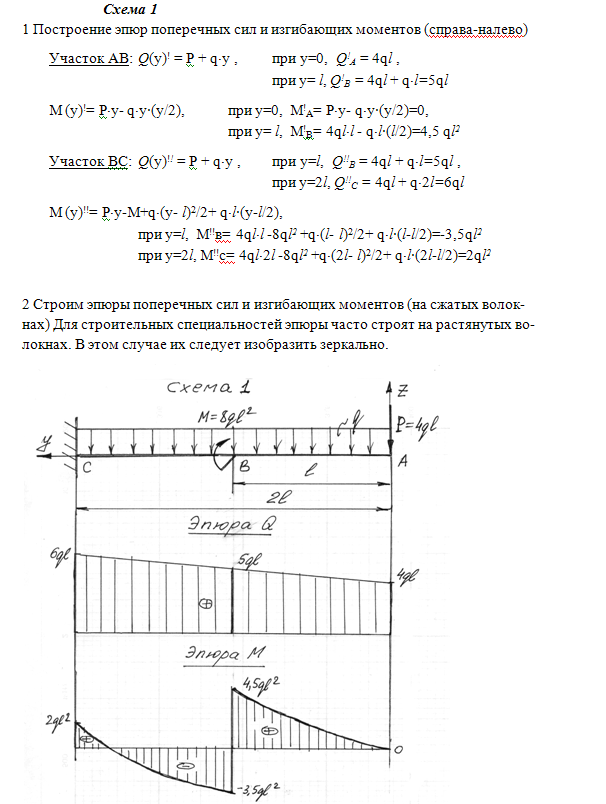 Находится на Красной площади, 1/2. М. Площадь Революции. Касса работает с 10.00 до 17.30, чт. 11.00-20.00, вторник выходной. 495-692-4019, www.shm.ru
Находится на Красной площади, 1/2. М. Площадь Революции. Касса работает с 10.00 до 17.30, чт. 11.00-20.00, вторник выходной. 495-692-4019, www.shm.ru
Музей истории евреев в России:
Постоянная экспозиция: подлинные артефакты, представляющие историю евреев, живших под властью России после трех разделов Польши.Адрес: Перовско-Разумовская аллея, 10, стр.3. М. Динамо. Пн. до ср. и пт. с полудня до 19:00, чт. с полудня до 21:00, вс. с полудня до 17:00, выходной — сб. Вход свободный. 495-656-4571, www.mievr.ru
Международный Центр Рерихов:
Внутреннее путешествие: картины Феодосии, до 16 июня.
Музей Николая Рериха: собрание произведений великого художника и философа, известного прежде всего своими пейзажами Индии, постоянная экспозиция. Адрес: Малый Знаменский переулок, 3/5.М. Кропоткинская. Касса открыта с 11.00 до 18.00, закрыта пн. 499-271-3417 / 20, www.icr.su
Музей Ивана Тургенева:
Москва. Остоженка. Тургенев: постоянная экспозиция о жизни и творчестве любимого писателя, драматурга и поэта. 37 Ul. Остоженка. М. Парк Культуры. Касса работает с 10.00 до 17.30, чт. с полудня до 20:30, выходной — пн, вт. и последняя пятница месяца. 495-695-1078, www.pushkinmuseum.ru
Остоженка. Тургенев: постоянная экспозиция о жизни и творчестве любимого писателя, драматурга и поэта. 37 Ul. Остоженка. М. Парк Культуры. Касса работает с 10.00 до 17.30, чт. с полудня до 20:30, выходной — пн, вт. и последняя пятница месяца. 495-695-1078, www.pushkinmuseum.ru
Еврейский музей и центр толерантности:
История евреев. Эта мультимедийная интерактивная экспозиция посвящена ключевым историческим периодам и начинается в «Начальном театре» с постоянной экспозиции 4D-фильма, основанного на Торе.Адрес: 11 Ul. Образцова, корп. 1А. М. Савеловская, затем две остановки на автобусе №12 до улицы Образцова. Солнце. по чт. с полудня до 22:00, пт. 10.00-15.00 закрыто сб. и еврейские праздники. 495-645-0550, www. jewish-museum.ru
Ходынка Галерея:
Птицы в Москве: фотографии, до 15 июня.
Николай и Сергей Андрияка: пейзажи маслом и акварелью, до 14 июня. Расположен на ул. Левченко. М. Октябрьское поле, автобус 691, 800 до улицы Вершинина. С полудня до 19:00, выходной — пн. и вт. 499-198-7684, www.arthodynka.ru
С полудня до 19:00, выходной — пн. и вт. 499-198-7684, www.arthodynka.ru
Музей-усадьба Коломенское:
Русская царская усадьба: построена между 15 и 17 веками, расположена на высоком берегу Москвы-реки и в настоящее время является архитектурным музеем.
Конюшенный двор (Конюшенный двор): Выставочный комплекс включает в себя конюшни с орловскими и русскими рысаками, каретный двор с экипажами и санями, кузницу и сеновал. Адрес: проспект Андропова, 39.М. Коломенская. С 10.00 до 18.00, выходной — пн. 495-232-6190, mgomz.ru/kolomenskoe
Музей Константина Станиславского:
Постоянная экспозиция: дом, в котором проживал соучредитель МХАТ и создатель знаменитой актерской системы. Адрес: Леонтьевский переулок, 6. М. Тверская. С 11.00 до 18.00, чт. С 11.00 до 21.00, выходной — пн. и вт. 495-629-2855, www.mxat.ru/museum
Дом-музей Корнея Чуковского:
Постоянная экспозиция: Знаменитая дача самого популярного детского поэта России, влиятельного литературного критика и публициста. Расположены в Переделкино, 3 Ул. Серафимовича. От Киевского вокзала до Переделкино. Касса работает с 11:00 до 17:30, чт. С 13 до 19:30, выходной — пн. и последний день месяца. 495-593-2670, goslitmuz.ru/ru/chukovsky-museum
Расположены в Переделкино, 3 Ул. Серафимовича. От Киевского вокзала до Переделкино. Касса работает с 11:00 до 17:30, чт. С 13 до 19:30, выходной — пн. и последний день месяца. 495-593-2670, goslitmuz.ru/ru/chukovsky-museum
Ковчег Галерея:
Май в мае: акварель и живопись Май Митурич (1925-2008), до 6 июля. Адрес: ул. Немчинова. М. Тимирязевская, далее автобус 87 или 206 до гостиницы Молодежная. Касса открыта в 11.00.до 20:15, выходной — пн. 499-977-0044 / 88, www.kovcheg-art.ru
Музей-усадьба Кузьминки:
Музей русской усадебной культуры (Музей Русской Усадебной Культуры): постоянная экспозиция. Находится в парке Кузьминки по адресу Тополевая аллея, 6. М. Рязанский проспект, далее автобус 29. Касса работает с 10.00 до 17.30, выходной — пн. и последний пт. месяца. 495-377-9457, 376-7610, www.kuzminky.ru
Музей Лефортово:
Лефортово.Вехи истории (Лефортово. Вехи Истории): история этого района Москвы, названного в честь ближайшего соратника царя Петра Великого Франца Лефорта, войска которого стояли неподалеку в Немецком квартале, постоянная экспозиция. Адрес: ул. Крюковская, 23. М. Семеновская, Авиамоторная. Касса открыта с 10.00 до 17.30, закрыта пн. и последний пт. месяца. 495-360-0147, www.mosmuseum.ru/museum-menu-lefortovo.html
Адрес: ул. Крюковская, 23. М. Семеновская, Авиамоторная. Касса открыта с 10.00 до 17.30, закрыта пн. и последний пт. месяца. 495-360-0147, www.mosmuseum.ru/museum-menu-lefortovo.html
Музей Льва Толстого:
Постоянная экспозиция: Музей, посвященный автору книг «Война и мир» и «Анны Карениной», имеет три филиала.Адрес: 11 Ul. Пречистенка. М. Кропоткинская. 499-766-9328. Филиал на Пятницкой ул., 12 М. Новокузнецкая. 495-951-5808. Филиал в г. Хамовники, ул. Льва Толстого. М. Парк Культуры. С 11.00 до 17.00, выходной — пн. 499-246-9444. Кассы открыты с 11:00 до 17:30, чт. с полудня до 19:30, выходной — пн. и Последняя пятница месяца. www.tolstoymuseum.org
Музей-усадьба Лопасня-Зачатьевское:
Постоянная экспозиция: парк с семью прудами и главным зданием, сначала Дом Гончарова, а затем Пушкинское гнездо.Экспозиция рассказывает о связях владельцев усадьбы Васильчиковых с Пушкиными, Ланскими и Гончаровыми. Адрес: г. Чехов, ул. Пушкина. М. Южная, далее автобус 365 до Сквера имени Чехова. 10.00-17.00, выходной — пн. и последняя пятница месяца. 496-723-0389, www.chekhov-melikhovo.com/index.php/en/museum-melikhovo/lopasnya
М. Южная, далее автобус 365 до Сквера имени Чехова. 10.00-17.00, выходной — пн. и последняя пятница месяца. 496-723-0389, www.chekhov-melikhovo.com/index.php/en/museum-melikhovo/lopasnya
Люблино-музей-усадьба:
Дворец Дурасовых: прекрасно сохранившаяся усадьба начала XIX века московского помещика Николая Дурасова, постоянная экспозиция.
Дворцово-парковый ансамбль, построенный московским помещиком Николаем Дурасовым, представляет собой образ жизни московского дворянства XIX века, постоянная экспозиция. Адрес: ул. Летняя, 1. М. Волжская. С 10.00 до 18.00, выходной — пн. 499-722-7189, 495-350-1553, mgomz.com, mgomz.ru/lublino
Манеж Выставочный зал:
Чемодан для последнего путешествия (Мой Самый Важный Чемодан): Московская версия немецкой выставки Фрица Рота 2012 года, которая побуждает людей задуматься о своей смертности и о том, что действительно имеет значение и что является устойчивым в жизни и смерти, до июня 26.
Коллектив: Это австрийское аудиовизуальное шоу включает инсталляцию и перформанс LWZ «Ring Ging Bing» и работу luma.laundisch «60 Seconds Somewhere» до 26 июня.
Созерцая смерть (Размышляя о Смерти): работы Джозефа Бойса, Билла Виолы, Феликса Гонсалеса-Торреса, Янга Чжэньчжуна, Он Кавара, Марселя Мита и других, до 30 июня.
MT PICK Дизайн упаковки. Сделано в России (Дизайн упаковки. Сделано в России): до 25 июня дореволюционные торговые марки, редкие образцы бутылок и банок, конструктивистские разработки Владимира Маяковского, Александра Родченко и др.
MT PICK Путешествие Одиссея (Путешествие Одиссея): иллюстрации к гомеровскому эпосу Андре Массона, Анри Матисса, Марка Шагала и Ганса Эрни к 26 июня. Расположен на Манежной площади, 1. М. Охотный ряд, Александровский сад. С полудня до 22:00, выходной — пн. 495-645-9277, www.moscowmanege.ru
Музей Марии Ермоловой:
Постоянная экспозиция: небольшая, но элегантная квартира-музей, посвященная великой актрисе Малого театра конца XIX века. Адрес: Тверской бульвар, 11. М. Тверская. С полудня до 19:00, чт. С 13:00 до 21:00 закрыто вт. и последний пт. месяц. 495-690-5416 / 4901, www.bakhrushin.theatre.ru/branches/dme
Адрес: Тверской бульвар, 11. М. Тверская. С полудня до 19:00, чт. С 13:00 до 21:00 закрыто вт. и последний пт. месяц. 495-690-5416 / 4901, www.bakhrushin.theatre.ru/branches/dme
Музей Марины Цветаевой:
Постоянная экспозиция: дом-музей, в котором поэт жил с 1914 по 1922 год. Расположен в Борисоглебском переулке, 6. М. Арбатская, Смоленская. С полудня до 17:30, чт. с полудня до 20:30, выходной — пн. и последняя пятница месяца. 495-697-5369, www.dommuseum.ru
Музей музыкальной культуры имени М.И. Глинки:
Постоянная экспозиция музыкальных инструментов. Адрес: 4 Ul. Фадеева. М. Маяковская. Касса открыта с 11.00 до 18.00, закрыта пн. и последний день месяца. 495-739-6226, www.glinka.museum
Дом-музей Михаила Пришвина:
Летняя усадьба русского писателя Михаила Пришвина (1873-1954). Адрес: пос. Дунино, 2. М. Молодежная, далее автобус 121 до Лесных Дали, касса открыта 11а.м. до 17:30, чт. С 13 до 18:30, выходной — пн.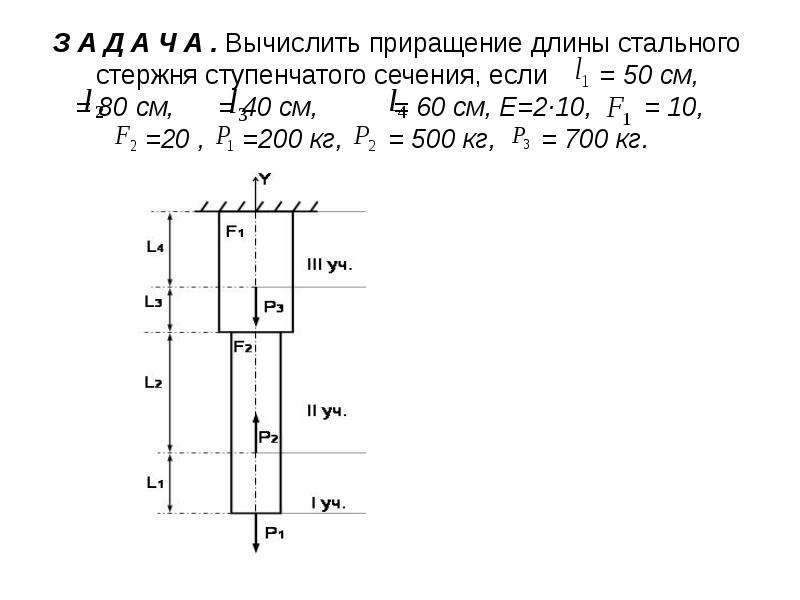 499-553-8132, www.prishvin.ru
499-553-8132, www.prishvin.ru
Московский музей современного искусства на Гоголевском:
MT PICK Хуан Миро: работы этого авангардного каталонского художника, скульптора и керамиста из Фонда Пилар и Хуана Миро в Пальма-де-Майорка для Sun.
Память платья («Память платья»): инсталляция Елизаветы Рабочих из смешанных белых арт-объектов, к 23 июня.
Искусство русского авангарда из собрания Самарского художественного музея.На выставке до 7 июля представлены работы Давида Бурлюка, Бориса Григорьева, Петра Кончаловского, Аристарха Лентулова, Казимира Малевича, Ольги Розановой и других. Расположен по адресу: Гоголевский бульвар, 10. Метро Кропоткинская. С полудня до 20:00, касса до 19:15, чт. 13.00 до 21.00, касса до 20:15, выходной — каждый третий понедельник месяца. 495-231-3660, www.mmoma.ru
Московский музей современного искусства на Петровке:
Сны для пробуждения (Сны Для Тех Кто Бодрствует): все жанры современного искусства из собрания музея, до сентября. 29.
29.
Расширение Объекта (Экспансия Предмета): преобразование предметов в изобразительном искусстве ХХ и ХХI веков, до 29 сентября. Расположен на Петровке, 25. М. Чеховская. С полудня до 20:00, касса до 19:15, чт. 13.00 до 21.00, касса до 20:15, выходной — каждый третий понедельник месяца. 495-231-3660, www.mmoma.ru
Московский музей современного искусства на Ермолаевском:
No Surprise (Удивляться Нечему): В ретроспективе работ Дмитрия Гутова представлены картины, видео, фотографии, инсталляции, металлические конструкции и графика до 30 июня.Адрес: Ермолаевский переулок, 17. М. Маяковская. С полудня до 20:00, касса до 19:15, чт. 13.00 до 21.00, касса до 20:15, выходной — каждый третий понедельник месяца. 495-231-3660, www.mmoma.ru
Московский планетарий:
Постоянные экспозиции: Интерактивный музей с Лунарием, Залами Большой и Малой Звезд, Музеем Урания и 4D Cinema Theater. Адрес: ул. Садовая-Кудринская, 5. М. Баррикадная. 9.00 — 21.00, выходные и праздничные дни 10.00м. до 22:00, вторник — выходной. 495-221-7690, www.planetarium-moscow.ru
9.00 — 21.00, выходные и праздничные дни 10.00м. до 22:00, вторник — выходной. 495-221-7690, www.planetarium-moscow.ru
Мультимедиа Арт Музей:
Меланхолический торнадо: кинетические объекты, фильмы и инсталляции немецкой современной художницы-классика Ребекки Хорн, Солнцу.
Натюрморт. Современная голландская фотография, до 14 июля.
NEW Формула времени (Формула времени): фотографии Всеволода Тарасевича, до 14 июля. Адрес: ул. Остоженка. М. Кропоткинская. Кассы открыты с 12:00 до 9ч.м., закрыто пн. 495-637-1100, www.mamm-mdf.ru
Музей прикладного, декоративного и народного искусства:
MT PICK Коллекционеры и коллекции: графика и декоративно-прикладное искусство из частных собраний Москвы, до 17 июня.
Шедевры советского фарфора 1920-1970-х годов, постоянная экспозиция.
Русское народное искусство XVIII — XX веков: постоянная экспозиция. Адрес: ул. Делегатская, 3. М. Цветной бульвар. Касса открыта 11 а.м. до 17:00, вторник выходной. и последний пн. месяца. 495-609-0146, чт. 10.00-20.00, www.vmdpni.ru
М. Цветной бульвар. Касса открыта 11 а.м. до 17:00, вторник выходной. и последний пн. месяца. 495-609-0146, чт. 10.00-20.00, www.vmdpni.ru
Музей Москвы:
История Москвы с древних времен до наших дней, постоянная экспозиция. Адрес: Зубовский бульвар, 2, вход с Остоженки. М. Парк Культуры. Кассы открыты вт., Ср., Пт. 10.00-17.30, сб, вс. С 11:00 до 17:30, выходной — пн. и последняя пятница месяца. 499-766-4196, www.mosmuseum.ru
Музей личных коллекций:
Девяносто девять имен Бога (Девяносто Девят Имён Всевышнего): классическое исламское искусство IX — XIX веков из собрания Фонда Марджани, до 16 июня.
Постоянная экспозиция в 23 залах включает 1500 произведений искусства.
Весна священная: Рождение легенды (Весна Священная: Зарождение легенды): Эта выставка, рассказывающая историю авангардного балета Стравинского с хореографией Вацлава Нижинского, декорациями и костюмами Николая Рериха, знаменует столетие своего существования. Премьера в Театре на Елисейских полях в Париже до 28 июля. Адрес: 10 Ul. Волхонка. М. Кропоткинская. С 11.00 до 19.00, чт.С 11.00 до 21.00, выходной — пн. и вт. 495-697-1610, www.arts-museum.ru, artprivatecollections.ru
Премьера в Театре на Елисейских полях в Париже до 28 июля. Адрес: 10 Ul. Волхонка. М. Кропоткинская. С 11.00 до 19.00, чт.С 11.00 до 21.00, выходной — пн. и вт. 495-697-1610, www.arts-museum.ru, artprivatecollections.ru
Музей русской иконы:
Постоянная экспозиция: Христианское искусство Восточной Европы с VI по XX век. Адрес: Гончарная набережная, 3, вход со стороны Большой Ватин переулок. М. Таганская. 11.00-19.00, среда — выходной. 495-221-5283, www.russikona.ru
Музей современной истории России:
От Английского клуба до Музея современной истории России: постоянная экспозиция.
Государственные символы России. История и современность (Государственная Символика России. История и Современность): постоянная экспозиция. Адрес: ул. Тверская, 21, м. Тверская. Касса работает вт., Ср. и пт. 10.00-17.30, чт. и сб. С 11:00 до 18:30, вс. 10.00 — 16.30, выходной — пн. 495-699-5458, www.sovr.ru
Музей уникальных кукол:
Постоянная экспозиция старинных кукол.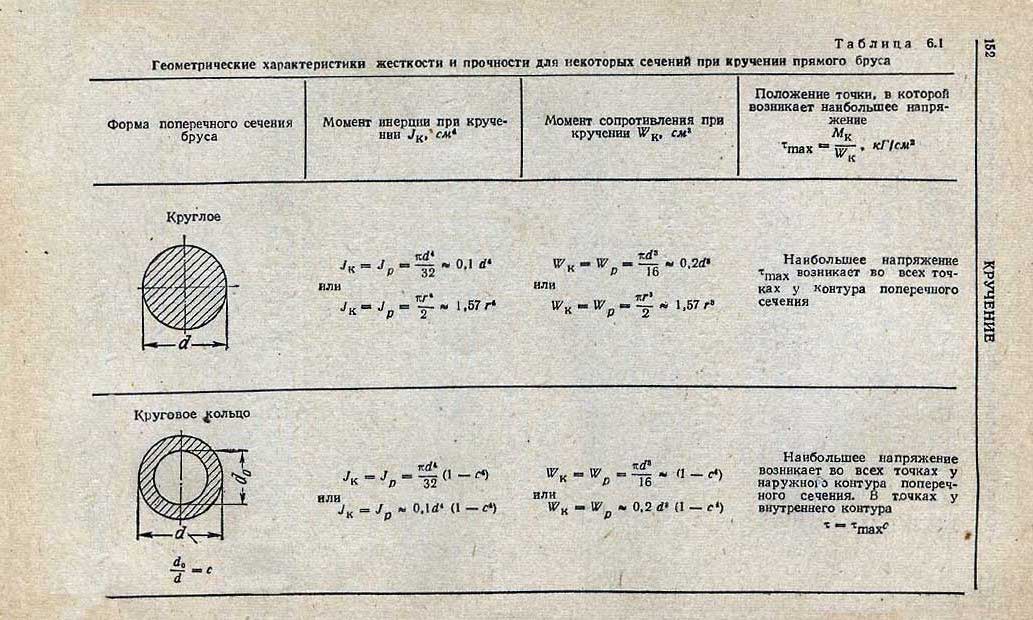 Адрес: 13 Ul. Покровка. М. Тургеневская, Китай-город, Чистые пруды.Пт, сб. Солнце. 10.00-18.00, вт, ср. Чт. экскурсии в полдень, 14 и 18 часов, выходной — пн. Вход свободный. 495-625-6405 / 7512, www.dollmuseum.ru
Адрес: 13 Ul. Покровка. М. Тургеневская, Китай-город, Чистые пруды.Пт, сб. Солнце. 10.00-18.00, вт, ср. Чт. экскурсии в полдень, 14 и 18 часов, выходной — пн. Вход свободный. 495-625-6405 / 7512, www.dollmuseum.ru
На Солянке Галерея:
MT PICK Милко Манчевски. Five Drops of Dream: работы этого известного американского македонского писателя-постановщика, фотографа и художника до 23 июня.
MT PICK Patriotic Tales: шедевр видеоарта 1997 года бельгийского художника Фрэнсиса Алиса, в котором он ведет круг овец вокруг флага на Пласа-де-ла-Конститусьон в Мехико, до 23 июня.
Петрушевская и Норштейн: спектакль, посвященный романистке, драматургу, певице, художнику-исполнителю Людмиле Петрушевской и ее диалогу с классическим аниматором Юрием Норштейном, до 22 июня. Расположен на Солянке, 1/2. М. Китай-город. Пн. по чт. С 14.00 до 22.00, пт. с полудня до полуночи, сб. и вс. с полудня до 22:00 495-621-5672, солянка.org
Музей-квартира Немировича-Данченко:
Постоянная экспозиция: дом, в котором жил режиссер и соучредитель МХАТ.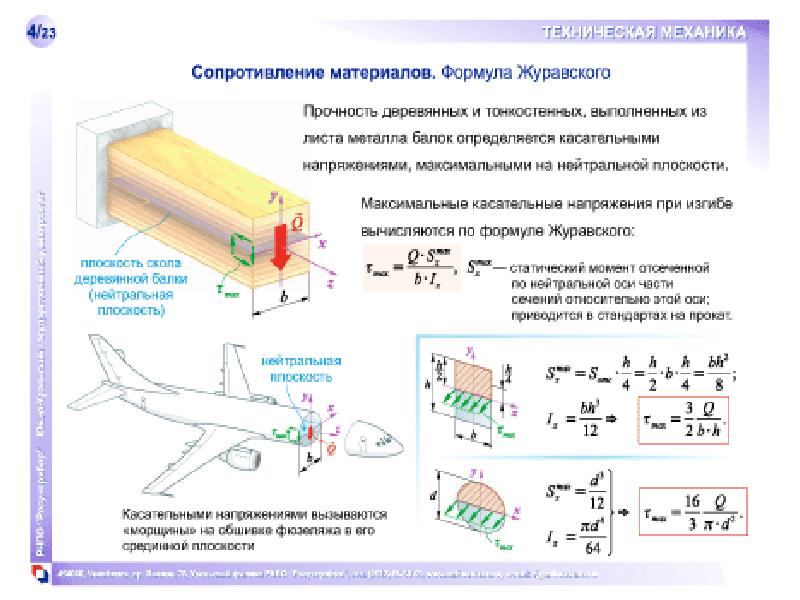 Адрес: Глинищевский переулок, 5/7, подъезд 5, кв. 52. М. Тверская. С 11:00 до 17:30, выходной — пн. и вт. 495-650-5391, www.mxat.ru/museum
Адрес: Глинищевский переулок, 5/7, подъезд 5, кв. 52. М. Тверская. С 11:00 до 17:30, выходной — пн. и вт. 495-650-5391, www.mxat.ru/museum
Новая Третьяковская галерея:
Александр Родченко. Рабочий клуб: (1885-1953): реконструированный интерьер рабочего клуба по проекту этого художника-конструктивиста, постоянная экспозиция.
Анатолий Комелин демонстрирует каменные рельефы и минималистичные скульптуры из дерева, к 11 августа.
НОВИНКА Густав Клуцис (1895-1938): картины, графика, эскизы, эскизы и фотоколлажи художника-конструктивиста-авангардиста, пт.по 22 сентября
Основные выставочные залы: экспозиция русского искусства ХХ века.
Михаил Нестеров (1862-1942): картины из музейных и частных собраний, до 18 августа.
«Фантомные боли»: скульптуры и живопись Бориса Орлова до 23 июня. Находится на Крымском валу, 10. М. Октябрьская, Парк Культуры. Касса открыта с 10.00 до 18.30, закрыта пн. 499-230-7788, 238-1378, 495-951-1362. Экскурсии 495-953-5223. Маршрутка Autoline отправляется от Новой Третьяковской галереи до Третьяковской галереи по адресу: Лаврушинский переулок, 10/12, ежедневно в 12:20, 1:20, 2:20, 3:20 и 16:20.м., www.tretyakovgallery.ru
Экскурсии 495-953-5223. Маршрутка Autoline отправляется от Новой Третьяковской галереи до Третьяковской галереи по адресу: Лаврушинский переулок, 10/12, ежедневно в 12:20, 1:20, 2:20, 3:20 и 16:20.м., www.tretyakovgallery.ru
Галерея нового западного искусства:
Искусство Европы и Америки XIX и XX веков.
Обнаженные. От мрамора до фотографии (Обнаженные. От Мрамора к фотографии), до 23 июня. Адрес: Волхонка, 14. М. Кропоткинская. 10.00-19.00, чт. 10.00 — 21.00, выходной — пн. 495-697-1546, www.arts-museum.ru, www.newpaintart.ru
Музей-квартира Николая Голованова:
Мемориальная квартира выдающегося дирижера, трижды исключенного из Большого театра — в 1928, 1936 и 1953 годах, постоянная экспозиция.Адрес: Брюсов переулок, 7, кв. 10. М. Тверская, Пушкинская. Открыто пн. и ср. С 14 до 17 часов 495-629-7083, www.glinka.museum/about/apartment_museum_golovanov
Новодевичий Богородице-Смоленский Новодевичий монастырь:
Новодевичий монастырь и кладбище: Красивый монастырский комплекс 17 века, который был основан в 1524 году царем Василием III, а затем, после Смутного времени, был значительно перестроен и улучшен регентшей Софией, которую позже заключил здесь Петр Великий. со своей нежеланной первой женой.Сейчас принадлежит Московской епархии Русской Православной Церкви. Адрес: Новодевичий проезд, 1. М. Спортивная. 499-245-3168, www.mepar.ru/eparhy/temples/?temple=1166
со своей нежеланной первой женой.Сейчас принадлежит Московской епархии Русской Православной Церкви. Адрес: Новодевичий проезд, 1. М. Спортивная. 499-245-3168, www.mepar.ru/eparhy/temples/?temple=1166
Новый Манеж:
NEW Stone. Ножницы. Бумага. Музейная попытка (Камень. Ножницы. Бумага. Попытка Музея): Экспериментальная инсталляция — совместная работа Лаборатории Дмитрия Крымова и Театрального музея имени Бахрушина до 7 июля. Расположена в Георгиевском переулке, 3. М. Охотный ряд, Театральная.С полудня до 21:00, выходной — пн. 495-645-9277, www.moscowmanege.ru
Музей искусства народов Востока:
Танцующая кисть (Танцующая кисть): Московские художники показывают картины в китайской и японской техниках, до 16 июня.
Мариус Бауэр (1867-1932): картины и графика этого голландского художника, до 9 сентября.
Постоянные экспозиции: искусство Кореи, Индии, Ирана, Китая, Азии, Сибири и др., Постоянная экспозиция. Адрес: Никитский бульвар, 12. М. Арбатская.Касса работает с 11:00 до 19:30, чт. с полудня до 20:30, выходной — пн. 495-691-9614 / 0212, www.orientmuseum.ru
Адрес: Никитский бульвар, 12. М. Арбатская.Касса работает с 11:00 до 19:30, чт. с полудня до 20:30, выходной — пн. 495-691-9614 / 0212, www.orientmuseum.ru
Галерея Pop / off / art в Центре современного искусства Винзавод:
No Comment: Олег Татаринцев и Ольга Татаринцева показывают концептуальную инсталляцию пост-минималистских керамических предметов до 30 июня. Расположена по адресу: 4-й Сыромятнический переулок, д. 1, корп. 6. М. Чкаловская, Курская. С полудня до 20:00, выходной — пн. 495-775-8706, popoffart.com
пр. Фабрика:
Ритуалы сопротивления (Ритуалы сопротивления): инсталляция Анны Титовой, к 20 июля.Адрес: Переведеновский переулок, 18. М. Бауманская, Электрозаводская, далее троллейбус 22 или 25 до Балакиревского переулка. С полудня до 20:00, выходной — пн. Вход свободный. 499-265-3926 / 3935, www.proektfabrika.ru
Галерея Проун в Центре современного искусства Винзавод:
MT PICK Пары (Вдвоем): работы Александра Родченко и Варвары Степановой, Александра Древина и Надежды Удальцовой, Ольги Розановой и Алексея Крученых, Натальи Гончаровой и Михаила Ларионова и др. , До августа.29. Адрес: 4-й Сыромятнический переулок, д. 1, корп. 6. М. Чкаловская, Курская. С полудня до 20:00, выходной — пн. 495-916-0900 www.winzavod.ru, www.proungallery.ru
, До августа.29. Адрес: 4-й Сыромятнический переулок, д. 1, корп. 6. М. Чкаловская, Курская. С полудня до 20:00, выходной — пн. 495-916-0900 www.winzavod.ru, www.proungallery.ru
ГМИИ им. А.С. Пушкина:
Выставка одной картины «Святой Марк» голландского мастера Франса Хальса из галереи Джонни Ван Хафтена (Лондон) до 28 июля.
Постоянная коллекция: произведения Древнего Египта, Ассирии, Греции и Рима, а также произведения средневековья до начала 20 века.
NEW MT PICK Прерафаэлиты: картины и предметы прикладного искусства викторианского авангарда из британских и американских музеев и частных коллекций, Вт. по 22 сентября. Адрес: Волхонка, 12. М. Кропоткинская. 10.00-19.00, чт. до 21:00, выходной — пн. 495-697-9578, www.arts-museum.ru
Галерея Красный Октябрь:
World Press Photo 2013, до 30 июня. Адрес: Берсеневская наб., 6. М. Кропоткинская, Полянка.С полудня до 21:00. 495-644-0143, 8-916-015-5166, www. redoctobergallery.com
redoctobergallery.com
Галерея Риджина в Центре современного искусства Винзавод:
MT PICK Frames (Ramy): арт-объекты Олега Кулика, до сб. Адрес: 4-й Сыромятнический переулок, дом 1. М. Чкаловская, Курская. С 11.00 до 19.00, выходной — вс. и пн. Вход свободный. 495-228-1330, www.reginagallery.com
Роза Азора Галерея:
High Style (Высокий стиль): фотоработы Владимира Клавихо-Телепнёва, до 17 июня.Адрес: Никитский бульвар, 14. Пн. до сб. с полудня до 20:00, вс. с полудня до 18:00 495-695-8119, www.rozaazora.ru
Галерея RuArts:
MT PICK Семен Агроскин. Реконструкция: росписи, до 22 июня. Находится по адресу 1-й Зачатьевский переулок, 10. М. Кропоткинская. С полудня до 20:00. Вход свободный. 495-637-4475, www.ruarts.ru
Выставочный зал Союза художников России:
NEW Евгений Жидков: Русские пейзажи традиционными маслами, до 16 июня.Адрес: Покровка, 37. М. Чистые пруды. Пн. до пт. С 11.00 до 17.30, сб. по предварительной записи, выходной — вс. 495-917-5880, www.shr.su
М. Чистые пруды. Пн. до пт. С 11.00 до 17.30, сб. по предварительной записи, выходной — вс. 495-917-5880, www.shr.su
Галерея S’Art:
Аниш Капур: фото-презентация его инсталляции «Вознесение»: столб дыма в церкви Сан-Джорджо-Маджоре, базилика, до 18 сентября.
Маурицио Каттелан: фото-презентация работ итальянского художника до 1 сентября.
Светлана К-Ли. Мясо: видеопрезентация работ этого концептуального русского художника, ныне живущего в Англии, до 15 июля.Адрес: Куркино, ул. Воротынская, 2, корп. 1. М. Планерная, затем автобус 268 до Микрорайона Четырнадцатый. По предварительной записи. 499-500-2366.
Музей-студия Сергея Коненкова:
Постоянная экспозиция: Работы этого влиятельного российского и советского скульптора, который провел более 20 лет в США и вернулся домой в 1945 году в возрасте 71 года. Расположен на Тверской ул., 17. М. Тверская, Пушкинская. Кассы открыты с 11.00 до 18.30, закрыты пн, вт.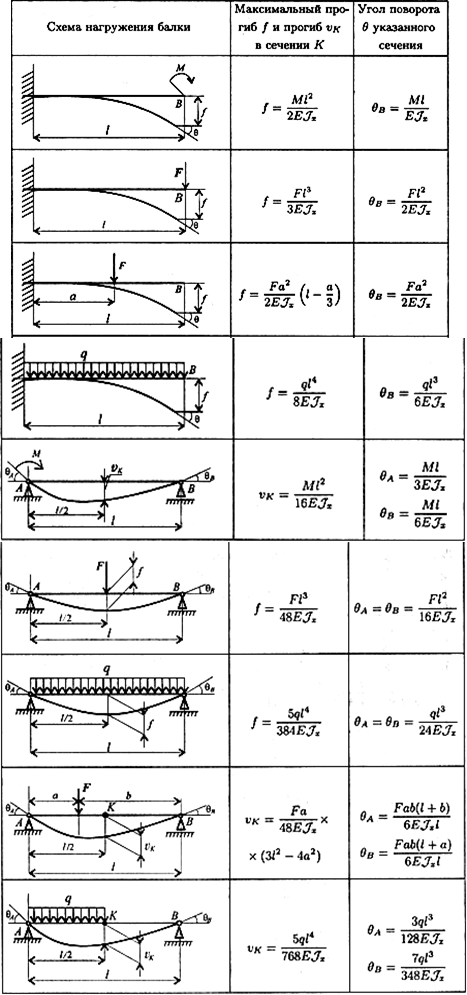 и последняя пятница месяца.495-629-6139, www.rah.ru/museums/muzey_masterskaya_s_t_konenkova.php
и последняя пятница месяца.495-629-6139, www.rah.ru/museums/muzey_masterskaya_s_t_konenkova.php
Музей Сергея Прокофьева:
Мемориальная квартира, в которой композитор жил с 1947 по 1953 год, постоянная экспозиция. Адрес: Камергерский переулок, 6. М. Театральная, Охотный ряд. Мы б. к вс. С 11.00 до 17.00, выходной — пн. и вт. 495-692-7959, www.glinka.museum/about/museum_of_prokofiev
Музей Серебряного века:
Дом Брюсова: «Кабинет-мемориал Валерия Брюсова» и «Пушкин и серебряный век русской литературы», постоянные экспозиции.Адрес: проспект Мира, 30. М. Проспект Мира (круговая линия). Касса работает с 11:00 до 17:30, чт. и пт. С 13 до 19:30, выходной — пн. и последний день месяца. 495-680-8683, www.goslitmuz.ru/ru/bryusov-museum
Собор Василия Блаженного:
Священные реликвии Покровского собора (Святыни Покровского Собора): потрясающий средневековый интерьер, иконы, книги и другие религиозные реликвии.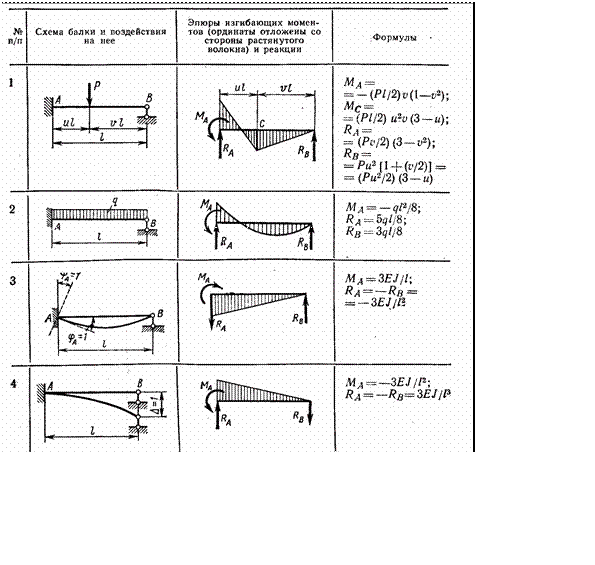 Адрес: Красная площадь, 2. М. Площадь Революции. Касса открыта летом, 11 а.м. до 17:30, зимой с 11:00 до 16:30, 495-698-3304 www.saintbasil.ru
Адрес: Красная площадь, 2. М. Площадь Революции. Касса открыта летом, 11 а.м. до 17:30, зимой с 11:00 до 16:30, 495-698-3304 www.saintbasil.ru
Государственный центр современного искусства:
NEW Маленькая теория всего, или Искусство познания: научно-популярные мультфильмы Владислава Ефимова, Евгения Стрелкова, Андрея Суздалева, а также короткометражки воспитанников Государственного центра науки и техники. Детская студия современного искусства, пт. по 23 июня.
Кино-Фото-Людогус: Владимир Маяковский и авангард ХХ века в фотографиях и фильмах до 18 июня.Адрес: Зоологическая ул., 13. М. Краснопресненская. С полудня до 20:00, чт. с полудня до 21:00, выходной — пн. 499-254-8492 / 0674, www.ncca.ru
Государственный литературный музей:
Постоянная экспозиция: книги, рукописи и другие предметы, рассказывающие о великих писателях России. Адрес: 28 Ul. Петровка. М. Чеховская. С 11.00 до 18.00, чт. С 14 до 20, выходной — пн. 495-625-1226, www.goslitmuz.ru/ru/gos-lit-museum
495-625-1226, www.goslitmuz.ru/ru/gos-lit-museum
Stella Art на Скарятинском:
Одиннадцать чемоданов для путешествия (Одиннадцат Чемоданов в Дорогу): инсталляции студентов Института База, до августа.4. Адрес: Скарятинский переулок, 7. М. Баррикадная. С полудня до 19:00, выходной — пн. 495-691-3407, www.safmuseum.org
Мемориал Святослава Рихтера Квартира:
Постоянная экспозиция: квартира великого пианиста, с экспозицией фотографий и картин, видео и звукозаписей.
Елена Колат: живопись, до 25 июля. Адрес: Большая Бронная ул., 2/6, кв. 59. М. Пушкинская. По предварительной записи вт., Чт. и третью субботу месяца с полудня до 2 р.м. 495-695-8346, 697-7205, www.sviatoslav-richter.ru
Чайковский и Музей Москвы:
Мемориальная квартира, в которой композитор жил с сентября 1872 г. по ноябрь 1873 г., постоянная экспозиция. Адрес: Кудринская площадь, 46/54. М. Баррикадная. 10.00-19.00, выходной — пн. и вт. 495-691-1514, www.glinka.museum/about/museum_of_moscow_tchaikovsky
и вт. 495-691-1514, www.glinka.museum/about/museum_of_moscow_tchaikovsky
Музей истории ГУЛАГа:
Постоянная экспозиция: Документы, письма, воспоминания и личные вещи узников ГУЛАГа.Адрес: 16 Ul. Петровка. М. Кузнецкий Мост, Театральная. Касса работает с 11.00 до 18.00, чт. с полудня до 19:00, выходной — пн. и последняя пятница недели. 495-621-7310, www.gmig.ru
Третьяковская галерея:
Борис Мессерер показывает картины, графику и инсталляции до 23 июня в Инженерном корпусе.
NEW Подарки и приобретения (Дары и Приобретения): новинки в коллекции графики XVIII — начала XX веков, до ноябрь.3.
Основные выставочные залы: шедевры русской иконописи и всемирно известные картины XIX — начала XX веков.
Православные церковные древности из собрания Серпуховского историко-художественного музея — иконы, предметы декоративно-прикладного искусства, рукописи и книги — до 28 июля в Инженерном корпусе. Адрес: Лаврушинский переулок, 10/12. М. Третьяковская. Касса работает вт., Ср., Сб. и вс. 10.00-17.00, чт. и пт. С 10 утра до 8 вечера.м., закрыто пн. 499-230-7788, 238-1378, 495-951-1362. Маршрутка Autoline отправляется от Третьяковской галереи до Новой Третьяковки на Крымском Валу, 10 ежедневно в полдень, 13, 14, 15, 16 и 17 часов, www.tretyakovgallery.ru
Адрес: Лаврушинский переулок, 10/12. М. Третьяковская. Касса работает вт., Ср., Сб. и вс. 10.00-17.00, чт. и пт. С 10 утра до 8 вечера.м., закрыто пн. 499-230-7788, 238-1378, 495-951-1362. Маршрутка Autoline отправляется от Третьяковской галереи до Новой Третьяковки на Крымском Валу, 10 ежедневно в полдень, 13, 14, 15, 16 и 17 часов, www.tretyakovgallery.ru
Музей Царицыно:
Екатерина Великая: (Великая Екатерина): экспонат, посвященный российской императрице, постоянная экспозиция.
Шедевры художественного собрания Царицыно (Шедевры Художественного Собрания Царицыно): западноевропейские гобелены XVI – XVIII веков, русское стекло и гобелены XX века, постоянная экспозиция.
Прошлое и настоящее Царицыно (Был и Нов Царицына): история Царицыно, постоянная экспозиция.
Кладовая серебра (Серебряная кладовая): произведения русского ювелирного искусства XVI — XX веков, постоянная экспозиция.
Царицынские древности: археологические находки, постоянная экспозиция.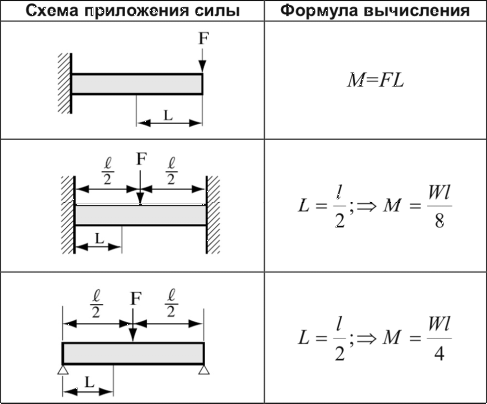 Адрес: ул. Дольская, 1. М. Царицыно, Орехово. Касса работает с 11.00 до 17.30, сб. С 11:00 до 19:30, вс. и праздники 11 а.м. до 18:30, выходной — пн. Парк открыт ежедневно с 6 утра до полуночи. 499-725-7287, www.tsaritsyno.net
Адрес: ул. Дольская, 1. М. Царицыно, Орехово. Касса работает с 11.00 до 17.30, сб. С 11:00 до 19:30, вс. и праздники 11 а.м. до 18:30, выходной — пн. Парк открыт ежедневно с 6 утра до полуночи. 499-725-7287, www.tsaritsyno.net
Ударник:
Гриша Брускин. Собрание археолога (Гриша Брускин. Коллекция археолога): инсталляция из 33 бронзовых скульптур, до 11 августа. Расположена на ул. Серафимовича. М. Полянка, Кропоткинская. С 11.00 до 20.00, выходной — пн. 495-657-9758.
Музей автомобилей Вадима Задорожного:
Постоянные экспозиции: ретро-автомобили, мотоциклы, вооружение и самолеты.Расположен в поселке Архангельское, 4 км Ильинского шоссе, корп. 8. М. Тушинская, автобус 541, 549, 568, 151, 541, 549, 568. М. Строгино, маршрутное такси Строгино-Зачарково до Липовой аллеи. Автомобилем по Новорижскому шоссе, возле Архангельского. Касса открыта вт. до пт. С 10.00 до 18.00, сб. и вс. 10.00-19.00, выходной — пн. 495-662-3818, www.tmuseum. ru
ru
Дом-музей Василия Пушкина:
NEW Небольшой особняк, в котором этот русский поэт-неоклассицизм и дядя Александра Пушкина жил с 1824 по 1830 год, открывается в четверг.Адрес: Старая Басманная ул., 36. М. Красные ворота. Касса работает с 10.00 до 17.30, чт. с полудня до 20:30, выходной — пн. и последний пт. месяца. 495-637-5674, www.pushkinmuseum.ru
Музей Владимира Маяковского:
Владимир Маяковский: документы и фотографии из жизни поэта-футуриста в доме, где он жил и покончил жизнь самоубийством. Адрес: Лубянский проезд, 3. М. Лубянка. 10.00-17.00, чт. С 13 до 20 часов, выходной — ср.и последний пт. месяца. 495-628-2569, www.mayakovsky.info
Геологический музей Владимира Вернадского:
Постоянные экспозиции: «Планета Земля», «История Земли», «Мир минералов», «Геологические раритеты» и другие экспозиции. Расположены по адресу: Моховая ул., 11, корп. 2. М. Охотный Ряд. Касса открыта вт. до пт. С 11.00 до 18.00, сб. и вс. с полудня до 18:00, выходной — пн. 495-692-0943, www.sgm.ru
С 11.00 до 18.00, сб. и вс. с полудня до 18:00, выходной — пн. 495-692-0943, www.sgm.ru
Музей-квартира Всеволода Мейерхольда:
Постоянная экспозиция: небольшой музей, посвященный директору, который до своего ареста и убийства в тюрьме в 1940 году был одним из мировых лидеров авангарда.Адрес: Брюсов переулок, 12, кв. 11. М. Пушкинская. Кассы открыты с полудня до 17:30, закрыты пн, вт. и последняя пятница месяца. 495-629-9437, www.bakhrushin.theatre.ru/branches/mkm
Академия акварели и изящных искусств:
Музей акварели: постоянная экспозиция. Адрес: 15 Ul. Академика Варги. М. Теплый Стан, автобусы 144, 227, 281 до улицы Академика Виноградова. С 11.00 до 19.00, выходной — пн. и вт. 495-531-5555, доб. 298, www.academy.andriaka.ru
Центр современного искусства Винзавод:
Позади тебя нет ничего (Позади Тебя Ничего Нет): последние абстрактные картины и две видеоинсталляции Виктора Алимпиева, до 23 июня. Расположен по адресу: 4-й Сыромятнический переулок, д. 1, корп. 6. М. Чкаловская, Курская. С полудня до 20:00. 495-917-4646, www.winzavod.ru
Расположен по адресу: 4-й Сыромятнический переулок, д. 1, корп. 6. М. Чкаловская, Курская. С полудня до 20:00. 495-917-4646, www.winzavod.ru
Фонд культуры Екатерины:
Хендрик Керстенс. Паула: серия портретов этого голландского фотографа к 28 июля.Адрес: Кузнецкий мост, 21, подъезд №8 с ул. Большая Лубянка. М. Кузнецкий мост. Касса работает с 11:00 до 19:30, закрыта по понедельникам. 495-621-5522, www.ekaterina-fondation.ru
Зоологический музей МГУ:
Постоянные экспозиции: Все группы животных, от одноклеточных до птиц и млекопитающих, в основном муляжи. Адрес: ул. Большая Никитская, 6. М. Охотный Ряд. 10.00-17.00, выходной — пн. и последний вт. месяца. 495-629-4435, змму.msu.ru
Галерея искусств Зураба Церетели:
Искусство и религия в современной культуре: византийские традиции в произведениях современных российских художников, до 30 июня.
Line Curve (Изгиб Линии): картины Григория Дембовского, до 22 июня.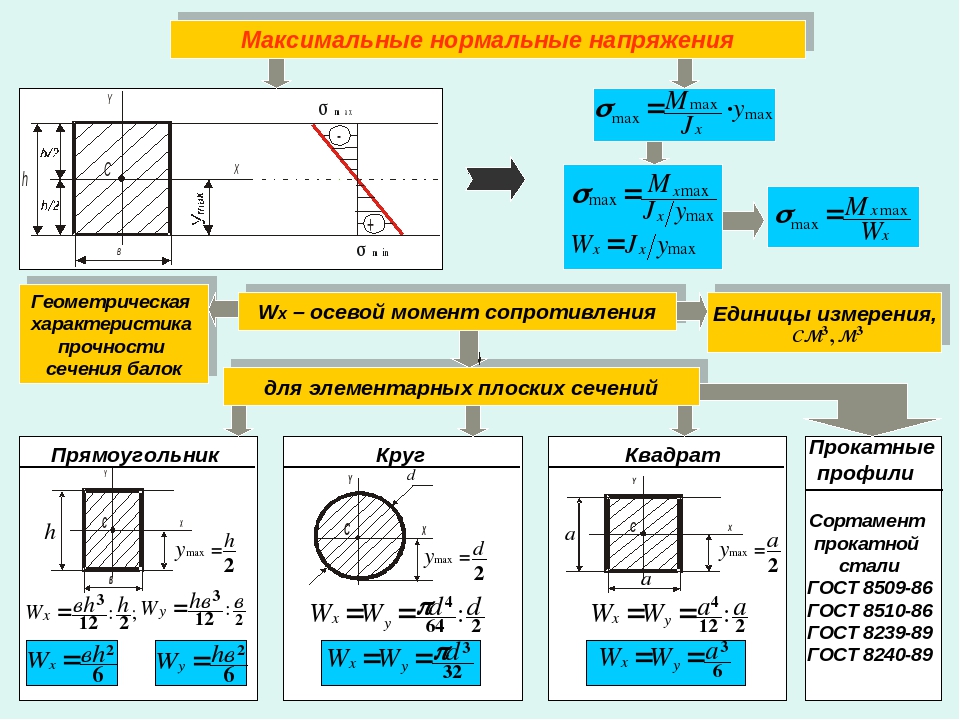
Старообрядческая иконопись из Ярославского областного краеведческого музея и частных собраний, до 10 августа. Находится на Пречистенке, 19. М. Кропоткинская. С полудня до 20:00, вс. полдень до 7 р.м., закрыто пн. 495-637-2569 / 4771, www.tsereteli.ru, www.rah.ru
Тригонометрическая таблица углов. Тригонометрические функции
Справочные данные для тангенса (tg x) и котангенса (ctg x). Геометрическое определение, свойства, графики, формулы. Таблица касательных и котангенсов, производных, интегралов, разложения в ряды. Выражения в терминах комплексных переменных. Связь с гиперболическими функциями.
Геометрическое определение
| BD | — длина дуги окружности с центром в точке A.
α — угол, выраженный в радианах.
Касательная (tg α) — тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равного отношению длины противоположного катета | BC | к длине соседней ноги | AB | . ..
..
Котангенс (ctg α) — тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равного отношению длины соседнего катета | AB | к длине противоположной ноги | BC | …
Касательная
Где n — целое.
В западной литературе тангенс обозначается следующим образом:
.
;
;
.
График функции касательной, y = tg x
Котангенс
Где n — целое.
В западной литературе котангенс обозначается следующим образом:
.
Также приняты следующие обозначения:
;
;
.
График функции котангенса, y = ctg x
Свойства тангенса и котангенса
Периодичность
Функции y = tg x и y = ctg x периодические с периодом π.
Четность
Функции тангенса и котангенса нечетные.
Области и значения, увеличение, уменьшение
Функции касательной и котангенса непрерывны в своей области определения (см. Доказательство непрерывности). Основные свойства тангенса и котангенса представлены в таблице ( n — целое).
Доказательство непрерывности). Основные свойства тангенса и котангенса представлены в таблице ( n — целое).
| y = tg x | y = ctg x | |
| Область определения и преемственности | ||
| Диапазон значений | -∞ | -∞ |
| По возрастанию | — | |
| По убыванию | — | |
| Крайности | — | — |
| Нули, y = 0 | ||
| Точки пересечения с осью y, x = 0 | у = 0 | — |
Формулы
Выражения в терминах синуса и косинуса
;
;
;
;
;
Формулы тангенса и котангенса суммы и разности
Остальные формулы легко получить, например
Произведение касательных
Формула суммы и разности касательных
В этой таблице показаны значения касательных и котангенсы для некоторых значений аргумента.
Выражения в терминах комплексных чисел
Выражения в терминах гиперболических функций
;
;
Производные инструменты
; .
.
Производная n-го порядка по переменной x функции:
.
Вывод формул касательной >>>; для котангенса >>>
Интегралы
Разложение в ряды
Чтобы получить разложение тангенса по степеням x, вам нужно взять несколько членов разложения в степенной ряд для функций sin x и cos x и разделить их. полиномы друг на друга.Это дает следующие формулы.
Ул.
в.
где B n — числа Бернулли. Они определяются либо из рекуррентного соотношения:
;
;
где.
Или по формуле Лапласа:
Обратные функции
Обратными функциями тангенса и котангенса являются арктангенс и аркотангенс, соответственно.
Арктангенс, arctg
, где n — целое.
Арккотангенс, arcctg
, где n — целое.
Литература:
И.Н. Бронштейн, К. Семендяев, Справочник по математике для инженеров и студентов технических вузов, «Лан», 2009.
Г. Корн, Справочник по математике для ученых и инженеров, 2012.
 Коды. Альфа, бета, гамма, дельта, эпсилон … Рейтинги электрических сетей. Преобразование единиц измерения Децибел. Мечтать. Задний план. Единицы измерения чего? Установки давления и вакуума. Преобразование единиц измерения давления и вакуума. Единицы длины. Преобразование единиц измерения длины (линейные размеры, расстояния). Единицы объема. Преобразование единиц объема. Единицы плотности. Преобразование единиц плотности. Единицы площади. Преобразование единиц площади. Единицы измерения твердости.2 (хладагент R702) Водяной пар. Воздух (атмосфера) Природный газ — природный газ. Биогаз — это канализационный газ. Сжиженный газ. NGL. СПГ. Пропан-бутан. Кислород O2 (хладагент R732) Масла и смазки Метан Ch5 (хладагент R50) Свойства воды. Окись углерода CO. Окись углерода. Двуокись углерода CO2. (Хладагент R744). Хлор Cl2 Хлороводород HCl, также известный как соляная кислота. Хладагенты (хладагенты). Хладагент (хладагент) R11 — Фтортрихлорметан (CFCI3) Хладагент (Хладагент) R12 — Дифтордихлорметан (CF2CCl2) Хладагент (Хладагент) R125 — Пентафторэтан (CF2HCF3).
Коды. Альфа, бета, гамма, дельта, эпсилон … Рейтинги электрических сетей. Преобразование единиц измерения Децибел. Мечтать. Задний план. Единицы измерения чего? Установки давления и вакуума. Преобразование единиц измерения давления и вакуума. Единицы длины. Преобразование единиц измерения длины (линейные размеры, расстояния). Единицы объема. Преобразование единиц объема. Единицы плотности. Преобразование единиц плотности. Единицы площади. Преобразование единиц площади. Единицы измерения твердости.2 (хладагент R702) Водяной пар. Воздух (атмосфера) Природный газ — природный газ. Биогаз — это канализационный газ. Сжиженный газ. NGL. СПГ. Пропан-бутан. Кислород O2 (хладагент R732) Масла и смазки Метан Ch5 (хладагент R50) Свойства воды. Окись углерода CO. Окись углерода. Двуокись углерода CO2. (Хладагент R744). Хлор Cl2 Хлороводород HCl, также известный как соляная кислота. Хладагенты (хладагенты). Хладагент (хладагент) R11 — Фтортрихлорметан (CFCI3) Хладагент (Хладагент) R12 — Дифтордихлорметан (CF2CCl2) Хладагент (Хладагент) R125 — Пентафторэтан (CF2HCF3). Хладагент (Хладагент) R134а — 1,1,1,2-Тетрафторэтан (CF3CFh3). Хладагент (Хладагент) R22 — Дифторхлорметан (CF2ClH) Хладагент (Хладагент) R32 — Дифторметан (Ch3F2). Хладагент (хладагент) R407C — R-32 (23%) / R-125 (25%) / R-134a (52%) / в процентах по весу. прочие Материалы — термические свойства. Абразивы — зернистость, крупность, шлифовальное оборудование. Почвы, земля, песок и другие породы. Показатели разрыхленности, усадки и плотности грунтов и горных пород. Усадка и расшатывание, нагрузки.Углы откоса, отвал. Высота скамеек, отвалов. Древесина. Пиломатериалы. Древесина. Журналы. Дрова … Керамика. Клеи и адгезивы Лед и снег (водяной лед) Металлы Алюминий и алюминиевые сплавы Медь, бронза и латунь Бронза Латунь Медь (и классификация медных сплавов) Никель и сплавы Соответствие марок сплавов Стали и сплавы Справочные таблицы веса проката и труб. +/- 5% Вес трубы. Металлический вес. Механические свойства сталей. Чугун Минералы. Асбест. Пищевые продукты и пищевое сырье.Свойства и т.д.
Хладагент (Хладагент) R134а — 1,1,1,2-Тетрафторэтан (CF3CFh3). Хладагент (Хладагент) R22 — Дифторхлорметан (CF2ClH) Хладагент (Хладагент) R32 — Дифторметан (Ch3F2). Хладагент (хладагент) R407C — R-32 (23%) / R-125 (25%) / R-134a (52%) / в процентах по весу. прочие Материалы — термические свойства. Абразивы — зернистость, крупность, шлифовальное оборудование. Почвы, земля, песок и другие породы. Показатели разрыхленности, усадки и плотности грунтов и горных пород. Усадка и расшатывание, нагрузки.Углы откоса, отвал. Высота скамеек, отвалов. Древесина. Пиломатериалы. Древесина. Журналы. Дрова … Керамика. Клеи и адгезивы Лед и снег (водяной лед) Металлы Алюминий и алюминиевые сплавы Медь, бронза и латунь Бронза Латунь Медь (и классификация медных сплавов) Никель и сплавы Соответствие марок сплавов Стали и сплавы Справочные таблицы веса проката и труб. +/- 5% Вес трубы. Металлический вес. Механические свойства сталей. Чугун Минералы. Асбест. Пищевые продукты и пищевое сырье.Свойства и т.д. Ссылка на другой раздел проекта. Резина, пластмассы, эластомеры, полимеры. Подробное описание эластомеров PU, TPU, X-PU, H-PU, XH-PU, S-PU, XS-PU, T-PU, G-PU (CPU), NBR, H-NBR, FPM, EPDM, MVQ , TFE / P, POM, PA-6, TPFE-1, TPFE-2, TPFE-3, TPFE-4, TPFE-5 (модифицированный PTFE), Сопротивление материалов. Сопромат. Строительные материалы. Физико-механические и термические свойства. Конкретный. Бетонный раствор. Решение. Строительная фурнитура. Сталь и др. Таблицы применимости материалов.Химическая устойчивость. Температурная применимость. Устойчивость к коррозии. Герметизирующие материалы — герметики для швов. ПТФЭ (фторопласт-4) и производные. ФУМ-лента. Анаэробные клеи. Невысыхающие герметики. Силиконовые герметики (кремнийорганические). Производные графита, асбеста, паронита и паронита. Пенографит (ТРГ, ТМГ), составы. Характеристики. Применение. Производство. Лен санитарный Уплотнения из резиновых эластомеров Утеплители и теплоизоляционные материалы. (ссылка на раздел проекта) Инженерные технологии и концепции Взрывозащита.
Ссылка на другой раздел проекта. Резина, пластмассы, эластомеры, полимеры. Подробное описание эластомеров PU, TPU, X-PU, H-PU, XH-PU, S-PU, XS-PU, T-PU, G-PU (CPU), NBR, H-NBR, FPM, EPDM, MVQ , TFE / P, POM, PA-6, TPFE-1, TPFE-2, TPFE-3, TPFE-4, TPFE-5 (модифицированный PTFE), Сопротивление материалов. Сопромат. Строительные материалы. Физико-механические и термические свойства. Конкретный. Бетонный раствор. Решение. Строительная фурнитура. Сталь и др. Таблицы применимости материалов.Химическая устойчивость. Температурная применимость. Устойчивость к коррозии. Герметизирующие материалы — герметики для швов. ПТФЭ (фторопласт-4) и производные. ФУМ-лента. Анаэробные клеи. Невысыхающие герметики. Силиконовые герметики (кремнийорганические). Производные графита, асбеста, паронита и паронита. Пенографит (ТРГ, ТМГ), составы. Характеристики. Применение. Производство. Лен санитарный Уплотнения из резиновых эластомеров Утеплители и теплоизоляционные материалы. (ссылка на раздел проекта) Инженерные технологии и концепции Взрывозащита. Защита от воздействий окружающей среды. Коррозия. Климатические исполнения (Таблицы совместимости материалов) Классы давления, температуры, герметичности Падение (потеря) давления. — Инженерная концепция. Противопожарная защита. Пожары. Теория автоматического управления (регулирования). ТАУ Математический справочник Арифметика, геометрические прогрессии и суммы некоторых числовых рядов. Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, прямоугольники и т. Д. Градусы в радианы. Плоские фигуры.Свойства, стороны, углы, знаки, периметры, равенства, сходства, хорды, сектора, площади и т. Д. Области неправильных фигур, объемы неправильных тел. Средняя мощность сигнала. Формулы и методы расчета площади. Графики. Построение графиков. Чтение графиков. Интегральное и дифференциальное исчисление. Табличные производные и интегралы. Таблица производных финансовых инструментов. Интегральный стол. Таблица первообразных. Найдите производную. Найдите интеграл. Диффурсы.
Защита от воздействий окружающей среды. Коррозия. Климатические исполнения (Таблицы совместимости материалов) Классы давления, температуры, герметичности Падение (потеря) давления. — Инженерная концепция. Противопожарная защита. Пожары. Теория автоматического управления (регулирования). ТАУ Математический справочник Арифметика, геометрические прогрессии и суммы некоторых числовых рядов. Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, прямоугольники и т. Д. Градусы в радианы. Плоские фигуры.Свойства, стороны, углы, знаки, периметры, равенства, сходства, хорды, сектора, площади и т. Д. Области неправильных фигур, объемы неправильных тел. Средняя мощность сигнала. Формулы и методы расчета площади. Графики. Построение графиков. Чтение графиков. Интегральное и дифференциальное исчисление. Табличные производные и интегралы. Таблица производных финансовых инструментов. Интегральный стол. Таблица первообразных. Найдите производную. Найдите интеграл. Диффурсы.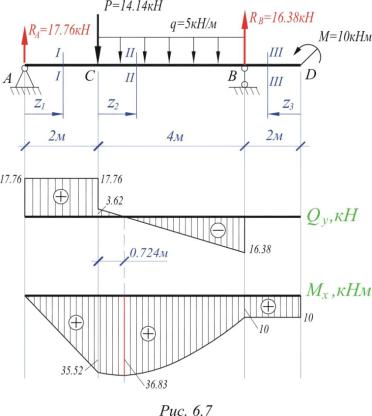 Комплексные числа. Мнимая единица.Линейная алгебра. (Векторы, матрицы) Математика для самых маленьких. Детский сад — 7 класс. Математическая логика. Решение уравнений. Квадратичные и биквадратные уравнения. Формулы. Методы. Решение дифференциальных уравнений Примеры решений обыкновенных дифференциальных уравнений более высокого порядка, чем первое. Примеры решений простейших = решаемых аналитически обыкновенных дифференциальных уравнений первого порядка. Системы координат. Прямоугольные декартовы, полярные, цилиндрические и сферические.2D и 3D. Системы счисления. Цифры и цифры (действительные, комплексные,….). Таблицы систем счисления. Степенные ряды Тейлора, Маклорена (= Макларена) и периодические ряды Фурье. Разложение функций на серии. Таблицы логарифмов и основных формул Таблицы числовых значений Таблицы Брадиса. Теория вероятностей и статистика Тригонометрические функции, формулы и графики. sin, cos, tg, ctg…. Значения тригонометрических функций. Формулы приведения тригонометрических функций.
Комплексные числа. Мнимая единица.Линейная алгебра. (Векторы, матрицы) Математика для самых маленьких. Детский сад — 7 класс. Математическая логика. Решение уравнений. Квадратичные и биквадратные уравнения. Формулы. Методы. Решение дифференциальных уравнений Примеры решений обыкновенных дифференциальных уравнений более высокого порядка, чем первое. Примеры решений простейших = решаемых аналитически обыкновенных дифференциальных уравнений первого порядка. Системы координат. Прямоугольные декартовы, полярные, цилиндрические и сферические.2D и 3D. Системы счисления. Цифры и цифры (действительные, комплексные,….). Таблицы систем счисления. Степенные ряды Тейлора, Маклорена (= Макларена) и периодические ряды Фурье. Разложение функций на серии. Таблицы логарифмов и основных формул Таблицы числовых значений Таблицы Брадиса. Теория вероятностей и статистика Тригонометрические функции, формулы и графики. sin, cos, tg, ctg…. Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества.Оборудование для численных методов — стандарты, размеры Бытовая техника, бытовая техника. Дренажные и дренажные системы. Емкости, резервуары, резервуары, резервуары. КИПиА. КИПиА. Измерение температуры. Конвейеры, ленточные конвейеры. Контейнеры (ссылка) Крепеж. Лабораторное оборудование. Насосы и насосные станции Насосы для жидкостей и шламов. Инженерный жаргон. Словарь. Скрининг. Фильтрация. Разделение частиц через сетки и сита.Примерная прочность канатов, канатов, шнуров, канатов из различных пластиков. Резиновые изделия. Суставы и соединения. Номинальные диаметры, DN, DN, NPS и NB. Метрические и дюймовые диаметры. SDR. Ключи и шпоночные пазы. Стандарты связи. Сигналы в системах автоматизации (КИПиА) Аналоговые входные и выходные сигналы приборов, датчиков, расходомеров и устройств автоматики. Интерфейсы подключения. Протоколы связи (коммуникации) Телефонная связь. Аксессуары для трубопроводов. Краны, задвижки, задвижки….Строительные длины. Фланцы и резьба.
Тригонометрические тождества.Оборудование для численных методов — стандарты, размеры Бытовая техника, бытовая техника. Дренажные и дренажные системы. Емкости, резервуары, резервуары, резервуары. КИПиА. КИПиА. Измерение температуры. Конвейеры, ленточные конвейеры. Контейнеры (ссылка) Крепеж. Лабораторное оборудование. Насосы и насосные станции Насосы для жидкостей и шламов. Инженерный жаргон. Словарь. Скрининг. Фильтрация. Разделение частиц через сетки и сита.Примерная прочность канатов, канатов, шнуров, канатов из различных пластиков. Резиновые изделия. Суставы и соединения. Номинальные диаметры, DN, DN, NPS и NB. Метрические и дюймовые диаметры. SDR. Ключи и шпоночные пазы. Стандарты связи. Сигналы в системах автоматизации (КИПиА) Аналоговые входные и выходные сигналы приборов, датчиков, расходомеров и устройств автоматики. Интерфейсы подключения. Протоколы связи (коммуникации) Телефонная связь. Аксессуары для трубопроводов. Краны, задвижки, задвижки….Строительные длины. Фланцы и резьба. Стандарты. Присоединительные размеры. Потоки. Обозначения, размеры, использование, типы… (ссылка на ссылку) Соединения («гигиенические», «асептические») трубопроводов в пищевой, молочной и фармацевтической промышленности. Трубы, трубопроводы. Диаметр труб и другие характеристики. Выбор диаметра трубопровода. Расходы. Расходы. Сила. Таблицы подбора, Падение давления. Медные трубы. Диаметр труб и другие характеристики. Трубы поливинилхлоридные (ПВХ).Диаметр труб и другие характеристики. Полиэтиленовые трубы. Диаметр труб и другие характеристики. Трубы полиэтиленовые ПНД. Диаметр труб и другие характеристики. Трубы стальные (в том числе нержавеющие). Диаметр труб и другие характеристики. Стальная труба. Труба нержавеющая. Трубы из нержавеющей стали. Диаметр труб и другие характеристики. Труба нержавеющая. Трубы из углеродистой стали. Диаметр труб и другие характеристики. Стальная труба. Примерка. Фланцы по ГОСТ, DIN (EN 1092-1) и ANSI (ASME).Фланцевое соединение. Фланцевые соединения. Фланцевое соединение.
Стандарты. Присоединительные размеры. Потоки. Обозначения, размеры, использование, типы… (ссылка на ссылку) Соединения («гигиенические», «асептические») трубопроводов в пищевой, молочной и фармацевтической промышленности. Трубы, трубопроводы. Диаметр труб и другие характеристики. Выбор диаметра трубопровода. Расходы. Расходы. Сила. Таблицы подбора, Падение давления. Медные трубы. Диаметр труб и другие характеристики. Трубы поливинилхлоридные (ПВХ).Диаметр труб и другие характеристики. Полиэтиленовые трубы. Диаметр труб и другие характеристики. Трубы полиэтиленовые ПНД. Диаметр труб и другие характеристики. Трубы стальные (в том числе нержавеющие). Диаметр труб и другие характеристики. Стальная труба. Труба нержавеющая. Трубы из нержавеющей стали. Диаметр труб и другие характеристики. Труба нержавеющая. Трубы из углеродистой стали. Диаметр труб и другие характеристики. Стальная труба. Примерка. Фланцы по ГОСТ, DIN (EN 1092-1) и ANSI (ASME).Фланцевое соединение. Фланцевые соединения. Фланцевое соединение. Элементы трубопроводов. Электрические лампы Электрические соединители и провода (кабели) Электродвигатели. Электродвигатели. Электрические коммутационные аппараты. (Ссылка на раздел) Стандарты личной жизни инженеров География для инженеров. Расстояния, маршруты, карты … .. Инженеры дома. Семья, дети, досуг, одежда и жилье. Дети инженеров. Инженеры в офисах. Инженеры и другие люди. Социализация инженеров. Курьезы.Отдыхающие инженеры. Это нас шокировало. Инженеры и еда. Рецепты, полезности. Уловки для ресторанов. Международная торговля для инженеров. Научиться думать по-хобби. Транспорт и путешествия. Личные автомобили, велосипеды…. Физика и химия человека. Экономика для инженеров. Болтовня финансистов — это человеческий язык. Технологические концепции и рисунки Писатель, рисунок, офисная бумага и конверты. Стандартные размеры фото. Вентиляция и кондиционирование. Водоснабжение и канализация. Горячее водоснабжение (ГВС).Питьевое водоснабжение Сточные воды. Холодное водоснабжение Гальваническая промышленность Охлаждение Паропроводы / системы.
Элементы трубопроводов. Электрические лампы Электрические соединители и провода (кабели) Электродвигатели. Электродвигатели. Электрические коммутационные аппараты. (Ссылка на раздел) Стандарты личной жизни инженеров География для инженеров. Расстояния, маршруты, карты … .. Инженеры дома. Семья, дети, досуг, одежда и жилье. Дети инженеров. Инженеры в офисах. Инженеры и другие люди. Социализация инженеров. Курьезы.Отдыхающие инженеры. Это нас шокировало. Инженеры и еда. Рецепты, полезности. Уловки для ресторанов. Международная торговля для инженеров. Научиться думать по-хобби. Транспорт и путешествия. Личные автомобили, велосипеды…. Физика и химия человека. Экономика для инженеров. Болтовня финансистов — это человеческий язык. Технологические концепции и рисунки Писатель, рисунок, офисная бумага и конверты. Стандартные размеры фото. Вентиляция и кондиционирование. Водоснабжение и канализация. Горячее водоснабжение (ГВС).Питьевое водоснабжение Сточные воды. Холодное водоснабжение Гальваническая промышленность Охлаждение Паропроводы / системы. Конденсатопроводы / системы. Паропроводы. Конденсатопроводы. Пищевая промышленность Газоснабжение Сварка металлов Условные обозначения и обозначения оборудования на чертежах и схемах. Условные графические изображения в проектах отопления, вентиляции, кондиционирования и отопления и охлаждения в соответствии со стандартом ANSI / ASHRAE 134-2005. Стерилизация оборудования и материалов Теплоснабжение Электронная промышленность Электроснабжение Физический справочник Азбуки.Принятые обозначения. Основные физические константы. Влажность бывает абсолютной, относительной и специфической. Влажность воздуха. Психрометрические таблицы. Диаграммы Рамзина. Временная вязкость, число Рейнольдса (Re). Единицы вязкости. Газы. Свойства газов. Индивидуальные газовые постоянные. Давление и вакуум Вакуум Длина, расстояние, линейный размер Звук. Ультразвук. Коэффициенты звукопоглощения (ссылка на другой раздел) Климат. Климатические данные. Натуральные данные. СНиП 23-01-99. Строительная климатология. (Статистика климатических данных) СНиП 23-01-99.
Конденсатопроводы / системы. Паропроводы. Конденсатопроводы. Пищевая промышленность Газоснабжение Сварка металлов Условные обозначения и обозначения оборудования на чертежах и схемах. Условные графические изображения в проектах отопления, вентиляции, кондиционирования и отопления и охлаждения в соответствии со стандартом ANSI / ASHRAE 134-2005. Стерилизация оборудования и материалов Теплоснабжение Электронная промышленность Электроснабжение Физический справочник Азбуки.Принятые обозначения. Основные физические константы. Влажность бывает абсолютной, относительной и специфической. Влажность воздуха. Психрометрические таблицы. Диаграммы Рамзина. Временная вязкость, число Рейнольдса (Re). Единицы вязкости. Газы. Свойства газов. Индивидуальные газовые постоянные. Давление и вакуум Вакуум Длина, расстояние, линейный размер Звук. Ультразвук. Коэффициенты звукопоглощения (ссылка на другой раздел) Климат. Климатические данные. Натуральные данные. СНиП 23-01-99. Строительная климатология. (Статистика климатических данных) СНиП 23-01-99. 2 Па. РФ. СНиП 23-01-99. Таблица 1. Климатические параметры холодного времени года. Бывший СССР. Плотность. Вес. Удельный вес. Объемная плотность. Поверхностное натяжение. Растворимость. Растворимость газов и твердых тел. Свет и цвет. Коэффициенты отражения, поглощения и преломления Цветовой алфавит 🙂 — Обозначения (кодировка) цвета (цветов). Свойства криогенных материалов и сред. Таблицы. Коэффициенты трения для различных материалов. Тепловые величины, включая кипение, плавление, пламя и т. Д.…… для получения дополнительной информации см .: Адиабатические коэффициенты (экспоненты). Конвекция и полная теплопередача. Коэффициенты теплового линейного расширения, теплового объемного расширения. Температуры, кипение, плавление, прочее … Перевод единиц измерения температуры. Воспламеняемость. Точка размягчения. Точки кипения Точки плавления Теплопроводность. Коэффициенты теплопроводности. Термодинамика. Удельная теплота испарения (конденсации). Энтальпия испарения. Удельная теплотворная способность (теплотворная способность).
2 Па. РФ. СНиП 23-01-99. Таблица 1. Климатические параметры холодного времени года. Бывший СССР. Плотность. Вес. Удельный вес. Объемная плотность. Поверхностное натяжение. Растворимость. Растворимость газов и твердых тел. Свет и цвет. Коэффициенты отражения, поглощения и преломления Цветовой алфавит 🙂 — Обозначения (кодировка) цвета (цветов). Свойства криогенных материалов и сред. Таблицы. Коэффициенты трения для различных материалов. Тепловые величины, включая кипение, плавление, пламя и т. Д.…… для получения дополнительной информации см .: Адиабатические коэффициенты (экспоненты). Конвекция и полная теплопередача. Коэффициенты теплового линейного расширения, теплового объемного расширения. Температуры, кипение, плавление, прочее … Перевод единиц измерения температуры. Воспламеняемость. Точка размягчения. Точки кипения Точки плавления Теплопроводность. Коэффициенты теплопроводности. Термодинамика. Удельная теплота испарения (конденсации). Энтальпия испарения. Удельная теплотворная способность (теплотворная способность). Потребность в кислороде. Электрические и магнитные величины. Электрические дипольные моменты. Диэлектрическая проницаемость. Электрическая постоянная. Длины электромагнитных волн (справочник другого раздела) Напряженности магнитного поля Понятия и формулы электричества и магнетизма. Электростатика. Пьезоэлектрические модули. Электрическая прочность материалов. Электрический ток. Электрическое сопротивление и проводимость. Электронные потенциалы. Химический справочник «Химический алфавит (словарь)» — названия, сокращения, префиксы, обозначения веществ и соединений.Водные растворы и смеси для обработки металлов. Водные растворы для нанесения и удаления металлических покрытий. Водные растворы для очистки от углеродных отложений (асфальтово-смолистые углеродистые отложения, углеродные отложения от двигателей внутреннего сгорания …) Водные растворы для пассивации. Водные растворы для травления — удаления оксидов с поверхности Водные растворы для фосфатирования Водные растворы и смеси для химического окисления и окраски металлов.
Потребность в кислороде. Электрические и магнитные величины. Электрические дипольные моменты. Диэлектрическая проницаемость. Электрическая постоянная. Длины электромагнитных волн (справочник другого раздела) Напряженности магнитного поля Понятия и формулы электричества и магнетизма. Электростатика. Пьезоэлектрические модули. Электрическая прочность материалов. Электрический ток. Электрическое сопротивление и проводимость. Электронные потенциалы. Химический справочник «Химический алфавит (словарь)» — названия, сокращения, префиксы, обозначения веществ и соединений.Водные растворы и смеси для обработки металлов. Водные растворы для нанесения и удаления металлических покрытий. Водные растворы для очистки от углеродных отложений (асфальтово-смолистые углеродистые отложения, углеродные отложения от двигателей внутреннего сгорания …) Водные растворы для пассивации. Водные растворы для травления — удаления оксидов с поверхности Водные растворы для фосфатирования Водные растворы и смеси для химического окисления и окраски металлов. Водные растворы и смеси для химической полировки. Обезжиривание водных растворов и органических растворителей pH.Таблицы PH. Горение и взрывы. Окисление и восстановление. Классы, категории, обозначения опасности (токсичности) химических веществ Периодическая система химических элементов Д. И. Менделеев. Таблица Менделеева. Плотность органических растворителей (г / см3) в зависимости от температуры. 0-100 ° С. Свойства растворов. Константы диссоциации, кислотность, основность. Растворимость. Смеси. Термические константы веществ. Энтальпии. Энтропия. Gibbs energy … (ссылка на химический справочник проекта) Электротехника Регуляторы Системы гарантированного и бесперебойного электроснабжения.Системы диспетчеризации и управления Структурированные кабельные системы Центры обработки данных
Водные растворы и смеси для химической полировки. Обезжиривание водных растворов и органических растворителей pH.Таблицы PH. Горение и взрывы. Окисление и восстановление. Классы, категории, обозначения опасности (токсичности) химических веществ Периодическая система химических элементов Д. И. Менделеев. Таблица Менделеева. Плотность органических растворителей (г / см3) в зависимости от температуры. 0-100 ° С. Свойства растворов. Константы диссоциации, кислотность, основность. Растворимость. Смеси. Термические константы веществ. Энтальпии. Энтропия. Gibbs energy … (ссылка на химический справочник проекта) Электротехника Регуляторы Системы гарантированного и бесперебойного электроснабжения.Системы диспетчеризации и управления Структурированные кабельные системы Центры обработки данных Тригонометрия как наука зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентации звезд. Эти расчеты относились к сферической тригонометрии, а в школьном курсе изучаются соотношения сторон и углов плоского треугольника.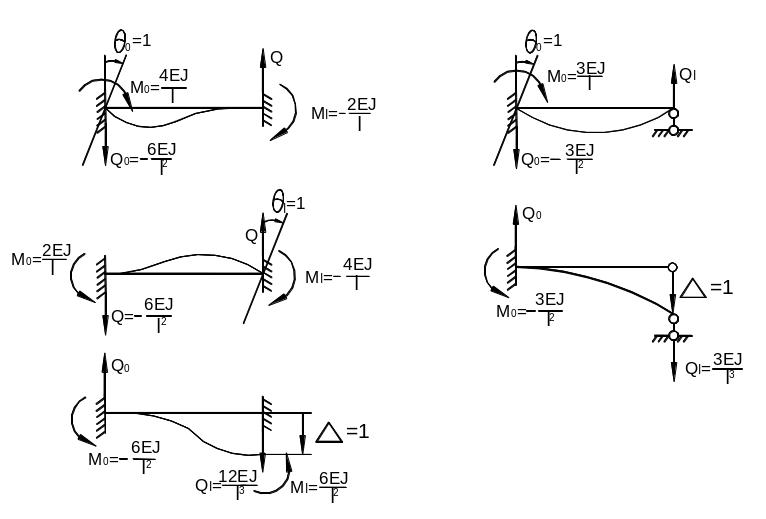
Тригонометрия — это раздел математики, изучающий свойства тригонометрических функций и отношения между сторонами и углами треугольников.
В период расцвета культуры и науки в I тысячелетии нашей эры знания распространились с Древнего Востока в Грецию. Но главные открытия тригонометрии — заслуга людей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений синусов, тангенсов и котангенсов. Понятие синуса и косинуса было введено индийскими учеными. Большое внимание тригонометрии уделяется в творчестве таких великих деятелей античности, как Евклид, Архимед и Эратосфен.
Основные параметры тригонометрии
Основными тригонометрическими функциями числового аргумента являются синус, косинус, тангенс и котангенс. Каждому из них соответствует свой график: синусоида, косинус, тангенс и котангенс.
Формулы для вычисления значений этих величин основаны на теореме Пифагора. Школьникам лучше знакома формулировка: «Пифагорейские штаны, равные во всех направлениях», так как доказательство дается на примере равнобедренного прямоугольного треугольника.
Школьникам лучше знакома формулировка: «Пифагорейские штаны, равные во всех направлениях», так как доказательство дается на примере равнобедренного прямоугольного треугольника.
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих значений для угла A и проследим взаимосвязь тригонометрических функций:
Как видите, tg и ctg — обратные функции. Если мы представим отрезок a как произведение sin A и гипотенузы c, а отрезок b как cos A * c, то мы получим следующие формулы для тангенса и котангенса:
Тригонометрический круг
Графически соотношение этих величин можно представить следующим образом:
Окружность в данном случае представляет все возможные значения угла α — от 0 ° до 360 °.Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от значения угла. Например, sin α будет со знаком «+», если α принадлежит I и II четвертям круга, то есть находится в диапазоне от 0 ° до 180 °. Когда α составляет от 180 ° до 360 ° (III и IV четверти), sin α может быть только отрицательным.
Когда α составляет от 180 ° до 360 ° (III и IV четверти), sin α может быть только отрицательным.
Попробуем построить тригонометрические таблицы для конкретных углов и узнать значения величин.
Значения α, равные 30 °, 45 °, 60 °, 90 °, 180 ° и т. Д., Называются частными случаями.Значения тригонометрических функций для них рассчитываются и представляются в виде специальных таблиц.
Эти углы выбраны не случайно. Обозначение π в таблицах означает радианы. Rad — это угол, при котором длина дуги окружности соответствует ее радиусу. Это значение было введено для установления универсальной зависимости; при расчете в радианах фактическая длина радиуса в см не имеет значения.
Углы в таблицах тригонометрических функций соответствуют значениям радианов:
Итак, нетрудно догадаться, что 2π — это полный круг или 360 °.
Свойства тригонометрических функций: синус и косинус
Чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо изобразить их функции. Это можно сделать в виде кривой, расположенной в двухмерной системе координат.
Это можно сделать в виде кривой, расположенной в двухмерной системе координат.
Рассмотрим сравнительную таблицу свойств для синусоиды и косинусоиды:
| Синусоида | Косинус |
|---|---|
| y = sin x | y = cos x |
| ODZ [-1; один] | ODZ [-1; один] |
| sin x = 0, для x = πk, где k ϵ Z | cos x = 0, для x = π / 2 + πk, где k ϵ Z |
| sin x = 1, для x = π / 2 + 2πk, где k ϵ Z | cos x = 1, для x = 2πk, где k ϵ Z |
| sin x = — 1, для x = 3π / 2 + 2πk, где k ϵ Z | cos x = — 1, для x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. Е.е. функция нечетная | cos (-x) = cos x, т.е. функция четная |
| функция периодическая, наименьший период 2π | |
| sin x ›0, для x, принадлежащих I и II четвертям, или от 0 ° до 180 ° (2πk, π + 2πk) | cos x› 0, для x, принадлежащих I и IV четвертям, или от 270 ° до 90 ° (- π / 2 + 2πk, π / 2 + 2πk) |
| sin x ‹0, для x, принадлежащих III и IV четвертям, или от 180 ° до 360 ° (π + 2πk, 2π + 2πk) | cos x‹ 0, при x, принадлежащих II и III четвертям, или от 90 ° до 270 ° (π / 2 + 2πk, 3π / 2 + 2πk) |
| увеличивается на интервале [- π / 2 + 2πk, π / 2 + 2πk] | увеличивается на интервале [-π + 2πk, 2πk] |
| убывает на интервалах [π / 2 + 2πk, 3π / 2 + 2πk] | убывает на интервалах |
| производная (sin x) ’= cos x | производная (cos x)’ = — sin x |
Определить, четная функция или нет, очень просто.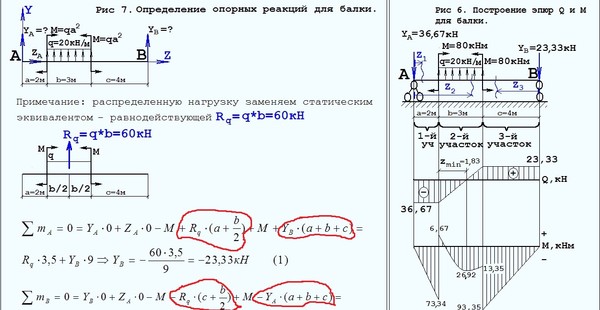 Достаточно представить себе тригонометрический круг со знаками тригонометрических величин и мысленно «свернуть» график вокруг оси OX. Если знаки совпадают, функция четная; в противном случае это странно.
Достаточно представить себе тригонометрический круг со знаками тригонометрических величин и мысленно «свернуть» график вокруг оси OX. Если знаки совпадают, функция четная; в противном случае это странно.
Введение радианов и перечисление основных свойств синусоиды и косинуса позволяют дать следующую закономерность:
Проверить правильность формулы очень просто. Например, для x = π / 2 синус равен 1, как и косинус x = 0.Проверку можно проводить, обращаясь к таблицам или отслеживая кривые функций для заданных значений.
Тангентоидные и котангентоидные свойства
Графики функций тангенса и котангенса существенно отличаются от синуса и косинуса. Значения tg и ctg противоположны друг другу.
- Y = tg x.
- Тангентоид стремится к значениям y при x = π / 2 + πk, но никогда не достигает их.
- Наименьший положительный период тангентоида равен π.
- Tg (- x) = — tg x, то есть функция нечетная.
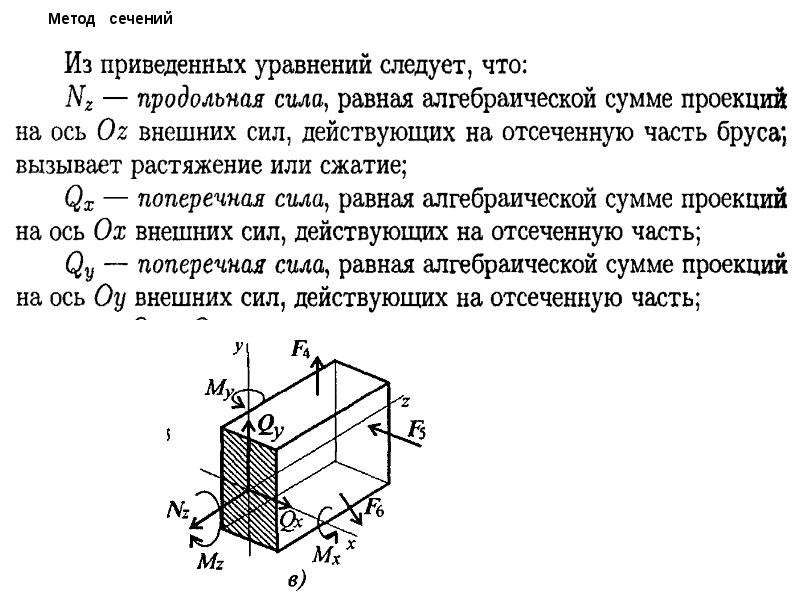
- Tg x = 0 для x = πk.
- Функция увеличивается.
- Tg x ›0, если x ϵ (πk, π / 2 + πk).
- Tg x ‹0, для x ϵ (- π / 2 + πk, πk).
- Производная (tg x) ’= 1 / cos 2 x.
Рассмотрим графическое представление котангентоида ниже в тексте.
Основные свойства котангенсоида:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангентоиде Y может принимать значения набора всех действительных чисел.
- Котангенсоид стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоида равен π.
- Ctg (- x) = — ctg x, то есть функция нечетная.
- Ctg x = 0, если x = π / 2 + πk.
- Функция убывает.
- Ctg x ›0, если x ϵ (πk, π / 2 + πk).
- Ctg x ‹0, если x ϵ (π / 2 + πk, πk).
- Производная (ctg x) ’= — 1 / sin 2 x Правильно
Примечание . .. В этой таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/».
.. В этой таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/».
см. Также полезные материалы:
Для , определяющего значение тригонометрической функции , найдите его на пересечении линии тригонометрической функции. Например, синус 30 градусов — ищем столбец с заголовком sin (синус) и находим пересечение этого столбца таблицы с линией «30 градусов», при их пересечении читаем результат — одну секунду.Точно так же мы находим косинус 60 градуса, синус 60 градуса (опять же, на пересечении столбца sin (синуса) и строки 60 градусов, мы находим значение sin 60 = √3 / 2) и т. Д. Таким же образом находятся значения синусов, косинусов и тангенсов других «популярных» углов.
Синус числа Пи, косинус числа Пи, тангенс числа Пи и другие углы в радианах
Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значений тригонометрических функций, аргумент которых задан в радианах .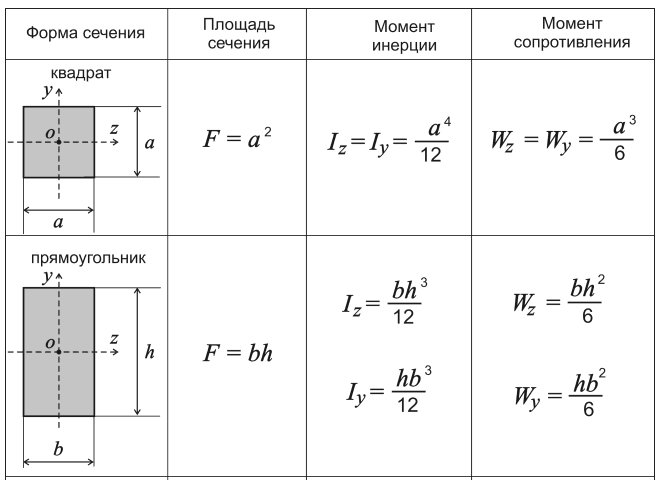 .. Для этого используйте второй столбец значений углов. Благодаря этому вы можете переводить значение популярных углов из градусов в радианы. Например, давайте найдем угол 60 градусов в первой строке и прочитаем его значение в радианах под ним. 60 градусов равны π / 3 радиан.
.. Для этого используйте второй столбец значений углов. Благодаря этому вы можете переводить значение популярных углов из градусов в радианы. Например, давайте найдем угол 60 градусов в первой строке и прочитаем его значение в радианах под ним. 60 градусов равны π / 3 радиан.
Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Итак, пи радианы равны 180 градусам.
Любое число, выраженное в единицах пи (радиан), можно легко преобразовать в градусы, заменив пи (π) на 180 .
Примеры :
1. Sine pi .
sin π = sin 180 = 0
, таким образом, синус числа пи такой же, как синус 180 градусов, и равен нулю.
2. Косинус пи .
cos π = cos 180 = -1
, таким образом, косинус числа пи совпадает с косинусом 180 градусов и равен минус единице.
3. Касательная пи
tg π = tg 180 = 0
Таким образом, тангенс числа пи такой же, как тангенс 180 градусов, и равен нулю.
Таблица значений синуса, косинуса и тангенса для углов 0 — 360 градусов (общие значения)
| значение угла α (градусы) | значение угла α (через число пи) | sin (синус) | cos (косинус) | тг (касательная) | ctg (котангенс) | сек (секанс) | косеканс (косеканс) |
| 0 | 0 | 0 | 1 | 0 | — | 1 | — |
| 15 | π / 12 | 2 — √3 | 2 + √3 | ||||
| 30 | π / 6 | 1/2 | √3 / 2 | 1 / √3 | √3 | 2 / √3 | 2 |
| 45 | π / 4 | √2 / 2 | √2 / 2 | 1 | 1 | √2 | √2 |
| 60 | π / 3 | √3 / 2 | 1/2 | √3 | 1 / √3 | 2 | 2 / √3 |
| 75 | 5π / 12 | 2 + √3 | 2 — √3 | ||||
| 90 | π / 2 | 1 | 0 | — | 0 | — | 1 |
| 105 | 7π / 12 | — | — 2 — √3 | √3 — 2 | |||
| 120 | 2π / 3 | √3 / 2 | -1/2 | -√3 | -√3 / 3 | ||
| 135 | 3π / 4 | √2 / 2 | -√2 / 2 | -1 | -1 | -√2 | √2 |
| 150 | 5π / 6 | 1/2 | -√3 / 2 | -√3 / 3 | -√3 | ||
| 180 | π | 0 | -1 | 0 | — | -1 | — |
| 210 | 7π / 6 | -1/2 | -√3 / 2 | √3 / 3 | √3 | ||
| 240 | 4π / 3 | -√3 / 2 | -1/2 | √3 | √3 / 3 | ||
| 270 | 3π / 2 | -1 | 0 | — | 0 | — | -1 |
| 360 | 2π | 0 | 1 | 0 | — | 1 | — |
Если в таблице значений тригонометрических функций вместо значения функции указано тире (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов), то функция не имеет определенного значения для этого значения градусной меры угла. Если дефиса нет — ячейка пуста, значит, мы еще не ввели нужное значение. Нас интересует, с какими запросами к нам приходят пользователи и дополняют таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов наиболее часто встречающихся значений углов вполне достаточно, чтобы решить большинство проблем.
Если дефиса нет — ячейка пуста, значит, мы еще не ввели нужное значение. Нас интересует, с какими запросами к нам приходят пользователи и дополняют таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов наиболее часто встречающихся значений углов вполне достаточно, чтобы решить большинство проблем.
Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов
0, 15, 30, 45, 60, 90 … 360 градусов
(числовые значения «как в таблицах Брадиса»)
| значение угла α (градусы) | значение угла α в радианах | грех (синус) | cos (косинус) | тг (касательная) | ctg (котангенс) |
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 15 | 0,2588 | 0,9659 | 0,2679 | ||
| 30 | 0,5000 | 0,5774 | |||
| 45 | 0,7071 | ||||
0,7660 | |||||
| 60 | 0,8660 | 0,5000 | 1,7321 | ||
7π / 18 |
Внимание!
В Особом разделе 555 есть дополнительные
материалов.
Для тех, кто очень «не очень …»
И для тех, кто «очень даже …»)
Прежде всего, напомню простой, но очень полезный вывод из урока «Что такое синус и косинус? Что такое тангенс и котангенс?»
Вот результат:
Синус, косинус, тангенс и котангенс тесно связаны со своими углами. Мы знаем одно — значит, знаем другое.
Другими словами, каждый угол имеет свой постоянный синус и косинус.И практически у каждого свой тангенс и котангенс. Почему почти ? Подробнее об этом ниже.
Эти знания очень помогают в обучении! Есть много задач, в которых вам нужно перейти от синусов к углам и наоборот. Для этого существует таблица синусов. Аналогично для задач с косинусом — таблица косинусов. И, как вы уже догадались, существует таблица касательных , и таблица котангенсов . )
Есть разные таблицы. Длинный, где вы можете увидеть, что равно, скажем, sin37 ° 6 ‘.Мы открываем таблицы Брадиса, ищем угол в тридцать семь градусов в течение шести минут и видим значение 0,6032.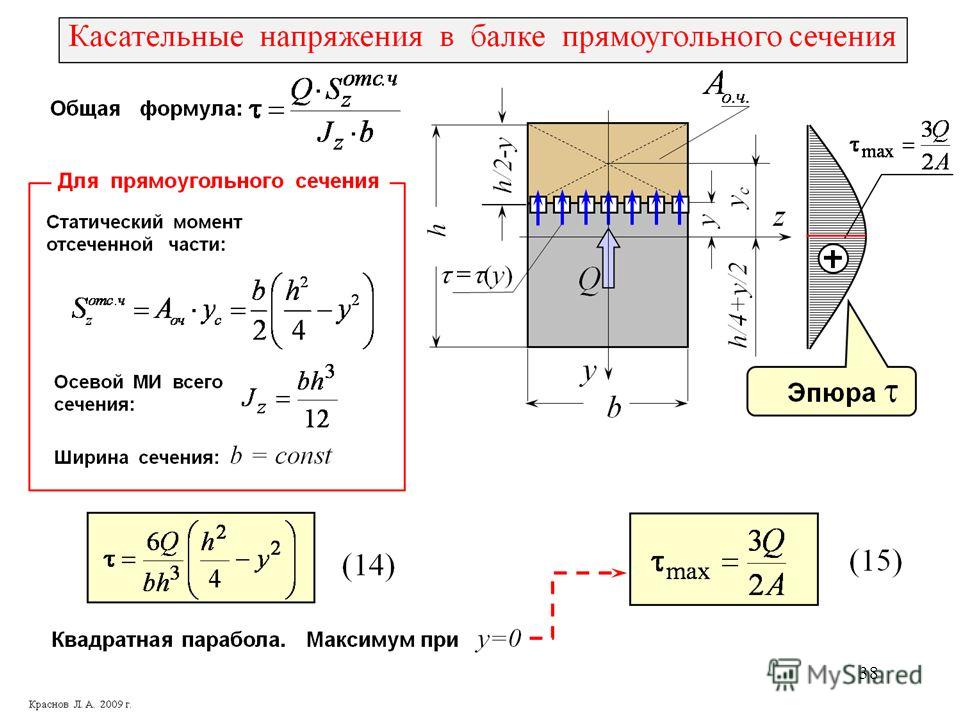 Понятно, что запоминание этого числа (и тысяч других табличных значений) вовсе не требуется.
Понятно, что запоминание этого числа (и тысяч других табличных значений) вовсе не требуется.
На самом деле, в наше время длинные таблицы косинусов синусов тангенсов котангенсов не особо нужны. Один хороший калькулятор полностью заменяет их. Но знать о существовании таких таблиц не помешает. Для общей эрудиции.)
А зачем тогда это занятие ?! — ты спрашиваешь.
Вот почему. Среди бесконечного количества углов есть особый, , о которых вы должны знать, все … Вся школьная геометрия и тригонометрия построены на этих углах. Это своего рода «таблица умножения» тригонометрии. Если вы не знаете, чему, например, равен sin50 °, никто вас не осудит.) Но если вы не знаете, что такое sin30 °, приготовьтесь получить заслуженные два …
Из таких также прилично набраны особые уголка.Школьные учебники обычно любезно предлагают для запоминания таблицу синусов и таблицу косинусов для семнадцати углов. И, конечно же, таблица тангенса и таблица котангенса для тех же семнадцати углов . .. предлагается запомнить 68 значений. Которые, кстати, очень похожи друг на друга, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти это все еще задача …)
.. предлагается запомнить 68 значений. Которые, кстати, очень похожи друг на друга, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти это все еще задача …)
Пойдем другим путем. Заменим механическое запоминание логикой и смекалкой.Затем мы должны запомнить 3 (три!) Значения для таблицы синусов и таблицы косинусов. И 3 (три!) Значения для таблицы касательных и таблицы котангенса. И это все. Шесть значений запомнить легче, чем 68, я думаю …)
Мы получим все остальные необходимые значения из этих шести, используя мощную юридическую шпаргалку. — тригонометрический круг. Если вы не изучали эту тему, переходите по ссылке, не поленитесь. Этот кружок нужен не только для этого урока. Незаменим для всей тригонометрии сразу … Просто грех не использовать такой инструмент! Ты не хочешь? Дело ваше. Запомните таблицу синусов . Таблица косинусов. Таблица касательных. Таблица котангенсов. Все 68 значений для разных углов.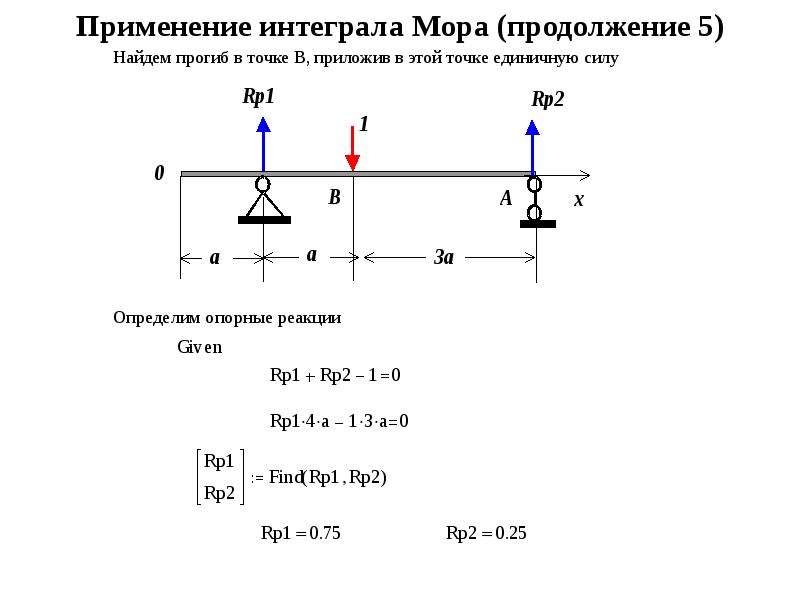 )
)
Итак, приступим. Для начала разделим все эти особые углы на три группы.
Первая группа углов.
Рассмотрим первую группу углов из семнадцати специальных … Это 5 углов: 0 °, 90 °, 180 °, 270 °, 360 °.
Вот так выглядит таблица синусов косинусов тангенсов котангенсов этих углов:
Угол x(в градусах) | 0 | 90 | 180 | 270 | 360 |
Угол x(в радианах) | 0 | ||||
sin x | 0 | 1 | 0 | -1 | 0 |
cos x | 1 | 0 | -1 | 0 | 1 |
тг x | 0 | не существительное | 0 | не существительное | 0 |
CTG x | не существительное | 0 | не существительное | 0 | не существительное |
Кто хочет вспомнить — помните.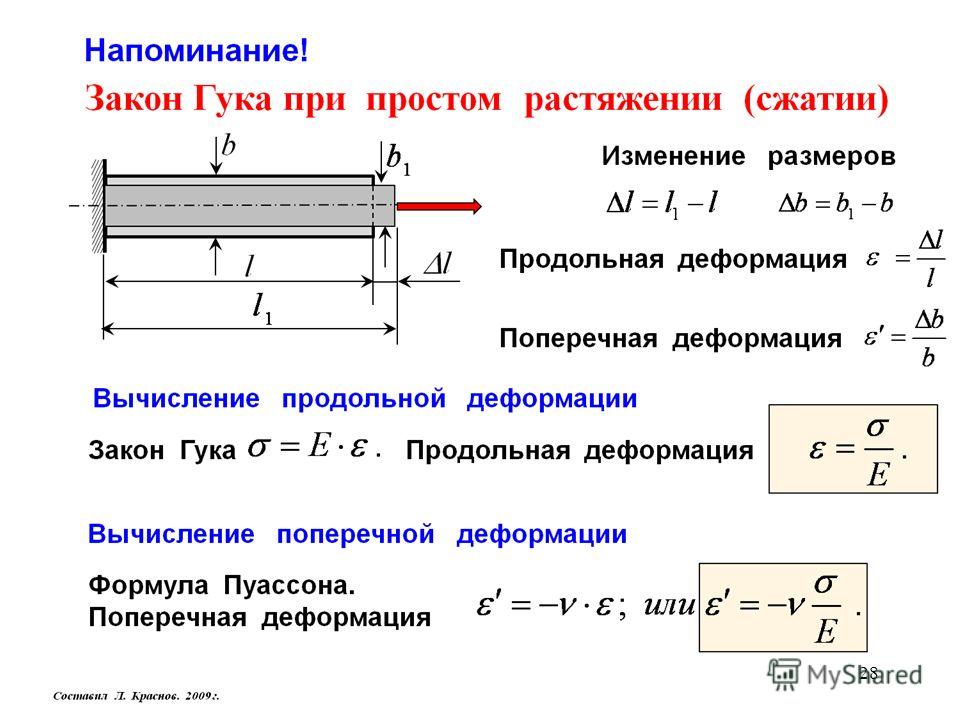 Но сразу скажу, что все эти единицы и нули очень запутаны в голове. Намного сильнее, чем вы хотите.) Поэтому включаем логику и тригонометрический круг.
Но сразу скажу, что все эти единицы и нули очень запутаны в голове. Намного сильнее, чем вы хотите.) Поэтому включаем логику и тригонометрический круг.
Нарисуйте круг и отметьте на нем те же углы: 0 °, 90 °, 180 °, 270 °, 360 °. Эти углы я обозначил красными точками:
Сразу видно, в чем особенность этих углов. Да! Это те углы, которые попадают точно на ось координат! Собственно поэтому народ и запутался… Но не запутаемся. Давайте разберемся, как без особого запоминания найти тригонометрические функции этих углов.
Кстати, угловое положение составляет 0 градусов полностью совпадает с с угловым положением 360 градусов. Это означает, что синусы, косинусы, тангенсы у этих углов в точности совпадают. Я отметил угол в 360 градусов, чтобы замкнуть круг.
Допустим, в сложной стрессовой обстановке экзамена вы как-то засомневались… Что такое пазуха 0 градусов? Вроде ноль … А если один ?! Механическое запоминание — это такая вещь. В суровых условиях начинают грызть сомнения .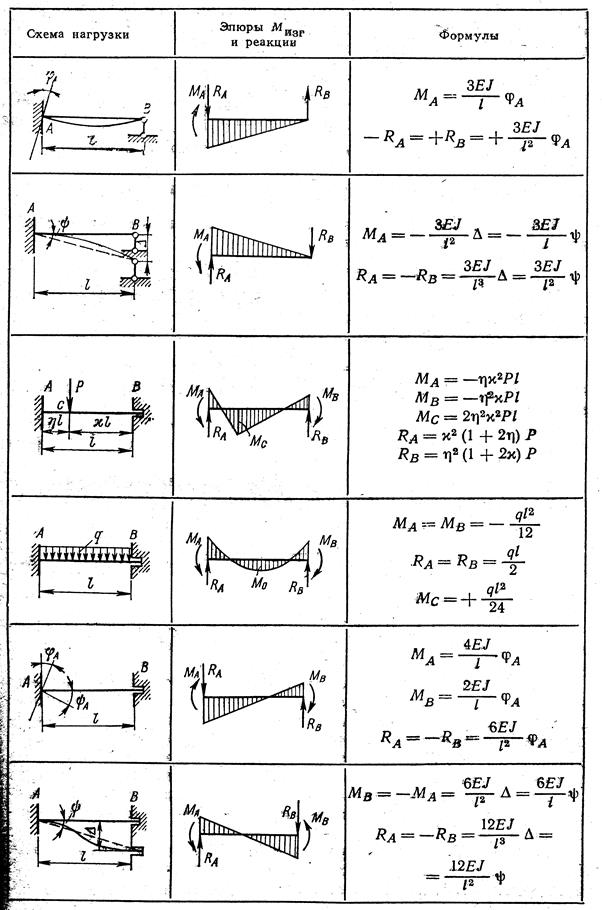 ..)
..)
Спокойствие, только спокойствие!) Подскажу практическую технику, которая даст 100% правильный ответ и полностью снимет все сомнения.
В качестве примера разберемся, как четко и надежно определить, скажем, синус 0 градусов. А заодно и косинус 0. Именно в этих значениях, как ни странно, люди часто путаются.
Для этого нарисуйте по окружности произвольный впрыск X … В первой четверти, чтобы было не далеко от 0 градусов. Обратите внимание на оси синуса и косинуса этого угла X, все является подбородком-подбородком. Как это:
А теперь — внимание! Уменьшаем угол X , приближаем подвижную сторону к оси OH. Наведите курсор на картинку (или нажмите на картинку на планшете), и вы все увидите.
А теперь включим элементарную логику !. Смотрим и думаем: Как ведет себя sinx при уменьшении угла x? Когда угол приближается к нулю? Уменьшается! И cosx увеличивается! Осталось выяснить, что станет с синусом, когда угол полностью схлопнется? Когда подвижная сторона угла (точка A) устанавливается на оси OX и угол становится равным нулю? Очевидно, синус угла тоже уйдет в ноль. И косинус увеличится до…к … Какова длина подвижной стороны угла (радиус тригонометрической окружности)? Один!
И косинус увеличится до…к … Какова длина подвижной стороны угла (радиус тригонометрической окружности)? Один!
Вот ответ. Синус 0 градусов равен 0. Косинус 0 градусов равен 1. Абсолютно железо и без сомнений!) Просто потому, что иначе быть не может.
Точно так же можно узнать (или уточнить) синус 270 градусов, например. Или косинус 180. Нарисуйте круг, произвольный угол в четверти рядом с интересующей нас координатной осью, мысленно переместите сторону угла и уловите, какими станут синус и косинус, когда сторона угла установится. на оси.Это все.
Как видите, для этой группы углов запоминать ничего не нужно. Здесь не нужна таблица синусов … да и таблица косинусов — тоже. Кстати, после нескольких применений тригонометрической окружности все эти значения запомнятся сами собой. А если забывают, я за 5 секунд рисовал кружок и уточнял. Намного проще, чем звонить другу из туалета с риском для справки, правда?)
Насчет тангенса и котангенса — все одинаково. Рисуем касательную (котангенс) на окружности — и все сразу видно. Где они равны нулю, а где их нет. Разве вы не знаете о касательных и котангенсах? Это печально, но поправимо.) Посетили Раздел 555 Тангенс и Котангенс на тригонометрической окружности — без проблем!
Рисуем касательную (котангенс) на окружности — и все сразу видно. Где они равны нулю, а где их нет. Разве вы не знаете о касательных и котангенсах? Это печально, но поправимо.) Посетили Раздел 555 Тангенс и Котангенс на тригонометрической окружности — без проблем!
Если вы догадались, как четко определить синус, косинус, тангенс и котангенс для этих пяти углов — поздравляем! На всякий случай сообщаю, что теперь вы можете определять функции любых углов, падающих на ось. А это и 450 °, и 540 °, и 1800 °, и бесконечное число …) Посчитал (правильно!) Угол на окружности — и с функциями проблем нет.
Но, просто, с подсчетом углов случаются проблемы и ошибки … Как их избежать, написано в уроке: Как нарисовать (посчитать) любой угол на тригонометрической окружности в градусах. Элементарно, но очень помогает при работе с ошибками.)
А вот и урок: Как нарисовать (посчитать) любой угол на тригонометрической окружности в радианах — будет круто.С точки зрения возможностей.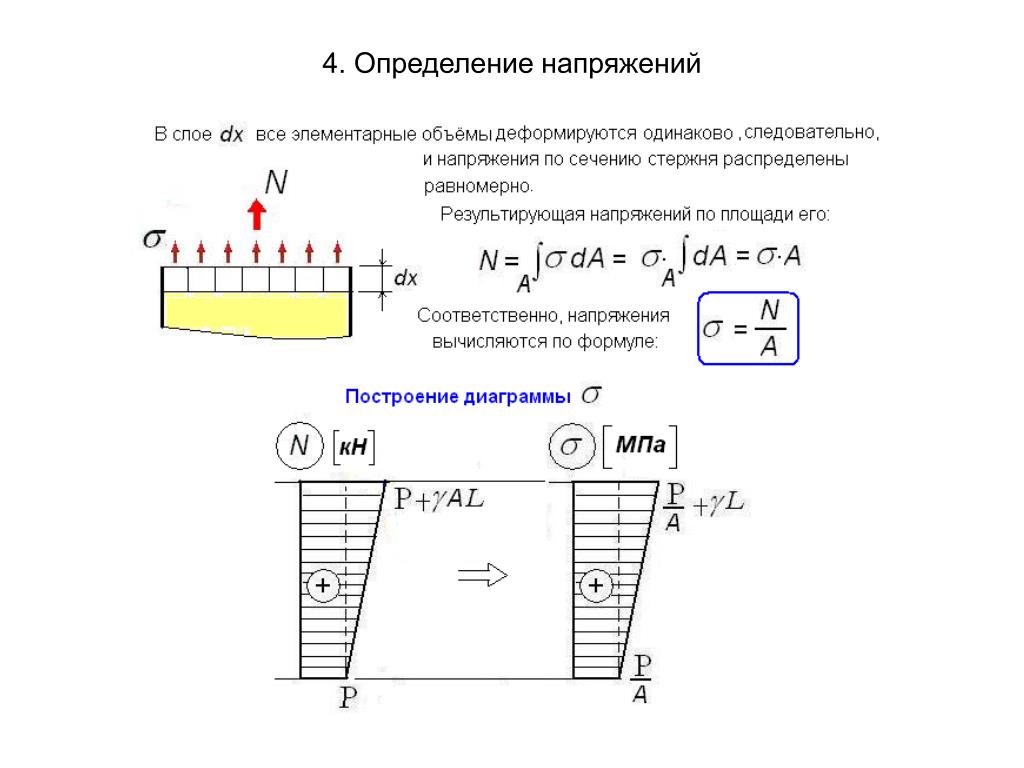 Допустим, определим, в какую из четырех полуосей угол падает на
Допустим, определим, в какую из четырех полуосей угол падает на
, вы можете сделать это за пару секунд. Я не шучу! Всего за пару секунд. Ну конечно не только 345 «пи» …) И 121, и 16, и -1345. Любой целый фактор хорош для мгновенного ответа.
А если угол
Подумать только! Правильный ответ приходит через 10 секунд. Для любого дробного значения радианов с двумя в знаменателе.
Собственно, для этого и годится тригонометрический круг.Дело в том, что возможность работы с некоторыми углами автоматически расширяется до бесконечного набора углов.
Итак, с пятью углами из семнадцати — разобрался.
Вторая группа углов.
Следующая группа углов — 30 °, 45 ° и 60 °. Почему именно эти, а не, например, 20, 50 и 80? Да, как-то так получилось … Исторически. Дальше будет видно, какие эти углы хороши.
Таблица синусов косинусов тангенсов котангенсов для этих углов выглядит так:
Угол x(в градусах) | 0 | 30 | 45 | 60 | 90 |
Угол x(в радианах) | 0 | ||||
sin x | 0 | 1 | |||
cos x | 1 | 0 | |||
тг x | 0 | 1 | не существительное | ||
CTG x | не существительное | 1 | 0 |
Я оставил значения для 0 ° и 90 ° из предыдущей таблицы, чтобы завершить картину. ) Так что вы можете видеть, что эти углы лежат в первой четверти и увеличиваются. От 0 до 90. Это нам пригодится в дальнейшем.
) Так что вы можете видеть, что эти углы лежат в первой четверти и увеличиваются. От 0 до 90. Это нам пригодится в дальнейшем.
Табличные значения углов 30 °, 45 ° и 60 ° необходимо запомнить. Подавайте, если хотите. Но даже здесь есть возможность облегчить себе жизнь.) Обратите внимание на значений таблицы синусов этих углов. И сравните со значениями таблицы косинусов …
Да! Они такие же! Только в обратном порядке.Углы увеличиваются (0, 30, 45, 60, 90) — и значения синуса увеличиваются с 0 до 1. Вы можете проверить это с помощью калькулятора. И значения косинуса уменьшаются от 1 до нуля. Причем сами значения одинаковые. Для углов 20, 50, 80 это не сработает …
Отсюда полезный вывод. Достаточно выучить три значения для углов 30, 45, 60 градусов. И помните, что они увеличиваются по синусу и уменьшаются по косинусу.По направлению к синусу.) На полпути (45 °) они встречаются, то есть синус 45 градусов равен косинусу 45 градусов.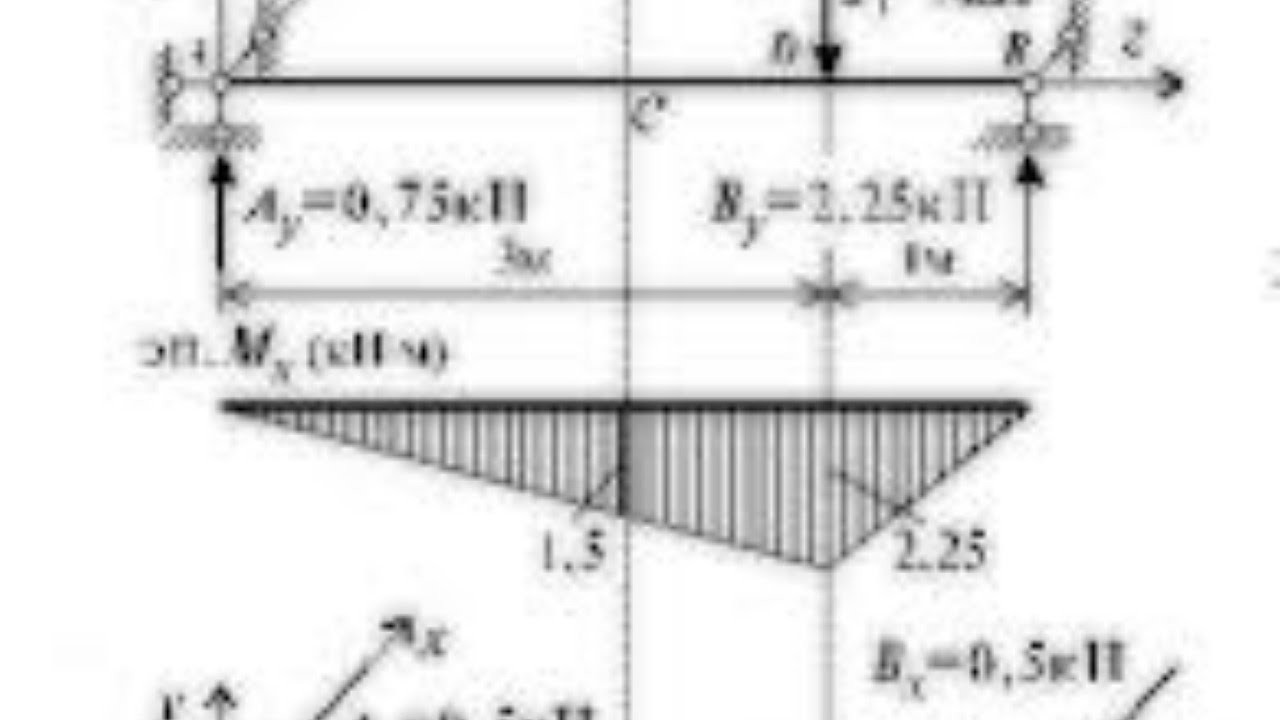 А потом они снова расходятся … Можно узнать три значения, не так ли?
А потом они снова расходятся … Можно узнать три значения, не так ли?
С касательными — котангенцами картина исключительно та же. Один к одному. Только значения разные. Эти значения (еще три!) Тоже нужно выучить.
Ну почти все запоминание окончено. Вы выяснили (надеюсь), как определить значения для пяти углов, которые попадают на ось, и узнали значения для углов 30, 45, 60 градусов.Только 8.
Осталось разобраться с последней группой из 9 угловых.
Это углы:
120 °; 135 °; 150 °; 210 °; 225 °; 240 °; 300 °; 315 °; 330 °. Для этих углов вам необходимо знать таблицу синусов, таблицу косинусов и т. Д.
Кошмар, да?)
А если мы добавим сюда углы, например: 405 °, 600 ° или 3000 ° и много-много таких же красивых?)
Или углы в радианах? Например, об углах:
и многие другие, вы должны знать все .
Самое смешное, что знать этот все — невозможно в принципе. Если вы используете механическую память.
И очень просто, на самом деле элементарно — если использовать тригонометрическую окружность. Как только вы освоите тригонометрический круг, все эти ужасные углы в градусах легко и элегантно сведутся к старому доброму:
Кстати, у меня для вас есть еще парочка интересных сайтов.)
Вы можете попрактиковаться в решении примеров и узнать свой уровень.Мгновенное проверочное тестирование. Учимся — с интересом!)
вы можете познакомиться с функциями и производными.
.

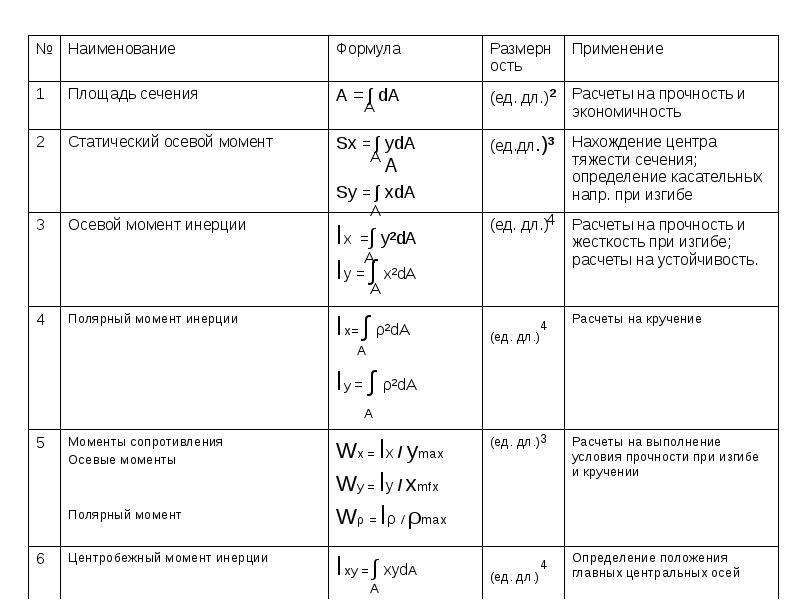
 2)
2)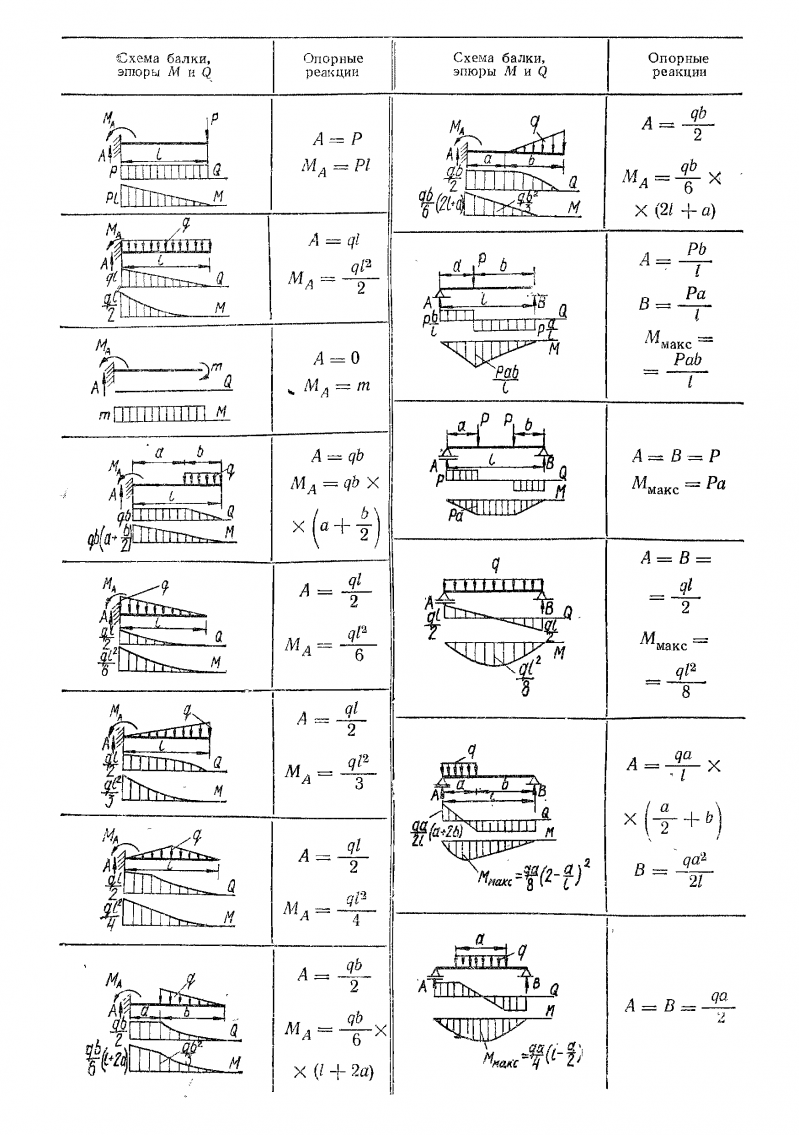 Выполнен с помощью он-лайн программы. (перейдя к примеру нажмите на одно из действий в блоке-меню «Расчет»)
Выполнен с помощью он-лайн программы. (перейдя к примеру нажмите на одно из действий в блоке-меню «Расчет»)
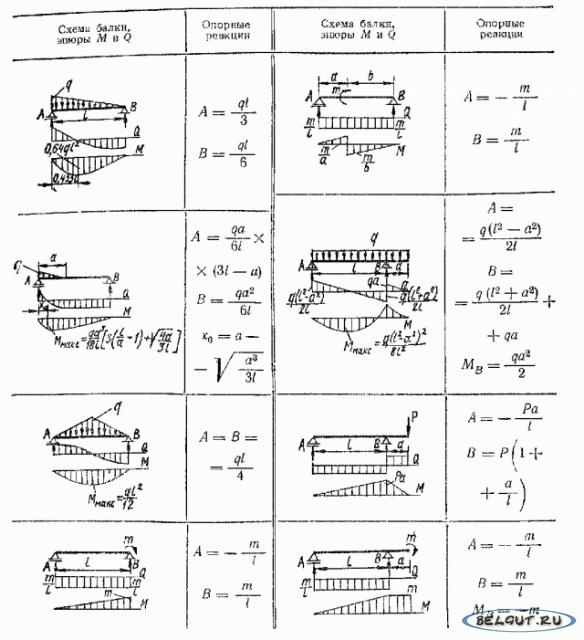 9)
9)