Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.
{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Биомеханика ходьбы и бега.
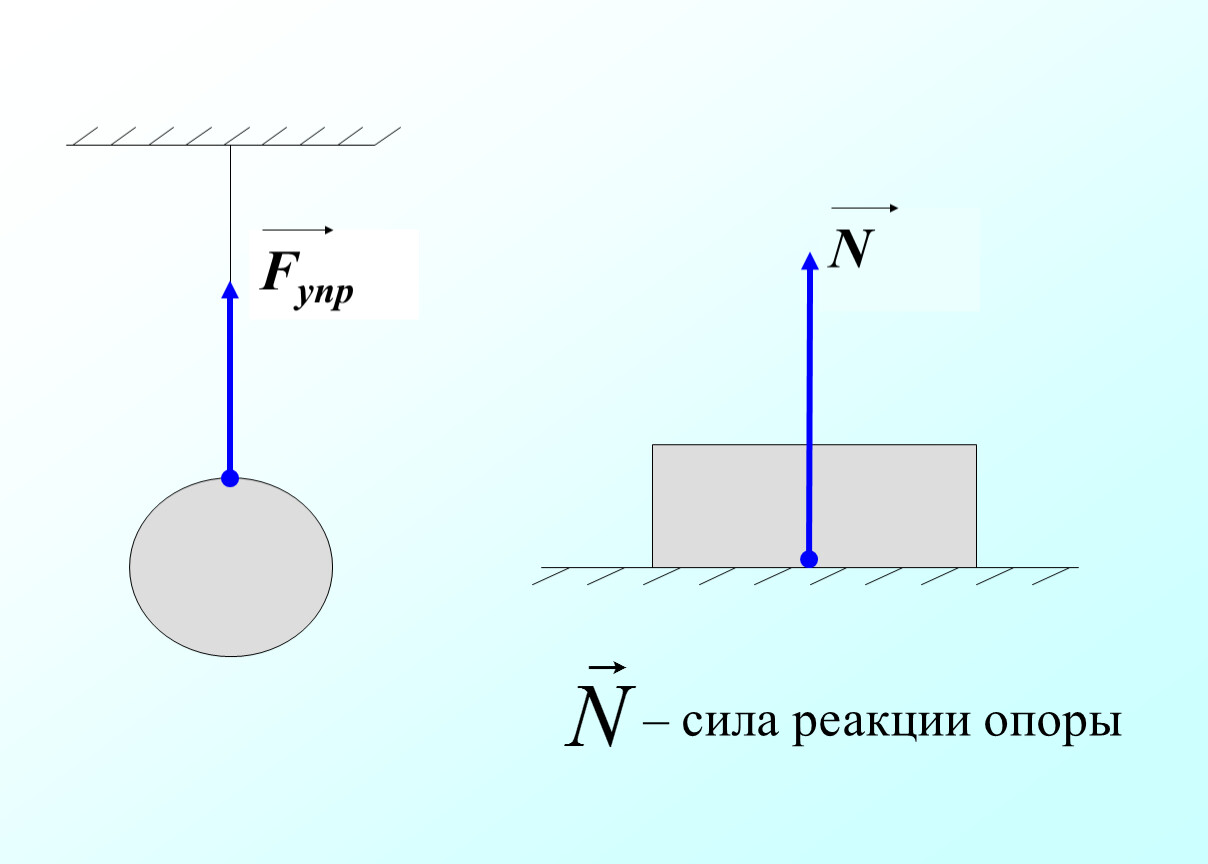 Величина силы реакции опоры
Величина силы реакции опоры Биомеханика ходьбы и бега. Величина силы реакции опоры
Динамометрические платформы позволяют зарегистрировать в обычной ходьбе три составляющие силы реакции опоры: вертикальную и горизонтальные (переднезаднюю и боковую). Повышенной скорости спортивной ходьбы сопутствуют более высокие, чем при обычной ходьбе, составляющие силы реакции опоры. Например, первый пик вертикальной составляющей может быть почти в два раза больше, чем при обычной ходьбе, но второй, относящийся к отталкиванию, больше только на 10 – 20 %. Переднезадняя составляющая обычно больше на 50 – 60 % в обеих своих частях, т. е. тормозящей и ускоряющей. Если движения бёдер и туловища, а также компенсирующие движения верхних конечностей выполняются технически правильно, то они уменьшают размах колебательного движения более высоко расположенных точек тела: таза, середины туловища и головы.
Скорость бега и способ постановки стопы на опору связаны с характером и величиной силы реакции опоры в беге.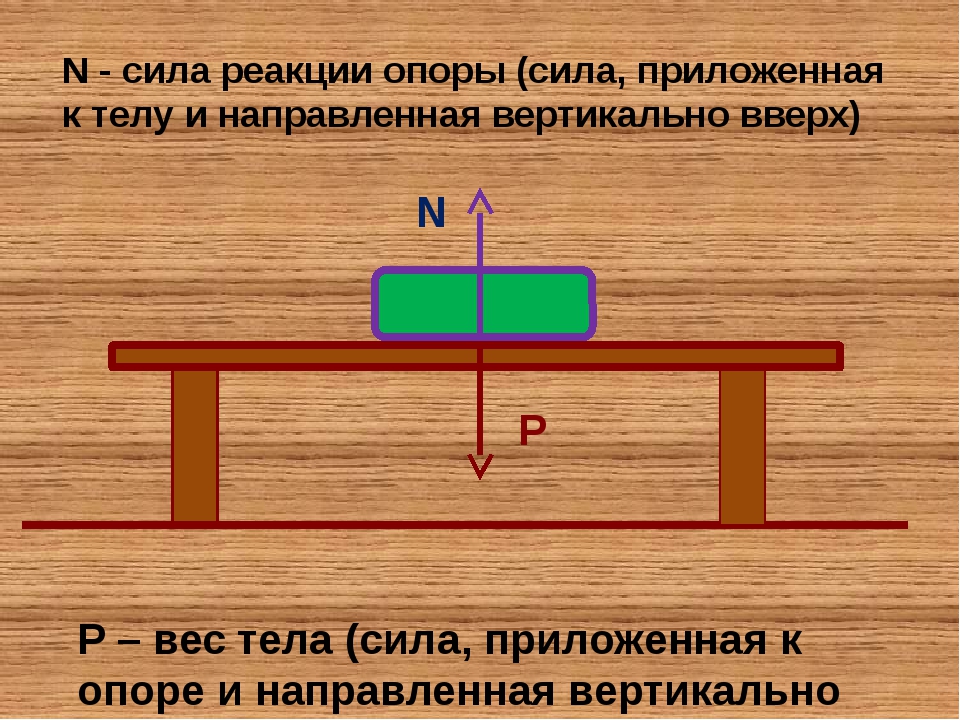 Нагрузка на нижние конечности, как правило, больше во время амортизации, чем отталкивания. При спринтерских скоростях в начале фазы опоры появляется высокий пик силы реакции опоры, который в пять раз превышает вес тела. Этот амортизационный пик снижается в соответствии со скоростью бега и способом постановки стопы на опору.
Нагрузка на нижние конечности, как правило, больше во время амортизации, чем отталкивания. При спринтерских скоростях в начале фазы опоры появляется высокий пик силы реакции опоры, который в пять раз превышает вес тела. Этот амортизационный пик снижается в соответствии со скоростью бега и способом постановки стопы на опору.
Различают четыре способа постановки стопы на опору. Основной заключается в том, что сначала в контакт с опорой вступает пятка и внешняя часть стопы: таким способом бегают спортсмены на всех дистанциях, но наиболее типичен он для стайеров. Плоскую постановку стопы применяют чаще на средних дистанциях. Более раннее вхождение в контакт с опорой внешней частью плюсны и последующая плоская опора на всю стопу типична для большинства спринтеров.
Отталкивание от опоры осуществляется посредством: 1) собственно отталкивания ногами от опоры; 2) маховыми движениями свободных конечностей тела. Эти движения должны быть тесно взаимосвязаны в едином действии – отталкивании.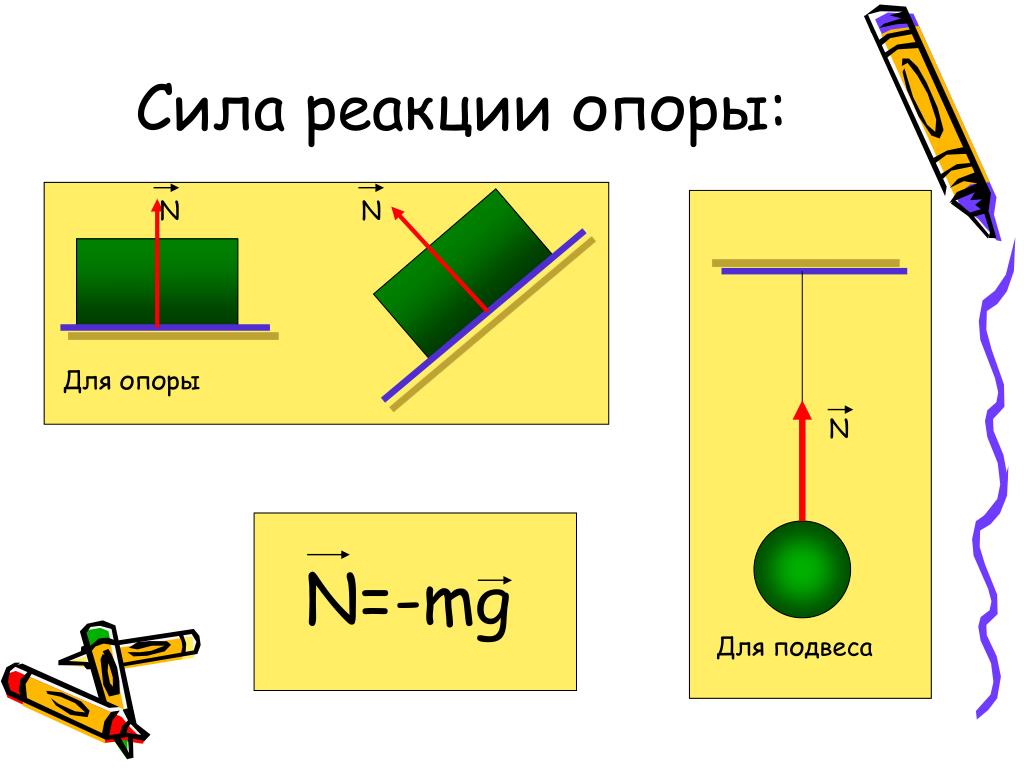 От их согласованности в значительной мере зависит совершенство отталкивания.
От их согласованности в значительной мере зависит совершенство отталкивания.
Во время отталкивания бегуна от опоры стопа зафиксирована неподвижно (трение покоя). На стопу как на опорное звено со стороны голени действует давление ускоряемых звеньев тела, направленное вниз и назад (F отт). Через стопу оно передаётся на опору. Противодействием этому давлению служит реакция опоры (R оп). Она приложена к стопе и направлена вперёд – вверх (рис. 1).
Рисунок 1. Отталкивание от опоры
Реакция опоры и давление голени приложены к стопе в противоположных направлениях; они взаимно уравновешиваются и фиксируют стопу на опоре. Реакция опоры и является той внешней силой, сообщающей ускорение ОЦТ тела во время отталкивания.
Маховые движения при отталкивании – это быстрые движения свободных звеньев тела, одинаковые в основном по направлению с отталкиванием ногой от опоры. При маховых движениях перемещаются ЦМ соответствующих звеньев тела.
Когда ускорения маховых звеньев направлены от опоры вверх вперёд, возникают силы инерции этих звеньев, направленные к опоре вниз назад.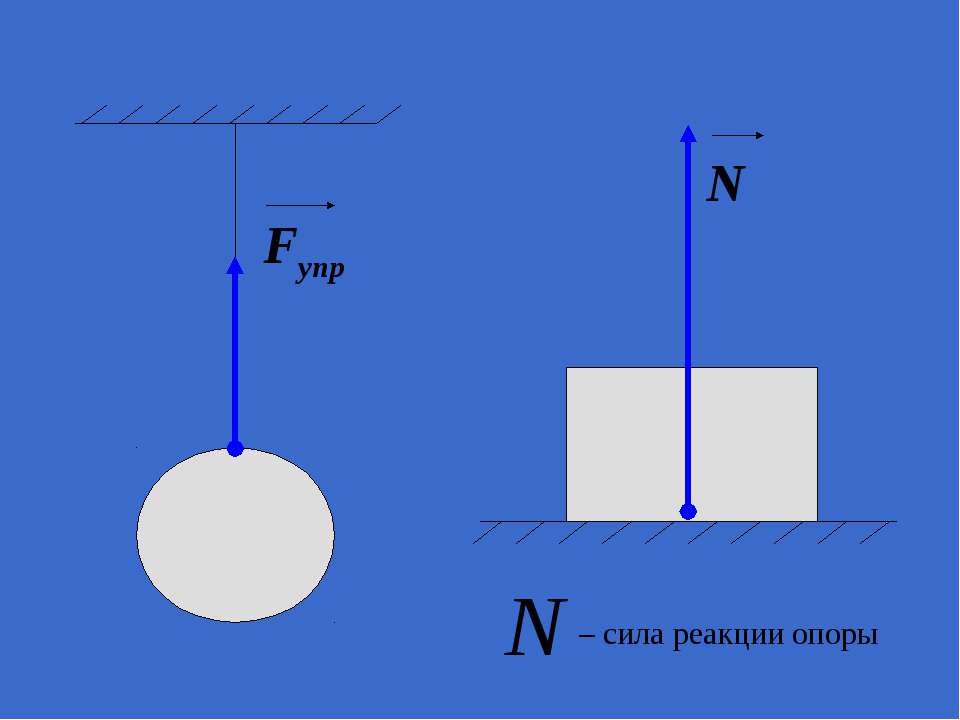 Совместно с весом тела бегуна, силой отталкивания опорной ноги – они увеличивают силу отталкивания, что дает прирост количества движения, т. е. увеличивают скорость ОЦМ тела.
Совместно с весом тела бегуна, силой отталкивания опорной ноги – они увеличивают силу отталкивания, что дает прирост количества движения, т. е. увеличивают скорость ОЦМ тела.
Таким образом, маховые движения свободных звеньев тела, одинаковые по направлению с отталкиванием ногой от опоры, можно считать составной частью отталкивания. Маховые движения увеличивают силу отталкивания и создают условия для быстрого завершения отталкивания.
Сила реакции опоры обозначение единицы измерения. Как найти силу реакции опоры
Сила реакции опоры относится к силам упругости, и всегда направлена перпендикулярно поверхности. Она противостоит любой силе, которая заставляет тело двигаться перпендикулярно опоре. Для того чтобы рассчитать ее нужно выявить и узнать числовое значение всех сил, которые действуют на тело, стоящее на опоре.
Вам понадобится
- — весы;
- — спидометр или радар;
- — угломер.
Инструкция
- Определите массу тела с помощью весов или любым другим способом.
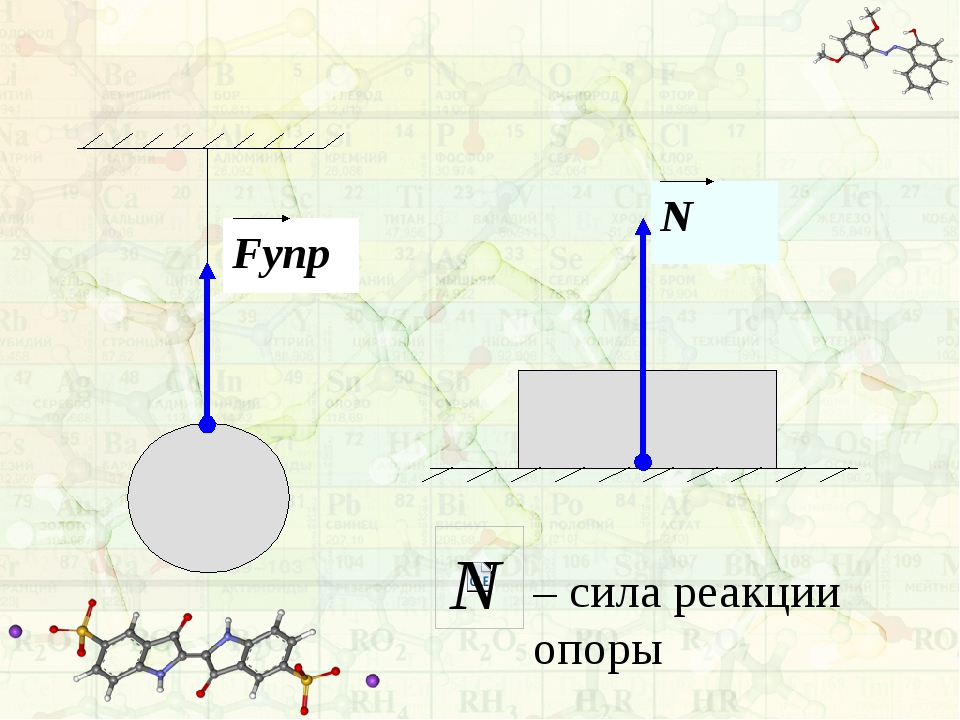 Если тело находится на горизонтальной поверхности (причем неважно, движется оно или пребывает в состоянии покоя), то сила реакции опоры равна силе тяжести действующей на тело. Для того чтобы рассчитать ее умножьте массу тела на ускорение свободного падения, которое равно 9,81 м/с² N=m g.
Если тело находится на горизонтальной поверхности (причем неважно, движется оно или пребывает в состоянии покоя), то сила реакции опоры равна силе тяжести действующей на тело. Для того чтобы рассчитать ее умножьте массу тела на ускорение свободного падения, которое равно 9,81 м/с² N=m g. - В том случае, если тело движется по поверхности, которая представляет собой часть окружности с радиусом R, например, мост, пригорок то сила реакции опоры учитывает силу, действующую по направлению из центра окружности, с ускорением, равным центростремительному, действующую на тело.
 Чтобы рассчитать силу реакции опоры в верхней точке, от ускорения свободного падения отнимите отношение квадрата скорости к радиусу кривизны траектории.
Чтобы рассчитать силу реакции опоры в верхней точке, от ускорения свободного падения отнимите отношение квадрата скорости к радиусу кривизны траектории. - Получившееся число умножьте на массу движущегося тела N=m (g-v²/R). Скорость должна быть измерена в метрах в секунду, а радиус в метрах. При определенной скорости значение ускорения, направленного от центра окружности, может сравняться, и даже превысить ускорение свободного падения, в этот момент сцепление тела с поверхностью пропадет, поэтому, например, автомобилистам, нужно четко контролировать скорость на таких участках дороги.
- Если же кривизна направлена вниз, и траектория тела вогнутая, то рассчитайте силу реакции опоры, прибавив к ускорению свободного падения отношение квадрата скорости и радиуса кривизны траектории, а получившийся результат умножьте на массу тела N=m (g+v²/R).
- Если известна сила трения и коэффициент трения, силу реакции опоры рассчитайте, поделив силу трения на этот коэффициент N=Fтр/μ.

Равномерное движение
S = v * t
S – путь, расстояние [м] (метр)
v – скорость [м/с] (метр в секунду)
t – время [ c ] (секунда)
Формула перевода скорости:
х км/ч= font-family:Arial»> м/с
Средняя скорость
v сред = EN-US»>s в – весь путь
t в – всё время
Плотность вещества
ρ= EN-US»>ρ – плотность
m – масса [кг] (килограмм)
V – объем [м3] (метр кубический)
Сила тяжести, вес и сила реакции опоры
Сила тяжести – сила притяжения к Земле. Приложена к телу. Направлена к центру Земли.
Вес – сила, с которой тело давит на опору или растягивает подвес. Приложена к телу. Направлена перпендикулярно опоре и параллельно подвесу вниз.
Сила реакции опоры – сила, с которой опора или подвес сопротивляется давлению или растяжению.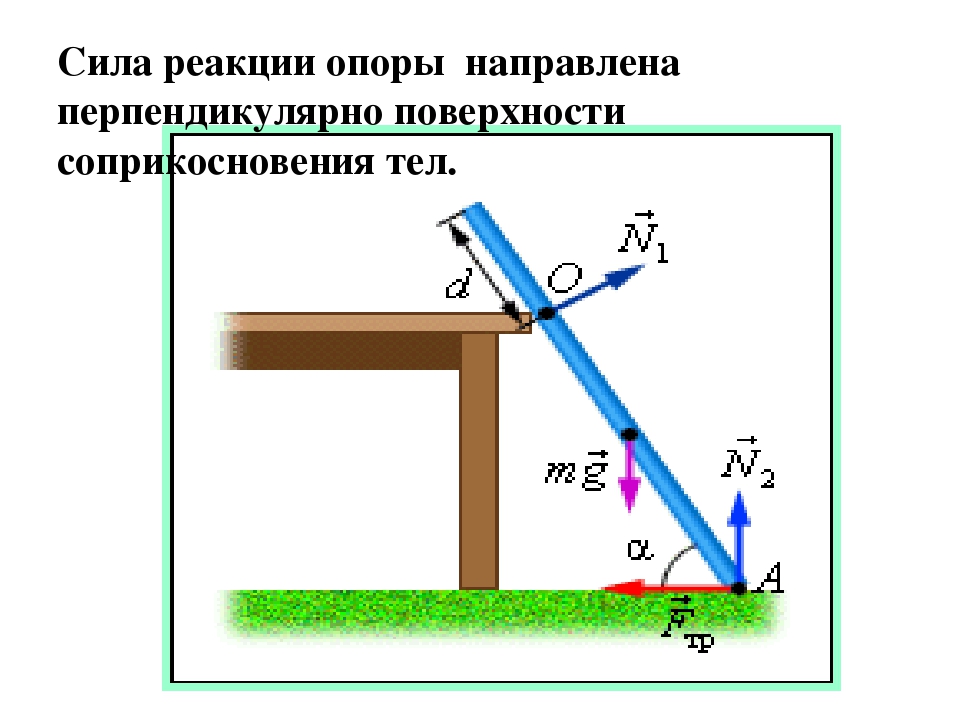
F т =m*g; P=m*g*cosα; N=m*g*cosα
F т – сила тяжести [Н] (Ньютон)
P – вес [ Н ]
N – сила реакции опоры [Н]
m – масса [кг] (килограмм)
α – угол между плоскостью горизонта и плоскостью опоры [º,рад] (градус, радиан)
g≈9,8 м / с2
Сила упругости (Закон Гука)
F упр = k * x
F упр — сила упругости [Н] (Ньютон)
k – коэффициент жёсткости [Н/м] (Ньютон на метр)
x – удлинение/сжатие пружины [м] (метр)
Механическая работа
A=F*l*cosα
A – работа [Дж] (Джоуль)
F – сила [Н] (Ньютон)
l – расстояние, на котором действует сила [м] (метр)
α – угол между направлением силы и направлением движения [º,рад] (градус, радиан)
Частные случаи:
1)α=0, т. е. направление действия силы совпадает с направлением движения
A=F*l;
2)
α
=
π
/2=90 º, т.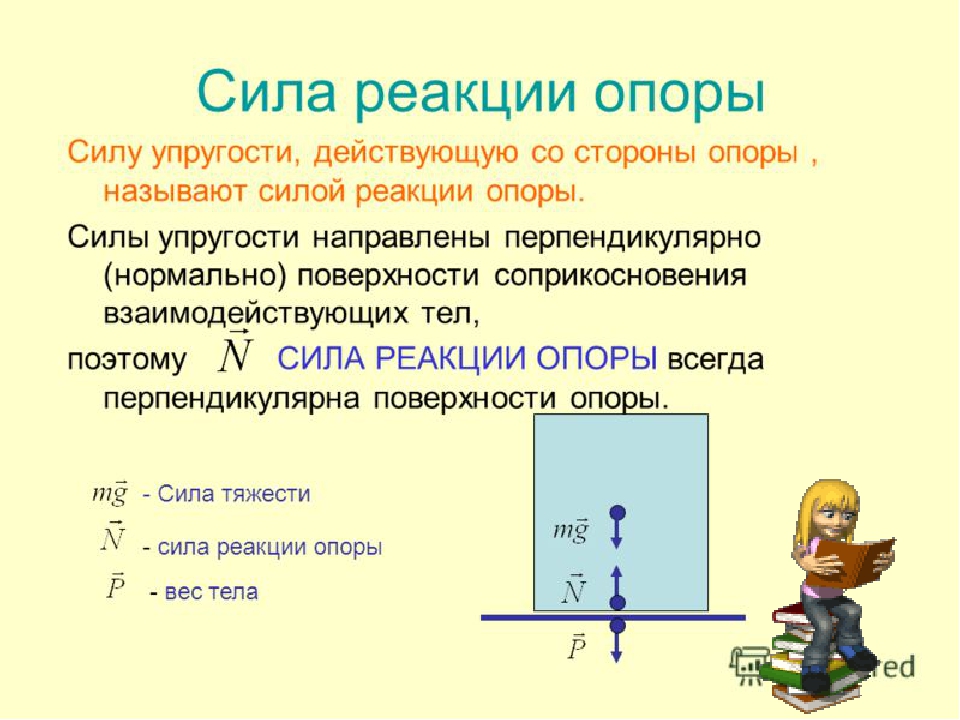 е. направление силы перпендикулярно направлению движения
е. направление силы перпендикулярно направлению движения
A=0;
3) α = π =180 º, т. е. направление силы противоположно направлению движения
A =- F * l ;
Мощность
N = EN-US»>N – мощность [Вт] (Ватт)
A – работа [Дж] (Джоуль)
t – время [с] (секунда)
Давление в жидкостях и твёрдых телах
P = font-family:Arial»>; P = ρ * g * h
P – давление [Па] (Паскаль)
F – сила давления [Н] (Ньютон)
s – площадь основания [м2] (квадратный метр)
ρ – плотность материала/жидкости [кг/м3] (килограмм на метр кубический)
g – ускорение свободного падения [м/с2] (метр на секунду в квадрате)
h – высота предмета/столба жидкости [м] (метр)
Сила Архимеда
Сила Архимеда – сила, с которой жидкость или газ стремятся вытолкнуть погруженное в них тело.
F Арх = ρ ж * V погр * g
F Арх – сила Архимеда [Н] (Ньютон)
ρ ж – плотность жидкости/газа [кг/м3] (килограмм на метр кубический)
V погр – объем погруженной части тела [м3] (метр кубический)
g – ускорение свободного падения [м/с2] (метр на секунду в квадрате)
Условие плавания тел:
ρ ж ≥ρ т
ρ т – плотность материала тела [кг/м3] (килограмм на метр кубический)
Правило рычага
F 1 * l 1 = F 2 * l 2 (равновесие рычага)
F 1,2 – сила, действующая на рычаг [Н] (Ньютон)
l 1,2 – длина плеча рычага соответствующей силы [м] (метр)
Правило моментов
M = F * l
M – момент силы [Н*м] (Ньютон-метр)
F – сила [Н] (Ньютон)
l – длина (рычага) [м] (метр)
M1=M2 (равновесие)
Сила трения
F тр =µ* N
F тр – сила трения [Н] (Ньютон)
µ — коэффициент трения [ , %]
N – сила реакции опоры [Н] (Ньютон)
Энергия тела
E кин = font-family:Arial»>; E п = m * g * h
E кин – кинетическая энергия [Дж] (Джоуль)
m – масса тела [кг] (килограмм)
v – скорость тела [м/с] (метр в секунду)
Еп – потенциальная энергия [Дж] (Джоуль)
g – ускорение свободного падения [м/с2] (метр на секунду в квадрате)
h – высота над землей [м] (метр)
Закон сохранения энергии: Энергия не исчезает в никуда и не появляется из ниоткуда, она лишь переходит из одних форм в другие.
Положим камень на горизонтальную крышку стола, стоящего на Земле (рис. 104). Поскольку ускорение камня относительно Земли равно пулю, то по второму закону Ньютона сумма действующих на него сил равна нулю. Следовательно, действие на камень силы тяжести m · g должно компенсироваться какими-то другими силами. Ясно, что под действием камня крышка стола деформируется. Поэтому со стороны стола на камень действует сила упругости. Если считать, что камень взаимодействует лишь с Землей и крышкой стола, то сила упругости должна уравновешивать силу тяжести: F упр = -m · g. Эту силу упругости называют силой реакции опоры и обозначают латинской буквой N. Так как ускорение свободного падения направлено вертикально вниз, сила N направлена вертикально вверх – перпендикулярно поверхности крышки стола.
Поскольку крышка стола действует на камень, то по третьему закону Ньютона и камень действует на крышку стола силой P = -N (рис. 105). Эту силу называют весом .
Весом тела называют силу, с которой это тело действует на подвес или опору, находясь относительно подвеса или опоры в неподвижном состоянии.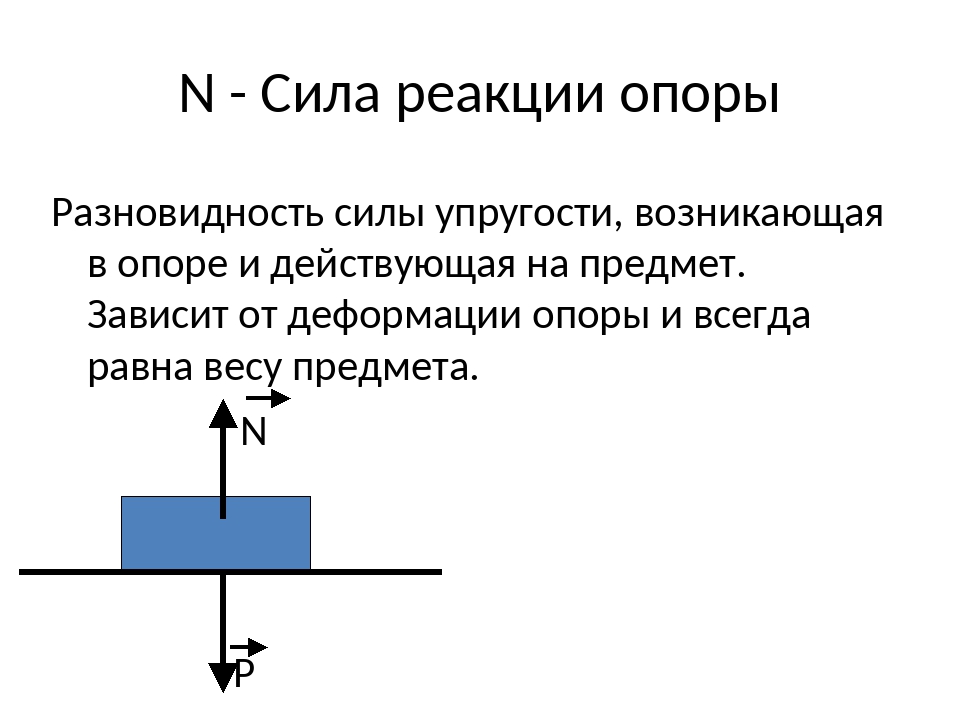
Ясно, что в рассмотренном случае вес камня равен силе тяжести: P = m · g. Это будет верно для любого тела, покоящегося на подвесе (опоре) относительно Земли (рис. 106). Очевидно, что в этом случае точка крепления подвеса (или опора) неподвижна относительно Земли.
Для тела, покоящегося на неподвижном относительно Земли подвесе (опоре), вес тела равен силе тяжести.
Вес тела также будет равен действующей на тело силе тяжести в случае, если тело и подвес (опора) движутся относительно Земли равномерно прямолинейно.
Если же тело и подвес (опора) движутся относительно Земли с ускорением так, что тело остается неподвижным относительно подвеса (опоры), то вес тела не будет равен силе тяжести.
Рассмотрим пример. Пусть тело массой m лежит на полу лифта, ускорение a которого направлено вертикально вверх (рис. 107). Будем считать, что на тело действуют только сила тяжести m · g и сила реакции пола N. (Вес тела действует не на тело, а на опору – пол лифта.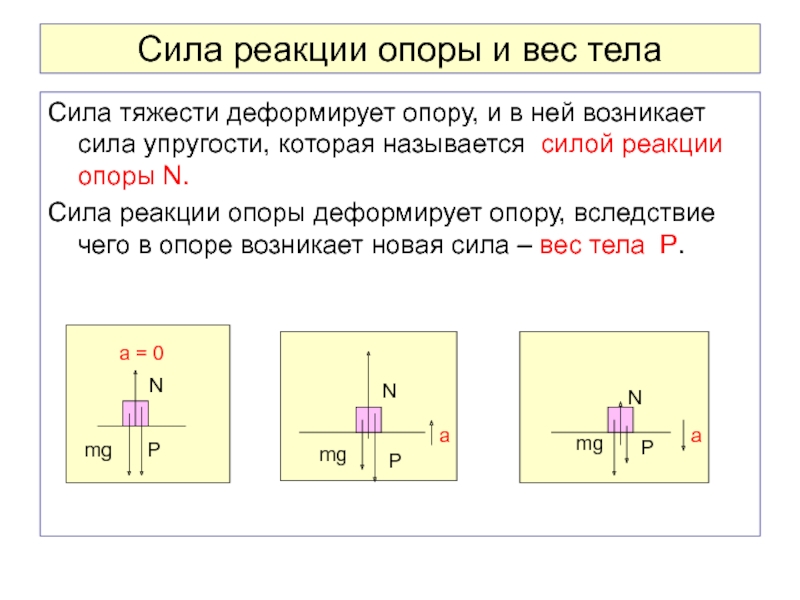 ) В системе отсчета, неподвижной относительно Земли, тело на полу лифта движется вместе с лифтом с ускорением a. В соответствии со вторым законом Ньютона произведение массы тела на ускорение равно сумме всех действующих на тело сил. Поэтому: m · a = N — m · g.
) В системе отсчета, неподвижной относительно Земли, тело на полу лифта движется вместе с лифтом с ускорением a. В соответствии со вторым законом Ньютона произведение массы тела на ускорение равно сумме всех действующих на тело сил. Поэтому: m · a = N — m · g.
Следовательно, N = m · a + m · g = m · (g + a). Значит, если лифт имеет ускорение, направленное вертикально вверх, то модуль силы N реакции пола будет больше модуля силы тяжести. В самом деле, сила реакции пола должна не только скомпенсировать действие силы тяжести, но и придать телу ускорение в положительном направлении оси X.
Сила N – это сила, с которой пол лифта действует на тело. По третьему закону Ньютона тело действует на пол с силой P, модуль которой равен модулю N, но направлена сила P в противоположную сторону. Эта сила является весом тела в движущемся лифте. Модуль этой силы P = N = m · (g + a). Таким образом, в лифте, движущемся с направленным вверх относительно Земли ускорением, модуль веса тела больше модуля силы тяжести .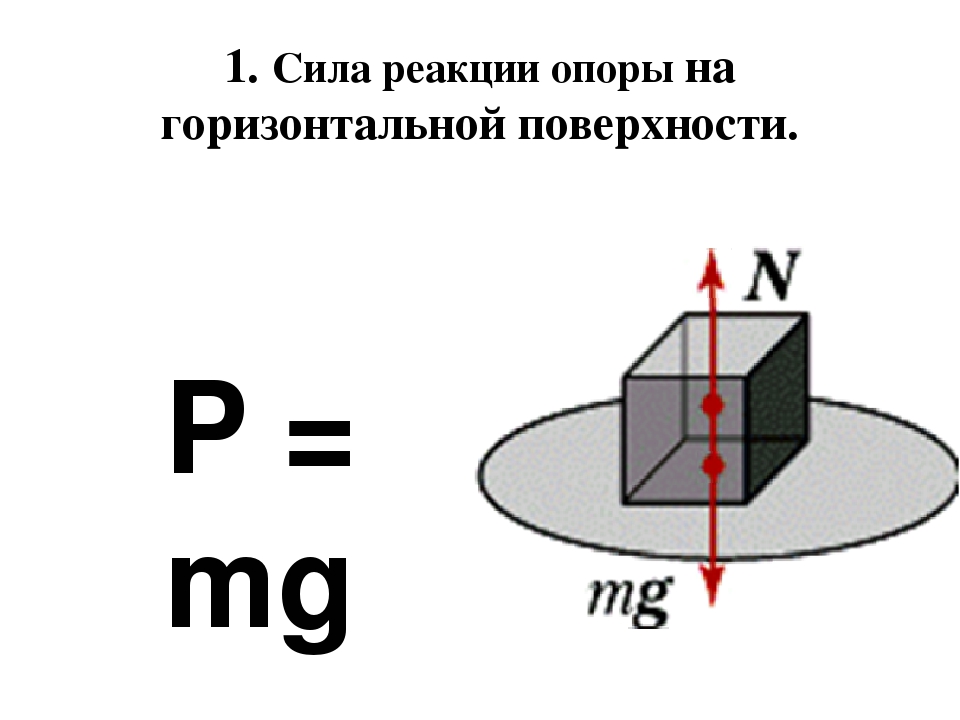
Такое явление называют перегрузкой .
Например, пусть ускорение а лифта направлено вертикально вверх и его значение равно g, т. е. a = g. В этом случае модуль веса тела – силы, действующей на пол лифта, – будет равен P = m · (g + a) = m · (g + g) = 2m · g. То есть вес тела при этом будет в два раза больше, чем в лифте, который относительно Земли покоится или движется равномерно прямолинейно.
Для тела на подвесе (или опоре), движущемся с ускорением относительно Земли, направленным вертикально вверх, вес тела больше силы тяжести.
Отношение веса тела в движущемся ускоренно относительно Земли лифте к весу этого же тела в покоящемся или движущемся равномерно прямолинейно лифте называют коэффициентом перегрузки или, более кратко, перегрузкой .
Коэффициент перегрузки (перегрузка) – отношение веса тела при перегрузке к силе тяжести, действующей на тело.
В рассмотренном выше случае перегрузка равна 2. Понятно, что если бы ускорение лифта было направлено вверх и его значение было равно a = 2g, то коэффициент перегрузки был бы равен 3.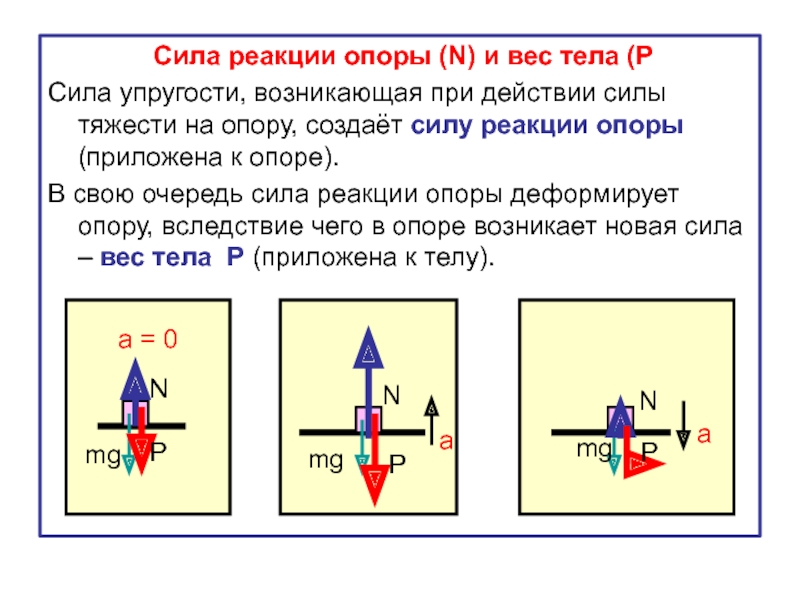
Теперь представим себе, что тело массой m лежит на полу лифта, ускорение которого a относительно Земли направлено вертикально вниз (противоположно оси X). Если модуль a ускорения лифта будет меньше модуля ускорения свободного падения, то сила реакции пола лифта по-прежнему будет направлена вверх, в положительном направлении оси X, а ее модуль будет равен N = m · (g — a). Следовательно, модуль веса тела будет равен P = N = m · (g — a), т. е. будет меньше модуля силы тяжести. Таким образом, тело будет давить на пол лифта с силой, модуль которой меньше модуля силы тяжести.
Это ощущение знакомо каждому, кто ездил на скоростном лифте или качался на больших качелях. При движении вниз из верхней точки вы чувствуете, что ваше давление на опору уменьшается. Если же ускорение опоры положительно (лифт и качели начинают подниматься), вас сильнее прижимает к опоре.
Если ускорение лифта относительно Земли будет направлено вниз и равно по модулю ускорению свободного падения (лифт свободно падает), то сила реакции пола станет равной нулю: N = m · (g — a) = m · (g — g) = 0.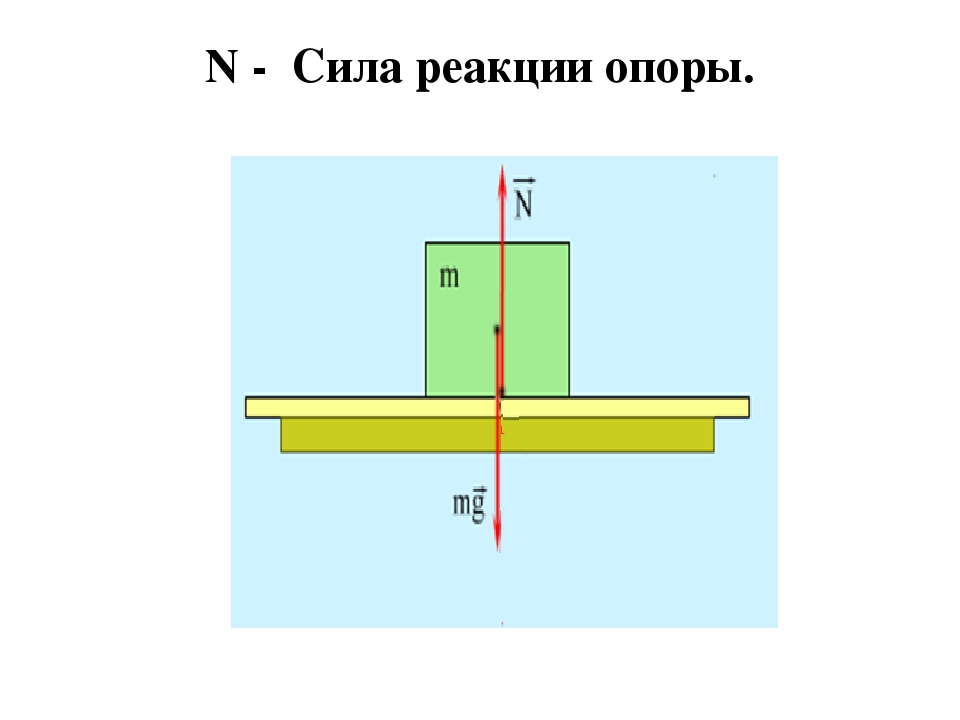 В этом случае пол лифта перестанет давить на лежащее на нем тело. Следовательно, согласно третьему закону Ньютона и тело не будет давить на пол лифта, совершая вместе с лифтом свободное падение. Вес тела станет равным нулю. Такое состояние называют состоянием невесомости .
В этом случае пол лифта перестанет давить на лежащее на нем тело. Следовательно, согласно третьему закону Ньютона и тело не будет давить на пол лифта, совершая вместе с лифтом свободное падение. Вес тела станет равным нулю. Такое состояние называют состоянием невесомости .
Состояние, при котором вес тела равен нулю, называют невесомостью.
Наконец, если ускорение лифта, направленное к Земле, станет больше ускорения свободного падения, тело окажется прижатым к потолку лифта. В этом случае вес тела изменит свое направление. Состояние невесомости исчезнет. В этом можно легко убедиться, если резко дернуть вниз банку с находящимся в ней предметом, закрыв верх банки ладонью, как показано на рис. 108.
Итоги
Весом тела называют силу, с которой это тело действует на поднес или опору, находясь относительно подвеса или опоры в неподвижном состоянии.
Вес тела в лифте, движущемся с направленным вверх относительно Земли ускорением, по модулю больше модуля силы тяжести.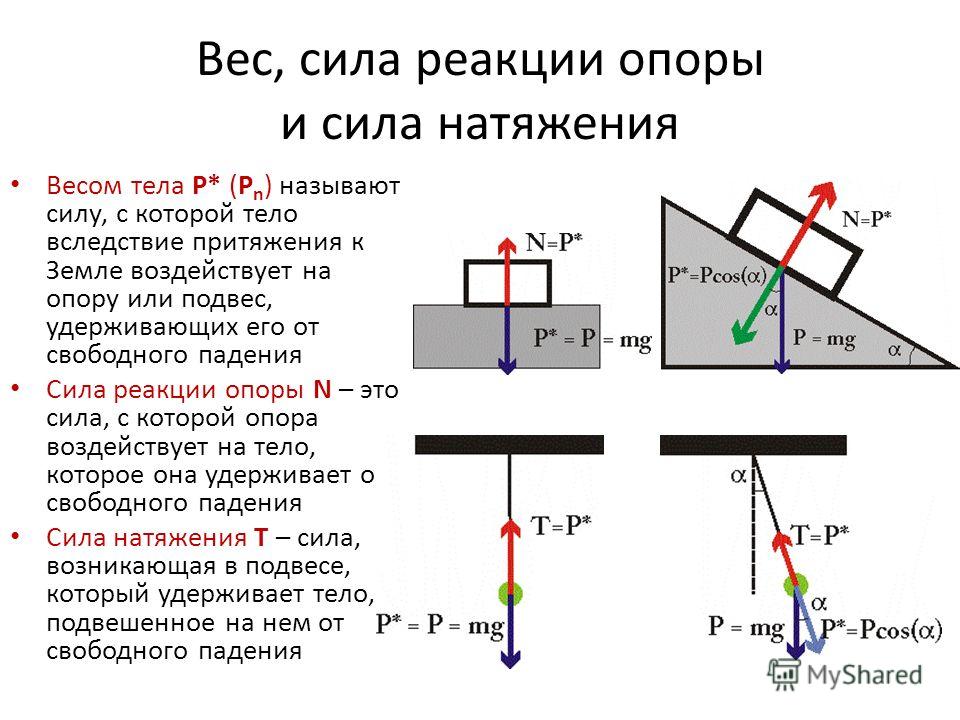 Такое явление называют перегрузкой .
Такое явление называют перегрузкой .
Коэффициент перегрузки (перегрузка) – отношение веса тела, при перегрузке к силе тяжести, действующей на это тело.
Если вес тела равен нулю, то такое состояние называют невесомостью .
Вопросы
- Какую силу называют силой реакции опоры? Что называют весом тела?
- К чему приложен вес тела?
- Приведите примеры, когда вес тела: а) равен силе тяжести; б) равен нулю; в) больше силы тяжести; г) меньше силы тяжести.
- Что называют перегрузкой?
- Какое состояние называют невесомостью?
Упражнения
- Семиклассник Сергей стоит на напольных весах в комнате. Стрелка прибора установилась напротив деления 50 кг. Определите модуль веса Сергея. Ответьте на остальные три вопроса об этой силе.
- Найдите перегрузку, испытываемую космонавтом, который находится в ракете, поднимающейся вертикально вверх с ускорением a = Зg.
- С какой силой действует космонавт массой m = 100 кг на ракету, указанную в упражнении 2? Как называется эта сила?
- Найдите вес космонавта массой m = 100 кг в ракете, которая: а) стоит неподвижно на пусковой установке; б) поднимается с ускорением a = 4g, направленным вертикально вверх.
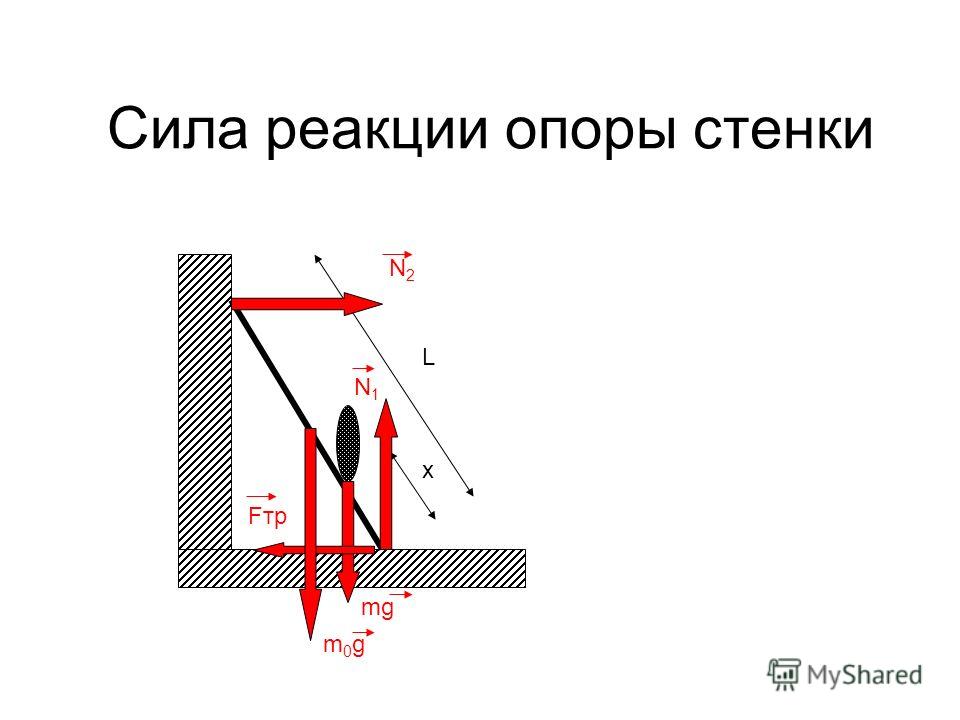
- Определите модули сил, действующих на гирю массой m = 2 кг, которая висит неподвижно На легкой нити, прикрепленной к потолку комнаты. Чему равны модули силы упругости, действующей со стороны нити: а) на гирю; б) на потолок? Чему равен вес гири? Указание: для ответа на поставленные вопросы воспользуйтесь законами Ньютона.
- Найдите вес груза массой m = 5 кг, подвешенного на нити к потолку скоростного лифта, если: а) лифт равномерно поднимается; б) лифт равномерно опускается; в) поднимающийся вверх со скоростью v = 2 м/с лифт начал торможение с ускорением a = 2 м/с 2 ; г) опускающийся вниз со скоростью v = 2 м/с лифт начал торможение с ускорением a = 2 м/с 2 ; д) лифт начал движение вверх с ускорением a = 2 м/с 2 ; е) лифт начал движение вниз с ускорением a = 2 м/с 2 .
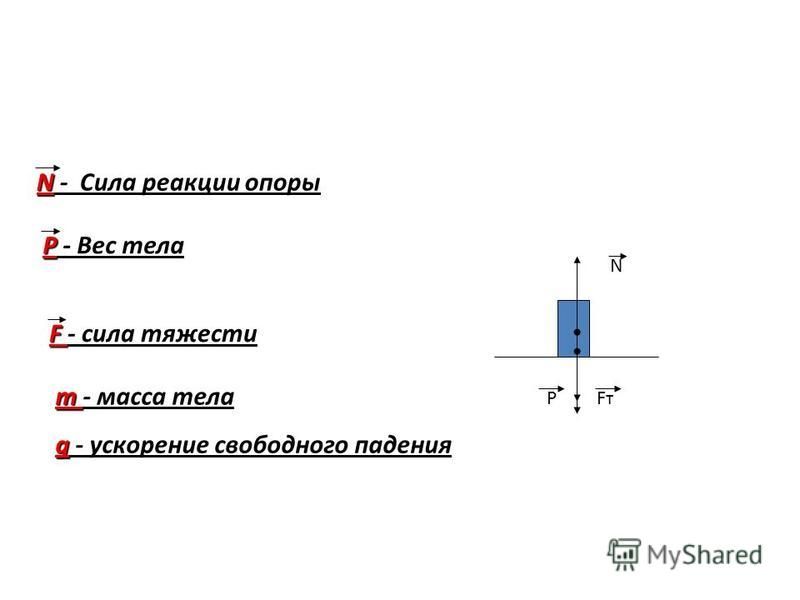
Силу действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести:
Wikimedia Foundation
. 2010
.
2010
.
Смотреть что такое «Сила нормальной реакции опоры» в других словарях:
Сила трения скольжения силы, возникающие между соприкасающимися телами при их относительном движении. Если между телами отсутствует жидкая или газообразная прослойка (смазка), то такое трение называется сухим. В противном случае, трение… … Википедия
Запрос «сила» перенаправляется сюда; см. также другие значения. Сила Размерность LMT−2 Единицы измерения СИ … Википедия
Запрос «сила» перенаправляется сюда; см. также другие значения. Сила Размерность LMT−2 Единицы измерения СИ ньютон … Википедия
Закон Амонтона Кулона эмпирический закон, устанавливающий связь между поверхностной силой трения, возникающей при относительном скольжении тела, с силой нормальной реакции, действующей на тело со стороны поверхности. Сила трения,… … Википедия
Силы трения скольжения силы, возникающие между соприкасающимися телами при их относительном движении. Если между телами отсутствует жидкая или газообразная прослойка (смазка), то такое трение называется сухим.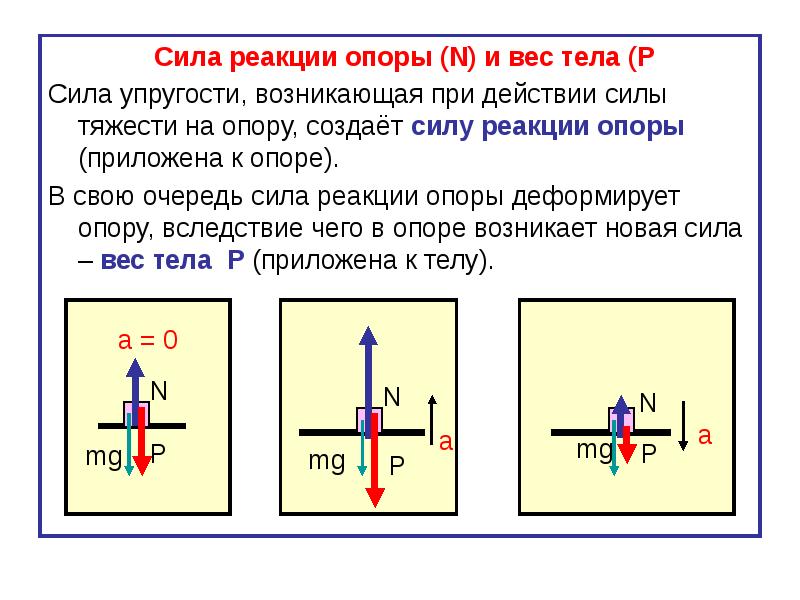 В противном случае, трение… … Википедия
В противном случае, трение… … Википедия
Трение покоя, трение сцепления сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг… … Википедия
Сюда перенаправляется запрос «Прямохождение». На эту тему нужна отдельная статья. Ходьба человека наиболее естественная локомоция человека. Автоматизированный двигательный акт, осуществляющийся в результате сложной координированной деятельности… … Википедия
Цикл ходьбы: опора на одну ногу двуопорный период опора на другую ногу… Ходьба человека наиболее естественная локомоция человека. Автоматизированный двигательный акт, осуществляющийся в результате сложной координированной деятельности скелетных … Википедия
Сила трения при скольжении тела о поверхность не зависит от площади соприкосновения тела с поверхностью, но зависит от силы нормальной реакции этого тела и от состояния окружающей среды. Сила трения скольжения возникает при скольжении данного… … Википедия
Сила трения скольжения возникает при скольжении данного… … Википедия
Закон Амонтона Кулона сила трения при скольжении тела о поверхность не зависит от площади соприкосновения тела с поверхностью, но зависит от силы нормальной реакции этого тела и от состояния окружающей среды. Сила трения скольжения возникает при… … Википедия
Инструкция
Случай 1. Формула для скольжения: Fтр = мN, где м – коэффициент трения скольжения, N – сила реакции опоры, Н. Для тела, скользящего по горизонтальной плоскости, N = G = mg, где G — вес тела, Н; m – масса тела, кг; g – ускорение свободного падения, м/с2. Значения безразмерного коэффициента м для данной пары материалов даны в справочной . Зная массу тела и пару материалов. скользящих друг относительно друга, найдите силу трения.
Случай 2. Рассмотрите тело, скользящее по горизонтальной поверхности и двигающееся равноускоренно. На него действуют четыре силы: сила, приводящее тело в движение, сила тяжести, сила реакции опоры, сила трения скольжения. 2 = 0,8 м/с2. Теперь найдите силу трения: Fтр = ma = 0,8*1 = 0,8 Н.
2 = 0,8 м/с2. Теперь найдите силу трения: Fтр = ma = 0,8*1 = 0,8 Н.
Случай 4. На тело, самопроизвольно скользящее по наклонной плоскости, действуют три силы: сила тяжести (G), сила реакции опоры (N) и сила трения (Fтр). Сила тяжести может быть записана в таком виде: G = mg, Н, где m – масса тела, кг; g – ускорение свободного падения, м/с2. Поскольку эти силы направлены не вдоль одной прямой, запишите уравнение движения в векторном виде.
Сложив по правилу параллелограмма силы N и mg, вы получите результирующую силу F’. Из рисунка можно сделать выводы: N = mg*cosα; F’ = mg*sinα. Где α – угол наклона плоскости. Силу трения можно записать формулой: Fтр = м*N = м*mg*cosα. Уравнение для движения принимает вид: F’-Fтр = ma. Или: Fтр = mg*sinα-ma.
Случай 5. Если же к телу приложена дополнительная сила F, направленная вдоль наклонной плоскости, то сила трения будет выражаться: Fтр = mg*sinα+F-ma, если направление движения и силы F совпадают. Или: Fтр = mg*sinα-F-ma, если сила F противодействует движению.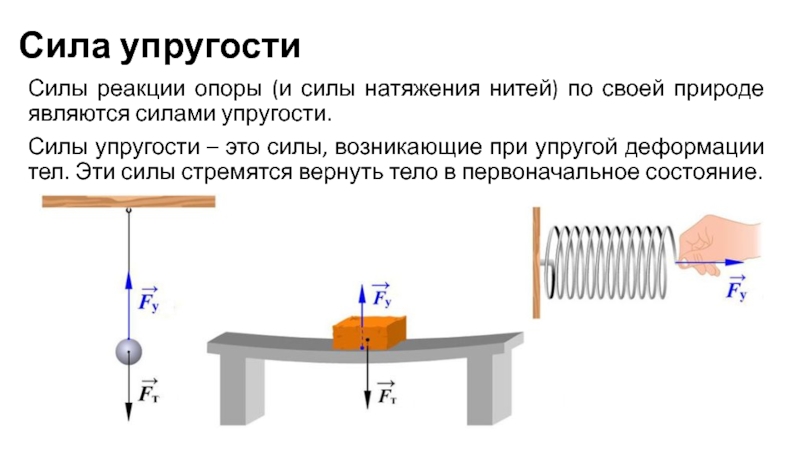 2 = 0,8 м/с2. Вычислите силу трения в первом случае: Fтр = 1*9,8*sin(45о)-1*0,8 = 7,53 Н. Определите силу трения во втором случае: Fтр = 1*9,8*sin(45о)+2-1*0,8= 9,53 Н.
2 = 0,8 м/с2. Вычислите силу трения в первом случае: Fтр = 1*9,8*sin(45о)-1*0,8 = 7,53 Н. Определите силу трения во втором случае: Fтр = 1*9,8*sin(45о)+2-1*0,8= 9,53 Н.
Случай 6. Тело двигается по наклонной поверхности равномерно. Значит, по второму закону Ньютона система находится в равновесии. Если скольжение самопроизвольное, движение тела подчиняется уравнению: mg*sinα = Fтр.
Если же к телу приложена дополнительная сила (F), препятствующая равноускоренному перемещению, выражение для движения имеет вид: mg*sinα–Fтр-F = 0. Отсюда найдите силу трения: Fтр = mg*sinα-F.
Источники:
- скольжение формула
Коэффициент трения – это совокупность характеристик двух тел, которые соприкасаются друг с другом. Существует несколько видов трения: трение покоя, трение скольжения и трение качения. Трение покоя представляет собой трение тело, которое находилось в покое, и было приведено в движение. Трение скольжения происходит при движении тела, данное трение меньше трения покоя.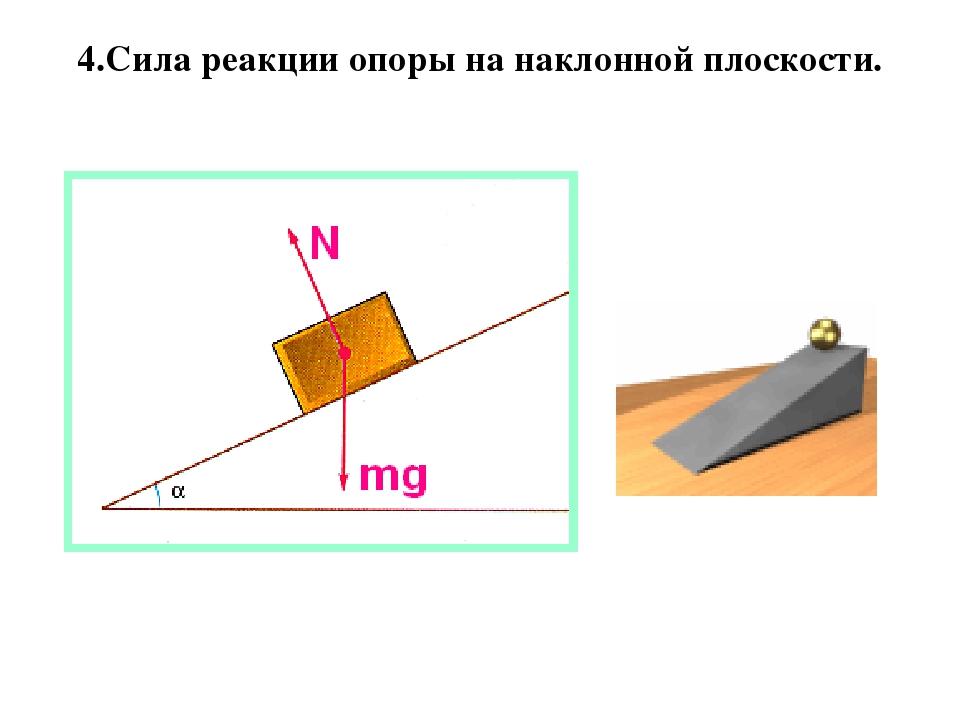 А трение качения происходит, когда тело катиться по поверхности. Обозначается трение в зависимости от вида, следующим образом: μск — трение скольжения, μо- трение покоя, μкач – трение качения.
А трение качения происходит, когда тело катиться по поверхности. Обозначается трение в зависимости от вида, следующим образом: μск — трение скольжения, μо- трение покоя, μкач – трение качения.
Инструкция
При определении коэффициента трения в ходе эксперимента, тело размещается на плоскости под наклоном и вычисляется угол наклона. При этом учитывать, что при определении коэффициента трения покоя заданное тело двигаться, а при определении коэффициента трения скольжения движется со скоростью, которая постоянна.
Коэффициент трения можно также вычислить в ходе эксперимента. Необходимо поместить объект на наклонную плоскость и вычислить угол наклона. Таким образом, коэффициент трения определяется по формуле: μ=tg(α), где μ — сила трения, α – угол наклона плоскости.
Видео по теме
При относительном движении двух тел между ними возникает трение. Оно также может возникнуть при движении в газообразной или жидкой среде. Трение может как мешать, так и способствовать нормальному движению. В результате этого явления на взаимодействующие тела действует сила трения .
В результате этого явления на взаимодействующие тела действует сила трения .
Инструкция
Наиболее общий случай рассматривает силу , когда одно из тел закреплено и покоится, а другое скользит по его поверхности. Со стороны тела, по которому скользит движущееся тело, на последнее действует сила реакции опоры, направленная перпендикулярно плоскости скольжения. Эта сила буквой N.Тело может также и покоится относительно закрепленного тела. Тогда сила трения, действующая на него Fтр
В случае движения тела относительно поверхности закрепленного тела сила трения скольжения становится равна произведения коэффициента трения на силу реакции опоры: Fтр = ?N.
Пусть теперь на тело действует постоянная сила F>Fтр = ?N, параллельная поверхности соприкасающихся тел. При скольжении тела, результирующая составляющая силы в горизонтальном направлении будет равна F-Fтр. Тогда по второму закону Ньютона, ускорение тела будет связано с результирующей силой по формуле: a = (F-Fтр)/m.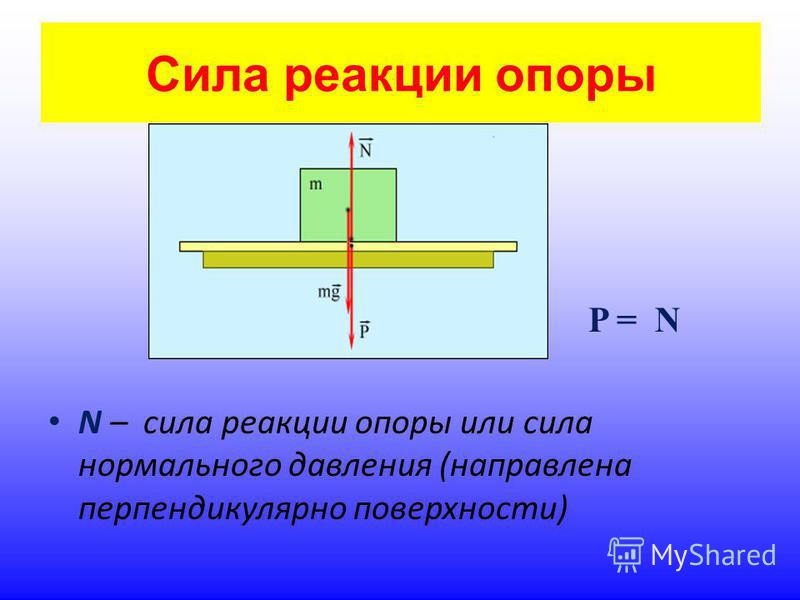 Отсюда, Fтр = F-ma. Ускорение тела можно найти из кинематических соображений.
Отсюда, Fтр = F-ma. Ускорение тела можно найти из кинематических соображений.
Часто рассматриваемый частный случай силы трения проявляется при соскальзывании тела с закрепленной наклонной плоскости. Пусть? — угол наклона плоскости и пусть тело соскальзывает равномерно, то есть без ускорения. Тогда уравнения движения тела будут выглядеть так: N = mg*cos?, mg*sin? = Fтр = ?N. Тогда из первого уравнения движения силу трения можно выразить как Fтр = ?mg*cos?.Если тело движется по наклонной плоскости с ускорением a, то второе уравнение движение будет иметь вид: mg*sin?-Fтр = ma. Тогда Fтр = mg*sin?-ma.
Видео по теме
Если сила, направленная параллельно поверхности, на которой стоит тело, превышает силу трения покоя, то начнется движение. Оно будет продолжаться до тех пор, пока движущая сила будет превышать силу трения скольжения, зависящую от коэффициента трения. Рассчитать этот коэффициент можно самостоятельно.
Вам понадобится
- Динамометр, весы, транспортир или угломер
Инструкция
Найдите массу тела в килограммах и установите его на ровную поверхность. Присоедините к нему динамометр, и начинайте двигать тело. Делайте это таким образом, чтобы показатели динамометра стабилизировались, поддерживая постоянную скорость . В этом случае сила тяги, измеренная динамометром, будет равна с одной стороны силе тяги, которую показывает динамометр, а с другой стороны силе , умноженной на скольжения.
Присоедините к нему динамометр, и начинайте двигать тело. Делайте это таким образом, чтобы показатели динамометра стабилизировались, поддерживая постоянную скорость . В этом случае сила тяги, измеренная динамометром, будет равна с одной стороны силе тяги, которую показывает динамометр, а с другой стороны силе , умноженной на скольжения.
Сделанные измерения позволят найти данный коэффициент из уравнения. Для этого поделите силу тяги на массу тела и число 9,81 (ускорение свободного падения) μ=F/(m g). Полученный коэффициент будет один и тот же для всех поверхностей такого же типа, как и те на которых производилось измерение. Например, если тело из двигалось по деревянной доске, то этот результат будет справедлив для всех деревянных тел, двигающихся скольжением по дереву, с учетом качества его обработки (если поверхности шершавые, значение коэффициента трения скольжения измениться).
Можно измерить коэффициент трения скольжения и другим способом. Для этого установите тело на плоскости, которая может менять свой угол относительно горизонта. Это может быть обыкновенная дощечка. Затем начинайте аккуратно поднимать ее за один край. В тот момент, когда тело придет в движение, скатываясь в плоскости как сани с горки, найдите угол ее уклона относительно горизонта. Важно, чтобы тело при этом не двигалось с ускорением. В этом случае, измеренный угол будет предельно малым, при котором тело начнет двигаться под действием силы тяжести. Коэффициент трения скольжения будет равен тангенсу этого угла μ=tg(α).
Это может быть обыкновенная дощечка. Затем начинайте аккуратно поднимать ее за один край. В тот момент, когда тело придет в движение, скатываясь в плоскости как сани с горки, найдите угол ее уклона относительно горизонта. Важно, чтобы тело при этом не двигалось с ускорением. В этом случае, измеренный угол будет предельно малым, при котором тело начнет двигаться под действием силы тяжести. Коэффициент трения скольжения будет равен тангенсу этого угла μ=tg(α).
Реакция опоры с трением — Энциклопедия по машиностроению XXL
Пусть на диск 5 помимо его веса р = mg и реакций опору с трением (скольжения и качения) действует горизонтальная сила,, приложенная к центру тяжести, и активная пара с моментом, перпендикулярным к диску. [c.31]Наконец, если имеется несколько опор с трением или без него, то при наличии условия (7) всегда можно будет бесконечным множеством способов выбрать систему реакций, результирующий момент которых относительно оси был бы равен М . Достаточно, например, предположить все реакции равными нулю, за исключением одной, которая определяется способом, указанным выше, в предположении, что имеется только одна опора. Равновесие оказывается поэтому действительно обеспеченным соотношением (7) во всех случаях, за исключением одного, рассмотренного выше (когда имеется только одна опора и притом абсолютно гладкая), мы встречаемся с неопределенностью реакций, которую нельзя устранить, если не обращаться к соображениям, выходящим за пределы статики твердых тел.
[c.125]
Достаточно, например, предположить все реакции равными нулю, за исключением одной, которая определяется способом, указанным выше, в предположении, что имеется только одна опора. Равновесие оказывается поэтому действительно обеспеченным соотношением (7) во всех случаях, за исключением одного, рассмотренного выше (когда имеется только одна опора и притом абсолютно гладкая), мы встречаемся с неопределенностью реакций, которую нельзя устранить, если не обращаться к соображениям, выходящим за пределы статики твердых тел.
[c.125]
Формула (88) и правило Жуковского легко объясняют поведение раскрученного волчка (рис. V.16). Действительно, пусть симметричный волчок вращается вокруг собственной оси если пренебречь трением в точке его касания с полом, то единственной действующей на него силой будет сила тяжести, приложенная в центре тяжести. Эта сила направлена в плоскости чертежа вниз, и чтобы выяснить направление скорости точки приложения силы, нужно разложить силу G на две составляющие вдоль оси симметрии (эта составляющая компенсируется реакцией опоры) и по перпендикуляру к этой оси.
 В соответствии с правилом Жуковского вторую составляющую надо повернуть на 90 по направлению вращения волчка. Поэтому скорость центра тяжести направлена перпендикулярно плоскости чертежа, например на нас . Однако, когда ось сдвинется в этом направлении, чертеж полностью сохранится, и таким образом, до тех нор, пока продолжается вращение с угловой скоростью o)i, продолжается и вращение оси волчка вокруг вертикального направления с некоторой угловой скоростью (0.2.
[c.206]
В соответствии с правилом Жуковского вторую составляющую надо повернуть на 90 по направлению вращения волчка. Поэтому скорость центра тяжести направлена перпендикулярно плоскости чертежа, например на нас . Однако, когда ось сдвинется в этом направлении, чертеж полностью сохранится, и таким образом, до тех нор, пока продолжается вращение с угловой скоростью o)i, продолжается и вращение оси волчка вокруг вертикального направления с некоторой угловой скоростью (0.2.
[c.206]На трубу действует задаваемая сила —вес Р. Связями являются опоры в точках А и С (рис. 153, б). Реакция точке С направлена перпендикулярно к АВ. Реакция в точке А имеет две составляющие нормальную и касательную — силу трения F. Выбрав координатные оси, как показано на рисунке, имеем следующие уравнения равновесия трубы [c.72]
Решение. Рассмотрим движение системы, состоящей из 1) диска А, 2) стрелки F, жестко соединенной с цилиндром В и представляющей с ним одно неразрывное целое, и 3) испытуемого тела D. Механическое движение диска передается другим телам системы в виде механического же движения. Тела совершают вращения вокруг оси и для решения задачи удобно воспользоваться теоремой (192) моментов системы относительно оси. На точки системы действуют только вертикальные внешние силы—веса тел и реакция в опоре С. Внешнее трение отсутствует. Трение между диском А и цилиндром В, возникающее при движении диска по винтовой резьбе, является внутренней силой и потому не входит в уравнение моментов. Моменты внешних сил относительно оси j равны нулю, и мы можем написать уравнение (193)
[c.346]
Механическое движение диска передается другим телам системы в виде механического же движения. Тела совершают вращения вокруг оси и для решения задачи удобно воспользоваться теоремой (192) моментов системы относительно оси. На точки системы действуют только вертикальные внешние силы—веса тел и реакция в опоре С. Внешнее трение отсутствует. Трение между диском А и цилиндром В, возникающее при движении диска по винтовой резьбе, является внутренней силой и потому не входит в уравнение моментов. Моменты внешних сил относительно оси j равны нулю, и мы можем написать уравнение (193)
[c.346]
Решение. В условиях задачи предполагается, что движение человека и тележки происходит относительно системы отсчета, связанной с Землей. На систему человек — тележка действуют внешние силы сила тяжести, сила реакции опоры и сила трения. [c.42]
На кулачок действуют следующие силы Дц=— 12 —реакция со стороны ролика Roi — реакция опоры вала О, касательная круга трения с радиусом poi-Обе реакции и Roi представляют собой пару сил с плечом Я, уравновешивающуюся движущим моментом М .
 [c.161]
[c.161]Тело, имеющее неподвижную ось. — Силами связи являются в данном случае реакции опор, которые удерживают ось неподвижной. Для отсутствия трения, очевидно, необходимо и достаточно, чтобы эти реакции могли быть приведены к силам, приложенным в точках оси. Тогда, в согласии с леммой, эти силы не будут производить работы при всяком перемещении, совместимом со связями, т. е. оставляющем неподвижными точки оси. Следовательно, принцип виртуальных перемещений применим в этом случае, и условие равновесия может быть из него выведено. Единственное виртуальное перемещение есть вращение ыЫ вокруг неподвижной оси. Уравнение (1) п 238 приводится к виду [c.294]
С другой стороны, если в фазе скольжения (т. е. в предположении 0 0) обозначим через N нормальную составляющую реакции опоры ф, а через А — силу трения (т, е. касательную составляющую Ф), то в силу законов динамического трения получим [c.185]
Далее мы исследовали движение чистого качения, допуская неявно, что плоскость в точке опоры С способна развить такую реакцию Ф, которая обеспечивает условия (6) неголономной связи (и согласуется с принципом виртуальных работ) теоретически этот способ правилен, так как, очевидно, выполняется условие, что работа реакции связи (в силу неподвижности точки С) равна нулю. Однако, физически, нельзя отвлечься от того факта, что реакция Ф как реакция опоры подчиняется закону статического трения, т. е. должна содержаться внутри конуса трения, имеющего вершиною С. Теперь важно отметить, что это условие будет, наверное, удовлетворено в нашем случае, потому что из равномерности горизонтального движения центра тяжести непосредственно следует, что реакция Ф будет вертикальной, т. е. нормальной к плоскости опоры.
[c.190]
Однако, физически, нельзя отвлечься от того факта, что реакция Ф как реакция опоры подчиняется закону статического трения, т. е. должна содержаться внутри конуса трения, имеющего вершиною С. Теперь важно отметить, что это условие будет, наверное, удовлетворено в нашем случае, потому что из равномерности горизонтального движения центра тяжести непосредственно следует, что реакция Ф будет вертикальной, т. е. нормальной к плоскости опоры.
[c.190]
Если упругие свойства опор различны в разных направлениях, задача сильно усложняется для анализа качественных особенностей движения рассмотрим наиболее простой вариант этой задачи главные оси жесткости опоры А совпадают с осями ц, а опора В вообще жесткая и внутреннее трение в роторе отсутствует. Тогда реакции опоры А выражаются формулами (11.15), а остальные уравнения (11.25) и (11.10) останутся прежними. Поэтому движение описывается четырьмя дифференциальными уравнениями, отличающимися от (11.26) только тем, что теперь
[c.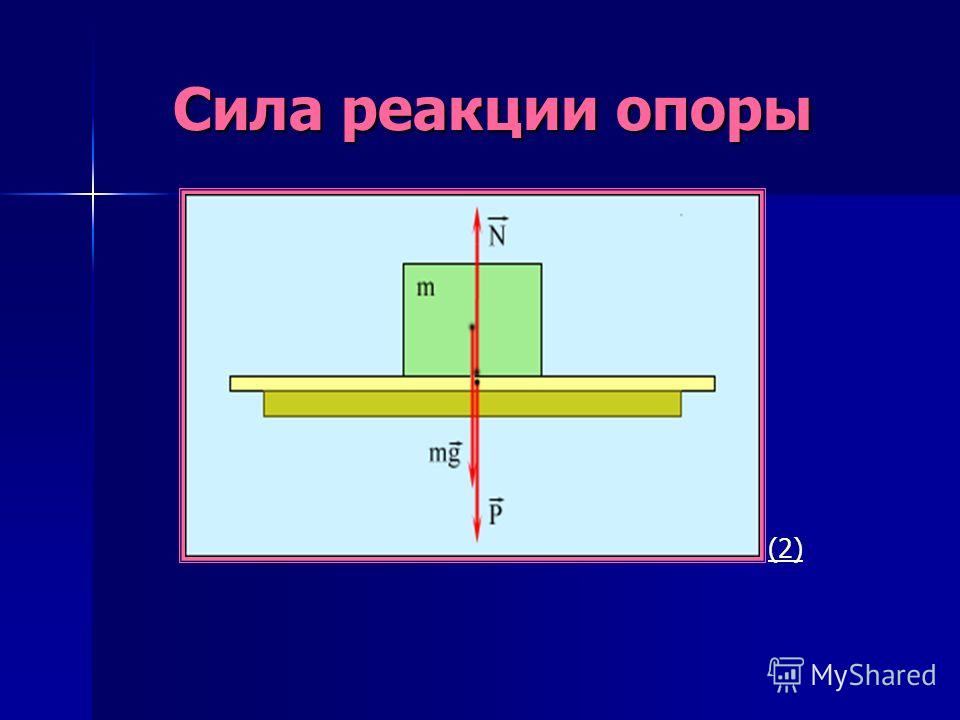 56]
56]
Верхняя опора сепаратора (рис. III.26) состоит из подшипника, помещенного во втулку с наружной шестигранной поверхностью, в грани которой упираются буферы, имеющие радиальные направляющие. Буферы прижимаются к втулке пружинами, установленными с некоторым предварительным поджатием. Такая схема сочетает в себе свойства упругой опоры и опоры сухого трения. И здесь необходимо так подобрать силу сухого трения, чтобы она была больше реакции в опоре при прохождении критической скорости, соответствующей ротору на упругой опоре. [c.154]
На фиг. 2 представлена схема несколько чаще применяемого колодочного тормоза Прони. Барабан 2 жёстко соединён с коленчатым валом двигателя и охватывается сверху и снизу деревянными колодками, которые между собой стягиваются болтами 1. Пусть вращение барабана происходит по часовой стрелке. Если под выступающий конец верхней колодки поставить опору, например, десятичные весы, то система колодок будет оставаться на месте, а барабан будет провёртываться с усилием, зависящим от степени затяжки болтов 1.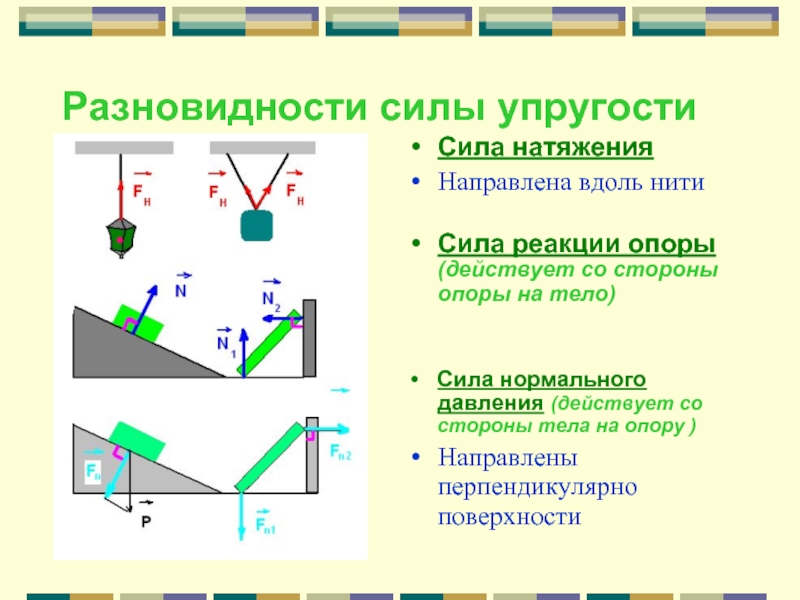 При установившемся числе оборотов момент Me, передаваемый от двигателя к барабану, должен быть равен моменту, действующему от колодок на барабан в противном случае число оборотов стало бы изменяться. Момент, передаваемый от колодок на барабан, равен произведению радиуса барабана R на силу трения F, развиваемую на ободе нажатием колодок. Точно такой же по величине момент, но действующий на схеме по часовой стрелке, передаётся на систему колодок и стремится их повернуть. Этот момент R F, равный моменту двигателя Mg, должен быть уравновешен моментом реакции опоры колодок Р 1, поскольку система колодок остаётся неподвижной. С другой стороны, Р равно давлению колодок на опору, т. е. величине Р, которая легко определяется по показанию весов.
[c.368]
При установившемся числе оборотов момент Me, передаваемый от двигателя к барабану, должен быть равен моменту, действующему от колодок на барабан в противном случае число оборотов стало бы изменяться. Момент, передаваемый от колодок на барабан, равен произведению радиуса барабана R на силу трения F, развиваемую на ободе нажатием колодок. Точно такой же по величине момент, но действующий на схеме по часовой стрелке, передаётся на систему колодок и стремится их повернуть. Этот момент R F, равный моменту двигателя Mg, должен быть уравновешен моментом реакции опоры колодок Р 1, поскольку система колодок остаётся неподвижной. С другой стороны, Р равно давлению колодок на опору, т. е. величине Р, которая легко определяется по показанию весов.
[c.368]
Задаемся углом 0 поворота балки на опоре. При изгибе балка скользит по опоре, и между ними возникает трение поэтому сила R реакции опоры составляет с нормалью к оси балки угол равный углу трения.
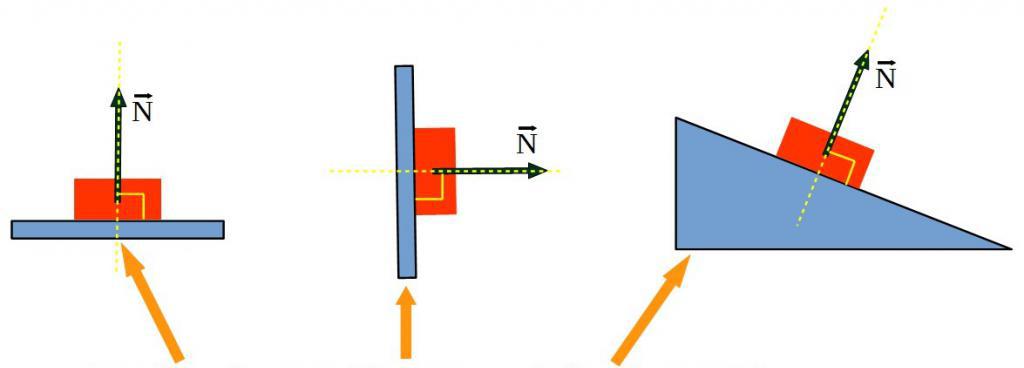 Величина силы определяется иа условия равенства ее вертикальной проекции половине силы Р, т. е.
[c.124]
Величина силы определяется иа условия равенства ее вертикальной проекции половине силы Р, т. е.
[c.124]С увеличением q уменьшаются габариты, измеряемые в плоскости, перпендикулярной осям, но растут размеры в направлении осей увеличивается неравномерность распределения нагрузки по ширине зубчатого венца и растут реакции опор. Это приводит к увеличению габаритов и веса подшипниковых узлов и потерь на трение в них. [c.832]
Заготовку закрепляют с помощью зажимных механизмов (ЗМ). Силу закрепления Р, определяют из условия равновесия заготовки под действием сил резания, реакций в опорах, сил трения по поверхностям контакта заготовки с опорами и ЗМ (табл. 7). При обработке массивных заготовок дополнительно учитывают силы веса, а при обработке с быстрыми перемещениями, резким торможением или реверсом — силы инерции. [c.157]
Задача 1.57. Вертикальная мачта весом g поддерживается кронштейном, опирающимся на ролик С. Коэффициент трения в направляющих А V. В одинаков и равен /. Размеры указаны на рис. а. Определить реакции опор А, В VI С.
[c.142]
Коэффициент трения в направляющих А V. В одинаков и равен /. Размеры указаны на рис. а. Определить реакции опор А, В VI С.
[c.142]
Если составная балка устроена без прокладок, как это часто бывает в деревянных конструкциях, то силы s прижатия одного бруса к другому создают добавочные препятствия сдвигу по шву в виде трения. При абсолютно жестких поперечных связях получаем сосредоточенные усилия 5, которые прижимают составляющие стержни по концам. Ограничимся (для простоты) рассмотрением симметрично составленной балки из двух брусьев. В конце п. 8 было установлено, что для такой балки усилия в поперечных связях при абсолютной жесткости последних равны полуразности поперечных нагрузок, приложенных к каждому из составляющих стержней. Следовательно, сосредоточенные усилия над опорами балки будут равны половине опорной реакции балки (при отсутствии сосредоточенного груза над опорой). Далее при более точном решении, учитывающем податливость поперечных связей, будет показано, что значения усилий 5, максимальные над опорами, быстро падают в пролете балки. Таким образом, общее усилие, близкое по величине к половине опорной реакции, передается с одного составляющего бруса на другой лишь на небольшом участке длины составной балки. То же самое можно установить и в других местах приложения сосредоточенных грузов. Поэтому будем считать, что силы трения, прямо пропорциональные давлению одного бруса на другой, сосредоточены в точках приложения опорных реакций и сосредоточенных грузов, действующих по направлению к шву составной балки, т.е. прижимающих брус к другому. Трение, противодействующее сдвигу.
[c.103]
Таким образом, общее усилие, близкое по величине к половине опорной реакции, передается с одного составляющего бруса на другой лишь на небольшом участке длины составной балки. То же самое можно установить и в других местах приложения сосредоточенных грузов. Поэтому будем считать, что силы трения, прямо пропорциональные давлению одного бруса на другой, сосредоточены в точках приложения опорных реакций и сосредоточенных грузов, действующих по направлению к шву составной балки, т.е. прижимающих брус к другому. Трение, противодействующее сдвигу.
[c.103]
При применении этого метода изгиба оказывается весьма удобным подвешивать грузы к прикрепленным к концам стеклянной полосы двум длинным выдающимся в стороны полосам из легкого дерева (см. фиг. 3.022). Это позволяет получить требуемый изгибающий момент с помощью гораздо меньших грузов. При таком способе реакции опор гораздо меньше, что имеет два преимущества 1) уменьшение местных искажений в поле напряжений, вызванных остриями ножей, и 2) столь значительное уменьшение возможного трения, что обычно пред-
[c.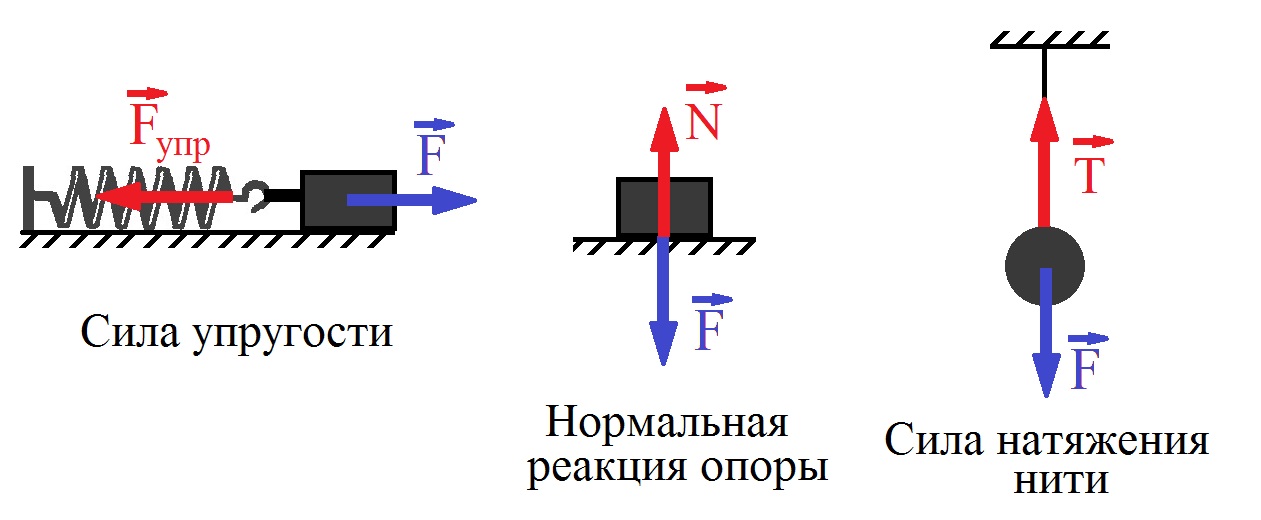 161]
161]
Тормоз с равными приводными силами и односторонним расположением опор изображен на рис. 166, а. Равные приводные силы и Ра возникают в результате того, что площади поршней цилиндра одинаковы. Чтобы оценить работу тормоза, на схеме показаны также реакции барабана на колодки, представленные в виде сосредоточенных сил и N2, а также силы трения и Т . Для упрощения схемы реакции опор на колодки не показаны. Если рассмотреть сумму моментов сил, действующих на каждую из колодок, то окажется, что тормозной момент, создаваемый колодкой 1, больше примерно в 2—3 раза тормозного момента колодки 2. Объясняется это тем, что момент силы трения, действующий на колодку 1, совпадает по направлению с моментом приводной силы, вследствие чего колодка захватывается вращающимся барабаном. Момент силы трения, действующий на колодку 2, противоположен по направлению моменту приводной силы, и поэтому сила трения препятствует прижатию колодки к барабану. Колодка 1 называется первичной, а колодка 2 вторичной.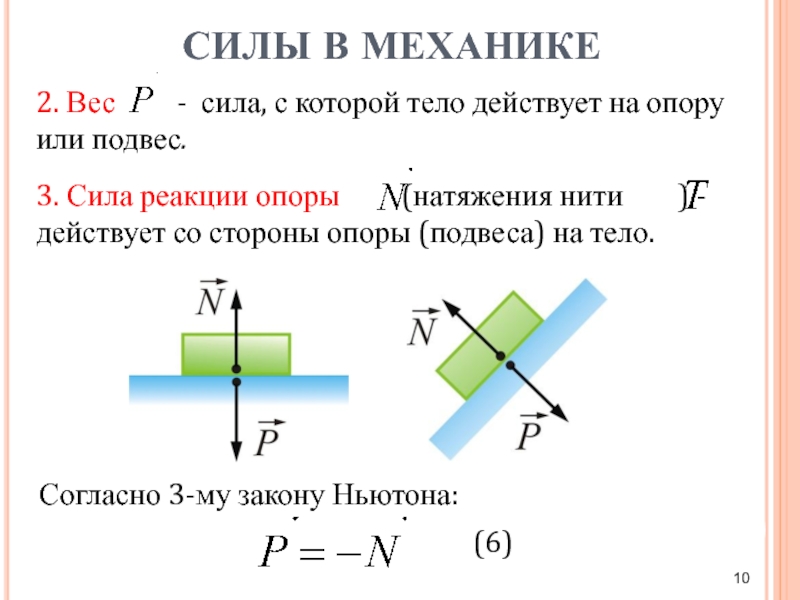 При вращении колеса в противоположную сторону функции колодок изменяются колодка работает как первичная, а колодка 1 — как вторичная.
[c.251]
При вращении колеса в противоположную сторону функции колодок изменяются колодка работает как первичная, а колодка 1 — как вторичная.
[c.251]
Искомыми величинами в задачах статики могут быть реакции опор, усилия в элементах конструкций, геометрические (размеры, углы) и материальные (вес, коэффициент трения) характеристики систем. В статически определимых задачах число уравнений равновесия совпадает с числом неизвестных. Именно такие задачи и будут рассмотрены в этой части. [c.11]
Вертикальная мачта весом С = 100 я, установленная в направляющих А и В, опирается на каток С. Пренебрегая трением в направляющих, определить реакции опор. [c.37]
Усилия в зацеплении и реакции опор находят путем последовательного рассмотрения условий равновесия каждого звена под действием внешних для данного звена сил, трение не учитывают. На рис. 11.3, а представлена схема усилий в одноступенчатой косозубой планетарной передаче с двумя сателлитами. [c.291]
[c.291]
Задача 9 (рис. 9). Брусок АВ длиной I, на конце которого прикреплен груз А1 весом Р, опирается в точке Л на гладкую вертикальную плоскость, а в точке С —на уступ. Определить, пренебрегая весом бруска и трением, реакции опор и расстояние АС при равЕЮвесии, если брусок образует с горизонтом угол а. [c.13]
Определить максимальную величпиу груза Р, который может быть поднят, а также реакции опор А и В, если дано диаметр вала Д = 10 см, Р = 45 см, а= 50 см. Трением в подшипниках пренебречь. Реакции в опорах обозначаем прописными буквами соответствеиио осям координат с индексами соответственно опорам. [c.82]
Гладкая поверхность — поверхность, при определении реакции которой силами трения мояшо пренебречь. Вектор реакции гладкой поверхности приложен в точке касания тела с поверхностью и направлен по нормали к поверхности, т е. перпендикулярно плоскости, касательной к данной поверхности ( рис.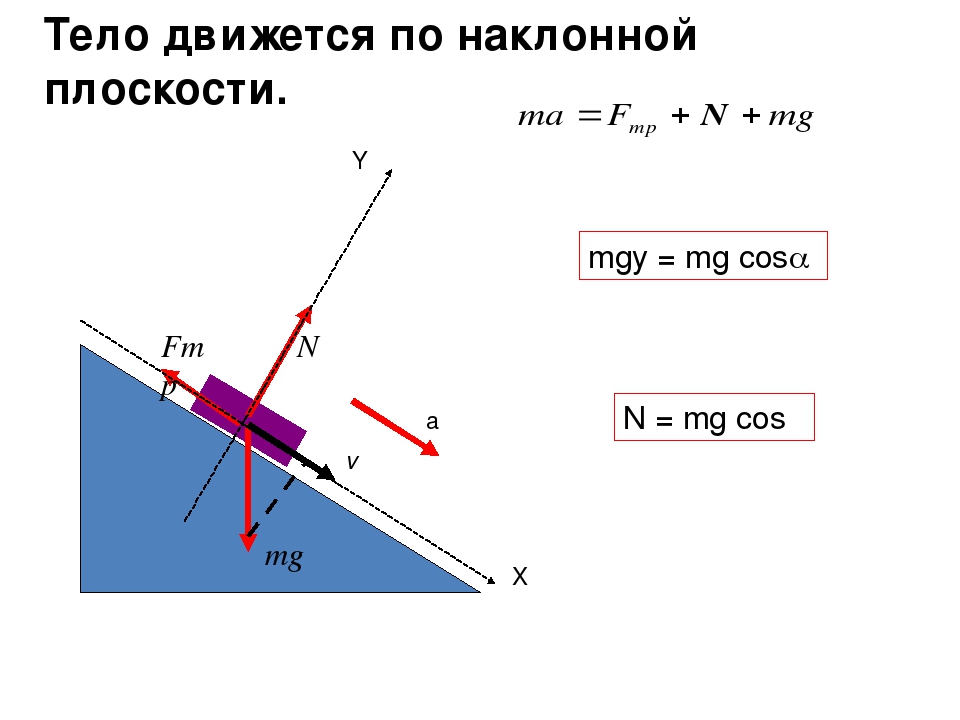 2.3 ). Разновидностью рассматриваемого типа связи является опора тела на уступ или острие, т.е. точечную опору. Гладкой в этом случае считается поверхность самого тела и вектор реакции направляется по нормали к повериости тела.
[c.46]
2.3 ). Разновидностью рассматриваемого типа связи является опора тела на уступ или острие, т.е. точечную опору. Гладкой в этом случае считается поверхность самого тела и вектор реакции направляется по нормали к повериости тела.
[c.46]
Рга аз в гз га 1а 23 вЛр-На толкатель действуют следующие силы Q3 —заданная сила сопротивления Л/оз —нормальная составляющая полной реакции Роз, возникающей в опоре С со стороны направляющей толкателя Т з —сила трения, возникающая в опоре С JVo3 — нормальная составляющая полной реакции Rob, возникающей в опоре С» со стороны направляющей толкателя — сила трения, [c.160]
Момент трения в шарнирах механизма в схемах привода, показанных на рис. IV.9, обеспечивающих отсутствие или малые значения реакций опор Ro и Af np, составляет 0,03Мдв (около 3%) им обычно пренебрегают. Силы и потери на трения играют большую роль в приводе с одним сервомотором, где Ron = Рсе >1 и в конических аппаратах, где велика вертикальная составляющая силы, действующей на опоре. В этих приводах силы трения надо учитывать.
[c.107]
В этих приводах силы трения надо учитывать.
[c.107]
На каждую из этих реакций можно распространить свойства, с которыми мы познакомились в случае одной материальной точки (см. гл. IX, п. 8). При этом мы должны опираться на один постулат, который подсказывается самой природой вещей и подтверждается ежедневным опытом, а именно мы доллсны считать, что любая опора Р способна обеспечить равновесие, развивая реакцию Ф, заранее неопределенную (и, возможно, равную нулю). Величина этой реакции зависит от действующих сил, но может быть какой угодно, а линия действия всегда остается внутри или на внешней полости конуса трения и совпадает с внешней нормалью (к телу, на котором находится опора), если опора лишена трения или рассматривается как свободная от трения (когда трение очень мало). На основании такого свойства реакции Ф мы всегда можем получить количественные условия равновесия, т. е. условия, которым должны удовлетворять силы F для того, чтобы вместе с реакциями Ф они могли составить систему, эквивалентную нулю.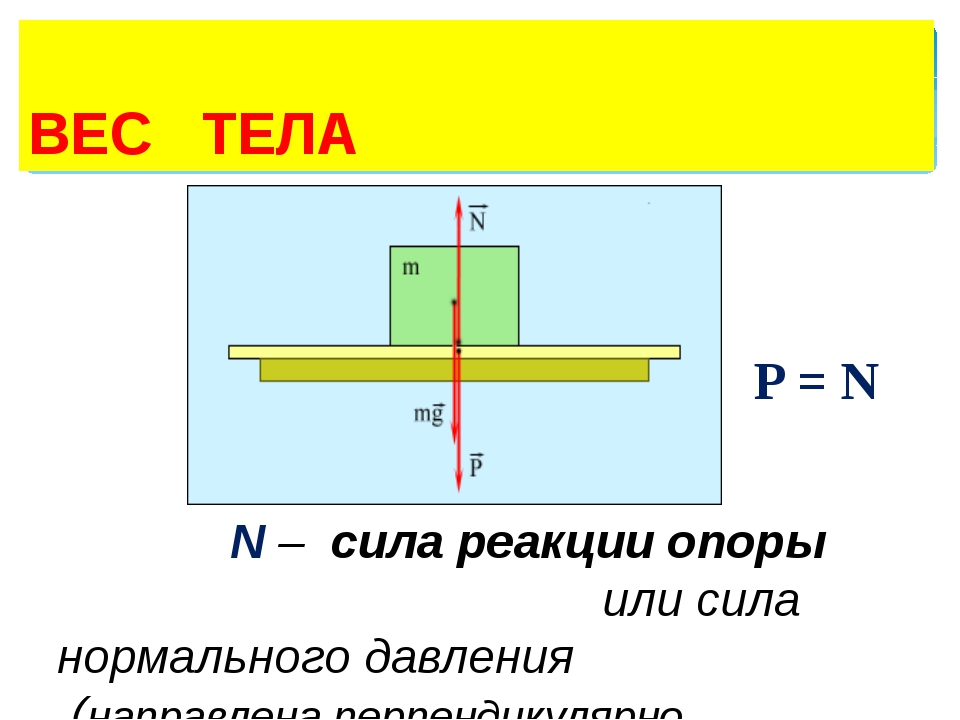 [c.116]
[c.116]
Рассмотрим вал с одним неуравновешенным диском, имеющим две основные опоры и одну промежуточную (рис. III.21), Промежуточная опора выполнена в виде опоры сухого трения [34]. Очевидно, что при низких скоростях вращения реакция в опоре будет меньше силы сухого трения и, следовательно, рассматриваемая система представляет собой ротор на трех жестких опорах, который имеет некоторую резонансную частоту (Окр-При возрастании угловой скорости прогиб диска будет изменяться согласно амплитудно-частотной характеристике трехопорного ротора (кривые ОА и А А» на рис. III.22). Однако развитие колебаний по этой характеристике будет происходить до тех пор, пока величина силы в промежуточной опоре не сравняется с величи- [c.152]
Действие системы из йп симметричных сосрёдоточбйных грузов расположенных в одной продольной плоскости попарно на одинаковых расстояниях от левой и правой опор с эксцентрицитетами b j, рассмотрено выше. Если не учитывать трение, то на основании выражений (6. 46)—(6. 48) для такой системы грузов уравнения упругой линии, изгибающих моментов и опорных реакций будут
[c.212]
46)—(6. 48) для такой системы грузов уравнения упругой линии, изгибающих моментов и опорных реакций будут
[c.212]
Силы трения в головке ветродвигателя существенно зависят от её конструкции и вызываются весом поворачивающейся конструкции, осевой нагрузкой, гироскопическим эффектом и реактивным моментом вертикального вала. На фиг. 42 дана схема верхней части ветродвигателя с виндро-зами [26], вес поворачивающейся части Q и координаты составляющих веса О, и О2 — и Ь. Реакции опор Bi и В2 определяются из [c.226]
Информация о типоразмерах зажимов и их расположении в пространстве в сочетании с данными об усп-лпях и месте резания позволяет осуществить силовой расчет системы деталь — приспособление, дает возможность уточнить выбранные типоразмеры зажпмов. Силовой расчет базируется на уравнениях статики. При этом рассматривается равновесие обрабатываемой детали иод влиянием усилий резания, сил зажима с j TieTOM возникающих при этом реакций опор и сил трения. [c.97]
[c.97]
Более общий случай произвольной нагрузки вала в параллельных плоскостях, перпендикулярных оси вращения, представлен на фиг. 174. Здесь имеется вал на двух опорах, несущий за опорами кривошипы, на которые действуют силы РI кг и Р 2 кг, и нагружённый между опорами маховиком весом О кг,служащий вместе с тем шкивом. Действие шкива-маховика может быть выражено вертикальной силой О и горизонтальной силой Рд, момент которой относи-, тельно оси вращения уравновешивает моменты сил Р, и Р, (в предположении равномерного вращения). Перенося все силы Р Рг и Рд на ось вращения, можно в дальнейшем сделать расчёт реакций опор, для чего каждую силу разлагаем по опорами получаем в плоскости опор известные горизонтальные и вертикальные силы X, Ух (фиг. 175) и АГг, При отсутствии трения силы Хи Ух уравно весились бы одной нормальной реакцией Ы,, трение же может быть [c.125]
Распространенные зажамные мехзниз.мы и вриво.эы стаиочяых приспособлений. Заготовку закрепляют с помощью зажимных механизмов (ЗМ). Силу закрепления Р3 определяют из условия равновесия заготовки под действием сил резания, реакций в опорах, сил трения по поверхностям контакта заготовки с опорами и ЗМ (табл. 6).
[c.245]
Заготовку закрепляют с помощью зажимных механизмов (ЗМ). Силу закрепления Р3 определяют из условия равновесия заготовки под действием сил резания, реакций в опорах, сил трения по поверхностям контакта заготовки с опорами и ЗМ (табл. 6).
[c.245]
Задаем направление возможного движения подвижной опоры, скользяБдей с трепием. Прикладываем к этой опоре силу трения, направляя ее в сторону противоположную возможному движению. Предельное значение силы трения связываем с величиной нормальной реакции опоры N по формуле Кулона = ТУ/, где / — коэффициент трения, зависяБдий от свойств коптактируюпдих материалов и заданный в условии задачи. [c.74]
Задаем направление возможного движения подвижной опоры, скользяБдей с трепием Предполагая возможное движение ползуна В влево, силу трения направим направо (рис. 53). Предельное значение силы трения связываем с нормальной реакцией опоры N по формуле Кулона [c.75]
Если пружина была нагружена большей силой и имела прогиб, превышающий величину а затем нагрузка уменьшилась, а прогиб стал равным /, то при этом сила трения Р будет иметь обратное направление (рис. 16, в). Равнодействующая сил Р и Р, т. е. истинная реакция опоры Рр, будет иметь ту же величину, что и в предыдущем случае, но будет отклонена от вертикали на угол, равный (0 + 7). Теперь ее проекция на вертикаль будет. меньше, чем проек.чия с 5. ы Р. и усилие Р/,-, т. е. иегинная нагрузка пружины, п11релел 1тся выражением
[c.177]
16, в). Равнодействующая сил Р и Р, т. е. истинная реакция опоры Рр, будет иметь ту же величину, что и в предыдущем случае, но будет отклонена от вертикали на угол, равный (0 + 7). Теперь ее проекция на вертикаль будет. меньше, чем проек.чия с 5. ы Р. и усилие Р/,-, т. е. иегинная нагрузка пружины, п11релел 1тся выражением
[c.177]
Сила реакции опоры. Вес ❤️
Положим камень на горизонтальную крышку стола, стоящего на Земле (рис. 104). Поскольку ускорение камня относительно Земли равно пулю, то по второму закону Ньютона сумма действующих на него сил равна нулю. Следовательно, действие на камень силы тяжести m — g должно компенсироваться какими-то другими силами. Ясно, что под действием камня крышка стола деформируется.
Поэтому со стороны стола на камень действует сила упругости. Если считать, что камень взаимодействует лишь с Землей и крышкой стола, то сила упругости должна уравновешивать силу
тяжести: Fупр = — m — g. Эту силу упругости называют силой реакции опоры и обозначают латинской буквой N.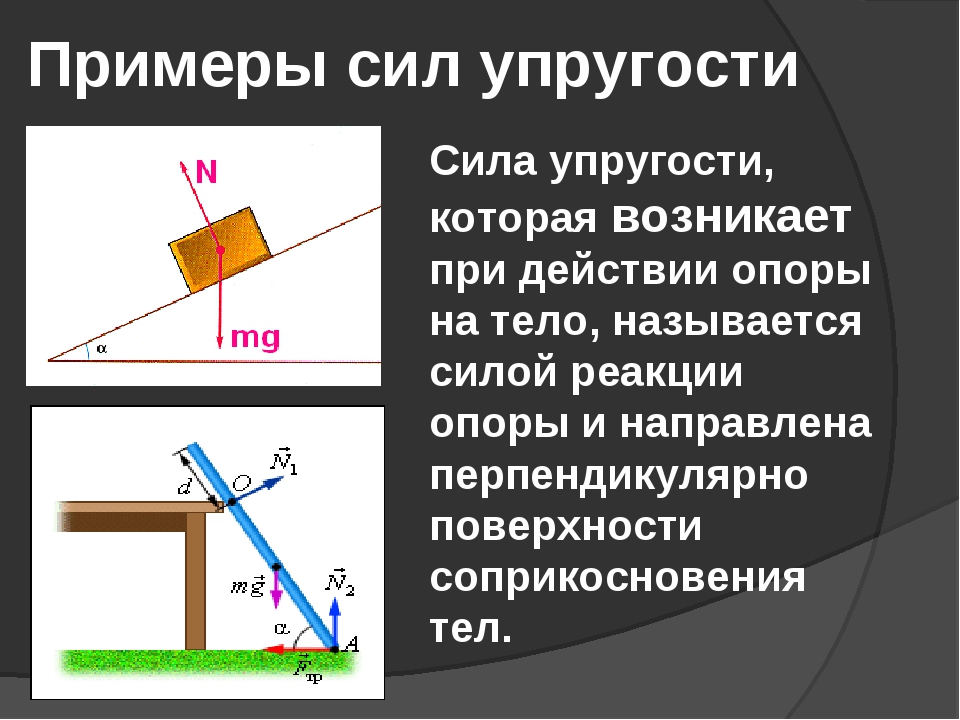 Так как ускорение свободного падения направлено вертикально вниз, сила N направлена вертикально вверх — перпендикулярно поверхности крышки стола.
Так как ускорение свободного падения направлено вертикально вниз, сила N направлена вертикально вверх — перпендикулярно поверхности крышки стола.Поскольку крышка стола действует на камень, то по третьему закону Ньютона и камень действует на крышку стола силой P = — N (рис. 105). Эту силу называют весом.
Весом тела называют силу, с которой это тело действует на подвес или опору, находясь относительно подвеса или опоры в неподвижном состоянии.
Ясно, что в рассмотренном случае вес камня равен силе тяжести: P = m — g. Это будет верно для любого тела, покоящегося на подвесе (опоре) относительно Земли (рис. 106). Очевидно, что в этом случае точка крепления подвеса (или опора) неподвижна относительно Земли.
Для тела, покоящегося на неподвижном относительно Земли подвесе (опоре), вес тела равен силе тяжести.
Вес тела также будет равен действующей на тело силе тяжести в случае, если тело и подвес (опора) движутся относительно Земли равномерно прямолинейно.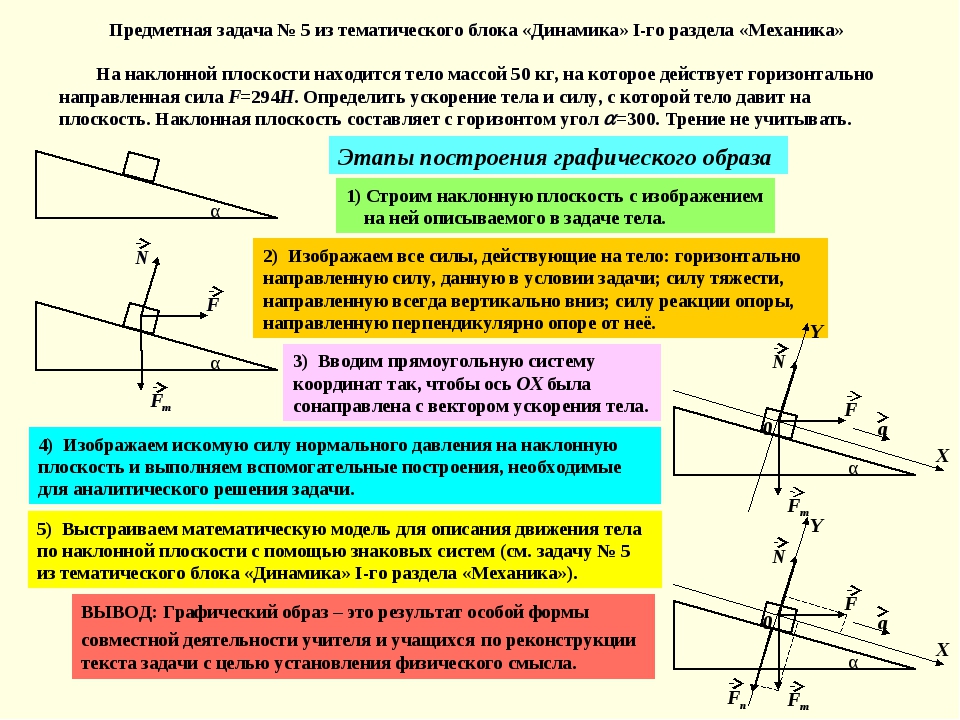
Если же тело и подвес (опора) движутся относительно Земли с ускорением так, что тело остается неподвижным относительно подвеса (опоры), то вес тела не будет равен силе тяжести.
Рассмотрим пример. Пусть тело массой m лежит на полу лифта, ускорение a которого направлено вертикально вверх (рис. 107).
Будем считать, что на тело действуют только сила тяжести m — g и сила реакции пола N. (Вес тела действует не на тело, а на опору — пол лифта.) В системе отсчета, неподвижной относительно Земли, тело на полу лифта движется вместе с лифтом с ускорением a. В соответствии со вторым законом Ньютона произведение массы тела на ускорение равно сумме всех действующих на тело сил. Поэтому: m — a = N — m — g.
Следовательно, N = m — a + m — g = m — (g + a). Значит, если лифт имеет ускорение, направленное вертикально вверх, то модуль силы N реакции пола будет больше модуля силы тяжести. В самом деле, сила реакции пола должна не только скомпенсировать действие силы тяжести, но и придать телу ускорение в положительном направлении оси X.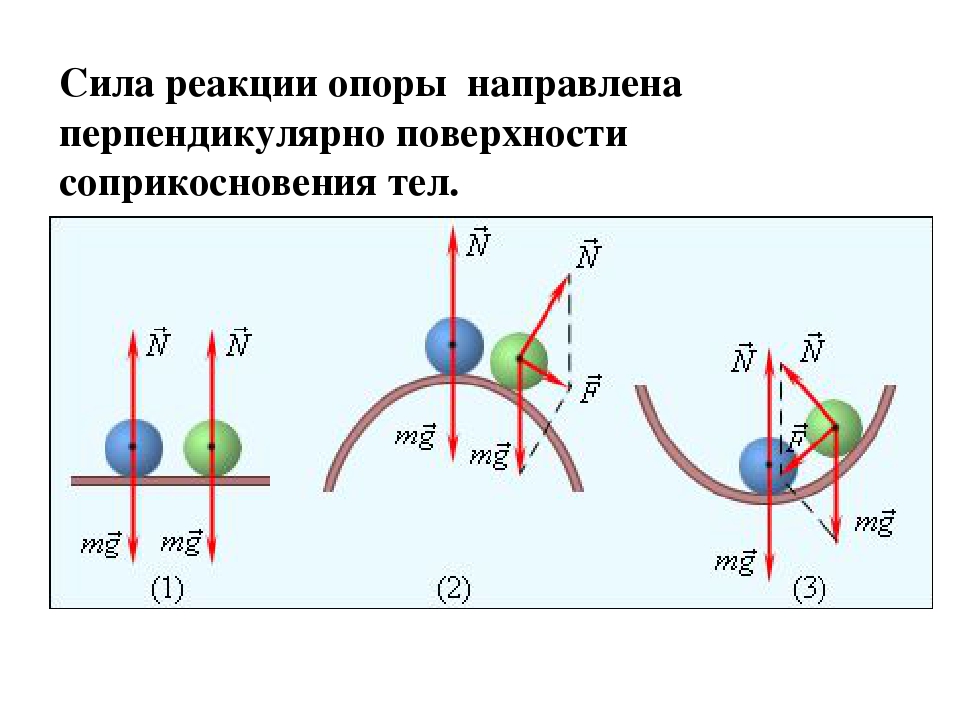
Сила N — это сила, с которой пол лифта действует на тело. По третьему закону Ньютона тело действует на пол с силой P, модуль которой равен модулю N, но направлена сила P в противоположную сторону. Эта сила является весом тела в движущемся лифте. Модуль этой силы P = N = m — (g + a).
Таким образом, в лифте, движущемся с направленным вверх относительно Земли ускорением, модуль веса тела больше модуля силы тяжести.
Такое явление называют перегрузкой.
Например, пусть ускорение а лифта направлено вертикально вверх и его значение равно g, т. е. a = g. В этом случае модуль веса тела — силы, действующей на пол лифта, — будет равен P = m — (g + a) = m — (g + g) = 2m — g. То есть вес тела при этом будет в два раза больше, чем в лифте, который относительно Земли покоится или движется равномерно прямолинейно.
Для тела на подвесе (или опоре), движущемся с ускорением относительно Земли, направленным вертикально вверх, вес тела больше силы тяжести.
Отношение веса тела в движущемся ускоренно относительно Земли лифте к весу этого же тела в покоящемся или движущемся равномерно прямолинейно лифте называют коэффициентом перегрузки или, более кратко, перегрузкой.
Коэффициент перегрузки (перегрузка) — отношение веса тела при перегрузке к силе тяжести, действующей на тело.
В рассмотренном выше случае перегрузка равна 2. Понятно, что если бы ускорение лифта было направлено вверх и его значение было равно a = 2g, то коэффициент перегрузки был бы равен 3.
Теперь представим себе, что тело массой m лежит на полу лифта, ускорение которого a относительно Земли направлено вертикально вниз (противоположно оси X). Если модуль a ускорения лифта будет меньше модуля ускорения свободного падения, то сила реакции пола лифта по-прежнему будет направлена вверх, в положительном направлении оси X, а ее модуль будет равен N = m — (g — a). Следовательно, модуль веса тела будет равен P = N = m — (g — a), т. е. будет меньше модуля силы тяжести.
Таким образом, тело будет давить на пол лифта с силой, модуль которой меньше модуля силы тяжести.
Это ощущение знакомо каждому, кто ездил на скоростном лифте или качался на больших качелях. При движении вниз из верхней точки вы чувствуете, что ваше давление на опору уменьшается. Если же ускорение опоры положительно (лифт и качели начинают подниматься), вас сильнее прижимает к опоре.
Если же ускорение опоры положительно (лифт и качели начинают подниматься), вас сильнее прижимает к опоре.
Если ускорение лифта относительно Земли будет направлено вниз и равно по модулю ускорению свободного падения (лифт свободно падает), то сила реакции пола станет равной нулю: N = m — (g — a) = m — (g — g) = 0. В этом случае пол лифта перестанет давить на лежащее на нем тело. Следовательно, согласно третьему закону Ньютона и тело не будет давить на пол лифта, совершая вместе с лифтом свободное падение. Вес тела станет равным нулю.
Такое состояние называют состоянием невесомости.
Состояние, при котором вес тела равен нулю, называют невесомостью.
Наконец, если ускорение лифта, направленное к Земле, станет больше ускорения свободного падения, тело окажется прижатым к потолку лифта. В этом случае вес тела изменит свое направление. Состояние невесомости исчезнет.
В этом можно легко убедиться, если резко дернуть вниз банку с находящимся в ней предметом, закрыв верх банки ладонью, как показано на рис.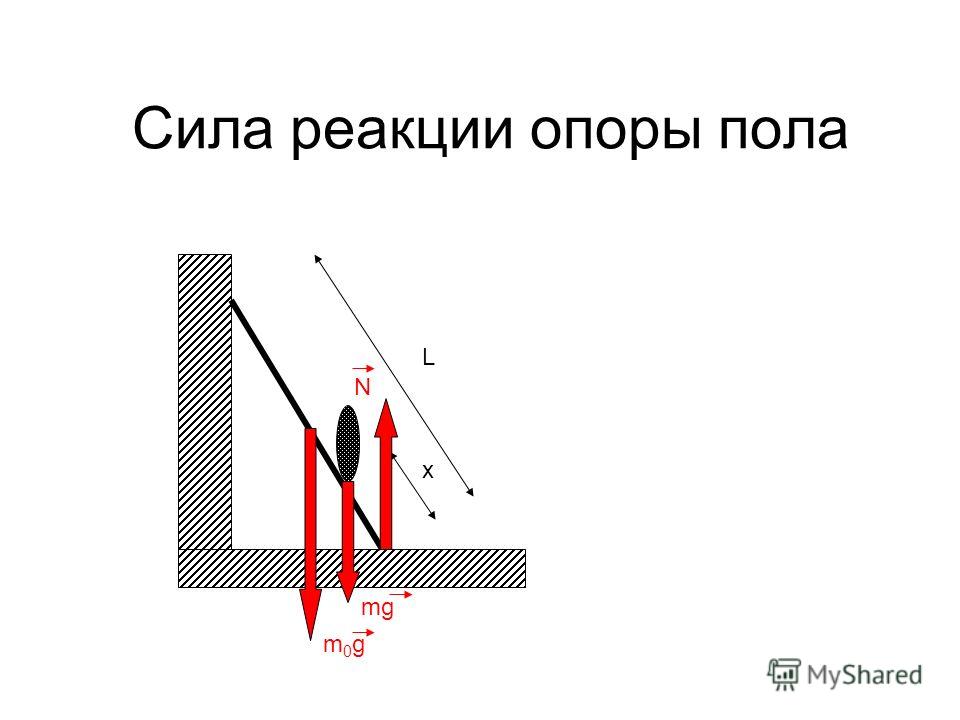 108.
108.
Итоги
Весом тела называют силу, с которой это тело действует на поднес или опору, находясь относительно подвеса или опоры в неподвижном состоянии.
Вес тела в лифте, движущемся с направленным вверх относительно Земли ускорением, по модулю больше модуля силы тяжести. Такое явление называют перегрузкой.
Коэффициент перегрузки (перегрузка) — отношение веса тела, при перегрузке к силе тяжести, действующей на это тело.
Если вес тела равен нулю, то такое состояние называют невесомостью.
Вопросы
Какую силу называют силой реакции опоры? Что называют весом тела? К чему приложен вес тела? Приведите примеры, когда вес тела: а) равен силе тяжести; б) равен нулю; в) больше силы тяжести; г) меньше силы тяжести. Что называют перегрузкой? Какое состояние называют невесомостью?
Упражнения
Семиклассник Сергей стоит на напольных весах в комнате. Стрелка прибора установилась напротив деления 50 кг. Определите модуль веса Сергея. Ответьте на остальные три вопроса об этой силе. Найдите перегрузку, испытываемую космонавтом, который находится в ракете, поднимающейся вертикально вверх с ускорением a = Зg. С какой силой действует космонавт массой m = 100 кг на ракету, указанную в упражнении 2? Как называется эта сила? Найдите вес космонавта массой m = 100 кг в ракете, которая: а) стоит неподвижно на пусковой установке; б) поднимается с ускорением a = 4g, направленным вертикально вверх. Определите модули сил, действующих на гирю массой m = 2 кг, которая висит неподвижно На легкой нити, прикрепленной к потолку комнаты. Чему равны модули силы упругости, действующей со стороны нити: а) на гирю; б) на потолок? Чему равен вес гири? Указание: для ответа на поставленные вопросы воспользуйтесь законами Ньютона. Найдите вес груза массой m = 5 кг, подвешенного на нити к потолку скоростного лифта, если: а) лифт равномерно поднимается; б) лифт равномерно опускается; в) поднимающийся вверх со скоростью v = 2 м/с лифт начал торможение с ускорением a = 2 м/с2; г) опускающийся вниз со скоростью v = 2 м/с лифт начал торможение с ускорением a = 2 м/с2; д) лифт начал движение вверх с ускорением a = 2 м/с2; е) лифт начал движение вниз с ускорением a = 2 м/с2.
Ответьте на остальные три вопроса об этой силе. Найдите перегрузку, испытываемую космонавтом, который находится в ракете, поднимающейся вертикально вверх с ускорением a = Зg. С какой силой действует космонавт массой m = 100 кг на ракету, указанную в упражнении 2? Как называется эта сила? Найдите вес космонавта массой m = 100 кг в ракете, которая: а) стоит неподвижно на пусковой установке; б) поднимается с ускорением a = 4g, направленным вертикально вверх. Определите модули сил, действующих на гирю массой m = 2 кг, которая висит неподвижно На легкой нити, прикрепленной к потолку комнаты. Чему равны модули силы упругости, действующей со стороны нити: а) на гирю; б) на потолок? Чему равен вес гири? Указание: для ответа на поставленные вопросы воспользуйтесь законами Ньютона. Найдите вес груза массой m = 5 кг, подвешенного на нити к потолку скоростного лифта, если: а) лифт равномерно поднимается; б) лифт равномерно опускается; в) поднимающийся вверх со скоростью v = 2 м/с лифт начал торможение с ускорением a = 2 м/с2; г) опускающийся вниз со скоростью v = 2 м/с лифт начал торможение с ускорением a = 2 м/с2; д) лифт начал движение вверх с ускорением a = 2 м/с2; е) лифт начал движение вниз с ускорением a = 2 м/с2.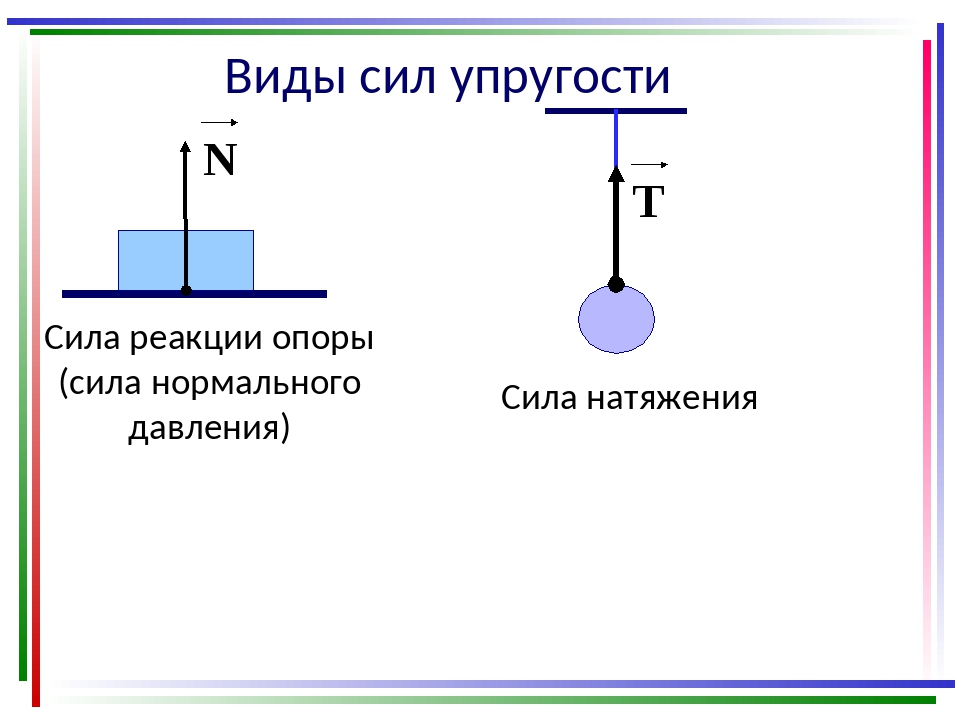
Силы реакции опоры
Механика Силы реакции опоры
просмотров — 990
Действие веса тела на опору встречает противодействие, ĸᴏᴛᴏᴩᴏᴇ называют реакцией опоры (или опорной реакцией).
Реакция опоры — это мера противодействия опоры действию на нее тела, находящегося с ней в контакте (в покое или движении). Она равна силе действия тела на опору, направлена в противоположную сторону и приложена к этому телу.
Обычно человек, находясь на горизонтальной опоре, испытывает противодействие своему весу. В этом случае опорная реакция, как и вес тела, направлена перпендикулярно к опоре. Это нормальная (или идеальная) реакция опоры. В случае если поверхность не плоская, то опорная реакция перпендикулярна к плоскости, касательной к точке опоры.
Когда вес статический, то реакция опоры статическая; по величине она равна статическому весу. В случае если человек на опоре движется с ускорением, направленным вверх, то к статическому весу добавляется сила инерции и возникает динамическая реакция о п о р ы (рис. 35). Реакция опоры — сила
35). Реакция опоры — сила
пассивная (реактивная). Она не может сама по себе вызвать положительные ускорения. Но без нее — если нет опоры, если не от чего оттолкнуться (или не к чему притянуться) — человек не может активно перемещаться.
В случае если отталкиваться от горизонтальной опоры не прямо вверх, то и сила давления на опору будет приложена не под прямым углом
к ее поверхности. Тогда реакция опоры также не будет перпендикулярна к поверхности, ее можно разложить на н о р м а л ь н у ю и касательную составляющие. Когда соприкасающиеся поверхности ровные, без выступов, шипов и т. п. (асфальт, подошва ботинка), то касательная составляющая реакции опоры и есть сила трения.
Касательная реакция может быть обусловлена не только трением (как, например, между лыжей и снегом), но и другими взаимодействиями (к примеру, шипы беговых туфель, вонзившиеся в дорожку).
Равнодействующая нормальной и касательной составляющих принято называть
о б щ е й реакцией опоры.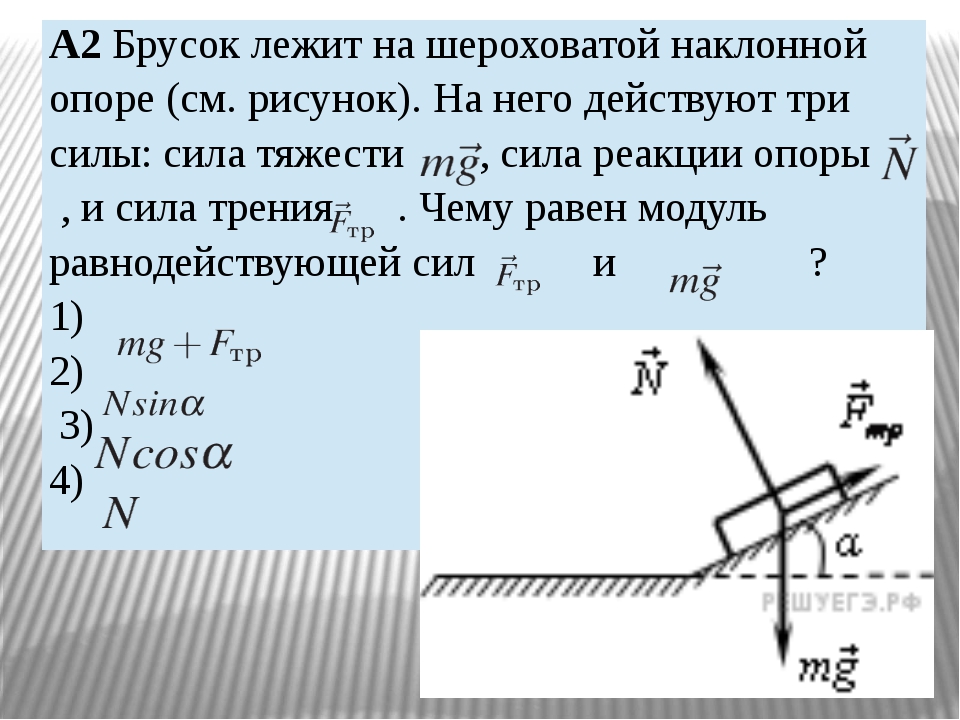 Она только при свободном неподвижном положении над опорой (или под опорой) проходит через ЦМ человека. Во время же движений, отталкивания или амортизации она обычно не проходит через ЦМ, образуя относительно него момент.
Она только при свободном неподвижном положении над опорой (или под опорой) проходит через ЦМ человека. Во время же движений, отталкивания или амортизации она обычно не проходит через ЦМ, образуя относительно него момент.
Читайте также
Действие веса тела на опору встречает противодействие, которое называют реакцией опоры (или опорной реакцией). Реакция опоры — это мера противодействия опоры действию на нее тела, находящегося с ней в контакте (в покое или движении). Она равна силе действия тела на опору,… [читать подробенее]
Технологическая карта урока физики по теме «Сила реакции опоры. Вес» по ФГОС
Технологическая карта урока физики по теме «Сила реакции опоры. Вес» по ФГОС
Класс: 7 класс
УМК: Грачев А.В., Погожев В.А., Селиверстов А.В.
Тема: Сила реакции опоры. Вес
Тип урока: урок получения новых знаний с элементами обобщения ранее изученного.
Технология построения урока: проблемное обучение.
Цель урока: сформировать представление о силе веса тела и силе нормальной реакции опоры.
Задачи
Обучающие: познакомить учащихся с новыми понятиями: вес тела, сила нормальной реакции опоры, перегрузка, невесомость, коэффициент перегрузки, с графическим изображением веса тела и силы реакции опоры, описать явления перегрузки и невесомости; применять алгоритм решения задач при расчете силы нормальной реакции опоры и веса тела.
Развивающие: развитие навыков логического мышления, развитие умения высказывать и обосновывать свою точку зрения, умения делать выводы
Воспитательные: убеждать учащихся в познаваемости окружающего мира; формировать интерес к познанию законов природы и их применению; создавать позитивное отношение к предмету; воспитывать чувство уважения к собеседнику.
Планируемый результат:
Личностные УУД:
формирование ответственного отношения к учению, готовности к саморазвитию и самообразованию;
формирование коммуникативной компетентности;
формирование устойчивой учебно-познавательной мотивации и интереса к учению.
Регулятивные УУД:
осуществление регулятивных действий самоконтроля и самооценки в процессе урока;
постановка учебной задачи на основе известного и неизвестного;
формирование умения самостоятельно контролировать своё время и управлять им.
Коммуникативные УУД:
организация и планирование учебного сотрудничества с учителем и сверстниками,
использование адекватных языковых средств для отображения своих чувств, мыслей, мотивов и потребностей.
построение устных высказываний, в соответствии с поставленной коммуникативной задачей.
Познавательные УУД:
построение логических рассуждений, включающих установление причинно-следственных связей;
формулирование проблемной задачи и поиск наиболее эффективных средств для ее решения.
Этапы урока, предполагаемый результат | Время, мин | Деятельность учителя | Деятельность учащихся | Формирование УУД |
Организационный момент | 1 | Приветствует учеников. | Приветствуют учителя, проверяют свои рабочие места | |
Актуализация знаний и фиксация затруднений в деятельности | 8 | Готовит учащихся к работе на уроке. Показывает демонстрации и формулирует вопросы, актуализирующие опорные знания: Демонстрация 1. Мячик, выпущенный из рук, падает вниз. Как движется мячик? Как направлено ускорение, с которым движется мячик? Почему он движется ускоренно? Сформулируйте второй закон Ньютона. Какая сила действует на мячик? Как направлена эта сила? По какой формуле ее можно рассчитать? Демонстрация 2. Тело подвешено на пружине. Почему оно находится в покое? Какие силы приложены к телу? Охарактеризуйте силу упругости, действующую на тело со стороны пружины (направление, величина). | Ученики отвечают на вопросы. | Регулятивные: самоконтроль и структурирование собственных знаний Познавательные: развитие умения проводить анализ и делать вывод, установление причинно-следственных связей Личностные: Самооценка имеющихся знаний Коммуникативные: развитие умения грамотно выражать свои мысли |
Постановка проблемных вопросов и выдвижение гипотез | 3 | Учитель предлагает ответить на следующие вопросы: 1. Почему книга, лежащая на столе, не движется ускоренно? С какими телами взаимодействует книга, лежащая на столе? Как называются силы, с которыми эти тела действуют на книгу? А с какой силой книга действует на стол? 2. | Отвечают на вопросы. Высказывают предположения, что на книгу действует сила упругости со стороны стола, т.к. она находится в покое относительно ИСО стола, а на пружину действует сила со стороны подвешенного тела. Формулируют тему урока, цель и задачи. Записывают тему урока в тетради. | Коммуникативные: развитие умения грамотно выражать свои мысли Познавательные: выдвижение гипотез и их обоснование Личностные: формирование познавательного интереса и понимание практической значимости выполняемой работы Регулятивные: постановка учебной задачи на основе известного и неизвестного. |
Решение проблемы | 20 | I. 1. На какое тело действует сила? 2. Какое тело действует с этой силой? 3. Чему равен модуль силы? 4. Куда направлена сила? Обращает внимание, что ее величину можно определить из второго закона Ньютона для тела. II. Определение модуля силы веса тела, стоящего на опоре, в случае ускоренного движения опоры вверх. Пусть тело массой m лежит на полу лифта, ускорение которого направлено вертикально вверх. Учитель решает эту задачу на доске, приходит к ответу, что вес тела P = m(g+a). Учитель просит класс проанализировать полученный результат. После анализа вводит понятие перегрузки и коэффициента перегрузки. III. Учитель просит определить модуль силы веса тела, стоящего на опоре, в случае ускоренного движения опоры вниз. Вызывает учащегося к доске и оказывает помощь при решении задачи. Анализируют ответ P = m (g – a). Выслушивает ответ ученика, поправляет в случае необходимости и вводит понятие невесомости тела. | I. Записывают определения. Делают поясняющие рисунки в тетрадях II. Решают задачу вместе с учителем. Делают вывод, что вес тела, лежащего на опоре, движущейся ускоренно вверх, больше силы тяжести. III. Учащийся решает задачу у доски при помощи учителя. | Коммуникативные: формулировать и аргументировать свою точку зрения. Познавательные: осмысление услышанной информации, построение логической цепочки рассуждений; знаково-символические действия (моделирование) |
Физкультминутка | 1 | Учитель читает стих: Шеей крутим осторожно — Голова кружиться может. Влево смотрим — раз, два, три. Так. И вправо посмотри. (Вращение головой вправо и влево.) Вверх потянемся, пройдёмся, (Потягивания —руки вверх, ходьба на месте. И за парты вновь вернёмся. | Обучающиеся делают зарядку | Коммуникативные: выполнять общие действия в коллективе |
Первичная проверка усвоения полученных знаний | 5 | Ответьте на вопросы: 1. Что показывают весы: массу или вес тела? 2. Может ли тело, имея массу, не иметь веса? Если да, то при каком условии? 3. Что общего у веса тела и силы тяжести? Чем они различаются? 4. Придумайте примеры, когда вес тела равен силе тяжести, меньше силы тяжести, больше силы тяжести, равен нулю. | Обучающиеся отвечают на вопросы | Коммуникативные: формулировать и аргументировать свою точку зрения. Познавательные: построение логических рассуждений, включающих установление причинно-следственных связей. Регулятивные: осознание качества и уровня усвоения знаний. |
Домашнее задание | 1 | §37, отв.на вопросы (с.168), упр. 1 – 3 (с.168) | Записывают домашнее задание | |
Рефлексия | 1 | Подводит итоги урока. Просит оценить учеников свою деятельность на уроке на листе самооценки. | Слушают учителя и проводят самооценку | Регулятивные: уметь соотносить цель и результат. |
Литература:
1. Грачев А.В. «Физика. 7 класс». Москва: Вентана-Граф, 2019 г.
2. Грачев А.В., Погожев В.А. и др. «Проектирование учебного курса: 7 класс. Методическое пособие», Москва: Вентана-Граф, 2014 г.
3. В.И. Коваленко «Школа физкультминуток», Москва: ВАКО, 2010 г.
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.ТЕГИ}} {{$элемент}} {{l10n_strings.ПРОДУКТЫ}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings. ЯЗЫК}}
{{$select.selected.display}}
ЯЗЫК}}
{{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.АВТОР}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Список сил реакции — 2017
Вы можете перечислить силы реакции на выбранные объекты для активного статического, нелинейного, испытания на падение и динамического исследования. Программное обеспечение перечисляет X-, Y-, Z-компоненты силы реакции и результирующую силу реакции на выбранных объектах, а также на всей модели.
Программное обеспечение перечисляет X-, Y-, Z-компоненты силы реакции и результирующую силу реакции на выбранных объектах, а также на всей модели.
Чтобы просмотреть силы реакции, после запуска анализа щелкните правой кнопкой мыши «Результаты» и выберите «Список сил реакции». В PropertyManager в разделе «Параметры» выберите «Сила реакции».
Вы также можете щелкнуть (Simulation CommandManager).
Силы реакции не рассчитываются для твердых тел.
Сила реакции
Перечисляет X-, Y-, Z-компоненты силы реакции и результирующую силу реакции на выбранных объектах и на всей модели.
| График отклика | Доступно только для нелинейных исследований, испытаний на падение и динамических исследований. Создает 2D-графики во времени для X-, Y-, Z-компонентов силы реакции и результирующей силы реакции на выбранных объектах и на всей модели. |
Момент реакции
Перечисляет X-, Y-, Z-компоненты момента реакции и результирующий момент реакции на выбранных объектах и на всей модели.
| График отклика | Доступно только для нелинейных исследований, испытаний на падение и динамических исследований. Создает 2D-графики во времени для X-, Y-, Z-компонентов момента реакции и результирующего момента реакции на выбранных объектах и на всей модели. |
Опции дисплея
| Отображение равнодействующей силы | Преобразует три вектора силы (X-, Y- и Z-компоненты) в результирующий вектор силы.Отображается только результирующий вектор силы. |
Расчет сил реакции в опорах котла по методу эквивалентной жесткости мембранной стенки
Значения сил реакции в опорах котла являются основой для расчета несущей металлоконструкции парового котла. В данной работе предлагается применение метода эквивалентной жесткости стенки мембраны для расчета сил реакции. Применен метод выравнивания смещения, как метод гомогенизации жесткости стенки мембраны.На примере котла «Милан» методом конечных элементов выполнен расчет реакций в опорах для реальной геометрии, дискретизированной конечным элементом оболочки. Второй расчет выполнен в предположении идеальной жесткости мембранных стенок, а третий – методом эквивалентной жесткости мембранных стенок. В третьем случае стенки мембраны аппроксимируются эквивалентной ортотропной пластиной. Аппроксимация жесткости стенки мембраны достигается с помощью матрицы упругости эквивалентной ортотропной пластины на уровне конечных элементов.Сопоставлены полученные результаты и подчеркнуты преимущества использования метода эквивалентной жесткости мембранной стенки для расчета реакций в опорах котлов.
В данной работе предлагается применение метода эквивалентной жесткости стенки мембраны для расчета сил реакции. Применен метод выравнивания смещения, как метод гомогенизации жесткости стенки мембраны.На примере котла «Милан» методом конечных элементов выполнен расчет реакций в опорах для реальной геометрии, дискретизированной конечным элементом оболочки. Второй расчет выполнен в предположении идеальной жесткости мембранных стенок, а третий – методом эквивалентной жесткости мембранных стенок. В третьем случае стенки мембраны аппроксимируются эквивалентной ортотропной пластиной. Аппроксимация жесткости стенки мембраны достигается с помощью матрицы упругости эквивалентной ортотропной пластины на уровне конечных элементов.Сопоставлены полученные результаты и подчеркнуты преимущества использования метода эквивалентной жесткости мембранной стенки для расчета реакций в опорах котлов.
1. Введение
В настоящее время паровые котлы мусоросжигательных электростанций изготавливаются специально в соответствии с требованиями инвесторов.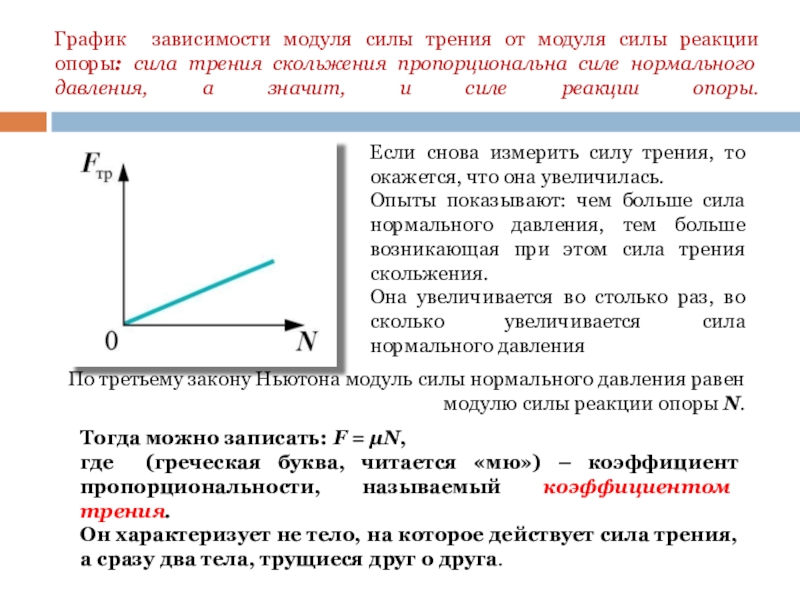 Из-за места, где будет установлен котел, количества и вида топлива, сжигаемого за определенное время, и технических параметров получаемого пара, производство паровых котлов в основном индивидуальное.Это представляет собой исключительное усилие дизайнеров. Трубы и листовой металл являются основными конструктивными элементами, используемыми для изготовления котлов. Более крупные структурные единицы, называемые мембранными стенками, получают путем сварки этих элементов. Мембранные стенки составляют основную конструкцию котла и выполняют двойную функцию. Теплообменник, то есть испаритель, является основной функцией, а второстепенной является передача нагрузки. Мембранные стенки парового котла нагружаются давлением рабочего тела (вода/пар), собственной массой и массой других конструктивных узлов, опирающихся на мембранные стенки, массой рабочего тела, массой изоляции и огнеупоров, и загрязняющая масса, которая откладывается в процессе горения.Нагрузка передается через мембранные стенки на опоры котла, а затем на несущую металлоконструкцию.
Из-за места, где будет установлен котел, количества и вида топлива, сжигаемого за определенное время, и технических параметров получаемого пара, производство паровых котлов в основном индивидуальное.Это представляет собой исключительное усилие дизайнеров. Трубы и листовой металл являются основными конструктивными элементами, используемыми для изготовления котлов. Более крупные структурные единицы, называемые мембранными стенками, получают путем сварки этих элементов. Мембранные стенки составляют основную конструкцию котла и выполняют двойную функцию. Теплообменник, то есть испаритель, является основной функцией, а второстепенной является передача нагрузки. Мембранные стенки парового котла нагружаются давлением рабочего тела (вода/пар), собственной массой и массой других конструктивных узлов, опирающихся на мембранные стенки, массой рабочего тела, массой изоляции и огнеупоров, и загрязняющая масса, которая откладывается в процессе горения.Нагрузка передается через мембранные стенки на опоры котла, а затем на несущую металлоконструкцию.
Поскольку водотрубные котлы представляют собой большие конструкции, состоящие из большого количества труб, соединенных с мембранными стенками, то точно рассчитать реакции в опорах очень сложно. На практике существует два подхода к расчету реакций в опорах паровых котлов. Первый подход основан на предположении, что жесткость мембраны мембранной стенки котла очень велика, поэтому котел рассчитывается как идеальное твердое тело.Второй подход учитывает конечную жесткость стенок мембраны с помощью метода конечных элементов. Дискретизация реальной геометрии котла (мембранных стенок) требует чрезвычайно большого количества конечных элементов, поэтому этот подход используется редко, особенно для небольших котлов. Чаще всего жесткость стенки мембраны аппроксимируется эквивалентной жесткостью ортотропной пластины/оболочки, что позволяет многократно уменьшить степени свободы численной модели.
Трудно найти более подробные исследования по теме гомогенизации мембранной стенки парового котла.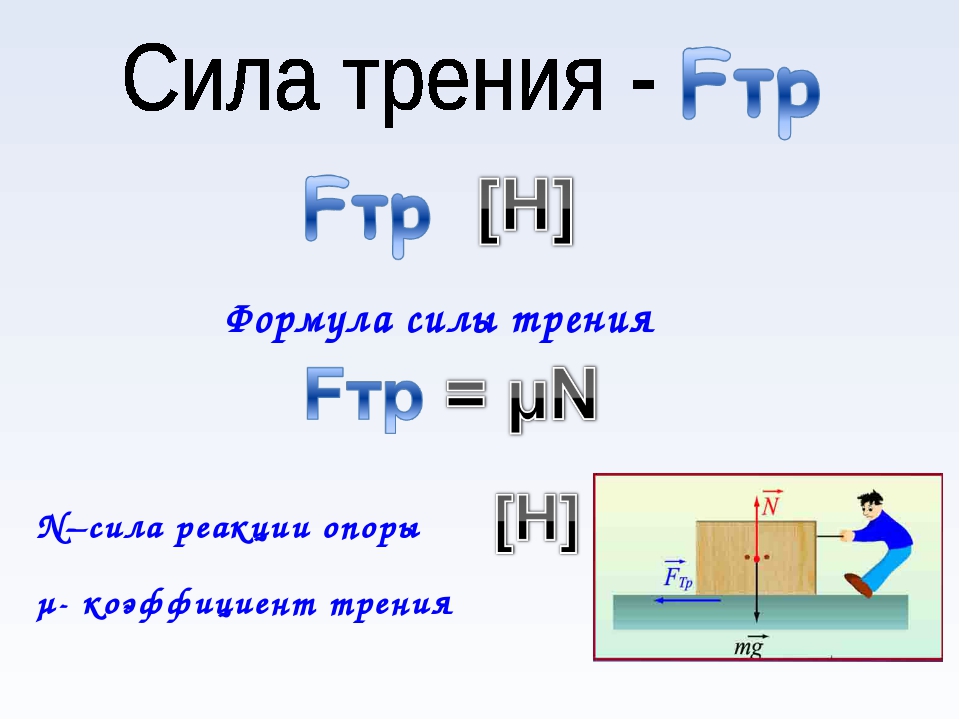 В 2012 году Милошевич-Митич [1] с группой авторов предложили методику расчета прочности водотрубного котла с использованием конечного элемента ортотропной плиты. Усреднение жесткости мембранных стенок проводится численно с использованием метода выравнивания перемещений.
В 2012 году Милошевич-Митич [1] с группой авторов предложили методику расчета прочности водотрубного котла с использованием конечного элемента ортотропной плиты. Усреднение жесткости мембранных стенок проводится численно с использованием метода выравнивания перемещений.
При расчете прогиба мембранных стенок под влиянием разрежения/избыточного давления дымовых газов на практике чаще всего используется метод эквивалентной толщины стенки. Жесткость на изгиб стеновой мембранной трубы равна жесткости на изгиб эквивалентной толщины стенки для оси, перпендикулярной продольной оси мембранной стеновой трубы, а жесткость на изгиб мембранной стеновой ленты равна жесткости на изгиб эквивалентной толщины стенки для ось параллельна продольной оси мембранной стенки трубы.
Мембранная стенка парового котла представляет собой конструктивно ортотропную плиту. К этому классу конструкций также относятся усиленные плиты, часто используемые как в строительстве, так и на перерабатывающих/энергетических установках, где необходимо добиться оптимального конструктивного решения с учетом массы конструкции. Самые ранние исследования по теме жесткости подкрепленных пластин, скорее всего, были выполнены Хубером [2–4]. Его исследования были вдохновлены отсутствием точных выражений для решения задач изгиба и потери устойчивости подкрепленных конструкций с использованием теории однородных ортотропных пластин.Точно так же Флюгге [5] опубликовал первую статью по теме структурно усиленной оболочки в 1932 г., а 15 лет спустя — Ван дер Нейт [6]. Со временем понимание теории деформирования конструктивно ортотропных пластин и оболочек продвинулось вперед. Термины «эквивалентная жесткость» и «эквивалентная толщина стенки» стали основой для анализа деформирования подкрепленных или конструктивно ортотропных плит/оболочек. Кроме того, Дейл и соавт. [7] применили эквивалентную жесткость при исследовании потери устойчивости сэндвич-панелей, нагруженных давлением.Смит и др. В [8] предложена улучшенная формулировка, учитывающая изменение положения нейтральной поверхности, связанное с локальным взаимодействием пластины и ребра жесткости.
Самые ранние исследования по теме жесткости подкрепленных пластин, скорее всего, были выполнены Хубером [2–4]. Его исследования были вдохновлены отсутствием точных выражений для решения задач изгиба и потери устойчивости подкрепленных конструкций с использованием теории однородных ортотропных пластин.Точно так же Флюгге [5] опубликовал первую статью по теме структурно усиленной оболочки в 1932 г., а 15 лет спустя — Ван дер Нейт [6]. Со временем понимание теории деформирования конструктивно ортотропных пластин и оболочек продвинулось вперед. Термины «эквивалентная жесткость» и «эквивалентная толщина стенки» стали основой для анализа деформирования подкрепленных или конструктивно ортотропных плит/оболочек. Кроме того, Дейл и соавт. [7] применили эквивалентную жесткость при исследовании потери устойчивости сэндвич-панелей, нагруженных давлением.Смит и др. В [8] предложена улучшенная формулировка, учитывающая изменение положения нейтральной поверхности, связанное с локальным взаимодействием пластины и ребра жесткости.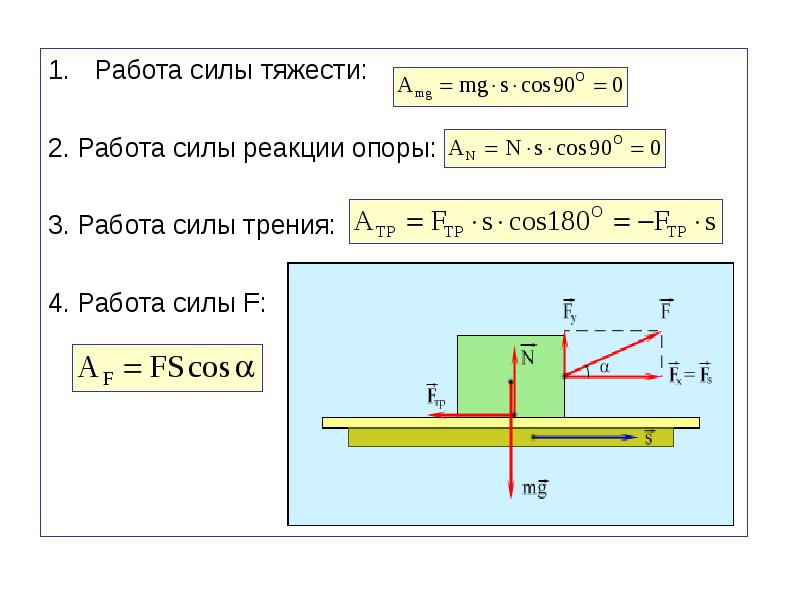 Пфлюгер [9], Гомза и Сейде [10], Либове и Хубка [11] применяли в своих исследованиях метод эквивалентной жесткости и толщины подкрепленной пластины/оболочки. В работах [12–14] применяется теория симметричных многослойных пластин с учетом поперечной сдвиговой жесткости. В 1956 году Хаффингтон мл.В работе [15] проанализирована эквивалентная жесткость ортогонально подкрепленной пластины без учета эксцентриситета ребра жесткости. В течение последних пятидесяти лет метод эквивалентной пластины или оболочки все еще использовался в качестве метода первого приближения [16–19]. Для экспериментального определения констант упругости чаще всего использовали метод испытаний нагрузочно-деформационных характеристик повторяющейся конструктивной части конструктивно-ортотропной плиты [20]. В 1969 г. Сунг [21–23] представил вывод выражений жесткости для ортотропных цилиндров на основе подхода энергии деформации.В последующие годы особое внимание уделялось взаимодействию между пластиной и элементами жесткости [24], при различной компоновке или сетке элементов жесткости [25–27] и различных сочетаниях нагрузок.
Пфлюгер [9], Гомза и Сейде [10], Либове и Хубка [11] применяли в своих исследованиях метод эквивалентной жесткости и толщины подкрепленной пластины/оболочки. В работах [12–14] применяется теория симметричных многослойных пластин с учетом поперечной сдвиговой жесткости. В 1956 году Хаффингтон мл.В работе [15] проанализирована эквивалентная жесткость ортогонально подкрепленной пластины без учета эксцентриситета ребра жесткости. В течение последних пятидесяти лет метод эквивалентной пластины или оболочки все еще использовался в качестве метода первого приближения [16–19]. Для экспериментального определения констант упругости чаще всего использовали метод испытаний нагрузочно-деформационных характеристик повторяющейся конструктивной части конструктивно-ортотропной плиты [20]. В 1969 г. Сунг [21–23] представил вывод выражений жесткости для ортотропных цилиндров на основе подхода энергии деформации.В последующие годы особое внимание уделялось взаимодействию между пластиной и элементами жесткости [24], при различной компоновке или сетке элементов жесткости [25–27] и различных сочетаниях нагрузок. В 1995 г. Jaunky и соавт. [28, 29] представили усовершенствованную теорию размазанных ребер жесткости для многослойных композитных панелей с ребрами жесткости, основанную на работе, представленной Smith et al. [8]. Точно так же Wodesenbet представила улучшенную теорию размазанных ребер жесткости для многослойных композитных цилиндров с ребрами жесткости в 2003 году.
В 1995 г. Jaunky и соавт. [28, 29] представили усовершенствованную теорию размазанных ребер жесткости для многослойных композитных панелей с ребрами жесткости, основанную на работе, представленной Smith et al. [8]. Точно так же Wodesenbet представила улучшенную теорию размазанных ребер жесткости для многослойных композитных цилиндров с ребрами жесткости в 2003 году.
Можно сделать вывод, что текущее исследование в основном основано на двух систематических аналитических методах, которые принимают во внимание или не принимают во внимание жесткость на поперечный сдвиг. Во-первых, существует прямой метод совместимости равновесия. Первый метод напрямую использует равновесие и совместимость для пластин, армированных ребрами жесткости. Второй называется методом энергетической эквивалентности базовой ячейки. Второй метод основан на определении эквивалентности между энергией деформации базовой повторяющейся ячейки и энергией деформации эквивалентной ортотропной пластины.Этот метод подходит для определения членов матрицы упругости для пластин с сеткой и многослойных пластин.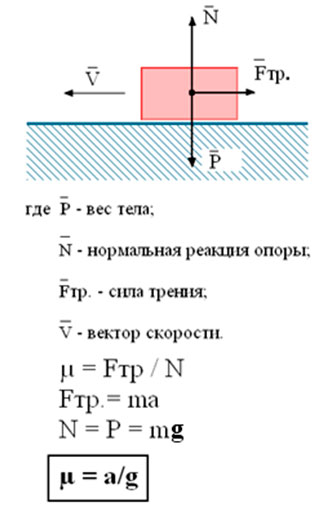
В отличие от ребер жесткости мембранная стенка парового котла состоит из однородной пластины с прикрепленными к ней ребрами жесткости. Поэтому два указанных метода не совсем подходят для определения эквивалентной жесткости стенки мембраны, то есть эквивалентных констант упругости. Процесс гомогенизации мембранной стенки парового котла представлен в работах [30–32].Константы упругости мембраны и изгибная жесткость мембранной стенки определяются теоретически путем уравнивания деформации мембранной стенки с деформацией эквивалентной ортотропной пластины. В этих работах жесткость на поперечный сдвиг не принимается во внимание.
2. Мембранная стенка парового котла как конструктивно ортотропная плита
Мембранная стенка парового котла может быть аппроксимирована как эквивалентная ортотропная плита, то есть ортотропная плита, которая будет иметь те же упругие свойства, что и реальная мембранная стенка.Используя теорию оболочек Кирхгофа-Лява [33, 34], определяющие уравнения эквивалентной ортотропной пластины или оболочки можно записать следующим образом: где – вектор сил сечения, – матрица упругости, – вектор деформации.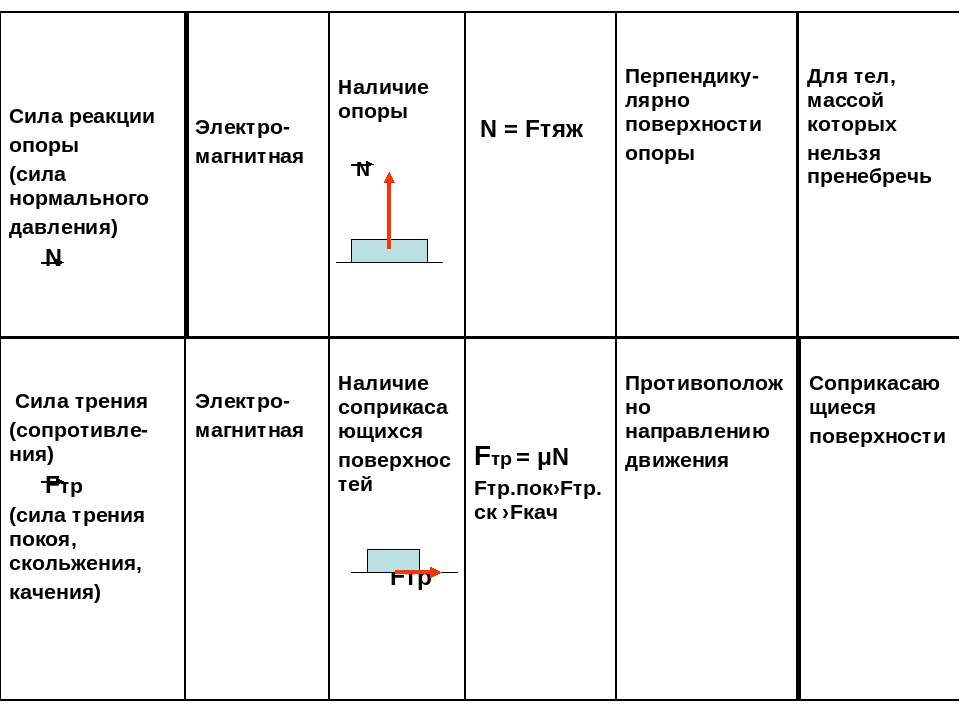 Согласно [35] можно сказать, что определяющие уравнения для расчета пластин и оболочек являются аналогами. Матричное выражение (1) представляет собой шесть составляющих уравнений мембранной стенки как конструктивно ортотропной плиты или эквивалентной ей ортотропной плиты, которые связывают силы сечения с соответствующими деформациями
, , и – силы сечения (рис. 1), а, и – моменты сечения (рис. 2) в стенке мембраны, т. е. эквивалентной ортотропной плите., , , и – элементы матрицы упругости для мембранных нагрузок, а , , , и – элементы матрицы упругости для изгибающих нагрузок эквивалентной ортотропной плиты. , , и – деформации мембраны, , , и – кривизны нейтральной поверхности конструктивно ортотропной плиты, т.е. эквивалентной ортотропной плиты.
Согласно [35] можно сказать, что определяющие уравнения для расчета пластин и оболочек являются аналогами. Матричное выражение (1) представляет собой шесть составляющих уравнений мембранной стенки как конструктивно ортотропной плиты или эквивалентной ей ортотропной плиты, которые связывают силы сечения с соответствующими деформациями
, , и – силы сечения (рис. 1), а, и – моменты сечения (рис. 2) в стенке мембраны, т. е. эквивалентной ортотропной плите., , , и – элементы матрицы упругости для мембранных нагрузок, а , , , и – элементы матрицы упругости для изгибающих нагрузок эквивалентной ортотропной плиты. , , и – деформации мембраны, , , и – кривизны нейтральной поверхности конструктивно ортотропной плиты, т.е. эквивалентной ортотропной плиты.
Члены матрицы упругости, относящиеся к жесткости мембраны [30, 34] стенки мембраны, могут быть рассчитаны с использованием следующих выражений: где – модуль упругости жесткости мембраны в направлении оси (ось параллельна оси трубы в стенке мембраны), – модуль упругости жесткости мембраны в направлении оси (ось перпендикулярна оси трубы в стенке мембраны), – коэффициент Пуассона для жесткости мембраны в направлении оси , – коэффициент Пуассона для жесткости мембраны в направлении оси , – модуль сдвига для жесткости мембраны. Члены матрицы упругости, относящиеся к изгибной жесткости [29, 33] стенки мембраны, могут быть рассчитаны с использованием следующих выражений: где константы упругости для изгибной жесткости обозначены индексом . Выражение для толщины стенки эквивалентной ортотропной плиты [30] можно получить из равенства момента инерции поперечного сечения мембранной стенки, рассматривая плоскость, перпендикулярную продольным осям мембранных труб (рис. 3), и поперечное сечение эквивалентной ортотропной пластины.Учитывать
Члены матрицы упругости, относящиеся к изгибной жесткости [29, 33] стенки мембраны, могут быть рассчитаны с использованием следующих выражений: где константы упругости для изгибной жесткости обозначены индексом . Выражение для толщины стенки эквивалентной ортотропной плиты [30] можно получить из равенства момента инерции поперечного сечения мембранной стенки, рассматривая плоскость, перпендикулярную продольным осям мембранных труб (рис. 3), и поперечное сечение эквивалентной ортотропной пластины.Учитывать
Константы упругости эквивалентной ортотропной пластины для жесткости мембраны могут быть рассчитаны с использованием аналитических выражений, предложенных в работе [31, 32]. Эти выражения получаются при уравнивании деформаций стенки мембраны и эквивалентной пластины (толщины) при эквивалентной нагрузке мембраны где – модуль упругости, – коэффициент Пуассона для изотропного материала стенки мембраны. Выражения для констант упругости эквивалентной ортотропной пластины и изгибной жесткости мембранной стенки предложены в работе [31, 32].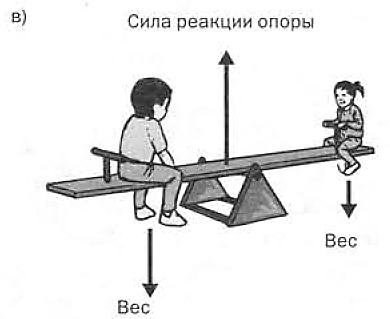 Как и для жесткости мембраны, эти выражения также получаются при уравнивании деформаций стенки мембраны и эквивалентной пластины (толщина) при эквивалентной изгибающей нагрузке где – количество труб в мембранной стене, – коэффициент Пуассона для изотропного материала мембранной стенки. После гомогенизации мембранной стенки парового котла матрица жесткости элемента оболочки может быть рассчитана по выражению где – поверхность элемента оболочки, – оператор граничной величины.
Как и для жесткости мембраны, эти выражения также получаются при уравнивании деформаций стенки мембраны и эквивалентной пластины (толщина) при эквивалентной изгибающей нагрузке где – количество труб в мембранной стене, – коэффициент Пуассона для изотропного материала мембранной стенки. После гомогенизации мембранной стенки парового котла матрица жесткости элемента оболочки может быть рассчитана по выражению где – поверхность элемента оболочки, – оператор граничной величины.
3. Расчет реакций в опорах парового котла для реальной модели геометрии мембранных стенок, для мембранных стенок, аппроксимированных эквивалентной ортотропной пластиной, и для идеально жесткой модели геометрии котла
Метод конечных элементов с использованием Abaqus 6.9 -3 будет применяться для расчета реакций в опорах. Реальная геометрия мембранных стенок (рис. 4) и мембранных стенок, аппроксимированных в виде эквивалентной ортотропной пластины (рис. 5), будет дискретизирована четырехузловым элементом тонкой оболочки с двойной кривизной с использованием сокращенной интеграции с контролем песочных часов.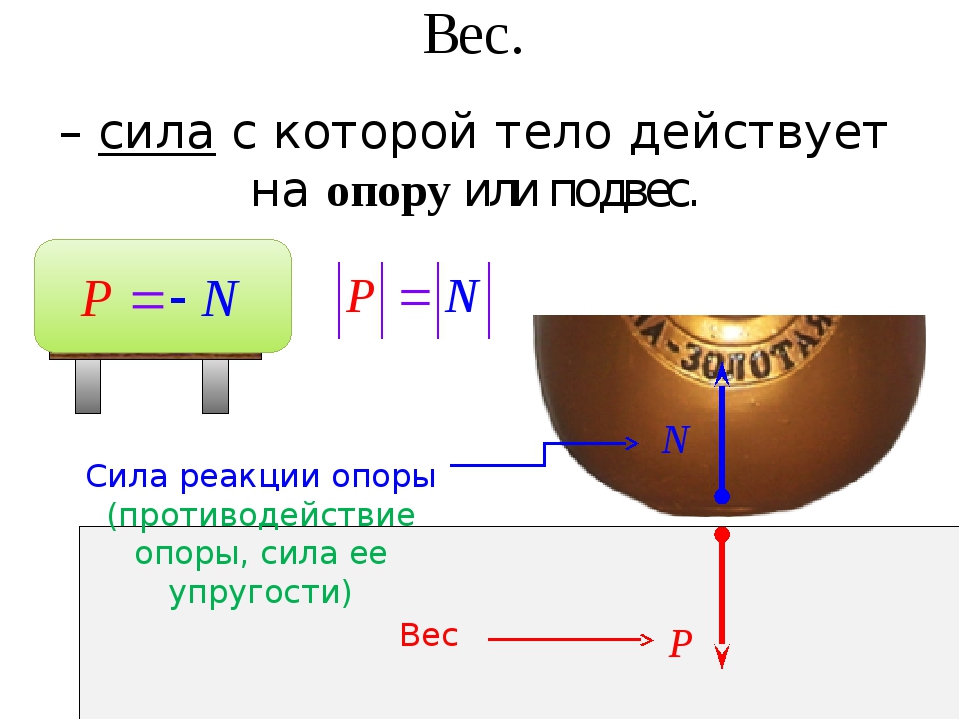 Конечный элемент имеет кодовое название S4R5, применяется для малых деформаций и имеет пять степеней свободы на узел.
Конечный элемент имеет кодовое название S4R5, применяется для малых деформаций и имеет пять степеней свободы на узел.
При расчете реакций в опорах парового котла «Милан» будет учитываться нагрузка массы конструкции котла (рис. 6). Другие нагрузки, такие как масса рабочего тела, масса отложений, осаждающихся на поверхностях нагрева в процессе горения, масса огнеупора, масса изоляции, здесь рассматриваться не будут.Материал труб мембранных стенок – P235GH, материал мембранной ленты и упоров – S235JRG2, материал камер – 16Mo3. Все три стали относятся к группе малоуглеродистых сталей с углеродом. Поскольку мембранные стенки котла являются поверхностями нагрева испарителя, расчетная температура составляет °С. Если предположить, что механические свойства конструкции котла изотропны, [36] модуль упругости для всех трех материалов примерно одинаков и составляет . Для значения коэффициента Пуассона используется .
Из-за симметрии одного котла для расчета методом конечных элементов достаточно смоделировать только половину геометрии котла (рис.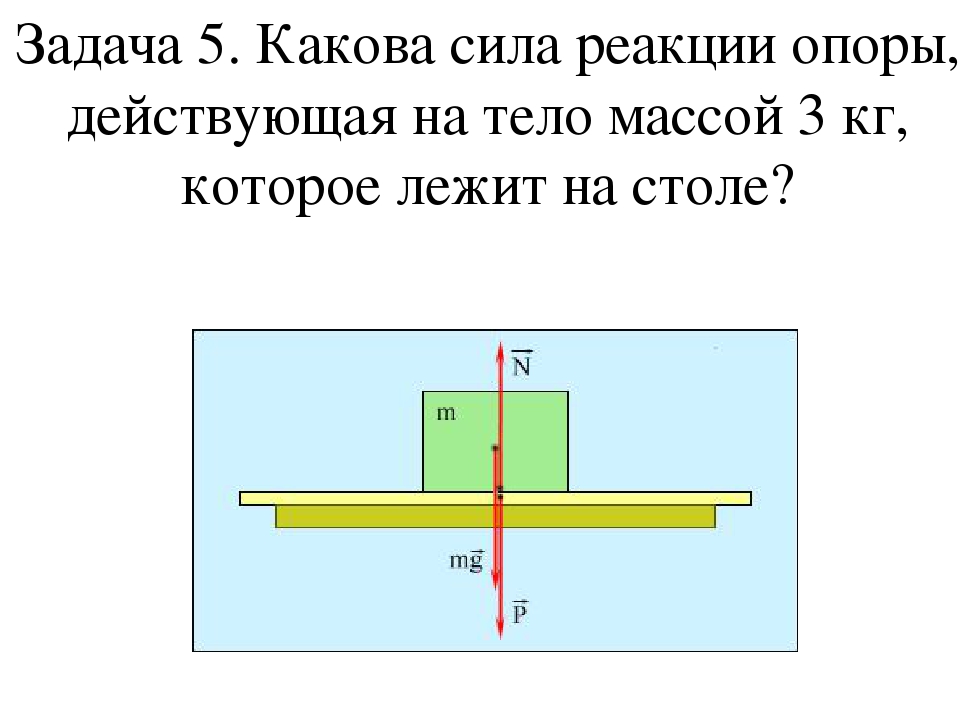 4 и 5). Котел опирается на десять опор, пять на распределительную камеру левой боковой стенки и пять на распределительную камеру правой боковой стенки (рис. 7). В третьем проходе котла были установлены теплообменники, то есть один испаритель и три пароперегревателя. Теплообменники опирались на боковые стенки третьего прохода.Из-за веса теплообменников нагрузка на левую и правую боковые стенки третьего прохода одинакова. Для расчета реакций в опорах котла половина веса индивидуального теплообменника будет использоваться как эквивалент тангенциального поверхностного давления на боковую стенку третьего прохода. Это давление прикладывается к поверхности А стенки мембраны, к которой приварены держатели теплообменников (рис. 7). Изгиб боковых стенок мембраны третьего прохода из-за нагрузки теплообменников не учитывался.
4 и 5). Котел опирается на десять опор, пять на распределительную камеру левой боковой стенки и пять на распределительную камеру правой боковой стенки (рис. 7). В третьем проходе котла были установлены теплообменники, то есть один испаритель и три пароперегревателя. Теплообменники опирались на боковые стенки третьего прохода.Из-за веса теплообменников нагрузка на левую и правую боковые стенки третьего прохода одинакова. Для расчета реакций в опорах котла половина веса индивидуального теплообменника будет использоваться как эквивалент тангенциального поверхностного давления на боковую стенку третьего прохода. Это давление прикладывается к поверхности А стенки мембраны, к которой приварены держатели теплообменников (рис. 7). Изгиб боковых стенок мембраны третьего прохода из-за нагрузки теплообменников не учитывался.
Массы отдельных элементов конструкции котла, маркированные по рисунку 4 и 7 и таблице 1, приведены в таблице 2. Неоднородность материала конструкции котла здесь учитываться не будет. Предполагается, что геометрия котла идеальна, без учета допусков изготовления и сборки, а также допусков заложенного в котел полуфабриката проката. Предполагается, что механические свойства материала конструкции котла изотропны, то есть анизотропия сварных соединений и полуфабрикатов проката не оказывает существенного влияния на реакции в опорах котла.
Предполагается, что геометрия котла идеальна, без учета допусков изготовления и сборки, а также допусков заложенного в котел полуфабриката проката. Предполагается, что механические свойства материала конструкции котла изотропны, то есть анизотропия сварных соединений и полуфабрикатов проката не оказывает существенного влияния на реакции в опорах котла.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
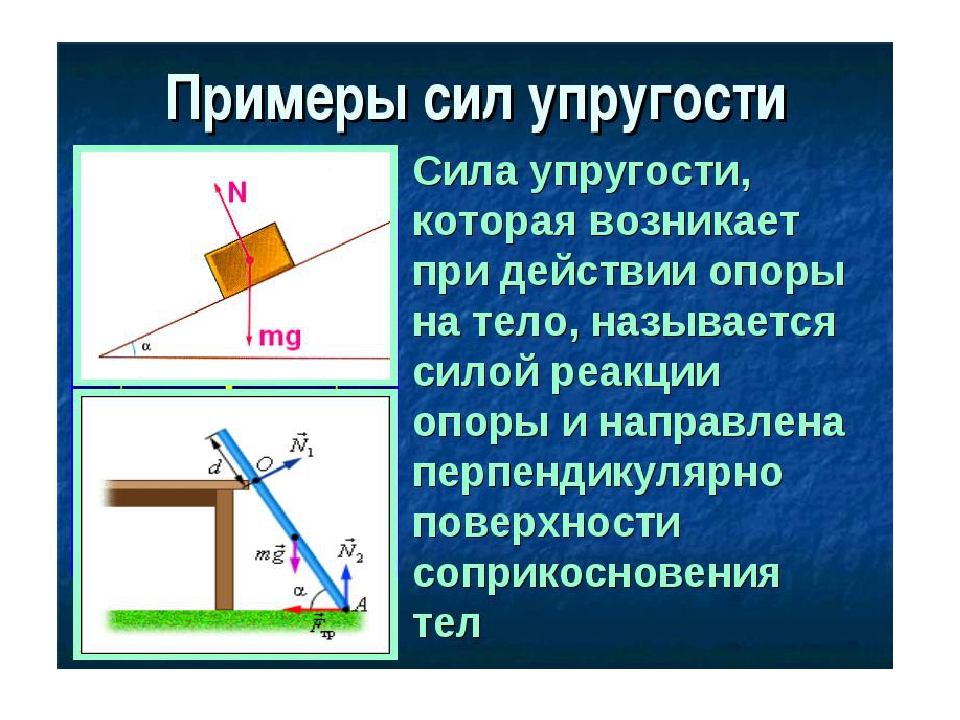 Проверяет готовность учеников к уроку
Проверяет готовность учеников к уроку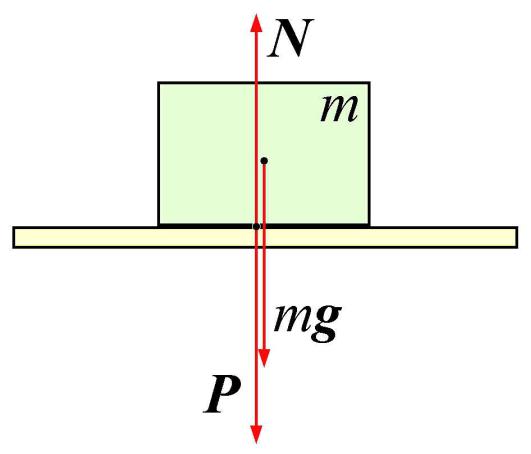 А что такое деформация?
А что такое деформация?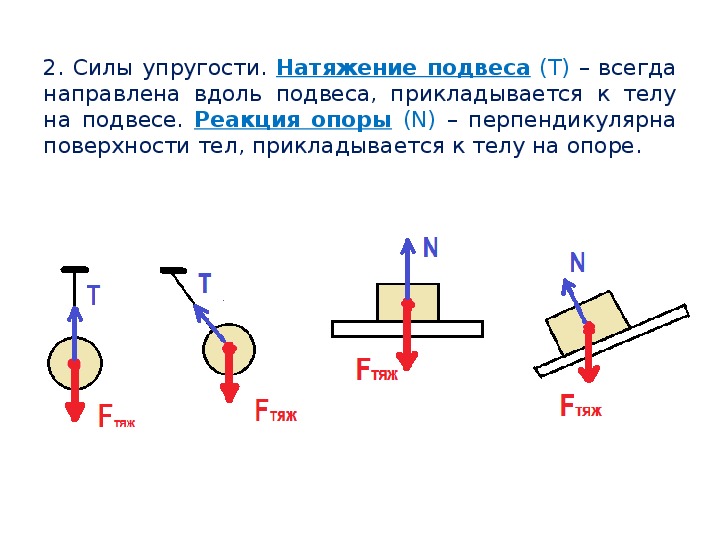 Почему ненагруженная пружина, висящая на штативе, при присоединении к ней тела начинает деформироваться?
Почему ненагруженная пружина, висящая на штативе, при присоединении к ней тела начинает деформироваться?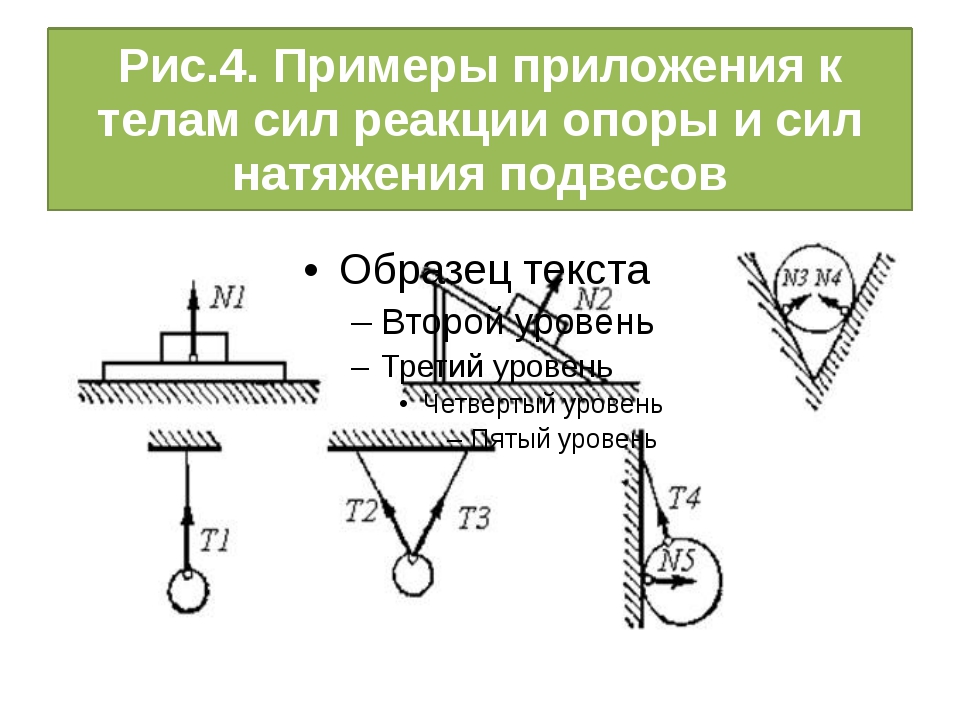 Учитель строит разъяснение, что сила упругости, действующая со стороны стола на книгу, называется силой нормальной реакции опоры, и характеризует ее по плану:
Учитель строит разъяснение, что сила упругости, действующая со стороны стола на книгу, называется силой нормальной реакции опоры, и характеризует ее по плану: Определить вес тела.
Определить вес тела.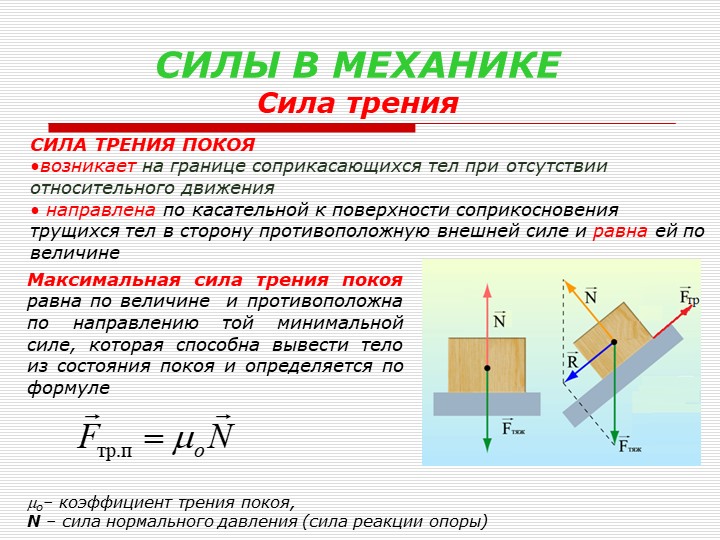 Анализирует полученный результат. Делает вывод, что вес тела, лежащего на опоре, движущейся ускоренно вниз, меньше силы тяжести и равен нулю при ускорении опоры, равном, ускорению свободного падения.
Анализирует полученный результат. Делает вывод, что вес тела, лежащего на опоре, движущейся ускоренно вниз, меньше силы тяжести и равен нулю при ускорении опоры, равном, ускорению свободного падения.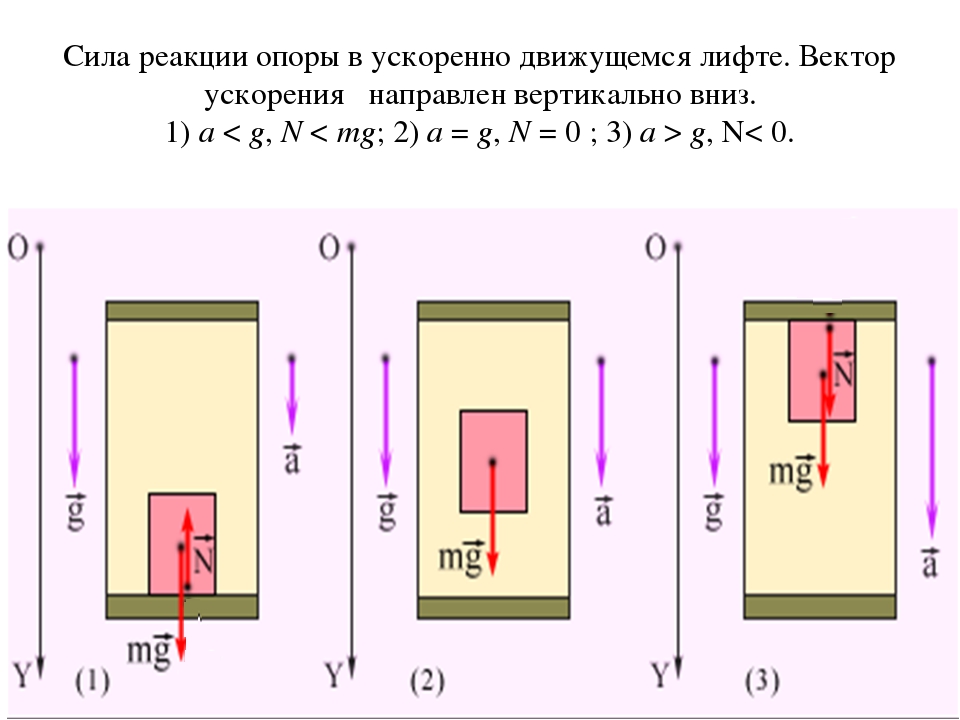 )
)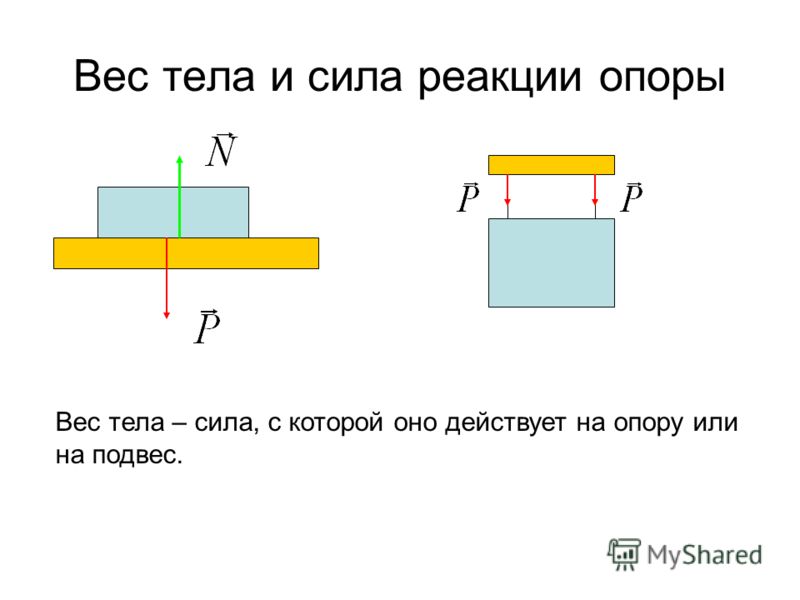
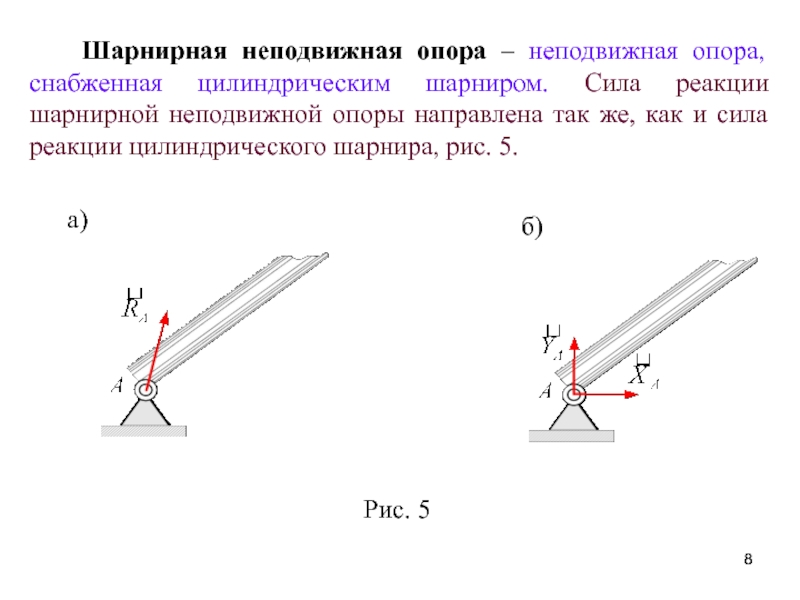
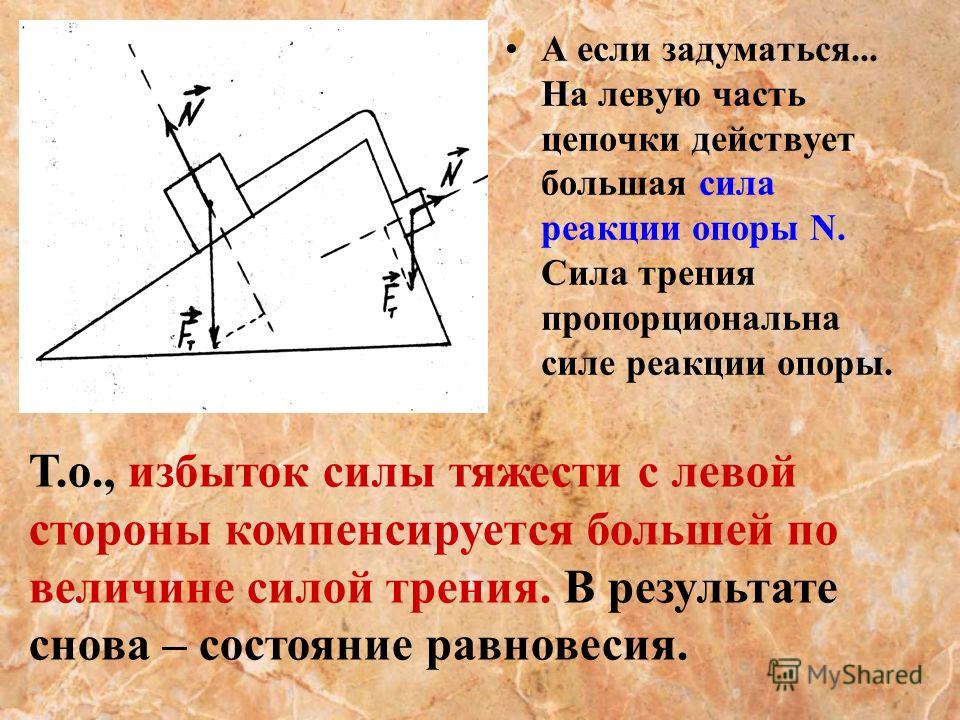 Мембранные стенки котла «Милан» выполнены с шагом 90 мм. Применяются два размера поперечного сечения трубы ( и ), а также мембранная лента (толщина 6 мм). Для мембранных стенок котла можно рассчитать константы упругости эквивалентной ортотропной плиты (табл. 3) по выражениям (6) и (7). Члены матрицы упругости (табл. 4 и 5), которые будут применяться к конечному элементу эквивалентной ортотропной пластины, будут рассчитываться по выражениям (3) и (4).
Мембранные стенки котла «Милан» выполнены с шагом 90 мм. Применяются два размера поперечного сечения трубы ( и ), а также мембранная лента (толщина 6 мм). Для мембранных стенок котла можно рассчитать константы упругости эквивалентной ортотропной плиты (табл. 3) по выражениям (6) и (7). Члены матрицы упругости (табл. 4 и 5), которые будут применяться к конечному элементу эквивалентной ортотропной пластины, будут рассчитываться по выражениям (3) и (4).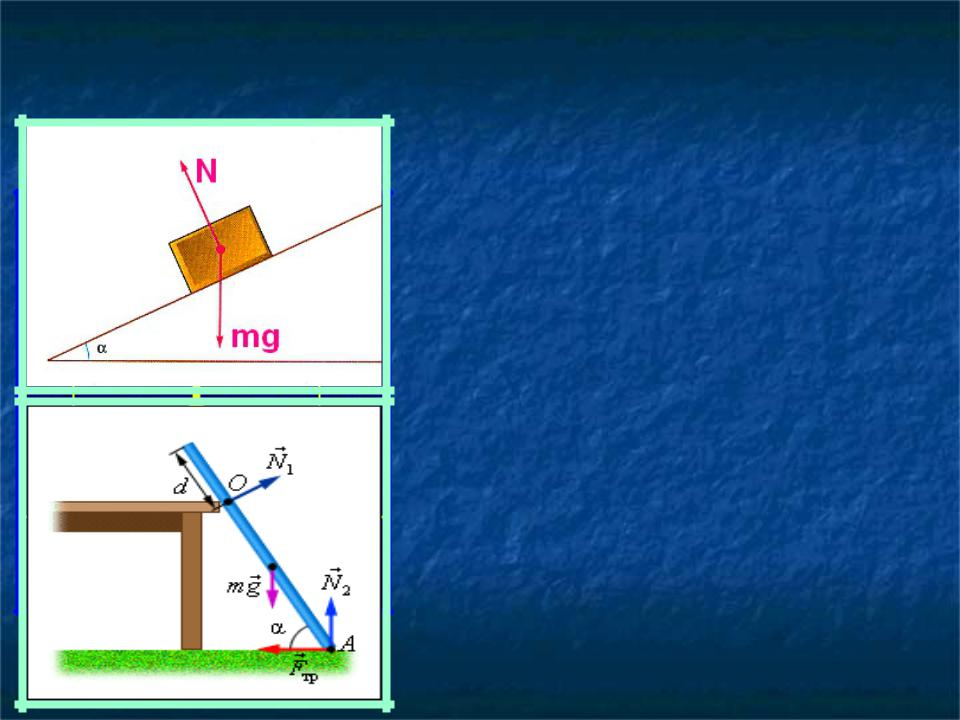 492
492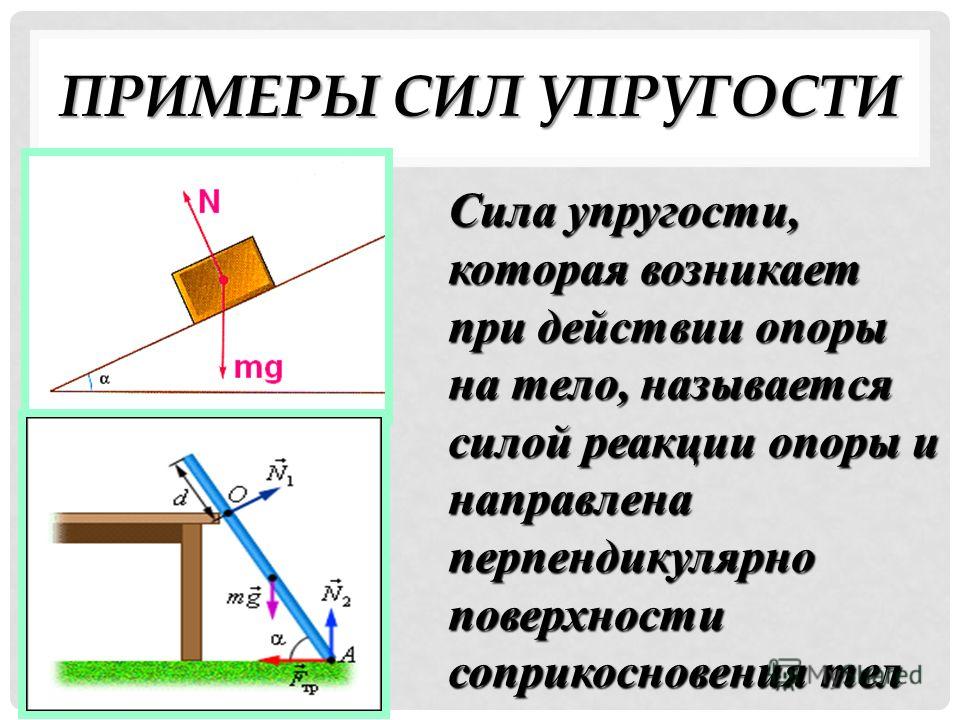 48
48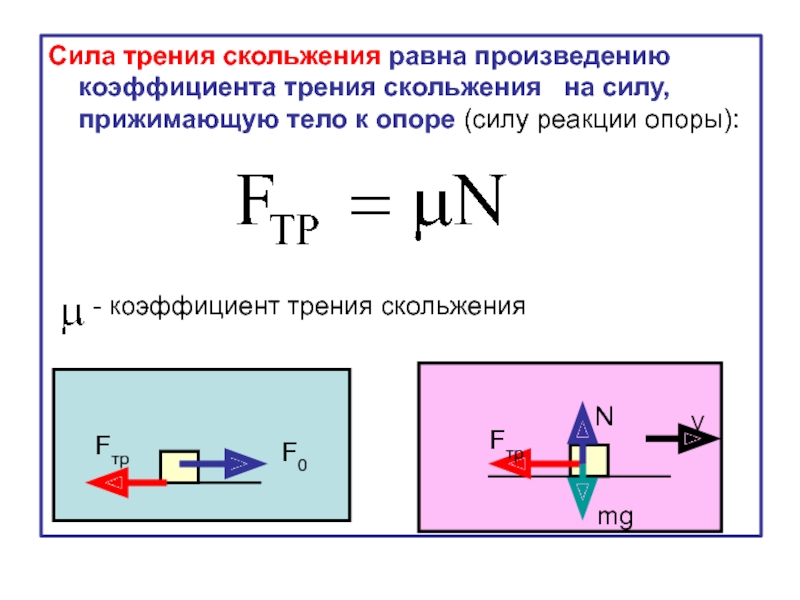 Каждый расчет производится с нагрузкой массы котла, с учетом и без учета массы теплообменников.
Каждый расчет производится с нагрузкой массы котла, с учетом и без учета массы теплообменников.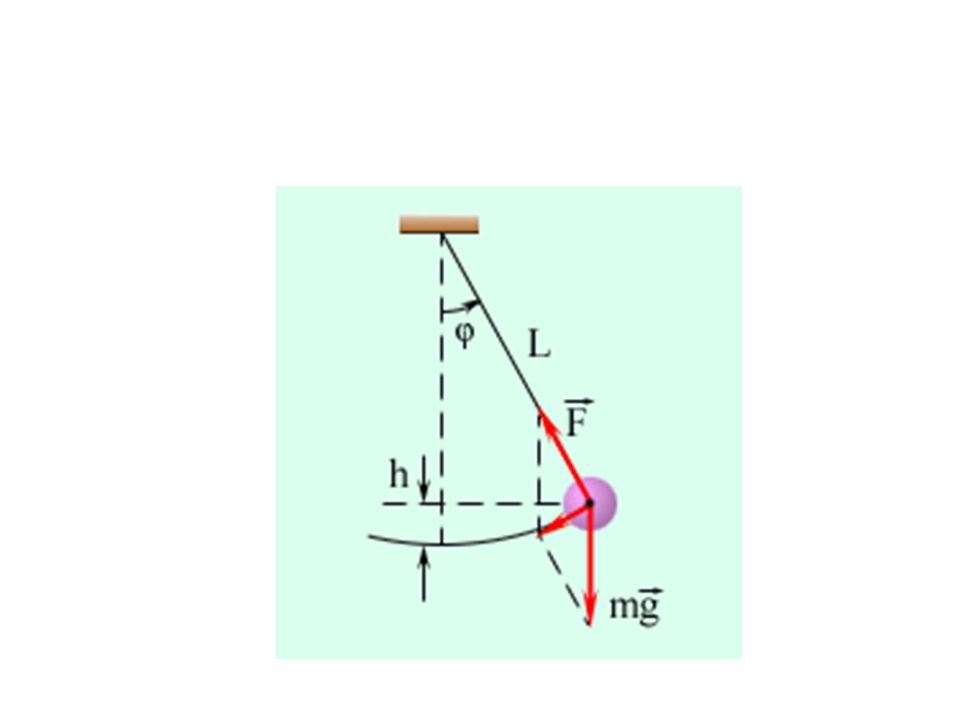 Таким же образом рассчитывалось отклонение сил реакции для расчета ЖЕСТКАЯ (по сравнению с расчетом РЕАЛЬНАЯ), выражалось в процентах и обозначалось как . Отклонения рассчитывали по следующим выражениям:
Таким же образом рассчитывалось отклонение сил реакции для расчета ЖЕСТКАЯ (по сравнению с расчетом РЕАЛЬНАЯ), выражалось в процентах и обозначалось как . Отклонения рассчитывали по следующим выражениям: 31
31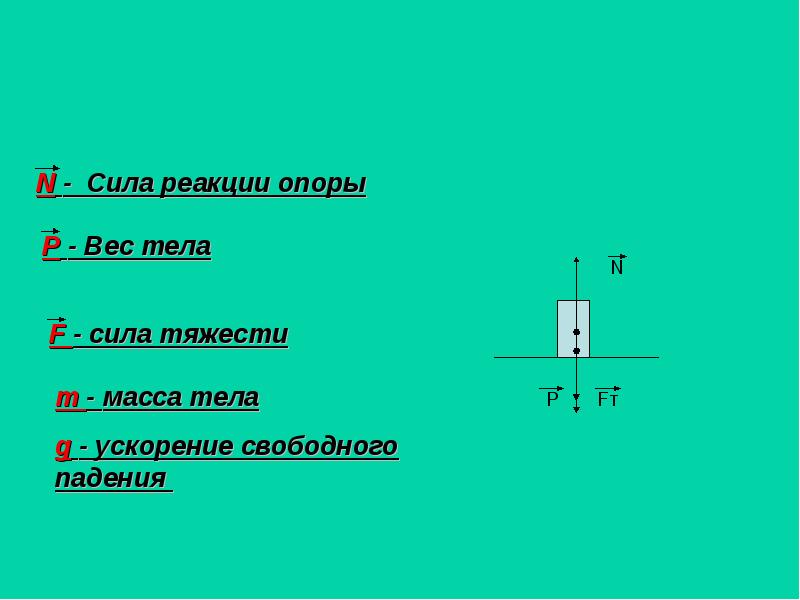 01
01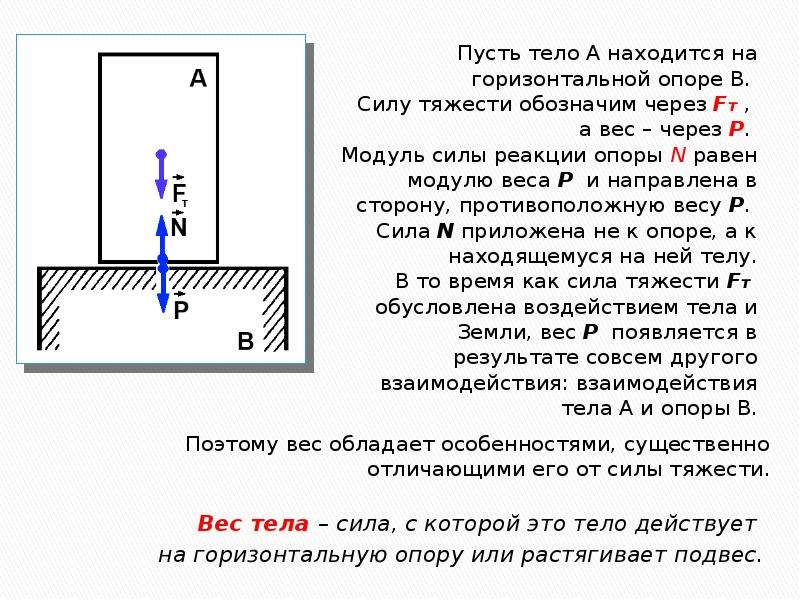 (viii) Дополнительные улучшения могут быть достигнуты за счет учета поперечной жесткости на сдвиг.
(viii) Дополнительные улучшения могут быть достигнуты за счет учета поперечной жесткости на сдвиг. 8.1, состоит в том, чтобы разбить задачу на определенные части (используя суперпозицию), а затем согласовать эти части друг с другом, используя совместимость.Напомним, что с точки зрения балки нет реальной разницы между нагрузкой, вызванной внешней силой, и нагрузкой, вызванной силой реакции. Единственная разница между внешними силами и силами реакции заключается в том, что мы знаем, что в месте расположения силы реакции деформация/вращение, связанные с этим компонентом реакции, равны нулю. Составляющая силы реакции служит для удержания конструкции на месте либо за счет сдерживания смещения, либо за счет сдерживания вращения. Это известное смещение/вращение в месте расположения реакционного компонента дает нам некоторую дополнительную информацию о том, как ведет себя структура, помимо того, что мы можем сказать о структуре только из равновесия.Например, на рисунке 8.1 на верхней диаграмме показана балка с показанными граничными условиями реакции, а на второй диаграмме сверху показана диаграмма свободного тела для этой балки, подвергаемой заданным внешним силам (с граничными условиями реакции, замененными результирующей реакцией компоненты силы).
8.1, состоит в том, чтобы разбить задачу на определенные части (используя суперпозицию), а затем согласовать эти части друг с другом, используя совместимость.Напомним, что с точки зрения балки нет реальной разницы между нагрузкой, вызванной внешней силой, и нагрузкой, вызванной силой реакции. Единственная разница между внешними силами и силами реакции заключается в том, что мы знаем, что в месте расположения силы реакции деформация/вращение, связанные с этим компонентом реакции, равны нулю. Составляющая силы реакции служит для удержания конструкции на месте либо за счет сдерживания смещения, либо за счет сдерживания вращения. Это известное смещение/вращение в месте расположения реакционного компонента дает нам некоторую дополнительную информацию о том, как ведет себя структура, помимо того, что мы можем сказать о структуре только из равновесия.Например, на рисунке 8.1 на верхней диаграмме показана балка с показанными граничными условиями реакции, а на второй диаграмме сверху показана диаграмма свободного тела для этой балки, подвергаемой заданным внешним силам (с граничными условиями реакции, замененными результирующей реакцией компоненты силы).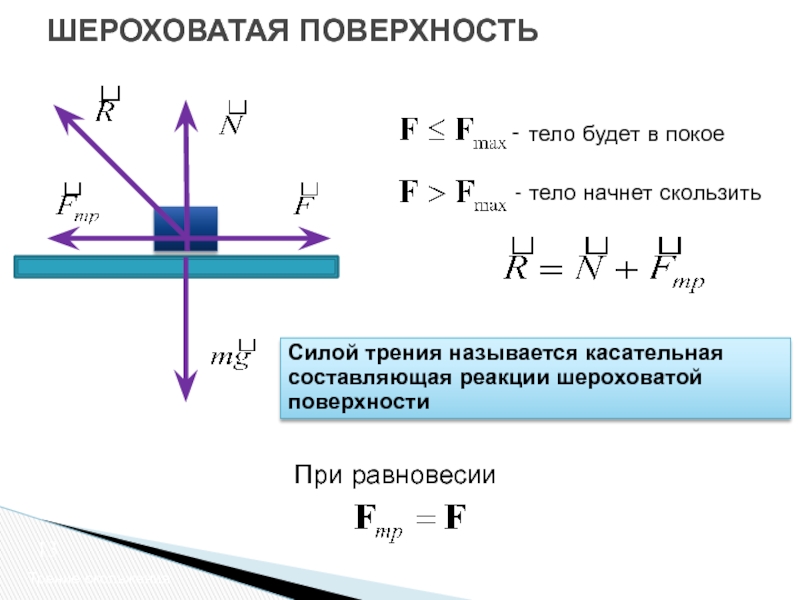 Верхняя диаграмма дает нам дополнительную информацию, которой нет на второй диаграмме (диаграмма свободного тела): она показывает, что луч удерживается от вертикального перемещения в точках A, C и E. Это информация о совместимости луч.Эта дополнительная информация о совместимости не требуется, когда мы анализируем сдвиги и моменты в определенной балке; однако, когда мы анализируем неопределенный луч, мы можем использовать его.
Верхняя диаграмма дает нам дополнительную информацию, которой нет на второй диаграмме (диаграмма свободного тела): она показывает, что луч удерживается от вертикального перемещения в точках A, C и E. Это информация о совместимости луч.Эта дополнительная информация о совместимости не требуется, когда мы анализируем сдвиги и моменты в определенной балке; однако, когда мы анализируем неопределенный луч, мы можем использовать его. \circ}$ в определенную систему.Эта новая детерминированная система без поддержки реакции, связанной с избыточной силой, называется первичной системой . Позже мы вернем в игру совместимость в точке C (т. е. тот факт, что там на самом деле есть реактивная опора и вертикальное смещение равно нулю).
\circ}$ в определенную систему.Эта новая детерминированная система без поддержки реакции, связанной с избыточной силой, называется первичной системой . Позже мы вернем в игру совместимость в точке C (т. е. тот факт, что там на самом деле есть реактивная опора и вертикальное смещение равно нулю).
 Для первого мы применяем только внешние реакции $P$ и $Q$ к первичной системе. Поскольку исходная система детерминирована, мы можем легко найти вертикальное перемещение в точке C ($\Delta_{C0}$) одним из методов из главы 5, предполагая, что нам заданы величины сил $P$ и $ Q$. Для второй из наложенных систем к основной системе прикладывается только избыточная сила $C_y$ с целью определения вертикального смещения, которое избыточная сила вызывает в точке C ($\Delta_{CC}$).Конечно, в отличие от $P$ и $Q$, мы на самом деле не знаем значения избыточной силы, поскольку именно это мы и пытаемся найти.
Для первого мы применяем только внешние реакции $P$ и $Q$ к первичной системе. Поскольку исходная система детерминирована, мы можем легко найти вертикальное перемещение в точке C ($\Delta_{C0}$) одним из методов из главы 5, предполагая, что нам заданы величины сил $P$ и $ Q$. Для второй из наложенных систем к основной системе прикладывается только избыточная сила $C_y$ с целью определения вертикального смещения, которое избыточная сила вызывает в точке C ($\Delta_{CC}$).Конечно, в отличие от $P$ и $Q$, мы на самом деле не знаем значения избыточной силы, поскольку именно это мы и пытаемся найти.
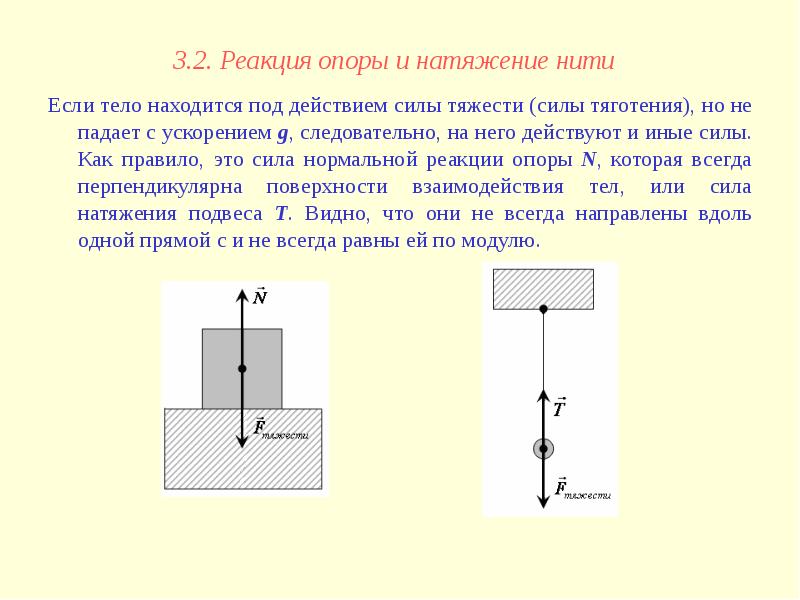 Если мы подставим уравнение \eqref{eq:flex-coeff} в уравнение \eqref{eq:compat-cond-1}, то получим:
Если мы подставим уравнение \eqref{eq:flex-coeff} в уравнение \eqref{eq:compat-cond-1}, то получим:
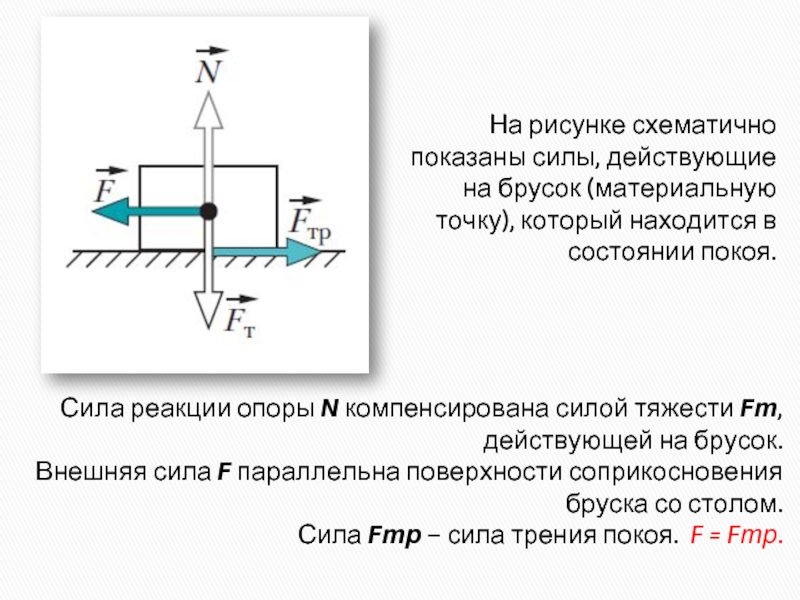 Перефразируя: если первичная система нестабильна, то выбранные избыточные реакции не подходят.
Перефразируя: если первичная система нестабильна, то выбранные избыточные реакции не подходят. В этом случае проще всего будет вертикальная реакция в точке C ($C_y$). Это связано с тем, что после устранения реакции в C первичная система фактически представляет собой кантилевер, который очень легко анализировать. Конечно, $A_y$ и $M_A$ также будут работать как избыточные (но не $C_x$, потому что их удаление сделает основную систему нестабильной).Полученная первичная структура показана на рисунке 8.4.
В этом случае проще всего будет вертикальная реакция в точке C ($C_y$). Это связано с тем, что после устранения реакции в C первичная система фактически представляет собой кантилевер, который очень легко анализировать. Конечно, $A_y$ и $M_A$ также будут работать как избыточные (но не $C_x$, потому что их удаление сделает основную систему нестабильной).Полученная первичная структура показана на рисунке 8.4.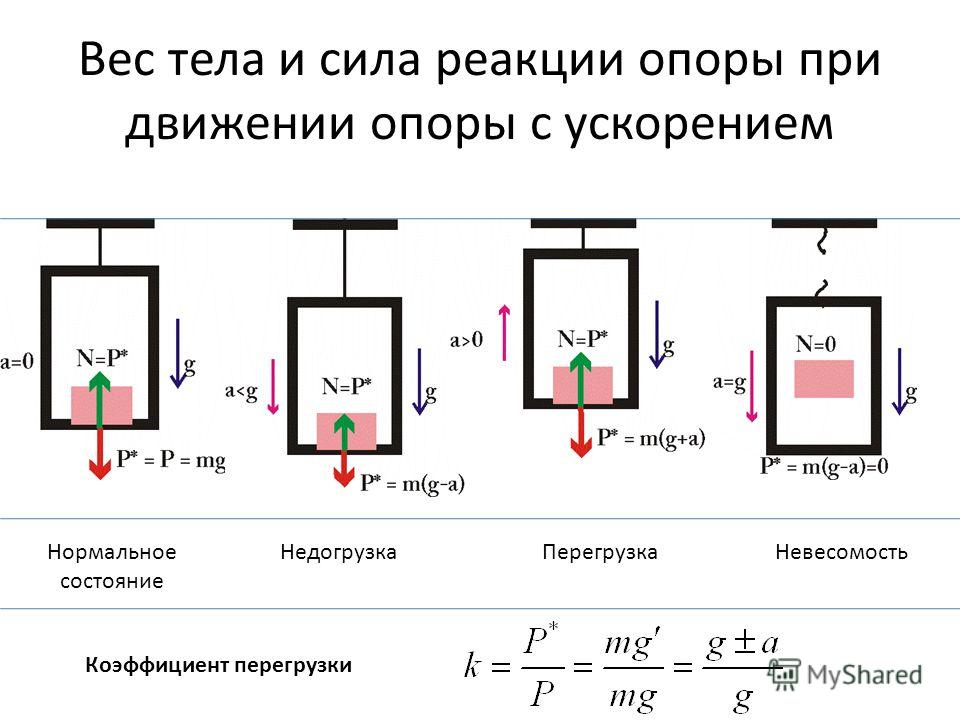
 Диаграмма моментов будет иметь ту же форму, что и диаграмма кривизны для этой системы (не показана), поскольку $EI$ постоянна для всех элементов. Также показаны виртуальная диаграмма сдвига и виртуальная диаграмма момента для виртуальной системы.
Диаграмма моментов будет иметь ту же форму, что и диаграмма кривизны для этой системы (не показана), поскольку $EI$ постоянна для всех элементов. Также показаны виртуальная диаграмма сдвига и виртуальная диаграмма момента для виртуальной системы.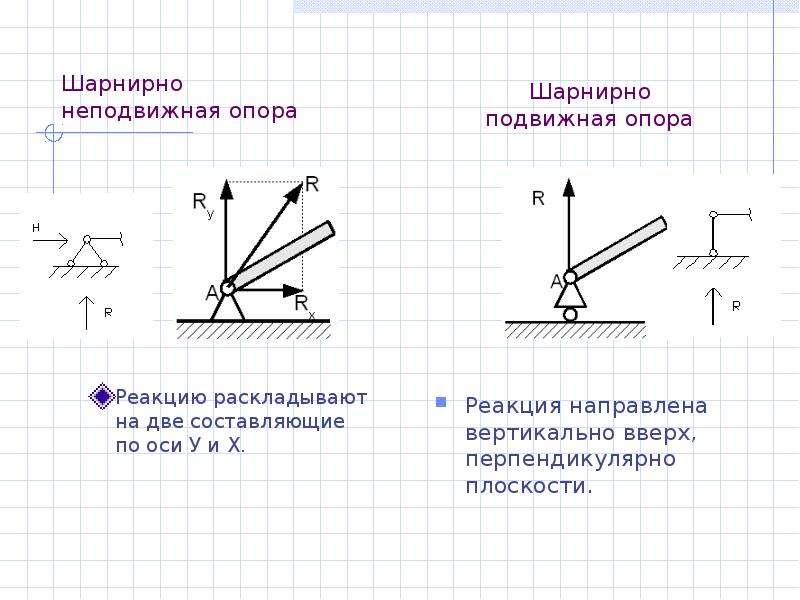 6 реальная система представляет собой первичную конструкцию с единичной избыточной силой в точке С, как показано на рисунке. Важно отметить, что единичная избыточная сила не применяется как $1\mathrm{\,kN}$, как виртуальная нагрузка, она является безразмерной (или в единицах $\mathrm{kN/kN}$), потому что мы хотим найти значения на кН приложенной избыточной силы. Чтобы найти отклонение в точке C из-за этой единичной избыточной силы, нам нужно создать виртуальную систему с виртуальной внешней единичной нагрузкой в точке C (в том же направлении, что и избыточная).Это означает, что реальная и виртуальная системы для нахождения эффекта единичной избыточной силы функционально идентичны, как показано на рисунке. Эти реальная и виртуальная системы, идентичные друг другу, также оказались идентичными виртуальной системе на рис. 8.5 (которая использовалась для нахождения отклонения основной системы, вызванного внешними нагрузками на систему без резервирования). . Таким образом, как реальная, так и виртуальная система являются результатами анализа избыточности модулей на рисунке 8.
6 реальная система представляет собой первичную конструкцию с единичной избыточной силой в точке С, как показано на рисунке. Важно отметить, что единичная избыточная сила не применяется как $1\mathrm{\,kN}$, как виртуальная нагрузка, она является безразмерной (или в единицах $\mathrm{kN/kN}$), потому что мы хотим найти значения на кН приложенной избыточной силы. Чтобы найти отклонение в точке C из-за этой единичной избыточной силы, нам нужно создать виртуальную систему с виртуальной внешней единичной нагрузкой в точке C (в том же направлении, что и избыточная).Это означает, что реальная и виртуальная системы для нахождения эффекта единичной избыточной силы функционально идентичны, как показано на рисунке. Эти реальная и виртуальная системы, идентичные друг другу, также оказались идентичными виртуальной системе на рис. 8.5 (которая использовалась для нахождения отклонения основной системы, вызванного внешними нагрузками на систему без резервирования). . Таким образом, как реальная, так и виртуальная система являются результатами анализа избыточности модулей на рисунке 8.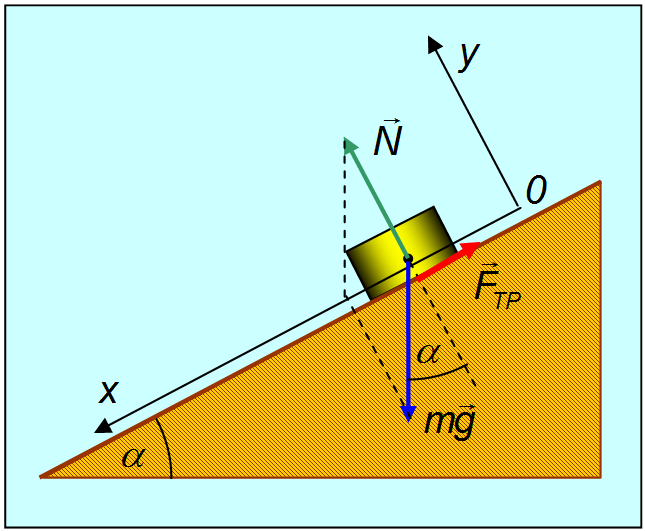 6 можно взять непосредственно из предыдущей виртуальной системы с рисунка 8.5. Это экономит некоторую работу по анализу, поскольку диаграммы моментов будут одинаковыми для всех трех. Единственная разница может состоять в том, что диаграмма кривизны для реальной системы на рис. 8.6 могла бы быть немного другой, если бы $EI$ не было постоянным. Надлежащие единицы для реальной системы также немного отличаются для анализа избыточности единиц, потому что избыточная единица не имеет единиц (т.е. она находится в единицах $\mathrm{кН/кН}$, как упоминалось ранее).3}} \right) \\ C_y &= +39,8\mathrm{\,kN} \\ C_y &= 39,8\mathrm{\,kN} \uparrow \end{align*}
6 можно взять непосредственно из предыдущей виртуальной системы с рисунка 8.5. Это экономит некоторую работу по анализу, поскольку диаграммы моментов будут одинаковыми для всех трех. Единственная разница может состоять в том, что диаграмма кривизны для реальной системы на рис. 8.6 могла бы быть немного другой, если бы $EI$ не было постоянным. Надлежащие единицы для реальной системы также немного отличаются для анализа избыточности единиц, потому что избыточная единица не имеет единиц (т.е. она находится в единицах $\mathrm{кН/кН}$, как упоминалось ранее).3}} \right) \\ C_y &= +39,8\mathrm{\,kN} \\ C_y &= 39,8\mathrm{\,kN} \uparrow \end{align*} 7, $A_x$, $A_y$ и $M_A$. Теперь их можно легко найти с помощью равновесия, и их значения показаны на рисунке 8.7. Когда все реакции известны, можно построить диаграммы сдвига и момента, как показано на рисунке.
7, $A_x$, $A_y$ и $M_A$. Теперь их можно легко найти с помощью равновесия, и их значения показаны на рисунке 8.7. Когда все реакции известны, можно построить диаграммы сдвига и момента, как показано на рисунке.
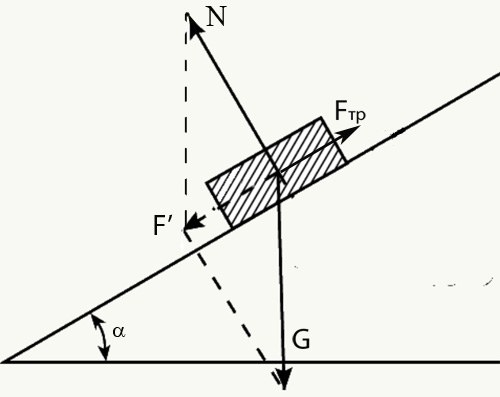 Нагрузки, воспринимаемые балкой, передаются
колонны, стены или балки, которые затем передают усилие на соседние структурные
элементы сжатия и, в конечном итоге, на землю.
Нагрузки, воспринимаемые балкой, передаются
колонны, стены или балки, которые затем передают усилие на соседние структурные
элементы сжатия и, в конечном итоге, на землю. 3: Прямая балка
3: Прямая балка 
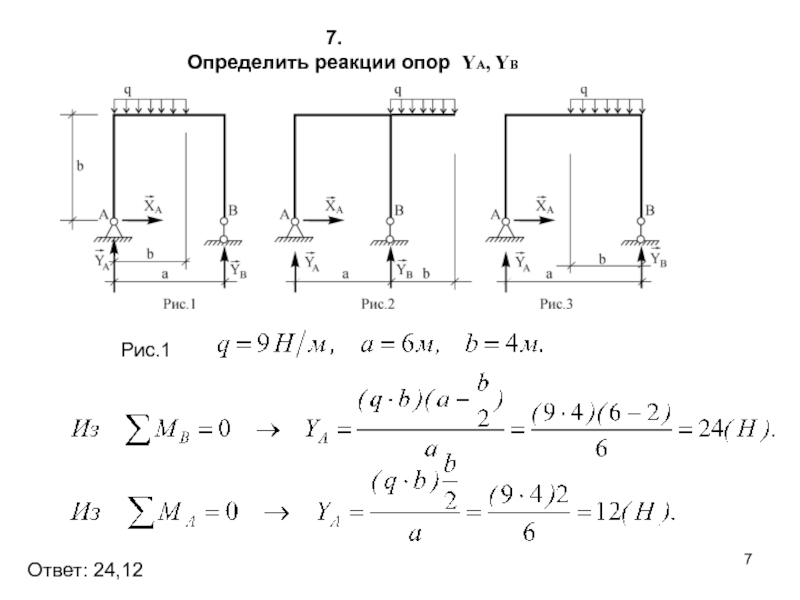 Настилы мостов и
сборные конструкции в основном поддерживаются свободно опертыми балками.
Настилы мостов и
сборные конструкции в основном поддерживаются свободно опертыми балками.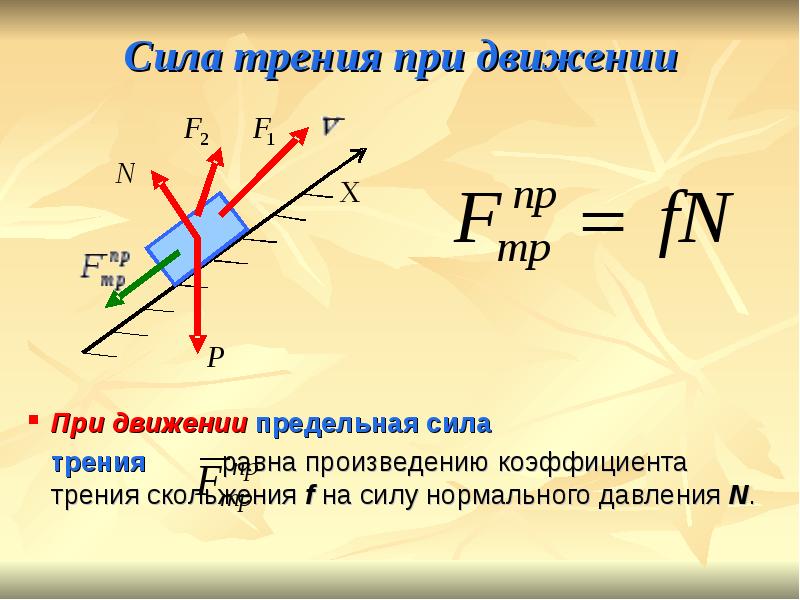
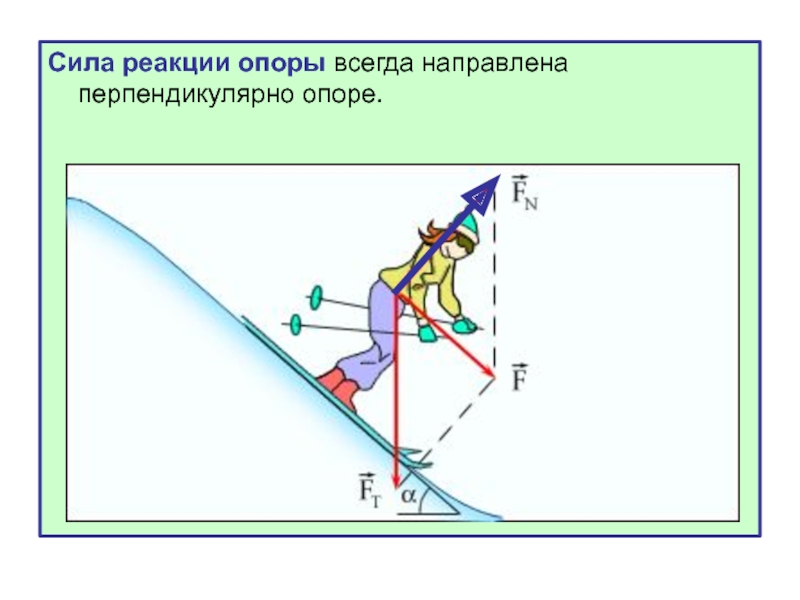 Центром реакции в этом случае является центр тяжести одинарной опоры.Если выбрано несколько опор (с помощью CTRL или SHIFT), то отображаются суммарная сила реакции и момент, а центром реакции является центр тяжести всех выбранных опор.
Центром реакции в этом случае является центр тяжести одинарной опоры.Если выбрано несколько опор (с помощью CTRL или SHIFT), то отображаются суммарная сила реакции и момент, а центром реакции является центр тяжести всех выбранных опор.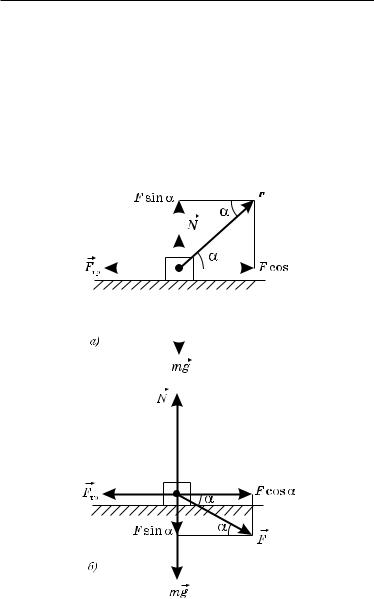 Это отфильтрует диалоговый список, чтобы показать только опоры и соединения, связанные с этой деталью.Теперь выберите любое соединение или опору для просмотра векторов силы и момента. Чтобы удалить фильтрацию, просто отмените выбор части, выбрав фон графики.
Это отфильтрует диалоговый список, чтобы показать только опоры и соединения, связанные с этой деталью.Теперь выберите любое соединение или опору для просмотра векторов силы и момента. Чтобы удалить фильтрацию, просто отмените выбор части, выбрав фон графики.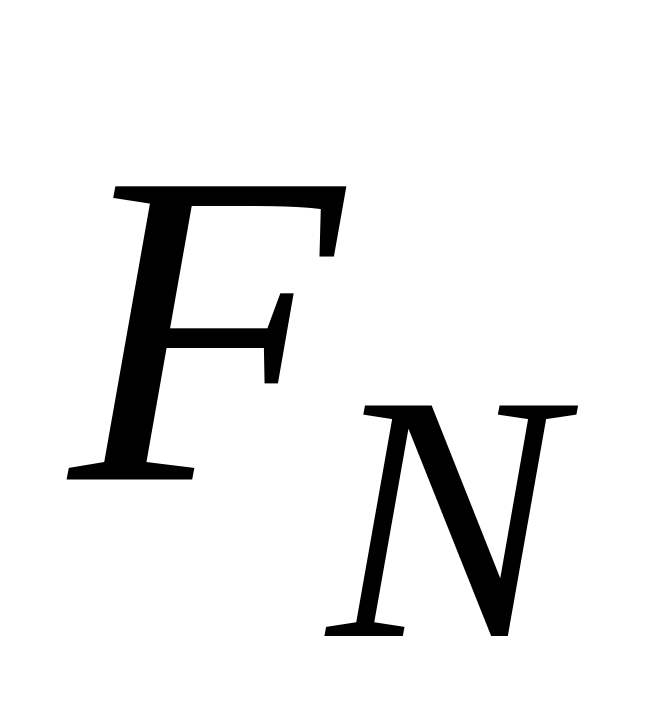 Это традиционно выполнялось в лаборатории ходьбы с использованием трехмерной оптической системы захвата движения и силовых пластин (Novacheck, 1998). Наиболее значимыми анализируемыми кинематическими и кинетическими параметрами являются: углы суставов (Devita and Skelly, 1992; Edwards et al., 2012) и силы реакции опоры (Cavanagh and Lafortune, 1980), поскольку они являются важными факторами, определяющими технику бега (Goss et al. ., 2012). Дискретными кинетическими параметрами, связанными с беговыми травмами и/или производительностью, являются: скорость нагрузки и пиковые вертикальные силы реакции опоры (Crowell and Davis, 2011; Goss et al., 2012; Schmitz et al., 2014), тогда как максимальное сгибание колена во время стояния является соответствующим дискретным кинематическим параметром (Edwards et al., 2012). Однако лабораторные условия не идентичны обычной беговой среде и поэтому могут привести к другой кинематике и кинетике (Sinclair et al., 2013). Предыдущие исследования подтвердили это, показав значительные различия между бегом на беговой дорожке и бегом на открытом воздухе (Nigg et al.
Это традиционно выполнялось в лаборатории ходьбы с использованием трехмерной оптической системы захвата движения и силовых пластин (Novacheck, 1998). Наиболее значимыми анализируемыми кинематическими и кинетическими параметрами являются: углы суставов (Devita and Skelly, 1992; Edwards et al., 2012) и силы реакции опоры (Cavanagh and Lafortune, 1980), поскольку они являются важными факторами, определяющими технику бега (Goss et al. ., 2012). Дискретными кинетическими параметрами, связанными с беговыми травмами и/или производительностью, являются: скорость нагрузки и пиковые вертикальные силы реакции опоры (Crowell and Davis, 2011; Goss et al., 2012; Schmitz et al., 2014), тогда как максимальное сгибание колена во время стояния является соответствующим дискретным кинематическим параметром (Edwards et al., 2012). Однако лабораторные условия не идентичны обычной беговой среде и поэтому могут привести к другой кинематике и кинетике (Sinclair et al., 2013). Предыдущие исследования подтвердили это, показав значительные различия между бегом на беговой дорожке и бегом на открытом воздухе (Nigg et al. , 1995). Кроме того, различия в кинематике бега также могут возникать в результате нацеливания силовой пластины при беге в надземной лаборатории (Challis, 2001).Таким образом, система, способная измерять соответствующие параметры вне лаборатории, может устранить эти недостатки.
, 1995). Кроме того, различия в кинематике бега также могут возникать в результате нацеливания силовой пластины при беге в надземной лаборатории (Challis, 2001).Таким образом, система, способная измерять соответствующие параметры вне лаборатории, может устранить эти недостатки.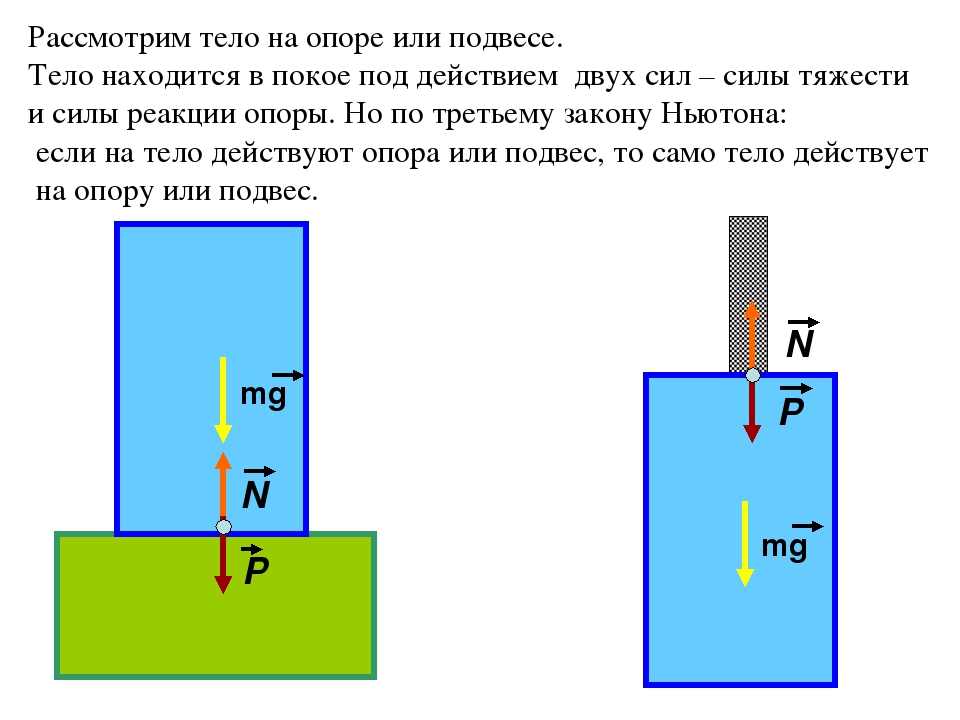 Вуда и др. (2016) продемонстрировали сопоставимую производительность с уменьшенной настройкой датчика с использованием искусственной нейронной сети (ИНС), обученной отображать пять ориентаций в позе всего тела.Преимущество ИНС заключается в создании «модели» для сопоставления определенных входных данных с выходными на основе набора данных, используемого для обучения (Алпайдин, 2009). Беговые приложения с использованием минимального набора инерционных датчиков в основном сосредоточены на временных результатах, таких как использование гироскопов на ногах для оценки временных параметров бега (McGrath et al., 2012). Бейли и Харле (2014, 2015) показали, что с помощью ИМУ, устанавливаемых на ноги, это можно расширить для оценки пространственно-временных параметров бега.
Вуда и др. (2016) продемонстрировали сопоставимую производительность с уменьшенной настройкой датчика с использованием искусственной нейронной сети (ИНС), обученной отображать пять ориентаций в позе всего тела.Преимущество ИНС заключается в создании «модели» для сопоставления определенных входных данных с выходными на основе набора данных, используемого для обучения (Алпайдин, 2009). Беговые приложения с использованием минимального набора инерционных датчиков в основном сосредоточены на временных результатах, таких как использование гироскопов на ногах для оценки временных параметров бега (McGrath et al., 2012). Бейли и Харле (2014, 2015) показали, что с помощью ИМУ, устанавливаемых на ноги, это можно расширить для оценки пространственно-временных параметров бега. , 2007). Однако ни один из вышеупомянутых подходов не предоставил пользователям кинетическую информацию. Попытки перенести кинетический анализ за пределы лабораторных условий оказались эффективными при сгибании туловища (Faber et al., 2016), походка (Karatsidis et al., 2017), танец (Shippen and May, 2012) и бег (Pavei et al., 2017). Однако вышеупомянутые подходы требуют кинематической информации всего тела. Метод оценки пиковых вертикальных сил реакции опоры (vGRF), предложенный Charry et al. (2013) опирались только на большеберцовые ускорения, но не подходили для оценки кинетики во время всей фазы опоры. Подход, основанный только на ускорении туловища, оказался недостаточным для оценки vGRF с использованием модели «масса-пружина-демпфер» (Nedergaard et al., 2017).
, 2007). Однако ни один из вышеупомянутых подходов не предоставил пользователям кинетическую информацию. Попытки перенести кинетический анализ за пределы лабораторных условий оказались эффективными при сгибании туловища (Faber et al., 2016), походка (Karatsidis et al., 2017), танец (Shippen and May, 2012) и бег (Pavei et al., 2017). Однако вышеупомянутые подходы требуют кинематической информации всего тела. Метод оценки пиковых вертикальных сил реакции опоры (vGRF), предложенный Charry et al. (2013) опирались только на большеберцовые ускорения, но не подходили для оценки кинетики во время всей фазы опоры. Подход, основанный только на ускорении туловища, оказался недостаточным для оценки vGRF с использованием модели «масса-пружина-демпфер» (Nedergaard et al., 2017). ИНС обучена оценивать углы суставов на основе ориентации голени относительно таза, аналогично подходу, представленному в предыдущей работе (Wouda et al., 2016). Соответствующие характеристики оцениваются с использованием как инерционных, так и оптических данных захвата движения всего тела. Расчетные углы сочленений в сочетании с ускорениями датчиков могут быть переданы во вторую ИНС, которая оценивает (вертикальные) силы реакции земли. Предлагаемый метод оценивался с использованием непрерывных результатов (vGRF и профили угла колена) и дискретных результатов (пиковая vGRF, скорость нагрузки и максимальное сгибание колена во время стояния). Результаты этого исследования могут быть использованы в будущем для предотвращения беговых травм и улучшения результатов бега.
ИНС обучена оценивать углы суставов на основе ориентации голени относительно таза, аналогично подходу, представленному в предыдущей работе (Wouda et al., 2016). Соответствующие характеристики оцениваются с использованием как инерционных, так и оптических данных захвата движения всего тела. Расчетные углы сочленений в сочетании с ускорениями датчиков могут быть переданы во вторую ИНС, которая оценивает (вертикальные) силы реакции земли. Предлагаемый метод оценивался с использованием непрерывных результатов (vGRF и профили угла колена) и дискретных результатов (пиковая vGRF, скорость нагрузки и максимальное сгибание колена во время стояния). Результаты этого исследования могут быть использованы в будущем для предотвращения беговых травм и улучшения результатов бега.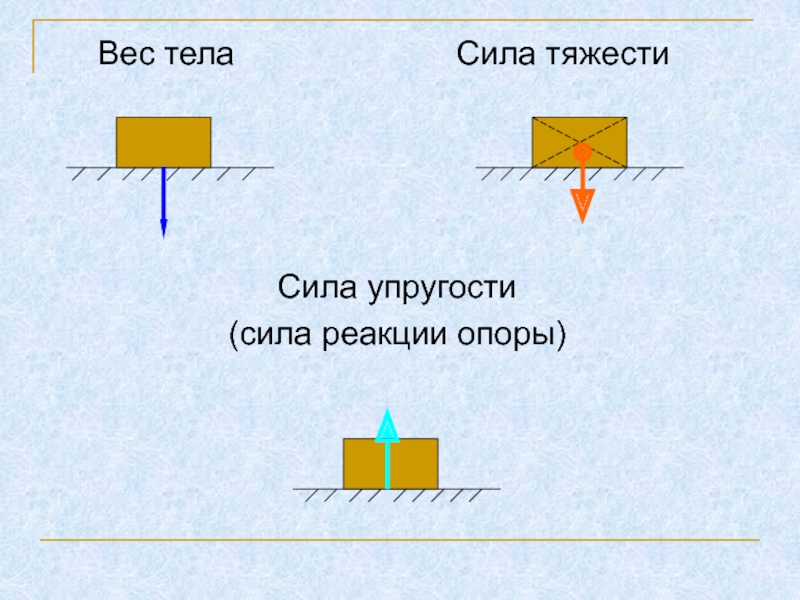 Бегуны были набраны из местного легкоатлетического клуба, и все они не сообщили о недавних травмах. Испытуемых проинструктировали бежать с 3 различными скоростями (10, 12 и 14 км/ч, в указанном порядке) в течение 3 минут на каждой беговой дорожке с приборами, расположенной в лаборатории ходьбы Roessingh Research and Development (Энсхеде, Нидерланды). .Сеанс разминки с самостоятельно выбранной скоростью бега (примерно 3 мин) выполнялся всеми испытуемыми перед измерениями. Комитет по этике факультета электротехники, математики и компьютерных наук Университета Твенте одобрил этот протокол, и все испытуемые дали письменное информированное согласие до проведения измерений.
Бегуны были набраны из местного легкоатлетического клуба, и все они не сообщили о недавних травмах. Испытуемых проинструктировали бежать с 3 различными скоростями (10, 12 и 14 км/ч, в указанном порядке) в течение 3 минут на каждой беговой дорожке с приборами, расположенной в лаборатории ходьбы Roessingh Research and Development (Энсхеде, Нидерланды). .Сеанс разминки с самостоятельно выбранной скоростью бега (примерно 3 мин) выполнялся всеми испытуемыми перед измерениями. Комитет по этике факультета электротехники, математики и компьютерных наук Университета Твенте одобрил этот протокол, и все испытуемые дали письменное информированное согласие до проведения измерений. , Викон, Оксфорд, Великобритания), расположенные вокруг беговой дорожки. Любой объект, который мог блокировать обзор камеры или создавать нежелательные отражения, был удален из среды измерения. Кроме того, кинематика была синхронно захвачена с помощью системы захвата инерциального движения Xsens MVN Link (Xsens, Enschede, Нидерланды), состоящей из 17 IMU, размещенных на обоих плечах, плечах, предплечьях, кистях, бедрах, голенях, ступнях, голове. , грудину и таз (Roetenberg et al., 2013). Необходимый полный костюм из лайкры (для размещения IMU) был модифицирован с отверстиями для уменьшения артефактов движения световозвращающих маркеров, которые размещаются непосредственно на коже субъекта. Кинематика всего тела экспортировалась с использованием прилагаемого программного обеспечения (MVN studio 4.3.7, Xsens, Enschede, Нидерланды) с выбранной частотой дискретизации 240 Гц. Испытуемые бежали на беговой дорожке с приборами S-Mill (ForceLink, Culemborg, Нидерланды) с площадью бега 250 × 100 см, что можно увидеть на рисунке 1.
, Викон, Оксфорд, Великобритания), расположенные вокруг беговой дорожки. Любой объект, который мог блокировать обзор камеры или создавать нежелательные отражения, был удален из среды измерения. Кроме того, кинематика была синхронно захвачена с помощью системы захвата инерциального движения Xsens MVN Link (Xsens, Enschede, Нидерланды), состоящей из 17 IMU, размещенных на обоих плечах, плечах, предплечьях, кистях, бедрах, голенях, ступнях, голове. , грудину и таз (Roetenberg et al., 2013). Необходимый полный костюм из лайкры (для размещения IMU) был модифицирован с отверстиями для уменьшения артефактов движения световозвращающих маркеров, которые размещаются непосредственно на коже субъекта. Кинематика всего тела экспортировалась с использованием прилагаемого программного обеспечения (MVN studio 4.3.7, Xsens, Enschede, Нидерланды) с выбранной частотой дискретизации 240 Гц. Испытуемые бежали на беговой дорожке с приборами S-Mill (ForceLink, Culemborg, Нидерланды) с площадью бега 250 × 100 см, что можно увидеть на рисунке 1.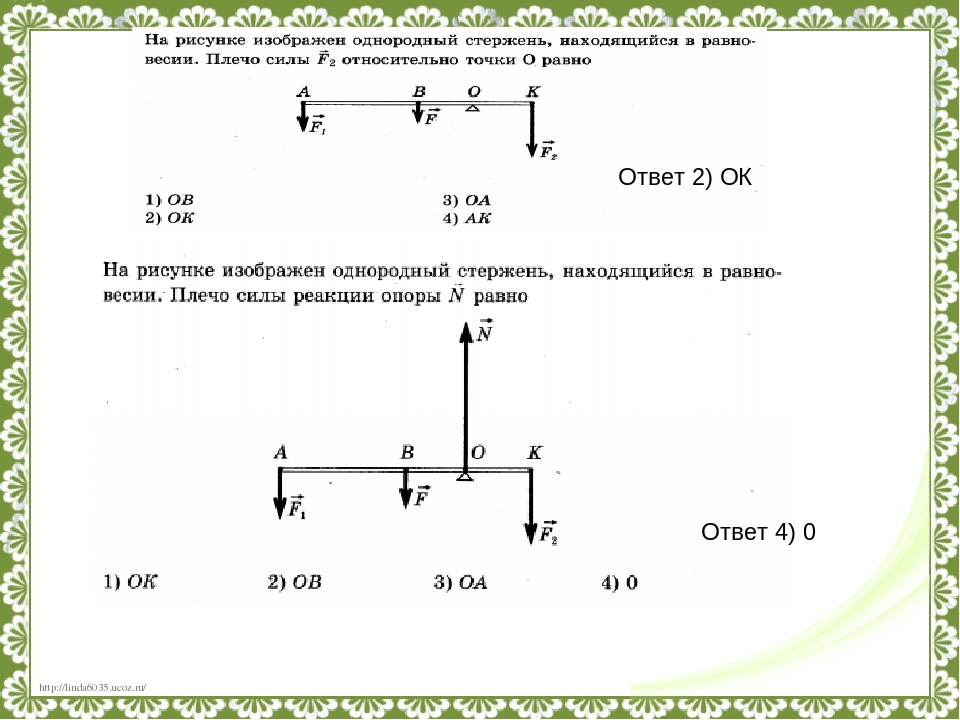 Беговая дорожка была оснащена одномерной силовой пластиной, способной измерять эталонную vGRF на частоте 1000 Гц. Данные различных систем синхронизировались с использованием аналогового сигнала синхронизации.
Беговая дорожка была оснащена одномерной силовой пластиной, способной измерять эталонную vGRF на частоте 1000 Гц. Данные различных систем синхронизировались с использованием аналогового сигнала синхронизации.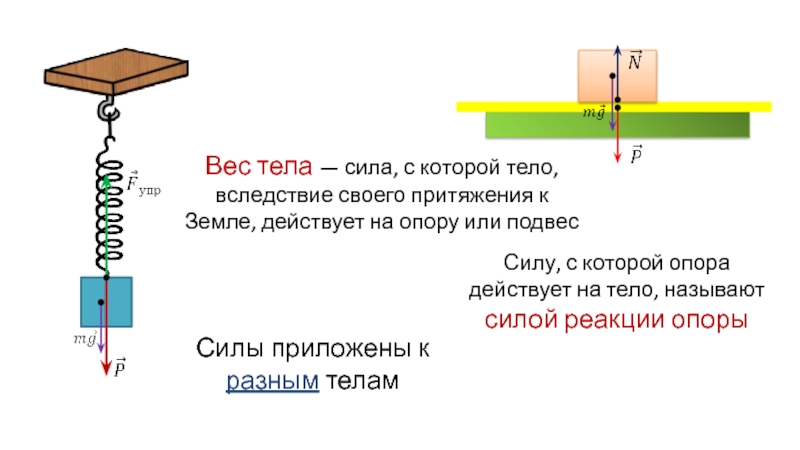
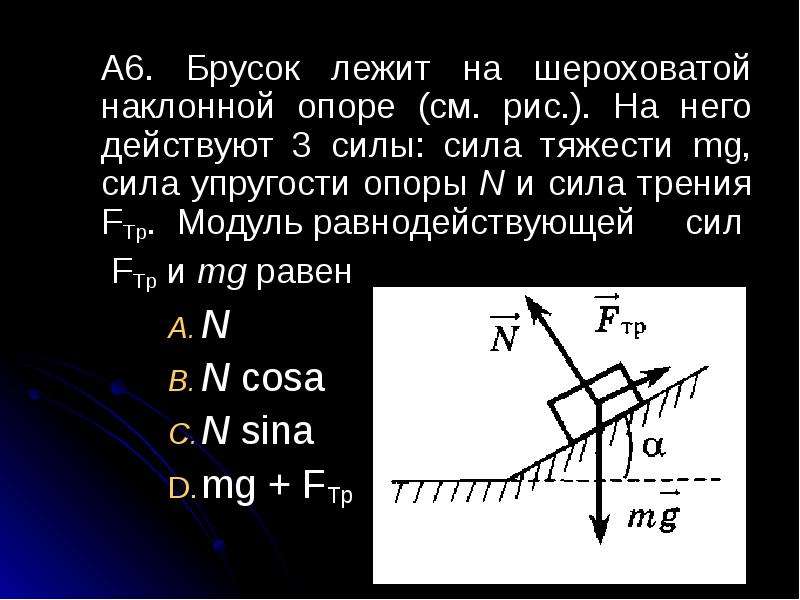 Эта повторная выборка данных не оказывает существенного влияния на измеренную кинематику и кинетику, как это также было сделано Pavei et al.(2017). Для анализа кинематические и кинетические данные были сегментированы по фазам опоры с использованием порога 20 Н (Milner and Paquette, 2015). Вся обработка данных и статистический анализ были выполнены в MATLAB R2017a (Mathworks, Inc., Натик, Массачусетс, США).
Эта повторная выборка данных не оказывает существенного влияния на измеренную кинематику и кинетику, как это также было сделано Pavei et al.(2017). Для анализа кинематические и кинетические данные были сегментированы по фазам опоры с использованием порога 20 Н (Milner and Paquette, 2015). Вся обработка данных и статистический анализ были выполнены в MATLAB R2017a (Mathworks, Inc., Натик, Массачусетс, США). ) к вертикальным силам реакции грунта.Эта архитектура была выбрана для обеспечения независимого обучения двух ИНС. Кроме того, предлагаемая архитектура разделяет проблемы обучения, позволяя проводить «выборочное» повторное обучение ИНС (например, в набор данных ИНС 1 можно включить дополнительные рабочие среды без одновременного измерения GRF).
) к вертикальным силам реакции грунта.Эта архитектура была выбрана для обеспечения независимого обучения двух ИНС. Кроме того, предлагаемая архитектура разделяет проблемы обучения, позволяя проводить «выборочное» повторное обучение ИНС (например, в набор данных ИНС 1 можно включить дополнительные рабочие среды без одновременного измерения GRF). С этой целью были оценены две схемы обучения, как показано в таблице 1, для проверки предложенного метода независимо от технологии захвата движения.
С этой целью были оценены две схемы обучения, как показано в таблице 1, для проверки предложенного метода независимо от технологии захвата движения. , 2016), для обеих ИНС использовалась двухуровневая (с 250 и 100 нейронами) функция, соответствующая архитектуре нейронной сети, способная отображать нелинейности между входом и выходом. Сети обучались в течение 2000 итераций, и обучение прекращалось досрочно, если градиент не уменьшался в течение 6 последовательных итераций или если градиент был меньше 1 × 10 -6 . Набор инструментов нейронной сети MATLAB R2017a (Mathworks, Inc., Натик, Массачусетс, США) использовался для проектирования, обучения и оценки ИНС, описанных выше.
, 2016), для обеих ИНС использовалась двухуровневая (с 250 и 100 нейронами) функция, соответствующая архитектуре нейронной сети, способная отображать нелинейности между входом и выходом. Сети обучались в течение 2000 итераций, и обучение прекращалось досрочно, если градиент не уменьшался в течение 6 последовательных итераций или если градиент был меньше 1 × 10 -6 . Набор инструментов нейронной сети MATLAB R2017a (Mathworks, Inc., Натик, Массачусетс, США) использовался для проектирования, обучения и оценки ИНС, описанных выше.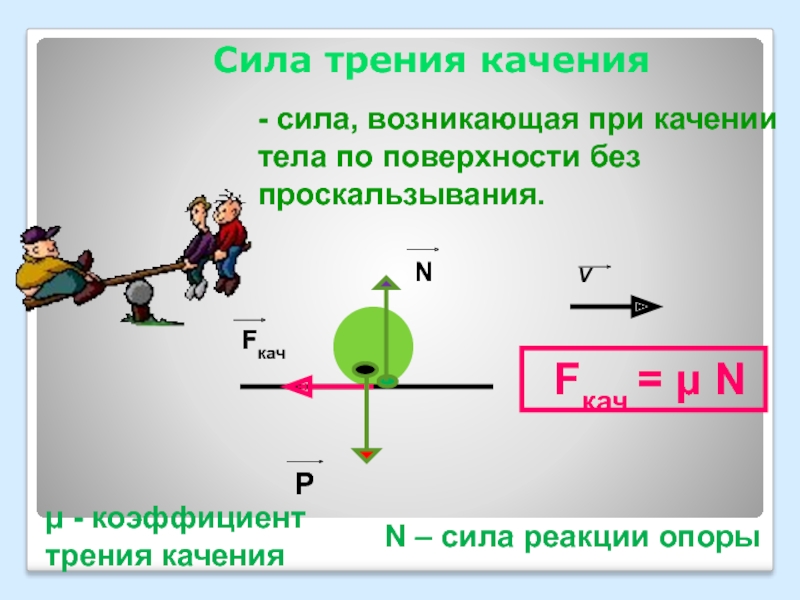 Обратите внимание, что для простоты мы будем показывать только результаты, соответствующие данным бега со скоростью 12 км/ч.
Обратите внимание, что для простоты мы будем показывать только результаты, соответствующие данным бега со скоростью 12 км/ч.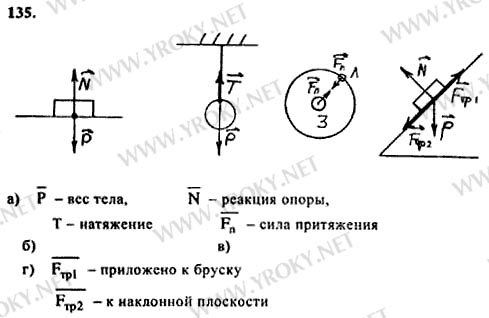 , 1998). Кроме того, максимальный угол F/E колена в фазе опоры оценивали с помощью парного теста t (уровень значимости 0.05) и график Бланда-Альтмана (Bland and Altman, 1986). Предполагаемые vGRF (нормализованные по массе тела, BW) также оценивали с использованием как непрерывных (ρ и RMSE), так и дискретных показателей (скорость нагрузки и пик vGRF). Однако кинетический анализ был ограничен фазой опоры каждой ноги (поскольку во время фазы переноса контакт отсутствует). Поскольку пик пассивной vGRF четко не определен для бегунов средней или передней части стопы, это событие было определено с использованием пикового ускорения от IMU голени (Willy et al., 2008).Используя это событие, скорость нагрузки была рассчитана как наклон vGRF между 20 и 80 процентами пикового времени пассивного vGRF (Willy et al., 2008; Crowell and Davis, 2011).
, 1998). Кроме того, максимальный угол F/E колена в фазе опоры оценивали с помощью парного теста t (уровень значимости 0.05) и график Бланда-Альтмана (Bland and Altman, 1986). Предполагаемые vGRF (нормализованные по массе тела, BW) также оценивали с использованием как непрерывных (ρ и RMSE), так и дискретных показателей (скорость нагрузки и пик vGRF). Однако кинетический анализ был ограничен фазой опоры каждой ноги (поскольку во время фазы переноса контакт отсутствует). Поскольку пик пассивной vGRF четко не определен для бегунов средней или передней части стопы, это событие было определено с использованием пикового ускорения от IMU голени (Willy et al., 2008).Используя это событие, скорость нагрузки была рассчитана как наклон vGRF между 20 и 80 процентами пикового времени пассивного vGRF (Willy et al., 2008; Crowell and Davis, 2011). Раздел 3.2 посвящен обобщению этого подхода на различные предметы (сценарий 2).
Раздел 3.2 посвящен обобщению этого подхода на различные предметы (сценарий 2).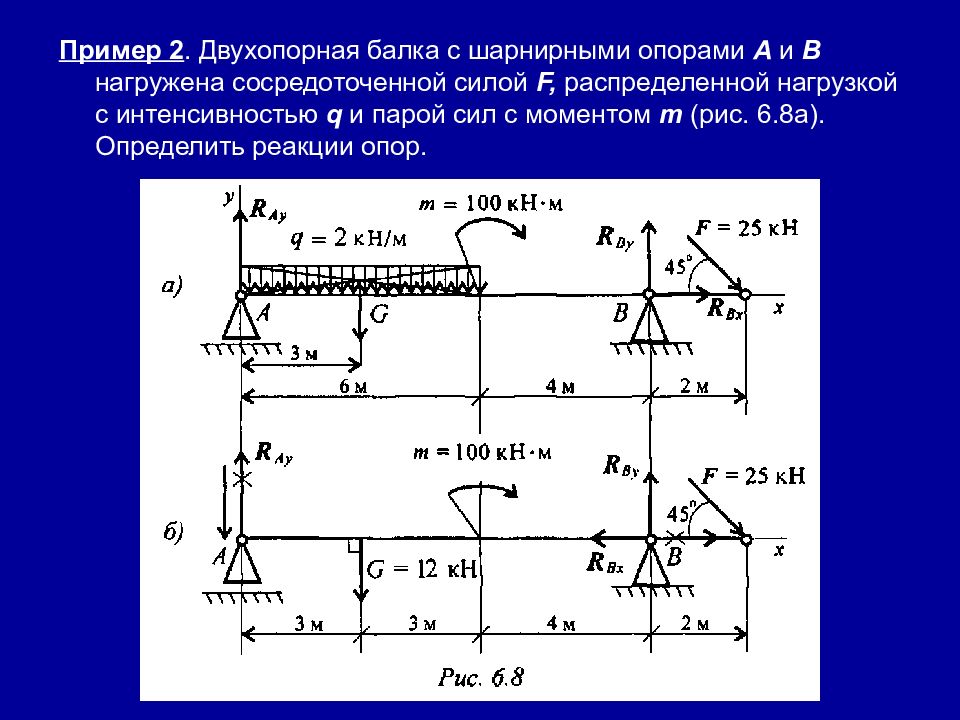 Наибольшая разница между оценкой и соответствующим эталоном наблюдается при наибольшем угле сгибания, который во всех случаях завышен. Как уже отмечалось в Таблице 2, различия между оценками, основанными на различных источниках, ограничены (в среднем 4°).
Наибольшая разница между оценкой и соответствующим эталоном наблюдается при наибольшем угле сгибания, который во всех случаях завышен. Как уже отмечалось в Таблице 2, различия между оценками, основанными на различных источниках, ограничены (в среднем 4°).