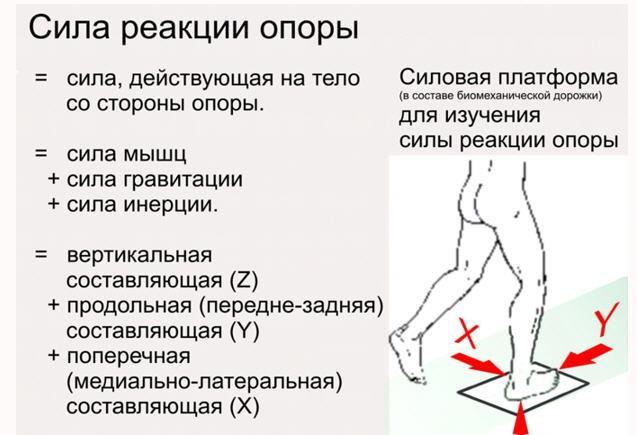
23.4. Силы реакции опоры

Действие веса тела на опору встречает противодействие, которое называют реакцией опоры (или опорной реакцией).

Реакция опоры — это мера противодействия опоры действию на нее тела, находящегося с ней в контакте (в покое или движении). Она равна силе действия тела на опору, направлена в противоположную сторону и приложена к этому телу.

Обычно человек, находясь на горизонтальной опоре, испытывает противодействие своему весу. В этом случае опорная реакция, как и вес тела, направлена перпендикулярно к опоре. Это нормальная (или идеальная) реакция опоры. Если поверхность не плоская, то опорная реакция перпендикулярна к плоскости, касательной к точке опоры.

Когда вес статический, то реакция опоры статическая; по величине она равна статическому весу. Если человек на опоре движется с ускорением, направленным вверх, то к статическому весу добавляется сила инерции и возникает динамическая реакция о п о р ы (рис.

35). Реакция опоры — сила

пассивная (реактивная). Она не может сама по себе вызвать положительные ускорения. Но без нее — если нет опоры, если не от чего оттолкнуться (или не к чему притянуться) — человек не может активно перемещаться.

Если отталкиваться от горизонтальной опоры не прямо вверх, то и сила давления на опору будет приложена не под прямым углом

к ее поверхности. Тогда реакция опоры также не будет перпендикулярна к поверх­ности, ее можно разложить на н о р м а л ь н у ю и касательную составляющие. Когда соприкасающиеся поверхности ров­ные, без выступов, шипов и т. п. (асфальт, подошва ботинка), то касательная состав­ляющая реакции опоры и есть сила трения.

Касательная реакция может быть обу­словлена не только трением (как, напри­мер, между лыжей и снегом), но и другими взаимодействиями (например, шипы бего­вых туфель, вонзившиеся в дорожку).

Равнодействующая нормальной и каса­тельной составляющих называется

о б щ е й реакцией опоры. Она только при свободном неподвижном положении над опорой (или под опорой) проходит через ЦМ человека. Во время же движений, отталкивания или амортизации она обычно не проходит через ЦМ, образуя относи­тельно него момент.

Спортсмену нередко приходится преодолевать сопротивление воз­духа или воды. Среда, в которой движется человек, оказывает свое действие на его тело. Это действие может быть статическим (выталкивающая сила) и динамическим (лобовое сопротивле­ние, нормальная реакция опоры).

Выталкивающая сила — это мера действия среды на погруженное в нее тело. Она измеряется весом вытесненного объема жидкости и направлена вверх.

Если выталкивающая сила (Q (рис. 36) больше силы тяжести тела (G), то тело всплывает. Если же сила тяжести тела больше вытал­кивающей силы, то оно тонет.

Лобовое сопротивление — это сила, с которой среда препятствует движению тела относительно нее. Величина лобового сопротивления (R_x) зависит от площади поперечного сечения тела, его обтекаемо­сти, платности и вязкости среды, а также относительной скорости тела:

Изменяя площадь поперечного сечения тела, можно изменить и действие среды. Так, у лыжника при спуске с горы в высокой стойке

эта площадь почти в 3 раза больше, чем в низкой стойке. Значит, сопротивление воздуха при спуске можно изменять почти в 3 раза. Принимая в воде позы с лучшей обтекаемостью, нужно уменьшать сопротивление воды. Как известно, с увеличением скорости передви­жения сопротивление воды или воздуха резко увеличивается (примерно пропорционально квадрату скорости).

Нормальная реакция среды — это сила, действующая со стороны среды на тело, расположенное под углом к направлению его движения. Она зависит от тех же факторов, что и лобовое сопротивление:

Нормальная реакция среды при гребке направлена перпендикулярно силе лобового сопротивления.

С нормальной реакцией среды как с подъемной силой приходится считаться (например, пловцу во время продвижения по дистанции, прыгуну на лыжах с трамплина во время полета в воздухе).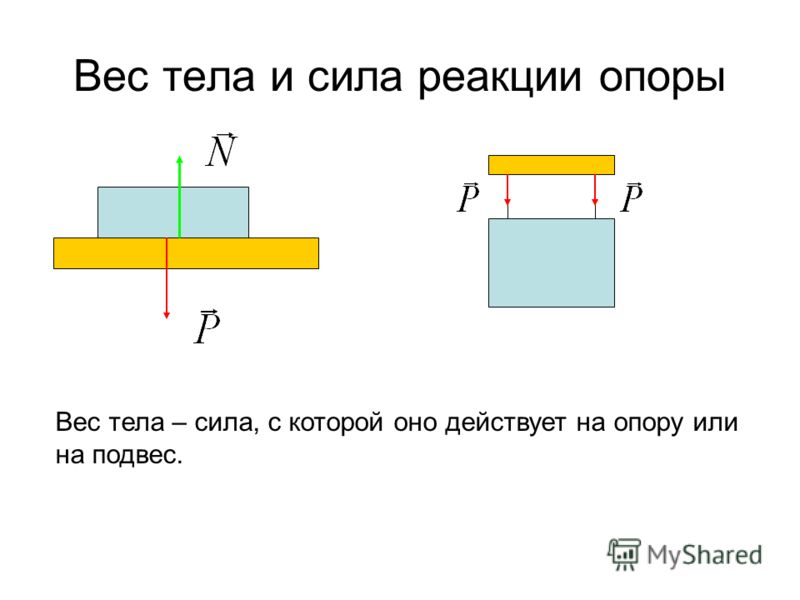

Сила реакция опоры и вес. — forlearn.ru

Перейти к содержимому

1. Опишите силу реакции опоры? Сделайте рисунок.
   Посмотрите на рис. 47.
   
   Рис. 47. Сила реакции опоры и вес тела.
   1 — первое тело, прижатое ко второму телу,
   2 — второе тело (оно конечно тоже будет прижато к первому телу),
   \overrightarrow{mg}~- сила тяжести, действующая на первое тело, её вектор изображён на рисунке ручкой,
   \vec{N}~- сила реакции опоры (её иногда называют силой нормальной реакции опоры, нормальной в смысле перпендикулярной), действующая на первое тело, её вектор изображён на рисунке карандашом сплошной линией,
   \vec{P}~- вес первого тела, его вектор изображён на рисунке карандашом пунктирной линией.
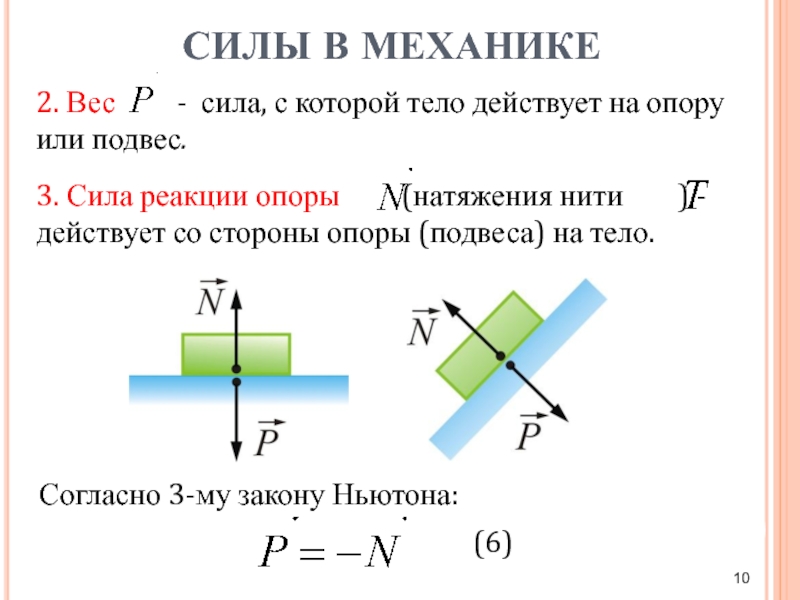
   1) Сила реакции опоры действует на тело (назовём его первым), прижатое ко второму телу.
   2) Сила реакции опоры направлена перпендикулярно поверхности второго тела в сторону от второго тела.
   3) Модуль силы реакции опоры находится из проекции на ось, направленную вдоль этой силы второго закона Ньютона, написанного для первого тела. Например, в случае, изображённом на данном рисунке, если на первое тело действуют только две силы \overrightarrow{mg} и \vec{N}:
   \overrightarrow{mg}+\vec{N}=m\cdot \vec{a};
   где \overrightarrow{mg}~- сила тяжести, действующая на первое тело,
   \vec{N}~- сила реакции опоры, действующая на первое тело,
   m~- масса первого тела,
   \vec{a}~- ускорение первого тела в ИСО.
   Тогда в проекции на ось сонаправленную с вектором \vec{N}, назовём эту ось \mathrm{y}:
   -m\cdot g+N=m\cdot a_y;
   Откуда выразим N:
   N= m\cdot g+m\cdot a_y;
   Если, например, ускорение первого тела в ИСО равно нулю, то получим:
   N= m\cdot g; ¹
   4) Второе тело действует на тело с этой силой реакции опоры.
   5) В случае, изображённом на рисунке (Когда первое тело прямоугольный параллелепипед, а поверхность соприкосновения ровная и перпендикулярна вектору \vec{g}), сила реакции опоры приложена к первому телу в точке, являющейся центром поверхности соприкосновения первого и второго тел.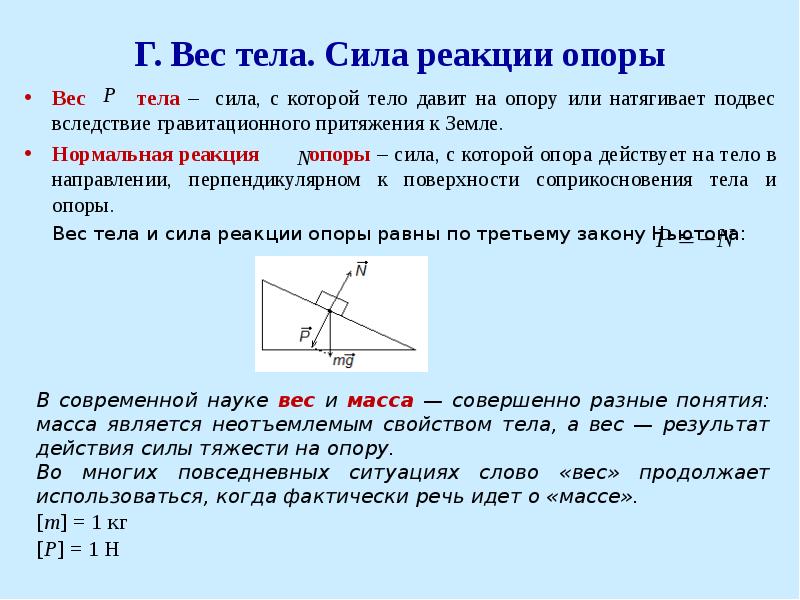 (В общем случае сила реакции опоры не обязательно будет приложена в точке, являющейся центром поверхности соприкосновения первого и второго тел).
2. Что такое вес тела? Сделайте рисунок. Опишите по нему вес тела.
   Вес тела — это сила, с которой это тело действует на горизонтальную опору² или растягивает подвес.³ Посмотрите на рис. 47.
   1) Вес действует на второе тело, поверхность которого горизонтальна, к которому прижато первое тело.
   2) Вес направлен противоположно силе реакции опоры \vec{N}, действующей на первое тело.
   3) \vec{P}=-\vec{N};
   где \vec{P}~- вес первого тела,
   \vec{N}~- сила реакции опоры второго тела с горизонтальной поверхностью, действующей на первое тело,
   4) Первое тело действует на второе своим весом,
   5) Вес приложен ко второму телу в точке поверхности второго тела, лежащей на прямой, содержащей вектор \vec{N}.
3. В чём измеряется вес в системе СИ?
   В СИ вес измеряется в Ньютонах [Н].
4. Модули каких сил, изображённых на рисунке, иллюстрирующем силу реакции опоры и вес, равны по 3-му закону Ньютона?
   На рисунке, иллюстрирующем силу реакции опоры и вес, равны по 3-му закону Ньютона модули силы реакции опоры и веса.
5. Модулю какой силы равен модуль силы тяжести, изображённой на рисунке, иллюстрирующем силу реакции опоры и вес, по 3-му закону Ньютона?
   На рисунке, иллюстрирующем силу реакции опоры и вес, по 3-му закону Ньютона модулю изображённой силы тяжести равен модуль силы тяготения, с которой первое тело действует на Землю.

Сноски:

1. Ещё раз подчеркну, полученные здесь результаты для модуля силы реакции опоры являются лишь частными случаями, сила реакции опоры не всегда находится по полученным формулам. В общем случае её модуль надо находить из проекции на ось, направленную вдоль этой силы второго закона Ньютона, написанного для первого тела.
2. Раз горизонтальную, значит имеется ввиду твёрдую?
3. Везде разные определения этого несчастного веса, и от того какое определение выбрать естественно будет зависеть решение задач на вес. А раз так будем руководствоваться определением, которое даётся в учебнике, рекомендованном для подготовки к ЕГЭ. Вообще обычно все задачи удаётся правильно решить, если считать весом, силу противоположную силе нормальной реакции опоры или силе натяжения нити по третьему закону Ньютона.

Ссылки:

1. Эти же вопросы без ответов.
2. Следующая тема (Сила натяжения и блоки).
3. Предыдущая тема (Закон Гука).
4. Для комментариев, касающихся не только ЕГЭ по физике или этого сайта.

Свежие комментарии

3.4 Реакции и опоры – инженерная механика: статика

Глава 3: Основы твердого тела

Представьте себе луч, выходящий из стены. Какой вес может выдержать балка, прежде чем она оторвется или упадет со стены? Это зависит от способа крепления к стене. Мы моделируем эти ситуации реального мира, используя силы и моменты. Например, пешеходный переход в Гранд-Каньоне позволяет людям пройтись по Гранд-Каньону. Вы хотите быть уверены, что пешеходный переход устроен таким образом, что люди, находящиеся на нем, находятся в безопасности.

Мы называем пешеходную дорожку консольной балкой и превращаем реальную балку в двухмерную модель с ограничениями. Таким образом, мы можем использовать ту же терминологию, это фиксированное ограничение , предотвращающее горизонтальное движение, вертикальное движение и вращение.

Силы и моменты реакции — это то, как мы моделируем ограничения на конструкции. Это внешние силы. В этом курсе мы сосредоточимся на 3 различных типах ограничений, и каждый из них имеет разные силы реакции и моменты:

1. Фиксированный (без трения)

• • Две силы реакции, действующие перпендикулярно в направлениях x и y.
  • Прикрепленное ограничение, а затем показана диаграмма его свободного тела:

 

2. Фиксированный

• • Две силы реакции, действующие перпендикулярно в направлениях x и y
  • Момент, вращающийся вокруг фиксированного ограничения (обычно стены), используйте правило правой руки, чтобы найти его направление
  • Это также называется консольной балкой.
  • Фиксированное ограничение, а затем показано FBD

 

3. Ролик (есть несколько видов)

• • Одиночная сила реакции, действующая в направлении Y
  • Момент не создается
  • Это также может быть земля, на которой стоит объект
  • Показана свободная схема корпуса для катка

 

Обратите внимание, что фиксированное ограничение является наиболее ограничивающим, а ролик — наименее ограничивающим. Вы прикладываете силу, чтобы показать, как ограничение ограничивает движение. Ролик только удерживает объект от перемещения по вертикали, поэтому действует только 1 сила. Штифтовое ограничение не допускает горизонтального или вертикального движения, отсюда и две силы. Неподвижная балка ограничивает вертикальное перемещение, горизонтальное перемещение и вращение, поэтому есть момент и две силы. Обратите внимание, что это относится только к 2d ограничениям.

Вот сводка, показывающая, какое движение разрешено ограничением этого типа:

 

 

 

 

Обычно силы реакции бывают следующими: закрепленная и фиксированная сила реакции вместе (1 сила реакции + 2 силы реакции = 3 ограничения) или неподвижная балка (2 силы реакции и 1 момент = 3 ограничения).

Показанная здесь информация предназначена для моделирования двухмерных ситуаций. В этом курсе статики мы не затрагиваем трехмерные задачи, разумеется, в трехмерном пространстве задействовано больше сил реакции и моментов, чем в двухмерном. В следующем разделе дается второе объяснение реакций и поддержки:

 

3.4.1 Штифтовая или шарнирная опора

Штифтовая опора позволяет вращаться вокруг любой оси, но предотвращает движение в горизонтальном и вертикальном направлениях. Его идеализированное представление и реакции показаны в таблице 3.1:

3.4.2 Роликовая опора

Роликовая опора допускает вращение вокруг любой оси и перемещение (горизонтальное перемещение) в любом направлении, параллельном поверхности, на которой она стоит. Он сдерживает конструкцию от перемещения в вертикальном направлении. Идеализированное представление ролика и его реакции также показаны в таблице 3.1.

3.4.3 Кулисная опора

Характеристики качающейся опоры аналогичны характеристикам роликовой опоры. Его идеализированная форма изображена в таблице 3.1.

3.4.4 Звено

Звено имеет два шарнира, по одному на каждом конце. Он допускает движение во всех направлениях, кроме направления, параллельного его продольной оси, которая проходит через два шарнира. Другими словами, сила реакции звена направлена ​​в направлении звена вдоль его продольной оси.

3.4.5 Фиксированная опора

Неподвижная опора препятствует вращению в любом направлении и предотвращает движение как в горизонтальном, так и в вертикальном направлениях.

Пример 1:

Пример 2 (A _x Добавлено, даже если оно оказывается 0):

Пример 3:

. Пример 4:

.

Источник: «Равновесные структуры, опорные реакции, детерминированность и устойчивость балок и рам» от LibreTexts под лицензией CC BY-NC-ND. https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1. 03%3A_Equilibrium_Structures_Support_Reactions_Determinacy_and_Stability_of_Beams_and_Frames

 

 

В основном: Реактивные силы и моменты (или ограничения) показывают, как движение ограничено, здесь в двух измерениях.

Применение

: Балка, прикрепленная к стене, имеет три способа ограничения движения: горизонтальное, вертикальное и вращательное.

Взгляд вперед: Каждый раз, когда мы моделируем сценарий, мы будем использовать силы реакции, чтобы показать, какой тип движения ограничивается. В главе 4 мы сможем рассчитать силы/моменты реакции.

 

Автор Гейла и Либби

Машиностроение — Силы реакции на трехопорную неразрезную балку, две из которых требуют уравнений совместности. Метод суперпозиции сделан неправильно!

Задавать вопрос

спросил 1 год, 6 месяцев назад

Изменено 1 год, 6 месяцев назад

Просмотрено 1к раз

$\begingroup$

Мне нужно проанализировать неразрезную балку длиной L и три опоры: A (при x=0), B (при x=L/2) и C (при x=L). Приложенная нагрузка P приложена при x=3L/4. Теперь в точке A неразрезная балка прикручена к кронштейну (обозначен оранжевым цветом). В точке C неразрезная балка крепится болтами к другому кронштейну, который приварен к другой балке (обозначен зеленым цветом) в ее середине (см. прилагаемое изображение). Балка с приваренным кронштейном перпендикулярна сплошной балке.

Если не ошибаюсь, кронштейн действует как консольная балка , а приложенная нагрузка вызывает кручение на перпендикулярной балке за счет приваренного кронштейна . Я попытался найти силы реакции, используя метод суперпозиции для статически неопределимых балок , описанный во многих книгах MoM (я консультировался с Филпотом).

В соответствии с этим методом при работе с балкой, поддерживаемой другой балкой, необходимо использовать уравнение совместимости после определения прогибов в интересующей точке. Первый шаг при решении задач такого типа состоит в устранении избыточной реакции (скажем, А в моей конструкции) и нахождении других реакций (В и С) с помощью уравнений статического равновесия, поскольку устранение избыточной реакции оставляет статически определимую балку ( выпущенный луч). В моем случае я считаю, что следующие шаги на самом деле не применимы, потому что сила реакции C определяется, когда уравнение совместимости используется при нахождении отклонений в точке C. Это что-то вроде парадокса: сила реакции A находится путем нахождения реакции C, но реакцию C можно найти, найдя реакцию A, и так далее. Как я могу решить эту проблему? Есть ли другой аналитический метод, который решает эти случаи? Я просто делаю что-то неправильно? Я на пороге открытия нового метода MoM? (просто шучу).

• машиностроение
• проектирование конструкций
• расчет конструкций
• механика твердого тела
• машиностроение

$\endgroup$

$\begingroup$

Кронштейны не играют никакой роли, если на них не действует какой-либо момент или внешняя нагрузка, или если их собственный вес не является значительным, что здесь не показано.

Это типичная проблема, решение которой легко найти во многих методических пособиях. путем поиска двухпролетной балки с сосредоточенной нагрузкой в ​​середине пролета. Простой способ расчета реакции состоит в том, чтобы отпустить третью опору, C, и позволить узлу C отклониться вверх, а затем рассчитать реакцию в C, которая отменит отклонение, как вы упомянули метод совместимости.

На рисунке ниже показаны момент и реакция средства проектирования DNS. источник.

.

$\endgroup$

$\begingroup$

Этот ответ указывает на возможную причину получения «неправильного» результата методом суперпозиции.

• Метод суперпозиции действителен и желателен для этой задачи, но ваши предположения о жесткости опоры могли быть неверными, что и привело к ошибке.

Конец балки справа (точка C) опирается на другую балку, которая может прогибаться и должна быть смоделирована как пружинная опора, как показано на графике ниже. На прочность жесткости пружины влияют характеристики и свойства поперечной балки — длина, жесткость, условия опирания, прогиб в точке «С».