Элементарный учебник физики Т1

Ландсберг Г.С. Элементарный учебник физики. Т.1. Механика. Теплота. Молекулярная физика. — М.: Наука, 1985. — 606 c. Один из лучших курсов элементарной физики, завоевавший огромную популярность. Достоинством курса является глубина изложения физической стороны рассматриваемых процессов и явлений в природе и технике. В новом издании структура курса осталась прежней, однако в изложении проведена система единиц СИ, терминология и обозначения единиц физических величин приведены в соответствие с действующим ГОСТ. Для слушателей и преподавателей подготовительных отделений и курсов вузов, старшеклассников общеобразовательных и профессиональных школ, а также лиц, занимающихся самообразованием и готовящихся к поступлению в вуз. Оглавление ОТ ИЗДАТЕЛЬСТВА ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ ВВЕДЕНИЕ Глава I. Кинематика § 1. Движение тел § 2. Кинематика. Относительность движения и покоя. § 3. Траектория движения § 4. Поступательное и вращательное движения тела § 5. Движение точки § 6. Описание движения точки § 7. Измерение длины § 8. Измерение промежутков времени § 9. Равномерное прямолинейное движение и его скорость § 10. Знак скорости при прямолинейном движении § 11. Единицы скорости § 12. Графики зависимости пути от времени § 13. Графики зависимости скорости от времени § 14. Неравномерное прямолинейное движение § 15. Мгновенная скорость § 16. Ускорение при прямолинейном движении § 17. Скорость прямолинейного равноускоренного движения § 18. Знак ускорения при прямолинейном движении § 19. Графики скорости при прямолинейном равноускоренном движении § 20. Графики скорости при произвольном неравномерном движении § 21. Нахождение пути, пройденного при неравномерном движении, при помощи графика скорости § 22. Путь, пройденный при равнопеременном движении § 23. Векторы § 24. Разложение вектора на составляющие § 25. Криволинейное движение § 26. Скорость криволинейного движения § 27. Ускорение при криволинейном движении § 28. Движение относительно разных систем отсчета § 29. Кинематика космических движений Глава II. Динамика § 30. Задачи динамики § 31. Закон инерции § 32. Инерциальные системы отсчета § 33. Принцип относительности Галилея § 34. Силы § 35. Уравновешивающиеся силы. О покое тела и о движении по инерции § 36. Сила — вектор. Эталон силы § 37. Динамометры § 38. Точка приложения силы § 39. Равнодействующая сила § 40. Сложение сил, направленных по одной прямой § 41. Сложение сил, направленных под углом друг к другу § 42. Связь между силой и ускорением § 43. Масса тела § 44. Второй закон Ньютона § 45. Единицы силы и массы § 46. Системы единиц § 47. Третий закон Ньютона § 48. Примеры применения третьего закона Ньютона § 49. Импульс тела § 50. Система тел. Закон сохранения импульса § 51. Применения закона сохранения импульса § 52. Свободное падение тел § 53. Ускорение свободного падения § 54. Падение тела без начальной скорости и движение тела, брошенного вертикально вверх § 55. Вес тела § 56. Масса и вес § 57. Плотность вещества § 58. Возникновение деформаций § 59. Деформации в покоящихся телах, вызванные действием только сил, возникающих при соприкосновении § 60. Деформации в покоящихся телах, вызванные силой тяжести § 61. Деформации тела, испытывающего ускорение § 62. Исчезновение деформаций при падении тел § 63. Разрушение движущихся тел § 64. Силы трения § 65. Трение качения § 66. Роль сил трения § 67. Сопротивление среды § 68. Падение тел в воздухе Глава III. Статика § 69. Задачи статики § 70. Абсолютно твердое тело § 71. Перенос точки приложения силы, действующей на твердое тело § 72. Равновесие тела под действием трех сил § 73. Разложение сил на составляющие § 74. Проекции сил. Общие условия равновесия § 75. Связи. Силы реакции связей. Тело, закрепленное на оси § 76. Равновесие тела, закрепленного на оси § 77. Момент силы § 78. Измерение момента силы § 79. Пара сил § 80. Сложение параллельных сил. Центр тяжести § 81. Определение центра тяжести тел § 82. Различные случаи равновесия тела под действием силы тяжести § 83. Условия устойчивого равновесия под действием силы тяжести § 84. Простые машины § 85. Клин и винт Глава IV. Работа и энергия § 86. «Золотое правило» механики § 87. Применения «золотого правила» § 88. Работа силы § 89. Работа при перемещении, перпендикулярном к направлению силы § 90. Работа силы, направленной под любым углом к перемещению § 91. Положительная и отрицательная работа § 92. Единица работы § 93. О движении по горизонтальной плоскости § 94. Работа силы тяжести при движении по наклонной плоскости § 95. Принцип сохранения работы § 96. Энергия § 97. Потенциальная энергия § 98. Потенциальная энергия упругой деформации § 99. Кинетическая энергия § 100. Выражение кинетической энергии через массу и скорость тела § 101. Полная энергия тела § 102. Закон сохранения энергии § 103. Силы трения и закон сохранения механической энергии § 104. Превращение механической энергии во внутреннюю энергию § 105. Всеобщий характер закона сохранения энергии § 106. Мощность § 107. Расчет мощности механизмов § 108. Мощность, быстроходность и размеры механизма § 109. Коэффициент полезного действия механизмов Глава V. Криволинейное движение § 110. Возникновение криволинейного движения § 111. Ускорение при криволинейном движении § 112. Движение тела, брошенного в горизонтальном направлении § 113. Движение тела, брошенного под углом к горизонту § 114. Полет пуль и снарядов § 115. Угловая скорость § 116. Силы при равномерном движении по окружности § 117. Возникновение силы, действующей на тело, движущееся по окружности § 118. Разрыв маховиков § 119. Деформация тела, движущегося по окружности § 120. «Американские горки» § 121. Движение на закруглениях пути § 122. Движение подвешенного тела по окружности § 123. Движение планет § 124. Закон всемирного тяготения § 125. Искусственные спутники Земли Глава VI. Движение в неинерциальных системах отсчета и силы инерции § 126. Роль системы отсчета § 127. Движение относительно разных инерциальных систем отсчета § 128. Движение относительно инерциальной и неинерциальной систем отсчета § 129. Поступательно движущиеся неинерциальиые системы § 130. Силы инерции § 131. Эквивалентность сил инерции и сил тяготения § 132. Невесомость и перегрузки § 133. Является ли Земля инерциальиой системой отсчета? § 134. Вращающиеся системы отсчета § 135. Силы инерции при движении тела относительно вращающейся системы отсчета § 136. Доказательство вращения Земли § 137. Приливы Глава VII. Гидростатика § 138. Подвижность жидкости § 139. Силы давления § 140. Измерение сжимаемости жидкости § 141. «Несжимаемая» жидкость § 142. Силы давления в жидкости передаются во все стороны § 143. Направление сил давления § 144. Давление § 145. Мембранный манометр § 146. Независимость давления от ориентации площадки § 147. Единицы давления § 148. Определение сил давления по давлению § 149. Распределение давления внутри жидкости § 150. Закон Паскаля § 151. Гидравлический пресс § 152. Жидкость под действием силы тяжести § 153. Сообщающиеся сосуды § 154. Жидкостный манометр § 155. Устройство водопровода. Нагнетательный насос § 156. Сифон § 157. Сила давления на дно сосуда § 158. Давление воды в морских глубинах § 159. Прочность подводной лодки § 160. Закон Архимеда § 161. Измерение плотности тел на основании закона Архимеда § 162. Плавание тел § 163. Плавание несплошных тел § 164. Устойчивость плавания кораблей § 165. Всплывание пузырьков § 166. Тела, лежащие на дне сосуда Глава VIII. Аэростатика § 167. Механические свойства газов § 168. Атмосфера § 169. Давление атмосферы § 170. Другие опыты, показывающие существование атмосферного давления § 171. Разрежающие насосы § 172. Влияние атмосферного давления на уровень жидкости в трубке § 173. Максимальная высота столба жидкости § 174. Опыт Торричелли. Ртутный барометр и барометр-анероид § 175. Распределение атмосферного давления по высоте § 176. Физиологическое действие пониженного давления воздуха § 177. Закон Архимеда для газов § 178. Воздушные шары и дирижабли § 179. Применение сжатого воздуха в технике Глава IX. Гидродинамика и аэродинамика § 180. Давление в движущейся жидкости § 181. Течение жидкости по трубам § 182. Закон Бернулли § 183. Жидкость в неинерциальных системах отсчета § 184. Реакция движущейся жидкости и ее использование § 185. Перемещение на воде § 186. Ракеты § 187. Реактивные двигатели § 188. Баллистические ракеты § 189. Взлет ракеты с Земли § 190. Сопротивление воздуха § 191. Эффект Магиуса и циркуляция § 192. Подъемная сила крыла и полет самолета § 193. Турбулентность в потоке жидкости или газа § 194. Ламинарное течение РАЗДЕЛ ВТОРОЙ. ТЕПЛОТА. МОЛЕКУЛЯРНАЯ ФИЗИКА Глава X. Тепловое расширение твердых и жидких тел § 195. Тепловое расширение твердых и жидких тел § 196. Термометры § 197. Формула линейного расширения § 198. Формула объемного расширения § 199. Связь между коэффициентами линейного и объемного расширения § 200. Измерение коэффициента объемного расширения жидкостей § 201. Особенности расширения воды Глава XI. Работа. Теплота. Закон сохранения энергии § 202. Изменения состояния тел § 203. Нагревание тел при совершении работы § 204. Изменение внутренней энергии тел при теплопередаче § 205. Единицы количества теплоты § 206. Зависимость внутренней энергии тела от его массы и вещества § 207. Теплоемкость тела § 208. Удельная теплоемкость § 209. Калориметр. Измерение теплоемкостей § 210. Закон сохранения энергии § 211. Невозможность «вечного двигателя» § 212. Различные виды процессов, при которых происходит передача теплоты Глава XII. Молекулярная теория § 213. Молекулы и атомы § 214. Размеры атомов и молекул § 215. Микромир § 216. Внутренняя энергия с точки зрения молекулярной теории § 217. Молекулярное движение § 218. Молекулярное движение в газах, жидкостях и твердых телах § 219. Броуновское движение § 220. Молекулярные силы Глава XIII. Свойства газов § 221. Давление газа § 222. Зависимость давления газа от температуры § 223. Формула, выражающая закон Шарля § 224. Закон Шарля с точки зрения молекулярной теории § 225. Изменение температуры газа при изменении его объема. Адиабатические и изотермические процессы § 226. Закон Бойля — Мариотта § 227. Формула, выражающая закон Бойля — Мариотта § 228. График, выражающий закон Бойля — Мариотта § 229. Зависимость между плотностью газа и его давлением § 230. Молекулярное толкование закона Бойля — Мариотта § 231. Изменение объема газа при изменении температуры § 232. Закон Гей-Люссака § 233. Графики, выражающие законы Шарля и Гей-Люссака § 234. Термодинамическая температура § 235. Газовый термометр § 236. Объем газа и термодинамическая температура § 237. Зависимость плотности газа от температуры § 238. Уравнение состояния газа § 239. Закон Дальтона § 240. Плотность газов § 241. Закон Авогадро § 242. Моль. Постоянная Авогадро § 243. Скорости молекул газа § 244. Об одном из способов измерения скоростей движения молекул газа (опыт Штерна) § 245. Удельные теплоемкости газов § 246. Молярные теплоемкости § 247. Закон Дюлонга и Пти Глава XIV. Свойства жидкостей § 248. Строение жидкостей § 249. Поверхностная энергия § 250. Поверхностное натяжение § 251. Жидкостные пленки § 252. Зависимость поверхностного натяжения от температуры § 253. Смачивание и несмачивание § 254. Расположение молекул у поверхности тел § 255. Значение кривизны свободной поверхности жидкости § 256. Капиллярные явления § 257. Высота поднятия жидкости в капиллярных трубках § 258. Адсорбция § 259. Флотация § 260. Растворение газов § 261. Взаимное растворение жидкостей § 262. Растворение твердых тел в жидкостях Глава XV. Свойства твердых тел. Переход тел из твердого состояния в жидкое § 263. Введение § 264. Кристаллические тела § 265. Аморфные тела § 266. Кристаллическая решетка § 267. Кристаллизация § 268. Плавление и отвердевание § 269. Удельная теплота плавления § 270. Переохлаждение § 271. Изменение плотности веществ при плавлении § 272. Полимеры § 273. Сплавы § 274. Затвердевание растворов § 275. Охлаждающие смеси § 276. Изменения свойств твердого тела Глава XVI. Упругость и прочность § 277. Введение § 278. Упругие и пластические деформации § 279. Закон Гука § 280. Растяжение и сжатие § 281. Сдвиг § 282. Кручение § 283. Изгиб § 284. Прочность § 285. Твердость § 286. Что происходит при деформации тел § 287. Изменение энергии при деформации тел Глава XVII. Свойства паров § 288. Введение § 289. Пар насыщенный и ненасыщенный § 290. Что происходит при изменении объема жидкости и насыщенного пара § 291. Закон Дальтона для пара § 292. Молекулярная картина испарения § 293. Зависимость давления насыщенного пара от температуры § 294. Кипение § 295. Удельная теплота парообразования § 296. Охлаждение при испарении § 297. Изменение внутренней энергии при переходе вещества из жидкого состояния в парообразное § 298. Испарение при кривых поверхностях жидкости § 299. Перегревание жидкости § 300. Пересыщение паров § 301. Насыщение пара при возгонке § 302. Превращение газа в жидкость § 303. Критическая температура § 304. Сжижение газов в технике § 305. Вакуумная техника § 306. Водяной пар в атмосфере Глава XVIII. Физика атмосферы § 307. Атмосфера § 308. Тепловой баланс Земли § 309. Адиабатические процессы в атмосфере § 310. Облака § 311. Искусственные осадки § 312. Ветер § 313. Предсказание погоды Глава XIX. Тепловые машины § 314. Условия, необходимые для работы тепловых двигателей § 315. Паросиловая станция § 316. Паровой котел § 317. Паровая турбина § 318. Поршневая паровая машина § 319. Конденсатор § 320. Коэффициент полезного действия теплового двигателя § 321. Коэффициент полезного действия паросиловой станции § 322. Бензиновый двигатель внутреннего сгорания § 323. Коэффициент полезного действия двигателя внутреннего сгорания § 324. Двигатель Дизеля § 325. Реактивные двигатели § 326. Передача теплоты от холодного тела к горячему Ответы и решения к упражнениям Предметный указатель

Силы реакции — определение термина

силы, которые возникают при взаимодействии тела с различными конструкциями (стол, стена, наклонная плоскость и т. д.), ограничивающими его положение в пространстве; силы реакции направлены по нормали к касательной плоскости в точке контакта.

Научные статьи на тему «Силы реакции»

действию сил….
Проекции всех сил на вертикальную ось равны нулю….
Первыми студенты рассматривают задачи определения опорных реакций, поперечной силы и изгибающего момента…
Опоры и опорные реакции балок….
систему уравновешивающихся сил, которые приложены к конструкции и заменяем шарниры или защемления реакциями

Статья от экспертов

На основе уравнений Максвелла получена формула, выражающая энергию излучения подвижного диполя, и вычислена сила реакции на излучение диполя, размеры плеча которого сравнимы со среднеквадратичными смещениями атомов кристаллов.

Creative Commons

Научный журнал

системы силам и реакциям наложенных связей, получаем уравновешенную систему. …
, $N_i$ — реакция связи, наложенной на точку; $J_i$ — сила инерции, определяемая формулой $J_i=-m_ia_i…
(реакциями связей)….
Реакции связей изначально не известны, поскольку зависят от характера действующих сил и могут определяться…
К первым относятся реакции связей, а категорию вторых составляют все остальные силы.

Статья от экспертов

Рассматривается задача о статическом нагружении системы двух колес с деформируемой периферией, закрепленных на общей оси с ненулевым углом развала. Протекторы колес моделируются множеством упругих стержней, взаимодействующих с плоскостью по закону сухого трения. Изучается влияние развала в колесной паре на проскальзывание в зоне контакта и величину реакций со стороны дороги. Рассмотрен аналог непрерывной модели стержневого протектора, найдены величины нормальных и касательных реакций в зависимости от вертикального перемещения центра системы.

Creative Commons

Научный журнал

Повышай знания с онлайн-тренажером от Автор24!

1. Напиши термин
2. Выбери определение из предложенных или загрузи свое
3. Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных карточек

Урок 17: 3-й закон Ньютона (действие-противодействие)

Ньютон вывел еще один закон, когда начал думать о взаимодействии объектов.

• Он уже говорил о том, что происходит, когда нет силы (1-й закон).
• Затем он рассказал о том, что происходит, когда есть сила (2-й закон).
• Но что происходит, когда объекты взаимодействуют, влияя друг на друга?

«Для каждой силы действия существует равная и противоположная сила противодействия».

Каждый раз, когда объект прикладывает силу к другому объекту, на исходный объект действует равная и противоположная сила.

• Если вы надавите на стену, вы почувствуете силу против вашей руки… стена давит на вас с той же силой, с какой вы к ней прикладываете.
• Если бы этого не происходило, ваша рука ускорилась бы сквозь стену!

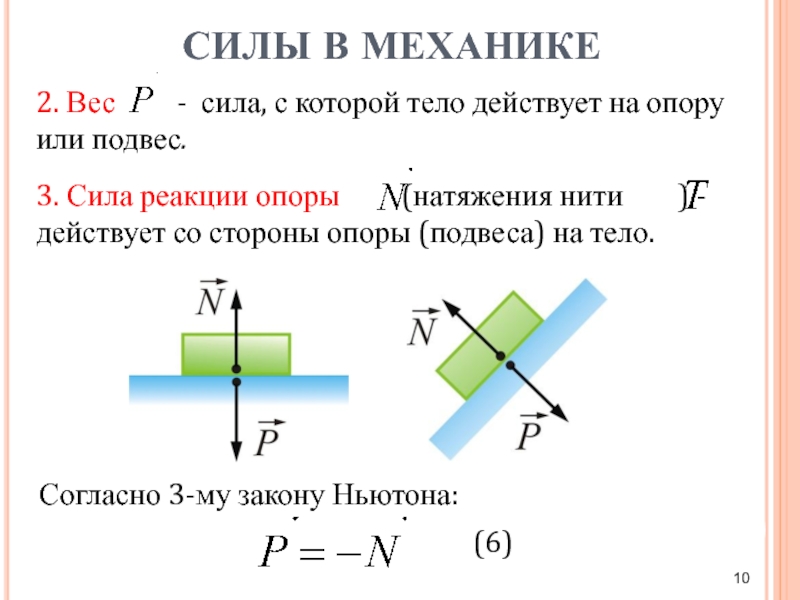
Стоя на земле, вы давите на землю с силой гравитации (F _g вниз), и земля давит на вас в ответ (F _N вверх).

Термин « нормальный » означает что-либо под прямым углом в математике или естественных науках.

• F _N это нормальная сила .
• Уравновешивает силу гравитации вниз.
• Нормальная сила всегда перпендикулярна поверхности, на которой находится объект.
• Без него на вас действовала бы чистая сила, и вы бы ускорялись вниз.
• Это пример пары действие-противодействие, двух сил, которые равны, но противоположны друг другу.

Есть одна очень важная вещь, которую следует помнить, когда вы смотрите на пары действие-противодействие.

• Две силы, на которые вы смотрите, действуют на разные объекты!
• Если вы исследуете то, что вы считаете силами действия-противодействия, и обе они действуют на один и тот же объект, это не так.
• В приведенном выше примере F _g — это человек, давит на землю, а F _N — это земля, давит на человека.

Вот несколько примеров сил действия-противодействия, которые зависят от объектов, находящихся в непосредственном контакте, что означает, что два вовлеченных объекта фактически касаются друг друга, чтобы воздействовать друг на друга. Они называются «контактными силами».

1. Действие: шины автомобиля давит на дорогу…
   Реакция: дорога давит на шины.
2. Действие: во время плавания вы толкаете воду назад…
   Реакция: вода толкает вас вперед.

Пары действие-противодействие также могут возникать без трения или даже с объектами, не касающимися друг друга, что известно как « действие на расстоянии » силы …

1. Действие: ракета выталкивает выхлоп…
   Реакция: выхлоп выталкивает ракета вперед.

Одним из первоначальных аргументов в пользу того, что полет в космическом вакууме невозможен, было то, что не на что было бы напирать. Это действие-реакция объясняет, как ракета может летать в космосе, где нет воздуха, на который можно было бы натолкнуться.

2. Действие: земля притягивает мяч…
   Реакция: мяч притягивается к земле.

Как второй пример может быть правдой?!?

Нижние индексы часто используются парами, чтобы показать, что делают силы. Обозначение « _E F _b » следует читать как «сила Земли, действующая на шар».

• Существует пара сил действие-противодействие, заданная формулой _E F _b = _b F _E
• Мы знаем, что мяч будет двигаться по направлению к Земле со скоростью 9,81 м/с ² , но ускоряется ли Земля по направлению к мячу с такой же скоростью?
  • Если это правда, вы должны ожидать, что земля будет постоянно подпрыгивать к падающим предметам.
• Внимательно запомните второй закон Ньютона (F = ma).
  • В этом примере силы равны, но масса земли значительно больше шара!
  • Земля имеет большую инерцию, чем мяч.
  • Предположим, что мяч имеет массу 2,00 кг, и произведем некоторые расчеты…

Сила Земли, действующая на шар

_E F _b = ma = мг

= (2,00 кг) (9,81 м/с ² )

90 031 Е Ф _б = 19,6 N

Это сила Земли, действующая на мяч, но, согласно 3-му закону Ньютона, это также сила мяча, действующая на Землю.

_Е Ф _b = _b F _E = 19,6N

Ускорение Земли из-за шара

_b F _E = ma

9000 2 а = _б F _Е / м = 19,6Н / 5,98e24 кг

a = 3,28e-24 м/с ²

Это настолько малое ускорение Земли по направлению к шару, что его даже нельзя измерить. Мы видим, что хотя силы равны, ускорения не обязательно должны быть одинаковыми!

Сэр Исаак Ньютон ненавидел свои собственные теории о том, что гравитация является силой, «действующей на расстоянии». Он так твердо верил, что должен существовать какой-то материал, который соединяет объекты, обладающие гравитационным притяжением друг к другу, что был одним из первых ученых, серьезно предположивших, что существует таинственная субстанция, называемая эфиром (иногда пишется как эфир), соединяющая все объекты. во вселенной.

Пример 1: Когда винтовка стреляет пулей, сила, с которой винтовка действует на пулю, точно такая же (но в противоположном направлении), как и сила, с которой пуля действует на винтовку… поэтому винтовка «отбрасывает». Пуля имеет массу 15 г, а масса винтовки 6,0 кг. Пуля покидает ствол винтовки длиной 75 см со скоростью 70 м/с.

а) Определить ускорение пули.

Рассчитайте это, используя формулу кинематики, например v _f ² = v _i ² + 2ad и вы должны получить 3,3e3 м/с ² .

б) Определить усилие, действующее на пулю.

F = ma позволит вам рассчитать ответ 49 N.

c) Определить ускорение винтовки.

Снова используйте F = ma, но убедитесь, что вы используете правильную массу. Вы должны получить 8,2 м/с ² .

г) Объясните , почему пуля ускоряется больше, чем винтовка, если силы одинаковы.

Несмотря на то, что на них действует одинаковая сила, каждый из них имеет разную массу (и, следовательно, разную инерцию).

Пример 2: Если я толкаю газонокосилку, она давит на меня с равной, но противоположной силой. Объясните , почему бы нам обоим не замолчать.

• Ответ заключается в том, что эти силы действуют на разные тела (и есть и другие силы, которые следует учитывать).
• Для газонокосилки не имеет значения, что на меня действует сила… газонокосилке важно лишь то, что на нее действует сила, поэтому она начинает двигаться!
• Еще одна пара действие-противодействие, которую вам нужно учитывать, это то, что я толкаю землю назад, а она толкает меня вперед.
  

3-й закон Ньютона

3-й закон Ньютона

Рассмотрим следующие ситуации:

• Вы с другом сидите на стульях с роликами. У вас обоих есть оторвите ноги от земли и своими ногами упираетесь в ноги своего друга стул. Ваш друг начинает отдаляться от вас, и вы начинаете двигаться подальше от своего друга. Вы оба ускоряетесь. Направление вашего ускорения противоположно направлению ускорения вашего друга ускорение.
• Вы оба протягиваете руки, хватаете своего друга и тянете его к вам. Он ускоряется к вам, и вы ускоряетесь к ему. Вы снова ускоряетесь.

Происходящее является следствием третьего закона Ньютона .

Для каждой силы, объект действует на другой объект, существует сила, равная по величине, но противоположное по направлению воздействие второго объекта на первый объект. Силы являются результатом взаимодействия.

Ты тянешь меня, я тяну тебя. Если других сил нет, я устремлюсь к вам. У меня ускорение величина силы, деленная на моей массы . Вы ускорите ко мне. Ваше ускорение имеет величину силы, деленную на вашей массы .

Вопрос:

Ты давишь на стол, стол давит на тебя. Ты ускориться от стола. Почему стол не ускоряется от вас?

• Если стол на роликах, он будет ускоряться от вас. Если таблица очень массивен, величина его ускорения будет намного меньше, чем величина вашего ускорения. Если не на роликах, то усилие на него также действует трение покоя, и векторная сумма двух силы равны нулю.

Стоя на очень скользкой поверхности или на скейтборде, вы бросаете тяжелый объект от вас в северном направлении. Для этого нужно приложить воздействие на объект в северном направлении. Объект действует с силой на вы, который имеет равную величину, но указывает на юг. Вы ускоряетесь на юг.

Третий закон Ньютона также называют законом Ньютона. действие и противодействие . Для каждой силы действия существует сила противодействия, равная по модулю и противоположные по направлению.   Объекты взаимодействуют.

Сила действия и противодействия всегда действуют на разные объекты.
Две силы, действующие на один и тот же объект, даже если они имеют одинаковую величина и точка в противоположном направлении никогда не образуют пару действие-противодействие.

Проблема:

Яблоко массой 0,2 кг лежит на столе в равновесии.
а) Какие силы действуют на него? Укажите их величину и направление.
б) Какова сила реакции на каждую из сил, действующих на яблоко?
(c) Что такое пары действие-реакция?

Решение:

• Обоснование:
  (a) Силы, действующие на яблоко, равны его весу W = mg = 1,96 Н, направленному вниз и нормальное усилие, указанное в таблице F _Н = 1,96 Н указывая вверх. Суммарная сила, действующая на яблоко, равна нулю.
  (b) Сила реакции на W представляет собой силу F _WR = 1,96 Н, направленную вверх и действующую в центре Земли. (Земля тянет яблоко и яблоко тянет землю.)
  Реакцией на F _N является сила F _NR = 1,96 Н, направленная вниз действует на столе. (Стол давит на яблоко, яблоко давит на стол.)
  (c) Пары действие-реакция: W – F _WR и N – F _NR .

Пары действие-противодействие представляют собой силы равной величины и противоположного направления которые действуют на разных объектов . Они никогда не действуют на один и тот же объект.

Третий закон Ньютона говорит нам, что силы — это взаимодействия. Объект не может воздействовать на другой объект, не чувствуя самой силы реакции. Сила реакции имеет ту же величину и направлена ​​в противоположном направлении. как сила, с которой объект действует на другой объект. Что и объект делает в результате действия силы реакции зависит не только от силы реакции, а на результирующую силу, действующую на объект. Чистая сила сумма силы реакции и всех других сил, действующих на объект.

Третий закон Ньютона прост, силы — это взаимодействия.
Второй закон Ньютона сложен, F _net = m a , потому что вам нужно знать все силы, и вам нужно сложить их в виде векторов. Только затем можете ли вы выяснить, ускоряется ли объект, и если да, то насколько и в каком направление.

Примеры пар действие-противодействие:

• Ружье давит на пулю — пуля давит на ружье (отдача)
• Игрок бросает мяч вперед, прикладывая силу к мячу рукой — мяч отталкивается от руки
• Ученик тянет за парту — стол тянет за собой ученика (вот как вы может «тянуть» себя вперед.)
• Земля притягивает человека (гравитация) — человек притягивает Землю

Примеры сил, имеющих одинаковую величину и противоположное направление, но НЕ пары действие-противодействие.

• Земля притягивает объект к полу — нормальная сила толкает человека вверх и предотвращает падение человека на пол (обе силы действуют на тот же объект. )
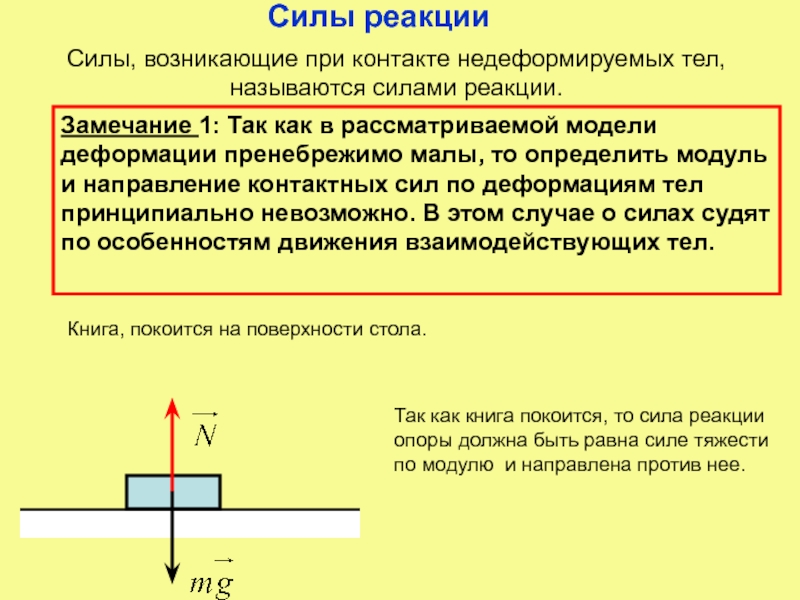• Человек 1 толкает объект влево — человек 2 толкает объект влево вправо, но объект остается в покое (обе силы действуют на один и тот же объект.)
• Автомобиль движется с постоянной скоростью. Мотор тянет машину вперед — точки трения в обратном направлении (обе силы действуют на одну и ту же объект.)

Внешняя ссылка: Физика Футбол — Третий закон движения Ньютона — YouTube

---

Встроенный вопрос 2

Устройство, используемое с 1940-х годов для измерения толчка или отдачи тела из-за к ударам сердца – «баллистокардиограф». Какой физический принцип(ы) участвуют здесь для измерения силы сердечного сокращения? Как может мы конструируем такое устройство?

Обсудите это со своими сокурсниками на форуме!

Встроенный вопрос 3

Предположим, вы держите в руке чашку кофе. Определить все силы, действующие на чашку, и реакция на каждую силу.

Обсудите это со своими сокурсниками на форуме!

---

Растяжение и сжатие

Предположим, что две противоборствующие команды и противоборствующая команда тянут веревку в противоположные направления. Есть ли результирующая сила на веревке?

Если веревка ускоряется в сторону одной из команд, то нет есть ненулевая результирующая сила. F = m a . Чистая сила представляет собой векторную сумму силы тяжести и сил приложили обе команды.
Противостоящая команда, так как веревка начинает ускоряться в их направление.

Если веревка не ускоряется, даже при этом каждая команда тянет изо всех сил может тогда нет чистой силы, действующей на веревку. Однако есть напряжение в веревка. Натяжение возникает из-за того, что на разные части тела действуют разные силы. тело. Напряжение может сломать вещи. Чистая сила, т.е. та же самая сила действуя на все части тела, не может сломать вещи.
Если вместо потянув за веревку, две команды толкают тяжелый камень, но камень не двигаться, то снова результирующая сила, действующая на камень, равна нулю. Однако теперь порода находится под сжатием .

Натяжение T является скаляром. Он определяется как величина сила, с которой натянутая веревка тянет все, к чему она прикреплена. Эту силу часто обозначают Т . Направление Т зависит от того, какой конец веревки рассматривается.

Суммарная сила, действующая на объект, всегда является векторной суммой всех сил. воздействуя на объект. Ускорение тела направлено в сторону эта чистая сила и имеет величину a = (чистая сила / масса объекта).

Возникает напряжение с выдвинутым объектом. На тело действуют две силы в разные точки, потянув в противоположном направлении. Чистая сила равна нулю две силы имеют равные величины.
Внутренние «контактные силы» удерживают объект от разрушения, но объект под напряжением. Обычно он немного растягивается, и если напряжение становится слишком большим, он ломается.
Сжатие также происходит с расширенным объектом. Две силы действуют на объект в разных точках, толкая в противоположном направлении, сжимая объект.

Проблема:

Блок весом 15 фунтов лежит на полу. (Примечание: фунт – это единица силы, вес блока 15 фунтов)
(a)  Что сила, с которой пол действует на блок?
(b) Если веревка привязана к блок и проходят вертикально над шкивом, а другой конец прикреплен к свободно висящий груз массой 10 фунтов, какова сила, с которой пол действует на 15-фунтовый блок?
(c) Если мы заменим 10-фунтовый груз в части (b) 20-фунтовый вес, какова сила, с которой пол действует на 15-фунтовый блок?

Решение:

• Обоснование:
  (а) Блок находится в состоянии покоя, результирующая сила равна нулю. Вес блок находится на 15 фунтов вниз. Таким образом, пол должен оказывать усилие 15 фунтов. вверх.
  (б) Блок по-прежнему находится в состоянии покоя. Вес 15 фунтов вниз, веревка тянет 10 фунтов вверх. из-за натяжения троса. Поэтому пол должен приложить силу 5 фунтов вверх.
  (c)  Вес на 15 фунтов направлен вниз, веревка тянет вверх с силой 20 фунтов из-за натяжения веревки. Блок будет ускоряться вверх, так как результирующая сила направлена ​​вверх.