Помогите решить / разобраться (Ф)
| wolf.ram |
| ||
04/06/10 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
wolf. ram ram |
| ||
04/06/10 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
wolf. ram ram |
| ||
04/06/10 |
| ||
| |||
| ukku |
| ||
20/04/11 |
| ||
| |||
| wolf.ram |
| ||
04/06/10 |
| ||
| |||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 8 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Сила реакции опоры: определение и формула
Статика — один из разделов современной физики, который изучает условия нахождения тел и систем в механическом равновесии.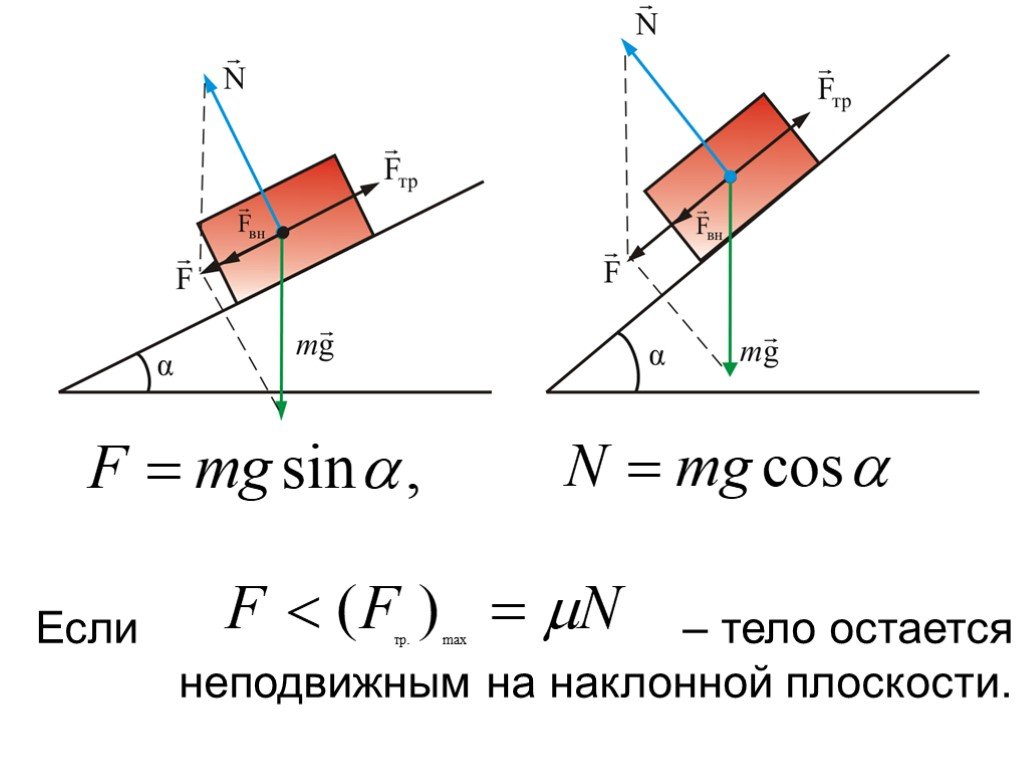 Для решения задач на равновесие важно знать, что такое сила реакции опоры. Данная статья посвящена подробному рассмотрению этого вопроса.
Для решения задач на равновесие важно знать, что такое сила реакции опоры. Данная статья посвящена подробному рассмотрению этого вопроса.
Второй и третий законы Ньютона
Прежде чем рассматривать определение силы реакции опоры, следует вспомнить о том, что вызывает движение тел.
Причиной нарушения механического равновесия является действие на тела внешних или внутренних сил. В результате этого действия тело приобретает определенное ускорение, которое вычисляется с помощью следующего равенства:
F = m*a
Эта запись известна как второй закон Ньютона. Здесь сила F является результирующей всех действующих на тело сил.
Если одно тело воздействует с некоторой силой F1¯ на второе тело, то второе оказывает действие на первое с точно такой же по абсолютной величине силой F2¯, но она направлена в противоположном направлении, чем F1¯. То есть справедливо равенство:
F1¯ = -F2¯
Эта запись является математическим выражением для третьего ньютоновского закона.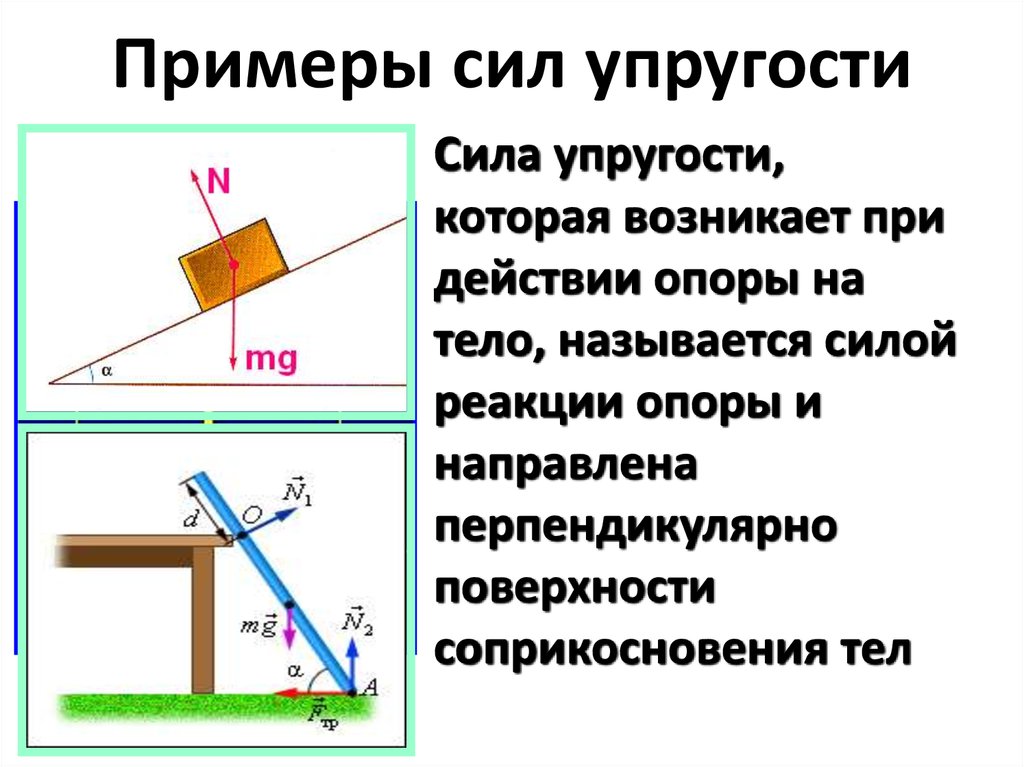
При решении задач с использованием этого закона школьники часто допускают ошибку, сравнивая эти силы. Например, лошадь везет телегу, при этом лошадь на телегу и телега на лошадь оказывают одинаковые по модулю силы. Почему же тогда вся система движется? Ответ на этот вопрос можно правильно дать, если вспомнить, что обе названные силы приложены к разным телам, поэтому они друг друга не уравновешивают.
Сила реакции опоры
Сначала дадим физическое определение этой силы, а затем поясним на примере, как она действует. Итак, силой нормальной реакции опоры называется сила, которая действует на тело со стороны поверхности. Например, мы поставили стакан с водой на стол. Чтобы стакан не двигался с ускорением свободного падения вниз, стол воздействует на него с силой, которая уравновешивает силу тяжести. Это и есть реакция опоры. Ее обычно обозначают буквой N.
Сила N — это контактная величина. Если имеется контакт между телами, то она появляется всегда. В примере выше значение величины N равно по модулю весу тела. Тем не менее это равенство является лишь частным случаем. Реакция опоры и вес тела — это совершенно разные силы, имеющие различную природу. Равенство между ними нарушается всегда, когда изменяется угол наклона плоскости, появляются дополнительные действующие силы, или когда система движется ускоренно.
Тем не менее это равенство является лишь частным случаем. Реакция опоры и вес тела — это совершенно разные силы, имеющие различную природу. Равенство между ними нарушается всегда, когда изменяется угол наклона плоскости, появляются дополнительные действующие силы, или когда система движется ускоренно.
Сила N называется нормальной потому, что она всегда направлена перпендикулярно плоскости поверхности.
Если говорить о третьем законе Ньютона, то в примере выше со стаканом воды на столе вес тела и нормальная сила N не являются действием и противодействием, поскольку обе они приложены к одному телу (стакану с водой).
Физическая причина появления силы N
Как было выяснено выше, сила реакции опоры препятствует проникновению одних твердых тел в другие. Почему появляется эта сила? Причина заключается в деформации. Любые твердые тела под воздействием нагрузки деформируются сначала упруго. Сила упругости стремится восстановить прежнюю форму тела, поэтому она оказывает выталкивающее воздействие, что проявляется в виде реакции опоры.
Если рассматривать вопрос на атомном уровне, то появление величины N — это результат действия принципа Паули. При небольшом сближении атомов их электронные оболочки начинают перекрываться, что приводит к появлению силы отталкивания.
Многим может показаться странным, что стакан с водой способен деформировать стол, но это так. Деформация настолько мала, что невооруженным глазом ее невозможно наблюдать.
Как вычислять силу N?
Сразу следует сказать, что какой-то определенной формулы силы реакции опоры не существует. Тем не менее имеется методика, применяя которую, можно определить N для совершенно любой системы взаимодействующих тел.
Методика определения величины N заключается в следующем:
- сначала записывают второй закон Ньютона для данной системы, учитывая все действующие в ней силы;
- находят результирующую проекцию всех сил на направление действия реакции опоры;
- решение полученного уравнения Ньютона на отмеченное направление приведет к искомому значению N.

При составлении динамического уравнения следует внимательно и правильно расставлять знаки действующих сил.
Найти реакцию опоры можно также, если пользоваться не понятием сил, а понятием их моментов. Привлечение моментов сил справедливо и является удобным для систем, которые имеют точки или оси вращения.
Далее приведем два примера решения задач, в которых покажем, как пользоваться вторым ньютоновским законом и понятием момента силы для нахождения величины N.
Задача со стаканом на столе
Выше уже был приведен этот пример. Предположим, что пластиковый стакан объемом 250 мл наполнен водой. Его поставили на стол, а сверху на стакан положили книгу массой 300 грамм. Чему равна сила реакции опоры стола?
Запишем динамическое уравнение. Имеем:
m*a = P1 + P2 — N
Здесь P1 и P2 — вес стакана с водой и книги соответственно. Поскольку система находится в равновесии, то a=0. Учитывая, что вес тела равен силе тяжести, а также пренебрегая массой пластикового стакана, получаем:
m1*g + m2*g — N = 0 =>
N = (m1 + m2)*g
Учитывая, что плотность воды равна 1 г/см3, и 1 мл равен 1 см3, получаем согласно выведенной формуле, что сила N равна 5,4 ньютона.
Задача с доской, двумя опорами и грузом
Доска, массой которой можно пренебречь, лежит на двух твердых опорах. Длина доски равна 2 метра. Чему будет равна сила реакции каждой опоры, если на эту доску посередине положить груз массой 3 кг?
Прежде чем переходить к решению задачи, следует ввести понятие момента силы. В физике этой величине соответствует произведение силы на длину рычага (расстояние от точки приложения силы до оси вращения). Система, имеющая ось вращения, будет находиться в равновесии, если суммарный момент сил равен нулю.
Возвращаясь к нашей задаче, вычислим суммарный момент сил относительно одной из опор (правой). Обозначим длину доски буквой L. Тогда момент силы тяжести груза будет равен:
M1 = -m*g*L/2
Здесь L/2 — рычаг действия силы тяжести. Знак минус появился потому, что момент M1 осуществляет вращение против часовой стрелки.
Момент силы реакции опоры будет равен:
M2 = N*L
Поскольку система находится в равновесии, то сумма моментов должна быть равной нулю. Получаем:
Получаем:
M1 + M2 = 0 =>
N*L + (-m*g*L/2) = 0 =>
N = m*g/2 = 3*9,81/2 = 14,7 Н
Заметим, что от длины доски сила N не зависит.
Учитывая симметричность расположения груза на доске относительно опор, сила реакции левой опоры также будет равна 14,7 Н.
изгиб — Какая сила создает реактивный момент в неподвижной опоре
Задавать вопрос
спросил
Изменено 1 год, 4 месяца назад
Просмотрено 614 раз
$\begingroup$
Вопрос: Какая сила вызывает реактивный момент в неподвижном соединении?
Давайте рассмотрим очень простой пример: балка, один конец которой соединен неподвижной опорой со стеной.
Я так понимаю, что в точке А будет вертикальная сила реакции, горизонтальная сила реакции и момент реакции. Насколько я понимаю, момент относительно оси всегда вызывается силой . Какая сила F вызывает реактивный момент?
Ориентируясь на этот пример, предположим F — сила горизонтальной реакции. Из условия равновесия сил вдоль направления x получаем, что эта сила имеет нулевую величину и, следовательно, не может создавать реактивный момент.
Предположим, F — вертикальная сила реакции. По-видимому, когда мы разрезаем балку в точке C и применяем условие равновесия моментов в точке C, мы должны учитывать как момент реакции, так и момент, создаваемый вертикальной силой реакции , что указывает на то, что момент, создаваемый вертикальной реакцией сила и момент реакции в точке А — это два разных момента, вызванные разными силами.
Итак, в заключение, если момент в точке А не вызван ни вертикальной, ни горизонтальной силой реакции, то какой силой он вызван?
- моменты
- изгиб
$\endgroup$
4
$\begingroup$
Я интерпретировал ваш вопрос как 2 отдельных запроса.
Какая фундаментальная физика заставляет неподвижную опору создавать момент вокруг центральной оси балки?
Как рассчитать внутренние силы в сечении «С» балки
Q1:
Вы можете представить, что балка крепится к стене с помощью клея. Когда луч пытается повернуться, луч будет вдавливаться в стену снизу и притягиваться к стене сверху клеем. Аналогичный процесс происходит, если балка прикручивается, приваривается или прикручивается к стене. Часть стенки внизу находится в состоянии «сжатия», и сжимаемый материал пытается расшириться до своего первоначального размера и, следовательно, помогает приложить силу, необходимую для вращения балки вокруг своей оси (момент).
Имейте в виду; >Чистая< сила в точке реакции в направлении х по-прежнему равна 0, потому что всасывание сверху и выталкивание снизу в сумме составляют ноль (0) ньютонов в направлении х.
Q2:
Вот окончательное решение для разреза сечения «С» на расстоянии 1 метра от балки. ПОЖАЛУЙСТА, имейте в виду, что вы должны убедиться, что вы полностью понимаете, как я рассчитал здесь все силы и моменты. По сути, вы хотите разрезать балку и убедиться, что сумма сил, воздействующих на (обе) балку (балки), и сумма моментов равна 0, как и для других задач статики. Опять же, новая точка разворота «фиксирована»
ПОЖАЛУЙСТА, имейте в виду, что вы должны убедиться, что вы полностью понимаете, как я рассчитал здесь все силы и моменты. По сути, вы хотите разрезать балку и убедиться, что сумма сил, воздействующих на (обе) балку (балки), и сумма моментов равна 0, как и для других задач статики. Опять же, новая точка разворота «фиксирована»
Внутренний момент балки на расстоянии 1 м от точки А равен 5 Н·м, так как при статическом равновесии:
$\Sigma Fx = 0; \Sigma F_y = 0 = F_{c_{y}} — 10(N)$
$\Sigma M = 0 = -10(N) * .5(m) + M_c$
$M_c = 5Nm$
$\endgroup$
7
$\begingroup$
момент в точке A представляет собой сумму вклада всех малых дифференциальных моментов dx по длине балки.
Его можно упростить как момент полной нагрузки, действующей в его ЦТ.
$$M_A=10N*2*1m=20Nm$$
Думаю, вы путаете момент свободного тела в случайной точке с моментом в точке A.
$\endgroup$
4
$\begingroup$
ИМХО вы путаете «момент силы относительно точки А», с «моментом реакции» который развивается при опоре конструкции, а точнее как они рассчитываются. Хотя они связаны, это не одно и то же.
Первое — очень фундаментальное понятие в физике. Момент силы равен произведению силы на расстояние точки от носителя силы (коллинеарная линия к силе).
Развивающийся реактивный момент создается конструкцией. Хотя в статике мы предполагаем жесткие конструкции (т. е. малые или несуществующие смещения), в реальной жизни все конструкции деформируются. Деформация конструкций может оказывать значительное влияние на конструкцию.
К чему я пытаюсь прийти, так это к тому, что «несущая конструкция, а также нагрузка определяют реакцию опоры».
Дополнительно по части вашего вопроса
По-видимому, когда мы разрезаем балку в точке C и применяем условие равновесия моментов в точке C, мы должны учитывать как момент реакции, так и момент, создаваемый вертикальной силой реакции, что указывает на то, что момент, создаваемый вертикальной силой реакции и момент реакции в точке А — это два разных момента, вызванных разными силами.
Это предложение неверно на многих уровнях, поэтому было бы лучше, если бы вы действительно сделали математику, чтобы мы могли сказать вам, где вы ошиблись. Я попытаюсь объяснить это на небольшом примере: предположим, что C находится прямо посередине луча в вашем посте.
В этом случае секция CB имеет длину 1 м, а общая поперечная сила на ней равна 10 Н. Реакция, которая развивается на C, основана на этих значениях, поэтому на C действует поперечная сила 10 Н и изгиб 5 Нм.
На участке АС длина опять 1м, а суммарная поперечная сила на участке АС 10Н, однако на участке С также присутствуют реакции от участка СВ. Эти силы представляют собой поперечную силу 10 Н и изгиб 5 Нм (с направлением, противоположным указанному выше). Таким образом, хотя в точке С имеется разрез, силы реакции, развивающиеся в точке С, таковы, что вся конструкция находится в статическом равновесии.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Глава 6, Вопрос 1PP | Решения для инженерной механики Хиббелера
Шаг 1
Нам даны две фермы, каждая из которых поддерживается штифтом и роликовой опорой.
Нас просят рассчитать силы реакции на опорах и нарисовать диаграммы свободного тела шарнира A, B и C.
Шаг 2 ферма.
Здесь ${A_y}$ — сила реакции в точке A, ${D_x}$ — горизонтальная сила реакции на опоре D, ${D_y}$ — вертикальная сила реакции на опоре D.
Применить уравнение равновесия для момента относительно точки D:
\[\begin{array}{c} \sum {{M_D}} = 0\\ — {A_y} \times 4\;{\rm{m} } + 400\;{\rm{N}} \times 2\;{\rm{m}} = 0\\ {A_y} = \frac{{400\;{\rm{N}} \times 2\ ;{\rm{m}}}}{{4\;{\rm{m}}}}\\ {A_y} = 200\;{\rm{N}} \end{массив}\]
Применить уравнение равновесия сил в горизонтальном направлении:
\[\begin{array}{c} \sum {{F_x}} = 0\\ {D_x} = 0 \end{array}\]
Применить уравнение равновесия сил в вертикальном направлении:
\[\begin{array}{c} \sum {{F_y}} = 0\\ {A_y} + {D_y} — 400\;{\rm{N}} = 0\\ {D_y} = 400 \;{\rm{N}} — {A_y} \end{array}\]
Подставьте значение ${A_y}$ в приведенное выше уравнение:
\[\begin{array}{c} {D_y } = 400\;{\rm{N}} — 200\;{\rm{N}}\\ = 200\;{\rm{N}} \end{массив}\]
Рассмотрим каждый элемент в напряжении .
Нарисуйте диаграмму свободного тела соединения A.
Здесь ${F_{AB}}$ и ${F_{AE}}$ — силы в элементах AB и AE.
Нарисуйте диаграмму свободного тела соединения B.
Здесь ${F_{BA}}$ — сила в стержне AB, ${F_{BC}}$ — сила в стержне BC, а ${ F_{BE}}$ — усилие в элементе BE.
Нарисуйте диаграмму свободного тела соединения C.
Здесь ${F_{BC}}$ — сила в стержне BC, ${F_{DC}}$ — сила в стержне DC, а $ {F_{EC}}$ — сила в члене EC.
Этап 3
Часть (b)
Нарисуйте схему фермы в свободном виде.
Здесь ${A_y}$ — сила реакции в точке A, ${C_x}$ — горизонтальная сила реакции на опоре C, ${C_y}$ — вертикальная сила реакции на опоре C.
Примените уравнение равновесия для момента относительно точки C:
\[\begin{array}{c} \sum {{M_C}} = 0\\ — {A_y} \times 4\;{\rm{m}} + 600\;{\rm{N}} \times 2\;{\rm{m}} = 0\\ {A_y} = \frac{{600\;{\rm{N}} \times 2\;{ \rm{m}}}}{{4\;{\rm{m}}}}\\ {A_y} = 300\;{\rm{N}} \end{массив}\]
Применить уравнение равновесия сил в горизонтальном направлении:
\[\begin{array}{c} \sum {{F_x}} = 0\\ {C_x} = 0 \end{array}\]
Применить уравнение равновесия сил в вертикальном направлении:
\[\begin{array}{c} \sum {{F_y}} = 0\\ {A_y} + {C_y} — 600\;{\rm{N}} = 0\\ {C_y} = 600\; {\rm{N}} — {A_y} \end{array}\]
Подставьте значение ${A_y}$ в приведенное выше уравнение:
\[\begin{array}{c} {C_y} = 600\;{\rm{N}} — 300\;{\rm{N}}\\ = 300\;{\rm{N}} \end{массив}\]
Рассмотрим каждый элемент в натяжении.
 2011, 13:37
2011, 13:37 
 04.2011, 16:24
04.2011, 16:24 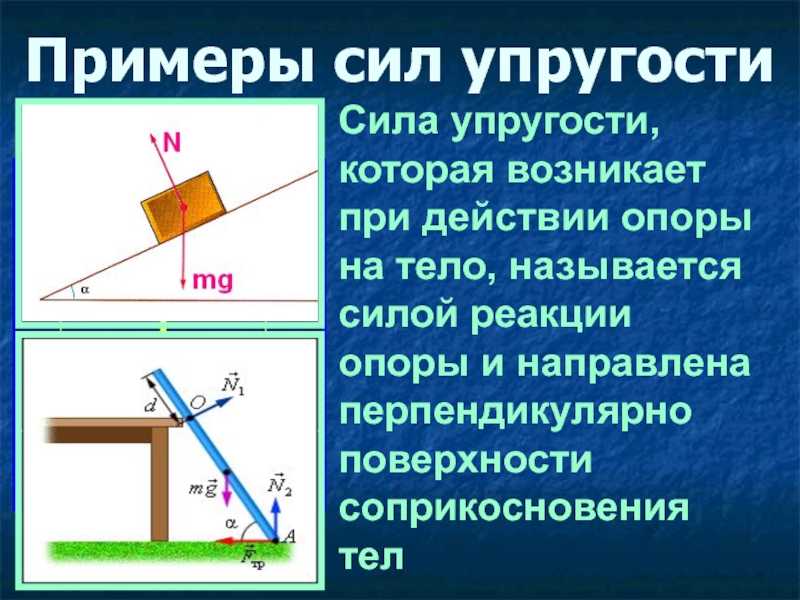 В данном случае сила взаимодействия равна силе реакции + сила трения. Сила взаимодействия между телами сонаправлена с , сила же реакции опоры такая же и соноправлена .
В данном случае сила взаимодействия равна силе реакции + сила трения. Сила взаимодействия между телами сонаправлена с , сила же реакции опоры такая же и соноправлена .