Сила реакция опоры: Что такое сила нормальной реакции? (статья)

Содержание

Алгоритм работы с силами — что это, определение и ответ

Прежде чем переходить к алгоритму, важно вспомнить направление сил в механике и от чего оно зависит:

Сила тяжести — всегда вертикально вниз

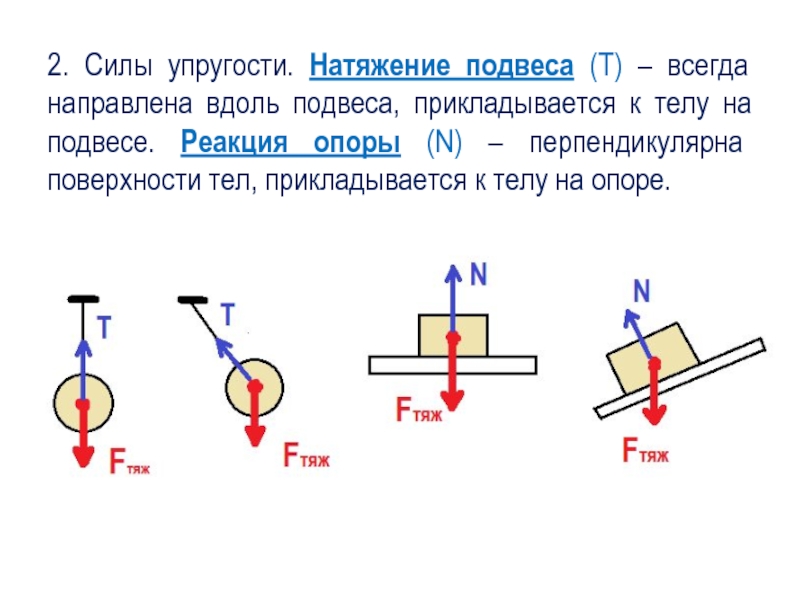
Сила реакции опоры — всегда перпендикулярно опоре (если тело касается опоры)

Сила натяжения нити: если тело подвешено с помощью нити — то от точки крепления нити к телу вдоль нити к ее центру; если тела связаны нитью — сила натяжения указывается от точек крепления нити к телам вдоль нити (или по касательной к нити, если нить не прямая) к центру нити.

Сила упругости — как и сила натяжения нити указывается от точки крепления пружины к телу. Направление — против деформации (если пружина сжата, сила упругости направлена от точки крепления сквозь тела, пытаясь разжать пружину, если растянута — от точки крепления противоположно телу, пытаясь сжать пружину).

Сила трения — всегда против скорости тела. Если тело покоится, то силу трения указывают против направления предполагаемого движения (на наклонной плоскости — против направления возможного соскальзывания тела с плоскости; на горизонтальной плоскости — против внешней силы, если такая имеется).

Сила давления — в сторону предполагаемого движения тела/поршня, если бы его ничто не удерживало.

Сила Архимеда — в сторону менее плотной среды. В большинстве задач направлена против силы тяжести.

Сила гравитационного притяжения тел — вдоль линии, соединяющей центры тел, направлена от одного тела к другому.

Теперь рассмотрим на практике расстановку и применение алгоритма.

Пример 1:

Тело расположено вплотную к вертикальной опоре, которая движется равноускорено так, как показано на рисунке. При каком ускорение тело не упадет? Коэффициент трения между телом и опорой принять равным 0,4.

Решение:

Тело не будет падать (то есть двигаться) при выполнении 1 закона Ньютона в проекции на вертикальную плоскость. \circ}.\) Трением между шаром и плоскостью пренебречь.

Решение:

Укажем действующие на шар силы и запишем 1 закон Ньютона (т.к. шар покоится):

\(\overrightarrow{N} + m\overrightarrow{g} + \overrightarrow{F_{арх}} + \overrightarrow{Т} = 0\)

Введем оси. Для удобства направим ось OX вдоль наклонной плоскости, а ось OY — перпендикулярно ей. Укажем угол альфа по условию.

Но также можешь указать накрестлежащий угол ддля угла альфа — он будет расположен между силой натяжения нити и силой Архимеда. После чего укажем вертикальный угол для этого угла (между силой тяжести и осью ОХ):

Теперь проецируем все силы на оси:

\(\left\{ \begin{matrix} OX:mg\cos\alpha — T — F_{арх} \bullet \cos\alpha = 0 \\ OY:N + F_{арх} \bullet \sin\alpha — mg \bullet \sin\alpha = 0 \\ \end{matrix} \right.\ \)

Выразим из первого уравнения силу натяжения нити, а из второго — силу Архимеда:

\(\left\{ \begin{matrix} T = mg\cos\alpha — F_{арх} \bullet \cos\alpha \\ F_{арх} = mg — \frac{N}{\sin\alpha} \\ \end{matrix} \right. \ \)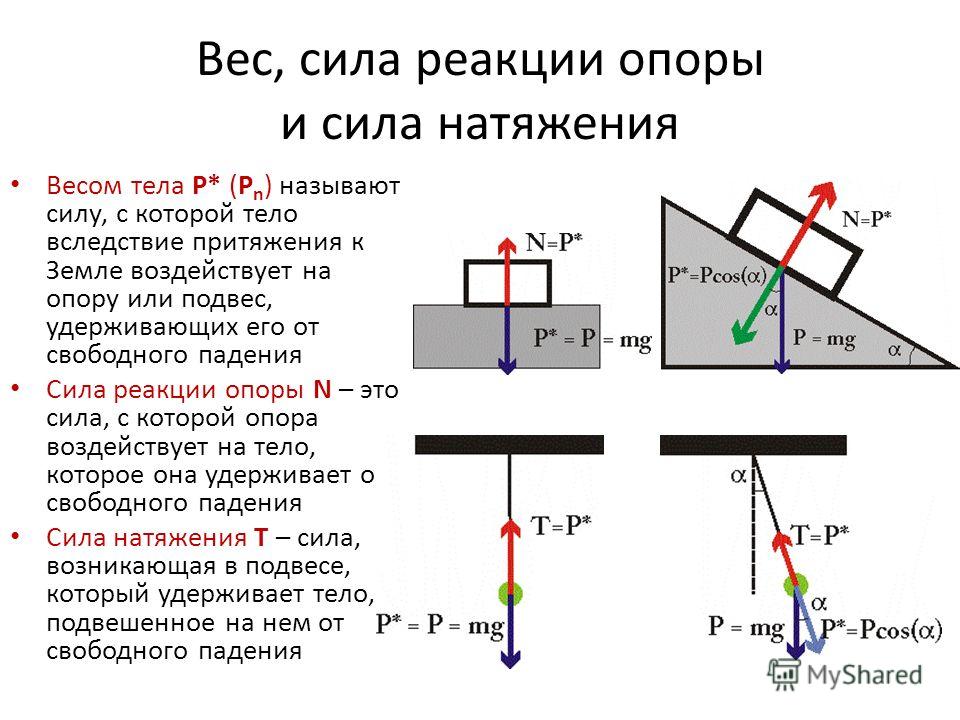

Подставляем второе уравнение в первое и завершаем задачу:

\(T = mg\cos\alpha — F_{арх} \bullet \cos\alpha = mg\cos\alpha — mg\cos\alpha + N \bullet ctg\left( \alpha \right) = N \bullet ctg\left( \alpha \right)\)

\(T = 19 \bullet 1 = 19\ Н\)

Ответ:19 Н

Физика — 10

Таблица 2.3. Некоторые характеристики тел Солнечной системы

Тела Солнечной системы	Ускорение свобод- ного падения на по- верхности (м/с²)	Среднее расстояние от Солнца (x10⁶км)	Масса (x10²⁴кг)	Диаметр экватора (км)
Меркурий	3,7	58	0,33	4 880
Венера	8,8	108	4,8	121
Земля	9,8	150	6	12 756
Марс	3,8	228	0,6	6 800
Юпитер	23,5	778	1 877	142 800
Сатурн	11,5	1 426	562	120 660
Уран	9,8	2 869	86	50 800
Нептун	11,6	4 496	102	49 600
Солнце	27,4	—	≈1 989 000	≈1 392 000
Луна	1,6	—	0,074	3 476

Обсуждение результатов:

Как изменяется масса астронавта на поверхности тел Солнечной системы?
На поверхности какого небесного тела вес астронавта наибольший (наименьший)? Почему?

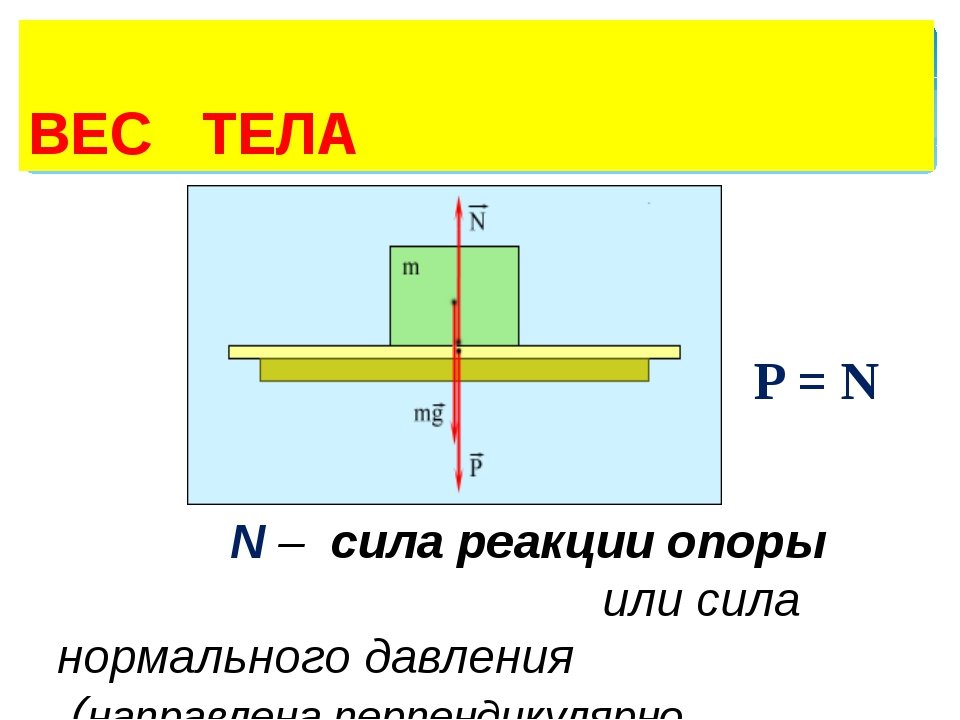
Вес.

● Вес — это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес. Вес тела обозначается буквой . Точка приложения веса находится на опоре (или подвесе). Вес направлен перпендикулярно поверхности опоры или вдоль подвеса. В зависимости от состояния тела его вес может изменяться или оставаться неизменным.

Случай, когда вес тела не меняется. Если тело находится в состоянии покоя или движется прямолинейно равномерно по горизонтальной поверхности, то его вес не изменяется. Почему?

Согласно III закону Ньютона, вес тела действует на опору и равен по модулю и противоположен по направлению силе реакции опоры . Сила реакции приложена к самому телу (b): (для удобства точка приложения силы реакции опоры смещается в центр тела).

Если тело на подвесе находится в состоянии покоя или вместе с подвесом движется прямолинейно равномерно, то, согласно III закону Ньютона, вес этого тела, действующий на подвес, равен по модулю и направлен противоположно силе натяжения нити .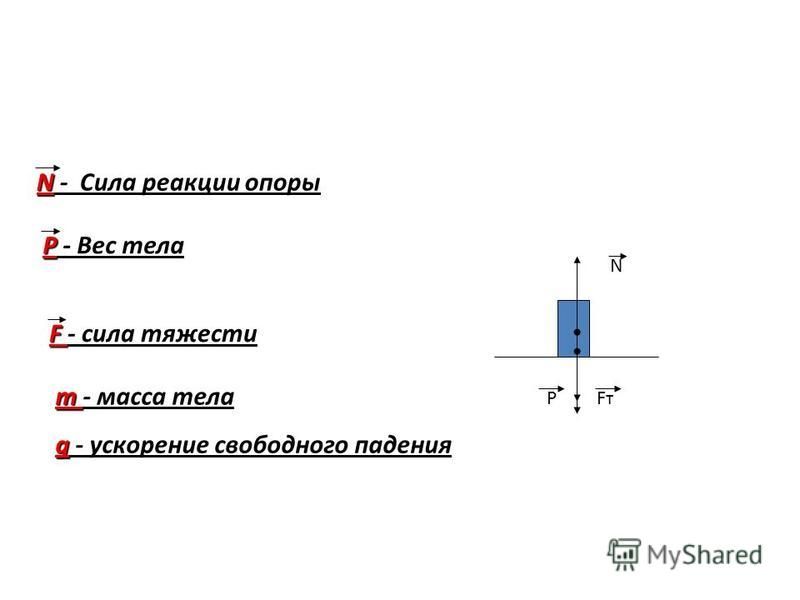

Сила натяжения прикладывается к самому телу (см: b )

Согласно II закону Ньютона, уравнение движения для тела, находящегося в состоянии покоя или прямолинейного равномерного движения на горизонтальной опоре, записывается в виде:

Принимая во внимание, что результирующая сила равна векторной сумме силы тяжести и силы реакции опоры, уравнение движения примет вид:

[Решено] Вертикальные опорные реакции RA и RB для данной балки

Вертикальные опорные реакции R _A и R _B для данной балки

Официальный доклад I за 2019 г. (состоялся 13 декабря 2020 г.)

Просмотреть все документы UPPSC AE >

R _A = 25 кН, R _B = 15 кН
R _{B 95003 1900} = 25 кН
R _A = 12,5 кН, R _B = 27,5 кН
RA = 27,5 кН, RB = 12,5 кН

Вариант 4: RA = 27,5 кН, RB = 12,5 кН

Free

CT 1: 1: кН = 12,5 кН

CT 1: Строительные материалы

6,9 тыс. пользователей

10 вопросов

20 баллов

12 минут

Концепция :

Сила сдвига является равнодействующей всех поперечных сил справа или слева от балки.
Изгибающий момент – результирующий момент в сечении под действием всех поперечных сил
либо слева, либо справа от сечения.

Расчет:

Указано

Интенсивность UDL = W1 = 10 кН/м, момент = M = 45 кН-M

∑ _A = 0, Момент около

∑ _a = 0,0.

= 10 × 4 × 4/2 + 45 — R _B × 10 = 0

= R _B = 12,5 кН

∑V = 0, принимая сумму всех вертикальных сил как 0

= R _A+ R _B = 10 × 4

= R _A = 40 — 12,5 =. 27,5 кН

Дополнительная информация

Наклон диаграммы поперечной силы = интенсивность распределенной нагрузки.

\(\frac{{dV}}{{dx}} = W\)

Sope на любом участке диаграммы изгибающего момента = поперечная сила на этом участке.

\(\frac{{dM}}{{dx}} = V\)

Точка обратного изгиба – это точка, в которой изгибающий момент меняет знак.
Точка изгиба это точка, где отклоненная форма балки изменяет свою кривизну.

Скачать решение PDF

Поделиться в WhatsApp

Последние обновления UPSC IES

Последнее обновление: 3 марта 2023 г.

Расписание экзаменов UPSC IES истекло! Основной экзамен состоится 25 июня 2023 года. 3 марта 2023 г. Союзная комиссия по государственной службе опубликовала результаты UPSC IES для предварительных экзаменов. Экзамен был проведен 19 февраля 2023 г. как для Paper I, так и для Paper II. Всего было освобождено 327 вакансий. Основной экзамен состоится 25 июня 2023 года. Кандидаты подали заявки в период с 14 сентября 2022 года по 4 октября 2022 года. Кандидаты должны соответствовать критериям приемлемости USPC IES, чтобы принять участие в наборе. Кандидаты должны попытаться пройти пробные тесты UPSC IES, чтобы повысить свою эффективность. Документы UPSC IES за предыдущий год можно скачать здесь.

Опорные реакции в балках из-за приложенной пары или момента

Пара сил

Пара определяется как две параллельные силы с одинаковой величиной , но противоположными по направлению, разделенные перпендикулярным расстоянием d.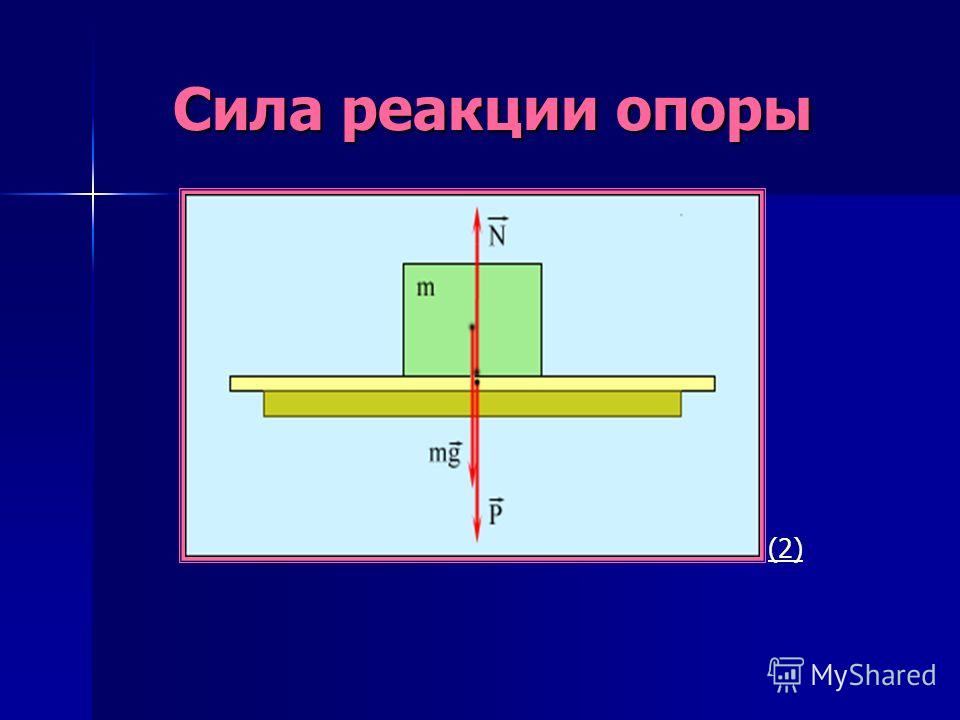

Чистый внешний эффект пары состоит в том, что результирующая сила равна нулю, а величина результирующего момента равна = F.d

Равнодействующая пары в любой точке всегда представляет собой чисто постоянный момент и равен

M = F d

пара против часовой стрелки 400 Нм и точечная нагрузка, как показано на рисунке. Рассчитайте опорные реакции

Решение:

Пусть вертикальная реакция на опоре A равна Ra, а на опоре B равна Rb.

Здесь вертикальные силы представляют собой направленные вверх реактивные силы Ra ,Rb и точечную направленную вниз нагрузку 1000 Н. Горизонтальная пара сил формируется как пара, и ее равнодействующая составляет момент 400 Н-м

Примените уравнение равновесия:

∑ fy = 0

RA+ RB-1000 = 0

RA+ RB = 1000 —— (1)

= 0

— 400 + 1000 х 4 — 6.Rb = 0

RB = 3600/6 = 600 N

Заменитель RB Значение в равенстве

в равенстве 1

Ra = 400N

Задача: 2,8

Свободно опертая балка несет пару M против часовой стрелки, как показано на рис.0172 RA и при поддержке B равен RB

Уравнение равновесия:

∑ FY = 0

RA+ RB = 0

RA+ RB = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0. )

Taking moments of the forces about end A,

∑ MA = 0

— M — L.Rb = 0

Rb = — M / L ( downward

реакция)
замена RB Значение в Equ.1
RA = + M/L ( Вверх Реакция ).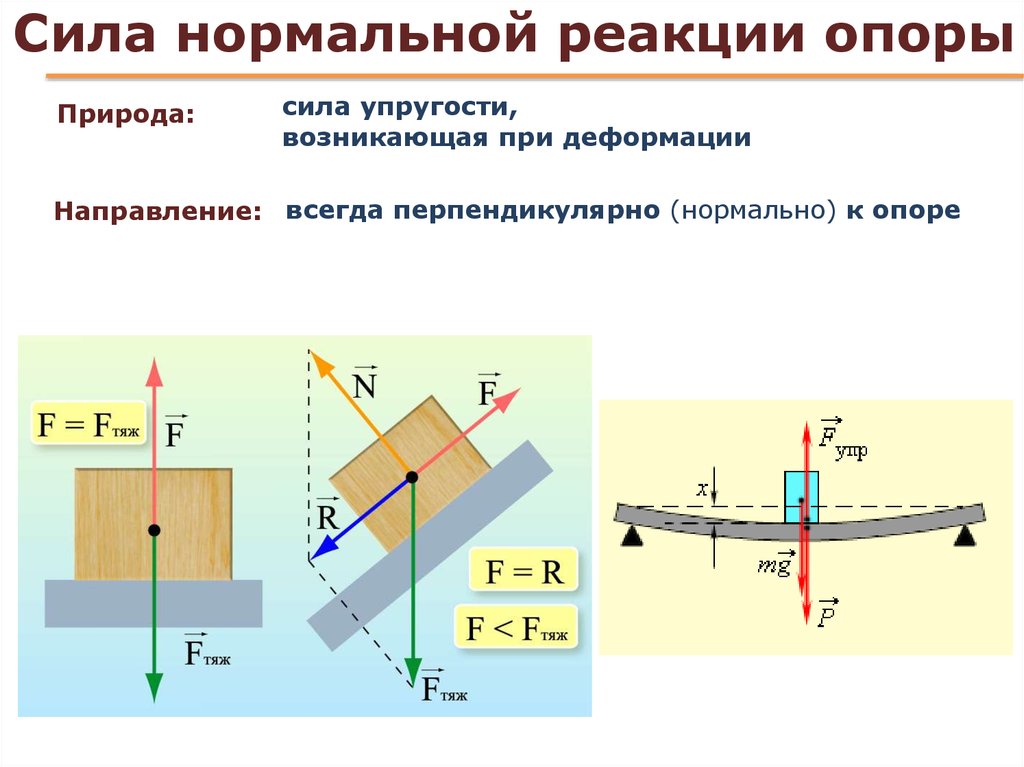 реакции не меняются поддержка реакции

Решение:
Пусть вертикальная реакция на опоре A равна Ra, а на опоре D равна Rd.
Применить уравнение равновесия:
∑ fy = 0
RA+ RD-4 = 0
RA+ RD = 4 KN —— (1)
Take Motment силы вокруг конца A,
∑ MA = 0
6 + 4×5 — 4.Rb   = 0
Rd   = 26/4 = 6,5 N ( Вверх Реакция)
Заместитель RD Значение в Equititute RD .
RA = -2,5 кН ( Вниз Реакция )
Присвоение:
Q 1. Определить. Обратите поддержку. СОДЕРЖА.
В 2. Определить опорные реакции свободно опертой консольной балки, нагруженной, как показано на рис. Q 3. Определите опорные реакции свободно опертой консольной балки, нагруженной, как показано на рис.
Популярные посты из этого блога
ПОРТАЛЬНЫЙ МЕТОД и КОНСОЛЬНЫЙ МЕТОД
Поведение конструкции под действием горизонтальных сил зависит от отношения ее высоты к ширине. Деформация в малоэтажных сооружениях, где высота меньше ширины, характеризуется преимущественно сдвиговыми деформациями. В высотном здании, где высота в несколько раз превышает его поперечные размеры, преобладает изгибающее действие. Для анализа конструкций, подверженных горизонтальному нагружению, у нас есть два метода. Портальный метод и консольный метод 1. ПОРТАЛЬНЫЙ МЕТОД Портальный метод представляет собой приблизительный анализ, используемый для анализа каркасов зданий, подверженных боковым нагрузкам, таким как ветровые нагрузки/сейсмические силы.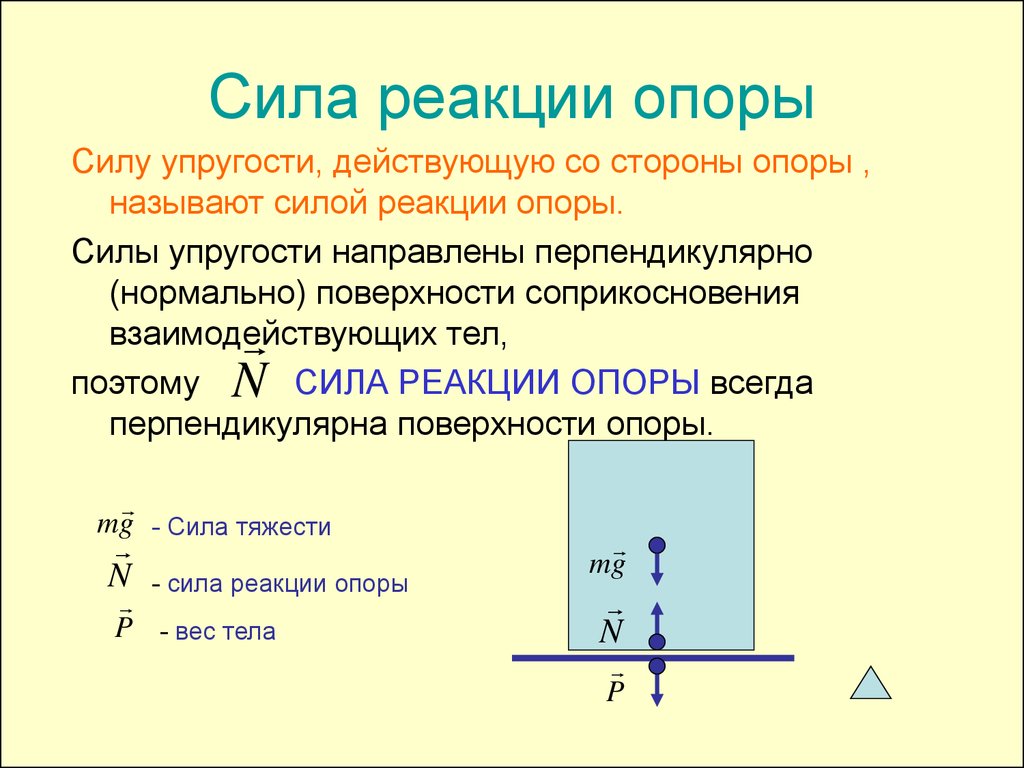 Поскольку деформации сдвига преобладают в малоэтажных конструкциях, метод делает упрощающие предположения относительно горизонтального сдвига в колоннах. Каждый пролет конструкции рассматривается как портальная рама, и горизонтальная сила распределяется между ними поровну. Допущения в портальном методе 1. Точки перегиба расположены на середине высоты каждого столбца выше 9-го столбца.0007
Связь между модулем упругости и модулем жесткости
Модуль упругости (E) Это отношение нормального напряжения к нормальной деформации в пределах предела упругости. Модуль упругости E = Нормальное напряжение/Нормальная деформация E = s/e Модуль жесткости (G) Это отношение между напряжением сдвига и деформацией сдвига в пределах предела упругости. Модуль жесткости G = напряжение сдвига/ деформация сдвига G = Ƭ / ø Соотношение между модулем упругости и модулем жесткости: рассмотрим сплошной куб PQRS , на который действует сила сдвига F. Пусть Ƭ   будет напряжением сдвига, возникающим на гранях PQ и RS благодаря этой силе сдвига.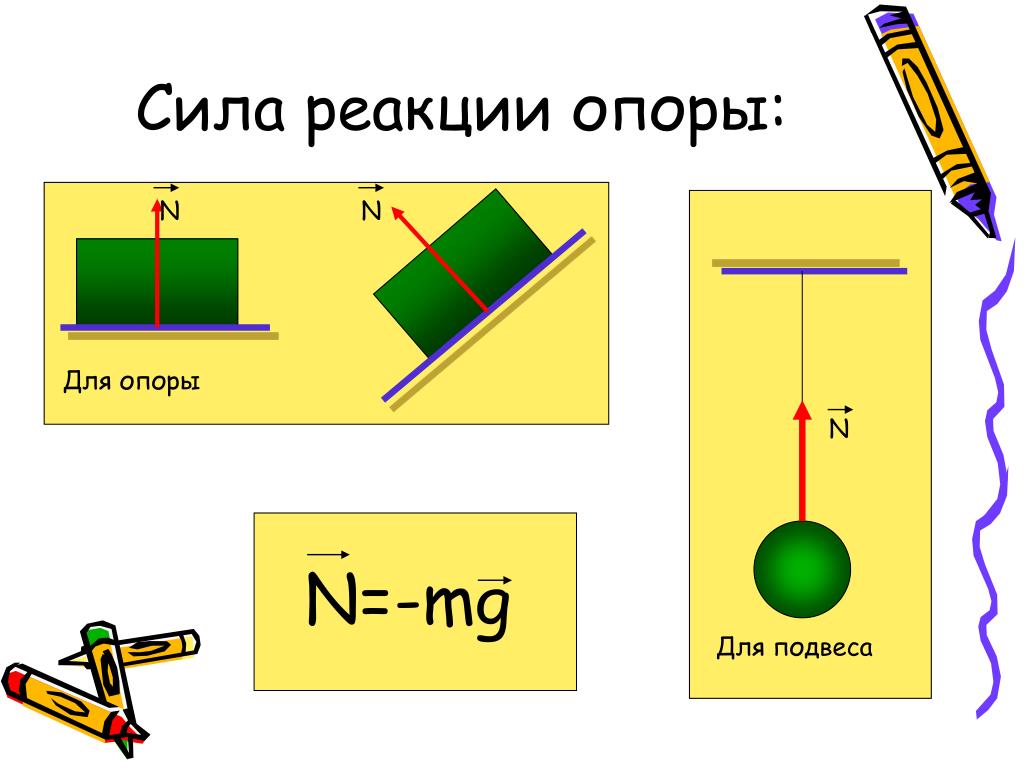 Дополнительное напряжение сдвига, возникающее в результате на вертикальных гранях PS и RQ, также одинаково и показано на рисунке как Ƭ Из-за чистой силы сдвига куб деформируется от PQRS до PQR’S’. Точка S переместилась в S’, а точка R переместилась в R’, как показано на рис. Деформация сдвига = угол деформации ø                ø = RR’/ RQ —(1) Деформация сдвига = напряжение сдвига / модуль жесткости
Прямые и изгибающие напряжения
Чаще всего элемент конструкции подвергается воздействию различных видов напряжений, действующих одновременно. К таким напряжениям относятся осевые, сдвигающие, изгибные и крутильные. Метод суперпозиции используется для определения совместного действия двух или более напряжений, действующих в поперечном сечении элемента. Комбинированные или составные напряжения. Комбинированное напряжение определяется как любая возможная комбинация прямого напряжения (растяжение, сжатие, сдвиг) и косвенного напряжения (изгиба, кручения, термического), возникающих внутри тела.