Силы в природе — что это, определение и ответ
Динамика — раздел механики, изучающий законы и причины, вызывающие движение тела, т.е. движение материальных тел под действием приложенных к ним сил. В механике имеют дело с тремя типами сил: силы тяготения, силы упругости и силы трения. Сила измеряется в ньютонах [Н].
Сила тяжести — это сила, с которой планета притягивает к себе тела, находящиеся на поверхности или вблизи неё. Сила тяжести направлена к центру планеты (вниз) и равна произведению массы тела m на ускорение свободного падения g:
\(F_{тяжести} = mg\)
Fтяжести — сила тяжести, [Н];
m — масса тела, [кг];
g — ускорение свободного падения, [Н/кг] или [м/c2].
Данная сила действует на любой объект, обладающий массой, и мы постоянно ощущаем действие этой силы на себе. Ускорение свободного падения не зависит от массы тела, вблизи Земли g ≈ 10м/c2.
Например, на человека массой 60 кг действует сила тяжести, равная 600 Н.
Вес тела — это сила, с которой тело действует на опору или растягивает подвес. В свою очередь со стороны опоры на тело действует сила реакции опоры. Сила реакции опоры равна по модулю весу тела и противоположна по направлению. Подвес действует на тело с силой натяжения подвеса, равной по модулю весу тела и противоположной по направлению.
\(\overrightarrow{P}\) — вес тела [Н]
\(\overrightarrow{Т}\) — сила натяжения подвеса [Н]
\(\overrightarrow{N}\) — сила реакции опоры [Н]
Если тело не касается опоры или подвеса, то его вес сила реакции опоры равны нулю.
Сила упругости — это сила, которая возникает внутри тела при деформации и стремится вернуть тело в исходное состояние. Деформацией называется изменение формы или размеров тела. При упругих деформациях тело восстанавливает свою форму и размер после прекращения действия деформирующей силы. Согласно закону Гука, деформация Δх, возникающая в упругом теле (пружине, стержне, и т. п.), пропорциональна приложенной к этому телу силе \(\overrightarrow{F_{внеш}}\):
Деформацией называется изменение формы или размеров тела. При упругих деформациях тело восстанавливает свою форму и размер после прекращения действия деформирующей силы. Согласно закону Гука, деформация Δх, возникающая в упругом теле (пружине, стержне, и т. п.), пропорциональна приложенной к этому телу силе \(\overrightarrow{F_{внеш}}\):
Fвнеш = kΔx. Коэффициент k называется жесткостью тела и измеряется в Н/м.
Сила упругости равна по модулю деформирующей силе и направлена в противоположную сторону:
\(\overrightarrow{F_{упр}} = — \overrightarrow{F_{внеш}}\)
Таким образом, сила упругости вычисляется по формуле: Fупр = kΔx.
При параллельном соединении двух пружин с коэффициентами жесткостей k1 и k2, жесткость системы равна сумме жесткостей k = k1 + k2. При последовательном соединении обратная общая жесткость системы равна сумме обратных жесткостей каждой из пружин:\(\frac{1}{k} = \frac{1}{k_{1}} + \frac{1}{k_{2}}\).
При последовательном соединении обратная общая жесткость системы равна сумме обратных жесткостей каждой из пружин:\(\frac{1}{k} = \frac{1}{k_{1}} + \frac{1}{k_{2}}\).
Сила трения — это сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению. Сила трения направлена в сторону, противоположную направлению движения или направлению предполагаемого движения. Причиной возникновения трения является шероховатость трущихся поверхностей и взаимодействие молекул этих поверхностей.
Если попробовать сдвинуть с места шкаф, то он будет оставаться в покое до тех пор, пока приложенная сила не достигнет определенного значения. Между шкафом и поверхностью пола возникает сила трения покоя Fтр.покоя, равная по модулю и противоположная направлению приложенной силы F:
\(\overrightarrow{F_{тр.покоя}} = — \overrightarrow{F}\)
С ростом приложенной силы, будет расти и сила трения покоя. Шкаф останется на месте до тех пор, пока приложенная сила не превысит максимально возможное значение силы трения покоя Fтр.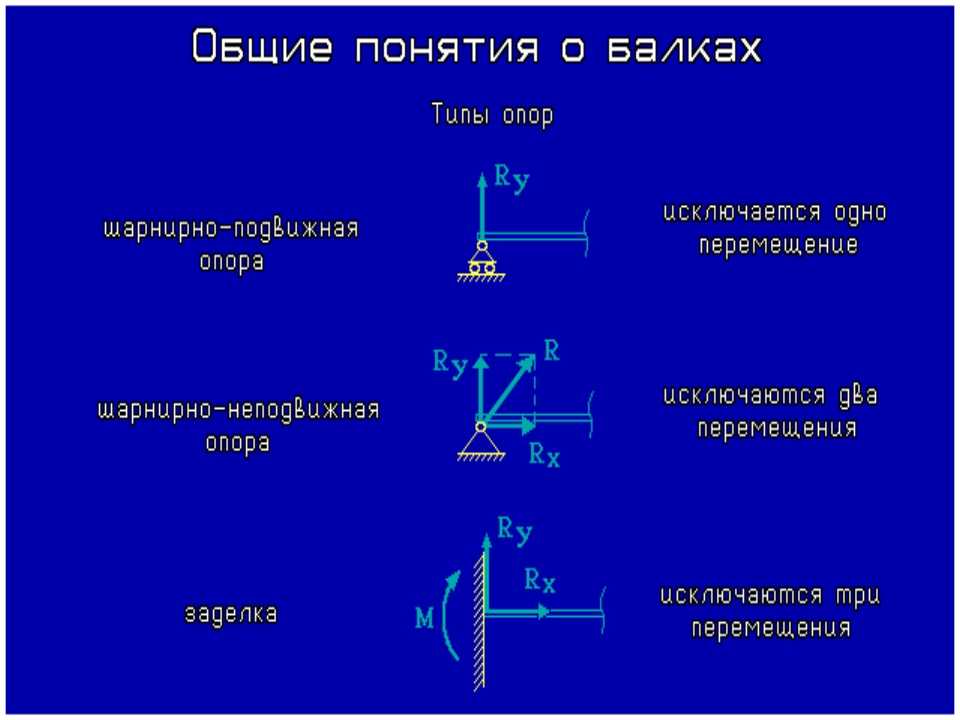 max, и уже после этого начнется движение.
max, и уже после этого начнется движение.
Сила трения скольжения равна максимальной силе трения покоя и пропорциональна силе реакции опоры N между трущимися поверхностями: Fтр = Fтр.max = μN. Сила реакции опоры N равна по модулю силе нормального давления P со стороны тела на опору. Значит, силу трения можно вычислять по формуле Fтр= μP. Коэффициент трения μ определяется материалами соприкасающихся тел. Сила трения скольжения не зависит от площади соприкосновения.
На тело, погруженное в жидкость или газ, действует выталкивающая сила. Данная сила называется силой Архимеда, направлена вверх и вычисляется по формуле: FA = ρgV. Здесь ρ — плотность тела, g — ускорение свободного падения, V — объем погруженной части тела.
Условия плавания тел:
\(F_{тяжести} > F_{А}\) — тело тонет
\(F_{тяжести} = F_{А}\) — тело плавает
\(F_{тяжести} < F_{А}\) — тело всплывает до тех пор, пока не начинает плавать
Условия плавания тел определяются соотношением между плотностью тела и плотностью жидкости:
ρтела > ρжидкости — тело тонет
ρтела = ρжидкости — тело плавает
ρтела < ρжидкости — тело всплывает до тех пор, пока не начнет плавать.
Если плотность тела меньше плотности жидкости, то объем погруженной части тела вычисляется по формуле:
\(V_{погруж} = V_{тела}\frac{\rho_{тела}}{\rho_{жидкости}}\)
Сила сопротивления возникает при движении тела в жидкости или газе. Она направлена противоположно скорости движения тела относительно среды и тормозит движение тела.
Величина силы сопротивления зависит от размеров, формы, состояния поверхности, скорости относительно среды и от свойств среды.
Частный случай силы реакции опоры, сила натяжения нити \(\overrightarrow{Т}\) точно также численно равна весу тела. При этом ее направление, как и у силы упругости пружины всегда против деформации — то есть от концов нити к ее центру.
Важно особенностью нити является равенство сил натяжения на ее концах, а в случае с нерастяжимой нитью — передача модуля ускорения от одного конца к другому (в задачах — от одного тела к другому, связанному с первым). При этом не обязательно должны совпадать направления ускорений тел, но обязательно совпадают модули.
Виды сил 7 класс онлайн-подготовка на Ростелеком Лицей
Введение
Тела взаимодействуют, и эти взаимодействия влияют на то, будет ли двигаться тело и как именно. Силы взаимодействия определяют ускорение. Какова природа этих сил? Можно толкнуть тело рукой, и оно сдвинется – с таким действием всё понятно. Но есть множество других взаимодействий. Например, если мы разожмём пальцы, то тело упадёт вниз. В воздухе тело упадет быстрее, чем тонуло бы в воде. Это означает, что на тело действуют какие-то силы. Тело лежит на столе и давит на него – тоже взаимодействие. Вещества состоят из структурных частиц – эти частицы как-то взаимодействуют друг с другом. Возникает вопрос, как это всё учесть и рассчитать, ведь нам приходится отвечать на вопрос: «Что, если…?», предсказывать явления.
Классификация сил
Любые два тела притягиваются. Явление притяжения по-другому называют гравитацией. Мы её ощущаем по тому, что Земля притягивает тела: преодолеваем гравитацию, когда поднимаем что-то тяжелое, и наблюдаем её действие, когда тело падает.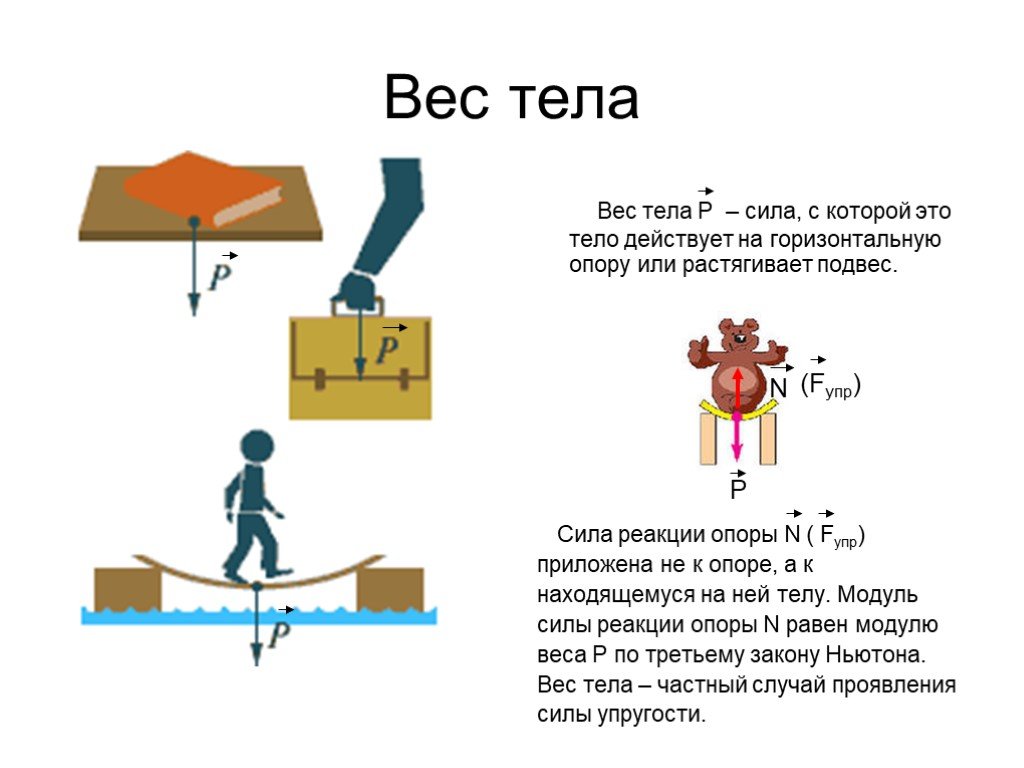 Сила притяжения зависит от масс тел и от расстояния между ними. Масса Земли огромна, поэтому к ней тела притягиваются заметно. Две книги на полке тоже притягиваются друг к другу, но так слабо из-за малых масс, что мы этого не замечаем.
Сила притяжения зависит от масс тел и от расстояния между ними. Масса Земли огромна, поэтому к ней тела притягиваются заметно. Две книги на полке тоже притягиваются друг к другу, но так слабо из-за малых масс, что мы этого не замечаем.
Притягивает ли нас Луна? А Солнце? Да, но намного меньше, чем Земля, из-за большого расстояния. Мы на себе притяжение Луны не ощущаем, а вот приливы и отливы происходят из-за притяжения Луны и Солнца. А черные дыры обладают настолько большой массой, что притягивают даже свет: проходящие мимо лучи искривляются.
Все тела притягиваются. Возьмем тело, которое лежит на столе. Оно притягивается к Земле, но остается на месте. Чтобы сохранялось состояние покоя, силы, действующие на тело, должны быть уравновешены. Значит должна быть сила, которая уравновешивает силу тяжести. В данном случае это сила, с которой на тело действует стол. Такую силу назвали силой реакции опоры (см. рис. 1).
При этом тело давит на стол. Если мы рассматриваем, как движется тело, нам не важно, что происходит со столом. Но если мы рассматриваем, что произойдет со столом, то нужно будет учесть это воздействие. Силу, с которой тело действует на опору или подвес, назвали весом:
Но если мы рассматриваем, что произойдет со столом, то нужно будет учесть это воздействие. Силу, с которой тело действует на опору или подвес, назвали весом:
Рис. 1. Взаимодействие гири и стола
Чтобы сдвинуть любое тело, надо приложить силу. В этом и заключается инертность. Если мы попробуем сдвинуть гирю на столе, она до некоторого предела вообще не сдвинется. Значит и здесь возникает некоторая сила, которая уравновешивает наше воздействие. Эта сила – сила трения:
Рис. 2. Сила трения
Что-то похожее происходит, когда мы поднимаем гирю. Она тоже сначала не поднимается, пока наша сила не превзойдет порог: здесь этот порог – сила притяжения Земли.
Если вместо стола будет пружина, она сожмется, и будет также действовать на это тело. Тело действует на стол или пружину, они прогибаются, их молекулы смещаются (см. рис. 3), а при смещении молекул между ними возникают силы отталкивания, препятствующие дальнейшей деформации:
Рис. 3. Сила отталкивания
3. Сила отталкивания
Отличие в том, что деформация стола чаще всего настолько мала, что ее трудно заметить, а некоторые тела деформируются значительно больше, как пружина или резинка. Мало того, по деформации такого тела можно судить о силе, которая в нем возникла. Это удобно для расчетов, поэтому эту силу изучают отдельно – ее назвали силой упругости.
А если тело положить на поверхность воды? В воде многие предметы становятся легче, значит, есть сила, которая их «приподнимает». Для некоторых тел ее достаточно, чтобы они плавали на поверхности – это и кусок пенопласта или древесины, и корабль. Благодаря этой силе мы вообще можем плавать. Эту силу назвали силой Архимеда.
Конечно, эта классификация достаточно условна. Природа силы реакции опоры и силы упругости одна и та же, но удобно их изучать отдельно. Или рассмотрим такой случай: гиря лежит на опоре и ее тянут вверх за нитку. Гиря действует и на опору, и на нитку – какую из этих сил считать весом и как назвать вторую силу? Важно рассмотреть две силы, на что они действуют, и решать задачу независимо от названий.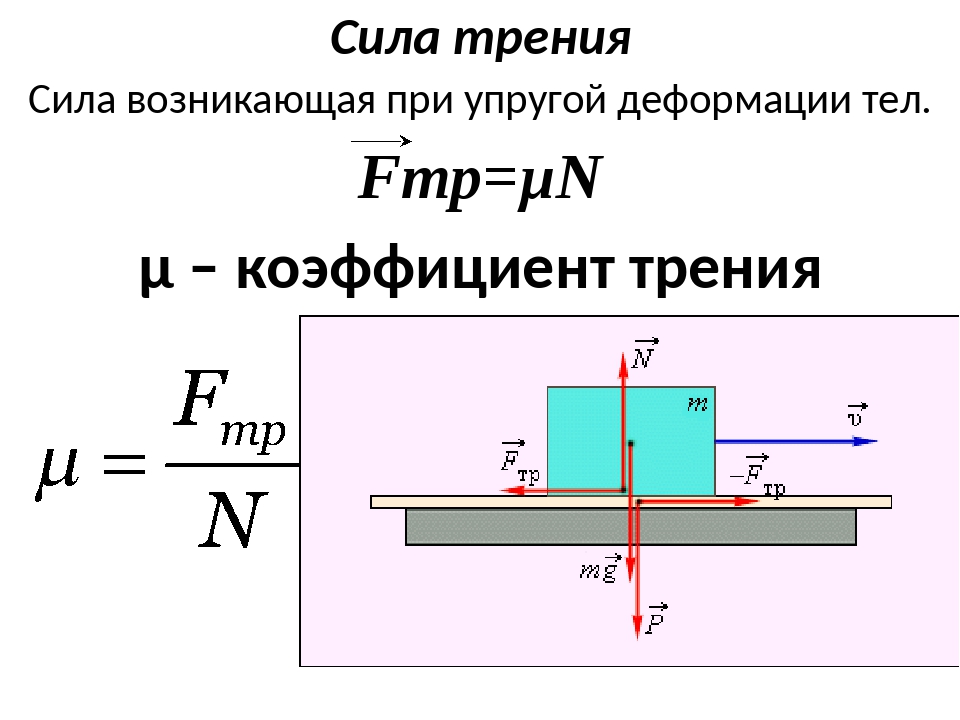 По большому счету есть только взаимодействие атомов, но для удобства мы придумали несколько моделей.
По большому счету есть только взаимодействие атомов, но для удобства мы придумали несколько моделей.
Сила притяжения
Можно провести опыт: подвесить на нити два груза на перекладине, чтобы они уравновесились. Если мы поднесём к одному из грузов гирю, система будет вращаться, это значит, что грузик и гиря притягиваются друг к другу. Действует закон всемирного тяготения.
Закон всемирного тяготения
Исаак Ньютон сформулировал закон всемирного тяготения:
Любые два тела притягиваются друг к другу, причем сила притяжения прямо пропорциональна массам этих тел, и обратно пропорциональна расстоянию между их центрами масс. Математически закон всемирного тяготения записывается так:
где m(1,2) – массы взаимодействующих тел, а R — расстояние между их центрами масс. Силы всемирного тяготения также называют гравитационными силами, а коэффициент пропорциональности G в законе всемирного тяготения называют гравитационной постоянной. Она равна .
Она равна .
Закон всемирного тяготения можно использовать для вычисления сил притяжения между любыми телами. Представьте, вы сидите перед монитором. Допустим, масса монитора равна 2 кг, а масса человека – 70 кг, расстояние примем равным 1 м. Тогда сила взаимодействия по формуле получится есть . Это настолько мало, что мы абсолютно не замечаем такое слабое взаимодействие. Коэффициент пропорциональности G в формуле принимает очень малое значение, . Если на земле будет лежать гвоздь и мы поднесем к нему магнит, то гвоздь притянется к маленькому магниту сильнее, чем к планете. Тем не менее, если взять взаимодействие двух небесных тел, например, планет, то в формулу надо будет подставлять огромные массы, тогда сила будет гораздо больше, несмотря на большие расстояния. Да и на движение небольших тел вблизи поверхности Земли, Земля оказывает значительное влияние.
Сила тяжести – это сила, с которой тело притягивается к Земле. Конечно, другие планеты тоже вступают в гравитационное взаимодействие и для них тоже можно вычислить силу тяжести. Гравитационные силы, а значит и сила тяжести, направлены по отрезку, соединяющему центры масс взаимодействующих тел. Мы привыкли направление к центру Земли называть «вниз».
Гравитационные силы, а значит и сила тяжести, направлены по отрезку, соединяющему центры масс взаимодействующих тел. Мы привыкли направление к центру Земли называть «вниз».
Галилео Галилей опытным путем установил: все тела вблизи поверхности Земли падают с одинаковым ускорением. Рассмотрим случай, когда на тело действует только сила тяжести. Эта сила и дает телу ускорение, по второму закону Ньютона . Дело в том, что если увеличить массу тела , сила тяжести увеличится во столько же раз , и из формулы увидим, что тело будет двигаться с тем же ускорением: То есть для разгона с тем же ускорением более тяжелых тел нужна бόльшая сила, и на них как раз и действует бόльшая сила тяжести. Это называется ускорением свободного падения. Для Земли оно равно примерно 9,8 м/.
Принято обозначать это ускорение буквой «g». Сама же сила тяжести чаще всего обозначается как Fтяжести, или кратко Fт. И по ускорению, которое создает сила, можно найти саму силу:
Почему бумага падает медленнее железа?
Мы рассматривали движение тел, на которые действует только сила тяжести. Эта сила сообщает всем телам одинаковое ускорение. Но не всегда действием остальных сил можно пренебречь. Например, при определенной форме тела существенной становится сила сопротивления воздуха. Возьмем железный шарик и скомканный лист бумаги такой же массы. Силы тяжести на них действуют одинаковые, но на бумагу дополнительно действует сопротивление воздуха, которым пренебречь нельзя, и поэтому бумага движется с другим ускорением. Если бросить железо и бумагу в безвоздушном пространстве, то можно снова рассматривать ситуацию, когда на тело действует только сила тяжести, и оба тела упадут с одним и тем же ускорением.
Эта сила сообщает всем телам одинаковое ускорение. Но не всегда действием остальных сил можно пренебречь. Например, при определенной форме тела существенной становится сила сопротивления воздуха. Возьмем железный шарик и скомканный лист бумаги такой же массы. Силы тяжести на них действуют одинаковые, но на бумагу дополнительно действует сопротивление воздуха, которым пренебречь нельзя, и поэтому бумага движется с другим ускорением. Если бросить железо и бумагу в безвоздушном пространстве, то можно снова рассматривать ситуацию, когда на тело действует только сила тяжести, и оба тела упадут с одним и тем же ускорением.
Даже если тело лежит на столе, на него действует та же сила тяжести, которую мы так же рассчитываем по формуле: масса на ускорение свободного падения. Казалось бы, при чем здесь ускорение, когда тело не движется? Так вот, это ускорение, с которым тело двигалось бы, если бы на него действовала только сила тяжести. По этому ускорению можно рассчитать силу, она будет той же: .
«Ускорение свободного падения в разных частях Земли»
Принято считать величину “g”, то есть ускорение свободного падения, величиной постоянной, равной около 9,8 м/с2. Но с оговоркой: «для нашей планеты». На других небесных телах так же действуют силы тяготения, но ускорение свободного падения там отличаются от нашего. Например, на Марсе ускорение свободного падения всего 3,71 м/с2.
Но на самом деле, даже на одной нашей планете это ускорение будет иметь разные значения в разных местах на Земле.
Известное число 9,8 – это усредненное значение для всей планеты. Наша планета, как известно, не круглая, а немного приплюснута на полюсах. И именно на этих полюсах, ускорение свободного падения немного больше, чем на других широтах: на полюсах g = 9,832 м/с2, а на экваторе — 9,78 м/с2.
Это объясняется тем, что ускорение свободного падения зависит от расстояния до центра Земли.
Формула, по которой можно найти ускорение: (сила тяжести, действующая на тело, делить на массу этого тела).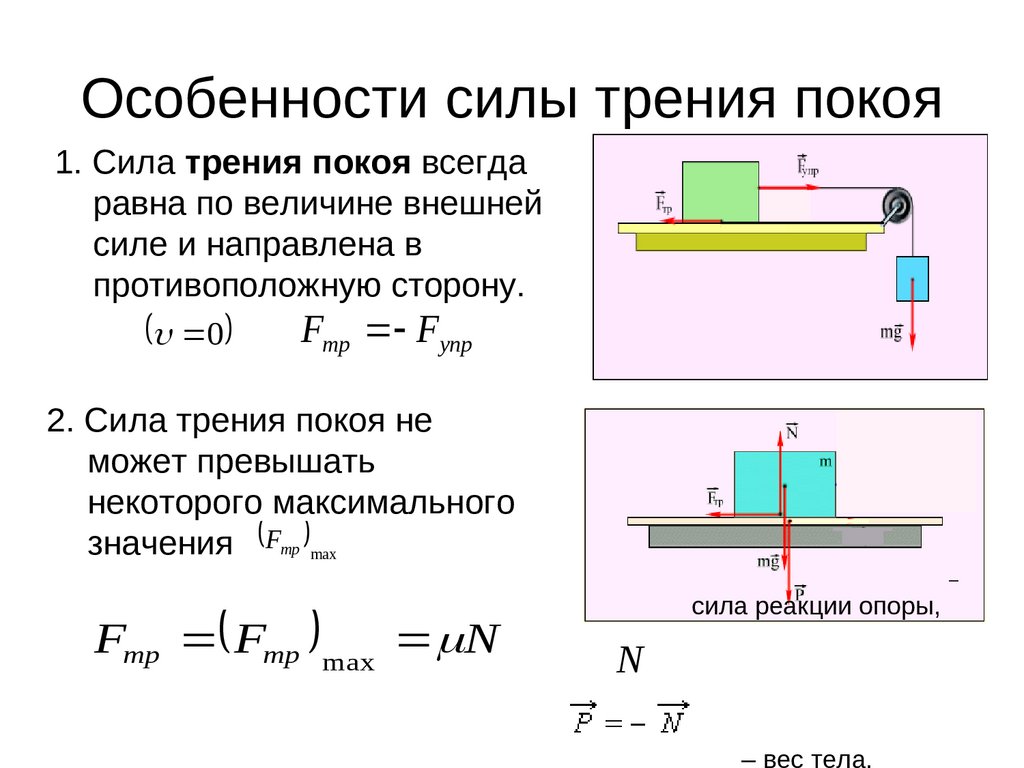
Чем больше расстояние, тем меньше ускорение свободного падения. Поэтому в горах оно меньше, чем у поверхности Земли.
Чем больше расстояние от тела до планеты, тем слабее действует на него сила тяжести и тем меньше ускорение свободного падения. Вблизи поверхности можно считать h равным нулю, тогда g будет постоянным и равным . Какую высоту мы еще можем считать «вблизи», а какую уже нет? Точность диктуется целью задачи. Для некоторых задач мы можем считать g постоянным на высотах в сотни километров. Если мы рассматриваем книгу, лежащую на столике в летящем самолете, то нам не так важно, что ускорение свободного падения будет отличаться на несколько сотых . А если мы рассчитываем запуск спутника, нам нужна бόльшая точность, эти несколько сотых нельзя опустить, приходится учитывать даже отличия радиуса Земли на экваторе и на полюсах.
Если тело покоится на какой-то поверхности (опоре), то на него действует сила тяжести и сила реакции опоры, и они уравновешиваются.
Сила реакции опоры – это сила, с которой опора действует на тело.
Силы тяжести и реакции опоры приложены к нашему телу и действуют на него. В рассмотренном примере, когда тело лежит на горизонтальной поверхности, сила реакции опоры равна силе тяжести, и направлена в противоположную сторону, то есть вертикально вверх:
Рис. 4. Сила реакции опоры
Обычно обозначают силу реакции опоры буквой N.
Опора действует на тело, а тело действует на опору (или нить, если оно висит на нити).
Вес тела – это сила, с которой тело действует на опору или подвес:
Рис. 5. Вес тела
Вес тела чаще всего обозначают буквой «Р», и по модулю он равен силе реакции опоры (по третьему закону Ньютона: с какой силой одно тело действует на другое, с такой же силой второе тело действует на первое): P=N.
Если тело покоится на горизонтальной поверхности, на него действуют сила тяжести и сила реакции опоры. Они уравновешиваются, . Тогда и вес равен .
Часто понятие «вес тела» путают с массой тела. Это уже стало нормой для разговорной речи: «взвесить», «сколько весишь», «весы». Вес – это сила, с которой тело действует, а масса – характеристика самого тела, мера инертности. Легко проверить: стоя на весах, мы видим значение массы, которое вычислено по весу. Если немного подпрыгнуть, то цифра изменится. Но ведь масса не поменялась. Это поменялся вес, сила, с которой мы давим на поверхность весов. А на МКС космонавт вообще не давит на весы, его вес равен нулю – и это состояние называется невесомость.
Тело тоже притягивает Землю, но на движение огромной Земли эта сила не влияет, поэтому ее не рассматривают. Прикасаясь к опоре, тело давит на опору своим весом, а опора на тело – с силой реакции опоры. Это вторая пара сил в этой системе. Если мы описываем движение конкретного тела, мы рассматриваем силы, которые действуют на него, например, сила тяжести и сила реакции опоры.
Сила трения
Рассмотрим силу, которая возникает, когда одни тела движутся относительно других, соприкасаясь с ними – силу трения.
Сила трения — сила, возникающая в месте соприкосновения тел и препятствующая их перемещению друг относительно друга:
Рис. 6. Сила трения
Если пнуть мяч – он покатится и через какое-то время остановится. Санки, с какой бы высокой горки ни съехали – также остановятся.
Рассмотрим два вида трения. Первое – это когда одно тело скользит по поверхности другого — например, при спуске с горы на санках, его назвали трение скольжения. Второе – когда одно тело катится по поверхности другого, например, мяч по земле, его назвали трение качения.
Обозначают силу трения , и вычисляют по формуле:
где N – сила реакции опоры, с которой мы уже познакомились, а µ — это коэффициент трения между данными двумя поверхностями.
Чем сильнее будут прижаты друг к другу тела, тем сила трения будет больше, то есть сила трения пропорциональна силе реакции опоры.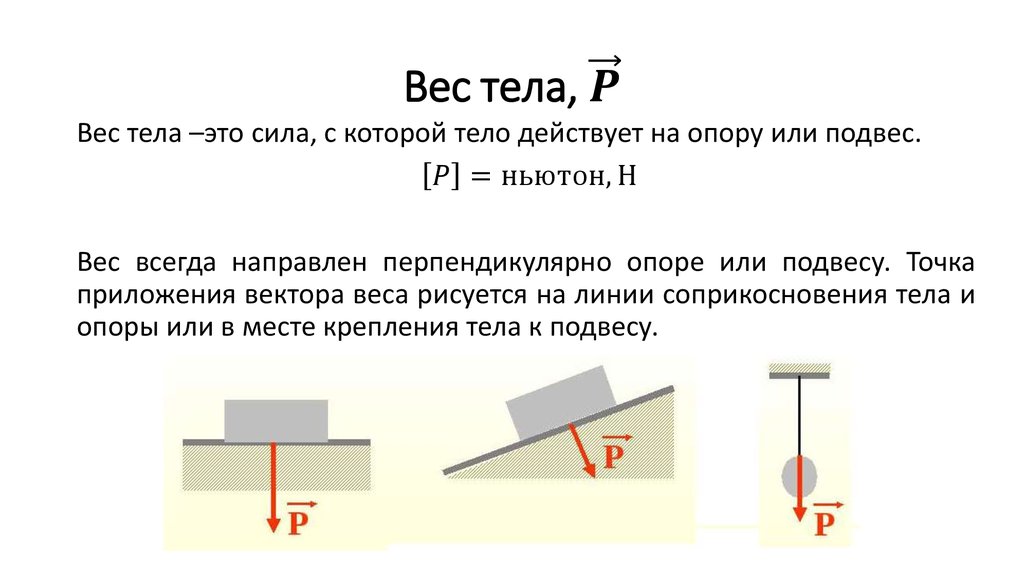
Трение возникает из-за взаимодействия частиц, из которых состоит вещество. Поверхность не может быть идеально гладкой, всегда есть выступы, шероховатости. Выступающие части поверхностей задевают друг друга и препятствуют движению тела. именно поэтому для движения по гладким (полированным) поверхностям требуется прикладывать меньшую силу, чем для движения по шероховатым.
Всегда ли трение уменьшается при полировке?
Полируя, мы уменьшаем количество и размер неровностей, которые препятствуют относительному движению двух поверхностей. Значит, чем лучше отполированы поверхности, тем лучше они будут скользить друг по другу и тем меньше будет сила трения между ними. Можно ли отполировать так, что сила трения вообще будет равна нулю? В какой-то момент неровности станут настолько незначительными, что в контакт придет огромное количество частиц двух поверхностей, а не только частицы шероховатостей, и эти все частицы будут взаимодействовать и препятствовать движению. Получается, что есть предел, до которого сила трения уменьшается при полировке поверхностей, а затем количество взаимодействий между частицами, а поэтому и сила трения, увеличивается. Поэтому мы иногда замечаем, что слишком гладкие поверхности «слипаются».
Получается, что есть предел, до которого сила трения уменьшается при полировке поверхностей, а затем количество взаимодействий между частицами, а поэтому и сила трения, увеличивается. Поэтому мы иногда замечаем, что слишком гладкие поверхности «слипаются».
Для тел из одних и тех же материалов сила трения при качении будет меньше, чем сила трения скольжения. Люди знали это уже давно, поэтому придумали колесо.
Но какое бы трение ни было, сила трения направлена в сторону, противоположную относительному смещению поверхностей. Причём направлена она вдоль линии, по которой тела соприкасаются.
«Разные виды трения»
Существуют разные виды сил трения.
Например, на столе лежит тяжёлая книга. Для того, чтобы ее сдвинуть, потребуется некоторое усилие. И если на книгу нажать слишком слабо — она не тронется с места. Мы же прикладываем силу, почему нет ускорения? Силу, с которой мы толкаем книгу, уравновешивает сила трения между нижней обложкой книги и столом.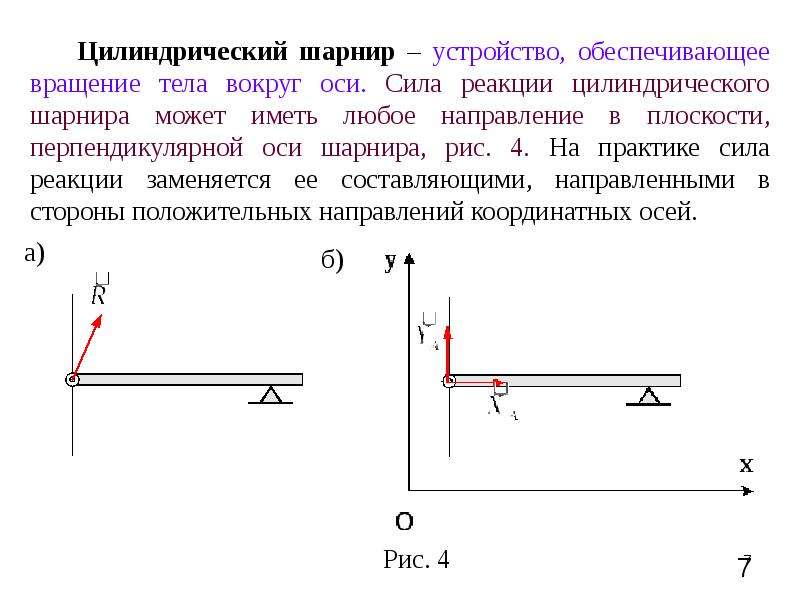 Эта сила трения препятствует твёрдым телам приходить в движение. Поэтому она называется силой трения покоя.
Эта сила трения препятствует твёрдым телам приходить в движение. Поэтому она называется силой трения покоя.
Сила трения покоя направлена также против движения — того движения, которое только ещё должно было бы возникнуть:
Рис. 7. Сила трения покоя
Чтобы сдвинуть что-то с места, нужно приложить силу, которая больше максимальной силы трения покоя.
При движении жидкости или газа, отдельные слои этих веществ движутся один относительно другого. Между ними возникают силы внутреннего или вязкого трения.
При небольшой скорости течения, в отсутствие вихрей, течение жидкости будет происходить послойно. То есть, жидкость можно мысленно разделить на параллельные слои, каждый слой имеет свою скорость. Слой, находящийся непосредственно у дна, будет неподвижен. Следующий слой будет «скользить» по неподвижному слою. Затем слой с еще большей скоростью относительно дна, скользящий по предыдущему, и т.д. (см. рис. 8). И таким образом, между более быстрым и более медленным слоями жидкости будет действовать сила вязкого трения. Возникает она из-за взаимодействия атомов и молекул жидкостей и газов, движущихся с разными скоростями: быстрые молекулы будут сталкиваться с медленными, при этом замедляясь.
Возникает она из-за взаимодействия атомов и молекул жидкостей и газов, движущихся с разными скоростями: быстрые молекулы будут сталкиваться с медленными, при этом замедляясь.
Рис. 8. Движение воды вблизи стенки сосуда
Почему предметы сдвигаются с рывком?
Когда мы пытаемся что-то сдвинуть, возникает сила трения покоя. Она уравновешивает силу F, которую мы прикладываем, и тело остается на месте. Чем бόльшую силу мы прикладываем, тем бόльшая сила трения покоя возникает. Сила трения покоя не может увеличиваться бесконечно, она имеет предел. Тело сдвинется: сила трения окажется меньше, чем приложенная нами сила F. Когда тело сдвинулось с места, возникает сила трения скольжения. Она немного меньшая, чем максимальная сила трения покоя. То есть в момент сдвига мы приложили силу, равную максимальной силе трения покоя, тело сдвинулось – а сила трения резко уменьшилась. Резче, чем мы можем уменьшить нашу силу F для равновесия. Поэтому в этот момент обычно происходит рывок: для сдвига тела, отрыва, мы прикладываем бόльшую силу, чем нужна потом при движении. Попробуйте одним пальцем сдвинуть книгу на столе на один миллиметр. С первого раза может не получиться, она из-за рывка будет сдвигаться на пару сантиметров.
Попробуйте одним пальцем сдвинуть книгу на столе на один миллиметр. С первого раза может не получиться, она из-за рывка будет сдвигаться на пару сантиметров.
Сила Архимеда
На все тела, погруженные в жидкость или газ, а в частности в воду, действует выталкивающая сила. Сила направлена вверх, против силы тяжести:
Рис. 9. Выталкивающая сила
Эта сила называется силой Архимеда, в честь древнегреческого физика и математика, открывшего ее.
Сила Архимеда – это выталкивающая сила, действующая на тело, погруженное в жидкость (газ) и равная весу вытесненной телом жидкости (газа). Обозначают ее обычно Fархимеда, или Fa.
Для ее вычисления пользуются формулой.
где ρ – это плотность жидкости, g – ускорение свободного падения и V – объем погруженной части тела.
Сила Архимеда равна весу вытесненной жидкости. Это похоже на весы, только противовесом нашему телу служит не груз на второй чаше весов, а вода вокруг тела.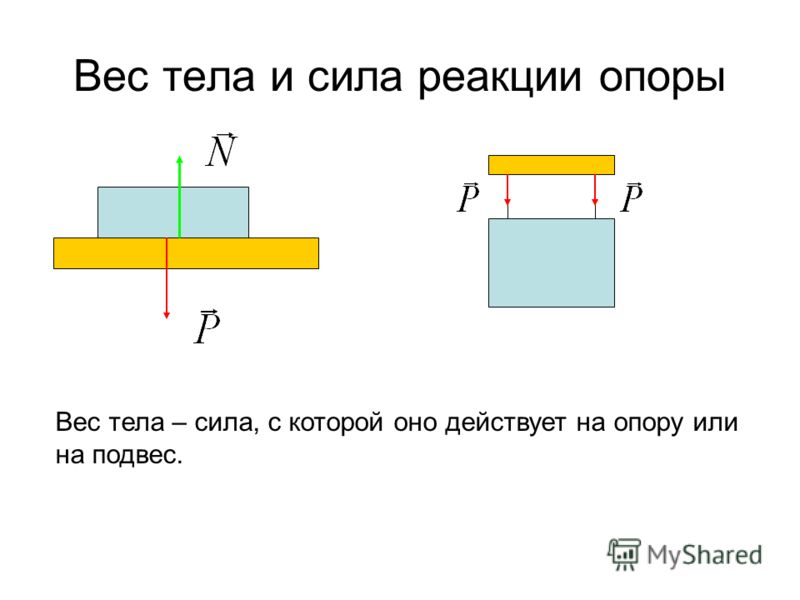
Вес вытесненной воды в состоянии покоя: . Массу вытесненной воды вычисляют через плотность и объем: . Объем вытесненной воды равен объему погруженной в нее части тела, . Если подставить все выражения:
.
В формуле для силы тяжести () тоже можно выразить массу через плотность, , тогда можно записать: .
Погрузим любое тело в воду и отпустим. На него действует сила тяжести и сила Архимеда. Если сила тяжести больше, то тело начинает двигаться вниз. Когда тело погружено в воду полностью, , сравнение силы тяжести и силы Архимеда сводится к сравнению плотностей тела и жидкости. То есть тело тонет, когда его плотность больше плотности жидкости. А если плотность тела меньше, то тело будет всплывать, пока не покажется из-под поверхности. Тогда объем погруженной части будет уменьшаться, пока сила тяжести не сравняется с силой Архимеда. И тогда тело будет плавать в состоянии равновесия на поверхности.
Точно так же сила Архимеда действует в любой жидкости и газе, в частности в воздухе.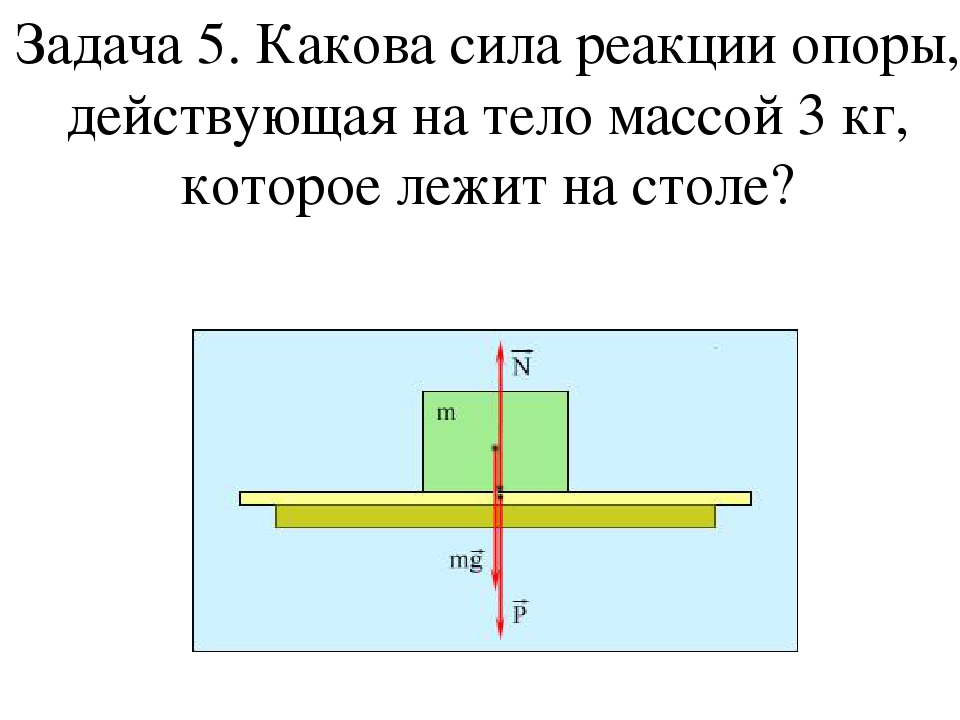 Ею пренебрегают, если она мала по сравнению с силой тяжести, действующей на тело. Но, например, гелиевый шарик обладает очень маленькой массой из-за маленькой плотности гелия, поэтому сила тяжести даже меньше, чем архимедова сила, с которой воздух выталкивает шарик. В данном случае учитывают архимедову силу, потому что благодаря ей гелиевый шарик взлетает.
Ею пренебрегают, если она мала по сравнению с силой тяжести, действующей на тело. Но, например, гелиевый шарик обладает очень маленькой массой из-за маленькой плотности гелия, поэтому сила тяжести даже меньше, чем архимедова сила, с которой воздух выталкивает шарик. В данном случае учитывают архимедову силу, потому что благодаря ей гелиевый шарик взлетает.
Сила упругости
Сила упругости – это сила, возникающая при деформации тела, которая стремится вернуть ему прежние размеры и форму:
Рис. 10. Сила упругости
Чем сильнее мы деформируем тело, чем большую приложим силу, тем больше тело будет сопротивляться деформации, то есть возникнет сила упругости (см. рис. 11). Величина силы упругости зависит от того, насколько удлинилось или сжалось тело, относительно исходного состояния.
Рис. 11. Большая сила упругости при большей деформации
Рассмотрим небольшую деформацию, при которой тело возвращается в исходное состояние. Такую деформацию назвали упругой. Рассмотрим пример: если мы растянули резинку для волос, и она стала длиннее на 3 см, то это называется абсолютным удлинением, это обычно записывают как Δх или Δl.
Такую деформацию назвали упругой. Рассмотрим пример: если мы растянули резинку для волос, и она стала длиннее на 3 см, то это называется абсолютным удлинением, это обычно записывают как Δх или Δl.
Силу упругости удобно обозначать Fупр, и рассчитывается она по формуле, которая является записью «закона Гука»:
Сила упругости, возникающая при упругой деформации тела, пропорциональна величине деформации.
k – это коэффициент жесткости материала, из которого изготовлено тело, а Δх — это разница между длиной тела до и после деформации ().
Рис.12. Сила упругости
Например, если для резинки , то чтобы растянуть ее на 3 см, нужно приложить силу 15 Н. По этой формуле можно рассчитать модуль силы. Сила направлена противоположно направлению деформации.
Чем мы пренебрегаем при описании взаимодействия тел
Заменим тело точкой — введем модель и назовем ее материальной точкой.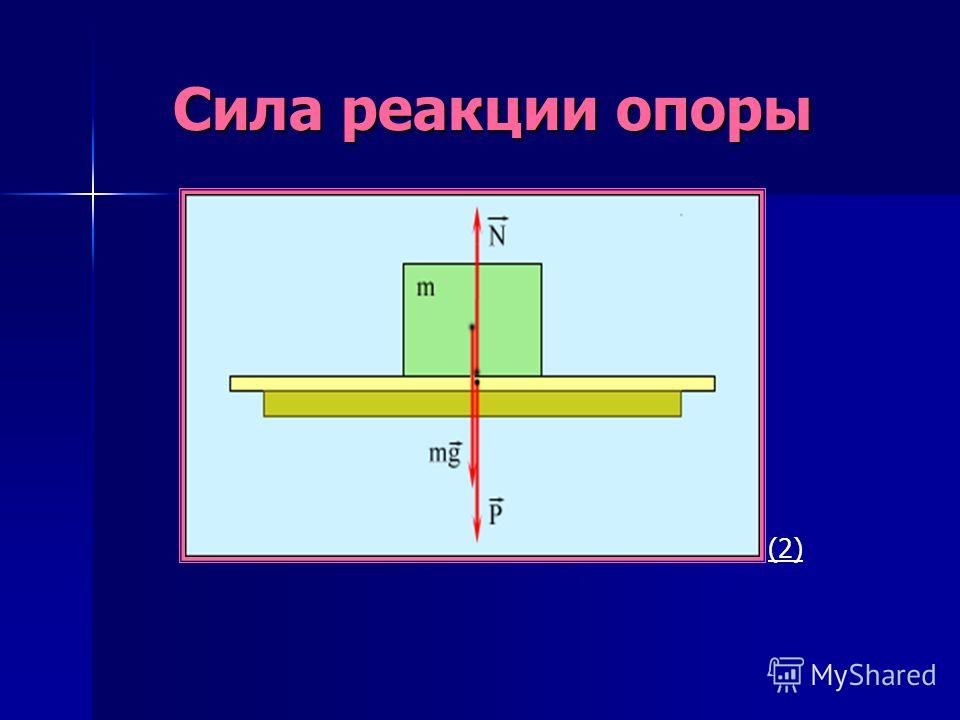 При этом мы пренебрегаем тем, куда именно к телу приложена сила. Когда бублик лежит на столе, на каждую его часть действует сила тяжести и сила реакции опоры, но мы можем заменить его точкой и считать, что к ней приложены силы, действующие на бублик. Такая точка опишет движение всего тела, без учета того, куда именно к телу приложена сила.
При этом мы пренебрегаем тем, куда именно к телу приложена сила. Когда бублик лежит на столе, на каждую его часть действует сила тяжести и сила реакции опоры, но мы можем заменить его точкой и считать, что к ней приложены силы, действующие на бублик. Такая точка опишет движение всего тела, без учета того, куда именно к телу приложена сила.
На каждое тело действует бесконечное множество сил, поэтому учесть их все просто невозможно. Например: ребенок скатывается с горки – влияет ли на него Луна? Как-то влияет: у нее есть масса, находится на некотором расстоянии… Но влияет настолько слабо, что ее можно не учитывать. Если же мы будем решать задачу о полете космического корабля, то нам конечно нужно учесть, с какими силами действуют на него ближайшие космические объекты. Мы часто даже не замечаем, что отбрасываем: всё, кроме того, что считаем существенным для движения тела. Для ребенка на санках это взаимодействие с Землей (сила тяжести) и с поверхностью (сила реакции опоры и сила трения). В некоторых задачах сразу говорится пренебречь какими-то силами, влияниями на тело. Поэтому в зависимости от целей, мы выбираем удобную нам модель, включающую все необходимые силы. Проводя измерения, мы тоже отбрасываем лишнее. Если мы захотим измерить расстояние от дома до школы, мы будем измерять его в километрах, или метрах, если она близко. Но мы ведь не будем измерять его в миллиметрах. А вот при изготовлении ключа, важен каждый миллиметр. Эти границы можно сравнить с точностью записи числа. Например, число Пи для обычных задач мы принимаем равное 3,14. Это правильное значение, но округленное, так как нам не нужна максимальная точность. Ведь если записать Пи = 3,14159, то у ответа поменяется только третий знак после запятой, а это одна тысячная ответа. Таким образом, точность вычислений зависит от цели.
В некоторых задачах сразу говорится пренебречь какими-то силами, влияниями на тело. Поэтому в зависимости от целей, мы выбираем удобную нам модель, включающую все необходимые силы. Проводя измерения, мы тоже отбрасываем лишнее. Если мы захотим измерить расстояние от дома до школы, мы будем измерять его в километрах, или метрах, если она близко. Но мы ведь не будем измерять его в миллиметрах. А вот при изготовлении ключа, важен каждый миллиметр. Эти границы можно сравнить с точностью записи числа. Например, число Пи для обычных задач мы принимаем равное 3,14. Это правильное значение, но округленное, так как нам не нужна максимальная точность. Ведь если записать Пи = 3,14159, то у ответа поменяется только третий знак после запятой, а это одна тысячная ответа. Таким образом, точность вычислений зависит от цели.
Равнодействующая сил
На тело может действовать одновременно несколько таких сил. Мы рассматриваем материальную точку и считаем, что все силы приложены к ней, в таком случае общий результат действия этих сил на тело можно заменить действием одной. Эта сила оказывает на тело такое действие, приводит к такому же результату, к какому приводит действие всех сил, приложенных к телу. Она показывает итоговое действие всех сил, приложенных к телу. Такую силу называют равнодействующей силой и обычно обозначают буквой R.
Эта сила оказывает на тело такое действие, приводит к такому же результату, к какому приводит действие всех сил, приложенных к телу. Она показывает итоговое действие всех сил, приложенных к телу. Такую силу называют равнодействующей силой и обычно обозначают буквой R.
Рассмотрим силы, которые действуют вдоль одной прямой. Если две силы действуют в одну сторону, то они друг другу «помогают», складываются, равнодействующая равна . А если в противоположные – то, наоборот, «мешают» друг другу, и их действия вычитаются, . Если силы равны, то равнодействующая равна .
Противоположным направлениям мы приписываем противоположные знаки. А перед какой силой ставить минус, или :
Рис. 13. Противоположные силы
Можно для каждой конкретной задачи выбрать направление, которое будем считать положительным, и тогда сколько бы ни было сил, мы просто расставим перед ними плюсы и минусы в зависимости от направлений, и сложим. И если, например, равнодействующая получилась отрицательной, значит она направлена против выбранного направления, и наоборот.
Применим нашу модель, где знак + или – соответствует направлению к закону Гука: . Сила упругости направлена противоположно деформации , значит, нужно поставить знак минус:
Задача
Определите вес человека массой m = 50 кг в лифте, движущемся с ускорением a = 0,8 м/с2:
а) вверх; б) вниз.
В задаче описано ускоренное движение человека в лифте. Это подчиняется второму закону Ньютона: равнодействующая сила создает ускорение, .
На человека действуют сила тяжести Земли, обозначим ее , и сила реакции опоры, с которой пол лифта действует на человека, обозначим её , она направлена вверх. Силу тяжести легко рассчитать по формуле .
Решим сначала часть а), лифт движется с ускорением вверх
Направление вверх удобно считать положительным, это направление силы N, которую мы ищем, минус сила тяжести, равная :
Теперь решим часть б), лифт движется вниз.
В уравнении перед ma поставим знак минус (ускорение направлено против выбранного положительного направления). Запишем:
Запишем:
Задача решена.
Список рекомендованной литературы
- Соколович Ю.А., Богданова Г.С. Физика: справочник с примерами решения задач. – 2-е издание, передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
- Перышкин А.В. Физика: учебник 7 класс. – М.: 2006. – 192 с.
Рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «files.school-collection.edu.ru» (Источник)
- Интернет-портал «files.school-collection.edu.ru» (Источник)
- Интернет-портал «files.school-collection.edu.ru» (Источник)
Домашнее задание
- Объясните с физической точки зрения, для чего в древнем Египте при строительстве пирамид, а именно при перемещении бетонных блоков, использовали бревна.
- Проведите свои собственные наблюдения по действию различных сил в быту и опишите несколько примеров.

1.10: Силовой метод анализа неопределенных конструкций
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 17617
- Феликс Удойо
- Temple University
Силовой метод анализа, также известный как метод согласованной деформации, использует уравнения равновесия и условия совместимости для определения неизвестных в статически неопределимых конструкциях. В этом методе неизвестные являются избыточными силами. Избыточная сила может быть внешней опорной силой реакции или внутренней силой стержня, которая, если ее убрать из конструкции, не вызовет нестабильности. Этот метод включает в себя формулировку набора уравнений совместимости в зависимости от количества избыточных сил в конструкции и одновременное решение этих уравнений для определения величины избыточных сил.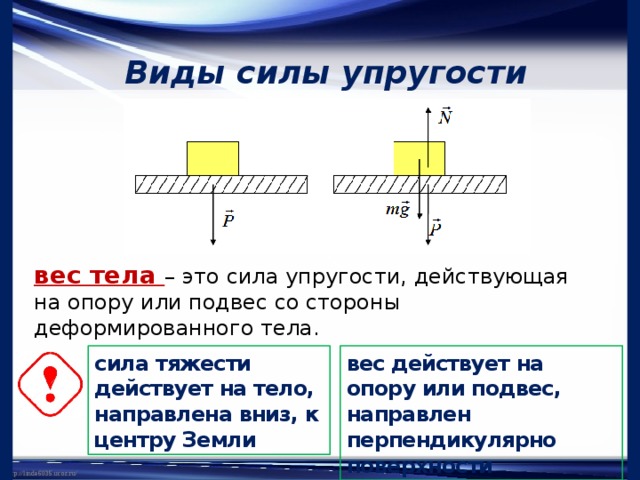
В качестве иллюстрации метода последовательной деформации рассмотрим подпертую консольную балку, показанную на рис. 10.1а. Балка имеет четыре неизвестные реакции, поэтому является неопределенной в первой степени. Это означает, что существует одна сила реакции, которую можно устранить без ущерба для устойчивости конструкции. Структура, которая остается после удаления избыточной реакции, называется первичной структурой. Первичная структура всегда должна соответствовать требованию равновесия. Внимательное наблюдение за рассматриваемой структурой покажет, что существуют две возможные избыточные реакции и две возможные первичные структуры (см. рис. 10b и рис. 10d). Снятие вертикальной реакции на опоре
 После выбора избыточных сил и установления первичных структур следующим шагом является формулировка уравнений совместимости для каждого случая путем суперпозиции некоторых наборов частных решений, удовлетворяющих требованиям равновесия. Уравнения 10.1 и 10.2 удовлетворяют вариантам 1 и 2 соответственно. Термы ∆ ВР , θ AP , δ BB и α AA относятся к коэффициентам гибкости или константам совместимости. Первый нижний индекс в коэффициенте указывает на положение смещения, а второй указывает на причину и направление смещения. Например, ∆ BP подразумевает смещение в точке B , вызванное нагрузкой P в направлении нагрузки Р . Коэффициенты совместимости можно вычислить с помощью закона взаимного обмена Максвелла-Бетти, который будет обсуждаться в следующем разделе.
После выбора избыточных сил и установления первичных структур следующим шагом является формулировка уравнений совместимости для каждого случая путем суперпозиции некоторых наборов частных решений, удовлетворяющих требованиям равновесия. Уравнения 10.1 и 10.2 удовлетворяют вариантам 1 и 2 соответственно. Термы ∆ ВР , θ AP , δ BB и α AA относятся к коэффициентам гибкости или константам совместимости. Первый нижний индекс в коэффициенте указывает на положение смещения, а второй указывает на причину и направление смещения. Например, ∆ BP подразумевает смещение в точке B , вызванное нагрузкой P в направлении нагрузки Р . Коэффициенты совместимости можно вычислить с помощью закона взаимного обмена Максвелла-Бетти, который будет обсуждаться в следующем разделе.Рис. 10.1. Подпертая консольная балка.
где
M = момент в основной конструкции из-за приложенной нагрузки P .
м = момент в основной конструкции из-за единичной нагрузки, приложенной к точке B .
м θ = момент в основной конструкции из-за единичного момента, приложенного к A .
Методика расчета неопределенных конструкций методом последовательного деформирования
- Определение степени неопределенности конструкции.
- Выберите избыточные реакции из неопределенной структуры.
- Удалите выбранные избыточные реакции, чтобы получить первичную структуру.
- Составьте уравнения совместимости. Количество уравнений должно соответствовать количеству избыточных сил.
- Вычислить коэффициенты гибкости.
- Подставить коэффициенты гибкости в уравнения совместимости.
- В случае нескольких избыточных реакций решить уравнения совместности одновременно для определения избыточных сил или моментов.
- Примените вычисленные избыточные силы или моменты к основной конструкции и оцените другие функции, такие как изгибающий момент, поперечная сила и отклонение, если это необходимо, используя условия равновесия.

Закон взаимных прогибов Максвелла-Бетти устанавливает тот факт, что смещения в двух точках упругой конструкции, подвергаемой последовательному воздействию единичной нагрузки в этих точках, одинаковы по величине. Этот закон позволяет уменьшить вычислительные затраты на получение коэффициентов гибкости для уравнений совместности при анализе неопределенных конструкций с несколькими избыточными связями силовым методом. Закон обратного отклонения Максвелла-Бетти утверждает, что линейное перемещение в точке A из-за единичной нагрузки, приложенной к B , равно по величине линейному смещению в точке B из-за единичной нагрузки, приложенной к A для устойчивой эластичной конструкции.
Для доказательства закона обратных прогибов Максвелла-Бетти рассмотрим балку, на которую действуют нагрузки P 1 и P 2 в точке 1 и точке 2 последовательно, как показано на рис. 10.2а и рис. 10.2б.
Рис. 10.2. Балка, подверженная нагрузкам.
10.2. Балка, подверженная нагрузкам.
Дело 1 :
Применить P 1 , затем P 2 .
Работа, выполняемая в точке 1, когда применяется P 1 :
, где
Δ 11 = отклонение в точке 1, посвященная постепенно прилагаемой нагрузке P8.
Работа, выполненная в точках 1 и 2, когда P 2 нанесен и P 1 все еще на месте:
, где
Δ 12 и Δ 22 = отклонения в точке 1 и точке 2 соответственно, когда нагрузка р 2 — грани. проделанная работа W T :
Случай 2:
Применить P 2 , затем P 1
Работа, выполненная в точке 1 при применении P 1 :
Work done at points 1 and 2 when P 1 is applied and P 2 is still in place:
Total work done W T :
Приравняем сумму обоих случаев (из уравнений 3 и 6).
Подстановка P 1 = P 2 = 1 в уравнение 7 дает следующее:
Закон Максвелла-Бетти также применим для обратного вращения. Теорема обратного вращения утверждает, что вращение в точке B из-за единичного парного момента, приложенного в точке A , равно по величине вращению в A из-за единичного парного момента, приложенного в точке B . This is expressed as follows:
where
α AB = the rotation at a point A due to a unit couple moment applied at B.
α BA = вращение в точке B из-за единичного парного момента, приложенного к A .
10.3 Анализ неопределенных балок и рам
Анализ неопределенных балок и рам проводится в соответствии с общей процедурой, описанной ранее. Сначала выбираются первичные структуры и избыточные неизвестные, затем формулируются уравнения совместности в зависимости от количества неизвестных и решаются. Существует несколько методов расчета коэффициентов гибкости при анализе неопределенных балок и рам. Эти методы включают использование интеграла Мора, таблиц отклонений и метода графического умножения. Эти методы проиллюстрированы в решенных примерах задач в этом разделе.
Существует несколько методов расчета коэффициентов гибкости при анализе неопределенных балок и рам. Эти методы включают использование интеграла Мора, таблиц отклонений и метода графического умножения. Эти методы проиллюстрированы в решенных примерах задач в этом разделе.
10.3.1 Расчет коэффициентов гибкости с использованием интеграла Мора
Интеграл Мора для получения коэффициента гибкости для балок и рам выражается следующим образом:
где к приложенной нагрузке P .
Пример 10.1
Определите реакции в балке, показанной на рис. 10.3а. Для проведения анализа используйте метод последовательной деформации. Все коэффициенты гибкости определяются интегрированием. EI = константа.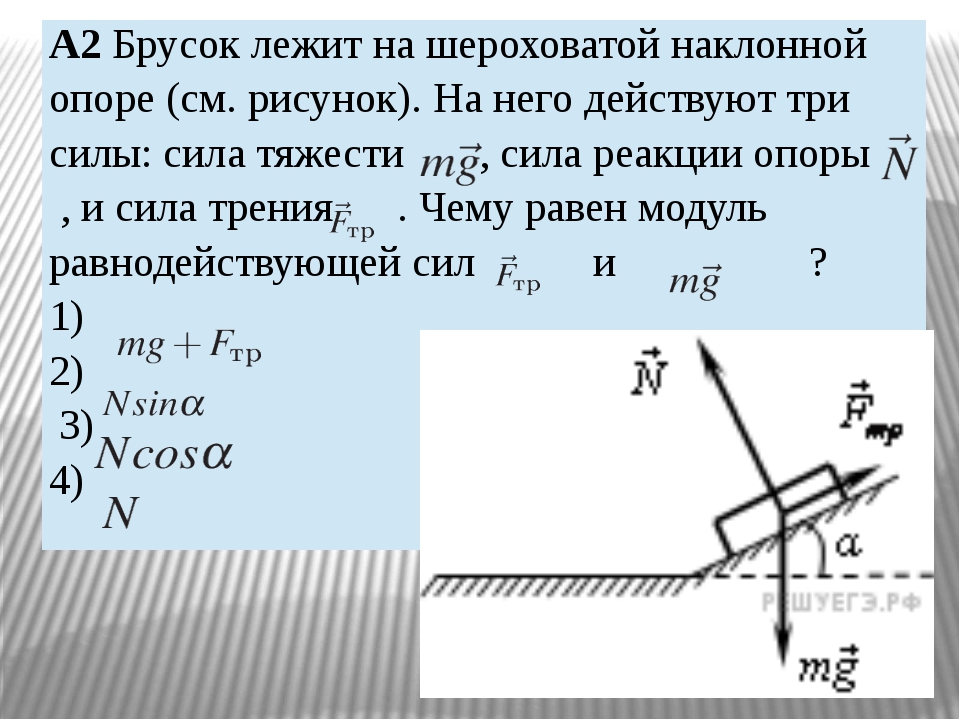
Рис. 10.3. Луч.
Раствор
Классификация структуры. В пучке четыре неизвестные реакции: три неизвестные реакции на закрепленном конце A и одна неизвестная реакция на объекте B . Поскольку на плоскости имеется три уравнения равновесия, это означает, что балка имеет одну неизвестную реакцию сверх уравнений равновесия на плоскости, таким образом, она является неопределенной в одной степени.
Выбор первичной конструкции. Может быть более одного возможного выбора первичной структуры. Для данной подпираемой консольной балки стойка B будет выбрана как избыточная. Таким образом, первичная структура показана на рис. 10.3b.
Уравнение совместимости. Количество уравнений совместимости всегда будет соответствовать количеству избыточных реакций в данной структуре. For the given cantilever beam, the number of compatibility equations is one and is written as follows:
∆ BP + B y δ BB = 0
The flexibility или коэффициенты совместимости ∆ BP и δ BB можно вычислить несколькими методами, включая метод интегрирования, метод графического умножения и табличный метод.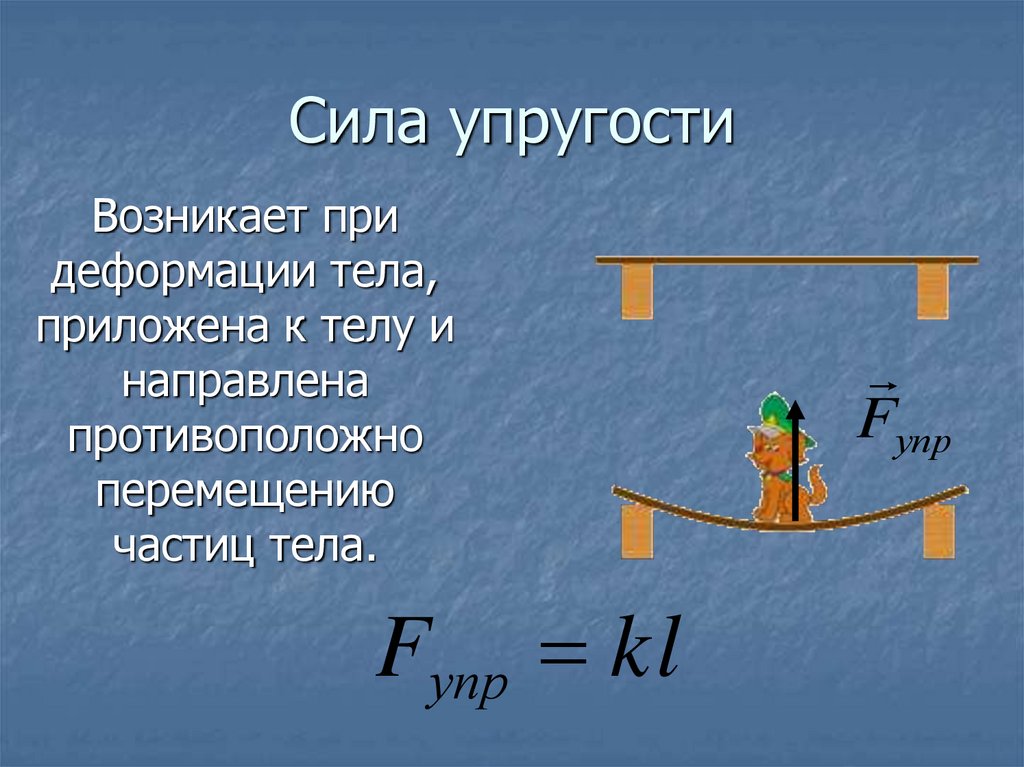 В этом примере коэффициенты гибкости вычисляются с использованием метода интегрирования.
В этом примере коэффициенты гибкости вычисляются с использованием метода интегрирования.
Выражения изгибающего момента для основной балки, подвергаемой внешней нагрузке, записываются следующим образом:
Изгибающий момент основной балки, подвергаемой B y = 1 кН, выглядит следующим образом:
Использование интегрирования для получения коэффициентов гибкости дает следующее:
Включение рассчитанных коэффициентов гибкости в уравнение совместимости дает следующее: диаграммы поперечной силы для неопределенной балки, показанные на рис. 10.4. Используйте метод последовательной деформации. EI = константа.
Рис. 10.4. Неопределенный луч.
Раствор
Классификация структуры. В балке четыре неизвестные реакции: три неизвестные реакции на неподвижном конце A и одна неизвестная реакция на опоре C . Поскольку на плоскости имеется три уравнения равновесия, это означает, что балка имеет одну неизвестную реакцию сверх уравнений равновесия на плоскости. Таким образом, оно неопределенно в одной степени.
Таким образом, оно неопределенно в одной степени.
Выбор первичной конструкции. Может быть более одного возможного выбора первичной структуры. Для данной подпираемой консольной балки реакция при C выбран в качестве избыточной реакции. Таким образом, первичная структура показана на рис. 10.4b.
Уравнение совместимости. Количество уравнений совместимости всегда будет соответствовать количеству избыточных реакций в данной структуре. Для данной консольной балки число уравнений совместности равно одному и записывается следующим образом:
∆ CP + C y δ CC = 0
Коэффициент гибкости или ∆совместимости0038 CP и δ CC вычисляются методом интегрирования.
Выражения изгибающего момента для сегментов AB и BC основной балки, подвергаемой внешней нагрузке, записываются следующим образом: записывается следующим образом:
M = x
Подстановка вычисленных коэффициентов гибкости в уравнение совместимости дает следующее:
Диаграмма поперечной силы и изгибающего момента.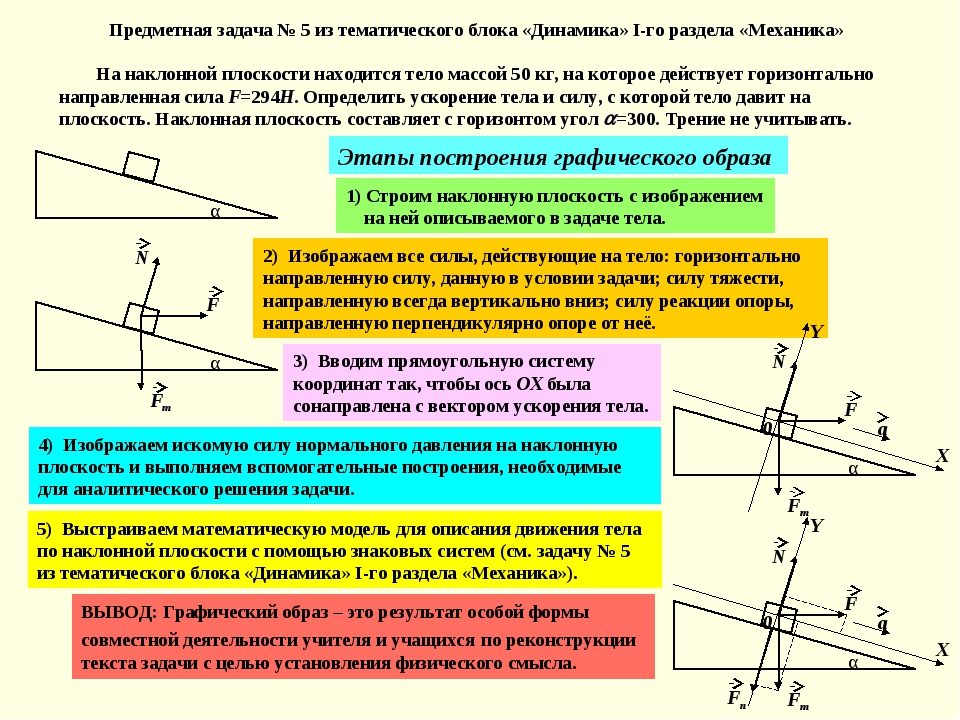 Для определения величин перерезывающей силы и изгибающего момента и построения их графиков прикладывают полученную избыточность к основной балке, как показано на рис. 10.4д.
Для определения величин перерезывающей силы и изгибающего момента и построения их графиков прикладывают полученную избыточность к основной балке, как показано на рис. 10.4д.
Диаграммы поперечной силы и изгибающего момента показаны на рис. 10.4h и рис. 10.4i.
10.3.2 Вычисление коэффициентов гибкости методом графического умножения
Вычисление коэффициентов гибкости для уравнений совместимости методом интегрирования может быть очень длительным и громоздким, особенно для неопределенных конструкций с несколькими неизвестными избыточными силами. В таких случаях получение коэффициентов методом графового умножения экономит время. Метод умножения графов основан на предположении, что интеграл содержит произведение двух графов моментов М и М . Чтобы вывести формулу для метода графового умножения, рассмотрим две диаграммы моментов M ′ и M , как показано на рис. 10.5. График M ′ является линейным, а график M представляет собой произвольную функцию.
Рис. 10.5. Диаграммы моментов.
Предполагая, что жесткость на изгиб EI постоянна, интеграл от произведения этих двух диаграмм моментов может быть выражен следующим образом:
Элементарная область диаграммы изгибающего момента на расстоянии х от левого конца, как показано на рисунке 10.5а, записывается следующим образом:
Используя тригонометрию, ордината линейный график M ′ на расстоянии x от начала координат, как показано на рис. 10.5b, может быть выражен следующим образом:
Подстановка уравнений 2 и 3 в уравнение 1 дает следующее:
Как следует из уравнения 10.6, интеграл произведения двух моментных диаграмм равен произведению площади одной из моментных диаграмм (предпочтительно диаграммы с произвольным контуром) на ординату второй моментной диаграммы с прямым контуром, лежащим на вертикальной линии, проходящей через центр тяжести первой диаграммы моментов.
Пример 10.3
Определить реакции на опорах A , C и D луча, показанного на рис. 10.6а. A — фиксированная опора, а C и D — роликовые опоры. EI = константа.
Рис. 10.6. Луч.
Раствор
Классификация структуры. В пучке пять неизвестных реакций. Таким образом, степень неопределенности структуры равна двум.
Выбор первичной конструкции. Опоры C и D выбраны как резервные реакции. Следовательно, основная конструкция представляет собой консольную балку, подверженную заданной сосредоточенной нагрузке, показанной на рис. 10.6b. Первичная структура с избыточными неизвестными показана на рис. 10.6c, рис. 10.6d, рис. 10.6e и рис. 10.6f.
Уравнение совместимости. Есть два уравнения совместимости, так как есть две избыточные неизвестные реакции. Уравнения имеют следующий вид:
Первые буквы нижнего индекса коэффициентов гибкости указывают место прогиба, а вторые буквы обозначают силу, вызывающую прогиб. При использовании метода умножения графа коэффициенты рассчитываются следующим образом:
При использовании метода умножения графа коэффициенты рассчитываются следующим образом:
При использовании метода умножения графа коэффициенты гибкости рассчитываются следующим образом:
Substituting the flexibility coefficients into the compatibility equation suggests the following two equations, with two unknowns:
–1600.8 + 170.56 C y + 426.56 D y = 0
–2560 + 426.56 C y + 1365,76 D y = 0
Одновременное решение обоих уравнений дает следующее:0034 D y = –4,83 k
Реакции на опоре A определяются следующим образом:
метод расчета коэффициентов гибкости. Он включает в себя получение констант из табличных отклонений на основе типов опор и конфигураций нагрузки, как показано в Таблице 10.1 и Таблице 10.2.
Таблица 10.1. Свободно поддерживаемые наклоны и прогибы балки.
Таблица 10. 2. Наклоны и прогибы консольных балок.
2. Наклоны и прогибы консольных балок.
Пример 10.4
Изобразите изгибающий момент и поперечную силу для неопределенной балки, показанной на рис. 10.7а. EI = константа.
Рис. 10.7. Неопределенный луч.
Раствор
Классификация структуры. В пучке происходят четыре неизвестные реакции. Таким образом, луч неопределен до одного градуса.
Выбор первичной структуры. Реакция по адресу B выбрана как избыточная реакция. Таким образом, первичная конструкция представляет собой свободно опертую балку, как показано на рис. 10.7b. На рис. 10.7c и рис. 10.7d показаны первичные структуры, загруженные избыточными реакциями.
Уравнение совместимости. Уравнение совместности для балки записывается следующим образом:
Для расчета коэффициентов гибкости ∆ BP и δ BB , используйте формулы отклонения луча из Таблицы 10.1.
Включение вычисленных коэффициентов гибкости в уравнение совместимости дает следующее:
Диаграммы поперечной силы и изгибающего момента. Как только величины избыточных реакций известны, балка становится определенной и строятся диаграммы изгибающего момента и силы сдвига, как показано на рис. 10.7g и рис. 10.7h.
Как только величины избыточных реакций известны, балка становится определенной и строятся диаграммы изгибающего момента и силы сдвига, как показано на рис. 10.7g и рис. 10.7h.
Пример 10.5
Чтобы получить коэффициенты гибкости, используйте таблицы прогиба балки для определения опорных реакций балок в примерах 10.1 и 10.2.
Раствор
Классификация структуры. Степень неопределенности балки в примерах 10.1 и 10.2 равна 2.
Коэффициенты гибкости. Используя информацию из таблицы 10.2, определите коэффициенты гибкости для примера 10.1 следующим образом:
Используя формулы прогиба балки, получите следующие коэффициенты гибкости для балки из примера 10.2 следующим образом:
Подстановка рассчитанных коэффициентов гибкости в уравнение совместимости дает следующий ответ: . EI = константа.
Рис. 10.8. Рамка.
Раствор
Классификация структуры. В кадре четыре неизвестные реакции: одна неизвестная реакция на свободном конце A и три неизвестные реакции на фиксированном конце C .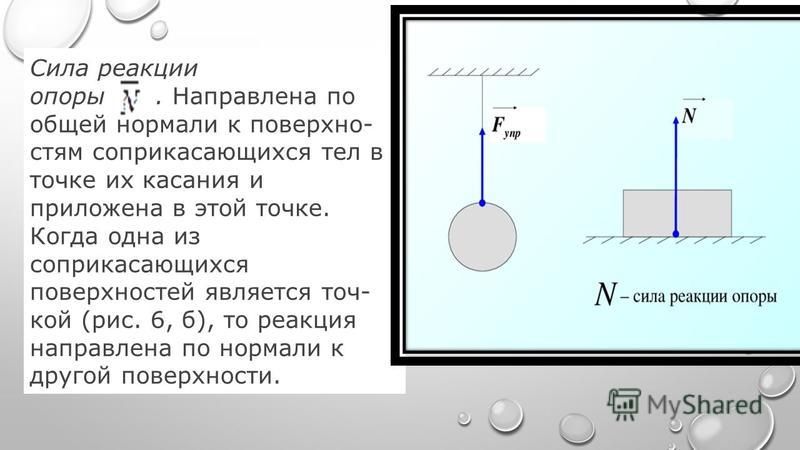 Таким образом, степень неопределенности структуры равна единице.
Таким образом, степень неопределенности структуры равна единице.
Выбор первичной конструкции. Выбор реакции на опоре A в качестве избыточной неизвестной силы предполагает, что первичная структура такая, как показано на рис. 10.8b. Первичная конструкция, нагруженная избыточной силой, показана на рис. 10.8c и 10.8d.
Уравнение совместимости. Уравнение совместимости для неопределенной системы отсчета выглядит следующим образом:
Коэффициенты гибкости или совместимости ∆ AP и Δ AA вычисляются методом размножения графика. Получение избыточной реакции предполагает следующее:
–562,5 + 41,67 A y = 0
A y = 13,5 кН
Определение реакций при C .
∑ M C = 0: –(13,5)(5) + (10 × 3)(1,5) + M C = 0
M
= 2 k
. м
Пример 10.7
Методом последовательной деформации определить опорные реакции фермы, показанной на рис. 10.9а. EI = константа.
10.9а. EI = константа.
Рис. 10.9. Ферма.
Решение
Классификация строения. В пучке пять неизвестных реакций. Таким образом, степень неопределенности структуры равна двум.
Выбор первичной конструкции. Две реакции штифтовой опоры в точке D выбраны как дублирующие реакции, поэтому основная конструкция представляет собой консольную балку, подверженную горизонтальной нагрузке в точке C , как показано на рис. 10.9b. Первичная структура, загруженная избыточными неизвестными, показана на рис. 10.9d и рис. 10.9.е.
Уравнение совместимости. Количество уравнений совместимости равно двум, так как есть два избыточных неизвестных. Уравнения записываются следующим образом:
Первое число нижнего индекса в коэффициентах гибкости указывает направление отклонения, а второе число или буква указывает силу, вызывающую отклонение. Коэффициенты вычисляются с использованием метода графического умножения следующим образом:
Подстановка коэффициентов гибкости в уравнение совместимости дает следующие два уравнения с двумя неизвестными:
7680 + 360 X 1 – 72 X 2 = 0
1707. 76 – 72 X 1 + 160.08 X 2 = 0
76 – 72 X 1 + 160.08 X 2 = 0
Solving both equations simultaneously suggests the Следующее:
x 1 = D Y = 25,79K
x 2 = D x = 22,27K D x = 22.27k
.0035 .
10.4 Расчет неопределенных ферм
Процедура расчета неопределенных ферм аналогична процедуре анализа балок. Для ферм с внешними избыточными связями процедура включает определение степени неопределенности конструкции, выбор избыточных реакций, запись уравнений совместности, определение прогиба от приложенной нагрузки и от единичной избыточной силы реакции, приложенной к опоре. первичная структура и решение уравнения (уравнений) совместимости для определения избыточных реакций. Для ферм с внутренними избыточными элементами процедура включает выбор избыточных элементов, вырезание избыточных элементов и представление каждого из них в виде пары сил в основной конструкции, а затем применение условия совместимости для определения осевых усилий в избыточных элементах.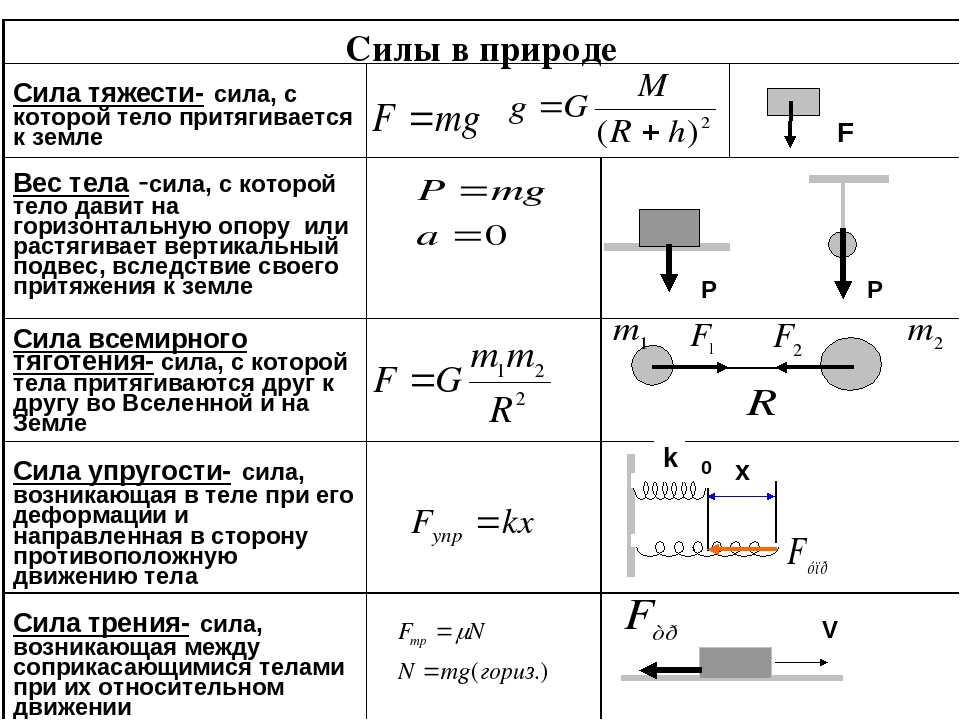 . В качестве примера рассмотрим ферму ниже. Эта ферма неопределима в первой степени. Участники AC и BD фермы представляют собой два отдельных перекрывающихся элемента. Любой из этих членов можно считать избыточным, так как первичная структура, полученная после удаления любого из них, останется устойчивой. Выбор BD в качестве избыточного элемента, разрезание его и приложение пары сил к поверхности разреза, а затем указание на то, что смещение фермы на поверхности разреза равно нулю, дает следующее выражение совместимости:
. В качестве примера рассмотрим ферму ниже. Эта ферма неопределима в первой степени. Участники AC и BD фермы представляют собой два отдельных перекрывающихся элемента. Любой из этих членов можно считать избыточным, так как первичная структура, полученная после удаления любого из них, останется устойчивой. Выбор BD в качестве избыточного элемента, разрезание его и приложение пары сил к поверхности разреза, а затем указание на то, что смещение фермы на поверхности разреза равно нулю, дает следующее выражение совместимости:
, где
∆ BD = относительное смещение поверхности разреза из-за приложенной нагрузки.
δ BD = относительное смещение поверхности среза из-за приложенной единичной избыточной нагрузки на поверхность среза.
Рис. 10.10
Коэффициенты гибкости для уравнения совместимости для неопределенного расчета фермы вычисляются следующим образом:
где
∆ XP = смещение в стыке X или элемента основной фермы из-за приложенной внешней нагрузки.
δ X 1 = смещение в стыке X или элемента основной фермы из-за единичной избыточной силы.
F = осевая сила в элементах фермы из-за приложенной внешней нагрузки, которая вызывает смещение ∆.
f = осевые усилия в элементах фермы из-за приложенной единичной избыточной нагрузки, вызывающей смещение δ .
L = длина элемента.
A = площадь поперечного сечения элемента.
Пример 10.8
Используя метод последовательных деформаций, определите осевую силу во всех элементах фермы, показанной на рисунке 10.11а. EA = константа. .
Рис. 10.11. Ферма.
Решение
Определение опорных реакций в первичной конструкции.
Уравнение совместимости.
∆ 1 P + X 1 δ 11 + X 2 δ 12 = 0
∆ 2 P + X 1 δ 21 + X 2 δ 22 = 0
Определение усилий в элементах от приложенной внешней нагрузки.
Соединение D .
Соединение А .
Соединение B .
Определение усилий в элементах из-за избыточности F BD = 1.
Соединение B .
Соединение D .
Соединение C . .
Определение осевых усилий стержня удобно выполнять в табличной форме, как показано в таблице 10.3.
Таблица 10.3.
Заменить коэффициент гибкости в уравнения совместимости и решения одновременных уравнений свидетельствуют о следующем:
x 1 = F BD = F BD 1 = F BD 1 = F BD 1 = F BD 1 = . = А 9
Пример 10.9 . EA = константа.
Рис.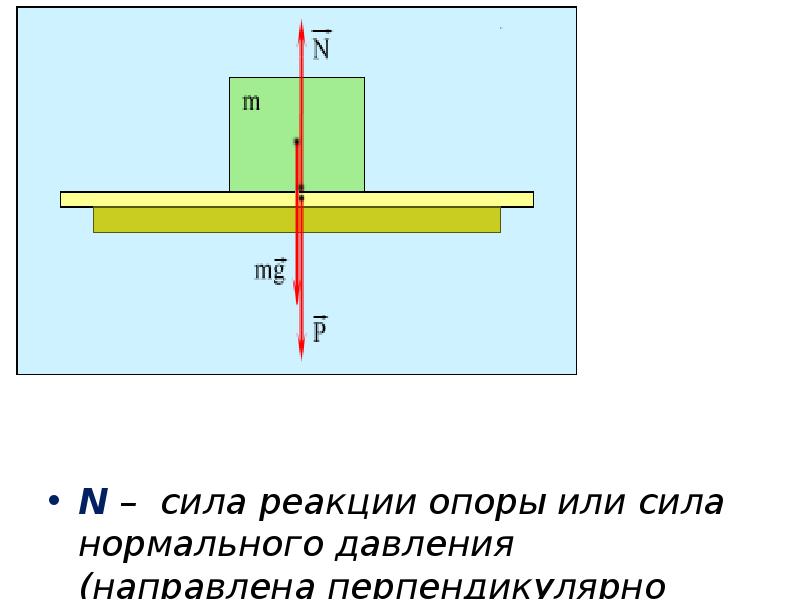 10.12. Ферма.
10.12. Ферма.
Решение
Определение осевых усилий в элементах из-за приложенных внешних нагрузок.
Определение усилий в стержнях из-за избыточных F AD = 1.
Определение осевых усилий стержня удобно выполнять в табличной форме, как показано в таблице 10.4.
Таблица 10.4.
Уравнение совместимости.
Краткое содержание главы
Силовой метод: Силовой метод или метод последовательной деформации основан на равновесии сил и совместимости конструкций. Этот метод включает в себя сначала выбор неизвестных избыточных элементов для структуры, а затем удаление избыточных реакций или элементов для получения первичной структуры.
Уравнения совместимости: Уравнения совместимости формулируются и используются вместе с уравнениями равновесия для определения неизвестных избыточных величин. Количество уравнений совместимости должно совпадать с количеством неизвестных избыточностей. Как только неизвестные избыточности определены, структура становится детерминированной. В главе рассматриваются методы вычисления коэффициентов совместимости или гибкости, такие как метод интегрирования, метод умножения графов и использование таблиц прогибов.
Как только неизвестные избыточности определены, структура становится детерминированной. В главе рассматриваются методы вычисления коэффициентов совместимости или гибкости, такие как метод интегрирования, метод умножения графов и использование таблиц прогибов.
Интеграл Мора для расчета коэффициентов гибкости балок и рам:
Закон взаимных прогибов Максвелла-Бетти: Закон Максвелла-Бетти помогает сократить вычислительные усилия, необходимые для получения коэффициентов гибкости для уравнений совместимости . Этот закон гласит, что линейное перемещение в точке A из-за единичной нагрузки, приложенной к B , равно по модулю линейному перемещению в точке B из-за единичной нагрузки, приложенной к A для стабильной эластичной конструкции. Этот закон выражается следующим образом:
Практические задачи
10.1 Используя метод последовательной деформации, рассчитайте опорные реакции и начертите диаграммы поперечной силы и изгибающего момента для балок, показанных на рисунках P10. 1–P10.4. . Выберите реакцию на внутренней опоре B как неизвестную избыточность.
1–P10.4. . Выберите реакцию на внутренней опоре B как неизвестную избыточность.
Рис. P10.1. Луч.
Рис. P10.2. Луч.
Рис. P10.3. Луч.
Рис. P10.4. Луч.
10.2 Используя метод последовательной деформации, рассчитайте опорные реакции и начертите диаграммы поперечной силы и изгибающего момента для рам, показанных на рисунках с P10.5 по P10.8. Выберите реакцию(и) на любой из опор в качестве неизвестной избыточной(ых). EI = константа.
Рис. P10.5. Рамка.
Рис. P10.6. Рамка.
Рис. P10.7. Рамка.
Рис. P10.8. Рамка.
10.3 Используя метод последовательных деформаций, определите реакции и осевые усилия в элементах ферм, показанных на рисунках с P10.9 по P10.13.
Рис. P10.9. Ферма.
Рис. P10.10. Ферма.
Рис. P10.11. Ферма.
Рис. P10.12. Ферма.
Рис. 10.13. Ферма.
10.13. Ферма.
Эта страница под названием 1.10: Силовой метод анализа неопределенных структур распространяется под лицензией CC BY-NC-ND 4.0 и была создана, изменена и/или курирована Феликсом Удоэйо посредством исходного контента, который был отредактирован в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Феликс Удоэйо
- Лицензия
- CC BY-NC-ND
- Версия лицензии
- 4,0
- Метки
- источник@https://temple.
 manifoldapp.org/projects/structural-analysis
manifoldapp.org/projects/structural-analysis
- источник@https://temple.
Как рисовать бесплатные диаграммы тела с примерами
доктора Шона Кэрролла
|
Опубликовано: 17 июля 2022 г.
|
Учебник
Добро пожаловать во вторую часть серии руководств по фундаментальной инженерной механике. В этой части основное внимание будет уделено тому, как использовать диаграммы свободного тела вместе с уравнениями равновесия для расчета опорных реакций. Предыдущий выпуск серии здесь. Эта серия предназначена для тех, кто только начинает изучать инженерное дело; Студенты первого курса технических специальностей должны найти эту серию особенно полезной.
Вы можете получить доступ ко всем видео из этой серии (по мере публикации каждой новой части), а также к загружаемым версиям заметок, присоединившись к сопровождающему курсу ниже. В этом уроке мы будем опираться на то, что рассмотрели в части 1, и сосредоточимся на диаграммах свободного тела, уравнениях равновесия и вычислении сил реакции.
1.0 Диаграммы свободного тела
В этом уроке мы рассмотрим диаграммы свободного тела и то, как их использовать для оценки сил, действующих на конструкцию в состоянии равновесия. Диаграмма свободного тела — это диаграмма, на которой показаны только силы, воздействующие на объект. Диаграммы свободного тела — это простой инструмент, помогающий определить все силы, воздействующие на объект или конструкцию. Как правило, одним из первых шагов при анализе конструкции является набросок диаграммы ее свободного тела с указанием всех сил, которые необходимо учитывать при анализе.
Ниже показан простой пример диаграммы свободного тела для массы, покоящейся на горизонтальной поверхности.
Рис. 1. Масса, покоящаяся на опорной поверхности (слева), простая диаграмма свободного тела (справа). Мы можем видеть влияние гравитации, представленное силой тяжести , в то время как равная по величине (противоположное направление) сила реакции , накладываемая опорной поверхностью, представлена .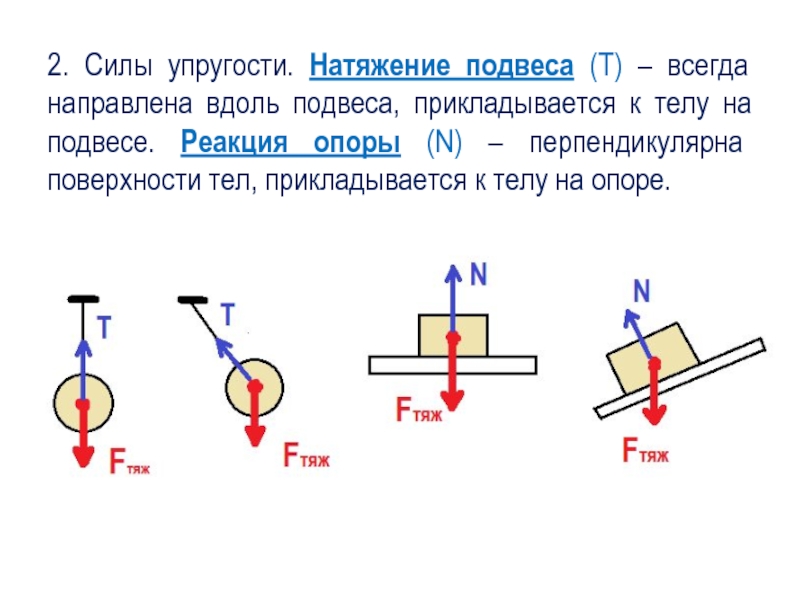 Отсюда мы определяем, что на массу действуют только две вертикальные силы. Это тривиальный пример, но диаграммы свободного тела особенно полезны при анализе более сложных систем.
Отсюда мы определяем, что на массу действуют только две вертикальные силы. Это тривиальный пример, но диаграммы свободного тела особенно полезны при анализе более сложных систем.
Рассмотрим немного более сложный пример маятника, раскачивающегося в воздухе.
Рис. 2. Диаграмма свободного тела для качающегося маятника (справа).В этом случае мы идентифицируем,
- Силу гравитации,
- Сила натяжения в подвесном тросе,
- Сила сопротивления из-за присутствия воздуха,
- Сила инерции присутствует из-за того, что масса имеет ускорение,
2.0 Равновесие
Объект находится в состоянии статического равновесия, если сумма всех сил и моментов, действующих на объект, равна нулю и объект покоится. Это прямое следствие первого закона Ньютона, который гласит, что тело остается в покое или движется с постоянной скоростью, если на него не действует неуравновешенная сила. Отсюда мы замечаем, что равновесие может также применяться к движущимся объектам при условии, что они движутся с постоянной скоростью. О таких объектах говорят, что они находятся в состоянии динамического равновесия. А пока мы просто займемся объектами в состоянии статического равновесия.
О таких объектах говорят, что они находятся в состоянии динамического равновесия. А пока мы просто займемся объектами в состоянии статического равновесия.
Если мы снова будем рассматривать силы и моменты только в 2D-плоскости (как мы делали это при обсуждении эквивалентных систем в предыдущем уроке), мы можем сказать, что объект находится в состоянии статического равновесия, если он удовлетворяет следующим трем условиям ,
(1)
(2)
(3)
Обратите внимание, что мы рассматриваем ортогональные компоненты сил, действующих на объект отдельно. Мы могли бы в равной степени сжать это и просто сказать, что сумма всех сил, действующих на объект, должна равняться нулю,
Если какое-либо из этих условий не выполняется, объект не будет находиться в состоянии статического равновесия и претерпит изменение своей скорости (т. е. испытает ускорение). Мы часто используем эти три уравнения для определения неизвестных сил или моментов в системе, находящейся в состоянии статического равновесия. Поскольку есть три уравнения, мы можем решить до трех неизвестных сил или моментов. Мы увидим это в действии, когда ниже будем оценивать силы и моменты реакции поддержки.
Поскольку есть три уравнения, мы можем решить до трех неизвестных сил или моментов. Мы увидим это в действии, когда ниже будем оценивать силы и моменты реакции поддержки.
3.0 Опоры и силы и моменты реакции
Выше мы видели, что на объект, покоящийся на горизонтальной поверхности, действует сила реакции. Третий закон Ньютона гласит, что на каждое действие существует равное (величина) и противоположное (направление) противодействие. Следовательно, сила реакции в данном случае — это сила, действующая со стороны опорной поверхности обратно на предмет. Эта сила реакции равна по величине силе гравитации, приложенной объектом к поверхности.
Как инженерам важно понимать силы и моменты, которые наши конструкции воздействуют на их опоры или фундаменты. Например, чтобы спроектировать фундамент, который не будет подвергаться недопустимым осадкам, нам необходимо знать силы и моменты, создаваемые конструкцией. Нам также необходимо знать, какая поддержка или ограничение нашей конструкции будет обеспечен определенный тип фундамента или опоры.
Существуют три общие модели опоры/ограничителя, которые мы используем для приближения к реальному поведению фундамента.
3.1 Встроенные/консольные/монолитные опорыЕсли конструкция поддерживается (или удерживается) встроенной опорой, конструкция теоретически будет удерживаться от:
- вертикального движения, т.е. сила реакции может быть создана на опоре
- горизонтальное движение, т.е. на опоре может создаваться горизонтальная сила реакции
- вращательное движение, т.е. на опоре может быть создана моментная реакция
Сейчас это может быть сложно визуализировать или понять, потому что мы рассматриваем модели поддержки изолированно. Но опоры и связанные с ними ограничения будут иметь больше смысла, если мы рассмотрим их применительно к структурам ниже.
Рис. 3. Встроенная опора с возможными реакциями. 3.2 Штифтовая опораШтифтовая опора сопротивляется:
- вертикальному движению, т.
 е. позволяет создавать вертикальную реакцию
е. позволяет создавать вертикальную реакцию - горизонтальное движение, т. е. позволяет генерировать горизонтальную реакцию
На штифтовой опоре отсутствует сопротивление вращению, поэтому не может быть создана реакция момента. Это означает, что если конструкция соединена со штифтовой опорой, сама опора не будет оказывать никакого сопротивления вращающейся в этой точке конструкции.
Рис. 4. Опора штифта с возможными реакциями. 3.3 Роликовая опораРоликовая опора сопротивляется прямолинейному движению только по одной оси, т. е. позволяет развивать силу реакции только по одной оси. Роликовая опора, показанная на рис. 5 ниже, позволяет соединенной конструкции свободно перемещаться в горизонтальном направлении, но ограничивает движение конструкции по вертикали. Как и штифтовые опоры, роликовые опоры не оказывают никакого сопротивления вращению.
Рис. 5. Роликовая опора с единственной возможной реакцией. Эти три типа поддержки являются идеализированными моделями поведения поддержки. Реально без поддержки ведет себя именно по этим моделям. Например, если мы планируем спроектировать фундамент, который остановит вращение нашей конструкции в этой точке, мы смоделируем фундамент как фиксированную или встроенную опору. Таким образом, наша модель не допускает вращения, и смоделированное поведение нашей конструкции будет отражать эту абсолютную неподвижность — это не означает, что фактическое основание будет иметь абсолютную неподвижность при вращении!
Реально без поддержки ведет себя именно по этим моделям. Например, если мы планируем спроектировать фундамент, который остановит вращение нашей конструкции в этой точке, мы смоделируем фундамент как фиксированную или встроенную опору. Таким образом, наша модель не допускает вращения, и смоделированное поведение нашей конструкции будет отражать эту абсолютную неподвижность — это не означает, что фактическое основание будет иметь абсолютную неподвижность при вращении!
С другой стороны, если, основываясь на инженерной оценке, мы не верим, что фундамент, когда он построен, будет оказывать значительное сопротивление вращению, мы могли бы смоделировать его в виде штифта или ролика, который предполагает нулевую фиксацию вращения. Опять же, маловероятно, что это будет соответствовать фактическому поведению фундамента в исходном состоянии. Подумайте, как опоры из трех колонн, изображенные ниже, соотносятся с нашими моделями опор.
Рис. 6. Три конфигурации опор фундамента (три верхние) и их возможные модели (две нижние).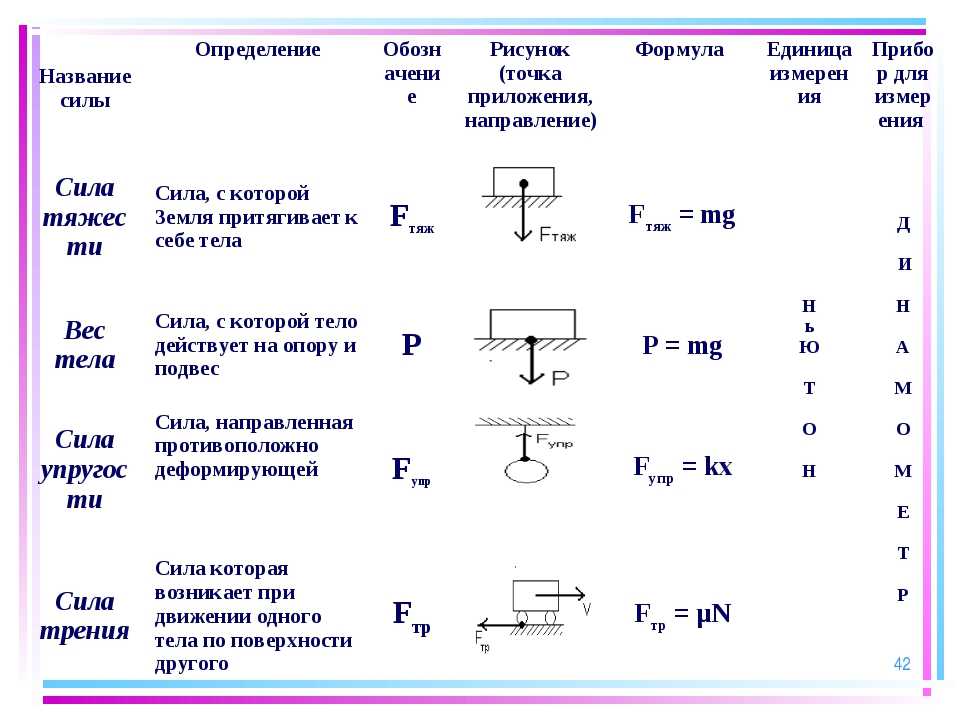
Способность соответствующим образом отображать реальное поведение в наших аналитических моделях является ключевой частью становления компетентным инженером и необходима для любого инженерного анализа. Интуитивное понимание того, насколько точно аналитические модели соответствуют реальному структурному поведению, приходит с практикой и опытом.
Вообще говоря, формальная инженерная подготовка будет в значительной степени сосредоточена на развитии знаний об аналитических моделях и о том, как ими манипулировать. В течение первых 3–5 лет работы инженером-практиком развивается интуиция, позволяющая связать поведение реального мира с математическими моделями. Это одна из причин, по которой обычно требуется минимум 4 или 5 лет последипломного опыта, прежде чем можно будет получить профессиональный диплом.
Один из ключевых выводов этого раздела заключается в том, что, хотя мы представили 3 четко определенные модели поддержки, мы должны быть осторожны, слишком доверяя результатам аналитического моделирования, и признавать, что фактические основания редко полностью соответствуют это идеализированное поведение.
После того, как опоры конструкции правильно смоделированы, мы должны определить величину и направление различных реакций, возникающих в опорах. Помните, что если наша конструкция подвергается воздействию внешних сил, в опорах должны развиваться реакции, чтобы гарантировать, что конструкция остается в состоянии статического равновесия. Опорные реакции развиваются непосредственно в ответ на нагрузки, приложенные к конструкции (и любой собственный вес конструкции).
Итак, для выявления опорных реакций мы делаем предположение, что наша структура находится в состоянии статического равновесия. Это позволяет нам использовать три приведенных выше уравнения равновесия для решения неизвестных реакций.
Пример №1
Рассмотрим следующую балку, на которую действует двухточечная нагрузка. Балка имеет штифтовую опору на левом конце и роликовую опору на правом конце. Эта конфигурация поддержки (шпилька и ролик) очень распространена, и о конструкции с такой конфигурацией поддержки часто говорят, что она 9. 1330 просто поддерживает .
1330 просто поддерживает .
Обратите внимание на стабильность, обеспечиваемую этой конфигурацией поддержки. Балка не могла двигаться горизонтально (даже если были приложены горизонтальные силы), потому что она удерживается в горизонтальном направлении опорой штифта в точке A. Она не может двигаться вертикально (сейчас игнорируем отклонение) из-за вертикального ограничения, обеспечиваемого штифтом. и ролик в A и B соответственно. Наконец, он не может вращаться (снова игнорируя прогиб между А и В) из-за способности вертикальных реакций в точках А и В образовывать пару, сопротивляющуюся любому вращению.
Теперь наша задача состоит в том, чтобы рассчитать значения опорных реакций, необходимых для поддержания этой балки в состоянии статического равновесия. Первое, что нам нужно сделать, это нарисовать диаграмму свободного тела для балки. Как мы уже говорили, это включает в себя рисование балки изолированно, а затем наложение всех сил, действующих на балку. В этом случае это довольно просто, как вы можете видеть ниже.
В этом случае это довольно просто, как вы можете видеть ниже.
У нас есть три неизвестные реакции. Мы можем рассматривать их как потенциальных реакций, так как мы еще не знаем, оценивается ли какая-либо из них как ноль. Поскольку необходимо определить три реакции, мы можем использовать три уравнения равновесия, определенные ранее. Начнем с оценки суммы сил в вертикальном направлении или направлении Y. Предположим, что силы, направленные вверх, положительны.
(4)
(5)
Далее мы можем вычислить сумму моментов относительно любой точки и положить ее равной нулю. Если мы возьмем сумму моментов относительно точки A или B, то одно из наших неизвестных пройдет через точку вращения и будет исключено из нашего уравнения моментов. Итак, взяв моменты относительно точки А и предполагая, что моменты по часовой стрелке положительны,
(6)
(7)
(8)
Теперь технически у нас все еще есть одна неизвестная сила реакции, . При осмотре мы можем видеть, что, поскольку нет внешних приложенных горизонтальных сил, в ответ не возникает горизонтальной реакции, поэтому . Вот почему мы сказали в начале, что у нас есть три потенциальных реакций. Получается, что в ответ на приложенные нагрузки эта конструкция развивает только две вертикальные реакции. Мы можем обобщить наши результаты с окончательным эскизом структуры.
При осмотре мы можем видеть, что, поскольку нет внешних приложенных горизонтальных сил, в ответ не возникает горизонтальной реакции, поэтому . Вот почему мы сказали в начале, что у нас есть три потенциальных реакций. Получается, что в ответ на приложенные нагрузки эта конструкция развивает только две вертикальные реакции. Мы можем обобщить наши результаты с окончательным эскизом структуры.
Наконец, для этого примера мы можем написать Python для выполнения вычислений за нас. Это ни в коем случае не является существенным, и на самом деле может считаться излишним для этой конкретной проблемы. Но если вы следите за этой серией «Фундаментальная механика» и пытаетесь попутно освоить Python, это хорошее упражнение. Это также дает нам возможность легко изменять входные параметры и быстро оценивать результат без повторной ручной обработки вычислений.
Обратите внимание, что в приведенном ниже закодированном решении мы вводим общую структуру программирования, известную как условие if/else . В предыдущем уроке из этой серии наше программирование на Python просто предлагало нам ту же функциональность, что и простой калькулятор. С этим введением l ogic gates ваше кодирование теперь может делать гораздо больше, чем простой калькулятор. Обратите особое внимание на то, как работает приведенный ниже код.
В предыдущем уроке из этой серии наше программирование на Python просто предлагало нам ту же функциональность, что и простой калькулятор. С этим введением l ogic gates ваше кодирование теперь может делать гораздо больше, чем простой калькулятор. Обратите особое внимание на то, как работает приведенный ниже код.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 32 27 32 28 |
#Определить некоторые переменные L = 15 #(м) Пролет балки между опорами P1 = 45 # (кН) Величина первой точечной нагрузки (слева направо) x1 = 3 # (м) Положение первой точечной нагрузки от левой опоры P2 = 30 # (кН) Величина вторая точечная нагрузка (слева направо) x2 = 9 #(м) Положение второй точечной нагрузки от левой опоры # Рассчитать реакции Vb = ((P1*x1) + (P2*x2)) /L Va = P1+P2-Vb #Определить направление Va if(Va>0): dirA = ‘вверх’ ELIF (VA <0): DIRA = ‘Downwards’ else: Dira = «» #determine направление VB IF (VB> 0): DIRB = ‘ IF (VB> 0): =’ . elif(Vb<0): dirB = ‘вниз’ else: dirB=»» #Выводные операторы print(‘1. Вертикальная реакция на опоре A равна {one} kN ‘. format(one=Va)+dirA) print(‘2. Вертикальная реакция на опоре B равна {one} кН ‘.format(one=Vb)+dirB) print(‘3. При осмотре горизонтальная реакция в точке A равна нулю’)
|
Этот кодовый блок выводит следующее:
- Вертикальная реакция на опоре А составляет 48,0 кН вверх
- Вертикальная реакция на опоре В 27,0 кН вверх
- При осмотре горизонтальная реакция в точке А равна нулю
Пример #2
В качестве следующего примера рассмотрим ту же балку, подверженную той же нагрузке, но с удаленной роликовой опорой в точке B и заменой штифтовой опоры в точке A на встроенную или консольную опору. Теперь у нас есть классическая консольная балка.
Рис. 10. Консольная балкаНачнем с оценки суммы вертикальных сил,
(9)
(10)
При осмотре мы снова видим, что горизонтальной реакции нет, поэтому . Наконец, мы можем оценить сумму моментов относительно точки A,
Наконец, мы можем оценить сумму моментов относительно точки A,
(11)
Знак минус здесь означает, что предполагаемое направление реакции момента на рис. 11 было неправильным, и момент реакции действительно действует в направлении против часовой стрелки. . Всякий раз, когда момент силы оценивается как отрицательное число, это говорит нам о том, что сила или момент действует в направлении, противоположном тому, которое первоначально предполагалось при расчете. Таким образом, мы можем переформулировать как положительное число и использовать стрелку, чтобы указать его направление.
(12)
Это имеет смысл, когда мы представляем, что влияние приложенных сил на балку заставит ее вращаться по часовой стрелке вокруг точки A. Следовательно, реактивный момент должен действовать против часовой стрелки, чтобы реагировать на это вращение и сопротивляться состав. Мы можем обобщить наши выводы с помощью краткого очерка.
Рис. 12. Консольная балка со всеми опорными реакциями.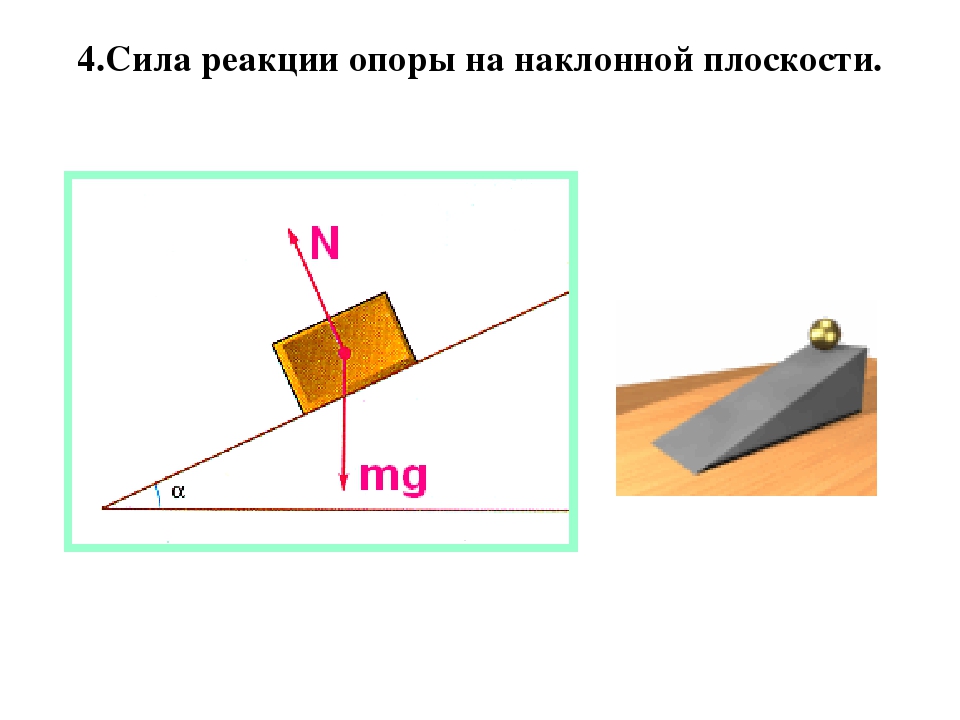
Опять же, давайте напишем решение, которое автоматизирует процесс вычислений.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# Расчет реакций Ma = -((P1*x1) + (P2*x2)) Va = P1+P2 Vb = 0 #determine Направление VA IF (VA> 0): Dira = ‘Upward’ ELIF (VA <0): Dira = ‘вниз’ ERSH: Dira = « ERST: Dira =» : Dira = « : Dira =» #Определить ориентацию Ma if(Ma>0): dirMa = ‘по часовой стрелке’ elif(Ma<0): dirMa = ‘против часовой стрелки’ =»»else: 90 dir Ma 90 #Выходные операторы print(‘1. print(‘2. Реакция момента на опоре A равна {один} кНм ‘.format(one=Ma)+dirMa) print(‘3. При осмотре горизонтальная реакция на A равна нулю’) |
Этот код выводит следующее:
- Вертикальная реакция на опоре А составляет 75 кН вверх
- Реакция момента на опоре А составляет -405 кНм против часовой стрелки
- При осмотре горизонтальная реакция в точке А равна нулю
Пример №3
Далее рассмотрим ту же балку и нагрузку, но на этот раз со встроенной опорой в точке А и роликовой опорой в точке В – комбинация двух предыдущих случаев. Эту конфигурацию балки и опор часто называют консольно-подпирающей.
Рис. 13. Подперто-консольная балка.Наша диаграмма свободного тела показывает 4 неизвестные потенциальные реакции и . Они представлены на диаграмме свободного тела ниже.
Рис. 14. Схема свободного тела с опорой и консолью.
Сразу видно, что у нас могут возникнуть проблемы — у нас 4 неизвестных, но только три уравнения, но давайте следовать нашей процедуре и посмотрим, куда она нас приведет. Оценка суммы сил в вертикальном направлении сначала дает
(13)
Рассмотрим сумму моментов относительно точки A далее,
(14)
До сих пор мы не смогли решить ни одно из наших неизвестных, и у нас есть только одно больше уравнения для использования. Оценка суммы сил в горизонтальном направлении или направлении x дает нам знакомый результат . Итак, мы не приблизились к решению для или . Эта конструкция называется статически неопределимой , поскольку одних только уравнений статики недостаточно для оценки неизвестных сил реакции. Чтобы найти реакции, нам нужно будет использовать более сложный метод анализа, который мы оставим на другой день. Этот последний пример просто демонстрирует то, что мы уже знаем; для решения неизвестных нам нужны независимые уравнения.
4.0 Примеры вопросов
Теперь, когда мы определились с основным рабочим процессом и понимаем ограничения нашего подхода, мы можем попрактиковаться в расчете опорных реакций для некоторых более интересных конструкций и конфигураций нагрузки.
4.1 Пример балкиОценим опорные реакции балки на рис. 15 ниже. В отличие от предыдущих балок, эта балка имеет консольный вылет справа между B и E. Однако процесс расчета опорных реакций остается прежним. В качестве примечания: в такой конфигурации балки и опоры, где у нас есть выступ с одной стороны, часть балки между опорами, в данном случае от А до В, часто называют задний пролет .
Рис. 15. Пример балки. Обратите внимание, что на балку действует равномерно распределенная нагрузка (UDL), т.е. она действует на каждый метр длины балки. Мы еще не видели этот тип нагрузки, но мы относимся к нему достаточно логично; для целей оценки опорных реакций мы можем просто определить эквивалентную точечную нагрузку.
Получается путем вычисления общего значения UDL, в данном случае . Эта эквивалентная точечная нагрузка будет действовать в средней точке UDL. Таким образом, UDL применяется, что означает его эквивалентную точечную нагрузку или равнодействующая будет действовать справа от точки D или справа от B. Затем мы можем нарисовать диаграмму свободного тела с результирующей силой, показанной зеленым цветом.
Рис. 16. Диаграмма свободного тела с результирующей силой UDL, показанной зеленым цветом и действующей справа от D.На этом этапе мы готовы приступить к оценке уравнений равновесия. Начнем с оценки суммы моментов относительно точки A,
(15)
(16)
Затем мы можем оценить сумму вертикальных сил, чтобы определить ,
(17)
(18)
Осмотром мы можем констатировать, что горизонтальная реакция равна нулю, так как отсутствуют внешние горизонтальные силы. Теперь мы можем суммировать эти силы реакции на окончательном эскизе конструкции, рис.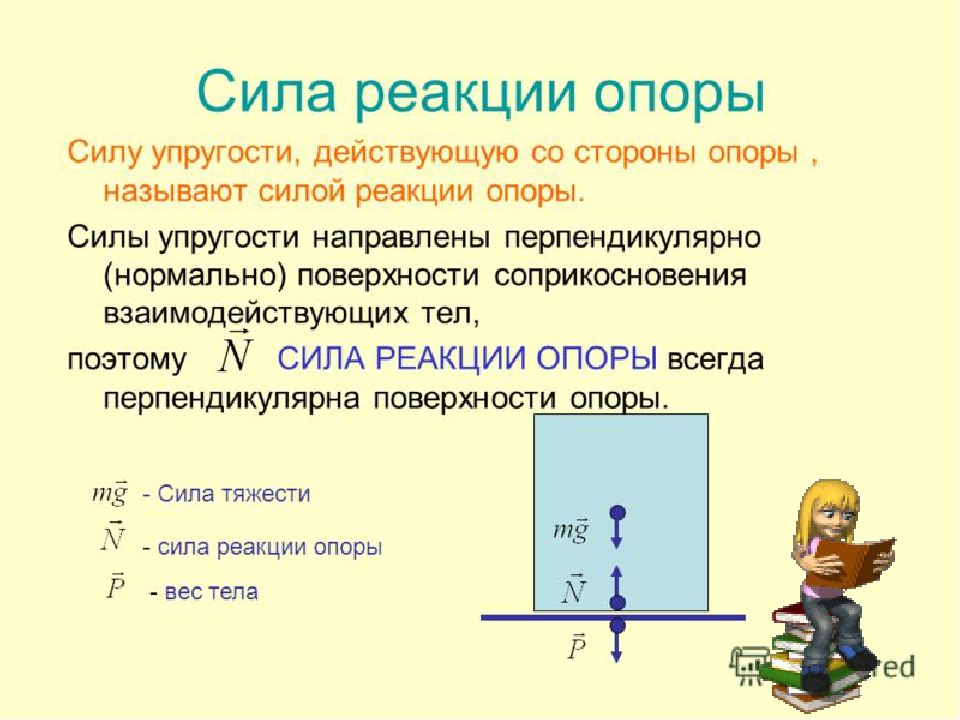 17.
17.
Чтобы еще немного попрактиковаться в Python, мы можем написать решение, следуя практически той же процедуре, что и выше.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 . |
#Определить некоторые переменные L1 = 11 #(м) Пролет балки между опорами L2 = 3 #(м) Длина свеса правой стороны P1 = 80 #(кН) Величина первой точечной нагрузки (лево- вправо) x1 = 5 #(м) Положение первой точечной нагрузки от левой опоры w = 25 #(кН/м) Величина равномерно распределенной нагрузки (UDL) x_start = 9 #(м) Положение начала UDL x_end = 14 #(м) Положение конца UDL M = 40 #(кНм) Величина приложенного момента #Рассчитать реакции Vb = ((P1*x1) + (w*(x_end-x_start)*(x_start+(x_end-x_start)/2)) + M)/L1 Va = P1-Vb+(w *(x_end-x_start)) #Определить направление Va if(Va>0): dirA = ‘вверх’ elif(Va<0): dirA = ‘вниз’ 2 else: dirA=»» #Определить направление Vb if(Vb>0): dirB = ‘вверх’ elif(Vb<0): dirB = ‘вниз’ else: dirB=»» #Выходные операторы print(‘1. print(‘2. Вертикальная реакция на опоре B равна {one} кН ‘.format(one=round(Vb,1))+dirB) print(‘3. При осмотре горизонтальная реакция в точке А равна нулю’)
|
Этот кодовый блок выводит:
- Вертикальная реакция на опоре А составляет 34,3 кН вверх
- Вертикальная реакция на опоре B 170,7 кН вверх
- При осмотре горизонтальная реакция в точке А равна нулю
Для нашего последнего примера давайте рассмотрим кое-что более интересное; каркасная конструкция, подверженная действию как вертикальных, так и горизонтальных сил, рис. 18. Хотя конструкция и нагрузка могут показаться немного более сложными, определение реакций на самом деле не сложнее, чем то, что мы уже сделали.
Рис. 18. Пример рамы. Первый шаг всегда один и тот же — нарисуйте диаграмму свободного тела.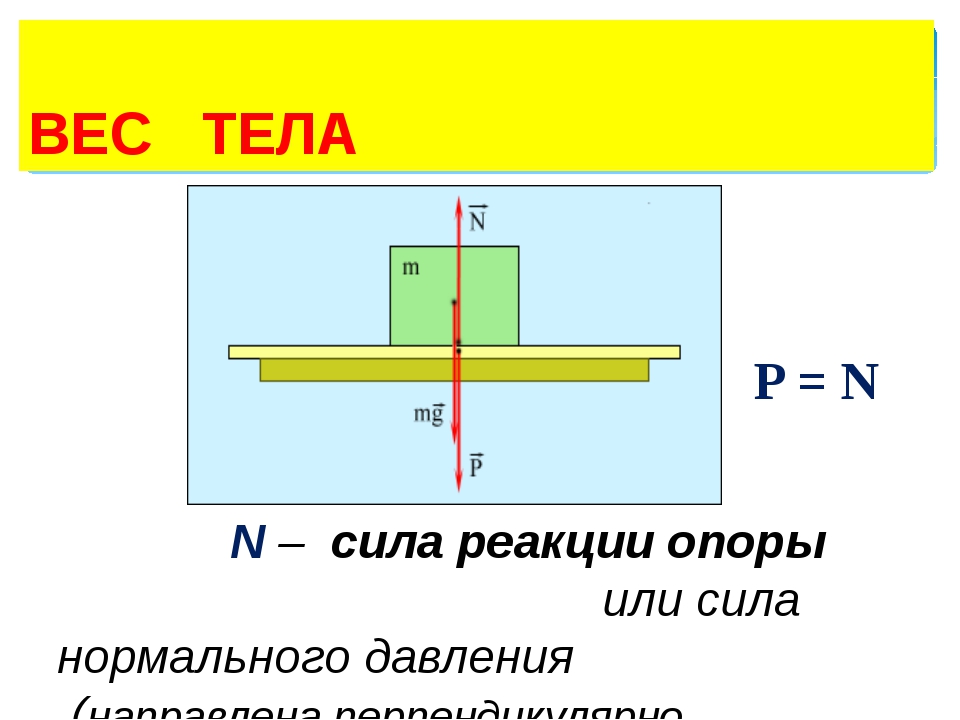 Так как эта структура имеет две UDL, мы также оценим и покажем величину и расположение их равнодействующих сил. Для UDL, применяемого слева к наклонному элементу балки, мы получаем результирующую величину, наблюдая, что UDL применяется вдоль наклонной длины . Это дает равнодействующую, действующую на полпути между A и B. UDL, применяемая между E и F, легко определяется как действующая горизонтально влево, на полпути между E и F. Теперь мы можем набросать полную диаграмму свободного тела, рис. 19..
Так как эта структура имеет две UDL, мы также оценим и покажем величину и расположение их равнодействующих сил. Для UDL, применяемого слева к наклонному элементу балки, мы получаем результирующую величину, наблюдая, что UDL применяется вдоль наклонной длины . Это дает равнодействующую, действующую на полпути между A и B. UDL, применяемая между E и F, легко определяется как действующая горизонтально влево, на полпути между E и F. Теперь мы можем набросать полную диаграмму свободного тела, рис. 19..
После того, как мы убедились, что существует не более 3 потенциальных реакций и структура статически определена, мы просто промываем и повторяем ту же процедуру, с которой мы уже знакомы. Неважно, с какого уравнения мы начнем; Я начну с оценки суммы горизонтальных сил,
(19)
Двигаясь дальше, мы можем оценить сумму сил в вертикальном направлении,
(20)
(21)
Наконец, вычисляя сумму моментов относительно точки A,
(22)
(23)
(24)
эскиз конструкции, рис. 20.
20.
5.0 Резюме
На этом мы завершаем обсуждение диаграмм свободного тела, уравнений равновесия и опорных реакций. На самом деле здесь есть только несколько важных выводов, о которых следует напомнить себе:
– Схемы произвольного тела невероятно полезны, когда мы начинаем анализировать более сложные конструкции – сделайте набросок диаграммы свободного тела первым шагом в любом структурном анализе.
— Мы представили три модели поддержки — помните, что они моделируют идеализированное поведение; либо полная фиксация, либо нулевая фиксация в различных степенях свободы. Это редко то, что мы видим в реальных структурах, поэтому помните об ограничениях и упрощениях, присущих вашему аналитическому моделированию.
– Для двухмерных плоских структур, которые мы проанализировали здесь, у нас есть только три уравнения равновесия, поэтому мы можем решить только для трех неизвестных реакций. Если условия опоры приводят к более чем трем неизвестным реакциям, конструкция является статически неопределимой, и нам нужно разбить более крупные пушки, чтобы проанализировать ее (см. , например, метод жесткости или анализ виртуальной работы).
, например, метод жесткости или анализ виртуальной работы).
Надеюсь, этот учебник по фундаментальной механике был вам полезен. Следите за следующим уроком из этой серии. Если вы хотите получать уведомления о публикации следующей части, присоединяйтесь к бесплатному курсу «Основы механики», зарегистрировавшись по ссылке в верхней части этого руководства.
Линкедин Твиттер YouTube
Автор
Доктор Шон Кэрролл
BEng (с отличием), MSc, PhD, CEng MIEI, FHEA
Привет, я Шон, основатель DegreeTutors.com. Я надеюсь, что вы нашли этот урок полезным. Проведя 10 лет в качестве преподавателя в университете по проектированию конструкций, я запустила DegreeTutors.com, чтобы помочь большему количеству людей понять инженерию и получить такое же удовольствие от ее изучения, как и я. Не стесняйтесь связаться или подписаться на DegreeTutors в любой из социальных сетей.
Если вам нужен полный доступ ко всей библиотеке курсов DegreeTutors (и коду!) за небольшую ежегодную плату, рассмотрите возможность подписки на DegreeTutors Членство с полным доступом .
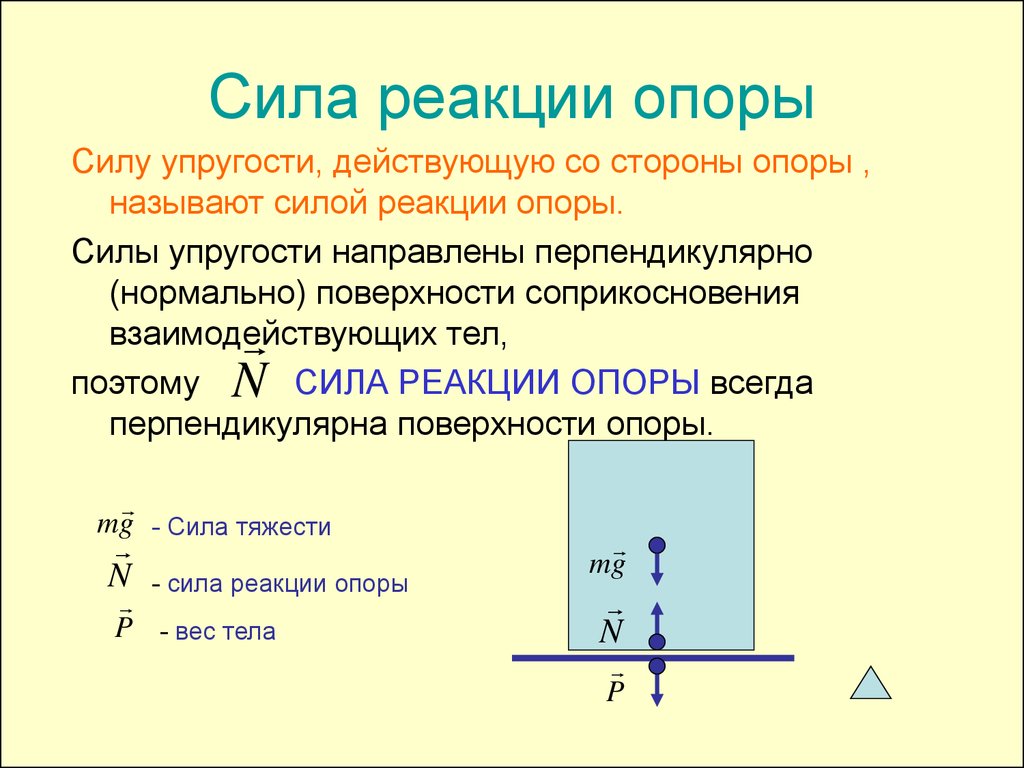 Вертикальная реакция на опоре A равна {one} kN ‘.format(one=Va)+dirA)
Вертикальная реакция на опоре A равна {one} kN ‘.format(one=Va)+dirA) Вертикальная реакция на опоре A равна {один} кН ‘.format(one=round(Va,1) ))+dirA)
Вертикальная реакция на опоре A равна {один} кН ‘.format(one=round(Va,1) ))+dirA)