Вес тела. Сила реакции опоры. Сила натяжения нити | LAMPA
Многие из вас пользуются или пользовались обычной проводной компьютерной мышкой. Если такая проводная мышка рядом с вами, то посмотрите на нее (а если ее нет рядом — то представьте). Мы знаем, что, как и на все тела на Земле, на нее действует сила тяжести Fтяготения=m⋅gF_{тяготения}=m\cdot gFтяготения=m⋅g.
Почему же она не падает вниз, а находится в состоянии покоя? Мы помним из 1-го закона Ньютона, что в инерциальных системах тело может находиться в состоянии покоя, если на него не действуют никакие силы (не наш случай) или действие всех сил скомпенсировано. Значит, что-то компенсирует действие силы тяжести. Но что? Мы забыли, что мышка лежит на столе. Мышка, на которую действует сила тяжести m⋅g⃗m\cdot\vec{g}m⋅g⃗, в свою очередь давит на стол с силой, которую называют вес тела. Обычно вес тела обозначается P⃗\vec{P}P⃗. Но из 3-го закона Ньютона мы знаем: с какой силой мышка давит на стол (мышка→\rightarrow→стол), с точно такой же по величине силой стол давит на мышку (стол→\rightarrow→мышка). Сила, с которой стол давит на мышку, называется силой реакции опоры. Чаще всего она обозначается N⃗\vec{N}N⃗. Из 3-го закона Ньютона следует, что N⃗=−P⃗.\vec{N}=-\vec{P}{.}N⃗=−P⃗.
Заметьте, что сил три:
- на тело действует сила тяжести m⋅g⃗m\cdot\vec{g}m⋅g⃗
- из-за действия силы тяжести на мышку мышка давит на стол с силой P⃗\vec{P}P⃗ (вес тела)
- и уже стол «отвечает» мышке на ее давление силой реакции опоры N⃗\vec{N}N⃗.
Важно помнить, что хотя силы N⃗\vec{N}N⃗ и P⃗\vec{P}P⃗ связаны друг с другом и равны по модулю, но приложены они к разным телам. Еще раз:
- вес тела P⃗\vec{P}P⃗ приложен к опоре (столу) со стороны мышки
- сила реакции опоры N⃗\vec{N}N⃗ приложена к мышке со стороны стола как «ответ» стола на действие мышки.
Давайте посмотрим, насколько хорошо вы усвоили разницу между весом P⃗\vec{P}P⃗ и силой реакции опоры N⃗\vec{N}N⃗. Попробуйте решить классическую задачу.
lampa.io
Материалы для урока «Сила реакции опоры»
Инфоурок › Физика ›Другие методич. материалы›Материалы для урока «Сила реакции опоры»Выберите документ из архива для просмотра:
Выбранный для просмотра документ Сила реакции опоры.pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:Сила реакции опоры.
2 слайд
Если тело находится на горизонтальной поверхности, на него действует сила тяжести, направленная вертикально вниз, и сила упругости, с которой опора действует на тело. Силу упругости в данном случае называют силой реакции опоры.
3 слайд Описание слайда:
Описание слайда:Сила упругости, которая возникает при действии опоры на тело, называется силой реакции опоры и направлена перпендикулярно поверхности соприкосновения тел
4 слайд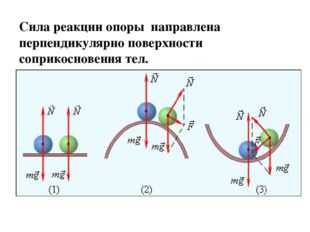 Описание слайда:
Описание слайда:Сила реакции опоры направлена перпендикулярно поверхности соприкосновения тел.
5 слайд Описание слайда:
Описание слайда:Сила реакции опоры направлена перпендикулярно поверхности соприкосновения тел.
6 слайд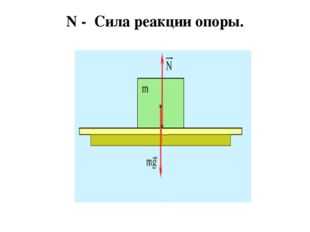 Описание слайда:
Описание слайда:N — Сила реакции опоры.
7 слайд Описание слайда:
Описание слайда:1. Сила реакции опоры на горизонтальной поверхности. P = mg
 Описание слайда:
Описание слайда:2.Сила реакции опоры в ускоренно движущемся лифте (ракете).
9 слайд Описание слайда:
Описание слайда:2.Сила реакции опоры в ускоренно движущемся лифте (ракете).
10 слайд Описание слайда:
Описание слайда:Сила реакции опоры в ускоренно движущемся лифте. Вектор ускорения направлен вертикально вниз. 1) a < g, N < mg; 2) a = g, N = 0 ; 3) a > g, N< 0.
11 слайд Описание слайда: 12 слайд
Описание слайда: 12 слайд  Описание слайда:
Описание слайда:Сила реакции опоры при вертикальном равноускоренном движении. а) ускорение направлено вверх P = m(g+a) б) ускорение направлено вниз P = m(g-a)
13 слайд Описание слайда:
Описание слайда:Тело массой 5 кг с помощью каната начинают равноускоренно поднимать вертикально вверх. Чему равна сила, действующая на тело со стороны каната, если известно, что за 3 с груз был поднят на высоту 12 м?
 Описание слайда:
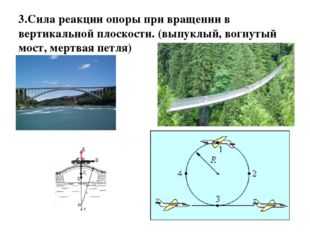
Описание слайда:3.Сила реакции опоры при вращении в вертикальной плоскости. (выпуклый, вогнутый мост, мертвая петля)
15 слайд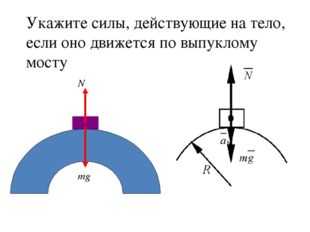 Описание слайда:
Описание слайда:Укажите силы, действующие на тело, если оно движется по выпуклому мосту mg N
16 слайд Описание слайда: 17 слайд
Описание слайда: 17 слайд 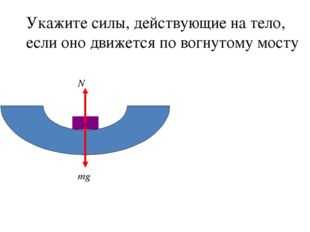 Описание слайда:
Описание слайда:Укажите силы, действующие на тело, если оно движется по вогнутому мосту mg N
18 слайд Описание слайда:
Описание слайда:Тело движется по мосту mg N mg N y
19 слайд Описание слайда:
Описание слайда:а) выпуклый мост N = m(g-a) б) вогнутый мост N = m(g+a)
 Описание слайда:
Описание слайда:Самолет выполняет фигуру высшего пилотажа «мертвая петля». В какой из отмеченных точек сила упругости, действующая на пилота со стороны кресла, максимальна? 4. 2. 3. 1.
21 слайд Описание слайда:
Описание слайда:Мальчик массой 40кг качается на качелях, длина которых 2м. Найдите силу реакции опоры со стороны качелей при прохождении нижней точки, если скорость в этот момент равна 3м/с.
22 слайд Описание слайда:
Описание слайда:4.Сила реакции опоры на наклонной плоскости.
23 слайд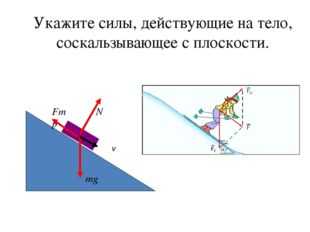 Описание слайда:
Описание слайда:Укажите силы, действующие на тело, соскальзывающее с плоскости. mg N v Fmр
24 слайд Описание слайда:
Описание слайда:Тело движется по наклонной плоскости. mg N v Fmр α а α N = mg cosα Y X mgy = mg cos
25 слайд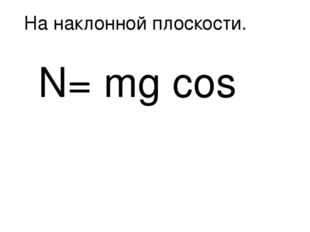
На наклонной плоскости. N= mg cos α
26 слайд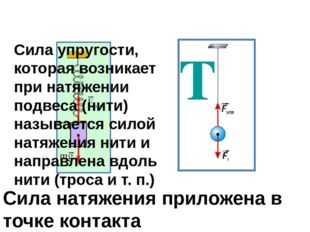 Описание слайда:
Описание слайда:Сила натяжения приложена в точке контакта Сила упругости, которая возникает при натяжении подвеса (нити) называется силой натяжения нити и направлена вдоль нити (троса и т. п.)
27 слайд Описание слайда: 28 слайд
Описание слайда: 28 слайд  Описание слайда:
Описание слайда:При отклонении подвеса. T= mg cos α

Курс профессиональной переподготовки
Учитель физики

Курс повышения квалификации

Курс повышения квалификации
infourok.ru
Равнодействующая сила, обозначение сил, нахождение проекций на оси
Тестирование онлайн
Определение
Это векторная сумма всех сил, действующих на тело.
Велосипедист наклоняется в сторону поворота. Сила тяжести и сила реакции опоры со стороны земли дают равнодействующую силу, сообщающую центростремительное ускорение, необходимое для движения по окружности
Взаимосвязь со вторым законом Ньютона
Вспомним закон Ньютона:
Равнодействующая сила может быть равна нулю в том случае, когда одна сила компенсируется другой, такой же силой, но противоположной по направлению. В этом случае тело находится в покое или движется равномерно.
Сила Архимеда уравновешивается силой тяжести, тело равномерно перемещается в жидкости вниз. | Сила тяжести уравновешивается силой упругости. Книга покоится |
Если равнодействующая сила НЕ равна нулю, то тело движется равноускоренно. Собственно именно эта сила является причиной неравномерного движения. Направление равнодействующей силы всегда совпадает по направлению с вектором ускорения.
Когда требуется изобразить силы, действующие на тело, при этом тело движется равноускоренно, значит в направлении ускорения действующая сила длиннее противоположной. Если тело движется равномерно или покоится длина векторов сил одинаковая.
Сила реакции опоры (сила, направленная вверх) длиннее силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вверх | Сила реакции опоры (сила, направленная вверх) короче силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вниз. Вектор силы тяжести, направленный вниз, длиннее. |
Нахождение равнодействующей силы
Для того, чтобы найти равнодействующую силу, необходимо: во-первых, верно обозначить все силы, действующие на тело; затем изобразить координатные оси, выбрать их направления; на третьем шаге необходимо определить проекции векторов на оси; записать уравнения. Кратко: 1) обозначить силы; 2) выбрать оси, их направления; 3) найти проекции сил на оси; 4) записать уравнения.
Как записать уравнения? Если в некотором направлении тело двигается равномерно или покоится, то алгебраическая сумма (с учетом знаков) проекций сил равна нулю. Если в некотором направлении тело движется равноускоренно, то алгебраическая сумма проекций сил равна произведению массы на ускорение, согласно второму закону Ньютона.
Примеры
На движущееся равномерно по горизонтальной поверхности тело, действуют сила тяжести, сила реакции опоры, сила трения и сила, под действием которой тело движется.
Обозначим силы, выберем координатные оси

Найдем проекции
Записываем уравнения
Тело, которое прижимают к вертикальной стенке, равноускоренно движется вниз. На тело действуют сила тяжести, сила трения, реакция опоры и сила, с которой прижимают тело. Вектор ускорения направлен вертикально вниз. Равнодействующая сила направлена вертикально вниз.
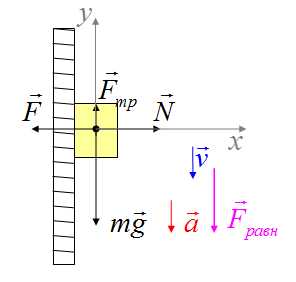
Тело равноускоренно движется по клину, наклон которого альфа. На тело действуют сила тяжести, сила реакции опоры, сила трения.

Главное запомнить
1) Если тело покоится или движется равномерно, то равнодействующая сила равна нулю и ускорение равно нулю;
2) Если тело движется равноускоренно, значит равнодействующая сила не нулевая;
3) Направление вектора равнодействующей силы всегда совпадает с направлением ускорения;
4) Уметь записывать уравнения проекций действующих на тело сил
Блок — механическое устройство, колесо, вращающееся вокруг своей оси. Блоки могут быть подвижными и неподвижными.
Неподвижный блок используется лишь для изменения направления силы.

Тела, связанные нерастяжимой нитью, имеют одинаковые по величине ускорения.
Подвижный блок предназначен для изменения величины прилагаемых усилий. Если концы веревки, обхватывающей блок, составляют с горизонтом равные между собой углы, то для подъёма груза потребуется сила вдвое меньше, чем вес груза. Действующая на груз сила относится к его весу, как радиус блока к хорде дуги, обхваченной канатом.

Ускорение тела А в два раза меньше ускорения тела В.
Фактически, любой блок представляет собой рычаг, в случае неподвижного блока — равноплечий, в случае подвижного — с соотношением плеч 1 к 2. Как и для всякого другого рычага, для блока справедливо правило: во сколько раз выигрываем в усилии, во столько же раз проигрываем в расстоянии
Также используется система, состоящая из комбинации нескольких подвижных и неподвижных блоков. Такая система называется полиспаст.

fizmat.by
1.2.2. Вес тела, сила реакции опоры,
сила натяжения нити
Вес
тела ( )
определяется силой, с которой тело
действует на опору или растягивает нить
подвеса. Вес тела измеряется в ньютонах.
Вес тела приложен не к самому телу, а к
опоре или подвесу. Если опора или подвеснеподвижны относительно Земли, то вес равен силе
тяжести тела.
)
определяется силой, с которой тело
действует на опору или растягивает нить
подвеса. Вес тела измеряется в ньютонах.
Вес тела приложен не к самому телу, а к
опоре или подвесу. Если опора или подвеснеподвижны относительно Земли, то вес равен силе
тяжести тела.
Реакция
опоры ( )
определяется силой, с которой опора
действует на находящееся на ней тело.
Реакция опоры всегда перпендикулярна
поверхности, на которую давит тело.
)
определяется силой, с которой опора
действует на находящееся на ней тело.
Реакция опоры всегда перпендикулярна
поверхности, на которую давит тело.
Рис. 5. Силы, действующие на тело в отсутствие сил трения
Рассмотрим силы, действующие на тело в первом и во втором случаях (рис.5, а, б), в отсутствие сил трения (рис.6).
Рис.6. Силы натяжения
Под
действием проекции силы тяжести  тело
будет перемещаться вдоль наклонной
плоскости (рис.6, в).
тело
будет перемещаться вдоль наклонной
плоскости (рис.6, в).
Сила
натяжения нити ( )
(рис.7).
)
(рис.7).
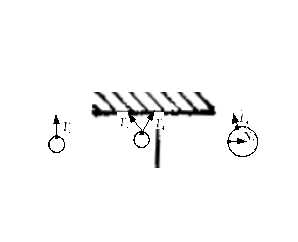
Рис. 7. Силы натяжения
Если реакция опоры становится равной нулю, говорят, что тело находится в состоянии невесомости. В состоянии невесомости тело движется только под действием силы тяжести.
1.2.3. Инертность и инерция. Инерциальные системы отсчета.
Первый закон Ньютона
Опыт показывает, что любое тело противится попыткам изменить его состояние вне зависимости от того, движется оно или покоится. Это свойство тел называется инертностью. Понятие инертности нельзя путать с инерцией тел. Инерция тел проявляется в том, что в отсутствие внешних воздействий тела находятся в состоянии покоя или прямолинейного и равномерного движения до тех пор, пока какое – либо внешнее воздействие не изменит этого состояния. Инерция, в отличие от инертности, не имеет количественной характеристики.
Задачи динамики решаются с помощью трех основных законов, получивших название законов Ньютона. Законы Ньютона выполняются в инерциальных системах отсчета. Инерциальные системы отсчета (ИСО) — это системы отсчета, в которых тела, не подверженные воздействию других тел, движутся без ускорения, то есть прямолинейно и равномерно, или покоятся.
Первый закон Ньютона (закон инерции): существуют такие системы отсчета (так называемые, инерциальные системы), для которых любая материальная точка в отсутствие внешних воздействий движется равномерно и прямолинейно или находится в состоянии покоя. Согласно принципу относительности Галилея все механические явления в различных инерциальных системах отсчета протекают одинаково и никакими механическими опытами невозможно установить, покоится данная система отсчета или движется прямолинейно и равномерно.
1.2.4. Второй закон Ньютона. Импульс тела и импульс силы.
Закон сохранения импульса. Третий закон Ньютона
Второй закон Ньютона: ускорение, приобретаемое материальной точкой под действием одной или нескольких сил, прямо пропорционально действующей силе (или равнодействующей всех сил), обратно пропорционально массе материальной точки и по направлению совпадает с направлением действующей силы (или равнодействующей):
 .
(8)
.
(8)
Второй закон Ньютона имеет еще одну форму записи. Введем понятие импульса тела.
Импульс
тела (или просто, импульс) – мера механического
движения, определяемая произведением
массы тела 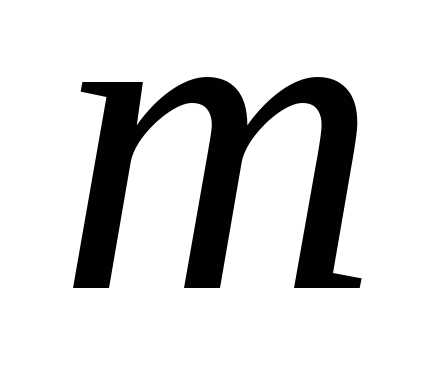 на его скорость
на его скорость 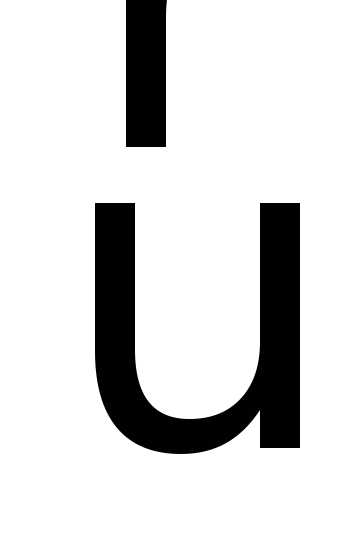 ,
т.е.,
,
т.е.,  .
Запишем второй закон Ньютона — основное
уравнение динамики поступательного
движения:
.
Запишем второй закон Ньютона — основное
уравнение динамики поступательного
движения:
.
Заменим
сумму сил на ее равнодействующую  и запись второго закона Ньютона принимает
следующий вид:
и запись второго закона Ньютона принимает
следующий вид:
 ,
(9)
,
(9)
а сам второй закон Ньютона закон может быть сформулирован еще и так: скорость изменения импульса определяет действующую на тело силу.
Преобразуем
последнюю формулу:
.
Величина получила названиеимпульса
силы. Импульс
силы
получила названиеимпульса
силы. Импульс
силы 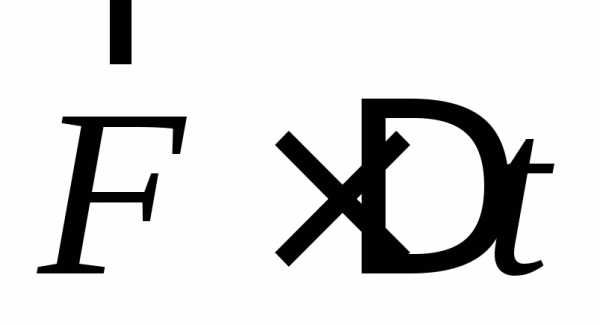 определяется
изменением импульса тела
определяется
изменением импульса тела  .
.
Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной).
Закон сохранения импульса: импульс замкнутой системы тел есть величина постоянная.
Третий закон Ньютона: силы, возникающие при взаимодействии тел, равны по величине, противоположны по направлению и приложены к разным телам (рис. 8):
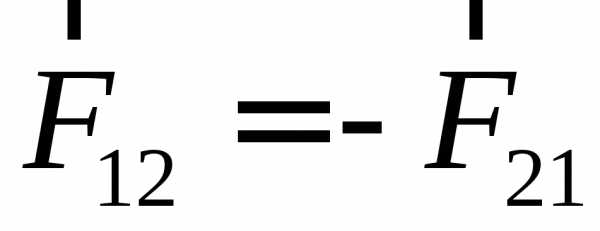 .
(10)
.
(10)
Рис. 8. Третий закон Ньютона
Из 3-го закона Ньютона следует, что при взаимодействии тел силы возникают парами. В полную систему законов динамики кроме законов Ньютона необходимо включить принцип независимости действия сил: действие какой-либо силы не зависит от присутствия или отсутствия других сил; совместное действие нескольких сил равно сумме независимых действий отдельных сил.
studfiles.net
Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.
 Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).
Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).
Все связи можно разделить на несколько типов.
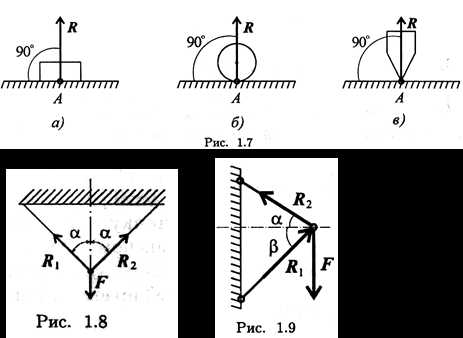
Связь — гладкая опора (без трения).Реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре (рис. 1.7).
Гибкая связь (нить, веревка, трос, цепь). Груз подвешен на двух нитях (рис. 1.8).
Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.
Жесткий стержень.
На схемах стержни изображают толстой сплошной линией (рис. 1.9).
Стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня.
Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.
Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент наложенными на него связями.
Убираем стержень 1, в этом случае стержень 2 падает вниз. Следовательно, сила от стержня 1 (реакция) направлена вверх. Убираем стержень 2. В этом случае точка А опускается вниз, отодвигаясь от стены. Следовательно, реакция стержня 2 направлена к стене.
Шарнирная опора
Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.
Подвижный шарнир. Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки) (рис. 1.10).
Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, т. к. не допускается только перемещение поперек опорной поверхности.
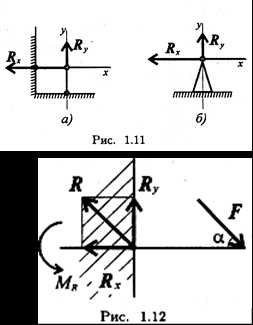 Неподвижный шарнир. Точка крепления перемещаться не может. Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Её принято изображать ввиде двух составляющих: горизонтальной и вертикальной (Rx, Ry) (рис. 1.11).
Неподвижный шарнир. Точка крепления перемещаться не может. Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Её принято изображать ввиде двух составляющих: горизонтальной и вертикальной (Rx, Ry) (рис. 1.11).
Защемление или «заделка». Любые перемещения точки крепления невозможны.
Под действием внешних сил в опоре возникают реактивная сила и реактивный момент МR, препятствующий повороту (рис. 1.12).
Реактивную силу принято представлять в виде двух составляющих вдоль осей координат
R = Rx + Ry
Примеры решения задач
Последовательность решения задач:
- Выбрать тело (точку), равновесие которого следует рассматривать.
- Освободить тело (шарнир) от связей и изобразить действующие на него активные силы и реакции отброшенных связей. Причем реакции стержней следует направить от шарнира, так как принято предполагать, что стержни растянуты.
- Выбрать оси координат и составить уравнения равновесия, используя условия равновесия системы сходящихся сил на плоскости ∑Xi = 0; ∑Yi = 0. Выбирая оси координат, следует учитывать, что полученные уравнения будут решаться проще, если одну из осей направить перпендикулярно одной из неизвестных сил.
- Определить реакции стержней из решения указанной системы уравнений.
- Проверить правильность полученных результатов, решив уравнения равновесия относительно заново выбранных координат х и у.
Пример 1. Груз подвешен на стержнях и канатах и находится в равновесии (рис. 1.13). Изобразить систему сил, действующих на шарнир А.
Решение
1. Реакции стержней направлены вдоль стержней, реакции гибких связей направлены вдоль нитей в сторону натяжения (рис. 1.13, а).
2. Для определения точного направления усилий в стержнях мысленно убираем последовательно стержни 1 и 2. Анализируем возможные перемещения точки А.
Неподвижный блок с действующими на него силами не рассматриваем.
3. Убираем стержень 1, точка А поднимается и отходит от стены, следовательно, реакция стержня 1 направлена к стене.
4. Убираем стержень 2, точка А поднимается и приближается к стене, следовательно, реакция стержня 2 направлена от стены вниз.
5. Канат тянет вправо.
6. Освобождаемся от связей (рис. 1.13, б).

Пример 2. Шар подвешен на нити и опирается на стену (рис. 1.14а). Определить реакции нити и гладкой опоры (стенки).
Решение
1. Реакция нити — вдоль нити к точке В вверх (рис. 1.14, б).
2. Реакция гладкой опоры (стенки) — по нормали от поверхности опоры.
Пример 3. Представим, что на горизонтально расположенный брус АБ, собственной массой которого пренебрегаем, действует вертикальная нагрузка F, приложенная в точке С бруса (рис. 1.14-1, а). Левый конец бруса А прикреплен к опоре шарниром, а правый В опирается на гладкую наклонную плоскость.
Изобразим брус схематично отрезком АВ, как на рис. 1.14-1, б, и приложим к нему в точке С вертикальную силу F. В точке В со стороны наклонной плоскости к брусу приложена ее реакция RB, направленная перпендикулярно плоскости; линии действия сил F и RBпересекаются в точке О. Кроме этих сил на брус действует еще одна сила — реакция шарнирно-неподвижной опоры. А так как брус находится в равновесии, то линия действия третьей силы также пройдет через точку О, т. е. реакция R шарнир-но-неподвижной опоры направлена вдоль отрезка АО.
Примененный здесь метод рассуждения называется принципом освобождения тела от связей и замены связей их реакциями.
Пример 4. Определить усилие в стержне CD и силу давления груза А на опорную плоскость EF (рис. 1.14-2, а). Массой стержня CD, блока К, каната и трением каната о блок пренебречь.
Решение
Натяжение каната во всех его точках одинаково и равно силе тяжести груза В, так как неподвижный блок изменяет только направление силы, действующей на канат.
Рассмотрим равновесие системы: стержень CD и блок К с прилегающим к нему отрезком каната ML. Отбросим связи и заменим их действие соответствующими реакциями (рис. 1.14-2, 6). Для полученной системы сил можно составить только одно уравнение равновесия:
На рис. 1.14-2, в показаны силы, действующие на груз А с прилегающим к нему отрезком каната ОН. REF — реакция опорной плоскости.
Так как груз А находится в равновесии, то
откуда
Rеf = Pa – Рв = 600 – 400 = 200 Н.
Сила давления груза А на опорную плоскость RA показана на рис, 1.14-2, г. Очевидно, RA = REF = 200 H (сила действия равна силе противодействия).
Пример 5.Определить реакции стержней, удерживающих грузы F1 = 70 кН и F2 = 100 кН (рис. а). Массой стержней пренебречь.
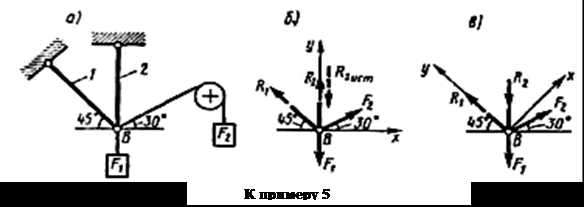 |
Решение
1. Рассматриваем равновесие шарнира В (рис. а).
2. Освобождаем шарнир В от связей и изображаем действующие на него активные силы и реакции связей (рис. б).
3. Выбираем систему координат, совместив ось у по направлению С реакцией R2 (рис. б) и составляем уравнения равновесия для системы сил, действующих на шарнир В:
3. Определяем реакции стержней R1 и R2, решая уравнения.
Подставляя найденное значение R1 в уравнение (2), получаем
Знак минус перед значением R2 указывает на то, что первоначально выбранное направление реакции неверное — следует направить реакцию R2 в противоположную сторону, т.е. к шарниру В (на рис. б истинное направление реакции R2 показано штриховым вектором).
5. Проверяем правильность полученных результатов, выбрав новое расположение осей координат х и у (рис. а). Относительно этих осей составляем уравнения равновесия:
Значения реакций R1 и R2, полученные при решении уравнений (1) и (2), совпадают по величине и направлению со значениями, найденными из уравнений (3) и (4), следовательно, задача решена правильно.
Контрольные вопросы и задания
1. Какая из приведенных систем сил (рис. 1.15) уравновешена?
2. Какие силы системы (рис. 1.16) можно убрать, не нарушая механического состояния тела:
3. Тела 1 и 2 (рис. 1.17) находятся в равновесии. Можно ли убрать действующие системы сил, если тела абсолютно твердые? Что изменится, если тела реальные, деформируемые?
4. Укажите возможное направление реакций в опорах (рис. 1.18).
ЛЕКЦИЯ 2
infopedia.su
сила нормального давления и сила реакции опоры это одно и тоже или нет????
Сила нормального давления — нормальная (перпендикулярная) составляющая силы давления, приложенной к телу (к опоре, к какой либо поверхности) . Сила реакции опоры — это сила, действующая на тело, находящегося на поверхности, со стороны этой поверхности. Силу реакции опоры принято раскладывать на две составляющие; перпендикулярную опоре и касательную. Перпендикулярная составляющая называется нормальной составляющей силы реакции опоры или просто — нормальной реакцией опоры, а касательная называется силой трения. Если тело (брусок) лежит на опоре (необязательно горизонтальной) , то оно давит на опору с силой, перпендикулярная поверхности составляющая которой — есть сила норм. давления (она приложена к опоре) , а на само тело действует перпендикулярная поверхности нормальная реакция опоры (приложена к телу) . По третьему закону Нютона эти силы равны по величине (и направлены противоположно) . Сила давления может быть совершенно не связана с силой тяжести.
они равны по модулю, но приложены к разным телам и противоположно направлены. сила нормального давления приложена со стороны тела к опоре и по своей природе — сила тяжести, направлена вертикально вниз. сила реакции опоры приложена со стороны опоры к телу и по своей природе — сила упругости, направлена вертикально вверх.
Ответил marat aminov верно в принципе, но неточно. если опора не горизонтальна, то соответственно и сила нормального давления, и реакция опоры отклоняются от вертикали. Интересные явления наступают, когда равнодействующая силы тяжести и реакции опоры на наклонной плоскости превышает силу трения — тело начинает скользить. И это весьма широко применяется в технике.
touch.otvet.mail.ru
какая формула силы реакции опоры
Сила реакции опоры это пассивная сила. То есть нет какой-то расчетной формулы. Она равна силе тяжести с которой тело давит на нее. N=mg и направлена в противоположную сторону. g=9,8
mg умножить на -1… g=9.8 <a rel=»nofollow» href=»http://www.hde.kurganobl.ru/dist/disk/Olimpiada/Praktikum/metodika/dinamika.html» target=»_blank»>http://www.hde.kurganobl.ru/dist/disk/Olimpiada/Praktikum/metodika/dinamika.html</a>
N=mg sina, N= -mg(только если sina=-1 т. е a=180
touch.otvet.mail.ru