Реакция опоры это: Что такое сила нормальной реакции? (статья)

Силы тяжести и вес — Вопросы к экзмену

 

Силы тяжести и вес

По закону всемирного тяготения все тела на Земле испытывают силу ее притяжения.

Сила тяжести тела —_это мера его притяжения к Земле (с учетом влияния вращения Земли):

G = т • g; [ G ] = ML T -2 .

  Сипа тяжести зависит от масс Земли и притягиваемого ею тела, а также от расстояния между ними. Расстояние от центра Земли до ее поверхности на полюсе меньше (6357 км), а на экваторе больше (6378 км), поэтому сила тяготения на экваторе на 0,2% меньше, чем на полюсах.

Так как Земля вращается вокруг своей оси, тела на ее поверхности испытывают действие центробежной силы инерции (фиктивной) в неинерционной (вращающейся) системе отсчета. Она больше всего на экваторе и уменьшает там силу тяготения еще на 0,3% (по сравнению с положением на полюсах). Поэтому сила тяжести равна геометрической сумме сил тяготения (гравитационной) и центробежной (инерционной).

 

На каждое звено и на все тело человека действуют силы тяжести как внешние силы, вызванные притяжением и вращением Земли. Равно­действующая параллельных сил тяжести тела приложена к его центру тяжести.

Когда тело покоится на опоре (или подвешено), сила тяжести, приложенная к телу, прижимает его к опоре (или отрывает от подвеса). Это действие тела на опору (нижнюю или верхнюю) измеряется весом тела . Вес тела (статический) — это мера воздействия тела в покое на покоящуюся же опору (или подвес), мешающую его падению. Значит, сила тяжести и вес тела не одна и та же сила. Вес всего тела человека приложен не к нему самому, а к его опоре (сила тяжести — дистантная, вес — контактная сила). В фазе полета в беге веса нет, это случай невесомости.

При воздействии головы на шейные позвонки взаимодействуют голова и позвоночный столб. Таким образом, вес головы относительно всего тела человека — сила внутренняя, относительно же позвоночного столба — внешняя. Вес, например, штанги, удерживаемой человеком, для него, конечно, внешняя сила.

При движении тела с ускорением, направленным по вертикали, возникает вертикальная сила инерции. Она направлена в сторону, противоположную ускорению. Если сила инерции направлена вниз, то она складывается со статическим весом; сила давления на опору при этом увеличивается. Если же сила инерции направлена вверх, то она вычитается из статического веса; сила давления на опору уменьшается. В обоих случаях измененный вес называют динамическим, он больше или меньше статического. Динамический вес штанги в руках спортсмена действует на него извне (внешняя сила). Динамический вес туловища при выпрыгивании вверх действует на ноги внутри тела (внутренняя сила относительно всего тела и внешняя — относительно ног).

 

Силы реакции опоры

 

Действие веса тела на опору встречает противодействие, которое называют реакцией опоры (или опорной реакцией).

Реакция опоры — это мера противодействия опоры действию на нее тела, находящегося с ней в контакте (в покое или движении). Она равна силе действия тела на опору, направлена в противоположную сторону и приложена к этому телу.

Обычно человек,, находясь на горизонтальной опоре, испытывает противодействие своему весу. В этом случае опорная реакция, как и вес тела, направлена перпендикулярно к опоре. Это нормальная (или идеальная) реакция опоры. Если поверхность не плоская, то опорная реакция перпендикулярна к плоскости, касательной к точке опоры.

Когда вес статический, то реакция опоры статическая; по величине она равна статическому весу. Если человек на опоре движется с ускорением, направленным вверх, то к статическому весу добавляется сила инерции и возникает динамическая реакция опоры. Реакция опоры — сила пассивная (реактивная). Она не может сама по себе вызвать положительные ускорения. Но без нее — если нет опоры, если не от чего оттолкнуться (или не к чему притянуться) — человек не может активно перемещаться.

Если отталкиваться от горизонтальной опоры не прямо вверх, то и сила давления на опору будет приложена не под прямым углом

к ее поверхности.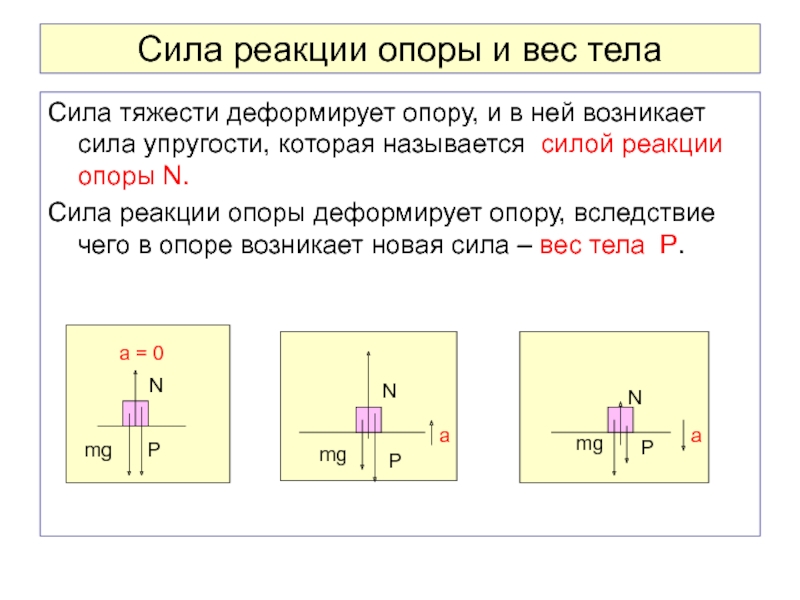 Тогда реакция опоры также не будет перпендикулярна к поверх­ности, ее можно разложить нанормальную и касательную составляющие. Когда соприкасающиеся поверхности ров­ные, без выступов, шипов и т. п. (асфальт, подошва ботинка), то касательная состав­ляющая реакции опоры и есть сила трения.

Касательная реакция может быть обу­словлена не только трением (как, напри­мер, между лыжей и снегом), но и другими взаимодействиями (например, шипы бего­вых туфель, вонзившиеся в дорожку).

Равнодействующая нормальной и каса­тельной составляющих называется об­щей реакцией опоры. Она только при свободном неподвижном положении над опорой (или под опорой) проходит через ЦМ человека. Во время же движений, отталкивания или амортизации она обычно не проходит через ЦМ, образуя относи­тельно него момент.

Еще статьи в этом разделе

Биомеханика как наука о движениях человека.

Биомеханическая характеристика силовых качеств

Биомеханическая характеристика скоростных качеств

Биомеханическая характеристика выносливости

Биомеханическая характеристика гибкости

Биомеханические методы изучения движения.

Временные характеристики.

Пространственно — временные характеристики.

Геометрия масс тела

Движения в биокинематических цепях

Задачи биомеханики спорта

Звенья тела как рычаги и маятники

Импульс силы и импульс момента силы

Инерционные характеристики

Кинематические характеристики

Динамические характеристики тела человека.

Механические свойства мышц

Развитие биомеханики спорта и связи ее с другими науками.

Разновидности работы мышц

Сила и момент силы

Силы действия среды

Силы трения

Соединение звеньев тела

Степени свободы и связи движений в биомеханических цепях

Выносливость и способы ее измерения

Строение биомеханической системы.

Разновидности работы мышц

Механизм отталкивания от опоры

Биодинамика прыжка

Онтогенез моторики

Телосложение и моторика человека

Эффективность владения спортивной техникой

Показатели технического мастерства

Реакция связи (опоры) — определение термина

сила, с которой связь действует на данное тело; реакция связи всегда направлена противоположно тому направлению, в котором связь противодействует возможному движению тела.

Научные статьи на тему «Реакция связи (опоры)»

Реакции, возникающие от наложенных связей, являются для нас неизвестной величиной….
Рассчитывая примеры из статики, определяют

реакции опоры сочлененной системы, которая состоит из более…
, на схеме показывают активные силы и реакции, которые остаются после отбрасывания внешних связей….
связей….
Расчет реакций опор в составных конструкциях Стандартной задачей будет определение реакции связей внутри

Статья от экспертов

В статье рассматривается алгоритм расчета систем с односторонними связями с заменой реакций опор на силовые неизвестные. Алгоритм расчета основывается на методе конечных элементов в форме классического смешанного метода. Алгоритм перебора вариантов рабочей конструктивной схемы основывается на модифицированном «физически очевидном» алгоритме расчетно конструктивно-нелинейных систем. В работе описываются особенности разрешающей системы предлагаемого авторами алгоритма и приводится блок-схема. Производится сравнительный анализ с алгоритмом расчета систем с односторонними опорами, предложенным авторами ранее, а также некоторыми другими. Эффективность алгоритма проверяется на численных примерах.

Creative Commons

Научный журнал

Реакции опор Определение 1 Реакция работы опоры – это силовой критерий, который возникает в опоре…
Для установления правильных реакций опор твердого тела в теоретической механике необходимо осуществить…
Способы определения реакций опор в теоретической механике Чтобы научиться использовать методы опорных…
Эти позиции в физике называются связями….
в теоретической механике Чтобы узнать количественное значение реакций опор, можно воспользоваться первой

Статья от экспертов

В статье приводятся результаты комплексного исследования реакции опоры и циклов дыхания человека в процессе выполнения физических упражнений. У спортсменов высокой квалификации обнаружено сопряженное изменение экстремумов графиков вертикальной составляющей реакции опоры и экстремумов пневмограммы дыхания во время выполнения физических упражнений, что указывает на тесные координационные связи между дыхательными движениями и двигательными действиями.

Creative Commons

Научный журнал

Повышай знания с онлайн-тренажером от Автор24!

  1. Напиши термин
  2. Выбери определение из предложенных или загрузи свое
  3. Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных карточек
\circ}$ неопределенный. Такая система показана на рисунке 8.1. Эта система представляет собой балку со штифтовой опорой и двумя роликовыми опорами, что дает ей четыре составляющие реакции, но только три уравнения равновесия. Мы не можем найти диаграмму моментов для этой балки ни одним из известных нам методов.

Рисунок 8.1: Силовой метод — использование суперпозиции для выделения избыточного компонента силы реакции частей друг с другом, используя совместимость. Напомним, что с точки зрения балки нет реальной разницы между нагрузкой, вызванной внешней силой, и нагрузкой, вызванной силой реакции. Единственная разница между внешними силами и силами реакции заключается в том, что мы знаем, что в месте расположения силы реакции деформация/вращение, связанные с этим компонентом реакции, равны нулю. Составляющая силы реакции служит для удержания конструкции на месте либо за счет сдерживания смещения, либо за счет сдерживания вращения. Это известное смещение/вращение в месте расположения реакционного компонента дает нам некоторую дополнительную информацию о том, как ведет себя структура, помимо того, что мы можем сказать о структуре только из равновесия. Например, на рисунке 8.1 на верхней диаграмме показана балка с показанными граничными условиями реакции, а на второй диаграмме сверху показана диаграмма свободного тела для этой балки, подвергаемой заданным внешним силам (с граничными условиями реакции, замененными результирующей реакцией компоненты силы).

Верхняя диаграмма дает нам дополнительную информацию, которой нет на второй диаграмме (диаграмма свободного тела): она показывает, что луч удерживается от вертикального движения в точках A, C и E. Это информация о
совместимость луча. Эта дополнительная информация о совместимости не требуется, когда мы анализируем сдвиги и моменты в определенной балке; однако, когда мы анализируем неопределенный луч, мы можем использовать его.

Чтобы воспользоваться этой дополнительной информацией о совместимости в реакционных опорах, мы разделим нашу диаграмму свободного тела на рисунке 8.1 на две отдельные системы, используя суперпозицию. Для начала выберем один из компонентов реакции в качестве 9.0009 избыточная сила . Мы рассмотрим эту составляющую реакции особым образом, рассмотрев, что было бы, если бы не было самой опорной реакции, а была бы силовая составляющая реакции (т.е. балка не удерживалась бы от смещения в этой точке). Для системы, показанной на рисунке 8.1, реакция ролика в точке C была выбрана в качестве избыточной силы.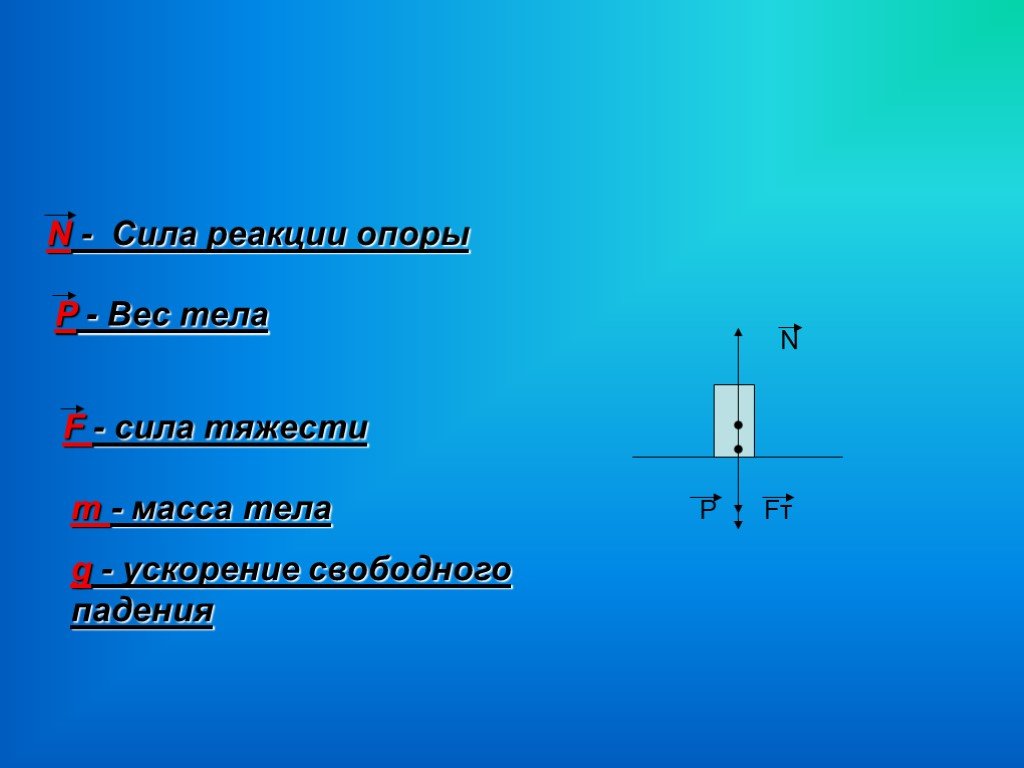 Итак, мы убираем опору, но сохраняем эквивалентную силу реакции $C_y$, которую мы теперь назовем нашей избыточной силой 9\circ}$ неопределенной системы в детерминированную систему. Эта новая детерминированная система без поддержки реакции, связанной с избыточной силой, называется первичной системой . Позже мы вернем в игру совместимость в точке C (т. е. тот факт, что там на самом деле есть реактивная опора и вертикальное смещение равно нулю).

Без опоры в точке C и рассматривая силу реакции $C_y$ как внешнюю силу, мы можем разделить полное поведение балки на две разные системы, используя суперпозицию, как показано на рисунке 8.1. В одной системе будут действовать реальные внешние силы $P$ и $Q$ («внешние силы без избыточных» на рисунке), а в другой системе будет действовать только избыточная сила $C_y$ («только избыточные силы» на рисунке) . Обеим этим системам будет позволено прогибаться в точке С, но не в точках А и Е (опоры в точках А и Е по-прежнему считаются существующими). Для каждой системы силы будут вызывать силы реакции в точках A и E и некоторое вертикальное отклонение в точке C. Если сила в точке C ($C_y$) верна, то суперпозиция этих двух систем вернет нам полную диаграмма свободного тела для балки, а сумма сил реакции для двух систем даст нам общие силы реакции для полной балочной системы.

Зачем мы все это делаем? Потому что теперь мы можем использовать суперпозицию деформаций двух отдельных систем, чтобы найти избыточную силу ($C_y$), которая является нашей истинной силой реакции в точке C в системе. Напомним из предыдущего обсуждения суперпозиции (см. главу 5), что суперпозиция применяется как к силам/моментам , так и к деформациям конструкции. Таким образом, деформация системы только с внешними силами (без избыточной силы) в сумме с деформацией системы только с избыточной силой будет равна полной деформации реальной полной балки. Это показано на рисунке 8.2.

Рисунок 8.2: Силовой метод. Наложение смещений, вызванных внешними силами, и избыточной составляющей силы реакции

На верхней диаграмме на рисунке 8. 2 показана деформация полной неопределенной балки при наличии реакции в точке C. Конечно, мы знаем, что вертикальная деформация в точке C ($\Delta_C$) должна быть равна нулю, как показано. Как только мы удалим опору в точке C, получив нашу первичную систему , мы сможем применить два компонента наложенной системы и измерить отклонение в точке C для каждого из них. Для первого мы применяем только внешние реакции $P$ и $Q$ к первичной системе. Поскольку первичная система детерминирована, мы можем легко найти вертикальное перемещение в точке C ($\Delta_{C0}$) одним из методов из главы 5, предполагая, что нам известны величины сил $P$ и $ Q$. Для второй из наложенных систем к основной системе прикладывается только избыточная сила $C_y$ с целью определения вертикального смещения, вызываемого избыточной силой в точке C ($\Delta_{CC}$). Конечно, в отличие от $P$ и $Q$, мы на самом деле не знаем значения избыточной силы, поскольку именно это мы и пытаемся найти.

Наложение и совместимость вместе дают нам одну дополнительную информацию. Два наложенных смещения в точке C ($\Delta_{C0}$ и $\Delta_{CC}$) должны суммироваться, чтобы получить полное перемещение в точке C ($\Delta_C$) в реальной балке, которое, как мы знаем, должно быть равным нулю, так как в этом месте действительно есть вертикальная опора. Это означает, что:

\begin{equation} \boxed{ \Delta_C = \Delta_{C0} + \Delta_{CC} = 0 } \label{eq:compat-cond-1} \tag{1} \end{ уравнение}

Это уравнение можно назвать нашим условием совместимости для этой задачи.

Мы не можем напрямую использовать это условие совместимости для решения $C_y$, потому что у нас нет доступного метода для расчета силы в конструкции, необходимой для достижения известного прогиба (все методы из главы 5 найти отклонение, вызванное данной силой). Но мы можем найти, какое отклонение в точке C (часть $\Delta_{CC}$) будет вызвано каждой единицей или каждой $1\mathrm{\,kN}$ частью силы $C_y$. Мы находим это, прикладывая единичную нагрузку в точке C в том же направлении, что и избыточная сила $C_y$, а затем находя отклонение в точке C, вызванное этой единичной силой. Это дает нам величину отклонения в точке C, вызванного каждым $\mathrm{kN}$ из $C_y$, и называется коэффициент гибкости ($f_{CC}$). Этот коэффициент гибкости имеет единицы длины, разделенные на силу (например, $\mathrm{мм/кН}$). Таким образом, полное отклонение, вызванное избыточной силой $C_y$, равно:

\begin{equation} \Delta_{CC} = f_{CC} C_y \label{eq:flex-coeff} \tag{2} \end {уравнение}

где $\Delta_{CC}$ — полный прогиб основной системы в точке C, вызванный избыточной силой $C_y$, а $f_{CC}$ — прогиб основной системы в точке C вызвано единичной нагрузкой ($1\mathrm{\,kN}$) в точке C. Если мы подставим уравнение \eqref{eq:flex-coeff} в уравнение \eqref{eq:compat-cond-1}, то мы получить:

\begin{equation} \boxed{ \Delta_{C0} + f_{CC} C_y = 0 } \tag{3} \end{equation}

и, тогда мы можем изменить порядок для решения избыточной силы $C_y $:

\begin{equation} \boxed{ C_y = \frac{-\Delta_{C0}}{f_{CC}} } \tag{4} \end{equation}

Это решение для $C_y$ дает Нам точное количество силы, необходимой в точке C, чтобы удерживать точку C в вертикальном положении (когда на систему действуют силы $P$ и $Q$). Таким образом, поскольку $C_y$ — это именно то количество силы, которое необходимо для удержания смещения в точке C равным нулю, на самом деле не имеет значения, что мы убрали опору в точке C, когда стали рассматривать реакцию в точке C как избыточную силу. силы реакции. Величина, на которую балка толкается вниз в точке C внешними силами $P$ и $Q$, точно уравновешивается величиной, на которую балка толкается вверх в точке C избыточной силой $C_y$.

После того, как мы нашли силу реакции в точке C ($C_y$), у нас остались только три неизвестные силы реакции: $A_x$, $A_y$ и $E_y$ (при условии, что известны $P$ и $Q$). ). Таким образом, использование трех уравнений равновесия для решения этих неизвестных теперь является тривиальным упражнением. Отсюда, когда мы знаем все реакции, мы можем нарисовать диаграммы сдвига и момента.

Выбор $C_y$ в качестве избыточной реакции был несколько произвольным. Вместо этого мы могли бы выбрать $A_y$ или $E_y$ в качестве избыточной силы; однако $C_y$ немного проще, потому что, когда опора в точке C удалена, мы остаемся с первичной системой, которая представляет собой свободно опертую балку, которую легко проанализировать на предмет прогибов. Мы не могли выбрать $A_x$ в качестве избыточной силы, поскольку удаление компоненты реакции $A_x$ сделало бы полученную первичную систему неустойчивой, а значит, невозможно было бы анализировать ее для определения прогибов.

Помните: если удаление компонента поддерживающего ограничения приведет к нестабильности конструкции, то этот компонент ограничения нельзя использовать в качестве резервного ограничения. Перефразируя: если первичная система нестабильна, то выбранные избыточные реакции не подходят.

Также важно отметить, что для конструкции с неподвижной опорой в качестве избыточной силы может быть выбран момент реакции. В этом случае условие совместимости будет связывать повороты в избыточном месте вместо деформаций, например:

\begin{align*} \theta_C = \theta_{C0} + \theta_{CC} = 0 \end{align*}

и коэффициент гибкости будет связывать единичный момент с вращением, вызванным этим моментом (единицы из $\mathrm{1/{кНм}}$):

\begin{equation} \boxed{ \theta_{CC} = -f_{CC} M_C } \label{eq:Moment-Compat} \tag{5 } \end{equation}

Как мы увидим, этот же метод напрямую применим к неопределенным рамам и фермам.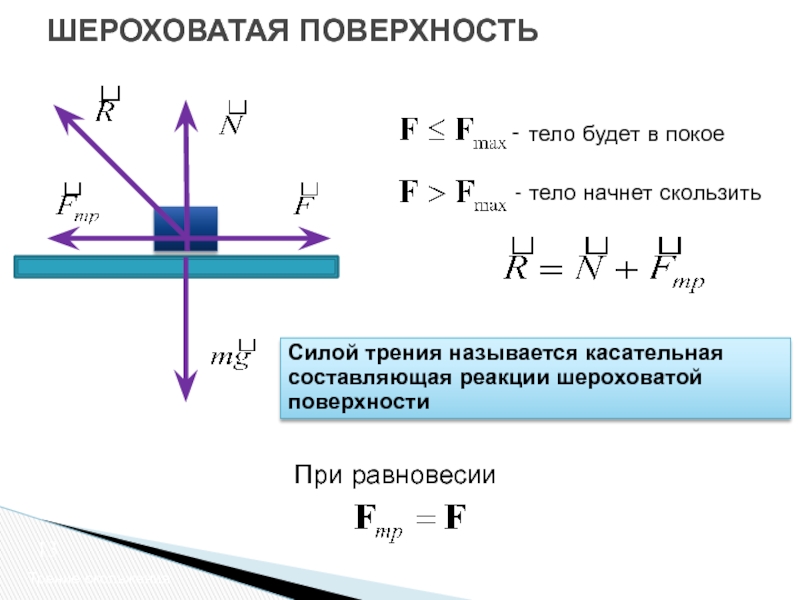 \circ}$ неопределенным и имеет постоянный $EI$ для всех членов.

Рисунок 8.3: Метод силы с использованием избыточной силы внешней реакции Пример

Первым шагом является выбор компонента реакции для использования в качестве избыточной силы. В этом случае проще всего будет вертикальная реакция в точке C ($C_y$). Это связано с тем, что после устранения реакции в C первичная система фактически представляет собой кантилевер, который очень легко анализировать. Конечно, $A_y$ и $M_A$ также будут работать как избыточные (но не $C_x$, потому что их удаление сделает основную систему нестабильной). Полученная первичная структура показана на рисунке 8.4.

Рисунок 8.4: Метод силы с использованием избыточной силы внешней реакции. Пример — основная конструкция с внешними нагрузками

При выборе $C_y$ в качестве избыточной силы условие совместимости для этой задачи: {C0} + \Delta_{CC} = 0 \end{align*}

где $\Delta_{C0}$ — прогиб основной системы в точке C только от внешних нагрузок, $\Delta_{CC} $ — отклонение первичной системы в точке C только за счет избыточной силы, а 0 — необходимый результат наложения двух отклонений. Сумма двух отклонений должна равняться нулю, поскольку в полностью неопределенной конструкции имеется вертикальная опора в точке С, которая ограничивает вертикальное отклонение конструкции в этом месте.

Как и в случае с балкой, рассмотренной ранее, первым шагом к нахождению избыточной силы является определение $\Delta_{C0}$, отклонения основной конструкции (основной системы) только от внешних нагрузок (без избыточной силы) . Эта структура и соответствующая изогнутая форма показаны на рисунке 8.4. Поскольку эта конструкция представляет собой раму, мы не можем использовать метод моментной площади или метод сопряженной балки для определения прогиба $\Delta_{C0}$, мы должны использовать метод виртуальной работы.

Анализ виртуальной работы основного строения с внешней нагрузкой показан на рисунке 8.5. Для этого анализа виртуальной работы реальная система является основной конструкцией с внешней нагрузкой (как показано), а виртуальная система является основной конструкцией с единичной вертикальной нагрузкой в ​​точке C (поскольку мы пытаемся найти вертикальное отклонение реальная система в точке С). Результирующая диаграмма реального сдвига и диаграмма реальной кривизны для реальной системы показаны на рисунке прямо под реальной системой. Диаграмма моментов будет иметь ту же форму, что и диаграмма кривизны для этой системы (не показана), поскольку $EI$ постоянна для всех элементов. Также показаны виртуальная диаграмма сдвига и виртуальная диаграмма момента для виртуальной системы. 93}}{EI} \end{align*}

Теперь мы нашли $\Delta_{C0}$, что является частью нашего условия совместимости. Далее необходимо найти влияние избыточного узла на прогиб основной системы в точке С (без учета внешних нагрузок). Мы также будем использовать для этого виртуальную работу, как показано на рисунке 8.6.

Рисунок 8.6: Метод силы с использованием избыточной силы внешней реакции Пример — отклонение основной конструкции из-за избыточной силы единицы в точке С, как показано на рисунке. Важно отметить, что единичная избыточная сила не применяется как $1\mathrm{\,kN}$, как виртуальная нагрузка, она является безразмерной (или в единицах $\mathrm{kN/kN}$), потому что мы хотим найти значения на кН приложенной избыточной силы. Чтобы найти отклонение в точке C из-за этой единичной избыточной силы, нам нужно создать виртуальную систему с виртуальной внешней единичной нагрузкой в ​​точке C (в том же направлении, что и избыточная). Это означает, что реальная и виртуальная системы для нахождения эффекта единичной избыточной силы функционально идентичны, как показано на рисунке. Эти реальная и виртуальная системы, идентичные друг другу, также оказались идентичными виртуальной системе на рис. 8.5 (которая использовалась для нахождения отклонения основной системы, вызванного внешними нагрузками на систему без резервирования). . Таким образом, как реальные, так и виртуальные результаты анализа избыточности блоков на рисунке 8.6 могут быть взяты непосредственно из предыдущей виртуальной системы на рисунке 8.5. Это экономит некоторую работу по анализу, поскольку диаграммы моментов будут одинаковыми для всех трех. Единственная разница может состоять в том, что диаграмма кривизны для реальной системы на рис. 8.6 могла бы быть немного другой, если бы $EI$ не было постоянным. Надлежащие единицы для реальной системы также немного отличаются для анализа избыточности единиц, потому что избыточная единица не имеет единиц (т.е. она находится в единицах $\mathrm{кН/кН}$, как упоминалось ранее). 93}} \right) \\ C_y &= +39.8\mathrm{\,kN} \\ C_y &= 39.8\mathrm{\,kN} \uparrow \end{align*}

Поскольку мы предположили, что блок избыточен сила, направленная вверх в нашем анализе (как показано на рисунке 8.6), положительный результат для $C_y$ подтверждает, что реакция действительно направлена ​​вверх.

После всего этого анализа нам удалось определить величину компоненты реакции $C_y$. Зная это, в неопределенной системе остаются только три неизвестные реакции, как показано на рисунке 8.7: $A_x$, $A_y$ и $M_A$. Теперь их можно легко найти с помощью равновесия, и их значения показаны на рисунке 8.7. Когда все реакции известны, можно построить диаграммы сдвига и момента, как показано на рисунке.

Рисунок 8.7: Метод силы с использованием избыточной силы внешней реакции Пример — момент и сдвиг в полной неопределенной системе отсчета Сааил Ашраф , опубликовано 18 мая 2022 г.

LinkedIn подвергся критике за излишнюю небрежность. А с реакциями дела обстоят еще более спорно. Так не навредит ли ожидаемая новая Реакция бренду?

LinkedIn продолжает расширять сферу своей деятельности, и вскоре появится потенциальная новая реакция. Для всех тех пользователей, которые жалуются на то, что платформа с каждым месяцем становится менее серьезной, этот случай не будет слишком хорошим.

В течение многих лет LinkedIn существовал где-то посередине серьезности и легкомыслия. Время от времени в вашей ленте появлялись более душевные и личные сообщения, но подавляющее большинство контента, который вы видели, был о работе и бизнесе. Это было уместно, потому что платформа была основана на необходимости сохранять профессионализм. В конце концов, это был сетевой сайт для профессионалов.

Затем LinkedIn стал менее серьезным. Вскоре личные посты стали нормой, а затем Реакции были включены в опции, доступные для постеров.

Реакции

LinkedIn создал Реакции, чтобы пользователи могли более плавно воспринимать свои разговоры на платформе. Вся идея заключалась в том, чтобы помочь пользователям легче общаться в LinkedIn. Важно было сообщить быстрый и четкий ответ.

Все, что нужно было сделать пользователям, — это навести курсор на значок «Мне нравится» в публикации, которую они просматривали, и появился ряд реакций.

Celebrate — это реакция, которая позволяет пользователям положительно реагировать на объявление, например, когда контактное лицо публикует информацию о том, что они приняли новую должность в компании. Или, может быть, только что случилась трудовая годовщина. Эта Реакция представляет собой хлопание в ладоши.

Затем у нас есть реакция поддержки. Это Реакция, напрямую связанная с проявлением эмпатии к связи, прошедшей какую-то профессиональную борьбу. Это может варьироваться от прохождения жесткого собеседования до управления изменениями на работе. Эта Реакция — рука с сердцем в ней.

Любовь — это реакция, которую LinkedIn намеревался использовать для контактов, опубликовавших что-то, что вызвало у вас отклик. Согласно LinkedIn, он может охватывать такие события, как:

  • Когда ваш ребенок приходит к вам на работу и думает, что у вас лучшая работа в мире
  • Публикации о важности баланса между работой и личной жизнью.
  • Наблюдение за достижением цели коллегой.
  • Благодарность вашим бывшим наставникам, которые помогли вам достичь того, что вы имеете сегодня.

Проницательный и Любопытный, далее:

Проницательный – Выражает, что вы считаете, что в сообщении содержится важная мысль, предложена новая идея или вы поделились полезными мыслями или советами. Например:

  • Когда ваша компания предлагает вам каждый месяц брать выходной для работы над проектом, которым вы увлечены.
  • Посты с советами и рекомендациями.

Любопытный. Выражает, что вы заинтригованы перспективой или вопросом, наводящим на размышления, и хотите узнать больше. Например:

  • Спросить, что люди думают о профессиональном тренде.
  • Спор о том, имеет ли смысл обучение в аспирантуре на данном этапе вашей карьеры

О том, почему LinkedIn создал Reacts:

Люди каждый день приходят в LinkedIn, чтобы узнать, что происходит в их профессиональных сообществах, и обсудить друг с другом темы и идеи, связанные с их работой. Эти разговоры охватывают широкий спектр вопросов, будь то обсуждение отраслевых новостей, празднование вехи компании, предоставление совета по поводу поиска работы или обмен мыслями о важных темах на рабочем месте, таких как работающий родитель.

Одна из вещей, которую мы регулярно слышим от всех вас, заключается в том, что вам нужны более выразительные способы, чем «Нравится», для ответа на различные сообщения, которые вы видите в своей ленте. В то же время вы также сказали нам, что когда вы публикуете сообщения в LinkedIn, вам нужно больше способов чувствовать себя услышанными и понимать, почему кому-то понравилось то, что вы сказали.

Мы тщательно подошли к разработке этих реакций, сосредоточившись на понимании того, какие из них будут наиболее ценными для типов разговоров участников в LinkedIn. Этот процесс включал изучение того, о чем люди уже говорят, чтобы лучше понять, какую обратную связь они хотели выразить и получить — например, мы проанализировали наиболее часто используемые комментарии из 1-2 слов и типы сообщений, которыми люди делятся чаще всего. Мы также провели глобальное исследование с участниками LinkedIn, чтобы получить отзывы о конкретных реакциях, чтобы убедиться, что они были понятны и полезны для всех.

Итак… Забавно

Забавно — ожидаемая новая Реакция. Это говорит само за себя, поскольку пользователи могут использовать эту реакцию, когда находят что-то смешное в своей ленте.

Очевидно, это одна из самых востребованных реакций со стороны пользователей. Таким образом, очевидно, что LinkedIn захочет хорошо обслуживать свою базу. В этом есть смысл.